Изобретение относится к измерительной технике, в частности к измерению сверхвысокочастотных параметров материалов в свободном пространстве.
Известны способы измерения диэлектрической и магнитной проницаемостей в объемном резонаторе на фиксированной частоте, когда образец измеряется в двух положениях: на поршне и на подставке [Е.Б. Зальцман. Измерение параметров магнитодиэлектриков и не намагниченных ферритов при помощи прямоугольного резонатора на волну Ню.//Радиотехника. - 1958. - Т. 13. - №10. - С. 76-80.].
Недостатком способов является узкополосность производимых измерений. При измерении парамагнитных и ферромагнитных материалов точность измерения снижается, потому что магнитное поле материала искажает структуру поля в резонаторе, метод малых возмущений, используемый в резонансном методе измерений не выполняется.
Волноводные и резонаторные методы измерения диэлектрической и магнитной проницаемостей имеют высокую точность и чувствительность измерения сверхвысокочастотных параметров, но обладают существенным недостатком - узкополосностью производимых измерений [В.Н. Егоров. Резонансные методы исследования диэлектриков на С.В.Ч.// Приборы и техника эксперимента. - 2007. - №2. - С. 5-38.].
Известны амплитудно-фазовые приборы, работающие на «прохождение» и «отражение» электромагнитной волны в свободном пространстве, используемые для измерения диэлектрической и магнитной проницаемости материалов [Приборы для неразрушающего контроля материалов и изделий. Справочник. В 2-х книгах. Кн. 1/Под ред. В.В. Клюева. - 2-е изд., перераб. и доп. - М: Машиностроение. 1986. - 488 с. (стр. 220-224, 233-234; рис. 17 стр. 217-219).].
Известны поляризационные приборы для измерения диэлектрической проницаемости оптическими методами в свободном пространстве, в которых контролируется изменение ориентации электрических векторов поля под влиянием свойств материалов [Приборы для неразрушающего контроля материалов и изделий. Справочник. В 2-х книгах. Кн. 1/Под ред. В.В. Клюева. - 2-e изд., перераб. и доп. - М: Машиностроение. 1986. - 488 с. (стр. 220-224, 233-234)].
Диэлектрические свойства материала в свободном пространстве определяют сравнительными измерениями мощности и фазы волны, распространяющейся между передающей и приемной антеннами без образца материала, и проходящей через образец материала или отражающейся от него [А.А. Брандт. Исследование диэлектриков на сверхвысоких частотах М.: Физматгиз, 1963. - 404 с; D.K. Ghodgaonkar, V.V. Varadan and V.K. Varadan. Free-Space Measurement of Complex Permittivity and Complex Permeability of Magnetic Materials at Microwave Frequencies. IEEE Transactions on Instrumentation and Measurement. Vol. 39 №2, April, 1990; В.И. Сусляев, В.А. Журавлев, E.Ю. Коровин, Ю.П. Землянухин. Рупорный метод измерения электромагнитного отклика от плоских образцов в диапазоне частот 26-37,5 ГГц с улучшенными метрологическими характеристиками. Радиотехника. Телекоммуникация. Антенны. Микроволновые устройства. Доклады ТУСУРа, №2 (24) часть 1, декабрь 2011. с. 227-231.].
Описаны способы определения диэлектрической проницаемости материала по мощности и фазе прошедшей и отраженной волны, а также применение СВЧ-измерителя в качестве приемной аппаратуры [Е.А. Воробьев. Радиоволновой контроль судовых радиотехнических конструкций и материалов. - Л.: Судостроение, 1986. - 81 с. (22 стр).].
Известны способы определения диэлектрической проницаемости материалов по мощности и фазе отраженной волны от пластины, расположенной под углом Брюстера [А.с. СССР №1550436, кл. G01R 27/26, 15.03.1990 Бюл. №10; Патент РФ №2249178 С2, МПК G01B 15/02, G01R 27/26, опубл. 27.03.2005 Бюл. №9; Патент РФ №2613810 С1, МПК G01R 27/00, опубл. 21.03.2017 Бюл. №9].
Недостатком этих способов является требование к высокой точности изготовления образцов пластин протяженных размеров на уровне 0,005 мм, что с технологической точки зрения при больших размерах образцов трудно выполнимо. Высокие требования предъявляются так же к радиотехническому качеству измерительного полигона и точности измерительной аппаратуры.
При всех недостатках присущих способу измерения сверхвысокочастотных параметров материала в свободном пространстве его важное преимущество состоит в возможности получения зависимостей диэлектрической проницаемости от частоты в широкой полосе.
Для получения расширенной информации об исследуемом материале требуется одновременное измерение его диэлектрических и магнитных свойств в широкой полосе частот с постоянным увеличением верхних граничных частот, где размеры резонансных систем становятся сравнимыми в длиной волны, поэтому направление развития методов исследований свойств материалов связано с использованием в радиодиапазоне оптических методов в свободном пространстве для которых, с созданием СВЧ-измерителей в виде широкополосных анализаторов цепей, достигнут прогресс в приборном обеспечении.
Вместе с тем известные способы измерения сверхвысокочастотных параметров материала в свободном пространстве обладают методическими недостатками, которые не позволяют одновременно производить измерение диэлектрических и магнитных свойств материалов с высокой точностью определения, диэлектрической и магнитной проницаемостей, тангенса угла диэлектрических и тангенса угла магнитных потерь.
Наиболее близким техническим решением является способ измерения диэлектрической и магнитной проницаемостей материала в свободном пространстве и устройство для его реализации, включающий измерение мощности и фазы прошедшей волны через образец материала, измерение мощности и фазы отраженной волны от образца материала, вычисление изменения мощности и фазы с образцом материала и без него, определение по изменениям величин мощностей и фаз комплексных S-параметров матрицы рассеяния диэлектрической и магнитной проницаемостей образца материала при неизменном взаимном положении приемной и передающей антенн [Nicolson, А.М. and G.F. Ross, "Measurement of the intrinsic properties of materials by time-domain techniques,"IEEE Trans. Instrum. Meas., Vol. 19, No. 4, 377-382, 1970.; А.А. Беляев, А.М. Романов, В.В. Широков, Е.М. Шульдешов. Измерение диэлектрической проницаемости стеклосотопласта в свободном пространстве. Электронный научный журнал «ТРУДЫ ВИАМ» - 2014. - №5. - С1-8.]
Условия проведения измерений в способе являются статическими для одного, неизменяемого, взаимного положения антенн по анализу результатов измерения и для одной неизменяемой поляризации падающей волны. Все эти условия проведения экспериментальных измерений не являются оптимальными для определения сверхвысокочастотных параметров, потому что в известных способах не достаточно экспериментальных данных для реализации высокой точности измерения и получения однозначных значений комплексных диэлектрической и магнитной проницаемостей. Кроме того, накладываются ограничения на толщину образца и диапазон изменения определяемых сверхвысокочастотных параметров.
Для устранения отражений электромагнитной волны от образца, которые снижают точность измерений, требуется значительно уменьшать электрическую толщину образца. Также представленные способы и устройства имеют низкую точность измерений тангенса угла диэлектрических и магнитных потерь, потому что алгоритмы расчетов основаны на оценке изменения мощности прошедшего через образец электромагнитного поля.
Приведено устройство, включающее СВЧ-измеритель, генераторный выход которого соединен с передающей антенной, а приемный вход с приемной антенной, подставку под образец, расположенную между антеннами, управляющий компьютер, соединенный с СВЧ-измерителем.
Определение только диэлектрической проницаемости и тангенса угла диэлектрических потерь материала для немагнитных материалов в свободном пространстве производится динамическим методом сравнения мощностей и фаз прошедшей или отраженной волн без образца и с образцом материала при его помещении на подставку между антеннами.
В качестве измерительных устройств применяются приемная и передающая антенны, настроенные специальным образом, так чтобы уменьшить искажения, вносимые вторичными волнами рассеяния и интерференции, возникающие на краях образца испытуемого материала.
Недостатком представленных способа и устройства является низкая точность измерения диэлектрической и магнитной проницаемостей в полосе частот.
Задачей настоящего изобретения является повышение точности измерения частотной зависимости комплексных диэлектрической и магнитной проницаемостей образца материала в широкой полосе частот в свободном пространстве.
Поставленная задача достигается тем, что предложен способ определения сверхвысокочастотных параметров материала в полосе частот, включающий измерение на СВЧ-измерителе в полосе частот мощности и фазы прошедшей волны между передающей и приемной антеннами без образца материала, установку образца материала на вращающую подставку в центре полигона между передающей и приемной антеннами, измерение на СВЧ-измерителе мощности и фазы прошедшей волны между передающей и приемной антеннами при повороте вращающейся подставки с образцом материала, вычисление в полосе частот изменения мощности и фазы прошедшей волны между передающей и приемной антеннами, с расположенным между ними образцом материала и без него, расчет по изменению мощности и фазы комплексных сверхвысокочастотных параметров материала, отличающийся тем, что на СВЧ-измерителе в полосе частот измеряют угловые зависимости мощности и фазы прошедшей и отраженной волн при повороте образца материала между передающей и приемной антеннами в двух перпендикулярных плоскостях поляризации, соответствующих плоскости поляризации с вектором электрического поля, лежащим в плоскости падения, и плоскости поляризации с вектором электрического поля перпендикулярным плоскости падения, по измеренным угловым зависимостям мощности и фазы отраженной волны определяют углы Брюстера для поляризации с вектором электрического поля в плоскости падения падающей волны и угол, соответствующий углу Брюстера для поляризации с вектором электрического поля перпендикулярным плоскости падения падающей волны, а комплексные величины сверхвысокочастотных параметров рассчитывают по мощностям и фазам для обеих поляризаций поля прошедшего через образец материала при нормальном падении и повернутого под углом Брюстера, причем, если не определяется угол соответствующий углу Брюстера для поляризации с вектором электрического поля перпендикулярным плоскости падения падающей волны, то для этой поляризации используется величина угла Брюстера для поляризации с вектором электрического поля в плоскости падения падающей волны.
В предлагаемом техническом решении определение комплексных сверхвысокочастотных параметров (диэлектрической и магнитной проницаемостей) осуществляется не по измеренным S-параметрам матрицы рассеяния для одного взаимного положения передающей приемной антенн и образца материала, как в известных технических решениях, а при одновременном решении задачи определения комплексной диэлектрической и комплексной магнитной проницаемостей с использованием экспериментальных данных, полученных в результате измерения необходимого и достаточного по объему набора угловых зависимостей амплитуд и фаз, коэффициентов прохождения и отражения электромагнитной волны через пластину образца материала при различных (не менее двух) угловых положениях антенн и образца материала, одновременно, при совпадающей ориентации антенн, в двух ортогональных плоскостях поляризации поля для каждой измеряемой частоты.
Экспериментально измеряются угловые зависимости амплитуд и фаз прошедшего поля для передающей и приемной антенн, расположенных напротив друг друга и при повороте образца материала на угол близкий к углу Брюстера при поляризации падающей волны у которой вектор Е лежит в плоскости падения (ТМ-волна) и для этого же угла для падающей волны у которой вектор Е лежит в плоскости перпендикулярной плоскости падения (ТЕ-волна) на пластину. Реализуя при взаимном повороте приемной антенны и образца материала относительно передающей антенны, закон Снеллиуса, экспериментально измеряются амплитуды и фазы отраженных волн.
Предложенный способ позволяет устранить неоднозначность, которая возникает из-за гармонического характера решений алгоритмов при определении комплексных диэлектрической и магнитной проницаемостей.
В предлагаемом техническом решении повышение точности определения тангенса угла диэлектрических потерь и тангенса угла магнитных потерь проводится с использованием фазовых измерений отраженной и проходящей волн. Реперными точками для определения величин диэлектрической и магнитной проницаемостей на частотной оси являются амплитуды и фазы прошедшего поля, соответствующие электрической толщинам образца материала кратным половине длины волны в материале для которых точность измерений самая высокая.
Авторами установлено, что изменение фазы прошедшей или отраженной волны, для любой частоты и при обеих поляризациях, любых углов падения волны на плоскую пластину при взаимодействии падающей и отраженной волн, в зависимости от электрической толщины, пластины имеют гармонический вид, кроме случая при падения плоской волны с параллельной поляризацией под углом Брюстера для которой зависимость изменения фазы от толщины пластины линейна из-за отсутствия отраженной волны.
Это приводит к тому, что методы определения, например, диэлектрической проницаемости в свободном пространстве, основанные на измерениях фазы прошедшей или отраженной волн, для несогласованной по электрической толщине стенки имеют значительную погрешность.
Для определения величины погрешности диэлектрической проницаемости методом свободного пространства при нулевом угле падения волны на плоскую пластину промоделируем условия эксперимента определив зависимость диэлектрической проницаемости от частоты, в полосе частот от 1 до 20 ГГц, считая пластину однородной и изготовленной из однородного материала толщиной d=9 мм, например, из диоксида кремния (кварцевого стекла) с диэлектрической проницаемостью ε=3,81 и тангенсом угла диэлектрических потерь tgδ=0,0001, которые измерены на частоте 10 ГГц по ГОСТ Р 8.623-2015 резонаторным методом.
На первом этапе рассчитываем мощность и фазу прошедшей волны (Δϕ(f)) для параллельной поляризации падающей волны в диапазоне частот от 1 до 20 ГГц, затем из этих расчетных данных определяем величину диэлектрической проницаемости по формуле:
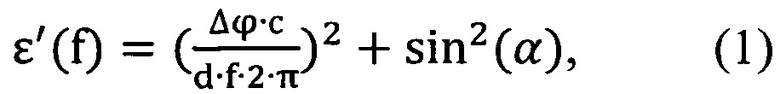
где с - скорость света;
Δϕ - фаза прошедшей волны;
d - толщина пластины;
f - частота;
α - угол падения волны на пластину.
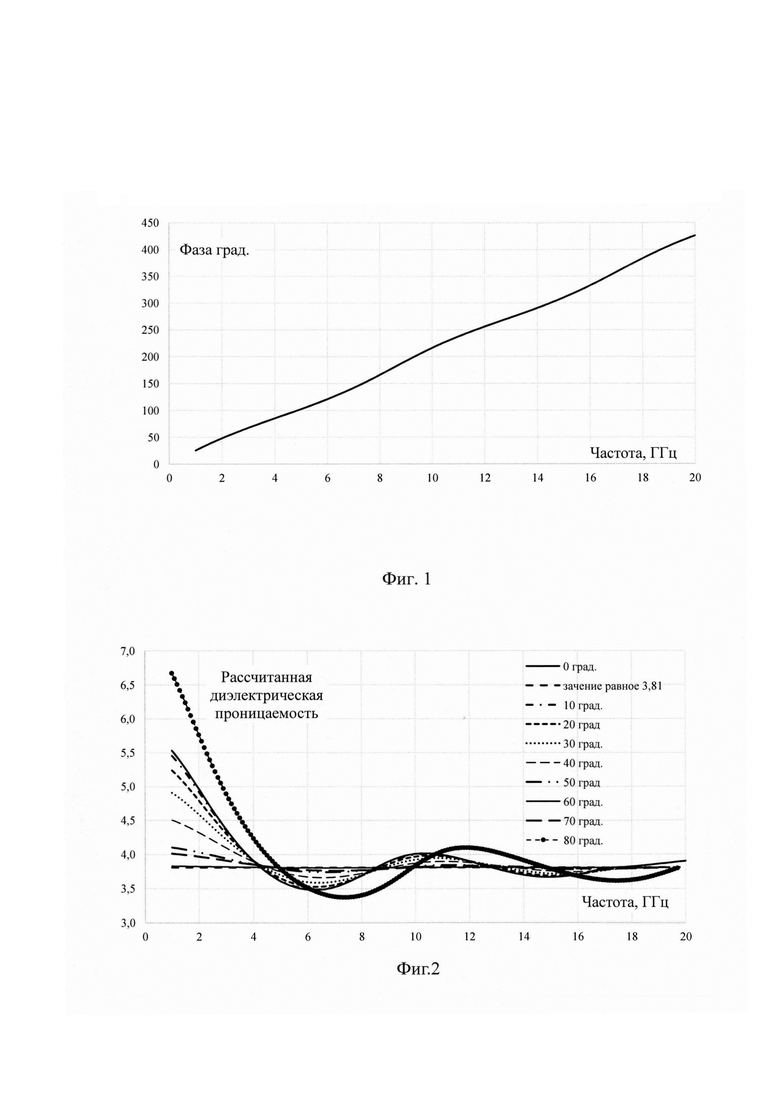
На фиг. 1 представлены результаты расчета частотной зависимости изменения фазы прошедшей волны по модели эксперимента.
Из фиг. 1 видно, что частотная зависимость фазы имеет гармонический вид.
Из частотных зависимостей фазы прошедшей волны по формуле (1) проведены расчеты диэлектрической проницаемости материала пластины из диоксида кремния для различных углов падения в зависимости от частоты, результаты которых представлены на фиг. 2.
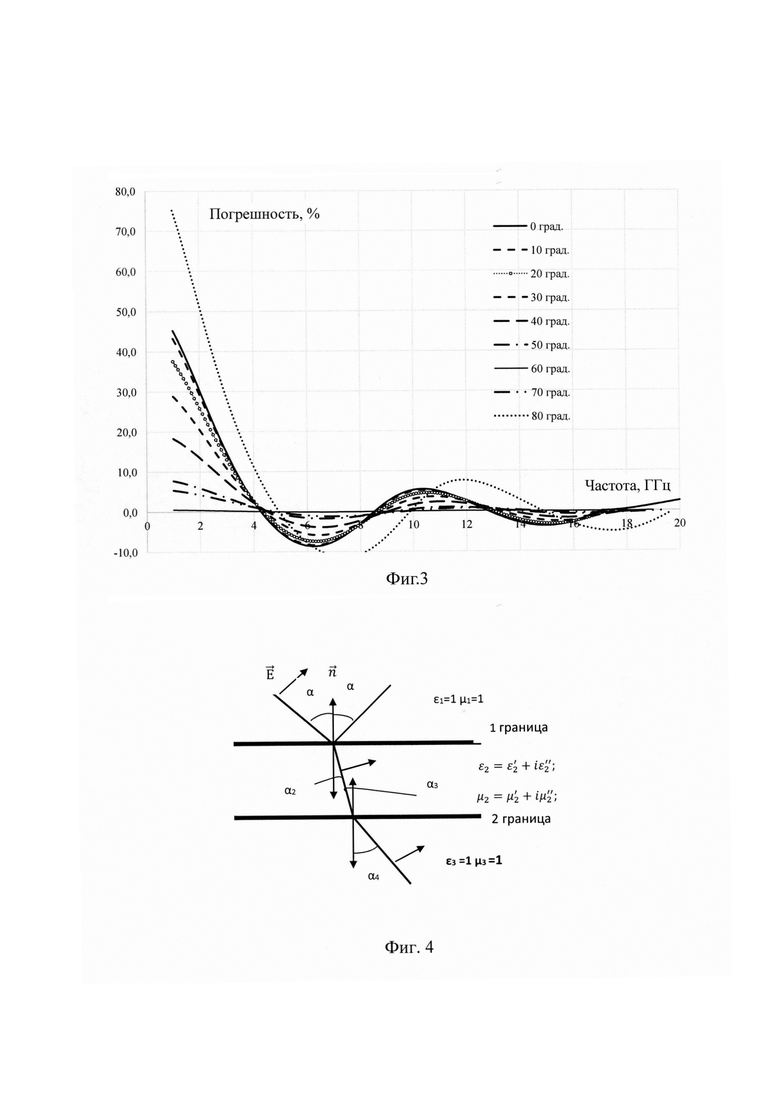
На фиг. 3 представлены частотные зависимости величин погрешности определения диэлектрической проницаемости материала пластины по фазе прошедшей волны для различных углов падения.
Из фиг. 3 видно, что для радиочастотного диапазона точность определения диэлектрической проницаемости материала пластины методом свободного пространства существенно зависит от электрической толщины пластины и становится приемлемой, когда она кратна четверти длины волны, то есть при четверть волновой электрической толщине пластины уменьшается величина отраженной волны и в этих точках зависимость фазы от электрической толщины становится линейной.
Из проведенного анализа видно, что в области радиодиапазона реализовать метод определения диэлектрической проницаемости в свободном пространстве в широкой полосе для малых величин угла падения с приемлемой для практики точностью не представляется возможным.
Как показывают проведенные расчеты основной причиной высокой погрешности определения диэлектрической проницаемости в методе свободного пространства является интерференция волн подающей и отраженной от образца материала. При отсутствии отраженной волны методическая погрешность определения диэлектрической проницаемости в свободном пространстве отсутствует.
При проведении расчетов изменения фазы прошедшей волны, было установлено, что для ТМ-поляризации при падении волны под углом Брюстера зависимость фазы прошедшей волны линейна и не зависит от электрической и геометрической толщин, а также от частоты электромагнитной волны.
Авторы установили, что определение сверхвысокочастотных параметров образца материала с использованием в расчетной процедуре одновременно результатов экспериментальных измерений не менее чем для двух углов поворота образца материала и не менее двух взаимных положений углов поляризации антенн позволяет повысить точность определения сверхвысокочастотных параметров образца материала и устранить неоднозначность их определения в полосе частот.
Определение диэлектрической проницаемости по фазе прошедшей волны через образец материала, установленного под углом Брюстера, устраняет неопределенность, связанную с кратностью резонансных электрических толщин и позволяет проводить измерение образцов с различными толщинами с более высокой точностью, чем в известных способах.
Известно, что для материала с потерями задача прохождения волны через плоский слой становится неоднородной, так как в окончательных выражениях формулы Френеля зависят только от вещественного угла падения, комплексный угол преломления исчезает, а моделирование задачи прохождения волны через слой с потерями заключается в решении классической задачи с использованием комплексного значения диэлектрической проницаемости материала.
Введение процедуры измерения частотных зависимостей модулей и фаз отраженной и прошедшей волн для двух взаимно перпендикулярных поляризаций, совпадающей с плоскостью падения и перпендикулярной ей, уравнений, решение которых позволит определить комплексные величины позволяет получить для каждой частоты систему из двух комплексных магнитной и диэлектрической проницаемостей материала измеряемой пластины.
На фиг. 4 показано прохождение и отражение волны через плоский слой, с учетом магнитных и диэлектрических свойств пластины с диэлектрической проницаемостью 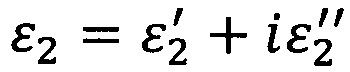 и магнитной проницаемостью
и магнитной проницаемостью 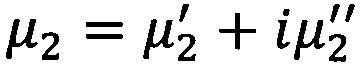 для угла падения падающей волны α.
для угла падения падающей волны α.
Для среды с магнитными и диэлектрическими свойствами при падении плоской волны с вектором электрического поля, лежащим в плоскости падения (ТМ-поляризация), как на фиг. 4, угол Брюстера α|| с минимальной амплитудой отраженной волны равен:
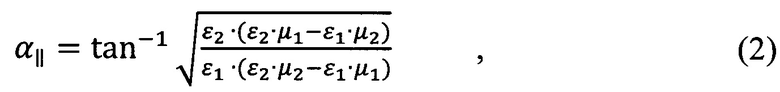
где ε1 - диэлектрическая проницаемость воздуха,
ε2 - диэлектрическая проницаемость материала,
μ1 - магнитная проницаемость воздуха,
μ2 - магнитная проницаемость материала.
Для среды с магнитными и диэлектрическими свойствами при падении плоской волны с вектором электрического поля, перпендикулярным плоскости падения (ТЕ-поляризация), угол α⊥ с минимальной величиной отраженной волны равен:
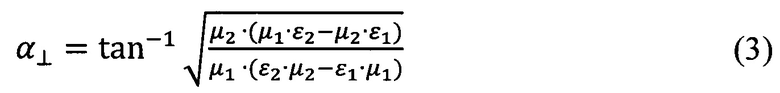
где ε1 - диэлектрическая проницаемость воздуха,
ε2 - диэлектрическая проницаемость материала,
μ1 - магнитная проницаемость воздуха,
μ2 - магнитная проницаемость материала.
Для среды с учетом электромагнитных свойств материала в воздушной среде ε1=1, μ1=1:
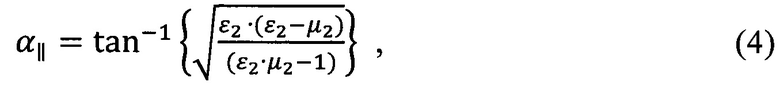
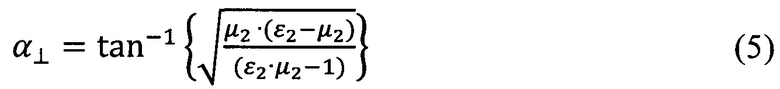
Для

Получим
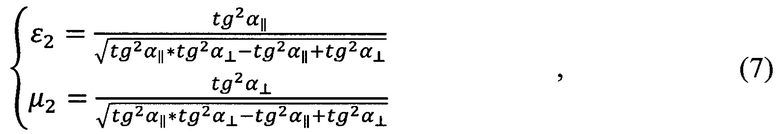
если 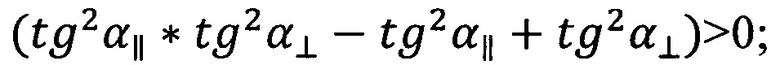
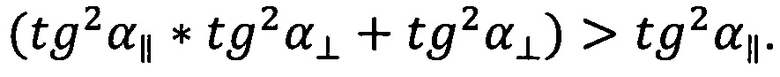
Если подкоренное выражение в формулах (7) больше нуля, то для выбранной поляризации наблюдается угол падения при котором находится минимум модуля коэффициента отражения.
В общем случае такой угол падения, или его отсутствие, находится в результате измерения угловой зависимости модуля и фазы отраженной волны на выбранной частоте для каждой поляризации.
Для поляризации у которой не существует угла с минимальной величиной отраженной волны выбирается угол падения для которого наблюдается максимум модуля прошедшей волны.
Если ε2>μ2, то существует вещественный угол α|| при котором наблюдается минимум отраженной волны от пластины материала.
Начальная процедура для обеих поляризаций заключается в определении величины угла падения при котором амплитуда отраженной волны минимальна.
Для ТМ-поляризации этот угол соответствует углу Брюстера. Углы падения волны на которых будут производиться измерения определяются экспериментально, потому что их величины зависят от частоты измерения, толщины пластины и комплексных величин электромагнитных параметров материала пластины.
При угле падения, для которого минимальна величина амплитуды отраженной волны наблюдается наибольшая точность измерения фазы отраженной и прошедшей волн, а значить наибольшая точность определения диэлектрической и магнитной проницаемостей материала.
После того, как установлен угол падения и соответствующий ему угол поворота пластины измеряется частотная зависимость модуля и фазы отраженной волны приемной антенной, установленной относительно пластины и падающей волны в соответствии с законом Снеллиуса (угол падения равняется углу отражения).
Затем приемная антенна устанавливается направленно на передающую антенну и измеряется частотная зависимость модуля и фазы коэффициента прохождения через пластину. Дальнейшие расчеты по определению комплексных величин диэлектрической и магнитной проницаемостей проводится с использованием алгоритма моделирования задачи прохождения плоской волны через пластину материала.
Расчетная модель, описывающая представленный эксперимент, основывается на матричном методе расчета прохождения плоской волны через пластину материала с известными величинами диэлектрической и магнитной проницаемостей [М. Борн, Э. Вольф. Основы оптики (2-е издание). М.: Наука, 1973].
При использовании алгоритма расчетной модели в виде программного продукта исчезает необходимость вывода аналитических формул, связывающих косвенные параметры, полученные в ходе эксперимента с сверхвысокочастотными параметрами материала, как это сделано, например, в формуле (1), при этом достаточно, моделируя в программе условия эксперимента, рассчитывать выходные данные [А.А. Брандт. Исследование диэлектриков на сверхвысоких частотах М.: Физматгиз, 1963. - 404 с].
Для доказательства преимущества предложенного способа определения комплексной диэлектрической проницаемости и комплексной магнитной проницаемости проведем расчетный эксперимент.
Сначала рассчитаем угловые зависимости модулей и фаз коэффициентов отражения и прохождения для падающей ТМ-волны и для падающей ТЕ-волны на пластину толщиной d, с диэлектрической проницаемостью ε=3,81, tgδ∈=0,0000 и магнитной проницаемостью μ=2,5, tgδμ=0,0000 (материал образца без потерь).
Угловые зависимости модулей и фаз прошедшей волны измеряются при расположении приемной и передающей антенн напротив друг друга и повороте образца материала, расположенного между ними, вокруг центральной оси измерительного полигона.
Угловые зависимости модулей и фаз отраженной волны измеряются при одновременном повороте, относительно падающего поля вокруг центральной оси измерительного полигона, образца материала и приемной антенны, которая, для реализации закона отражения Снеллиуса, поворачивается в два раза быстрее образца материала.
Используя сформированный массив данных, путем перебора искомых значений диэлектрической проницаемости ε в диапазоне от 1,3 до 40 и магнитной проницаемости μ в диапазоне от 0,1 до 40 на частоте ƒ=10 ГГц и толщине пластины, равной полуволновому значению, d=7,685 мм определим искомые результаты для одного угла падения падающей волны на пластину α=0 град, что соответствует алгоритму прототипа.
В результате расчета получены следующие результаты:
вариант 1 ε=3,81, μ=2,5;
вариант 2 ε=1,4, μ=7,01;
вариант 3 ε=4,36, μ=11,25;
вариант 4 ε=3,55, μ=13,89;
вариант 5 ε=3,27, μ=18,24;
вариант 6 ε=2,73, μ=18,31;
вариант 7 ε=1,87, μ=27,18;
вариант 8 ε=1,71, μ=29,9;
вариант 9 ε=3,78, μ=31,89.
Из результатов расчетов видно, что применение в известных технических решениях способа определения комплексной диэлектрической проницаемости и комплексной магнитной проницаемости при анализе амплитуды и фазы для одного угла взаимного положения антенн, например, напротив друг друга, и образца материала расположенного при нормальном падании волны, не приводит к получению единственного решения, даже для материала без потерь.
Подобный результат получен и для пластины не полуволновой толщины на частоте ƒ=10 ГГц d=8,685 мм.
В результате расчета получены следующие результаты:
вариант 1 ε=3,81, μ=2,5;
вариант 2 ε=10,02, μ=1,03;
вариант 3 ε=14,45, μ=0,74;
вариант 4 ε=15,36, μ=2,85;
вариант 5 ε=15,59, μ=2,81;
вариант 6 ε=19,70, μ=2,25;
вариант 7 ε=35,89, μ=1,27.
Используя сформированный массив данных, путем перебора искомых значений диэлектрической проницаемости ε в диапазоне от 1,3 до 40 и магнитной проницаемости μ в диапазоне от 0,1 до 40 на частоте f=\0 ГГц и толщине пластины, равной полуволновому значению, d=7,685 мм, и сравнивая их с полученными расчетным способом, определяем искомые результаты для двух углов падения падающей волны на пластину α1=0 град, (нормальное падение волны) и α2=60 град., близкому к углу Брюстера для ТМ-поляризации падающей волны, для измерения фазы прошедшей волны при неизменном положении антенн напротив друг друга, расчет, соответствующий одному из вариантов по предложенному техническому решению. В результате расчета получен единственный результат: единственный вариант решения - ε=3,81, μ=2,5, совпадающий с данными для выбранной пластины.
Для определения диэлектрических и магнитных потерь к анализу экспериментального изменения фазы прошедшей волны необходимо добавить анализ изменения модуля прошедшего поля.
На первом этапе, для ТМ-волны, поворачивают образец материала вокруг центральной оси измерительного полигона на угол αобр и одновременно поворачивают приемную антенну в два раза быстрее, на угол α-прием=2⋅αобр, выполняют закон Снеллиуса, по положению минимума коэффициента отражения и изменению фазы на 180 град, определяют угол Брюстера αo. Затем, для ТЕ-волны, поворачивают образец материала вокруг центральной оси измерительного полигона на угол αо1 и одновременно поворачивают приемную антенну в два раза быстрее на угол αприем=2⋅αо, выполняя закон Снеллиуса, определяют минимум коэффициента отражения определяют угол аналогичный углу Брюстера αо2. Углы αо1 и αо2 запоминают (фиксируют). Если минимум отраженной волны для какой-то поляризации не определяется, то для этой поляризации выбирается угол, соответствующий другой поляризации или соответствующий максимуму амплитуды прошедшей волны.
На втором этапе, экспериментально измеряя амплитуды (Ап) и фазы (Фп) прошедшего и амплитуды (Ao) и фазы (Фо) отраженного полей, составляют массив данных:

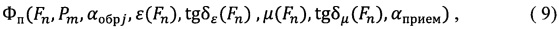
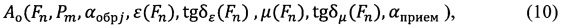
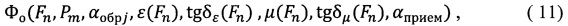
где Fn - частота измерений в n-точке, n=1, …N,
Pm - поляризация падающей волны, для ТМ-волны m=1, для ТЕ-волны m=2, αобрim - угол поворота образца материала, диапазон от -90 до 90 град.,
при чем αобр=0 град., соответствует нормальному падению волны на образец материала, когда волновой вектор падающего поля совпадает с нормалью к поверхности образца материала, число угловых точек измерения соответствует j=0, …J,
αприем - угол поворота приемной антенны относительно волнового вектора падающей волны, α-прием=0 град., соответствует направлению на передающую антенну,
ε(Fn) - диэлектрическая проницаемость образца материала на частоте Fn, tgδε(Fn) - тангенс угла диэлектрических потерь образца материала на частоте Fn,
μ(Fn) - магнитная проницаемость образца материала на частоте Fn,
tgδμ(Fn) - тангенс угла магнитных потерь образца материала на частоте Fn.
Далее для каждой частоты Fn составляется система уравнений:
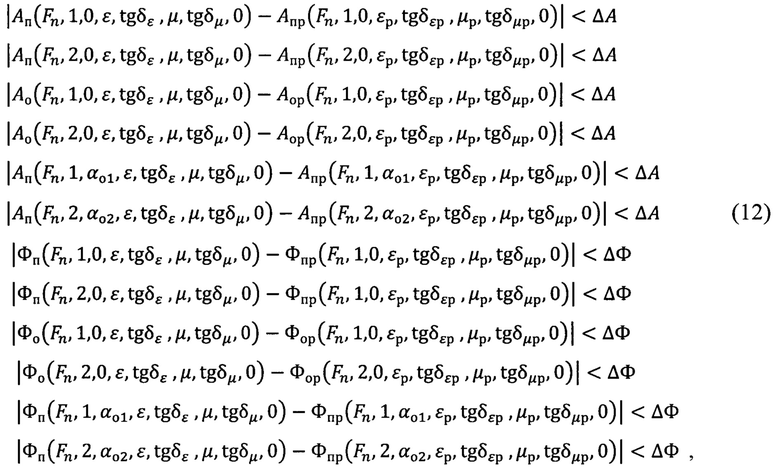
где ΔА - погрешность определения амплитуды,
ΔФ - погрешность определения фазы,
εр - расчетная диэлектрическая проницаемость образца материала,
tgδεp - расчетный тангенс угла диэлектрических потерь образца материала, изменяющийся в диапазоне его изменений,
μр - расчетная магнитная проницаемость образца материала, изменяющаяся в диапазоне ее изменений,
tgδμp - расчетный тангенс угла магнитных потерь образца материала, изменяющийся в диапазоне его изменений,
Апр - расчетная амплитуда прошедшей волны, соответствующая εp, tgδεp, μр, tgδεp,
Фпр - расчетная фаза прошедшей волны, соответствующая εp, tgδεp; μp, tgδμp,
Aop - расчетная амплитуда отраженной волны, соответствующая εр, tgδεp, μр, tgδμp,
Фор - расчетная фаза отраженной волны, соответствующая εр, tgδεp, μр, tgδμp.
Изменяя в расчете величины εр, tgδεp, μр, tgδμp сравниваются одновременно значения расчетные значения амплитуды Апр и фазы Фпр прошедшей и Аор, Фор отраженной волн с экспериментальными данными из массивов Ап, Фп, Ao, Фo добиваясь их совпадения, не выше погрешности ΔА, ΔФ, которые уточняются для каждого измерительного устройства.
Устройство для измерения сверхвысокочастотных параметров материалов в полосе частот, включающее вращающуюся подставку для крепления образца материала, оборудованную для вращения вокруг оси двигателем с блоком управления и датчиком угла поворота и расположенную в центре измерительного полигона между передающей и приемной антеннами, СВЧ-измеритель, соединенный с управляющим компьютером, отличающееся тем, что линейно-поляризованные антенны установлены с возможностью вращения вокруг продольной оси посредством двигателей с блоками управления и оборудованы датчиками для определения положения антенн относительно плоскости полигона, приемная антенна, расположена на платформе, закрепленной соосно с вращающейся подставкой для крепления образца материала с двигателем и блоком управления для вращения вокруг оси, и оборудованной датчиком угла поворота, причем датчики угла поворота и двигатели с блоками управления для вращения платформы и подставки расположены соосно и подключены к управляющему компьютеру.
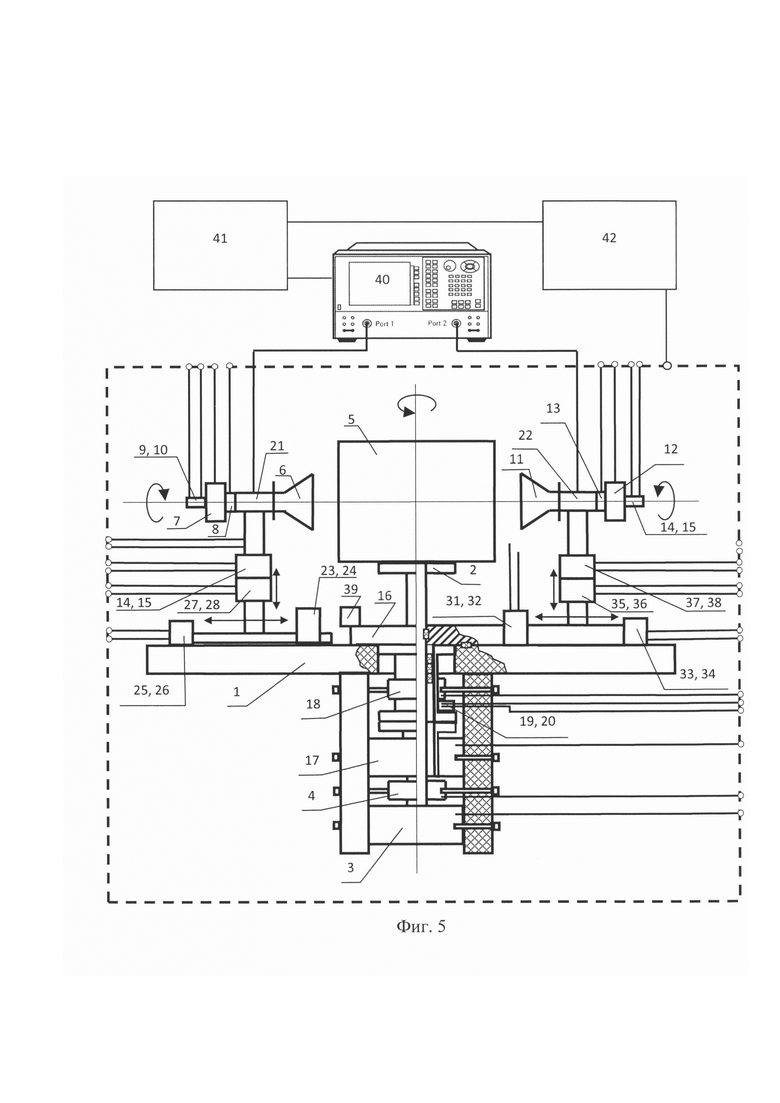
На фиг. 5 представлено устройство для измерения диэлектрических свойств образца материала в свободном пространстве.
Устройство предназначено для измерения параметров сверхвысоких частот (СВЧ) прошедшей и отраженной СВЧ волн и содержит основание полигона 1, вращающуюся подставку 2 с управляемым приводом 3 и датчиком угла поворота 4 с установленным образцом материала 5, передающую антенну 6, с управляемым приводом вращения для изменения поляризации 7, датчиком угла поворота 8 и концевыми датчиками 9, 10, приемную антенну 11с управляемым приводом вращения для изменения поляризации 12, датчиком угла поворота 13 и концевыми датчиками 14 и 15, принимающую отраженную волну от панели и установленную на вращающейся платформе 16, с управляемым приводом 17, датчиком угла поворота 18, концевыми датчиками 19 и 20, коаксиально-волновые переходы 21 и 22, платформу для линейного перемещения передающей антенны с управляемыми приводами 23 с датчиком линейного перемещения 24 и концевыми выключателями 25 и 26, механизм вертикального перемещения передающей антенны вдоль вертикальной штанги с управляемыми приводами 27 с датчиком линейного перемещения 28, концевыми выключателями 29 и 30, платформу для линейного перемещения приемной антенны с управляемыми приводами 31 с датчиком линейного перемещения 32, концевыми выключателями 33 и 34, механизм вертикального перемещения приемной антенны вдоль вертикальной штанги с управляемыми приводами 35 с датчиком линейного перемещения 36, концевыми выключателями 37 и 38.
На фиг. 5 показано, когда измеряют амплитуду и фазу отраженной и прошедшей волн с выхода СВЧ измерителя в виде анализатора цепей 40, фиксируют эти показания в компьютере 41, одновременно измеряя углы поворота образца материала и положение антенн управляя ими с управляющего компьютера 42.
Управляемые привода 3 поворота подставки 2 и вращающейся платформы 16, приемной антенны 6, датчики 4 и 18 должны располагаться на одной оси конструктивно используя прецизионный сервопривод 17 с полым валом.
Механические устройства работают следующим образом.
Управляемыми приводами 23 и 31 устанавливают расстояние антенн относительно центра полигона, контролируя расстояние до центра датчиками 3 и 24.
Управляемыми приводами 27 и 35 устанавливают высоту расположения антенн относительно плоскости стола полигона, контролируя высоту до плоскости стола датчиками 28 и 36.
Управляемыми приводами 7 и 12 устанавливают совпадающие поляризации передающей антенны 6 и приемной антенны 11, контролируя поляризацию датчиками 8 и 18.
Поворачивают приемную антенну и записывают значения измеренных параметров СВЧ. Закрепляют образец материала 5 на подставке 2.
Приводом 3 поворачивают подставку на заданный угол, контролируя ее положение датчиком угла 4.
Приводом 17 поворачивают приемную антенну 6 на угол в два раза превосходящий заданный угол на который повернут образец материала, контролируя угол поворота датчиком 18.
По изменению измеренных амплитуд и фаз с образцом и без него расчетом в компьютере определяются сверхвысокочастотные параметры материала.
Основанием для введения в устройство для измерения диэлектрической проницаемости образца материала в свободном пространстве дополнительной платформы с закрепленной антенной, принимающей при различных угловых положениях образца материала относительно передающей антенны, отраженную или прошедшую волны, моторов с блоками управления и датчиками угла поворота, является необходимость проведения высокоточных измерений угловых зависимостей мощности и фазы отраженной волны для определения тангенса угла диэлектрических потерь образца материала по градиенту угловой зависимости фазы отраженной волны и для высокоточной установки величины угла Брюстера падающей волны для точного измерения сверхвысокочастотных параметров образца материала по измерению угловой зависимости мощности и фазе прошедшей волны.
Основным источником аппаратных ошибок в определении диэлектрической проницаемости является погрешность измерения фазы прошедшей волны. Расчеты показывают, что инструментальная погрешность 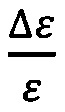 при использовании в расчете погрешностей составляющих, входящих в формулу (3), и со значениями, указанными выше, составит 3%.
при использовании в расчете погрешностей составляющих, входящих в формулу (3), и со значениями, указанными выше, составит 3%.
Использование в приемном канале одного приемного рупора для последовательного измерения коэффициентов прохождения при повороте пластины и угловых зависимостей коэффициента отражения позволяет снизить стоимость устройства за счет оптимизации схемы измерения и устранения СВЧ элементов: коммутатора и дополнительных: рупора, КВП и кабелей, а также применить не четырех, а двухпортовый анализатор цепей.
С использованием в качестве СВЧ измерителя векторного анализатора цепей, появляется возможность перекрыть единым приборным измерительным комплексом весь используемый в настоящее время радиочастотный диапазон для исследования материалов.
Для решения методических вопросов применения метода измерения диэлектрических свойств материалов в широкой полосе частот рассмотрим модель измерительного полигона с расположением линейно-поляризованных рупорных антенн в ближней зоне по схеме (фиг. 5).
На фиг. 5 представлены измерительные антенны в виде линейно-поляризованных рупоров, расположенных для измерения в совпадающих поляризациях так, что вектора электрического поля (Е) рупоров лежат в плоскости падения электромагнитной волны на пластину из испытуемого материала толщиной d. Применение линейно-поляризованных секториальных рупоров и экспериментальные измерения, произведенные при совпадающих поляризациях передающей и приемной антенн, позволяет получить дополнительные измерительные данные для последующих расчетных процедур по определению диэлектрической и магнитной проницаемостей. Применение линейно-поляризованных секториальных рупоров позволяет значительно сократить эффективную поверхность раскрыва и тем самым сократить расстояния от антенн до поверхности образца, что особенно важно при практической реализации устройства для сокращения его размеров. Приемный и передающий рупор соединены с анализатором цепей. Излучаемая передающим рупором электромагнитная волна, проходя через пластину, принимается приемным рупором. На фигуре образец материала повернут на угол α, равный углу падения плоской волны, в модели, с помощью которой описывается данный измерительный эксперимент. Элементы радиоизмерительного тракта хорошо разработаны и имеют погрешность определения фазы в СВЧ диапазоне от 1,5 град до 2 град.
Передающий рупор 6 и приемный рупор 11 соединены с СВЧ-измерителем, представленным в виде анализатора цепей 40 (фиг. 5), при повороте подставки 2 с образцом материала 5 на угол α относительно падающей волны, платформа 3 с приемной антенной 11, принимающей отраженную волну, поворачивается на угол 2⋅α. Управление электромеханической частью устройства производится управляющим компьютером 42. Величины углов, а также мощность и фаза отраженной волны фиксируются в компьютере 41. При изменении положения приемного рупора 11 измеряются величины мощности и фазы прошедшей волны, которые также запоминаются в компьютере 41, в котором определяются сверхвысокочастотные параметры материала образца.
Таким образом, использование в способе измерения диэлектрической проницаемости материала в широкой полосе частот падение волны под углом близким к углу Брюстера по анализу фазы прошедшей волны по процедуре изложенной в предлагаемом техническом решении позволяет определить частотную зависимость диэлектрической проницаемости с более высокой точностью, чем при использовании известных способов, а анализируя по предложенному техническому решению фазы отраженной волны с более высокой разрешающей способностью определить частотную зависимость тангенса угла диэлектрических потерь по сравнению с известными способами.
Предложенное устройство, реализующее способ определения сверхвысокочастотных параметров материала в полосе частот, позволяет производить измерение в широкой частотной полосе с точностью более высокой, чем в известных устройствах.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ измерения диэлектрических свойств материала и устройство для его осуществления | 2017 |
|
RU2665593C1 |
| СПОСОБ ДИСТАНЦИОННОГО ИЗМЕРЕНИЯ КОМПЛЕКСНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПЛОСКОСЛОИСТЫХ ДИЭЛЕКТРИКОВ ЕСТЕСТВЕННОГО ПРОИСХОЖДЕНИЯ | 2022 |
|
RU2790085C1 |
| Способ определения диэлектрической проницаемости материала | 2019 |
|
RU2713162C1 |
| СВЧ-СПОСОБ ОПРЕДЕЛЕНИЯ КОМПЛЕКСНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ И ТОЛЩИНЫ ДИЭЛЕКТРИЧЕСКИХ ПЛАСТИН | 2003 |
|
RU2249178C2 |
| Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями | 2022 |
|
RU2789626C1 |
| Способ пеленгации и устройство для его осуществления | 2019 |
|
RU2716273C1 |
| Способ пеленгации и широкополосный пеленгатор для его осуществления | 2018 |
|
RU2699079C1 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ОБРАЗЦА МАТЕРИАЛА ПРИ ВОЗДЕЙСТВИИ ВНЕШНИХ ФАКТОРОВ | 2011 |
|
RU2453856C1 |
| ШИРОКОПОЛОСНЫЙ ОБТЕКАТЕЛЬ | 2013 |
|
RU2559730C2 |
| Устройство дистанционного измерения диэлектрической проницаемости плоскослоистых диэлектриков естественного происхождения с суммарно-разностной обработкой интерференционных сигналов | 2024 |
|
RU2821440C1 |
Использование: для определения сверхвысокочастотных параметров материала. Сущность изобретения заключается в том, что способ включает измерение мощности и фазы прошедшей волны между передающей и приемной антеннами без образца материала, установку образца материала на вращающую подставку в центре полигона между передающей и приемной антеннами, измерение мощности и фазы прошедшей волны между передающей и приемной антеннами с образцом материала, вычисление мощности и фазы прошедшей волны между передающей и приемной антеннами с расположенным между ними образцом материала и без него, расчет мощности и фазы комплексных сверхвысокочастотных параметров материала, при этом в полосе частот измеряют угловые зависимости мощности и фазы прошедшей и отраженной волн при повороте образца материала между передающей и приемной антеннами в двух перпендикулярных плоскостях поляризации, по измеренным угловым зависимостям мощности и фазы отраженной волны определяют углы Брюстера, а комплексные величины сверхвысокочастотных параметров рассчитывают по мощностям и фазам поля прошедшего через образец материала при нормальном падении и повернутого под углом Брюстера, причем, если не определяется угол, соответствующий углу Брюстера для поляризации с вектором электрического поля, перпендикулярным плоскости падения падающей волны, то для этой поляризации используется величина угла Брюстера для поляризации с вектором электрического поля в плоскости падения падающей волны. Технический результат: обеспечение возможности повышения точности измерения частотной зависимости комплексных диэлектрической и магнитной проницаемости образца материала. 2 н.п. ф-лы, 5 ил.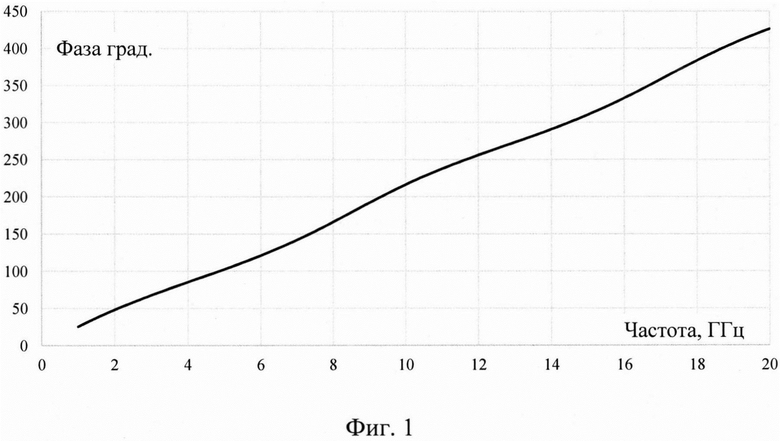
1. Способ определения сверхвысокочастотных параметров материала в полосе частот, включающий измерение на СВЧ-измерителе в полосе частот мощности и фазы прошедшей волны между передающей и приемной антеннами без образца материала, установку образца материала на вращающую подставку в центре полигона между передающей и приемной антеннами, измерение на СВЧ-измерителе мощности и фазы прошедшей волны между передающей и приемной антеннами при повороте вращающейся подставки с образцом материала, вычисление в полосе частот изменения мощности и фазы прошедшей волны между передающей и приемной антеннами с расположенным между ними образцом материала и без него, расчет по изменению мощности и фазы комплексных сверхвысокочастотных параметров материала, отличающийся тем, что на СВЧ-измерителе в полосе частот измеряют угловые зависимости мощности и фазы прошедшей и отраженной волн при повороте образца материала между передающей и приемной антеннами в двух перпендикулярных плоскостях поляризации, соответствующих плоскости поляризации с вектором электрического поля, лежащим в плоскости падения, и плоскости поляризации с вектором электрического поля, перпендикулярным плоскости падения, по измеренным угловым зависимостям мощности и фазы отраженной волны определяют углы Брюстера для поляризации с вектором электрического поля в плоскости падения падающей волны и угол, соответствующий углу Брюстера для поляризации с вектором электрического поля, перпендикулярным плоскости падения падающей волны, а комплексные величины сверхвысокочастотных параметров рассчитывают по мощностям и фазам для обеих поляризаций поля, прошедшего через образец материала при нормальном падении и повернутого под углом Брюстера, причем, если не определяется угол, соответствующий углу Брюстера для поляризации с вектором электрического поля, перпендикулярным плоскости падения падающей волны, то для этой поляризации используется величина угла Брюстера для поляризации с вектором электрического поля в плоскости падения падающей волны.
2. Устройство для измерения параметров материалов в полосе частот, включающее вращающуюся подставку для крепления образца материала, оборудованную для вращения вокруг оси двигателем с блоком управления и датчиком угла поворота и расположенную в центре измерительного полигона между передающей и приемной антеннами, СВЧ-измеритель, соединенный с управляющим компьютером, отличающееся тем, что линейно-поляризованные антенны установлены с возможностью вращения вокруг продольной оси посредством двигателей с блоками управления и оборудованы датчиками определения угла поворота положения антенн относительно плоскости полигона, приемная антенна расположена на платформе, закрепленной соосно с вращающейся подставкой для крепления образца материала с двигателем и блоком управления для вращения вокруг оси и оборудованной датчиком угла поворота, причем датчики угла поворота и двигатели с блоками управления для вращения платформы и подставки установлены соосно и подключены к управляющему компьютеру.
| Устройство для промежуточного останова рамы кегельбана | 1976 |
|
SU657733A3 |
| US 20170336452 A1,23.11.2017 | |||
| US 5532604 A1, 02.07.1996 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ КРИВОЛИНЕЙНОГО СЛОЯ МАТЕРИАЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2365926C1 |
| US 20050230619 A1, 20.10.2005. | |||
Авторы
Даты
2019-05-21—Публикация
2018-07-25—Подача