Изобретение относится к измерительной технике, в частности к измерению сверхвысокочастотных параметров материалов в свободном пространстве.
Известны способы измерения относительной диэлектрической и магнитной проницаемостей в объемном резонаторе на фиксированной частоте, когда образец измеряется в двух положениях: на поршне и на подставке (Е.Б.Зальцман. Измерение параметров магнитодиэлектриков и не намагниченных ферритов при помощи прямоугольного резонатора на волну Н10.// Радиотехника, 1958, с.13, №10, с.76-80).
Недостатком способов является узкополосность производимых измерений. При измерении параметров парамагнитных и ферромагнитных материалов точность измерения снижается, потому что магнитное поле материала искажает структуру поля в резонаторе и метод малых возмущений, используемый в резонансном методе измерений не выполняется.
Волноводные и резонаторные методы измерения относительной диэлектрической и магнитной проницаемостей имеют высокую точность и чувствительность измерения сверхвысокочастотных параметров, но обладают существенным недостатком – узкополосностью производимых измерений (В.Н.Егоров. Резонансные методы исследования диэлектриков на СВЧ.// Приборы и техника эксперимента. – 2007, №2, с.5-38).
Известны амплитудно-фазовые приборы, работающие на «прохождение» и «отражение» электромагнитной волны в свободном пространстве, используемые для измерения относительной диэлектрической и магнитной проницаемости материалов (Приборы для неразрушающего контроля материалов и изделий. Справочник в 2-х книгах, кн.1 под ред. В.В.Клюева. 2-е изд., перераб. и доп., М.: Машиностроение. 1986, с.220-224, 233-234, рис.17 с. 217-219).
Описаны способы определения относительной диэлектрической проницаемости материала по мощности и фазе прошедшей и отраженной волны (Е.А.Воробьев. Радиоволновой контроль судовых радиотехнических конструкций и материалов, Л.: Судостроение, 1986, 81, с. 22).
Известны способы определения относительной диэлектрической проницаемости материалов по мощности и фазе отраженной волны от пластины, расположенной под углом Брюстера (А.с. СССР №1550436, кл. G01R 27/26, опубл.15.03.1990 Бюл. №10; Патент РФ №2249178, МПК G01B 15/02, G01R 27/26, опубл. 27.03.2005, Бюл. №9, Заявка на изобретение 2003 106 528 , опубл. 10.09.2004).
Недостатком этих способов является требование к высокой точности изготовления плоских образцов протяженных размеров на уровне 0,005 мм, что с технологической точки зрения при больших размерах образцов трудновыполнимо. Высокие требования предъявляются также к радиотехническому качеству измерительного полигона и точности измерительной аппаратуры.
При всех недостатках, присущих способу измерения сверхвысокочастотных параметров материала в свободном пространстве, его важное преимущество состоит в возможности получения зависимостей относительной диэлектрической проницаемости от частоты в широкой полосе.
Для получения расширенной информации об исследуемом материале требуется измерение его диэлектрических свойств в широкой полосе частот с постоянным увеличением верхних граничных частот, где размеры резонансных систем становятся сравнимыми в длиной волны, поэтому направление развития методов исследований свойств материалов связано с использованием в радиодиапазоне оптических методов в свободном пространстве, для которых с созданием СВЧ-измерителей в виде широкополосных анализаторов цепей достигнут прогресс в приборном обеспечении.
Вместе с тем известные способы измерения сверхвысокочастотных параметров материала в свободном пространстве обладают методическими недостатками, которые не позволяют одновременно производить измерение относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь материалов с высокой точностью.
Наиболее близким техническим решением является способ измерения относительной комплексной диэлектрической проницаемости (Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями. Патент РФ № 2613810, МПК G01R 27/00, опубл. 21.03.2017, Бюл. № 9).
В этом методе при изменении угла падающей электромагнитной линейно поляризованной волны с вектором электрического поля, лежащим в плоскости падения, на плоский образец материала (ТМ-волна) находится угол, который определяется из условия перпендикулярности между направлениями прошедшей и отраженной волнами, исходя из которого устанавливается взаимосвязь между углом Брюстера и электродинамическими параметрами материала пластины в виде формулы Брюстера:

где 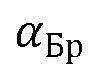 – угол, при котором выполняются условия закона Брюстера;
– угол, при котором выполняются условия закона Брюстера;
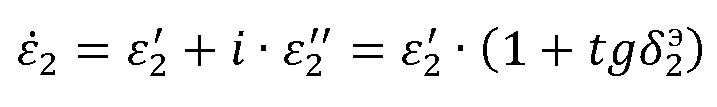 – относительная комплексная диэлектрическая проницаемость материала;
– относительная комплексная диэлектрическая проницаемость материала;
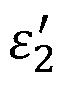 – относительная диэлектрическая проницаемость;
– относительная диэлектрическая проницаемость;
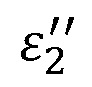 – мнимая часть диэлектрической проницаемости;
– мнимая часть диэлектрической проницаемости;
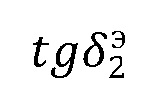 – тангенс угла диэлектрических потерь в материале.
– тангенс угла диэлектрических потерь в материале.
Как установили авторы, формула (1) выполняется только при отсутствии потерь в материале, но с увеличением тангенса угла диэлектрических потерь наблюдаются значительные расхождения между условиями выполнения закона Брюстера, что снижает точность определения относительной комплексной диэлектрической проницаемости.
Задачей настоящего изобретения является повышение точности измерения частотной зависимости относительной комплексной диэлектрической проницаемости материала плоского образца в широкой полосе частот в свободном пространстве.
Поставленная задача достигается тем, что предложен способ измерения комплексной относительной диэлектрической проницаемости плоского образца материала с диэлектрическими потерями в полосе частот СВЧ диапазона, в котором с помощью СВЧ-измерителя измеряют зависимость комплексного коэффициента отражения, когда электрическое поле падающей волны параллельно плоскости падения и определяют относительную комплексную диэлектрическую проницаемость, отличающийся тем, что для каждой частоты СВЧ диапазона с помощью метода прогонки с заранее заданным шагом итераций рассчитывают относительную комплексную диэлектрическую проницаемость по формуле:

где i – мнимая единица;
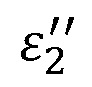 – мнимая часть диэлектрической проницаемости;
– мнимая часть диэлектрической проницаемости;
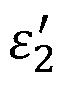 – относительная диэлектрическая проницаемость,
– относительная диэлектрическая проницаемость,
путем решения двух совместных уравнений, первое из которых составлено для значения угла 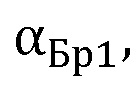 найденного из измеренной угловой зависимости амплитуды коэффициента отражения Френеля и соответствующего расчетному минимуму отраженной волны по формуле:
найденного из измеренной угловой зависимости амплитуды коэффициента отражения Френеля и соответствующего расчетному минимуму отраженной волны по формуле:
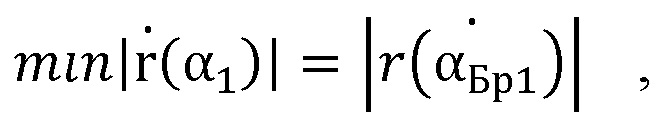
где: 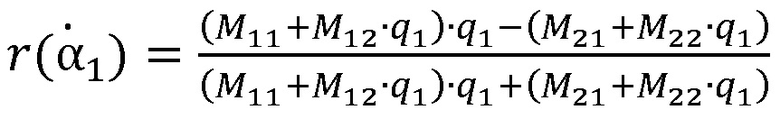 – расчетная угловая зависимость комплексного коэффициента отраженной волны;
– расчетная угловая зависимость комплексного коэффициента отраженной волны;
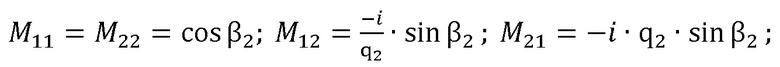
 – параметр, соответствующий плоскому образцу толщиной d2;
– параметр, соответствующий плоскому образцу толщиной d2;
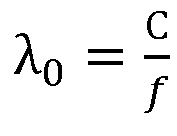 – длина волны, f – частота измерений, C – скорость света;
– длина волны, f – частота измерений, C – скорость света;

α1 – угол падения волны на плоский образец;
α2 – угол преломления,
и второе составлено для значения угла 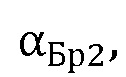 найденного из измеренной угловой зависимости фазы коэффициента отражения Френеля и соответствующего расчетной фазе, по формуле:
найденного из измеренной угловой зависимости фазы коэффициента отражения Френеля и соответствующего расчетной фазе, по формуле:
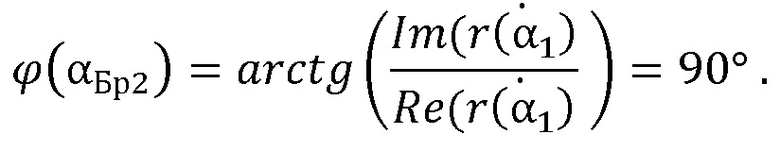
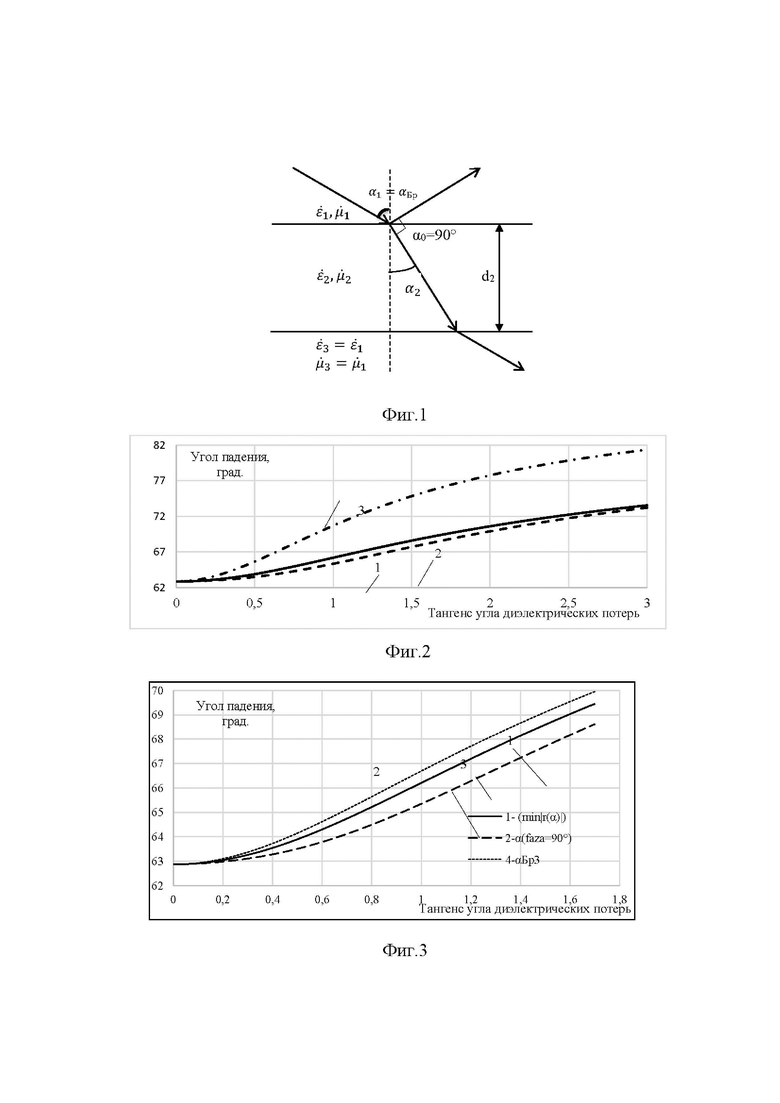
Для анализа условий проведения измерений относительной комплексной диэлектрической проницаемости авторы использовали задачу наклонного падения электромагнитной волны на бесконечную пластину диэлектрика, в которой по рассчитанным величинам амплитуды и фазы отраженной волны в рамках геометрической оптики, определяли относительную комплексную диэлектрическую проницаемость образца. Параметры образца в виде пластины указаны на фиг. 1, на которой между первой и третьей средами с электродинамическими параметрами 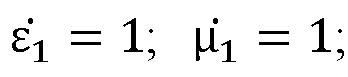 и
и 
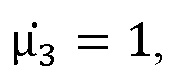
где  – относительные комплексные диэлектрические проницаемости сред,
– относительные комплексные диэлектрические проницаемости сред,  – относительные комплексные магнитные проницаемости сред, располагается исследуемый плоский образец с относительной комплексной диэлектрической проницаемостью
– относительные комплексные магнитные проницаемости сред, располагается исследуемый плоский образец с относительной комплексной диэлектрической проницаемостью 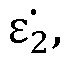 и относительной комплексной магнитной проницаемостью
и относительной комплексной магнитной проницаемостью 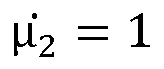 и геометрической толщиной d2. Падающая волна изображена в виде луча, составляющего с перпендикуляром к границе пластины угол
и геометрической толщиной d2. Падающая волна изображена в виде луча, составляющего с перпендикуляром к границе пластины угол  а преломленная волна изображена в виде луча под углом α2 к перпендикуляру.
а преломленная волна изображена в виде луча под углом α2 к перпендикуляру.
Модель расчета коэффициента отражения для задачи в рамках геометрической оптики построена на основе матричного метода для плоского образца (Борн М., Вольф Э. Основы оптики. Изд. 2-е. М.: Из-во «Наука», Главная редакция физико-математической литературы, 1973, 720 с.).
Расчетная угловая зависимость комплексного коэффициента отраженной волны равна:
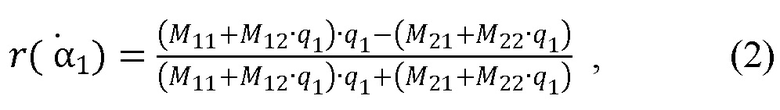
где: 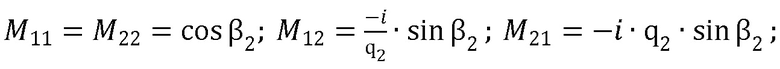
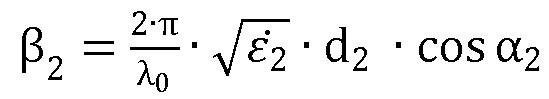 – параметр, соответствующий плоскому образцу толщиной d2,
– параметр, соответствующий плоскому образцу толщиной d2,
i – мнимая единица,
λ0 – длина волны,
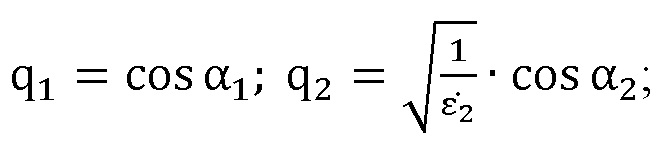 ;
; 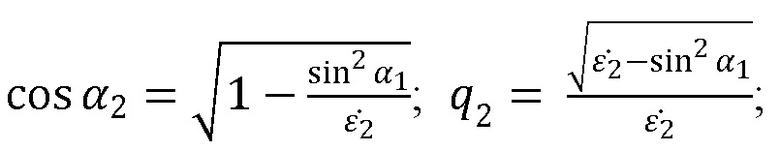
α1 – угол падения волны на плоский образец;
α2 – угол преломления.
Авторы установили, что левая часть формулы равна действительному углу, а правая тангенсу от комплексной величины, поэтому она выполняется только при действительной величине относительной комплексной диэлектрической проницаемости, то есть для материала без потерь.
При падении электромагнитной линейно-поляризованной волны с вектором электрического поля, лежащим в плоскости падения, под углом Брюстера на пластину материала с потерями, угол между отраженной и прошедшей волнами отличается от 90° и растет с увеличением диэлектрических и магнитных потерь.
Для определения относительной комплексной диэлектрической проницаемости с использованием измеренных параметров отраженной волны в виде определения угла, соответствующего углу Брюстера, не достаточно.
Обобщая полученные результаты теоретических и экспериментальных исследований и анализируя математические формулы определения фазы и амплитуды электромагнитных волн в виде:
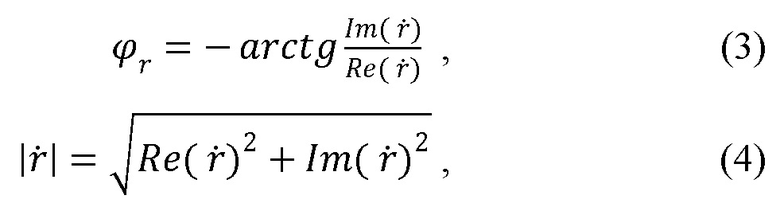
можно делать вывод, что скачок фазы электромагнитной волны на 180° в области угла Брюстера происходит тогда, когда выполняется условие равенства нулю действительной части амплитуды:

а условие минимума амплитуды при равенстве нулю модуля амплитуды:

выполняется только при условии равенства нулю действительной и мнимой частей амплитуды электромагнитной волны:

поэтому, как видно из сравнения условий (5) и (7), в общем случае точки минимума амплитуды и скачка фазы на 180° не должны совпадать. Но так как в основе математического описания электромагнитных амплитуд лежат гармонические функции, то очевидно, что для среды с электромагнитными параметрами с незначительными диэлектрическими и магнитными потерями совпадение условий (5) и (7) достаточно часто наблюдается для частотных зависимостей и реже для угловых зависимостей, как для отраженных, так и для прошедших волн.
Поэтому разница в угловых положениях минимума и скачка фазы на 180° отраженной волны в области угла Брюстера, наблюдаемая в экспериментах, связана не с отклонениями в законах Френеля, а в разнице условий их природного положения, что видно при проведении расчетов отраженных волн в пределах геометрической оптики при учете комплексных величин электродинамических параметров среды.
Поэтому предлагается проводить измерение:
– угла падения α1, равного углу 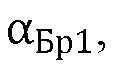 для условия минимума модуля коэффициента отражения:
для условия минимума модуля коэффициента отражения:

– угла падения α1, равного углу 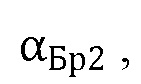 для условия равенства фазы коэффициента отражения:
для условия равенства фазы коэффициента отражения:
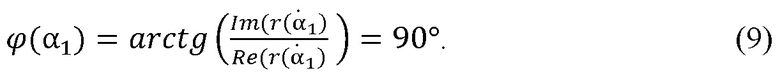
Данные значений углов падения 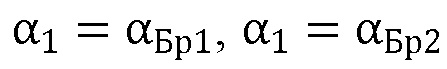 используются для проведения расчетов относительной комплексной диэлектрической проницаемости в виде относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь с использованием формулы (2).
используются для проведения расчетов относительной комплексной диэлектрической проницаемости в виде относительной диэлектрической проницаемости и тангенса угла диэлектрических потерь с использованием формулы (2).
При этом для угла Брюстера, определяемого по формуле (1), углы, определенные для условий (8) и (9), совпадают 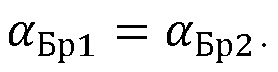
Авторы провели сравнительный расчет величины угла Брюстера по формуле (1) в зависимости от возрастающих диэлектрических потерь 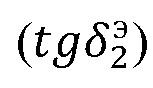 для материала с
для материала с 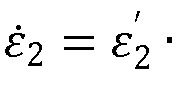
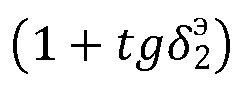 и с магнитной проницаемостью
и с магнитной проницаемостью 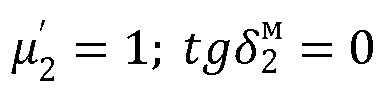 с расчетами углов.
с расчетами углов.
Численным расчетом по формуле (2) определялась угловая зависимость модуля коэффициента отражения, по которой определялся угол с минимальной амплитудой отраженной волны из условия: 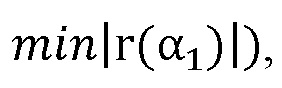 соответствующий углу
соответствующий углу  и второму следствию закона Брюстера для каждого значения возрастающего тангенса угла диэлектрических потерь материала
и второму следствию закона Брюстера для каждого значения возрастающего тангенса угла диэлектрических потерь материала 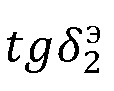 при неизменном значении относительной диэлектрической проницаемости
при неизменном значении относительной диэлектрической проницаемости 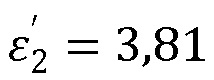 при отсутствии относительной комплексной магнитной проницаемости
при отсутствии относительной комплексной магнитной проницаемости 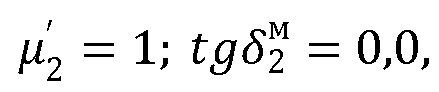 на длине волны λ0=30 мм, и толщине пластины, равной
на длине волны λ0=30 мм, и толщине пластины, равной 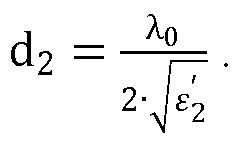
Проведенные расчеты углов, соответствующих условиям (8) и (9), в зависимости от диэлектрических потерь материала пластины, приведенные на фиг.2, на которой представлены зависимости углов от тангенса угла диэлектрических потерь, соответствующих: для кривой 1 минимуму модуля коэффициента отражения, для кривой 2 - фазе коэффициента отражения равной 90 град, кривой 3 - для угла, равного 90 град между направлениями прошедшей и отраженной волнами, при отражении от пластины с 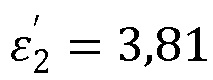 толщиной в четверть волновой электрической толщины.
толщиной в четверть волновой электрической толщины.
Из сравнения кривых, представленных на фиг.2 видно, что с увеличением потерь в материале пластины увеличивается разница между кривыми 1 и 2, то есть условие совпадения, как по формуле (1) между углами, при которых наблюдается минимум амплитуды и при котором фаза равняется 90 град, при наличии потерь в материале не выполняется и соответствует только условию для материала пластины без потерь.
Из фиг.2 также видно, что угол, при котором наблюдается направление отраженной волны, составляющий с направлением прошедшей волны 90 град с ростом потерь в материале пластины всё больше отличается от того, который рассчитывается по формуле (1) для материала пластины без потерь.
Из анализа полученных расчетных зависимостей, моделирование которых не выходило за пределы геометрической оптики, видно, что отклонения от законов Френеля не наблюдаются, а результаты расчетов совпадают с экспериментальными наблюдениями, что говорит о неприменимости формулы Брюстера в виде (1) для определения углов, соответствующих его следствиям.
Проведем расчеты величины углов Брюстера, используя различные критерии, следующие из закона Брюстера, и сравним их с расчетами по формулам (9) и (10) в зависимости от величины потерь материала пластины.
Результаты расчетов приведены на фиг. 3 для материала пластины с 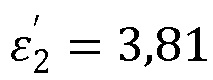 , толщиной в четверть волновой электрической толщины. Кривая 1 - это зависимость положения угла, соответствующего минимуму модуля амплитуды отраженной волны от тангенса угла диэлектрических потерь. Кривая 2 - это зависимость положения угла, соответствующего значению фазы отраженной волны, равной 90° от тангенса угла диэлектрических потерь. Кривая 3 - это зависимость положения угла Брюстера, рассчитываемого по более корректной формуле
, толщиной в четверть волновой электрической толщины. Кривая 1 - это зависимость положения угла, соответствующего минимуму модуля амплитуды отраженной волны от тангенса угла диэлектрических потерь. Кривая 2 - это зависимость положения угла, соответствующего значению фазы отраженной волны, равной 90° от тангенса угла диэлектрических потерь. Кривая 3 - это зависимость положения угла Брюстера, рассчитываемого по более корректной формуле
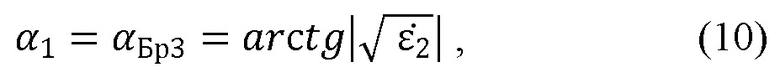
чем формула (1), в зависимости от потерь в материале или тангенса угла диэлектрических потерь.
Но тем не менее из фиг. 3 видно, что расчеты по формуле (10) не совпадают ни с кривой 1, ни с кривой 2, причем с увеличением потерь в материале, это различие растет. Поэтому очевидно, что при определении относительной комплексной диэлектрической проницаемости материалов с потерями необходимо производить расчет по формуле (2), как в предлагаемом в техническом решении.
Расчеты проводились с использованием программной платформы Microsoft Visual Studio стандарта FORTRAN 2008 с применением дополнительных опций для чисел с плавающими запятыми для уменьшения ошибок расчетов при моделировании задачи наклонного падения электромагнитной волны на бесконечную пластину из однородного диэлектрического материала с потерями.
Таким образом, авторы за счет экспериментального определения положения углов, соответствующих минимуму угловой зависимости амплитуды и фазы, равной 90° отраженной волны, и последующего использования этих значений для расчета относительной комплексной диэлектрической проницаемости одновременно соответствующей уравнению (2), повысили точность её определения для материалов с потерями в широкой полосе частот.
Изобретение относится к измерительной технике, в частности к измерению сверхвысокочастотных параметров материалов в свободном пространстве. Способ измерения относительной комплексной диэлектрической проницаемости плоского образца материала с диэлектрическими потерями в полосе частот СВЧ диапазона, в котором с помощью СВЧ-измерителя измеряют зависимость комплексного коэффициента отражения, когда электрическое поле падающей волны параллельно плоскости падения и определяют относительную комплексную диэлектрическую проницаемость. Для каждой частоты СВЧ диапазона с помощью метода прогонки с заранее заданным шагом итераций рассчитывают относительную комплексную диэлектрическую проницаемость по формуле:
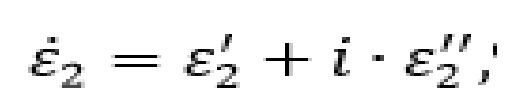
где i – мнимая единица;
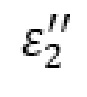 – мнимая часть диэлектрической проницаемости;
– мнимая часть диэлектрической проницаемости;
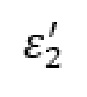 – относительная диэлектрическая проницаемость.
– относительная диэлектрическая проницаемость.
Техническим результатом при реализации заявленного решения является повышение точности измерения частотной зависимости относительной комплексной диэлектрической проницаемости материала плоского образца в широкой полосе частот в свободном пространстве. 3 ил.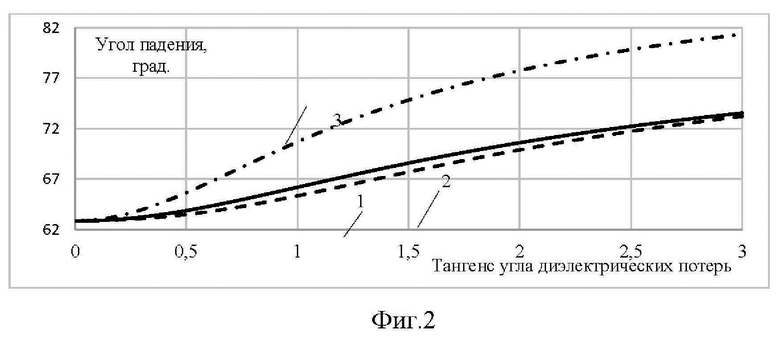
Способ измерения комплексной относительной диэлектрической проницаемости материала с потерями в полосе частот СВЧ диапазона, в котором с помощью СВЧ-измерителя измеряют зависимость комплексного коэффициента отражения, когда электрическое поле падающей волны параллельно плоскости падения и определяют относительную комплексную диэлектрическую проницаемость, отличающийся тем, что для каждой частоты СВЧ диапазона с помощью метода прогонки с заранее заданным шагом итераций рассчитывают относительную комплексную диэлектрическую проницаемость по формуле:
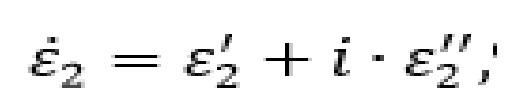
где i – мнимая единица;
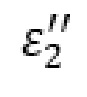 – мнимая часть диэлектрической проницаемости;
– мнимая часть диэлектрической проницаемости;
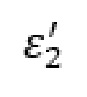 – относительная диэлектрическая проницаемость,
– относительная диэлектрическая проницаемость,
путем решения двух совместных уравнений, первое из которых составлено для значения угла 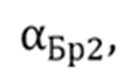 найденного из измеренной угловой зависимости амплитуды коэффициента отражения Френеля и соответствующего расчетному минимуму отраженной волны по формуле:
найденного из измеренной угловой зависимости амплитуды коэффициента отражения Френеля и соответствующего расчетному минимуму отраженной волны по формуле:
где: 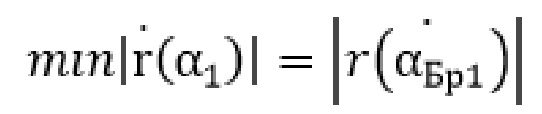
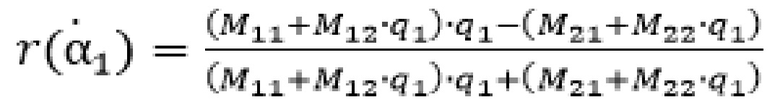 – расчетная угловая зависимость комплексного коэффициента отраженной волны;
– расчетная угловая зависимость комплексного коэффициента отраженной волны;
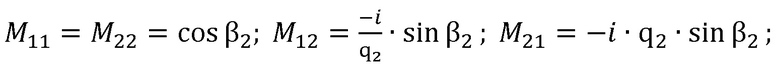
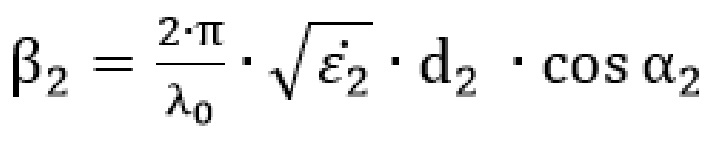 – параметр, соответствующий плоскому образцу толщиной d2;
– параметр, соответствующий плоскому образцу толщиной d2;
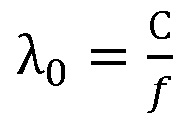 – длина волны, f – частота измерений, C – скорость света;
– длина волны, f – частота измерений, C – скорость света;
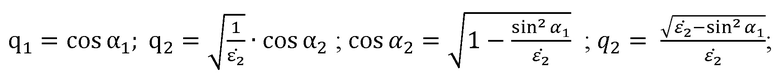
α1 – угол падения волны на плоский образец;
α2 – угол преломления,
и второе составлено для значения угла 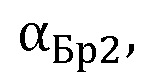 найденного из измеренной угловой зависимости фазы коэффициента отражения Френеля и соответствующего расчетной фазе, по формуле:
найденного из измеренной угловой зависимости фазы коэффициента отражения Френеля и соответствующего расчетной фазе, по формуле:
| Способ измерения относительной комплексной диэлектрической проницаемости материала с потерями в СВЧ диапазоне | 2015 |
|
RU2613810C1 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ЭЛЕКТРОФИЗИЧЕСКИХ ПАРАМЕТРОВ ТОНКИХ ПЛОСКИХ ПЛЕНОК ИЗ НЕМАГНИТНОГО ИМПЕДАНСНОГО ИЛИ ПРОВОДЯЩЕГО МАТЕРИАЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2005 |
|
RU2284533C1 |
| СПОСОБ ИЗМЕРЕНИЯ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2548064C1 |
| US 4818930 A1, 04.04.1989 | |||
| Способ измерения диэлектрических свойств материала и устройство для его осуществления | 2017 |
|
RU2665593C1 |
| US 10542906 B2, 28.01.2020. | |||
Авторы
Даты
2023-02-06—Публикация
2022-01-10—Подача