Изобретение относится к получению состава полимерных композиционных материалов (ПКМ) и может быть использовано для получения полимерных композиционных материалов с требуемыми теплофизическими и электрофизическими свойствами, применяемыми в различных отраслях промышленности.
Современная наука о полимерах позволяет конструировать на их основе материалы с заданными свойствами, отличающимися на несколько порядков. Достигается это путем создания композиционных материалов с использованием различных ингредиентов.
При создании новых композиционных материалов требуется проводить определение характеристик соответствующих свойств: механических, теплофизических, электрофизических и т.д., присущих не полимеру и наполнителю, а материалу в целом. Такие характеристики определяются в результате численного или натурного экспериментов и называются эффективными [1-3]. При получении состава полимерных композиционных материалов, например, электротехнических, требуется получить такие необходимые эффективные характеристики, как диэлектрическая проницаемость, удельная электрическая проводимость и теплоотвод, оцениваемый коэффициентом теплопроводности.
Цикл работ по решению подобного рода задач дисперсно-наполненных композиционных материалов был опубликован авторами [1-5].
Известен способ получения состава композиционного полимерного материала с заданными свойствами в виде многофакторного планирования эксперимента, т.е. многофакторный анализ (факторный анализ) [6, 7].
Предлагаемый способ получения материалов с заданными свойствами заключается в построении поверхностей, отражающих зависимости эффективных характеристик от управляющих параметров, различие состоит в самом способе построения поверхностей, которые строятся не на основе полученных функций, а на основе прямого использования экспериментальных данных, и получаются совмещением контурных кривых (изолиний).
Наиболее близким решением, использующим методы совмещения контурных кривых, является работа [7]. Для графического анализа полученных целевых функций с целью оптимизации необходимо построить контурные графики. Для построения контурных кривых изменения свойств в зависимости от содержания двух компонентов по осям откладывают дозировки компонентов в условных единицах. Контурные кривые позволяют определить, при каких дозировках компонентов свойства материала характеризуются наиболее высокими показателями и в какой области показатель изменяется в допустимых пределах. Для определения оптимальных условий, удовлетворяющих комплексу требований, используют метод совмещения контурных кривых для исследуемых показателей [8].
Этот подход является трудоемким, требует проведения полного цикла экспериментов и большого расхода материалов. Кроме того, недостатком этого способа является то, что связь между входными (управляющими) и выходными параметрами системы описывается обычно полиномом. Необходимость расположить экспериментальные точки неким оптимальным образом является одной из основных задач планирования эксперимента.
Основное отличие задачи получения материалов с заданными свойствами от традиционных задач оптимизации заключается в том, что необходимо найти не экстремальное значение параметра, а некоторое наперед заданное.
Рецептура (значения управляющих параметров), обеспечивающих требуемые значения эффективных характеристик композиционного материала (эффективного коэффициента теплопроводности, диэлектрической проницаемости и удельной электрической проводимости) определяются на основе данных из натурных экспериментов, при необходимости используются данные из вычислительных экспериментов, получаемые на основе решения задач теплопроводности [1, 2] и электростатики [10, 11].
Эти данные представляются в виде поверхностей значений теплофизических (коэффициента теплопроводности) и электрофизических характеристик (диэлектрической проницаемости и удельной электрической проводимости), зависящих от рецептурного состава (степени наполнения, типа и радиуса наполнителя).
Для построения гладких поверхностей по дискретным неполным данным используется полином Лагранжа.
Чтобы найти рецептуру, придающую требуемые значения эффективным характеристикам (в виде заданных интервалов), нужно наложить полученные зависимости в виде изолиний.
Получаем область, обеспечивающую попадание эффективных характеристик (коэффициента теплопроводности, диэлектрической проницаемости и удельной электрической проводимости) в заданные интервалы, а значения управляющих параметров по осям абсцисс и ординат определяют рецептуру композиционного материала.
Технический результат изобретения связан со способом получения рецептуры композиционного полимерного материала с комплексом теплофизических и электрофизических характеристик в заданных интервалах
Описанный подход распространяется на случай, когда нужно обеспечить получение одновременно двух, трех и более эффективных характеристик.
ПРИМЕР ПРАКТИЧЕСКОЙ РЕАЛИЗАЦИИ
Пусть необходимо определить степень наполнения и радиус частиц наполнителя для получения ПКМ на основе политетрафторэтилен (ПТФЭ), например, фторопласт - 4, с заданным коэффициентом теплопроводности в интервале 0,42÷0,37 Вт/м*К, диэлектрической проницаемостью 3,4÷2,9 и удельной электрической проводимостью 0,8*10-14÷0,4*10-14 Ом-1м-1, наполненной порошком меди ПСМ-1.
В таблице 1 представлены физические характеристики матрицы и наполнителя.
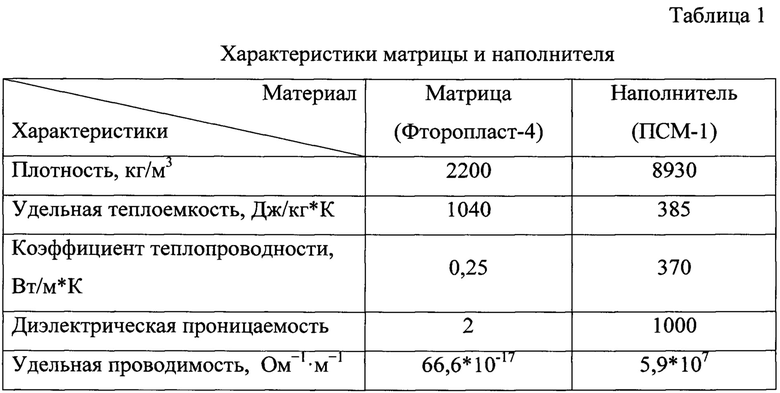
Ниже (табл. 2-4) приведены экспериментальные результаты, полученные для фторопласта с различной степенью наполнения порошком меди (10, 20 и 30%) и разным радиусом частиц наполнителя (10 и 30 мкм).
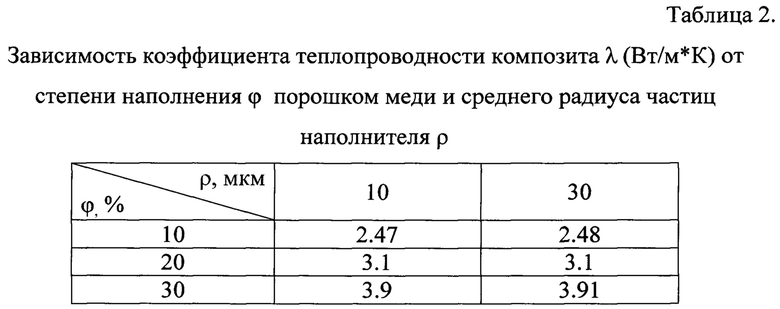


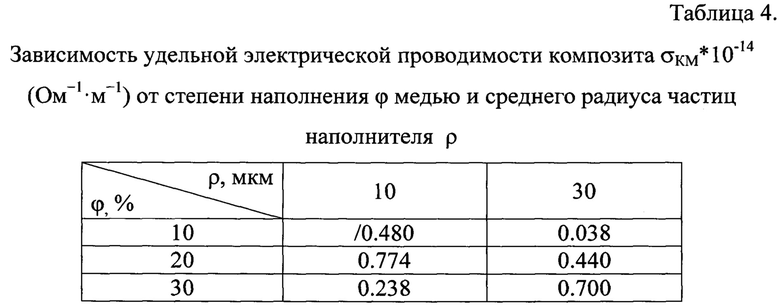
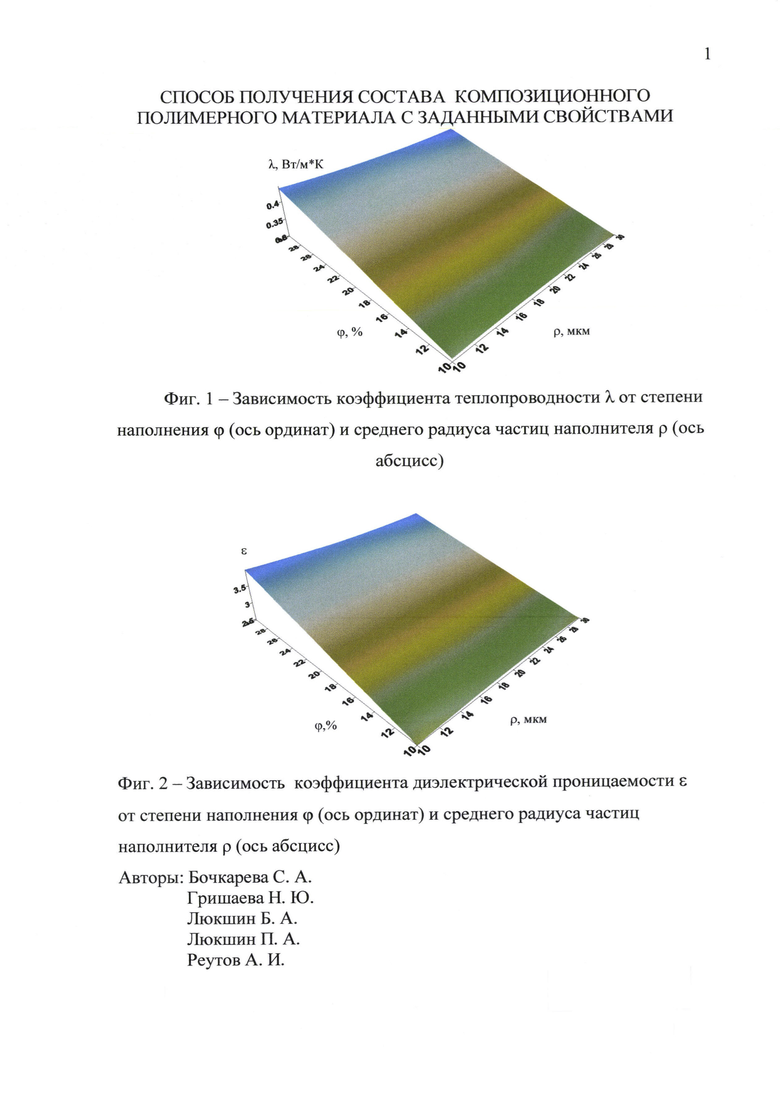
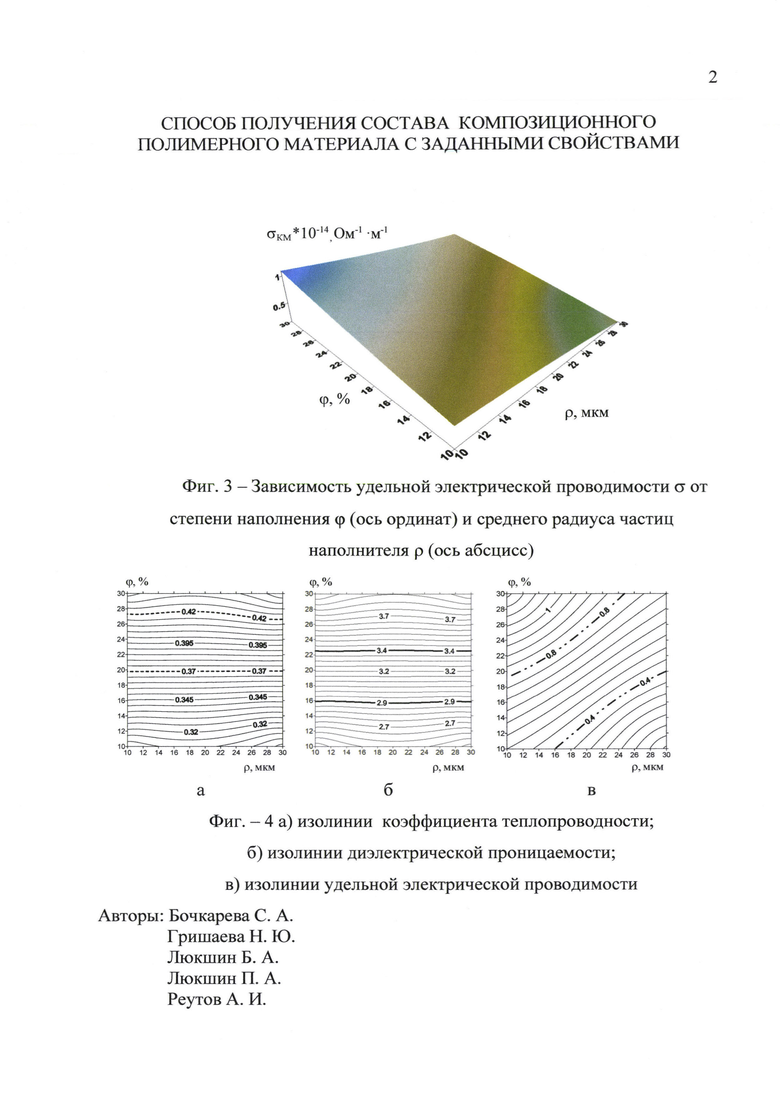
На основе полученных значений, можно найти значение рассматриваемых эффективных характеристик в любой точке плоскости (ϕ, ρ) с использованием интерполяционного полинома Лагранжа и построить зависимости эффективных характеристик от относительного радиуса частиц наполнителя и степени наполнения в виде поверхностей (фиг 1-3): фиг. 1 отражает зависимость коэффициента теплопроводности λ от степени наполнения ϕ (ось ординат) и среднего радиуса частиц наполнителя ρ (ось абсцисс), фиг. 2 соответствует диэлектрической проницаемости, фиг. 3 - удельной проводимости.
Используя способ представления скалярной функции от двух переменных на плоскости, соединяем одинаковые значения эффективных характеристик на каждой из этих поверхностей линией - получаем изолинии (фиг. 4) или линии одинаковых значений. Поскольку речь идет об интервале заданных значений, то на каждом из графиков оставляем полосу, ограниченную двумя изолиниями, отвечающими верхней и нижней границам заданного интервала (фиг 4).
0,42÷0,37 Вт/м*К - коэффициента теплопроводности (пунктирные линии);
3,4÷2,9 - диэлектрической проницаемости (жирные линии);
0,8*10-14÷0,4*10-14 Ом-1⋅м-1 - удельной электрической проводимости (штрихпунктирные линии).
Чтобы найти рецептуру (управляющие параметры), придающих требуемые значения эффективных характеристик (в виде заданных интервалов), нужно наложить полученные графики в виде изолиний друг на друга.
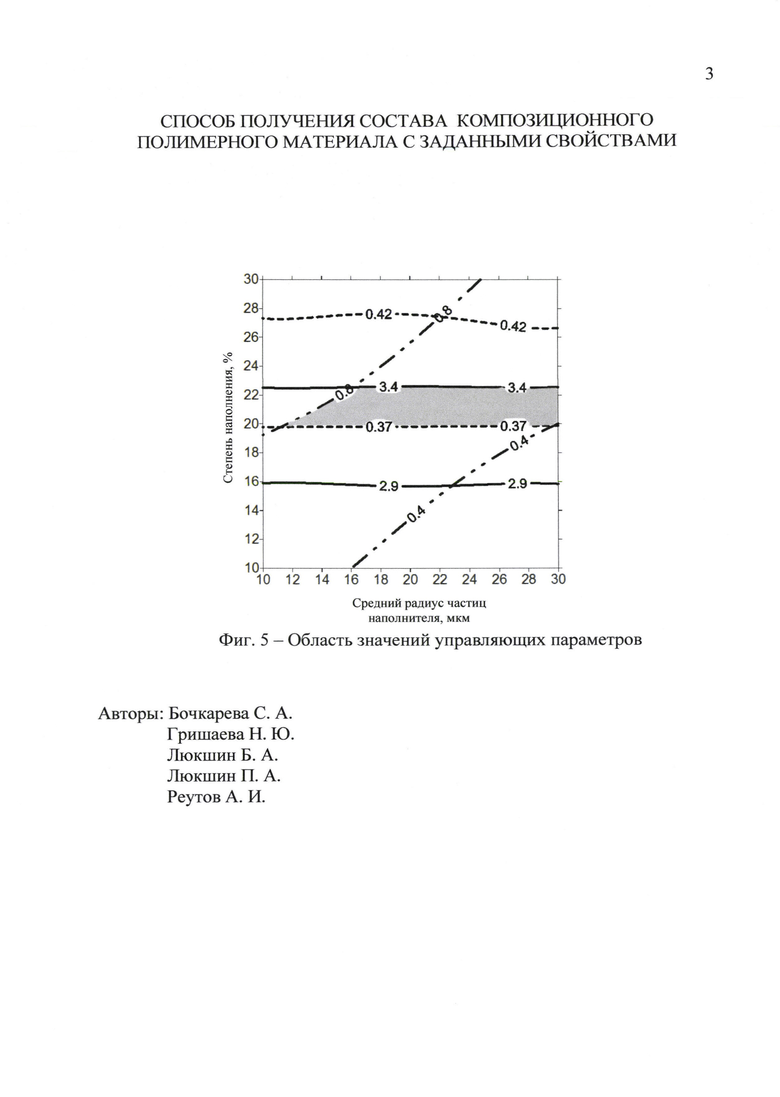
На фиг. 5 полученный неправильный затемненный криволинейный многоугольник и есть область необходимых значений эффективных характеристик, а значения по осям - это управляющие параметры: по оси абсцисс - средний радиус частиц наполнителя, а по оси ординат - степень наполнения.
С формальной точки зрения любое сочетание управляющих параметров, попадающих в полученную область, дает решение поставленной задачи. В то же время, очевидно, что с практической точки зрения следует придерживаться вариантов (точек), наиболее удаленных от границ области. Тогда при случайных отклонениях значений управляющих параметров от номинальных значений, не превосходящих расстояние до границы, результат будет соответствовать полученному варианту; в других случаях можно легко выйти за границу области.
Таким образом, для получения заданных значений эффективных характеристик выбираем точки расположенные ближе к центру полученной области с координатами по оси абсцисс, соответствующими 20-25 мкм, а по оси ординат - 21% и, следовательно, композиционный материал на основе фторопласта должен содержать порошка меди 21% с радиусом частиц от 20-25 мкм.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОЗДАНИЯ ДВУХКОМПОНЕНТНОГО КОМПОЗИТА С ЗАДАННОЙ ТЕПЛОПРОВОДНОСТЬЮ | 2020 |
|
RU2748669C1 |
| СПОСОБ СОЗДАНИЯ МЕТАЛЛОКОМПОЗИТА С ПРЕДСКАЗУЕМОЙ ТЕПЛОПРОВОДНОСТЬЮ | 2020 |
|
RU2739728C1 |
| КОМПОЗИЦИОННЫЙ ТЕПЛОПРОВОДЯЩИЙ МАТЕРИАЛ НА ОСНОВЕ НАНОЖИДКОСТИ | 2020 |
|
RU2764219C1 |
| Композиция теплопроводящего герметизирующего материала | 2020 |
|
RU2761621C1 |
| СПОСОБ ПОЛУЧЕНИЯ ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ | 2006 |
|
RU2327717C1 |
| ПОЛИМЕРНАЯ КОМПОЗИЦИЯ ДЛЯ РАДИАТОРОВ ОХЛАЖДЕНИЯ СВЕТОИЗЛУЧАЮЩИХ ДИОДОВ (СИД) И СПОСОБ ЕЕ ПОЛУЧЕНИЯ | 2012 |
|
RU2522573C2 |
| Электропроводящий морозостойкий полимерный композиционный материал | 2024 |
|
RU2832823C1 |
| Композиционный полимерный материал для герметизации | 2020 |
|
RU2745193C1 |
| СПОСОБ ПОЛУЧЕНИЯ МЕТАЛЛ-ПОЛИМЕРНОГО КОМПОЗИТНОГО МАТЕРИАЛА ДЛЯ РАДИОТЕХНИЧЕСКОЙ АППАРАТУРЫ | 2012 |
|
RU2506224C1 |
| Полимерный теплопроводящий высокоэластичный композиционный материал | 2019 |
|
RU2727401C1 |
Изобретение относится к способу получения состава композиционного полимерного материала - степени наполнения и среднего радиуса частиц наполнителя с эффективными теплофизическими и электрофизическими характеристиками в заданных интервалах. Способ характеризуется тем, что по экспериментальным данным строятся поверхности и соответствующие им изолинии эффективных характеристик - коэффициента теплопроводности, диэлектрической проницаемости и удельной электрической проводимости, зависящие от управляющих параметров - степени наполнения, типа и среднего радиуса частиц наполнителя и наложение изолиний определяет рецептуру - значения управляющих параметров, которая обеспечивает попадание указанных эффективных характеристик в заданные интервалы значений. Способ позволяет исключать нереализуемые варианты рецептуры. 5 ил., 4 табл.
Способ получения рецептуры композиционного полимерного материала с эффективными теплофизическими и электрофизическими характеристиками в заданных интервалах, отличающийся тем, что по экспериментальным данным строятся поверхности и соответствующие им изолинии эффективных характеристик, зависящие от управляющих параметров - степени наполнения, типа и среднего радиуса частиц наполнителя, и наложение изолиний определяет рецептуру - значения управляющих параметров, обеспечивающую попадание эффективных характеристик в заданные интервалы значений.
| АНОХИНА Н.Ю | |||
| и др., Компьютерное конструирование наполненной полимерной композиции с требуемыми деформационно-прочностными свойствами, Механика композиционных материалов и конструкций, 2009, т.15, N4, с | |||
| Динамометрическая втулка | 1921 |
|
SU600A1 |
| Анисимов И.И | |||
| и др., Разработка расчетно-экспериментальных методов оптимизации механических характеристик высокоэнергетических материалов и конструкций, Механика композиционных материалов и конструкций, 2011, т.17, N3, с.293-305 | |||
| ЗЕДГИНИДЗЕ И.Г., Планирование эксперимента для исследования многокомпонентных систем, Москва, НАУКА, 1976, с | |||
| Поливное приспособление для паровозов | 1922 |
|
SU390A1 |
| RU 2013101191 A, 20.07.2014. | |||
Авторы
Даты
2018-10-04—Публикация
2015-09-28—Подача