Изобретение относится к медицине и предназначено для определения упругих свойств биологических тканей.
Известен способ определения упругости артерий - измерение скорости распространения пульсовой волны (сфигмометрия), основанный на графическом исследовании механических колебаний артериальной стенки, возникающих при прохождении пульсовой волны [1]. Однако при этом существует возможность определять упругость лишь сосудистой стенки и только прижизненно, но таким способом невозможно определять упругость других биологических тканей - связок, апоневрозов и т.п.
Целью изобретения является разработка способа определения упругих свойств биологических тканей.
Цель изобретения достигается тем, что производят прямые измерения зависимости абсолютного удлинения исследуемых образцов биологической ткани под действием дискретно возрастающей силы с последующим преобразованием экспериментальных данных в аналитические выражения с использованием общей аппроксимирующей функции, производная от которой является выражением для расчета упругости образцов.
Способ осуществляется следующим образом.
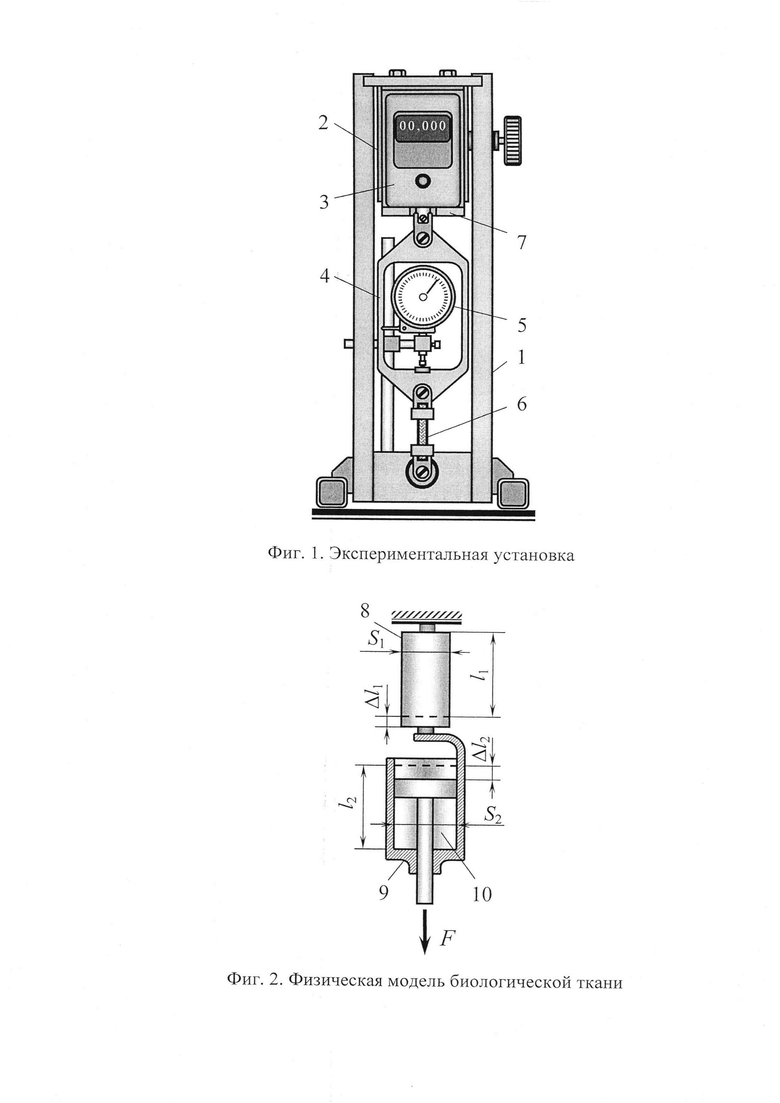
Измерения зависимости абсолютного удлинения образцов под действием дискретно возрастающей силы F проводятся на специально спроектированной установке (фиг. 1), состоящей из жесткой рамы 1, силового механизма 2, динамометра 3, тяги 4, и индикатора линейных перемещений 5.
Силовой механизм 2, установленный на верхней перекладине рамы 1, оснащен редуктором, позволяющим обеспечивать плавное перемещение его платформы 7 в вертикальной плоскости. Измерение силовой нагрузки, подводимой к исследуемому образцу, осуществляется с помощью цифрового динамометра 3, жестко закрепленного на платформе силового механизма.
Кинематическая связь динамометра 3 с исследуемым образцом 6 осуществляется с помощью тяги 4. Индикатор линейных перемещений 5, установленный в проеме тяги 4, представляет собой рычажно-зубчатую многооборотную измерительную головку 1 МИГ ГОСТ 9996-82.
В процессе исследований образцы 6 устанавливаются и закрепляются с помощью резьбового соединения между тягой 4 и нижней перекладиной рамы 1, после чего к нижнему срезу проема тяги подводится подвижный шток индикатора перемещений 5. Далее образцы подвергаются воздействию дискретно возрастающей силы F с фиксацией соответствующих абсолютных приращений их длины 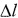 .
.
Последующая математическая обработка экспериментальных результатов заключается в преобразовании массива дискретных данных в аналитические зависимости вида:

где  и S - исходная длина и площадь поперечного сечения образцов соответственно.
и S - исходная длина и площадь поперечного сечения образцов соответственно.
Процесс преобразования осуществляется с использованием общей аппроксимирующей функции, наиболее полно отражающей упругие свойства большинства биологических тканей: достаточно быстрый рост относительных приращений длины 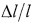 на начальном участке соотношения (1) и их последующее снижение с плавным переходом к практически линейной зависимости от величины механического напряжения F/S.
на начальном участке соотношения (1) и их последующее снижение с плавным переходом к практически линейной зависимости от величины механического напряжения F/S.
Такая реакция образцов сопоставима с реакцией физической модели (фиг. 2), состоящей из двух, соединенных последовательно элементов: упругого стержня 8 и цилиндра 9, под поршнем которого находится идеальный газ 10.
Полное абсолютное приращение длины такой модели, обусловленное воздействием внешней силы F, определяется выражением:

где 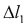 и
и 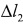 - абсолютные приращения длины стержня и цилиндра с поршнем соответственно.
- абсолютные приращения длины стержня и цилиндра с поршнем соответственно.
В случае стержня, сила растяжения F вызывает приращение длины:

где Е - модуль упругости стержня или модуль Юнга; 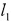 и S1 - исходная длина стержня и площадь его поперечного сечения соответственно.
и S1 - исходная длина стержня и площадь его поперечного сечения соответственно.
Согласно уравнению (3), величина абсолютных приращений стержня находится в прямой пропорциональной зависимости от механического напряжения F/S1, что обеспечивает линейный характер зависимости (1)
при больших силовых нагрузках.
Что касается цилиндра, то в исходном состоянии давление газа под поршнем равно внешнему давлению Р0. Под действием внешней силы F смещение поршня вниз приведет к увеличению давления на величину ΔP=F/S2 и, следовательно, будет составлять:

Для идеального газа при постоянной температуре справедливо следующее соотношение:

где 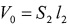 - исходный объем газа;
- исходный объем газа; 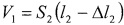 - объем газа при смещении поршня на величину
- объем газа при смещении поршня на величину 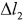 .
.
Из совместного решения уравнений (4) и (5) получаем:
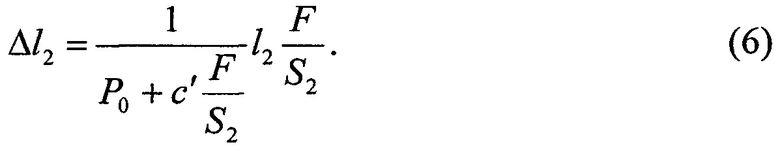
Существенно нелинейный характер данной зависимости обеспечивает относительно высокие значения абсолютных приращений длины при малых силовых нагрузка. С ростом механического напряжения величина приращений стремится к насыщению, асимптотически приближающийся к постоянному значению 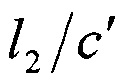 . Искусственно введенный безразмерный коэффициент с' характеризует максимально возможный уровень приращений относительно значения исходной длины
. Искусственно введенный безразмерный коэффициент с' характеризует максимально возможный уровень приращений относительно значения исходной длины 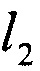 .
.
Чтобы привести в соответствие размеры принятой модели с геометрией образцов, запишем:
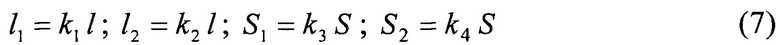
где k1, k2, k3 и k4 - некоторые постоянные безразмерные коэффициенты. В частности, коэффициенты k1 и k2 учитывают какую часть длина стержня 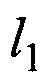 и цилиндра с поршнем
и цилиндра с поршнем 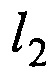 составляют от длины образца
составляют от длины образца  . Коэффициенты k3 и k4 учитывают какую часть площадь сечения стержня S1 и цилиндра S2 составляют от площади сечения образца S.
. Коэффициенты k3 и k4 учитывают какую часть площадь сечения стержня S1 и цилиндра S2 составляют от площади сечения образца S.
Подстановка соотношений (3) и (6) с учетом (7) в уравнение (2) приводит к выражению:
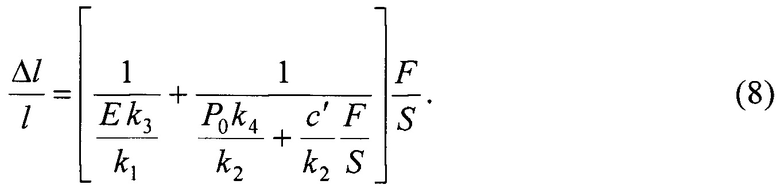
Поскольку величины Е и Р0 для конкретного образца являются константами, введем новые обозначения:
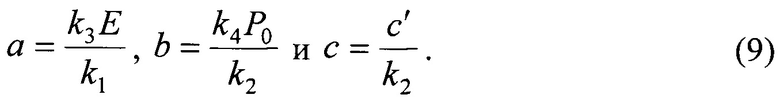
С учетом (9) общая аппроксимирующая функция (8) окончательно принимает вид:
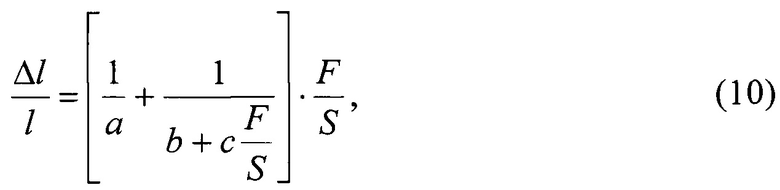
Далее отметим, что согласно определению понятия упругости α, ее численное значение равно тангенсу угла наклона касательной к зависимости (10) и, следовательно, определяется выражением:
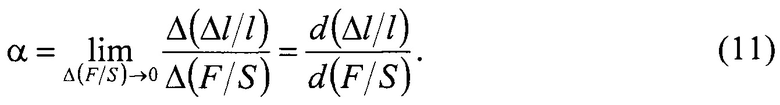
После дифференцирования уравнения (10), выражение для расчета коэффициента упругости (м2/Н) принимает вид:
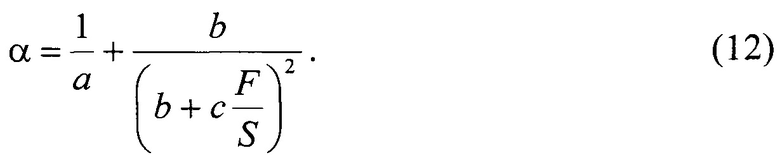
Таким образом, упругие свойства конкретного образца однозначно определяются значениями соответствующих ему коэффициентов а, b и с.
Как следует из (12), упругость биологических тканей зависит от прилагаемой силовой нагрузки и, следовательно, не имеет статуса константы. Поэтом можно говорить о ее исходном значении α0 как о некотором пределе, к которому стремится упругость α при малых силовых нагрузках, то есть при F/S→0. В этом случае уравнение (12) сводится к виду:
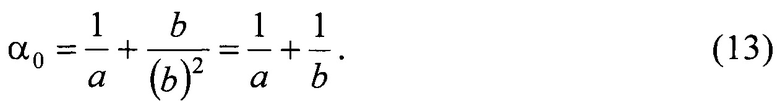
Согласно (9), константа с является безразмерной величиной. Чтобы пояснить смысл коэффициентов а и b воспользуемся общеизвестным законом Гука:

Отсюда следует, что упругость равна обратной величине модуля Юнга,

Сравнивая это соотношение с формулой (13), видно, что применительно к биологическим тканям константы а и b имеют размерность (F/S) и смысл модуля Юнга.
Обработка экспериментальных данных осуществляется следующим образом. Допустим, что под действием дискретно возрастающей силы F1, F2 и F3 абсолютное удлинение образца составило 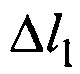 ,
, 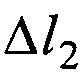 и
и 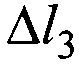 соответственно. В результате этого получаем систему, состоящую из следующих уравнений:
соответственно. В результате этого получаем систему, состоящую из следующих уравнений:
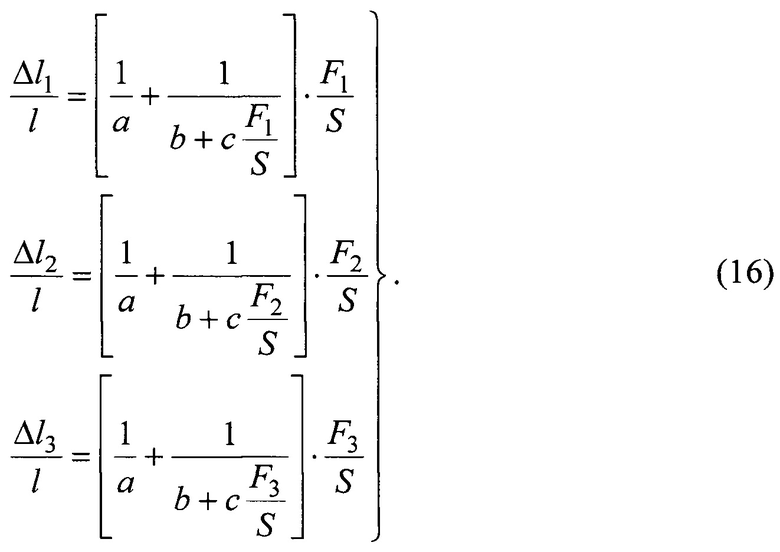
Здесь все величины кроме коэффициентов а, b и с известны. Поэтому перепишем первое уравнение относительно коэффициента а и подставим его во второе уравнение. Далее перепишем второе уравнение относительно коэффициента b и подставим его в третье уравнение. Из решения третьего уравнения получаем значение коэффициента с. После этого, проводя операцию вычислений в обратной последовательности, определяем значения коэффициентов b и а. Затем по формулам (12) и (13) рассчитываем значения α и α0.
Эта процедура достаточно трудоемка, поэтому в случае большого числа образцов, вычисления целесообразно производить в пакете расширения Curve Fitting Toolbox вычислительной среды Matlab. В этом случае, дополнительно к значениям искомых коэффициентов получаем величину достоверности аппроксимации экспериментальных данных с помощью соотношения (10).
Предлагаемый способ определения упругости, основанный на математической обработке результатов прямых измерений зависимости абсолютного удлинения исследуемых образцов под действием дискретно возрастающей силы, позволяет с высокой точностью определять упругость различных биологических тканей, а также динамику ее изменения в зависимости от изменения силовой нагрузки или степени удлинения, в клинической и экспериментальной медицине.
Источник информации:
1. Asmar R. Pulse wave velocity as endpoint in large-scale intervention trial. The Complior study / R. Asmar, J. Topouchian, B. Pannier [et al.] // J. Hypertens. - 2001. - Vol. 19, №4. - P. 813-818.
.
Изобретение относится к медицине. Способ основан на математической обработке результатов прямых измерений зависимости абсолютного удлинения исследуемых образцов под действием дискретно возрастающей силы с использованием общей аппроксимирующей функции:
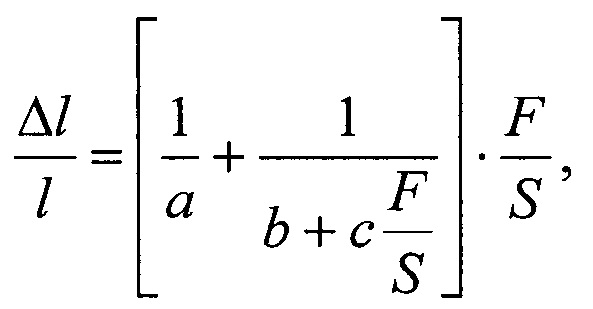
где Δl - абсолютное удлинение образца, l и S - исходная длина и площадь поперечного сечения образцов соответственно, F - прилагаемая сила. Исходя из численных значений коэффициентов a, b и с, характеризующих свойства исследуемых образцов, расчет коэффициента упругости α (м2/Н) производится по формуле:
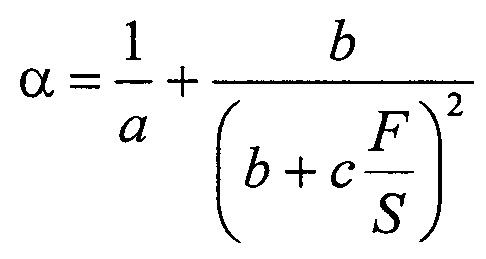
Достигается возможность с высокой точностью определять упругость различных биологических тканей, а также динамику ее изменения в зависимости от изменения силовой нагрузки или степени удлинения, в клинической и экспериментальной медицине. 2 ил.
Способ определения упругости биологических тканей, отличающийся тем, что производят прямые измерения зависимости абсолютного удлинения 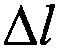 исследуемых образцов под действием дискретно возрастающей силы F с последующим преобразованием экспериментальных данных в аналитические выражения в виде общей аппроксимирующей функции:
исследуемых образцов под действием дискретно возрастающей силы F с последующим преобразованием экспериментальных данных в аналитические выражения в виде общей аппроксимирующей функции:
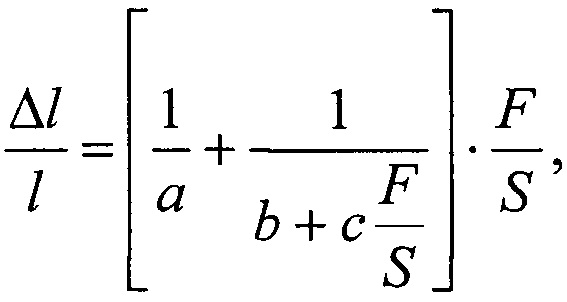
где 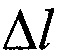 - абсолютное удлинение образца,
- абсолютное удлинение образца,  и S - исходная длина и площадь поперечного сечения образцов соответственно, F - прилагаемая сила, и далее, по установленным численным значениям коэффициентов a, b и c, характеризующих свойства исследуемых образцов, рассчитывается их коэффициент упругости (м2/Н) по формуле:
и S - исходная длина и площадь поперечного сечения образцов соответственно, F - прилагаемая сила, и далее, по установленным численным значениям коэффициентов a, b и c, характеризующих свойства исследуемых образцов, рассчитывается их коэффициент упругости (м2/Н) по формуле:
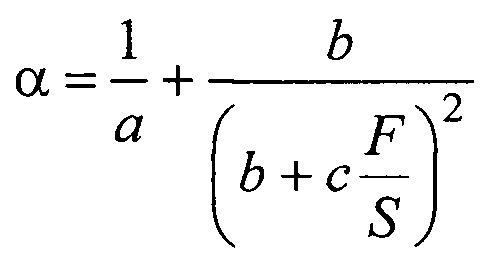 .
.
| СПОСОБ ИЗГОТОВЛЕНИЯ ОБРАЗЦОВ БИОЛОГИЧЕСКИХ ТКАНЕЙ В КОМПЛЕКСЕ С ИМПЛАНТИРОВАННЫМИ ЭЛЕМЕНТАМИ ДЛЯ ИССЛЕДОВАНИЯ СВЕТОВОЙ МИКРОСКОПИЕЙ | 2014 |
|
RU2564895C1 |
| Способ определения механических свойств биологических мягких тканей | 1987 |
|
SU1644029A1 |
| Устройство для определения жесткости и упругости эластичных материалов | 1990 |
|
SU1803778A1 |
| СПОСОБ ДИАГНОСТИКИ СОСТОЯНИЯ КОЖИ ПАЦИЕНТА (ВАРИАНТЫ) | 2011 |
|
RU2466680C1 |
| УСТРОЙСТВО ДЛЯ РЕГИСТРАЦИИ УПРУГО-ВЯЗКИХ СВОЙСТВ БИОЛОГИЧЕСКИХ ТКАНЕЙ | 1972 |
|
SU420928A1 |
| US 9330461 B2, 03.05.2016 | |||
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
Авторы
Даты
2018-10-23—Публикация
2016-06-21—Подача