Изобретение относится к измерительной технике, в частности - к измерениям теплофизических свойств материалов, которые эксплуатируются в области высоких температур, где свойства имеют ярко выраженную зависимость от температуры. Изобретение предназначено для изучения свойств электропроводных материалов, применяемых в энергетике, авиационно-космической, химической и других отраслях промышленности.
Наиболее распространенными способами измерения температурной зависимости коэффициента теплопроводности электропроводных материалов при высоких температурах являются способы, основанные на разогреве исследуемого образца постоянным электрическим током. Из них близкими по сути к предлагаемому являются следующие способы.
Известен способ определения температурной зависимости коэффициента теплопроводности твердых изотропных электропроводящих материалов, включающий нагрев образцов пропусканием постоянного тока по двум полым цилиндрическим образцам с разной толщиной стенки, измерение значений силы тока, падения напряжения и истинной температуры внутренней поверхности для каждого цилиндра, построение зависимостей плотности теплового потока с единицы поверхности от температуры и определение истинных температур внутренней поверхности двух полых цилиндрических образцов при одинаковых значениях плотностей тепловых потоков, определение в первом приближении зависимости коэффициента теплопроводности от температуры, представление ее в виде линейной функции, дополнительное определение по падению напряжения и силе тока зависимости коэффициента удельного электрического сопротивления от температуры отнесения, использование полученных зависимостей при численном решении стационарного нелинейного дифференциального уравнения теплопроводности с внутренними источниками теплоты, зависящими от температуры, для выбранных значений силы тока и истинной температуры внутренней поверхности одного из двух полых цилиндрических образцов, нахождение реального распределения температуры по толщине цилиндрической стенки, определение на его основе уточненного значения коэффициента теплопроводности и температуры отнесения, окончательное определение температурной зависимости коэффициента теплопроводности в изучаемой области температур (Патент РФ №2419782, МПК G01N 25/18, опубл. 27.05.11).
Также известен способ определения температурной зависимости коэффициента теплопроводности твердых, изотропных электропроводящих материалов, включающий нагрев постоянным током двух полых цилиндрических образцов с разной толщиной стенки, измерение на изотермических участках заданной длины силы тока, падения напряжения, истинной температуры внутренней поверхности, построение зависимостей плотностей теплового потока от температуры, определение соответствующих температур внутренней поверхности двух полых цилиндрических образцов и расчет значения коэффициента теплопроводности (Петров В.А. Излучательная способность высокотемпературных материалов. Москва: Наука, 1969 г., стр. 28). Уравнение измерения способа основано на совместном решении стационарных линейных дифференциальных уравнений теплопроводности с постоянно действующими внутренними источниками теплоты для двух полых цилиндров различной толщины.
Общие недостатки перечисленных способов заключаются в том, что в них либо используются простые аналитические решения уравнения теплопроводности, либо решаются дифференциальные уравнения, в которых учитываются функциональные зависимости свойств исследуемого материала от температуры, решения которых могут быть получены только численными методами. Это снижает достоверность получаемых результатов и неизбежно приводит к потере точности. Кроме того ни в одном из известных способов не приводится оценка ожидаемой неопределенности измерений.
Наиболее близким по сути к предлагаемому является способ (прототип) способ определения коэффициента теплопроводности λ (Пелецкий В.Э., Тимрот Д.Л., Воскресенский В.Ю. Высокотемпературные исследования тепло- и электропроводности твердых тел, Москва: Энергия, 1971 г., стр. 89), включающий нагрев постоянным током одного толстостенного образца в виде цилиндрической трубки с радиусами R и r, измерение на изотермическом участке длиной L силы тока I, падения напряжения U, истинной температуры внутренней поверхности полого цилиндрического образца Т и определение коэффициента теплопроводности. В качестве первого приближения для определения среднего в интервале температур (T2-Т1) коэффициента λ используется выражение, отвечающее решению задачи теплопроводности через цилиндрическую стенку с внутренними источниками теплоты qv=const и при постоянных свойствах материала:
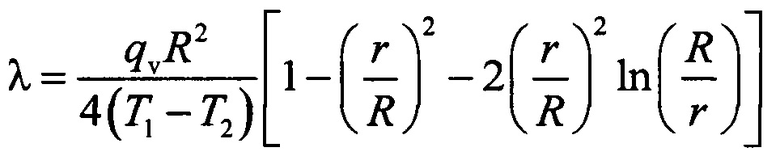
где qv=4IU/π(R2-r2)L.
Во втором приближении для определения окончательных значений коэффициента теплопроводности и температуры отнесения используются линейные зависимости коэффициентов теплопроводности и удельного электрического сопротивления от температуры, полученные в первом приближении, а температурное распределение по радиусу цилиндрического образца находится расчетным путем.
Недостатком данного способа является то, что для второго приближения используется аналитическое выражение, которое получено при допущении, что внутренний радиус полого образца равен нулю (r=0), - это эквивалентно сплошному цилиндру, в то время как эксперимент проводится на полом цилиндрическом образце. Соответствующие ряды уравнения для второго приближения для полых цилиндрических образцов с увеличением внутреннего радиуса сходятся все медленнее, что снижает точность способа, так как усложняет задачу отыскания локальных значений исследуемых параметров. Применение выбранного аналитического решения диктует необходимость использования в эксперименте толстостенных образцов, что приводит к большим перепадам температуры по радиусу образца, что также понижает точность определения локальных значений коэффициента теплопроводности. Другим недостатком способа является ограничение на использование только линейной зависимости свойств теплопроводности и удельного электрического сопротивления от температуры, что дополнительно снижает точность определения коэффициента теплопроводности.
Технический результат, достигаемый от применения предлагаемого способа - повышение точности измерений.
Указанный результат достигается тем, что в предлагаемом способе измерения температурной зависимости коэффициента теплопроводности электропроводящих материалов при высоких температурах, образец выполняют в виде тонкой ленты, при этом длину и ширину ленты выбирают исходя из заданной точности и пространственного разрешения бесконтактного средства измерения температуры, толщину ленты выбирают таким образом, чтобы площадь поперечного сечения ленты была так много меньше площади поперечного сечения токоподводов, чтобы обеспечивался максимальный градиент температуры по длине образца не меньший, чем 10 К/мм, закрепляют образец между токоподводами так, чтобы плоскость ленты была ориентирована горизонтально, помещают образец и токоподводы в герметичную камеру с инертным газом, при этом стенки камеры выполняют прозрачными для излучения на рабочей длине волны бесконтактного средства измерения температуры, нагревают образец постоянным электрическим током до заданной температуры, измеряют стационарное распределение температуры вдоль образца с помощью бесконтактного средства измерения температуры, измеряют силу тока, протекающего через образец, изменяют направление постоянного тока через образец на противоположное, измеряют стационарное распределение температуры вдоль образца при противоположном направлении тока, по измеренным распределениям температуры графическим способом находят координату сечения образца, для которой с заданной точностью выполняется условие равенства градиентов температуры полученных распределений температуры, находят значение указанных градиентов, рассчитывают температурный коэффициент теплопроводности материала образца по соотношению
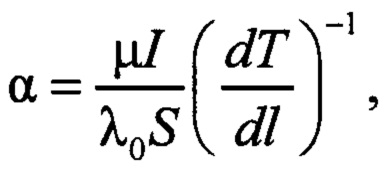
а температурную зависимость коэффициента теплопроводности находят по соотношению
λ(Т)=λ0(1+α(Т-Т0)),
где
α - температурный коэффициент теплопроводности материала образца,
λ0(Т0) - теплопроводность образца при температуре Т0,
Т0 - опорная температура, для которой значение теплопроводности материала образца известно точно и измерено другими способами,
λ(Т) - теплопроводность образца при температуре Т>Т0,
μ - коэффициент Томсона материала образца,
I - сила постоянного электрического тока, проходящего через образец,
S - площадь поперечного сечения ленты образца,
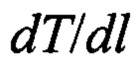 - измеренный температурный градиент.
- измеренный температурный градиент.
В другом варианте предлагаемого способа измерения выполняют для нескольких значений заданной температуры образца, для каждой заданной температуры выполняют расчет температурного коэффициента теплопроводности, находят аппроксимирующую математическую зависимость температурного коэффициента теплопроводности от температуры, а температурную зависимость коэффициента теплопроводности находят расчетным путем по соотношению

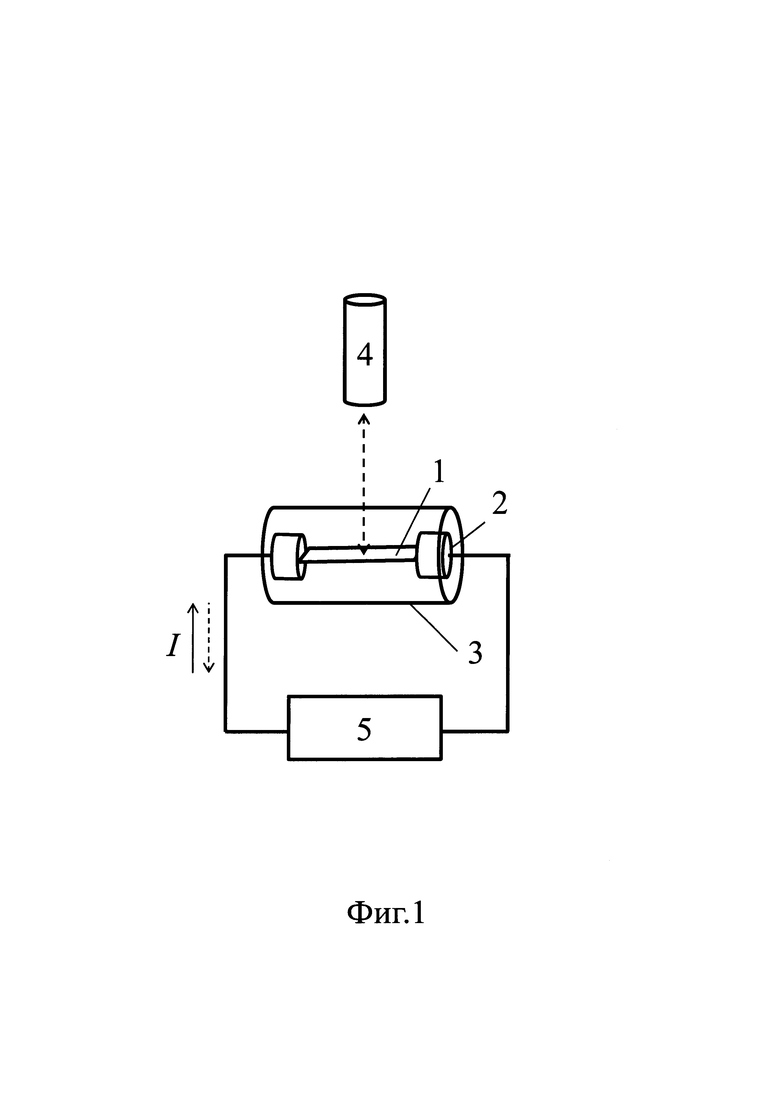
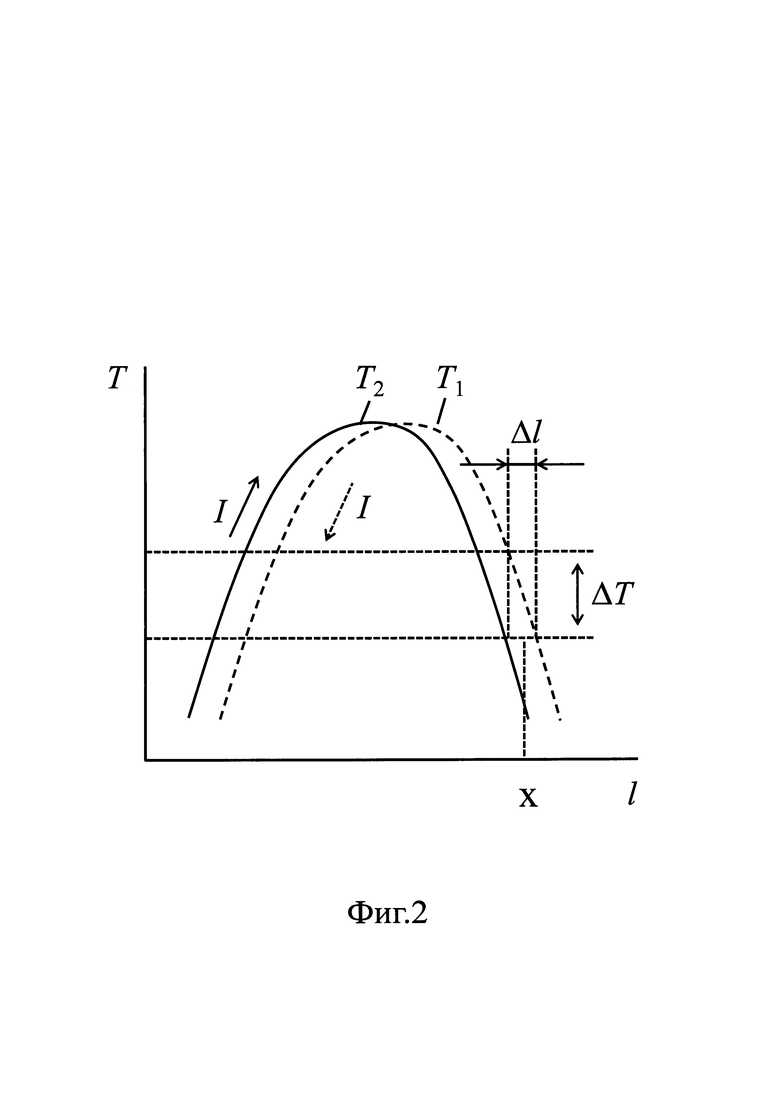
Сущность способа поясняется фигурами 1, 2. На фиг. 1 представлена структурная схема устройства для реализации способа, где: 1 - исследуемый образец. 2 - токоподводы, 3 - герметичная камера с инертным газом. 4 - бесконтактное средство измерения температуры, 5 - источник постоянного тока. На фиг. 2 представлен пример распределения температуры вдоль образца 1 (ленты) при различных направлениях электрического тока в нем, а также - параметры, входящие в уравнение измерения.
Сущность способа заключается в следующем.
Способ базируется на уравнении в частных производных, описывающем поток тепла в цилиндрическом проводнике (Поуэлл Р. Наиболее важные достижения в изучении теплопроводности металлов // Успехи физических наук, 1971, т. 105, вып. 2. - С. 329-351):
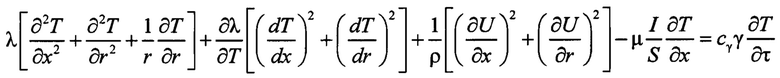
где
λ - теплопроводность образца,
х, r - осевая и радиальная координаты, соответственно,
ρ - удельное электрическое сопротивление,
μ - коэффициент Томсона,
I - сила тока,
U - электрический потенциал, напряжение,
S - площадь поперечного сечения образца,
сγ - удельная теплоемкость,
γ - плотность образца.
Для длинного и тонкого образца оно сводится к уравнению:
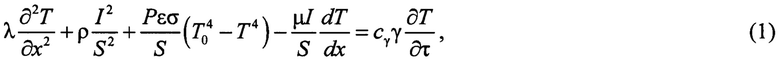
где σ=5,67⋅10-8 Вт/(м2⋅К4) - постоянная Стефана-Больцмана, P - периметр образца, м; ε - коэффициент излучения образца. В заявляемом способе, в противоположность известным способам, где теплотой Томсона пренебрегается, предлагается использовать данный эффект Томсона для нахождения искомой теплопроводности. Суть эффекта Томсона заключается в том, что на участке проводника длиной 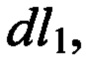 находящемся в градиенте температур
находящемся в градиенте температур 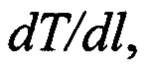 при прохождении постоянного электрического тока I в зависимости от его направления либо выделяется, либо поглощается теплота Томсона dQT (Яворский Б.М., Детлаф А.А. Справочник по физике. // Изд. 7-е, М.: Наука, 1977, 421 с.):
при прохождении постоянного электрического тока I в зависимости от его направления либо выделяется, либо поглощается теплота Томсона dQT (Яворский Б.М., Детлаф А.А. Справочник по физике. // Изд. 7-е, М.: Наука, 1977, 421 с.):

где
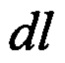 - длина участка проводника,
- длина участка проводника,
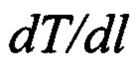 - градиент температуры по длине участка.
- градиент температуры по длине участка.
Для элемента испытуемого образца длиной 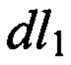 стационарный тепловой поток, проходящий через его поперечное сечение x, при питании переменным током, когда теплота Томсона не выделяется, равен:
стационарный тепловой поток, проходящий через его поперечное сечение x, при питании переменным током, когда теплота Томсона не выделяется, равен:

Стационарные тепловые потоки, переносимые через то же самое сечение х образца, при прохождении через образец постоянного тока различного направления, равны dQ1 и dQ2:

Тепловые потоки dQ1 и dQ2 отличаются от dQ0 на величину теплоты Томсона dQT, т.е.:
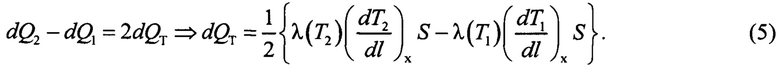
Если принять, что λ(T2)=λ(T1)+dλ, то уравнение (5) можно переписать в виде:
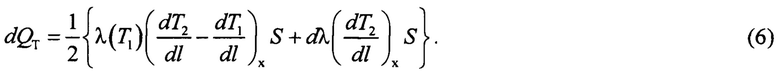
Экспериментально установлено, что, как в параболическом, так и в экспоненциальном распределениях температуры по длине образца на нем имеются участки, где с заданной точностью выполняется условие равенства градиентов 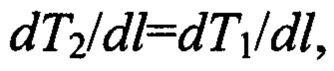 следовательно, для таких участков образца уравнение (6) принимает вид:
следовательно, для таких участков образца уравнение (6) принимает вид:
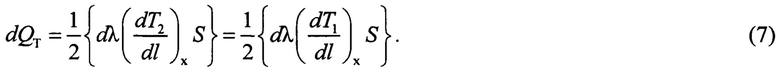
Совместное решение уравнений (7), (2) дает соотношение для приращения теплопроводности dλ, соответствующего приращению температуры ΔТ=Т1-T2, (фиг. 2):

но поскольку на рассматриваемом участке градиенты температуры равны 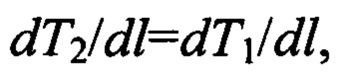 то выражение (8) принимает вид:
то выражение (8) принимает вид:

Введем в рассмотрение температурный коэффициент теплопроводности α, который, согласно определению, вычисляется по известной формуле:

где
λ0 - теплопроводность материала образца при некоторой взятой температуре T0. Отношение приращения теплопроводности dλ к соответствующему изменению температуры ΔТ=Т1-Т2 есть производная от теплопроводности по температуре на данном уровне температур ΔT=(T1+T2)/2. При этом при воздействии двух теплот Томсона температурное распределение в сечении х образца смещается на величину 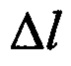 (фиг. 2), следовательно, при действии одной теплоты Томсона - смещение составит
(фиг. 2), следовательно, при действии одной теплоты Томсона - смещение составит 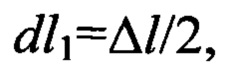 поэтому выражение (10), с учетом (9) и изложенного выше, примет вид:
поэтому выражение (10), с учетом (9) и изложенного выше, примет вид:

Используя уравнение (11) можно рассчитать значение теплопроводности образца при заданной температуре T двумя способами:
- первый способ используется для материалов, у которых зависимость коэффициента теплопроводности от температуры носит линейный характер, в этом случае уравнение измерения имеет вид:

Для этого случая достаточно выполнить измерения температурного коэффициента теплопроводности при одной заданной температуре, как указано в п. 1 формулы изобретения.
- второй способ (п. 2 формулы) используется для материалов, у которых зависимость коэффициента теплопроводности от температуры носит нелинейный характер, в этом случае уравнение измерения имеет вид:

Для этого случая в заданном температурном диапазоне необходимо выполнить измерения температурного коэффициента теплопроводности при нескольких заданных температурах и найти его математическую зависимость от температуры. Искомое значение теплопроводности при заданной температуре Т находится путем интегрирования, как показано в уравнении (13).
Таким образом, способ измерения сводится к определению температурного коэффициента теплопроводности α либо его температурной зависимости α(Т) по формуле (11). Параметры, входящие в (11), являются величинами, определяемыми с достаточно высокой точностью.
Оценка неопределенности измерений. Расчетное соотношение неопределенности измерения температурного коэффициента теплопроводности а для косвенных измерений получено из уравнения измерения (11) и имеет вид:
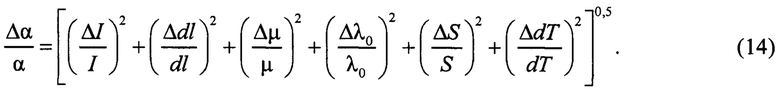
Расчетное соотношение неопределенности измерения коэффициента теплопроводности λ для косвенных измерений получено из уравнения измерения (12) и имеет вид:
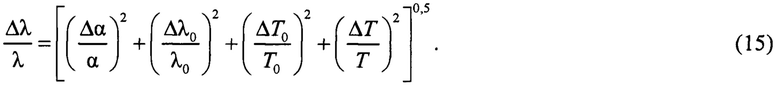
Пример расчета неопределенности измерений. Для расчета взяты следующие экспериментальные данные. λ0=162,8 Вт/(м⋅К) - теплопроводность вольфрама при температуре T0=300 К известна с относительной неопределенностью Δλ/λ≈0,06; μ(T) - коэффициент Томсона - с относительной неопределенностью Δμ/μ≈0,03 (Рудницкий А.А. Термоэлектрические свойства благородных металлов и их сплавов. // М.: АН СССР, 1956, с. 18-20, с. 36-132); I - сила тока, измерена с относительной неопределенностью ΔI/I≈0,001; 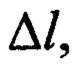 S, Т - с относительными неопределенностями ≈ 0,01; 0,001; 0,002, соответственно. Суммарная неопределенность α(T), рассчитанная по соотношению (14) составляет ~6,8%. Относительная неопределенность λ(Т), рассчитанная по соотношению (15) составляет ~9,1%. Данный результат превосходит известные аналоги и прототип. Следует заметить, что погрешность определения данного параметра другими известными способами достигает 70% (Пелецкий В.Э., Тимрот Д.Л., Воскресенский В.Ю. Высокотемпературные исследования тепло- и электропроводности твердых тел. // М.: Энергия, 1971, 182 с.).
S, Т - с относительными неопределенностями ≈ 0,01; 0,001; 0,002, соответственно. Суммарная неопределенность α(T), рассчитанная по соотношению (14) составляет ~6,8%. Относительная неопределенность λ(Т), рассчитанная по соотношению (15) составляет ~9,1%. Данный результат превосходит известные аналоги и прототип. Следует заметить, что погрешность определения данного параметра другими известными способами достигает 70% (Пелецкий В.Э., Тимрот Д.Л., Воскресенский В.Ю. Высокотемпературные исследования тепло- и электропроводности твердых тел. // М.: Энергия, 1971, 182 с.).
Для осуществления способа необходимо, чтобы образец имел геометрические размеры, которые обеспечат с заданной точностью измерение температурной зависимости теплопроводности. Выбор геометрических размеров образца, главным образом, зависит от технических характеристик применяемого бесконтактного средства измерения температуры, таких как - пространственное разрешение и температурная чувствительность. В качестве такого средства измерения, может быть использован, например, тепловизор. Возьмем тепловизор «FLIR SC2500», спектральный диапазон длин волн λ=0,4-1,7 мкм, температурная чувствительность δT=25 мК, диапазон измеряемых температур T=400-3000°С, размер приемной матрицы dm=0,02 м (320×256 пикселей), размер пикселя Δ1=30 мкм, угловое поле зрения FOV=12×160, фокусное расстояние объектива тепловизора F=0,5 м. Пространственное разрешение тепловизора на расстоянии визирования L=1 м рассчитывается по соотношению:
δx=NDdmL/(Nx⋅F),
где
dm/(NxF) - угловое разрешение тепловизора, приходящееся на один пиксельный элемент. Пространственное разрешение тепловизора на расстоянии визирования L=1 м, рассчитанное исходя из значения критерия Джонсона, равного количеству пикселей ND=16, составляет δx=0,002 м или δх=2 мм. Значение критерия Джонсона выбрано равным ND=16 согласно рекомендациям, данным в литературе (Dulnev G.N., Pokhodun A.I., Khodunkov V.P. A thermal analysis of quality of infrared images of distant low-contrast objects // Measurement Techniques. 2013. Vol. 56. №3. P. 289-296).
Исходя из рассчитанного значения δх=2 мм ширина ленты образца должна быть не менее 2 мм, при этом обеспечивается степень достоверности измерений температуры, равная 95%. Длина ленты совместно площадью ее поперечного сечения должна обеспечить градиент температуры по длине ленты не меньший 10 К/мм. При градиенте 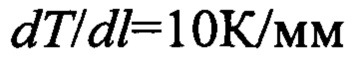 при смещении температурного распределения на
при смещении температурного распределения на 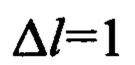 мм соответствующая разность температуры составит ΔT=10 К. При температурной чувствительности тепловизора δT=25 мК неопределенность измерений температуры составит ±δT/ΔT=0,0025 отн. ед. или 0,25%. Подбор требуемой толщины и длины ленты осуществляют экспериментальным путем, при этом толщину ленты выбирают всегда много меньшей толщины токоподводов.
мм соответствующая разность температуры составит ΔT=10 К. При температурной чувствительности тепловизора δT=25 мК неопределенность измерений температуры составит ±δT/ΔT=0,0025 отн. ед. или 0,25%. Подбор требуемой толщины и длины ленты осуществляют экспериментальным путем, при этом толщину ленты выбирают всегда много меньшей толщины токоподводов.
Образец между токоподводами устанавливают строго горизонтально. Это необходимо для обеспечения более симметричного температурного распределения вдоль образца (при этом максимально исключается влияние вертикальной конвекции на температурное распределение). Установка образца в герметичную камеру с инертным газом, например с высокочистым аргоном, исключает испарение материала образца при высоких температурах и обеспечивает более высокий диапазон температурных измерений. При этом должно соблюдаться условие, чтобы стенки камеры были прозрачными для спектрального диапазона применяемого бесконтактного средства итзмерения температуры. В рассмотренном примере с тепловизором данный диапазон должен находиться в пределах λ=0,4-1,7 мкм.
Пример осуществления способа.
Согласно предложенному способу была измерена температурная зависимость коэффициента теплопроводности вольфрама. Образец был выполнен в виде ленты с габаритными размерами 20×2×0,03 мм, диаметр токоподводов составлял ∅2 мм. Образец и токоподводы были запаяны в герметичную колбу из кварцевого стекла. Нагрев образца производился от стабилизированного источника постоянного тока. При измерениях выполнялись следующие операции:
- измерения стационарного температурного поля вдоль ленты при одном направлении тока через образец;
- измерения стационарного температурного поля вдоль ленты при противоположном направлении тока через образец.
В качестве бесконтактного средства измерения температуры использовался пирометр с исчезающей нитью. В результате для вольфрама для диапазона температуры 1100-1700 К экспериментально получено постоянное значение температурного коэффициента теплопроводности α=6,71⋅10-5 К-1 и соответствующее ему расчетное соотношение для температурной зависимости коэффициента теплопроводности (согласно п. 1 формулы изобретения):
λ(Т)=λ0(1+α(T-T0))=115(1-6,71⋅10-5(T-1100)),
при этом значение коэффициента теплопроводности вольфрама λ0(T0)=115 Вт/(м⋅К) взято для температуры T0=1100 К (Зиновьев В.Е. Теплофизические свойства металлов при высоких температурах. Справ. изд., М.: Металлургия, 1989. - 384 с.).
Способ применим для электропроводящих материалов, которые имеют выраженную зависимость коэффициента теплопроводности от температуры. Одно из главных преимуществ способа - его реализуемость в стационарных условиях, что отвечает максимальному приближению к реальным условиям работы высокотемпературных материалов.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения коэффициента теплопроводности при температурах до 2800 К полупроводниковых, композиционных материалов | 2020 |
|
RU2748985C1 |
| Способ определения температуропроводности и коэффициента теплопроводности | 2022 |
|
RU2785084C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ТВЕРДЫХ ИЗОТРОПНЫХ ЭЛЕКТРОПРОВОДЯЩИХ МАТЕРИАЛОВ | 2009 |
|
RU2419782C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОПРОВОДНОСТИ ТВЕРДОГО ТЕЛА АКТИВНЫМ МЕТОДОМ ТЕПЛОВОГО НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ | 2012 |
|
RU2488102C1 |
| СПОСОБ ТЕПЛОВОГО НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ РАБОЧЕГО ТЕЛА | 2008 |
|
RU2379668C1 |
| Способ определения теплофизических свойств веществ при химической реакции | 2025 |
|
RU2841507C1 |
| Способ определения теплофизических свойств веществ в области фазовых переходов | 2024 |
|
RU2830045C1 |
| СПОСОБ КОМПЛЕКСНОГО ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 2003 |
|
RU2243543C1 |
| СПОСОБ ТЕПЛОВОГО КОНТРОЛЯ ОСТАТОЧНЫХ НАПРЯЖЕНИЙ И ДЕФЕКТОВ КОНСТРУКЦИЙ | 2007 |
|
RU2383009C2 |
| СПОСОБ НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ СТЕПЕНИ ИСЧЕРПАНИЯ ЗАЩИТНЫХ СВОЙСТВ ФИЛЬТРУЮЩЕ-ПОГЛОЩАЮЩИХ ИЗДЕЛИЙ | 2014 |
|
RU2561014C1 |
Изобретение относится к измерительной технике, в частности - к измерениям теплофизических свойств материалов, которые эксплуатируются в области высоких температур, где свойства имеют ярко выраженную зависимость от температуры. Сущность изобретения заключается в том, что для получения температурной зависимости теплопроводности измеряют температурный коэффициент теплопроводности исследуемого образца, при этом используют эффект Томсона, а искомую теплопроводность находят расчетным путем. Технический результат – повышение точности измерений. 1 з.п. ф-лы, 2 ил.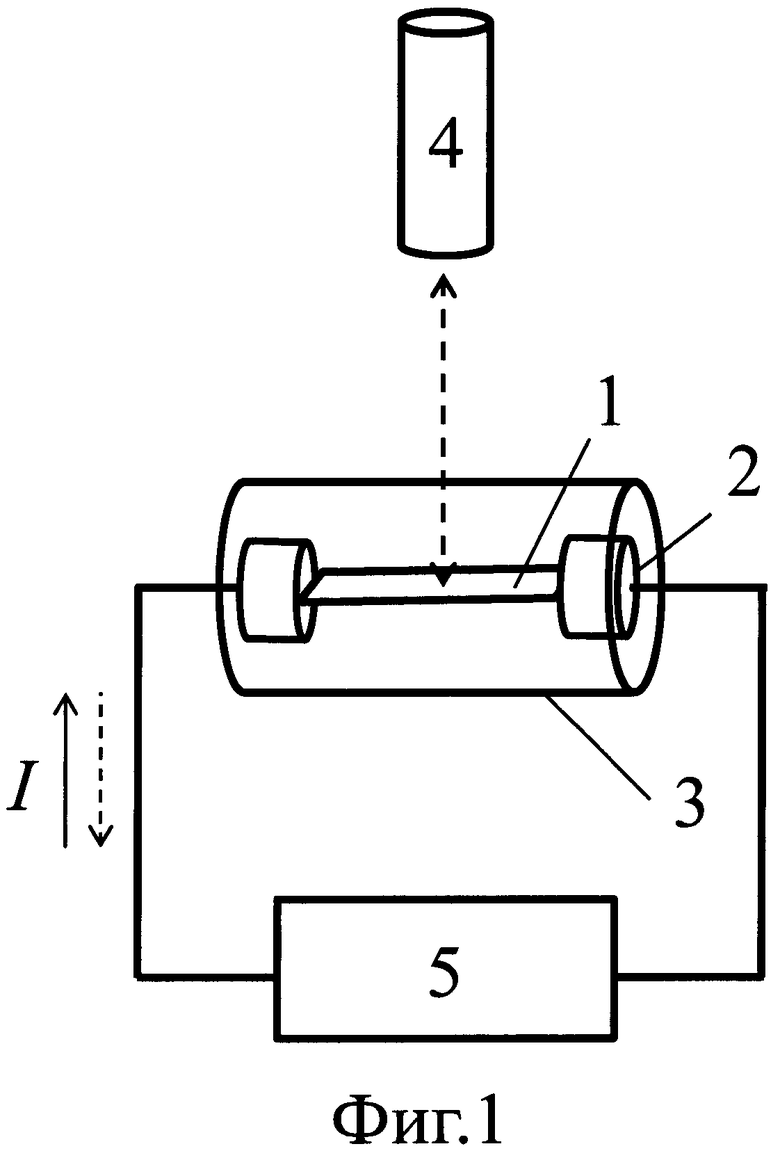
1. Способ измерения температурной зависимости коэффициента теплопроводности электропроводящих материалов при высоких температурах, заключающийся в том, что образец выполняют в виде тонкой ленты, при этом длину и ширину ленты выбирают исходя из заданной точности и пространственного разрешения бесконтактного средства измерения температуры, толщину ленты выбирают таким образом, чтобы площадь поперечного сечения ленты была так много меньше площади поперечного сечения токоподводов, чтобы обеспечивала максимальный градиент температуры по длине образца не меньший чем 10 K/мм, закрепляют образец между токоподводами так, чтобы плоскость ленты была ориентирована горизонтально, помещают образец и токоподводы в герметичную камеру с инертным газом, при этом стенки камеры выполняют прозрачными для излучения на рабочей длине волны бесконтактного средства измерения температуры, нагревают образец постоянным электрическим током до заданной температуры, измеряют стационарное распределение температуры вдоль образца с помощью бесконтактного средства измерения температуры, измеряют силу тока, протекающего через образец, изменяют направление постоянного тока через образец на противоположное, измеряют стационарное распределение температуры вдоль образца при противоположном направлении тока, по измеренным распределениям температуры графическим способом находят координату сечения образца, для которой с заданной точностью выполняется условие равенства градиентов температуры полученных распределений температуры, находят значение указанных градиентов, рассчитывают температурный коэффициент теплопроводности материала образца по соотношению
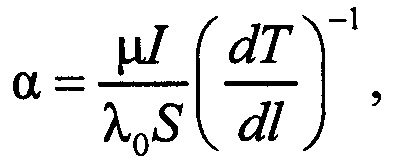
а температурную зависимость коэффициента теплопроводности находят по соотношению
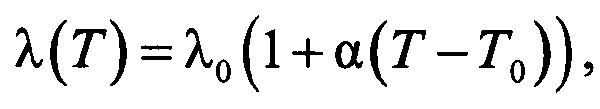
где
α - температурный коэффициент теплопроводности материала образца;
λ0(T0) - теплопроводность образца при температуре Т0;
Т0 - опорная температура, для которой значение теплопроводности материала образца известно точно и измерено другими способами;
λ(Т) - теплопроводность образца при температуре Т>Т0;
μ - коэффициент Томсона материала образца;
I - сила постоянного электрического тока, проходящего через образец;
S - площадь поперечного сечения ленты образца;
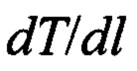 - измеренный температурный градиент.
- измеренный температурный градиент.
2. Способ по п. 1, отличающийся тем, что измерения выполняют для нескольких значений заданной температуры образца, для каждой заданной температуры выполняют расчет температурного коэффициента теплопроводности, находят аппроксимирующую математическую зависимость температурного коэффициента теплопроводности от температуры, а температурную зависимость коэффициента теплопроводности находят расчетным путем по соотношению
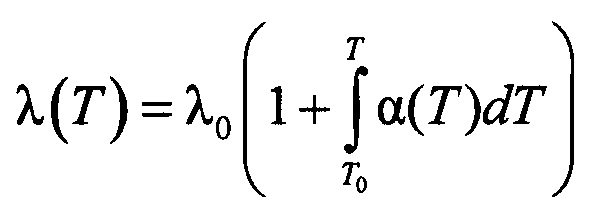
| ХОДУНКОВ В.П., "ОПРЕДЕЛЕНИЕ ТЕПЛОПРОВОДНОСТИ ЭЛЕКТРОПРОВОДНЫХ МАТЕРИАЛОВ МЕТОДАМИ РАДИАЦИОННОЙ ПИРОМЕТРИИ", ИЗВ.ВУЗОВ.ПРИБОРОСТРОЕНИЕ, 2013, ТОМ 56, НОМЕР 3, С.93-97 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ТВЕРДЫХ ИЗОТРОПНЫХ ЭЛЕКТРОПРОВОДЯЩИХ МАТЕРИАЛОВ | 2009 |
|
RU2419782C2 |
| Сплав на медной основе для изготовления радиаторных трубок | 1944 |
|
SU66055A1 |
| УСТРОЙСТВО ДЛЯ БЕСКОНТАКТНОГО ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ТЕМПЕРАТУРОПРОВОДНОСТИ ТВЕРДЫХ ТЕЛ | 2014 |
|
RU2549549C1 |
| US 7407325 В2, 05.08.2008 | |||
| US 20150003492 A1, 01.01.2015. | |||
Авторы
Даты
2019-12-19—Публикация
2019-05-29—Подача