Способ относится к радиотехнике, а именно к способам определения местоположения источников радиоизлучения, и может быть использован для определения местоположения абонентского терминала спутниковой связи (AT) посредством приема и обработки их сигналов от спутника-ретранслятора на низкой околоземной орбите (CP).
Известен способ определения местоположения пользовательского терминала с использованием двух спутников-ретрансляторов [1]. Указанный способ заключается в том, что на основе измерений временных задержек и частотных сдвигов между переданными и принятыми тестовыми сигналами системы, с учетом известных координат первого и второго спутников-ретрансляторов CP1, СР2, векторов их скоростей 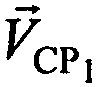 ,
, 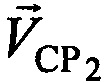 , координат узла межсетевого сопряжения (УМС) и предварительно заданных частот конвертирования
, координат узла межсетевого сопряжения (УМС) и предварительно заданных частот конвертирования 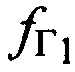 ,
, 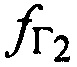 рабочих частот СР1 СР2, вычисляют широту ϕПТ и долготу λПТ пользовательского терминала (ПТ).
рабочих частот СР1 СР2, вычисляют широту ϕПТ и долготу λПТ пользовательского терминала (ПТ).
Для реализации указанного известного способа выполняют следующие этапы:
определяют расстояние 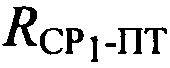 между первым CP1 и ПТ;
между первым CP1 и ПТ;
определяют расстояние 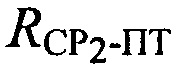 между вторым СР2 и ПТ;
между вторым СР2 и ПТ;
измеряют модуль 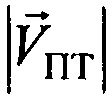 , азимут αПТ вектора скорости пользовательского терминала и его высоту hПТ относительно земной поверхности;
, азимут αПТ вектора скорости пользовательского терминала и его высоту hПТ относительно земной поверхности;
вычисляют в УМС доплеровские сдвиги частот 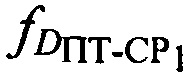 и
и 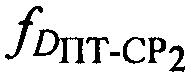 первого и второго узкополосных тестовых сигналов, обусловленные радиальными скоростями ПТ относительно CP1 и СР2, для чего предварительно определяют вероятные местоположения ПТ с учетом известных координат CP1, СР2 и определенных параметров
первого и второго узкополосных тестовых сигналов, обусловленные радиальными скоростями ПТ относительно CP1 и СР2, для чего предварительно определяют вероятные местоположения ПТ с учетом известных координат CP1, СР2 и определенных параметров 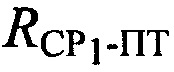 и
и 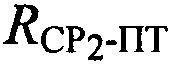 ;
;
определяют, по меньшей мере, один из параметров: радиальную скорость 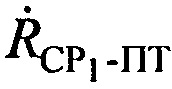 перемещения первого CP1 относительно ПТ, и/или радиальную скорость
перемещения первого CP1 относительно ПТ, и/или радиальную скорость 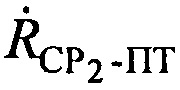 перемещения второго СР2 относительно ПТ, с учетом доплеровских сдвигов частот
перемещения второго СР2 относительно ПТ, с учетом доплеровских сдвигов частот 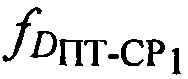 и
и 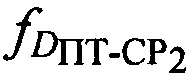 ;
;
вычисляют широту ϕПТ и долготу λПТ ПТ.
Недостатками способа определения местоположения ПТ с использованием двух спутников-ретрансляторов [1] являются:
длительное время определения координат ЗС, связанное с необходимостью проведения дополнительных измерений модуля, азимута вектора скорости ПТ и его высоты относительно земной поверхности,
необходимость ответной передачи тестовых сигналов с ПТ, чьи координаты необходимо определить в УМС через СР.
Известен способ определения местоположения земной станции спутниковой связи [2], заключающийся в том, что координаты земной станции (ЗС) определяют на основе анализа условий распространения радиоволн на трассе ЗС-СР. Падение уровня сигналов связывают с ослаблением при прохождении трассы ЗС-СР через области объемно распределенных гидрометеоров (ООРГ). Выявляют сходство замираний амплитуды между искомой и хотя бы одной из опорных ЗС.
Для реализации указанного известного способа выполняют следующие этапы:
принимают и измеряют параметров ретранслируемых сигналов земных станций (ЗС) спутниковой связи на станции спутникового радиоконтроля (ССРК), в дискретные моменты времени;
измеряют уровни ретранслируемых сигналов от одновременно работающих через CP опорных земных станций (ОЗС) спутниковой связи с известными географическими координатами и искомой ЗС;
регистрируют результаты измерений в виде последовательностей дискретных отсчетов, равных уровням сигналов;
с помощью визуального анализа этих зависимостей выявляют долговременные циклические повторения падения уровня сигналов на фоне короткоживущих высокочастотных компонентов;
связывают падение уровня сигналов с их ослаблением при прохождении трасс ЗС-СР через области ООРГ;
выявляют сходства падений уровней сигналов между искомой ЗС и хотя бы одной из ОЗС;
причиной данного сходства считают прохождение трасс ЗС-СР и ОЗС-СР через одну и ту же область ООРГ с ограниченным размером занимаемого пространства;
в качестве условия прохождения разных трасс ЗС-СР через ООРГ с такими характеристиками принимают территориальную близость ЗС и ОЗС;
определяют привязкой к географическим координатам выявленной ОЗС район наиболее вероятного местоположения искомой ЗС;
осуществляют окончательный поиск и локализацию искомой ЗС относительно выявленной ОЗС в радиусе горизонтальной протяженности проекции локальной однородной ООРГ на Землю.
К недостаткам способа определения местоположения земной станции спутниковой связи [2] относят:
длительное время определения координат ЗС, связанное с необходимостью многократного измерения уровней ретранслируемых сигналов ЗС и множества ОЗС, поиска вероятных ООРГ и взаимного сравнения результатов измерения;
высокую стоимость устройства, реализующего способ, обусловленную необходимостью размещения на борту навигационных CP дополнительных передатчиков, приемников, а также аппаратуры обработки информации.
Из известных способов наиболее близким аналогом (прототипом) предлагаемого способа по технической сущности является способ определения местоположения с помощью одного спутника на низкой околоземной орбите [3]. Для реализации данного способа последовательно выполняют следующие этапы:
измеряют в AT частоту первого сигнала, принятого с узловой станции (УС) через CP;
посылают результат измерения частоты первого сигнала в УС;
передают второй сигнал с AT в УС через CP;
измеряют в УС частоту второго сигнала, принятого с AT через CP;
измеряют в узловой станции задержку при двойном прохождении сигнала, переданного с УС в AT через CP и переданного повторно с AT в УС через CP;
определяют параметр дальности - расстояние между CP и AT;
осуществляют деление частоты первого сигнала на номинальную частоту первого сигнала для получения первого отношения, деление частоты второго сигнала на номинальную частоту второго сигнала для получения второго отношения, и умножение суммы первого и второго отношений на половину скорости света;
определяют параметр скорости изменения дальности - радиальную скорость между CP и AT;
определяют местоположение AT на поверхности Земли на основании известных положения и скорости CP, упомянутых параметра дальности и параметра скорости изменения дальности.
Недостатками способа прототипа являются:
относительно невысокая точность определения координат AT;
необходимость ответной передачи тестовых сигналов с AT, чьи координаты необходимо определить в КРМ через СР.
Целью изобретения является разработка способа определения местоположения AT с помощью CP на низкой околоземной орбите, обеспечивающего более высокую точность определения координат AT за счет более точного определения частотных сдвигов сигналов системы и одновременно исключающего необходимость ответной передачи тестовых сигналов с AT.
Поставленная цель достигается тем, что в известном способе определения местоположения AT с помощью CP на низкой околоземной орбите включающим: размещение КРМ, содержащего приемную и передающую аппаратуру, на позиции с известными координатами xK, yK, zK, выбор в качестве объекта радиоэлектронного мониторинга CP с известным номиналом частоты конвертирования ƒG, излучение с помощью аппаратуры КРМ тестового радиосигнала с номиналом средней частоты (НСЧ) 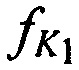 в направлении на CP в момент времени t1, измерение в КРМ НСЧ радиосигнала
в направлении на CP в момент времени t1, измерение в КРМ НСЧ радиосигнала 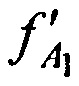 , принятого от AT через CP в момент времени t1, вычисление местоположения AT на поверхности земли на основании известных координат КРМ xK, yK, zK, номинала частоты конвертирования /с, запомненных НСЧ
, принятого от AT через CP в момент времени t1, вычисление местоположения AT на поверхности земли на основании известных координат КРМ xK, yK, zK, номинала частоты конвертирования /с, запомненных НСЧ 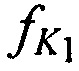 и
и 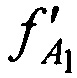 переданного тестового радиосигнала и принятого от AT через CP радиосигнала в момент времени t1, дополнительно устанавливают на земной поверхности М≥2 излучающих опорных реперных станции (ИОРС) на позициях с известными координатами xIm, yIm, zIm, где m=1…М - номер ИОРС.
переданного тестового радиосигнала и принятого от AT через CP радиосигнала в момент времени t1, дополнительно устанавливают на земной поверхности М≥2 излучающих опорных реперных станции (ИОРС) на позициях с известными координатами xIm, yIm, zIm, где m=1…М - номер ИОРС.
Для выбора CP в качестве объекта радиоэлектронного мониторинга предварительно задают район ведения радиомониторинга (РВРМ), как область на поверхности земли, в которой необходимо определить местоположение AT и выбирают n-е моменты времени tn, где n=1…N, N≥3, при которых зона освещенности указанного CP охватывает и КРМ, и РВРМ, и позиции всех М ИОРС.
Определяют n-е канонические параметры (КП) CP, включающие координаты CP 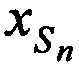 ,
, 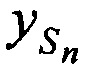 ,
, 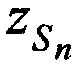 и ортогональные составляющие вектора его скорости
и ортогональные составляющие вектора его скорости 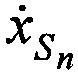 ,
, 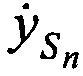 ,
, 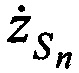 на основе излучения тестовых сигналов КРМ и m-ми ИОРС в моменты времени tn в направлении на CP и их последующего приема КРМ после переизлучения указанным CP,
на основе излучения тестовых сигналов КРМ и m-ми ИОРС в моменты времени tn в направлении на CP и их последующего приема КРМ после переизлучения указанным CP,
Измеряют в КРМ НСЧ радиосигналов 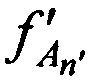 , принятых от AT через CP в моменты времени tn', где n'=2…N.
, принятых от AT через CP в моменты времени tn', где n'=2…N.
Выделяют в качестве опорных g-е, где g=1, …, N КП CP для момента времени tg.
Формируют N-1 отличающихся друг от друга пар КП CP, в каждой из которых первые КП CP соответствуют моменту времени tg, а вторые КП CP соответствуют моменту времени 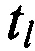 , где
, где 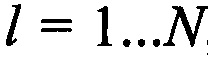 ,
, 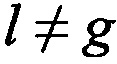 .
.
Вычисляют N-1 разностей радиальных скоростей 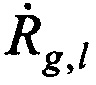 для каждой сформированной пары КП CP на основе g-x и
для каждой сформированной пары КП CP на основе g-x и 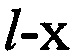 КП CP, координат КРМ xK, yK, zK, номинала частоты конвертирования ƒG, НСЧ радиосигналов
КП CP, координат КРМ xK, yK, zK, номинала частоты конвертирования ƒG, НСЧ радиосигналов 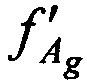 ,
, 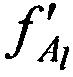 принятых от AT через CP в моменты времени tg и
принятых от AT через CP в моменты времени tg и  соответственно.
соответственно.
В качестве поверхности земли принимают сферу с радиусом 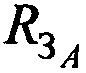 , который рассчитывается на основе средней широты РВРМ ϕA.
, который рассчитывается на основе средней широты РВРМ ϕA.
Определение местоположения AT на поверхности земли производят с использованием n-х КП CP, N-1 разностей радиальных скоростей 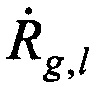 и радиуса сферы поверхности земли
и радиуса сферы поверхности земли 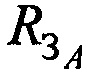 .
.
Для определения n-х КП CP в моменты времени tn, дополнительно выполняют ниже следующие процедуры.
Излучают с помощью аппаратуры КРМ тестовые радиосигналы с НСЧ 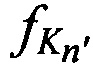 в направлении на CP в моменты времени tn'.
в направлении на CP в моменты времени tn'.
Излучают m-ми ИОРС тестовые радиосигналы с НСЧ 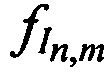 в направлении на CP в моменты времени tn.
в направлении на CP в моменты времени tn.
Принимают с помощью КРМ переизлученные CP тестовые радиосигналы с НСЧ 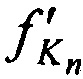 и
и 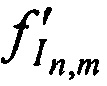 в моменты времени
в моменты времени 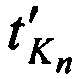 и
и 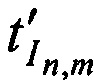 соответственно.
соответственно.
Передают в КРМ НСЧ тестовых радиосигналов 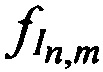 от m-х ИОРС.
от m-х ИОРС.
Измеряют задержки во времени 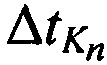 ,
, 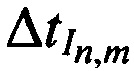 между излученными и принятыми тестовыми радиосигналами.
между излученными и принятыми тестовыми радиосигналами.
Вычисляют наклонные дальности от CP до КРМ 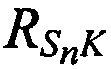 и до m-х ИОРС
и до m-х ИОРС 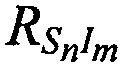 соответствующие моментам времени tn.
соответствующие моментам времени tn.
Рассчитывают координаты CP 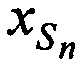 ,
, 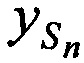 ,
, 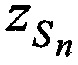 в моменты времени tn по известным координатам КРМ и m-х ИОРС, а также измеренным наклонным дальностям
в моменты времени tn по известным координатам КРМ и m-х ИОРС, а также измеренным наклонным дальностям 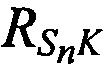 , и
, и 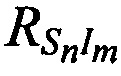 .
.
Измеряют радиальные скорости CP относительно КРМ 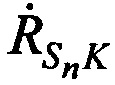 и m-х ИОРС
и m-х ИОРС 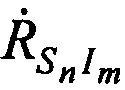 в моменты времени tn на основе известных координат КРМ и m-х ИОРС, рассчитанных координат CP
в моменты времени tn на основе известных координат КРМ и m-х ИОРС, рассчитанных координат CP 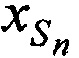 ,
, 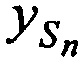 ,
, 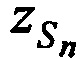 , а также запомненных НСЧ переданных
, а также запомненных НСЧ переданных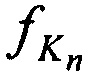 ,
, 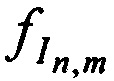 и принятых
и принятых 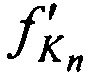 ,
, 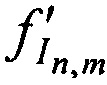 тестовых радиосигналов.
тестовых радиосигналов.
Вычисляют ортогональные составляющие вектора скорости CP 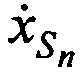 ,
, 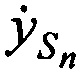 ,
, 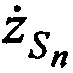 в моменты времени tn используя известные координаты КРМ и m-х ИОРС, вычисленные координаты CP
в моменты времени tn используя известные координаты КРМ и m-х ИОРС, вычисленные координаты CP 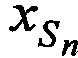 ,
, 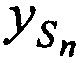 ,
, 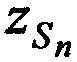 и измеренные радиальные скорости
и измеренные радиальные скорости 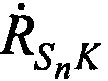 и
и 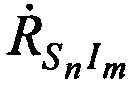 .
.
В качестве n-х КП CP принимают совокупность координат CP 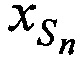 ,
, 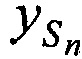 ,
, 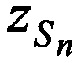 и ортогональных составляющих вектора его скорости
и ортогональных составляющих вектора его скорости 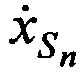 ,
, 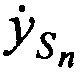 ,
, 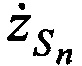 в момент времени tn.
в момент времени tn.
Благодаря перечисленной новой совокупности существенных признаков, при использовании тестовых радиосигналов М ИОРС на позициях с известными координатами достигается цель изобретения: обеспечение высокой точности определения координат AT за счет более точного измерения частотных сдвигов сигналов системы, и исключении необходимости ответной передачи тестовых сигналов с AT.
Заявленный способ поясняется чертежами, на которых показаны:
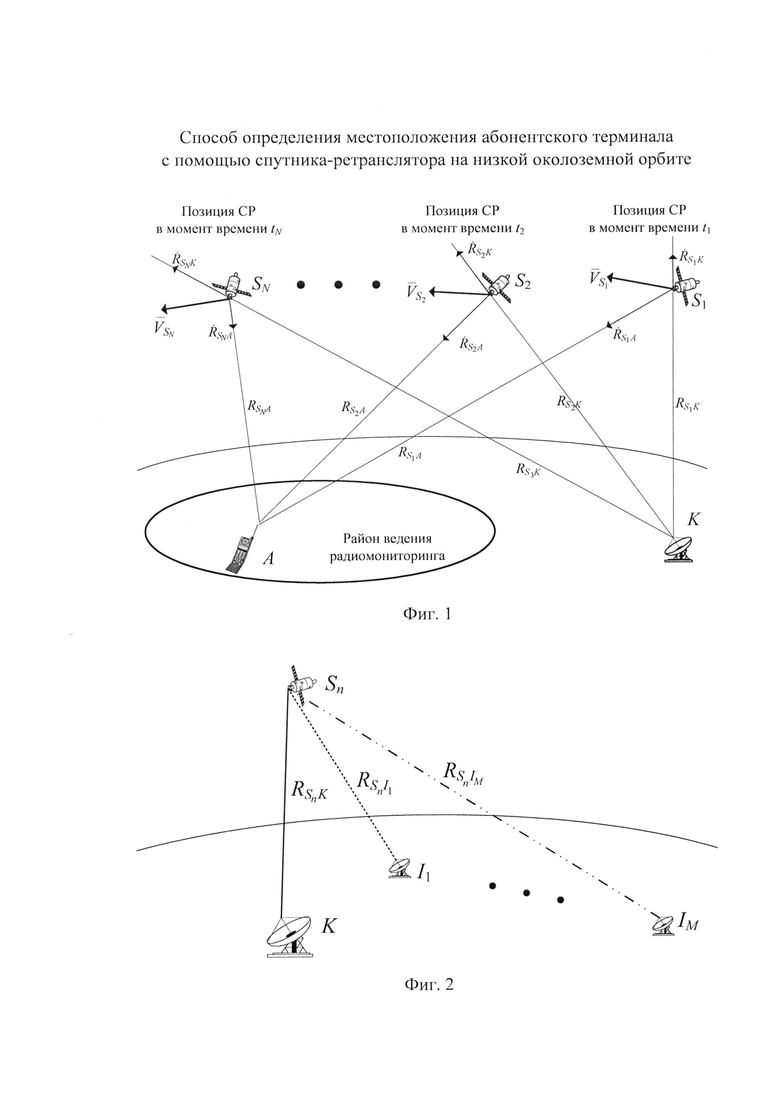
на фиг. 1 - типовая схема ведения радиомониторинга для позиций CP S1, S2 и Sn в моменты времени t1 t2 и tn,
на фиг. 2 - схема подсистемы определения координат CP 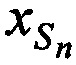 ,
, 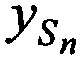 ,
, 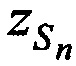 в моменты времени tn,
в моменты времени tn,
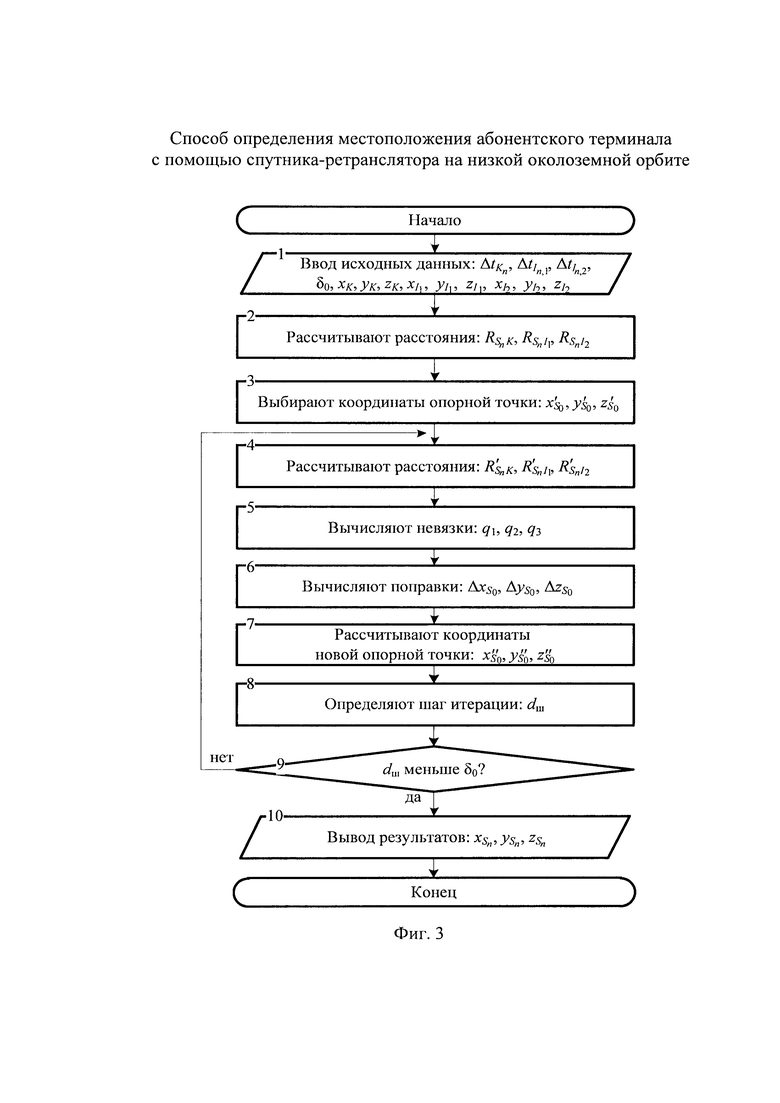
на фиг. 3 - схема алгоритма определения координат CP в моменты времени tn при использовании двух ИОРС,
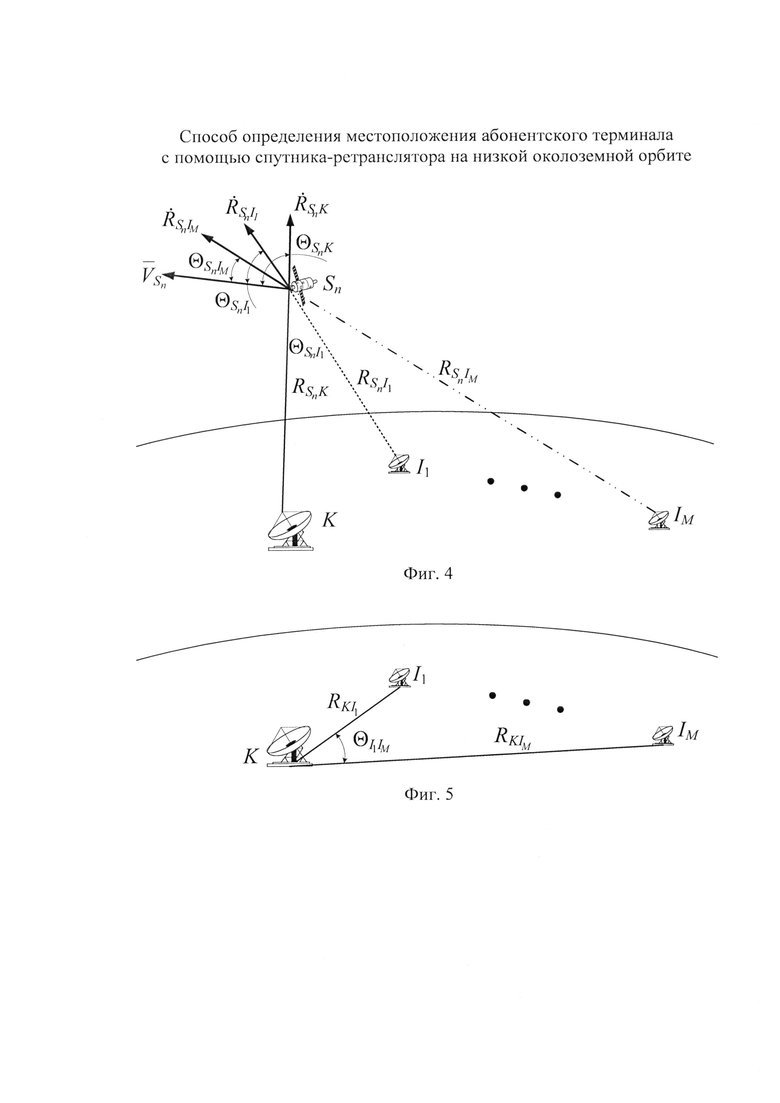
на фиг. 4 - схема подсистемы определения ортогональных составляющих вектора скорости CP в моменты времени tn,
на фиг.5 - топология размещения КРМ и М ИОРС.
Для реализации заявленного способа определения местоположения AT используют один CP, а измерения проводят в моменты времени tn, где n=1…N, a N≥3 - номер временного отсчета, соответствующих положению CP, при котором и КРМ, и РВРМ, и позиции всех М ИОРС находились бы в зоне радиовидимости (ЗРВ) указанного СР.
На фиг. 1 представлена типовая схема ведения радиомониторинга включающая позиции CP S1, S2 и SN в моменты времени t1, t2 и tN, КРМ K, AT А. На фиг. 1 введены следующие обозначения: 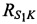 ,
, 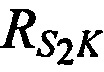 и
и 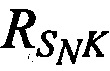 - расстояния от КРМ до CP,
- расстояния от КРМ до CP, 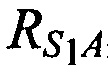 ,
, 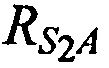 и
и 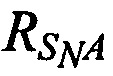 - расстояния от AT до CP,
- расстояния от AT до CP, 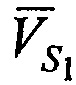 ,
, 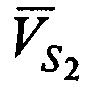 ,
, 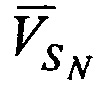 - векторы скорости CP,
- векторы скорости CP, 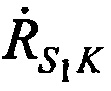 ,
, 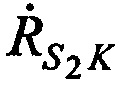 ,
, 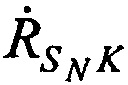 - радиальные скорости CP относительно КРМ (проекции векторов скорости CP
- радиальные скорости CP относительно КРМ (проекции векторов скорости CP 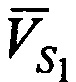 ,
, 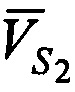 ,
, 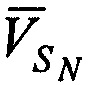 на оси
на оси 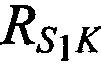 ,
, 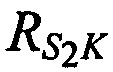 и
и 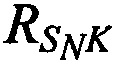 соответственно),
соответственно), 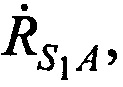
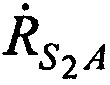 ,
, 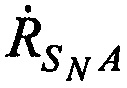 - радиальные скорости CP относительно AT (проекции векторов скорости CP
- радиальные скорости CP относительно AT (проекции векторов скорости CP 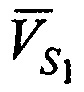 ,
, 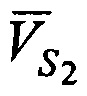 ,
, 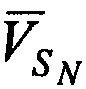 на оси
на оси 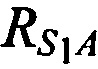 ,
, 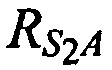 и
и 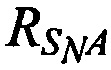 соответственно) в моменты времени t1, t2 и tN.
соответственно) в моменты времени t1, t2 и tN.
КРМ является стационарным, его координаты xK, yK, zK, считают известными.
Предполагают, что AT размещен в предварительно выбранном РВРМ.
Заявленный способ определения местоположения AT основан на использовании КП CP в различные моменты времени tn, что накладывает требования к точности определения указанных КП СР.
Теория полета CP, или, как ее еще называют, астродинамика, небесная механика, космическая баллистика, основана на законах И. Кеплера и законе всемирного тяготения И. Ньютона.
В первом приближении движение CP представляется как невозмущенное - такое движение, которое происходило бы только под влиянием силы притяжения Земли по закону Ньютона, т.е. точно соответствует задаче двух тел (Земля - CP) в небесной механике. Это движение называется движением по Кеплеровой орбите, так как подчиняется трем законам Кеплера [4].
Достоинством Кеплеровой орбиты является простота вычисления координат и вектора скорости CP в прогнозируемые моменты времени. Это предопределило широкое использование элементов Кеплеровой орбиты. В настоящем изобретении с помощью этих элементов выбирают CP в качестве объекта радиоэлектронного мониторинга и выбирают моменты времени tn, соответствующие положению CP, при котором и КРМ, и РВРМ, и позиции всех М ИОРС находились бы в ЗРВ указанного СР.
Кроме того элементы Кеплеровой орбиты CP служат для ориентирования приемной и передающей антенн КРМ, а также передающих антенн всех М ИОРС на выбранный CP при передаче и приеме тестовых радиосигналов и приема радиосигналов AT, ретранслированных СР.
Недостатком Кеплеровой орбиты является относительно низкая точность определения координат и вектора скорости CP, которая в большинстве случаев недостаточна для реализации заявленного способа определения местоположения AT с помощью одного CP на низкой околоземной орбите.
Более точно канонические параметры (КП) CP, включающие координаты CP 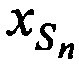 ,
, 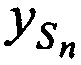 ,
, 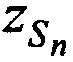 и ортогональные составляющие вектора его скорости
и ортогональные составляющие вектора его скорости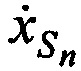 ,
, 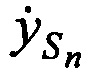 ,
, 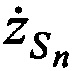 в моменты времени tn, определяют по радиосигналам ИОРС, размещенных на позициях с известными координатами [5].
в моменты времени tn, определяют по радиосигналам ИОРС, размещенных на позициях с известными координатами [5].
На фиг. 2 и фиг. 4 представлены схемы подсистем определения координаты CP 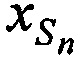 ,
, 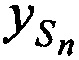 ,
, 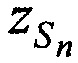 и ортогональных составляющих вектора его скорости
и ортогональных составляющих вектора его скорости 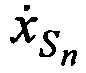 ,
, 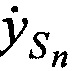 ,
, 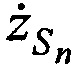 в моменты времени tn. Эти подсистемы состоят из КРМ и М≥2 ИОРС, размещенных на позициях с известными координатами
в моменты времени tn. Эти подсистемы состоят из КРМ и М≥2 ИОРС, размещенных на позициях с известными координатами 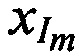 ,
,  ,
, 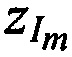 , где m=1…М - номер ИОРС.
, где m=1…М - номер ИОРС.
На фиг. 2 введены обозначения: 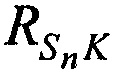 - расстояния между CP и КРМ,
- расстояния между CP и КРМ, 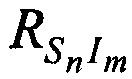 - расстояния между CP и m-и ИОРС в моменты времени tn.
- расстояния между CP и m-и ИОРС в моменты времени tn.
На фиг. 4 дополнительно введены обозначения: 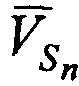 - векторы скоростей CP,
- векторы скоростей CP, 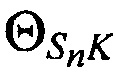 - углы между векторами
- углы между векторами 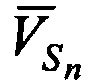 и направлениями на КРМ,
и направлениями на КРМ, 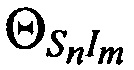 - углы между векторами
- углы между векторами 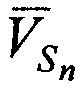 и направлениями на m-ю ИОРС,
и направлениями на m-ю ИОРС, 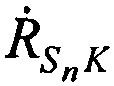 -радиальные скорости CP относительно КРМ;
-радиальные скорости CP относительно КРМ; 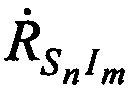 - радиальные скорости CP относительно m-й ИОРС.
- радиальные скорости CP относительно m-й ИОРС.
Синхронность работы передатчиков КРМ и М ИОРС обеспечивают за счет использования меток времени высокостабильного генератора частот.
Для определения КП CP в момент времени tn используют временные задержки и частотные сдвиги тестовых радиосигналов [6].
В моменты времени tn синхронно излучают тестовые радиосигналы КРМ и М ИОРС с номиналами средних частот (НСЧ) 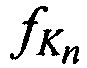 и
и 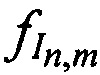 соответственно. Далее принимают в КРМ переизлученные CP тестовые радиосигналы в моменты времени
соответственно. Далее принимают в КРМ переизлученные CP тестовые радиосигналы в моменты времени 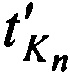 и
и 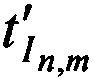 с НСЧ
с НСЧ 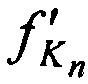 и
и 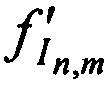 . Определяют в КРМ задержки во времени
. Определяют в КРМ задержки во времени 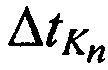 ,
, 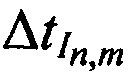 между излученными и принятыми тестовыми радиосигналами:
между излученными и принятыми тестовыми радиосигналами:
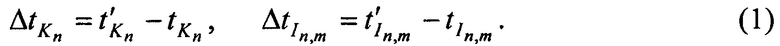
На основе полученных задержек во времени 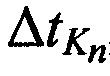 ,
, 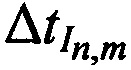 измеряют наклонные дальности от CP до КРМ
измеряют наклонные дальности от CP до КРМ 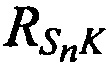 и наклонные дальности от CP до каждой из М ИОРС
и наклонные дальности от CP до каждой из М ИОРС  для каждого момента времени tn:
для каждого момента времени tn:
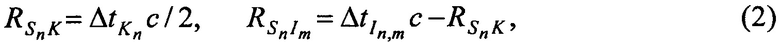
где с=3×108 м/с - скорость света в вакууме.
С помощью полученных наклонных дальностей 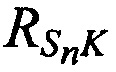 и
и 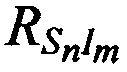 определяют координаты CP
определяют координаты CP 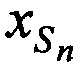 ,
, 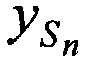 ,
, 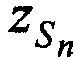 в моменты времени tn.
в моменты времени tn.
Для одномоментного и однозначного определения координат CP 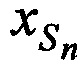 ,
, 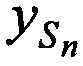 ,
, 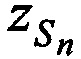 в каждый момент времени tn, необходимо и достаточно измерить минимум три наклонные дальности, например,
в каждый момент времени tn, необходимо и достаточно измерить минимум три наклонные дальности, например, 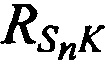 ,
, 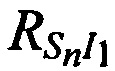 и
и 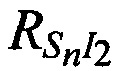 , следовательно, конфигурация подсистемы определения координат CP должна включать минимум две ИОРС I1 и I2.
, следовательно, конфигурация подсистемы определения координат CP должна включать минимум две ИОРС I1 и I2.
В качестве примера, для частного случая, когда количество ИОРС равно двум (М=2), в приложении А представлена аналитическая интерпретация алгоритма определения координат CP 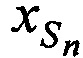 ,
, 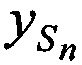 ,
, 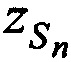 в моменты времени tn.
в моменты времени tn.
Дальнейшее увеличение количества ИОРС (М≥3) приводит к повышению точности определения координат CP и к сопутствующему увеличению суммарной стоимости устройства, реализующего заявленный способ.
Алгоритм определения координат CP при использовании М≥3 ИОРС будет аналогичен алгоритму, описанному в приложении А, с той лишь разницей, что система (А.1), составляемая на этапе 6 приложения А, будет содержать М+1 (более четырех) линейных уравнений с тремя неизвестными. Тогда систему (А.1) решают одним из известных численных методов, например, методом наименьших квадратов.
Для одномоментного и однозначного определения ортогональных составляющих вектора скорости CP 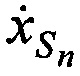 ,
, 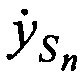 ,
, 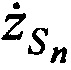 в каждый момент времени tn, необходимо и достаточно измерить минимум три радиальные скорости, например,
в каждый момент времени tn, необходимо и достаточно измерить минимум три радиальные скорости, например, 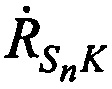 ,
, 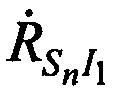 и
и 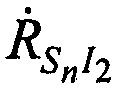 , следовательно, конфигурация подсистемы определения ортогональных составляющих вектора скорости CP должна включать минимум две ИОРС I\ и I2.
, следовательно, конфигурация подсистемы определения ортогональных составляющих вектора скорости CP должна включать минимум две ИОРС I\ и I2.
В качестве примера, для частного случая, когда количество ИОРС равно двум (М=2), в приложении Б представлена аналитическая интерпретация алгоритма определения ортогональных составляющих вектора скорости CP 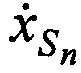 ,
, 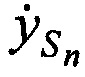 ,
, 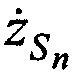 в моменты времени tn.
в моменты времени tn.
Дальнейшее увеличение количества ИОРС (М≥3) приводит к повышению точности определения ортогональных составляющих вектора скорости CP и к сопутствующему увеличению суммарной стоимости устройства, реализующего заявленный способ.
Алгоритм определения ортогональных составляющих вектора скорости CP при использовании М≥3 ИОРС будет аналогичен алгоритму, описанному в приложении Б, с той лишь разницей, что система (Б.8), составляемая на этапе 3 в приложения Б, будет содержать М+1 (более четырех) линейных уравнений с тремя неизвестными. Тогда систему (Б.8) решают одним из известных численных методов, например, методом наименьших квадратов.
В качестве КП CP в моменты времени принимают координаты CP 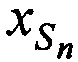 ,
, 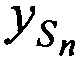 ,
, 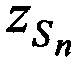 и ортогональные составляющие вектора его скорости
и ортогональные составляющие вектора его скорости 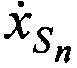 ,
, 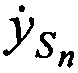 ,
, 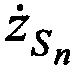 .
.
Для определения местоположения AT в КРМ измеряют НСЧ радиосигналов 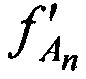 , принятых от AT через CP в моменты времени tn.
, принятых от AT через CP в моменты времени tn.
Предполагают, что AT в моменты времени tn излучает в направлении на CP радиосигналы с постоянным НСЧ равным ƒA, однако, в КРМ этот НСЧ не известен. НСЧ радиосигналов AT в моменты времени tn претерпевают следующие сдвиги на трассе АТ-СР-КРМ [7]:
доплеровские сдвиги НСЧ радиосигналов AT на входе CP 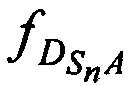 за счет его сближения (удаления) с (от) AT;
за счет его сближения (удаления) с (от) AT;
сдвиг НСЧ радиосигналов AT на предварительно заданную величину номинала частоты конвертирования ƒG;
доплеровские сдвиги НСЧ радиосигналов AT на выходе CP 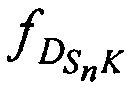 за счет его сближения (удаления) с (от) K.
за счет его сближения (удаления) с (от) K.
Считают, что нестабильность генератора частот CP в моменты времени tn известна и возможна ее компенсация. Влияние других эффектов на изменение частоты, например гравитационный и релятивистский эффекты в рамках рассматриваемого способа пренебрежимо малы и поэтому не учитывают.
Доплеровские сдвиги НСЧ радиосигналов AT на выходе CP 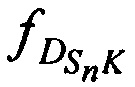 за счет его сближения (удаления) с (от) K, рассчитываются на основе известных координат КРМ xK, yK, zK и КП CP определенных n-х КП СР.
за счет его сближения (удаления) с (от) K, рассчитываются на основе известных координат КРМ xK, yK, zK и КП CP определенных n-х КП СР.
В свою очередь доплеровские сдвиги НСЧ радиосигналов AT на входе CP 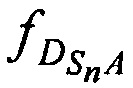 за счет сближения (удаления) CP с (от) AT используют для определения местоположения самого AT хА, yA и zA. В условиях, когда НСЧ радиосигнала ƒА в КРМ не известен, рассчитывают разности указанных доплеровских сдвигов НСЧ радиосигналов AT на входе CP в различные моменты времени. Для этого предварительно выделяют в качестве опорных g-e, где g=1, ..., N, КП CP для момента времени tg.
за счет сближения (удаления) CP с (от) AT используют для определения местоположения самого AT хА, yA и zA. В условиях, когда НСЧ радиосигнала ƒА в КРМ не известен, рассчитывают разности указанных доплеровских сдвигов НСЧ радиосигналов AT на входе CP в различные моменты времени. Для этого предварительно выделяют в качестве опорных g-e, где g=1, ..., N, КП CP для момента времени tg.
Далее формируют отличающихся друг от друга пары КП CP, в каждой из которых первые КП CP соответствуют моменту времени tg, а вторые КП CP соответствуют моменту времени 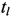 , где
, где 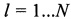 ,
, 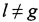 . Всего получают N-1 таких пар.
. Всего получают N-1 таких пар.
Для каждой сформированной пары КП CP вычисляют разность радиальных скоростей 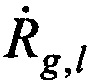 на основе g-x и
на основе g-x и 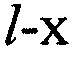 КП CP, координат КРМ xK, yK, zK, номинала частоты конвертирования ƒG, НСЧ радиосигналов
КП CP, координат КРМ xK, yK, zK, номинала частоты конвертирования ƒG, НСЧ радиосигналов 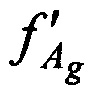 ,
, 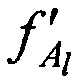 принятых от AT через CP в моменты времени tg и
принятых от AT через CP в моменты времени tg и 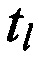 соответственно.
соответственно.
В качестве модели поверхности Земли выбирают сферу с переменным радиусом [8], зависящим от широты и определяемым из известного соотношения, который в РВРМ будет равен 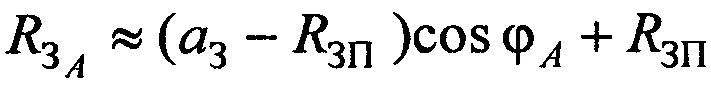 , где aЗ=6378136 м - большая полуось эллипсоида Земли;
, где aЗ=6378136 м - большая полуось эллипсоида Земли; 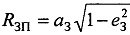 - радиус Земли на полюсе;
- радиус Земли на полюсе; 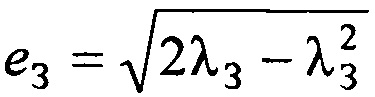 - эксцентриситет эллипсоида Земли; λЗ=1/298,25784 - сжатие эллипсоида Земли, ϕA - средняя широта РВРМ.
- эксцентриситет эллипсоида Земли; λЗ=1/298,25784 - сжатие эллипсоида Земли, ϕA - средняя широта РВРМ.
На завершающем этапе рассчитывают координаты AT хА, уА, zA используя n-e КП CP, N-1 разность радиальных скоростей 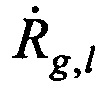 и радиус сферы поверхности земли
и радиус сферы поверхности земли 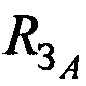 .
.
Для одномоментного и однозначного определения местоположения AT (расчета координат AT хА, уА, zA) с помощью заявленного способа необходимо и достаточно вычислить минимум две разности радиальных скоростей 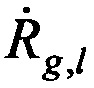 , следовательно, требуется проведение измерений в три момента времени (N=3).
, следовательно, требуется проведение измерений в три момента времени (N=3).
В качестве примера реализации заявленного способа в приложении В приводится аналитическая интерпретация алгоритма определения местоположения AT с помощью CP на низкой околоземной орбите для N=3, то есть для трех моментов времени t1, t2, t3. В указанном примере в качестве опорных выбраны первые (g=1) КП CP для момента времени t1.
Дальнейшее увеличение количества измерений (N≥4) приводит к повышению точности определения местоположения AT и к сопутствующему увеличению суммарной стоимости устройства, реализующего заявленный способ.
Алгоритм определения местоположения AT с помощью CP на низкой околоземной орбите для N≥4 моментов измерения будет аналогичен алгоритму, описанному в приложении В, с той лишь разницей, что система уравнений (В.14), будет содержать N (более четырех) уравнений второго порядка с тремя неизвестными. Это в свою очередь приведет к тому, что последующая система линейных уравнений (В.15) с тремя неизвестными будет включать более четырех уравнений. Тогда систему (В.15) решают одним из известных численных методов, например, методом наименьших квадратов.
На точность определения местоположения AT с помощью заявленного способа оказывают влияние множество факторов, основными из которых являются:
количество установленных на земной поверхности М ИОРС;
топология размещения КРМ и m-x ИОРС;
точность синхронизации излучений КРМ и m-x ИОРС;
количество проводимых измерений N;
временные интервалы между моментами времени tg и 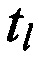 ,
,
погрешности измерения НСЧ переданных и принятых тестовых радиосигналов и принятых радиосигналов от AT;
Увеличение количества установленных на земной поверхности М ИОРС приводит к повышению точности определения координат CP 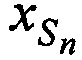 ,
, 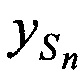 ,
, 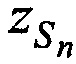 и ортогональных составляющих вектора скорости CP
и ортогональных составляющих вектора скорости CP 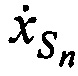 ,
, 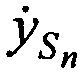 ,
, 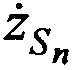 в каждый момент времени tn. Это в свою очередь способствует повышению точности определения местоположения AT.
в каждый момент времени tn. Это в свою очередь способствует повышению точности определения местоположения AT.
Под топологией размещения КРМ и m-x ИОРС понимают совокупность таких параметров, как 1) расстояния между КРМ и m-ми ИОРС 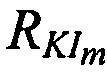 , 2) величины углов
, 2) величины углов 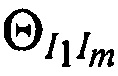 , образованных отрезками
, образованных отрезками 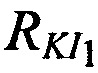 и
и 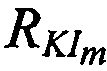 . На фиг. 5, в качестве примера, представлена топология КРМ и М ИОРС, а также показаны расстояния
. На фиг. 5, в качестве примера, представлена топология КРМ и М ИОРС, а также показаны расстояния 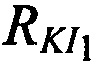 ,
, 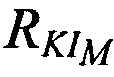 . и угол
. и угол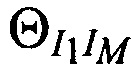 . Для повышения точности определения местоположения AT необходимо увеличивать расстояния
. Для повышения точности определения местоположения AT необходимо увеличивать расстояния 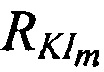 и увеличивать углы
и увеличивать углы 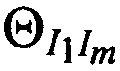 .
.
Высокую точность синхронизации излучений КРМ и m-х ИОРС и низкую погрешности измерения НСЧ переданных и принятых тестовых радиосигналов и принятых радиосигналов от AT обеспечивают за счет использования высокоточных генераторов частот в КРМ и m-x ИОРС.
При выборе количества проводимых измерений N и связанных с ним временных интервалов между моментами времени tg и 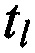 решают противоречивую задачу: с одной стороны количество проводимых измерений необходимо увеличивать с целью повышения точности определения местоположения AT; с другой стороны увеличение проводимых измерений снижает производительность КРМ.
решают противоречивую задачу: с одной стороны количество проводимых измерений необходимо увеличивать с целью повышения точности определения местоположения AT; с другой стороны увеличение проводимых измерений снижает производительность КРМ.
Произведено имитационное моделирование заявленного способа определения местоположения абонентского терминала с помощью одного спутника-ретранслятора на низкой околоземной орбите и способа-прототипа с помощью разработанных программ на ЭВМ [9, 10] при одинаковых исходных данных.
Результаты моделирования свидетельствуют о существенном повышении точности определения местоположения AT с помощью заявленного способа по сравнению со способом прототипом на 60…80% (в зависимости от топологии размещения КРМ и М ИОРС, а также количества проведенных измерений N), при одновременном исключении необходимости ответной передачи тестовых сигналов с AT, что указывает на возможность достижения технического результата при использовании заявленного технического решения.
Источники информации
1. Волков Р.В., Саяпин В.Н., Севидов В.В. Способ определения местоположения пользовательского терминала с использованием двух спутников-ретрансляторов. Патент RU №2605457, опубл. 20.12.2016 Бюл. №35.
2. Басукинский А.Б., Кизима С.В., Лисица Г.В., Митченков С.Г. Способ определения местоположения земной станции спутниковой связи. Патент RU №2442996, опубл. 20.02.2012 Бюл. №5.
3. Леванон Н. Определение местоположения с помощью одного спутника на низкой околоземной орбите. Патент RU №2241239, опубл. 27.11.2004 Бюл. №33.
4. Абалакин В.К. Астрономический календарь. Постоянная часть. - М.: Наука, 1981. - 704 с.
5. Волков Р.В., Малышев С.Р., Симонов А.Н., Севидов В.В. Определение канонических параметров спутников-ретрансляторов по радиосигналам опорных реперных станций // Труды Военно-космической академии им. А.Ф. Можайского. 2016. Вып. 655. С. 88-92.
6. Кельян А.Х., Чемаров А.О., Волков Р.В., Севидов В.В. Определение параметров движения летательного аппарата системой геолокации по излучениям находящейся на его борту станции спутниковой связи // Успехи современной радиоэлектроники. 2016. №5. С. 10-14.
7. Волков Р.В., Саяпин В.Н., Севидов В.В. Модель измерения временной задержки и частотного сдвига радиосигнала, принятого от спутника-ретранслятора при определении местоположения земной станции // T-Comm: Телекоммуникации и транспорт. 2016. Том 10. №9. С. 14-18.
8. Богдановский С.В., Волков Р.В., Севидов В.В., Теслевич С.Ф. Модель поверхности Земли при определении местоположения земной станции по сигналам спутников-ретрансляторов // Наукоемкие технологии. 2016. №12. С. 44-50.
9. Волков Р.В., Саяпин В.Н., Севидов В.В. Модель движения искусственного спутника Земли // Программы для ЭВМ. Базы данных. Топологии интегральных микросхем. 2016. №2. С 112.
10. Севидов В.В. Определение координат и параметров движения источника радиоизлучения на основе разностно-временных и разностно-доплеровских измерений // Программы для ЭВМ. Базы данных. Топологии интегральных микросхем. 2015. №11. С. 2.
Приложение А
Алгоритм определения координат спутника-ретранслятора при использовании двух ИОРС
Для расчета координат CP в моменты времени tn в частном случае, когда количество ИОРС равно двум (М=2) разработан алгоритм, схема которого представлена на фиг. 3.
На этапе 1 производят ввод исходных данных, в качестве которых выступают координаты КРМ xK, yK, zK; координаты двух ИОРС 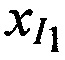 ,
, 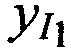 ,
, 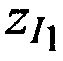 и
и 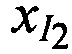 ,
, 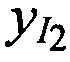 ,
, 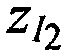 ; временные задержки между излученными КРМ, двумя ИОРС и принятыми КРМ тестовыми радиосигналами
; временные задержки между излученными КРМ, двумя ИОРС и принятыми КРМ тестовыми радиосигналами 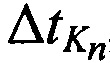 ,
, 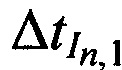 , и
, и 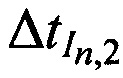 , предварительно определенные в соответствии с формулами (1); порог точности δ0 расчета координат СР.
, предварительно определенные в соответствии с формулами (1); порог точности δ0 расчета координат СР.
На этапе 2 рассчитывают расстояния 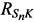 ,
, 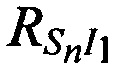 и
и 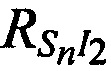 по формулам (2).
по формулам (2).
На этапе 3 выбирают, на основе элементов Кеплеровой орбиты CP, координаты опорной точки 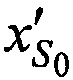 ,
, 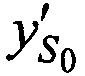 ,
, 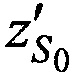 .
.
На этапе 4 рассчитывают расстояния 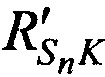 ,
, 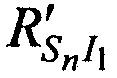 и
и 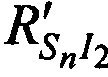 , при условии равенства координат CP координатам опорной точки
, при условии равенства координат CP координатам опорной точки 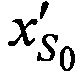 ,
, 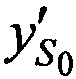 ,
, 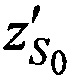 по формулам
по формулам
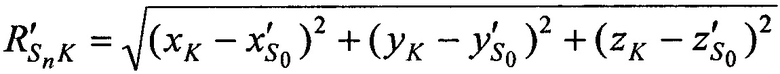 ,
,
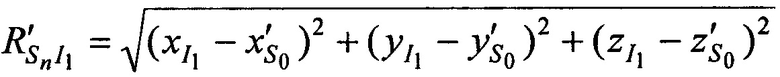 ,
,
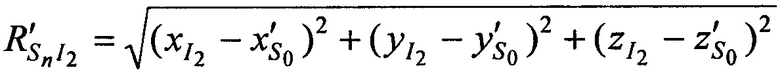 .
.
На этапе 5 вычисляют невязки q1, q2 и q3 как разницы между расстояниями 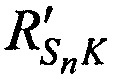 ,
, 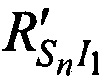 и
и 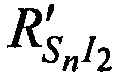 , рассчитанными на этапе 4, и расстояниями
, рассчитанными на этапе 4, и расстояниями 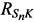 ,
, 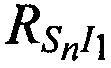 и
и 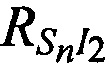 , рассчитанными на этапе 2 и соответственно
, рассчитанными на этапе 2 и соответственно
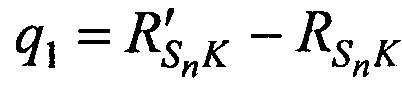 ,
, 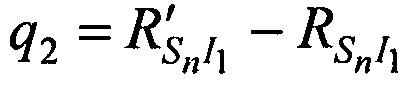 ,
,  .
.
На этапе 6 получают поправки к координатам CP 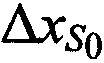 ,
, 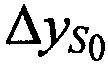 ,
, 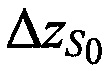 для чего предварительно формируют систему линейных уравнений путем разложении в ряд Тейлора функций
для чего предварительно формируют систему линейных уравнений путем разложении в ряд Тейлора функций 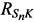 ,
,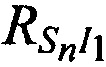 и
и 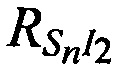 , с точностью до первых членов, где в качестве переменных выступают поправки к координатам CP
, с точностью до первых членов, где в качестве переменных выступают поправки к координатам CP 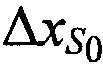 ,
, 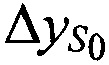 ,
, 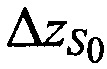 :
:
с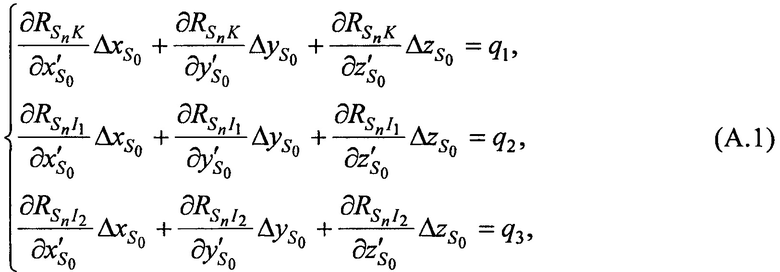
где частные производные, в свою очередь, рассчитываются согласно выражениям
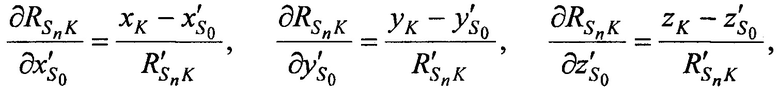
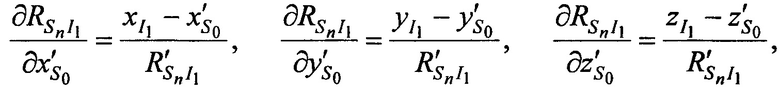
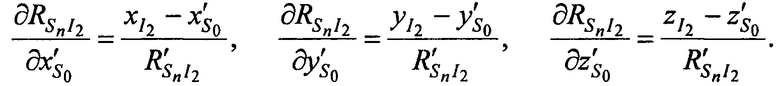
Решают систему линейных уравнений (А.1) одним из известных методов, например методом Крамера, получают поправки к координатам CP 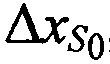 ,
, 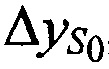 ,
, 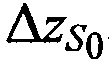
На этапе 7 рассчитывают координаты новой опорной точки 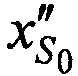 ,
, 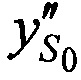 ,
, 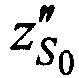 :
:
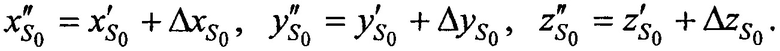
Этапы 4…7 в совокупности составляют первую итерацию. Далее итерации повторяют, используя каждый раз координаты новой опорной точки, рассчитанные на предыдущей итерации. Количество необходимых итераций зависит требуемой точности определения координат СР. С точностью определения координат CP напрямую связан шаг итерации dш.
На этапе 8 определяют шаг итерации dш как расстояние между текущей и предыдущей опорными точками:
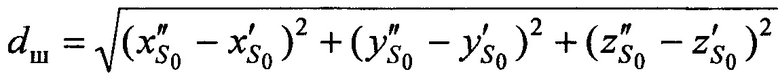
На этапе 9 сравнивают dш с порогом δ0, задаваемом на этапе 1. По результату сравнения либо выполняют следующую итерацию (этапы 4…7), если dш>δ0, либо переходят к этапу 10, если dш<δ0. Необходимое число итераций, как правило, составляет 2, …, 4.
На этапе 10 осуществляют вывод координат CP 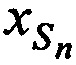 ,
, 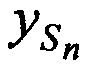 ,
, 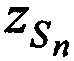 в качестве которых предварительно выбирают значения координат опорной точки на последней итерации.
в качестве которых предварительно выбирают значения координат опорной точки на последней итерации.
Приложение Б
Алгоритм определения ортогональных составляющих вектора скорости спутника-ретранслятора при использовании двух ИОРС
Для расчета ортогональных составляющих вектора скорости CP в моменты времени tn в частном случае, когда количество ИОРС равно двум (М=2) разработан алгоритм, основные этапы которого раскрыты ниже.
На этапе 1 производят ввод исходных данных, в качестве которых выступают: координаты КРМ xK yK, zK, координаты двух ИОРС 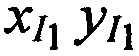 ,
, 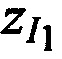 и
и 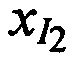
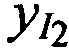 ,
, 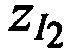 ; координаты CP
; координаты CP 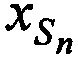 ,
,  ,
, 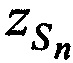 , рассчитанные в соответствии с алгоритмом, представленном в приложении А; НСЧ тестовых радиосигналов
, рассчитанные в соответствии с алгоритмом, представленном в приложении А; НСЧ тестовых радиосигналов 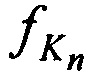 ,
, 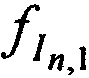 ,
, 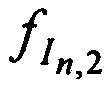 переданных КРМ и двумя ИОРС и
переданных КРМ и двумя ИОРС и 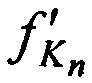 ,
, 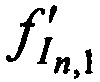 ,
, 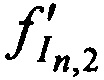 принятых тестовых радиосигналов КРМ после их переизлучения CP; номинал частоты конвертирования CP ƒG.
принятых тестовых радиосигналов КРМ после их переизлучения CP; номинал частоты конвертирования CP ƒG.
На этапе 2 рассчитывают значения радиальных скоростей 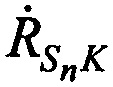 ,
, 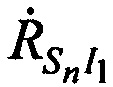 и
и 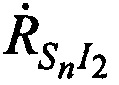 CP относительно КРМ, 1-й, 2-й ИОРС в моменты времени tn.
CP относительно КРМ, 1-й, 2-й ИОРС в моменты времени tn.
Соотношения НСЧ 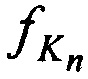 ,
, 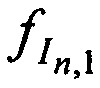 ,
, 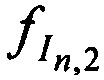 переданных тестовых радиосигналов КРМ и двумя ИОРС и
переданных тестовых радиосигналов КРМ и двумя ИОРС и 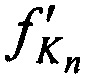 ,
, 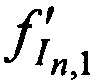 ,
, 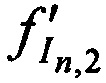 принятых тестовых радиосигналов КРМ после их переизлучения CP, имеют вид
принятых тестовых радиосигналов КРМ после их переизлучения CP, имеют вид
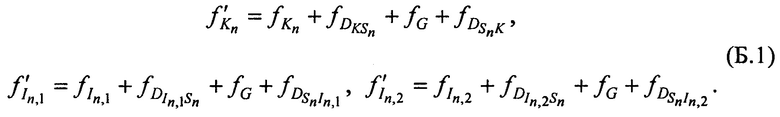
где ƒG - номиналом частоты конвертирования CP, 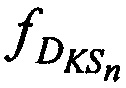 ,
,  и
и 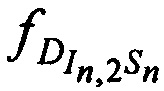 - доплеровские сдвиги частот тестовых радиосигналов на входе CP за счет его сближения (удаления) с (от) КРМ, 1-й и 2-й ИОРС в моменты времени tn,
- доплеровские сдвиги частот тестовых радиосигналов на входе CP за счет его сближения (удаления) с (от) КРМ, 1-й и 2-й ИОРС в моменты времени tn, 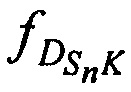 ,
, 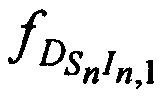 и
и 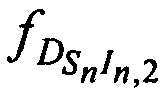 - доплеровские сдвиги частот тестовых радиосигналов на выходе CP за счет его сближения (удаления) с (от) КРМ, 1-й и 2-й ИОРС в моменты времени tn.
- доплеровские сдвиги частот тестовых радиосигналов на выходе CP за счет его сближения (удаления) с (от) КРМ, 1-й и 2-й ИОРС в моменты времени tn.
Предполагают, что нестабильность генератора частот CP известна и компенсируется. Влияние других эффектов на изменение частоты, например гравитационный и релятивистский эффекты в рамках рассматриваемого способа пренебрежимо малы и поэтому не учитывают.
Выражения для доплеровских сдвигов частот тестовых радиосигналов 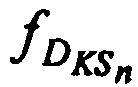 ,
, 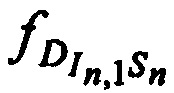 и
и 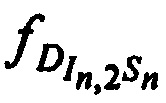 на входе CP и для доплеровских сдвигов частот тестовых радиосигналов
на входе CP и для доплеровских сдвигов частот тестовых радиосигналов 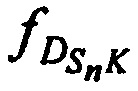 ,
, 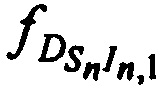 и
и 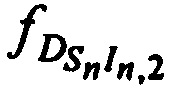 на выходе CP, с учетом того, что
на выходе CP, с учетом того, что 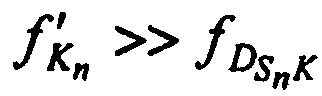 ,
, 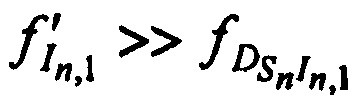 и
и 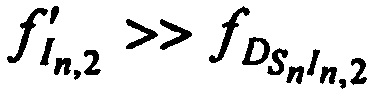 , имеют следующие виды:
, имеют следующие виды:
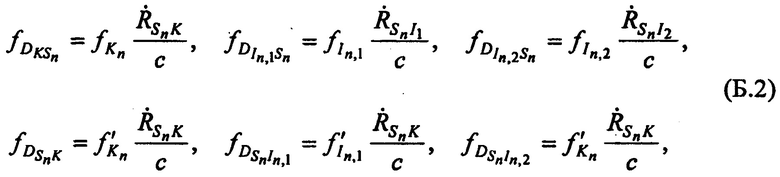
Из равенств (Б.1) и (Б.2) получают выражения для расчета радиальных скоростей 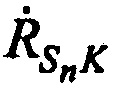 ,
, 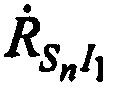 и
и 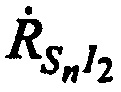 :
:
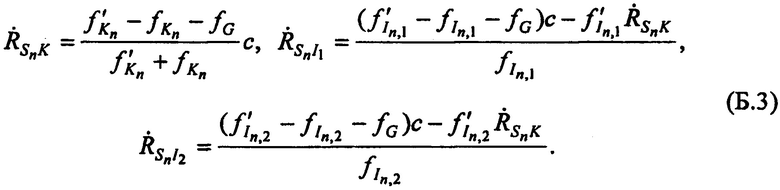
На этапе 3 рассчитывают ортогональные составляющие вектора скорости CP 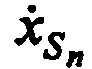 ,
, 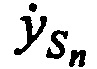 ,
, 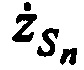 .
.
Справедливы тождества, связывающие радиальные скорости 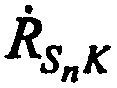 ,
, 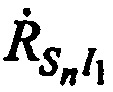 и
и 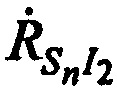 с векторами скоростей CP
с векторами скоростей CP 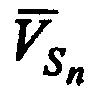 , через углы
, через углы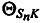 ,
, 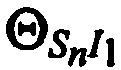 и
и  :
:

Согласно теореме о скалярном произведении векторов
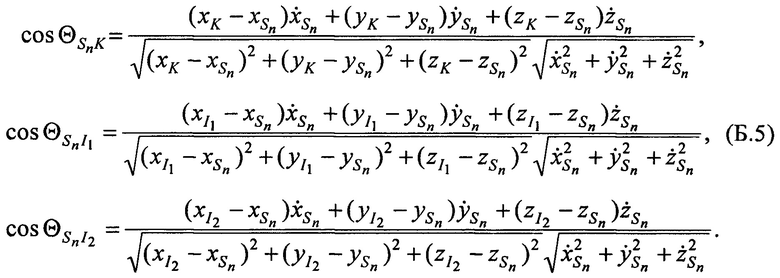
Модуль вектора скорости CP равен:

а расстояния от КРМ, 1-й, 2-й ИОРС до CP 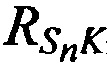 ,
, 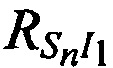 ,
, 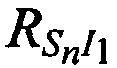 рассчитывают как
рассчитывают как
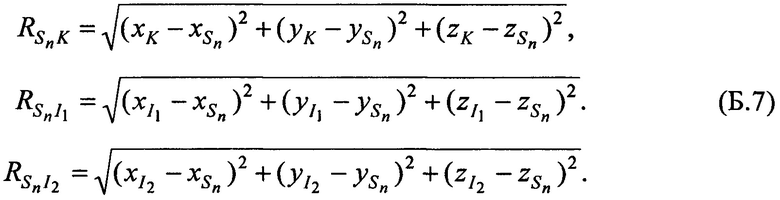
Выражения (Б.1) с учетом уравнений (Б.4)…(Б.7) для частного случая, когда n=1…2, преобразуют в систему линейных уравнений:
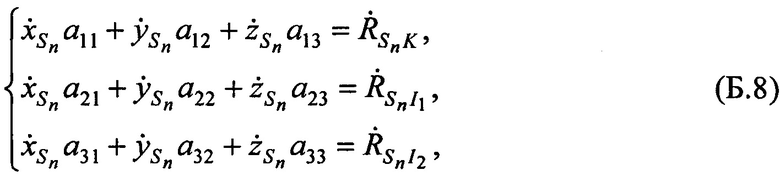
где коэффициенты при переменных 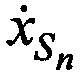 ,
, 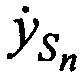 ,
, 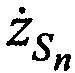 равны:
равны:
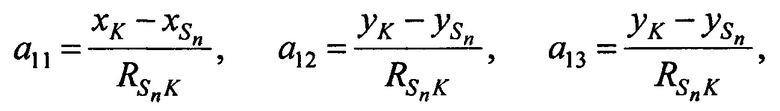
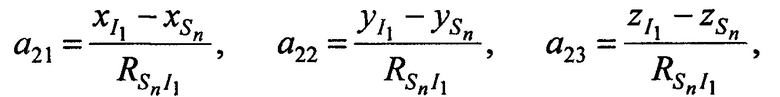
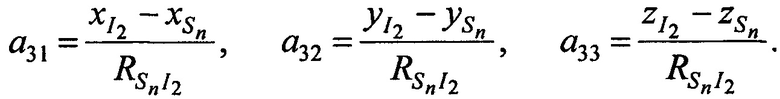
Систему из трех линейных уравнений (Б.8) с тремя неизвестными решают одним из известных методов, например, методом Крамера. Результатом решения системы уравнении (Б.8) выступают ортогональные составляющие вектора скорости CP 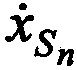 ,
, 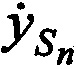 ,
, 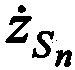 .
.
Приложение В
Алгоритм определения местоположения AT с помощью CP на низкой околоземной орбите для трех моментов измерения
В качестве исходных данных разработанного алгоритма выступают: координаты КРМ xK, yK, zK; КП CP - координаты CP 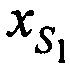 ,
, 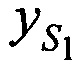 ,
, 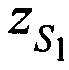 ,
, 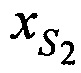 ,
, 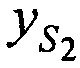 ,
, 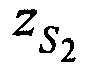 ,
, 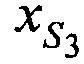 ,
, 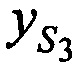 ,
, 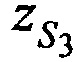 и ортогональные составляющие вектора его скорости
и ортогональные составляющие вектора его скорости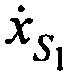 ,
,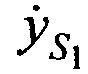 ,
, 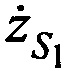 ,
, 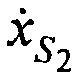 ,
, 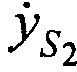 ,
, 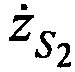 ,
, 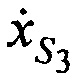 ,
, 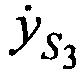 ,
, 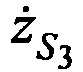 в моменты времени t1, t2 и t3; радиус сферы поверхности земли
в моменты времени t1, t2 и t3; радиус сферы поверхности земли 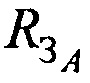 .
.
В КРМ измеряют НСЧ радиосигналов 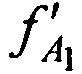 ,
, 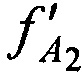 и
и 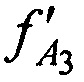 , принятых от AT через CP в моменты времени t1, t2 и t3. Вместе с тем указанные НСЧ представляют в следующем виде:
, принятых от AT через CP в моменты времени t1, t2 и t3. Вместе с тем указанные НСЧ представляют в следующем виде:
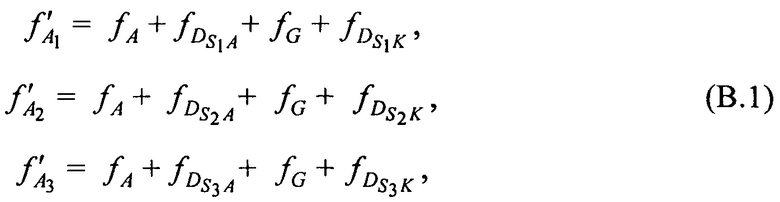
где ƒG - номинала частоты конвертирования, 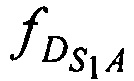 ,
, 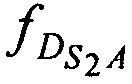 ,
, 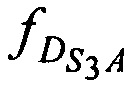 - доплеровские сдвиги частот радиосигналов AT на входе CP за счет его сближения (удаления) с (от) AT в моменты времени tn
- доплеровские сдвиги частот радиосигналов AT на входе CP за счет его сближения (удаления) с (от) AT в моменты времени tn 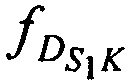 ,
, 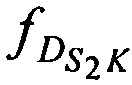 ,
, 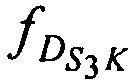 - доплеровские сдвиги частот радиосигналов AT на выходе CP за счет его сближения (удаления) с (от) K в моменты времени tn.
- доплеровские сдвиги частот радиосигналов AT на выходе CP за счет его сближения (удаления) с (от) K в моменты времени tn.
Для компенсации неизвестного НСЧ радиосигнала AT ƒA на основе тождеств (В.1) составляют разностные уравнения:
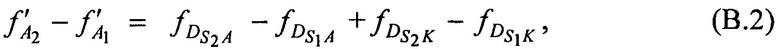
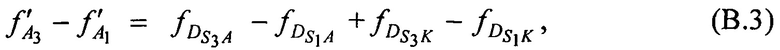
Поскольку справедливы неравенства 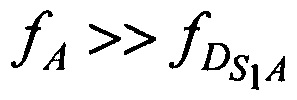 ,
, 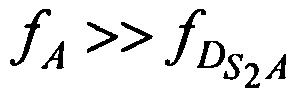 ,
, 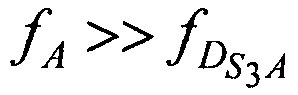 и
и 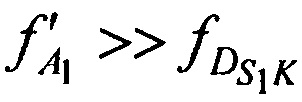 ,
, 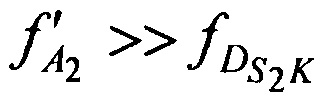 ,
, 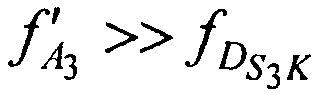 , то выражения для расчета доплеровских сдвигов частот имеют следующий вид:
, то выражения для расчета доплеровских сдвигов частот имеют следующий вид:
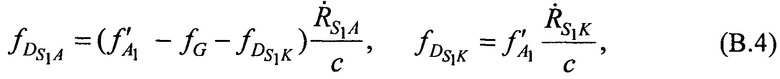
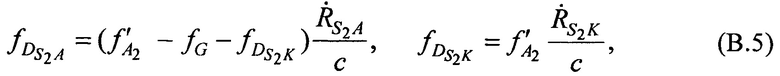
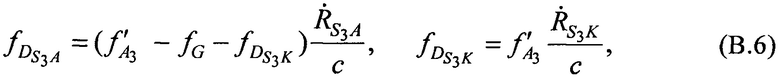
где 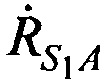 ,
, 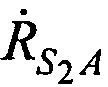 ,
, 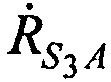 и
и 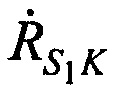 ,
, 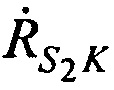 ,
, 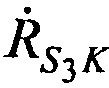 - радиальные скорости CP относительно AT и КРМ в моменты времени t1, t2, t3.
- радиальные скорости CP относительно AT и КРМ в моменты времени t1, t2, t3.
Рассчитывают значения радиальных скоростей CP относительно КРМ 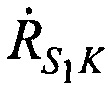 ,
, 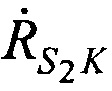 ,
, 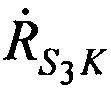 в моменты времени t1, t2, t3 по формулам:
в моменты времени t1, t2, t3 по формулам:
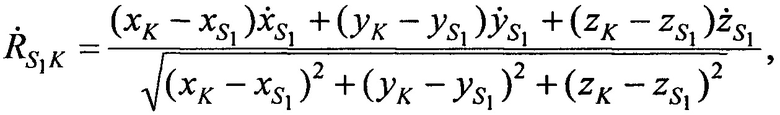
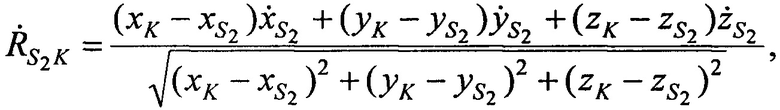
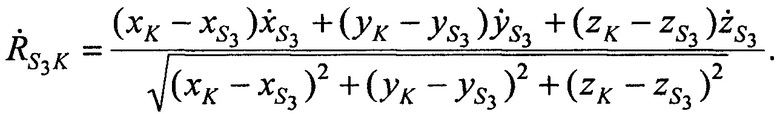
Составляют тождества для расчета радиальных скоростей CP относительно AT 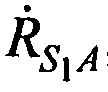 ,
, 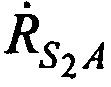 ,
, 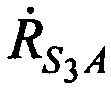 в моменты времени t1, t2, t3:
в моменты времени t1, t2, t3:
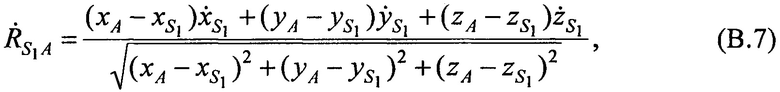
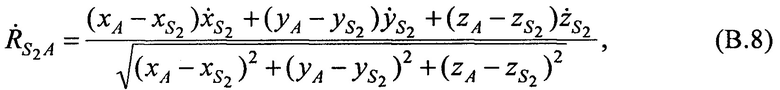
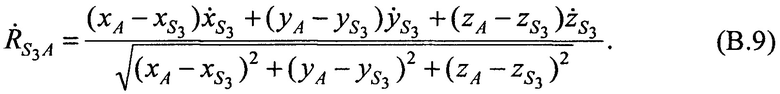
где хА, уА и zA - искомые координаты AT.
Разностное уравнение (В.2) с учетом (В.4), (В.5), (В.7) и (В.8), приобретает вид:
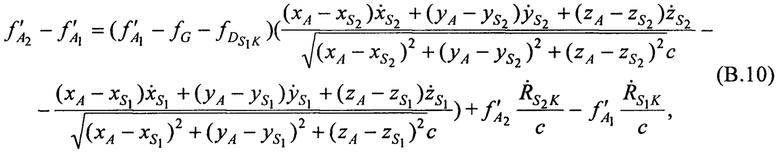
Выражение (В.10), содержащее три неизвестных переменные хА, уА и zA, преобразуют к виду:
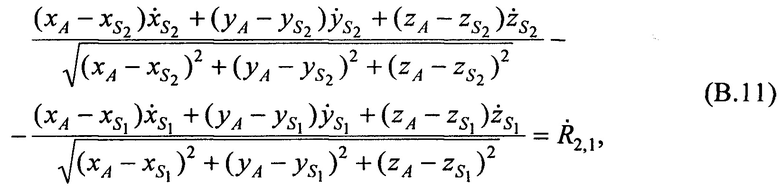
где коэффициент в правой части 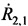 - разность радиальных скоростей CP относительно AT в моменты времени t2 и t1, которая вычисляется в соответствии с выражением:
- разность радиальных скоростей CP относительно AT в моменты времени t2 и t1, которая вычисляется в соответствии с выражением:
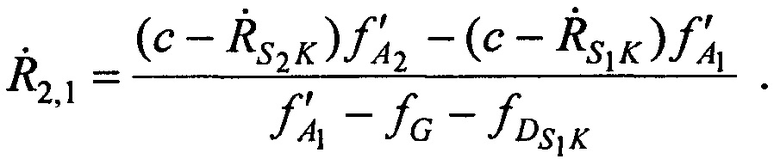
Аналогично преобразуя (В.3), с учетом (В.5), (В.6), (В.8) и (В.9) получают:
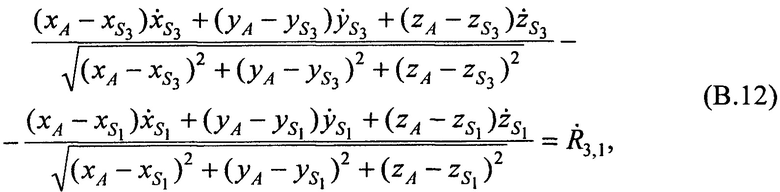
где коэффициент в правой части 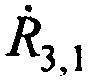 - разность радиальных скоростей CP относительно AT в моменты времени t3 и t1, которая вычисляется в соответствии с выражением:
- разность радиальных скоростей CP относительно AT в моменты времени t3 и t1, которая вычисляется в соответствии с выражением:
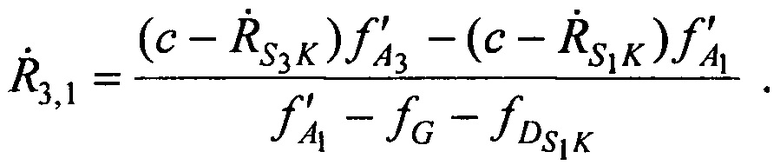
В предположении, что AT расположен на земной поверхности, составляют еще одно уравнение с переменными хА, уА и zA:

Уравнения (В.11), (В.12) и (В.13) в совокупности образуют систему уравнений
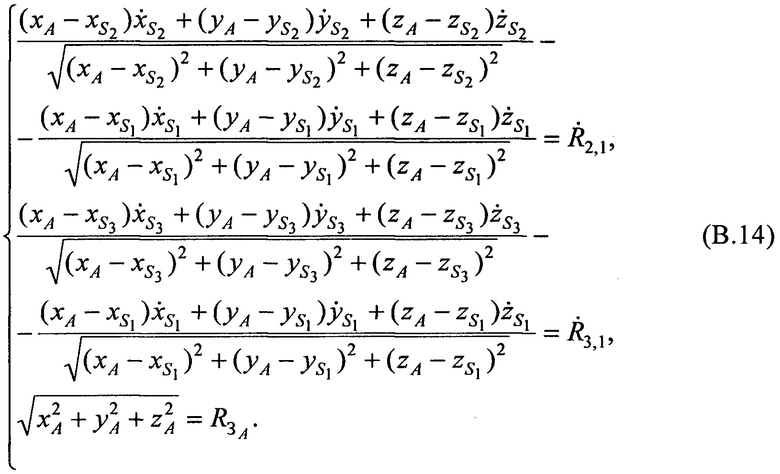
Для решения системы уравнений второго порядка (В.14) применяют итерационный алгоритм, включающий следующие этапы:
Этап 1. Задают произвольные, но для быстрой сходимости наиболее правдоподобные опорные координаты AT: x'A, y'A, z'A.
Этап 2. Определяют значения функций 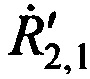 ,
, 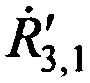 и
и 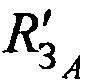 системы уравнений (В.14) в точке с опорными координатами AT х'А, у'А, z'A:
системы уравнений (В.14) в точке с опорными координатами AT х'А, у'А, z'A:
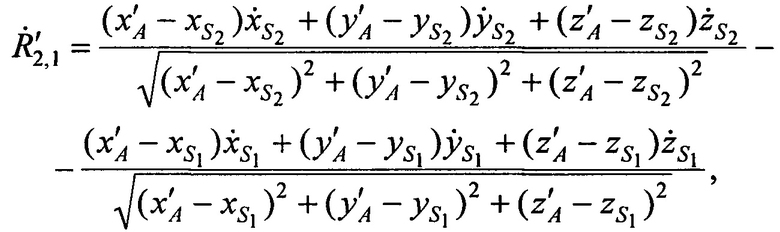
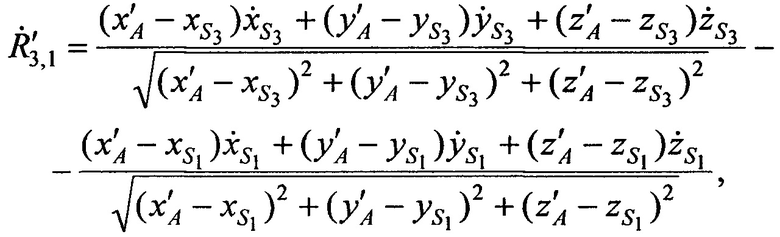
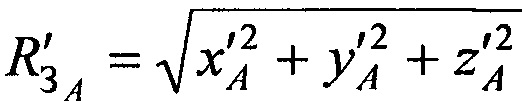
Этап 3. Рассчитывают невязки q4, q5 и q6 по формулам
 ,
, 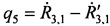 ,
, 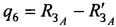 .
.
Этап 4. Составляют систему трех линейных уравнений, в которой в качестве неизвестных выступают поправки к точке с опорными координатами AT ΔхА, ΔуА и ΔzA, на основе разложений функций 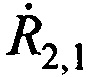 ,
, 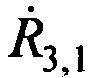 и
и 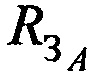 в ряды Тейлора с точностью до первых производных:
в ряды Тейлора с точностью до первых производных:
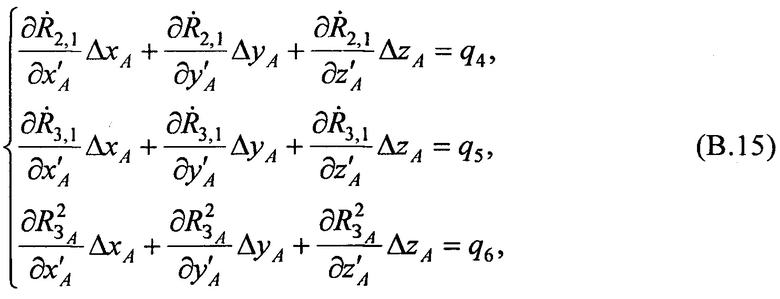
где значения частных производных в точке с опорными координатами AT х'А, y'A, z'А равны:
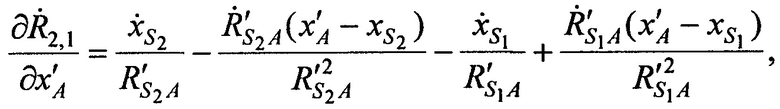
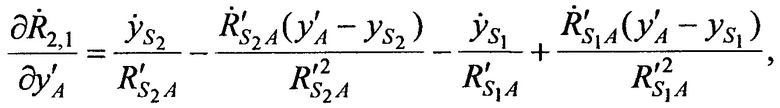
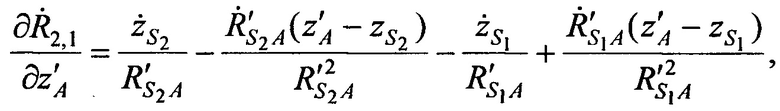
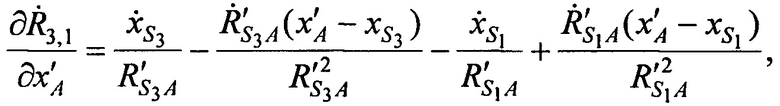
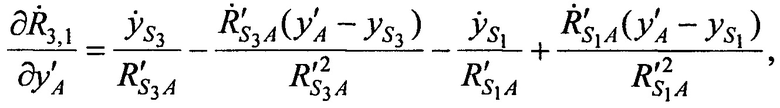
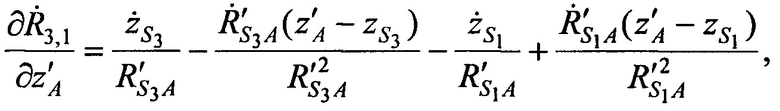
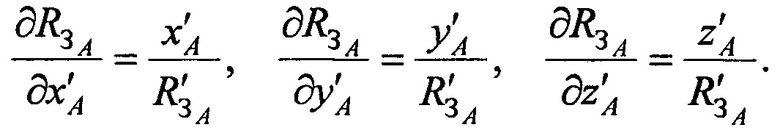
а, расстояния 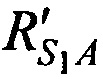 ,
, 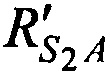 ,
, 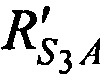 от CP в моменты времени t1, t2, t3 до точки с опорными координатами AT х'А, у'А, z'A и радиальные скорости
от CP в моменты времени t1, t2, t3 до точки с опорными координатами AT х'А, у'А, z'A и радиальные скорости 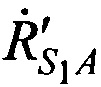 ,
, 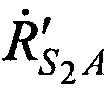 ,
, 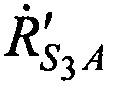 CP в моменты времени t1, t2, t3 относительно точки с опорными координатами AT x'A, y'A, z'A равны:
CP в моменты времени t1, t2, t3 относительно точки с опорными координатами AT x'A, y'A, z'A равны:
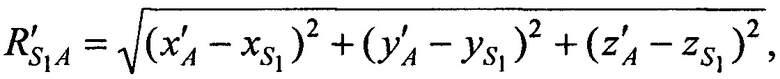
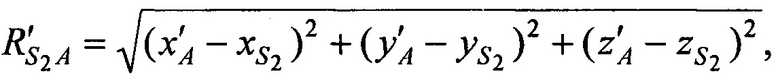
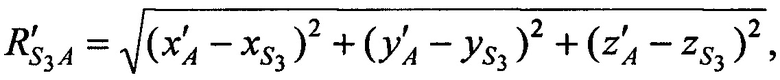
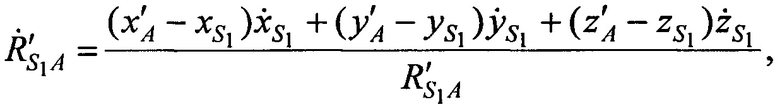
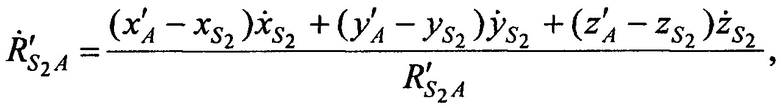
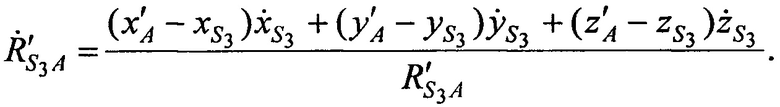
Этап 5. Решают систему трех линейных уравнений (В.15), с тремя неизвестными одним из известных методов, например, методом Крамера.
Результатом решения системы уравнений (В.15) выступают поправки к опорным координатам AT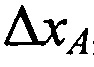 ,
,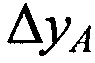 ,
,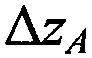
Этап 6. Определяют новые опорные координаты AT 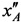 ,
, 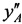 ,
, 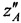 :
:
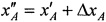 ;
; 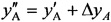 ;
; 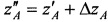 .
.
Этапы 1…6 в совокупности образуют первую итерацию. Далее итерации повторяют, используя каждый раз новые опорные координаты AT, полученные на этапе 6 предыдущей итерации. Количество необходимых итераций зависит от корректности выбора начальных опорных координаты (этап 1) и требуемой точности определения координат AT.
Окончательно, в качестве координат AT xA, yA, zA принимают значения опорных координат AT на последней итерации.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ АБОНЕНТСКОГО ТЕРМИНАЛА С ПОМОЩЬЮ НЕ МЕНЕЕ ДВУХ СПУТНИКОВ-РЕТРАНСЛЯТОРОВ НА НИЗКОЙ ОКОЛОЗЕМНОЙ ОРБИТЕ | 2017 |
|
RU2684740C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ СКОРОСТИ ДВУХ КОСМИЧЕСКИХ АППАРАТОВ С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ И ИЗЛУЧАЮЩЕЙ ОПОРНОЙ РЕПЕРНОЙ СТАНЦИИ | 2022 |
|
RU2791153C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ КОСМИЧЕСКОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ И ИЗЛУЧАЮЩЕЙ ОПОРНОЙ РЕПЕРНОЙ СТАНЦИИ | 2021 |
|
RU2788518C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ДВУХ КОСМИЧЕСКИХ АППАРАТОВ С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ И ИЗЛУЧАЮЩЕЙ ОПОРНОЙ РЕПЕРНОЙ СТАНЦИИ | 2022 |
|
RU2787890C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ И СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ КОСМИЧЕСКОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ | 2020 |
|
RU2750753C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРА СКОРОСТИ И СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ КОСМИЧЕСКОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ | 2020 |
|
RU2750228C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ С ИСПОЛЬЗОВАНИЕМ ПРИЕМО-ПЕРЕДАЮЩИХ ОПОРНЫХ РЕПЕРНЫХ СТАНЦИЙ | 2018 |
|
RU2708883C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРТОГОНАЛЬНЫХ СОСТАВЛЯЮЩИХ ВЕКТОРОВ СКОРОСТЕЙ И СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ДВУХ КОСМИЧЕСКИХ АППАРАТОВ С ИСПОЛЬЗОВАНИЕМ ЗЕМНЫХ СТАНЦИЙ | 2020 |
|
RU2750983C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ С ИСПОЛЬЗОВАНИЕМ ПРИЕМНЫХ ОПОРНЫХ РЕПЕРНЫХ СТАНЦИЙ | 2018 |
|
RU2702098C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ОРБИТЫ ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ | 2017 |
|
RU2652603C1 |
Изобретение относится к радиотехнике, а именно к способам определения местоположения источника радиоизлучения (ИРИ), и может быть использовано в навигационных, пеленгационных, локационных средствах для определения местоположения абонентского терминала (AT) по радиосигналам, принятым от спутника-ретранслятора (CP) на низкой околоземной орбите. Технический результат состоит в повышении точности определения частотных сдвигов сигналов системы. Для этого способ основан на размещении комплекса радиоэлектронного мониторинга (КРМ) и М≥2 излучающих опорных реперных станций (ИОРС) на позициях с известными координатами, задании района ведения радиомониторинга (РВРМ), излучении с помощью аппаратуры КРМ и m-ми, где m=1…М, ИОРС тестовых радиосигналов в моменты времени tn, где n=1…N, N≥3, приеме в КРМ указанных тестовых радиосигналов после их ретрансляции CP, определении канонических параметров CP в моменты времени tn, выборе в качестве поверхности земли сферы с радиусом, рассчитываемым на основе средней широты РВРМ, и последующем определении местоположения AT на поверхности земли. 1 з.п. ф-лы, 5 ил.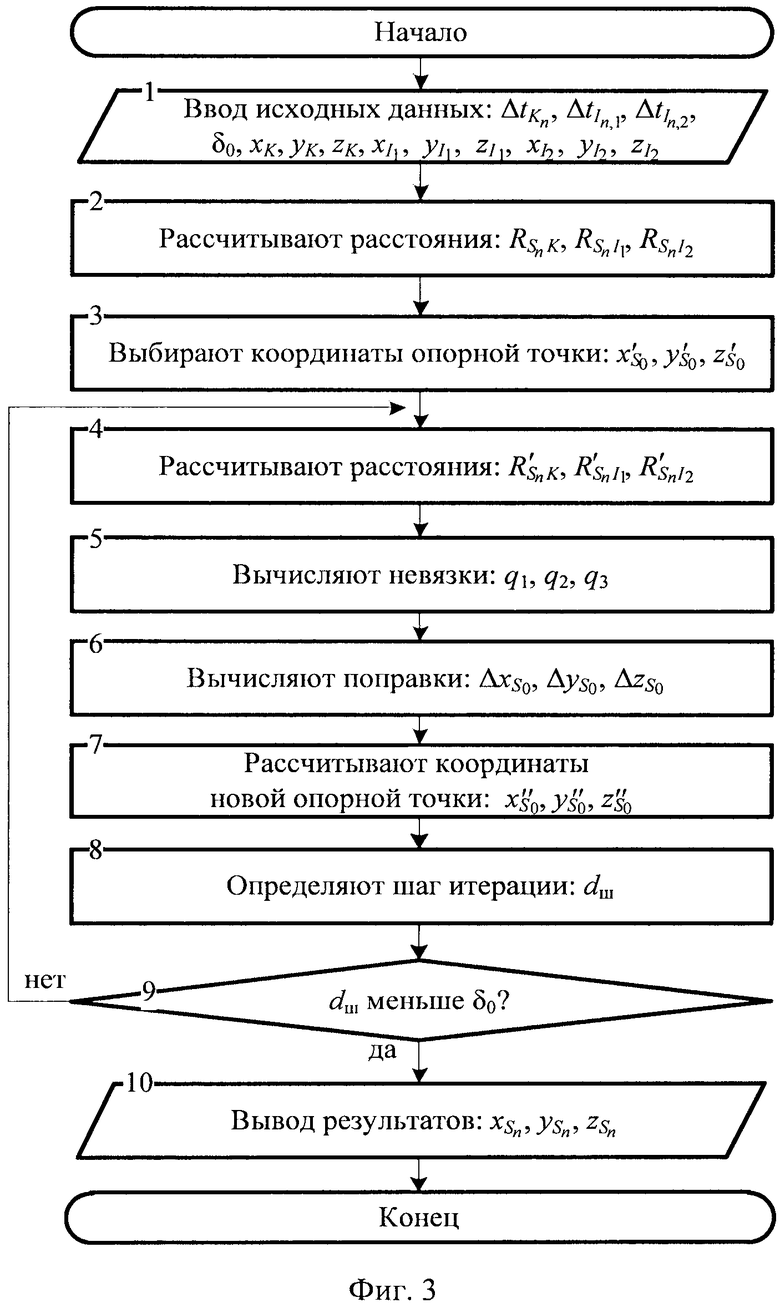
1. Способ определения местоположения абонентского терминала (AT) с помощью спутника-ретранслятора (CP) на низкой околоземной орбите, заключающийся в том, что размещают комплекс радиоэлектронного мониторинга (КРМ), содержащий приемную и передающую аппаратуру, на позиции с известными координатами xK, yK, zK, в качестве объекта радиоэлектронного мониторинга выбирают CP с известным номиналом частоты конвертирования ƒG, излучают с помощью аппаратуры КРМ тестовый радиосигнал с номиналом средней частоты (НСЧ) 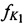 в направлении на CP в момент времени t1, измеряют в КРМ НСЧ радиосигнала
в направлении на CP в момент времени t1, измеряют в КРМ НСЧ радиосигнала 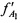 , принятого от AT через CP в момент времени t1, на основании известных координат КРМ xK, yK, zK, номинала частоты конвертирования ƒG, НСЧ
, принятого от AT через CP в момент времени t1, на основании известных координат КРМ xK, yK, zK, номинала частоты конвертирования ƒG, НСЧ 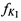 и
и 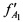 переданного тестового радиосигнала и принятого от AT через CP радиосигнала в момент времени t1 вычисляют местоположение AT на поверхности земли, отличающийся тем, что дополнительно устанавливают на земной поверхности М≥2 излучающих опорных реперных станций (ИОРС) на позициях с известными координатами xIm, yIm, zIm, где m=1…М - номер ИОРС, а для выбора CP в качестве объекта радиоэлектронного мониторинга предварительно задают район ведения радиомониторинга (РВРМ) как область на поверхности земли, в которой необходимо определить местоположение AT, и выбирают n-е моменты времени tn, где n=1…N, N≥3, при которых зона освещенности указанного CP охватывает и КРМ, и РВРМ, и позиции всех m-х ИОРС, определяют n-е канонические параметры (КП) CP, включающие координаты CP
переданного тестового радиосигнала и принятого от AT через CP радиосигнала в момент времени t1 вычисляют местоположение AT на поверхности земли, отличающийся тем, что дополнительно устанавливают на земной поверхности М≥2 излучающих опорных реперных станций (ИОРС) на позициях с известными координатами xIm, yIm, zIm, где m=1…М - номер ИОРС, а для выбора CP в качестве объекта радиоэлектронного мониторинга предварительно задают район ведения радиомониторинга (РВРМ) как область на поверхности земли, в которой необходимо определить местоположение AT, и выбирают n-е моменты времени tn, где n=1…N, N≥3, при которых зона освещенности указанного CP охватывает и КРМ, и РВРМ, и позиции всех m-х ИОРС, определяют n-е канонические параметры (КП) CP, включающие координаты CP 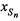 ,
, 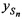 ,
, 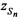 и ортогональные составляющие вектора его скорости
и ортогональные составляющие вектора его скорости 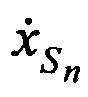 ,
, 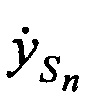 ,
, 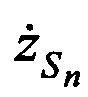 в моменты времени tn, на основе излучения тестовых радиосигналов КРМ и m-ми ИОРС в направлении на CP и их последующего приема КРМ после переизлучения указанным CP, измеряют в КРМ НСЧ радиосигналов
в моменты времени tn, на основе излучения тестовых радиосигналов КРМ и m-ми ИОРС в направлении на CP и их последующего приема КРМ после переизлучения указанным CP, измеряют в КРМ НСЧ радиосигналов 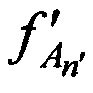 , принятых от AT через CP, в моменты времени
, принятых от AT через CP, в моменты времени 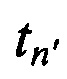 , где n'=2…N, выделяют в качестве опорных g-e, где g=1,…,N, КП CP для момента времени tg, формируют N-1 отличающихся друг от друга пар КП CP, в каждой из которых первые КП CP соответствуют моменту времени tg, а вторые КП CP соответствуют моменту времени t1, где l=1…N, l≠g, вычисляют N-1 разностей радиальных скоростей
, где n'=2…N, выделяют в качестве опорных g-e, где g=1,…,N, КП CP для момента времени tg, формируют N-1 отличающихся друг от друга пар КП CP, в каждой из которых первые КП CP соответствуют моменту времени tg, а вторые КП CP соответствуют моменту времени t1, где l=1…N, l≠g, вычисляют N-1 разностей радиальных скоростей 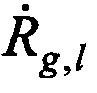 для каждой сформированной пары КП CP на основе g-x и l-х КП CP, координат КРМ xK, yK, zK, номинала частоты конвертирования ƒG, НСЧ радиосигналов
для каждой сформированной пары КП CP на основе g-x и l-х КП CP, координат КРМ xK, yK, zK, номинала частоты конвертирования ƒG, НСЧ радиосигналов 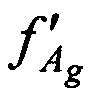 ,
, 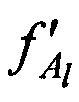 принятых от AT через CP в моменты времени tg и tl соответственно, в качестве поверхности земли принимают сферу с радиусом
принятых от AT через CP в моменты времени tg и tl соответственно, в качестве поверхности земли принимают сферу с радиусом 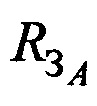 , который рассчитывается на основе средней широты РВРМ ϕA, а определение местоположения AT на поверхности земли производят с использованием n-х КП CP, N-1 разностей радиальных скоростей
, который рассчитывается на основе средней широты РВРМ ϕA, а определение местоположения AT на поверхности земли производят с использованием n-х КП CP, N-1 разностей радиальных скоростей 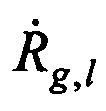 и радиуса сферы поверхности земли
и радиуса сферы поверхности земли 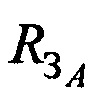 .
.
2. Способ по п. 1. отличающийся тем, что для определения n-х КП CP в моменты времени tn, предварительно излучают с помощью аппаратуры КРМ тестовые радиосигналы с НСЧ 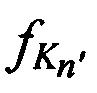 в направлении на CP в моменты времени
в направлении на CP в моменты времени 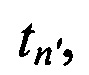 излучают m-ми ИОРС тестовые радиосигналы с НСЧ
излучают m-ми ИОРС тестовые радиосигналы с НСЧ 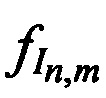 в направлении на CP в моменты времени tn, принимают с помощью КРМ переизлученные CP тестовые радиосигналы с НСЧ
в направлении на CP в моменты времени tn, принимают с помощью КРМ переизлученные CP тестовые радиосигналы с НСЧ 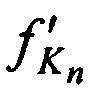 и
и 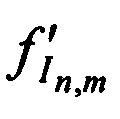 в моменты времени
в моменты времени 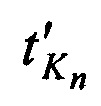 и
и 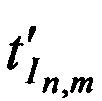 соответственно, передают в КРМ НСЧ тестовых радиосигналов
соответственно, передают в КРМ НСЧ тестовых радиосигналов 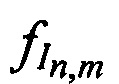 от m-х ИОРС, измеряют задержки во времени
от m-х ИОРС, измеряют задержки во времени 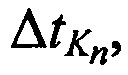
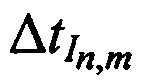 между излученными и принятыми тестовыми радиосигналами, после чего вычисляют наклонные дальности от CP до КРМ
между излученными и принятыми тестовыми радиосигналами, после чего вычисляют наклонные дальности от CP до КРМ 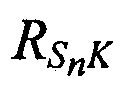 и до m-х ИОРС
и до m-х ИОРС 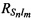 , соответствующие моментам времени tn, рассчитывают координаты CP
, соответствующие моментам времени tn, рассчитывают координаты CP 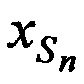 ,
, 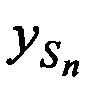 ,
, 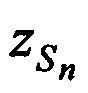 в моменты времени tn по известным координатам КРМ и m-х ИОРС, а также измеренным наклонным дальностям
в моменты времени tn по известным координатам КРМ и m-х ИОРС, а также измеренным наклонным дальностям 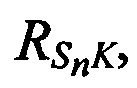 и
и 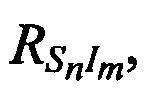 измеряют радиальные скорости CP относительно КРМ
измеряют радиальные скорости CP относительно КРМ 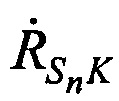 и m-х ИОРС
и m-х ИОРС 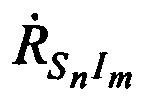 в моменты времени tn на основе известных координат КРМ и m-х ИОРС, рассчитанных координат CP
в моменты времени tn на основе известных координат КРМ и m-х ИОРС, рассчитанных координат CP 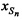 ,
, 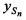 ,
, 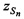 , а также запомненных НСЧ переданных
, а также запомненных НСЧ переданных 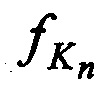 ,
, 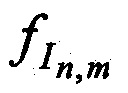 и принятых
и принятых 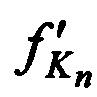 ,
, 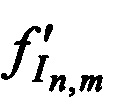 тестовых радиосигналов, вычисляют ортогональные составляющие вектора скорости CP
тестовых радиосигналов, вычисляют ортогональные составляющие вектора скорости CP 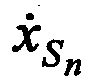 ,
, 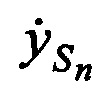 ,
, 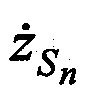 в моменты времени tn используя известные координаты КРМ и m-х ИОРС, вычисленные координаты CP
в моменты времени tn используя известные координаты КРМ и m-х ИОРС, вычисленные координаты CP 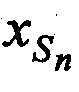 ,
, 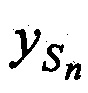 ,
, 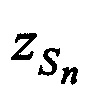 и измеренные радиальные скорости
и измеренные радиальные скорости 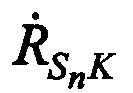 и
и 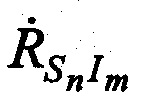 , а в качестве n-х КП CP принимают совокупность координат CP
, а в качестве n-х КП CP принимают совокупность координат CP 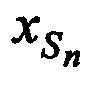 ,
, 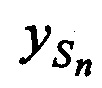 ,
, 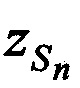 и ортогональных составляющих вектора его скорости
и ортогональных составляющих вектора его скорости 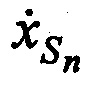 ,
, 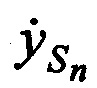 ,
, 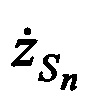 в момент времени tn.
в момент времени tn.
| МОБИЛЬНАЯ СТАНЦИЯ ВИДЕОМОНИТОРИНГА И СВЯЗИ | 2008 |
|
RU2398353C2 |
| СИСТЕМА ГЛОБАЛЬНОГО МОНИТОРИНГА В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ ПАРАМЕТРОВ СОСТОЯНИЯ МНОГОПАРАМЕТРИЧЕСКИХ ОБЪЕКТОВ | 2014 |
|
RU2568291C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ПОЛЬЗОВАТЕЛЬСКОГО ТЕРМИНАЛА С ИСПОЛЬЗОВАНИЕМ ДВУХ СПУТНИКОВ-РЕТРАНСЛЯТОРОВ | 2015 |
|
RU2605457C1 |
| Перекатываемый затвор для водоемов | 1922 |
|
SU2001A1 |
| Дорожная спиртовая кухня | 1918 |
|
SU98A1 |
Авторы
Даты
2019-02-14—Публикация
2017-10-06—Подача