Заявленное техническое решение относится к области радиотехники, а именно к способам определения местоположения (ОМП) источников радиоизлучения.
Заявленное изобретение может быть использовано при построении подсистемы ОМП пользовательских терминалов (ПТ) спутниковой системы связи (ССС).
Известен способ ОМП ПТ с использованием глобальной спутниковой радионавигационной системы ГЛОНАСС. Данный способ широко известен и описан, например, в книге Тяпкина В.Н. и Гарина Е.Н. «Методы определения навигационных параметров подвижных средств с использованием спутниковой радионавигационной системы ГЛОНАСС». - Красноярск: Сиб. федер. ун-т, 2012. - 260 с. При этом для одномоментного ОМП ПТ в пространстве требуется наличие сигналов минимум четырех спутников. Однако указанный аналог имеет недостатки. Так, ПТ должен иметь отдельный приемник, принимающий сигналы системы ГЛОНАСС. Еще одним недостатком является повышение требований к вычислительным ресурсам ПТ, позволяющим рассчитывать свои координаты по сигналам системы ГЛОНАСС.
Известен также аналог-способ определения местоположения земной станции спутниковой связи по ретранслированному сигналу из патента РФ 2172495 МПК G01S 5/06 (2006.01) от 06.05.00. Данный способ основывается на измерении доплеровских сдвигов частот сигналов, ретранслированных одним спутником-ретранслятором (CP1 в течение нескольких часов. Указанный аналог также имеет существенные недостатки. Первый недостаток связан с недопустимо длительным интервалом времени ОМП ПТ, необходимым для наблюдения за сигналами системы. Второй недостаток - громоздкость вычислений, которые влекут существенное удорожание стоимости системы, его реализующего.
Наиболее близким по своей технической сущности к заявленному способу ОМП ПТ является способ ОМП ПТ, описанный в патенте РФ 2256935 МПК G01S 5/02 (2006.01) от 26.09.1997. Способ-прототип, включающий в себя ПТ, по меньшей мере два спутника с известными местоположениями и известными скоростями и узел межсетевого сопряжения (УМС) для осуществления связи с ПТ через упомянутые спутники, включающий этап определения параметра дальности, представляющего собой расстояние между одним из спутников и ПТ, этап определения параметра разности дальностей, представляющего собой разность расстояний одного и другого спутника от ПТ, этап определения по меньшей мере одного из следующих параметров: параметра скорости изменения дальности, представляющего собой радиальную скорость одного из спутников относительно ПТ, параметра разности скоростей изменения дальностей, представляющего собой разность радиальных скоростей одного и другого спутника относительно ПТ, этап определения положения ПТ на поверхности Земли на основе известных местоположений и известных скоростей CP, а также указанных параметра дальности, параметра скорости изменения дальности и по меньшей мере одного из упомянутых параметров разности дальностей и разности скоростей изменения дальностей.
При таком способе обеспечивается высокое быстродействие ОМП ПТ без существенного усложнения аппаратуры ПТ и УМС.
Недостатком ближайшего аналога (прототипа) является относительно-невысокая точность определения координат ПТ при изменении скорости перемещения ПТ, вследствие возможности размещения его на широком классе движущихся объектов (автомобиль, вертолет, самолет и т.д.).
Техническим результатом при использовании заявленного решения является разработка способа ОМП ПТ с использованием двух CP, обеспечивающего повышение точности определения координат ПТ при изменении скорости его перемещения.
Указанный технический результат в заявляемом способе ОМП ПТ достигается тем, что в известном способе ОМП ПТ с использованием двух спутников-ретрансляторов CP1, СР2 и узла межсетевого соединения (УМС), заключающемся в том, что на основе измерений временных задержек и частотных сдвигов между переданными и принятыми тестовыми сигналами системы, известных модуля 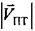 , азимута αПТ вектора скорости
, азимута αПТ вектора скорости 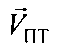 пользовательского терминала и его высоты hПТ, относительно земной поверхности, с учетом координат CP1, CP2, векторов их скоростей
пользовательского терминала и его высоты hПТ, относительно земной поверхности, с учетом координат CP1, CP2, векторов их скоростей 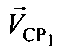 ,
, 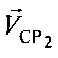 координат УМС и предварительно заданных частотных сдвигов
координат УМС и предварительно заданных частотных сдвигов 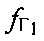 ,
, 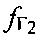 рабочих частот CP1, СР2, определяют расстояние
рабочих частот CP1, СР2, определяют расстояние 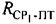 между первым CP1 и ПТ, определяют расстояние
между первым CP1 и ПТ, определяют расстояние 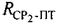 между вторым CP2 и ПТ, определяют, по меньшей мере, один из параметров: радиальную скорость
между вторым CP2 и ПТ, определяют, по меньшей мере, один из параметров: радиальную скорость 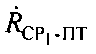 перемещения первого CP1 относительно ПТ, и/или радиальную скорость
перемещения первого CP1 относительно ПТ, и/или радиальную скорость 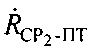 перемещения второго СР2 относительно ПТ, после чего с учетом координат CP1, СР2, векторов их скоростей
перемещения второго СР2 относительно ПТ, после чего с учетом координат CP1, СР2, векторов их скоростей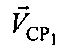 ,
, 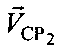 , определенных параметров
, определенных параметров 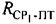 ,
, 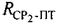 , а также радиальной скорости
, а также радиальной скорости 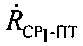 и/или радиальной скорости
и/или радиальной скорости 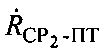 , вычисляют широту φПТ и долготу λПТ пользовательского терминала, дополнительно на основе известных модуля
, вычисляют широту φПТ и долготу λПТ пользовательского терминала, дополнительно на основе известных модуля 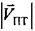 , азимута αПТ вектора скорости
, азимута αПТ вектора скорости 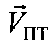 пользовательского терминала и его высоты hПТ относительно земной поверхности вычисляют в УМС доплеровские сдвиги частот
пользовательского терминала и его высоты hПТ относительно земной поверхности вычисляют в УМС доплеровские сдвиги частот 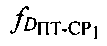 и
и 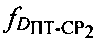 первого и второго узкополосных тестовых сигналов, обусловленные изменениями радиальных скоростей ПТ относительно CP1 и CP2, для чего предварительно определяют вероятные местоположения ПТ с учетом координат спутников-ретрансляторов CP1, CP2, определенных параметров
первого и второго узкополосных тестовых сигналов, обусловленные изменениями радиальных скоростей ПТ относительно CP1 и CP2, для чего предварительно определяют вероятные местоположения ПТ с учетом координат спутников-ретрансляторов CP1, CP2, определенных параметров 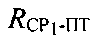 и
и 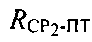 , а при определении по меньшей мере одного из параметров:
, а при определении по меньшей мере одного из параметров: 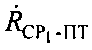 и/или
и/или 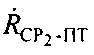 учитывают дополнительно доплеровские сдвиги частот
учитывают дополнительно доплеровские сдвиги частот 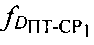 и
и 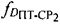 .
.
Дополнительные доплеровские сдвиги частот 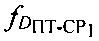 и
и 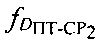 обусловлены изменениями радиальных скоростей ПТ относительно CP1 и CP2. При их вычислении предварительно определяют вероятные местоположения ПТ с учетом координат спутников-ретрансляторов CP1, CP2, определенных параметров
обусловлены изменениями радиальных скоростей ПТ относительно CP1 и CP2. При их вычислении предварительно определяют вероятные местоположения ПТ с учетом координат спутников-ретрансляторов CP1, CP2, определенных параметров 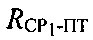 и
и 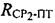 , известных модуля
, известных модуля 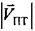 , азимута αПТ вектора скорости
, азимута αПТ вектора скорости 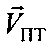 пользовательского терминала и его высоты hПТ относительно земной поверхности.
пользовательского терминала и его высоты hПТ относительно земной поверхности.
Для определения параметра 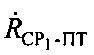 , в ПТ измеряют частоту
, в ПТ измеряют частоту 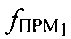 первого узкополосного тестового сигнала, излученного УМС на частоте
первого узкополосного тестового сигнала, излученного УМС на частоте 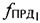 и ретранслированного через CP1, передают результат измерения в УМС и рассчитывают доплеровский сдвиг частоты
и ретранслированного через CP1, передают результат измерения в УМС и рассчитывают доплеровский сдвиг частоты 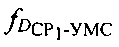 первого сигнала, обусловленного изменением радиальной скорости CP1 относительно УМС. Далее рассчитывают доплеровский сдвиг частоты
первого сигнала, обусловленного изменением радиальной скорости CP1 относительно УМС. Далее рассчитывают доплеровский сдвиг частоты 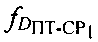 первого сигнала, обусловленного изменением радиальной скорости ПТ относительно CP1 и вычисляют параметр
первого сигнала, обусловленного изменением радиальной скорости ПТ относительно CP1 и вычисляют параметр 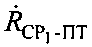 на основе первого сигнала, излучаемого на частоте
на основе первого сигнала, излучаемого на частоте 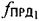 , предварительно заданной частоте сдвига
, предварительно заданной частоте сдвига 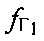 рабочей частоты CP1, измеренной частоты
рабочей частоты CP1, измеренной частоты 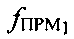 первого сигнала, принятого после прохождения им трассы УМС-CP1-ПТ, рассчитанных доплеровских сдвигов частот
первого сигнала, принятого после прохождения им трассы УМС-CP1-ПТ, рассчитанных доплеровских сдвигов частот 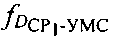 и
и 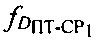 первого сигнала.
первого сигнала.
Для определения параметра 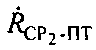 , в ПТ измеряют частоту
, в ПТ измеряют частоту 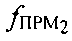 второго узкополосного тестового сигнала, излученного УМС на частоте
второго узкополосного тестового сигнала, излученного УМС на частоте 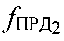 и ретранслированного через CP2, передают результат измерения в УМС и рассчитывают доплеровский сдвиг частоты
и ретранслированного через CP2, передают результат измерения в УМС и рассчитывают доплеровский сдвиг частоты 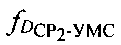 второго сигнала, обусловленного изменением радиальной скорости CP2 относительно УМС. Далее рассчитывают доплеровский сдвиг частоты
второго сигнала, обусловленного изменением радиальной скорости CP2 относительно УМС. Далее рассчитывают доплеровский сдвиг частоты 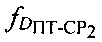 второго сигнала, обусловленного изменением радиальной скорости ПТ относительно СР2 и вычисляют параметр
второго сигнала, обусловленного изменением радиальной скорости ПТ относительно СР2 и вычисляют параметр 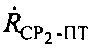 на основе второго сигнала, излучаемого на частоте
на основе второго сигнала, излучаемого на частоте 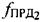 , предварительно заданной частоте сдвига
, предварительно заданной частоте сдвига 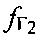 рабочей частоты СР2, измеренной частоты
рабочей частоты СР2, измеренной частоты 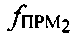 второго сигнала, принятого после прохождения им трассы УМС-CP2-ПТ, рассчитанных доплеровских сдвигов частот
второго сигнала, принятого после прохождения им трассы УМС-CP2-ПТ, рассчитанных доплеровских сдвигов частот 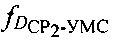 и
и 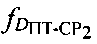 второго сигнала.
второго сигнала.
В альтернативном варианте при ОМП ПТ используют различные комбинации из четырех параметров: 1) дальность, 2) разность дальностей, 3) скорость изменения дальности, 4) разность скоростей изменения дальностей.
Однако совместное использование параметров: дальности от одного CP до ПТ и разности дальностей от одного и другого CP до ПТ, эквивалентно использованию двух параметров дальности: 1) дальности от CP1 до ПТ, 2) дальности от СР2 до ПТ. Аналогично, совместное использование параметров: скорости изменения дальности одного CP относительно ПТ и разности скоростей изменения дальностей одного и другого CP относительно ПТ, эквивалентно использованию двух параметров скоростей изменения дальности: 1) скорости изменения дальности CP1 относительно ПТ, 2) скорости изменения дальности СР2 относительно ПТ.
Вместе с тем, составление и решение уравнений, соответствующих параметрам положения для дальностей и скоростей изменения дальностей, значительно проще, чем для разности дальностей и разности скоростей изменения дальности, поэтому в предпочтительном варианте настоящего изобретения используют следующие параметры положения: 1) дальность 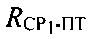 от CP1 до ПТ, 2) дальность
от CP1 до ПТ, 2) дальность 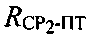 от CP2 до ПТ, 3) скорость
от CP2 до ПТ, 3) скорость 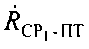 изменения дальности CP1 относительно ПТ, 4) скорость
изменения дальности CP1 относительно ПТ, 4) скорость 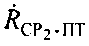 изменения дальности CP2 относительно ПТ.
изменения дальности CP2 относительно ПТ.
В альтернативном варианте рассматривают проекции линий положения на поверхности Земли, тем самым ограничивая пространственное расположение ПТ. В предпочтительном варианте рассматривают проекции линий положения на плоскость, параллельную поверхности Земли, имеющую произвольную известную высоту hПТ.
Параметры 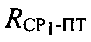 и
и 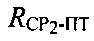 определяют на основе измерений временных задержек между переданными и принятыми тестовыми сигналами системы.
определяют на основе измерений временных задержек между переданными и принятыми тестовыми сигналами системы.
Параметры 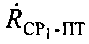 и
и 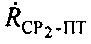 определяют на основе частотных сдвигов между переданными и принятыми тестовыми сигналами системы. Сдвиги тестовых сигналов системы являются суммой предварительно заданных частотных сдвигов
определяют на основе частотных сдвигов между переданными и принятыми тестовыми сигналами системы. Сдвиги тестовых сигналов системы являются суммой предварительно заданных частотных сдвигов 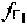 ,
, 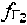 рабочих частот CP1, СР2 и доплеровскими сдвигами частот, обусловленными суммарными радиальными скоростями соответствующего CP относительно ПТ и УМС.
рабочих частот CP1, СР2 и доплеровскими сдвигами частот, обусловленными суммарными радиальными скоростями соответствующего CP относительно ПТ и УМС.
В альтернативном варианте предполагают, что ПТ не движется относительно земной поверхности. В реальных условиях ПТ может быть размещен на широком классе движущихся объектов (автомобиль, вертолет, самолет и т.д.). Движение ПТ относительно земной поверхности вносит в принятые тестовые сигналы системы дополнительные доплеровские сдвиги частот. Такие сдвиги можно не учитывать, если скорость CP относительно земной поверхности значительно превосходит скорость ПТ относительно земной поверхности. Но когда эти скорости соизмеримы, то для расчета параметров скорости изменения дальности и разности скоростей изменения дальностей необходимо учитывать дополнительные доплеровские сдвиги частот тестовых сигналов системы, обусловленных движением ПТ относительно земной поверхности.
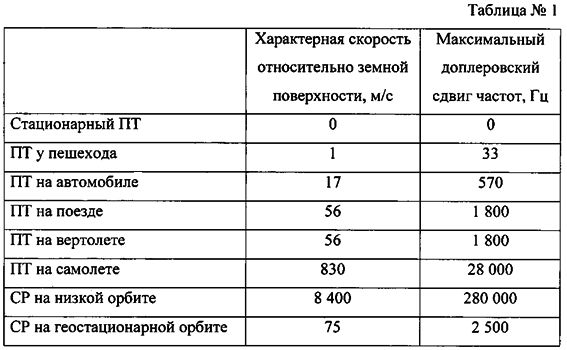
В таблице №1 приведены значения характерных скоростей и соответствующих им максимальных доплеровских сдвигов частот, вносимых некоторыми типами ПТ и CP при несущей частоте, равной 10 ГГц.
Анализ значений, приведенных в таблице, позволяет сделать вывод, что во многих случаях при определении суммарной радиальной скорости существенным фактором является учет скорости ПТ. Особенно это характерно для ССС на геостационарной орбите (ГСО).
Учет скорости ПТ приводит к повышению точности определения параметров 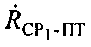 и/или
и/или 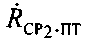 , что в свою очередь ведет к повышению точности ОМП ПТ.
, что в свою очередь ведет к повышению точности ОМП ПТ.
Одним из преимуществ настоящего изобретения является повышение точности ОМП ПТ.
Другим преимуществом настоящего изобретения является возможность ОМП ПТ на произвольной известной высоте hПТ.
Заявленный способ поясняется чертежами, на которых показаны:
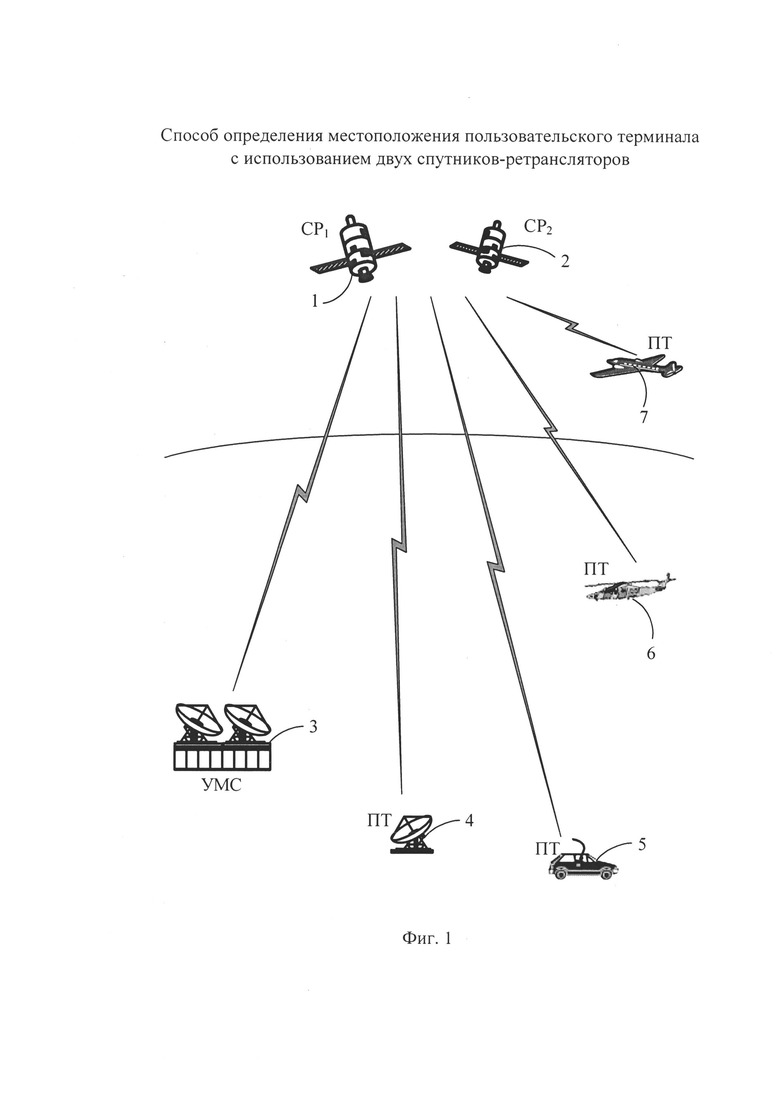
- на фиг. 1 - типовая спутниковая система связи;
- на фиг. 2 - геометрическая основа типовой спутниковой системы связи;
- на фиг. 3 - схема отсутствия эффекта Доплера;
- на фиг. 4 - схема проявления эффекта Доплера;
- на фиг. 5 - варианты нахождения взаимной радиальной скорости движущихся приемника и передатчика;
- на фиг. 6 - иллюстрация нахождения линии положения ПТ, как пересечения поверхности положения параметра дальности с плоскостью 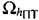 ;
;
- на фиг. 7 - иллюстрация нахождения линии положения ПТ, как пересечения поверхности положения параметра скорости изменения дальности с плоскостью 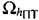 ;
;
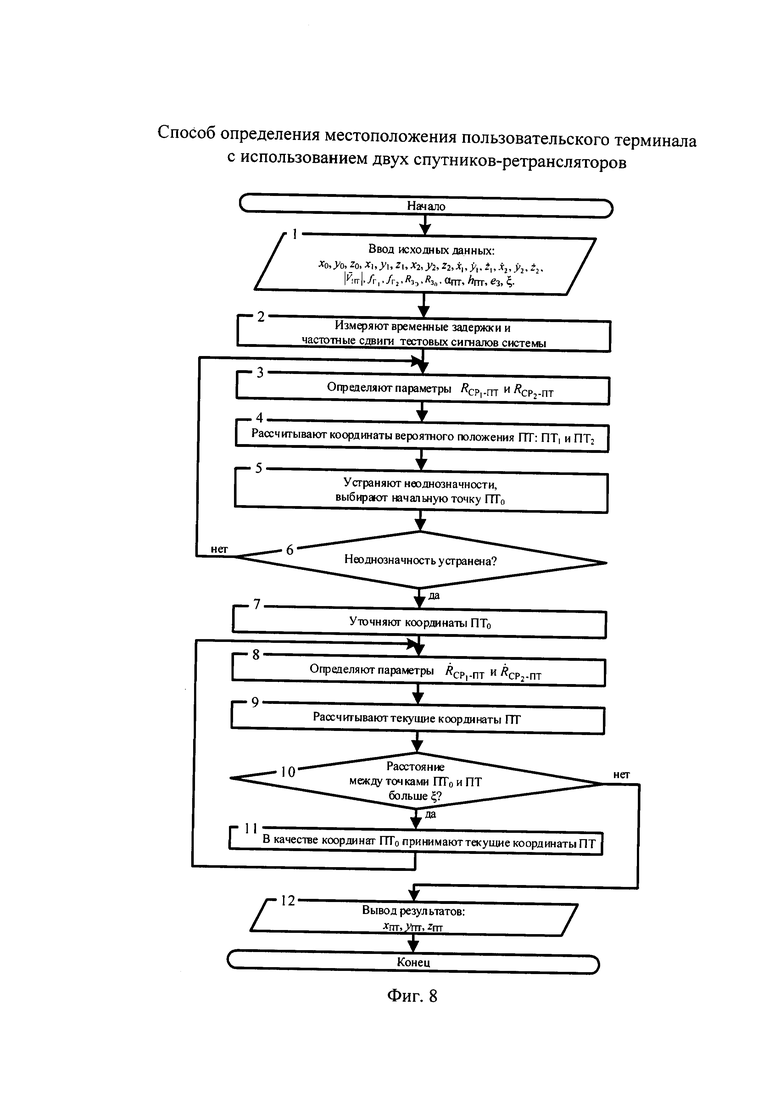
- на фиг. 8 - алгоритм определения местоположения пользовательского терминала;
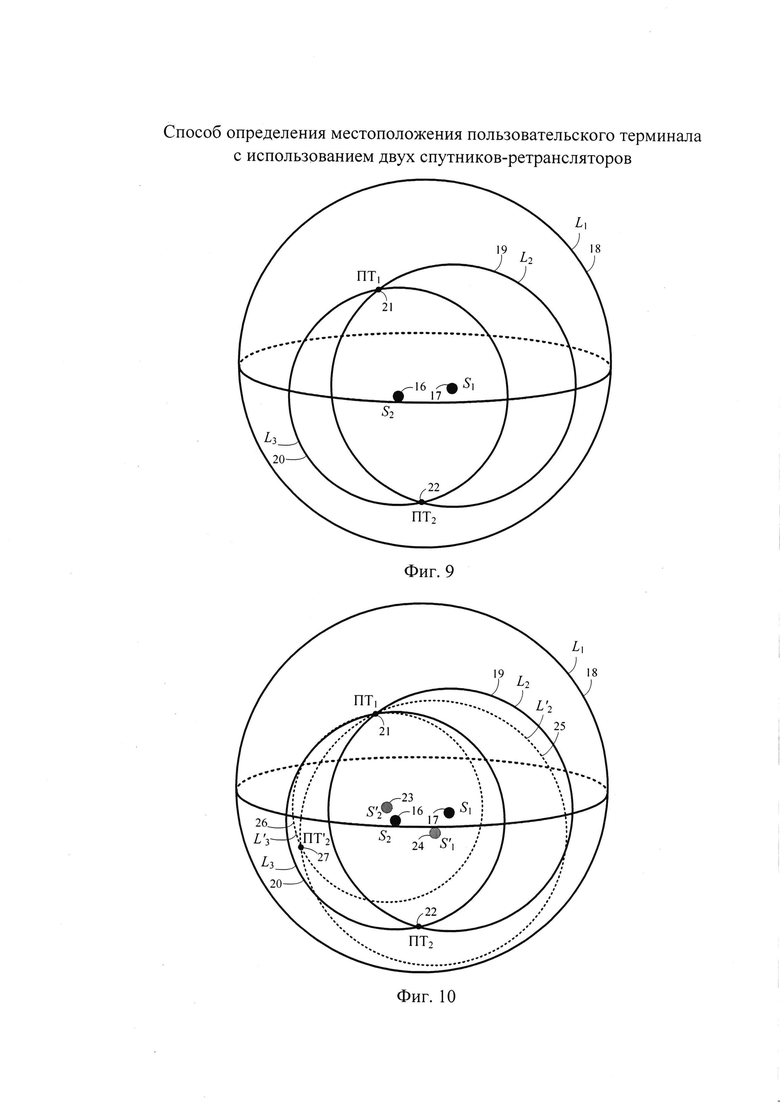
- на фиг. 9 - определение вероятных местоположений пользовательского терминала с использованием дальностей в качестве параметров положения;
- на фиг. 10 - принцип устранения неоднозначности для неподвижного пользовательского терминала;
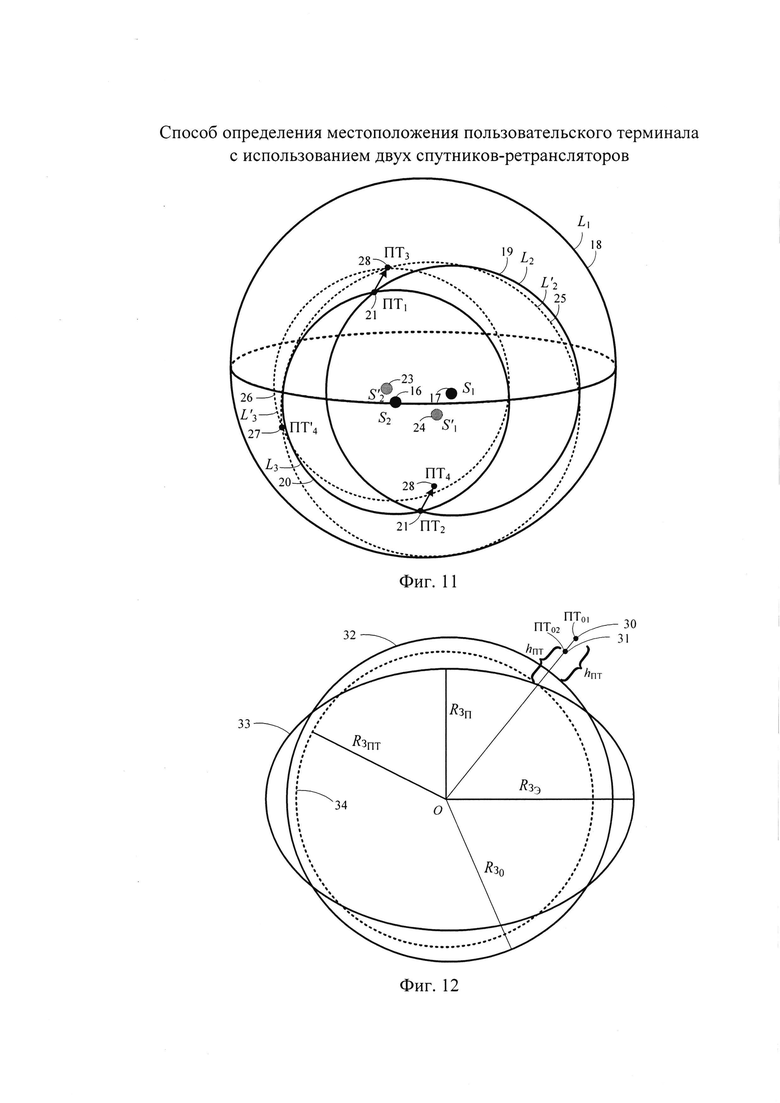
- на фиг. 11 - принцип устранения неоднозначности для подвижного пользовательского терминала;
- на фиг. 12 - уточнение радиуса Земли;
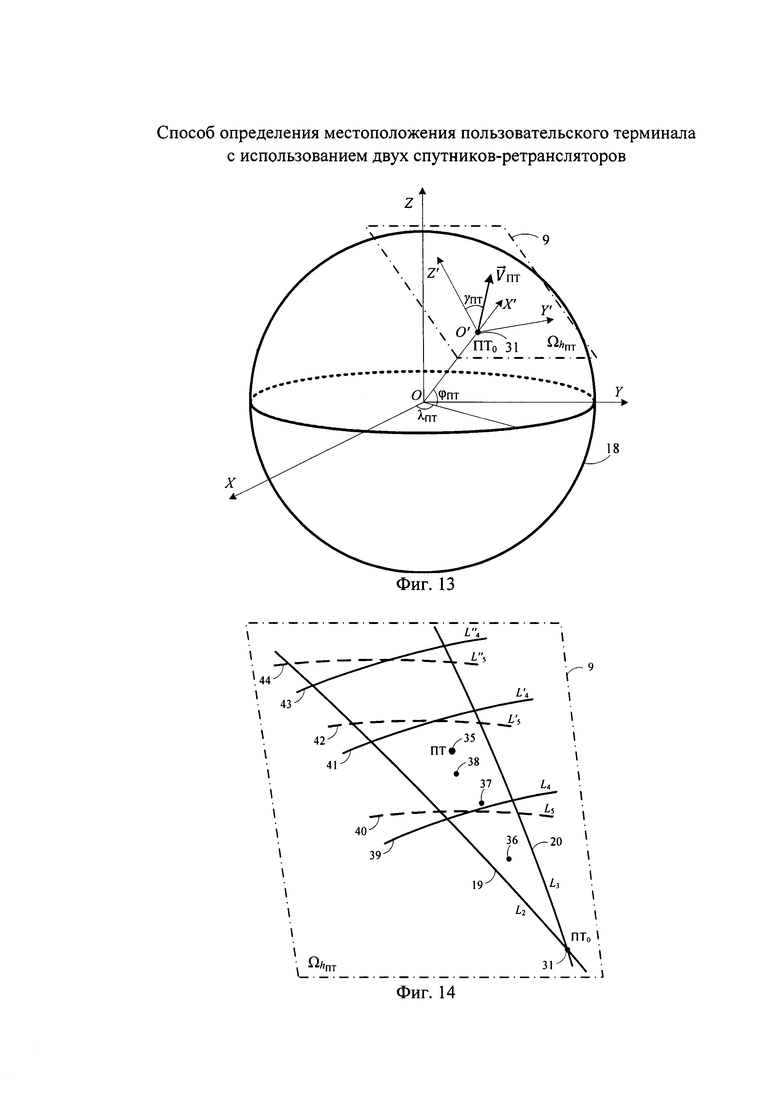
- на фиг. 13 - определение координат вектора скорости пользовательского терминала в геоцентрической системе координат;
- на фиг. 14 - итерационный метод повышения точности определения координат пользовательского терминала;
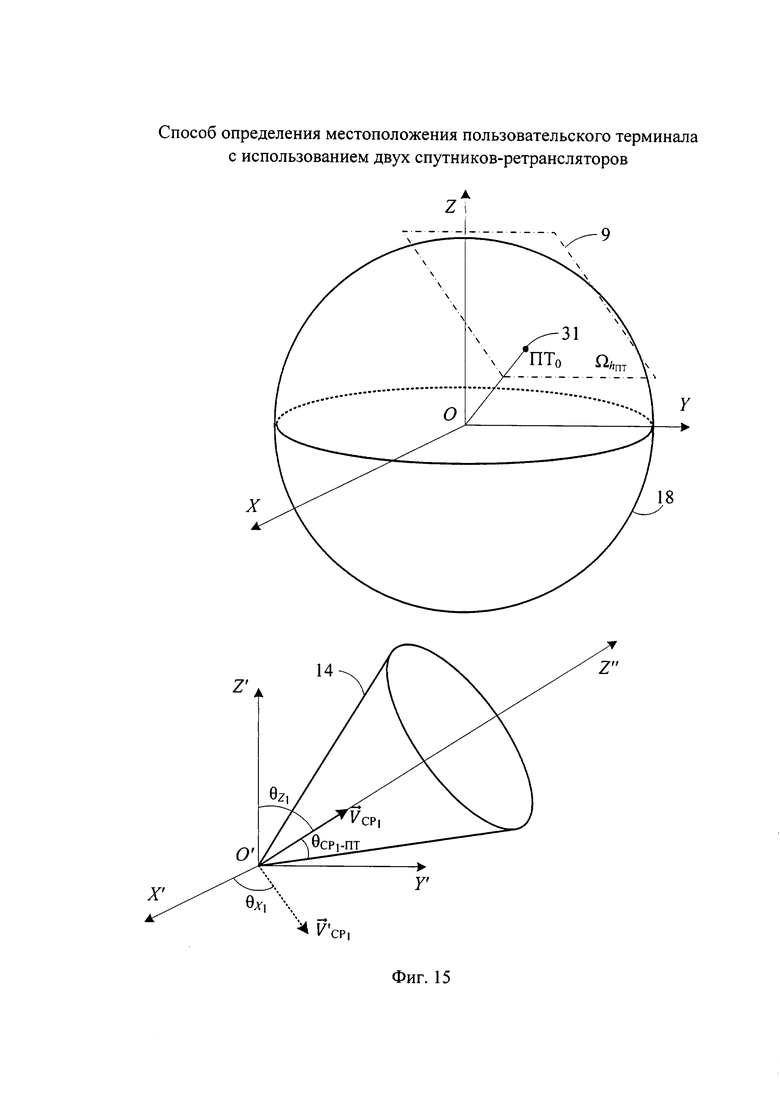
- на фиг. 15 - геометрическая основа составления уравнения круглого конуса в геоцентрической системе координат.
Реализация заявленного способа представлена на примере типовой спутниковой системы связи, представленной на фиг. 1. Она содержит один узел межсетевого сопряжения (УМС), пользовательские терминалы, которые могут быть в стационарном исполнении 4 (см. фиг. 1), либо размещены на движущихся объектах: на автомобиле 5, на вертолете 6, на самолете 7 (см. фиг. 1) и т.д., а также два спутника-ретранслятора: CP1 и СР2 для обеспечения связи между УМС и ПТ.
Современные ССС позволяют предоставлять услуги связи как стационарным ПТ, так и ПТ, размещенным на широком классе движущихся объектов (автомобиль, вертолет, самолет).
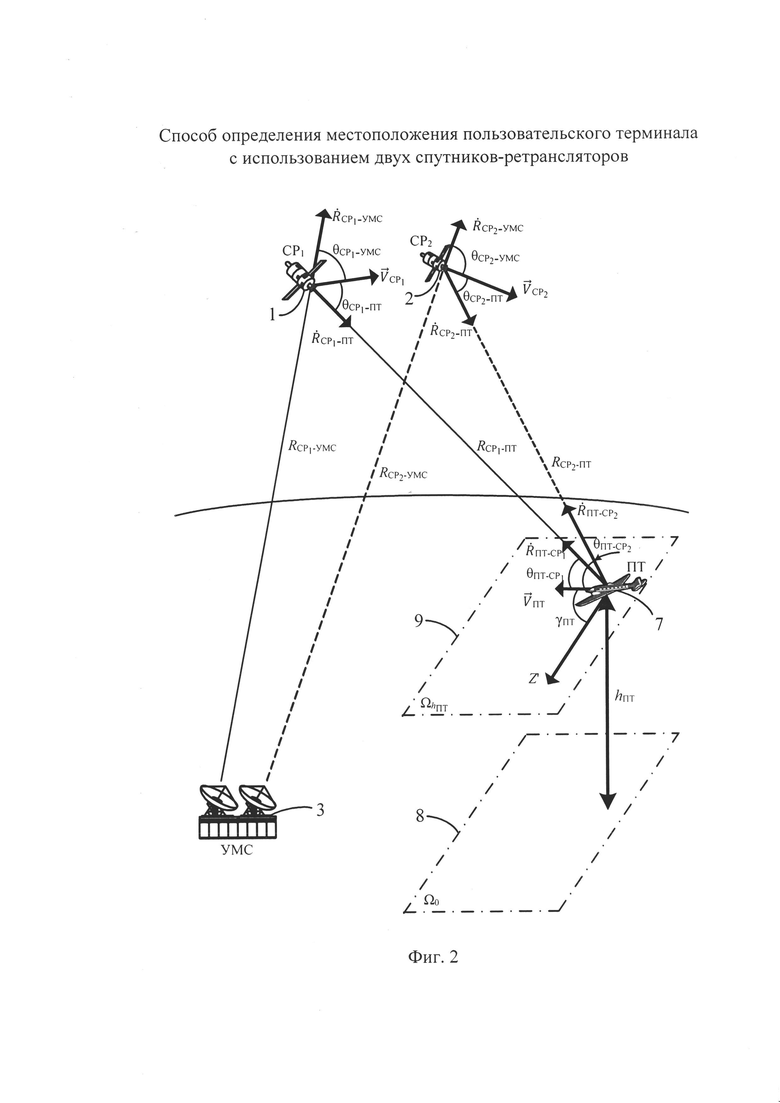
В качестве примера для описания изобретения рассматривают ПТ, размещенный на самолете. Геометрическая основа спутниковой линии связи в таком исполнении раскрыта на фиг. 2.
УМС является стационарным, его координаты, а точнее координаты оптических фокусов антенн, хорошо известны.
ПТ размещен на самолете, который движется со скоростью 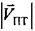 в плоскости
в плоскости 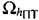 , параллельной горизонтальной плоскости Ω0 (на нулевой высоте) и находящейся на высоте hПТ от нее. Азимутом движения самолета является угол γПТ, отсчитываемый между направлением на север, обозначенным стрелкой Z′ и направлением движения самолета. В дальнейшем будем считать, что параметры
, параллельной горизонтальной плоскости Ω0 (на нулевой высоте) и находящейся на высоте hПТ от нее. Азимутом движения самолета является угол γПТ, отсчитываемый между направлением на север, обозначенным стрелкой Z′ и направлением движения самолета. В дальнейшем будем считать, что параметры 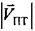 , hПТ и γПТ известны, так как большинство самолетов оборудованы приборами, позволяющими измерить указанные параметры в любой момент времени.
, hПТ и γПТ известны, так как большинство самолетов оборудованы приборами, позволяющими измерить указанные параметры в любой момент времени.
Идеальная ГСО CP характеризуется следующими параметрами: эксцентриситет орбиты равен нулю е=0, наклонение орбиты равно i=0°, период обращения CP равен периоду обращения Земли (звездные сутки, которые составляют 23 часа 56 минут 04 секунды), компенсация влияний возмущающих факторов, таких как неравномерное гравитационное поле Земли, сила притяжения Солнца, Луны и др. космических объектов. В этом случае CP оказывается «висячим» над определенной точкой земной поверхности, на определенной долготе, строго над экватором, на высоте 35875 км над поверхностью Земли.
Однако на практике перечисленные условия являются недостижимыми. Спутники-ретрансляторы CP1 и CP2 находятся на так называемой квазистационарной орбите, при этом их суточное смещение, как правило, составляет единицы градусов. Вследствие этого CP не являются «висячими» над определенными точками земной поверхности, а совершают колебательные движения.
Суточное смещение CP1 и СР2 является причиной наличия векторов скоростей 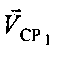 ,
, 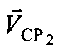 , обозначенных на фиг. 2 стрелками. Очевидно, что векторы скоростей
, обозначенных на фиг. 2 стрелками. Очевидно, что векторы скоростей 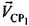 ,
, 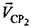 в течение суток меняют и модуль, и направление, однако на малом интервале времени, исчисляемом минутами, можно считать их постоянными. В дальнейших рассуждениях считают, что векторы
в течение суток меняют и модуль, и направление, однако на малом интервале времени, исчисляемом минутами, можно считать их постоянными. В дальнейших рассуждениях считают, что векторы 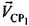 ,
, 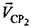 , равно как и координаты CP1 и CP2, известны в любой момент времени. Действительно, операторам-владельцам ССС должны быть известны эти параметры, существуют методики, с помощью которых либо измеряют, либо рассчитывают координаты CP и параметры их движения. Они описаны, например, в монографии Дубошина Г.Н. Небесная механика. Методы теории движения искусственных небесных тел. - М.: Наука. Главная редакция физико-математической литературы, 1983. - 352 с.
, равно как и координаты CP1 и CP2, известны в любой момент времени. Действительно, операторам-владельцам ССС должны быть известны эти параметры, существуют методики, с помощью которых либо измеряют, либо рассчитывают координаты CP и параметры их движения. Они описаны, например, в монографии Дубошина Г.Н. Небесная механика. Методы теории движения искусственных небесных тел. - М.: Наука. Главная редакция физико-математической литературы, 1983. - 352 с.
В конкретный момент времени топология системы характеризуется расстояниями спутников ретрансляторов от УМС и ПТ, обозначенными на фиг. 2 сплошными и пунктирными отрезками:
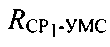 - расстояние между CP1 и УМС,
- расстояние между CP1 и УМС,
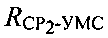 - расстояние между CP2 и УМС,
- расстояние между CP2 и УМС,
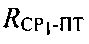 - расстояние между CP1 и ПТ,
- расстояние между CP1 и ПТ,
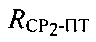 - расстояние между CP2 и ПТ.
- расстояние между CP2 и ПТ.
В любой момент времени расстояния 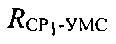 и
и 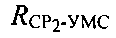 можно вычислить, основываясь на известных координатах УМС, CP1 и CP2.
можно вычислить, основываясь на известных координатах УМС, CP1 и CP2.
Расстояния 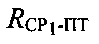 и
и 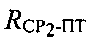 являются параметрами положения, вычисление которых производится при использовании тестовых сигналов системы.
являются параметрами положения, вычисление которых производится при использовании тестовых сигналов системы.
На фиг. 2 также показаны угловые величины между векторами скоростей 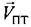 ,
, 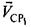 ,
, 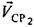 и соответствующими направлениями:
и соответствующими направлениями:
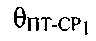 - угол между вектором
- угол между вектором 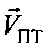 и направлением ПТ-CP1,
и направлением ПТ-CP1,
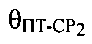 - угол между вектором
- угол между вектором 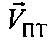 и направлением ПТ-СР2,
и направлением ПТ-СР2,
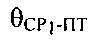 - угол между вектором
- угол между вектором 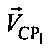 и направлением CP1-ПТ,
и направлением CP1-ПТ,
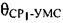 - угол между вектором
- угол между вектором 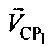 и направлением CP1-УМС,
и направлением CP1-УМС,
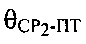 - угол между вектором
- угол между вектором 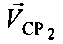 и направлением CP2-ПТ,
и направлением CP2-ПТ,
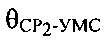 - угол между вектором
- угол между вектором 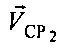 и направлением СР2-УМС.
и направлением СР2-УМС.
Данные угловые величины связывают векторы скоростей 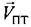 ,
, 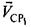 ,
, 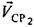 с их проекциями на соответствующую ось. Такие проекции являются радиальными скоростями:
с их проекциями на соответствующую ось. Такие проекции являются радиальными скоростями:
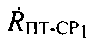 - радиальная скорость ПТ относительно CP1 - проекция вектора
- радиальная скорость ПТ относительно CP1 - проекция вектора 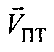 на ось ПТ-CP1,
на ось ПТ-CP1,
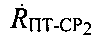 - радиальная скорость ПТ относительно CP2 - проекция вектора
- радиальная скорость ПТ относительно CP2 - проекция вектора 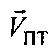 на ось ПТ-CP2,
на ось ПТ-CP2,
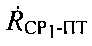 - радиальная скорость CP1 относительно ПТ - проекция вектора
- радиальная скорость CP1 относительно ПТ - проекция вектора 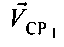 на ось CP1-ПТ,
на ось CP1-ПТ,
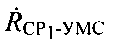 - радиальная скорость CP1 относительно УМС - проекция вектора
- радиальная скорость CP1 относительно УМС - проекция вектора 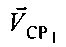 на ось CP1-УМС,
на ось CP1-УМС,
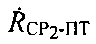 - радиальная скорость CP2 относительно ПТ - проекция вектора
- радиальная скорость CP2 относительно ПТ - проекция вектора 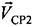 на ось CP2-ПТ,
на ось CP2-ПТ,
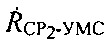 - радиальная скорость CP2 относительно УМС - проекция вектора
- радиальная скорость CP2 относительно УМС - проекция вектора 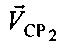 на ось CP2-УМС.
на ось CP2-УМС.
В любой момент времени радиальные скорости 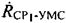 ,
, 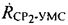 ,
, 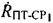 ,
, 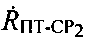 можно вычислить, основываясь на известных координатах УМС, CP1 и CP2, известных векторах
можно вычислить, основываясь на известных координатах УМС, CP1 и CP2, известных векторах 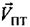 ,
, 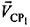 ,
, 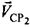 .
.
Радиальные скорости 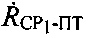 и
и 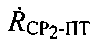 являются параметрами положения, вычисление которых производится при использовании тестовых сигналов системы.
являются параметрами положения, вычисление которых производится при использовании тестовых сигналов системы.
Параметры 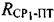 и
и 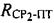 определяют на основе измерений временных задержек между переданными и принятыми тестовыми сигналами системы. Измеренные временные задержки умножают на скорость распространения радиоволны, равную скорости света в вакууме: с=3×108 м/с.
определяют на основе измерений временных задержек между переданными и принятыми тестовыми сигналами системы. Измеренные временные задержки умножают на скорость распространения радиоволны, равную скорости света в вакууме: с=3×108 м/с.
Параметры 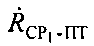 и
и 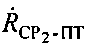 определяют на основе частотных сдвигов между переданными и принятыми тестовыми сигналами системы. Сдвиги тестовых сигналов системы являются суммой предварительно заданных частотных сдвигов
определяют на основе частотных сдвигов между переданными и принятыми тестовыми сигналами системы. Сдвиги тестовых сигналов системы являются суммой предварительно заданных частотных сдвигов 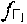 ,
, 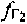 рабочих частот CP1, CP2 и доплеровскими сдвигами частот, обусловленными суммарными радиальными скоростями соответствующего CP относительно ПТ и УМС.
рабочих частот CP1, CP2 и доплеровскими сдвигами частот, обусловленными суммарными радиальными скоростями соответствующего CP относительно ПТ и УМС.
Рассмотрим в общих чертах причину возникновения доплеровского эффекта, его связь с радиальной скоростью передатчика (приемника), а также порядок расчета взаимной радиальной скорости при движении и передатчика, и приемника.
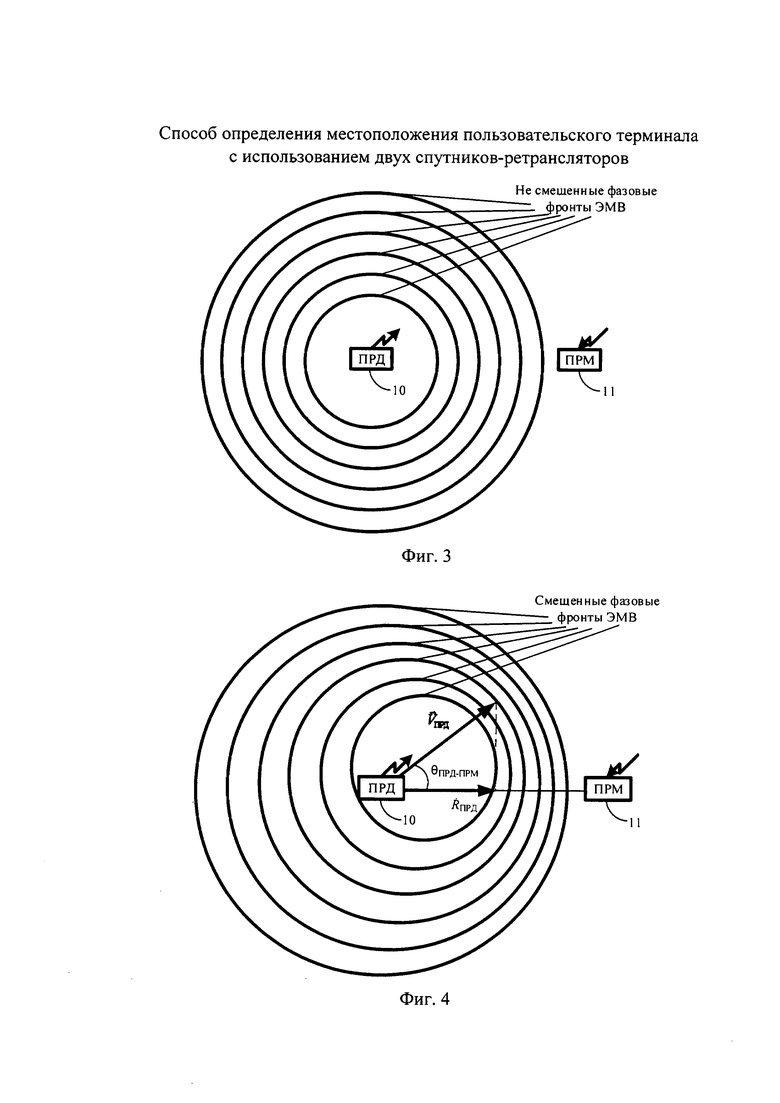
Доплеровский эффект в определенном смысле универсален. Его проявления можно проследить и в механических (звуковых) волнах, и в электромагнитных волнах как оптического диапазона, так и радиодиапазона. Доплеровский эффект можно пояснить с помощью фиг. 3 и фиг. 4.
На фиг. 3 изображены передатчик (ПРД) и приемник (ПРМ). Концентрическими окружностями схематично изображены фазовые фронты радиоволн, излучаемых ПРД, расстояния между которыми соответствует длине волны. При отсутствии относительного движения ПРД и ПРМ эффект Доплера отсутствует: длина волны ПРМ равна длине волны ПРД. Из последнего утверждения следует, что и частота ПРМ 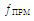 равна частоте ПРД
равна частоте ПРД 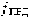 :
:
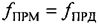 .
.
На фиг. 4 изображен ПРД, движущийся со скоростью 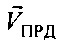 с углом θПРД-ПРМ к направлению ПРД-ПРМ. Такое движение приводит к изменению длины волны в ПРМ по отношению к длине волны ПРД. Такое изменение называется эффектом Доплера. Частота ПРМ в этом случае изменяется на величину доплеровского смещения частоты
с углом θПРД-ПРМ к направлению ПРД-ПРМ. Такое движение приводит к изменению длины волны в ПРМ по отношению к длине волны ПРД. Такое изменение называется эффектом Доплера. Частота ПРМ в этом случае изменяется на величину доплеровского смещения частоты 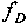 , относительно частоты ПРД:
, относительно частоты ПРД:
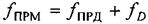
Знак этого смещения может быть положительным, если ПРМ и ПРД сближаются, и отрицательным, если ПРМ и ПРД удаляются друг относительно друга.
Аналитическое выражение для расчета доплеровского смещения частоты без учета релятивистского эффекта выглядит следующим образом:
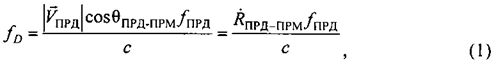
где 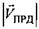 - модуль вектора скорости ПРД,
- модуль вектора скорости ПРД, 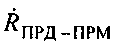 - радиальная скорость ПРД относительно ПРМ - проекция вектора
- радиальная скорость ПРД относительно ПРМ - проекция вектора 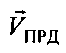 на ось ПРД-ПРМ, θПРД-ПРМ - угол между вектором
на ось ПРД-ПРМ, θПРД-ПРМ - угол между вектором 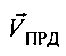 и направлением ПРД-ПРМ.
и направлением ПРД-ПРМ.
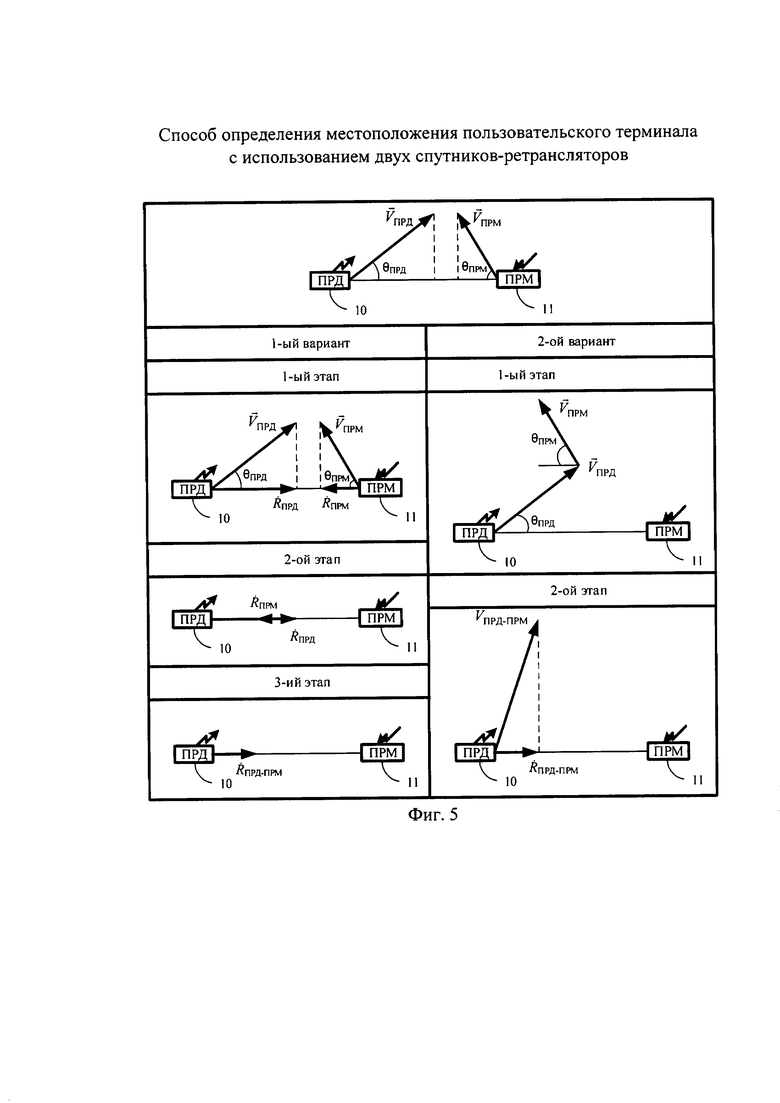
В ряде случаев в движении могут находиться и ПРД, и ПРМ. Тогда нахождение взаимной радиальной скорости движущихся ПРМ и ПРД возможно по двум вариантам, представленным на фиг. 5.
В первом варианте сначала определяют радиальные скорости ПРД и ПРМ 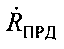 и
и 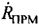 , как проекции векторов
, как проекции векторов 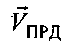 и
и 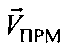 на ось ПРД-ПРМ, затем находят взаимную радиальную скорость движущихся ПРМ и ПРД
на ось ПРД-ПРМ, затем находят взаимную радиальную скорость движущихся ПРМ и ПРД 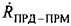 , как вектор суммы
, как вектор суммы 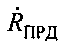 и
и 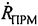 .
.
Во втором варианте сначала определяют результирующую относительную скорость 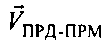 движущихся ПРМ и ПРД, как вектор суммы их скоростей
движущихся ПРМ и ПРД, как вектор суммы их скоростей 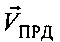 и
и 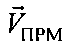 , затем находят взаимную радиальную скорость движущихся ПРМ и ПРД
, затем находят взаимную радиальную скорость движущихся ПРМ и ПРД 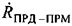 , как проекцию вектора
, как проекцию вектора 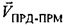 на ось ПРД-ПРМ.
на ось ПРД-ПРМ.
Вышеуказанные варианты справедливы и для ССС, использующей подвижный CP, с той лишь разницей, что при расчете взаимной радиальной скорости движущихся ПРМ и ПРД будут участвовать три радиальные скорости (см. фиг. 5). В таком случае целесообразно использовать первый вариант нахождения взаимной радиальной скорости движущихся ПРМ и ПРД.
При ОМП ПТ используют следующие параметры положения: 1) дальность 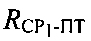 от CP1 до ПТ, 2) дальность
от CP1 до ПТ, 2) дальность 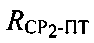 от СР2 до ПТ, 3) скорость
от СР2 до ПТ, 3) скорость 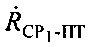 изменения дальности CP1 относительно ПТ, 4) скорость
изменения дальности CP1 относительно ПТ, 4) скорость 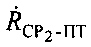 изменения дальности CP2 относительно ПТ.
изменения дальности CP2 относительно ПТ.
Эти параметры могут характеризоваться поверхностями положения и линиями положений.
Поверхность положения (какого-либо параметра положения) - поверхность в пространстве, соединяющая все точки, имеющие одинаковое значение данного параметра. В качестве поверхности положения в некоторых случаях может выступать поверхность Земли.
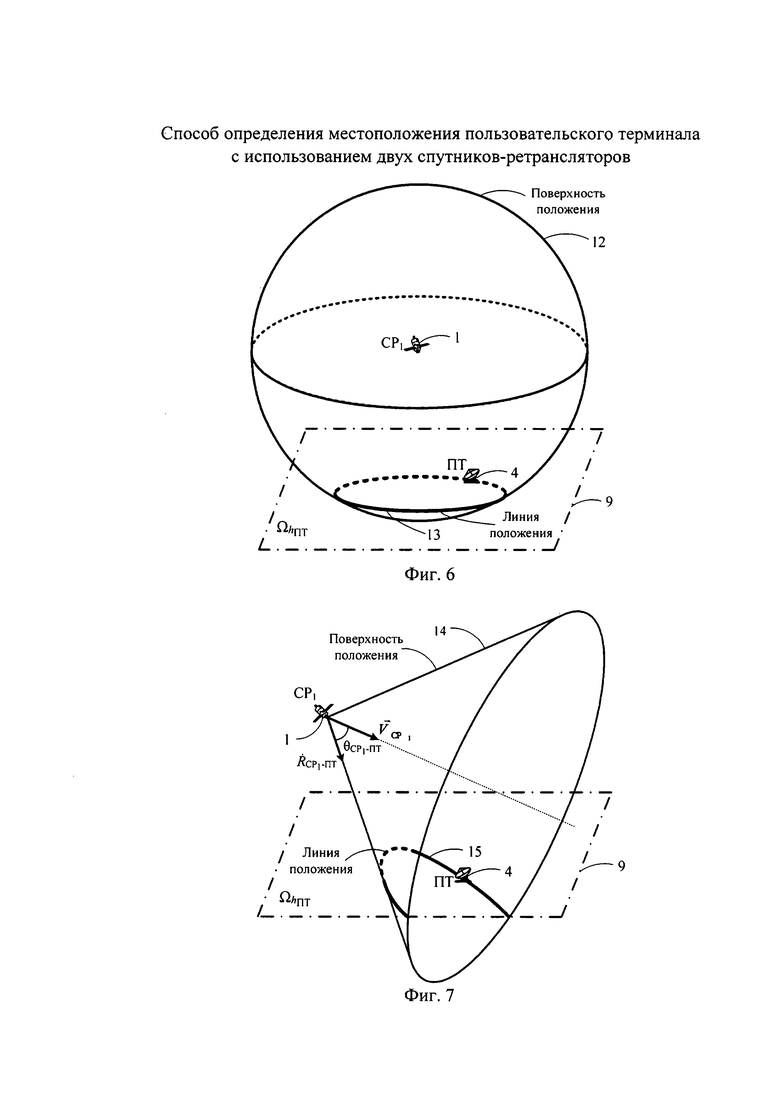
Линия положения (какого-либо параметра положения) - кривая на поверхности Земли или на какой-либо другой поверхности, соединяющая все точки, имеющие одинаковое значение данного параметра. Линии положений рассматриваемых параметров положений выделены жирными линиями на соответствующих рисунках (см фиг. 6, 7). В альтернативном варианте рассматривают линии положения только на земной поверхности, при этом земную поверхность аппроксимируют плоскостью. В предпочтительном варианте рассматривают плоскость 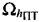 , параллельную земной поверхности (горизонтальной плоскости Ω0 на нулевой высоте) и находящейся на известной высоте hПТ от нее.
, параллельную земной поверхности (горизонтальной плоскости Ω0 на нулевой высоте) и находящейся на известной высоте hПТ от нее.
Параметр положения дальность RСР-ПТ представляет собой расстояние между CP и ПТ. Поверхность положения параметра дальности - сфера с центром, совпадающим с оптическим центром антенны CP и радиусом RСР-ПТ. Линия положения параметра дальности на плоскости 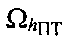 - окружность, центр которой совпадает с подспутниковой точкой CP (см. фиг. 6). Рассмотрение в качестве CP поочередно CP1 и СР2 приводит к получению параметров положения
- окружность, центр которой совпадает с подспутниковой точкой CP (см. фиг. 6). Рассмотрение в качестве CP поочередно CP1 и СР2 приводит к получению параметров положения 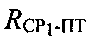 и
и 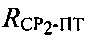 соответственно.
соответственно.
Параметр положения скорость изменения дальности 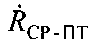 представляет собой относительную радиальную скорость между ПТ и СР. Поверхность положения параметра скорости изменения дальности - круглый конус (далее просто конус) с вершиной, совпадающей с оптическим центром антенны CP, с осью, совпадающей с вектором
представляет собой относительную радиальную скорость между ПТ и СР. Поверхность положения параметра скорости изменения дальности - круглый конус (далее просто конус) с вершиной, совпадающей с оптическим центром антенны CP, с осью, совпадающей с вектором 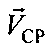 и с углом вращения, равным θСР-ПТ. Линия положения параметра скорости изменения дальности на плоскости
и с углом вращения, равным θСР-ПТ. Линия положения параметра скорости изменения дальности на плоскости 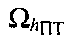 - гипербола, симметричная относительно
- гипербола, симметричная относительно 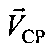 (см. фиг. 7). Рассмотрение в качестве CP поочередно CP1 и СР2 приводит к получению параметров положения
(см. фиг. 7). Рассмотрение в качестве CP поочередно CP1 и СР2 приводит к получению параметров положения 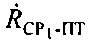 и
и 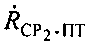 соответственно.
соответственно.
В альтернативном варианте предполагают, что ПТ не движется относительно земной поверхности. В реальных условиях ПТ может быть размещен на широком классе движущихся объектов (автомобиль, вертолет, самолет и т.д.). Движение ПТ относительно земной поверхности вносит в принятые и переданные тестовые сигналы системы дополнительные доплеровские сдвиги частот. Такие сдвиги можно не учитывать, если скорость CP относительно земной поверхности значительно превосходит скорость ПТ относительно земной поверхности. Но когда эти скорости соизмеримы, то для расчета параметров скорости изменения дальности и разности скоростей изменения дальностей необходимо учитывать дополнительные доплеровские сдвиги частот тестовых сигналов системы, обусловленных движением ПТ относительно земной поверхности.
Последовательность этапов реализации заявленного способа ОМП ПТ можно рассмотреть с использованием представленного на фиг. 8 алгоритма.
Этап 1. Ввод исходных данных. Исходными данными, в соответствии с введенными выше обозначениями являются: 1) координаты УМС (x0, y0, z0), 2) координаты CP1 (x1, y1, z1) и CP2 (х2, y2, z2), 3) векторы скоростей 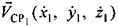 ,
, 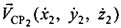 , 4) частотные сдвиги
, 4) частотные сдвиги 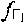 ,
, 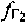 рабочих частот CP1, CP2, 5) модуль
рабочих частот CP1, CP2, 5) модуль 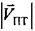 , азимут γПТ вектора скорости ПТ и его высота hПТ, 6)
, азимут γПТ вектора скорости ПТ и его высота hПТ, 6) 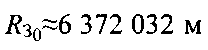 - средний радиус Земли,
- средний радиус Земли, 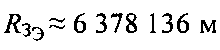 - радиус Земли на экваторе; еЗ≈0,081819 - эксцентриситет эллипсоида Земли, 5) порог ξ - допустимое расстояние между истинными и определенными координатами ПТ.
- радиус Земли на экваторе; еЗ≈0,081819 - эксцентриситет эллипсоида Земли, 5) порог ξ - допустимое расстояние между истинными и определенными координатами ПТ.
Этап 2. Измерение временных задержек и частотных сдвигов тестовых сигналов системы.
Временные задержки между переданными и принятыми тестовыми сигналами системы используют для определения параметров положения 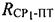 и
и 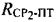 . Тестовыми сигналами при этом являются две известные псевдошумовые (ПШ) последовательности.
. Тестовыми сигналами при этом являются две известные псевдошумовые (ПШ) последовательности.
Для измерения временных задержек выполняют следующие операции:
1. УМС излучает два известных тестовых сигнала, представляющих собой ПШ последовательности и запоминает время излучения каждого из этих сигналов 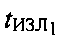 и
и 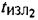 .
.
2. ПТ принимает первый тестовый сигнал через CP1, второй тестовый сигнал через CP2 и переизлучает их сразу, либо с известными задержками 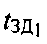 и
и 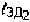 .
.
3. УМС принимает первый тестовый сигнал через CP1, второй тестовый сигнал через CP2, измеряет время приема каждого из этих сигналов 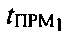 и
и 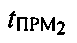 и вычисляет задержки двусторонних распространений сигналов
и вычисляет задержки двусторонних распространений сигналов 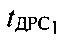 и
и 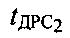 , соответствующих траекториям УМС-СР1-ПТ-CP1-УМС и УМС-СР2-ПТ-СР2-УМС:
, соответствующих траекториям УМС-СР1-ПТ-CP1-УМС и УМС-СР2-ПТ-СР2-УМС:
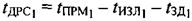 ,
,
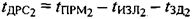 .
.
Частотные сдвиги между переданными и принятыми тестовыми сигналами системы используют для определения параметров положения 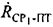 и
и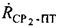 . Тестовые сигналы, представляющие собой два узкополосных сигнала с центральными частотами
. Тестовые сигналы, представляющие собой два узкополосных сигнала с центральными частотами 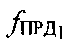 и
и 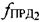 , передают УМС через СР1, СР2 и принимают ПТ. На траекториях УМС-СР1-ПТ и УМС-CP2-ПТ центральные частоты сигналов подвержены сдвигам, среди которых можно выделить:
, передают УМС через СР1, СР2 и принимают ПТ. На траекториях УМС-СР1-ПТ и УМС-CP2-ПТ центральные частоты сигналов подвержены сдвигам, среди которых можно выделить:
- заданные частотные сдвиги 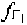 ,
, 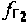 рабочих частот CP1, СР2,
рабочих частот CP1, СР2,
- доплеровские сдвиги частот 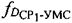 ,
, 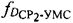 , обусловленные движением CP1 и CP2 относительно УМС,
, обусловленные движением CP1 и CP2 относительно УМС,
- доплеровские сдвиги частот 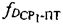 ,
, 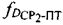 , обусловленные движением CP1 и CP2 относительно ПТ,
, обусловленные движением CP1 и CP2 относительно ПТ,
- доплеровские сдвиги частот  ,
, 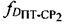 , обусловленные движением ПТ относительно CP1 и CP2.
, обусловленные движением ПТ относительно CP1 и CP2.
Указанные сдвиги центральных частот тестовых сигналов можно выразить аналитически:
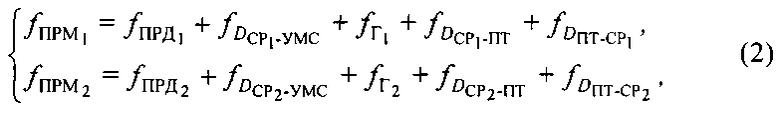
где 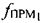 ,
, 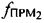 - значения центральных частот тестовых сигналов после прохождения обозначенных траекторий и соответствующих сдвигов.
- значения центральных частот тестовых сигналов после прохождения обозначенных траекторий и соответствующих сдвигов.
В рассматриваемом способе предусмотрена возможность измерения центральных частот тестовых сигналов в ПТ с последующей передачей информации о них в УМС.
Таким образом, в ходе данного этапа определены временные задержки 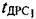 и
и 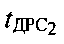 и частотные сдвиги
и частотные сдвиги 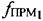 ,
, 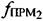 тестовых сигналов системы.
тестовых сигналов системы.
Этап 3. Определение параметров 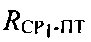 и
и 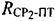 .
.
Известные координаты CP1, CP2 и УМС позволяют рассчитать расстояния 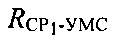 и
и 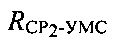 в момент времени измерения временных задержек
в момент времени измерения временных задержек 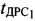 и
и 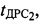 используя выражения:
используя выражения:
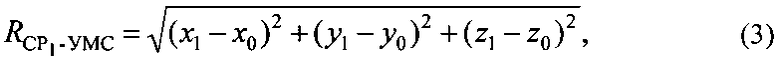
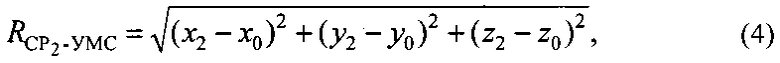
где x0, y0, z0 - координаты УМС, х1, y1, z1 - координаты CP1, х2, y2, z2 - координаты CP2.
Параметры положения 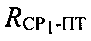 и
и 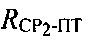 можно рассчитать по формулам:
можно рассчитать по формулам:
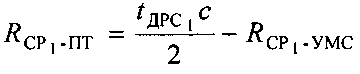
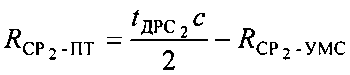
Этап 4. Расчет координат вероятного положения ПТ; ПТ) и ПТ2.
В ходе данного этапа рассчитывают координаты ПТ с большой ошибкой, достигающей 500 км и, как будет показано ниже, с не устраненной неоднозначностью.
В качестве поверхности Земли в данном этапе используют сферу с радиусом 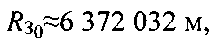 представляющим собой средний радиус Земли, что для приблизительных расчетов вполне допустимо.
представляющим собой средний радиус Земли, что для приблизительных расчетов вполне допустимо.
Задачу по расчету координат вероятного положения ПТ можно свести к решению системы из трех уравнений с тремя неизвестными х, y и z, являющимися декартовыми геоцентрическими координатами ПТ:
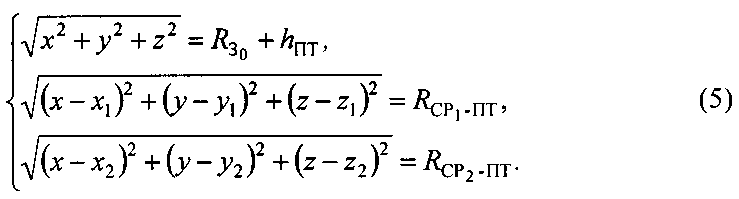
В системе уравнений (5) первое выражение - уравнение сферы с центром, совпадающим с центром Земли и радиусом, равным сумме среднего радиуса Земли RЗ и высоты ПТ hПТ, второе выражение - уравнение сферы с центром, совпадающим с оптическим центром антенны CP1 и радиусом 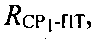 третье выражение - уравнение сферы с центром, совпадающим с оптическим центром антенны СР2 и радиусом
третье выражение - уравнение сферы с центром, совпадающим с оптическим центром антенны СР2 и радиусом 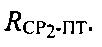
На фиг. 9 схематично показаны: L1 - поверхность положения, соответствующая первому выражению системы уравнений (5), L2 - линия положения на поверхности L1, соответствующая второму выражению системы уравнений (5), L1 - линия положения на поверхности L1, соответствующая третьему выражению системы уравнений (5). Точками S1 и S2 показаны подспутниковые точки CP1 и СР2.
Из-за геометрических особенностей построения ССС для CP на геостационарной орбите возникает неоднозначность результатов ОМП ПТ, так как линии положения Z2 и L3 пересекаются в двух точках ПТ1 и ПТ2, что показано на фиг. 9, при этом одна точка будет находиться в северном полушарии Земли, другая - в южном.
Аналитическим решением системы уравнений (5) будут две тройки действительных корней 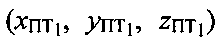 и
и  являющихся декартовыми координатами точек ПТ1 и ПТ2, соответственно.
являющихся декартовыми координатами точек ПТ1 и ПТ2, соответственно.
Этап 5. Устранение неоднозначности, выбор начальной точки ПТ0.
В большинстве случаев неоднозначность с точностью до полушария возможно устранить еще до установления ПТ сеанса связи. Возможно также использование дополнительной априорной информации о ПТ, например, вероятность его одновременного попадания в зоны радиовидимости CP1 и СР2.
Однако в общем случае в УМС ССС нет никакой информации о местоположении ПТ. В этом случае используют способ устранения возникшей неоднозначности, реализация которого для неподвижного ПТ показана на фиг. 10. Первая часть на фиг. 10, отображенная сплошными линиями, аналогична рисунку на фиг. 9 и соответствует первому моменту времени. Второй момент времени характеризуется тем, что в результате своего движения CP1 и CP2 сместятся, при этом подспутниковые точки также меняют свои координаты на 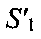 и
и 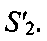 В результате новыми линиями положения будут
В результате новыми линиями положения будут 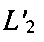 и
и 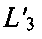 (штриховые линии) и, как следствие, искомая точка ПТ1 останется в том же месте, а ложная изменит свое положение на
(штриховые линии) и, как следствие, искомая точка ПТ1 останется в том же месте, а ложная изменит свое положение на 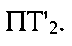 Аналитически такая трансформация выразится в повторном составлении и решении системы уравнений (5) с новыми координатами CP1 и СР2, а также новыми параметрами положения
Аналитически такая трансформация выразится в повторном составлении и решении системы уравнений (5) с новыми координатами CP1 и СР2, а также новыми параметрами положения 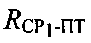 и
и 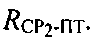
В случае с подвижным ПТ, представленным на фиг. 11, рассуждения, аналогичные с той разницей, что за время смещения CP1 и СР2 переместится и ПТ. Известные модуль 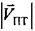 и азимут αПТ вектора скорости ПТ позволяют рассчитать смещение ПТ, которое считают одинаковым для обеих вероятных точек. В качестве примера на фиг. 11 показано перемещение ПТ в северовосточном направлении, в результате чего точки ПТ1 и ПТ2 сместятся соответственно в точки ПТ3 и ПТ4. Процедура построения новых линий положений
и азимут αПТ вектора скорости ПТ позволяют рассчитать смещение ПТ, которое считают одинаковым для обеих вероятных точек. В качестве примера на фиг. 11 показано перемещение ПТ в северовосточном направлении, в результате чего точки ПТ1 и ПТ2 сместятся соответственно в точки ПТ3 и ПТ4. Процедура построения новых линий положений 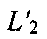 и
и 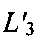 (штриховые линии) через определенное время позволяет сделать выбор в пользу точек ПТ1 и ПТ3, исключив точки ПТ2 и ПТ4, тем самым устранив неоднозначности ОМП ПТ.
(штриховые линии) через определенное время позволяет сделать выбор в пользу точек ПТ1 и ПТ3, исключив точки ПТ2 и ПТ4, тем самым устранив неоднозначности ОМП ПТ.
Таким образом, и для неподвижного, и для подвижного ПТ возможно устранить неоднозначность его ОМП, указанным выше способом. В представленных вариантах выбор делают в пользу координат северного полушария Земли - точки ПТ. Далее выбранная точка выступает в качестве начальной точки ПТ0 с координатами 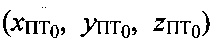 для поиска более точных координат ПТ итерационным методом с использованием параметров
для поиска более точных координат ПТ итерационным методом с использованием параметров 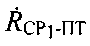 и/или
и/или 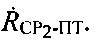
Этап 6. Неоднозначность устранена?
Сущность данного этапа частично раскрыта при пояснении этапа 5. Так, если при первом прохождении алгоритма нет дополнительной априорной информации о ПТ, то неоднозначность устранить невозможно. Тогда производится переход на этап 3, где через некоторое время повторно определяют параметры 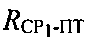 и
и 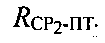 Затем на этапе 4 повторно рассчитывают вероятные координаты ПТ и на этапе 5 устраняют неоднозначность. При следующем прохождении этапа 6 неоднозначность уже устранена и выполняют переход к следующему этапу.
Затем на этапе 4 повторно рассчитывают вероятные координаты ПТ и на этапе 5 устраняют неоднозначность. При следующем прохождении этапа 6 неоднозначность уже устранена и выполняют переход к следующему этапу.
Для достаточного смещения CP1 и CP2 необходимо относительно небольшое время - несколько минут. Кроме того, в целях экономии времени, устранение неоднозначности необходимо выполнять при регистрации абонента в сети. Тогда на момент установления связи неоднозначность уже будет устранена.
Этап 7. Уточнение координат ПТ0.
На данном этапе уточняют координаты начальной точки ПТ0 по высоте с учетом сферичности Земли, а также находят эквивалентный радиус Земли 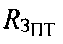 в точке ПТ0. Обозначим, полученную на этапе 5, исходную точку ПТ0, как ПТ01, а ее координаты
в точке ПТ0. Обозначим, полученную на этапе 5, исходную точку ПТ0, как ПТ01, а ее координаты  Точку с учетом корректировки по высоте обозначим ПТ02, а ее координаты
Точку с учетом корректировки по высоте обозначим ПТ02, а ее координаты 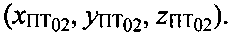
На фиг. 12 показаны сечения трех поверхностей меридианной плоскостью, проходящей через центр Земли - точку О и ПТ01. Первая поверхность - сфера с центром в точке О и радиусом, равным среднему радиусу Земли 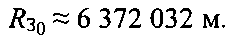 Вторая поверхность - эллипсоида вращения с центром в точке О, большой полуосью, равной радиусу Земли на экваторе
Вторая поверхность - эллипсоида вращения с центром в точке О, большой полуосью, равной радиусу Земли на экваторе 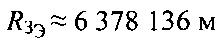 и эксцентриситетом eЗ≈0,081819 (модель Земли - ПЗ.90.02). Третья поверхность - сфера с центром в точке О и радиусом, равным радиусу Земли
и эксцентриситетом eЗ≈0,081819 (модель Земли - ПЗ.90.02). Третья поверхность - сфера с центром в точке О и радиусом, равным радиусу Земли 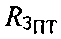 в точке ПТ.
в точке ПТ.
Также на фиг. 12 показаны точка ПТ01, расположенная на высоте hПТ от сферы с радиусом 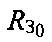 , и точка ПТ02, расположенная на высоте hПТ от сферы с радиусом
, и точка ПТ02, расположенная на высоте hПТ от сферы с радиусом 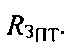
Радиус сферы 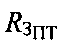 зависит от широты φПТ и максимален на экваторе, где принимает значение
зависит от широты φПТ и максимален на экваторе, где принимает значение 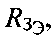 минимален на полюсах, где принимает значение
минимален на полюсах, где принимает значение 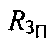 (радиус Земли на полюсе). В общем случае выражение для расчета
(радиус Земли на полюсе). В общем случае выражение для расчета 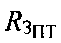 выглядит следующим образом:
выглядит следующим образом:
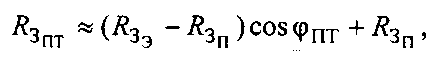
где 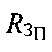 - радиус Земли на полюсе, вычисляемый по формуле:
- радиус Земли на полюсе, вычисляемый по формуле:
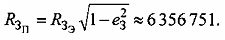
Геоцентрическая широта φПТ и геоцентрическая долгота λПТ начальной точки ПТ01 рассчитываются по формулам:
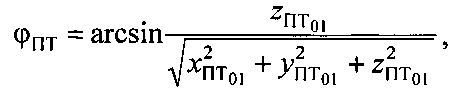
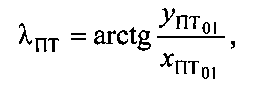
где 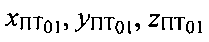 - декартовы координаты точки ПТ01,
- декартовы координаты точки ПТ01,
Величины φПТ и λПТ оставляют неизменными и для ПТ02. Тогда декартовы координаты ПТ02 равны:
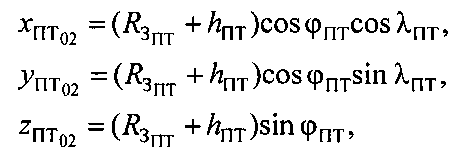
где 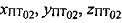 - декартовы координаты точки ПТ02.
- декартовы координаты точки ПТ02.
Далее в качестве координат начальной точки ПТ0 принимают координаты ПТ02 и обозначают их как 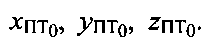 В качестве земной поверхности используют сферу с центром в точке О и радиусом
В качестве земной поверхности используют сферу с центром в точке О и радиусом 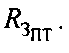
Этап 8. Определение параметров 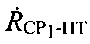 и
и 
Известные координаты точек расположения УМС (х0, y0, z0), CP1 (х1, y1, z1), СР2 (х2, y2, z2), а также известные координаты векторов 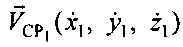 и
и 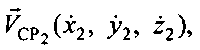 позволяют рассчитать радиальные скорости
позволяют рассчитать радиальные скорости 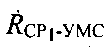 и
и 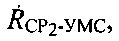 показанные на фиг. 2.
показанные на фиг. 2.
Согласно уравнению (1) радиальная скорость 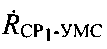 равна:
равна:
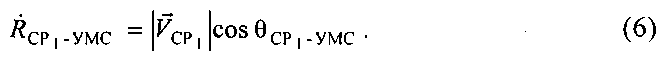
Модуль вектора 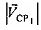 скорости CP1 равен:
скорости CP1 равен:
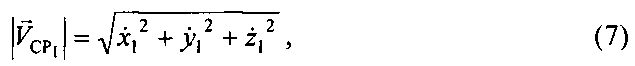
где 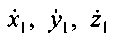 - декартовы координаты вектора
- декартовы координаты вектора 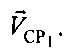
Из теоремы о скалярном произведении векторов имеем:
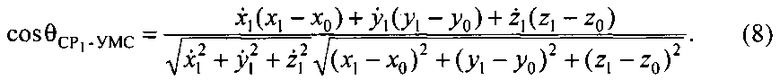
Подставив (7) и (8) в (6), получим:
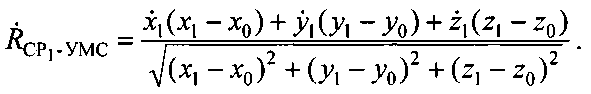
Аналогично рассчитывают радиальную скорость 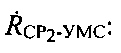
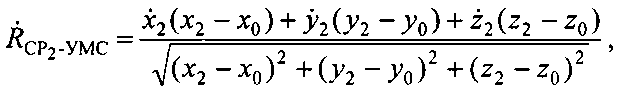
где 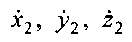 - декартовы координаты вектора
- декартовы координаты вектора 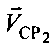 .
.
С учетом нахождения ПТ в начальной точке ПТ0 с координатами 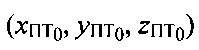 рассчитывают радиальные скорости
рассчитывают радиальные скорости 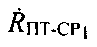 и
и 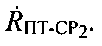
Согласно уравнению (1) 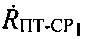 и
и 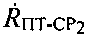 равны:
равны:

Модуль вектора 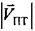 скорости ПТ известен.
скорости ПТ известен.
Используя теорему о скалярном произведении векторов, с учетом (9) имеем:
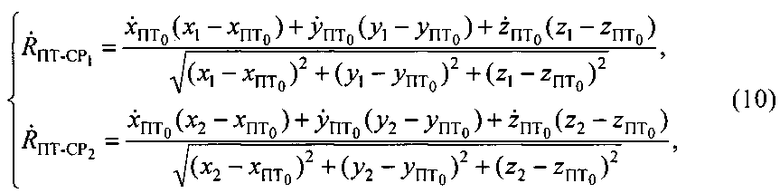
где 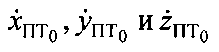 - координаты вектора
- координаты вектора 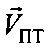 скорости ПТ в декартовой геоцентрической системе координат при условии нахождении ПТ в начальной точке ПТ0.
скорости ПТ в декартовой геоцентрической системе координат при условии нахождении ПТ в начальной точке ПТ0.
На фиг. 13 представлена геоцентрическая декартова система координат, где начало координат - точка О, совпадающая с центром Земли, плоскость OXY совпадает с плоскостью экватора, ось ОХ лежит в плоскости нулевого (гринвичского) меридиана, ось OZ - направлена вдоль оси вращения Земли, ось OY дополняет систему координат до правой.
Для нахождения координат 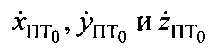 в геоцентрической декартовой системе рассмотрим сначала местную топоцентрическую декартову систему координат Z′O′Y′X′, представленную на фиг. 13, начало которой - точка О′ - совмещена с точкой ПТ0, а плоскость Z′O′Y′ совмещена с плоскостью
в геоцентрической декартовой системе рассмотрим сначала местную топоцентрическую декартову систему координат Z′O′Y′X′, представленную на фиг. 13, начало которой - точка О′ - совмещена с точкой ПТ0, а плоскость Z′O′Y′ совмещена с плоскостью 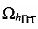 .
.
Очевидно, что в системе координат Z′O′Y′X′ координаты вектора 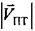 скорости ПТ будут равны:
скорости ПТ будут равны:

где 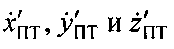 - топоцентрические декартовы координаты вектора
- топоцентрические декартовы координаты вектора 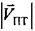 скорости ПТ в системе координат Z′O′YX′.
скорости ПТ в системе координат Z′O′YX′.
Переход от топоцентрических декартовых координат 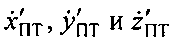 к геоцентрическим декартовым координатам производится посредством поворота системы координат относительно осей O′Y′ и О′Х′ на углы φПТ и λПТ соответственно и смещения начала координат из точки О′ в точку О.
к геоцентрическим декартовым координатам производится посредством поворота системы координат относительно осей O′Y′ и О′Х′ на углы φПТ и λПТ соответственно и смещения начала координат из точки О′ в точку О.
Аналитическое выражение таких преобразований, с учетом (11) можно представить в матричном виде:
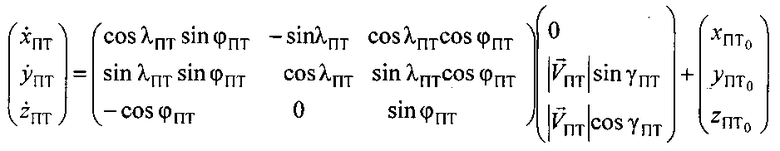
Систему уравнений (2) с учетом (1) можно переписать в виде:
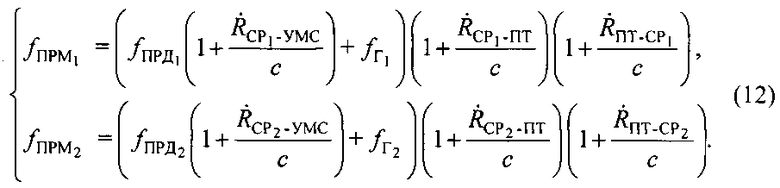
В системе уравнений (12) неизвестными величинами выступают только 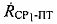 и
и 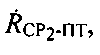 которые можно выразить следующим образом:
которые можно выразить следующим образом:
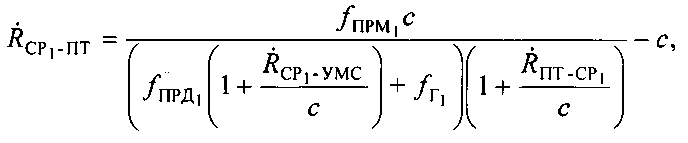
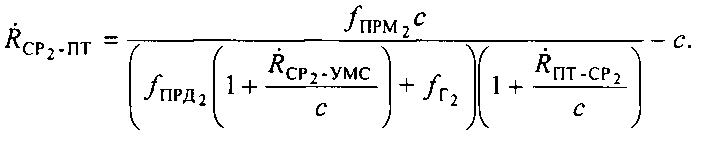
Этап 9. Расчет текущих координат ПТ.
При расчете и уточнении координат начальной точки ПТ0 (этапы 3…7) могут возникать ситуации, при которых имеет место геометрический фактор снижения точности, обусловленный малым углом между линиями положений L2 и L3, вследствие чего ошибка ОМП ПТ достигает 500 км, что не приемлемо для ССС.
Использование параметров положения 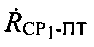 и/или
и/или 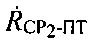 призвано повысить точность ОМП ПТ. Схема реализации итерационного метода повышения точности ОМП ПТ представлена на фиг. 14. Сущность метода можно описать следующим алгоритмом:
призвано повысить точность ОМП ПТ. Схема реализации итерационного метода повышения точности ОМП ПТ представлена на фиг. 14. Сущность метода можно описать следующим алгоритмом:
1) На основе рассчитанных параметров положения 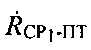 и/или
и/или 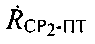 (этап 8) в плоскости
(этап 8) в плоскости 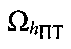 определяют линии положения L3 и/или L4;
определяют линии положения L3 и/или L4;
2) По выбранному решающему правилу, с использованием линий положения L2 и L3, а также L3 и/или L4, определяют точку 36 (см. фиг. 14), являющуюся текущей точкой ПТ (xПТ, yПТ, zПТ).
3) Поскольку истинные координаты ПТ, обозначенной на фиг. 14 точкой 35, то и неизвестно насколько близко текущая точка 36 с координатами (xПТ, yПТ, zПТ) к точке с истинными координатами. Однако косвенно о приближении точки с текущими координатами к точке с истинными координатами можно судить по так называемому расстоянию шага между предыдущей и текущей точками координат ПТ, оцениваемому по неравенству:
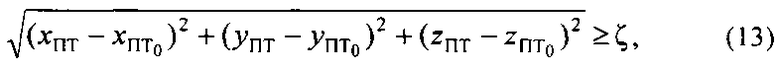
где ξ - предварительно заданное (этап 1) допустимое расстояние между истинными и определенными координатами ПТ.
4) В том случае, если неравенство (13) верно, в качестве координат ПТ0 принимают текущие координаты ПТ. Далее заново определяют параметры положения 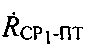 и/или
и/или 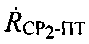 (этап 8). На основе новых параметров положения
(этап 8). На основе новых параметров положения 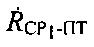 и/или
и/или 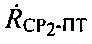 заново определяют соответствующие им линии положения, обозначенные на фиг. 14
заново определяют соответствующие им линии положения, обозначенные на фиг. 14 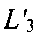 и
и 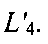 Определяют точку 37 и проверяют неравенство (13).
Определяют точку 37 и проверяют неравенство (13).
5) Если расстояние между точками 36 и 37 больше ξ, то есть неравенство (13) снова верно, процедуры 4-го пункта алгоритма повторяют: определяют линии положения, обозначенные на фиг. 14 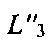 и
и 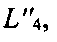 получают координаты точки 38 и снова проверяют неравенство (13). Количество шагов (итераций), как правило, не превышает пяти.
получают координаты точки 38 и снова проверяют неравенство (13). Количество шагов (итераций), как правило, не превышает пяти.
6) В том случае, если неравенство (13) неверно, итерационный алгоритм завершают, в качестве искомых координат ПТ принимают координаты текущей точки.
Рассмотрим аналитическое решение представленного алгоритма.
Поверхность положения, соответствующая параметру положения 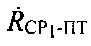 , представляет собой круглый конус, схематически изображенный на фиг. 15, с вершиной О′, совпадающей с оптическим центром антенны CP1, направляющей осью Z″, совпадающей с вектором
, представляет собой круглый конус, схематически изображенный на фиг. 15, с вершиной О′, совпадающей с оптическим центром антенны CP1, направляющей осью Z″, совпадающей с вектором 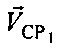 скорости CP1 и углом вращения
скорости CP1 и углом вращения 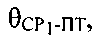 который можно рассчитать по формуле:
который можно рассчитать по формуле:
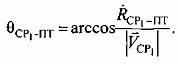
На фиг. 15 представлена геоцентрическая декартова система координат ZOXY, рассматриваемая ранее, а также система координат Z′O′X′Y′, полученная параллельным переносом ZOXY в начало координат, совпадающее с оптическим центром антенны СP1.
Уравнение круглого конуса в системе координат Z″O′X″T″ (оси О′Х″ и O′Y″ на фиг. 15 не изображены, чтобы не загромождать рисунок) имеет вид:
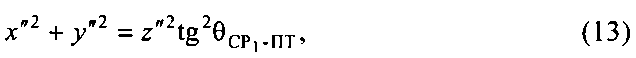
где x″, y″ и z″ - координаты в системе координат Z″O″X″Y″, связаны с координатами в геоцентрической системе координат ZOXY следующим соотношением в матричной форме:
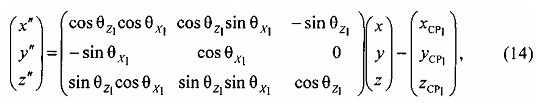
где 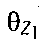 - угол между осью O′Z″ и осью O′Z′,
- угол между осью O′Z″ и осью O′Z′, 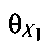 - угол между
- угол между 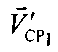 и осью ОХ′,
и осью ОХ′, 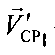 - проекцией вектора
- проекцией вектора  на плоскость O′X′Y′.
на плоскость O′X′Y′.
Углы 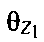 и
и 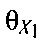 рассчитывают по формулам:
рассчитывают по формулам:
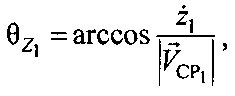
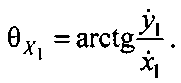
Уравнение круглого конуса в геоцентрической системе координат ZOXY с учетом (13) и (14) приобретает вид:
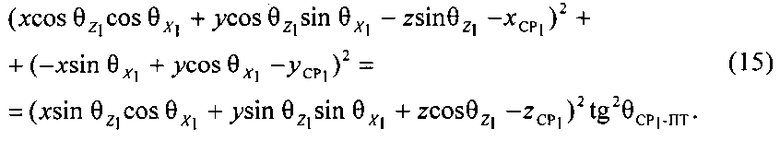
Аналогично, уравнение круглого конуса в геоцентрической системе координат ZOXY, соответствующее параметру положения 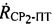 , имеет вид:
, имеет вид:
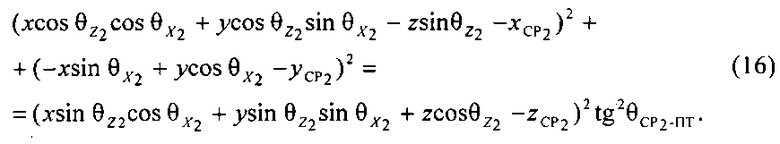
где угловые величины 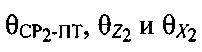 рассчитывают по формулам:
рассчитывают по формулам:
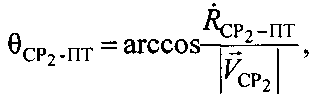
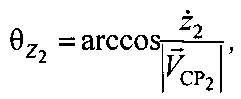
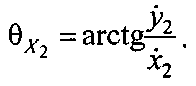
Реализация рассматриваемого алгоритма итерационного метода повышения точности ОМП ПТ в аналитическом виде сводится к добавлению в систему уравнений (5) уравнения (15) и/или уравнения (16) и решению полученной системы. В новой системе уравнений в первом выражении заменяют значение среднего радиуса Земли 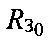 на радиус Земли
на радиус Земли 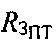 в точке ПТ, который был рассчитан на этапе 7.
в точке ПТ, который был рассчитан на этапе 7.
Полученная таким образом система уравнений будет состоять из четырех либо из пяти уравнений и будет включать три неизвестные хПТ, yПТ, zПТ. Вычисление корней таких уравнений возможно с использованием широко известных численных методов, например, с использованием метода наименьших квадратов. Решением системы уравнений будут координаты ПТ в декартовой геоцентрической системе.
Этап 10. Расстояние между точками ПТ0 и ПТ больше ξ?
Сущность данного этапа раскрыта при пояснении 3-го пункта итерационного метода повышения точности ОМП ПТ этапа 9.
Этап 11. В качестве координат ПТ0 принимают координаты ПТ.
Сущность данного этапа раскрыта при пояснении 6-го пункта итерационного метода повышения точности ОМП ПТ этапа 9.
Этап 12. Вывод результатов.
В качестве результатов рассмотренного алгоритма выступают декартовые координаты ПТ (хПТ, yПТ, zПТ), из которых вычисляют полярные координаты - геоцентрическая широта и геоцентрическая долгота по формулам:
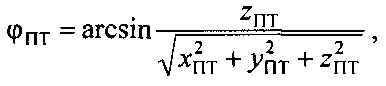
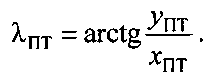
Имитационное моделирование заявленного способа ОМП ПТ с использованием двух CP показало повышение точности определения координат ПТ при изменении скорости его перемещения на 20…50% (в зависимости от величины вектора скорости ПТ), за счет более точного определения частотных сдвигов сигналов системы без существенного усложнения аппаратуры ПТ и УМС, его реализующего.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ТРИОРТОГОНАЛЬНОЙ РАМОЧНОЙ АНТЕННОЙ СИСТЕМЫ | 2020 |
|
RU2741074C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ КОМБИНИРОВАННОЙ ТРИОРТОГОНАЛЬНОЙ АНТЕННОЙ СИСТЕМЫ | 2020 |
|
RU2741068C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ АБОНЕНТСКОГО ТЕРМИНАЛА С ПОМОЩЬЮ НЕ МЕНЕЕ ДВУХ СПУТНИКОВ-РЕТРАНСЛЯТОРОВ НА НИЗКОЙ ОКОЛОЗЕМНОЙ ОРБИТЕ | 2017 |
|
RU2684740C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ АБОНЕНТСКОГО ТЕРМИНАЛА С ПОМОЩЬЮ СПУТНИКА-РЕТРАНСЛЯТОРА НА НИЗКОЙ ОКОЛОЗЕМНОЙ ОРБИТЕ | 2017 |
|
RU2679890C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ТРИОРТОГОНАЛЬНОЙ ВИБРАТОРНОЙ АНТЕННОЙ СИСТЕМЫ | 2020 |
|
RU2741072C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЙ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ТРИОРТОГОНАЛЬНОЙ АНТЕННОЙ СИСТЕМЫ | 2019 |
|
RU2714502C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЙ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ТРИОРТОГОНАЛЬНОЙ ВИБРАТОРНОЙ АНТЕННОЙ СИСТЕМЫ | 2023 |
|
RU2822686C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЙ С БОРТА ЛЕТАТЕЛЬНОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ТРИОРТОГОНАЛЬНОЙ АНТЕННОЙ СИСТЕМЫ | 2019 |
|
RU2709607C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2018 |
|
RU2696086C1 |
| Разностно-дальномерный способ определения местоположения источника радиоизлучения в условиях многолучевого распространения радиоволн | 2019 |
|
RU2714303C1 |
Изобретение относится к технике связи и может использоваться для определения местоположения источников радиоизлучения при построении подсистемы определения местоположения пользовательского терминала спутниковой системы связи. Техническим результатом изобретения является повышение точности определения координат пользовательского терминала в широком диапазоне скоростей его перемещения за счет более точного определения частотных сдвигов сигналов системы. Для этого способ основан на измерении временных задержек и частотных сдвигов между переданными и принятыми тестовыми сигналами системы. По результатам измерений, с использованием известных координат узла межсетевого соединения, координат и параметров движения спутников ретрансляторов, модуля 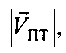 азимута αПТ вектора скорости
азимута αПТ вектора скорости 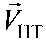 пользовательского терминала и его высоты hПТ, относительно земной поверхности и предварительно заданных частотных сдвигов
пользовательского терминала и его высоты hПТ, относительно земной поверхности и предварительно заданных частотных сдвигов 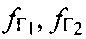 рабочих частот спутников ретрансляторов вычисляют координаты пользовательского терминала. 1 табл., 15 ил.
рабочих частот спутников ретрансляторов вычисляют координаты пользовательского терминала. 1 табл., 15 ил.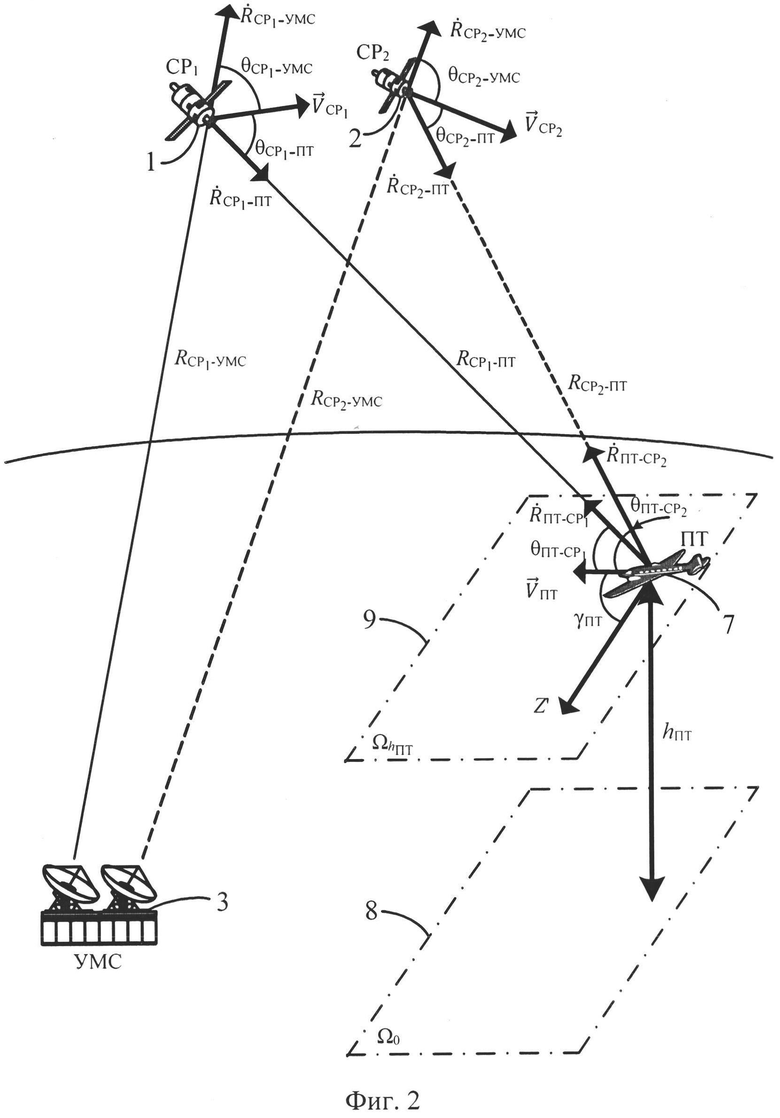
Способ определения местоположения (ОМП) пользовательского терминала (ПТ) с использованием двух спутников-ретрансляторов (CP) CP1, СР2 и узла межсетевого сопряжения (УМС), заключающийся в том, что на основе измерений временных задержек и частотных сдвигов между переданными и принятыми тестовыми сигналами системы, с учетом известных координат CP1, СР2, векторов их скоростей 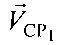 ,
, 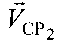 , координат УМС и предварительно заданных частотных сдвигов
, координат УМС и предварительно заданных частотных сдвигов 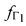 ,
, 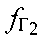 рабочих частот CP1, СР2, определяют расстояние
рабочих частот CP1, СР2, определяют расстояние 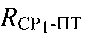 между первым CP1 и ПТ, определяют расстояние
между первым CP1 и ПТ, определяют расстояние 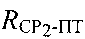 между вторым СР2 и ПТ, определяют, по меньшей мере, один из параметров: радиальную скорость
между вторым СР2 и ПТ, определяют, по меньшей мере, один из параметров: радиальную скорость 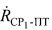 перемещения первого CP1 относительно ПТ, и/или радиальную скорость
перемещения первого CP1 относительно ПТ, и/или радиальную скорость 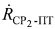 перемещения второго СР2 относительно ПТ, после чего вычисляют широту φПТ и долготу λПТ пользовательского терминала, отличающийся тем, что для вычисления широты φПТ и долготы λПТ пользовательского терминала дополнительно измеряют модуль
перемещения второго СР2 относительно ПТ, после чего вычисляют широту φПТ и долготу λПТ пользовательского терминала, отличающийся тем, что для вычисления широты φПТ и долготы λПТ пользовательского терминала дополнительно измеряют модуль 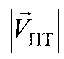 , азимут αПТ вектора скорости пользовательского терминала и его высоту hПТ относительно земной поверхности, вычисляют в УМС доплеровские сдвиги частот
, азимут αПТ вектора скорости пользовательского терминала и его высоту hПТ относительно земной поверхности, вычисляют в УМС доплеровские сдвиги частот 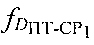 и
и 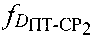 первого и второго узкополосных тестовых сигналов, обусловленные радиальными скоростями ПТ относительно CP1 и СР2, для чего предварительно определяют вероятные местоположения ПТ с учетом известных координат CP1, СР2 и определенных параметров
первого и второго узкополосных тестовых сигналов, обусловленные радиальными скоростями ПТ относительно CP1 и СР2, для чего предварительно определяют вероятные местоположения ПТ с учетом известных координат CP1, СР2 и определенных параметров 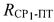 и
и 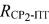 , а при определении по меньшей мере одного из параметров:
, а при определении по меньшей мере одного из параметров: 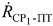 и/или
и/или 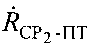 учитывают дополнительно доплеровские сдвиги частот
учитывают дополнительно доплеровские сдвиги частот 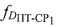 и
и 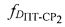 , причем для определения параметра
, причем для определения параметра 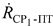 в ПТ измеряют частоту
в ПТ измеряют частоту 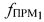 первого узкополосного тестового сигнала излученного УМС на частоте
первого узкополосного тестового сигнала излученного УМС на частоте 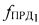 и ретранслированного через CP1 с частотой сдвига сигнала
и ретранслированного через CP1 с частотой сдвига сигнала 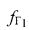 , передают результат измерения в УМС, определяют доплеровский сдвиг частоты
, передают результат измерения в УМС, определяют доплеровский сдвиг частоты 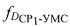 первого сигнала, обусловленного радиальной скоростью CP1 относительно УМС, определяют доплеровский сдвиг частоты
первого сигнала, обусловленного радиальной скоростью CP1 относительно УМС, определяют доплеровский сдвиг частоты 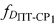 первого сигнала, обусловленного радиальной скоростью ПТ относительно CP1, затем вычисляют параметр
первого сигнала, обусловленного радиальной скоростью ПТ относительно CP1, затем вычисляют параметр 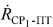 , кроме того, для определения параметра
, кроме того, для определения параметра 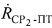 в ПТ измеряют частоту
в ПТ измеряют частоту 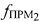 второго узкополосного тестового сигнала, излученного УМС на частоте
второго узкополосного тестового сигнала, излученного УМС на частоте 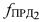 и ретранслированного через СР2 с частотой сдвига сигнала
и ретранслированного через СР2 с частотой сдвига сигнала 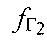 , передают результат измерения в УМС, определяют доплеровский сдвиг частоты
, передают результат измерения в УМС, определяют доплеровский сдвиг частоты 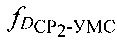 второго сигнала, обусловленного радиальной скоростью СР2 относительно УМС, определяют доплеровский сдвиг частоты
второго сигнала, обусловленного радиальной скоростью СР2 относительно УМС, определяют доплеровский сдвиг частоты 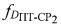 второго сигнала, обусловленного радиальной скоростью ПТ относительно СР2, затем вычисляют параметр
второго сигнала, обусловленного радиальной скоростью ПТ относительно СР2, затем вычисляют параметр 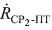 .
.
| СИСТЕМА, СПОСОБ И ПОЛЬЗОВАТЕЛЬСКИЙ ТЕРМИНАЛ В СИСТЕМЕ ОДНОЗНАЧНОГО ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ С ИСПОЛЬЗОВАНИЕМ ДВУХ СПУТНИКОВ НА НИЗКОЙ ОКОЛОЗЕМНОЙ ОРБИТЕ | 1997 |
|
RU2256935C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ЗЕМНОЙ СТАНЦИИ СПУТНИКОВОЙ СВЯЗИ ПО РЕТРАНСЛИРОВАННОМУ СИГНАЛУ | 2000 |
|
RU2172495C1 |
| US6664923B1, 16.12.2003. | |||
Авторы
Даты
2016-12-20—Публикация
2015-09-18—Подача