Изобретение относится к области техники и информатики, а более конкретно - к способу предсказания состояния технической системы при помощи аппроксимации ее параметров к непрерывной функции.
Настоящее изобретение может найти применение при создании, эксплуатации и управлении различных технических систем, включая сложные технические и технологические системы, в которых интегрированы ресурсы различного назначения и архитектуры, используемые в энергетике, машиностроении, коммунальном и сельском хозяйстве, медицине и других отраслях.
В основу настоящего изобретения положена задача создания такого способа предсказания состояния технической системы, который позволил бы объективно оценивать и прогнозировать состояние технической или технологической системы, используя обширный математический аппарат непрерывных функция, включая производные функций, а также позволял бы достигать оптимального функционирования системы ее агрегатов и подсистем, оценивать возможные последствий изменения параметров системы и управляющих ею процессов даже при малых управляющих воздействиях.
Наиболее близким по технической сущности к заявляемому изобретению является устройство автоматического прогнозирования технического состояния систем, содержащее сумматор, регистр хранения-сдвига, блок определения степени полинома, схему подключения конечных разностей, блоки умножения, схему временных коэффициентов Ньютона, элемент задержки, шину задания временной точки, на которую необходимо осуществить прогноз технического состояния систем, причем вход сумматора соединен с выходом блоков умножения и выходом элемента задержки, вход которого соединен с последней ячейкой регистра сдвига-хранения, выходы которого являются входами блока определения степени полинома, второй выход которого является первым входом схемы временных коэффициентов Ньютона и вторым входом схемы подключения конечных разностей, первые входы которой соединены с выходами блока определения степени полинома, а выходы схемы подключения конечных разностей являются первыми входами блоков умножения, второй вход которых соединен с выходами схемы временных коэффициентов Ньютона, второй вход которой соединен с шиной задания временной точки прогнозирования (Петриченко Г.С., Тартачный С.Н., «Устройство автоматического прогнозирования технического состояния систем», по заявке №92011675/09, 14.12.1992), которое можно принять за прототип.
Недостатком данного устройства является то, что оно не позволяет бороться со случайной ошибкой прогноза, возникающей за счет ошибки измерения, которая резко увеличивается с увеличением степени аппроксимирующего полинома и времени прогноза.
Задачи изобретения решены и недостатки прототипа устранены в реализованном согласно настоящему изобретению способе предсказания состояния технической системы при помощи аппроксимации ее параметров к непрерывной функции на основе данных о функционировании агрегатов и/или подсистем агрегатов, из которых состоит рассматриваемая техническая система, при этом данные о функционировании представлены в виде показателей в различных материальных формах в их дискретном цифровом представление и характеризуют технологические параметры системы и/или ее подсистем, и предусматривающий следующие стадии:
1) накапливают данные о функционировании в виде показателей в различных материальных формах в их дискретном цифровом представление о функционировании агрегатов и/или подсистем агрегатов и передают их эксперту;
2) эксперт на основе выбора методов построения моделей функционирования отдельных агрегатов и/или подсистем агрегатов, и/или системы в целом и показателей функционирования, либо их подмножества выбирает по меньшей одну из моделей функционирования отдельных агрегатов и/или подсистем агрегатов, и/или системы в целом, допускающую представление в виде непрерывной функции;
3) эксперт исходя из данных, полученных на стадиях 1 и 2 получает аппроксимацию показателей в их дискретном цифровом представление о функционировании агрегатов и/или подсистем агрегатов к непрерывной функции, таким образом, что она принимает значения показателей в реальные или условные моменты времени, которые являются единственным аргументом или несколькими аргументами этой функции
4) в процессе функционирования отдельных агрегатов и сложных технологических комплексов, состоящих из отдельных агрегатов и/или подсистем агрегатов получают текущие показатели функционирования;
5) полученные текущие показатели в автоматизированном режиме сравнивают со значениями аппроксимирующей функции, полученной на стадии 3 и оценивают размер отклонений текущих показателей от значений аппроксимирующей функции;
6) определяют с помощью внешнего критерия размер отклонения поступающих показателей от значений аппроксимирующей функции и делают вывод о нормальности или аномальности текущих отклонений;
7) при помощи аппроксимирующей функции прогнозируют состояние отдельных агрегатов и/или подсистем агрегатов, и/или системы в целом в следующие моменты времени, осуществляя прогнозирование;
8) полученные показатели и состояния необязательно сохраняют и используют в качестве управляющих воздействий для данной или аналогичной технической системы, позволяющих достичь оптимального функционирования отдельных агрегатов и/или подсистем агрегатов, и/или системы в целом.
Технически целесообразно в данном способе рассматривать ситуацию, когда эксперт при помощи вычисления производных анализирует аппроксимирующую функцию, выявляя ее экстремумы, а также характер убывания или возрастания для прогнозирования поведения данной или аналогичной технической системы.
Также технически целесообразно в данном способе рассматривать ситуацию, когда эксперт при принятии решений использует технологии искусственного интеллекта.
За счет реализации заявленного способа достигаются следующие технические результаты:
- возможно скомпенсировать случайную ошибку прогноза, возникающей за счет ошибки измерения, тем самым устранив недостаток прототипа,
- возможно объективно оценивать и прогнозировать состояние технической или технологической системы, используя обширный математический аппарат непрерывных функция, включая производные функций,
- возможно достигать оптимального функционирования системы ее агрегатов и подсистем,
- возможно оценивать возможные последствий изменения параметров системы и управляющих ею процессов даже при малых управляющих воздействиях.
Настоящее изобретение будет раскрыто в нижеследующих примерах вычисления аппроксимирующих функций второй степени, поскольку ошибки измерения резко увеличиваются с увеличением степени аппроксимирующего полинома и времени прогноза.
Первоначально накапливают данные о функционировании узла двигателя в виде показателей его температуры в дискретном цифровом представление.
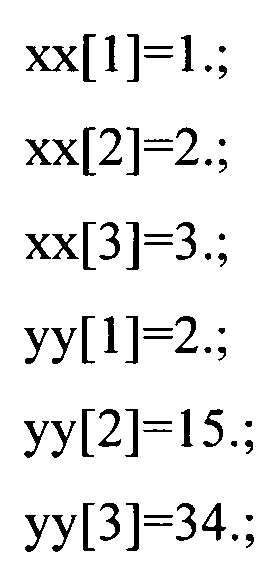
Моменты условного времени указаны в параметрах хх, а значения температуры в градусах Цельсия - в параметрах yy.
После получения данных эксперт на основе выбора методов построения моделей функционирования определяет одну из моделей функционирования отдельных агрегатов и/или подсистем агрегатов, и/или системы в целом, допускающую представление в виде непрерывной функции, а именно - представление в виде функции квадратичной функции вида Т=ах2+bx+с, где x - указанные выше моменты времени (минуты).
Эксперт исходя из полученных данных находит аппроксимацию показателей в их дискретном цифровом представление о функционировании агрегатов и/или подсистем агрегатов к непрерывной функции, таким образом, что она принимает значения показателей в реальные или условные моменты времени, которые являются единственным аргументом или несколькими аргументами этой функции, для чего вычисляет следующие параметры: abc[0] - коэффициент а квадратичной функции вида Т=ах+bx+c, abc[1] - коэффициент b квадратичной функции вида Т, abc[2] - коэффициент с квадратичной функции вида Т при помощи следующей вычислительной процедуры.

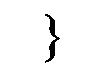
При указанных параметрах xx и yy эксперт получает значения:
Т=3х2+4х-5
а=3.000000b=4.000000с=-5.000000
Далее в процессе функционирования изучаемого узла двигателя получают текущие показатели функционирования при помощи вычисления необходимых значений по функции Т=3х2+4х-5.
Полученные текущие показатели в автоматизированном режиме сравнивают со значениями аппроксимирующей функции и оценивают размер отклонений текущих показателей от значений аппроксимирующей функции.
Далее определяют с помощью внешнего критерия размер отклонения поступающих показателей от значений аппроксимирующей функции и делают вывод о нормальности или аномальности текущих отклонений.
Проиллюстрируем данную стадию на примере аппроксимации одного периода периодической функции sin x, определяющую колебания механической системы:
Для этого эксперт вычисляет аппроксимирующую функцию, как указано выше, но для других значений:
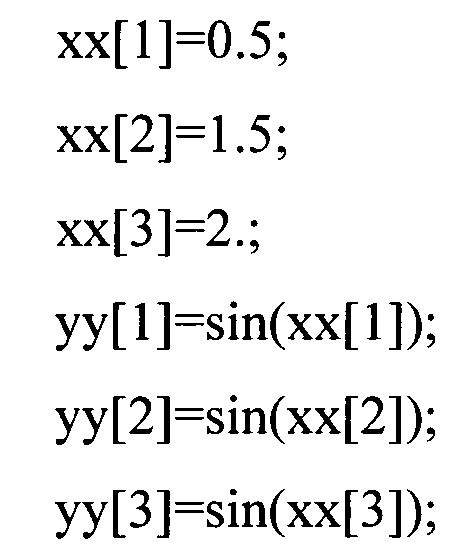
При помощи вычислительной процедуры
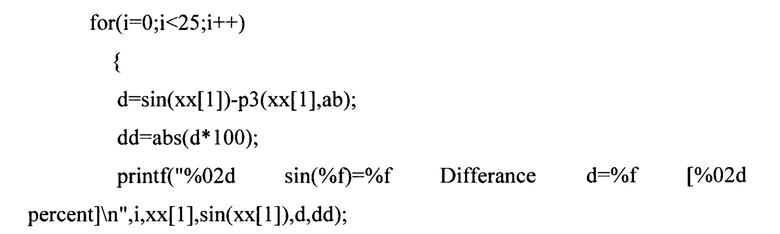
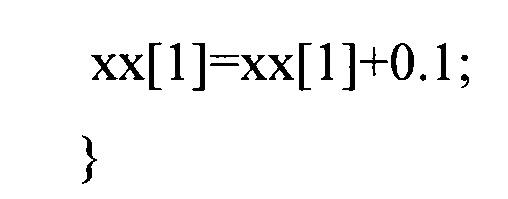
Вычислительная процедура

реализует вычисления экспертом значений функции вида T=ax2+bx+с.
Эксперт получает следующую таблицу результатов:






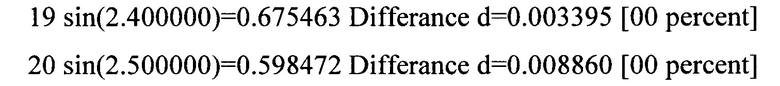

Позиции с 16-й по 24-ю относятся к области прогнозирования колебаний механической системы вне интервала измерений (0.5-2 секунды), при этом ошибка до 20-го шага составляет менее одного процента, а далее, несмотря на рост, остается в интервале допустимых инженерных погрешностей (около 7 процентов).
При этом
y1=0.479426y2=0.997495y3=0.909297?
а коэффициенты аппроксимирующей функции следующие:
a=-0.462976 b=1.444022 c=-0.126842
Таким образом, при помощи аппроксимирующей функции прогнозируют состояние отдельных агрегатов и/или подсистем агрегатов, и/или системы в целом в следующие моменты времени, осуществляя прогнозирование.
Полученные показатели и состояния сохраняют и используют в качестве управляющих воздействий для данной или аналогичной технической системы, позволяющих достичь оптимального функционирования отдельных агрегатов и/или подсистем агрегатов, и/или системы в целом.
По сравнению со способами, известными авторам, заявляемый способ позволяет объективно оценивать и прогнозировать состояние технической или технологической системы, позволяет эффективно бороться со случайной ошибкой прогноза, возникающей за счет ошибки измерения, а также достигать оптимального функционирования системы ее агрегатов и подсистем и оценивать возможные последствий изменения параметров системы и управляющих ею процессов даже при малых управляющих воздействиях.
Изобретение относится к области техники и информатики. В способе предсказания состояния технической системы при помощи аппроксимации ее параметров к непрерывной функции на основе данных о функционировании агрегатов накапливают данные о функционировании; выбирают одну из моделей функционирования отдельных агрегатов, допускающую представление в виде непрерывной функции. Далее получают аппроксимацию показателей в их дискретном цифровом представлении. Получают текущие показатели функционирования, сравнивают их со значениями полученной функции и оценивают размер отклонений текущих показателей от значений аппроксимирующей функции. Определяют размер отклонения поступающих показателей от значений аппроксимирующей функции и делают вывод о нормальности или аномальности текущих отклонений. Прогнозируют состояние отдельных агрегатов, и/или подсистем агрегатов, и/или системы в целом. Полученные показатели и состояния сохраняют и используют в качестве управляющих воздействий. Достигается оптимальное функционирование системы. 2 з.п. ф-лы.
1. Способ предсказания состояния технической системы при помощи аппроксимации ее параметров к непрерывной функции на основе данных о функционировании агрегатов и/или подсистем агрегатов, из которых состоит рассматриваемая техническая система, при этом данные о функционировании представлены в виде показателей в различных материальных формах в их дискретном цифровом представлении и характеризуют технологические параметры системы и/или ее подсистем, предусматривающий следующие стадии:
1) накапливают данные о функционировании в виде показателей в различных материальных формах в их дискретном цифровом представлении о функционировании агрегатов и/или подсистем агрегатов;
2) на основе методов построения моделей функционирования отдельных агрегатов, и/или подсистем агрегатов, и/или системы в целом и показателей функционирования либо их подмножества, выбирают по меньшей мере одну из моделей функционирования отдельных агрегатов, и/или подсистем агрегатов, и/или системы в целом, допускающую представление в виде непрерывной функции;
3) исходя из накопленных данных и выбранной модели функционирования отдельных агрегатов, и/или подсистем агрегатов, и/или системы в целом и показателей функционирования либо их подмножества получают аппроксимацию показателей в их дискретном цифровом представлении о функционировании агрегатов и/или подсистем агрегатов к непрерывной функции таким образом, что непрерывная функция принимает значения показателей в реальные или условные моменты времени, которые являются одним или несколькими аргументами этой функции;
4) в процессе функционирования отдельных агрегатов и сложных технологических комплексов, состоящих из отдельных агрегатов и/или подсистем агрегатов, получают текущие показатели функционирования;
5) полученные текущие показатели в автоматизированном режиме сравнивают со значениями полученной аппроксимирующей функции и оценивают размер отклонений текущих показателей от значений аппроксимирующей функции как модуль разности значений текущих показателей и значений аппроксимирующей функции;
6) определяют с помощью внешнего критерия размер отклонения поступающих показателей от значений аппроксимирующей функции и делают вывод о нормальности или аномальности текущих отклонений;
7) при помощи аппроксимирующей функции прогнозируют состояние отдельных агрегатов, и/или подсистем агрегатов, и/или системы в целом в следующие моменты времени, осуществляя прогнозирование;
8) полученные показатели и состояния сохраняют и используют в качестве управляющих воздействий для данной или аналогичной технической системы, позволяющих достичь оптимального функционирования отдельных агрегатов и/или подсистем агрегатов, и/или системы в целом.
2. Способ по п. 1, отличающийся тем, что при помощи вычисления производных аппроксимирующей функции анализируют ее, выявляя ее экстремумы, а также характер убывания или возрастания для прогнозирования поведения данной или аналогичной технической системы.
3. Способ по п. 1, отличающийся тем, что при принятии решений используют технологии искусственного интеллекта.
| 0 |
|
SU160950A1 | |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ И ЭКСПЕРТНАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2571693C1 |
| RU 92011675 A, 20.11.1996 | |||
| WO 2013052318 A1, 11.04.2013. | |||
Авторы
Даты
2019-03-06—Публикация
2017-05-02—Подача