Настоящее техническое решение относится к измерительной технике сверхвысоких частот.
Известен способ определения модуля и аргумента комплексного коэффициента отражения СВЧ-двуполюсника, основанный на анализе амплитудного распределения поля в линии передачи. Способ заключается в возбуждении в линии передачи, подключенной к исследуемому двухполюснику, гармонического колебания, ответвлении сигнала из линии передачи с помощью подвижного ненаправленного зонда, квадратичном детектировании ответвленного сигнала, измерении максимального и минимального значений этого сигнала, фиксации положения минимума и определение модуля и аргумента комплексного коэффициента отражения по известным формулам (см., например, Данилин А.А. Измерения в технике СВЧ / А.А. Данилин - М.: «Радиотехника», 2008. - 94 с. ). Недостатком этого способа является малый динамический диапазон изменения входного сигнала. Это связано с неквадратичностью вольт-амперной характеристики устройств, применяемых для реализации операции квадратичного детектирования (СВЧ-диодов). Динамический диапазон квадратичного детектирования у них составляет (30-40 дБ). В частности, это приводит к существенной погрешности измерения при больших значениях коэффициента стоячей волны (КСВ), а также невозможности проведения измерений в условиях, когда мощность СВЧ генератора изменяется в широких пределах.
Этот недостаток устранен за счет перехода к анализу фазового распределения поля в линии передачи в авторском свидетельстве (Гимпилевич Ю.Б. А.с. 1633367 СССР, МКИ 5 G01R 27/06. Способ определения модуля и фазы коэффициента отражения СВЧ-двуполюсника / Ю.Б. Гимпилевич (СССР). - №4407549/09; заявл. 11.04.88; опубл. 07.03.91, Бюл. №9). При этом динамический диапазон изменения входного сигнала расширен до (70-80) дБ. Этот способ наиболее близок по технической сущности к заявляемому способу определения модуля и аргумента комплексного коэффициента отражения микроволнового двухполюсника и поэтому выбран в качестве прототипа.
Указанный способ заключается в возбуждении в линии передачи зондирующего гармонического колебания и измерении параметров сигнала, ответвленного из линии передачи с помощью подвижного зонда при подключении к выходу линии передачи исследуемого двухполюсника, формировании опорного сигнала той же частоты, что и у зондирующего сигнала, начальную фазу которого изменяют по линейному закону синхронно с перемещением подвижного зонда, измерении фазового сдвига между ответвленным и опорным сигналами, определении максимального отклонения фазового сдвига Δψmax относительно нулевого значения, фиксации положения подвижного зонда, соответствующего нулевому значению фазового сдвига, определении величины смещения  положения подвижного зонда, соответствующего нулевому значению фазового сдвига относительно опорной плоскости в режиме короткого замыкания и расчете модуля
положения подвижного зонда, соответствующего нулевому значению фазового сдвига относительно опорной плоскости в режиме короткого замыкания и расчете модуля  и аргумента ϕ комплексного коэффициента отражения
и аргумента ϕ комплексного коэффициента отражения  по формулам:
по формулам:

где λ - длина волны в линии передачи.
Этот способ обладает следующими недостатками: пониженная точность ввиду отсутствия избыточности, что связано с анализом только фазового распределения поля в линии передачи, а также значительные габариты, масса и стоимость аппаратурной реализации (необходимость применения СВЧ фазометра для измерения фазового сдвига, а также необходимость применения второй измерительной линии для формирования опорного сигнала с линейным изменением фазового сдвига.
Целью изобретения является увеличение точности, а также уменьшение габаритов, массы и стоимости аппаратурной реализации.
Данная цель достигается за счет того, что в заявленном способе определения модуля и аргумента комплексного коэффициента отражения микроволнового двухполюсника заключающемся в возбуждении в линии передачи зондирующего гармонического микроволнового колебания, формировании опорного микроволнового колебания той же частоты, что и у зондирующего сигнала, и измерении параметров сигнала, ответвленного из линии передачи с помощью ненаправленного подвижного зонда при подключении к выходу линии передачи микроволнового двухполюсника, дополнительно осуществляют квадратурное детектирование ответвленного ненаправленным подвижным зондом сигнала с использованием сформированного опорного колебания, в результате которого получают I и Q составляющие, используя которые рассчитывают амплитудное  и фазовое
и фазовое  распределения поля вдоль линии передачи по формулам:
распределения поля вдоль линии передачи по формулам:  - расстояние от плоскости подключения нагрузки до подвижного зонда, для каждого из распределений рассчитывают оценки модуля и оценки аргумента комплексного коэффициента отражения микроволнового двухполюсника, а результаты определяют как среднее арифметическое этих оценок.
- расстояние от плоскости подключения нагрузки до подвижного зонда, для каждого из распределений рассчитывают оценки модуля и оценки аргумента комплексного коэффициента отражения микроволнового двухполюсника, а результаты определяют как среднее арифметическое этих оценок.
На фиг. 1 изображена структурная электрическая схема устройства, реализующего заявленный способ определения модуля и аргумента комплексного коэффициента отражения микроволнового двухполюсника.
Устройство содержит СВЧ генератор 1, микроволновый двухполюсник 2, отрезок линии передачи с продольной щелью 3, ненаправленный зонд 4, каретку 5, направленный ответвитель 6, фазовращатель 7, смесители 8 и 9, фильтры нижних частот 10 и 11, устройства возведения в квадрат 12 и 13, устройство суммирования 14, устройство деления 15, устройство извлечения квадратного корня 16, арктангесный преобразователь 17, квадратурный детектор 18, блок квадратурной обработки 19.
Способ измерения модуля и аргумента комплексного коэффициента отражения реализуют следующим образом.
Гармоническое колебание от СВЧ генератора 1 через отрезок линии передачи с продольной щелью 3, в которую введен ненаправленный зонд 4, поступает на микроволновый двухполюсник 2, модуль и аргумент комплексного коэффициента отражения которого необходимо определить. Ненаправленный зонд 4 установлен на каретке 5, которая может перемещаться вдоль отрезка линии передачи 3. Направленный ответвитель 6 установлен на выходе СВЧ генератора 1 и ориентирован на падающую волну. В результате на выходе вторичного канала направленного ответвителя 6 формируется сигнал той же частоты, что и сигнал, ответвляемый ненаправленным зондом 4. Сигналы с ненаправленного зонда 4 и направленного ответвителя 6, подаются на входы смесителей 8 и 9. Причем сигнал с выхода направленного ответвителя 6 перед тем как попасть на вход смесителя 9 сдвигается по фазе на -90° при помощи фазовращателя 7. При этом в спектре тока смесителей 8 и 9 появляются комбинационные составляющие нулевой частоты, то есть обеспечивается квадратурное детектирование СВЧ сигналов. Фазовращатель 7 и смесители 8 и 9 образуют так называемый квадратурный детектор 18, который может быть реализован в интегральном исполнении на основе стандартной микросхемы (например, микросхемы ADL53S2). На выходах фильтров нижних частот 10 и 11 при перемещении ненаправленного зонда 4 вдоль отрезка линии передачи 3 формируется пара напряжений, называемых квадратурными составляющими, 
Эти составляющие поступают в блок квадратурной обработки 19, который состоит из следующих устройств: устройства возведения в квадрат 12 и 13, устройство суммирования 14, устройство деления 15, устройство извлечения квадратного корня 16, арктангесный преобразователь 17. Блок квадратурной обработки 19 может быть реализован на основе персонального компьютера либо микроконтроллера.
На выходах блока квадратурной обработки 19 получаем амплитудное  и фазовое
и фазовое  распределения поля в линии передачи, для каждого из которых рассчитывают оценки модуля и аргумента ККО, а результаты получают путем усреднения этих оценок.
распределения поля в линии передачи, для каждого из которых рассчитывают оценки модуля и аргумента ККО, а результаты получают путем усреднения этих оценок.
Проведем теоретический анализ заявляемого способа определения модуля и аргумента комплексного коэффициента отражения микроволнового двухполюсника.
В результате интерференции падающей и отраженной волн в отрезке линии передачи 3 возникает режим смешанной волны. Комплексную амплитуду суммарной волны  в плоскости подключения подвижного зонда 4, находящемся на расстоянии
в плоскости подключения подвижного зонда 4, находящемся на расстоянии  от плоскости подключения микроволнового двухполюсника 2, с учетом отсутствия потерь в линии передачи и идеального согласования с СВЧ генератором 1 можно записать (см. Силаев М.А., Брянцев С.Ф. Приложение матриц и графов к анализу СВЧ устройств / М.А. Силаев, С.Ф. Брянцев - М.: «Сов. радио», 1970. - 248 с. ) как
от плоскости подключения микроволнового двухполюсника 2, с учетом отсутствия потерь в линии передачи и идеального согласования с СВЧ генератором 1 можно записать (см. Силаев М.А., Брянцев С.Ф. Приложение матриц и графов к анализу СВЧ устройств / М.А. Силаев, С.Ф. Брянцев - М.: «Сов. радио», 1970. - 248 с. ) как

где Еп- амплитуда падающей волны;  - комплексный коэффициент отражения микроволнового двухполюсника 2; β=2π/λ - фазовая постоянная; λ - длина волны в линии передачи; L - длина отрезка линии передачи 3.
- комплексный коэффициент отражения микроволнового двухполюсника 2; β=2π/λ - фазовая постоянная; λ - длина волны в линии передачи; L - длина отрезка линии передачи 3.
Представим в формуле (1) комплексный коэффициент отражения двухполюсника  в алгебраическом виде, применив формулу Эйлера
в алгебраическом виде, применив формулу Эйлера

Определим амплитуду суммарной волны  взяв модуль выражения для комплексной амплитуды (2):
взяв модуль выражения для комплексной амплитуды (2):

Определим начальную фазу суммарной волны, взяв аргумент выражения для комплексной амплитуды (2):

Зная амплитуду (3) и начальную фазу (4) суммарной волны, запишем выражение для гармонического колебания, ответвляемого ненаправленным зондом 4:

где K - коэффициент передачи ненаправленного зонда 4; ω - круговая частота микроволнового колебания; t - текущее время.
Это колебание подается на сигнальные входы смесителей 8 и 9. Опорное колебание  формируемое на выходе вторичного канала, направленного ответвителя 6 можно записать в виде
формируемое на выходе вторичного канала, направленного ответвителя 6 можно записать в виде
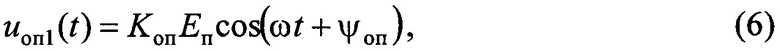
где Kоп - коэффициент передачи опорного канала; ψоп - начальная фаза опорного колебания.
Опорное колебание (6) подается на опорный вход смесителя 8 и одновременно на вход фазовращателя 7, на выходе которого формируется колебание  сдвинутое по фазе на угол -90° относительно
сдвинутое по фазе на угол -90° относительно  то есть
то есть
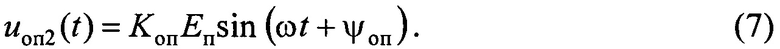
Это колебание подается на опорный вход смесителя 9. Смесители 8 и 9 осуществляют перемножение колебаний, поступающих на их входы. Запишем выражения для произведений этих колебаний с учетом формул (5), (6) и (7):

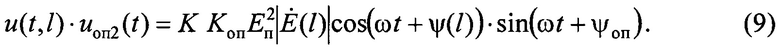
Применив в (8) и (9) известные тригонометрические формулы, получаем


Таким образом, в спектрах выходных сигналов смесителей 8 и 9 появляются постоянные составляющие (первые члены в выражения 10 и 11), а также составляющие, частоты которых вдвое превышают частоту микроволнового колебания (вторые члены в выражениях 10 и 11).
Сигналы с выходов смесителей 8 и 9 поступают на входы фильтров нижних частот 10 и 11, что обеспечивает выделение низкочастотных составляющих и подавление высокочастотных составляющих, то есть осуществляется квадратурное детектирование. При этом на выходах фильтров нижних частот 10 и 11 квадратурного детектора 18, с учетом (3) и (4), получаем следующие соотношения для квадратурных составляющих:


где  - сквозной коэффициент преобразования; Kкд - коэффициент преобразования квадратурного детектора.
- сквозной коэффициент преобразования; Kкд - коэффициент преобразования квадратурного детектора.
В блоке квадратурной обработки 19 определяются амплитуда  и начальная фаза
и начальная фаза  ответвленного ненаправленным зондом 3 колебания. Для определения амплитуды квадратурные составляющие
ответвленного ненаправленным зондом 3 колебания. Для определения амплитуды квадратурные составляющие  подают на входы устройств возведения в квадрат 12 и 13 соответственно, с выходов которых квадраты квадратурных составляющих
подают на входы устройств возведения в квадрат 12 и 13 соответственно, с выходов которых квадраты квадратурных составляющих  поступают на входы устройства суммирования 14, с выхода которого сигнал поступает на вход устройства извлечения квадратного корня 16, на выходе которого получаем
поступают на входы устройства суммирования 14, с выхода которого сигнал поступает на вход устройства извлечения квадратного корня 16, на выходе которого получаем

Для определения начальной фазы квадратурные составляющие  и
и  подают на входы устройства деления 15, с выхода которого отношение квадратурных составляющих
подают на входы устройства деления 15, с выхода которого отношение квадратурных составляющих  поступает на вход арктангенсного преобразователя 17, на выходе которого получаем
поступает на вход арктангенсного преобразователя 17, на выходе которого получаем

Подставляя (12) и (13) в формулы (14) и (15), получаем следующие соотношения для амплитудного и фазового распределений:


Проанализируем фазовое распределение  Из формулы (17) следует, что три первые составляющая
Из формулы (17) следует, что три первые составляющая  не несут информации об измеряемых параметрах
не несут информации об измеряемых параметрах  а значит, что эти составляющие можно исключить при обработке измерительной информации в режиме калибровки прибора. При дальнейшем рассмотрении не будем учитывать эти составляющие, сосредоточив внимание на третьей составляющей, которая несет информацию об измеряемых параметрах. Назовем эту составляющую «информационной составляющей» и обозначим как
а значит, что эти составляющие можно исключить при обработке измерительной информации в режиме калибровки прибора. При дальнейшем рассмотрении не будем учитывать эти составляющие, сосредоточив внимание на третьей составляющей, которая несет информацию об измеряемых параметрах. Назовем эту составляющую «информационной составляющей» и обозначим как 

Для удобства дальнейшего анализа введем переменную х:

Тогда выражение (18) для информационной составляющей фазового распределения поля приобретает вид

Проанализируем информационную составляющую фазового распределения Δψ(x). Из выражения (20) следует, что Δψ(x) - периодическая функция аргумента х с периодом 2π. Сначала определим экстремальные значения этой функции. Для этого найдем производную по переменной х выражения (20) и приравняем ее к нулю, что приводит к уравнению

Решая уравнение (21) определим значения х, соответствующие экстремумам. Исключая тривиальный случай  при х≥0 решение имеет вид
при х≥0 решение имеет вид

где n=0, 1, 2, ….
Анализ показывает, что на одном периоде функции Δψ(x) существует один максимум и один минимум. Экстремальные значения фазового распределения определим, подставив xn в формулу (20). В результате получим:


где Δψ1 и Δψ2 - максимальное и минимальное значения фазового сдвига соответственно.
Из (23) и (24) следует, что экстремальные значения имеют одинаковую абсолютную величину и отличаются только знаками. В дальнейшем будем пользоваться термином «максимальное отклонение фазового распределения Δψmax относительно нуля», понимая под этим абсолютное значение экстремумов

Из (25) следует, что Δψmax зависит только от модуля комплексного коэффициента отражения, что позволяет определить Для этого решим (25) относительно
Для этого решим (25) относительно Из формулы (25) следует
Из формулы (25) следует 
Из выражения (26) следует

Применив известное тригонометрическое соотношение tgα=sinα/cosα, из (27) получаем, следующую формулу для определения модуля комплексного коэффициента отражения

Далее определим положение нулей фазового распределения, приравняв (20) к нулю, что приводит к уравнению

Решение уравнения (29) при х≥0 имеет вид

где k=0, 1, 2 ….
Из (30) следует, что положение нулей фазового распределения не зависит от значения модуля 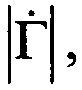 а зависит только от координаты х, то есть только от аргумента комплексного коэффициента отражения, что позволяет определить ϕ. Проведя обратную замену переменных в соответствии с (19), из формулы (30) находим
а зависит только от координаты х, то есть только от аргумента комплексного коэффициента отражения, что позволяет определить ϕ. Проведя обратную замену переменных в соответствии с (19), из формулы (30) находим

Выражение (31) позволяет однозначно определить аргумент комплексного коэффициента отражения по положению нулей фазового распределения. Сначала в качестве нагрузки подключим образцовый короткозамыкатель, аргумент комплексного коэффициента отражения которого равен ϕкз=-π. При этом фиксируем положение нулей фазового распределения  которые в соответствии с (31) будут расположены в точках с координатами
которые в соответствии с (31) будут расположены в точках с координатами

Затем фиксируем положение нулей фазового распределения при подключенном измеряемом двухполюснике. Величину смещения нулей фазового распределения  определим, используя (31) и (32):
определим, используя (31) и (32):

Из формулы (33) выразим ϕ следующим образом

Таким образом, по фазовому распределению с помощью формул (28) и (34) можно определить модуль и аргумент комплексного коэффициента отражения.
Теперь проанализируем амплитудное распределение  С учетом (19) выражение для амплитудного распределения (16) принимает вид
С учетом (19) выражение для амплитудного распределения (16) принимает вид

Найдем минимальное Umin и максимальное Umax значения функции U(x). Для этого продифференцируем выражение (35) по х и приравняем производную к нулю, что приводит к уравнению

из которого следует

Исключая тривиальный случай при х≥0 решение имеет вид
при х≥0 решение имеет вид

Анализируя (35) легко убедиться в том, что минимумы амплитудного распределения будут наблюдаться при нечетных значениях n, а максимумы - при четных значениях n. Подставляя (38) в формулу (35), с учетом этого получаем:

Из (39) следует, что минимальное и максимальное значения амплитуды зависят только от модуля комплексного коэффициента отражения и не зависят от аргумента, что позволяет определить значение 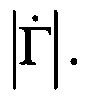 Для этого решим систему уравнений (39) относительно модуля комплексного коэффициента отражения. В результате получаем следующее выражение для расчета модуля
Для этого решим систему уравнений (39) относительно модуля комплексного коэффициента отражения. В результате получаем следующее выражение для расчета модуля 

Из (38) следует, что положение минимумов амплитудного распределения не зависит от значения модуля  а зависит только от координаты х, то есть только от аргумента комплексного коэффициента отражения, что позволяет определить ϕ.
а зависит только от координаты х, то есть только от аргумента комплексного коэффициента отражения, что позволяет определить ϕ.
Из предыдущего анализа следует, что минимумы амплитудного распределения будут наблюдаться при

где m=0, 1, 2, ….
Проведя обратную замену переменных в соответствии с (19), из формулы (41) находим

Выражение (42) позволяет однозначно определить аргумент комплексного коэффициента отражения по положению минимумов амплитудного распределения. Сначала в качестве нагрузки подключим образцовый короткозамыкатель, аргумент комплексного коэффициента отражения которого равен ϕкз=-π. При этом фиксируем положение нулей амплитудного распределения  которые в соответствии с (42) будут расположены в точках с координатами
которые в соответствии с (42) будут расположены в точках с координатами

Затем фиксируем положение минимумов амплитудного распределения при подключенном измеряемом двухполюснике. Величину смещения минимумов амплитудного распределения  определим, используя (42) и (43):
определим, используя (42) и (43):
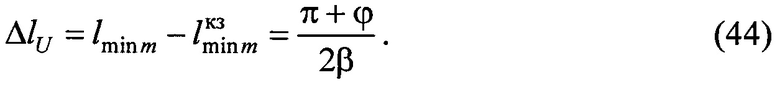
Из формулы (44) выразим ϕ следующим образом

Таким образом, по амплитудному распределению с помощью формул (40) и (45) можно определить модуль и аргумент комплексного коэффициента отражения.
Проведенный анализ заявленного способа показал, что он обеспечивает одномоментное определение двух пар независимых оценок значений модуля и аргумента измеряемого комплексного коэффициента отражения, а это приводит к двукратной избыточности, что позволяет повысить точность путем усреднения. При этом результаты измерения следует определять, как среднее арифметические (для модуля и аргумента) от двух измерений, выполненных посредством анализа амплитудного и фазового распределений полей по формулам (28), (40) - для модуля и по формулам (34), (45) - для аргумента.
Предлагаемый способ определения модуля и аргумента комплексного коэффициента отражения микроволнового двухполюсника обладает следующими преимуществами:
- высокая точность, получаемая за счет избыточности при одновременном использовании амплитудного и фазового распределений электромагнитной волны в линии передачи;
- малые габариты и масса аппаратурной реализации СВЧ части устройства, поскольку при этом исключается из схемы измерения вторая измерительная линия и громоздкий СВЧ фазометр.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОГО ИЗМЕРЕНИЯ МОДУЛЯ И АРГУМЕНТА КОМПЛЕКСНОГО КОЭФФИЦИЕНТА ОТРАЖЕНИЯ МИКРОВОЛНОВЫХ УЗЛОВ | 2020 |
|
RU2752022C1 |
| Измеритель модуля и фазы коэффициента отражения | 1990 |
|
SU1793392A1 |
| Измеритель комплексного коэффициента отражения | 1990 |
|
SU1727088A1 |
| Способ определения модуля и фазы коэффициента отражения СВЧ-двухполюсника | 1988 |
|
SU1633367A1 |
| СПОСОБ ВСТРОЕННОГО КОНТРОЛЯ ХАРАКТЕРИСТИК ЦИФРОВОЙ АКТИВНОЙ ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКИ | 2020 |
|
RU2752553C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОМПЛЕКСНЫХ ПАРАМЕТРОВ СВЧ-УСТРОЙСТВ | 1991 |
|
RU2022284C1 |
| АВТОДИННЫЙ ФОТОДЕТЕКТОРНЫЙ ПРИЕМОПЕРЕДАТЧИК ДЛЯ СИСТЕМ БЛИЖНЕЙ РАДИОЛОКАЦИИ | 2023 |
|
RU2824039C1 |
| СПОСОБ И СИСТЕМА ДЛЯ РАДИОЛОКАЦИОННОГО ИЗМЕРЕНИЯ СКОРОСТЕЙ И КООРДИНАТ ОБЪЕКТОВ (ВАРИАНТЫ) | 2002 |
|
RU2239845C2 |
| Способ обработки радиолокационных сигналов в моноимпульсной РЛС | 2016 |
|
RU2636058C1 |
| Способ определения угла сдвига фаз СВЧ-устройства с преобразованием частоты | 2016 |
|
RU2621368C1 |

Изобретение относится к измерительной технике сверхвысоких частот, в частности к измерениям параметров СВЧ-двухполюсников. Технический результат - увеличение точности, а также уменьшение габаритов, массы и стоимости аппаратурной реализации. Способ определения комплексного коэффициента отражения микроволнового двухполюсника заключается в возбуждении в линии передачи зондирующего гармонического микроволнового колебания, формировании опорного микроволнового колебания той же частоты, что и у зондирующего сигнала, и измерении параметров сигнала, ответвленного из линии передачи с помощью ненаправленного подвижного зонда при подключении к выходу линии передачи микроволнового двухполюсника. При этом дополнительно осуществляют квадратурное детектирование ответвленного ненаправленным подвижным зондом сигнала с использованием сформированного опорного колебания, в результате которого получают I и Q составляющие, используя которые рассчитывают амплитудное  и фазовое
и фазовое  распределения поля вдоль линии передачи по формулам
распределения поля вдоль линии передачи по формулам 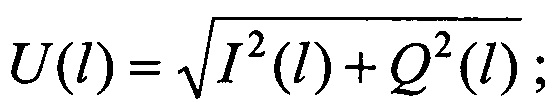
 где
где  - расстояние от плоскости подключения нагрузки до подвижного зонда, для каждого из распределений рассчитывают оценки модуля и оценки аргумента комплексного коэффициента отражения микроволнового двухполюсника, а результаты определяют как среднее арифметическое этих оценок. 1 ил.
- расстояние от плоскости подключения нагрузки до подвижного зонда, для каждого из распределений рассчитывают оценки модуля и оценки аргумента комплексного коэффициента отражения микроволнового двухполюсника, а результаты определяют как среднее арифметическое этих оценок. 1 ил.
Способ определения комплексного коэффициента отражения микроволнового двухполюсника, заключающийся в возбуждении в линии передачи зондирующего гармонического микроволнового колебания, формировании опорного микроволнового колебания той же частоты, что и у зондирующего сигнала, и измерении параметров сигнала, ответвленного из линии передачи с помощью ненаправленного подвижного зонда при подключении к выходу линии передачи микроволнового двухполюсника, отличающийся тем, что дополнительно осуществляют квадратурное детектирование ответвленного ненаправленным подвижным зондом сигнала с использованием сформированного опорного колебания, в результате которого получают I и Q составляющие, используя которые рассчитывают амплитудное  и фазовое
и фазовое  распределения поля вдоль линии передачи по формулам
распределения поля вдоль линии передачи по формулам 
 где
где  - расстояние от плоскости подключения нагрузки до подвижного зонда, для каждого из распределений рассчитывают оценки модуля и оценки аргумента комплексного коэффициента отражения микроволнового двухполюсника, а результаты определяют как среднее арифметическое этих оценок.
- расстояние от плоскости подключения нагрузки до подвижного зонда, для каждого из распределений рассчитывают оценки модуля и оценки аргумента комплексного коэффициента отражения микроволнового двухполюсника, а результаты определяют как среднее арифметическое этих оценок.
| Способ определения модуля и фазы коэффициента отражения СВЧ-двухполюсника | 1988 |
|
SU1633367A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОМПЛЕКСНЫХ ПАРАМЕТРОВ СВЧ-УСТРОЙСТВ | 1991 |
|
RU2022284C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ПАРАМЕТРОВ РАССЕЯНИЯ ЧЕТЫРЕХПОЛЮСНИКА НА СВЧ | 2012 |
|
RU2494408C1 |
| Способ измерения комплексных параметров двухполюсника | 1990 |
|
SU1756832A1 |
| Способ измерения величин составляющих комплексного сопротивления двухполюсника | 1977 |
|
SU962818A2 |
| СПОСОБ ЛИТЬЯ МЕТАЛЛА | 1998 |
|
RU2209841C2 |
Авторы
Даты
2019-04-02—Публикация
2018-03-06—Подача