1 СВЯЗАННЫЕ ЗАЯВКИ
Данная заявка ссылается на предварительную заявку на патент США №61/865,134 "NADO криптография с использованием односторонних функций", внесенную в реестр 13 августа 2013 г.; данная заявка ссылается на предварительную заявку на патент США №61/992,915 "NADO криптография с генераторами ключей с использованием односторонних функций", внесенную в реестр 14 мая 2014 г.; данная заявка ссылается на предварительную заявку на патент США №62/004,852 "NADO криптография с использованием односторонних функций", внесенную в реестр 29 мая 2014 г.; данная заявка ссылается на Международную заявку на патент PCT/US14/50462 "NADO криптография с использованием односторонних функций", внесенную в реестр 10 августа 2014 г.; данная заявка ссылается на предварительную заявку на патент США №62/056,537 "Генераторы ключей усиливают симметричную криптографию", внесенную в реестр 28 сентября 2014 г.; данная заявка ссылается на заявку на патент США №14/292,935 "NADO криптография с использованием односторонних функций", внесенную в реестр 1 июня 2014 г.; данная заявка ссылается на заявку на патент США №14/843,999 "NADO криптография при помощи генераторов ключей", внесенную в реестр 3 сентября 2015 г.
2 ОБЛАСТЬ ИЗОБРЕТЕНИЯ
Настоящее изобретение, в общем, относится к криптографическим методам и устройствам. В некоторых его примерах осуществления, оно относится к симметричным методам и устройствам для криптографии. Криптографические устройства и методы в основном используются для шифрования и дешифрования информации, которая передается посредством систем связи и передачи данных. Например, криптографические методы могут использоваться для того, чтобы шифровать телефонный звонок; в некоторых примерах осуществления изобретения телефонный звонок может передаваться при помощи голоса посредством IP (интернет-протокола), используя мобильный телефон. Эти методы также могут использоваться для шифрования пассивных данных на компьютере или другом физическом устройстве, таком как накопитель на магнитной ленте. Обычно информация, которая шифруется отправителем, который иногда называется Боб, с использованием его уникального(ых) ключа(ей), а зашифрованная информация, которая называется зашифрованное сообщение, передается получателю, который иногда называется Элис. Получатель, Элис, использует свой(и) уникальный(е) ключ(и), чтобы применить устройство или метод шифрования к зашифрованному сообщению. На выходе из этого устройства или метода шифрования получается та же информация, которую отправитель собрал перед тем, как ее зашифровать и отправить. Ева - это название агента, который пытается расшифровать зашифрованное сообщение. Одной из первичных целей Элис или Боба является гарантия того, что Ева не сможет расшифровать зашифрованное сообщение, которое передается между ними.
3 УРОВЕНЬ ТЕХНИКИ
Объект изобретения, который описывается в данном разделе, не следует считать предшествующим уровнем техники только в результате упоминания о нем в данном разделе. Точно также, задача, которая указана в разделе, или связана с объектом изобретения раздела, не должна считаться такой, которая ранее была признана в предшествующем уровне техники. Объект изобретения в разделе "Суть изобретения" представляет собой различные подходы, которые сами по себе также могут быть изобретениями, а также различные проблемы, которые возможно изобретатель распознал первым.
Ссылка [1] предоставляет практическое и теоретическое описание криптографии и криптографических методов. Ссылки [2, 3, 4] также предоставляют описание известных криптографических методов, которые находятся в открытом доступе. Криптографическая защита с открытым ключом обычно используется для управления ключами и огромного числа протоколов. Симметричная традиционная криптография является полезной для шифрования данных и защиты частных голосовых и письменных передач данных.
В симметричной криптографии Элис шифрует свой открытый текст, а Боб расшифровывает зашифрованное сообщение, полученное от Элис, используя тот же закрытый ключ. Ключ называется закрытым, чтобы продемонстрировать то, что Элис и Боб не хотят, чтобы Ева получила этот ключ. Например, алгоритм блочного шифрования ЕА:{0,1}m×{0,1}κ→{0,1}m использует κ-битный ключ K в качестве параметра и шифрует m-битный блок открытого текста М, именуемый как ЕА(М, K). Вместимость ключа блочного шифра {0,1}κ имеет размер 2κ. Вместимость ключа блочного шифра {0,1}m имеет размер 2m. Алгоритм расшифровки DA:{0,1}m×{0,1}κ→{0,1}m имеет обратную особенность, что DA(EA(x,K),K)=x для каждого открытого текста х∈{0,1}m и каждого ключа K∈{0,1}κ.
Стандарт AES (усовершенствованный стандарт шифрования) представляет собой блочный шифр с размером блока 16 байт (128 бит), который представляет собой симметричный криптографический алгоритм [5, 6]. Стандарт AES широко используется в промышленности, рекомендован NIST (Национальный институт стандартов и технологии) и используется Министерством Обороны Соединенных Штатов Америки. Стандарт AES является наиболее широко используемым ключом блочного шифрования на сегодняшний день. Например, стандарт AES-128, который использует 128-битные статические ключи, в настоящее время используется приложением FileVault на компьютерах Apple. FileVault шифрует жесткий диск внутри компьютера Apple.
В течение последних лет, различные атаки на шифр стандарта AES (известный уровень техники) продемонстрировали слабость в этом шифре. В некоторых случаях практические атаки дополнением на Oracle (oracle padded attacks) [7] были в состоянии получить обычный текст из зашифрованного текста, который шифровался по стандарту AES. По крайней мере, частью слабого места является медленное преобразование открытого текста для нарушения его статистической структуры в планировании ключа [8, 9, 10]. Слабые места стандарта AES далее усиливаются статическим блоком подстановки, и из-за своего статического ключа стандарт AES преобразовывает два идентичных блока открытого текста в два идентичных блока зашифрованного текста. В частности, вероятную атаку на стандарт AES-256 демонстрирует меньшее на 1 число циклов - 13 циклов вместо 14 - в таблице ключей [11]. Вообще, в последние годы были открыты дополнительные общеизвестные (не засекреченные) атаки на стандарт шифрования AES [12, 13, 14, 15], которые предполагают, что стандарт AES не является, таким же криптостойким шифром, как полагало ранее криптографическое сообщество.
Более того, известный уровень техники [1, 2, 6, 16] не раскрывает понятие последовательности генератора ключа, ни получения нового ключа, исходя из обновления генератора ключа. Использование генераторов ключа в данном изобретении исключает зависимость криптографической надежности от одного статического крипотографического ключа. Обычно, криптографические данные в известном уровне техники используют статический ключ К на протяжении всего выполнения алгоритма шифрования. Использование статического ключа в известном уровне техники далее вытекает из некоторых атак, как описано в предыдущем абзаце, которые пытаются получить или воссоздать статический ключ. В известном уровне техники, если статический ключ получен, то криптографическая безопасность полностью скомпрометирована. Напротив, в примерах осуществления, описанных в данном изобретении, если один из динамических ключей получен Евой, то Ева все равно не может найти предшествующие динамические ключи, которые используют Элис и Боб, а также Ева не может найти или получить будущие динамические ключи, которые используют Элис и Боб.
В качестве примера предположения статического ключа в известном уровне техники, некоторые атаки, связанные с дополнениями Oracle [7] полагаются на тот факт, что у Евы имеется некоторая информация о последнем блоке. Это помогает Еве работать в обратном направлении для нахождения статического ключа. В данном изобретении использование односторонней функции для создания динамических ключей препятствует Еве получить даже тот ключ, который используется для того одного блока открытого текста, поскольку для этого потребовалась бы атака нахождения прообраза на одностороннюю функцию без какой-либо прямой информации, касающейся профиля, и трудноразрешимый поиск по огромной последовательности непредсказуемых ключей. В известном уровне техники Еве приходится осуществлять поиск только одного статического ключа, который используется для шифрования каждого блока обычного текста.
4 СУТЬ ИЗОБРЕТЕНИЯ
Изобретение(я), описанное(ые) в данном документе представляет собой процесс шифрования и расшифровки информации, который используется в системах связи, передачи и хранения данных.
Термин "генератор ключа" используется в данном описании, чтобы обозначить значение или совокупность значений, по которым выполняется одна или несколько операций для создания другого значения или набора значений, из которого получают или можно получить ключ. "Последовательность генераторов ключей" представляет собой последовательность генераторов ключей. В примере осуществления изобретения присваивание обозначения для "последовательности генераторов ключей" может быть автоматически представлено, как функция Г:N→Sn где N - это натуральные числа, a S - конечный алфавит значений, а {0,1}n - множество всех строк значений длиной n. Размер генератора ключей - n.
В варианте осуществления изобретения S={0,1}, значения которого равны 0 и 1. В этом варианте значения 0 и 1 являются битами. В другом варианте осуществления S={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е}, которые называются шестнадцатеричными значениями. В другом варианте осуществления S может быть алфавитом значений {а, b, с, d, е, f, g, h}. В другом варианте осуществления S имеет 256 значений и S={0, 1, 2, 3, 4, …, 255}.
Например, строка значений 10101 представляет собой элемент {0,1}5, где S={0,1}. Например, множество всех строк значений длиной 3 представляет собой {0,1}3={000, 001, 010, 011, 100, 101, 110, 111}. Иногда в описании k-тый генератор последовательности генератора ключей Г будет обозначаться, как Г(k).
В некоторых примерах осуществления изобретения фактическое получение ключа является необязательным. Например, часть k-того генератора ключей могла бы использоваться в качестве k-того ключа. В данном описании в тех случаях, когда упоминаются ключ и генератор ключей, имеется отдельный ключ и генератор ключей, где ключ получают из генератора ключей. В другом примере осуществления изобретения отсутствует отдельный ключ, который получают фактически, а часть нынешнего генератора ключей может использоваться в качестве ключа.
В данном описании слово "ключ" и термин "криптографический ключ" используются взаимозаменяемо для обозначения одного и того же. Ключ представляет собой одно или несколько значений, которые описывают, как конкретная функция шифрования будет шифровать сообщение. Например, ключ может представлять собой последовательность нулей и единиц, которые побитово исключают или исключаются биты / битами, которые составляют сообщение, чтобы сформировать зашифрованное сообщение. В другом варианте осществления изобретения, ключ может быть последовательностью значений от 0 до 255 включительно. Другие примеры использования ключей, как части методов шифрования, приводятся в других местах в данном описании.
В некоторых примерах осуществления изобретения, Н-процесс может быть реализован при помощи блочного шифра, где генератор ключей Г обновляется после того, как один или нескольких блоков обычного текста были зашифрованы при помощи блочного шифра. Иногда последовательность всех блоков простого текста, которые шифруются во время сессии шифрования, именуются, как сообщение обычным текстом или сообщение. В некоторых примерах осуществления изобретения, данный блочный шифр может представлять собой улучшенным AES-256 или улучшенный AES-128, или же улучшенный Serpent. В данном описании, когда используются термины "улучшенный" AES или "улучшенный" Serpent, это означает, что улучшенный AES и улучшенный Serpent более не используют статический ключ во время шифрования или дешифрования. Далее, в другом контексте улучшенный AES или улучшенный Serpent означают, что используется динамический ключ, который получен из генератора ключей. Эти улучшения используют последовательности генераторов ключей и динамические ключи. В данном описании "стандартный" AES [5, 6] или "стандартный" Serpent [39] будут использоваться для описания известного уровня техники AES и Serpent, соответственно, в тех случаях, когда для каждого зашифрованного блока или дешифрованного используется статический ключ.
Изобретение вводит понятие последовательности генераторов ключей, обновления генератора ключей и динамических ключей. Это дает возможность каждому ключу, который используется Н-процессом непредсказуемо обновляться после того, как процесс зашифровал один или более блоков обычного текста. Более того, во всем данном описании генератор ключей может быть значительно больше, чем тот ключ, который используется Н-процессом. Обновление генератора ключей создает благоприятные криптографические особенности и укрепляет криптографические шифры, которые уже существуют и уже проверены.
В примере осуществления изобретения, j-тый генератор ключей Г(j) представляет собой n бит по длине. Г(j) обновляется до Г(j+1) путем применения односторонней функции хеширования к q бит Г(j), где q<n, а профиль сообщения соединяется с оставшимися n-q бит Г(j). Вообще, n-q бит Г(j) остаются без изменений, а другие q бит изменяются, благодаря односторонней функции хеширования. В примере осуществления изобретения, динамический ключ получают из Г(j), и он используется блочным шифром для шифрования обычного текста. В примере осуществления изобретения, данное шифрование может работать, как автономная симметричная криптография. В альтернативном примере осуществления изобретения, данное шифрование с помощью динамического ключа работает, как Н-процесс.
Данный метод обновления генератора ключей использует лавинный эффект односторонних функций хеширования и приводит к тому, что начальный генератор ключей Г(0) выполняет перебор по огромной орбите подстановок. На Рисунке 1С показан пример лавинного эффекта для односторонней функции хеширования SHA-1 [18]. Если говорить более конкретно, последовательность Г(0), Г(1), Г(2), …, Г(n) … не имеет наложений до тех пор, пока последовательность генераторов ключей напоминает длину, которая предсказана парадоксом дней рождений, исходя их равномерного распределения вероятностей. На странице 77 источника [1] представлено описание хорошо известного парадокса дней рождений.
Говоря более детально, каждый генератор ключей может быть представлен, как окончательная последовательность символов: например, каждый генератор ключей может быть представлен J битами. В связи с этим, эффект дня рождения может использоваться в качестве одной статистической проверки непредсказуемости последовательности генераторов ключей, если вероятность повторения (т.е. наложения) какого-либо данного генератора ключей в последовательности имеет такой же порядок, как и прогнозирует эффект дня рождения.
Предположим, что m=2J является общим числом возможных генераторов ключей. Тогда n, которая удовлетворяет уравнению 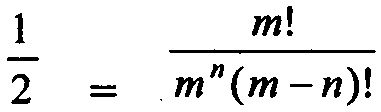 обозначает размер последовательности генераторов ключей, которая имеет примерно 50-процентную вероятность возникновения наложения при допущении равномерной распределения вероятностей. Для конечной последовательности генераторов ключей, в которой начало последовательности генератора ключей короче, чем n имеет менее, чем 50% вероятности возникновения наложения.
обозначает размер последовательности генераторов ключей, которая имеет примерно 50-процентную вероятность возникновения наложения при допущении равномерной распределения вероятностей. Для конечной последовательности генераторов ключей, в которой начало последовательности генератора ключей короче, чем n имеет менее, чем 50% вероятности возникновения наложения.
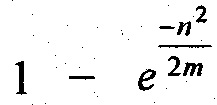 это удовлетворительное приближение для
это удовлетворительное приближение для 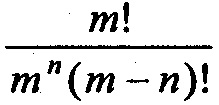 . В данном приближении, решение
. В данном приближении, решение 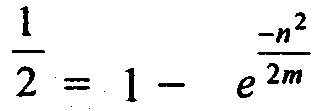 дает примерно размер образца, при котором имеется 50-процентная вероятность наложения. Решение для n, число n примерно является квадратным корнем из (2m ln 2), где ln х обозначает логарифм натуральный действительного числа х. В данной спецификации, по крайней мере, некоторая полезность в связи с лавинным эффектом может измеряться, как самое большое число генераторов ключей в последовательности, которая вероятно не будет иметь повторения. В примере осуществления изобретения хороший лавинный эффект возникает, когда усредненные последовательности генераторов ключей, которые меньше или равны произведению 0,9 и квадратного корня из (2m ln 2), вероятно не будут иметь наложения. В другом примере осуществления изобретения, если количество генераторов ключей в последовательности задается квадратным корнем из (2m ln 2), тогда последовательность имеет вероятность наложения 55% или меньше.
дает примерно размер образца, при котором имеется 50-процентная вероятность наложения. Решение для n, число n примерно является квадратным корнем из (2m ln 2), где ln х обозначает логарифм натуральный действительного числа х. В данной спецификации, по крайней мере, некоторая полезность в связи с лавинным эффектом может измеряться, как самое большое число генераторов ключей в последовательности, которая вероятно не будет иметь повторения. В примере осуществления изобретения хороший лавинный эффект возникает, когда усредненные последовательности генераторов ключей, которые меньше или равны произведению 0,9 и квадратного корня из (2m ln 2), вероятно не будут иметь наложения. В другом примере осуществления изобретения, если количество генераторов ключей в последовательности задается квадратным корнем из (2m ln 2), тогда последовательность имеет вероятность наложения 55% или меньше.
Более того, вообще, период орбиты Г значительно больше, чем количество возможных ключей и обычно находится в порядке 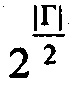 , где |Г| - это длина генератора ключа Г. Например, если |Г|=1024 бита, а генератор ключей Г(n) используется для получения нового улучшенного 256-битного ключа AES для n-го блока из 16 байт обычного текста, тогда ожидаемая длина период этой орбиты существенно больше, чем 2256, несмотря на то, что для Н-процесса получение 256-битного ключа от каждого генератора ключей представляет собой орбиту {0,1}256.
, где |Г| - это длина генератора ключа Г. Например, если |Г|=1024 бита, а генератор ключей Г(n) используется для получения нового улучшенного 256-битного ключа AES для n-го блока из 16 байт обычного текста, тогда ожидаемая длина период этой орбиты существенно больше, чем 2256, несмотря на то, что для Н-процесса получение 256-битного ключа от каждого генератора ключей представляет собой орбиту {0,1}256.
В частности, 50-процентная вероятность наложения в последовательности генератора ключей Г(0), Г(1) … предполагается для последовательности длинной n = корень квадратный из (21025 ln 2)>10154. Когда используется данный метод обновления генератора ключей - использование одной или нескольких односторонних функций с хорошим лавинным эффектом - где улучшенный AES-256 является блочным шифром в Н-процессе, то это существенно увеличивает сложность расчета, которую необходимо преодолеть для того, чтобы нарушить Н-процесс, по сравнению со стандартным шифром AES.
Мотивацию для нового понятия генератора ключей, а также его конструкцию также можно понять с точки зрения дифференциального криптоанализа [19]. В улучшенном шифре AES-256, каждый уникальный 256-битный ключ К создает логическую функцию шифрования Е(K, ⋅), где Е:{0,1}256×{0,1}128→{0,1}128. Другими словами, ключ K действует в качестве параметра, где каждое Е(К, ⋅) является функцией f:{0,1}128→{0,1}128 при f=(f1, …, f128) и каждая fk:{0,1}128→{0,1}. Как обсуждалось в [20], каждая fk имеет степень ≤128. С этой точки зрения последовательность динамических ключей создает высокую, трехмерную орбиту над пространством функции {f|f:{0,1}128→{0,1}128}, которая существенным образом повышает эффективную степень. Общие, динамические ключи, полученные при обновлении генератора ключей и на основании односторонних функций с хорошим лавинным эффектом, создают мощный криптографический метод, который может улучшать криптографическую стойкость примитива, такого как блочный шифр AES-256, который уже анализируется в течение многих лет.
Далее, в некоторых примерах осуществления изобретения, свойство полноты и лавинный эффект хорошей(их) односторонней(их) функции(й) обеспечивает возможность, чтобы генераторы последовательных ключей Г(n) и Г(n+1) имели хемминговское расстояние, которое составляет примерно 1/2 от |Г(n)|, которое означает, что Г(n)⊕Г(n+1) составляет примерно половину единиц и половину нулей, а их порядок является непредсказуемым. Данное выгодное свойство мешает атакам, связанным с ключами.
Обычно односторонние функции хеширования используются для проверки подлинности информации. Информацию, подлинность которой проверяется, иногда называют сообщением в криптографической литературе, которая обсуждает односторонние функции хеширования. В известном уровне техники односторонние функции хеширования не использовались непосредственно в зашифровывании и дешифровке, поскольку односторонние функции хеширования не являются однозначными.
Функция σ:X→X преобразует элементы X в элементы X. Функция σ является однозначной; это означает, что никакие два различных элемента X не преобразуются при помощи σ в одинаковый элемент. Более формально, если s1, s2 представляют собой два различных элемента из X, другими словами, если s1 не равняется s2, то σ(s1) не равняется σ(s2).
В известном уровне техники обычно односторонняя функция применяется непосредственно к обычному тексту в процессе зашифровывания, или же односторонняя функция непосредственно применяется к шифрованному тексту в процессе расшифровки. Для этого метода, в котором односторонняя функция применяется непосредственно к обычному тексту или шифрованному тексту, если односторонняя функция, которая используется в известном уровне техники, не является однозначной, тогда два или более обычных текста могут быть привязаны при помощи этой односторонней функции к тому же шифрованному тексту. В публикациях FIPS 180-4, Стандарт по безопасному хешированию, написанному Национальным институтом Стандартов (NIST), в аннотациях [21] сказано:
В данном стандарте приводятся алгоритмы хеширования, которые могут использоваться для создания профилей сообщений.
Профили используются для того, чтобы определить, менялись ли сообщения с тех пор, как были созданы профили.
Данное описание приводит принципиально новое использование односторонних функций для непредсказуемого обновления генераторов ключей, а также искажения Н-процесса, который используется в криптографии. В примерах осуществления изобретения Н-процесс использует односторонние функции. Лавинное свойство односторонних функций помогает укреплению NADO-криптографии против атак с помощью дифференциального криптоанализа и других видов атак.
NADO может быть эффективно реализовано в аппаратном или программном обеспечении. В некоторых примерах осуществления изобретения процесс Н является блочным шифром. Другим улучшением является сложность взлома этого метода шифрования, как функция его скорости выполнения. Для исполняемого кода, который реализует пример осуществления изобретения NADO, требуется небольшое количество компьютерной памяти, менее, чем 20К оперативной памяти для даже относительно больших генераторов ключей Г и менее, чем 5 К в других примерах осуществления изобретения. Пример осуществления изобретения может исполняться с процессором 150 МГЦ на компьютере с архитектурой сокращенного набора команд (Reduced Instruction Set Computer (RISC)) [22]: данный пример защищает конфиденциальность беседы по мобильному телефону в режиме реального времени. Для данного примера осуществления изобретения, генератор ключа Г для H-процесса имеет размер, как минимум, 512 бит; Далее в данном примере осуществления изобретения, в мобильном телефоне в режиме реального времени, каждые из этих генераторов ключей являются независимыми от других двух и обновляются при помощи односторонней функции хеширования SHA-512 [23] или другой односторонней функции хеширования, такой как Keccak, Blake, Skein or Gr∅stl. Некоторые примеры осуществления изобретения NADO являются достаточно быстрыми для того, чтобы позволить приложениям, таким как шифрование в режиме реального времени беспроводной передачи данных, встроенные системы реального времени, безопасная связь между спутниками и безопасной маршрутизации и передачи Интернет-трафика.
5 КРАТКОЕ ОПИСАНИЕ РИСУНКОВ
В следующих рисунках, хотя они и могут отражать различные примеры осуществления изобретения, изобретения не ограничиваются примерами, которые приведены на рисунках.
Рисунок 1А демонстрирует пример осуществления информационной системы для отправки и получения зашифрованной информации.
Рисунок 1В демонстрирует пример осуществления процесса для кодирования информации, который может использоваться в примере осуществления изобретения на Рисунке 1А.
Рисунок 1С демонстрирует пример лавинного эффекта после 16 циклов односторонней функции хеширования SHA-1 на первых 46 битах выходных данных SHA-1, которые могут использоваться в примере осуществления изобретения на Рисунке 1А.
Рисунок 1D демонстрирует схему примера осуществления полупроводникового микропроцессора, который определяет фотоны и генерирует недетерминированный процесс, который может использоваться в примере осуществления изобретения на Рисунке 1А.
На Рисунке 1Е показана схема примера осуществления одного этапа обновляемого генератора ключей при помощи односторонней функции хеширования Ф. Размер генератора ключа составляет « значений. В некоторых примерах осуществления изобретения значением является бит (0 или 1). Выходной размер функции хеширования Ф составляет q значений. В данном примере осуществления изобретения, на этапе обновления генератора ключа односторонняя функция Φ применяется к первым q значениям генератора ключей, а последние n-q значения генератора ключей остаются без изменений. Как описано в методе 1, рисунок 1Е демонстрирует этап Серия (Гi+1,0 Гi+1,1 … Гi+1,q-1)=Φ((Гi,0 Гi,1 … Гi,q-1), выраженный как Φ(b1 … bq)=(c1 … cq). На Рисунке IE также показан следующий этап Серия Гi+1,j=Гi,j для каждой j, удовлетворяющей q≤j≤n-1, выражена как (a1 а2 … аn-q)=(а1 а2 … аn-q) на этом рисунке.
На Рисунке 1F показана схема альтернативного примера осуществления изобретения одного этапа обновляемого генератора ключей при помощи односторонней функции хеширования Φ. Размер генератора ключа составляет n значений. Выходной размер функции хеширования Φ составляет q значений. В данном альтернативном примере осуществления изобретения на этапе обновления генератора ключа односторонняя функция Φ применяется к последним q значениям генератора ключей, а первые n-q значения генератора ключей остаются без изменений.
На Рисунке 1G показана схема ключа с к значениями, который получен из генератора ключей. Односторонняя функция Ψ применяется к генератору ключей, а первые к значения этих выходных данных выбираются в качестве динамического ключа. Рисунок 1G представляет собой этап получения ключа, который соответствует этапу обновления генератора ключа, показанному на Рисунке 1Е.
На Рисунке 1Н показана схема ключа с к значениями, который получен из генератора ключей. Односторонняя функция Ψ применяется к генератору ключей, а первые κ значения этих выходных данных выбираются в качестве динамического ключа. Рисунок 1Н представляет собой этап получения ключа, который соответствует этапу обновления генератора ключа, показанному на Рисунке 1F.
Рисунок 1I демонстрирует пример осуществления изобретения в форме процесса для кодирования информации, который может использоваться в примере осуществления изобретения на Рисунке 1А.
На Рисунке 2А показан пример осуществления изобретения в форме компьютерной сети, передающей зашифрованный обычный текст, которая в некоторых примерах осуществления изобретения может быть сетью Интернет или частью сети, которая поддерживает инфраструктуру, такую как электрическая сеть, финансовая биржа, или электростанция, которая может использоваться с примером осуществления изобретения на Рисунке 1А.
На Рисунке 2В показан пример осуществления изобретения в форме защищенной вычислительной зоны для шифрования информации, которая включает в себя процессор, память и систему ввода / вывода, которой могут быть передающие и/или принимающие устройства на Рисунке 1А.
На Рисунке 3А показан пример осуществления изобретения в форме USB-диска, который может действовать в качестве отправляющего устройства и принимающего устройства для хранения и защиты данных пользователя путем шифрования данных.
На Рисунке 3В показан пример осуществления изобретения в форме аутентификационного маркера, который может включать в себя устройства для отправки и/или приема с Рисунка 1А, который содержит компьютерный процессор, который может зашифровать обычный текст, который представляет собой данные аутентификации.
На Рисунке 4 показан пример осуществления изобретения в виде мобильного телефона 400, который зашифровывает беспроводные голосовые данные, которые могут включать в себя передающие и/или принимающие устройства Рисунка 1А. Мобильный телефон 500 представляет собой пример осуществления изобретения, который отправляет беспроводной зашифрованный обычный текст в автомобиль, который может содержать передающие / принимающие устройства на Рисунке 1А.
На Рисунке 5А показан пример осуществления изобретения в Н-процессе, реализованный при помощи улучшенного блочного шифра AES-256 [5], который может использоваться в передающих / принимающих устройствах на Рисунке 1А.
На Рисунке 5В показан другой пример осуществления изобретения в Н-процессе, реализованный при помощи улучшенного блочного шифра Serpent [39], который может использоваться в передающих / принимающих устройствах на Рисунке 1А.
6 ПОДРОБНОЕ ОПИСАНИЕ
Хотя различные примеры осуществления изобретений возможно и были продиктованы различными недочетами в известном уровне техники, которые могут обсуждаться или упоминаться в одном или нескольких местах в описании, примеры осуществления изобретения не обязательно затрагивают какие-либо из этих недочетах. Другими словами, различные примеры осуществления изобретения могут затрагивать различные недочеты, которые могут обсуждаться в описании. Некоторые примеры осуществления изобретения могут только частично упоминать некоторые недочеты или только один недочет, которые могут обсуждаться в описании, а некоторые могут не упоминать какие-либо из этих недочетов.
Раздел 6.1 описывает информационные системы, которые используют криптографический процесс. Раздел 6.2 описывает лавинный эффект и односторонние функции. Раздел 6.4 описывает способы шифрования при помощи блочного шифра, который использует динамические ключи, полученные из генераторов ключей и обновлений генерации ключей при помощи односторонних функций хеширования. Раздел 6.8 объясняет, как использование динамических ключей останавливает простую атаку на блочный шифр. Разделы 6.5, 6.6, 6.7, 6.9, 6.10 и 6.11 описывают принципиально новые алгоритмы, концепции, аппаратное обеспечение, инфраструктуру, устройства, математику, способы, методику и системы, которые делают вклад в некоторые примеры осуществления криптографического процесса.
6.1 ИНФОРМАЦИОННАЯ СИСТЕМА
На Рисунке 1А показана информационная система 100 для шифрования информации способом, который, как предполагается, является надежным. Информационная система 100 включает в себя обычный текст (незашифрованная информация), процессы шифрования 106, генераторы ключей 107 и одностороннее хеширование 107, передающее устройство 102, зашифрованный обычный текст (зашифрованная информация) 109 и путь передачи 110, принимающее устройство 112, процесс расшифровки 116, расшифрованный обычный текст 114, генераторы ключей 117 и одностороннее хеширование 117. В других примерах осуществления изобретения информационная система 100 может не иметь всех компонентов, котрые перечислены выше, или может иметь другие компоненты вместо и/или в дополнение к перечисленным выше.
Информационная система 100 может использоваться для передачи зашифрованного обычного текста. Обычный текст 104 относится к информации, которая еще не была зашифрована, которую предполагается доставить в другое место, программный блок, устройство, другому лицу или объекту. Хотя термин "обычный текст" и содержит в себе слово "текст", значение обычного текста в данном описании шире и касается любого типа информации, которая не была зашифрована. Например, обычным текстом могут быть голосовые данные, которые еще не были зашифрованы. В примере осуществления изобретения обычный текст может быть расшифрованной информацией, которая передается по беспроводной связи между спутниками. Обычный текст может быть представлен в некоторых примерах осуществления изобретения в аналоговой форме, а также может быть представлен в цифровой форме. В примере осуществления изобретения звуковые волны, которые передаются изо рта говорящего в микрофон мобильного телефона, представляют собой обычный текст. Представление информации в этом обычном тексте перед тем, как она попадает в микрофон, происходит в аналоговой форме. Впоследствии, информация в форме обычного текста может быть дискретизирована цифровым способом, поэтому она представлена в цифровой форме после того, как ее принимает микрофон мобильного телефона. Вообще, обычный текст в данном документе относится к любому роду информации, которая не была зашифрована.
В данном описании, термин "местоположение" может относиться к географическим местоположениям и/или местам хранения. Конкретное место хранения может представлять собой совокупность смежных и/или несмежных мест на одном или нескольких машиночитаемых носителях. Два различных места хранения могут обозначать два различных набора местоположений на одном или нескольких машиночитаемых носителях, в которых местоположения одного комплекта может переплетаться с местоположениями другого комплекта. В данном описании термин "машиночитаемый носитель" используется для обозначения какого-либо носителя, который может нести в себе информацию, которая читается устройством. Одним из примеров машиночитаемого носителя является носитель, читаемый компьютером. Другим примером машиночитаемого носителя является бумага с отверстиями, которые определяются, как такие, которые запускают различные механические, электрические и/или логические отклики. Термин "машиночитаемый носитель" также включает в себя носители, которые несут в себе информацию, пока информация находится в процессе передачи от одного местоположения в другое, такие как медный провод и/или оптоволокно, и/или атмосферу, и/или космическое пространство. Возможно, желательно сохранять содержание обычного текста 104 в тайне. Впоследствии, может быть желательно, зашифровать обычный текст 104 таким образом, чтобы предполагалось, что переданная информация не была понятной незаконному получателю в случае, если незаконный получатель пытается прочитать и/или расшифровать переданный зашифрованный обычный текст. Обычный текст 104 может представлять собой совокупность нескольких незашифрованных информационных блоков, весь обычный текст, сегмент обычного текста (информацию) или какую-либо другую часть обычного текста.
Процесс расшифровки 106 может представлять собой серию этапов, которые выполняются с обычным текстом 104. В данном описании термин "процесс" обозначает серию из одной или нескольких операций. В одном примере осуществления изобретения термин "процесс" обозначает одну или несколько инструкций для устройства шифрования 102 для выполнения серии операций, которые могут храниться на машиночитаемом носителе. В другом случае, процесс может выполняться оборудованием, и, таким образом, обозначать оборудование (например, логические схемы), или может представлять собой комбинацию из инструкций, которые хранятся на машиночитаемом носителе, и оборудования, которые приводят к исполнению операций передающим устройством 102 или принимающим устройством 112. Обычный текст 104 может быть вводными данными для процесса шифрования 106. Шаги, которые входят в состав процесса шифрования 106, могут включать в себя одну или несколько математических операций и/или одну или несколько других операций. В примере осуществления изобретения "процесс" может также включать в себя операции или действия, которые лучше всего описываются, как "недетерминированные". В примере осуществления изобретения "процесс" может включать некоторые операции, которые могут исполняться цифровой компьютерной программой и некоторыми физическими операциями, которые являются недетерминированными.
В настоящем документе термин "процесс" обозначает и выражает более широкое понятие, чем "алгоритм". Формальное понятие "алгоритм" было представлено в документе Тьюринга [24] и обозначает конечное устройство, которое выполняет конечное число инструкций при помощи ограниченной памяти. "Алгоритм" представляет собой детерминированный процесс в следующем смысле: если конечное устройство полностью известно, и известны входные данные для устройства, тогда может быть определено будущее поведение устройства. Однако, имеется оборудование для квантового генератора случайных чисел (QRNG) [25, 26] и другие примеры осуществления изобретения, которые измеряют квантовые действия фотонов (или других физически недетерминированных процессов), физический процесс которых является недетерминированным. Признание недетерминированности, которое наблюдается квантовыми генераторами случайных чисел и другими квантовыми примерами осуществления изобретения, основано на экспериментальном доказательстве и многих годах статистических испытаний. Более того, квантовая теория - выведенная из теоремы Кохена-Шпекера и ее обобщений [27, 28, 29] -подразумевает, что выходные данные квантового измерения не могут быть заранее известны и не могут быть сгенерированы машиной Тьюринга (цифровой компьютерной программой). В результате, физически недетерминированный процесс не может генерироваться алгоритмом: конкретно, последовательностью операций, выполняемых цифровой компьютерной программой. На Рисунке 1D показан пример осуществления изобретения недетерминированного процесса, который возникает из квантовых событий, т.е. входящих потоков фотонов.
Некоторые примеры физически недетерминированных процессов приведены ниже. В некоторых примерах осуществления изобретения, которые используют недетерминированность, может использоваться полупрозрачное зеркало, где фотоны, которые ударяются об зеркало, могут принимать два или более путей в пространстве. В одном примере осуществления изобретения, если фотон отражается, тогда он принимает одно битовое значение b∈{0,1}; если фотон передается, тогда он принимает другое битовое значение 1-b. В другом примере осуществления изобретения можно отобрать направление движение электрона, чтобы сгенерировать следующий недетерминированный бит. В еще одном примере осуществления изобретения, белок, который состоит из аминокислот, заполняющих мембрану клетки или искусственную мембрану, которая имеет две или более конформаций, может использоваться для того, чтобы определить недетерминированность: отобранная конформация белка может использоваться для того, чтобы сгенерировать недетерминированное значение в {0, … n-1}, где белок имеет n неповторимых конформаций. В другом примере осуществления изобретения один или несколько белков родопсина могли бы использоваться для определения времени поступления фотонов, а разница во времени поступления могла бы использоваться для создания недетерминированных битов. В некоторых примерах осуществления изобретения для выбора недетерминированности может использоваться счетчик Гейгера. В некоторых примерах осуществления изобретения недетерминированная величина основана на погрешности округления в наименее значимом бите при вычислении в связи с ограничениями в аппаратном обеспечении. Наконец, любая из односторонних функций данного описания может быть основана на случайном событии, таком как квантовое событие (недетерминированное), сгенерированное квантовым генератором случайных чисел с Рисунка 1D, который описывается далее в разделе 6.3.
На Рисунке 1А генераторы ключей 107 могут включать в себя один или несколько генераторов ключей. Генераторы ключей 107 могут использоваться процессом расшифровки 106, чтобы помочь получить один или несколько ключей, которые используются для шифрования, как минимум, части обычного текста 104. Генераторы ключей 117 могут использоваться процессом шифрования 116, чтобы помочь получить один или несколько ключей, которые используются для расшифровывания, как минимум, части шифрованного обычного текста 109. В примере осуществления изобретения один или несколько генераторов ключей 107 и генератор ключей 117 получены из недетерминированного генератора 136 в Рисунке 1В. В другом примере осуществления изобретения при использовании генератора ключей 107 две стороны могут использовать один и тот же процесс шифрования, но все равно не предполагается, что они смогут расшифровать зашифрованную информацию друг друга, если они не используют одинаковые генераторы ключей 107 в том же порядке в криптографическом процессе. Генераторы ключей 107 могут иметь большой диапазон размеров. Например, если размер генератора ключей 107 измеряется в битах; один или несколько генераторов ключей могут быть 256-битными, 512-битными, 1000-битными, 1024-битными, 4096-битными или больше. В примере осуществления изобретения две стороны (Элис и Боб) могут назначать одинаковые генераторы ключей 107, сначала создавая генераторы закрытых ключей из своих соответствующих недетерминированных генераторов 136, а затем производя обмен генераторами ключей. В примере осуществления изобретения аппаратное устройство, показанное на Рисунке 1D, может представлять собой часть недетерминированного генератора 136.
Передающее устройство 102 может представлять собой информационную машину, которая передает информацию в первое местоположение, программный блок, устройство, лицу, отправителю или другому объекту, либо связана с ними. Передающим устройством 102 может быть компьютер, телефон, мобильный телефон, телеграф, спутник или другой тип электронного устройства, механическое устройство или другой вид устройства, которое передает информацию. Передающее устройство 102 может включать в себя один или несколько процессоров и/или может включать в себя специализированную компоновку схем для работы с информацией. Передающее устройство 102 может получать обычный текст 104 из другого источника (например, преобразователя, такого как микрофон), может производить весь или часть обычного текста 104, может реализовывать процесс шифрования 106 и/или может передавать выходные данные другому объекту. В другом примере осуществления изобретения передающее устройство 102 принимает обычный текст 104 из другого источника, тогда как процесс шифрования 106 и доставка результатов процесса шифрования 106 реализуются вручную. В другом примере осуществления изобретения передающее устройство 102 реализует процесс шифрования 106 при вводе обычного текста 104 при помощи клавиатуры (например) или при помощи микрофона мобильного телефона в передающее устройство 102. В другом примере осуществления изобретения передающее устройство 102 принимает результат процесса шифрования 106 и отправляет его другому объекту. В одном из примеров осуществления изобретения передающее устройство 102 может генерировать новые генераторы ключей 107 для других информационных машин.
Передающее устройство 102 может реализовывать любой из методов шифрования, описанных в данном описании. Процесс шифрования 106 может включать в себя какой-либо из способов шифрования, описанных в данном описании (например, процесс шифрования 106 может реализовать какой-либо пример осуществления изобретения Н-процесса). Зашифрованный обычный текст 109 включает в себя, как минимум, некоторый обычный текст 104, который шифруется процессом шифрования 106.
Канал передачи 110 представляет собой путь, который занимает зашифрованный обычный текст 109, чтобы дойти до места назначения, в которое был отправлен зашифрованный обычный текст 109. Канал передачи 110 может включать в себя одну или несколько сетей. Например, канал передачи 110 может представлять собой Интернет; например, канал передачи 110 может быть беспроводным с использованием голоса по Интернет-протоколу. Канал передачи 110 может включать в себя какую-либо комбинацию какого-либо прямого подключения, ручной доставки, голосовой передачи, одной или нескольких локальных вычислительных сетей (LAN), одной или нескольких глобальных сетей (WAN), одной или нескольких телефонных сетей, включая подземные трассы через оптоволоконные кабели и/или одну или несколько беспроводных сетей, и/или беспроводную передачу данных в атмосфере Земли или за ее пределами.
Приемное устройство 112 может представлять собой информационную машину, которая обрабатывает информацию в месте назначения зашифрованного обычного текста 109. Приемным устройством 112 может быть компьютер, телефон, телеграф, маршрутизатор, спутник или другой тип электронного устройства, механическое устройство или другой вид устройства, которое принимает информацию. Принимающее устройство 112 может включать в себя один или несколько процессоров и/или специализированную компоновку схем, сконфигурированную для обработки такой информации, как зашифрованный обычный текст 109. Принимающее устройство 112 может принимать зашифрованный обычный текст 109 из другого источника и/или воссоздать (например, расшифровать) весь зашифрованный обычный текст 109 или его часть. Принимающее устройство 112 может реализовать какой-либо из методов шифрования, описанных в данном описании, и может расшифровать какое-либо сообщение, зашифрованное передающим устройством 102 и процессом шифрования 106.
В одном из примеров осуществления изобретения принимающее устройство 112 только принимает зашифрованный обычный текст 109 из канала передачи 110, тогда как процесс расшифровки 106 реализуется вручную и/или при помощи другой информационной машины. В другом примере осуществления изобретения принимающее устройство 112 реализует процесс расшифровки 116, который воспроизводит весь обычный текст 104 или его часть, который называется расшифрованный обычный текст 114. В другом примере осуществления изобретения принимающее устройство 112 принимает зашифрованный обычный текст 109 из канала передачи 110 и воссоздает весть расшифрованный текст 114 или его часть с помощью процесса расшифровки 116.
Процесс расшифровки 116 может хранить любой из процессов расшифровки информации, описанных в этом описании. Процесс расшифровки 116 может включать в себя какой-либо из способов расшифровки, описанных в данном описании (например, процесс расшифровки 106 может реализовать любой из методов для расшифровки какого-либо примера осуществления изобретения Н-процесса).
Принимающее устройство 112 может быть идентичным передающему устройству 102. В примере осуществления изобретения, в котором приемное устройство и передающее устройство одинаковые, как передающее, так и приемное устройство, каждое включает в себя обычный текст 104 (незашифрованную информацию), процесс шифрования 106, генераторы ключей 107 (которые могут включать в себя одностороннее хеширование), зашифрованный обычный текст (зашифрованная информация) 109, процессы дешифровки 116, расшифрованный обычный текст 114 и генераторы ключей 117 (которые могут включать в себя одностороннее хеширование), и они оба могут реализовывать какие-либо процессы шифрования, процесс расшифровки и методы обмена генераторами ключей, представленные в данном описании.
Например, принимающее устройство 112 может принимать обычный текст 104 из другого источника, формировать весь обычный текст или его часть 104 и/или реализовывать процесс шифрования 106. Подобно передающему устройству, приемное устройство 112 может создавать генераторы ключей 117. Приемное устройство 112 может передавать результат процесса расшифровки 116 по каналу передачи 110 в другой объект и/или принимать зашифрованный обычный текст 109 (по каналу передачи 110) от другого объекта. Приемное устройство 112 может предоставлять зашифрованный обычный текст 109 для использования в качестве входящих данных для процесса расшифровки 116.
6.2 ЛАВИННЫЙ ЭФФЕКТ И ОДНОСТОРОННИЕ ФУНКЦИИ
Односторонняя функция 107 на Рисунке 1А и односторонняя функция 126 на Рисунке 1В могут включать в себя одну или несколько односторонних функций. Односторонняя функция Φ имеет такое свойство, что имея выходное значение z, она является сложной для вычисления, чтобы определить информационный элемент mz такой, чтобы Φ(mz)=z. Другими словами, односторонняя функция Φ представляет собой функцию, которую можно легко вычислить, но ее обратная величина Φ-1 является сложной для вычисления. Вычисление, для которого требуется 10101 шагов вычисления считается таким, которое имеет вычислительную нераскрываемость 10101. Больше информации представлено в разделе о вычислительной нераскрываемости. В одном из примеров осуществления изобретения существует количество времени Т, в течение которого зашифрованная информация должна оставаться секретной. Если у зашифрованной информации нет экономической ценности или стратегической ценности после времени Т, то "вычислительная нераскрываемость" означает, что число вычислительных шагов, которые необходимы для всей вычислительной мощности мира, займет больше времени для вычисления, чем время Т. Допустим, C(t) обозначает всю вычислительную мощность мира при времени /, выраженном в годах.
Рассмотрим банковскую онлайн-транзакцию, которая зашифровывает сведения по данной транзакции. В таком случае, в большинстве примеров осуществления изобретения изобретения количество вычислительных шагов, которые могут быть произведены всеми компьютерами мира в течение следующих 30 лет во многих примерах осуществления изобретения вероятно являются вычислительно нераскрываемыми, поскольку такой конкретный банковский счет вероятно не будет более существовать через 30 лет, или будет иметь другой интерфейс для аутентификации.
Чтобы сделать числа более конкретными, китайский суперкомпьютер 2013 года, который побил мировой рекорд скорости вычисления, производит примерно 33000 триллионов вычислений в секунду [30]. Если Т=1 один год, и мы можем предположить, что существует максимум 1 миллиард этих суперкопьютеров. (Это можно логически вывести из экономических соображений, исходя из слишком заниженной цены в 1 миллион долларов за каждый суперкомпьютер. Тогда эти 1 миллиард суперкомпьютеров стоили бы 1000 триллионов долларов). Таким образом, С(2014)×1 год менее, чем 109×33×1015×3600×24 ×365=1.04×1033 вычислительных шагов. Для получения некоторого восприятия в отношении крпитографии, криптография на основе 25519 эллиптических кривых [31] имеет предполагает сложность [32] в 2128 вычислительных шагов. Также, 2128>1038, поэтому в рамках этого измерения вычислительной нераскрываемости, криптография на основе 25519 эллиптических кривых имеет вычислительную нераскрываемость, как минимум, 1038 вычислительных шагов.
Как только что обсуждалось, в некоторых примерах осуществления изобретения и применениях, вычислительная нераскрываемость может быть измерена в рамках того, сколько стоит зашифрованная информация в экономической стоимости, и какова нынешняя стоимость вычислительной мощности, которая необходима для расшифровки такой зашифрованной информации. В других примерах осуществления изобретения экономическая вычислительная нераскрываемость может быть бесполезной. Например, предположим, семья хочет сохранить местоположение своего ребенка неизвестным для жестоких похитителей. Предположим, что Т=100 лет, поскольку это примерно в два раза больше, чем их предполагаемый срок жизни. Тогда 100 лет×С(2064) является лучшим измерением вычислительной нераскрываемости для данного использования. Другими словами, для ключевых способов применения, которые выходят за пределы экономической стоимости, необходимо стремиться к хорошей оценке мировой вычислительной мощности.
Односторонние функции, которые демонстрируют полноту и надлежащий лавинный эффект или строгий лавинный критерий [33], представляют собой предпочтительные примеры осуществления изобретения: эти свойства являются благоприятными для обновления генератора ключей. На Рисунке 1С показан лавинный эффект через 16 циклов SHA-1 на первые 46 битов выходных данных SHA-1. Размер профиля SHA-1 составляет 160 бит (т.е. длина его выходных данных). Только один бит был переключен с b на 1-b во входных данных. Переключенный бит во входных данных отображается небольшим белым прямоугольником возле верхней части Рисунка 1С. Белые квадраты показывают биты, которые переключились с 0 на 1 или с 1 на 0 в результате переключения одного бита входных данных. На 16ом цикле имеется больше белых битов, чем черных битов. Строгий лавинный критерий говорит, что существует 50-процентная вероятность того, что появится переключение битов. Предполагается, что 80 циклов SHA-1 обеспечивают достаточное преобразование обычного текста для нарушения его статистической структуры.
Определение полноты и надлежащий лавинный эффект цитируются непосредственно из [33]:
Если криптографическая трансформация является полной, тогда каждый бит зашифрованного текста должен зависеть от всех битов обычного текста. Таким образом, если бы было возможно найти самое простое булевское выражение для каждого бита зашифрованного текста в переводе на биты обычного текста, каждое из этих выражений должно было бы содержать все биты обычного текста, если бы функция была полной. В другом случае, если имеется, как минимум, одна пара n-битных векторов обычного текста X и Xi которые отличаются только битом i, а ƒ(X) и ƒ(Xi) отличаются, как минимум, битом j для всего: {(i,j):1≤i,j≤n}, то функция ƒ должна быть полной.
Для данной трансформации, чтобы продемонстрировать лавинный эффект, среднее значение половины выходных битов должно изменяться в тех случаях, когда будет дополняться один входной бит. Для того чтобы определить удовлетворяет ли этому требованию m×n (m входных битов и n выходных битов) функция ƒ, векторы обычного текста 2m должны разделяться на 2m-1 пар, X и Xj, такие как X и Xj отличаются только битом i. Тогда необходимо рассчитать суммы Vi=ƒ(X)⊕ƒ(Xi) строгой дизъюнкции 2m-1. Эти суммы строгой дизъюнкции будут указываться в качестве лавинных векторов, каждый из которых содержит n бит, или лавинные переменные.
Если процедура повторяется для всех i, таких как 1≤i≤m, а половина лавинных переменных равняется 1 для каждой i, то функция ƒ имеет хороший лавинный эффект. Конечно данному методу можно следовать, только если m является весьма маленькой величиной; в противном случае количество векторов обычного текста становится слишком большим. Если ситуация именно такова, тогда лучшее, что можно сделать - это взять случайный образец векторов обычного текста X и для каждого значения i рассчитать все лавинные векторы Vi. Если приблизительно половина получившихся лавинных переменных равняется 1 для величин i, тогда мы можем сделать вывод, что функция имеет хороший лавинный эффект.
Функция хеширования, также обозначенная, как Φ, представляет собой функцию, которая принимает в качестве своего входящего аргумента достаточно длинную строку бит (или байтов) и создает выходную информацию с фиксированным размером. Информация на выходе обычно называется профилем сообщения или цифровым отпечатком пальца. Другими словами, функция хеширования преобразует переменную длину m входной информации в выходные данные с фиксированным размером, Φ(m), которые представляют собой профиль сообщения или профиль информации. Стандартный диапазон размеров выходных данных составляет от 160 до 512 бит, но также может быть и больше. Идеальная функция хеширования представляет собой функцию Φ, выходные данные которой равномерно распределяются следующим образом: Предположим, что выходной размер Φ составляет n бит. Если сообщение m выбирается случайным образом, тогда для каждого из 2n возможных выходов z, вероятность того, что Φ(m)=z составляет 2-n. В примере осуществления изобретения, функции хеширования, которые используются, являются односторонними.
Хорошая односторонняя функция хеширования также является устойчивой к наложению. Наложение возникает, когда два различных элемента информации преобразуются при помощи односторонней функции хеширования Ф в такой же профиль. Устойчивость к наложению означает, что противник не может произвести вычисления, чтобы выявить наложение: точнее, невозможно произвести вычисления, чтобы выявить два различных элемента информации m1, m2, где m1 не был равен m2, и так чтобы Ф(m1)=Ф(m2). Может использоваться ряд функций одностороннего хеширования. SHA-512 представляет собой одностороннюю функцию хеширования, разработанную АНБ и стандартизированную NIST [23]. Размер профиля сообщения SHA-512 составляет 512 бит. Другими альтернативными функциями хеширования является тот тип, который соответствует стандарту SHA-384, который создает размер профиля сообщения 384 бит. SHA-1 имеет размер профиля сообщения 160 бит. Примером осуществления изобретения односторонней функции хеширования является Keccak [34]. Примером осуществления изобретения односторонней функции хеширования является BLAKE [35]. Примером осуществления изобретения односторонней функции хеширования является Gr∅stl [36]. Примером осуществления изобретения односторонней функции хеширования является JH [37]. Еще одним примером осуществления изобретения односторонней функций хеширования является Skein [38]. В других примерах осуществления изобретения, вместо односторонней функции хеширования могут использоваться другие односторонние функции. Например, эллиптическая кривая по полю с конечным числом элементов может использоваться в качестве односторонней функции. Для этих альтернативных односторонних функцию полнота и хороший лавинный эффект являются благоприятными свойствами, которые демонстрируют эти функции. Строгий лавинный критерий также является благоприятным свойством для этих альтернативных односторонних функций.
В одном из примеров осуществления изобретения, односторонняя функция 126 на Рисунке 1В может быть реализована, как исполняемые инструкции устройства во внутренних инструкциях устройства микропроцессора. В еще одном примере осуществления изобретения, односторонняя функция 126 на Рисунке 1В может быть реализована в таком оборудовании, как программируемая пользователем матрица логических элементов (FPGA), которая может обеспечить надежную зону для выполнения расчетов. Надежная зона показана на Рисунке 2В. В некоторых примерах осуществления изобретения безопасная зона находится внутри пластиковой карточки с микропроцессором.
6.3 ОБОРУДОВАНИЕ И ИНФРАСТРУКТУРА ДЛЯ КРИПТОГРАФИИ
На Рисунке 1D показан пример осуществления изобретения недетерминированного процесса, который определяет время поступления фотонов. Время поступления фотонов считается квантовым событием. На Рисунке 1D приводится пример осуществления изобретения недетерминированного генератора 136. hν обозначает энергию поступающего фотона, где h - это постоянная Планка, а ν - это частота. В одном из примеров осуществления изобретения можно сравнивать 3 последовательных времени прибытия t1<t2<t3 трех последовательных фотонов. Если t2-t1>t3-t2, то недетерминированный генератор 142 формирует бит 1. Если t2-t1<t3-t2, то недетерминированный генератор 142 формирует бит 0. Если t2-t1=t3-t2, то не формируется недетерминированная информация, и этот недетерминированный процесс выбирает еще три времени прибытия.
На Рисунке 2А информационная система 200 демонстрирует некоторые из вариаций реализации информационной системы 100. Передающее устройство 202 представляет собой один из примеров осуществления изобретения передающего устройства 101. Передающее устройство 202 может быть защищенным запоминающим устройством USB, как показано на 3А. Передающее устройство 202 может представлять собой аутентификационный маркер, как показано на Рисунке 3В. Пример осуществления передающего устройства 202 в форме мобильного телефона, как показано на Рисунке Передающего устройства 202 или передающего устройства 400 может сообщаться беспроводным способом с компьютером 204. В одном из примеров осуществления изобретения компьютер 204 может представляться собой станцию вызова для приема зашифрованного обычного текста 109 от передающего устройства 400. Пользователь может использовать систему ввода 254 и систему вывода 252 передающего устройства (мобильный телефон) 400 для передачи зашифрованных голосовых данных в приемное устройство, которое представляет собой мобильный телефон. В одном из примеров осуществления изобретения система ввода 254 на Рисунке 2В включает в себя микрофон, который интегрирован с передающим устройством (мобильным телефоном) 400. В одном из примеров осуществления изобретения система вывода 252 на Рисунке 2В включает в себя динамик, который интегрирован с передающим устройством (мобильным телефоном) 400. В другом примере осуществления изобретения передающее устройство 202 имеет возможность подключения и обмена данными с компьютером 20 или с другими системами посредством компьютера 204.
Компьютер 204 подключается к системе 210 и подключается по сети 212 к системе 214, системе 216 и системе 218, которая подключена к системе 220. Сеть 212 может быть одной из или комбинацией из одной или нескольких локальных вычислительных сетей (LAN), глобальных сетей (WAN), беспроводных сетей, телефонных сетей и/или других сетей. Система 218 может напрямую подключаться к системе 220 или подключаться по LAN к системе 220. Сеть 212 и система 214, 216, 218 и 220 могут представлять собой Интернет-серверы или узлы, которые маршрутизируют зашифрованный обычный текст (голосовые данные), полученные от передающего устройства 400, показанного на Рисунке 4. На Рисунке 2А система 214, 216, 218 и система 220, а также сеть 220 могут совместно выступать в качестве канала передачи 110 для зашифрованного обычного текста 109. В одном из примеров осуществления изобретения система 214, 216, 218 и система 220, а также сеть 212 могут исполнять Интернет-протокол совместно выступать в качестве канала передачи 110 для зашифрованного обычного текста 109. В одном из примеров осуществления изобретения зашифрованный обычный текст 102 может представлять собой голосовые данные. В одном из примеров осуществления изобретения зашифрованный обычный текст 109 может представлять собой данные маршрутизации. В одном из примеров осуществления изобретения зашифрованный обычный текст 109 может представлять собой сообщение электронной почты. В одном из примеров осуществления изобретения зашифрованный обычный текст 109 может представлять собой текстовые данные, отправленные с передающего устройства 400.
На Рисунке 1В процесс дешифровки 122 может быть реализован при помощи любой из, какой-либо, или какой-либо комбинации любой системы 210, сети 212, системы 214, системы 216, системы 218 и/или системы 220. Например, информация маршрутизации канала передачи ПО может быть зашифрована при помощи процесса шифрования 122, который исполняется в системном компьютере 210, сетевых компьютерах 212, системном компьютере 214, системном компьютере 216, системном компьютере 218 и/или системном компьютере 220. Процесс шифрования 106 может исполняться в передающем устройстве 400, а процесс расшифровки 116 может исполняться в приемном устройстве 400 на Рисунке 4.
В одном из примеров осуществления изобретения H-процесс NADO исполняется в безопасной зоне системы процессора 258 Рисунка 2В. В одном из примеров осуществления изобретения в системе процессора 258 может использоваться специализированное оборудование для ускорения вычисления односторонних функций 126 на Рисунке 1В, который используется в H процессе. В одном из примеров осуществления изобретения данное специализированное аппаратное обеспечение в системе процессора 258 может быть реализовано в виде ASIC (заказная специализированная микросхема), которая вычисляет SHA-1 и/или SHA-512, и/или Keccak, и/или BLAKE, и/или JH, и/или Skein. Микросхема ASIC может увеличивать скорость выполнения вычислений H-процесса. В одном из примеров осуществления изобретения система ввода данных 256 принимает голосовые данные и отправляет их в систему процессора 258, где голосовые данные расшифровываются. Система выходных данных 252 отправляет зашифрованные голосовые данные 109 в телекоммуникационную сеть 212. В одном из примеров осуществления изобретения система памяти 256 сохраняет генераторы ключей 124 и обрабатывает инструкции по Н-блочному шифрованию 130.
Состояние относится к конкретному значению или набору значений из какого-либо набора одной или нескольких внутренних переменных, при котором способ, которым выполняются операции нарушается при выборе значения или набора значений, которые составляют состояние. Генератор состояний выполняет одну или несколько операций для обновления состояния.
В одном из примеров осуществления изобретения инструкции H-процесса 130 выполняются в надежной зоне системы процессора 258, которая находится внутри автономного USB-диска, представленного на Рисунке 3А. В одном из примеров осуществления изобретения процесс шифрования 122 зашифровывает данные, которые хранятся на USB-диске, для защиты конфиденциальности данных.
В одном из примеров осуществления изобретения инструкции H-процесса 130 шифруют голосовую бесуде в надежной зоне системы процессора 258, которая находится в мобильном телефоне 400, который представляет собой пример осуществления изобретения передающего устройства 102 и приемного устройства 112.
В одном из примеров осуществления изобретения на Рисунке 1В инструкции H-процесса 130 выполняются в надежной зоне каждой системы процессора 258 (Рисунок 2В), которая содержится в системных компьютерах 210, 214, 216, 218 и 220 и внутри сети 212, показанной на Рисунке 2А.
6.4 ШИФРОВАНИЕ ПРИ ПОМОЩИ ДИНАМИЧЕСКИХ КЛЮЧЕЙ
Создание и использование динамических ключей зависит от согласования Элис и Бобом элемента следующего генератора ключей Г(i+1) от предыдущего генератора ключей Г(i), и именно так построена последовательность генератора ключей Г(0), Г(1), …, Г(i), Г(i+1), … Бесчисленное количество последовательностей генераторов ключей являются невычислимыми по Тьюрингу; в данном документе наши примеры осуществления изобретения описывают вычислимые по Тьюрингу последовательности генераторов ключей, поскольку вычислимость помогает упростить координацию обновления генератора ключей между Элис и Бобом.
Наши односторонние функции прообраза имеют принципиально новое использование при типичном применении аутентификации сообщений, которое выполняется односторонними функциями хеширования в известном уровне техники. В криптографическом методе 1 Ф представляет собой одностороннюю функцию прообраза с размером профиля q.
Пусть S - конечный алфавит символов или значений. В примере осуществления изобретения S=, значения которого равны 0 и 1. В этом примере осуществления изобретения значения 0 и 1 являются битами. В другом примере осуществления изобретения S={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е}, которые называются шестнадцатеричными значениями. В другом примере осуществления изобретения S может быть алфавитом значений {а, b, с, d, е, f, g, h}. В ином примере осуществления изобретения S имеет 256 значений и S={0, 1, 2, 3, 4, …, 255}.
Последовательность генераторов ключей Г:N×Sn удовлетворяет q<n. Размер генератора ключей - n. Символ Гij является j-тым значением или символом i-го генератора ключей Г(i). Первый этап использует подписанный обмен генераторами ключей, когда в некоторых примерах осуществления изобретения частные секреты Элис и Боба создаются из недетерминированного генератора 172, как показано на Рисунке 1I. В некоторых примерах осуществления изобретения инструкции по обмену генераторами ключей 170 определяют первый генератор ключей, который создается из недетерминированного процесса. Обмен генераторами ключей обсуждается далее в разделах 6.9, 6.10 и 6.11.
Криптографический метод 1. Обновление генератора ключей при помощи односторонней функции прообраза
Элис и Боб осуществляют подписанный обмен генератором ключей, чтобы создать совместно используемый генератор ключей
Г(0)=Г0,0 … Г0,n-1

Метод 1 предназначен для создания многомерной орбиты на первых q значениях Гi,0 Гi,1 … Гi,q-1, под воздействием лавинных свойств [33] функции Φ; для сохранения оставшихся n-q значений постоянными для всех i; и для обеспечения того, чтобы никакая информация из последних n-q значений не влияла на орбиту первых q значений.
На Рисунке 1Е показан этап обновления генератора ключей: Задать, что (Гi+1,0 Гi+1,1 … Гi+1,q-1)=Φ(Гi,0 Гi,1 … Гi,q-1). На Рисунке 1Е первые q значения (Гi,0 Гi,1 … Гi,q-1) i-гo генератора ключей выражаются, как b1 b2 … bq. На Рисунке 1Е последние n-q значения i-го генератора ключей (Гi,q, Гi,q+1 … Гi,n-1) выражены, как а1 а2 … аn-q. На Рисунке 1Е выражение (c1 с2 … cq)=Φ(b1 b2 … bq) представляет первые q значения (Гi+1.0 Гi+1.1 … Гi+1,q-1) i+1-го генератора ключей. Далее, на Рисунке 1Е биты а1 а2 … аn-q представляют последние n-q значения (Гi+1,q Гi+1,q+1 … Гi+1,n-1), поскольку эти значения остаются без изменений. В одном из примеров осуществления изобретения n=128, а q=32 и алфавит S - 256 значений. В другом примере осуществления изобретения n=768, а q=512 и S - 2 значения. В ином примере осуществления изобретения S - 8 значений. В еще одном примере осуществления изобретения n=1024, а q=512. Ив еще одном примере осуществления изобретения, n=20000, a q=1000.
В случае обычного использования противник - Ева - никогда не получит доступа ни к каким-либо значениям генератора ключей Элис Г(i). Это аналогично тому, что Ева не имеет доступа к каким-либо значениям статического ключа Элис, который используется в реализациях симметричной криптографии в известном уровне техники.
В другом примере осуществления изобретения односторонняя функция Ф может применяться к последним q значениям, оставшиеся n-q значния остаются неизменными для всех i. Данный пример осуществления изобретения показано на Рисунке 1F, где последние q значения генератора ключей обновляются, как (с1 с2 … cq)=Φ(b1 b2 … bq). В других примерах осуществления изобретения постоянные (неизменные) значения аk1 аk2 … аkn-q могут перемежаться между значениями генератора ключей, которые обновляются, как (cj1 … cjq)=Ф(bj1 bj2 … bjq), где набор заданых местоположений {k1, k2, … kn-q} для постоянных значений отделен от набора заданых местоположений {j1, j2, … Jq},q), что указывает на значения (bj1 bj2 Bjq),jq), которые обновляются. То есть, {k1, k2, … kn-q}∩{j1, j2, … jq)=∅.
В некоторый примерах осуществления изобретения различные односторонние функции могут применяться на разных этапах обновления генератора ключей. Например, для вычислений первого генератора ключей Г(1) из генератора ключей Г(0) может использоваться SHA-512; SHA-384 может использоваться для вычисления второго генератора ключей Г(2) из генератора ключей Г(1); Keccak может использоваться для вычисления третьего генератора ключей Г(3) из генератора ключей Г(2); и т.д. В этих примерах осуществления изобретения имеются инструкции для генераторов ключей 162 (рисунок 1I), которые вызывают различные инструкции односторонних функций 164 в зависимости от j-го генератора ключей. Инструкции односторонних функций 164 могут реализовывать SHA-384, Keccak, SHA-512 и другие односторонние функции.
Метод 2 получает динамический ключ Ki для блочного шифра А из i-го генератора ключей Г(i) последовательности генераторов ключей, как показано на рисунках 1G и 1Н. Символ Ψ обозначает одностороннюю функцию, выходной размер которой составляет r значений, где κ≤r. Как показано на рисунках 1G и 1Н, Ψ применяется к конкатенации динамической части Гi,0 Гi,1 … Гi,q-1 из Г(i) и постоянной части Гi,q … Гi,n-1 для того, чтобы получить различный ключ Кi для каждого блока, который шифруется. На рисунке 1G первые q значения (b1 b2 … bq) являются частью генератора ключей, которые меняются после каждого этапа обновления генератора ключей, показанного на рисунке 1Е; на рисунке 1G, последние n-q значения (a1 а2… an-q) остаются неизменными. На рисунке 1Н первые n-q бит (a1 а2… an-q) остаются неизменными; на рисунке 1Н последние q значения (b1 b2 … bq) являются частью генератора ключей, которые меняются после каждого этапа обновления генератора ключей, показанного на рисунке 1F.
В некоторых примерах осуществления изобретения Ψ является отличной от Ф односторонней функцией. Например, в некоторых примерах осуществления изобретения Ψ может быть реализована с помощью Keccak, а Φ может быть реализована с помощью SHA-512. В некоторых примерах осуществления изобретения Ψ может использоваться для получения первого динамического ключа, а другая односторонняя функция Ψ' может использоваться для получения второго динамического ключа, и т.д.
Выражение 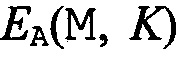 представляет собой блочный шифр
представляет собой блочный шифр  , зашифровывающий блок обычного текста М при помощи ключа К, a
, зашифровывающий блок обычного текста М при помощи ключа К, a 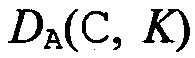 представляет собой блочный шифр А, расшифровывающий шифрованный текст С с помощью ключа K. Размер ключа |K| блочного шифра составляет к значений и удовлетворяет κ≤r. Определим проекционную карту πκ:{0;1}r→{0;1}κ, где πκ(x1 х2 …хr)=( x1 х2 …хκ).
представляет собой блочный шифр А, расшифровывающий шифрованный текст С с помощью ключа K. Размер ключа |K| блочного шифра составляет к значений и удовлетворяет κ≤r. Определим проекционную карту πκ:{0;1}r→{0;1}κ, где πκ(x1 х2 …хr)=( x1 х2 …хκ).
В других частях описания Н-процесс будет указан в некоторых примерах осуществления изобретения, как такой, который реализуется при помощи блочного шифра, который использует динамические ключи, полученные из обновления генератора ключей. В связи с этим, криптографические методы 1, 2, 3, 4, 5 могут реализовывать Н-процесс.
Криптографический метод 2.
Блочный шифр А выполняет шифрование при помощи Динамических Ключей, полученных из Генератора Ключей
Элис вычисляет используемый совместно генератор Г(0) при помощи 1го этапа метода 1.

Криптографический метод 3.
Блочный шифр А выполняет расшифровку при помощи Динамических Ключей, полученных из Генератора Ключей
Боб вычисляет используемый совместно генератор Г(0) при помощи 1го этапа метода 1.

Реализация стандартного Serpent представляет собой 16-байтный блочный шифр с 256-битным ключом [39]. Образец обновления генератора ключей и получения динамического ключа для улучшенного Serpent описывается ниже и показан на Рисунке 5В. "Фотоны являются ключами" представляет собой 16-байтный блок обычного текста, который соединяется вместе 4 раза для создания 64-байтного обычного текста. Другими словами, В1=В2=В3=В4="Фотоны являются ключами".
В описании ниже приведено каждое значение генератора ключей и выражено, как число между 0 и 255 включительно. Другими словами, алфавит значений S={0, 1, 2, 3,…, 253,
254, 255}. Как показано на рисунке 5В, 16-байтный блок В1 обычного текста "Фотоны являются ключами" - это
80 104 111 116 111 110 115 32 97 114 101 32 107 101 121 115
Генератор ключей Г(1) - это 96 значений и показан ниже.
112 132 168 213 84 252 132 50 143 235 140 71 123 248 243 160 240 248 237 200 113 43
65 95 208 97 175 125 184 234 154 227 130 187 104 4 131 204 239 92 44 187 34 166 71
146 186 241 108 149 70 166 66 35 108 195 13 235 58 218 85 229 180 66 109 55 178 123
110 135 57 238 177 21 29 225 222 84 215 155 21 179 210 201 122 202 210 208 51 104
213 58 247 238 139 116
Первые 16 значений ключа K1, полученный из генератора ключей Г(1) - это 32 23 248 49 234 86 223 193 83 37 87 247 191 22 112 130 34 177 54 67 56 186 154 188 149 130 23 146 220 118 192 55
После шифрования первый 16-байтный блок обычного текста В1="Фотоны являются ключи" с улучшенным Serpent и динамическим ключом K1, зашифрованный текст - 33 175 244 28 210 147 63 101 221 74 197 89 195 30 31 228, который выражен, как Δ(В1, Г(1)) на Рисунке 5В.
Генератор ключей Г(2) это 96 значений и показан ниже.
219 14 199 128 227 62 241 230 111 13 179 127 82 52 211 235 216 220 52 233 191 255 22
121 103 165 109 90 168 10 36 23 172 246 97 184 183 134 6 195 84 171 123 50 184 60
112 217 7 249 224 23 186 238 174 199 235 214 22 152 211 212 186 202 240 109 55
178 123 110 135 57 238 177 21 29 225 222 84 215 155 21 179 210 201 122 202 210
208 51 104 213 58 247 238 139 116
Второй ключ K2, полученный из генератора ключей Г(2) - это 86 35 129 230 137 79 46 48 202 130 242 209 127 25 84 159 185 250 154 249 12 245 176 61 12 242 200 226 63 90 62 44 После шифрования второй 16-байтный блок обычного текста "Фотоны являются ключи" с улучшенным Serpent и ключом K2, зашифрованный текст - 79 101 31 159 181 228 83 121 166 170 215 94 99 67 100 139, который выражен, как Δ(В2, Г(2)) на Рисунке 5В.
Генератор ключей Г(3 это 96 значений и показан ниже.
106 83 207 235 94 38 238 182 252 52 145 130 208 170 9 222 90 70 48 182 140 87 211
89 241 135 27 217 27 4 83 65 122 137 153 188 253 116 162 45 70 34 57 162 77 45
116 126 190 163 194 142 206 195 184 102 154 112 164 53 38 215 50 187 109 55 178
123 110 135 57 238 177 21 29 225 222 84 215 155 21 179 210 201 122 202 210 208 51
104 213 58 247 238 139 116
Третий ключ K3, полученный из генератора ключей Г(3) - это 137 141 95 102 34 68 172 9 169 183 22 154 200 144 84 232 251 87 33 62 155 72 214 82 81 119 46 198 52 253 120 133 После шифрования третий 16-байтный блок обычного текста "Фотоны являются ключи" с улучшенным Serpent и ключом K3, зашифрованный текст - 138 83 40 138 141 153 198 180 164 108 233 135 99 130 205 34, который выражен, как Δ(В3, Г(3)) на Рисунке 5В.
Генератор ключей Г(4) это 96 значений и показан ниже.
22 228 65 144 60 200 76 27 17 148 227 251 74 182 41 167 6 215 249 33 9 219 36 170
139 106 189 109 42 190 115 21 220 162 232 214 66 167 48 226 230 77 73 198 147 180
29 41 103 238 224 24 103 225 181 252 103 103 194 164 76 132 242 207 109 55 178
123 110 135 57 238 177 21 29 225 222 84 215 155 21 179 210 201 122 202 210 208 51
104 213 58 247 238 139 116
Четвертый ключ K4, полученный из генератора ключей Г(4) - это 184 244 102 78 50 249 102 189 46 27 147 31 37 96 37 36 50 13 62 209 109 30 126 93 248 239 161 157 195 223 108 48
После шифрования четвертый 16-байтный блок обычного текста "Фотоны являются ключи" с улучшенным Serpent и ключом K4, зашифрованный текст - 248 255 208 238 140 14 26 6 121 1 52 78 22 48 168 112, который выражен, как Δ(В4, Г(4)) на Рисунке 5В.
В некоторых примерах осуществления изобретения обновление генератора ключей Г возникает после каждого шифрования блока: обновление происходит после блоков B2, В4, В6 …, но не после блоков В1, В3, B5, …. В других примерах осуществления изобретения обновление генератора ключей возникает только после блоков В1, В3, B5, …, но не после блоков B2, В4, В6 …. В некоторых примерах осуществления изобретения обновление генератора ключей Г возникает только после четвертых блоков B4, В8, В12 … шифрования. В других примерах осуществления изобретения обновление генератора ключей выполняется апериодически; например, обновление генератора ключей происходит только после блоков В2, В3, В5, В7, В11, В13, B19, и так далее.
Использование генератора ключей, который обновляется в методах 2 и 3, не следует путать с существующими режимами работы блочного шифра, таким как СВС или CTR. Во-первых, каждый из этих режимов все еще опирается на статический ключ. Даже CTR, где 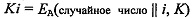 и i-ый блок зашифрованного текста представляет собой Сi=Mi⊕K, опирается на статический ключ K. Во-вторых, обновление генератора ключей использует значения n для генератора ключей, который может быть существенно больше, чем размер блочного и статического ключа. То есть, обычно n>>|Mi| и n>>κ, где >> означает "намного больше, чем". В некоторых примерах осуществления изобретения n=1024, тогда как размер ключа κ=128, а размер блока |Мi| - 128; это пример, где n>>κ. Как объясняется в разделе 6.7, периодичность орбиты динамических ключей, созданных генератором ключей, может быть значительно больше, чем 2κ.
и i-ый блок зашифрованного текста представляет собой Сi=Mi⊕K, опирается на статический ключ K. Во-вторых, обновление генератора ключей использует значения n для генератора ключей, который может быть существенно больше, чем размер блочного и статического ключа. То есть, обычно n>>|Mi| и n>>κ, где >> означает "намного больше, чем". В некоторых примерах осуществления изобретения n=1024, тогда как размер ключа κ=128, а размер блока |Мi| - 128; это пример, где n>>κ. Как объясняется в разделе 6.7, периодичность орбиты динамических ключей, созданных генератором ключей, может быть значительно больше, чем 2κ.
Каждый из этих режимов устанавливает верхнее предельное значение для суммы увеличения энтропия, исходя из размеров блока или размера ключа. В случае ЕСВ, не возникает увеличения энтропии. В случае СВС, увеличение энтропии ограничено сверху размером области сообщения. В случае CTR, случайное число, которое соединяется со счетчиком i, ограничено сверху размером области сообщения, а полученная орбита ключа ограничена сверху размером области сообщения. Поскольку n может быть значительно больше, чем размер ключа или блока, более значительное увеличение энтропии может произойти при обновлении генератора ключей.
Более того, ничто не препятствует комбинации обновления генератора ключей с режимом СВС или режимом CTR. В альтернативных примерах осуществления изобретения криптографический режим, такой как режим сцепления блоков шифрованного текста (СВС), может добавляться к криптографическим методам 2 и 3. Методы 4 и 5 демонстрируют обновление генератора ключей в комбинации с режимом СВС.
Криптографический метод 4. Блочный шифр А выполняет шифрование при помощи динамических ключей и режима СВС
Элис вычисляет секреты 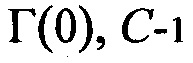 с помощью 1го этапа криптографического метода 1.
с помощью 1го этапа криптографического метода 1.

В методах 4 и 5 символ  представляет собой вектор инициализации, установленный между Элис и Бобом в процессе обмена генераторами ключей.
представляет собой вектор инициализации, установленный между Элис и Бобом в процессе обмена генераторами ключей.
Криптографический метод 5. Блочный шифр А выполняет расшифровку при помощи динамических ключей и режима СВС
Боб вычисляет секреты 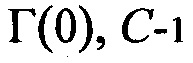 с помощью 1-го этапа криптографического метода 1.
с помощью 1-го этапа криптографического метода 1.

В других примерах осуществления изобретения могут использоваться другие криптографические режимы, такие как CTR или OFB. В одном из примеров осуществления изобретения метод 1 исполняется в передающем устройстве 102, а также приемном устройстве 112, как показано на Рисунке 1А. В одном из примеров осуществления изобретения методы 2 и 3 исполняются в передающем устройстве 102, а также приемном устройстве 112, как показано на Рисунке 1А. В другом примере осуществления изобретения методы 4 и 5 исполняются в передающем устройстве 102, а также приемном устройстве 112, как показано на Рисунке 1А. В некоторых примерах осуществления изобретения недетерминированный генератор 172 на рисунке 1I, который используется в первом этапе метода 1, может использовать фотоны, как показано на рисунке 1D, или другие виды квантовых эффектов для создания недетерминированности.
В некоторых примерах осуществления изобретения, которые показаны на рисунке 1I, инструкции по обновлению генератора ключей 162 и инструкции по получению ключей 168, описанные в методах 1, 2, 3, 4 и 5 являются частью процесса шифрования 160. В некоторых примерах осуществления изобретения, которые показаны на рисунках 1I, 1Е и 1F, генератор ключей при обновлении в методах 1, 2, 3, 4 и 5 может быть реализован, как исполняемые инструкции устройства в собственных инструкциях к микропроцессору устройства. В других примерах осуществления изобретения генератор ключей при обновлении по методам 1, 2, 3, 4 и 5 может быть реализован в оборудовании, таком как FPGA (программируемая пользователем матрица логических элементов) или ASIC (заказная специализированная микросхема). В других примерах осуществления изобретения инструкции по обновлению генератора ключей 162 по методам 1, 2, 3, 4 и 5 могут быть реализованы, как исходный код с и скомпилированы с внутренними инструкциями для ASIC, микропроцессора или FPGA.
6.5 ОБНОВЛЕНИЕ ГЕНЕРАТОРА КЛЮЧЕЙ И ДИНАМИЧЕСКИЕ КЛЮЧИ С ОДНОСТОРОННИМИ ФУНКЦИЯМИ ХЕШИРОВАНИЯ
В данном разделе описывается одно из примеров осуществления изобретения, которое является вариацией метода 2: улучшенный AES-128 является блочным шифром, который использует 128-битные (16 значений, где каждое значение представляет собой число от 0 до 255 включительно) динамические ключи. Keccak действует, как односторонняя функция хеширования Φ, которая выполняет обновление генератора ключей. SHA-512 [23] реализует одностороннюю функцию хеширования Ψ, которая помогает выполнять получение динамических ключей. Два шага для изменения метода 2:
SHA-512 имеет размер профиля в 512 бит (64 значения), поэтому вычисление одиночного профиля может создать четыре различных 128-битных ключа. Таким образом, скорости выполнения шифрования и расшифровки увеличиваются при выполнении этих двух шагов, только когда i mod 4=0. Определить функцию П:{0,1,2,3}×{0,1}512→{0,1}128, так как П(а, (х0, х1 …, х511))=(х128a, x128а+1 … x128a+127), где a∈{0,1,2,3} и (х0, х1,…, x511)∈{0,1}512. Задать, что n=1024, поэтому для всех i и для каждого j∈{512, …, 1023}, тогда Гi,j=Гi+1,j. Функция Φ=Keccak, а Ψ=SHA=512.
Криптографический метод 6. Обновление генератора ключей при помощи Keccak и получение динамических ключей при помощи SHA-512
Метод шифровки Элис
Первый шаг метода 1 предоставляет Элис общий секрет Г(0).

Метод расшифровки Боба
Первый шаг метода 1 предоставляет Бобу общий секрет Г(0).


6.6 ВЫЧИСЛИТЕЛЬНАЯ СЛОЖНОСТЬ И ОДНОСТОРОННИЕ ФУНКЦИИ ПРООБРАЗА
На основе машин Тьюринга данный раздел вводит понятие вычислительной сложности, а затем определяет одностороннюю функцию хеширования прообраза. Первой целью наших определений является исключить сложность того, что асимптотические определения сложности не могут моделировать односторонние функции хеширования, которые используются на практике. Второй более долгосрочной целью является дальнейшее развитие надлежащей структуры для описания односторонности, путем применения мощных инструментов на основе динамических систем к машине Тьюринга.
Если говорить коротко, то машина Тьюринга представляет собой тройное (Q, Σ, η), где Q представляет собой конечный набор состояний, который не содержит уникального состояния приостановки h. Когда начинается машинное выполнение, то машина находится в начальном состоянии s∈Q. Σ - это конечный алфавит, символы которого читаются с ленты T и записываются на нее: Z→Σ. Символ алфавита в кой клетке ленты - это Т(k). -1 и +1 представляют собой подачу головки ленты в левую или правую клетку ленты соответственно, η - это программная функция, где η:Q×Σ→Q∪{h}×Σ×{-1,+1}.
Для каждого q в Q и α в Σ, инструкция η(q, α)=(r, β, х) описывает то, как машина выполняет один шаг расчета. Находясь в состоянии q и читая символ алфавита α на ленте: машина переходит в состояние r. На ленте машина заменяет символ алфавита α на символ β. Если х=-1 или х=+1, тогда машина передвигает свою головку ленты на одну клетку влево или вправо соответственно, а потом читает символ в этой новой клетке. Если r=h, то машина достигает состояния приостановки и прекращает выполнение.
Определение 1. Вычислительная сложность Для величины u∈Σ*, которая вводится в машину, допустим, |u| будет длинной u. Допустим, g:N→N будет функцией |u|. Машина М=(Q, Σ, η) имеет вычислительную сложность C(g, σ, ρ, |u|), если соблюдаются три следующих условия:
При вводе u, машине М требуется, как минимум, g(|u|) шагов вычисления для приостановки. Алфавит М удовлетворяет условию |Σ|≤σ.
Состояния М удовлетворяют условию |Q|≤ρ.
Примечание 1.
Параметры σ и ρ вводят ограничения на размер программы η машины Тьюринга для того, чтобы исключить предварительные вычисления (табличные подстановки). Предполагается, что предварительные вычисления будут закодированы в η или / вводные данные u.
Примечание 2.
Отметим, что предварительные определения сложности зависят от значения алгоритма. Для любого данного алгоритма может быть неопределенное количество машин Тьюринга, которое реализует алгоритм, в котором каждая из этих машин имеет Сложность Шеннона Состояние × Символ [40], такую что |Q| |Σ|>ρ σ. Различие между реализацией машиной алгоритма и абстрактным алгоритмом может привести к глубоким тонкостям [41, 42, 43]. В [44], черный ящик создан при помощи самоизменяемой, параллельной машиной, которая используется квантовую случайность; данный неисчислимый метод поднимает больше вопросов о различиях между алгоритмом и "машиной", которая выполняет его. Также смотрите [45].
Примечание 3.
С точки зрения практики, атаки по побочным каналам обычно используют реализацию алгоритма конкретной машиной. (Например, смотрите [46].) Это тем более поддерживает наш тезис о том, что определение сложности должно быть основано на машине, а не на алгоритме.
Произвольно, h:{0,1}<N→{0,1}q является (N, σ, ρ, r) односторонней функцией прообраза, если А и В соответствуют условиям:
A. Машина Тьюринга М принимает, что на входном значении х выводится h(x) в допустимом количестве шагов вычисления.
B. Любое вероятностное Р машины Тьюринга, которому присваивается у∈{0,1}q в качестве вводных данных, и которое ищет точку полного прообраза х∈h-1({у}), является успешным только при экспоненциально низкой возможности при следующих трех условиях: (1) Машина Тьюринга Р имеет максимум σ алфавитных символов. (2) Машина Тьюринга Р имеет максимум ρ состояний. (3) Имеется некоторая фиксированная степень r и каждая является успешной, как минимум |х|r шагов.
В нашем формальном определении никаких допущений не делается относительно стойкости к наложениям.
Определение 2. Односторонняя функция прообраза Допустим, σ, ρ, r∈N. Допустим, N∈N∪{ω0}. Функция h:{0,1}<N→{0,1}q называется (N, σ, ρ, r) односторонняя функция прообраза с размером профиля q, если соблюдаются два следующих условия:
A. Легко оценить: Существует машина Тьюринга для полиномиального времени А, такая чтобы М(х)=h(x) для каждого х∈{0,1}<N.
B. Вычислительно сложная для инверсии: Для каждого вероятностного Р машины Тьюринга и каждого n, такого чтобы q≤n≤N, вероятность множества
Следующие примечания помогают более объяснить определение 2.
Примечание 4.
ω0 - это первое счетно-бесконечное порядковое числительное. Когда N=ω0, это подразумевает, что область определения h составляет {0,1}*, и в этом случае определение 2 является асимптотическим.
Примечание 5.
Устройство противника Р получает h(х) в качестве исходных данных и вспомогательные исходные данные 1n, которые представляют собой двоичную длину х. Целью вспомогательных исходных данных 1n является возможность того, что функция ложным образом считается односторонней, поскольку устройство Р не имеет достаточно времени, что вывести на печать ее выходные данные. Например, функция h(x)=у, где у=log n наименее значимых битов х с |x|=n. Ни одно устройство не может найти точку h-1({у}) во времени полиномиальном в |h(x)|; однако, существует устройство, которое находит точку h-1(y) во времени полиномиальном в |х|.
Примечание 6.
Для наших целей только n≥q требуется в алгоритмах 1 и 2. Имеется некоторое k<q, такое которое противник может с использованием грубой силы вычислить h(x) для каждого х∈{0,1)j во всех случаях, когда j≤k. Число k зависит от вычислительных ресурсов противника.
Примечание 7.
Односторонняя концепция является вероятностной. Определение не указывает, что для устройства противника Р является невозможным найти точку в полном прообразе h-1({h(x)}); оно утверждает, что Р имеет вероятность≤2-n в нахождении точки в полном прообразе, где устройству требуется, как минимум nr шагов вычисления для того, чтобы найти ее. Здесь g(|u|)=(|u|-q)r, где u=h(x) 1n. Для "успеха" устройство противника Р должно только определить некоторую точку в h-1({h(x)}). Р не требуется определять х, которую использовала машина М. Более того, распределение вероятности является равномерным в отношении входных данных х, и возможного подбрасывания монет машины противника Р.
Примечание 8.
Интуиция для верхней границы 2-n по вероятностным ответвлениям на основе парадокса дня рождения: при условии, что случайно выбранный профиль у, для Евы должно быть намного сложнее с вычислительной точки зрения найти точку прообраза x∈h-1({y})∩{0,1}n, чем для случайного выбора Евой точек прообразов х1, х2,. …, хm вычислить h(x1), h(x2), …, h(xm), и найти наложение в { h(x1), h(x2), … h(xm)}.
Пример 1.
Допустим, 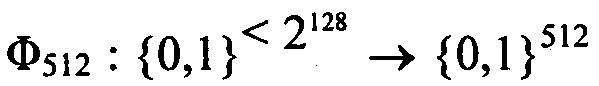 обозначает SHA-512. Для Φ512, N=2128, a q=512. В настоящее время, не существует никакого математического доказательства того, что SHA-512 является односторонней функцией прообраза не некоторых значений r, σ и ρ. В связи с этим полезно будет упомянуть о недавней атаке нахождения прообраза по полному двудольному графу [47] на сокращенных 50 циклах Φ512: их оценка сложности прообраза в 2511.5 все же поддерживает такую возможность и намного превышает сегодняшнюю вычислительную мощность. На практике входные строки ≥2128 бит не появляются. Однако, на основании определения(й) односторонности нынешней практики SHA-512 не удовлетворяет их математическому определению односторонней функции хеширования, поскольку область определения SHA-512 не составляет {0,1}* и в последствии не может удовлетворять асимптотические требования определения.
обозначает SHA-512. Для Φ512, N=2128, a q=512. В настоящее время, не существует никакого математического доказательства того, что SHA-512 является односторонней функцией прообраза не некоторых значений r, σ и ρ. В связи с этим полезно будет упомянуть о недавней атаке нахождения прообраза по полному двудольному графу [47] на сокращенных 50 циклах Φ512: их оценка сложности прообраза в 2511.5 все же поддерживает такую возможность и намного превышает сегодняшнюю вычислительную мощность. На практике входные строки ≥2128 бит не появляются. Однако, на основании определения(й) односторонности нынешней практики SHA-512 не удовлетворяет их математическому определению односторонней функции хеширования, поскольку область определения SHA-512 не составляет {0,1}* и в последствии не может удовлетворять асимптотические требования определения.
6.7 АНАЛИЗ КРИПТОГРАФИЧЕСКИХ МЕТОДОВ 1, 2, 3, 4 И 5
Допустим, ƒ:X→X является функцией на некотором топологическом пространстве X. Орбитой точки р∈X является 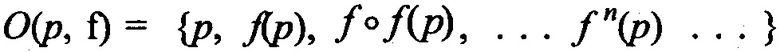 . Вообще, орбита может представлять собой бесконечное множество. В криптографических методах 1, 2, 3, 4 и 5, пространство X={0,1}m для некоторого m∈N, поэтому наши орбиты ключей и орбиты генератора ключей являются конечными. Точка р∈X представляет собой периодическую точку, если имеется j∈N, при котором ƒj(p)=р. Точка x∈X является эвентуально периодической, если имеется k∈N, при котором ƒk(х)=р, и р является периодической точкой.
. Вообще, орбита может представлять собой бесконечное множество. В криптографических методах 1, 2, 3, 4 и 5, пространство X={0,1}m для некоторого m∈N, поэтому наши орбиты ключей и орбиты генератора ключей являются конечными. Точка р∈X представляет собой периодическую точку, если имеется j∈N, при котором ƒj(p)=р. Точка x∈X является эвентуально периодической, если имеется k∈N, при котором ƒk(х)=р, и р является периодической точкой.
Предположим, ƒ:{0,1}m→{0,1}m является функцией. Принцип Дирихле предполагает, что каждая точка х∈{0,1}m является эвентуально периодической с периодом максимум 2m. Каждая функция ƒ:{0,1}m→{0,1}m выводит отношение эквивалентности по множеству {0,1}m следующим образом. Если х и y являются эвентуально периодическими в той же орбите в отношении ƒ, тогда х и y называются эвентуально периодическим эквивалентом, выраженным как х~ƒу. Допустим, [х] обозначает класс эквивалентности {y∈{0,1}m:х~ƒу}.
Орбита генератора ключей  Размер орбиты генератора ключей представляет собой количество точек в О(Г, Ф, А1). Также, А2 и А4 обозначают криптографические методы 2 и 4 соответственно.
Размер орбиты генератора ключей представляет собой количество точек в О(Г, Ф, А1). Также, А2 и А4 обозначают криптографические методы 2 и 4 соответственно.
Определение 3. Допустим ϕ:{0, 1}<N→{0,1}q является функцией с размером профиля q. (Никаких допущений не делается относительно односторонности ϕ) ϕ имеет периодическую точку р∈{0,1}q с периодом m, если m является самым мелким положительным числом, при котором ϕm(р)=р.
Периодическая орбита, которая заключена в О(Г, Ф, А1) имеет период ≤|О(Г, Ф, А1)|. Один из наших инструментов использует теорему 1, чтобы предоставить метод для определения атаки нахождения прообраза на Φ на основании эвентуально периодических классов эквивалентности.
Когда q>κ, где κ=|Kj|, необходимо упомянуть важные тонкости. С первого взгляда, можно предположить, что последовательность динамических ключей K1, K2, … должна всегда иметь период ≤2κ, поскольку множество { K1, К2,… K2κ+1} должно иметь наложение. Оно еще больше увеличивается парадоксом дня рождения, который для последовательности  возможно содержит два идентичных динамических ключа.
возможно содержит два идентичных динамических ключа.
Если бы эта последовательность динамических ключей была создана дискретной, автономной динамической системой ƒ:{0,1}κ→{0,1}κ, то первое наложение определило бы периодичность последовательности ключей. Вместо этого орбита О(Г, ϕ, А1)⊆{0,1}q используется для получения динамических ключей K1, K2, …. Таким образом, размер О(Г, ϕ, А1) может быть значительно больше, чем 2κ, в частности, когда q существенно больше, чем κ. Данное наблюдение приводит нас к теореме 1.
Теорема 1. Предположим, что z∈{0,1}q имеет период m относительно ϕ. Затем на z происходит атака нахождения прообраза путем вычисления m-1 итераций ϕ.
ДОКАЗАТЕЛЬСТВО. Вычислить х=ϕm-1(z). Затем ϕ(х)=ϕm(z)=z.
Следующее определение помогает проанализировать криптографические методы 2 и 4.
Определение 4. Функция ϕ:{0,1}<N→{0,1}q является регулярной в своей подобласти {0,1}k при k≥q, если для каждого у∈{0,1}q, то пересечение полного прообраза ϕ-1({у}) и имеют {0,1}k одинаковое количество точек. Это означает, что для каждого у∈{0,1}q, тогда |ϕ-1({у})∩{0,1}k|=2k-q.
Теорема 2. Предположим, что функция ϕ:{0, 1}<N→{0,1}q является регулярной в подобласти {0,1}q. Тогда каждая точка в {0,1}q является периодической точкой и находится в уникальной периодической орбите относительно ϕ.
ДОКАЗАТЕЛЬСТВО. При приведении к абсурду, предположим, что х∈{0,1}q не является периодической точкой. Допустим, k является наименьшим положительным натуральным числом у=ϕk(х) является периодическим числом. Допустим, m будет периодом у. Тогда ϕ-1({у}) содержит, как минимум, две точки ϕm-1(у) и ϕk-1(x). Эти две точки противоречат условию регулярности ϕ. Уникальность периодической орбиты х непосредственно следует из отношения эквивалентности ~ϕ, которое ϕ обуславливает на {0,1}q.
Когда ϕ удовлетворяет условию регулярности на подобласти {0,1}q, полезными являются теоремы 1 и 2, поскольку нет необходимости искать умные атаки нахождения прообраза. Вместо этого, можно проанализировать размер и количество периодических орбит ϕ на {0,1}q. Следствие 3 говорит о том, что 2q равняется суме периодов каждой периодической орбиты относительно ϕ.
Следствие 3. Допустим, что функция ϕ:{0, 1}<N→{0,1}q является регулярной в подобласти {0,1}q. Тогда сумма всех |[х]|= 2q, где сумма находится в диапазоне каждого класса эквивалентности [х], обусловленных ~ϕ и |[х]|, представляет собой число точек в [х]. То есть, |[х]| представляет собой период х относительно ϕ.ДОКАЗАТЕЛЬСТВО. ~ϕ представляет собой отношение эквивалентности по {0,1}q. Использовать теорему 2.
Следствие 3 создает инструмент вычисления для определения вероятности того, что точка находится в периодической орбите с периодом m. В качестве простого примера допустим, что S:{0,1}8→{0,1}8 обозначает блок замены, который используется в AES. Затем ~S обуславливает пять классов эквивалентности [0], [1], [4], [11], [115] по {0,1}8. Класс эквивалентности [0] имеет 59 элементов. Это предполагает, что S59(0)=0 поскольку S является взаимно-однозначным соответствием. Отметим, что [11]={43, 241, 161, 50, 35, 38, 247, 104, 69, 110, 159, 219, 185, 86, 177, 200, 232, 155, 20, 250 45, 216, 97, 239, 223, 158}. Также, |[1]|=81, |[4]|=87, |[11]|=27 и |[115]|=2 и |[0]|+|[1]|+|[4]|+|[11]|+|[115]|=28.
В процессе однократного выполнения криптографического метода 2 присутствует низкая вероятность шифрования двух различных блоков с идентичными ключами. Другими словами, когда i не равно j, то событие Ki=Kj имеет низкую вероятность. Следующая лемма помогает усилить выражение "низкая вероятность".
Лемма 4. Предположим, Φ:{0, 1}<N→{0,1}q является односторонней функцией прообраза (N, σ, ρ, r+m+2), которая удовлетворяет условию регулярности по подобласти {0,1}q, где r, m≥1, N=n+1, a σ=q и ρ=q2. Предположим, что машина М вычисляет Φ по каким-либо входящим данным х∈{0,1}q за максимум qm шагов вычисления. Предположим, что Элис случайно выбирает х∈{0,1}q и вычисляет Φ(х)=у. Предположим, что Ева видит только у. Задать, что 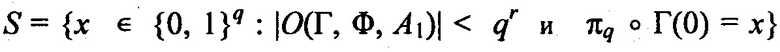 Тогда |S|≤2-q/2.
Тогда |S|≤2-q/2.
СХЕМА ДОКАЗАТЕЛЬСТВА. Используя машину М, Ева вычисляет орбиту [у, Φ(у), Ф2(у), …] с максимум qr итераций. После выполнения вычисления каждой итерации Φk(у), Ева осуществляет поиск на предмет наложения в {у, Φ(у), Φ2(у), …, Φk(у)}. Если наложение найдено, то устройство Евы приостанавливается. Если устройство Евы достигает  и не выявляет наложения, тогда устройство Евы приостанавливается.
и не выявляет наложения, тогда устройство Евы приостанавливается.
Там, где присутствует наложение в {у, Φ(у), … Φk(у)}, по теореме 2, условие регулярности предполагает, что у находится в данной периодической орбите (класс эквивалентности). Допустим, а=|[у]|. Тогда теорема 1 предполагает, что х=Φа-1(у) является точкой прообраза, которую ищет Ева. Если |S|>2-q/2, тогда устройство Евы найдет точку прообраза х за менее чем qr+m-1 log q шагов вычисления с вероятностью более, чем 2-q/2, противореча утверждению, что Ф является односторонней функцией прообраза (N, σ, ρ, r+m+2).
Пример 2.
Рассмотрим Φ512, где q=512. Предположим, что m=3, потому что 5123 шага являются более консервативной верхней границей для вычисления машиной Тьюринга Φ512 по х∈{0,1}512, чем 5122. Если Φ512 удовлетворяет условию регулярности по подообласти {0,1}512, а Φ512 является функцией прообраза (2128, q, q2, 9), тогда вероятность составляет ≤2-256, что генератор ключей в криптографическом методе 2 имеет орбиту, которая удовлетворяет |0(Г, Φ512, А2)|<q4 вероятностью, как минимум, 1-2-256, в тех случаях, когда j не равняется k, тогда Г(j) не равняется Г(k) для длины шифрования до 8,5 миллиардов байт. Видение двух идентичных ключей, которые шифруют различные блоки, требует наложения SHA-512 только после 134217728 итераций SHA-512. В настоящее время не существует никаких математических доказательств односторонности Φ512; однако, (2128, q, q2, 9) кажется консервативным, исходя из атаки нахождения прообраза по полному двудольному графу [47], которая зависит от сокращенных 50 циклов вместо стандартных 80 циклов.
Примечание 9.
В известном уровне техники стандартные алгоритмы блочного шифра, такие как AES, Serpent или DES не должны показывать статический ключ Еве; в известном уровне технике, если статический ключ скомпрометирован, то и криптографическая безопасность фатально скомпрометирована. Примеры осуществления изобретения, которые приведены в данном описании, являются лучшими: Если динамический ключ, который использован в методах 2, 3, 4 и 5, взломан Евой, то такой взлом не открывает предшествующих динамических ключей и будущих динамических ключей, которые используются блочным шифром А.
Для создания будущих динамических ключей Kk, при которых k>j, Ева должна найти точку прообраза Г(j), j-ый генератор ключей. В криптографическом методе 2, предположим, что блочный шифр А - это AES-256, q=512, а n=1024 и предположим, что из пути обхода системы защиты процессора Ева получает 256-битный ключ Kleak. Даже после утечки, чтобы построить будущие ключи, Еве необходимо знать Г(j). Для алгоритма 2 построение будущих ключей требует от Евы значительно больше вычислительных шагов, чем определение одной точки прообраза x∈{0,1}1024, при которой Φ512(x)=Kleak. Если Φ512 является регулярной на субообласти {0,1}1024, тогда |Φ512-1(Kleak)|=2512. Условие регулярности предполагает, что Ева должна угадать Г(j) из 2512 возможных точек прообразов. Когда Ева пытается выяснить динамические ключи, которые предшествуют Kj, тогда у нее есть даже меньше информации, чем когда она пытается построить будущие ключи. Тогда как последние n-q бит из Г(j) являются постоянными, даже если Еве известен генератор ключей Г(j), то знание Евы не позволяют ей незамедлительно получить Г(j-1), поскольку Φ512(Гj-1,0 … Гj-1,q-1)=Гj-1,0 … Гj-1,q-1, а Φ512 выдерживает атаки нахождения прообраза.
Примечание 10.
Логическая функция ƒ:{0,1}n→{0,1} может быть выражена, как 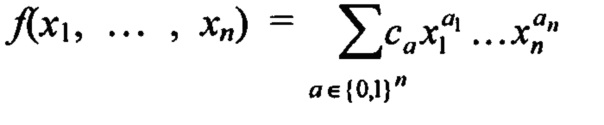 по F2[x1, …, хn]/(х12-х1, …, хn2-хn), где
по F2[x1, …, хn]/(х12-х1, …, хn2-хn), где  , а х≤а, если хi≤аi, для каждого i. Алгебраическая степень ƒ определяется, как
, а х≤а, если хi≤аi, для каждого i. Алгебраическая степень ƒ определяется, как 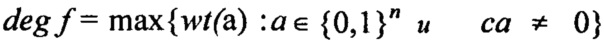 , где wt(a) - это вес Хэмминга a. Рассмотрим функции ƒ1, ƒ2 … ƒn:{0,1}n→{0,1} и функцию F:{0,1}n→{0,1}n, которые определяются, как F(х)=(ƒ1(x), ƒ2(x), … ƒn(x)). Алгебраическая степень F=max{degƒ1, degƒ2, … degƒn}. Для статического ключа AES K, функция шифрования AES ЕK:{0,1}128→{0,1}128 имеет алгебраическую степень ≤128, и ЕK является функцией из 128 булевых логических переменных. Хорошо известно, что сопротивление булевой функции дифференциальному криптоанализу и дифференциалам высокого порядка зависит от ее алгебраической степени и от того, насколько быстро ее степень может быть уменьшена при взятии дискретных производных [48, 49, 50].
, где wt(a) - это вес Хэмминга a. Рассмотрим функции ƒ1, ƒ2 … ƒn:{0,1}n→{0,1} и функцию F:{0,1}n→{0,1}n, которые определяются, как F(х)=(ƒ1(x), ƒ2(x), … ƒn(x)). Алгебраическая степень F=max{degƒ1, degƒ2, … degƒn}. Для статического ключа AES K, функция шифрования AES ЕK:{0,1}128→{0,1}128 имеет алгебраическую степень ≤128, и ЕK является функцией из 128 булевых логических переменных. Хорошо известно, что сопротивление булевой функции дифференциальному криптоанализу и дифференциалам высокого порядка зависит от ее алгебраической степени и от того, насколько быстро ее степень может быть уменьшена при взятии дискретных производных [48, 49, 50].
Задать, что М=|O(Г, Φ, А4)|. Для каждого динамического ключа Ki, допустим, что ЕKi:{0,1}128→{0,1}128, обозначают функцию кодирования блочного шифра; таким блочным шифром может быть AES, Serpent или другой блочный шифр, размер блока которого составляет 16 байт. В процессе выполнения криптографического метода 4 имеются 4М различные функции ЕK0 … ЕK4M-1, где функция шифрования ЕK0 применяется к блоку обычного текста M0, функция шифрования ЕK1 применяется к блоку М1, и так далее. Такая последовательность шифрования обуславливает функцию ƒГ:{0,1}512М→{0,1}512М, где ƒГ=(ƒ1, ƒ2 … ƒ512М). Как обсуждалось в примере 2, даже для исключительно маловероятного события, такого как наложение после всего 134217728 итераций SHA-512 (если такая орбита существует), обусловленная ƒГ будет представлять собой функцию из 68719476736 булевых переменных по сравнению со 128 булевыми переменными для ЕK. Сцепление блоков шифрованного текста и орбита генератора ключей создает компоновку функций шифрования блоков шифрованного текста ЕK0, ЕK1 …; например, С2= ЕK2(M2⊕ЕK1|(M1⊕ЕK0(М0⊕С-1))). Таким образом, функции ƒ1+128k, … ƒ128(k+i) являются функцией из 128(k+1) переменных x1, …, х128(k+i) для 0≤k≤4М. Более того, данное примечание и факт того, что 68719476736 намного больше, чем 128, объясняет то, как метод 4 существенно увеличивает алгебраическую степень по сравнению с максимальной алгебраической степенью фонового блочного шифрования, которое использует статический ключ в известном уровне техники.
6.8 ДИНАМИЧЕСКИЕ КЛЮЧИ ОСТАНАВЛИВАЮТ ПРОСТУЮ АТАКУ НА БЛОЧНЫЙ ШИФР
Динамические ключи, полученные при криптографических методах 2, 3, 4 и 5 помогают остановить простую атаку Хуанга и Лаи на блочный шифр [51], которая описана ниже в алгоритме Хуанга и Лаи 7. Следующий перечень описывает символы, которые используются в их алгоритме атаке 7.
Р - обычный текст
С - шифрованный текст
n - размер блока
K - основной ключ
k - размер основного ключа R - число циклов S - нелинейный слойL - линейный слой
Kr - подключ, используемый в цикле rХr - входной блок в цикл r, где Х0=Р
Yr - выходной блок ключа, который смешивается в цикле r
Zr - выходной блок нелиниейного слоя в цикле r
Zir - i-ый подблок в Zr
S1 представляет собой внутреннее состояние, которое может рассчитываться на основании Р только при помощи k1 бит подключей, где k1 является максимально меньшей, чем k, которая может быть получена. Точно также S2 - это внутреннее состояние, которое может быть получено только из С при помощи (других) подключей k1 бит. Для какого-либо блочного шифра можно определить состояния S1 и S2. Алгоритм атаки имеет два этапа:
1. Стадия "встреча посредине" создает перечень кандидатов, который содержит 2k-M ключей, где М - это соблюдаемый промежуточный размер.
2. Стадия проверки, которая исследует ключи в перечне кандидатов.
Линейные числа были добавлены в этот алгоритм атаки [51], чтобы помочь объяснить как криптографические методы 2 и 4 мешают этой атаке.


Метод алгоритма 7, который использует перечень ключей-кандидатов для определения статического ключа блочного шифра не является эффективным против криптографических методов 2 и 4. Чтобы это проиллюстрировать, рассмотрим криптографический метод 2, например, с использованием 16-байтного блочного шифра, такого как Serpent, при q=512 и n=768. После того, как каждый 16-байтный блок зашифрован, перечень кандидатов-ключей изменяется, потому что следующий 256-битный ключ получается из обновленного генератора ключей Гj,0 … Гj,767, а среднее расстояние Хэмминга между Гj,0 … Гj,511 and Гj-1,0 … Гj-1,511 составляет 256. Рассмотрим криптографический метод 2, который шифрует 256000 байт голосовых данных в секунду. При такой скорости для одночасовой телефонной беседы потребуется орбита генератора ключей (Г0,0… Г0,511) Ф512(Г0,0 … Г0,511), … Ф5121440000(Г0,0 … Г0,512) с размером 1440001. Если в этой орбите возникает наложение в процессе одночасового телефонного звонка, тогда теорема 1 обеспечивает подавляющую атаку нахождения прообраза на SHA-512, как минимум, с 1440000 итераций SHA-512. Исходя из чрезвычайно низкой вероятности этого редкого события (такие обиты могут даже не существовать), наложение также привело бы к тому, что SHA-512 не удовлетворяло бы какие-либо обоснованные значения сложности прообраза (2128, σ, ρ, r). "Обоснованные" означает, что они не ограничивают устройство Евы Р настолько сильно, что она не может вычислить, например, SHA-512. Допустим, ρ=1, поэтому устройство Р может иметь только одно состояние.
Напоминаем, что атака нахождения прообраза по полному двудольному графу [47] - на сокращенные 50 циклов SHA-512 вместо полных 80 - имеет расчетную сложность прообраза в 2511.5. Для типичной орбиты чрезвычайно вероятно, что O(Г, Ф512, A2) имеет размер намного больший, чем число итераций SHA-512, чтобы обеспечить полное шифрование для какого-либо прогнозируемого применения. В таком случае допущение, что имеются пары 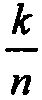 (обычный текст, шифрованный текст), не подходит для метода 2. Более того, отсутствие пар
(обычный текст, шифрованный текст), не подходит для метода 2. Более того, отсутствие пар 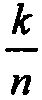 (обычный текст, шифрованный текст) делает недействительным эффективность контура, который состоит из линий от 1 до 7 включительно, и контура, который состоит из линий от 8 до 18 включительно.
(обычный текст, шифрованный текст) делает недействительным эффективность контура, который состоит из линий от 1 до 7 включительно, и контура, который состоит из линий от 8 до 18 включительно.
6.9 РАСПРЕДЕЛЕНИЕ ГЕНЕРАТОРОВ КЛЮЧЕЙ NADO
NADO использует симметричный генератор закрытых ключей. Это означает, что начальный закрытый ключ, который используется шифратором для каждого процессе, является таким же, как и генератор закрытых ключей, который используется дешифратором для соответствующего процесса. Существуют различные методы для распространения генератора закрытых ключей NADO.
1. Может использоваться электронный обмен генераторами ключей между сторонами. 2. Курьер может передать непосредственно генераторы ключей двум или более сторонам. Метод 1 является предпочтительным, когда количество потенциальных получателей зашифрованной передачи данных является большим, а потенциальные получатели неизвестны. Данные способы использования включают в себя: Защищенные беспроводные способы использования, такие как разговоры по мобильному телефону, беспроводные передачи сообщений электронной почты, транзакции по беспроводной сети, электронная торговля по беспроводной сети и спутниковая передача данных. Защищенные программные способы использования, такие как приложения для работы с сообщениями электронной почты, корпоративные вычисления, электронная торговля в режиме реального времени, отправка сообщений в режиме реального времени, корпоративные портальные программы и другие интернет-приложения.
В способах использования, где количество потенциальных получателей зашифрованной передачи данных является небольшим, а получатели известны заранее, можно использовать метод 2, при котором отправители и получатели могут договориться о передаче их генераторов закрытых ключей безопасным образом. Этот метод может использоваться, когда имеются опасения относительно атаки с применением технологии «незаконный посредник» при обмене ключами.
6.10 ОБМЕН ГЕНЕРАТОРАМИ КЛЮЧЕЙ
В имеющемся уровне техники обмен ключами по методу Диффи-Хеллмана-Меркле является методом обмена ключами, при котором две стороны (Элис и Боб), которые предварительно не знают друг друга, устанавливают общий секретный ключ на небезопасный канал связи. В данном описании дополнение к этому методу обмена используют две стороны (Элис и Боб), чтобы создать начальный генератор общего ключа Г(0) для H-процесса; Обмен генераторами ключей зависит от характеристик коммутативных групп. Группа G представляет собой множество с операцией с двоичными числами*, (g2 означает g*g, a g5 означает g*g*g*g*g), при котором выдерживаются четыре следующих свойства:
Операция с двоичными числами* замыкается на G. Другими словами, а*b находится в G для всех элементов а и b в G.
Операция с двоичными числами* является ассоциативной по G. а*(b*с)=(а*b)*с для всех элементов а, b и с в G.
BG. а*е=е*а=а присутствует уникальный элемент тождества е.
Каждый элемент а в G имеет уникальную обратную величину, которая обозначается, как а-1 а*а-1=а-1*а=е.
В абстрактном смысле, иногда оператором пренебрегают, поэтому а*b пишется, как аb. Иногда тождество группы представлена, как 1, когда групповая операция представляет собой некоторую форму умножения. Иногда тождество группы представлена, как 0, когда групповая операция представляет собой некоторую форму сложения. Числа {…, -2, -1, 0, 1, 2, …} относительно их операции с двоичными числами+являются примером бесконечной группы. 0 является элементом тождества. Например, обратная величина от 5 - это 5, а обратная величина от 107 - это 107. Множество перестановок n элементов {1, 2,…, n}, обозначенное, как Sn, является примером конечной группы с n! элементами, где операция с двоичными числами является композицией функцией. Каждый элемент Sn является функцией σ:{1, 2, …, n}→{1, 2, …, n}, т.е. от 1 до 1 и далее. В этом контексте, а называется перестановкой. Тождественная перестановка е представляет собой элемент тождества Sn, при котором е(k)=k для каждой k в {1, 2, …, n}.
Если Н является непустым подмножеством группы G, а Н является группой относительно групповой операции с двоичными числами * из G, тогда Н называется подгруппой G. Н является собственной подгруппой G, если Н не равняется G G (т.е., Н является собственным подмножеством G). G является циклической группой, если G не имеет собственных подгрупп. Числа по модулю n (т.е., Zn={[0], [1], … [N-1]}n-1]} являются примером конечной группы относительно добавления по модулю n. Если n=5, [4]+[4]=[3] в Z5, потому что 5 делит (4+4). Точно также, [3]+[4]=[3] в Z5. Z5 является циклической группой, поскольку 5 является простым числом. Когда р является простым числом, Zp является циклической группой, содержащей р элементов {[0], [1],… [р-1]}. [1] называется генерирующим элементом для циклической группы Zp, поскольку [1]m=[m], где m является натуральным числом, при котором 0<m<=р-1, a [1]p=[0]. Эта мультипликативная концепция работает следующим образом: [1]2=[1]+[1]; [1]3=[1]+[1]+[1]; и так далее. Эта мультипликативная концепция (т.е. с использованием верхних индексов) используется в описании обмена генераторами ключей, описанного ниже.
Имеется бесконечное число циклических групп, и бесконечное число этих циклических групп является чрезвычайно большим. Концепция чрезвычайно большого числа означает следующее: если считать, что 21024 является чрезвычайно большим числом, исходя из вычислительной мощности нынешних компьютеров, то тогда все еще имеется бесконечное число конечных циклических групп, и при этом каждая циклическая группа содержит более, чем 21024 элементов.
Шаги 1, 2, 3, 4 и 5 описывают обмен генераторами ключей.
1. Элис и Боб соглашаются на чрезвычайно большую, конечную, циклическую группу G и генерирующий элемент g в G. Эта группа G пишется мультипликативно, как объяснялось ранее.
2. Элис выбирает случайное натуральное число а и отправляет ga Бобу.
3. Боб выбирает случайное натуральное число b и отправляет gb Элис.
4. Элис вычисляет 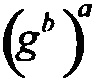 .
.
5. Боб вычисляет 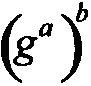 .
.
Элис и Боб иногда договариваются о конечной циклической группе G и об элементе g задолго до остальной части протокола обмена ключами; предполагается, что g известна всем атакующим. Математическая концепция циклической группы, генерирующий элемент и конечное поле представлены в [55].
Как Элис, так и Боб теперь обладают групповым элементом gab, который может служить в качестве общего секретного ключа. Величины 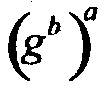 и
и 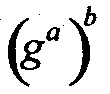 являются одинаковыми, потому что g является элементом группы G. Элис может зашифровать информацию m, как m*(gab), и направляет m*(gab) Бобу. Боб знает |G|, b и ga. Для конечных групп теорема Лагранжа предполагает, что порядок каждого элемента группы разделяет число элементов в группе, обозначенных как |G|. Это означает х|G|=1 для всех х в G, где 1 является элементом тождества в группе G. Боб вычисляет
являются одинаковыми, потому что g является элементом группы G. Элис может зашифровать информацию m, как m*(gab), и направляет m*(gab) Бобу. Боб знает |G|, b и ga. Для конечных групп теорема Лагранжа предполагает, что порядок каждого элемента группы разделяет число элементов в группе, обозначенных как |G|. Это означает х|G|=1 для всех х в G, где 1 является элементом тождества в группе G. Боб вычисляет 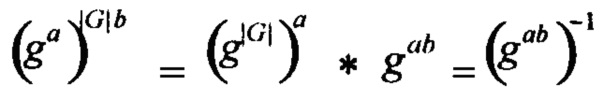 . После того, как Боб получает зашифрованную информацию m*(gab) от Элис, тогда Боб применяет
. После того, как Боб получает зашифрованную информацию m*(gab) от Элис, тогда Боб применяет  и расшифровывает зашифрованную информацию путем вычисления
и расшифровывает зашифрованную информацию путем вычисления  .
.
6.11 ОБМЕН ГЕНЕРАТОРАМИ КЛЮЧЕЙ НА ОСНОВЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ
Данный раздел описывает криптографию на основе ассиметричных ключей, которая называется криптографией на основе эллиптических кривых, которая в некоторых примерах осуществления изобретения может использоваться для того, чтобы реализовать обмен генераторами ключей. Концепция Еnc(Е, m) используется для того, чтобы представить результат шифрования обычного текста т с использованием эллиптической кривой Е. Из чего следует, что концепция Dec(E, с) используется для представления результата расшифровки шифрованного текста с, который включен, как точка на эллиптической кривой Е. В одном из примеров осуществления изобретения криптография на основе эллиптической кривой представляет собой метод асимметричной криптографии, который используется для создания генераторов ключей общих для Элис и Боба.
В одном из примеров осуществления изобретения предполагается, что Е представляет собой эллиптическую кривую по конечному полю Fp, где р - это простой число, а Н - это циклическая подгруппа E(FP), генерируемая точкой Р, которая находится в E(FP). Элис хочет безопасно отправлять информацию Бобу, общеизвестным ключом которого является (Е, Р, аР), и закрытым ключом которого является натуральное число а<р-1.
Элис выполняет следующий Этап Кодирования. Выбрать случайное натуральное число b<р-1. Принять во внимание, что информация обычного текста вставлена, как точки m на Е. Вычислить β=bР и γ=m+b(aР). Направить зашифрованный Еnc(Е, m)=с=(β, γ) Бобу.
Боб выполняет следующий Этап Расшифровки после получения зашифрованного текста с=(β, γ). Обычный текст m извлекается при помощи закрытого ключа, как Dec(E, с)=m=γ-аβ.
Вычисления эллиптической кривой по конечному полю, также дают возможность Элис и Бобу создать общие генераторы закрытых ключей перед тем, как начнется симметричная криптография. Ниже приводится простой пример, описанный здесь для иллюстрации, а не для целей безопасности. Принять во внимание, что эллиптическая кривая Е задана у2=х3+4х+4 по F13. Можно показать, что E(F13) имеет 15 элементов, которая обязательно является цикличной. Также Р=(1,3) представляет собой генератор Е. Предполагая, что общеизвестным ключом Боба является (Е, Р, 4Р), где a=4 является закрытым ключом, а m=(10, 2) - это информация, которую Элис хочет направить Бобу, то Элис выполняет следующее. Элис выбирает b=7 случайным образом. Затем Элис вычисляет Еnc(Е, m)=Еnc(E, (10, 2))=(bР, m+b(aР))=(7P, (10, 2)+7(4Р))=((0, 2), (10, 2)+7(6, 6))=((0, 2), (10, 2)+(12, 5))=((0, 2), (3, 2))=(β, γ)=с. Затем Элис направляет зашифрованный текст с=(β, γ)=((0, 2), (3, 2)) Бобу, который использует свой закрытый ключ для расшифровки зашифрованного текста и получения информации m=(10, 2) следующим образом: Dec(E, с)=(3,2) 4(0,2)=(3,2) (12,5)=(3,2)+(12,8)=(10,2). Дополнительная информация по эллиптическим кривым приводится в [56, 57].
В одном из примеров осуществления изобретения, эллиптическая кривая с формой у2=х3+Ах+х, которая предложена Монтгомери [58], может использоваться для выполнения обмена генераторами ключей на основе эллиптических кривых. В одном из примеров осуществления изобретения закрытый ключ может быть создан с помощью последовательности из 96 байт (768 бит). В другом примере осуществления изобретения закрытый ключ может быть из 1024 байт (8192 бит). В примере осуществления изобретения, который показано под номером 136 на Рисунке 1В и под номером 140 на Рисунке 1D недетерминированный генератор создает эти биты путем измерения времени наступления события для фотонов, как описано в разделе 6.3, который называется КРИПТОГРАФИЧЕСКОЕ ОБОРУДОВАНИЕ И ИНФРАСТРУКТУРА. В одном из примерах осуществления изобретения 768 различных точек времени наступления события для фотонов (t(1,1), t(1,2), t(1,3)), (t(2,1), t(2,2), t(2,3)) … (t(k,1), t(k,2), t(k,3)), … (t(256,1), t(256,2), t(256,3)), которые для каждого k удовлетворяют условию t(k,1)<t(k,2)<'(U) и t(k,2)-t(k,1) не равняется t(k,3)-t(k,2), наблюдаются при использовании недетерминированного генератора. Каждая тройка создает "1" или "0" в зависимости от того будет ли t(k,2)-t(k,1)>t(k,3)_t(k,2) ИЛИ t(k,2)- t(k,1)<t(k,3)-t(k,2).
Каждая соответствующая общедоступная точка на эллиптической кривой вычисляется при помощи базовой точки на эллиптической кривой у2=х3+Ах+х и 96-байтного закрытого ключа, который был получен на основании недетерминированного генератора 136 на Рисунке 1В. В одном из примеров осуществления изобретения Элис создает свою общедоступную точку на эллиптической кривой на основании своего закрытого ключа и базовой точки; Боб вычисляет свою общедоступную точку на эллиптической кривой при помощи той же кривой у2=x3+Ах+х и такой же базовой точки на этой кривой. В некоторых примерах осуществления изобретения Элис и Боб могут выполнять обмен генераторами ключей несколько раз.
В результате выполнения этого обмена один раз Элис и Боб могут создать общие 96 байт для генератора ключей (0). В данном примере осуществления изобретения и других примерах осуществления изобретения, новый общий генератор ключей может быть создан независимо от предыдущих генераторов ключей. В одном из примеров осуществления изобретения эллиптическая кривая с формой кривой у2=х3+Ах+х описана ниже. В одном из примеров осуществления изобретения, число А выбирается таким образом, чтобы (А-2)/4 было небольшим числом. Это помогает ускорить умножение.
На основании недетерминированного генератора (например, оборудования на Рисунке 1D) Элис создает следующий 96-байтный закрытый ключ.
56 118 47 136 134 34 224 68 132 171 49 19 207 117 184 159 218 125 120 98 138 117 103 249
109 235 127 143 11 246 210 126 88 145 54 249 200 62 228 161 5 98 23 4 203 144 24 232 148
196 78 37 85 58 13 45 188 136 220 254 9 32 236 76 192 39 121 233 214 163 41 88 26 164 6
203 186 154 41 146 254 13 249 232 109 68 146 91 167 54 202 82 235 81 230 83
Элис использует свой закрытый ключ и базовую точку для вычисления на кривой у2=х3+Ах+х следующей общедоступной точки эллиптической кривой.
236 131 148 127 55 62 150 40 81 11 71 122 94 145 91 37 181 245 124 3 254 164 47 75 129
171 56 128 8 237 202 24 56 227 93 5 194 105 0 228 9 29 86 101 156 203 48 118 152 142
190 28 179 174 106 86 122 89 54 193 192 234 83 50 40 146 144 54 136 94 200 4 144 123
190 191 246 167 128 76 97 219 54 233 114 37 145 207 155 98 195 89 137 56 225 80
Элис отправляет свою точку эллиптической кривой Бобу. На основании недетерминированного оборудования, показанного на Рисунке 1D, Боб создает следующий 96-байтный закрытый ключ.
176 99 149 32 146 54 112 229 54 146 107 179 39 0 64 13 38 201 241 89 203 87 41 227 95
183 205 206 133 201 117 92 40 134 199 246 72 205 82 245 119 149 67 30 151 73 154 238
25 96 96 106 175 247 80 69 174 13 220 219 115 243 152 71 168 237 59 17 227 94 148 27
190 90 48 139 16 141 20 89 71 51 159 23 63 70 175 239 0 144 130 90 208 84 150 64
Боб использует свой закрытый ключ и базовую точку для вычисления на кривой у2=х3+Ах+х следующей общедоступной точки эллиптической кривой.
78 33 138 252 54 163 232 126 202 160 84 232 216 188 31 8 131 133 101 195 178 208 241 223 127 35 129 40 42 137 40 95 25 113 231 248 138 236 54 147 113 119 226 59 141 6 27 192 175 179 56 187 151 93 151 106 228 52 58 96 87 26 249 121 164 164 41 244 19 183 74 32 189 249 124 109 246 68 254 173 186 233 187 57 118 242 197 140 135 199 90 254 200 227 14 33
Боб отправляет свою точку эллиптической кривой Элис. Далее Элис использует свой закрытый ключ и общедоступную току эллиптической кривой Боба, чтобы вычислить на кривой у2=х3+Ах+х общую точку, показанную ниже, которая представляет собой генератор кривой Г(0).
235 126 229 251 14 146 63 250 203 150 6 199 175 116 50 153 21 37 23 64 172 71 113 143
125 226 131 23 41 73 63 72 227 109 78 221 181 3 6 204 128 84 141 146 60 218 238 121
98 245 57 203 26 192 215 170 218 148 42 176 14 142 193 8 29 157 107 135 231 5 222 171
5 227 97 236 110 144 214 165 76 246 193 22 84 220 92 202 3 219 10 253 231 45 13 114
Данный обмен дает возможность Бобу и Элис создавать 96 байт общего генератора ключей Г(0).
Хотя изобретение и было описано в отношении конкретных примеров осуществления изобретения, те, кто имеет специальные знания, понимают, что могут быть внесены различные изменения, а эквиваленты могут быть заменены на соответствующие элементы без выхода за пределы истинного духа и объема изобретения. К тому же, изменения могут быть внесены, не отклоняясь от фундаментальных идей изобретения.
Список литературы
[1] Mihir Bellare and Phillip Rogaway. Introduction to Modern Cryptography. 2005.
http://www.cs.ucdavis.edu/~rogaway/classes/227/spring05/book/main.pdf
[2] Oded Goldreich. Foundations of Cryptography. Volumes I Basic Tools. Cambridge University Press 2001.
[3] Oded Goldreich. Foundations of Cryptography. Volume II Basic Applications. Cambridge University Press. 2004.
[4] T.W. Cusick and P. Stanica. Cryptographic Boolean Functions and Applications. Academic Press, Elsevier, 2009.
[5] NIST. Advanced Encryption Standard (AES), FIPS 197. Nov. 2001.
http://csrc.nist.gov/publications/fips/fipsl97/fips-197.pdf
[6] R. A. Mollin. Codes: The Guide to Secrecy From Ancient to Modern Times. Chapman & Hall. 527-530, 2005.
[7] Juliano Rizzo and Thai Duong. Practical Padding Oracle Attacks. Black Hat Conference. 201
https://www.usenix.org/legacy/event/woot10/tech/full_papers/Rizzo.pdf
http://en.wikipedia.org/wiki/Padding_oracle_attack
http://people.cs.kuleuven.be/~andre.marien/security/playing%20with%20cbc.pdf
[8] Alex Biryukov and Khovratovich, D.: Related-Key Cryptanalysis of the Full AES-192 and AES-256. In Matsui, M., ed.: Asiacrypt. LNCS 5912, Springer, 1-18, 2009.
[9] Alex Biryukov, Khovratovich, D., Nikolic, I. Distinguisher and Related-Key Attack on the Full AES-256. Advances in Cryptology - Crypto 2009. LNCS 5677. Springer, 231-249, 2009.
[10] Patrick Derbez, Pierre-Alain Fouque and Jeremy Jean. Improved Key Recovery Attacks on Reduced-Round AES in the Single-Key Setting. Advances in Cryptology - Eurocrypt 2011. LNCS 7881. Springer, 371-387, 2011.
[11] Alex Biryukov and Dmitry Khovratovich. Feasible Attack on the 13-round AES-256. 2010.
[12] Andrey Bogdanov, Dmitry Khovratovich, and Christian Rechberger. Biclique Cryptanalysis of the Full AES. Advances in Cryptology - Asiacrypt 2011. LNCS 7073, Springer, 344-371, 2011.
[13] Daniel Bernstein and Tanja Lange. Non-uniform cracks in the concrete: the power of free precomputation. Advances in Cryptology - Asiacrypt. LNCS 8270. Springer, 321-340, 2013.
[14] Orr Dunkelman, Nathan Keller, Adi Shamir. Improved Single-Key Attacks on 8-round AES. Cryptology ePrint Archive, Report 2010:322, 2010.
http://eprint.iacr.org/2010/322.pdf
[15] Jon Passki and Tom Ritter. An Adaptive-Ciphertext Attack against I ⊕ C Block Cipher Modes with Oracle. IACR Cryptology ePrint Archive 2012:292, 2012.
http://eprint.iacr.org/2012/292.pdf http://ritter.vg/blog- separator_oracle.html
[16] Horst Feistel. Cryptography and Computer Privacy. Scientific American. 228, No. 5, 15-23, 1973.
[17] Clark Robinson. Dynamical Systems Stability, Symbolic Dynamics, and Chaos. CRC Press. 1995.
[18] Dake. Image of SHA-1 avalanche effect.
http://commons.wikimedia.Org/wiki/File:Sha1_avalanche_effect.png#
[19] Xuejia Lai. Higher Order Derivatives and Differential Cryptanalysis. In Communications and Cryptography: Two Sides of One Tapestry, R.E. Blahut et al., eds., Kluwer Adademic Publishers, 227-233, 1994.
[20] Ming Duan, Xuejia Lai, Mohan Yang, Xiaorui Sun and Bo Zhu. Distinguishing Properties of Higher Order Derivatives of Boolean Functions. IACR Cryptology ePrint. 2010. https://eprint.iacr.org/2010/417.pdf.
[21] NIST. FIPS-180-4. Secure Hash Standard, March 2012.
http://csrc.nist.gov/publications/fips/fips180-4/fips-180-4.pdf
[22] John Hennessy, David Patterson. Computer Architecture. 5th Edition, Morgan Kaufmann, 2012.
[23] NIST. FIPS-180-2: Secure Hash Standard, August 2002.
http://www.itl.nist.gov/fipspubs/.
[24] Alan M. Turing. On computable numbers, with an application to the Entscheidungsproblem. Proc. London Math. Soc. Series 2 42 (Parts 3 and 4), 230-265, 1936.
[25] Andre Stefanov, Nicolas Gisin, Olivier Guinnard, Laurent Guinnard, and Hugo Zbinden. Optical quantum random number generator. Journal of Modern Optics, 47(4):595 598, 2000.
[26] Mario Stipcevic and B. Medved Rogina. Quantum random number generator based on photonic emission in semiconductors. Review of Scientific Instruments. 78, 045104: 1-7, 2007.
[27] A. A. Abbott, С.S. Calude, J. Conder & К. Svozil. Strong Kochen-Specker theorem and incomputability of quantum randomness. Physical Review A. 86 062109, 1-11, 2012.
[28] John Conway and Simon Kochen. The Strong Free Will Theorem. Notices of the American Mathematical Society. 56 (2), 226-232, February 2009.
[29] Simon Kochen and Ernst P. Specker. The Problem of Hidden Variables in Quantum Mechanics. Journal of Mathematics and Mechanics (now Indiana Univ. Math Journal) 17 No. 1, 59-87, 1967.
[30] Klint Finley. Chinese Supercomputer Is Still the Worlds Most Powerful. Wired Magazine. Nov. 18, 2013.
[31] Daniel Bernstein. Curve25519: new Diffie-Hellman speed records. Public Key Cryptography. LNCS 3958. New York, Springer. 207-228, 2006.
http://cr.yp.to/ecdh/curve25519-20060209.pdf
[32] Stephen Cook. The P VS NP Problem,
http://www.claymath.org/sites/default/files/pvsnp.pdf
[33] A.F. Webster and S.E. Tavares. On the Design of S-Boxes. Advances in Cryptology. CRYPTO 85 Proceedings. LNCS 218. Springer, 523-534, 1986.
[34] Guido Bertoni, Joan Daemen, Michael Peeters, Gilles Van Assche. Keccak Reference 3.0 2011.
http://keccak.noekeon.org/http://en.wikipedia.org/wiki/Keccak
[35] Jean-Philippe Aumasson, Samuel Neves, Zooko Wilcox-O'Hearn, Christian Winnerlein. BLAKE.
https://131002.net/blake/http://en.wikipedia.org/wiki/BLAKE_(hash_function)
[36] Praveen Gauravaram, Lars Knudsen, Krystian Matusiewicz, Florian Mendel, Christian Rechberger, Martin Schlffer, and Sren S. Thomsen. Grstl a SHA-3 candidate.
http://www.groestl.info http://www.groestl.info/Groestl.pdf
[37] HongjunWu. The Hash Function JH. 2011.
http://ehash.iaik.tugraz.at/wiki/JH http://www3.ntu.edu.sg/home/wuhj/research/jh/jh_round3.pdf
[38] Niels Ferguson, Stefan Lucks, Bruce Schneier, Doug Whiting, Mihir Bellare, Tadayoshi Kohno, Jon Callas, Jesse Walker. The Skein Hash Function Family. 2010.
https://www.schneier.com/skein1.3.pdf http://en.wikipedia.org/wiki/Skein_(hash_function)
[39] Ross Anderson, Eli Biham, Lars Knudsen. A Proposal for the Advanced Encryption Standard.
http://www.cl.cam.ac.uk/~rja14/Papers/serpent.pdf http://www.cl.cam.ac.uk/~rja14/serpent.html
[40] Claude Shannon. A universal Turing machine with two internal states. Automata Studies, C.E. Shannon and J. McCarthy (eds.). Princeton University Press, 129-153, 1956.
[41] Yiannis N. Moschovakis. What is an algorithm? In Mathematics Unlimited 2001 and beyond (eds. B. Engquist and W. Schmid), Springer. 919-936, 2001.
[42] Yiannis N. Moschovakis. Algorithms and Implementations. Tarski Lecture 1, March 3, 2008.
http://www.math.ucla.edu/~ynm/lectures/tlectl.pdf
[43] Yuri Gurevich. What is an algorithm? In SOFSEM: Theory and Practice of Computer Science (eds. M. Bielikova et al.), LNCS 7147. Springer. 31-42, 2012.
http://research.microsoft.com/pubs/155608/209-3.pdf
http://link.springer.com/chapter/10.1007%2F978-3-642-27660-6_3#page-1
[44] Michael S. Fiske. Turing Incomputable Computation. Turing-100 Proceedings. Alan Turing Centenary. EasyChair 10, 69-91, 2012.
http://www.aemea.org/Turing100.
[45] Michael S. Fiske. Quantum Random Active Element Machine. UCNC 2013 Proceedings. LNCS 7956, 252-254, Springer, 2013.
http://www.aemea.org/UCNC2013.
[46] Daniel Bernstein. Cache-timing attack on AES. 2005.
http://cr.yp.to/antiforgery/cachetiming-20050414.pdf
[47] Dmitry Khovratovich, Christian Rechberger and Alexandra Savelieva. Bicliques for Preimages: Attacks on Skein-512 and the SHA-2 family. FSE, 244-263, 2012.
[48] E. Biham and Adi Shamir. Differential Cryptanalysis of DES-like Cryptosystems. Advances in Cryptology. CRYPTO 90 Proceedings. LNCS 537. Springer, 2-21, 1990.
[49] Xuejia Lai. Higher Order Derivatives and Differential Cryptanalysis. In Communications and Cryptography: Two Sides of One Tapestry, R.E. Blahut et al., eds., Kluwer Adademic Publishers, 227-233, 1994.
[50] L. Knudsen. Truncated and higher order differentials. In Fast Software Encryption. Springer, 196-211, 1995.
[51] Jialin Huang and Xuejia Lai. What is the Effective Key Length for a Block Cipher: an Attack on Every Block Cipher. Science China Information Sciences. 57, Issue 7, Springer, 1-11, 2014.
[52] Fouz Sattar and Muid Mufti. Spectral Characterization and Analysis of Avalanche in Cryptographic Substitution Boxes using Walsh-Hadamard Transformations. International Journal of Computer Applications. 28 No.6. August 2011.
[53] Michael Stephen Fiske. Non-autonomous Dynamical Systems Applicable to Neural Computation. Northwestern University. 1996.
[54] Mike Spivak. Differential Geometry. Volume I. Publish or Perish, Inc. 1979.
[55] Nathan Jacobson. Basic Algebra I. W.H. Freeman and Company. 1985.
[56] Neil Koblitz. Introduction to Elliptic Curves and Modular Forms. Springer-Verlag 1984.
[57] Joseph Silverman and John Tate. Rational Points on Elliptic Curves. Springer-Verlag 1992.
[58] Peter L. Montgomery. Speeding the Pollard and elliptic curve methods of factorization. Mathematics of Computation 48, 243-264, 1987.
http://cr.yp.to/bib/entries.html#1987/montgomery.
| название | год | авторы | номер документа |
|---|---|---|---|
| КОМАНДА НА ШИФРОВАНИЕ СООБЩЕНИЯ С АУТЕНТИФИКАЦИЕЙ | 2017 |
|
RU2727152C1 |
| Повышение неоднозначности | 2016 |
|
RU2737917C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОБЕСПЕЧЕНИЯ ЗАЩИТЫ В СИСТЕМЕ ОБРАБОТКИ ДАННЫХ | 2002 |
|
RU2333608C2 |
| УПРАВЛЕНИЕ КОНФИДЕНЦИАЛЬНОЙ СВЯЗЬЮ | 2016 |
|
RU2718689C2 |
| СПОСОБ И СИСТЕМА ДЛЯ МАРКИРОВКИ ГОТОВЫХ ИЗДЕЛИЙ С ЦЕЛЬЮ ОБНАРУЖЕНИЯ НЕСАНКЦИОНИРОВАННОГО ПОВТОРНОГО ЗАПОЛНЕНИЯ | 2015 |
|
RU2787209C2 |
| СПОСОБ И СИСТЕМА ДЛЯ МАРКИРОВКИ ГОТОВЫХ ИЗДЕЛИЙ С ЦЕЛЬЮ ОБНАРУЖЕНИЯ НЕСАНКЦИОНИРОВАННОГО ПОВТОРНОГО ЗАПОЛНЕНИЯ | 2015 |
|
RU2698768C2 |
| ЗАЩИТА ОТ ПАССИВНОГО СНИФФИНГА | 2011 |
|
RU2579990C2 |
| АУТЕНТИФИКАЦИЯ В ЗАЩИЩЕННОЙ КОМПЬЮТЕРИЗОВАННОЙ ИГРОВОЙ СИСТЕМЕ | 2003 |
|
RU2302276C2 |
| СПУТНИКОВЫЕ РАДИОНАВИГАЦИОННЫЕ СИГНАЛЫ С ЦИФРОВОЙ ПОДПИСЬЮ | 2014 |
|
RU2635368C2 |
| СПОСОБ ОБЕСПЕЧЕНИЯ БЕЗОПАСНОСТИ ИГРОВЫХ УСТРОЙСТВ И ИГРОВОЕ УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2310907C1 |
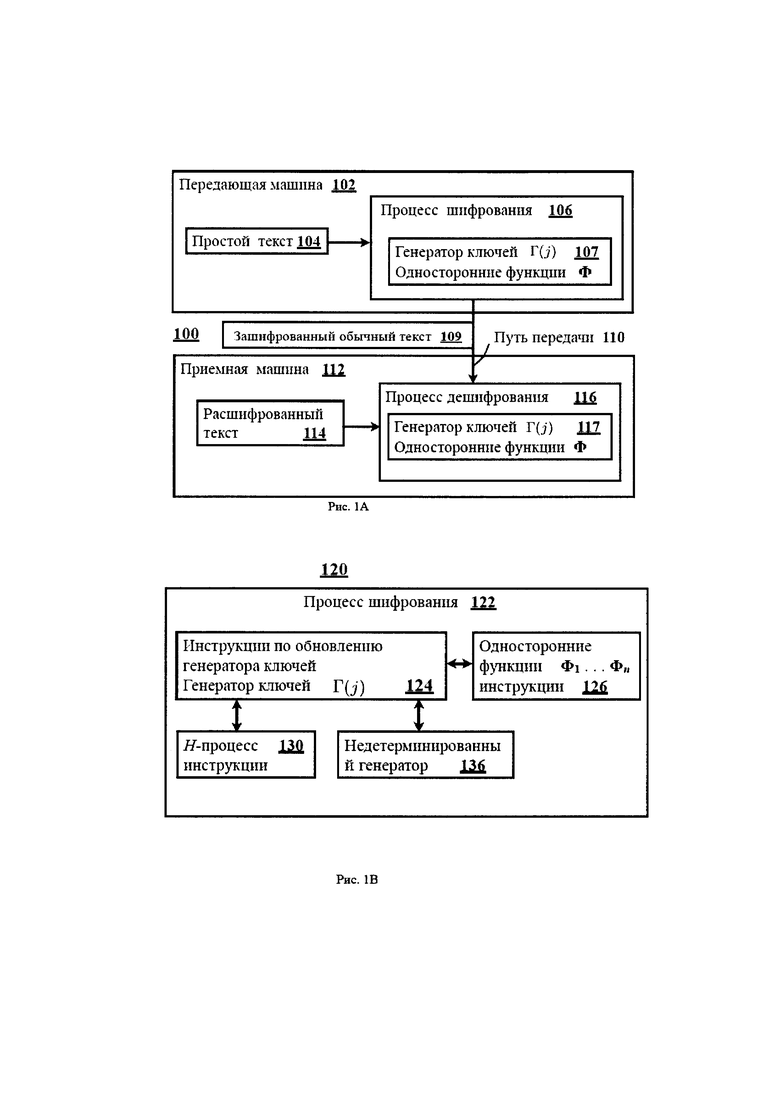
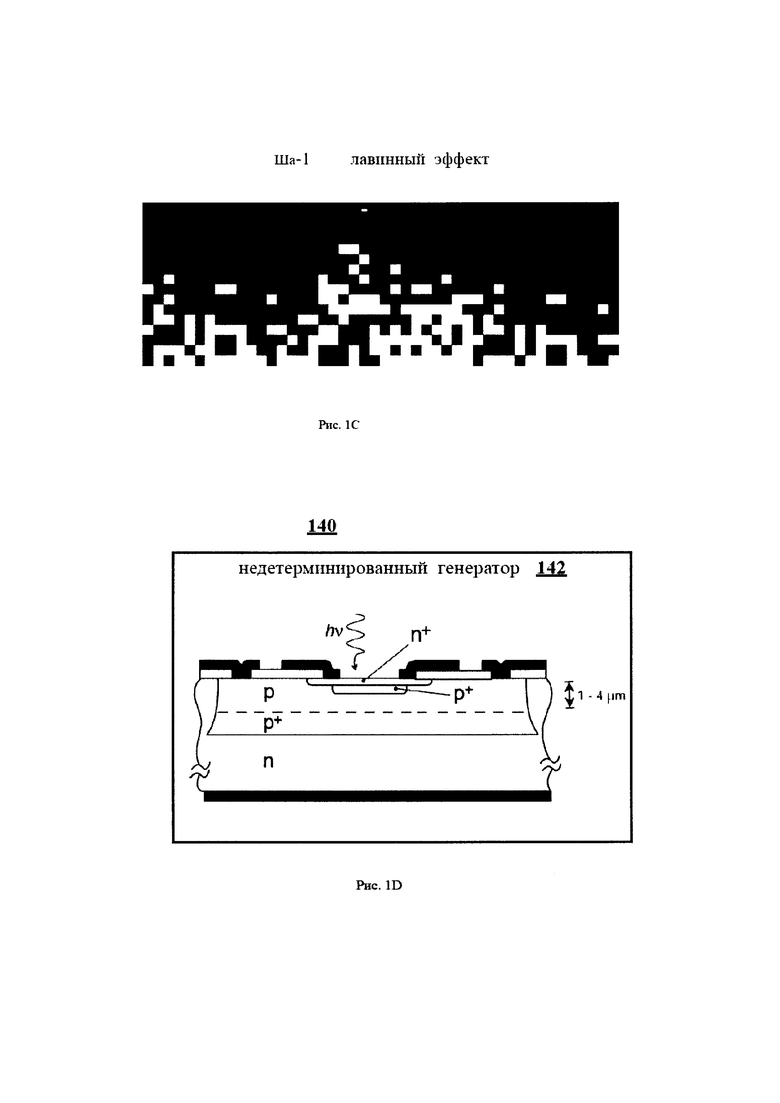

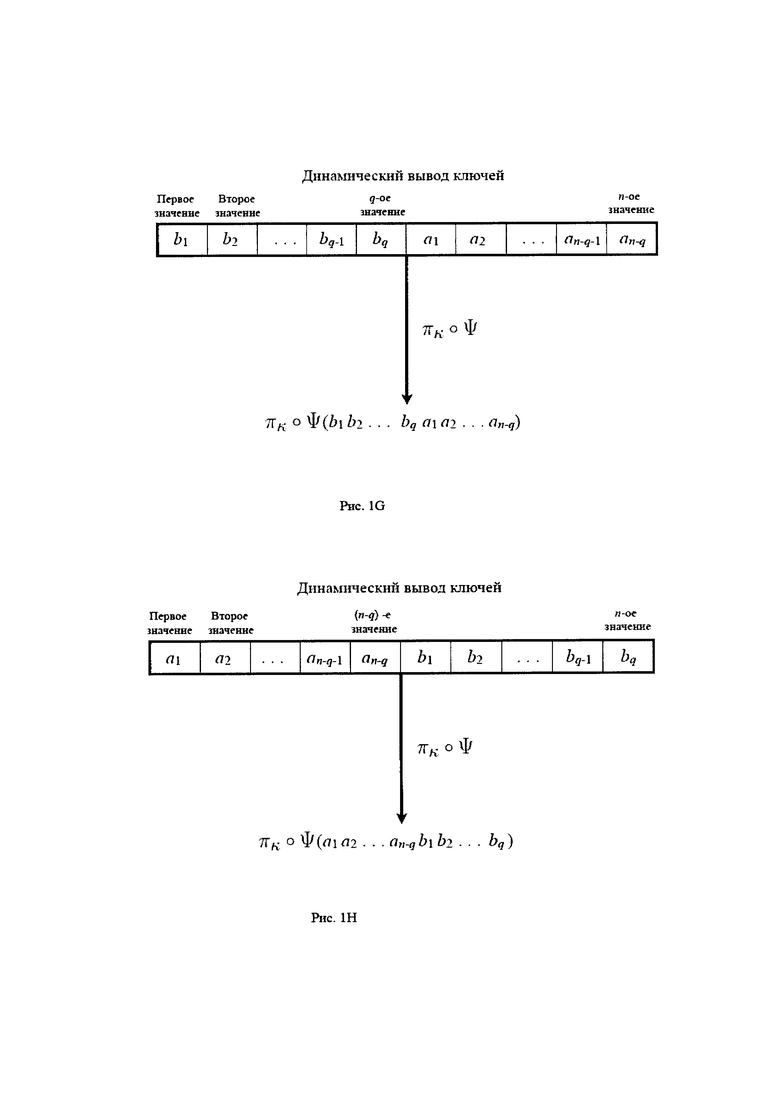
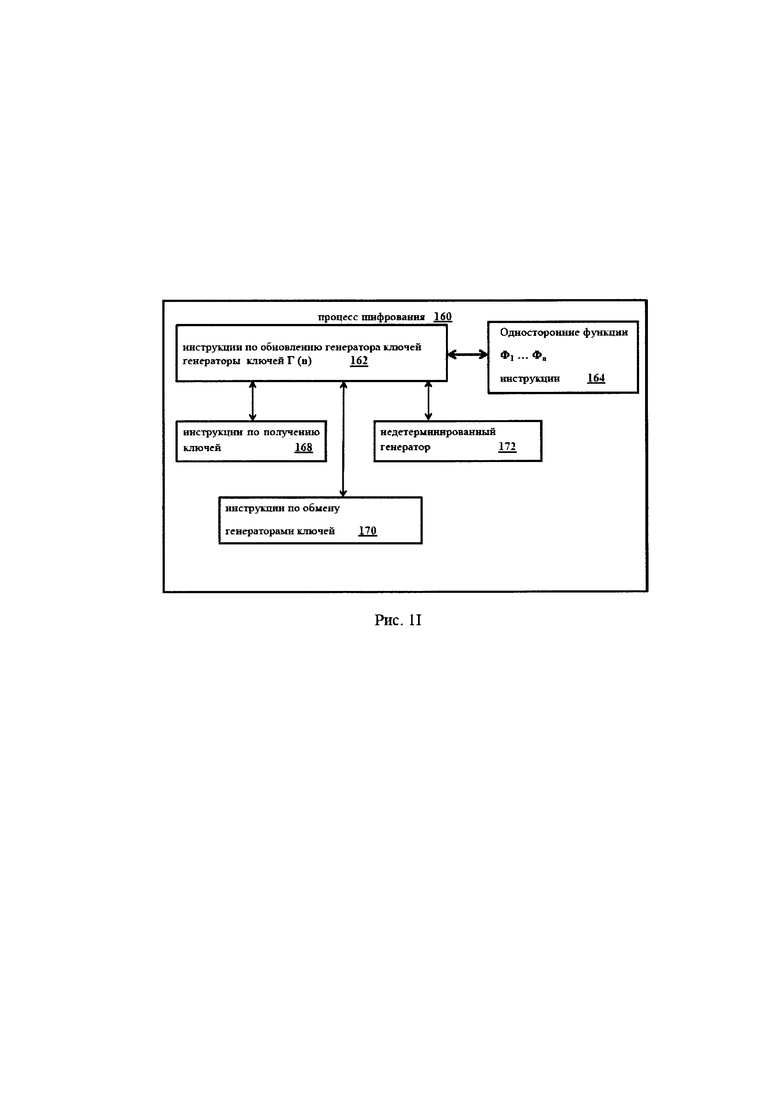
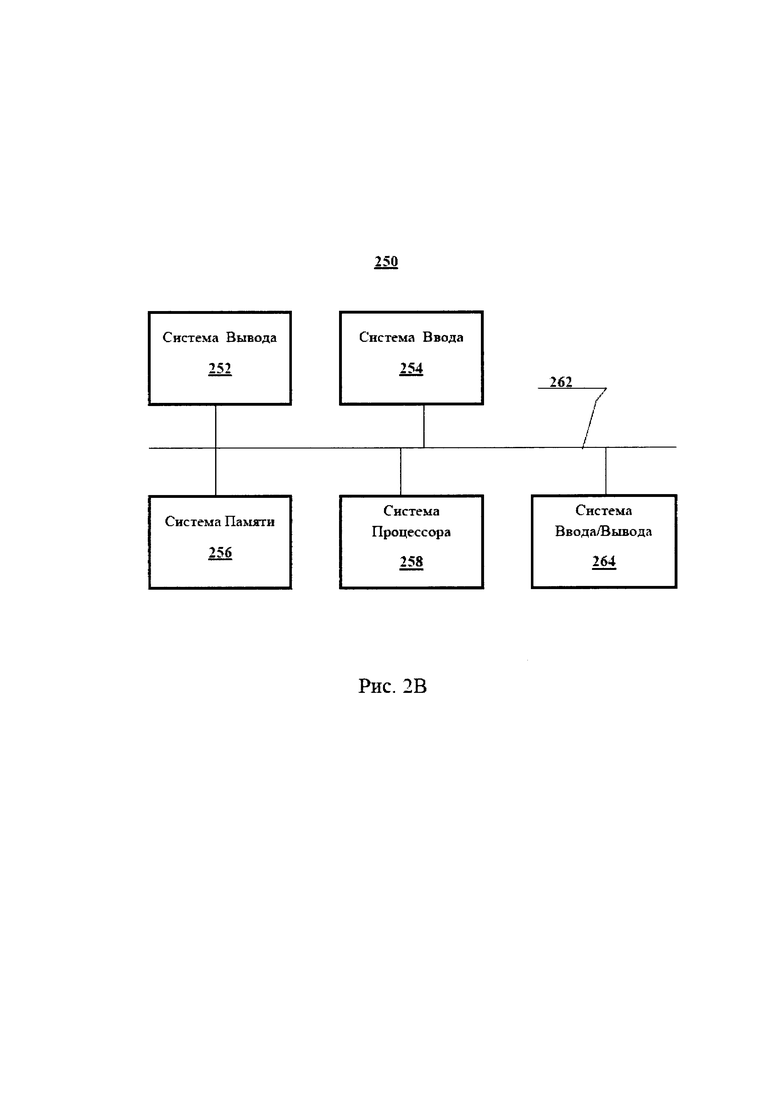


Изобретение относится к симметричной криптографии для шифрования и расшифровки информации. Технический результат – повышение эффективности шифрования информации. Способ для шифрования информации включает в себя шифрование одного или нескольких блоков информации сообщения при помощи блочного шифра на основании первого ключа, получение первого ключа из генератора первого ключа, обновление указанного генератора первого ключа, на основании функции для вычисления генератора второго ключа, при котором обновление не изменяет, как минимум, часть генератора ключей, получение второго ключа из генератора второго ключа, шифрование одного или нескольких блоков информации сообщения при помощи блочного шифра на основании второго ключа, при котором в процессе получения первого ключа односторонняя функция применяется как к первым, так и ко вторым частям генератора первого ключа, и при котором размер первого ключа меньше, чем размер генератора первого ключа. 4 н. и 10 з.п. ф-лы, 16 ил.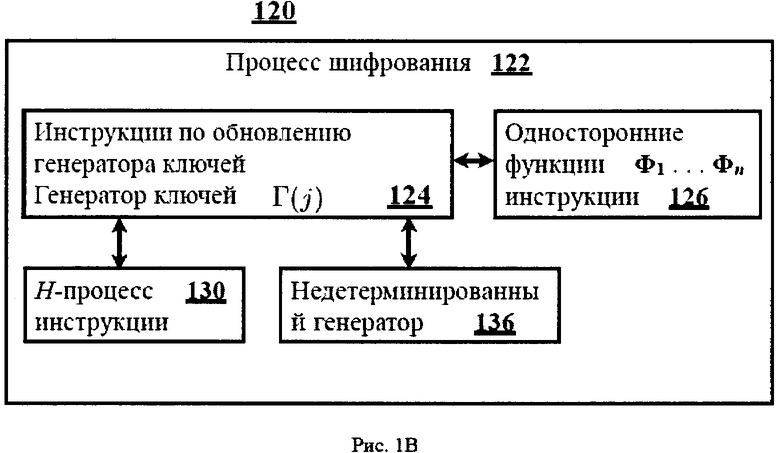
1. Способ, реализованный с помощью криптографического устройства, для шифрования информации, включающий в себя шифрование (106, 122, 160) одного или нескольких блоков информации сообщения при помощи блочного шифра на основании первого ключа;
получение (155, 158, 168) первого ключа (156, 159) из генератора первого ключа (107,117,124,154,157,162);
обновление указанного генератора первого ключа (107, 117, 124, 150, 151, 152, 153, 162), на основании функции (107, 117, 126, 164) для вычисления генератора второго ключа (107, 117, 124, 150, 151, 152, 153, 162);
при котором обновление не изменяет, как минимум, часть генератора ключей (151, 153);
получение (155, 158, 168) второго ключа (156, 159) из генератора второго ключа (107, 117, 124, 154, 157, 162);
шифрование (106, 122, 160) одного или нескольких блоков информации сообщения при помощи блочного шифра на основании второго ключа;
при котором в процессе получения первого ключа односторонняя функция (107, 117, 126, 155, 158, 164) применяется как к первым, так и ко вторым частям (150, 151, 152, 153, 154, 157) генератора первого ключа;
и при котором размер первого ключа меньше, чем размер генератора первого ключа.
2. Способ по п. 1, при котором в ходе указанного обновления оставшаяся часть генератора первого ключа (107, 117, 124, 150, 152, 162) изменяется, как минимум, частично при применении односторонней функции хеширования (107, 117, 126, 155, 158, 164) или односторонней функции прообраза (107,117, 126, 155, 158, 164).
3. Способ по п. 2, при котором указанные односторонние функции (107, 117, 126, 155, 158, 164) требуют как минимум 264 шагов для вычисления точки прообраза или как минимум 264 шагов для вычисления, чтобы определить наложение.
4. Способ по п. 1, 2 или 3, при котором в процессе получения второго ключа односторонняя функция (107, 117, 126, 155, 158, 164) применяется как к первым, так и ко вторым частям (150, 151, 152,153, 154, 157) генератора второго ключа;
и при котором размер второго ключа меньше, чем размер генератора второго ключа.
5. Система (210, 214, 216, 218, 220, 250) шифрования информации, которая включает в себя
шифрование (106, 122, 160) одного или нескольких блоков информации сообщения при помощи блочного шифра на основании первого ключа;
получение (155, 158, 168) первого ключа (156, 159) из генератора первого ключа (107, 117, 124, 154, 157, 162);
обновление указанного генератора первого ключа (107, 117, 124, 150, 151, 152, 153, 162), на основании функции (107, 117, 126, 164) для вычисления генератора второго ключа (107, 117, 124, 150, 151, 152, 153, 162);
при котором обновление не изменяет, как минимум, часть генератора ключей (151, 153);
получение (155, 158, 168) второго ключа (156, 159) из генератора второго ключа (107, 117, 124, 154, 157, 162);
шифрование (106, 122, 160) одного или нескольких блоков информации сообщения при помощи блочного шифра на основании второго ключа;
при котором в процессе получения первого ключа односторонняя функция (107, 117, 126, 155, 158, 164) применяется как к первым, так и ко вторым частям (150, 151, 152, 153, 154, 157) генератора первого ключа;
и при котором размер первого ключа меньше, чем размер генератора первого ключа.
6. Система (210, 214, 216, 218, 220, 250) по п. 5, при котором в ходе указанного обновления оставшаяся часть генератора первого ключа (107, 117, 124, 150, 152, 162) изменяется, как минимум, частично при применении односторонней функции хеширования (107, 117, 126, 155, 158, 164) или односторонней функции прообраза (107, 117, 126, 155, 158, 164).
7. Система (210, 214, 216, 218, 220, 250) по п. 5 или 6, при котором указанные односторонние функции (107, 117, 126, 155, 158, 164) требуют, как минимум, 264 шагов для вычисления точки прообраза или, как минимум, 264 шагов для вычисления, чтобы определить наложение.
8. Способ шифрования по п. 1, при котором указанный генератор первого ключа (107, 117, 124, 162) создается на основании недетерминированного процесса (142, 172), который использует фотоны.
9. Способ шифрования по п. 1, при котором указанная односторонняя функция (107, 117, 126, 155, 158, 164), которая используется при получении первого ключа требует, как минимум, 264 шагов для определения точки прообраза.
10. Способ обновления генератора ключей, реализованный с помощью устройства, включающий в себя:
обновление генератора первого ключа (107, 117, 124, 154, 157, 162), в процессе которого в результате получается генератор второго ключа (107, 117, 124, 154, 157, 162);
генератор первого ключа (107, 117, 124, 154, 157, 162) представляет собой первый набор значений;
генератор второго ключа (107, 117, 124, 154, 157, 162) представляет собой второй набор значений;
при котором в процессе обновления, как минимум, часть генератора первого ключа (107, 117, 124, 151, 153, 162) не изменяется;
при котором в процессе обновления ко второй части генератора первого ключа применяется односторонняя функция (107, 117, 124, 150, 152, 162);
получение первого ключа (156, 159) из генератора первого ключа (107, 117, 124; 154, 157, 162);
при котором первый ключ представляет собой третье значение или третий набор значений;
получение второго ключа (156, 159) из генератора второго ключа (107, 117, 124, 154, 157, 162);
при котором второй ключ представляет собой четвертое значение или четвертый набор значений;
при котором в процессе получения первого ключа односторонняя функция (107, 117, 126, 155, 158, 164) применяется как к первым, так и ко вторым частям генератора первого ключа;
и при котором количество значений первого ключа меньше, чем количество значений в генераторе первого ключа.
11. Способ по п. 10, при котором обновление использует, как минимум, функцию обновления (107, 117, 126, 150, 152);
функция (107, 117, 126, 150, 152) принимает комбинацию значений в качестве вводных данных;
комбинация значений вводных данных может иметь различные длины;
функция (107, 117, 126, 150, 152) вычисляет в качестве выходного результата комбинацию значений;
комбинация значений выходного результата имеет фиксированную, предварительно определенную длину;
функция (107, 117, 126, 150, 152) может быть вычислена при помощи машины Тьюринга, у которой это займет не более указанного количества шагов вычисления;
указанное количество вычисляется с помощью полиномиальной функции с длиной в комбинацию вводных данных.
12. Способ по п. 10 или 11, при котором для какой-либо машины Тьюринга, которая имеет не более первого указанного числа состояний машины, и не более второго указанного числа символов на ленте, вероятность при максимальном 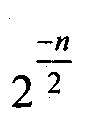 того, что машина Тьюринга может определить полиномиальное число шагов вычисления, как функцию от n, комбинацию вводных данных, которая привела в результате к комбинации результатов обновляющейся функции (107, 117, 126, 150, 152), не имея комбинации вводных данных, где n - это размер комбинации вводных данных, которую пытается найти машина Тьюринга.
того, что машина Тьюринга может определить полиномиальное число шагов вычисления, как функцию от n, комбинацию вводных данных, которая привела в результате к комбинации результатов обновляющейся функции (107, 117, 126, 150, 152), не имея комбинации вводных данных, где n - это размер комбинации вводных данных, которую пытается найти машина Тьюринга.
13. Способ по пп. 10, 11 или 12, который далее включает в себя;
при котором в процессе получения (155, 158, 168) второго ключа односторонняя функция (107, 117, 126, 155, 158, 164) применяется как к первым, так и ко вторым частям генератора второго ключа;
и при котором количество значений второго ключа меньше, чем количество значений в генераторе второго ключа.
14. Система обновления генератора ключей (210, 214, 216, 218, 220, 250), которая включает в себя процессор для обновления,
обновление генератора первого ключа (107, 117, 124, 154, 157, 162), в процессе которого в результате получается генератор второго ключа (107, 117, 124, 154, 157, 162);
генератор первого ключа (107, 117, 124, 154, 157, 162) представляет собой первый набор значений;
генератор второго ключа (107, 117, 124, 154, 157, 162) представляет собой второй набор значений;
при котором в процессе обновления, как минимум, часть генератора первого ключа (107, 117, 124, 151, 153, 162) не изменяется;
при котором в процессе обновления ко второй части генератора первого ключа применяется односторонняя функция (107, 117, 124, 150, 152, 162);
получение первого ключа (156, 159) из генератора первого ключа (107, 117, 124, 154, 157, 162);
при котором первый ключ представляет собой третье значение или третий набор значений;
получение второго ключа (156, 159) из генератора второго ключа (107, 117, 124, 154, 157, 162);
при котором второй ключ представляет собой четвертое значение или четвертый набор значений;
при котором в процессе получения первого ключа односторонняя функция (107, 117, 126, 155, 158, 164) применяется как к первым, так и ко вторым частям генератора первого ключа;
и при котором количество значений первого ключа меньше, чем количество значений в генераторе первого ключа.
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| Пресс для выдавливания из деревянных дисков заготовок для ниточных катушек | 1923 |
|
SU2007A1 |
| Многоступенчатая активно-реактивная турбина | 1924 |
|
SU2013A1 |
| СПОСОБ АДАПТИВНОГО ПОТОЧНОГО ШИФРОВАНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2329544C2 |
Авторы
Даты
2019-06-11—Публикация
2015-09-28—Подача