Изобретение относится к цифровой вычислительной технике и предназначено для автоматического преобразования произвольной Булевой функции, зависящей от n аргументов, к полиномиальной нормальной форме - к полиному Жегалкина или к полиномам Рида - Маллера с фиксированной полярностью (positive-polarity Reed-Muller expressions - PPRM).
Наиболее близким по технической сути является широко известный регистр сдвига, смотри, например, [Новожилов О.П. Основы цифровой техники. - М: ИП РадиоСофт, 2004. - 528 с.].
Данный регистр сдвига состоит из нескольких последовательно расположенных однотипных секций, выходы которых являются параллельным выходом регистра сдвига, причем выход каждой предшествующей секций соединен с первым входом последующей секции, первый вход первой секции и выход последней секции не подключены ни к одной из цепей, вторые входы секций объединены между собой и подключены к входу сигнала сброса регистра сдвига, третьи входы секций объединены между собой и подключены к входу сигнала синхронизации, при этом каждая секция содержит синхронный JK-триггер и один инвертор, преобразующий JK-триггер в синхронный D-триггер.
Данный регистр сдвига реализует несколько операций: установка в нулевое состояние всех триггеров регистра; последовательный синхронный прием входных данных при их подаче на первый вход первой секции регистра; хранение принятых данных, которые могут быть считаны параллельно со всех выходов регистра или последовательно с выхода последней секции регистра.
Изобретение направлено на расширение функциональных возможностей регистра сдвига за счет реализации дополнительной операции, обеспечивающей возможность автоматического преобразования произвольной Булевой функции, зависящей от n аргументов, к полиномиальной нормальной форме - к полиному Жегалкина или к полиномам Рида - Маллера с фиксированной полярностью (positive-polarity Reed-Muller expressions - PPRM).
Это достигается тем, что в каждую регистровую секцию 1,2 дополнительно вводится схема управления режимами работы JK-триггера, содержащая элемент ИЛИ 4, два элемента И 5,6 и второй инвертор 7, вход первого инвертора 8 подключен к первому входу первого элемента И 5 и четвертому входу 1.5 регистровой секции, выход инвертора 8 подключен к второму входу второго элемента И 6, первый вход которого подключен к входу второго инвертора 7, к входу J триггера и первому входу 1.2 регистровой секции, выход первого инвертора 7 подключен к второму входу первого элемента И 5, выход которого подключен к первому входу элемента ИЛИ 4, второй вход которого подключен к выходу второго элемента И 6, а выход элемента ИЛИ 4 подключен к входу K триггера, вход С которого подключен к третьему входу 1.4 регистровой секции, а вход R триггера подключен к второму входу 1.3 регистровой секции, четвертые входы 1.5 и 2.5 всех регистровых секций соединены между собой и подключены к сигналу управления режимами работы JK-триггера.
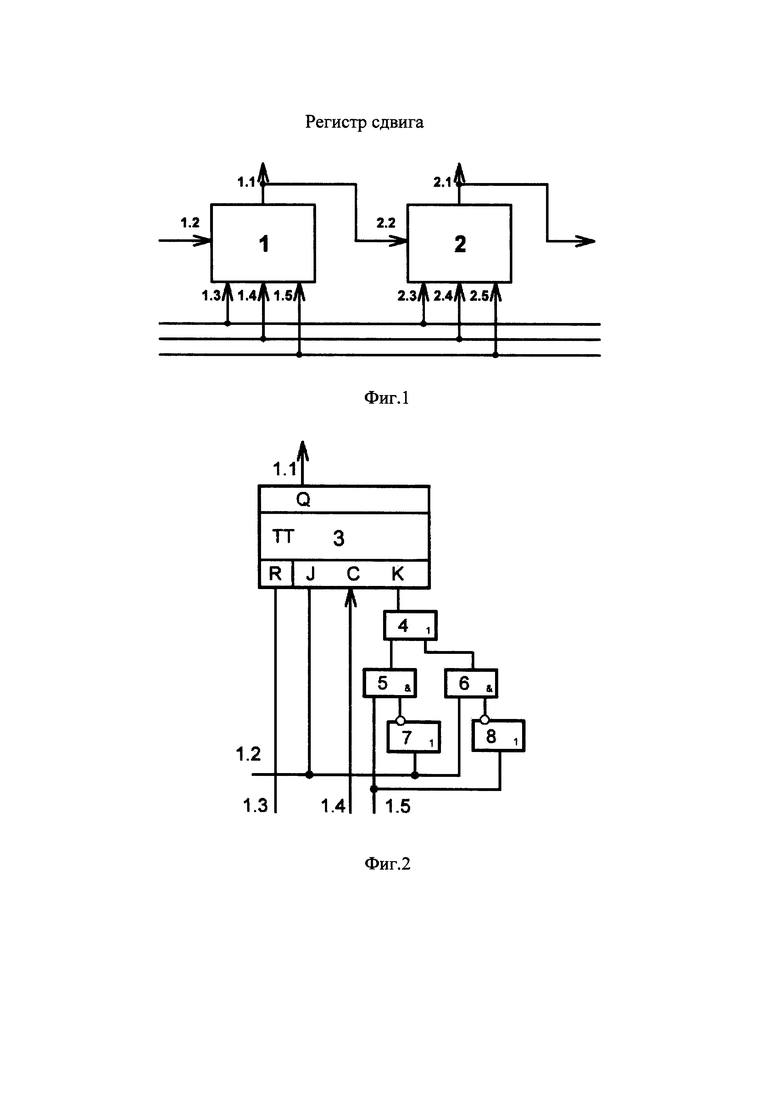
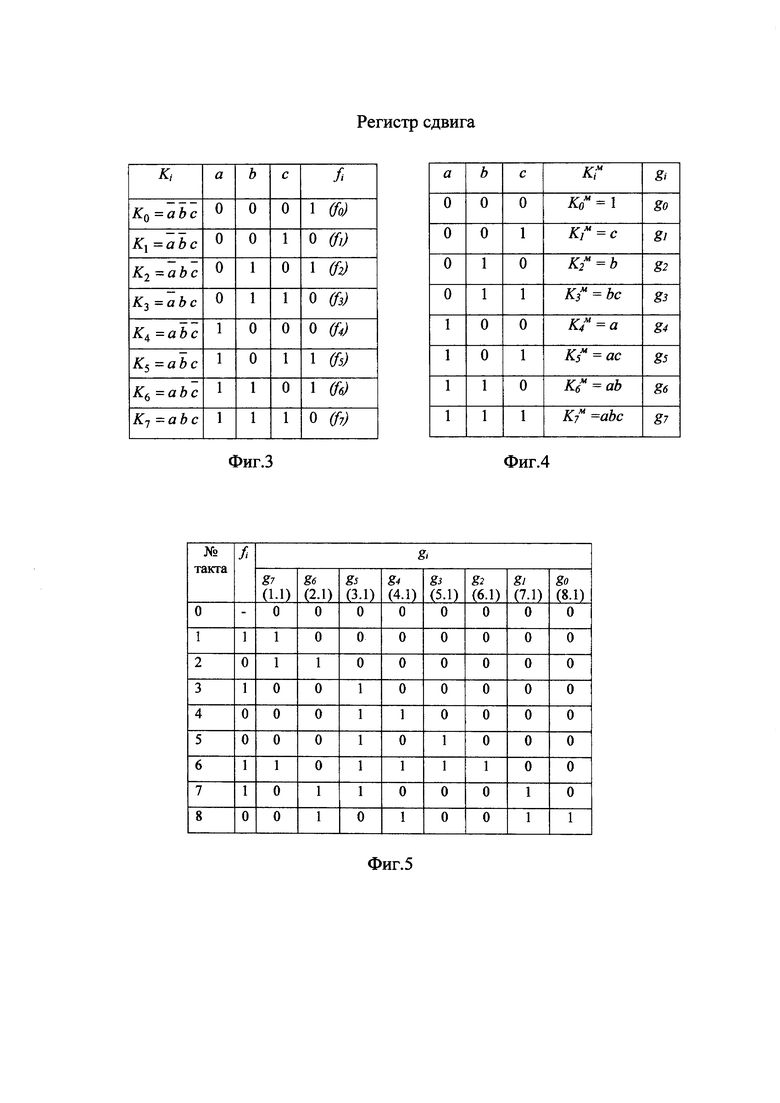
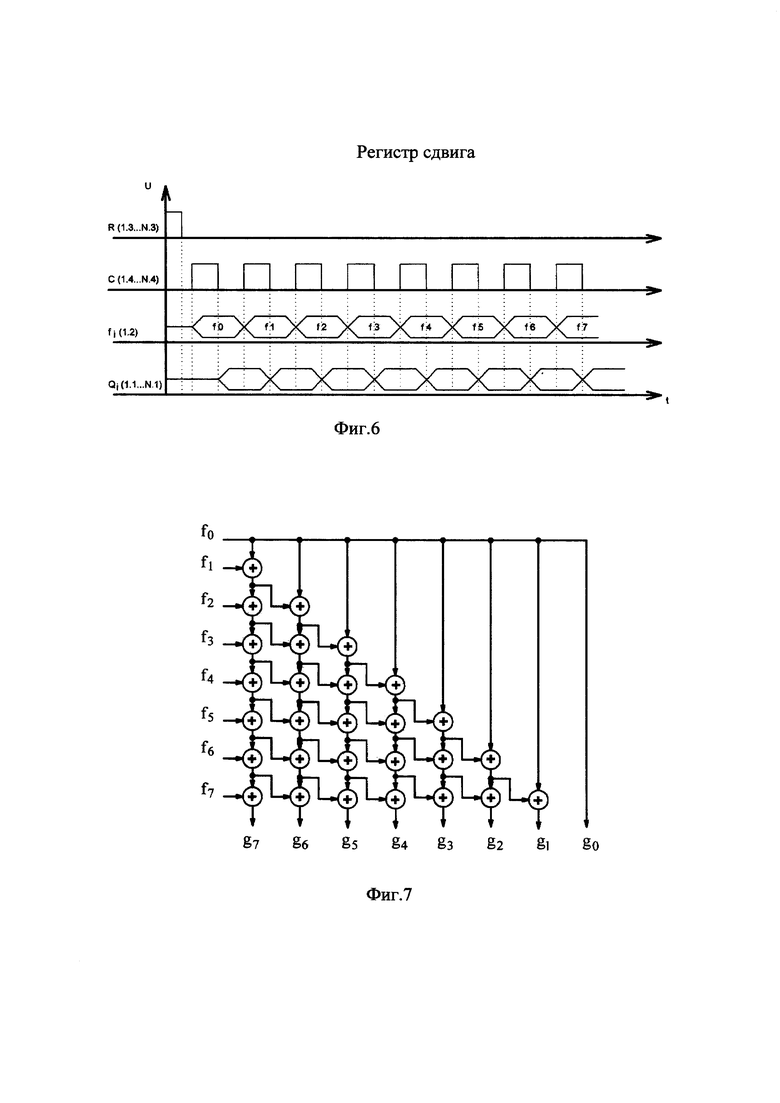
На фиг. 1 представлена структурная схема предлагаемого регистра сдвига; на фиг. 2 - функциональная схема регистровой секции. На фиг. 3 представлена таблица истинности некоторой Булевой функции F (а, b, с) и двоичное кодирование ее элементарных конъюнкций, а на фиг. 4 - монотонные конъюнкции функции F (а, b, с), их двоичное кодирование и соответствие коэффициентам полиномиальной формы. На фиг. 5 представлена таблица, иллюстрирующая процесс последовательного преобразования заявляемым регистром сдвига Булевой функции F (а, b, с) в полином Жегалкина (положительно поляризованный полином Рида - Маллера). На фиг. 6 представлена временная диаграмма работы заявляемого регистра сдвига в режиме полиномиального преобразования Булевой функции. На фиг. 7 представлена функциональная схема, реализующая последовательно-параллельные свертки по модулю два значений Булевой функции и являющаяся комбинационным эквивалентом заявляемого регистра сдвига при его работе в режиме полиномиального преобразования.
Регистр сдвига работает следующим образом. Если на входы 1.5, 2.5 … всех регистровых секций подается сигнал управления, равный логической единице (U=1), то JK - триггер будет функционировать как синхронный D-триггер. В этом режиме выполняются все прежние операции: установка в нулевое состояние всех триггеров регистра; последовательный синхронный прием входных данных при их подаче на первый вход первой секции регистра; хранение принятых данных, которые могут быть считаны параллельно со всех выходов регистра или последовательно с выхода последней секции регистра. Если же на входы 1.5, 2.5 … всех регистровых секций подается сигнал управления, равный логическому нулю (U=0), то JK-триггер будет функционировать как синхронный Т-триггер, а регистр сдвига - как полиномиальный преобразователь произвольной Булевой функции, битовые значения которой последовательно подают на первый вход 1.1 первой секции. Для полиномиального преобразования Булевой функции, зависящей от n аргументов, потребуется 2n регистровых секций и 2n рабочих такта. При этом каждая регистровая секция трансформируется в накапливающий сумматор по модулю 2 (⊕), то есть каждая регистровая секция реализует следующее логическое выражение:

где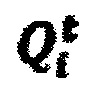 - текущее логическое значение на выходе i-го триггера;
- текущее логическое значение на выходе i-го триггера;
 - текущее логическое значение на выходе (i-1)-го триггера;
- текущее логическое значение на выходе (i-1)-го триггера;
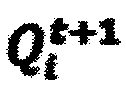 - следующее логическое значение на выходе i-го триггера.
- следующее логическое значение на выходе i-го триггера.
Из соотношения (1) следует, что во втором режиме работы при U=0 регистр сдвига преобразуется в специфический синхронный счетчик, в котором после установки этого счетчика в ноль в каждой i-ой его секции определяется четное или нечетное количество единичных значений, которое принимал выход (i-1)-ой секции на некотором количестве тактов счета. Если количество входных для i-ой секции единичных значений было четным, то на выходе i-ой секции формируется логический ноль, а если количество входных для i-ой секции единичных значений было нечетным, то на выходе i-ой секции формируется логическая единица. Предлагаемое преобразование регистра сдвига позволяет его использовать как полиномиальный преобразователь произвольной Булевой функции, зависящей от n аргументов, к полиномиальной нормальной форме - к полиному Жегалкина или к полиномам Рида - Маллера с фиксированной полярностью (positive-polarity Reed-Muller expressions - PPRM).
Рассмотрим подробнее работу предлагаемого регистра сдвига в режиме полиномиального преобразователя.
Широко известно, например, (Акинин А.А., Акинина Ю.С., Подвальный С.Л., Тюрин С.В. Автоматизация полиномиального разложения булевых функций на основе метода неопределенных коэффициентов // Системы управления и информационные технологии. 2011. Т. 44. №2. С. 4-8.), что существуют следующие тождественные аналитические представления Булевых функций (БФ), зависящих от n переменных:
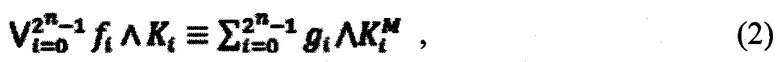
где 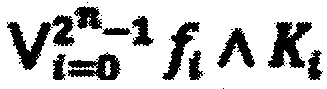 - совершенная дизъюнктивная нормальная форма БФ;
- совершенная дизъюнктивная нормальная форма БФ;
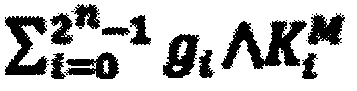 - полиномиальная нормальная форма;
- полиномиальная нормальная форма;
Λ - знак конъюнкции;
V - знак дизъюнкции;
Σ - знак суммы по модулю два;
ƒi - значение (0, 1) БФ на i-ом наборе аргументов;
Ki - элементарная конъюнкция максимального ранга на i-ом наборе аргументов;
gi - коэффициенты (0, 1) полиномиальной нормальной формы;
 - монотонная конъюнкция на i-ом наборе аргументов.
- монотонная конъюнкция на i-ом наборе аргументов.
С учетом (2) и данных, представленных на фиг. 3 и фиг. 4 для Булевой функции F (а, b, с), имеем:
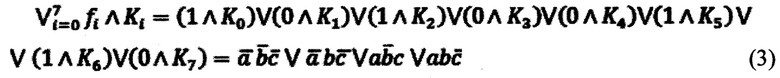
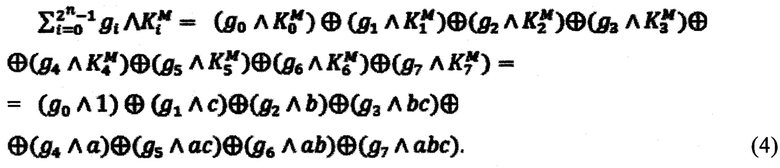
Из (4) следует, что для получения аналитического представления БФ в полиномиальной нормальной форме необходимо и достаточно определить значения коэффициентов gi. Именно такую задачу и решает предлагаемый регистр сдвига, работающий в режиме полиномиального преобразователя. На фиг. 5 поясняется работа заявляемого регистра сдвига, имеющего восемь секций и преобразующего Булеву функцию F (а, b, с), таблица истинности которой представлена на фиг. 3. На фиг. 6 показана временная диаграмма, соблюдение которой необходимо для корректной работы заявляемого регистра сдвига в режиме полиномиального преобразователя. Важным является и то, что значение коэффициента 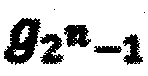 всегда формируется на выходе 1.1 первой регистровой секции.
всегда формируется на выходе 1.1 первой регистровой секции.
На основании данных, представленных на фиг. 5, имеем следующую полиномиальную форму (полином Жегалкина) для функции F (а, b, с):
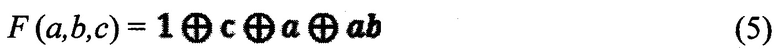
На фиг. 7 представлена функциональная схема, реализующая последовательно-параллельные свертки по модулю два значений Булевой функции и являющаяся комбинационным эквивалентом заявляемого регистра сдвига при его работе в режиме полиномиального преобразования. На основе анализа этого комбинационного эквивалента не трудно получить известную из дискретной математики систему уравнений, которую, по математической сути, реализует заявляемый регистр сдвига в режиме полиномиального преобразования Булевых функций:

Техническим результатом от использования заявляемого изобретения является дополнительная возможность простого решения задачи автоматического преобразования произвольной Булевой функции, зависящей от n аргументов, к полиномиальной нормальной форме с минимальными аппаратурными и временными затратами: требуется 2n регистровых секций и 2n тактов работы заявляемого регистра сдвига.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ | 2014 |
|
RU2541905C1 |
| Функциональный преобразователь | 1978 |
|
SU781822A1 |
| Устройство для вычисления булевых производных | 1988 |
|
SU1518825A2 |
| СПОСОБ ТЕСТОПРИГОДНОСТИ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ПРЕОБРАЗОВАТЕЛЕЙ | 2011 |
|
RU2497182C2 |
| ГЕНЕРАТОР СИГНАЛОВ, ИЗМЕНЯЮЩИХСЯ ПО БУЛЕВЫМ ФУНКЦИЯМ | 2010 |
|
RU2505849C2 |
| Устройство для преобразования булевых функций | 1988 |
|
SU1532946A1 |
| Магнитооптическое устройство для реализации дискретного преобразования Фурье | 1990 |
|
SU1795472A1 |
| ПОЛИНОМИАЛЬНЫЙ МОДУЛЯРНЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ С ОБНАРУЖЕНИЕМ ОШИБОК | 2015 |
|
RU2586574C1 |
| Устройство для решения булевых дифференциальных уравнений | 1989 |
|
SU1661791A1 |
| Функциональный преобразователь | 1983 |
|
SU1140130A1 |
Изобретение относится к цифровой вычислительной технике. Технический результат заключается в расширении функциональных возможностей регистра сдвига за счет возможности автоматического преобразования произвольной Булевой функции, зависящей от n аргументов, к полиномиальной нормальной форме - к полиному Жегалкина или к полиномам Рида - Маллера с фиксированной полярностью. Регистр сдвига состоит из нескольких последовательно расположенных однотипных секций, каждая секция содержит синхронный JK-триггер и один инвертор, в каждую регистровую секцию дополнительно вводится схема управления режимами работы JK-триггера, содержащая элемент ИЛИ, два элемента И и второй инвертор. 7 ил.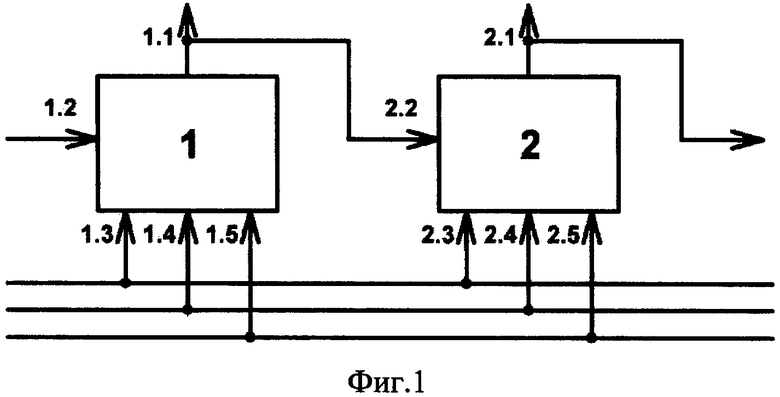
Регистр сдвига, состоящий из последовательно расположенных однотипных секций, выходы которых являются параллельным выходом регистра сдвига, причем выход каждой предшествующей секций соединен с первым входом последующей секции, первый вход первой секции и выход последней секции не подключены ни к одной из цепей, вторые входы секций объединены между собой и подключены к входу сигнала сброса регистра сдвига, третьи входы секций объединены между собой и подключены к входу сигнала синхронизации, при этом каждая секция содержит синхронный JK-триггер и один инвертор, отличающийся тем, что в каждую регистровую секцию дополнительно вводится схема управления режимами работы JK -триггера, содержащая элемент ИЛИ, два элемента И и второй инвертор, вход первого инвертора подключен к первому входу первого элемента И и четвертому входу регистровой секции, выход инвертора подключен к второму входу второго элемента И, первый вход которого подключен к входу второго инвертора, к входу J триггера и первому входу регистровой секции, выход первого инвертора подключен к второму входу первого элемента И, выход которого подключен к первому входу элемента ИЛИ, второй вход которого подключен к выходу второго элемента И, а выход элемента ИЛИ подключен к входу К триггера, вход С которого подключен к третьему входу регистровой секции, а вход R триггера подключен к второму входу регистровой секции, четвертые входы всех регистровых секций соединены между собой и подключены к сигналу управления режимами работы JK -триггера.
| Регистр сдвига | 1975 |
|
SU666583A1 |
| Реверсивный регистр сдвига | 1983 |
|
SU1140176A1 |
| МОДУЛЬ МАНИПУЛЯТОРА | 1991 |
|
RU2022773C1 |
| ОДНОТАКТНЫЙ РЕГИСТР СДВИГА | 1990 |
|
RU2047922C1 |
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
Авторы
Даты
2019-06-18—Публикация
2017-10-30—Подача