Изобретение относится к области метеорологии, а именно к способам определения изменения давления атмосферы с изменением высоты. Оно может быть применено для определения давления атмосферы на различных высотах как для накопления статистического материала для анализа, так и для практики, где требуется знание текущего давления атмосферы на различных высотах.
Получение достоверной оценки изменения давления в атмосфере по ее профилю особенно важно для больших высот, где обычные способы непосредственного измерения давления не обеспечивают необходимой точности.
Известны способы определения давления атмосферы на различных высотах путем решения уравнения статики атмосферы и уравнения состояния идеального газа [ГОСТ 4401-81. Атмосфера стандартная. Параметры. М.: ИПК Издательство стандартов, 2004. - 180 с.], а также путем учета изменения газового состава атмосферы, изменения длины свободного пробега частиц, изменения количества частиц в единице объема газа [Матвеев Л.Т. Курс общей метеорологии. Физика атмосферы. Изд. 2-е, перераб. и доп.Л.: Гидрометеоиздат, 1984. - 752 с.]. Всем им присущ существенный недостаток, заключающийся в том, что они требуют знания дополнительных параметров, не поддающихся измерениям или определяемых косвенными методами. Поэтому только в отдельных случаях применение перечисленных способов позволяет получить приемлемую точность определения давления атмосферы.
Известен баллистический способ определения изменения давления атмосферы на различных высотах, изложенный в изобретении [Патент RU №2643705 C2 от 05.02.2018, опубликовано 05.02.2018, Бюл. №4]. Он наиболее близок к предлагаемому способу определения изменения давления атмосферы по ее профилю и принят за прототип.Здесь предложено определять изменение давления атмосферы с изменением высоты по результатам внешнетраекторных измерений параметров движения в атмосфере объекта с известным значением его баллистического коэффициента, который представляет собой совокупную характеристику аэродинамических, массовых и геометрических свойств объекта. По результатам измерений параметров полета объекта вычисляют в дискретных точках траектории высоту точки над поверхностью земного эллипсоида, скорость движения объекта, угол наклона вектора скорости к плоскости местного горизонта, ускорение силы притяжения Земли. На основании этих сведений получают изменения давления атмосферы для каждой пары соседних точек траектории по совокупности аналитических зависимостей, которые обоснованы и получены в предложенном изобретении. Имея значение давления атмосферы с приемлемой точностью в одной из точек траектории движения объекта (например, в приземном слое атмосферы), восстанавливают значения давления по всему профилю атмосферы с использованием вычисленных разностей давления на каждом интервале траектории. Под интервалом траектории здесь понимается интервал между двумя соседними точками измерения параметров траектории.
Недостатком предложенного способа является снижение точности определения разности давлений атмосферы на интервале траектории движения объекта вследствие принятого допущения, что значение баллистического коэффициента объекта является константой. Известно [Основы теории полета космических аппаратов. Под ред. Г.С.Нариманова и М.К.Тихонравова. М.: Машиностроение, 1972. - 608 с.], что баллистический коэффициент 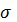 определяется из следующего выражения:
определяется из следующего выражения:
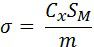
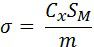 ,
,
где 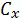 - аэродинамический коэффициент силы лобового сопротивления объекта;
- аэродинамический коэффициент силы лобового сопротивления объекта;
SM - площадь миделевого сечения объекта;
m - масса объекта.
Массу (m) объекта и площадь его миделевого сечения (SM) допустимо принять за константы без заметного снижения точности определения изменения давления атмосферы. Эти параметры хотя и могут изменяться за счет обгара объекта, но только на высоких скоростях, близких к гиперзвуковым. Такие скорости нецелесообразно использовать при проведении измерений для целей решения рассматриваемой задачи. А значение аэродинамического коэффициента силы лобового сопротивления (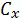 ) начинает меняться уже на дозвуковых скоростях движения объекта, достигая максимума в окрестности M=1, где M - число Маха [Лебедев А.А., Герасюта Н.Ф. Баллистика ракет. М.: Машиностроение, 1970. - 244 с.]. Отсутствие в прототипе учета изменения величины аэродинамического коэффициента силы лобового сопротивления от скорости движения объекта и состояния среды движения может приводить к значимым погрешностям определения разности давлений на интервале траектории.
) начинает меняться уже на дозвуковых скоростях движения объекта, достигая максимума в окрестности M=1, где M - число Маха [Лебедев А.А., Герасюта Н.Ф. Баллистика ракет. М.: Машиностроение, 1970. - 244 с.]. Отсутствие в прототипе учета изменения величины аэродинамического коэффициента силы лобового сопротивления от скорости движения объекта и состояния среды движения может приводить к значимым погрешностям определения разности давлений на интервале траектории.
Целью и техническим результатом настоящего изобретения является повышение точности определения изменения давления атмосферы по ее профилю.
Технический результат, на достижение которого направлено изобретение, достигнут учетом переменной величины аэродинамического коэффициента силы лобового сопротивления объекта в аналитическом представлении зависимости изменения давления атмосферы на интервале траектории пассивного полета объекта от параметров его движения.
Для определения вида аналитической зависимости изменения давления атмосферы от измеренных параметров траектории движения объекта воспользуемся порядком вывода аналогичной зависимости, предложенной в прототипе [Патент RU №2643705 C2 от 05.02.2018, опубликовано 05.02.2018, Бюл. №4]. При этом учтем такую особенность, как зависимость величины аэродинамического коэффициента силы лобового сопротивления объекта от условий его полета.
В основу вывода искомой зависимости положим систему дифференциальных уравнений, описывающих движение центра масс объекта в скоростной системе координат.При этом из всей системы дифференциальных уравнений выделим уравнение, описывающее изменение скорости движения объекта [Лебедев А.А., Герасюта Н.Ф. Баллистика ракет.М.: Машиностроение, 1970. - 244 с.]:
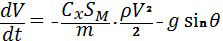
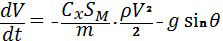 ,
,
где 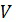 - относительная скорость движения объекта в скоростной системе координат;
- относительная скорость движения объекта в скоростной системе координат;
 - плотность воздуха атмосферы;
- плотность воздуха атмосферы;
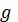 - ускорение силы притяжения Земли;
- ускорение силы притяжения Земли;
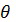 - угол наклона вектора относительной скорости к плоскости
- угол наклона вектора относительной скорости к плоскости
местного горизонта.
Правая часть уравнения (2) характеризуется сложной зависимостью от времени, которую не представляется возможным указать в явном виде. Это затрудняет решение уравнения. Некоторые параметры, входящие в состав уравнения (плотность воздуха атмосферы, ускорение силы притяжения Земли), в неявном виде зависят от высоты траектории полета над поверхностью земного эллипсоида. Исходя из изложенных соображений, для решения дифференциального уравнения (2) перейдем от независимой переменной времени ( ) к высоте траектории полета (
) к высоте траектории полета ( ). Используем для этого известное соотношение [Лебедев А.А., Герасюта Н.Ф. Баллистика ракет.М.: Машиностроение, 1970. - 244 с.]:
). Используем для этого известное соотношение [Лебедев А.А., Герасюта Н.Ф. Баллистика ракет.М.: Машиностроение, 1970. - 244 с.]:

 ,
,
или эквивалентное ему:
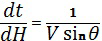
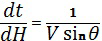 .
.
Для замены переменной  на переменную
на переменную  умножим уравнение (2) слева на выражение
умножим уравнение (2) слева на выражение  , а справа - на выражение
, а справа - на выражение  В результате исходное уравнение (2) преобразуется к виду:
В результате исходное уравнение (2) преобразуется к виду:

 .
.
Воспользуемся формулой производной от квадрата переменной: 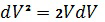 . Умножив на обе части уравнения (5), получим:
. Умножив на обе части уравнения (5), получим:

 .
.
Уравнение (6) представляет собой дифференциальное уравнение относительно неизвестной функции  и ее производной. Для его решения обозначим
и ее производной. Для его решения обозначим  . При этом уравнение (6) запишется в виде:
. При этом уравнение (6) запишется в виде:
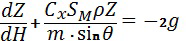
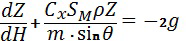 .
.
Для решения уравнения (7) принимаем допущение, что изменения параметров: аэродинамический коэффициент силы лобового сопротивления объекта (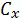 ), плотность атмосферы (ρ), синус угла наклона вектора скорости к плоскости местного горизонта (
), плотность атмосферы (ρ), синус угла наклона вектора скорости к плоскости местного горизонта ( ), ускорение силы притяжения Земли (
), ускорение силы притяжения Земли (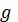 ) незначительны на каждом интервале траектории. Это позволяет принять величины указанных параметров постоянными и равными их средним значениям на интервале траектории. Другое допущение заключается в том, что площадь миделевого сечения SM объекта и его масса m постоянны во всех условиях полета объекта. При таких допущениях уравнение (7) представляет собой дифференциальное уравнение первого порядка, линейное относительно неизвестной функции
) незначительны на каждом интервале траектории. Это позволяет принять величины указанных параметров постоянными и равными их средним значениям на интервале траектории. Другое допущение заключается в том, что площадь миделевого сечения SM объекта и его масса m постоянны во всех условиях полета объекта. При таких допущениях уравнение (7) представляет собой дифференциальное уравнение первого порядка, линейное относительно неизвестной функции  и ее производной.
и ее производной.
Решение уравнения (7) будем искать в виде произведения двух функций, зависящих от  :
:
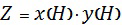
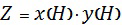 .
.
Дифференцируя обе части этого выражения по переменной  , получаем:
, получаем:

 .
.
Подставляя выражения (8) и (9) в дифференциальное уравнение (7), имеем:
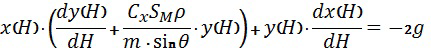
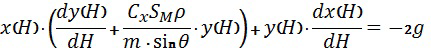 .
.
Одну из функций 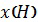 и
и 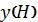 можно взять произвольной. Тогда вид другой функции определится из решения уравнения (10). Выберем функцию
можно взять произвольной. Тогда вид другой функции определится из решения уравнения (10). Выберем функцию 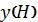 такой, чтобы выражение в скобках левой части уравнения (10) равнялось нулю:
такой, чтобы выражение в скобках левой части уравнения (10) равнялось нулю:

 .
.
Разделив переменные в этом уравнении, получаем следующую зависимость:
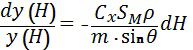
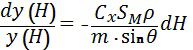 .
.
Для нахождения вида функции 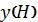 воспользуемся основным уравнением статики атмосферы [Матвеев Л.Т. Курс общей метеорологии. Физика атмосферы. Изд. 2-е, перераб. и доп.Л.: Гидрометеоиздат, 1984. - 752 с.]:
воспользуемся основным уравнением статики атмосферы [Матвеев Л.Т. Курс общей метеорологии. Физика атмосферы. Изд. 2-е, перераб. и доп.Л.: Гидрометеоиздат, 1984. - 752 с.]:
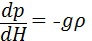
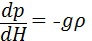 ,
,
из которого получаем:

 ,
,
где  - давление атмосферы.
- давление атмосферы.
Подставив выражение (14) в (12), получаем:
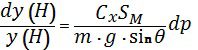
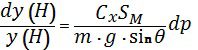 .
.
Проинтегрируем (15), принимая выражение 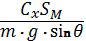 постоянным вследствие принятых выше допущений. В результате получим уравнение:
постоянным вследствие принятых выше допущений. В результате получим уравнение:

 ,
,
откуда находим его решение относительно искомой функции 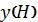 :
:
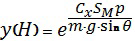
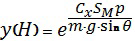 .
.
Функцию 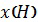 определим путем подстановки функции
определим путем подстановки функции 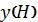 из формулы (17) в выражение (10) с учетом условия (11), т.е. равенства нулю соотношения, стоящего в скобках.
из формулы (17) в выражение (10) с учетом условия (11), т.е. равенства нулю соотношения, стоящего в скобках.
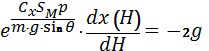
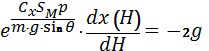 ,
,
или
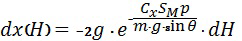
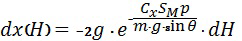 .
.
Проинтегрируем последнее выражение и получим зависимость:
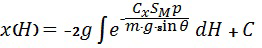
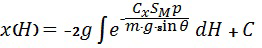 ,
,
где 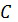 - произвольная постоянная.
- произвольная постоянная.
Для получения общего решения исходного уравнения (2) запишем выражение (8) с подстановкой в него найденных функций 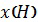 и
и 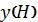 :
:

 .
.
Из выражения (21) определим произвольную постоянную 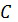 при условиях
при условиях  ,
, 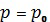 и
и 
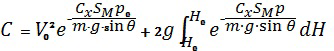
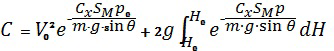 .
.
Учитывая, что второе слагаемое выражения (22) равно нулю, получаем выражение для определения произвольной постоянной:

 .
.
Подставив выражение (23) в (21), найдем следующую зависимость:
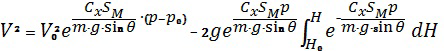
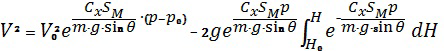 .
.
Подынтегральная функция во втором слагаемом непрерывна и монотонна, что позволяет воспользоваться теоремой о среднем [Выгодский М.Я. Справочник по высшей математике. 11-е изд. М.: Наука, 1976. - 872 с.]. При таком допущении решение (24) запишем в следующем виде:

где - среднее значение давления атмосферы на интервале траектории.
Формульную зависимость для расчета представим в виде:

После подстановки выражения для (26) в решение (25) и преобразований, получаем:
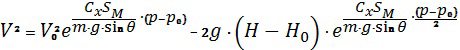
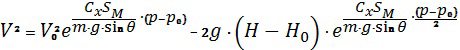 .
.
Анализ величин параметров второго члена решения (27) показывает, что его показательная функция 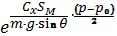 уточняет не более чем на 1-2% величину второго члена, который сам по себе мал относительно общего решения. Приведенные выкладки позволили принять показательную функцию равной единице. При таком допущении можно получить выражение первого приближения для решения дифференциального уравнения (2), которое принимает следующий вид:
уточняет не более чем на 1-2% величину второго члена, который сам по себе мал относительно общего решения. Приведенные выкладки позволили принять показательную функцию равной единице. При таком допущении можно получить выражение первого приближения для решения дифференциального уравнения (2), которое принимает следующий вид:
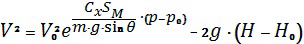
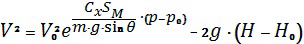 .
.
В качестве второго приближения предлагается использовать выражение, вытекающее из (27), в котором величина множителя 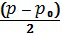 берется из решения (28).
берется из решения (28).
Полученные выражения (27) и (28) не предъявляют особых условий применения и охватывают движение тел как малоскоростных (с тормозным парашютом), так и высокоскоростных (при больших числах Маха), как в приземных, так и в верхних слоях атмосферы.
Из решения (27) и (28) нетрудно получить выражения для определения разности давлений в первом приближении:


и во втором приближении:
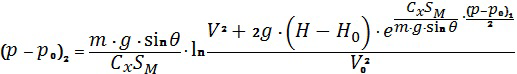
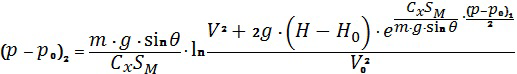 .
.
В силу принятых допущений, под обозначениями 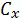 ,
, 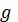 ,
, 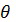 в формулах (29) и (30) следует понимать средние значения величин обозначаемых ими параметров на каждом интервале траектории полета. Поэтому применительно к обработке дискретных значений результатов измерений формульные зависимости определения разности давлений в окончательном виде принимают следующий вид:
в формулах (29) и (30) следует понимать средние значения величин обозначаемых ими параметров на каждом интервале траектории полета. Поэтому применительно к обработке дискретных значений результатов измерений формульные зависимости определения разности давлений в окончательном виде принимают следующий вид:

 ;
;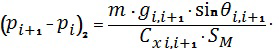
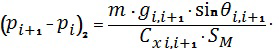

 ,
,
где  - давление атмосферы в i-ой и
- давление атмосферы в i-ой и  -ой точках траектории;
-ой точках траектории;
m - масса объекта;
 - среднее значение ускорения силы притяжения Земли на интервале траектории между i-ой и
- среднее значение ускорения силы притяжения Земли на интервале траектории между i-ой и  -ой точками;
-ой точками;
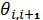 - среднее значение угла наклона вектора относительной скорости к плоскости местного горизонта на интервале траектории между i-ой и
- среднее значение угла наклона вектора относительной скорости к плоскости местного горизонта на интервале траектории между i-ой и  -ой точками;
-ой точками;
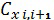 - среднее значение аэродинамического коэффициента силы лобового сопротивления объекта на интервале траектории между i-ой и
- среднее значение аэродинамического коэффициента силы лобового сопротивления объекта на интервале траектории между i-ой и  -ой точками;
-ой точками;
SM - площадь миделевого сечения объекта;
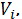
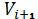 - относительная скорость движения объекта в i-ой и
- относительная скорость движения объекта в i-ой и  -ой точках траектории;
-ой точках траектории;
 - высота расположения i-ой и
- высота расположения i-ой и  -ой точек траектории полета объекта над поверхностью земного эллипсоида.
-ой точек траектории полета объекта над поверхностью земного эллипсоида.
Значения большинства параметров, входящих в выражения (31) и (32), могут быть определены по результатам измерений траектории полета объекта. Исключение составляет один параметр - аэродинамический коэффициент силы лобового сопротивления объекта (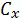 ), который не может быть определен таким образом. Но он может быть вычислен на основе имеющейся информации. Теоретические предпосылки для получения его значений в каждой i-ой точке траектории заключаются в следующем.
), который не может быть определен таким образом. Но он может быть вычислен на основе имеющейся информации. Теоретические предпосылки для получения его значений в каждой i-ой точке траектории заключаются в следующем.
Значение аэродинамического коэффициента зависит от числа Маха (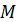 ):
):
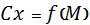
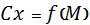 .
.
Число Маха для каждой i-ой точки траектории ( ) определяется из формулы:
) определяется из формулы:
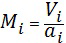
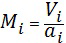 ,
,
где Vi - скорость объекта в i-ой точке траектории;
ai - скорость распространения звука в воздухе в i-ой точке.
Для определения скорости распространения звука в воздухе принято [ГОСТ 4401-81. Атмосфера стандартная. Параметры. М.: ИПК Издательство стандартов, 2004. - 180 с.] следующее выражение:
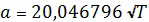
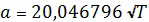 ,
,
где T - температура атмосферы по Кельвину.
Температура атмосферы ( ) для каждой дискретной точки траектории в функции высоты расположения точки траектории относительно поверхности земного эллипсоида
) для каждой дискретной точки траектории в функции высоты расположения точки траектории относительно поверхности земного эллипсоида 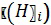 может быть определена по одной из существующих моделей (например, ГОСТ 4401-81. Атмосфера стандартная. Параметры. М.: ИПК Издательство стандартов, 2004. - 180 с.) или из результатов измерений температуры, совмещенных со временем проведения баллистического эксперимента. По полученным значениям температуры, последовательно применяя формулы (35), (34), (33), вычисляют значения Cx i в каждой i-ой точке траектории.
может быть определена по одной из существующих моделей (например, ГОСТ 4401-81. Атмосфера стандартная. Параметры. М.: ИПК Издательство стандартов, 2004. - 180 с.) или из результатов измерений температуры, совмещенных со временем проведения баллистического эксперимента. По полученным значениям температуры, последовательно применяя формулы (35), (34), (33), вычисляют значения Cx i в каждой i-ой точке траектории.
Следует отметить, что погрешность вычисления аэродинамического коэффициента 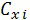 , вызванная неточностью определения температуры Ti, в несколько раз меньше, чем вызвавшая ее погрешность температуры. Отсюда следует, что требования к точности определения температуры Ti могут быть существенно ниже, чем к точности аэродинамического коэффициента
, вызванная неточностью определения температуры Ti, в несколько раз меньше, чем вызвавшая ее погрешность температуры. Отсюда следует, что требования к точности определения температуры Ti могут быть существенно ниже, чем к точности аэродинамического коэффициента 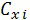 и конечного результата в целом.
и конечного результата в целом.
Предлагаемый способ определения изменения давления атмосферы по ее профилю осуществляется следующим образом.
Для проведения баллистического эксперимента по определению изменения давления атмосферы используют объект массой m, площадью миделевого сечения SM и известной зависимостью аэродинамического коэффициента силы лобового сопротивления объекта от числа Маха Cx=f(M). Доставляют объект в некоторую расчетную точку пространства и обеспечивают его свободный полет в атмосфере с заданной высоты. С требуемой дискретностью измеряют параметры движения объекта. Для этого могут быть использованы средства измерения, расположенные в объекте, средства внешнетраекторных измерений или их комбинация. По результатам обработки измерений определяют в каждом i-ом такте измерений:
- высоту расположения i-ой точки траектории полета объекта над поверхностью земного эллипсоида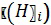 ;
;
- относительную скорость движения объекта 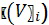 ;
;
- угол наклона вектора скорости к плоскости местного горизонта 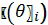 ;
;
- ускорение силы притяжения Земли  .
.
Для каждого интервала траектории, ограниченного парой соседних точек (i-ой и (i+1)-ой), вычисляют средние значения:
- ускорения силы притяжения Земли ( );
);
- угла наклона вектора относительной скорости к плоскости местного горизонта (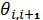 );
);
- аэродинамического коэффициента силы лобового сопротивления объекта (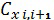 ).
).
Средние значения каждого из указанных параметров определяют как полсуммы значений соответствующих им параметров в граничных точках интервала. Для первых двух параметров ( и
и 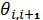 ) такие значения (
) такие значения ( ) получены по результатам обработки измерений. Для третьего параметра (
) получены по результатам обработки измерений. Для третьего параметра (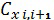 ) необходимо предварительно найти его значения
) необходимо предварительно найти его значения 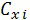 в граничных точках интервала. Исходной информацией для получения
в граничных точках интервала. Исходной информацией для получения 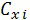 в каждой граничной точке является:
в каждой граничной точке является:
- высота расположения i-ой точки траектории над поверхностью земного эллипсоида 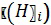 ;
;
- зависимость температуры атмосферы (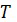 ) от высоты над поверхностью земного эллипсоида (
) от высоты над поверхностью земного эллипсоида ( );
);
- зависимость аэродинамического коэффициента силы лобового сопротивления объекта (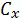 ) от числа Маха (
) от числа Маха (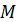 ).
).
По известной высоте  расположения точки траектории определяют соответствующую ей температуру
расположения точки траектории определяют соответствующую ей температуру  атмосферы в этой точке. Затем по формулам (35), (34), (33) находят значение
атмосферы в этой точке. Затем по формулам (35), (34), (33) находят значение 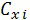 . На основании значений аэродинамического коэффициента в двух соседних точках траектории вычисляют средние значения
. На основании значений аэродинамического коэффициента в двух соседних точках траектории вычисляют средние значения 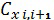 на интервалах.
на интервалах.
С использованием полученных значений вышеперечисленных параметров вычисляют изменение давления на интервале по формулам (31) и (32) для каждого интервала траектории, ограниченного парой соседних точек (i-ой и (i+1)-ой). По известному значению давления в одной из точек траектории (например, в приземном слое атмосферы) восстанавливают значения давления атмосферы по всему профилю атмосферы с применением полученных изменений давления на каждом интервале.
Оценка методической погрешности определения разности давлений показала, что она достигает порядка 1% при шаге измерений по высоте до 5 км. Уменьшение шага ведет к заметному снижению методической погрешности. В реальном полете шаг может быть уменьшен более чем на порядок. Отсюда следует, что предлагаемый способ обеспечивает приемлемую точность определения изменения давления и вычисления давления атмосферы для многих практических приложений. Кроме методической погрешности, на точность оценки разности давлений оказывает влияние погрешность определения измеряемых параметров  , что требует использования в баллистическом эксперименте высокоточных средств измерения.
, что требует использования в баллистическом эксперименте высокоточных средств измерения.
Предлагаемый способ определения изменения давления атмосферы по ее профилю может быть использован для определения давления на различных высотах, прежде всего в случаях, когда непосредственное измерение давления невозможно, либо погрешность таких измерений неадекватно отражает состояние среды.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ БАЛЛИСТИЧЕСКОГО КОЭФФИЦИЕНТА ОБЪЕКТА | 2015 |
|
RU2600515C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗМЕНЕНИЯ ДАВЛЕНИЯ АТМОСФЕРЫ С ИЗМЕНЕНИЕМ ВЫСОТЫ | 2016 |
|
RU2643705C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАВЛЕНИЯ АТМОСФЕРЫ ПО ЕЁ ПРОФИЛЮ | 2021 |
|
RU2759851C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ БАЛЛИСТИЧЕСКОГО КОЭФФИЦИЕНТА ОБЪЕКТА | 2018 |
|
RU2679910C1 |
| СПОСОБ УПРАВЛЕНИЯ СПУСКОМ КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТЫ | 2013 |
|
RU2537193C1 |
| СПОСОБ УПРАВЛЕНИЯ СПУСКОМ КОСМИЧЕСКОГО АППАРАТА В АТМОСФЕРЕ ПЛАНЕТЫ | 2013 |
|
RU2537192C1 |
| Способ управления беспилотным планирующим летательным аппаратом | 2017 |
|
RU2654238C1 |
| СПОСОБ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ С ИСПОЛЬЗОВАНИЕМ АЭРОДИНАМИЧЕСКОГО КАЧЕСТВА ПРИ СПУСКЕ В АТМОСФЕРЕ | 2014 |
|
RU2552770C1 |
| СПОСОБ ЗОНДИРОВАНИЯ СЕЙСМООРБИТАЛЬНЫХ ЭФФЕКТОВ И ВАРИАЦИЙ ПЛОТНОСТИ ВЕРХНЕЙ АТМОСФЕРЫ | 2019 |
|
RU2705161C1 |
| СПОСОБ РЕШЕНИЯ ОСНОВНОЙ ЗАДАЧИ ВНЕШНЕЙ БАЛЛИСТИКИ НЕУПРАВЛЯЕМЫХ РЕАКТИВНЫХ СНАРЯДОВ ДЛИТЕЛЬНЫХ СРОКОВ ХРАНЕНИЯ | 2014 |
|
RU2590841C2 |
Изобретение относится к области метеорологии и может быть использовано для определения изменения давления атмосферы с изменением высоты. Сущность: измеряют параметры пассивного полета в атмосфере объекта с известными массово-геометрическими и аэродинамическими характеристиками в дискретных точках траектории. Вычисляют координаты и скорость движения объекта, угол наклона вектора скорости к плоскости местного горизонта, ускорение силы притяжения Земли. Для каждой пары соседних точек траектории движения объекта определяют величину изменения давления атмосферы, учитывая полученные параметры, а также величину аэродинамического коэффициента силы лобового сопротивления объекта. Технический результат: повышение точности определения изменения давления атмосферы по ее профилю.
Способ определения изменения давления атмосферы по ее профилю, основанный на измерениях параметров пассивного полета в атмосфере объекта с известными массово-геометрическими и аэродинамическими характеристиками, по результатам которых в дискретных точках траектории полета определяют координаты, скорость движения объекта, угол наклона вектора скорости к плоскости местного горизонта и ускорение силы притяжения Земли, на основании чего для каждой пары соседних точек траектории движения объекта определяют разность давления атмосферы с использованием совокупности аналитических зависимостей, отличающийся тем, что в аналитических зависимостях учитывают переменную величину аэродинамического коэффициента силы лобового сопротивления объекта в соответствии с изменяющимися скоростью движения объекта и температурой окружающей среды.
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗМЕНЕНИЯ ДАВЛЕНИЯ АТМОСФЕРЫ С ИЗМЕНЕНИЕМ ВЫСОТЫ | 2016 |
|
RU2643705C2 |
| RU 2014125773 A, 27.12.2015 | |||
| СПОСОБ ЗОНДИРОВАНИЯ ИОНОСФЕРЫ, ТРОПОСФЕРЫ, ГЕОДВИЖЕНИЙ И КОМПЛЕКС ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2011 |
|
RU2502080C2 |
Авторы
Даты
2019-06-18—Публикация
2018-10-04—Подача