Изобретение относится к системам управления летательными аппаратами (ЛА) и может быть использовано в комплексе функциональных программ управления и наведения ЛА авиационных комплексов для построения траекторий обхода опасных зон.
Повышение живучести ЛА в процессе решения ими различных задач является одной из основных тенденций развития радиоэлектронных систем управления. Одним из способов повышения живучести является использование скрытых методов наведения. Среди этих методов можно выделить [1]:
• командный вывод самолета непосредственно в область целевого применения,
• использование полуактивного режима,
• использование многопозиционного варианта наведения на одну цель,
Однако, если некоторые опасные зоны, например, наземные зоны ПВО, не являются объектом поражения, то их лучше избегать. Тем самым, еще одним направлением повышения живучести является обход (облет) опасных зон. Существует множество подходов к решению этой задачи. В [2] рассматривается способ, при котором сначала с помощью диаграмм Вороного строится кусочно-линейная траектория полета, которая затем сглаживается при помощи спиралей Корню. В [3] путь обхода строится по седловым точкам потенциала с помощью теории графов.
Целью предлагаемого изобретения является разработка простого алгоритма формирования пути обхода ЛА опасных зон в плоскости, способного быстро построить требуемую траекторию без участия человека.
В качестве прототипа был выбран способ обхода опасных зон, предлагаемый в работе [4].
Предлагаемый в прототипе подход к формированию предполагаемой траектории обхода основывается на построении сетки точек в пространстве координат и скоростей. К сетке также добавляются заданные начальная и конечная точки. Затем эти точки соединяются между собой участками траекторий, удовлетворяющими заданным условиям. Такой способ построения сетки обеспечивает плавный переход между участками. Затем из этих точек и участков траекторий строится граф путей, в котором ищется кратчайший путь.
Преимуществом прототипа является то, что он позволяет решить задачу построения оптимального по заданному критерию пути, удовлетворяющего заданным ограничениям, при наличии препятствий произвольного вида, причем можно строить траекторию, как на плоскости, так и в пространстве.
Однако такая универсальность заставляет жертвовать скоростью решения задачи. В [4] разбирается пример обхода двух эллипсов на плоскости при заданных начальной и конечной точках и направлениях. Для ее решения в [4] строится граф путей из 4140 вершин и порядка 300,000 ребер. Для сравнения, в предлагаемом изобретении граф путей будет состоять из 144 вершин и 432 ребер. Видно, что наш способ для частного, но наиболее естественного вида опасных зон, гораздо более экономичен, чем прототип. Кроме того, наш способ строит действительно кратчайший путь, хотя при достаточном количестве точек алгоритм из прототипа дает практически ту же самую длину траектории.
Технический результат, который может быть получен от использования предлагаемого изобретения, заключается в возможности автоматического построения кратчайшей траектории облета опасных зон, что снижает информационную нагрузку на операторов (штурманов наведения).
Заявленный технический результат, который может быть получен от реализации предлагаемого технического решения, достигается тем, что решение задачи сводится численному решению серии уравнений не выше четвертого порядка и последующему применению известного алгоритма Дейкстры нахождения кратчайшего пути в графе.
Возможность достижения технического результата обусловлена следующими причинами:
• предлагаемый способ позволяет быстро и эффективно строить траектории обхода достаточно большого количества опасных зон, что подтверждено компьютерным моделированием;
• построенная траектория обхода задается аналитически в виде набора отрезков и дуг эллипсов, что позволяет использовать известные алгоритмы следования заданной траектории при выполнении облета.
Сущность предлагаемого изобретения заключается в разработке нового способа автоматического построения кратчайшей траектории обхода опасных зон, основанного на решении серии несложных вспомогательных геометрических задач и применении алгоритма Дейкстры поиска кратчайшего пути в графе.
Задача построения траектории, обходящей опасные зоны, решается при следующих условиях:
1) зоны обхода сохраняют свою конфигурацию в пространстве достаточно продолжительное время;
2) зоны описываются эллипсами в горизонтальной плоскости. Это довольно точное приближение, если опасные зоны представляют собой средства ПВО;
3) известны начальная точка А и конечная точка В полета ЛА, а также направление движения в начальной точке и минимально допустимый радиус разворота R;
4) ЛА обладает достаточной маневренностью, чтобы двигаться по границам эллипсов, задающих опасные зоны. Как правило, это предположение оправдано, поскольку размер опасных зон обычно значительно больше радиуса разворота ЛА.
5) известен перечень эллипсов, определяющих опасные зоны. Эллипсы задаются параметрами (х,у,а,b,ϕ) (фиг. 1), где (х,у) - координаты центра эллипса, а,b - полуоси эллипса, ϕ - угол наклона оси а в системе координат XY.
Ставится задача движения ЛА из точки А в точку В с заданным направлением движения в точке А, причем этот ЛА не должен заходить внутрь опасных зон.
Траектория облета опасных зон, задающая самый короткий путь из А в B, должна удовлетворять ограничениям на допустимый радиус разворота ЛА. Легко понять, что она будет состоять из дуги окружности с заданным радиусом разворота R и последовательно чередующихся отрезков и дуг эллипсов. При этом в точках пересечения отрезки будут касаться эллипсов. Тем самым отрезки пути между эллипсами будут отрезками общих касательных. Т.к. между двумя эллипсами может быть не более четырех общих касательных (фиг. 4), то имеется конечное число возможных промежуточных точек, и для решения задачи можно применить методы теории графов [5].
В соответствии со сказанным выше, результатом работы алгоритма будет массив элементарных участков пути: отрезков и дуг эллипсов, которые вместе и составляют искомую траекторию.
Сначала приводится общее описание алгоритма. Реализация его отдельных частей, связанная с решением частных геометрических задач, будет рассмотрена после.
К списку эллипсов, задающих опасные зоны, добавляют две окружности, радиус которых равен радиусу разворота R, проходящих через начальную точку А так, чтобы начальное направление движения в точке А было касательным к этим окружностям. Перебирают все возможные пары эллипсов из этого списка. Для каждой пары строят все возможные отрезки, соединяющие их, причем эти отрезки должны касаться эллипсов в точке пересечения (способ построения отрезков будет указан в пункте 2 далее). Далее для каждого эллипса строятся все касательные к нему, исходящие из конечной точки (способ построения касательной будет указан в пункте 5 далее).
Затем строится граф путей. Вершинами графа будут пары, состоящие из точки на эллипсе и направления движения по границе эллипса в этой точке. Кроме того в графе будет отдельная вершина, соответствующая конечной точке пути. Построение вершин графа производится следующим образом.
Для каждой точки построенного касательного отрезка между двумя эллипсами, лежащей на эллипсе, в граф добавляются две вершины, соответствующие этой точке и двум возможным направлениям движения по границе эллипса. Для каждой точки касательной, лежащей на эллипсе и проходящей через конечную точку, в граф добавляются две вершины, соответствующие точке на эллипсе и двум возможным направлениям обхода эллипса. Также в граф добавляется вершина, соответствующая конечной точке. Наконец, в граф добавляются две вершины, соответствующие начальной точке на двух построенных окружностях, с направлением движения по окружности, совпадающим с направлением начальной скорости. Для N опасных зон число вершин не превышает величины порядка N2.
Ребра графа являются направленными и имеют определенную длину. Они строятся следующим образом.
Две вершины графа, соответствующие двум точкам, лежащим на разных эллипсах, соединяются ребром, если эти являются концами одного из построенных отрезков, причем этот отрезок не пересекается ни с какими реальными опасными зонами, кроме двух рассматриваемых (алгоритм проверки пересечения будет указан в пункте 4 далее). Кроме того, должно быть выполнено условие согласования направлений, которое проиллюстрировано фигурой 2. Двигаясь в точке А в направлении 1 можно перейти на касательную и попасть в точку В, причем направлением движения в точке В будет 1. Поэтому в граф добавляется ребро (А1,В1), где А1 -начальная точка ребра, В1 - конечная точка. Также в граф добавляется ребро (В2,А2). Все другие комбинации условиям согласования не удовлетворяют. Длина ребра полагается равной длине отрезка касательной.
Две вершины графа, первая из которых соответствует точке на эллипсе, а вторая соответствует конечной точке движения, соединяются ребром, конец которого соответствует конечной точке, если точка на эллипсе лежит на касательной, проведенной из конечной точки, и отрезок между этими двумя точками не пересекается с другими опасными зонами. Длина ребра полагается равной длине отрезка касательной.
Две вершины графа, соответствующие двум точкам, лежащим на одном эллипсе, соединяются ребром, если конечная точка ребра следует сразу после начальной, направления движения совпадают, а путь по эллипсу между двумя этими точками не пересекается с другими опасными зонами (алгоритм проверки пересечения эллипсов приводится в пункте 2 далее). Пример приведен на фигуре 3. Ребрами, в которых начальная вершина соответствует точке А, будут (А1,В1) и (А2,Е2). Длина ребра полагается равной длине пути между точками на эллипсе.
Затем для построенного графа выполняется алгоритм Дейкстры [5] поиска кратчайшего пути. Начальными данными в алгоритме будет нуль в двух вершинах, соответствующих начальной точке на двух проходящих через нее окружностях, и бесконечность во всех остальных вершинах.
В результате для каждой точки графа будет построен кратчайший путь в нее из начальной точки. Путь в конечную точку и будет искомым путем. Вычислительная сложность алгоритма при количестве опасных зон N пропорциональна N3. Отметим, что если вместо двух окружностей добавить начальную точку, то можно построить кратчайший путь без учета начального направления движения.
В приведенном выше описании алгоритма указано, что для построения требуемой траектории необходимо решить ряд частных геометрических задач, к которым относятся:
• нахождение общих касательных к эллипсам,
• проверка пересечения эллипсов,
• определение пересечения отрезка с эллипсом,
• нахождение касательных к эллипсу, проходящих через заданную точку.
1. Решение задачи нахождения общих касательных в частном случае, когда один эллипс является единичной окружностью с центром в начале координат, а оси другого эллипса ориентированы по координатным осям, проиллюстрировано фигурой 5.
Эллипс задается координатами центра (х0,у0) и полуосями а,b. Уравнение эллипса определяется соотношением
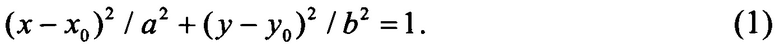
Точки касательной к окружности, проходящей через точку (cosϕ, sinϕ), определяются в параметрическом виде через параметр t выражениями

Условие касания эллипса записывается в виде
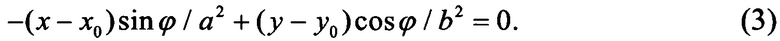
Для нахождения касательной нужно решить систему (1)-(3). Исключив t из уравнений (2), получим:

откуда следует
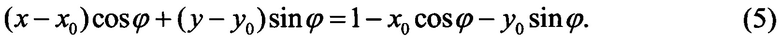
Решив систему (3), (5) относительно (x-х0) и (у-у0) и подставив ее решение в (1), получим уравнение
a 2cos2ϕ+b2sin2ϕ=(1-x0cosϕ-y0sinϕ)2.
Это уравнение заменой z=tg(ϕ/2) приводится к уравнению четвертой степени
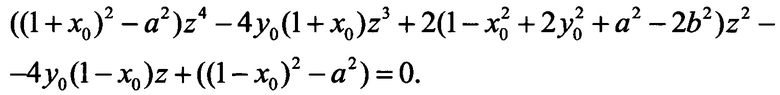
Каждое его действительное решение определяет общую касательную, идущую от точки (cosϕ, sinϕ) окружности к точке (х,у) эллипса, определяемой из системы линейных уравнений (3), (4) при найденном значении ϕ.
Нахождение общих касательных к двум эллипсам произвольного вида, при условии, что они заданы параметрами (xl,yl,al,bl,ϕ1) и (х2,у2,а2,b2,ϕ2) иллюстрируется фигурой 4. Приведем последовательность преобразований, сводящих задачу к рассмотренному выше частному случаю.
a) Сдвигаем эллипсы на -x1, по оси X и на -у1 по оси Y так чтобы центр первого эллипса оказался в начале координат. При этом изменятся координаты центра второго эллипса.
b) Поворачиваем эллипсы на угол -ϕ1 вокруг начала координат. Угол поворота первого эллипса станет равным нулю, угол поворота второго эллипса будет равен ϕ2-ϕ1, вектор центра (х2,у2) тоже повернется.
c) Используя преобразование 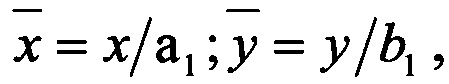 изменяем масштаб осей так, чтобы первый эллипс стал единичной окружностью. Преобразование второго эллипса производится следующим образом. Оставляя для координат его центра и угла поворота после преобразований а) и b) исходные обозначения (х2,у2,ϕ2), запишем его уравнение в виде
изменяем масштаб осей так, чтобы первый эллипс стал единичной окружностью. Преобразование второго эллипса производится следующим образом. Оставляя для координат его центра и угла поворота после преобразований а) и b) исходные обозначения (х2,у2,ϕ2), запишем его уравнение в виде
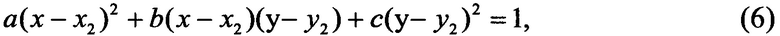
где
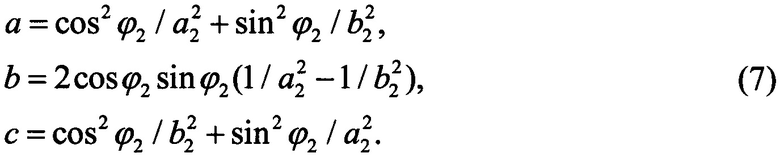
В новых координатах уравнение (6) примет вид
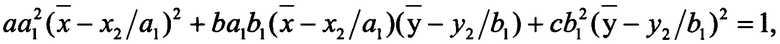
откуда следует, что координаты центра второго эллипса будут (х2/а1,у2/b1). Для нахождения новых полуосей запишем матрицу
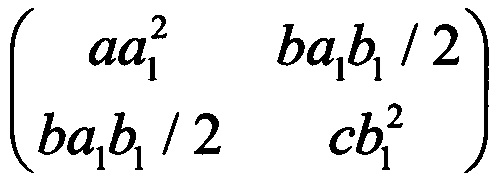
и найдем ее собственные значения λ1, λ2 и собственный вектор, соответствующий λ1. Тогда новые полуоси эллипса будут 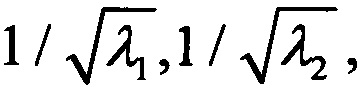 а направление собственного вектора определит новый угол ϕ2 поворота эллипса.
а направление собственного вектора определит новый угол ϕ2 поворота эллипса.
d) Поворачиваем эллипсы на угол -ϕ2 вокруг начала координат. Вектор центра второго эллипса (х2/а1,у2/b1) повернется, а новое значения угла ϕ2 будет равным нулю. Первый эллипс при этом не изменится, т.к. он является окружностью с центром в начале координат.
В результате проделанных преобразований первый эллипс стал единичной окружностью с центром в начале координат, а оси второго эллипса ориентированы по координатным осям. В соответствии с рассмотренным ранее алгоритмом, найдем отрезки общих касательных, соединяющие окружность с эллипсом. Эти отрезки задаются декартовыми координатами двух точек, одна из которых лежит на окружности, а другая на эллипсе. Проведем над этими точками преобразования, обратные к преобразованиям d), с), b), а). Получим координаты точек отрезка касательной, соединяющей исходные эллипсы в первоначальной системе координат.
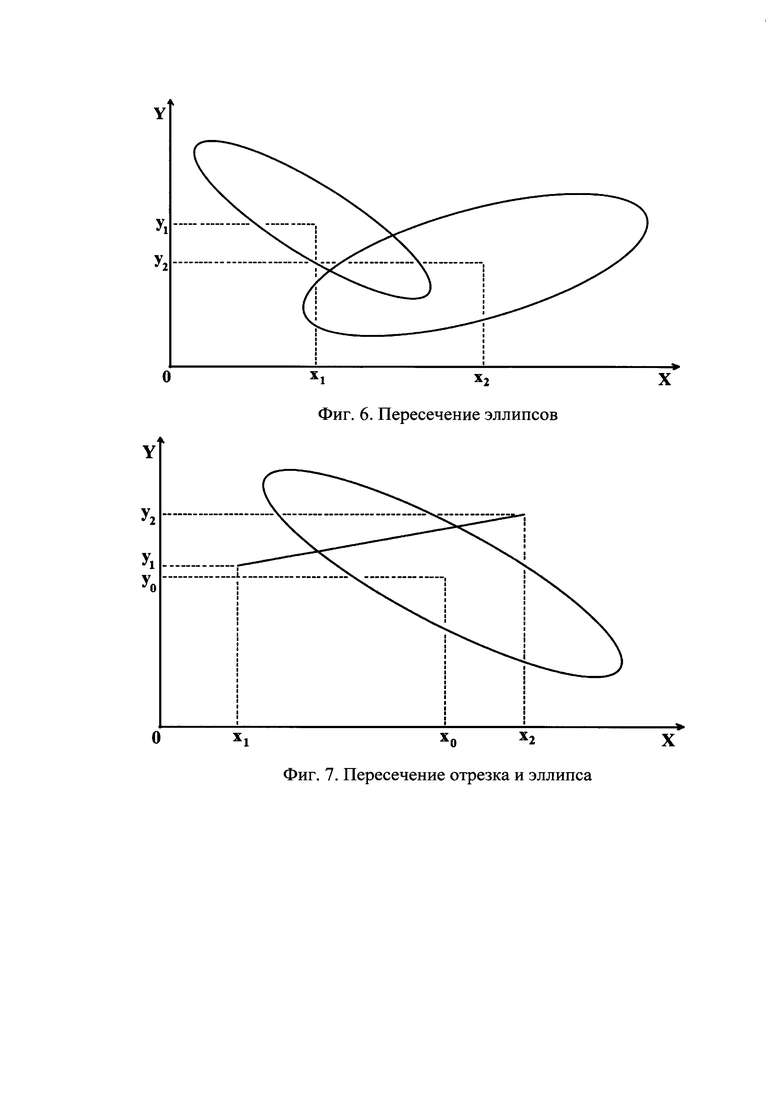
2. Проверка пересечения эллипсов иллюстрируется фигурой 6. Два эллипса заданы параметрами (x1,y1,a1,b1,ϕ1) и (x2,y2,a2,b2,ϕ2). На первом эллипсе задана дуга, определяемая интервалом углов при задании эллипса в параметрическом виде

в связанной с ним системе координат. Нужно определить, пересекается ли эта дуга со вторым эллипсом или лежит внутри него.
Сдвигаем и поворачиваем эллипсы вокруг начала координат, так чтобы центр первого эллипса попал в начало координат, а его оси были направлены по координатным осям, и обозначим новые параметры эллипсов теми же символами, что и до преобразований. Тогда уравнение второго эллипса примет вид
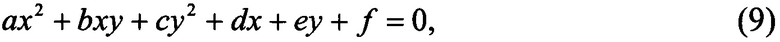
где первые три коэффициента определяются по формулам (7), а остальные вычисляются по формулам
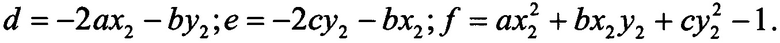
После подстановки (8) в (9), получим уравнение
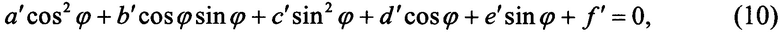
где
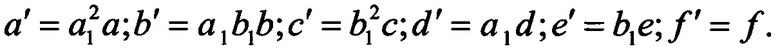
Заменой t=tg(ϕ/2) уравнение (10) приводится к виду
(a'-d'+ƒ')t4+(2е'-2b')t3+(2ƒ'+4с'-2a')t2+(2b'+2e')t+(a'+d'+ƒ')=0.
Найдем его действительные корни и соответствующие значения ϕ. Они определяют разбиение первого эллипса на участки, лежащие внутри или вне второго эллипса. Остается лишь проверить пересекается ли заданный участок с участками, лежащими внутри второго эллипса.
3. Определение пересечения отрезка с эллипсом иллюстрируется фигурой 7. Эллипс задан параметрами (х0,у0,а,b,ϕ), а координаты концов отрезка (х1,у1) и (х2,у2). Сдвигаем и поворачиваем эллипс и отрезок вокруг начала координат, так чтобы центр эллипса попал в начало координат, а его оси были направлены по координатным осям. Обозначим новые координаты концов отрезка 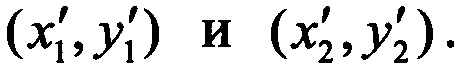 Отрезок пересекается с эллипсом, если квадратное уравнение
Отрезок пересекается с эллипсом, если квадратное уравнение
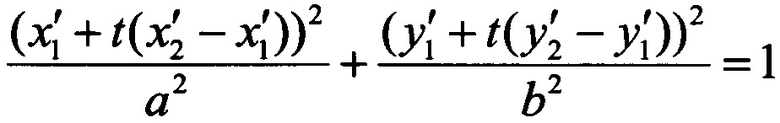
имеет корни, лежащие на отрезке [0,1].
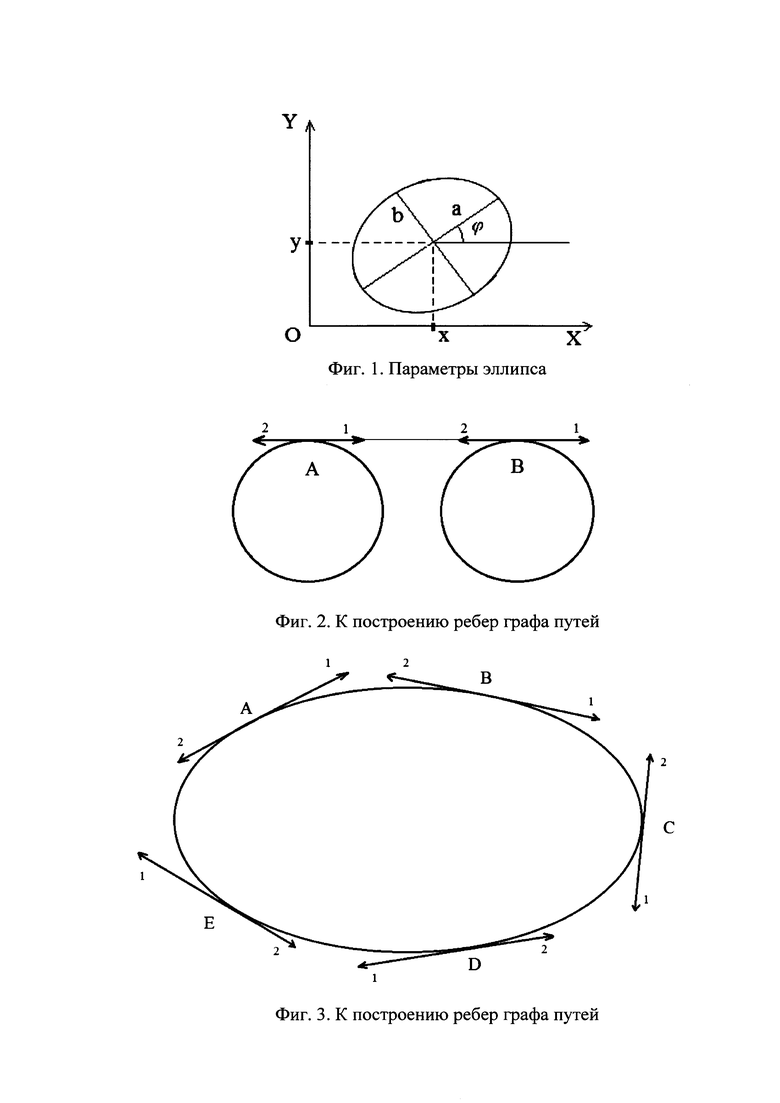
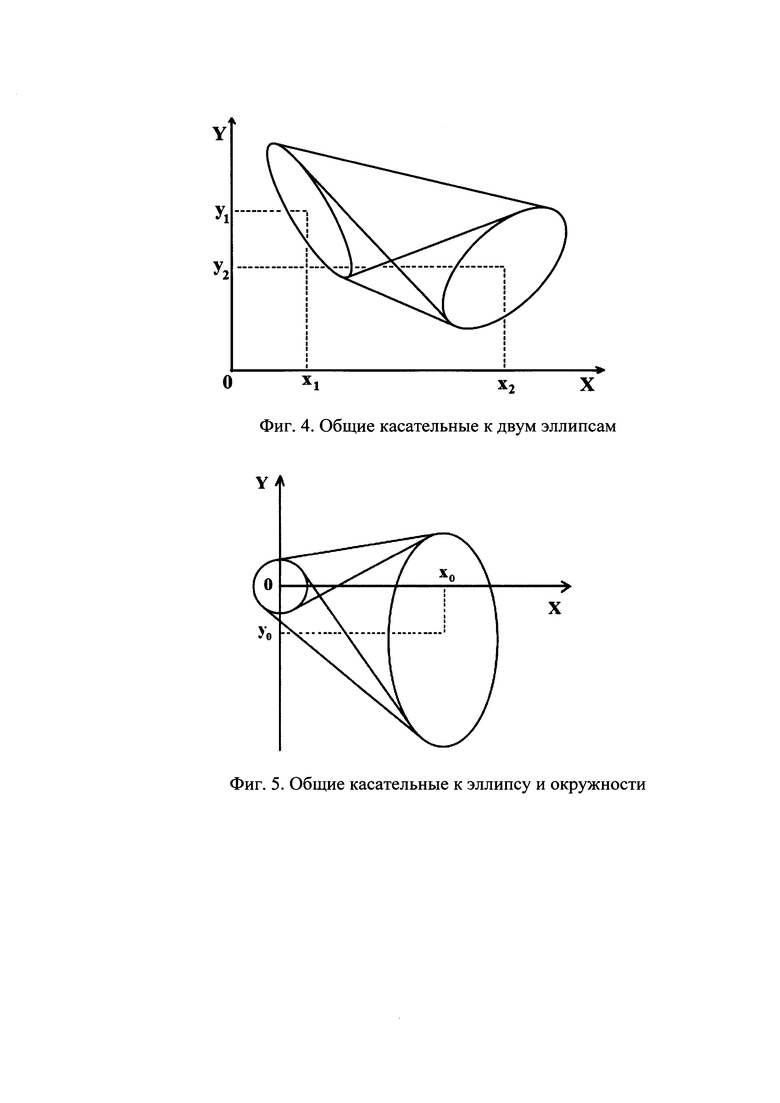
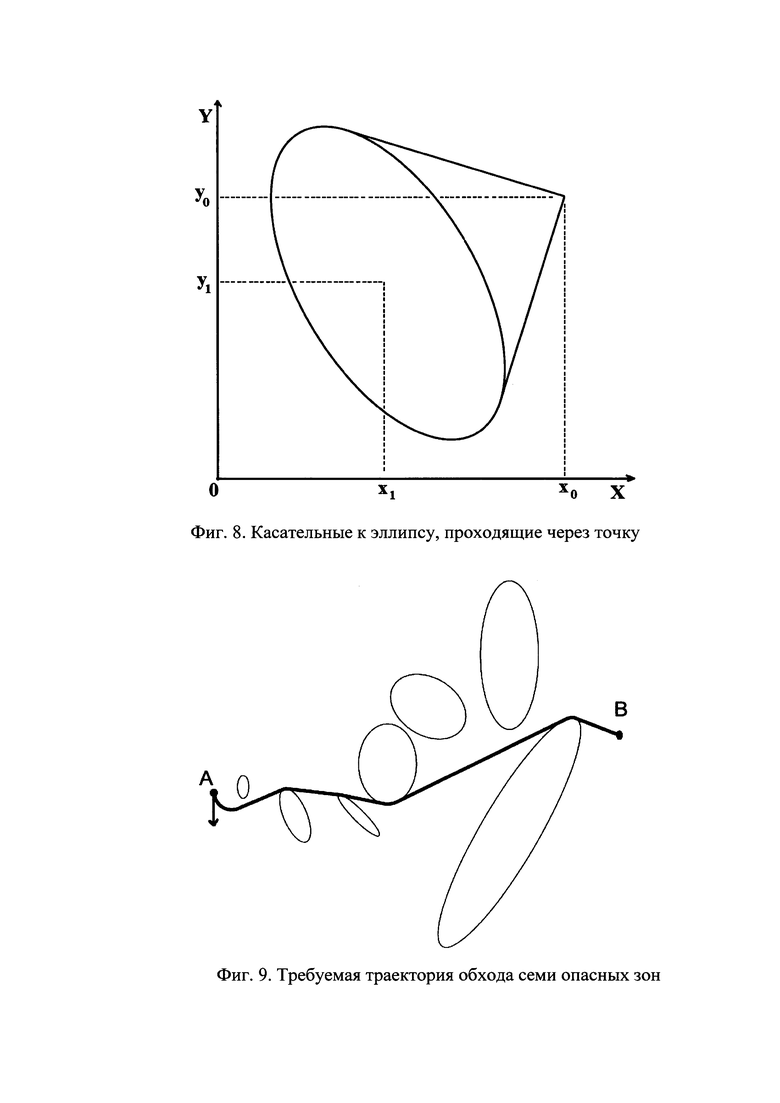
4. Нахождение касательных к эллипсу, проходящих через заданную точку иллюстрируется фигурой 8. Эллипс задан параметрами (x1,y1,a,b,ϕ1), а координаты точки (х0,у0). Сдвигаем и поворачиваем эллипс и точку вокруг начала координат, так чтобы центр эллипса попал в начало координат, а его оси были направлены по координатным осям. Если координаты точки после преобразований равны 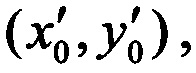 то значения угла ϕ на эллипсе, определяющие точки, через которые проходит касательная, определяются из уравнения
то значения угла ϕ на эллипсе, определяющие точки, через которые проходит касательная, определяются из уравнения
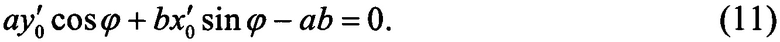
Работоспособность разработанного алгоритма исследовалась в процессе имитационного моделирования. На фигуре 9 представлен результат построения кратчайшей траектории между точками А и В при наличии N=7 опасных зон при заданном начальном направлении движения в точке А. Для наглядности радиус поворота выбран сравнимым с размерами некоторых опасных зон, несмотря на то, что реализация полученной траектории может оказаться невозможной.
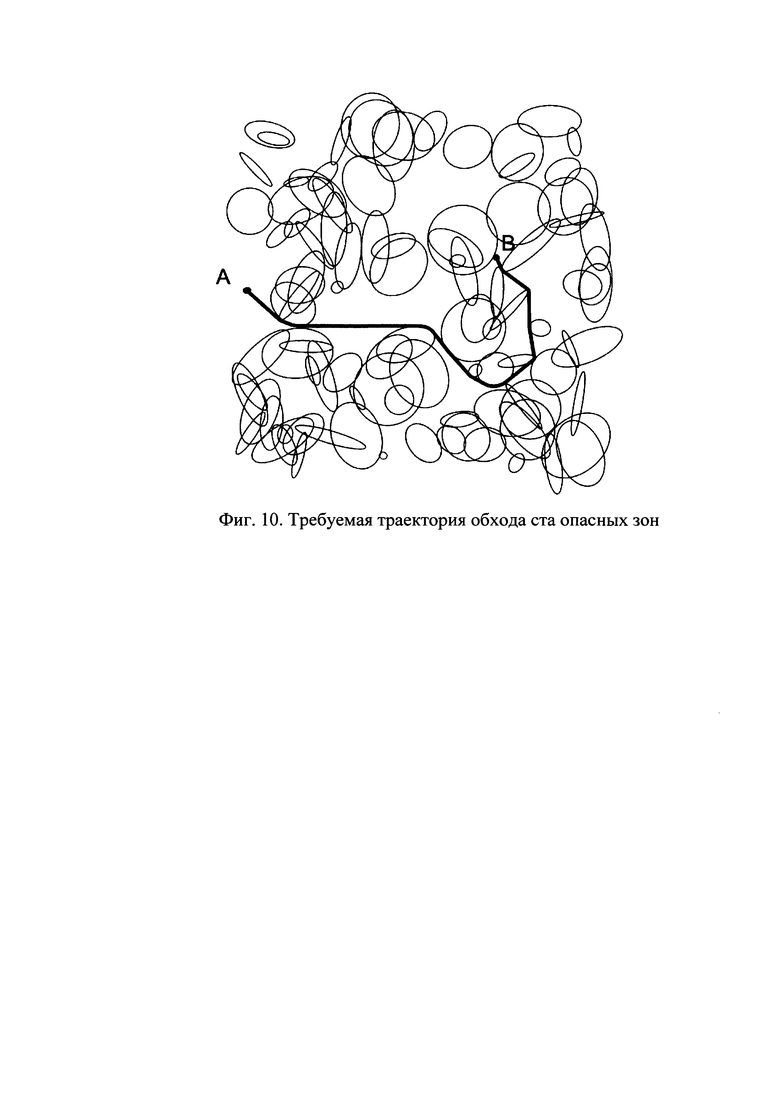
Другой вариант поиска кратчайшей траектории, приведенный на фигуре 10, проводился при количестве опасных зон N=100, плотно расположенных на пути между начальной и конечной точкой без учета начального направления движения. Время расчета пути при наличии ста зон составляет около одной секунды.
Полученный алгоритм построения траектории обхода опасных зон подтвердил свою эффективность в широком поле условий применения. Его достоинством является то, что он позволяет обеспечить построение требуемой траектории практически любой конфигурации опасных зон, которые могут быть заданы эллипсами.
Предложенный алгоритм можно использовать в комбинации с любыми методами движения по заданной траектории.
Промышленная применимость предлагаемого технического решения подтверждается также возможностью реализации его назначения с помощью стандартных бортовых вычислительных средств.
Список использованных источников
1. Верба B.C. Авиационные комплексы радиолокационного дозора и наведения. Принципы построения, проблемы разработки и особенности функционирования. - М.: Радиотехника, 2014.
2. Ran D., Cochran J.E. Path Planning and State Estimation for Unmanned Aerial Vehicles in Hostile Environments - Journal of Guidance, Control, and Dynamics, 2010, Vol. 33, No. 2.
3. Hwang Y.K., Ahuja N. A Potential Field Approach to Path Planning - IEEE Transactions On Robotics And Automation, 1992, Vol. 8, No. 1.
4. Mattei M., Blasi L. Smooth Flight Trajectory Planning in the Presence of No-Fly Zones and Obstacles - Journal of Guidance, Control, and Dynamics, 2010, Vol. 33, No. 2.
5. Кристофидес H. Теория графов. Алгоритмический подход. - М.: Мир, 1978.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ ОБХОДА И ПРЕОДОЛЕНИЯ ОПАСНЫХ ЗОН БЕСПИЛОТНЫМ ЛЕТАТЕЛЬНЫМ АППАРАТОМ | 2022 |
|
RU2797956C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО МАРШРУТА ОБХОДА ЛЕТАТЕЛЬНЫМ АППАРАТОМ ЗОН ГРОЗОВОЙ ДЕЯТЕЛЬНОСТИ И ЛИВНЕВЫХ ОСАДКОВ | 2023 |
|
RU2798628C1 |
| Способ нахождения надежных кратчайших путей в сети связи | 2019 |
|
RU2700547C1 |
| Способ детекции протяженных линейных объектов на изображении | 2022 |
|
RU2802991C1 |
| СПОСОБ ПОСТРОЕНИЯ МАРШРУТА ПЕРЕДВИЖЕНИЯ НА ПЕРЕСЕЧЕННОЙ МЕСТНОСТИ | 2014 |
|
RU2594374C2 |
| СПОСОБ ПРОКЛАДЫВАНИЯ МАРШРУТА ПЕРЕДВИЖЕНИЯ НА ПЕРЕСЕЧЕННОЙ МЕСТНОСТИ | 2010 |
|
RU2439496C1 |
| Способ минимизации многоадресного трафика и обеспечение его отказоустойчивости в ПКС сетях | 2017 |
|
RU2676239C1 |
| СПОСОБ АДАПТИВНО-МАРШРУТНОГО УПРАВЛЕНИЯ ПИЛОТИРУЕМЫМ ЛЕТАТЕЛЬНЫМ АППАРАТОМ | 2013 |
|
RU2568161C2 |
| СПОСОБ СЪЕМКИ НИЖНЕЙ ПОВЕРХНОСТИ ЛЕДЯНОГО ПОКРОВА | 2013 |
|
RU2549683C2 |
| Способ оптимальной адаптации маршрута перехвата воздушной цели при нахождении в районе полетов группировки зенитных ракетных комплексов | 2020 |
|
RU2734171C1 |
Изобретение относится к способу построения траектории летательного аппарата (ЛА) обхода опасных зон. Для построения траектории по известным координатам начальной и конечной точек пути, направлению скорости ЛА в начальной точке, допустимому радиусу разворота, а также множеству опасных зон определенным образом решают задачу нахождения кратчайшего пути с помощью метода Дейкстры. Обеспечивается автоматическое построение кратчайшей траектории облета опасных зон и снижение информационной нагрузки на операторов. 10 ил.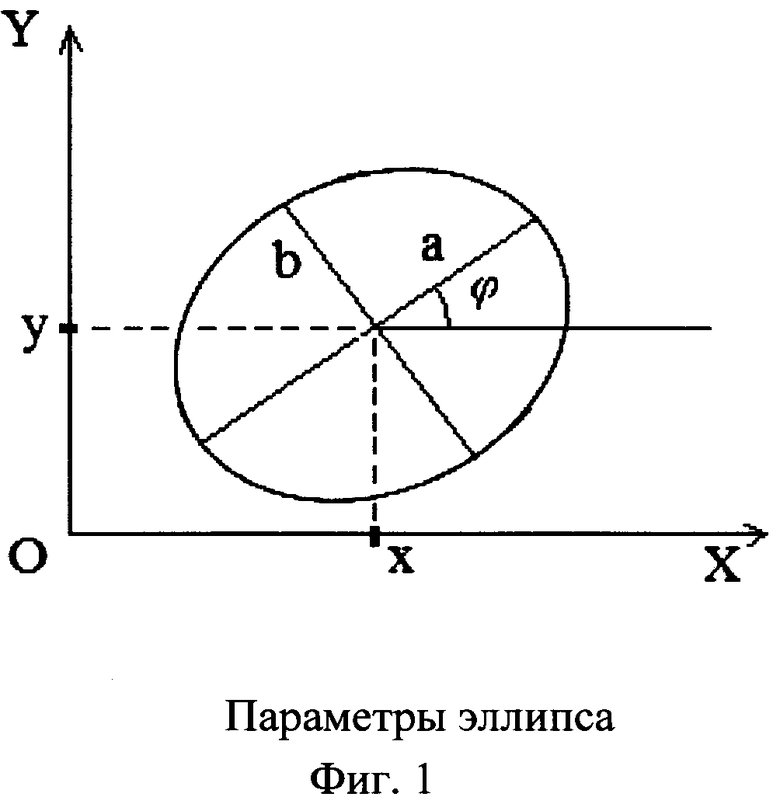
Способ управления летательным аппаратом (ЛА), заключающийся в том, что производят автоматическое построение траектории обхода опасных зон из заданной начальной точки в заданную конечную точку пути по известным координатам начальной и конечной точек пути, направлению скорости ЛА в начальной точке и допустимому радиусу его разворота R, а также множеству опасных зон по назначенным потребителем заранее узлам расчетной сетки строят множество вершин графа путей обхода опасных зон, затем строят множество ребер графа путей обхода опасных зон, затем методом Дейкстры решают задачу нахождения кратчайшего пути в графе; отличающийся тем, что алгоритм построения графа путей обхода опасных зон формируют в виде следующей последовательности действий:
опасные зоны задают эллипсами, для каждого из которых известны координаты х, у центра, длины полуосей а, b и угол ϕ поворота полуоси а относительно оси координат X, затем к списку полученных эллипсов добавляют две окружности радиуса R, проходящие через начальную точку пути, причем направление движения в начальной точке является общей касательной к этим окружностям,
далее строят множество вершин графа путей следующим образом:
1) формируют начальное множество вершин графа, состоящее из вершины, соответствующей конечной точке пути,
2) для каждой пары различных эллипсов из списка опасных зон решают задачу нахождения всех общих касательных отрезков к обоим эллипсам и для каждой точки касательной, лежащей на эллипсе, в граф добавляют две вершины, соответствующие двум направлениям движения по границе эллипса;
3) для каждого эллипса и конечной точки пути решают задачу построения касательных к эллипсу, выходящих из этой точки; затем для каждой точки касательной, лежащей на эллипсе, в граф добавляют две вершины, соответствующие этой точке и двум направлениям обхода эллипса;
4) в граф добавляют две вершины, соответствующие начальной точке пути, лежащие на двух построенных окружностях, причем направление обхода окружностей в этих вершинах совпадает с направлением начальной скорости;
далее строят множество ребер графа путей, где ребра имеют направление и длину, следующим образом:
1) для каждой пары вершин, соответствующих точкам на различных эллипсах, лежащих на общем касательном отрезке, решают задачу о пересечении этого отрезка со всеми остальными эллипсами; если пересечения нет и направления в вершинах согласованы с движением из первой точки во вторую (т.е. при движении по общей касательной между двумя эллипсами из первой точки в заданном направлении попадают во вторую точку, причем направление движения будет совпадать с заданным во второй точке направлением), то эту пару вершин соединяют ребром, длина которого равна расстоянию между этими точками;
2) для конечной точки пути и каждой точки выходящей из нее касательной к эллипсу, лежащей на нем, решают задачу о пересечении отрезка между этими двумя точками со всеми остальными эллипсами, при этом если пересечения нет, то в граф добавляют ребро с начальной вершиной, лежащей на эллипсе, и заданным направлением движения на конечную точку пути, и конечной вершиной, соответствующей конечной точке пути, при этом длину ребра полагают равной расстоянию между конечной точкой пути и соответствующей точкой на эллипсе;
3) пару вершин, соответствующих точкам, лежащим на одном эллипсе, соединяют ребром, если эти точки на эллипсе являются соседними и направления движения из первой точки во вторую согласованы (т.е. при движении по границе эллипса из первой точки в заданном направлении вторая точка будет первой из встреченных и направление движения во второй точке совпадает с заданным направлением), а путь между этими точками по границе эллипса не пересекается с другими опасными зонами, при этом длину ребра полагают равной расстоянию на эллипсе между двумя точками;
затем к построенному графу путей обхода опасных зон применяют алгоритм Дейкстры поиска кратчайшего пути в графе, где в качестве начальных условий выбраны нули в двух вершинах, соответствующих начальной точке пути на двух построенных окружностях, и бесконечности во всех остальных точках;
в результате выполнения алгоритма Дейкстры получают кратчайший путь в каждую вершину графа, при этом путь в вершину, соответствующую конечной точке, является требуемым путем, затем по последовательности вершин этого пути формируют кратчайшую траекторию ЛА обхода опасных зон, состоящую из прямолинейных участков и дуг эллипсов, после чего построенную траекторию по командным радиолиниям связи передают в систему командного управления, в которой формируют сигналы управления ЛА, обеспечивающие движение по построенной траектории.
| EP 3118840 A1, 18.01.2017 | |||
| WO 2017124331 A1, 27.07.2017 | |||
| СПОСОБ МНОГОПУТЕВОЙ МАРШРУТИЗАЦИИ С ИСПОЛЬЗОВАНИЕМ РАСЩЕПЛЕНИЯ ПОТОКА ТРАФИКА ДАННЫХ | 2017 |
|
RU2636665C1 |
| RU 2012145652 A, 27.04.2014 | |||
| НАВИГАЦИОННАЯ СИСТЕМА И СПОСОБ ПОИСКА МАРШРУТА | 2009 |
|
RU2445577C2 |
Авторы
Даты
2019-09-12—Публикация
2018-08-01—Подача