Область техники
Изобретение относится к области оптики, а именно к способам создания линейных оптических устройств, осуществляющих линейные преобразования между большим числом каналов. Изобретение может быть использовано в качестве элемента коммуникационных и вычислительных сетей, обслуживающих большое число абонентов и вычислительных узлов; эти сети могут быть как классическими, так и квантовыми. Изобретение может быть элементом, использующимся в квантовых оптических вычислителях, в частности, при реализации алгоритма бозонного сэмплинга (boson sampling). Также изобретение может быть элементом квантового оптического генератора случайных чисел.
Уровень техники
Линейные оптические преобразования являются необходимой частью в фундаментальных оптических исследованиях. Они играют большую роль в реализациях многих прикладных алгоритмов обработки, получения и передачи информации. Линейные преобразования между двумя каналами могут быть реализованы с помощью одного делителя и элемента фазового сдвига - основных оптических элементов, доступных в разных типах устройств.
Из уровня техники известен способ реализации двухканального линейного преобразования с возможностью изменения его конфигурации. Такой способ использует двухканальный интерферометр с двумя сбалансированными делителями и двумя варьируемыми фазовыми сдвигами (М. Рэк с соавторами, «Экспериментальная реализация любого дискретного унитарного оператора» // Phys. Rev. Lett. Т. 73, №1, С. 58 (1994)).
Известен универсальный способ представления многоканальных линейных преобразований в виде планарных массивов объединенных друг с другом двухканальных преобразований, раскрытый в работах М. Ржа с соавторами, «Экспериментальная реализация любого дискретного унитарного оператора» // Phys. Rev. Lett. Т. 73, №1, С. 58 (1994) и В.Р. Клеменса с соавторами, «Оптимальный дизайн универсальных многопортовых интерферометров» // Optica, Т. 3, №12, С. 1460 (2016). Этот способ позволяет конструировать произвольные линейные преобразования, соединяя друг с другом двухканальные преобразования, упомянутые выше, и надлежащим выбором параметров этих двухканальных преобразований. Суть способа заключается в аналитическом методе расчета параметров составляющих двухканальных преобразований по заданной матрице требуемого многоканального преобразования.
Недостатком универсального способа представления многоканальных линейных преобразований при реализациях является рост потерь при увеличении размерности преобразования (числа каналов), связанный с увеличением глубины планарной схемы - максимального числа оптических элементов, через которые проходят сигналы от входа до выхода схемы. При этом наименьшая глубина получаемых планарных схем равна N, где N - число каналов схемы.
Известен неуниверсальный способ разложения линейных преобразований, который может быть использован в частных случаях для осуществления дискретного преобразования Фурье и преобразования Сильвестра, изложенный, например, в работах П. Торма с соавторами, «Реализация полностью симметричных преобразователей мод с помощью делителей» // Jour. Modern Optics, Т. 43, №2, С. 245-251 (1996) (на анг. яз.) и Ф. Фламини с соавторами, «Бенчмаркинг интегральных линейно-оптических архитектур для квантовой обработки информации» // Sci. Reps Т. 7, 15133 (2017) (на анг. яз.). Суть этого способа заключается в последовательном конструировании матриц требуемой размерности из матриц размерности 2×2, таким образом увеличивая на каждом шаге размерность в 2 раза. Глубина полученной оптической схемы при этом равна log2N, где N - число каналов схемы, которое должно быть четным числом. Разложения, получаемые таким способом, могут быть более компактными по сравнению с универсальными, т.к. глубина последних в лучшем случае равна N.
Недостаток такого способа заключается в узком классе преобразований, которые можно реализовать с его помощью. Требование четности числа каналов преобразования также является недостатком этого метода.
Известны технологии интегральной оптики, позволяющие создавать на практике большие оптические схемы, описанные, например, в работах В. Богэртс с соавторами, «Изготовление фотонных кристаллов в кремний-на-изоляторе с использованием 248-нм глубокой ультрафиолетовой литографии» // IEEE J. Sel. Top.Quantum. Electron., Т. 8, №4, С. 928-934 (2002) и Т. Мини с соавторами «Квантовые оптические схемы, изготовленные лазерной печатью» //Laser & Photon. Rev., Т. 9, №4, С. 363-384 (2015). Суть этих технологий заключается в создании схемы, в которой функциональные оптические элементы и их соединения размещаются на монолитной площадке интегрального чипа. Все элементы и их соединения в интегральной схеме создают параллельно.
Недостатком интегральных оптических схем является невозможность адресного устранения ошибок и исправления отклонений параметров оптических элементов схемы от заданных в изначальном дизайне после ее создания. Данное обстоятельство ограничивает максимальные размерности схем, которые можно создать технологиями интегральной оптики.
Известны методы создания многоканальных оптических схем из модулей меньшего масштаба. Суть этих методов заключается в непосредственном разбиении оптических схем на модули, каждый из которых представляет собой часть схемы. Соединения модулей друг с другом формирует многоканальную схему (П. Менеа с соавторами «Модульные линейно-оптические схемы» // Optica, Т. 5, №9, С. 1087-1090 (2018) (на англ. яз.)). В таком случае изготовление модулей мелкого масштаба является технически менее сложной процедурой и каждый из модулей может быть предварительно отобран, чтобы соответствовать требуемым параметрам точности.
Недостатком описанных модульных способов разбиения схем являются дополнительные оптические потери, возникающие на стыках между модулями, а число стыков возрастает при более мелком разбиении на модули. Еще одним недостатком известных модульных способов является увеличение потерь с ростом числа каналов преобразования, связанное с ростом глубины схем.
Наиболее близким по сущности к заявляемому техническому решению является изобретение, описанное в патенте US 6427037 от 30 июля 2002 г. (X. Окаяма «Двухэтапная переключающая оптическая сетевая схема»). В этом изобретении реализуют преобразования перестановок, т.е. изменение порядка следования каналов, большого числа оптических каналов используя множество устройств, реализующих преобразования перестановок меньшего числа каналов. Схема представляет собой последовательность из как минимум двух этапов, каждый из которых составлен из независимых устройств-модулей, реализующих преобразования каналов число которых меньше, чем число исходного преобразования перестановок. Возможность реализации всего класса преобразований перестановок обусловлено созданием связи между преобразованиями следующих друг за другом этапов.
Недостатком такого изобретения является возможность реализовывать только преобразования перестановок. В таком классе преобразований сигналы, распространяющиеся по разным каналам, никогда не взаимодействуют друг с другом, т.е. это очень узкий класс возможных преобразований между большим числом каналов.
В заявляемом изобретении предложен способ реализации многоканальных линейно-оптических преобразований, который может быть использован для случаев, когда число входных каналов, на которые подаются преобразуемые сигналы, намного меньше, чем общее число каналов преобразования (т.е. число каналов на выходе преобразования). Изобретение может реализовывать широкий класс преобразований, включая перестановки.
Раскрытие изобретения
Техническая проблема, на решение которой направлено заявляемое изобретение, заключается в преодолении недостатков, присущих аналогам и прототипу, за счет создания многоканального оптического интерферометра, обеспечивающего возможность линейного оптического преобразования сигналов для большого числа каналов, обеспечивая при этом минимальную глубину оптической схемы.
Технический результат, достигаемый при использовании заявляемого изобретения, заключается в обеспечении возможности реализации многоканального линейного оптического преобразования, когда число выходных каналов оптической схемы, по меньшей мере, в два раза больше числа входных каналов оптической схемы. Кроме того, технический результат заключается в упрощении требований к технологии изготовления оптической схемы за счет ее модульного выполнения из схем меньшей размерности, которые могут быть изготовлены и верифицированы по отдельности. Помимо этого, техническим результатом является уменьшение потерь при реализации преобразования за счет сокращения «глубины» оптической схемы - минимального числа функциональных элементов, через которые проходят сигналы от входа до выхода схемы.
1. Поставленная задача решается тем, что в способе линейного оптического преобразования М входных сигналов в N выходных сигналов в N - канальном интерферометре, согласно техническому решению, каждый из М входных сигналов, где N>M, по меньшей мере в два раза, подвергают преобразованию рассеяния с получением множества промежуточных сигналов, амплитуда каждого из которых равна
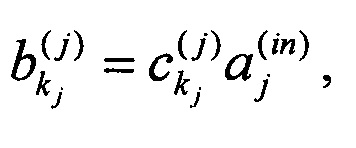
где 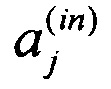 - амплитуда j-того входного сигнала,
- амплитуда j-того входного сигнала,
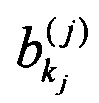 - амплитуда промежуточного сигнала на выходе j-того преобразования рассеяния в его kj-ом промежуточном канале,
- амплитуда промежуточного сигнала на выходе j-того преобразования рассеяния в его kj-ом промежуточном канале,
 - коэффициент, характеризующий рассеяние j-того входного сигнала в kj-том промежуточном канале,
- коэффициент, характеризующий рассеяние j-того входного сигнала в kj-том промежуточном канале,
j = от 1 до М, индекс, нумерующий входной сигнал,
kj = от 1 до Kj, номер промежуточного канала в j-том преобразовании рассеяния,
Kj - число каналов в j-том преобразовании рассеяния, после чего
каждый из промежуточных сигналов в kj канале каждого j-ого преобразования рассеяния подвергают преобразованию смешения с получением N выходных сигналов, каждый из которых получен из промежуточных сигналов из каналов количеством от 2 до М и имеет амплитуду
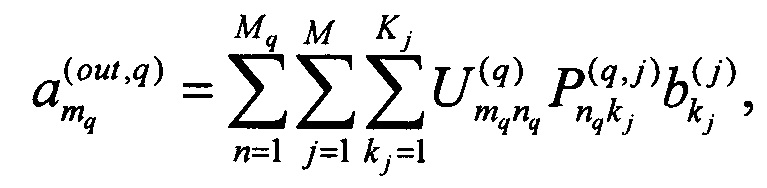 где
где
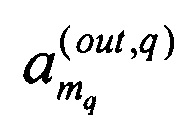 - амплитуда выходного сигнала на выходе mq-ого канала q-ого преобразования смешения, являющаяся амплитудой выходного сигнала интерферометра,
- амплитуда выходного сигнала на выходе mq-ого канала q-ого преобразования смешения, являющаяся амплитудой выходного сигнала интерферометра,
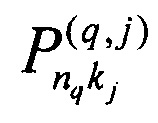 - элементы матрицы, описывающей соединение промежуточных каналов преобразований рассеяния с входными каналами преобразований смешения, соответствующие коэффициенту передачи от kj-ого канала j-ого преобразования рассеяния к nq-ому каналу q-ого преобразования смешения,
- элементы матрицы, описывающей соединение промежуточных каналов преобразований рассеяния с входными каналами преобразований смешения, соответствующие коэффициенту передачи от kj-ого канала j-ого преобразования рассеяния к nq-ому каналу q-ого преобразования смешения,
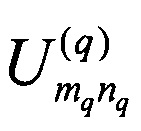 - элементы матрицы q-ого преобразования смешения,
- элементы матрицы q-ого преобразования смешения,
Mq - размерность q-ого преобразования смешения,
nq = от 1 до М - индекс, нумерующий входной канал q-ого преобразования смешения,
mq = от 1 до М - индекс, нумерующий выходной канал q-ого преобразования смешения,
q = от 1 до Q,
Q - число преобразований смешения.
N и М связаны соотношением N=Q*M, где Q - целое и больше либо равно 2.
Поставленная задача решается также тем, что линейный оптический N-канальный интерферометр, включает, по меньшей мере, один блок рассеяния, имеющий входные и выходные каналы, и, по меньшей мере, один блок смешения, имеющий входные и выходные каналы, обеспечивающие преобразование рассеяния и смешения в соответствии с заявляемым способом. Блок рассеяния и блок смешения могут быть выполнены, по меньшей мере, из одного интегрального оптического устройства, методом планарной литографии или методом трехмерной лазерной модификации. Интерферометр также может быть снабжен соединительным блоком, выполненным методом планарной литографии или методом трехмерной лазерной модификации (печати), и расположенным между блоками рассеяния и смешения с обеспечением соединения выходных каналов блока рассеяния и входных каналов блока смешения.
Краткое описание чертежей
На фиг. 1-4 приведены поясняющие уровень техники изображения и схемы, а именно:
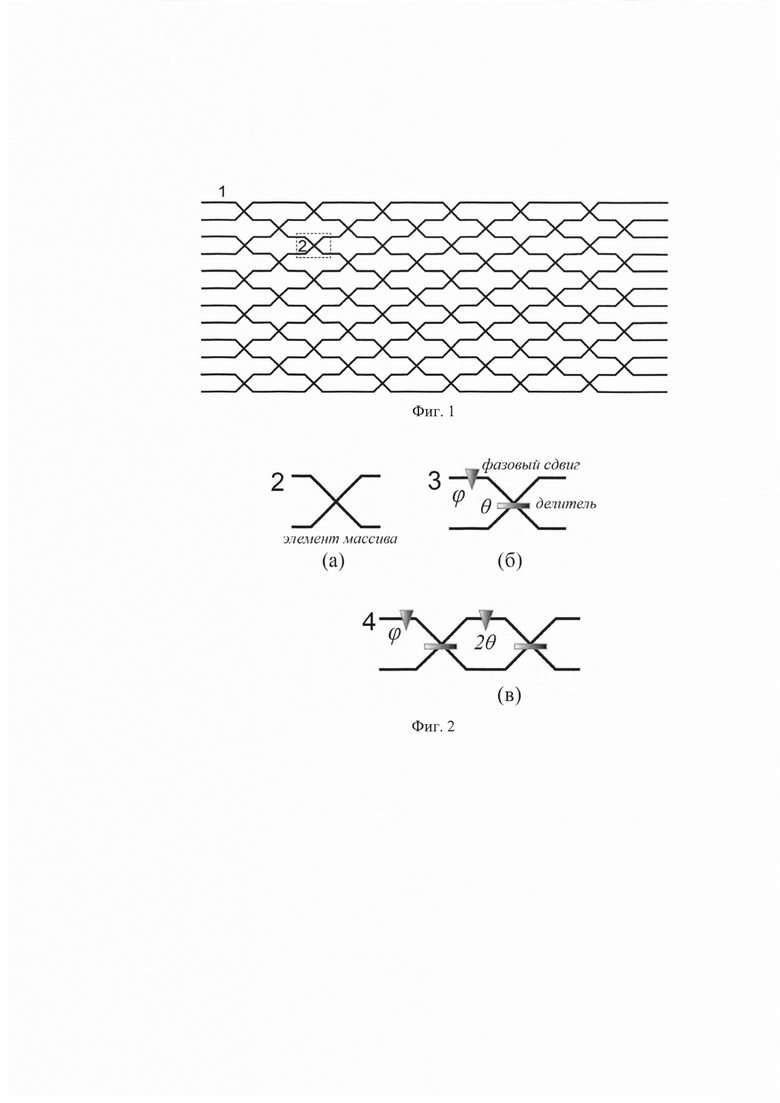
На Фиг. 1 изображена планарная схема универсального многоканального линейного преобразования 1 для случая 12 каналов, известная из уровня техники.
На Фиг. 2 схематически изображено пояснение к обозначению элементарного канального преобразования (а), которое представляет собой делитель, характеризуемый угловым параметром θ, который определяет коэффициент деления, и фазовым сдвигом в одном из каналов ϕ (б). На схеме (в) представлен вариант реализации реконфигурируемого преобразования с использованием интерферометра, известный из уровня техники.
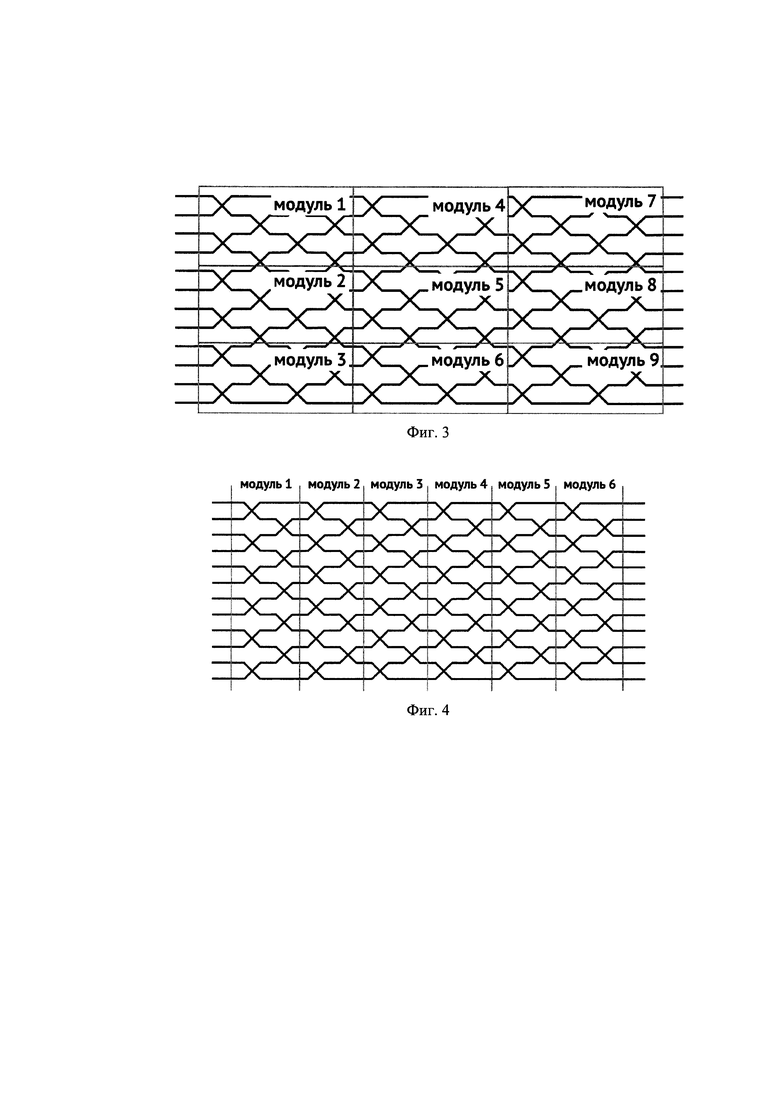
На Фиг. 3 изображен пример разбиения 12-канальной универсальной планарной топологии на модули, представляющие собой соединенные блоки размером 4×4.
На Фиг. 4 изображен пример разбиения 12-канальной универсальной планарной топологии на модули, представляющие собой 12-канальные слои, соединенные последовательно.
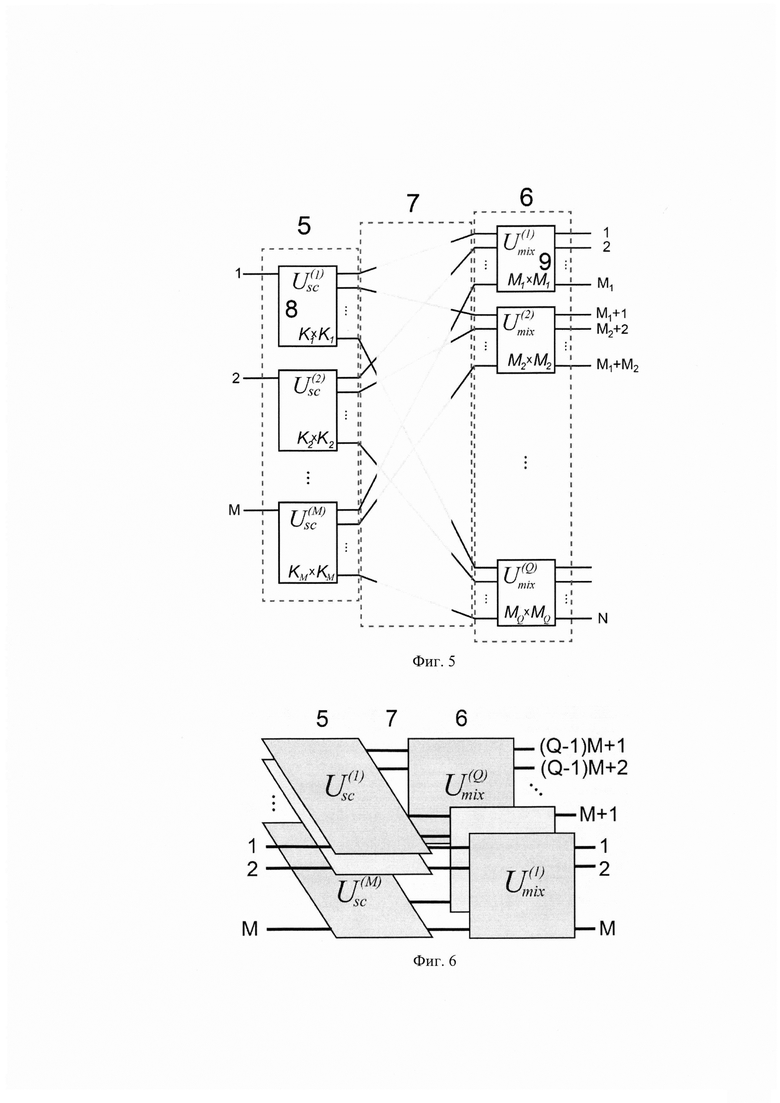
На фиг. 5-12 приведены поясняющие изобретение схемы и графики, а именно: На Фиг. 5 изображена общая схема многоканального линейного преобразования М входных сигналов в N выходных каналов, состоящая из двух последовательных блоков - рассеяния (5) и смешения (6), соединенных друг с другом оптическими каналами (соединение 7), которая предлагается в настоящем изобретении. При этом блоки составлены из модулей разных размерностей. На Фиг. 5 выделены два модуля, отвечающие за рассеяние (8) и смешение (9).
На Фиг. 6 изображена схема интерферометра для случая, когда число выходных каналов преобразования N кратно больше числа входных каналов М:N=QM. В таком случае соединения (7) выходных каналов модулей блока рассеяния (5) с входными каналами модулей блока смешения (6) возможны без пересечений используя изображенную конфигурацию размещения модулей.
На Фиг. 7 изображена схема соединения выходных каналов модулей блока рассеяния (5) с входными каналами модулей блока смешения (6) для случая, представленного на Фиг. 6.
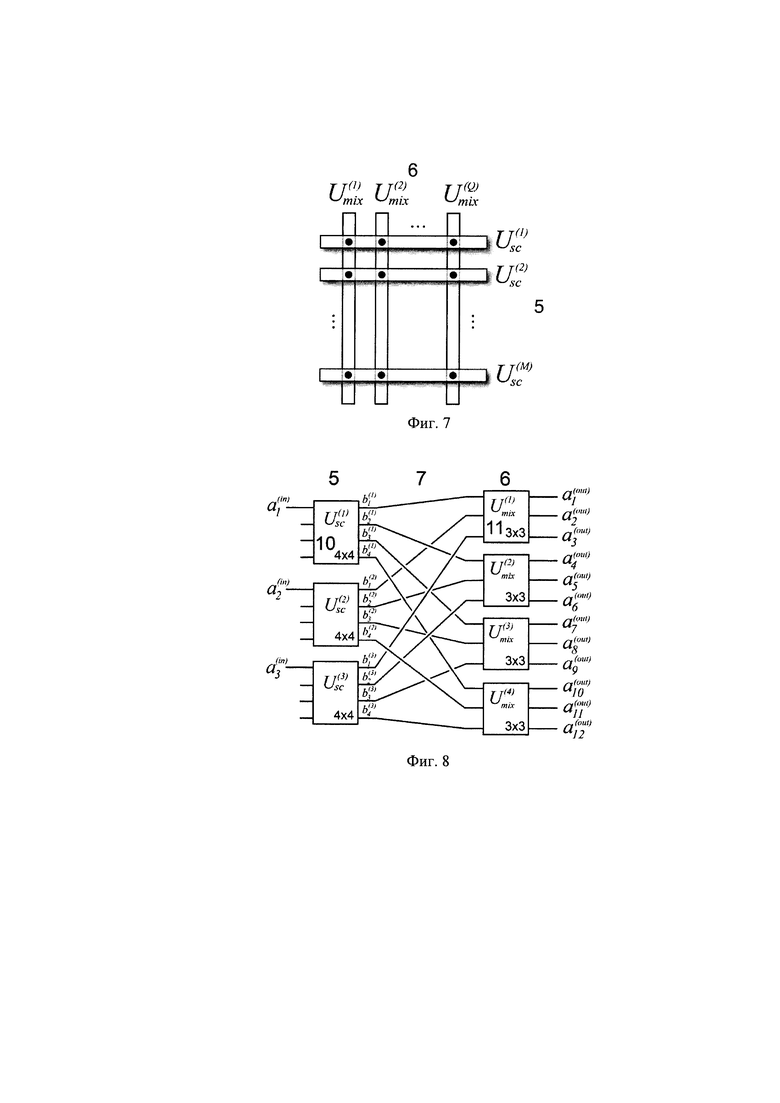
На Фиг. 8 изображен пример многоканальной линейной оптической схемы при М=3 входных каналов и N=12 выходных каналов, для частного случая 3-х модулей преобразования рассеяния размерности K=4 (10), и 4-х модулей преобразования смешения размерности М=3 (11).
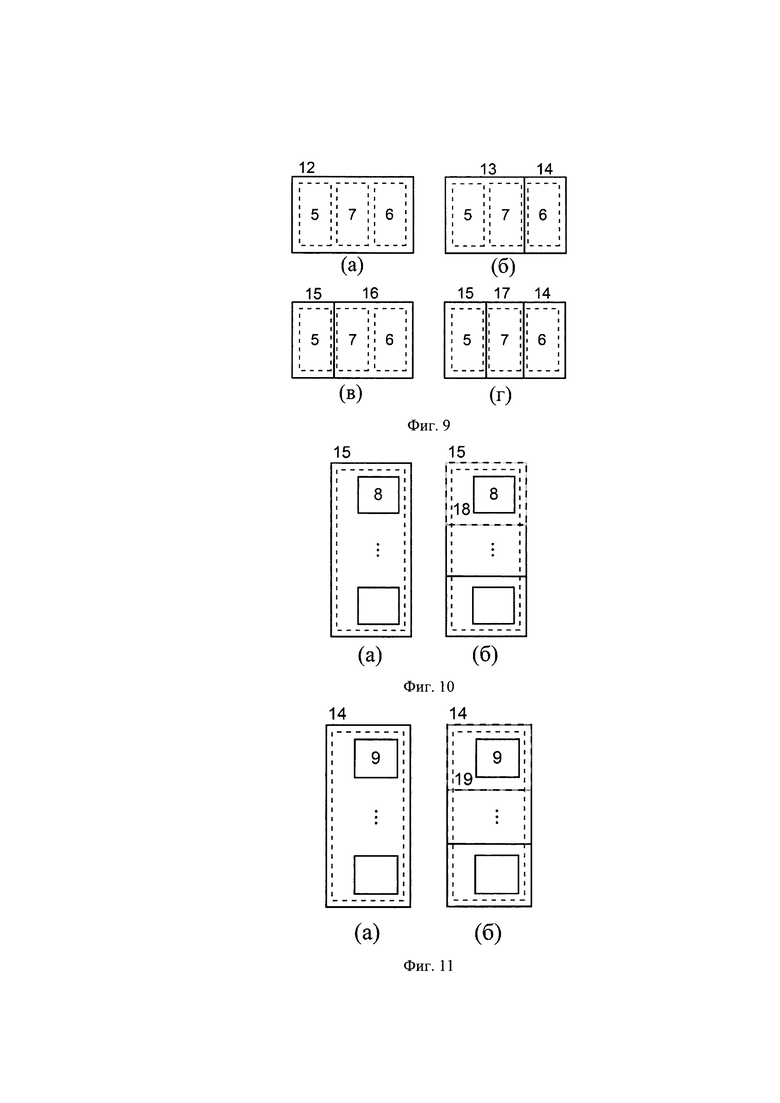
На Фиг. 9 приведены возможные схемы осуществления интерферометра, реализующего предложенный способ многоканальных оптических преобразований:
а) в виде одиночного монолитного устройства (12), в котором реализованы блоки рассеяния (5), смешения (6) и их соединения (7);
б) в виде двух соединенных монолитных схем, одна из которых (13) содержит блок рассеяния (5) и соединения (7), а другая (14) содержит блок смешения;
в) в виде двух соединенных монолитных схем, одна из которых (15) содержит блок рассеяния (5), а другая (16) содержит блок смешения (6) и соединения (7), объединяющие преобразования двух блоков;
г) в виде трех монолитных схем, каждое из которых в отдельности реализует блок рассеяния (5) (схема (15)), блок смешения (6) (схема (14)) и соединения (7) (схема (17)).
Фиг. 10 иллюстрирует возможные способы реализации схем блока рассеяния в добавлении к разбиению интерферометра, изображенным на Фиг. 7:
а) все схемы модулей блока (одно из них (8)) реализованы на одной монолитной схеме (15),
б) каждое преобразование реализовано на отдельной монолитной схеме (например, модуль (8) на отдельной монолитной схеме (18)). Монолитные схемы соединены друг с другом.
Фиг. 11 иллюстрирует возможные способы реализации схем блока смешения дополнительно к разбиению интерферометра, изображенным на Фиг. 9:
а) все схемы модулей блока (одной из них (9)) реализованы на одной монолитной схеме (14),
б) каждое преобразование (9) реализовано на отдельной монолитной схеме (17). Монолитные схемы соединены друг с другом.
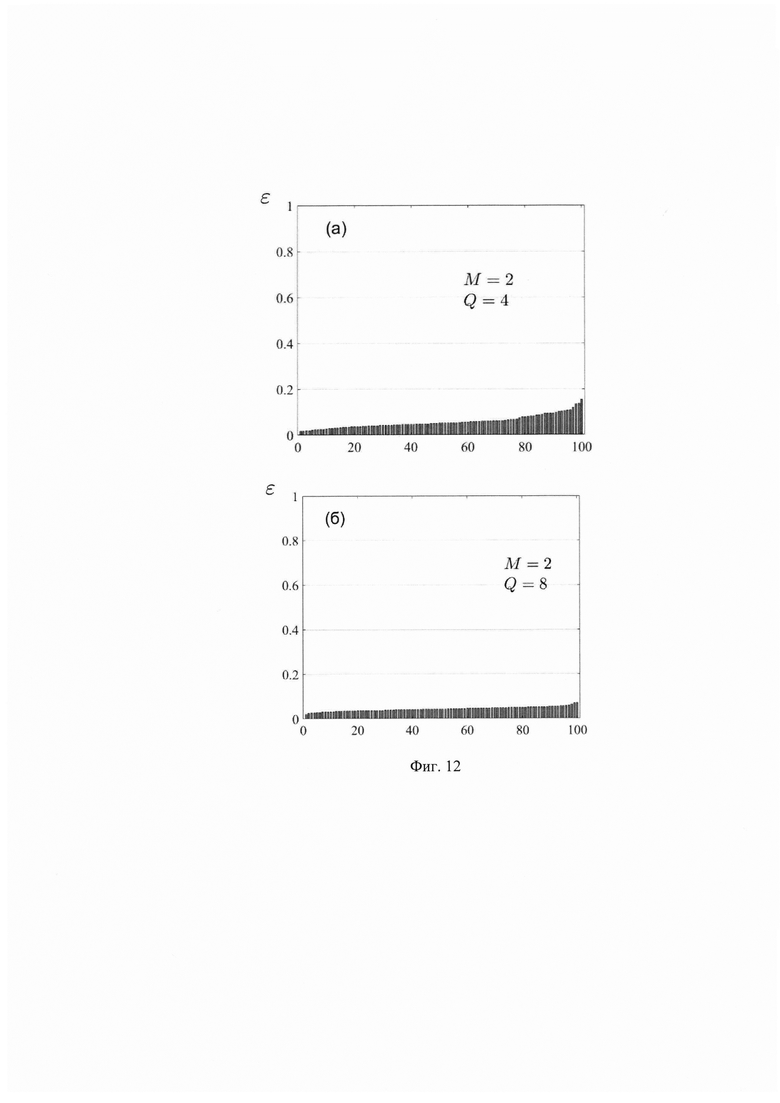
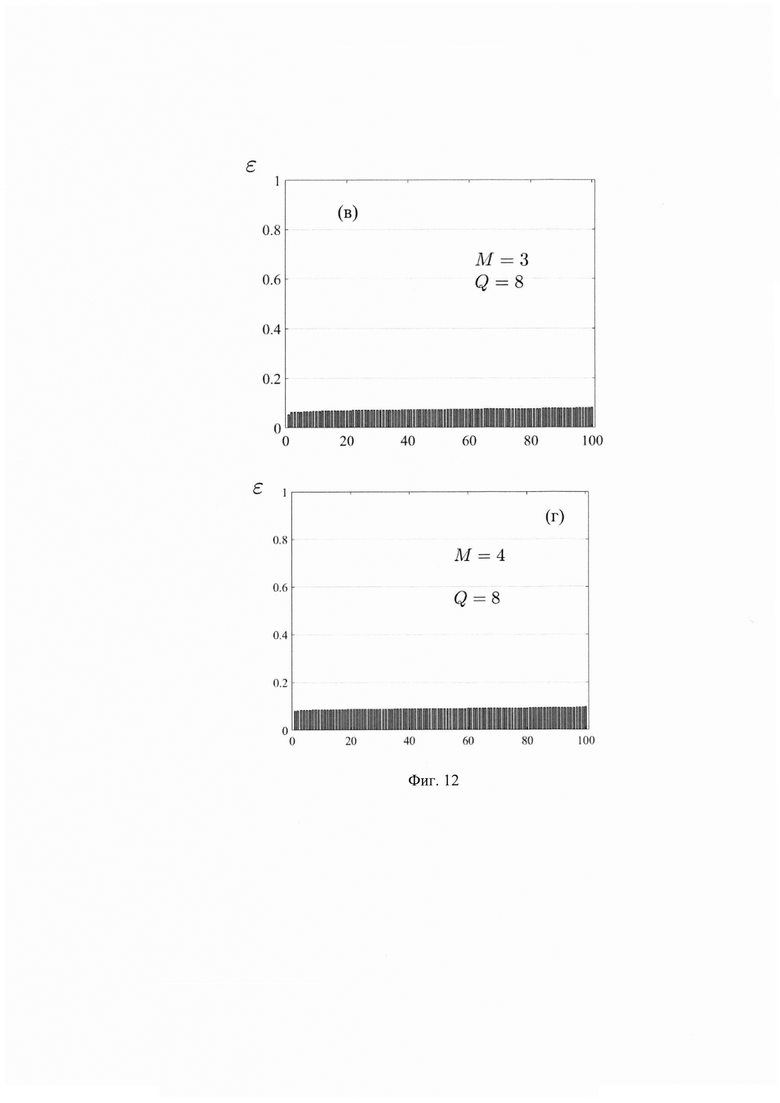
На Фиг. 12 изображены графики зависимостей параметра ошибки (1.14) для набора 100 унитарных матриц, которые были сгенерированы случайным равномерным образом, при их аппроксимации с помощью блочной схемы интерферометра, изображенной на Фиг. 5. Размерности модулей в каждом блоке интерферометра одинаковы. Значения параметра ошибки упорядочены по их возрастанию.
Осуществление изобретения
Многоканальные линейные оптические преобразования необходимы в фундаментальных экспериментальных исследованиях и осуществлении на практике алгоритмов по обработке, получению и передачи информации. В частности, особый интерес многоканальные преобразования представляют для области прикладной квантовой информации в связи с задачей бозонного сэмплинга, осуществление которой на практике рассматривается в качестве удобной демонстрации вычислительных преимуществ квантовых устройств над классическими (С. Ааронсон, А. Архипов, «Вычислительная сложность линейной оптики» // Theory of Computing, Т. 9, С. 143-252 (2013)).
Характеристики многоканальных устройств линейно-оптических интерферометров описывают комплексными матрицами (матрицами преобразований), элементы которых имеют смысл коэффициентов передачи, а их размерность задает число каналов преобразования, т.е. матрица преобразования U имеет смысл «соотношений вход-выход» между амплитудами сигналов на входе 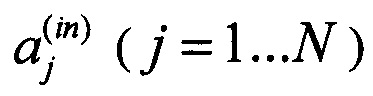 и амплитудами сигналов на выходе после преобразования
и амплитудами сигналов на выходе после преобразования 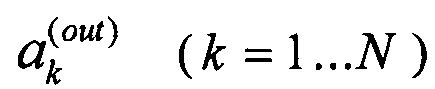 (промежуточных сигналов):
(промежуточных сигналов):

где N - число каналов преобразования (размерность преобразования). Описание линейных преобразований квантовых сигналов может быть описано также соотношением (1.1) (Ландау, Л.Д., Лифшиц, Е.М. Квантовая механика (нерелятивистская теория), 1974 («Теоретическая физика», том III).). Без ограничения общности, можно рассматривать преобразования U без потерь, т.к. преобразование с потерями можно представить в виде части другого преобразования без потерь более высокой размерности.
Для более однозначного понимания сущности заявленного изобретения ниже представлены основные термины и определения, используемые в рамках настоящего описания.
Преобразование смешения - линейное преобразование общего вида (1.1).
Преобразование рассеяния - частный вид многоканального линейного преобразования (1.1), в котором используется только один вполне определенный входной канал. В дальнейшем полагаем, что в преобразованиях рассеяния используют первый входной канал, таким образом матрица рассеяния  имеет вид:
имеет вид:
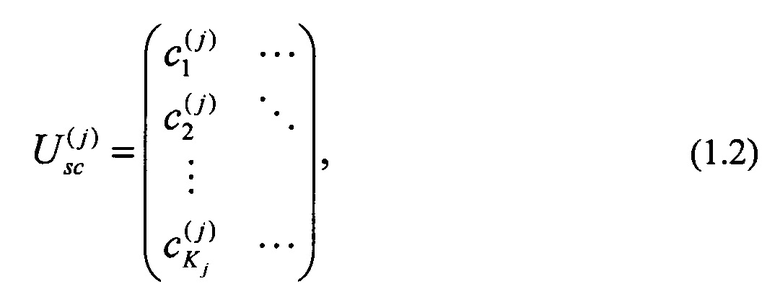
где 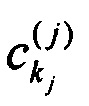 - комплексные коэффициенты, описывающие амплитуды рассеянных сигналов в kj-м выходном порте
- комплексные коэффициенты, описывающие амплитуды рассеянных сигналов в kj-м выходном порте 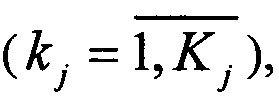 Kj - размерность преобразования, j - индекс, нумерующий преобразование рассеяния. Для этих коэффициентов справедливо условие нормировки:
Kj - размерность преобразования, j - индекс, нумерующий преобразование рассеяния. Для этих коэффициентов справедливо условие нормировки: 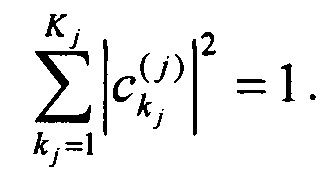 В (1.2) важны только коэффициенты первого столбца матрицы, т.е. число независимых параметров, задающих преобразование рассеяния, равно 2Kj-1. В дальнейшем интерес представляют схемы интерферометра, которые содержат несколько преобразования рассеяния, поэтому здесь введен индекс j, который нумерует конкретное преобразование и который также нумерует размерность этого преобразования Kj.
В (1.2) важны только коэффициенты первого столбца матрицы, т.е. число независимых параметров, задающих преобразование рассеяния, равно 2Kj-1. В дальнейшем интерес представляют схемы интерферометра, которые содержат несколько преобразования рассеяния, поэтому здесь введен индекс j, который нумерует конкретное преобразование и который также нумерует размерность этого преобразования Kj.
Преобразования перестановок - преобразование, описываемое матрицей перестановок, которое описывает изменение порядка следования каналов на выходах блока рассеяния в соответствии с нумерацией входных каналов блока смешения. Т.е. это преобразование задается необходимыми соединениями каналов блока рассеяния с каналами блока смешения. Например, преобразование перестановки 7, изображенное на Фиг. 8 (для 3 входных каналов и 12 выходных каналов), описывается матрицей следующего вида:

Как и элементы произвольной матрицы линейного преобразования (1.1), элементы матрицы перестановок имеют смысл коэффициентов передачи, однако, могут принимать только «0» или «1». При этом в одной строке и в одном столбце не может быть больше одного элемента со значением «1» - это отражает отсутствие взаимодействия между сигналами, распространяющимися по разным каналам преобразования перестановки. Также следует отметить, что матрица перестановок не обязана быть квадратной, как в примере (1.3). В общем случае число строк Nr и число столбцов Ncol матрицы Р может быть разным. Если Nr<Ncol, то матрица описывает преобразование перестановки, в котором не все сигналы, поступающие на его вход, используют в дальнейшем на ее выходе. Действительно, предполагая, что на все Ncol входных каналов поступают сигналы, и учитывая, что в один выходной канал не могут поступать сигналы от двух и более входов, до выхода перестановки дойдет Nr<Ncol сигналов. В противоположном случае (Nr>Ncol) все входные сигналы доходят до выхода перестановки. Однако имеются дополнительные Nr-Ncol каналов на выходе перестановки, и в преобразование, следующим за перестановкой, сигналы в эти каналы никогда не поступают.
Промежуточные каналы - каналы, исходящие из преобразований рассеяния.
Промежуточные амплитуды - амплитуды поля, выходящего из преобразований рассеяния, т.е. из промежуточных каналов.
Модуль рассеяния - часть устройства заявляемого оптического интерферометра, в котором осуществляется одно независимое преобразование рассеяния входного сигнала.
Модуль смешения - часть устройства заявляемого оптического интерферометра, в котором осуществляется одно независимое преобразование смешения. На модуль смешения могут поступать промежуточные амплитуды, исходящие от разных модулей рассеяния.
Блок рассеяния - часть устройства заявляемого оптического интерферометра, в котором реализуются все независимые преобразования рассеяния. Таким образом, блок рассеяния включает все модули рассеяния.
Блок смешения - часть устройства заявляемого оптического интерферометра, в котором реализуются все преобразования смешения. Таким образом, блок рассеяния включает все модули смешения.
Соединительный блок (блок соединения) - часть устройства заявляемого оптического интерферометра, в котором осуществляется соединение выходных каналов блока рассеяния с входными каналами блока смешения. Преобразование соединительного блока описывается матрицей перестановок (см. выше).
В настоящем изобретении предложена архитектура оптической схемы многоканального интерферометра, которая реализует широкий класс линейных преобразований. Предлагаемый класс оптических схем может быть использован для случаев, когда число сигналов М, поступающих на вход преобразования, (минимум вдвое) меньше, чем общее число каналов преобразования N. Использование этого обстоятельства дает возможность предложить следующую архитектуру для многоканальных линейных оптических преобразований. Идея, лежащая в основе архитектуры, состоит в разложении многоканального преобразования на два последовательных этапа. На первом этапе каждый из входных сигналов независимо подвергается преобразованию рассеяния. На втором этапе эти сигналы подвергаются взаимной интерференции - они «смешиваются» друг с другом, поэтому в дальнейшем этот этап называется смешением (преобразование смешения).
Фиг. 5 иллюстрирует предложенный способ многоканального преобразования. На приведенной схеме М входных сигналов подвергаются преобразованию М независимыми преобразованиями рассеяния. Очевидно, что число преобразований рассеяния фиксировано и равно М, т.е. блок рассеяния (5) состоит из М независимых модулей 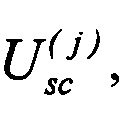 каждый из которых осуществляет независимые преобразования рассеяния между Kj промежуточными каналами
каждый из которых осуществляет независимые преобразования рассеяния между Kj промежуточными каналами 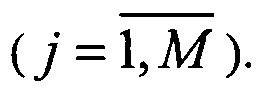 В блоке рассеяния преобразование j-го сигнала описывается унитарной матрицей
В блоке рассеяния преобразование j-го сигнала описывается унитарной матрицей 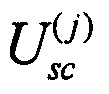 размером Kj×Kj. Таким образом, j-тое преобразование рассеяния по смыслу эквивалентно преобразованию рассеяния j-го входного сигнала. При этом общее число промежуточных каналов на выходе блока рассеяния равно:
размером Kj×Kj. Таким образом, j-тое преобразование рассеяния по смыслу эквивалентно преобразованию рассеяния j-го входного сигнала. При этом общее число промежуточных каналов на выходе блока рассеяния равно: 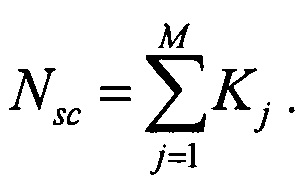 Для преобразования рассеяния определяющими являются элементы матрицы
Для преобразования рассеяния определяющими являются элементы матрицы 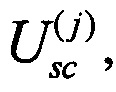 стоящие только в одном ее столбце - операция рассеяния одиночного сигнала является узким подклассом более широкого класса всех унитарных преобразований. Полагаем, что сигналы подаются на первый порт преобразований рассеяния и, таким образом, матрица имеет вид (1.2). Общее преобразование первой стадии оптической схемы описывается известной блочно-диагональной матрицей (https://dic.academic.ru/dic.nsf/aiwiki/813058):
стоящие только в одном ее столбце - операция рассеяния одиночного сигнала является узким подклассом более широкого класса всех унитарных преобразований. Полагаем, что сигналы подаются на первый порт преобразований рассеяния и, таким образом, матрица имеет вид (1.2). Общее преобразование первой стадии оптической схемы описывается известной блочно-диагональной матрицей (https://dic.academic.ru/dic.nsf/aiwiki/813058):
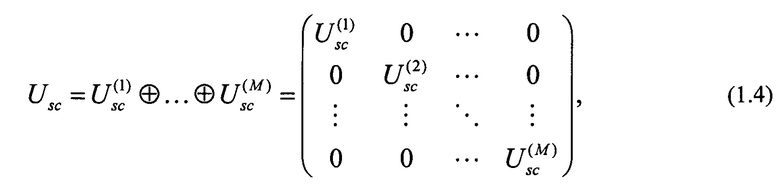
В (1.4) символами "0" обозначены матрицы, составленные из нулевых элементов; эти матрицы в общем случае имеют различающуюся размерность. Число независимых параметров, задающих матрицу Usc (1.4), равно 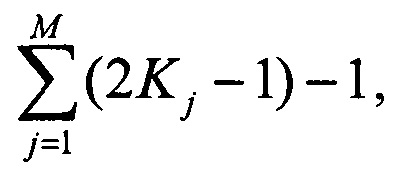 где учтены условия нормировки и произвольность выбора глобальной фазы для Nsc промежуточных каналов на выходе блока U(sc).
где учтены условия нормировки и произвольность выбора глобальной фазы для Nsc промежуточных каналов на выходе блока U(sc).
На втором этапе происходит смешение рассеянных сигналов. Для этого используют Q преобразований 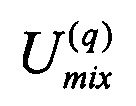 с размерностями Mq×Mq, где индекс q нумерует конкретное преобразование смешения
с размерностями Mq×Mq, где индекс q нумерует конкретное преобразование смешения 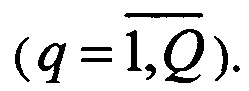 Общая размерность блока смешения равна
Общая размерность блока смешения равна  В отличие от преобразования рассеяния, матрицы преобразований смешения - произвольные унитарные матрицы размерности Mq×Mq. Общее преобразование первой стадии оптической схемы описывается матрицей блочно-диагональной матрицей:
В отличие от преобразования рассеяния, матрицы преобразований смешения - произвольные унитарные матрицы размерности Mq×Mq. Общее преобразование первой стадии оптической схемы описывается матрицей блочно-диагональной матрицей:
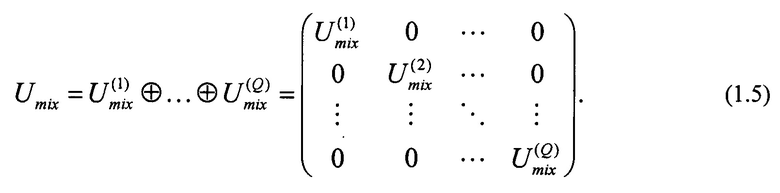
Необходимо, чтобы 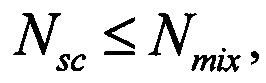 т.к. в противном случае останутся неиспользованными промежуточные каналы. С точки зрения универсальности интерферометра, построенного при заданных М и N, нужно, чтобы каждый из Q модулей смешения принимал на вход сигналы от всех М модулей рассеяния, т.е. должно быть Kj i Q и, следовательно, Nsc i QM. Таким образом, в дальнейшем подразумеваем, что справедлива следующая цепочка неравенств:
т.к. в противном случае останутся неиспользованными промежуточные каналы. С точки зрения универсальности интерферометра, построенного при заданных М и N, нужно, чтобы каждый из Q модулей смешения принимал на вход сигналы от всех М модулей рассеяния, т.е. должно быть Kj i Q и, следовательно, Nsc i QM. Таким образом, в дальнейшем подразумеваем, что справедлива следующая цепочка неравенств:

Отметим также, что должно быть 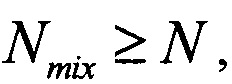 т.к. иначе каналов на выходе не хватит для реализации интерферометра.
т.к. иначе каналов на выходе не хватит для реализации интерферометра.
В зависимости от конкретного преобразования, которое нужно реализовать в j интерферометре, на вход каждого из преобразований смешения могут подаваться промежуточные сигналы от всех преобразований рассеяния или только от части из них. В соответствии с этим выбирают размерности Kj и Mq. Для выбора конкретной архитектуры оптической схемы интерферометра, которая задается набором параметров размерности Kj и Mq, где 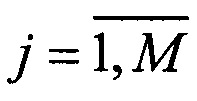 и
и 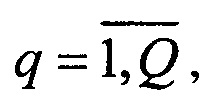 можно пользоваться известными мерами близости (различия) двух матриц, которые характеризуют степень совпадения или различия двух матриц. Выбор размерностей блоков преобразований основан на максимизации (минимизации) меры соответствия (различия). Например, можно использовать следующую меру:
можно пользоваться известными мерами близости (различия) двух матриц, которые характеризуют степень совпадения или различия двух матриц. Выбор размерностей блоков преобразований основан на максимизации (минимизации) меры соответствия (различия). Например, можно использовать следующую меру:
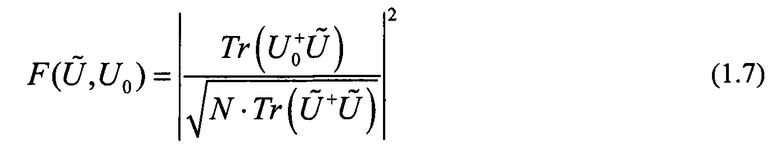 !
!
где U0 - матрица преобразования, которое нужно осуществить в интерферометре, 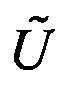 - матрица преобразования схемы интерферометра (1.9), Tr означает операцию взятия следа матрицы,
- матрица преобразования схемы интерферометра (1.9), Tr означает операцию взятия следа матрицы, 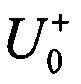 и
и 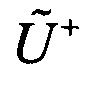 - матрицы, комплексно-сопряженные к U0 и
- матрицы, комплексно-сопряженные к U0 и  соответственно.
соответственно.
Выбор параметров оптической схемы интерферометра состоит из следующих шагов:
1) Задают число входных и выходных каналов преобразования - М и N.
2) Задают множество линейно-оптических преобразований, которые нужно осуществить с помощью интерферометра. Множество преобразований может представлять собой как счетное множество матриц U0n, где n - индекс матрицы, или как класс матриц 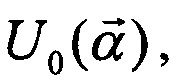 где
где 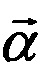 - набор параметров. Матрицы могут быть заданы как численно (матрицы из чисел), так и аналитически (матричные функции в зависимости от параметров).
- набор параметров. Матрицы могут быть заданы как численно (матрицы из чисел), так и аналитически (матричные функции в зависимости от параметров).
3) В дополнении к п. 2 могут быть заданы весовые коэффициенты для множества матриц: w(n) для счетного множества или 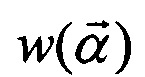 для класса параметризованных матриц. Весовые коэффициент определяют приоритет конкретного подмножества матриц - чем выше весовой коэффициент, тем важнее приблизить именно это подмножество матриц с наибольшей точностью.
для класса параметризованных матриц. Весовые коэффициент определяют приоритет конкретного подмножества матриц - чем выше весовой коэффициент, тем важнее приблизить именно это подмножество матриц с наибольшей точностью.
4) Получают параметры оптической схемы (параметры размерности преобразований Kj и Mq в блоках рассеяния и смешения) как значения, которые максимизируют среднюю меру: 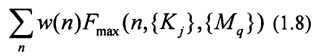
относительно Kj и Mq. В (1.8) 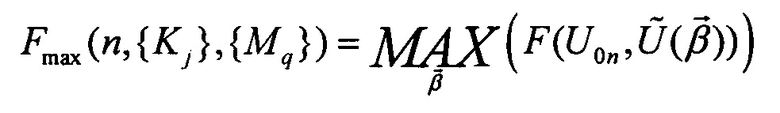 означает максимум по параметрам схемы интерферометра
означает максимум по параметрам схемы интерферометра 
5) В соответствии с полученными Kj и Mq конструируют схему интерферометра (Фиг. 5).
6) Конкретное преобразование из заданного множества матриц получают с помощью надлежащего выбора параметров 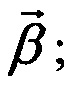 оно максимизирует (1.7).
оно максимизирует (1.7).
Матрица общего преобразования полученной оптической схемы может быть записана в виде:

где Р - матрица перестановки, которая приводит в соответствие нумерацию каналов на первой стадии рассеяния с нумерацией каналов на второй стадии смешения. Размерность матрицы перестановки в (1.9) равна N×Nsc. Фиг. 6 иллюстрирует принцип, в соответствии с которым получается матрица перестановок Р для частного случая N=QM. На Фиг. 7 приведена схема соответствия промежуточных выходных каналов блока рассеяния входным каналам блока смешения.
В дальнейшем для элементов матрицы перестановки удобно перейти от I нумерации двумя индексами, обозначающих элемент, стоящий на пересечении соответствующих столбца и строки матрицы Pmn, к нумерации двумя парами индексов 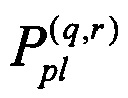 (пара «верхний и нижний индексы»). В таких обозначениях элемент матрицы
(пара «верхний и нижний индексы»). В таких обозначениях элемент матрицы 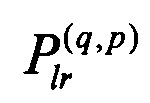 описывает соединение промежуточных каналов преобразований рассеяния с входными каналами преобразований смешения, соответствующие коэффициенту передачи от r-ого канала р-ого преобразования рассеяния к
описывает соединение промежуточных каналов преобразований рассеяния с входными каналами преобразований смешения, соответствующие коэффициенту передачи от r-ого канала р-ого преобразования рассеяния к 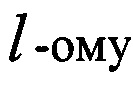 каналу q-ого преобразования смешения. Переход от двухиндексного обозначения к четырехиндексному может быть выполнен согласно соотношениям:
каналу q-ого преобразования смешения. Переход от двухиндексного обозначения к четырехиндексному может быть выполнен согласно соотношениям:

и

где K - размерность j-го преобразования рассеяния, Mi - размерность i-го преобразования смешения. Таким образом, верхний индекс отвечает за номер преобразования, а соответствующий ему нижний индекс отвечает за номер канала в этом преобразовании.
В таком же ключе удобно ввести двухиндексную нумерацию и для амплитуд на выходе интерферометра. Амплитуда на выходе преобразования (1.1) 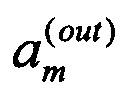 с одним индексом m
с одним индексом m 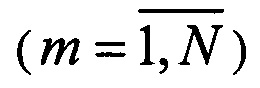 в двухиндексном обозначении запишется как
в двухиндексном обозначении запишется как 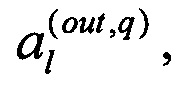 где индексы связаны соотношением (1.11).
где индексы связаны соотношением (1.11).
Фиг. 9-11 иллюстрируют возможные способы изготовления схем блоков рассеяния, смешения и их соединения, которые отличаются по их разделению на монолитные схемы.
На Фиг. 9а приведен возможный способ осуществления интерферометра, реализующего предложенный способ многоканальных оптических преобразований в виде одного монолитного устройства (12), в котором реализованы блоки рассеяния (5), смешения (6) и их соединения (7). Более практичным подходом может быть создание интерферометра в виде двух соединенных монолитных схем, изображенным на Фиг. 9б. В этом случае интерферометр представляет собой две соединенные монолитные схемы, одна из которых (13) содержит блок рассеяния (5) и соединения (7), а другая (14) содержит блок смешения. На Фиг. 9в приведен возможные способ осуществления интерферометра в виде двух соединенных монолитных схем, одна из которых (15) содержит блок рассеяния (5), а другая (16) содержит блок смешения (6) и соединения (7), объединяющие преобразования двух блоков. Фиг. 9г иллюстрирует возможный способ осуществления интерферометра в виде трех монолитных схем, каждое из которых в отдельности реализует блок рассеяния (5) (схема (15)), блок смешения (6) (схема (14)) и соединения (7) (схема (17)).
В добавление к разделению схемы интерферометра на отдельные монолитные схемы, содержащие блоки преобразования и их объединения, Фиг. 10 иллюстрирует возможные способы реализации схем блока рассеяния в добавлении к разбиению интерферометра, изображенным на Фиг. 7: а) все схемы модулей блока (одно из них (8)) реализованы на одной монолитной схеме (15), б) каждое преобразование реализовано на отдельной монолитной схеме (например, модуль (8) на отдельной монолитной схеме (18)). Монолитные схемы соединены друг с другом. Фиг. 11 иллюстрирует возможные способы реализации схем блока смешения дополнительно к разбиению интерферометра, изображенным на Фиг. 9.
Точность осуществления преобразований U0 предлагаемым способом подтверждена в результате проведения экспериментов. Например, реализован вариант, когда размерности модулей в каждом блоке одинаковы, т.е. Kj=Q, Mq=М, и, следовательно, справедливо простое соотношение между число входных и выходных каналов: N=QM. Класс универсальных унитарных матриц, описывающих линейные преобразования М сигналов между N≥M выходными каналами, имеет 2NM - М2 действительных параметров. Число независимых параметров, полностью описывающих рассматриваемую модульную схему (для случая N=QM), равно Q(M2+M+Y)-M-2. Сравнение числа параметров, необходимых для полного описания предлагаемой модульной оптической схемы, с числом параметров общего класса унитарных преобразований (М→QM) говорит о неполной универсальности предлагаемой схемы.
Очевидно, что предлагаемый тип оптических схем может реализовать тривиальные линейные преобразования перестановок: М входных сигналов можно переставить в любые из N выходных каналов без их смешения друг с другом. Также очевидно, что такие схемы могут осуществлять произвольные преобразования над одиночными сигналами (М=1).
Используя (1.2) и (1.9), можно предложить альтернативную (1.7) меру соответствия матриц преобразования. Для U0 можно воспользоваться мерой соответствия, которая следует из (1.9). Для этого необходимо рассмотреть матрицу
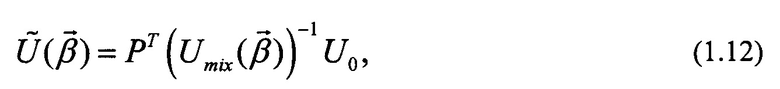
которая зависит от набора параметров 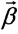 (всего Q(M2-М+1)-1 параметров), задающих матрицу смешения. Величина
(всего Q(M2-М+1)-1 параметров), задающих матрицу смешения. Величина
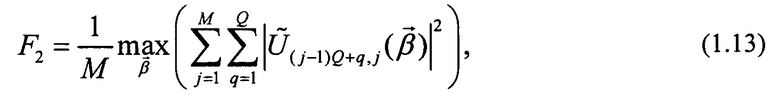
получается из элементов матрицы (1.12) в результате максимизации по параметрам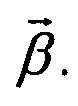 Значение F2=1 отвечает возможности абсолютно точного соответствия преобразования модульной схемы заданному U0. При анализе удобно рассматривать величину F3=(F2M-1)/(М-1), которая получаем на основе F2. Отличие F3 от F2 заключается в области значений, которые они могут принимать - минимально возможное значение F3=0 отвечает наихудшим результатом, тогда как максимально возможное значение F3=1 соответствует идеальному результату. Далее, можно ввести параметр ошибки:
Значение F2=1 отвечает возможности абсолютно точного соответствия преобразования модульной схемы заданному U0. При анализе удобно рассматривать величину F3=(F2M-1)/(М-1), которая получаем на основе F2. Отличие F3 от F2 заключается в области значений, которые они могут принимать - минимально возможное значение F3=0 отвечает наихудшим результатом, тогда как максимально возможное значение F3=1 соответствует идеальному результату. Далее, можно ввести параметр ошибки:

принимающий значения от 0 (наилучший случай) до 1/Q (наихудший случай). На Фиг. 12 изображены графики зависимостей параметра ошибки (1.14) при аппроксимации набора 100 унитарных матриц, сгенерированных случайным образом из равномерного распределения, для различных значений числа входных каналов М и числа преобразований смешения Q (в рассматриваемом случае N=QM). Уровни ошибок на графиках приведены в отсортированном возрастающем порядке.
Для иллюстрации работы интерферометра, реализующего заявляемый способ преобразования, предложен конкретный пример преобразования с параметрами М=3, N=12, изображенный на Фиг. 6. На вход трех каналов интерферометра подают сигналы с амплитудами 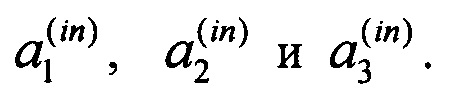 Сигналы поступают на блок рассеивания (3), в котором они преобразуются независимыми преобразованиями (1.2) (8). Каждое преобразование амплитуд сигналов
Сигналы поступают на блок рассеивания (3), в котором они преобразуются независимыми преобразованиями (1.2) (8). Каждое преобразование амплитуд сигналов 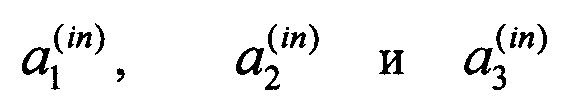 описывается 4-мя коэффициентами -
описывается 4-мя коэффициентами -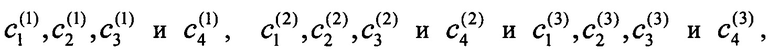 соответственно. Амплитуды промежуточных сигналов на выходе блока рассеяния рассчитываются согласно формулам:
соответственно. Амплитуды промежуточных сигналов на выходе блока рассеяния рассчитываются согласно формулам:

где индексы могут принимать следующие значения: j=1, 2, 3; kj=1, 2, 3, 4.
Далее, 12 сигналов (1.15) с выхода блока рассеивания (3) поступают на блок смешения (4) через соединения (5), которые реализуют необходимые перестановки каналов Р (см. Фиг. 6). Блок смешения реализован в виде четырех 3-канальных преобразований (9). В общем виде матрицы, задающие эти преобразования имеют вид:
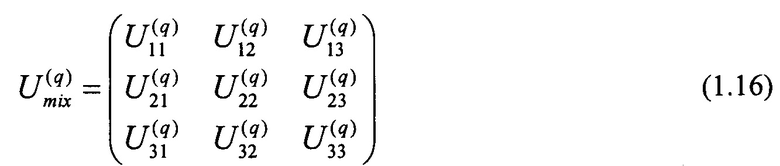
Преобразуя промежуточные амплитуды 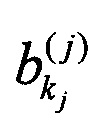 матрицами смешения (1.16) в соответствии с Фиг. 6, получают следующие соотношения, связывающие амплитуды сигналов на входе, с амплитудами на выходе:
матрицами смешения (1.16) в соответствии с Фиг. 6, получают следующие соотношения, связывающие амплитуды сигналов на входе, с амплитудами на выходе:
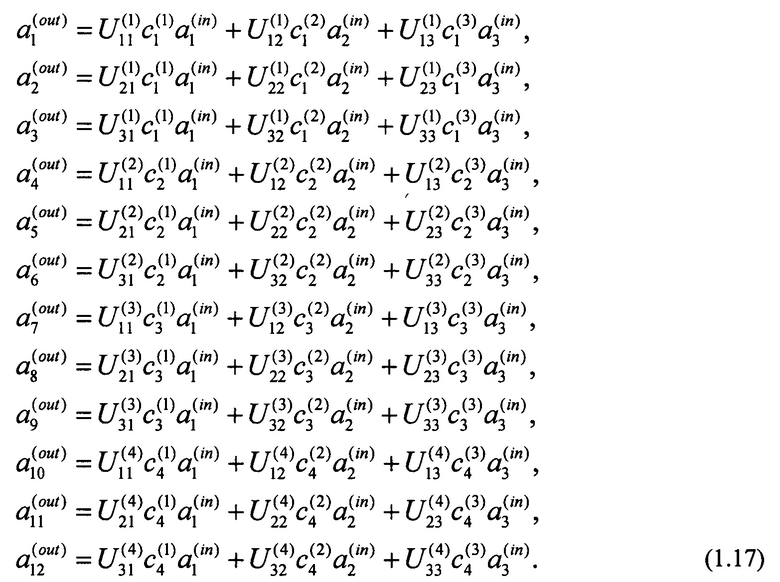
Задание параметров  и
и  в (1.17) определяет конкретное преобразование.
в (1.17) определяет конкретное преобразование.
При практических реализациях эти параметры определяются фазовыми параметрами реконфигурируемых интерферометров (см. Фиг. 2), из которых построены оптические схемы. Как правило, это осуществляется с использованием термо-оптического эффекта, при котором локальный нагрев вызывает изменение показателя преломления области нагрева, который, в свою очередь, приводит к дополнительному набегу фазы. При этом локальный нагрев осуществляется теплом, которое выделяется на электрическом элементе с сопротивлением, на который подается разность потенциалов. Величина разности потенциалов для каждого 2-канального интерферометра служит управляющим параметром, т.к. они определяет нагрев и, следовательно, набеги фаз θ и ϕ оптического сигнала, проходящего рядом с электрическим элементом.
В качестве примера рассмотрим интерферометр, изображенным на рис. 6 и описывающейся матрицей преобразования (1.17), с точки зрения возможности реализовывать перестановки между каналами. Суть перестановок заключается в изменении канала, по которому распространяется сигнал. При этом перестановки являются независимыми преобразованиями, поэтому достаточно рассмотреть перестановку только одного из каналов. Например, для перестановки 1-го канала, на который подается сигнал с амплитудой  в 12-й выходной канал, необходимо, чтобы
в 12-й выходной канал, необходимо, чтобы 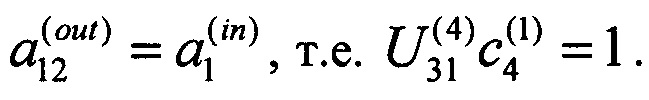 Для этого необходимо, чтобы
Для этого необходимо, чтобы 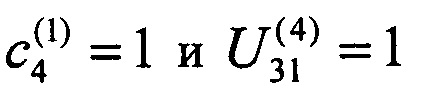 - это всегда можно осуществить соответствующей перестройкой схемы интерферометра. При такой перестановке сигнал
- это всегда можно осуществить соответствующей перестройкой схемы интерферометра. При такой перестановке сигнал 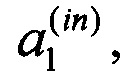 поступающий на первый входной канал, полностью передается преобразованием рассеяния в 4-й промежуточный канал:
поступающий на первый входной канал, полностью передается преобразованием рассеяния в 4-й промежуточный канал: 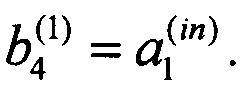 Далее этот сигнал поступает на 1-й входной канал преобразования смешения
Далее этот сигнал поступает на 1-й входной канал преобразования смешения 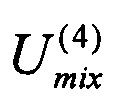 (10-й канал всей схемы интерферометра), которые направляет его на 4-й выходной канал (12-й канал всей схемы интерферометра). Таким образом, для перестановок схема предлагаемого интерферометра вырождается в два последовательных блока перестановок.
(10-й канал всей схемы интерферометра), которые направляет его на 4-й выходной канал (12-й канал всей схемы интерферометра). Таким образом, для перестановок схема предлагаемого интерферометра вырождается в два последовательных блока перестановок.
Перестановки между оптическими каналами - важный элемента классических коммуникационных сетей, вместе с тем, это очень узкий класс преобразований. Больший интерес представляют канальные оптические преобразования, допускающие взаимодействие между сигналами. В частности, случай преобразования (1.17) позволяет создать интерферометр, который при поступлении на него только одного сигнала в любой из 3-х входных каналов равномерно распределяет мощность между всеми 12 выходными каналами. Очевидно, что такой случай реализуется, если для всех параметров преобразования справедливо: 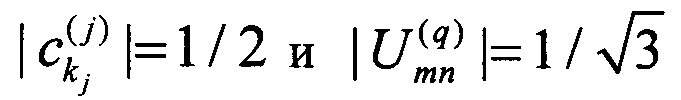 (m, n=1, 2, 3; j=1, 2, 3; kj=1, 2, 3, 4; q=1, 2, 3, 4). Произвол в фазах комплексных параметров определяет множество преобразований, удовлетворяющих условию равномерности мощности на выходе. Отметим, что при поступлении на вход таких интерферометров сигналов в два или три канала мощностью на выходе в общем случае будет неравномерным и будет зависеть от величин амплитуд этих сигналов. Отметим, что особым частным случаем унитарной матрицы, удовлетворяющей условию
(m, n=1, 2, 3; j=1, 2, 3; kj=1, 2, 3, 4; q=1, 2, 3, 4). Произвол в фазах комплексных параметров определяет множество преобразований, удовлетворяющих условию равномерности мощности на выходе. Отметим, что при поступлении на вход таких интерферометров сигналов в два или три канала мощностью на выходе в общем случае будет неравномерным и будет зависеть от величин амплитуд этих сигналов. Отметим, что особым частным случаем унитарной матрицы, удовлетворяющей условию 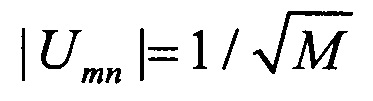 для произвольной размерности М является матрица дискретного преобразования Фурье с элементами:
для произвольной размерности М является матрица дискретного преобразования Фурье с элементами:
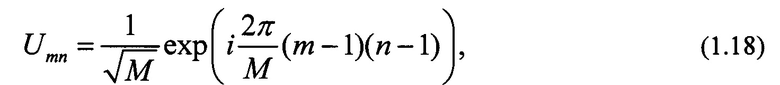
(m, n=1…М).
Используя выкладки для случая произвольных значений М и N, которые были представлены выше, в общем случае преобразования интерферометра (1.17) полностью определяется 47 действительными параметрами. В свою очередь, полностью универсальные преобразований аналогичной размерности имеют 63 параметрами. Глубина оптической схемы интерферометра для предложенного метода равна 7, тогда как универсальный интерферометр имеет глубину 12.
Предложенный метод реализации многоканальных преобразований был реализован в эксперименте для случая М=3, N=12 (см. ф-лу (1.17)). Для создания блоков рассеяния и смешения была использована технология фемтосекундной лазерной печати волноводных элементов, с помощью которой создавались интегральные оптические схемы в заготовке из плавленого кварца. В эксперименте каждый блок собирался из отдельных интегральных оптических схем. Для изменения конфигурации оптических схем был использован традиционный способ, основанный на термооптическом эффекте - изменении показателя преломления вещества под действием температурных изменений. Для этой цели на поверхность кварцевого чипа над участками волноводов, в которых необходимо менять набег фазы сигналов, наносились металлические резистивные нагреватели. Под действием разности потенциалов резистивные нагреватели разогревались. Детали технологии изготовления можно найти в работе https://arxiv.org/abs/1805.05323. При создании интерферометра с М=3 и N=12 применялись 3 интегральных чипа размерности 4×4 и 4 интегральных схемы размерности 3×3, изготовленных по-отдельности описанным способом. Интегральные схемы были соединены друг с другом (см. Фиг. 6) посредством оптических волокон, при этом блоки состояли из отдельных схем модулей (случай Фиг. 9г и Фиг. 10б).
Для исследования качества преобразования в сконструированном интерферометре проводились два типа экспериментов - 1) реализация перестановок одиночных сигналов, посылаемых по-отдельности в каждый из 3-х входных каналов, 2) реализация равномерного распределения мощности между выходными каналами одиночных выходных сигналов, посылаемых по-отдельности в каждый из 3-х входных каналов. В первом эксперименте, качество перестановок исследовалось с помощью максимизации величины мощности, направляемой в заданный выходной канал из заданного входного. Усредненное значение мощности (нормированную на общую мощность на всех выходах), полученное усреднением по всем 36 возможным вариантам перестановок, равно 0.95 при значении 1.0 соответствующем идеальному случаю. При этом наихудший вариант перестановки характеризовался значением 0.91.
Во втором эксперименте изучалось отклонение распределение мощности на выходе от равномерного. При поступлении входного сигнала на каждый из 3 входов по-отдельности, были получены следующие нормированные величина отклонения распределения мощности от равномерного: 0.05, 0.07, 0.09. Значение 0 отвечало идеальному случаю.
Заявляемый способ преобразования и интерферометр могут быть использованы в качестве
- элемента коммуникационных сетей (классических и квантовых) с большим числом абонентов;
- элемента вычислительных сетей (классических и квантовых), например, нейронных;
- элемента квантовых оптических вычислителей и симуляторов, например, реализации бозонного сэмплинга (Boson sampling);
- элемента квантового оптического генератора случайных чисел.
Заявляемое изобретение позволяет достичь технический результат за счет использования не планарной модульной архитектуры схемы, возможной, когда число входных портов, на которые подаются преобразуемые сигналы, меньше числа каналов преобразования. Преобразования каждого этапа реализуется параллельно несколькими модулями, размерности которых намного меньшей размерности общего преобразования. В двухэтапной схеме необходим только один слой интерконнекта между модулями. Таким образом изобретение решает технологическую проблему сложности изготовления оптических схем с большим числом каналов и проблему увеличения потерь, связанную с возрастанием глубины многоканальной оптической схемы.
| название | год | авторы | номер документа |
|---|---|---|---|
| N-КАНАЛЬНЫЙ ЛИНЕЙНЫЙ ПРЕОБРАЗОВАТЕЛЬ ЭЛЕКТРОМАГНИТНЫХ СИГНАЛОВ И СПОСОБ ОСУЩЕСТВЛЕНИЯ МНОГОКАНАЛЬНОГО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ | 2019 |
|
RU2723970C1 |
| Архитектура квантовых вычислительных устройств для решения прикладных задач в области материаловедения | 2023 |
|
RU2821360C1 |
| Система и способ решения прикладных задач материаловедения с помощью сопряжения квантовых и классических устройств | 2023 |
|
RU2814969C1 |
| УСТОЙЧИВЫЙ К ОШИБКАМ МНОГОКАНАЛЬНЫЙ ПОЛЯРИЗАЦИОННЫЙ ПРЕОБРАЗОВАТЕЛЬ ЭЛЕКТРОМАГНИТНЫХ СИГНАЛОВ | 2020 |
|
RU2745979C1 |
| N-КАНАЛЬНЫЙ ЛИНЕЙНЫЙ ПРЕОБРАЗОВАТЕЛЬ ЭЛЕКТРОМАГНИТНЫХ СИГНАЛОВ | 2019 |
|
RU2734454C1 |
| Квантовая вычислительная система на основе фотонных чипов | 2023 |
|
RU2806840C1 |
| СПОСОБ ФИЛЬТРАЦИИ ФОТОНОВ ОТ ОСТАТОЧНОГО ИЗЛУЧЕНИЯ КОГЕРЕНТНОЙ НАКАЧКИ | 2021 |
|
RU2783222C1 |
| СПОСОБ БЛОЧНОГО КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ | 1998 |
|
RU2140713C1 |
| Способ определения результатов векторно-матричных преобразований в параллельных акустооптических процессорах | 1989 |
|
SU1735836A1 |
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ В СКРУЧЕННОМ ПОЛЯРНОМ КОДЕ | 2014 |
|
RU2571587C2 |
Изобретение относится к области оптики, а именно к способам создания линейных оптических устройств, осуществляющих линейные преобразования между большим числом каналов. Изобретение позволяет обеспечить возможность реализации многоканального линейного оптического преобразования, уменьшить потери за счет использования непланарной модульной архитектуры схемы, возможной, когда число входных портов, на которые подаются преобразуемые сигналы, меньше числа каналов преобразования. Преобразование каждого этапа реализуется параллельно несколькими модулями, размерности которых намного меньше размерности общего преобразования. В двухэтапной схеме необходим только один слой интерконнекта между модулями. 2 н. и 3 з.п. ф-лы, 12 ил.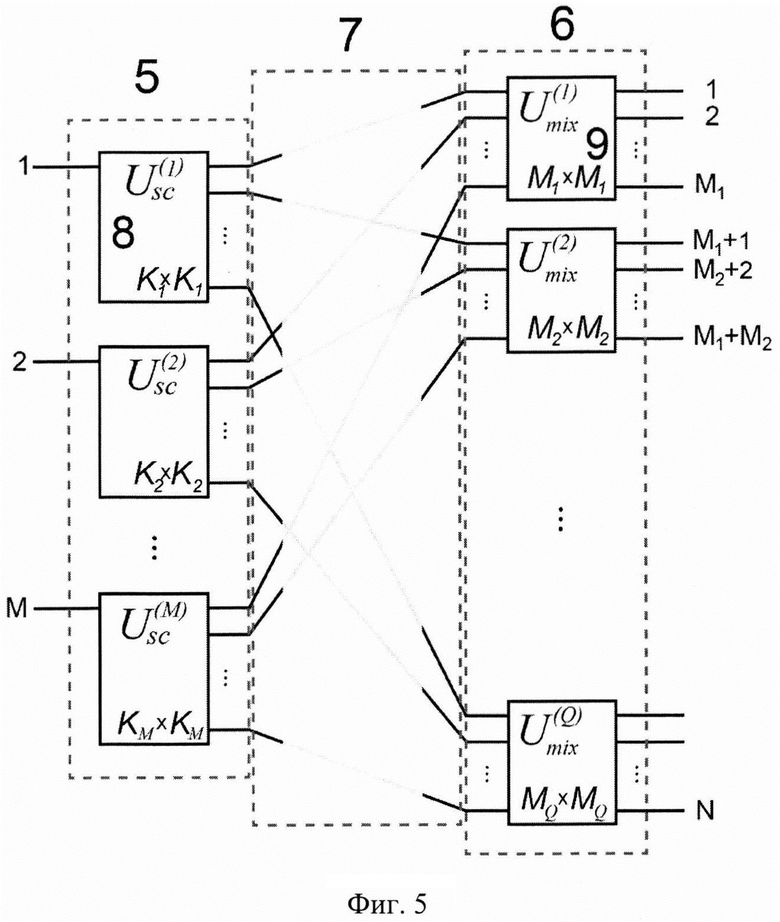
1. Способ линейного оптического преобразования М входных сигналов в N выходных сигналов в N-канальном интерферометре, характеризующийся тем, что каждый из М входных сигналов, где N>M по меньшей мере в два раза, подвергают преобразованию рассеяния с получением множества промежуточных сигналов, амплитуда каждого из которых равна
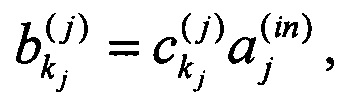
где  - амплитуда j-го входного сигнала,
- амплитуда j-го входного сигнала,
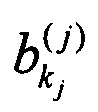 - амплитуда промежуточного сигнала на выходе j-го преобразования рассеяния в его kj-м промежуточном канале,
- амплитуда промежуточного сигнала на выходе j-го преобразования рассеяния в его kj-м промежуточном канале,
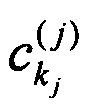 - коэффициент, характеризующий рассеяние j-го входного сигнала в kj-м промежуточном канале,
- коэффициент, характеризующий рассеяние j-го входного сигнала в kj-м промежуточном канале,
j = от 1 до М, индекс, нумерующий входной сигнал,
kj = от 1 до Kj, номер промежуточного канала в j-м преобразовании рассеяния,
Kj - число каналов в j-м преобразовании рассеяния, после чего каждый из промежуточных сигналов в kj канале каждого j-го преобразования рассеяния подвергают преобразованию смешения с получением N выходных сигналов, каждый из которых получен из промежуточных сигналов из каналов количеством от 2 до М и имеет амплитуду
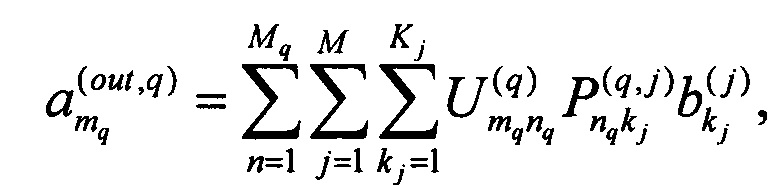
где 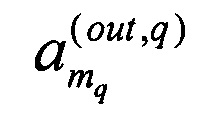 - амплитуда выходного сигнала на выходе mq-го канала q-го преобразования смешения, являющаяся амплитудой выходного сигнала интерферометра,
- амплитуда выходного сигнала на выходе mq-го канала q-го преобразования смешения, являющаяся амплитудой выходного сигнала интерферометра,
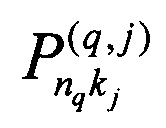 - элементы матрицы, описывающей соединение промежуточных каналов преобразований рассеяния с входными каналами преобразований смешения, соответствующие коэффициенту передачи от kj-го канала j-го преобразования рассеяния к nq-му каналу q-го преобразования смешения,
- элементы матрицы, описывающей соединение промежуточных каналов преобразований рассеяния с входными каналами преобразований смешения, соответствующие коэффициенту передачи от kj-го канала j-го преобразования рассеяния к nq-му каналу q-го преобразования смешения,
 - элементы матрицы q-го преобразования смешения,
- элементы матрицы q-го преобразования смешения,
Mq - размерность q-го преобразования смешения,
nq = от 1 до Мq - индекс, нумерующий входной канал q-го преобразования смешения,
mq = от 1 до Mq - индекс, нумерующий выходной канал q-го преобразования смешения,
q = от 1 до Q,
Q - число преобразований смешения.
2. Способ по п. 1, отличающийся тем, что N и М связаны соотношением N=Q*M, где Q - целое и больше либо равно 2.
3. Линейный оптический N-канальный интерферометр, включающий по меньшей мере один блок рассеяния, имеющий входные и выходные каналы, и по меньшей мере один блок смешения, имеющий входные и выходные каналы, обеспечивающие преобразование рассеяния и смешения в соответствии со способом по п. 1.
4. Интерферометр по п. 3, отличающийся тем, что блок рассеяния и блок смешения выполнены по меньшей мере из одного интегрального оптического устройства методом планарной литографии или методом трехмерной лазерной модификации.
5. Интерферометр по п. 3, отличающийся тем, что он снабжен соединительным блоком, выполненным методом планарной литографии или методом трехмерной лазерной модификации (печати) и расположенным между блоками рассеяния и смешения с обеспечением соединения выходных каналов блока рассеяния и входных каналов блока смешения.
| EP 1098219 A1, 09.05.2001 | |||
| US 6606427 B1, 12.08.2003 | |||
| US 6771905 B1, 03.08.2004. |
Авторы
Даты
2019-10-11—Публикация
2018-12-03—Подача