Область техники, к которой относится изобретение
Изобретение относится к области квантовых вычислений, а именно к устройствам, реализующим квантовые вычислительные алгоритмы с целью решения некоторых классов вычислительных задач. В частности, изобретение может быть использовано для решения задач симуляции свойств молекул и материалов, задач глобальной оптимизации сложных функций со многими параметрами, поиска решений больших систем алгебраических уравнений быстрее и точнее, чем устройства, использующие классические вычислительные алгоритмы.
Уровень техники
Из уровня техники известны квантовые вычислительные алгоритмы, которые могут решать некоторые классы задач быстрее и/или точнее, чем классические алгоритмы, которые раскрыты, например, в книге М. Нильсен, И. Чанг «Квантовые вычисления и квантовая информация», Москва: Мир, 2006. Решение задач квантовыми алгоритмами выполняют с помощью приготовления квантового состояния посредством применения последовательности квантовых преобразований над изначальным квантовым состоянием. Ответ к решаемой задаче получают из результатов измерений, выполняемых над приготовленным таким образом квантовым состоянием. Квантовые преобразования обычно имеют вид последовательности слоев одно- и двухкубитовых гейтов. Для заданного квантового алгоритма изначальное состояние не зависит от конкретной решаемой задачи. Конкретная решаемая задача определяет последовательность квантовых преобразований над изначальным состоянием. С возрастанием сложности решаемых задач требования к числу кубитов возрастает. Также с ростом сложности задач возрастает число слоев преобразований.
Недостатком квантовых вычислительных алгоритмов является сложность их реализации на квантовых устройствах по причине их чувствительности к шумам и ошибками. Решение задач на квантовых вычислителях быстрее и точнее, чем решение этих же задач на традиционных классических компьютерах, но требует очень малых уровней шумов и ошибок, вносимых реальными квантовыми операциями (гейтами) в преобразуемые квантовые состояния кубитов. Одновременно с этим сложные задачи требуют приготовления квантовых состояний, состоящих из большого числа кубитов. Вероятность внесения ошибок в получаемый ответ возрастает с ростом числа кубитов в квантовом вычислителе, снижая точность ответа или саму возможность выполнения квантового алгоритма. Решение практически значимых задач на квантовых компьютерах с современным уровнем развития технологий эффективнее классических компьютеров крайне сложно и поэтому превосходства квантовых вычислителей над классическими продемонстрировано на практике не было.
Из уровня техники известны квантовые вычислители, основанные на материальных кубитах, раскрытые, например, в патентной публикации R.G. Clark, A.S. Dzurak, J.L. O'Brien, S.R. Schofield, M.Y. Simmons, "Single molecule array on silicon substrate for quantum computer" // WO 02/18266 (2002). В таких вычислителях квантовая информация хранится в материальных кубитах, которые могут представлять собой, например, сверхпроводниковые контуры, квантовые точки, дефекты в твердом теле или плененные одиночные нейтральные атомы или заряженные ионы. Наиболее удобной геометрией расположения материальных кубитов на чипе квантового вычислителя или в ловушке, удерживающей атомы или ионы квантового вычислителя, является одномерная и двумерная геометрия. При этом за одно применение квантовых гейтов, перепутывающие два или большее число кубитов, могут выполняться только между кубитами, которые расположены по соседству друг с другом.
Недостатком планарного одномерного или двумерного расположения кубитов является ограниченная связанность кубитов из-за невозможности за одно применение гейтов перепутывать кубиты удаленные друг от друга. Перепутывающие квантовые операции обычно всегда присутствуют в квантовых логических схемах, которые описывают последовательность применения гейтов при приготовлении квантовых состояний. Как следствие, в таких квантовых вычислителях для выполнения одного перепутывающего гейта между удаленными кубитами необходимо применять последовательность дополнительных двухкубитных гейтов, попеременно действующих на соседние кубиты. Зависимость числа дополнительных гейтов, необходимых для одной перепутывающей операции между удаленными кубитами, растет с удалением кубитов друг от друга. Время, затрачиваемое на выполнение гейтов между удаленными кубитами, растет пропорционально числу дополнительных гейтов, что приводит к росту вносимых шумов и ошибок и, следовательно, ограничивает применение квантовых вычислителей с одномерным и двумерным размещением кубитов.
Из уровня техники известны квантовые вычислители, основанные на материальных кубитах, представляющие собой ионы в ловушках, которые раскрыты в работе CD. Bruzewics, J. Chiaverihi, R. McConnell, J.M. Sage, «Trapped-ion quantum computing: Progress and challenges» // Appl. Phys. Rev. v. 6, 021314 (2019). В этих вычислителях кубиты располагаются в одномерном массиве. Специфика физического взаимодействия ионов в ловушке квантового вычислителя позволяет реализовывать перепутывающие операции между удаленными кубитами за один подход.
Недостатком квантовых вычислителей на ионах является ограничение на число кубитов в квантовом вычислителе из-за невозможности создания условий для удержания большого числа ионов в ловушке с одновременной возможностью их адресного управления. Наибольшее число кубитов в одной ионной ловушке не превышает ~100, что намного меньше, чем требуется для возможности решения практически значимых задач эффективнее, чем на классических вычислителях.
Из уровня техники известны линейно-оптические квантовые вычислители, которые используют оптические фотоны, которые распространяются через линейно-оптические схемы, например, выполненные в интегральном исполнении, для хранения и преобразования квантовой информации, которые раскрыты в патентной публикации К. Bradler, D. Su, N. Killoran, М. Schuld, Z. Vernon, L. Helt, B. Morrison, D. Mahler, "Apparatus and methods for Gaussian boson sampling" // WO 2020/232546 (2020). Такие вычислители используют квантовые свойства интерференции фотонов и способны реализовывать некоторые классы квантовых алгоритмов.
Недостатком известных линейно-оптических квантовых вычислителей является большой объем физических ресурсов: источников фотонов или сжатых квантовых состояний, программируемых многоканальных интерферометров, детекторов фотонов и быстрых переключателей. С увеличением сложности решаемых задач и применяемых для этого квантовых алгоритмов для их решения объем этих физических ресурсов растет. Кроме этого, с ростом размеров интерферометров возрастают потери, которые препятствуют выполнению квантовых вычислений. Настоящий уровень развития технологий не позволяет создать линейно-оптические квантовые вычислители с традиционной архитектурой с масштабом и качеством квантовых операций, способных обеспечить решение практически значимых задач эффективнее, чем классические компьютеры.
Наиболее близкими к заявляемому техническому решению являются способ и устройство для приготовления квантовых состояний фотонов, раскрытые в патентной публикации J.C. Mower, N.C. Harris, D. Englund, G. Steinbrecher, "Methods, systems, and apparatus for programmable quantum photonic processing" // US 9354039 (2016). Изобретение основано на многоканальном программируемом интерферометре с обратной связью, в котором сигналы от части выходов перенаправляются на часть входов через линии обратной связи. Преобразуемые состояния подаются на входные каналы интерферометра и могут многократно проходить через интерферометр, благодаря чему глубина эффективной схемы - параметр, характеризующий сложность линейно-оптического преобразования, увеличивается по сравнению с глубиной физической схемы используемого устройства интерферометра. Таким образом, можно использовать программируемые интерферометры с меньшим числом каналов и меньшее число источников и детекторов фотонов, чем необходимо при использовании способа без обратной связи.
Недостатком этого технического решения является ограниченная связанность квантовых схем, которые могут быть реализованы в линейно-оптическом квантовом вычислителе, что ограничивает класс квантовых алгоритмов, которые можно реализовать в вычислителе на базе такого интерферометра, и класс задач, которые можно решать с его помощью. Еще одним недостатком является ограниченная глубина квантовых логических схем, которые можно реализовать в таком интерферометре, что ограничивает возможность использования его использования.
Технической проблемой, решаемой заявляемым изобретением, является ограниченный класс квантовых преобразований, которые можно реализовывать в известных квантовых схемах с обратной связью. Также решаемой технической проблемой является высокий уровень шумов, ошибок и потерь, которые сопутствуют квантовым вычислителям с ограниченной связанностью кубитов при увеличении их числа.
Раскрытие изобретения
Техническим результатом изобретения является повышение связанности между кубитами квантовых вычислителей с обратной связью и увеличение глубины реализуемых квантовых логических схем, что позволяет выполнять более широкий класс квантовых преобразований и снижает уровень шумов, ошибок и потерь в квантовом вычислителе.
Технический результат достигается квантовым вычислителем, который может иметь несколько вариантов осуществления.
Согласно первому варианту осуществления изобретения квантовое вычислительное устройство включает по меньшей мере один блок 1-го типа, имеющий N входов и N выходов, где N>=3, выполненный с возможностью синхронного преобразования сигналов, описываемых квантовыми состояниями, за время т; по меньшей мере один блок 2-го типа, имеющий M<N входов и М выходов, где М>=2, выполненный с возможностью внесения временных задержек в сигналы, описываемые квантовыми состояниями, поступающие на его входы, с возможностью перестановки каналов на выходах относительно каналов на входах; блок измерений, выполненный с возможностью измерения и обработки результатов измерений квантовых состояний сигналов, поступающих на входы блока с N-M выходов блока 1-го типа; блок формирования входных сигналов, выполненный с возможностью подачи сигналов на N-M входов блока 1 -го типа, описываемых одинаковыми квантовыми состояниями, с периодом Т, равным или кратным τ; компьютер, выполненный с возможностью управления преобразованиями по меньшей мере одного блока 1-го типа и по меньшей мере одного блока 2-го типа, управления блоком измерений и обработки результатов измерений этого блока; при этом М выходов блока 1 -го типа соединены с М входами блока 2-го типа, а М выходов блока 2-го типа соединены с М входами блока 1 -го типа, a N-M выходов блока 1 -го типа соединены с N-M входами блока измерений.
Квантовое вычислительное устройство может содержать не менее двух блоков 1 -го типа, при этом блоки соединены последовательно таким образом, что выходы с предыдущего блока соединены с соответствующими входами последующего блока.
Блок 2-го типа может быть выполнен с возможностью изменения временных задержек по меньшей мере в одном пространственном канале данного блока; с возможностью внесения временных задержек кратных Т и их программируемого изменения. По меньшей мере один из блоков преобразований 1-го и 2-го типа, блок измерений и компьютер могут быть выполнены с возможностью изменения преобразования квантовых состояний за время меньшее, чем Т.
В качестве сигналов могут быть использованы оптические сигналы, которые кодируют квантовые состояния, при этом в качестве блоков 1-го и 2-го типа предпочтительно использование программируемых интерферометров, где блок 2-го типа дополнительно содержит петли временной задержки.
В квантовом вычислительном устройстве блок 2-го типа может содержать элементы квантовой памяти, выполненные с возможностью записи и считывания оптических сигналов. Элемент квантовой памяти может иметь различную конструктивную реализацию, например, представлять собой твердотельную квантовую систему, выполненную с возможностью хранения квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее, чем 2Т. В другом варианте элемент квантовой памяти может представлять собой квантовую систему, реализованную на базе паров щелочных металлов, выполненную с возможностью хранения квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее, чем 2Т. Кроме того, элемент квантовой памяти может представлять собой квантовую систему одиночных нейтральных атомов в ловушке или ионов в ловушке, выполненную с возможностью хранения квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее, чем 2Т.
Согласно второму варианту осуществления изобретения квантовое вычислительное устройство включает по меньшей мере один блок 1-го типа, имеющий N входов и N выходов, где N>=3, выполненный с возможностью синхронного преобразования сигналов, описываемых квантовыми состояниями, за время τ; по меньшей мере один блок 2-го типа, имеющий совокупно N входов и M<N выходов, где М>=2, содержащий по меньшей мере 2 модуля, соединенные параллельно или последовательно и выполненные с возможностью внесения временных задержек в сигналы, описываемые квантовыми состояниями, поступающие с соответствующих выходов блока 1-го типа на входы блока 2-го типа, с возможностью перестановки каналов на выходах относительно каналов на входах; по меньшей мере один блок измерений, выполненный с возможностью измерения квантовых состояний сигналов, поступающих на D>=1 его входов с D выходов модуля блока 2-го типа; блок формирования входных сигналов, выполненный с возможностью подачи сигналов на N-M входов блока 1-го типа, описываемых одинаковыми квантовыми состояниями, с периодом Т, равным или кратным τ; компьютер, выполненный с возможностью управления преобразованиями блока 1-го типа и блока 2-го типа, управления блоком измерений и обработки результатов измерений этого блока.
Блок 2-го типа может состоять из двух модулей и иметь по меньшей мере четыре варианта реализации схемы их соединения с остальными блоками квантового вычислительного устройства.
Согласно первому варианту два модуля блока 2-го типа подключены к блоку 1 -го типа параллельно, при этом подмножество из M1 выходов блока 1-го типа соединены с M1 входами первого модуля блока 2-го типа, M1 выходов которого соединены с подмножеством из M1 входов блока 1-го типа, при этом оставшиеся N-M1 выходов блока 1-го типа соединены с N-M1 входами второго модуля блока 2-го типа, D выходы второго модуля блока 2-го типа соединены с D входами блока измерений, а оставшиеся M2=N-M1-D выходов второго модуля блока 2-го типа соединены с М2 входами блока 1-го типа.
Согласно второму варианту модули блока 2-го типа подключены к блоку 1-го типа последовательно, при этом подмножество из M1 выходов блока 1-го типа соединены с подмножеством из M1 входов первого модуля блока 2-го типа, M1 выходов которого соединены с подмножеством из M1 входов блока 1-го типа, при этом оставшиеся N-M1 выходов блока 1-го типа соединены с N-M1 входами второго модуля блока 2-го типа, D выходов которого соединены с D входами блока измерений, при этом оставшиеся M2=N-M1-D выходов второго модуля блока 2-го типа соединены с подмножеством из М2 входов первого модуля блока 2-го типа.
Согласно третьему варианту модули блока 2-го типа подключены к блоку 1-го типа последовательно, при этом N выходов блока 1-го типа соединены с N входами второго модуля блока 2-го типа, подмножество из D выходов которого соединено с D входами блока измерений, оставшиеся N-D выходов второго модуля блока 2-го типа соединены с N-D входами первого модуля блока 2-го типа, N-D выходов которого соединены с подмножеством из N-D входов блока 1-го типа.
Согласно четвертому варианту модули блока 2-го типа подключены к блоку 1-го типа последовательно, при этом N выходов блока 1-го типа соединены с N входами первого модуля блока 2-го типа, N выходов которого соединены с N входами второго модуля блока 2-го типа, при этом подмножество из D выходов второго модуля блока 2-го типа соединены с D входами блока измерений, а оставшиеся N-D выходов второго модуля блока 2-го типа соединены с N-D входами блока 1-го типа.
Кроме того, в квантовом вычислительном устройстве может быть реализован алгоритм, согласно которому на N-M входы блока 1-го типа подаются сигналы, описываемые одинаковыми квантовыми состояниями, с периодом Т, равным или кратным т, при этом временные задержки, вносимые блоком 2-го типа, кратны Т и выполнены с возможностью программируемого изменения.
Компьютер может быть выполнен с возможностью изменения преобразования квантовых состояний, выполняемых блоком 1-го типа, за время меньшее, чем Т; с возможностью изменения базиса измерений, выполняемых блоком измерений, за время меньшее, чем Т.
В качестве сигналов предпочтительно использование оптических сигналов, которые кодируют квантовые состояния, в этом случае блоки 1-го и 2-го типа и элементы квантовой памяти могут иметь реализацию, описанную выше, характеризующую первый вариант осуществления изобретения.
Квантовое вычислительное устройство может быть выполнено на основе квантовой системы одиночных нейтральных атомов в ловушке, или на основе квантовой системы одиночных ионов в ловушке, или на основе квантовой системы сверхпроводниковых цепочек, или на основе квантовой системы квантовых точек, или на основе квантовой системы дефектов в кремнии или алмазе. При этом в одном из вариантов осуществления изобретения блок 1-го типа и блок 2-го типа могут быть выполнены на основе разных квантовых систем.
В квантовом вычислительном устройстве компьютер выполнен с возможностью реализации квантовых вариационных алгоритмов.
Изобретение характеризуется возможностью повторного использования ресурсов -ограниченного числа кубитов доступных в квантовых системах на основе материальных носителей квантовой информации или источников и детекторов фотонов и интерферометров в линейно-оптических квантовых вычислителях - по сравнению с известными до этого времени способами с таким же количеством ресурсов и наличием в каналах обратной связи дополнительного блока или блоков, задерживающих и переставляющих квантовые состояния, поступающие в каналы обратной связи. Благодаря этому удается повысить размерность приготавливаемых квантовых оптических состояний и уменьшить влияние шумов, ошибок и потерь на результаты квантовых вычислений.
Наличие дополнительного блока или блоков в каналах обратной связи позволяет повысить связанность и глубину квантовых логических схем, которые можно реализовать в квантовом вычислителе. Таким образом, решается проблема ограниченной связанности традиционных архитектур квантовых вычислителей, например, в случае связанности, при которой перепутывающие квантовые операции возможны только между близко расположенными кубитами. Также решается проблема ограниченной глубины квантовых логических схем.
Краткое описание чертежей
Изобретение поясняется чертежами и схемами.
На фиг. 1 приведена схема архитектуры квантового вычислителя, предлагаемого в настоящем изобретении.
Фиг. 2 поясняет пространственно-временной способ кодирования квантовой информации, используемый в настоящем изобретении.
На фиг. 3 приведена схема известной архитектуры квантового вычислителя со статическими линиями задержки.
На фиг. 4 приведена квантовая схема, которую можно реализовать в квантовом вычислителе, изображенном на фиг. 3.
На фиг. 5 представлена схема, иллюстрирующая конечную связанность кубитов в квантовом процессоре.
На фиг. 6 представлена квантовая логическая схема, реализующая преобразование квантового преобразования Фурье.
На фиг. 7 представлен пример выполнения двухкубитного гейта между удаленными кубитами в квантовых вычислителях с ограниченной связанностью кубитов. На фиг. 7а приведен пример двухкубитного гейта CRj между удаленными друг от друга кубитами. На Фиг. 7б представлен пример квантовой логической схемы, которую необходимо реализовать на квантовом вычислителе с ограниченной связанностью для осуществления двухкубитного гейта CRj из фиг. 7а.
На фиг. 8 изображена схема разложения SWAP-гейта на последовательность трех CNOT-гейтов.
На фиг. 9 представлен пример квантовой логической схемы, которую можно реализовать в квантовом вычислителе, изображенном на фиг. 1.
Фиг.10 иллюстрирует возможные конструкции квантовых вычислителей, выполненных по предлагаемой архитектуре.
Фиг. 11 иллюстрирует примеры блоков преобразователей 2-го типа, используемые в предлагаемой архитектуре квантовых вычислителей.
На фиг. 12 приведен пример программируемой линии временной задержки с двумя возможными значениями вносимой временной задержки.
На фиг. 13 приведены схемы оптических установок, которые были использованы для конкретной демонстрации заявляемого изобретения.
Позициями на фигурах обозначены:
1 - блок преобразователя 1-го типа;
2 - блок преобразователя 2-го типа, 2а и 2б - модули блока преобразователя 2-го типа;
3 - блок измерений;
4 - компьютер, управляющий квантовым вычислителем;
5 - множество входов блока преобразователя 1-го типа, где 5а - подмножество входов, используемые для входа изначальных состояний, 5б - подмножество входов, используемых в линиях обратной связи;
6 - множество выходов блока преобразователя 1-го типа, где 6а - подмножество выходов, в которых генерируются приготавливаемые состояния, поступающие на входы блока измерений, 6б - подмножество выходов, используемых в линиях обратной связи;
7 - множество входов блока преобразователя 2-го типа;
8 - множество выходов блока преобразователя 2-го типа;
9 - линии, по которым компьютер осуществляет управление блоком преобразования 1-го типа;
10 - линии, по которым компьютер осуществляет управление блоком преобразования 2-го типа;
11 - линии, по которым компьютер осуществляет управление блоком измерений;
12 - линии, по которым результаты измерений блоком измерений поступают в компьютер;
13 - квантовые состояния, входящие во входы 5а блока преобразователя 1-го типа, где 13а и 13б - два состояния, следующих друг за другом в разные временные отрезки;
14 - квантовые состояния, приготавливаемые квантовым вычислителем и выходящие из выходов 6а блока преобразователя 1-го типа, где 14а и 14б - два состояния, следующих друг за другом в разные временные отрезки;
15 - квантовые состояния, выходящие из выходов 6б блока преобразоателя 1-го типа и поступающие на входы 7 блока преобразователя 2-го типа, где 15а и 15б - два состояния, следующих друг за другом в разные временные отрезки;
16 - квантовые состояния, выходящие из выходов 8 блока преобразователя 2-го типа и поступающие на подмножество входов 56 блока преобразователя 1-го типа, 16а и 16б -два состояния, следующих друг за другом в разные временные отрезки;
17 - блок временных задержек;
18 - квантовое преобразование, которое реализуется блоком преобразователя 1 -го типа за М шагов работы квантового вычислителя; 18а и 18б - два преобразования блока преобразователя 1-го типа, которые реализуются за два последовательных шага работы схемы; преобразования, выполняемые на разных шагах работы схемы обозначены Vm, где m - номер шага;
19а и 19б - два канала, которые реализуются линией обратной связи за 2 последовательных шага работы квантового вычислителя;
20 - чип квантового процессора с планарным размещением кубитов;
21 - кубиты квантового процессора; 21а - один кубит, который может взаимодействовать с кубитами 21б за одно применение двухкубитового гейта; 21в - кубит, удаленный от кубита 21а;
22 - входное N-кубитное квантовое состояние;
23 - двухкубитный гейт, действующий на соседние кубиты;
24 - двухкубитный гейт, действующий на удаленные друг от друга кубиты;
25 - преобразованное N-кубитное квантовое состояние;
26 - последовательности применения SWAP-гейтов, необходимых для выполнения двухкубитного гейта между удаленными друг от друга кубитами;
27 - SWAP-гейт;
28 - двухкубитный гейт, действующий на соседние кубиты;
29а, 296 - два канала, которые реализуются линией обратной связи за 2 последовательных шага работы квантового вычислителя;
30 - линия задержки;
30а, 30б, 30в - программируемые задержки;
31 - программируемый блок перестановок;
31а, 31б, 31 в - программируемые перестановки; 32а, 32б - статические задержки;
33а, 33б - входной и выходной переключатель программируемой задержки;
34 - 4-канальный интерферометр;
35 - блок 2-го типа, 35а и 35б - волоконные линии обратной связи;
36 - источник пар фотонов;
37 - блок измерений, 37а и 37б - детекторы одиночных фотонов;
38 - линии, по которым результаты измерений измерительным блоком поступают в компьютер, 38а и 38б - электрические линии, идущие от детекторов одиночных фотонов 37а и 37б, соответственно.
Осуществление изобретения
В изобретении речь идет об архитектуре квантовых вычислителей способных решать задачи из области материаловедения. Предлагаемая архитектура может быть использована для построения квантовых вычислителей на разных физических платформах, как на основе материальных систем, в которых информация в форме квантовых состояний может храниться и обрабатываться в материальных носителях, так и на основе оптических систем, в которых носителем информации являются летящие оптические фотоны.
Для более однозначного понимания сущности заявленного изобретения ниже представлены основные термины и определения, используемые в рамках настоящего описания.
Логическим кубитом или просто кубитом называют квантовую физическую систему или часть физической системы, позволяющую хранить два квантовых состояния, обозначаемых |0) и |1) и называемых логическим «0» и логическим «1», а также любую их линейную суперпозицию вида α |0)+β|1), где α и β - комплексные числа, подчиняющиеся условию нормировки: |α|2+|β|2=1. Кодирование логических состояний кубитов |0) и |1) проводят в квантовые состояния физической системы.
Существует множество способов кодирования логических состояний кубитов в физические состояния системы. При кодировании кубита в оптические фотоны выбор конкретного кодирования кубитов обусловлен наличием требуемых для этого ресурсов, например, числом каналов в оптических схемах и числом фотонов, и удобством выполнения преобразований над кубитами. В линейно-оптических квантовых вычислениях распространено кодирование кубитов в «двухрельсовый базис» (от термина dual-rail encoding в англоязычной литературе), использующий два оптических канала/моды, состоящий из двух физических состояний |0>m|1>n и |1>m|0>n, где |0> и |1> - фоковские состояния с числом фотонов 0 и 1, соответственно, а индексы тип обозначают номера оптических каналов, к которым относится фоковское состояние (Р. Kоk et al. "Linear optical quantum computing" // Rev. Mod. Phys., vol. 79, 135 (2007)). Также распространено кодирование в так называемый «однорельсовый базис» (от термина single-rail encoding в англоязычной литературе), использующий фоковские состояния в одном оптическом канале |0>m и |1>m.В настоящем изобретении речь идет о двухрельсовой кодировке. В квантовых системах, использующих для хранения и преобразования кубитов материальные элементы, например, нейтральные атомы в ловушках, ионы в ловушках, дефекты в твердотельных структурах, квантовые точки, кубиты могут кодировать в электронные состояния и двумя уровнями энергии.
Квантовым вычислителем или квантовым компьютером называют устройство, которое использует квантовые свойства реальных физических систем для практической реализации квантовых вычислительных алгоритмов.
Особенности квантовых физических систем, отличающие их от классических, можно описывать с помощью математического понятия вектора состояния системы. Если D возможным состояниям квантовой системы можно приписать набор состояний |ϕj) (j=1…D), которые попарно ортогональны ((<ϕi|ϕj>=δij), то квантовая система может также находиться в состоянии с наблюдаемыми в эксперименте характеристиками, описываемыми суперпозицией состояний |(ϕ>:

где cj - коэффициенты разложения, которые задают конкретное квантовое состояние (j=1…D), для которых справедливо нормировочное соотношение: 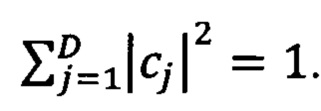 Даже для сравнительно малых физических систем, состоящих из Q кубитов - двухуровневых квантовых систем, число различных базисных состояний |ϕj> и коэффициентов разложения cj в (1) экспоненциально велико: D=2Q. Для хранения всей информации о квантовом состоянии (1) на классических компьютерах требуется память для 2Q+1 - 1 действительных параметров, задающих коэффициенты cj, что не представляется возможным даже для сравнительно малых значений Q ≈ 50. Преобразования над векторами состояний (1) описывают матрицами размерности D × D, что на классическом компьютере требует еще большей памяти, чем хранение вектора состояния. Здесь следует отметить отличие в сложности классического описания преобразования Q классических амплитуд, задаваемого умножением матрицы размерности Q × Q, и классического описания преобразования Q-кубитового квантового состояния, где требуется перемножение на матрицу размерности 2Q×2Q.
Даже для сравнительно малых физических систем, состоящих из Q кубитов - двухуровневых квантовых систем, число различных базисных состояний |ϕj> и коэффициентов разложения cj в (1) экспоненциально велико: D=2Q. Для хранения всей информации о квантовом состоянии (1) на классических компьютерах требуется память для 2Q+1 - 1 действительных параметров, задающих коэффициенты cj, что не представляется возможным даже для сравнительно малых значений Q ≈ 50. Преобразования над векторами состояний (1) описывают матрицами размерности D × D, что на классическом компьютере требует еще большей памяти, чем хранение вектора состояния. Здесь следует отметить отличие в сложности классического описания преобразования Q классических амплитуд, задаваемого умножением матрицы размерности Q × Q, и классического описания преобразования Q-кубитового квантового состояния, где требуется перемножение на матрицу размерности 2Q×2Q.
В отличие от классических компьютеров, устройства квантовых вычислителей предоставляют реальные возможности для выполнения вычислений посредством преобразования экспоненциально емких по информации квантовых состояний, выполняя манипуляции над сравнительно небольшим числом физических кубитов. Базовым функционалом квантовых симуляторов является возможность приготовления квантовых физических систем, используемых в устройствах-симуляторах, в состояния, которыми можно управлять внешними классическими воздействиями.
Параметризованными квантовыми состояниями называют квантовые состояния, которые можно задавать на этапе приготовления, выставляя управляющие параметры.
Параметризованными квантовыми схемами называют квантовые преобразователи, осуществляющие преобразования квантовых состояний, конкретный вид которых зависит от набора управляющих параметров 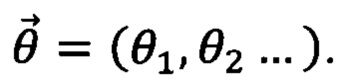 Параметризованные квантовые схемы используют для приготовления параметризованных квантовых состояний
Параметризованные квантовые схемы используют для приготовления параметризованных квантовых состояний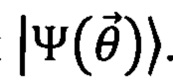
Квантовыми логическими гейтами, квантовыми гейтами или просто гейтами называют элементарные заранее известные квантовые операции, с помощью которых конструируют более сложные квантовые алгоритмы и схемы. Гейты различают в соответствии с числом кубитов, на которые они действуют. Так, говорят об однокубитовых гейтах, двухкубитовых гейтах, трехкубитовых гейтах и т.д. Наиболее распространенные наборы гейтов, из которых конструируют преобразования многокубитовых квантовых состояний, содержат одно- и двухкубитовые гейты. Например, распространены однокубитовые гейты, действие которых описывается матрицами:
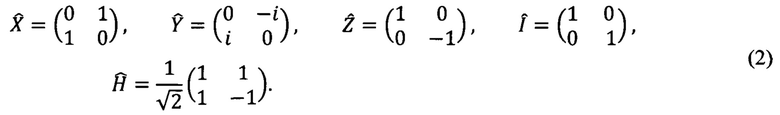
Однокубитовые операторы, описываемые матрицами (2), называют операторами Паули, а сами матрицы - матрицами Паули. Однокубитовые преобразования состояния кубита α|0) +β|1) сводятся к перемножению столбца 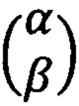 на матрицу, отвечающую этому преобразованию. Среди множества двухкубитовых гейтов распространены следующие:
на матрицу, отвечающую этому преобразованию. Среди множества двухкубитовых гейтов распространены следующие:
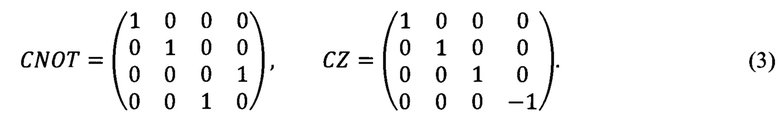
Двухкубитовым преобразованиям отвечает перемножение матриц на столбец амплитуд, отвечающий состояниям двух кубитов: 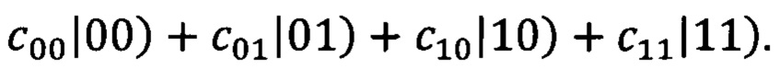 В этом случае столбец амплитуд имеет вид
В этом случае столбец амплитуд имеет вид 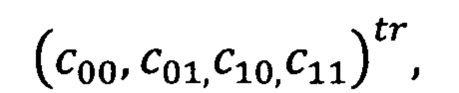 где tr означает транспонирование строки. Применение некоторых двухкубитных гейтов, например, гейтов (3), к изначально независимым (неперепутанным) состояниям приготавливает перепутанные состояния. По этой причине такие гейты называют перепутывающими. Примером неперепутывающего гейта является SWAP-гейт (см. формулу (4) ниже).
где tr означает транспонирование строки. Применение некоторых двухкубитных гейтов, например, гейтов (3), к изначально независимым (неперепутанным) состояниям приготавливает перепутанные состояния. По этой причине такие гейты называют перепутывающими. Примером неперепутывающего гейта является SWAP-гейт (см. формулу (4) ниже).
Квантовой логической схемой или просто квантовой схемой называют последовательность применения квантовых гейтов над логическими состояниями кубитов, которые описывают выполнение квантового алгоритма или квантового преобразования. Стоит отметить, что квантовые схемы описывают преобразования на высоком уровне абстракции, выполняемые над логическими состояниями безотносительно конкретных реализаций кодирования кубитовых состояний и преобразующих их гейтов.
Связанностью кубитов в квантовом вычислителе называют характеристику этого вычислителя, описывающего множество двухкубитных операций, которые можно выполнять над кубитами вычислителя за одно применение этих операций. Связанность кубитов можно описать в виде графа, вершинами которого являются физические кубиты в квантовом вычислителе, а ребра, связывающие пары кубитов - возможные взаимодействия между парами кубитов, которые могут реализовать двухкубитные гейты. Связанность кубитов определяется платформой, на базе которой изготовлен квантовый вычислитель, и конкретной технологией его изготовления. Типично связанность кубитов в квантовых вычислителях характеризуется возможностью выполнять двухкубитные операции только между кубитами, которые физически расположены по соседствую друг с другом.
Вариационным квантовым алгоритмом называют квантовый алгоритм, основанный на попеременном использовании физической системы для приготовления параметризованного квантового состояния 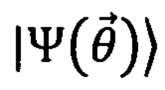 и классического оптимизационного алгоритма, который принимает результаты измерения приготовленного состояния. В соответствии с результатами измерений оптимизационный алгоритм выдает обновленный набор управляющих параметров
и классического оптимизационного алгоритма, который принимает результаты измерения приготовленного состояния. В соответствии с результатами измерений оптимизационный алгоритм выдает обновленный набор управляющих параметров 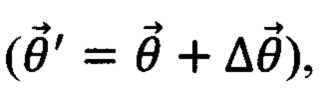 который меняет состояние, приготавливаемое квантовым симулятором:
который меняет состояние, приготавливаемое квантовым симулятором: 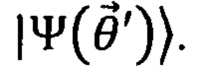 Измерения, проводимые с помощью вариационного квантового состояния, представляют собой среднее от некоторой физической величины, минимум которой необходимо найти и обычно представляющем собой гамильтониан системы Я. Задачи материаловедения, связанные с нахождением новых веществ и материалов или исследованием свойств существующих веществ и материалов, могут быть сведены к нахождению энергии основного состояния гамильтониана (Н. Ma, М. Govoni, G. Galli "Quantum simulations of material on near-term quantum computers" // NPJ Computational Materials v. 6, No. 85 (2020)).
Измерения, проводимые с помощью вариационного квантового состояния, представляют собой среднее от некоторой физической величины, минимум которой необходимо найти и обычно представляющем собой гамильтониан системы Я. Задачи материаловедения, связанные с нахождением новых веществ и материалов или исследованием свойств существующих веществ и материалов, могут быть сведены к нахождению энергии основного состояния гамильтониана (Н. Ma, М. Govoni, G. Galli "Quantum simulations of material on near-term quantum computers" // NPJ Computational Materials v. 6, No. 85 (2020)).
Алгоритм нахождения энергии основного состояния гамильтониана, описывающего симулируемую систему, состоит из последовательных шагов:
1) Симулятор приготавливает квантовое состояние 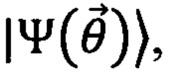 состоящее из Р кубитов, которое зависит от набора параметров
состоящее из Р кубитов, которое зависит от набора параметров 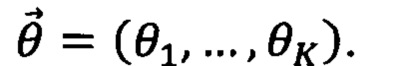 Приготовление осуществляют посредством последовательного применения гейтов, которые задают квантовую схему симулятора, к фиксированному начальному состоянию Набор гейтов, доступных в используемом симуляторе, и их качество определяет класс приготавливаемых состояний. В качестве гейтов могут выступать как стандартные одно- и двухкубитовые гейты, так и многокубитовые преобразования. Изменение параметров
Приготовление осуществляют посредством последовательного применения гейтов, которые задают квантовую схему симулятора, к фиксированному начальному состоянию Набор гейтов, доступных в используемом симуляторе, и их качество определяет класс приготавливаемых состояний. В качестве гейтов могут выступать как стандартные одно- и двухкубитовые гейты, так и многокубитовые преобразования. Изменение параметров 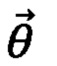 позволяет варьировать приготавливаемое состояние.
позволяет варьировать приготавливаемое состояние.
2) Производят серию измерений приготавливаемых состояний, в каждом из которых получают среднее каждого из слагаемых 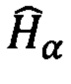 гамильтониана задачи
гамильтониана задачи 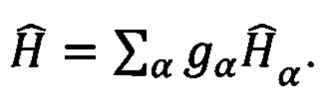 Переход от измерения одного слагаемого к другому осуществляется сменой измерительного базиса. Сумма измеренных средних (с коэффициентами gα)
Переход от измерения одного слагаемого к другому осуществляется сменой измерительного базиса. Сумма измеренных средних (с коэффициентами gα) 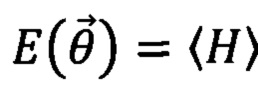 является оценкой ожидаемой величины энергии квантовой системы для заданного состояния
является оценкой ожидаемой величины энергии квантовой системы для заданного состояния 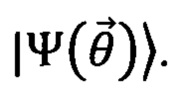
3) Величина (Н) поступает на классический компьютер как значение оптимизируемой функции энергии гамильтониана, после чего компьютер выполняет классическую процедуру численной оптимизации. Классический оптимизационный алгоритм выдает новое значение набора параметров 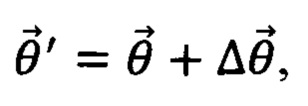 поступающего на квантовое устройство симулятора и симуляция продолжается, начиная с первого шага.
поступающего на квантовое устройство симулятора и симуляция продолжается, начиная с первого шага.
4) Итерациями, описанными в пунктах 1-3, находят минимум энергии 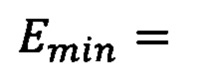
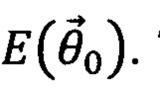 Таким образом, последовательность итераций представляет собой шаги с разными значениями набора параметров, которые могут быть описаны выражением:
Таким образом, последовательность итераций представляет собой шаги с разными значениями набора параметров, которые могут быть описаны выражением: 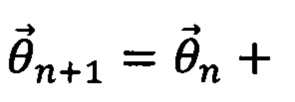
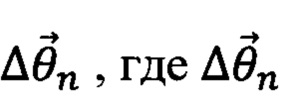 - приращение набора параметров на n+1 шаге итерации.
- приращение набора параметров на n+1 шаге итерации.
Члены 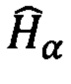 оптимизируемого гамильтониана
оптимизируемого гамильтониана 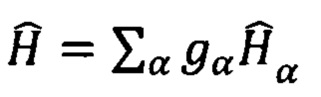 для Р-кубитовых состояний можно представить в виде произведения N операторов Паули, имеющих матричное представление (2):
для Р-кубитовых состояний можно представить в виде произведения N операторов Паули, имеющих матричное представление (2): 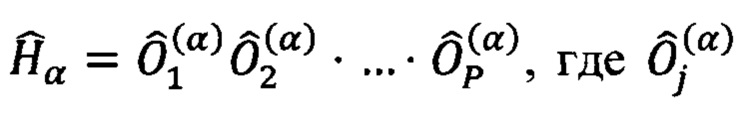 - обозначение оператора
- обозначение оператора
Паули из набора (2) (см., например, работу Y.Cao et al., "Quantum chemistry in the age of quantum computing"//Chem. Rev., vol. 119, No 19, p.10856-10915 (2019)). Конкретная задача, определяемая гамильтонианом 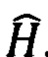 , задается числом и величинами коэффициентов gα и последовательностями произведений операторов Паули, средние которых необходимо рассчитывать с помощью квантового симулятора. Таким образом при решении оптимизационной задачи с помощью квантового вариационного алгоритма рассчитывают средние
, задается числом и величинами коэффициентов gα и последовательностями произведений операторов Паули, средние которых необходимо рассчитывать с помощью квантового симулятора. Таким образом при решении оптимизационной задачи с помощью квантового вариационного алгоритма рассчитывают средние 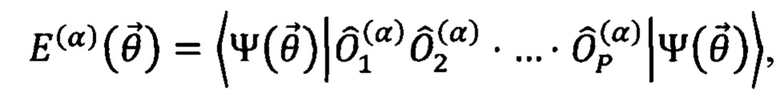 а оптимизируемая функция при заданном наборе варьируемых параметров
а оптимизируемая функция при заданном наборе варьируемых параметров 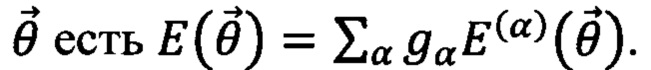
Канал блока преобразователя или канал преобразователя - понятие, которому соответствует единица квантовой информации, хранящейся в одной части квантовых состояний, преобразуемых этим преобразователем, и порядковый номер, однозначно определяющий один канал преобразователя от другого. Каждому каналу отвечает свой вход и свой выход в преобразователе. Преобразуемые квантовые состояния поступают в каналы преобразователя через соответствующие входы, а преобразованные состояния выходят из его каналов через выходы. Например, если преобразователь выполняет преобразования над квантовыми состояниями, кодирующими кубиты, то единицей информации, отвечающей каналу, является кубит. В тексте будет говориться о квантовых вычислителях, преобразующих состояния кубитов, однако предлагаемое изобретение также справедливо и для общего случая, когда единицами информации, которыми оперируют квантовые вычислители, являются кудиты или другие единицы квантовой информации.
Преобразованием 1-го типа называют преобразование, выполняемое над двумя или большим числом каналов, которое может перепутывать изначально независимые состояния, поступающих на вход преобразования. Например, для реализации преобразований 1-го типа можно использовать гейтовые квантовые логические схемы, которые применяют в традиционных квантовых вычислителях. Преобразования 1-го типа характеризуются синхронным выполнением преобразований квантовых состояний, поступающих на его вход, при котором квантовое состояние, поступающее одновременно на его входы, преобразуется в квантовое состояние, одновременно выходящее из всех выходов. Таким образом преобразование 1-го типа может вносить только постоянную временную задержку в преобразуемые состояния. Эта задержка связана с временем выполнения преобразования в конкретной его реализации.
Преобразованием 2-го типа называют преобразование, которое может вносить временные задержки независимо в разные каналы преобразования, а также выполнять перестановку каналов.
Блоком преобразований 1-го типа или преобразователем 1-го типа называют часть квантового вычислителя, который выполняет преобразования 1 -го типа.
Блоком преобразований 2-го типа или преобразователем 2-го типа называют часть квантового вычислителя, который выполняет преобразования 2-го типа.
На фиг. 1 представлена схема, поясняющая предлагаемую архитектуру квантового вычислителя. Основными элементами схемы являются: блок преобразователя 1 -го типа 1, блок преобразователя 2-го типа 2, блок измерений 3, компьютер 4. Блок 1 выполняет преобразования квантовых состояний, которые поступают на его входы 5, результатом которого являются квантовые состояния, выходящие из его выходов 6. Блок 2 осуществляет преобразование квантовых состояний, которые поступают на его входы 7, результатом которого являются квантовые состояния выходящие из его выходов 8. На подмножество входов 5а блока преобразователя 1-го типа 1 поступают квантовые состояния 13. Подмножество 6а выходов 6 соединено с входами измерительного блока 3. Подмножество выходов 66 выходов 6 соединено с входами 7. Выходы 8 блока преобразователя 2-го типа 2 соединены с подмножеством входов 56 блока преобразователя 1-го типа 1. Компьютер 4 управляет блоками преобразователя 1-го типа 1 и блоками преобразователя 2-го типа 2 через линии 9 и 10, соответственно, по которым передается классическая информация. Также компьютер 4 управляет блоком измерений 3 через линии 11, по которым передается классическая информация. Результаты измерений поступают в компьютер 4 через линии 12.
Блок преобразователя 2-го типа 2 представляет собой основное дополнение к уже известным архитектурами вычислителей с обратной связью. Он способен выполнять преобразования как между пространственными каналами (имеющие входы 7 и выходы 8), так и между временными каналами, которые характеризуются разными временными отрезками, в которых расположены квантовые состояния в пространственных каналах. Блок преобразователя 1-го типа 1 способен выполнять преобразования только между пространственными каналами. Ниже функциональные особенности этих блоков будут пояснены более детально.
На выполнение преобразования в блоке преобразователя 1-го типа затрачивается некоторое время τ1. По этой причине во время выполнения конкретного квантового алгоритма, решающего задачи на представленном вычислителе, на подмножество входов блока преобразователя 1-го типа 1 поступают квантовые состояния 13 |ψin> с периодом следования Т>τ1г.На фиг. 1 изображены два следующих друг за другом состояния 13а и 13б. Состояния |ψ0> не меняются от задачи к задаче и служат для инициализации состояния квантового вычислителя. Их выбирают исходя из простоты приготовления. Например, если входам и выходам соответствуют логические кубиты, то для каждого кубита обычно выбирают 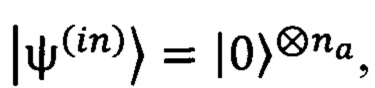 где nα - число входов/кубитов подмножества входов 5а блока преобразователя 1-го типа 1. Входные состояния характеризуются тем, что каждое такое состояние локализовано во времени во временном отрезке длительностью τ≤τ1 и поступают на подмножество входов с некоторым периодом следования Т>τ1 в количестве min. Блок преобразователя 1-го типа 1 характеризуется тем, что состояния, поступившие на его входы в разные временные отрезки, преобразуются независимо, а состояния, поступившие на входы в один отрезок времени, преобразуются этим блоком и поступают из выходов синхронно в один отрезок времени.
где nα - число входов/кубитов подмножества входов 5а блока преобразователя 1-го типа 1. Входные состояния характеризуются тем, что каждое такое состояние локализовано во времени во временном отрезке длительностью τ≤τ1 и поступают на подмножество входов с некоторым периодом следования Т>τ1 в количестве min. Блок преобразователя 1-го типа 1 характеризуется тем, что состояния, поступившие на его входы в разные временные отрезки, преобразуются независимо, а состояния, поступившие на входы в один отрезок времени, преобразуются этим блоком и поступают из выходов синхронно в один отрезок времени.
Квантовое вычислительное устройство приготавливает квантовые состояния, которые измеряются блоком измерений 3. Приготавливаемые состояния поступают на блок измерений в виде последовательности импульсов - квантовых состояний, приготавливаемых квантовым вычислительным устройством и выходящих из выходов 6а блока преобразователя 1-го типа, где 14а и 14б - два состояния, следующих друг за другом в разные временные отрезки с периодом Т.
Блок преобразователя 2-типа 2 характеризуется тем, что он может вносить временные задержки в квантовые состояния, поступающие на его входы: квантовые состояния, поступающие на его входы синхронно в один временной отрезок, могут покидать его выходы в разные отрезки времени. При этом блок преобразователя выполнен таким образом, что разница во времени между временными отрезками, в которых локализованы состояния на выходах блока кратно периоду Т при условии соблюдения этого условия для состояний, поступающих на его входы. Другими словами, временные отрезки, в которые состояния из блока преобразователя 2-го типа 2 поступают на подмножество входов 5б блока преобразователя 1-го типа 1, должны быть синхронизированы.
Вычислители с обратной связью используют пространственно-временное кодирование для расширения размерности обрабатываемой информации. Благодаря такому кодированию удается использовать ограниченные физические ресурсы для построения крупномасштабных вычислителей. В вычислителях - как квантовых, так и классических -обрабатываемая информация локализована в пространстве, например, в физических материальных кубитах на чипе процессора или в пространственной моде, в которой распространяется кубит, кодируемый оптическим фотоном. Каждый кубит может быть преобразован независимо от остальных; к ним можно адресно применять гейты. Помимо этого, квантовая информация также локализована во времени в виде импульсов конечной длительности, которые задаются, например, характерными временами длительности квантовых операций (гейтов), выполняемых над материальными кубитами и/или длительности оптических импульсов, которые кодируют квантовые состояния. При пространственно-временном кодировании используют как пространственную, так и временную степень свободы, в которых локализована обрабатываемая информация. Таким образом, пространственно-временным каналам можно поставить в соответствие неперекрывающиеся пространственные моды и временные интервалы, в которые кодируются каналы.
Фиг. 2 поясняет пространственно-временной способ кодирования информации, в котором N пространственных каналов состоят из М временных каналов. Временные каналы в каждом пространственном канале кодируется во временные интервалы, следующие друг за другом с периодом Т. Временной канал с индексом m (m=1…М) в составе пространственного канала с индексом n (n=1…N) характеризуется временными отсчетами tm=t1+(m-1)Т, описывающими временные отсчеты центров временных интервалов, в которые попадают импульсы, хранящие информацию. При этом временной отсчет первого временного окна t1 определяется временем начала работы квантового вычислителя. Чтобы информацию, которая хранится в разных временных каналах, можно было преобразовывать независимо соответствующие временные интервалы не должны перекрываются друг с другом, поэтому период следования Т>τ, где τ - характерная ширина временного окна, в которое попадают импульсы, несущие информацию. Использование не одного, а N пространственных каналов, состоящих из М временных каналов, увеличивает объем информации, обрабатываемой системами с пространственно-временным кодированием в М раз, т.е. число информационных импульсов равно М ⋅ N. Каждый из импульсов несет часть квантового состояния. При использовании только пространственного кодирования доступна обработка только N временных импульсов. Выполнение произвольных преобразований над состояниями в пространственно-временной кодировке требует наличия задержек, которые, во-первых, могут сводить в один интервал времени части состояний, поступающих на преобразователь в отличающиеся интервалы (отличающиеся временные каналы с разными индексами m), и, во-вторых, разводить в разные временные интервалы состояния, поступающие на преобразователь синхронно в одинаковые временные интервалы (временные каналы с одинаковыми m).
Для использования пространственно-временного кодирования информации необходимо иметь возможность преобразовьюать информацию в такой кодировке. На фиг. 3 представлена архитектура квантового вычислителя с обратной связью, который способен выполнять квантовые преобразования в пространственно-временной кодировке. Данная архитектура известна из области оптических вычислителей (J.С.Mower, N.С.Harris, D. Englund, G. Steinbrecher, "Methods, systems, and apparatus for programmable quantum photonic processing" // US 9354039 (2016)).B таком квантовом вычислителе подмножество выходов 66 блока преобразователя 1-го типа 1 направлены на блок временной задержки 15. Выходы блока задержки направлены на подмножество входов 5б блока преобразователя 1-го типа 1. Блок временных задержек 17 вносит задержку Т во все каналы. Отличием этой архитектуры от заявляемого является невозможность выполнения программируемых задержек и перестановок в блоке 2-го типа.
На фиг. 4 представлена эффективная квантовая логическая схема, которую можно реализовать с помощь квантового вычислителя с обратной связью, изображенного на фиг. 3, за М циклов его работы. На схеме обозначены преобразования над квантовыми состояниями 18, которые можно реализовать блоком преобразователя 1-го типа 1. В общем случае преобразованиями блока 1-го типа 1 можно управлять с компьютера и поэтому для разных шагов работы схемы преобразования на разных шагах, описываемые матрицами Vm, где m - номер шага, могут меняться (на рисунке отдельно обозначены преобразования 18а и 18б, выполняемые на первых двух шагах). На часть входов схемы поступают входные состояния |ψ(in)> (на рисунке они обозначены 13а и 13б для первых двух шагов). На схеме обозначены преобразования 18а и 18б для первых двух циклов (шагов). Часть состояний на выходе из блока преобразователя 1-типа 1 после выполнения цикла поступает на вход преобразования Vm+1 на следующем цикле. На схеме обозначены части состояний 19а и 19б для первых двух циклов. Часть состояний, приготавливаемых на выходах блока преобразователя 1-го типа 1 на каждом цикле, формирует приготавливаемое состояние 14, которое может быть использовано в дальнейшем в работе квантового алгоритма, например, в квантовом вариационном алгоритме.
Из фиг. 4 видно, что схема с обратной связью, изображенная на фиг. 3, может приготавливать состояния с размерностью превосходящую размерность состояния, приготавливаемой в блоке преобразователя 1-го типа 1 без обратной связи: если размерность состояний, приготавливаемого за один шаг (например, состояния 14а или 14б) равно Q кубитам, то за М шагов размерность приготавливаемого квантового состояния 14 равно М ⋅ Q. Это возможно благодаря пространственному-временному кодированию информации, при которой приготавливаемое квантовое состояние 14 генерируется по частям в последовательные интервалы времени.
Недостатком архитектуры квантовых вычислителей, изображенной на фиг. 3, является ограниченный класс квантовых преобразований, которые можно реализовать на этой платформе. В результате такие схемы могут быть использованы только для решения ограниченных классов задач.
Ограниченная связанность кубитов в квантовых вычислителях является одним из ограничивающих факторов, препятствующим их использованию для решения практически значимых задач. Фиг. 5 иллюстрирует причину конечной связанности кубитов в квантовых вычислителях, построенных на основе традиционной архитектуры без обратной связи.
Традиционная архитектура квантовых вычислителей может быть использована для создания блока преобразователя 1-го типа в предлагаемой архитектуре. На фиг. 5 изображен чип 20 квантового процессора с планарным размещением кубитов и связью только между соседними кубитами. Кубиты 21 на чипе 20 располагаются в виде двумерного массива. Чип 20 выполнен таким образом, что реализовывать взаимодействие (за одно применение), необходимое для выполнения двухкубитовых и/или многокубитовых гейтов, возможно только между соседними кубитами. В качестве примера на фигуре выделен один кубит 21а и 4 кубита 21б, с которыми кубит 21а может приводиться во взаимодействие. При необходимости выполнения перепутывающих квантовых операций, вовлекающих кубит 21а и удаленные кубиты, приходится применять промежуточные гейты между кубитами, расположенными на чипе 20 между кубитом 21а и удаленными кубитами, например, кубитом 21в. Дополнительные квантовые гейты вносят шумы, ошибки и потери в дополнении к таковым, которые бы имелись в квантовых вычислителях с большей степенью связанности. Представленный пример не ограничивает все возможные случаи квантовых вычислителей. Квантовые вычислители с планарным расположением кубитов и возможным взаимодействием только между соседними кубитами могут иметь более разряженную структуру.
Для иллюстрации важности высокой связанности кубитов для квантовых вычислений на фиг. 6 представлена квантовая логическая схема, реализующая квантовое преобразование Фурье (КПФ). КПФ находит применения в ряде важнейших квантовых алгоритмов, например, в алгоритме Шора, решающего задачу разложения чисел на простые множители. КПФ также применяется в квантовом алгоритме оценки фазы, который может рассчитывать уровни энергии квантовых систем. Квантовыми системами могут выступать молекулы или материалы (М Нильсен, И. Чанг «Квантовые вычисления и квантовая информация», Москва: Мир, 2006). Квантовая логическая схема КПФ, изображенная на фиг. 6, представляет собой последовательность применения слоев из однокубитных гейтов Адамара Н и двухкубитовых гейтов условного поворота фазы CRj, которые применяются к входному N-кубитному квантовому состоянию 22. Двухкубитные гейты CRj вращают фазу целевого кубита на угол 2π/2j (на схеме эти кубиты пересекают квадраты с надписью R с нижним индексом), если соответствующий управляющий кубит в состоянии |1). Как видно из фиг. 6 значительная часть двухкубитных гейтов CRj на представленной логической схеме действует на удаленные друг от друга кубиты, большая часть которых отвечает кубитам, которые удалены друг от друга на квантовом чипе вычислителя. Таким образом, выполнение значительной части гейтов CRj на реальном квантовом вычислителе, например, со связанностью, проиллюстрированной на фиг. 6 требует применения промежуточных гейтов, которые вносят шумы, ошибки и потери. На фиг. 6 выделены двухкубитный гейт 23, который действует на соседние кубиты. Он может быть применен на квантовом вычислителе за одно применение без промежуточных двухкубитных гейтов. В то же время, например, двухкубитный гейт 24, действующий на 1-й и N-й кубит в квантовой логической схеме вряд ли можно применить за один подход на реальном квантовом вычислителе, т.к. физические кубиты вряд ли будут расположены по соседству друг к другу. Такая ситуация все же возможна, например, если при нумерации кубитов на квантовом чипе с планарным размещение, изображенной на фиг. 5, 1-й и N-й кубит расположены по соседствую, однако даже в этом случае большая часть других двухкубитных гейтов будет действовать на удаленные друг от друга кубиты. Преобразованное N-кубитное квантовое состояние 25 на выходе КПФ используют при дальнейшем выполнении алгоритмов, например, в алгоритме Шора или алгоритме оценки фазы.
Для выполнения двухкубитных операций между кубитами, расположенными не по соседству друг с другом, промежуточные квантовые гейты могут представлять собой SWAP-гейты, которые действуют на двухкубитные состояния согласно следующей матрице:

Результатом действия SWAP-гейта на двухкубитные состояния является перестановка информации между двумя кубитами.
Фиг. 7 поясняет необходимость применения промежуточных операций, выполняемых SWAP-гейтами для выполнения двухкубитных гейтов между удаленными друг от друга кубитами. На фиг. 7а представлен слой (преобразованное N-кубитное квантовое состояние 25) квантовой логической схемы выполняющей двухкубитный гейт условного сдвига фазы CRj. На фиг. 76 приведен пример реализация этой операции на квантовом вычислителе с ограниченной связанностью, позволяющей за одно применение реализовывать двухкубитные операции только между соседними кубитами. Реализация операции требует привлечение последовательностей применения SWAP-гейтов 26 из дополнительных двухкубитных SWAP-гейтов 27 для перемещения информации, содержащейся в одном из кубитов, участвующем в выполнении гейта CRj, ко второму такому кубиту. Целевая операций двухкубитного гейта 28 проводится между соседними кубитами. Из представленной квантовой схемы видно, что число необходимых дополнительных SWAP-гейтов растет пропорционально удалению кубитов, участвующих в двухкубитной операции. Как правило, в квантовых вычислителях, построенных по традиционным архитектурам, SWAP-гейт не входит в набор операций, которые могут выполняться за одно применение. По этой причине для выполнения SWAP-гейта используют последовательность других гейтов, которые поддерживаются квантовым вычислителем. Часто к набору поддерживаемых квантовых гейтов, которые можно выполнять за один подход, относится CNOT-гейт с матрицей преобразования, приведенной в выражении (3). На фиг. 8 приведено разложение квантовой операции, выполняемой SWAP-гейтом, на последовательность трех двухкубитных гейтов CNOT с матрицей преобразования (3). Таким образом, реализация операций перестановки состояний между удаленными друг относительно друга кубитами очень затратна с точки зрения внесения дополнительных шумов и ошибок, вносимых в квантовое состояние. Предлагаемое изобретение решает проблему конечной связанности кубитов в квантовых вычислителях с обратной связью.
Таким образом, квантовые вычислители с обратной связью, с архитектурой, изображенной на фиг. 3, не могут реализовывать многослойные квантовые логические схемы КПФ. Множество других схем также нельзя реализовать в этой архитектуре.
На фиг. 9 представлен пример схемы квантового преобразования, которую можно реализовать в квантовом вычислителе с обратной связью с блоком преобразователя 2-го типа 2 с архитектурой, изображенной на фиг. 1. Благодаря возможности хранения квантовой информации преобразователем 2-го типа 2 в течении нескольких шагов работы схемы удается повысить связанность квантовых логических схем. На фиг. 9 представлен пример, отвечающий задержке/хранению квантовых состояний 29а, сгенерированных в блоке преобразователя 1-го типа 1 на выходах 66 после первого шага работы вычислителя на протяжении следующих за этим j-1 шагов. После чего состояние поступает в блок преобразователя 1-го типа 1, начинающем выполнять j-й шаг. Блок преобразователя 2-го типа 2 может одновременно хранить состояния, сгенерированные на нескольких предыдущих шагах, которые могут подаваться на блоке преобразователя 1-го типа 1 в соответствии с конкретной реализуемой квантовой схемой.
На фиг. 10 представлены схемы архитектур квантовых вычислителей с обратной связью, которые могут реализовывать более сложные квантовые логические схемы, чем рассмотренная до этого архитектура. Квантовые схемы, реализуемые квантовыми вычислителями с архитектурами, изображенными на фиг. 10, могут быть более глубокими, т.к. они могут состоять из множества следующих друг за другом диагональных квантовых преобразований 18. Отличие этой архитектуры от архитектуры, изображенной на фиг. 1, заключается в том, что блок преобразователя 2-го типа 2 разделен и состоит из двух блоков 2а и 2б и приготавливаемое состояние измеряется на выходе блока 2б. Блок 2а служит для внесения задержки и возможного переключения каналов для выполнения одной диагонали квантовых преобразований 18 - Vj. Блок 2б служит для задержки и возможного переключения каналов между диагоналями квантовых преобразований 18, генерируемых последовательно, а также для выведения состояния на блок измерений 3. Рисунки, изображенные на фиг. 10 (а)-(г), иллюстрируют возможные варианты предлагаемой архитектуры квантовых вычислителей, которые отличаются соединением блоков преобразователя 1-го типа и блоков преобразователя 2-го типа.
Согласно варианту, изображенному на фиг. 10а, два модуля блока преобразований 2-го типа подключены к блоку преобразователя 1-го типа параллельно, при этом подмножество из M1 выходов блока преобразователя 1-го типа соединены с M1 входами первого модуля блока преобразователя 2-го типа, M1 выходов которого соединены с подмножеством из M1 входов блока преобразователя 1-го типа, при этом оставшиеся N-M1 выходов блока преобразователя 1-го типа соединены с N-M1 входами второго модуля блока преобразователя 2-го типа, D выходы второго модуля блока преобразователя 2-го типа соединены с D входами блока измерений, а оставшиеся M2=N-M1-D выходов второго модуля блока преобразователя 2-го типа соединены с М2 входами блока преобразователя 1-го типа.
Согласно варианту, изображенному на фиг. 10б, модули блока преобразователя 2-го типа подключены к блоку преобразователя 1-го типа последовательно, при этом подмножество из M1 выходов блока преобразователя 1-го типа соединены с подмножеством из M1 входов первого модуля блока преобразователя 2-го типа, M1 выходов которого соединены с подмножеством из M1 входов блока преобразователя 1-го типа, при этом оставшиеся N-M1 выходов блока преобразователя 1-го типа соединены с N-М1 входами второго модуля блока преобразователя 2-го типа, D выходов которого соединены с D входами блока измерений, при этом оставшиеся M2=N-M1-D выходов второго модуля блока преобразователя 2-го типа соединены с подмножеством из М2 входов первого модуля блока преобразователя 2-го типа.
Согласно варианту, изображенному на фиг. 10в, модули блока преобразователя 2-го типа подключены к блоку преобразователя 1 -го типа последовательно, при этом N выходов блока преобразователя 1-го типа соединены с N входами второго модуля блока преобразователя 2-го типа, подмножество из D выходов которого соединено с D входами блока измерений, оставшиеся N-D выходов второго модуля блока преобразователя 2-го типа соединены с N-D входами первого модуля блока преобразователя 2-го типа, N-D выходов которого соединены с подмножеством из N-D входов блока преобразователя 1 -го типа.
Согласно варианту, изображенному на фиг. 10г, модули блока преобразователя 2-го типа подключены к блоку преобразователя 1-го типа последовательно, при этом N выходов блока преобразователя 1-го типа соединены с N входами первого модуля блока преобразователя 2-го типа, N выходов которого соединены с N входами второго модуля блока преобразователя 2-го типа, при этом подмножество из D выходов второго модуля блока преобразователя 2-го типа соединены с D входами блока измерений, а оставшиеся N-D выходов второго модуля блока преобразователя 2-го типа соединены с N-D входами блока преобразователя 1-го типа.
Блоки преобразователей 1-го типа могут представлять собой системы квантовых вычислителей, основанные на традиционной гейтовой модели: оптические кубиты и линейно-оптические схемы, сверхпроводниковые цепи, ионы и нейтральные атомы, плененные в ловушках и др.
На фиг. 11 приведены примеры квантовых схем, которые могут быть использованы для осуществления блоков преобразователей 2-го типа. На фиг. 11 (а) приведен преобразователь 2-го типа, который состоит из набора программируемых задержек 30а, 30б, … 30в. Величина временной задержки, вносимой в канал, задается с компьютера через линии 9а, 9б…9в. На фиг. 11 (6) изображен преобразователь 2-го типа, который помимо программируемых задержек также содержит программируемый блок перестановок 31. Блок перестановок 31 выполняет преобразования перестановок между каналами в пространственной кодировке, т.е. состояния в разных пространственных каналах, входящие в него синхронно в один отрезок времени, переставляются в состояния, выходящие из него синхронно в один отрезок времени. Конкретное преобразование перестановки выполняется в соответствии с управлением от компьютера через линии 9. Временные программируемые задержки 30а, 30б…30в, вносимые в каналы после перестановки 31, могут менять временные каналы преобразуемых состояний. На фиг. 11 (в) изображен преобразователь 2-го типа, который состоит из последовательности чередующихся блоков перестановок 31а, 31б… и независимых временных задержек 30а, 30б…
Рабочий принцип простейшей программируемой линии задержки 30 поясняется на фиг. 12. Задержка может вносить два предварительно заданных значения временной статической задержки 32а или 32б в зависимости от положения входного и выходного переключателей программируемой задержки 33а и 33б соответственно. Одна из двух задержек реализуется в зависимости от режима, в который выставлены переключатели 33а и 33б. Конкретная реализация переключения между разными линиями задержки зависит от физической платформы, на которой основан квантовый вычислитель.
Преобразователи 2-го типа, осуществляющие программируемые задержки и перестановки, также можно изготовить на базе существующих квантовых систем или в полной совместимости с ними. Например, для оптической платформы квантовых вычислений, в которой квантовые состояния кодируются в оптические фотоны, задержки могут быть реализованы в виде программируемых оптических интерферометров, например, в виде оптоволоконных петель, соединенных посредством программируемых переключателей и/или делителей (Н. Qi et al, "Linear multiportphotonic interferometers: loss analysis of temporally-encoded architectures"// arxiv:1812.07015 (2018); K.R. Motes at al, "Scalable boson sampling with time-bin encoding using a loop-based architecture " // Phys. Rev. Lett. V. 113, 120501 (2015)). Вместо оптических волокон могут быть использованы резонаторы, сконструированные из зеркал на оптическом столе или в монолитном интегрально-оптическом исполнении. Помимо этого, для преобразователей 2-го типа можно использовать элементы квантовой оптической памяти, которая может хранить квантовые оптические состояния и по требования выдавать эти состояния в преобразователь 1 -го типа. В отличие от преобразователей на основе задержек, в которых фотоны распространяются в оптоволоконных или резонаторных петлях после их поступления на входы, при записи состояний в квантовую память происходит конвертация состояний в возбуждение материальной среды, например, возбуждение уровней энергий паров металлов (K.F. Reim at al. "Quantum memory" // WO 2011073656A1 (2011)) или твердотельной структуры (A. Ortu et al. "Storage of photonic time-bin qubits for up to 20 ms in a rare-earth doped crystal" // NPJ Quantum Information v. 8, No. 29 (2022)). Таким образом, входные квантовые состояния фотонов, распространяющиеся со скоростью света, конвертируются в квантовое состояние покоящейся материальной среды. Вывод состояний из квантовой памяти происходит управляющим воздействием, которое стимулирует конвертация возбуждения материальной среды в состояния распространяющихся фотонов. Существует множество типов квантовой памяти, которые отличаются материальной квантовой системой, используемой хранения информации принципом работы процедур записи и считывания квантовых состояний.
В квантовых вычислителях, основанных на кодировании квантовых состояний в состояния материальных систем, квантовую память, необходимую для построения преобразователей 2-го типа, также можно реализовать на практике. Например, продемонстрированное время хранения квантовых состояний кубитов на уровнях в ионах в ловушках составляет десятки минут, что на несколько порядков превосходит типичные времена выполнения квантовых логических операций на этой платформе (P. Want et al., "Single ion qubit with estimated coherence time exceeding one hour" // Nature Communications v. 12, No 233 (2021)). Время хранения квантовых состояний в центрах окраски в алмазе может превышать 10 миллисекунд (D.D. Sukachov et al., "Silicon-Vacancy spin qubit in diamond: a quantum memory exceeding 10 ms with single-shot state readout" // Phys. Rev. Lett, v. 119, 223602 (2017)). Времена хранения в квантовой памяти на много порядков превышают время, затрачиваемое на выполнение квантовых логических операций, т.е. на основе таких элементов квантовой памяти можно построить квантовые вычислители по предложенной архитектуре, которые будут реализовывать задержки достаточно долгое время, для реализации многокубитных и глубоких квантовых логических цепей.
Пример конкретной реализации
Для демонстрации работы заявленного изобретения был использован линейно-оптический квантовый компьютер, в котором квантовая информация кодируется в летящие одиночные фотоны, преобразование блока 1-го типа выполнялось многоканальным интерферометрам, а преобразование блока 2-го типа выполнялось волоконными линиями задержки с разными длинами.
На фиг. 13 представлены схемы оптических установок, использованных в демонстрации заявленного изобретения. На фиг. 13 (а) изображена схема, реализующая известный квантовый оптический вычислитель. Этот вычислитель использует независимые линии временной задержки, которые вносят одинаковые задержки. На фиг. 13б изображена схема, которая является простейшим вариантом квантового вычислителя, выполненного по предлагаемой архитектуре. Ее отличие от схемы, изображенной на фиг. 13а, состоит в том, что в линиях задержки выполняется перестановка двух каналов и относительная задержка сигналов. Основными элементами схем являлись: блок преобразований 1-го типа, представляющий собой многоканальный программируемый 4-х канальный интерферометр 34, блок преобразований 2-го типа, состоящий из линий задержки с разными длинами волоконных линий 35 и состоящий из двух оптических волокон 35а и 35б, источник пар фотонов 36, основанный на спонтанном параметрическом рассеянии, блок измерений, состоящий в реализуемом примере из двух детекторов одиночных фотонов 37а и 37б, компьютера 4. Схемы отличаются конструкцией блока преобразователя 2-го типа, а именно волоконными линиями задержки.
В качестве многоканального программируемого интерферометра использовался интегрально-оптический чип, созданный с помощью технологии фемтосекундной лазерной печати, которая позволяет изготавливать как планарные, так и трехмерные интегрально-оптические схемы. Для создания интегрального чипа оптической схемы использовалась кварцевая заготовка в форме прямоугольника с длиной 10 см, шириной 5 см и толщиной 0.5 см. На первом этапе изготовления чипа в объеме заготовки создавались пассивные волноводные структуры, формирующие статическую оптическую схему, представляющую собой пучок из пяти волноводов, которые сводились близко друг к другу для формирования области взаимодействия, где энергии оптических сигналов переходят из волновода в волновод за счет эванесцентного взаимодействия между ними, и разносились на удаление для предотвращения взаимодействия и внесения сдвигов фаз программируемым образом. Начала и концы волноводов доводились до противоположных торцов стеклянной заготовки для обеспечения возможности заведения и выведения оптических сигналов.
Для реализации программируемое™ на чипе изготавливались элементы сдвига фазы, с помощью которых осуществлялась реконфигурация интерферометров. Элементы сдвига фазы были основаны на термо-оптическом эффекте. Элементы изменяемых фазовых сдвигов представляли собой металлические полоски, располагаемые над участками волноводов, на которых было необходимо реализовать эти элементы. При подаче напряжен на элементы происходил нагрев соответствующих участков волноводов, в результате чего коэффициент преломления стекла в этой области менялся, вызывая таким образом сдвиг фазы относительно не нагретых участков. Детали использованной технологии изготовления можно найти в работе Z V. Dyakonov et al., "Reconfigurablephotonics on a glass chip" // Phys. Rev. Applied, vol. 10, 044048 (2018).
Два одиночных фотона, поступающих одновременно на 2 входа 4-х канального интерферометра 34, представляют собой входные состояния, инициализирующие состояние квантового вычислителя. Источником пар фотонов 36 являлся процесс спонтанного параметрического рассеяния, протекающий в нелинейном кристалле бета-бората бария. В процессе спонтанного параметрического рассеяния рождались пары фотонов, каждый из которых выходил из кристалла под своим углом, что давало возможность собирать фотоны в волокна и заводить в интерферометр. В качестве накачки использовался лазер, генерирующий импульсы на центральной длине волны 816 нм длительностью ~100 фс и частотой следования f=83 МГц. Излучение накачки поступало на удвоитель частоты, где его длина волны становилось в 2 раза меньше изначальной, после чего оно поступало на нелинейный кристалл. Импульс накачки в нелинейном кристалле недетерминистическим образом рождал пару одиночных фотонов на длине волны 816 нм в разных пространственных модах. Через оптоволоконный ввод пары фотонов поступали на два канала интерферометра. Т.к. длина волны накачки, поступающая в нелинейный кристалл, намного отличается от длин волн генерируемых пар фотонов, и направления распространения фотонов отличается от направления распространения волны накачки, частотных фильтров не требовалось.
Для детектирования использовались сверхпроводниковые детекторы. Сигналы с выхода интерферометра заводились в криостат, в котором располагались детекторы, с помощью волокон. Эффективность детектирования одиночных фотонов составляла -85%. Электрические сигналы с электронной системы считывания фотоотсчетов поступали на персональный компьютер 4, через электрические линии 38а и 38,. Компьютерная программа обрабатывала сигналы, поступающие на компьютер от детекторов 37а и 37,, соответственно.
Для реализации блока преобразователя 2-го типа использовались оптические волокна, концы которых соединялись с входами и выходами интегрального чипа. В схеме, изображенной на фиг. 13 а, волокна имели одинаковую длину, которая обеспечивала синхронное поступление фотонов от источника пар фотонов 36 и сигналов из петли на входы в чип. Таким образом длина волокон, составляла « 2,4 м и подгонялась чтобы с высокой степенью точности (не хуже 0,1 мм) давать время полного обхода оптических сигналов, равное периоду следования импульсов накачки 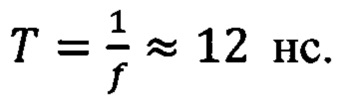 Для этой цели несколько раз проводилось укорачивание/сошлифовывание волокна (волокно бралось заведомо длиннее, чем необходимо). После каждого раза волокно соединялось с чипом и изучалась возможность наблюдения эффекта квантовой интерференции при поступлении на чип одиночных фотонов с частотой f, который возможен только, если задержанный фотон или волокна поступает в интерферометр одновременно с заново сгенерированным. Укорачивание волокна продолжалось до наблюдения эффекта. Также проводился контроль поляризации сигналов, выходящих из волокна - она всегда должна совпадать с поляризацией фотонов, поступающих на интерферометр. Нужная поляризация подбиралась контроллером поляризации.
Для этой цели несколько раз проводилось укорачивание/сошлифовывание волокна (волокно бралось заведомо длиннее, чем необходимо). После каждого раза волокно соединялось с чипом и изучалась возможность наблюдения эффекта квантовой интерференции при поступлении на чип одиночных фотонов с частотой f, который возможен только, если задержанный фотон или волокна поступает в интерферометр одновременно с заново сгенерированным. Укорачивание волокна продолжалось до наблюдения эффекта. Также проводился контроль поляризации сигналов, выходящих из волокна - она всегда должна совпадать с поляризацией фотонов, поступающих на интерферометр. Нужная поляризация подбиралась контроллером поляризации.
В схеме, изображенной на фиг. 136, волокна имели разную длину. Одно из волокон обеспечивало задержку 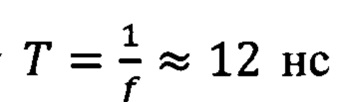 и имело длину ≈2,4 м, тогда как другое волокно имело длину ≈4,8 м, обеспечивающую задержку 2Т ≈ 24 нc. Точный подгон длин волокон осуществлялся таким же методом, что и для схемы, изображенной на фиг. 13а. Помимо этого, выходы волокон были переставлены относительно входов, таким образом было реализовано преобразование перестановки.
и имело длину ≈2,4 м, тогда как другое волокно имело длину ≈4,8 м, обеспечивающую задержку 2Т ≈ 24 нc. Точный подгон длин волокон осуществлялся таким же методом, что и для схемы, изображенной на фиг. 13а. Помимо этого, выходы волокон были переставлены относительно входов, таким образом было реализовано преобразование перестановки.
Для сравнения сложности выполняемых задач квантовыми вычислителями друг с другом была рассмотрена задача приготовления квантовых состояний в пространственно-временной кодировке и генерация статистики фотоотсчетов на основе измерений этих состояний детекторами одиночных фотонов. Т.к. за один шаг работы схемы измеряются 2 пространственных канала, то состояние, приготавливаемой схемами за W шагов их работы, может быть описано суперпозицией по 2W пространственно-временным каналам:

где  - фоковское состояние с числом фотонов в j-ой моде Sj (j=1…2W),
- фоковское состояние с числом фотонов в j-ой моде Sj (j=1…2W), 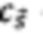 - амплитуда вероятности, соответствующая состоянию
- амплитуда вероятности, соответствующая состоянию 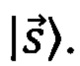 В эксперименте анализировались распределения вероятностей
В эксперименте анализировались распределения вероятностей 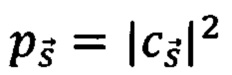 фотоотсчетов, измеренных детекторами одиночных фотонов на выходе из квантовой схемы. Для сравнения информационной емкости генерируемых квантовых состояний рассчитывались энтропия Шеннона:
фотоотсчетов, измеренных детекторами одиночных фотонов на выходе из квантовой схемы. Для сравнения информационной емкости генерируемых квантовых состояний рассчитывались энтропия Шеннона:
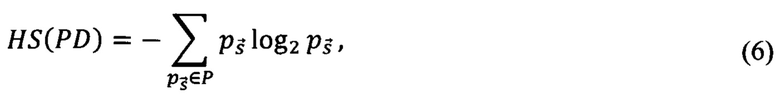
где PD - распределение вероятностей pi, полученное в эксперименте. Чем выше значение энтропии Шеннона, тем больше информации несет квантовое состояние с распределением 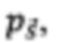 (J.V. Stone, "Information theory: a tutorial introduction" // arxiv:1802.59068 (2018)).
(J.V. Stone, "Information theory: a tutorial introduction" // arxiv:1802.59068 (2018)).
В двух оптических схемах, изображенных на фиг. 1 За и фиг. 136, использовался один и тот же интегральный чип: 4-х канальный интерферометр 34. Сначала выполнялся эксперимент со схемой, изображенной на фиг. 13 а, для чего к чипу подключалась линия задержки из двух одинаковых волокон (с процедурой подстройки длины, описанной ранее). Выбиралось W=5 шагов работы схемы, таким образом измерялась статистика фотоотсчетов для квантовых состояний, сгенерированных в 10 пространственно-временных каналах на выходе из чипа интерферометра 34. Для этого лазер, используемый для накачки источника пар фотонов, включался и работал в течение ~100 периодов (шагов работы схемы) следования импульсов. В силу высокой частоты следования импульсов лазера включение лазера на меньшее количество времени было невозможным из-за отсутствия технических средств для этого. Из 100 шагов выбирались только те фотоотсчеты, которые были получены за первые W шагов. Данная процедура автоматически повторялась 1 млн. раз в 10 разных экспериментах, отличающихся передаточной матрицей многоканального интерферометра. В каждом новом эксперименте передаточная матрица многоканального интерферометра устанавливалась заново случайным выставлением сдвигов фаз на интегральном чипе. Таким образом, были получены распределения PD(1) вероятностей 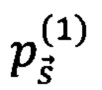 для схемы, изображенной на фиг. 13а.
для схемы, изображенной на фиг. 13а.
Аналогичная серия экспериментов повторялась для схемы, изображенной на фиг. 13. Для этого в установке волоконные линии обратной связи менялись соответствующим образом и выполнялось точно такое же количество измерений и экспериментов, как и в предыдущей схеме. Были получены распределения вероятностей 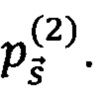
На основе полученных распределений вероятностей рассчитаны средние значения энтропии Шеннона для вычислителей, изображенных на фиг. 13а и фиг. 13б. Энтропия фотоотсчетов, полученная в первой схеме, оказалась равной H5(PD(1))=65,3, тогда как энтропия, полученная во второй схеме, реализующей предлагаемое изобретение, была равна HS(PD(2))=94,6.
Таким образом, изобретение решает проблему ограниченной связанности в квантовых вычислителях с обратной связью. Помимо этого, продемонстрированное превышение сложности квантовых состояний в схеме, использующей предлагаемую архитектуру квантовых вычислителей, по сравнению со схемой, выполненной по известной архитектуре, свидетельствует о необходимости реализации более глубоких квантовых схем в известной архитектуре, чтобы достичь преобразований, которые реализуются в заявляемых архитектурах на схемах с меньшей глубиной.
| название | год | авторы | номер документа |
|---|---|---|---|
| Квантовая вычислительная система на основе фотонных чипов | 2023 |
|
RU2806840C1 |
| Система и способ решения прикладных задач материаловедения с помощью сопряжения квантовых и классических устройств | 2023 |
|
RU2814969C1 |
| СПОСОБ ВЫПОЛНЕНИЯ КВАНТОВЫХ ВЫЧИСЛЕНИЙ С ИСПОЛЬЗОВАНИЕМ КУДИТОВ | 2020 |
|
RU2761771C1 |
| СПОСОБ И СИСТЕМА КОМПЕНСАЦИИ ШУМОВ НА КВАНТОВОМ ПРОЦЕССОРЕ С ПОМОЩЬЮ КВАНТОВОЙ ТОМОГРАФИИ ОПЕРАЦИЙ | 2022 |
|
RU2786349C1 |
| Квантовая вычислительная система на основе нейтральных атомов | 2023 |
|
RU2814970C1 |
| Управляющая система для квантовых вычислительных устройств | 2023 |
|
RU2814936C1 |
| СПОСОБ ФИЛЬТРАЦИИ ФОТОНОВ ОТ ОСТАТОЧНОГО ИЗЛУЧЕНИЯ КОГЕРЕНТНОЙ НАКАЧКИ | 2021 |
|
RU2783222C1 |
| ВОЛОКОННО-ОПТИЧЕСКИЙ КВАНТОВЫЙ КОМПЬЮТЕР (ВАРИАНТЫ) | 2023 |
|
RU2813708C1 |
| СПОСОБ ЛИНЕЙНОГО ОПТИЧЕСКОГО ПРЕОБРАЗОВАНИЯ СИГНАЛОВ И ИНТЕРФЕРОМЕТР, РЕАЛИЗУЮЩИЙ ТАКОЕ ПРЕОБРАЗОВАНИЕ | 2018 |
|
RU2702806C1 |
| Устройство для реализации двухкубитного вентиля CZ между сверхпроводниковыми кубитами на основе высокой кинетической индуктивности | 2022 |
|
RU2795679C1 |
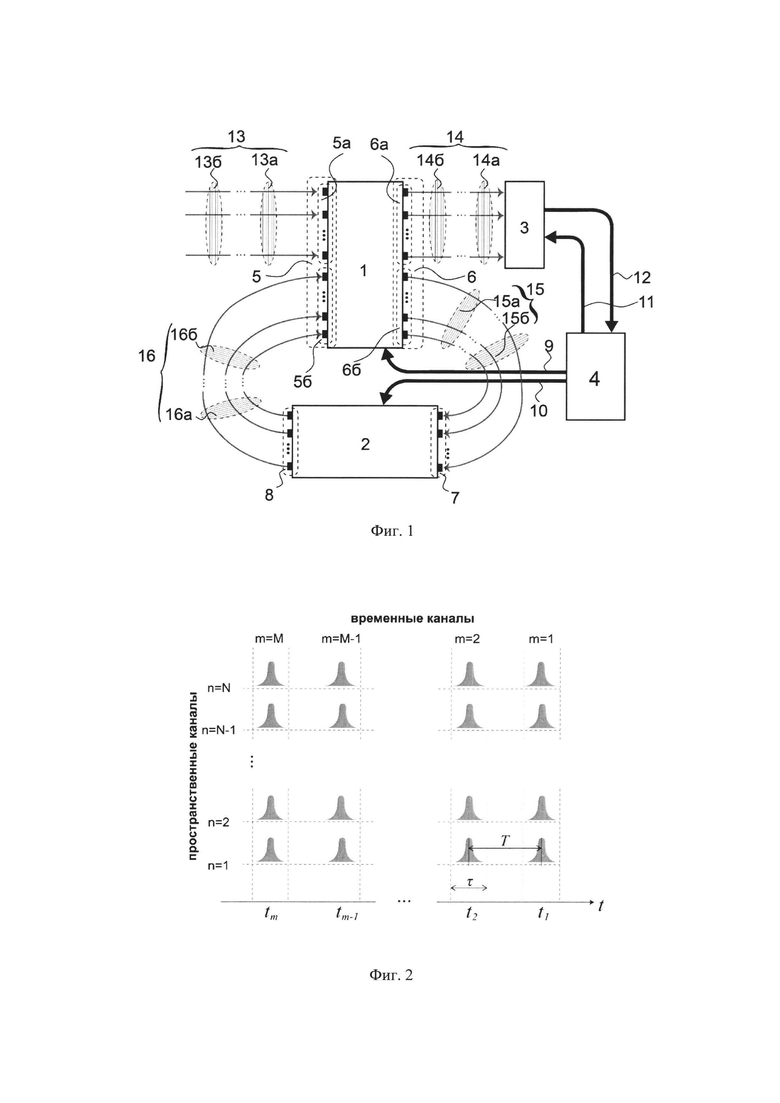
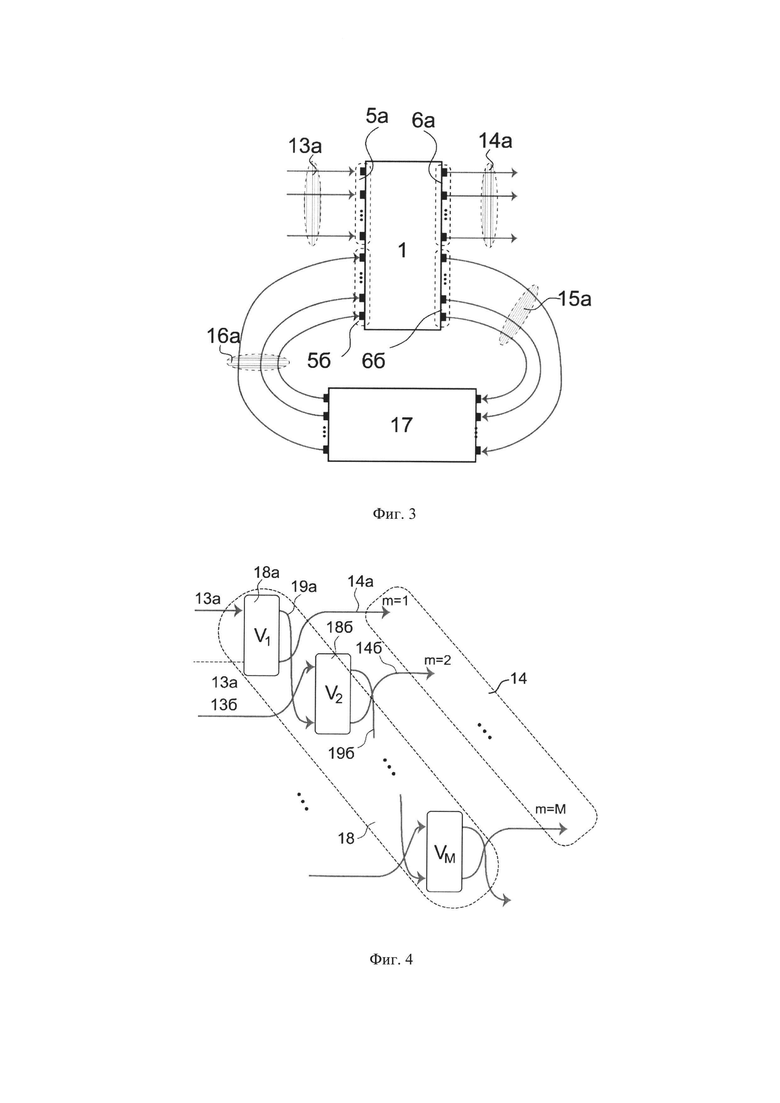
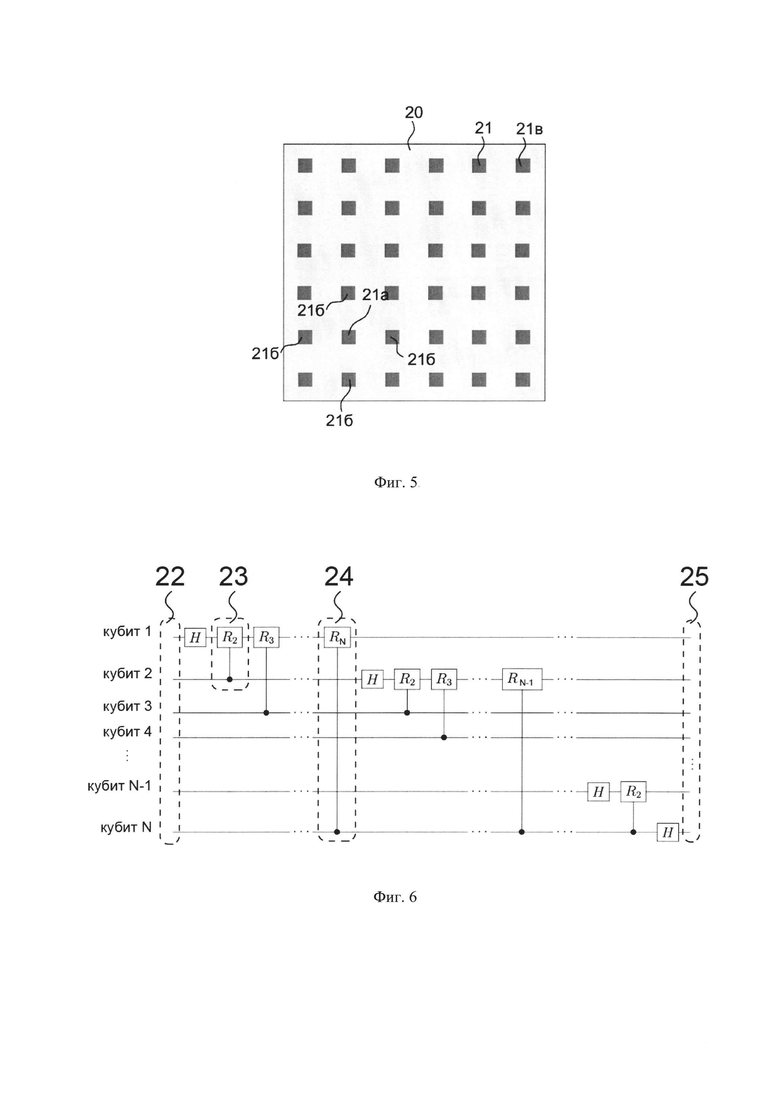
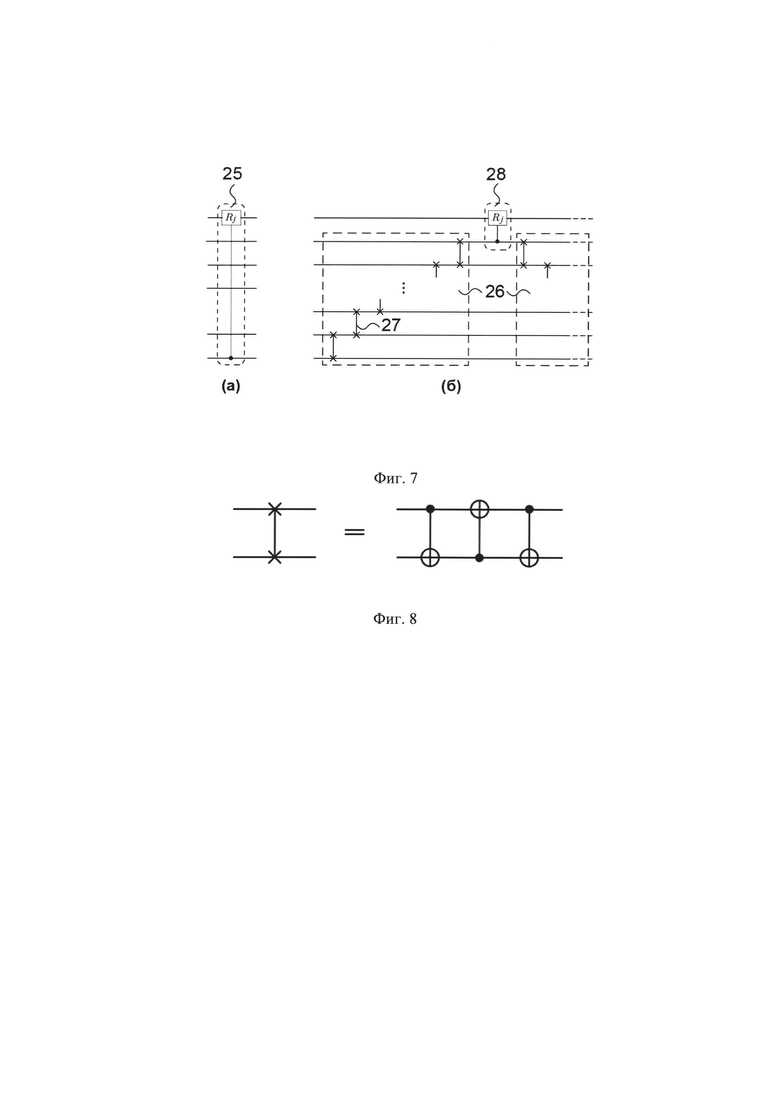
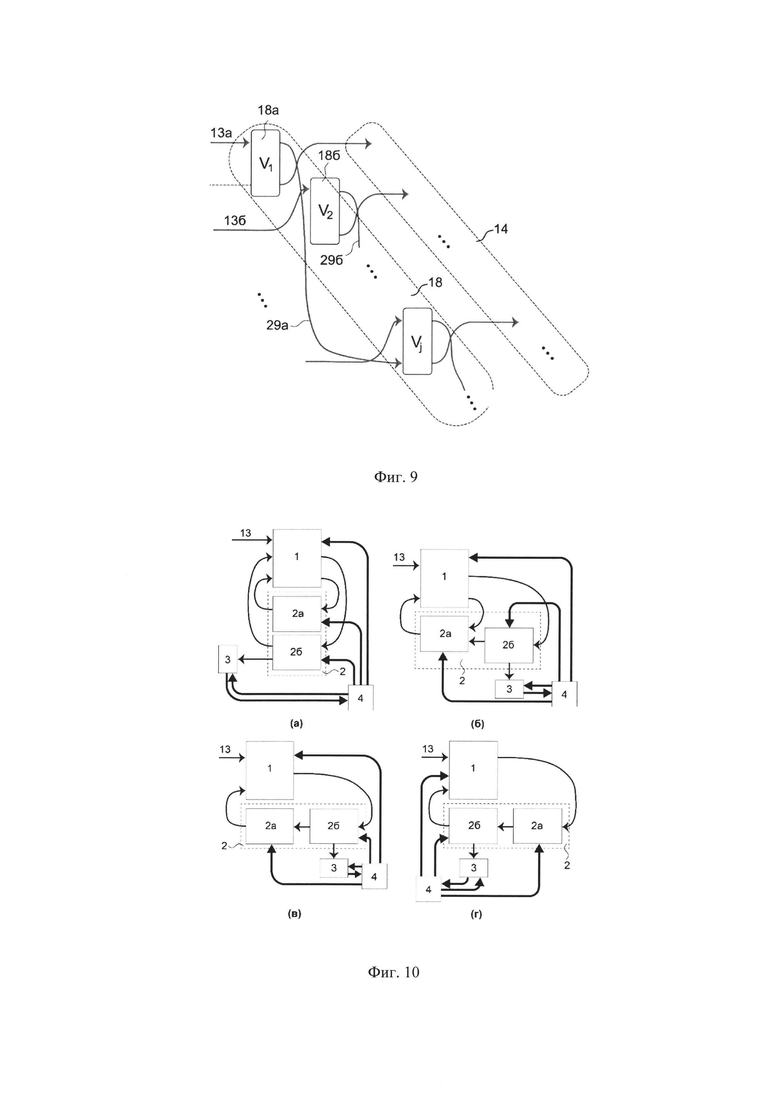
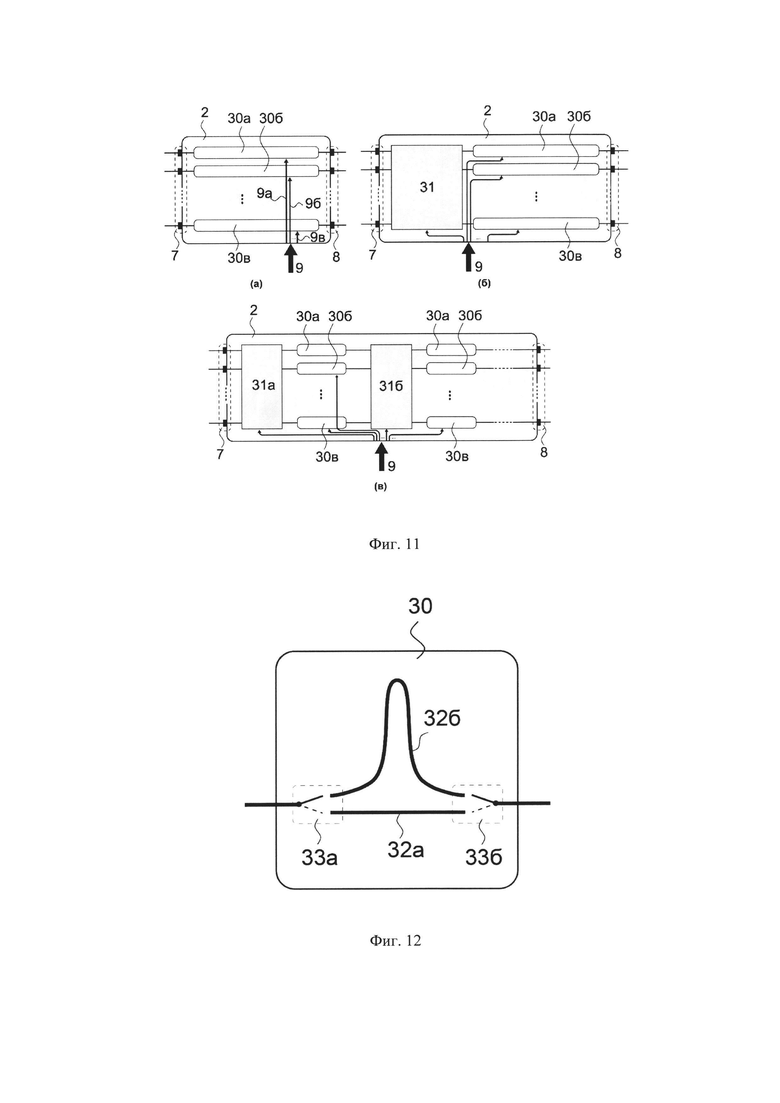
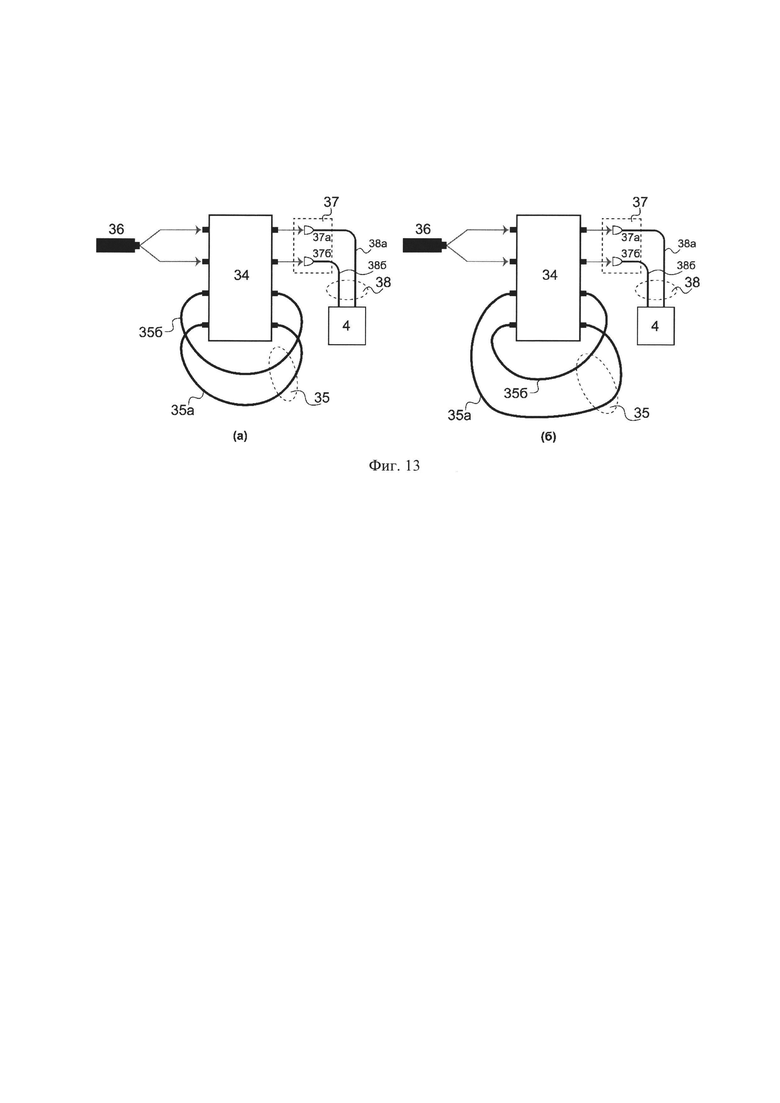
Изобретение относится к области квантовых вычислений, а именно к устройствам, реализующим квантовые вычислительные алгоритмы. Технический результат заключается в повышении связанности между кубитами квантовых вычислителей с обратной связью и увеличении глубины реализуемых квантовых логических схем, что позволяет выполнять более широкий класс квантовых преобразований и снижает уровень шумов, ошибок и потерь в квантовом вычислителе. Технический результат достигается за счет того, что архитектура квантового вычислителя включает блоки преобразований двух типов, выполненных с возможностью программируемого изменения преобразований; причем один из блоков имеет возможность вносить временные задержки и выполнять перестановки каналов. 2 н. и 28 з.п. ф-лы, 13 ил.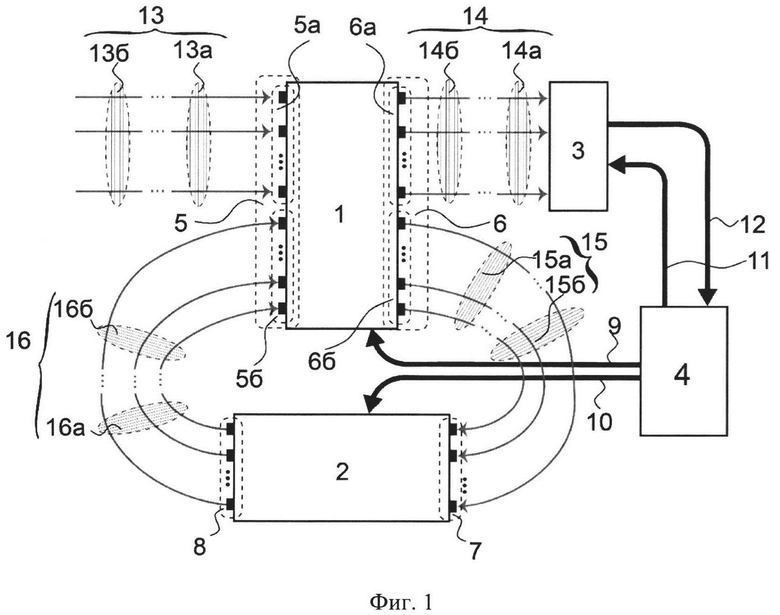
1. Квантовое вычислительное устройство, включающее
по меньшей мере один блок 1-го типа, имеющий N входов и N выходов, где N≥3, выполненный с возможностью синхронного преобразования сигналов, описываемых квантовыми состояниями, за время τ,
по меньшей мере один блок 2-го типа, имеющий M<N входов и М выходов, где М≥2, выполненный с возможностью внесения временных задержек в сигналы, описываемые квантовыми состояниями, поступающие на его входы, с возможностью перестановки каналов на выходах относительно каналов на входах,
блок измерений, выполненный с возможностью измерения и обработки результатов измерений квантовых состояний сигналов, поступающих на входы блока с N-M выходов блока 1-го типа,
блок формирования входных сигналов, выполненный с возможностью подачи сигналов на N-M входов блока 1-го типа, описываемых одинаковыми квантовыми состояниями, с периодом Т, равным или кратным τ,
компьютер, выполненный с возможностью управления преобразованиями по меньшей мере одного блока 1-го типа и по меньшей мере одного блока 2-го типа, управления блоком измерений и обработки результатов измерений этого блока,
при этом М выходов блока 1-го типа соединены с М входами блока 2-го типа, а М выходов блока 2-го типа соединены с М входами блока 1-го типа, a N-M выходов блока 1-го типа соединены с N-M входами блока измерений.
2. Квантовое вычислительное устройство по п. 1, отличающееся тем, что содержит не менее двух блоков 1-го типа, при этом блоки соединены последовательно таким образом, что выходы с предыдущего блока соединены с соответствующими входами последующего блока.
3. Квантовое вычислительное устройство по п. 1, отличающееся тем, что блок 2-го типа выполнен с возможностью изменения временных задержек по меньшей мере в одном пространственном канале данного блока.
4. Квантовое вычислительное устройство по п. 1, отличающееся тем, что блок 2-го типа выполнен с возможностью внесения временных задержек, кратных Т, и возможностью их программируемого изменения.
5. Квантовое вычислительное устройство по п. 1, отличающееся тем, что по меньшей мере один из блоков преобразований 1-го и 2-го типа, блок измерений и компьютер выполнены с возможностью изменения преобразования квантовых состояний за время меньшее, чем Т.
6. Квантовое вычислительное устройство по п. 1, отличающееся тем, что в качестве сигналов использованы оптические сигналы, которые кодируют квантовые состояния,
при этом в качестве блоков 1-го и 2-го типа использованы программируемые интерферометры, где блок 2-го типа дополнительно содержит петли временной задержки.
7. Квантовое вычислительное устройство по п. 6, отличающееся тем, что блок 2-го типа содержит элементы квантовой памяти, выполненные с возможностью записи и считывания оптических сигналов.
8. Квантовое вычислительное устройство по п. 7, отличающееся тем, что элемент квантовой памяти представляет собой твердотельную квантовую систему, выполненную с возможностью хранения квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее чем 2Т.
9. Квантовое вычислительное устройство по п. 7, отличающееся тем, что элемент квантовой памяти представляет собой квантовую систему, реализованную на базе паров щелочных металлов, выполненную с возможностью хранения квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее чем 2Т.
10. Квантовое вычислительное устройство по п. 7, отличающееся тем, что элемент квантовой памяти представляет собой квантовую систему одиночных нейтральных атомов в ловушке или ионов в ловушке, выполненную с возможностью хранения квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее чем 2Т.
11. Квантовое вычислительное устройство по п. 1, отличающееся тем, что выполнено на основе квантовой системы одиночных нейтральных атомов в ловушке, или на основе квантовой системы одиночных ионов в ловушке, или на основе квантовой системы сверхпроводниковых цепочек, или на основе квантовой системы квантовых точек, или на основе квантовой системы дефектов в кремнии или алмазе.
12. Квантовое вычислительное устройство по п. 11, отличающееся тем, что блок 1-го типа и блок 2-го типа выполнены на основе разных квантовых систем.
13. Квантовое вычислительное устройство по п. 1, отличающееся тем, что компьютер выполнен с возможностью реализации квантовых вариационных алгоритмов.
14. Квантовое вычислительное устройство, включающее
по меньшей мере один блок 1-го типа, имеющий N входов и N выходов, где N≥3, выполненный с возможностью синхронного преобразования сигналов, описываемых квантовыми состояниями, за время τ,
по меньшей мере один блок 2-го типа, имеющий совокупно N входов и M<N выходов, где М≥2, содержащий по меньшей мере 2 модуля, соединенные параллельно или последовательно и выполненные с возможностью внесения временных задержек в сигналы, описываемые квантовыми состояниями, поступающие с соответствующих выходов блока 1-го типа на входы блока 2-го типа, с возможностью перестановки каналов на выходах относительно каналов на входах,
по меньшей мере один блок измерений, выполненный с возможностью измерения квантовых состояний сигналов, поступающих на D≥1 его входов с D выходов модуля блока 2-го типа,
блок формирования входных сигналов, выполненный с возможностью подачи сигналов на N-M входов блока 1-го типа, описываемых одинаковыми квантовыми состояниями, с периодом Т, равным или кратным τ,
компьютер, выполненный с возможностью управления преобразованиями блока 1-го типа и блока 2-го типа, управления блоком измерений и обработки результатов измерений этого блока.
15. Квантовое вычислительное устройство по п. 14, отличающееся тем, что число модулей в блоке 2-го типа равно двум, и они подключены к блоку 1-го типа параллельно, при этом подмножество из M1 выходов блока 1-го типа соединено с M1 входами первого модуля блока 2-го типа, M1 выходов которого соединены с подмножеством из M1 входов блока 1-го типа, при этом оставшиеся N-M1 выходов блока 1-го типа соединены с N-M1 входами второго модуля блока 2-го типа, D выходы второго модуля блока 2-го типа соединены с D входами блока измерений, а оставшиеся M2=N-M1-D выходов второго модуля блока 2-го типа соединены с М2 входами блока 1-го типа.
16. Квантовое вычислительное устройство по п. 14, отличающееся тем, что число модулей в блоке 2-го типа равно двум, и они подключены к блоку 1-го типа последовательно, при этом подмножество из M1 выходов блока 1-го типа соединено с подмножеством из M1 входов первого модуля блока 2-го типа, M1 выходов которого соединены с подмножеством из M1 входов блока 1-го типа, при этом оставшиеся N-M1 выходов блока 1-го типа соединены с N-M1 входами второго модуля блока 2-го типа, D выходов которого соединены с D входами блока измерений, при этом оставшиеся M2=N-M1-D выходов второго модуля блока 2-го типа соединены с подмножеством из М2 входов первого модуля блока 2-го типа.
17. Квантовое вычислительное устройство по п. 14, отличающееся тем, что число модулей в блоке 2-го типа равно двум, и они подключены к блоку 1-го типа последовательно, при этом N выходов блока 1-го типа соединены с N входами второго модуля блока 2-го типа, подмножество из D выходов которого соединено с D входами блока измерений, оставшиеся N-D выходов второго модуля блока 2-го типа соединены с N-D входами первого модуля блока 2-го типа, N-D выходов которого соединены с подмножеством из N-D входов блока 1-го типа.
18. Квантовое вычислительное устройство по п. 14, отличающееся тем, что число модулей в блоке 2-го типа равно двум, и они подключены к блоку 1-го типа последовательно, при этом N выходов блока 1-го типа соединены с N входами первого модуля блока 2-го типа, N выходов которого соединены с N входами второго модуля блока 2-го типа, при этом подмножество из D выходов второго модуля блока 2-го типа соединено с D входами блока измерений, а оставшиеся N-D выходов второго модуля блока 2-го типа соединены с N-D входами блока 1-го типа.
19. Квантовое вычислительное устройство по п. 14, отличающееся тем, что на N-M входов блока 1-го типа подаются сигналы, описываемые одинаковыми квантовыми состояниями, с периодом Т, равным или кратным т, при этом временные задержки, вносимые блоком 2-го типа, кратны Т и выполнены с возможностью программируемого изменения.
20. Квантовое вычислительное устройство по п. 14, отличающееся тем, что компьютер выполнен с возможностью изменения преобразования квантовых состояний, выполняемых блоком 1-го типа, за время меньшее, чем Т.
21. Квантовое вычислительное устройство по п. 14, отличающееся тем, что компьютер выполнен с возможностью изменения базиса измерений, выполняемых блоком измерений, за время меньшее, чем Т.
22. Квантовое вычислительное устройство по п. 14, отличающееся тем, что в качестве сигналов используются оптические сигналы, которые кодируют квантовые состояния, при этом в качестве блоков 1-го и 2-го типа использованы программируемые интерферометры, где блок 2-го типа дополнительно содержит петли временной задержки.
23. Квантовое вычислительное устройство по п. 22, отличающееся тем, что блок 2-го типа содержит элементы квантовой памяти, выполненные с возможностью записи и считывания оптических сигналов.
24. Квантовое вычислительное устройство по п. 23, отличающееся тем, что элемент квантовой памяти представляет собой твердотельную квантовую систему, в которой возможно хранение квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее чем 2Т.
25. Квантовое вычислительное устройство по п. 23, отличающееся тем, что элемент квантовой памяти представляет собой квантовую систему, реализованную на базе паров щелочных металлов, выполненную с возможностью хранения квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее чем 2Т.
26. Квантовое вычислительное устройство по п. 24, отличающееся тем, что элемент квантовой памяти представляет собой квантовую систему одиночных нейтральных атомов в ловушке или ионов в ловушке, в которой возможно хранение квантовых состояний поступающих сигналов в форме возбуждения квантовых состояний этой квантовой системы на протяжении отрезка времени не менее чем 2Т.
27. Квантовое вычислительное устройство по п. 14, отличающееся тем, что выполнено на основе квантовой системы одиночных нейтральных атомов в ловушке, или на основе квантовой системы одиночных ионов в ловушке, или на основе квантовой системы сверхпроводниковых цепочек, или на основе квантовой системы квантовых точек, или на основе квантовой системы дефектов в кремнии или алмазе.
28. Квантовое вычислительное устройство по п. 14, отличающееся тем, что блок 1-го типа и блоки 2-го типа выполнены на основе разных квантовых систем.
29. Квантовое вычислительное устройство по п. 14, отличающееся тем, что блоки 2-го типа выполнены на основе разных квантовых систем.
30. Квантовое вычислительное устройство по п. 14, отличающееся тем, что компьютер выполнен с возможностью выполнения квантовых вариационных алгоритмов.
| Способ восстановления спиралей из вольфрамовой проволоки для электрических ламп накаливания, наполненных газом | 1924 |
|
SU2020A1 |
| СПОСОБ ЛИНЕЙНОГО ОПТИЧЕСКОГО ПРЕОБРАЗОВАНИЯ СИГНАЛОВ И ИНТЕРФЕРОМЕТР, РЕАЛИЗУЮЩИЙ ТАКОЕ ПРЕОБРАЗОВАНИЕ | 2018 |
|
RU2702806C1 |
| Способ регенерирования сульфо-кислот, употребленных при гидролизе жиров | 1924 |
|
SU2021A1 |
| Способ получения продуктов конденсации фенолов с формальдегидом | 1924 |
|
SU2022A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТОЯНИЯ КУБИТА | 2013 |
|
RU2538296C2 |
Авторы
Даты
2024-06-24—Публикация
2023-04-06—Подача