Область техники, к которой относится изобретение
Изобретение относится к области квантовой оптики и квантовой информации, а именно к методам реализации квантовых вычислительных алгоритмов с помощью линейно-оптических устройств. Изобретение может быть использовано для реализации на практике квантовых вычислительных алгоритмов с целью решения некоторых классов вычислительных задач. В частности, для решения задач глобальной оптимизации сложных функций со многими параметрами, поиска решений больших систем алгебраических уравнений, симуляции свойств молекул и материалов быстрее и точнее, чем устройства, рабочий принцип которых основан на классических вычислительных алгоритмах.
Уровень техники
Из уровня техники известны квантовые вариационные алгоритмы, применяемые для решения вычислительных задач, которые раскрыты в изобретении R. Babbush, Н. Neven, «Simulating materials using quantum computation» // WO 2018 080553 (2018). В своей основе эти алгоритмы используют квантовые особенности физических систем, которые позволяют решать некоторые классы вычислительных задач быстрее, чем традиционные компьютеры, основанные на традиционных классических подходах. Примером вычислительных задач, которые можно решать квантовыми вариационными алгоритмами, является нахождение энергии состояний молекул - важной характеристики при расчете химических реакций. В квантовых вариационных алгоритмах решаемую задачу кодируют в квантовые операторы. Решение задачи выполняют посредством поиска глобального экстремума величин от ожидаемых средних этих операторов, которые рассчитываются с использованием квантовых состояний, приготавливаемых на квантовых физических устройствах. Для расчета экстремума ожидаемого среднего от операторов в практических реализациях необходимо приготавливать квантовые состояния реальных физических систем, которые должны допускать управление изменением внешних параметров.
Недостатком квантовых вариационных алгоритмов является сложность приготовления многокубитовых параметризованных квантовых состояний в реальных физических системах. Размерность приготавливаемых состояний определяет сложность задач, которые можно решать с помощью квантового устройства.
Из уровня техники известны способ и устройство для реализации квантового вариационного алгоритма с помощью линейно-оптических гейтовых схем, изложенные в работе A. Peruzzo et al., "A variational eigenvalue solver on a photonic quantum processor"// Nature Communications, v. 5, 4213 (2014). Для приготовления параметризованного квантового состояния фотонов используют параметризованную гейтовую схему, основанную на логической кодировке кубитов с одним двухкубитовым линейно-оптическим гейтом CNOT. Максимальная вероятность успешного срабатывания этой схемы ограничена вероятностью срабатывания линейно-оптического гейта, которая равна 1/9. Устройство позволяет изменять приготавливаемое состояние с помощью варьирования параметров элементов сдвигов фазы, задающих параметры однокубитных гейтов, также входящих в квантовую схему.
Недостатком известного технического решения является невозможность применения данного способа для приготовления вариационных состояний, состоящих из большого числа кубитов. Рост числа кубитов в схеме приводит к схемам, содержащим возрастающее число недетерминистических двухкубитовых гейтов, что делает вероятность успешного приготовления состояний крайне низкой. Еще одним недостатком, проявляющимся при реализации многокубитовых вариационных алгоритмов, является большой размер перепрограммируемых линейно-оптических схем, которые сложно изготовить и которые сложно перепрограммировать.
Из уровня техники известна архитектура универсальных перепрограммируемых интерферометров, раскрытая в изобретении W. Clements et al, "Interferometer and method of designing an interferometer" // US 20190086610 (2020). Многоканальные интерферометры, созданные по этой архитектуре, представляют собой прямоугольные массивы перепрограммируемых двухканальных делителей, типично реализуемых в виде интерферометров Маха-Цендера. Массивы сформированы последовательно соединенными слоями, состоящими из интерферометров Маха-Цендера, таким образом, что глубина схемы интерферометра - максимальное число делителей, через которые проходят оптические сигналы от входа до выхода, равна числу каналов в многоканальном интерферометре. Число элементов сдвига фазы, необходимое для реализации произвольных передаточных матриц в сконструированных таким способом интерферометрах, растет по квадратичному закону в зависимости от числа каналов в интерферометре.
Недостатком этого способа являются высокие потери в интерферометре, которые пропорциональны глубине схемы, которая растет линейно с ростом числа каналов. Одинаковый уровень потерь испытывают все оптические сигналы, поступающие на вход интерферометра. Высокие потери приводят к снижению эффективности квантовых вычислителей, основанных на этих универсальных перепрограммируемых интерферометрах. Еще одним недостатком является большое число фазовых сдвигов, которые необходимы для программирования интерферометра, что повышает сложность приготовления вариационного квантового состояния, обеспечивающего решение задачи. Также недостатком является необходимость подавать одновременно большое число одиночных фотонов на вход интерферометра для приготовления многокубитного параметризованного состояния.
Наиболее близкими к заявляемому техническому решению являются способ и устройство для приготовления квантовых состояний фотонов, раскрытые в патентной публикации J.C. Mower, N.C. Harris, D.r. Englund, G. Steinbrecher, "Methods, systems, and apparatus for programmable quantum photonic processing" // US 9354039 (2016). Изобретение основано на многоканальном программируемом интерферометре, в котором сигналы от части выходов перенаправляются на часть входов. Преобразуемые состояния подаются на входные каналы интерферометра и могут многократно проходить через интерферометр, благодаря чему глубина эффективной схемы - параметр, характеризующий сложность линейно-оптического преобразования, увеличивается по сравнению с глубиной физической схемы используемого устройства интерферометра. В этом техническом решении для расчета качества приготовления требуемого квантового состояния используют результаты измерений, выполняемые над преобразованными сигналами после многократного прохождения сигналов через интерферометр, из которых извлекается информация о приготавливаемом квантовом состоянии. При несоответствии приготовленного состояния требуемому выполняют перепрограммирование интерферометра и преобразование выполняют снова до тех пор, пока не будет достигнут максимум соответствия между приготавливаемым и целевым состоянием.
Недостатком этого технического решения (прототипа) является необходимость получения информации о приготавливаемом квантовом состоянии для сравнения с требуемым с целью расчета ошибки линейно-оптического преобразования и последующей корректировки параметров многоканального интерферометра. Получение точной информации о квантовом состоянии на основе измерений представляется сложной задачей: число измерений, необходимых для получения полной информации о Q-кубитном состоянии, растет по экспоненциальному закону. Даже для сравнительно небольшого числа кубитов, которое намного меньше, чем необходимо для достижения практических преимуществ использования квантовых вычислителей над классическими, измерения занимают очень много времени. Таким образом, получение информации о квантовом состоянии является непрактичным при оптимизации многокубитовых линейно-оптических квантовых вычислителей, состоящих из большого числа элементов, которые необходимо варьировать при оптимизации. Использование данного технического решения требует чрезвычайно больших временных затрат.
Технической проблемой, решаемой заявляемым изобретением, является высокий уровень временных затрат, требуемых для приготовления многокубитных квантовых состояний для квантовых вариационных алгоритмов. Затраты времени возникают по двум причинам. Во-первых, процесс приготовления включает в себя многошаговую процедуру оптимизации параметров многоканальных интерферометров, которая требует одновременной генерации и преобразования большого числа фотонов. Во-вторых, имеется необходимость проведения большого количества измерений над приготавливаемыми состояниями. Данное обстоятельство препятствует реализации квантовых вариационных алгоритмов вовсе или ограничивает размерности квантовых состояний, которые можно приготавливать линейно-оптическими методами, и, следовательно, вычислительную сложность задач, которые можно решать с помощью этих алгоритмов. Еще одной технической проблемой, решаемой заявляемым изобретением, является большой объем физических ресурсов, необходимых для приготовления многокубитных квантовых состояний для квантовых вариационных алгоритмов, что делает известные способы непригодными.
Раскрытие изобретения
Техническим результатом изобретения является снижение времени, затрачиваемого на решение задач с помощью квантовых вариационных алгоритмов на линейно-оптической платформе по сравнению с прототипом.
Снижение времени достигается благодаря многошаговой процедуре приготовления параметризованных квантовых состояний, используемых в квантовых вариационных алгоритмах, и измерениям, выполняемым на каждом шаге. Схема содержит программируемый интерферометр, снабженный оптическими линиями обратной связи, перенаправляющими сигналы, выходящие из части выходов интерферометра на часть его входов, и одновременно задерживающие эти сигналы. Процесс приготовления многокубитных состояний делится на несколько последовательных шагов, на каждом из которых происходит генерация новой части квантового состояния и его частичное измерение двумя измерительными блоками, один из которых измеряет состояние фотонов непосредственно, а другой преобразует состояния в соответствии с измеряемой средней величиной. Первый блок выполняет измерение и его используют для проверки на соответствие наперед заданному паттерну. Второй блок используют для измерения рассчитываемой средней величины по приготавливаемому состоянию. Ускорение решения вычислительных задач достигается по трем причинам. Во-первых, измерения, проводимые на каждом шаге работы схемы, позволяют быстрее заканчивать неудачные попытки генерации параметризованного квантового состояния, которые не соответствуют выбираемому паттерну измерений или логической кодировке кубитов. При пошаговом подходе с измерениями на каждом шаге попытка прерывается после первого несоответствия без необходимости генерировать, преобразовывать и детектировать все фотоны, необходимые для требуемого многокубитного состояния, как в случае схем, где необходима одновременная генерация сразу всех фотонов и их одновременное преобразование и детектирование. Во-вторых, уменьшается время перепрограммирования интерферометра, т.к. для этого требуется рассчитывать средние от наблюдаемых величин, представляющих собой средние по квантовому состоянию, приготавливаемому в схеме, а не получение полной информации об этом квантовом состоянии. В-третьих, пошаговое приготовление многокубитового состояния происходит быстрее, чем одновременное приготовление такого состояния, т.к. в первом случае используется меньшее количество ресурсов - источников и детекторов фотонов и каналов программируемых интерферометров, что, в свою очередь, обеспечивает меньшее время ожидания успешной генерации фотонов по причине более низких потерь и более высокого качества квантовой интерференции, которая получается от меньшего количества источников, чем в схемах, где необходима одновременная генерация сразу всех фотонов и их одновременное преобразование и детектирование.
Технический результат достигается системой, реализующей квантовый вариационный алгоритм, включающей:
М источников одиночных фотонов;
интерферометр для выполнения линейно-оптических преобразований над квантовыми состояниями фотонов, снабженный управляющим входом для управления линейным преобразованием, N входами, из которых М входов предназначены для приема одиночных фотонов, L входов - для линий обратной связи, где  а также N выходами, из которых L выходов предназначены для подключения линий обратной связи, J выходов - для соединения с измерительным блоком первого типа, R выходов - для соединения с измерительным блоком второго типа, при этом
а также N выходами, из которых L выходов предназначены для подключения линий обратной связи, J выходов - для соединения с измерительным блоком первого типа, R выходов - для соединения с измерительным блоком второго типа, при этом 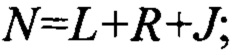
L линий обратной связи, соединяющих соответствующие выходы и входы интерферометра;
измерительный блок первого типа для измерения состояний фотонов, снабженный J входами и включающий J детекторов фотонов, каждый из которых выполнен с возможностью измерения сигналов с выхода одного канала интерферометра;
измерительный блок второго типа, снабженный R входами, управляющим входом измерительного блока второго типа и выходом, предназначенным для подключения к компьютеру, выполненный с возможностью измерения средних значений произведения однокубитовых операторов по квантовым состояниям фотонов, и изменения измерительного базиса по сигналу с управляющего входа измерительного блока второго типа;
компьютер для вычисления результата шага квантового вариационного алгоритма, снабженный входами для подключения измерительного блока первого типа и для подключения измерительного блока второго типа, управляющими выходами для подключения к управляющим входам измерительного блока второго типа и интерферометра;
при этом:
линии обратной связи выбраны с обеспечением возможности синхронного поступления сигналов на входы для фотонов и на входы для линий обратной связи интерферометра с сохранением поляризации сигналов;
выход измерительного блока первого типа соединен со входом компьютера для измерительного блока первого типа; выход измерительного блока второго типа соединен со входом компьютера для измерительного блока второго типа;
М источников фотонов выполнены с возможностью генерации одиночных фотонов с обеспечением одновременного поступления на соответствующие входы интерферометра.
М источников одиночных фотонов могут быть реализованы с помощью лазера, выполненного с возможностью генерации периодических последовательностей импульсов когерентного излучения, снабженного управляющим входом для управления генерацией, соединенным с компьютером, при этом компьютер снабжен соответствующим управляющим выходом;
при этом система содержит блок делителей для формирования разделенных на М каналов последовательностей импульсов когерентного излучения, снабженный входом и М выходами для вывода разделенных последовательностей импульсов, а также М фильтров для отсечения остаточной мощности импульсов когерентного излучения от одиночных фотонов, каждый из М фильтров снабжен входом и выходом для вывода одиночных фотонов, очищенных от остаточной мощности импульсов когерентного излучения.
Система может быть снабжена блоком переключателей для вывода сигналов обратной связи интерферометра, снабженным управляющим входом для управления выводом сигналов обратной связи, L входами, L выходами обратной связи и L выходами для подключения к блоку измерения части приготавливаемого состояния, снабженному L соответствующими входами, управляющим входом, соединенным с соответствующим управляющим выходом компьютера для управления параметрами блока и выходом для вывода сигнала измерения, соединенным со входом компьютера для блока измерения приготавливаемого состояния.
Источники одиночных фотонов, интерферометр для выполнения линейно-оптических преобразований над квантовыми состояниями фотонов и линии обратной связи, соединяющие соответствующие выходы и входы интерферометра, используют для приготовления параметризованных квантовых состояний. Управление параметрами приготавливаемых квантовых состояний осуществляют компьютером. Измерения данных квантовых состояний осуществляют измерительными блоками первого и второго типа.
Технический результат достигается также способом, реализующим квантовые вычисления на основе описанной выше системы, включающим следующие этапы:
1) представление вычислительной задачи в виде суммы произведений операторов с весовыми коэффициентами для каждого слагаемого;
2) определение максимального числа кубитов Q, необходимого для расчетов средних значений от произведений операторов;
3) выбор числа шагов работы схемы  с округлением до наибольшего целого значения;
с округлением до наибольшего целого значения;
4) формирование произвольных значений фазовых сдвигов интерферометра путем подачи электромагнитных сигналов на его управляющие входы;
5) выбор вектора (паттерна) измерений фотонов для измерительного блока первого типа (на протяжении W шагов работы схемы по подэтапам а - d этапа 6);
6) выбор слагаемого в сумме произведений операторов, для которого производят следующие подэтапы:
a) генерацию фотонов и подачу их на вход интерферометра,
b) конфигурирование измерительного блока второго типа с обеспечением соответствия передаточной матрицы по меньшей мере одного интерферометра Маха-Цендера соответствующему множителю произведении операторов,
c) проведение измерений фотонов на выходе из блока первого типа с проверкой соответствия заданному вектору (паттерну) (соответствующих пятому этапу), и измерений фотонов на выходе из блока второго типа с проверкой соответствия кодировке кубитов,
d) в случае, если результаты измерений фотонов с выхода блоков первого и второго типов соответствуют заданному вектору (паттерну) и кодировке кубитов, то этапы b) и с) повторяют, с конфигурированием измерительного блока второго типа в соответствии с измеряемым на данном шаге произведением однокубитовых операторов и элементов вектора измерений блока первого типа, а в случае несоответствия - возвращаются к подэтапу а),
e) определение среднего значения измеренных чисел фотонов на выходах интерферометров в измерительном блоке второго типа для попыток, прошедших все W шагов (свидетельствующее об измерении всего произведения операторов в данном слагаемом),
f) повтор подэтапов а)-е) до выполнения критерия статистической сходимости применительно к среднему значению измерения числа фотонов на выходах измерительного блока второго типа;
7) повтор этапа 6 для каждого слагаемого в сумме произведений операторов с суммированием средних значений измерений числа фотонов с весовым коэффициентом, соответствующим выбранному слагаемому;
8) применение оптимизационного алгоритма к полученной на этапе 7 сумме с соответствующим изменением параметров интерферометра и числом повторений этапов 6 и 7, обеспечивающим решение оптимизационной задачи.
Краткое описание чертежей
Изобретение поясняется чертежами и схемами.
На фиг. 1 приведена схема, иллюстрирующая приготовление параметризованного квантового состояния предложенным способом.
На фиг. 2 представлена схема системы, реализующая квантовый вариационный алгоритм с помощью предлагаемого способа приготовления и измерения параметризованных квантовых состояний.
На фиг. 3 представлена традиционная схема для приготовления квантового состояния фотонов с помощью программируемого интерферометра.
На фиг. 4 представлена зависимость размерности квантового состояния от числа каналов  в которых приготовлено это состояние, для разного количества фотонов
в которых приготовлено это состояние, для разного количества фотонов  в этом состоянии. Размерность приведена в числе кубитов Q.
в этом состоянии. Размерность приведена в числе кубитов Q.
Фиг. 5 иллюстрирует преобразование схемы, изображенной на аиг. 1, при двух шагах работы схемы.
Фиг. 6 схематически иллюстрирует работу квантового вариационного алгоритма. В этом алгоритме классический компьютер управляет квантовым состоянием, которое приготавливается на квантовом устройстве, с помощь набора параметров 
Фиг. 7 иллюстрирует оптическую схему для измерения средних от произведения однокубитных операторов при двухрельсовой кодировке кубитов: а) оптическая схема одновременного измерения среднего однокубитового оператора, которая представляет собой интерферометр Маха-Цендера, которая позволяет проводить измерение одного оператора из произведения операторов, б) оптическая схема измерительного блока второго типа, для одновременного измерения произведения из F однокубитовых операторов.
Фиг. 8 иллюстрирует оптическую схему, которая была использована при реализации предлагаемого способа: а) общий вид схемы с 5-канальным программируемым интерферометром, б) схема 5-канального интегрально-оптического интерферометра.
На фиг. 9 изображена гистограмма, демонстрирующая распределение точности приготовления двухкубитных состояний в двухрельсовой кодировке, выполненного в примере конкретной реализации с помощью схемы, изображенной на фиг. 8. Точность рассчитывалась как скалярное произведение двух векторов коэффициентов, составленных из коэффициентов разложения заданного вектора квантового состояния и вектора получаемого квантового состояния.
Позициями на фигурах обозначены:
1 - многоканальный программируемый интерферометр,
2 - источники одиночных фотонов,
3 - измерительный блок первого типа, включающий детекторы одиночных фотонов,
4 - оптические линии обратной связи,
5 - входные каналы (или входы) программируемого интерферометра,
6 - выходные каналы (или выходы) программируемого интерферометра,
7 - множество фотонов, сгенерированное источниками одиночных фотонов,
8 - множество входных каналов (или входов) программируемого интерферометра, на которые поступают фотоны от источников,
9 - множество выходных каналов (или выходов) программируемого интерферометра, с которых сигналы поступают на вход измерительного блока первого типа,
10 - множество выходных каналов (или выходов) программируемого интерферометра, с которых сигналы поступают в линии обратной связи,
11 - множество входных каналов (или входов) программируемого интерферометра, в которые поступают сигналы из линий обратной связи,
12 - множество выходных каналов (или выходов) программируемого интерферометра, на которых генерируется приготавливаемое параметризованное квантовое состояние,
13 - часть генерируемого параметризованного состояния,
14 - вход с параметрами, управляющими преобразованием интерферометра,
15 - переключатели, способные выводить сигналы из линий обратной связи,
16 - часть параметризованного состояния, сгенерированная в линиях обратной связи,
17 - лазер (или лазер накачки), генерирующий импульсы когерентого излучения,
18 - блок, разделяющий одиночные импульсы лазера на множество импульсов,
19 - фильтры, отсекающие остаточное излучение лазера от сгенерированных одиночных фотонов,
20 - измерительный блок второго типа, выполняющий измерения приготавливаемого состояния,
21 - электрические каналы, по которым результаты измерений в измерительном блоке второго типа поступают на компьютер,
22 - компьютер, обрабатывающий результаты измерений и управляющий работой оптической схемы,
23 - электрические каналы, по которым результаты измерений в измерительном блоке первого типа поступают на компьютер,
24 - измерительный блок, выполняющий измерения сигналов, выведенных из линий обратной связи,
25 - электрические каналы, по которым компьютер управляет измерительным блоком, второго типа,
26 - электрические каналы, по которым передаются результаты от измерительного блока, измеряющего сигналы, выведенные из линий обратной связи,
27 - электрические каналы, по которым компьютер управляет измерительным блоком, измеряющим сигналы, выведенные из линий обратной связи,
28 - электрические каналы, по которым компьютер управляет переключателями,
29 - электрический канал, по которой компьютер управляет работой лазера,
30 - сбалансированные элементы статических делителей,
31 - варьируемые элементы сдвига фазы,
32 - детекторы одиночных фотонов,
33 - 2 детектора одиночных фотонов в составе измерительного блока второго типа,
34 - 2 детектора одиночных фотонов в составе измерительного блока первого типа,
35 - электрические каналы, по которым сигналы с детекторов фотонов в составе измерительного блока второго типа передаются на компьютер,
36 - электрические каналы, по которым сигналы с детекторов фотонов в составе блока первого типа передаются на компьютер,
37 - область связи в 5-канальном интегральном оптическом чипе,
38 - термо-оптический элемент сдвига фазы.
Осуществление изобретения
В изобретении речь идет о способе и устройстве, реализующих квантовые вариационные алгоритмы, использующие преобразования квантовых состояний фотонов. Фотоны, в которые кодируют квантовые состояния, могут принадлежать к разным диапазонам длин волн - от радио- до оптического.
Для более однозначного понимания сущности заявленного изобретения ниже представлены основные термины и определения, используемые в рамках настоящего описания.
Линейно-оптическим преобразованием или просто линейным преобразованием называют преобразование, действие которого на классические амплитуды электромагнитных сигналов можно описать линейным законом:

где N - число входных каналов преобразования, 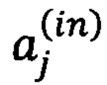 - комплексные амплитуды поля на входе преобразования,
- комплексные амплитуды поля на входе преобразования,  - комплексные амплитуды поля на выходе преобразования. Здесь индекс j, нумерующий входной канал, принимает значения от 1 до N. Число выходных каналов преобразования в общем случае может не совпадать с числом входных каналов, соответственно, индекс k, нумерующий выходной канал в (1), может пробегать диапазон с длиной отличной от N. Однако, в дальнейшем без ограничения общности будем полагать, что в линейном преобразовании число выходных каналов равно числу входных каналов.
- комплексные амплитуды поля на выходе преобразования. Здесь индекс j, нумерующий входной канал, принимает значения от 1 до N. Число выходных каналов преобразования в общем случае может не совпадать с числом входных каналов, соответственно, индекс k, нумерующий выходной канал в (1), может пробегать диапазон с длиной отличной от N. Однако, в дальнейшем без ограничения общности будем полагать, что в линейном преобразовании число выходных каналов равно числу входных каналов.
В (1) комплексные коэффициенты  формируют матрицу U размерности
формируют матрицу U размерности  которая и определяет конкретное линейное преобразование. Выражение (1) может быть представлено в матричном виде:
которая и определяет конкретное линейное преобразование. Выражение (1) может быть представлено в матричном виде:

где  и
и  - столбцы, составленные из амплитуд сигналов на входе и выходе преобразования, соответственно. Число каналов преобразования N характеризует размерность линейного преобразования классических амплитуд электромагнитных полей.
- столбцы, составленные из амплитуд сигналов на входе и выходе преобразования, соответственно. Число каналов преобразования N характеризует размерность линейного преобразования классических амплитуд электромагнитных полей.
Передаточной матрицей линейного преобразования или просто матрицей преобразования называют матрицу U, которая связывает друг с другом столбец классических амплитуд электромагнитных сигналов на выходе преобразования  со столбцом амплитуд на его входе
со столбцом амплитуд на его входе  (см. выражение (2)).
(см. выражение (2)).
N-канальным линейным преобразователем или линейным N-канальным устройством или линейным N-канальным интерферометром или просто N-канальным интерферометром называют любое устройство, осуществляющее линейное N-канальное преобразование электромагнитных сигналов в соответствии с выражением (2). Если 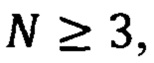 то N-канальный интерферометр называют многоканальным.
то N-канальный интерферометр называют многоканальным.
Программируемым N-канальным интерферометром или просто программируемым интерферометром называют интерферометр, передаточную матрицу которого можно менять внешним управлением.
Логическим кубитом или просто кубитом называют квантовую физическую систему или часть физической системы, позволяющую хранить два квантовых состояния, обозначаемых  и
и  и называемых логическим «0» и логической «1», а также любую их линейную суперпозицию вида
и называемых логическим «0» и логической «1», а также любую их линейную суперпозицию вида  где α и β - комплексные числа, подчиняющиеся условию нормировки:
где α и β - комплексные числа, подчиняющиеся условию нормировки:  Кодирование логических состояний кубитов
Кодирование логических состояний кубитов  и
и  проводят в квантовые состояния физической системы.
проводят в квантовые состояния физической системы.
Существует множество способов кодирования логических состояний кубитов в физические состояния системы. Выбор конкретного кодирования кубитов обусловлен наличием требуемых для этого ресурсов, например, числом каналов в оптических схемах и числом фотонов, и удобством выполнения преобразований над кубитами. В линейно-оптических квантовых вычислениях распространено кодирование кубитов в «двухрельсовый базис» (от термина dual-rail encoding в англоязычной литературе), использующий два оптических канала/моды, состоящий из двух физических состояний  и
и  где
где 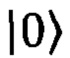 и
и  - фоковские состояния с числом фотонов 0 и 1, соответственно, а индексы m и n обозначают номера оптических каналов, к которым относится фоковское состояние (Р. Kok et al. "Linear optical quantum computing" //Rev. Mod. Phys., vol. 79, 135 (2007)). Также распространено кодирование в так называемый «однорельсовый базис» (от термина single-rail encoding в англоязычной литературе), использующий фоковские состояния в одном оптическом канале
- фоковские состояния с числом фотонов 0 и 1, соответственно, а индексы m и n обозначают номера оптических каналов, к которым относится фоковское состояние (Р. Kok et al. "Linear optical quantum computing" //Rev. Mod. Phys., vol. 79, 135 (2007)). Также распространено кодирование в так называемый «однорельсовый базис» (от термина single-rail encoding в англоязычной литературе), использующий фоковские состояния в одном оптическом канале  и
и 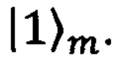 В настоящем изобретении речь идет о двухрельсовой кодировке.
В настоящем изобретении речь идет о двухрельсовой кодировке.
Квантовым вычислителем или квантовым симулятором называют устройство, которое использует квантовые свойства реальных физических систем для практической реализации квантовых вычислительных алгоритмов.
Особенности квантовых физических систем, отличающие их от классических, можно описывать с помощью математического понятия вектора состояния системы (Л.Д. Ландау, Е.М. Лифшиц, Теоретическая физика т.3. Квантовая механика. Нерелятивистская теория // 4-е изд., испр. - М.: Наука. Гл. ред. физ.-мат. лит., 1989 - 768 с.). Если D возможным состояниям квантовой системы можно приписать набор состояний 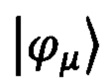 (μ=1…D), которые попарно ортогональны
(μ=1…D), которые попарно ортогональны  где
где  - символ Кронекера), то квантовая система может также находиться в состоянии с наблюдаемыми в эксперименте характеристиками, описываемыми суперпозицией состояний
- символ Кронекера), то квантовая система может также находиться в состоянии с наблюдаемыми в эксперименте характеристиками, описываемыми суперпозицией состояний 

где  - коэффициенты разложения, которые задают конкретное квантовое состояние (μ=1…D), для которых справедливо нормировочное соотношение:
- коэффициенты разложения, которые задают конкретное квантовое состояние (μ=1…D), для которых справедливо нормировочное соотношение:  Даже для сравнительно малых физических систем, состоящих из Q кубитов - двухуровневых квантовых систем, число различных базисных состояний
Даже для сравнительно малых физических систем, состоящих из Q кубитов - двухуровневых квантовых систем, число различных базисных состояний  и коэффициентов разложения в (3) растет по экспоненциальному закону:
и коэффициентов разложения в (3) растет по экспоненциальному закону:  Для хранения всей информации о квантовом состоянии (3) на классических компьютерах требуется память для
Для хранения всей информации о квантовом состоянии (3) на классических компьютерах требуется память для 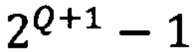 действительных параметров, задающих коэффициенты
действительных параметров, задающих коэффициенты 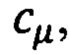 что не представляется возможным даже для сравнительно малых значений
что не представляется возможным даже для сравнительно малых значений  Преобразования над векторами состояний (3) описывают матрицами размерности
Преобразования над векторами состояний (3) описывают матрицами размерности  что на классическом компьютере требует еще большей памяти, чем хранение вектора состояния. Здесь следует отметить отличие в сложности классического описания преобразования Q классических амплитуд, задаваемого умножением матрицы размерности
что на классическом компьютере требует еще большей памяти, чем хранение вектора состояния. Здесь следует отметить отличие в сложности классического описания преобразования Q классических амплитуд, задаваемого умножением матрицы размерности  (см. выражение (2)), и классического описания преобразования Q-кубитового квантового состояния, где требуется перемножение на матрицу размерности
(см. выражение (2)), и классического описания преобразования Q-кубитового квантового состояния, где требуется перемножение на матрицу размерности 
В отличие от классических компьютеров, устройства квантовых вычислителей предоставляют реальные возможности для выполнения вычислений посредством преобразования экспоненциально емких по информации квантовых состояний, выполняя манипуляции над сравнительно небольшим числом физических кубитов. Базовым функционалом квантовых симуляторов является возможность приготовления квантовых физических систем, используемых в устройствах-симуляторах, в состояниях, которыми можно управлять внешними классическими воздействиями.
Параметризованными квантовыми состояниями называют квантовые состояния, которые можно задавать на этапе приготовления, выставляя управляющие параметры.
Параметризованными квантовыми схемами называют квантовые преобразователи, осуществляющие преобразования квантовых состояний, конкретный вид которых зависит от набора управляющих параметров  Параметризованные квантовые схемы используют для приготовления параметризованных квантовых состояний
Параметризованные квантовые схемы используют для приготовления параметризованных квантовых состояний 
Квантовыми логическими гейтами, квантовыми гейтами или просто гейтами называют элементарные заранее известные квантовые операции, с помощью которых конструируют более сложные квантовые алгоритмы и схемы. Гейты различают в соответствии с числом кубитов, на которые они действуют. Так, говорят об однокубитовых гейтах, двухкубитовых гейтах, трехкубитовых гейтах и т.д. Наиболее распространенные наборы гейтов, из которых конструируют преобразования многокубитовых квантовых состояний, содержат одно- и двухкубитовые гейты. Например, распространены однокубитовые гейты, действие которых описывается матрицами:

Однокубитовые операторы, описываемые матрицами (4), называют операторами Паули, а сами матрицы - матрицами Паули. Однокубитовые преобразования состояния кубита  сводятся к перемножению столбца
сводятся к перемножению столбца  на матрицу, отвечающую этому преобразованию. Среди множества двухкубитовых гейтов распространены следующие:
на матрицу, отвечающую этому преобразованию. Среди множества двухкубитовых гейтов распространены следующие:
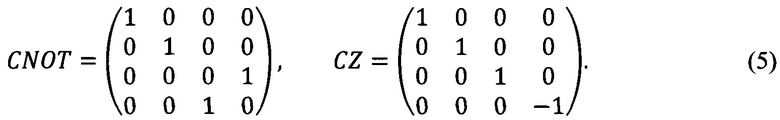
Двухкубитовым преобразованиям отвечает перемножение матриц на столбец амплитуд, отвечающий состояниям двух кубитов: 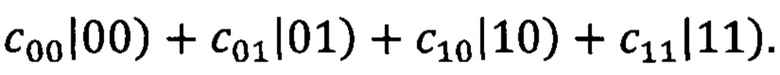 В этом случае столбец амплитуд имеет вид
В этом случае столбец амплитуд имеет вид  где Т означает транспонирование строки.
где Т означает транспонирование строки.
Квантовой логической схемой или просто квантовой схемой называют последовательность применения квантовых гейтов над логическими состояниями кубитов, которые описывают выполнение квантового алгоритма или квантового преобразования. Стоит отметить, что квантовые схемы описывают преобразования на высоком уровне абстракции, выполняемые над логическими состояниями безотносительно конкретных реализаций кодирования кубитовых состояний и преобразующих их гейтов.
Вариационным квантовым алгоритмом называют квантовый алгоритм, основанный на попеременном использовании физической системы для приготовления параметризованного квантового состояния  на j-м шаге и классического оптимизационного алгоритма, который принимает результаты измерения приготовленного состояния. В соответствии с результатами измерений на j-м шаге оптимизационный алгоритм выдает обновленный набор управляющих параметров
на j-м шаге и классического оптимизационного алгоритма, который принимает результаты измерения приготовленного состояния. В соответствии с результатами измерений на j-м шаге оптимизационный алгоритм выдает обновленный набор управляющих параметров  который меняет состояние, приготавливаемое квантовьм симулятором:
который меняет состояние, приготавливаемое квантовьм симулятором:  Измерения, проводимые с помощью вариационного квантового состояния, представляют собой среднее от некоторой физической величины, минимум которой необходимо найти и обычно представляющем собой гамильтониан системы
Измерения, проводимые с помощью вариационного квантового состояния, представляют собой среднее от некоторой физической величины, минимум которой необходимо найти и обычно представляющем собой гамильтониан системы 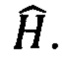 Квантовые вариационные алгоритмы предложено использовать при решении задач материаловедения, например, при расчетах энергий основных состояний молекул (Y.Nam et al. "Ground-state energy estimation of the water molecule on a trapped-ion quantum computer" // NPJ quantum information, vol. 7, 33 (2020)).
Квантовые вариационные алгоритмы предложено использовать при решении задач материаловедения, например, при расчетах энергий основных состояний молекул (Y.Nam et al. "Ground-state energy estimation of the water molecule on a trapped-ion quantum computer" // NPJ quantum information, vol. 7, 33 (2020)).
Алгоритм нахождения энергии основного состояния гамильтониана, описывающего симулируемую систему, состоит из последовательных шагов:
1) симулятор приготавливают в Р-кубитном квантовом состоянии  которое зависит от набора параметров
которое зависит от набора параметров  Приготовление осуществляют посредством последовательного применения гейтов, которые задают квантовую схему симулятора, к фиксированному начальному состоянию
Приготовление осуществляют посредством последовательного применения гейтов, которые задают квантовую схему симулятора, к фиксированному начальному состоянию  Набор гейтов, доступных в используемом симуляторе, и их качество определяет класс приготавливаемых состояний. В качестве гейтов могут выступать как стандартные одно- и двухкубитовые гейты, так и многокубитовые преобразования. Изменение параметров
Набор гейтов, доступных в используемом симуляторе, и их качество определяет класс приготавливаемых состояний. В качестве гейтов могут выступать как стандартные одно- и двухкубитовые гейты, так и многокубитовые преобразования. Изменение параметров  позволяет варьировать приготавливаемое состояние.
позволяет варьировать приготавливаемое состояние.
2) производят серию измерений приготавливаемых состояний, в каждом из которых получают среднее каждого из слагаемых  гамильтониана задачи
гамильтониана задачи  Переход от измерения одного слагаемого к другому осуществляется сменой измерительного базиса. Сумма измеренных средних (с коэффициентами
Переход от измерения одного слагаемого к другому осуществляется сменой измерительного базиса. Сумма измеренных средних (с коэффициентами  )
)  является оценкой ожидаемой величины энергии квантовой системы для заданного состояния
является оценкой ожидаемой величины энергии квантовой системы для заданного состояния 
3) величина  поступает на классический компьютер как значение оптимизируемой функции энергии гамильтониана, которое поступает на классический компьютер, который выполняет классическую процедуру численной оптимизации. Классический оптимизационный алгоритм выдает новое значение набора параметров
поступает на классический компьютер как значение оптимизируемой функции энергии гамильтониана, которое поступает на классический компьютер, который выполняет классическую процедуру численной оптимизации. Классический оптимизационный алгоритм выдает новое значение набора параметров  поступающего на квантовое устройство симулятора и симуляция продолжается, начиная с шага 1).
поступающего на квантовое устройство симулятора и симуляция продолжается, начиная с шага 1).
4) Итерациями, описанными в пунктах 1-3, находят минимум энергии  Таким образом, последовательность итераций представляет собой шаги с разными значениями набора параметров, которые могут быть описаны выражением:
Таким образом, последовательность итераций представляет собой шаги с разными значениями набора параметров, которые могут быть описаны выражением:  где
где  - приращение набора параметров на n+1 шаге итерации.
- приращение набора параметров на n+1 шаге итерации.
Члены 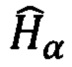 оптимизируемого гамильтониана
оптимизируемого гамильтониана  для Р-кубитовых состояний можно представить в виде произведения N операторов Паули, имеющих матричное представление (4):
для Р-кубитовых состояний можно представить в виде произведения N операторов Паули, имеющих матричное представление (4):  где
где  - обозначение оператора Паули из набора (4) (см., например, работу Y. Cao et al., "Quantum chemistry in the age of quantum computing"//Chem. Rev., vol. 119, No 19, p. 10856-10915 (2019)). Конкретная задача, определяемая гамильтонианом
- обозначение оператора Паули из набора (4) (см., например, работу Y. Cao et al., "Quantum chemistry in the age of quantum computing"//Chem. Rev., vol. 119, No 19, p. 10856-10915 (2019)). Конкретная задача, определяемая гамильтонианом  задается числом и величинами весовых коэффициентов
задается числом и величинами весовых коэффициентов  и последовательностями произведений операторов Паули, средние которых необходимо рассчитывать с помощью квантового симулятора. Таким образом при решении оптимизационной задачи с помощью квантового вариационного алгоритма рассчитывают средние
и последовательностями произведений операторов Паули, средние которых необходимо рассчитывать с помощью квантового симулятора. Таким образом при решении оптимизационной задачи с помощью квантового вариационного алгоритма рассчитывают средние  а оптимизируемая функция при заданном наборе варьируемых параметров
а оптимизируемая функция при заданном наборе варьируемых параметров  есть
есть 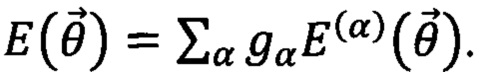
Предлагаемый способ приготовления высокоразмерных параметризованных квантовых оптических состояний, составляющих основу для вариационных квантовых алгоритмов, проиллюстрирован на фиг. 1. Основными элементами схемы являются многоканальный программируемый интерферометр 1, источники одиночных фотонов 2, измерительный блок первого типа 3, который состоит из детекторов фотонов, оптических линий обратной связи 4, перенаправляющие и задерживающие сигналы из части выходов интерферометра 1 в его входы. Многоканальный интерферометр 1 имеет по N входных каналов 5 и выходных каналов 6. М источников одиночных фотонов 2 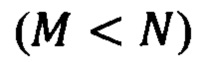 одновременно генерируют импульсы М одиночных фотонов 7, которые синхронно поступают на множество входных каналов 8 интерферометра 1. Эти независимо сгенерированные фотоны претерпевают линейно-оптическую интерференцию в интерферометре 1. Генерация множества одиночных фотонов происходит периодически с интервалом Т. Сигналы, выходящие из множества выходных каналов 9, состоящего из J каналов, поступают на измерительный блок первого типа 3, который производит их измерения. Сигналы, выходящие из множества выходных каналов 10, состоящего из L каналов, поступают в оптические линии обратной связи 4. Сигналы из оптических линий обратной связи 4 поступают на множество входов 11 интерферометра. Оптические сигналы, выходящие из множества выходных каналов 12, которое содержит
одновременно генерируют импульсы М одиночных фотонов 7, которые синхронно поступают на множество входных каналов 8 интерферометра 1. Эти независимо сгенерированные фотоны претерпевают линейно-оптическую интерференцию в интерферометре 1. Генерация множества одиночных фотонов происходит периодически с интервалом Т. Сигналы, выходящие из множества выходных каналов 9, состоящего из J каналов, поступают на измерительный блок первого типа 3, который производит их измерения. Сигналы, выходящие из множества выходных каналов 10, состоящего из L каналов, поступают в оптические линии обратной связи 4. Сигналы из оптических линий обратной связи 4 поступают на множество входов 11 интерферометра. Оптические сигналы, выходящие из множества выходных каналов 12, которое содержит  каналов, несут часть генерируемого параметризованного квантового состояния 13. Наличие входа 14 позволяет управлять параметрами интерферометра извне, служит для задания передаточной матрицы многоканального интерферометра 1. В одном из вариантов осуществления изобретения в схеме могут быть использованы переключатели 15, которые позволяют выводить сигналы из обратной связи 4 на последнем шаге выполнения алгоритма. В таком случае эти сигналы несут часть приготавливаемого параметризованного состояния 16.
каналов, несут часть генерируемого параметризованного квантового состояния 13. Наличие входа 14 позволяет управлять параметрами интерферометра извне, служит для задания передаточной матрицы многоканального интерферометра 1. В одном из вариантов осуществления изобретения в схеме могут быть использованы переключатели 15, которые позволяют выводить сигналы из обратной связи 4 на последнем шаге выполнения алгоритма. В таком случае эти сигналы несут часть приготавливаемого параметризованного состояния 16.
Время обхода импульсных сигналов от входа в интерферометр, их выхода через каналы 10, их прохождения через линии 4 до входа в каналы 11 совпадает или кратно периоду Т следования однофотонных импульсов. В таком случае в интерферометре 1 происходит интерференция одиночных фотонов, сгенерированных источниками на шаге  которые только поступают на входные каналы 8, с квантовыми состояниями, полученными в результате интерференции на предыдущем шаге j, которые поступают на входные каналы 11. Сигналы, выходящие из одного пространственного канала интерферометра 1, но на разных временных шагах могут быть измерены и преобразованы независимо друг от друга и поэтому принадлежат разным каналам. В таком случае эти каналы можно назвать пространственно-временными.
которые только поступают на входные каналы 8, с квантовыми состояниями, полученными в результате интерференции на предыдущем шаге j, которые поступают на входные каналы 11. Сигналы, выходящие из одного пространственного канала интерферометра 1, но на разных временных шагах могут быть измерены и преобразованы независимо друг от друга и поэтому принадлежат разным каналам. В таком случае эти каналы можно назвать пространственно-временными.
Таким образом, по прошествии периода Т в каналах 12 генерируется новая часть квантового состояния - размерность приготавливаемого состояния увеличивается с каждым шагом. Связь между состояниями, сгенерированными на разных шагах, обусловлена линиями обратной связи 4 и интерференционным взаимодействием в интерферометре 1. Конкретное квантовое состояние, генерируемое за W шагов, каждый из которых длится в течении периода времени T, от начала периодического поступления импульсов до их окончания, определяется параметрами с входа 14, управляющими преобразованиями интерферометра, которые управляют передаточной матрицей интерферометра 1. Число шагов W, в течение которых работает схема для генерации одного квантового состояния, определяется размерностью этого состояния. Так, в случае двухрельсового базиса, который кодирует кубит в два канала, состояние из Q кубитов требует  шагов (округление до наибольшего целого значения). Помимо этого, генерируемое состояние зависит от всех результатов измерений детекторами измерительного блока 3 множества выходных каналов 9, выполненных во время работы схемы. Квантовое состояние, генерируемое в схеме, изображенной на Фиг. 1, представляет собой суперпозицию состояния множества фотонов, распределенных по WR каналам.
шагов (округление до наибольшего целого значения). Помимо этого, генерируемое состояние зависит от всех результатов измерений детекторами измерительного блока 3 множества выходных каналов 9, выполненных во время работы схемы. Квантовое состояние, генерируемое в схеме, изображенной на Фиг. 1, представляет собой суперпозицию состояния множества фотонов, распределенных по WR каналам.
На фиг. 2 представлена общая оптическая схема системы для реализации квантовых вариационных алгоритмов с использованием способа и системы для приготовления параметризованных квантовых состояний, предложенного в настоящем изобретении, который проиллюстрирован на фиг. 1. В схеме используется лазер 17, который может генерировать периодические последовательности импульсов. Каждый из импульсов последовательности разделяется в блоке 18 на М штук в соответствии с количеством используемых далее источников одиночных фотонов 2. Разделенные лазерные импульсы используются для возбуждения источников фотонов 2 с целью излучения ими одиночных фотонов. Каждый из М полученных лазерных импульсов поступает на один источник одиночных фотонов. В результате М источников излучают по фотону. Т.к. после возбуждения источников и излучения ими фотонов имеется остаточная мощность лазерных импульсов, которые распространяются вместе с одиночными фотонами, для предотвращения попадания лазерных импульсов в многоканальную схему и на детекторы, стоящие за ней, перед интерферометром 1 располагают фильтры 19, которые пропускают только однофотонные сигналы. На выходе из интерферометра 1 происходит измерение в измерительном блоке первого типа 3, который состоит из однофотонных детекторов, и измерительным блоком второго типа 20, который применяется для измерений с целью получения оценки средних значений с помощью приготавливаемых квантовых состояний. Результаты измерений фотонов измерительным блоком второго типа 20 поступают по электрическому каналу 21 на классический компьютер 22. Результаты, полученные измерением в измерительном блоке первого типа 3 также поступают на компьютер 22 по электрическому каналу 23. Кроме этого, измерительный блок, выполняющий измерения сигналов 24 (второго типа), выведенных из линий обратной связи служит также для измерения части приготавливаемого состояния на последнем шаге W, на котором переключатели 15 производят вывод сигналов из оптических линий обратной связи 4 для измерений. Результаты измерений из блока 24 поступают на компьютер 22 по электрическим каналам 26. Функциональное предназначение блока 24 совпадает с предназначением блока 20; различие состоит в том, что блок 24 работает только на последнем шаге, тогда как блок 20 производит измерения на всех шагах. Компьютер 22 управляет параметрами измерительных блоков 20 и 24 с помощью электрических каналов 25 и 27, соответственно. Конкретные параметры блоков 20 и 24 задают измерительный базис для оценки среднего по многокубитовому состоянию, приготавливаемому интерферометром 1. Посредством электрического канала 29 компьютер 22 управляет лазером накачки 17. Компьютер 22 управляет переключателями 15 по электрическому каналу 28.
На каждом из W шагов выполнения алгоритма, который сопровождается поступлением в интерферометр новых М фотонов от источников 2, происходит расширение размерности приготавливаемого состояния за счет добавления сигналов в новых пространственно-временных каналах. Кубит, закодированный в отдельные пространственно-временные каналы, которые на каждом шаге отвечают некоторому множеству пространственных выходных каналов 12 интерферометра 1, требует измерения в базисе, который в общем случае отличается от базиса, который использовался для измерений в этих же пространственных каналах на предыдущих шагах. По этой причине на каждом шаге компьютер 22 устанавливает новый базис измерений с помощью реконфигурирования схемы блока 20. Базис измерения состояния, поступающего на блок 24 на последнем шаге, задается компьютером посылкой электрических сигналов по электрическому каналу 27.
Реконфигурирование переключателей 15 в режим вывода сигналов из линий 4 на вход блока 24 осуществляется посылкой электрического сигнала с компьютера по электрическому каналу 28. Компьютер также управляет временем работы лазера 17 - он включает его для начала генерации фотонов, поступающих на схему, и выключает для прекращения генерации квантового состояния. Управление работой лазера осуществляется посылкой электрических сигналов по электрическому каналу 29.
Альтернативной возможностью управления началом и окончанием поступления фотонов в интерферометр является, соответственно, открытие и перекрытие каналов перед интерферометром при постоянно работающем лазере, что также требует управления с компьютера. Способ включения и выключения не влияет на работу схемы в общем.
На фиг. 3 представлена схема приготовления параметризованных квантовых состояний с помощью программируемого интерферометра 1 без использования задерживающих и перенаправляющих оптических линий. На вход интерферометра с N входами и N выходами, передаточная матрица которого U задается набором параметров  поступающих на вход 14 интерферометра 1, поступают одновременно одиночные фотоны. Квантовое состояние фотонов, приготавливаемое на выходе из интерферометра, можно представить в виде разложения по базису фоковских состояний основных - неизмеряемых - каналов (s) и измеряемых каналов (а):
поступающих на вход 14 интерферометра 1, поступают одновременно одиночные фотоны. Квантовое состояние фотонов, приготавливаемое на выходе из интерферометра, можно представить в виде разложения по базису фоковских состояний основных - неизмеряемых - каналов (s) и измеряемых каналов (а):
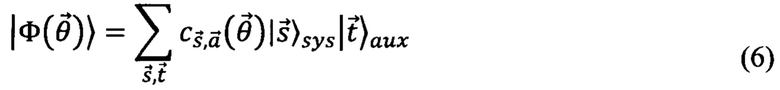
где  и
и  - строки чисел заполнения фотонов, использующиеся для нумерации базисных состояний фотонов в основных и вспомогательных каналах, соответственно,
- строки чисел заполнения фотонов, использующиеся для нумерации базисных состояний фотонов в основных и вспомогательных каналах, соответственно,  - коэффициент разложения по базисному состоянию
- коэффициент разложения по базисному состоянию  В случае, когда на вход перепрограммируемого интерферометра 1 поступает М одиночных фотонов и потери в интерферометре малы суммарное число фотонов, выходящих из интерферометра также должно быть равно М, поэтому в разложении (6) принимают только базисные состояния, удовлетворяющие равенству:
В случае, когда на вход перепрограммируемого интерферометра 1 поступает М одиночных фотонов и потери в интерферометре малы суммарное число фотонов, выходящих из интерферометра также должно быть равно М, поэтому в разложении (6) принимают только базисные состояния, удовлетворяющие равенству: 
Коэффициенты разложения состояния  в (6) зависят от передаточной матрицы интерферометра
в (6) зависят от передаточной матрицы интерферометра  которая управляется набором параметров
которая управляется набором параметров  поступающих на вход 14, благодаря чему и возможно приготовление параметризованного квантового состояния фотонов. Стоит отметить, что расчет коэффициентов разложения состояния представляется вычислительно сложной задачей для классических компьютеров, т.к. связан с вычислением перманентов матриц (S. Aaronson, S. Arkhipov "The computational complexity of linear optics" //arxiv:1011.3245 (2010)).
поступающих на вход 14, благодаря чему и возможно приготовление параметризованного квантового состояния фотонов. Стоит отметить, что расчет коэффициентов разложения состояния представляется вычислительно сложной задачей для классических компьютеров, т.к. связан с вычислением перманентов матриц (S. Aaronson, S. Arkhipov "The computational complexity of linear optics" //arxiv:1011.3245 (2010)).
Величина размерности квантового состояния равна количеству базисных состояний в суперпозиции и определяется числом фотонов М и числом мод N (здесь мода - общее понятие для канала, способного к независимому преобразованию или измерению при этом нет привязки к конкретному кодированию каналов - это могут быть пространственные, пространственно-временные каналы.) в системе. Кроме этого, размерность квантового состояния зависит от выбранного способа кодирования кубитов. При кодировании кубитов в однорельсовый базис, когда число фотонов в одном канале не превышает 1, размерность приготавливаемого квантового состояния (6) до измерения детекторами блока 3 определяется числом соответствующих базисных состояний в суперпозиции, равное сочетанию  На Фиг. 4 представлен график, демонстрирующий зависимость размерности гильбертова пространства квантовых состояний при однорельсовой кодировке кубитов от числа фотонов и числа каналов преобразования. Единицей размерности квантовых состояний на графике является число кубитов Q, которое рассчитано по формуле
На Фиг. 4 представлен график, демонстрирующий зависимость размерности гильбертова пространства квантовых состояний при однорельсовой кодировке кубитов от числа фотонов и числа каналов преобразования. Единицей размерности квантовых состояний на графике является число кубитов Q, которое рассчитано по формуле  где
где  - число базисных состояний, рассчитанное согласно способу, изложенному выше,
- число базисных состояний, рассчитанное согласно способу, изложенному выше, 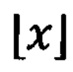 - операция взятия целой части числа х. Размерность квантового состояния, которое приготавливается в основной части 13 после измерения детекторами 3, зависит от числа измеренных фотонов М'. Если на вход N-канального интерферометра поступает М фотонов, а на выходе из интерферометра проводят измерения в J выходах
- операция взятия целой части числа х. Размерность квантового состояния, которое приготавливается в основной части 13 после измерения детекторами 3, зависит от числа измеренных фотонов М'. Если на вход N-канального интерферометра поступает М фотонов, а на выходе из интерферометра проводят измерения в J выходах  и было измерено М' фотонов
и было измерено М' фотонов  то квантовое состояние оптических сигналов в неизмеренных
то квантовое состояние оптических сигналов в неизмеренных 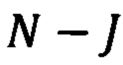 (в этой схеме
(в этой схеме  ) выходах будет содержать
) выходах будет содержать  фотонов.
фотонов.
График, изображенный на фиг. 4, свидетельствует о том, что реализация линейно-оптических устройств с вычислительной мощностью, которая может быть потенциально выше, чем у самых мощных классических компьютеров, требуются интерферометры с большим числом каналов. Как уже упоминалось выше, наименьшая размерность квантовых состояний, при которой их хранение и расчет невозможен на самых мощных классических компьютерах, составляет ~ 50 кубитов (H. Wang et al., "Boson sampling with 20 input photons and a 60-mode interferometer in a 1014-dimensional Hilbert space" //Phys. Rev. Lett., vol. 123, 250503 (2019)). При числе фотонов M=10, что все еще сложно получить на современном уровне развития технологий, используемый интерферометр должен иметь N≥150 каналов; при М=8, N≥300. Реализация программируемых многоканальных интерферометров с таким числом каналов находится на грани или за пределами возможностей современного уровня технологий (W. Bogaerts et al., "Programmable photonic circuits" // Nature, vol. 586, p. 207-216 (2020)).
В случае кодирования кубитов в двухрельсовый базис на М фотонов требуется N-J=2М каналов. Размерность пространства таких состояний в таком случае равно Q=М кубитов. Для Q=50 кубитов необходимо 50 фотонов и 100 каналов. Современный уровень развития технологий не позволяет эффективно получать такое число фотонов одновременно.
На фиг. 5 представлена схема, поясняющая преобразование схемы, изображенной на фиг. 1, при двух шагах ее работы. Для более наглядного представления расположение обозначений позиций на фигуре изменено в сравнении со схемой, изображенной на фиг. 2. Сигналы, поступающие в линии обратной связи на первом шаге, выходят из множества каналов 10 и входят в множество каналов 11 в начале второго шага работы схемы. На каждом шаге измерительный блок первого типа 3 проводит измерение на множестве выходных каналов 9, а на множестве выходных каналов 12 генерируется часть параметризованного состояния. Таким образом, число каналов и фотонов приготавливаемого квантового состояния, которое генерируется на множестве выходов 12, удваивается. Кроме этого, если второй шаг является последним, то на нем также генерируется часть параметризованного состояния 16, выходящее из линии обратной связи.
Передаточная матрица линейно-оптической схемы, изображенной на фиг. 1, которую можно рассчитать из соответствующей эффективной схемы, представленной на фиг. 4, имеет вид произведения матриц:

где

- передаточная матрица, описывающая действие схемы на j-ом шаге с начала работы и имеющая блочно-диагональную форму. В (8) введены следующие обозначения для блоков матриц:  - единичная матрица размером
- единичная матрица размером 
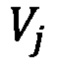 - передаточная матрица интерферометра 1 на j-ом шаге с начала работы схемы. Выражения (7) и (8) учитывают возможность перепрограммирования передаточной матрицы интерферометра заново при каждом новом обходе сигналов. По истечении W шагов работы схемы, эффективная размерность передаточной матрицы (7) равна
- передаточная матрица интерферометра 1 на j-ом шаге с начала работы схемы. Выражения (7) и (8) учитывают возможность перепрограммирования передаточной матрицы интерферометра заново при каждом новом обходе сигналов. По истечении W шагов работы схемы, эффективная размерность передаточной матрицы (7) равна 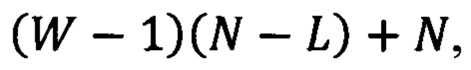 что превышает размерность передаточной матрицы интерферометра. Таким образом, перенаправление сигналов с части выходных каналов интерферометра 1 во входные каналы с одновременной их задержкой позволяет кратно увеличить эффективные размеры схемы. Несмотря на то, что на всех шагах работы схемы используются одни и те же пространственные каналы 12, каждому новому шагу отвечает набор новых временных каналов, т.к. сигналы, выходящие из этих каналов, можно преобразовывать и изменять независимо от предыдущих.
что превышает размерность передаточной матрицы интерферометра. Таким образом, перенаправление сигналов с части выходных каналов интерферометра 1 во входные каналы с одновременной их задержкой позволяет кратно увеличить эффективные размеры схемы. Несмотря на то, что на всех шагах работы схемы используются одни и те же пространственные каналы 12, каждому новому шагу отвечает набор новых временных каналов, т.к. сигналы, выходящие из этих каналов, можно преобразовывать и изменять независимо от предыдущих.
Число каналов, сигналы с которых поступают на измерительный блок первого типа 3, равно WJ. Каждый новый шаг увеличивает число каналов, которые используют для приготовления параметризованного квантового состояния, на R, следовательно, число каналов приготавливаемого состояния равно  где дополнительное слагаемое учитывает возможность использования L каналов на последнем шаге W перенаправлением сигналов из линий 4 с помощью L варьируемых переключателей 15. Часть параметризованного состояния 16 также входит в приготавливаемое состояние, которое на последнем шаге используется в квантовом алгоритме наравне с состояниями 13, приготавливаемыми во множестве выходных каналов 12.
где дополнительное слагаемое учитывает возможность использования L каналов на последнем шаге W перенаправлением сигналов из линий 4 с помощью L варьируемых переключателей 15. Часть параметризованного состояния 16 также входит в приготавливаемое состояние, которое на последнем шаге используется в квантовом алгоритме наравне с состояниями 13, приготавливаемыми во множестве выходных каналов 12.
Помимо увеличения числа каналов линейно-оптического преобразования, схема, изображенная на фиг. 1, также позволяет увеличить число фотонов в приготавливаемых состояниях без увеличения размеров используемых физических устройств интерферометров, числа источников и детекторов фотонов. Если за один шаг работы схемы на ее вход одновременно подается М фотонов, по прошествии W шагов работы схемы, число фотонов, которые могут провзаимодействовать друг с другом равно MW.
Фиг. 6 схематически иллюстрирует работу квантовых вариационных алгоритмов, в которых может использоваться предлагаемый способ и устройство приготовления параметризованных квантовых состояний 
Способ приготовления параметризованного квантового состояния за W шагов работы предлагаемой схемы заключается в следующем. Квантовое состояние, которое генерируется в множестве выходных каналов 12 интерферометра 1 после измерения в измерительном блоке первого типа 3, измеряющих множество выходных каналов 9, на множестве временных шагов зависит от характеристик этих детекторов. В случае, когда детекторы позволяют получать информацию о числе измеренных фотонов (детекторы с разрешением по числу фотонов), приготавливаемое состояние чистое и описывается вектором состояния. Такой способ приготовления квантовых состояний, при котором над частью каналов проводят измерения, называют условным, т.к. нужное состояние или множество квантовых состояний получают при условии реализации определенных результатов измерений в измерительном блоке первого типа.
При последующим описании работы схемы нумерация пространственно-временных каналов будет вестись согласно следующему порядку. При рассмотрении множества пространственных каналов интерферометра в количестве А пространственно-временной канал с индексом j отвечает сигналу, выходящему на временном шаге с индексом 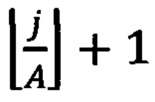
 - операция взятия целой части числа х), из пространственного канала с индексом, равным остатку от деления j на A. В соответствии с такой нумерацией, при измерении каналов измерительным блоком первого типа 3, включающего детекторы одиночных фотонов, в схеме, изображенной на фиг. 1, информация, получаемая при измерении, будет описываться вектором
- операция взятия целой части числа х), из пространственного канала с индексом, равным остатку от деления j на A. В соответствии с такой нумерацией, при измерении каналов измерительным блоком первого типа 3, включающего детекторы одиночных фотонов, в схеме, изображенной на фиг. 1, информация, получаемая при измерении, будет описываться вектором  Вектор
Вектор  составлен согласно описанному порядку нумерации: величина j-го элемента mj вектора равна числу фотонов, которые были зарегистрированы на временном шаге с индексом, равным
составлен согласно описанному порядку нумерации: величина j-го элемента mj вектора равна числу фотонов, которые были зарегистрированы на временном шаге с индексом, равным  - операция взятия целой части числа х), физическим детектором с индексом, равным остатку от деления j на J.
- операция взятия целой части числа х), физическим детектором с индексом, равным остатку от деления j на J.
После выполнения всех шагов измерения фотонов во множестве выходных каналов 9, квантовое состояние фотонов во множестве выходных каналов 12 принимает вид:

которое осталось во вспомогательных каналах после W шагов.
Случай, когда детекторы не различают число поступающих на них фотонов (детектор не срабатывает, если ни один фотон не поступает на него, и срабатывает если на него поступает любое число фотонов отличное от 0) - отличается от предыдущего. В такой ситуации информация, получаемая от детекторов, измеряющих вспомогательные каналы, описывается строкой 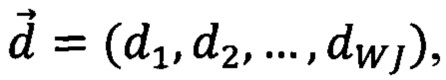 где dj принимает значения 1 и 0, если детектор сработал или не сработал, соответственно. Вектор
где dj принимает значения 1 и 0, если детектор сработал или не сработал, соответственно. Вектор  составлен по такому же принципу, что и вектор
составлен по такому же принципу, что и вектор 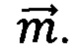 Квантовое состояние неизмеренной части в общем случае оказывается смешанным. Однако, в частном случае, когда
Квантовое состояние неизмеренной части в общем случае оказывается смешанным. Однако, в частном случае, когда 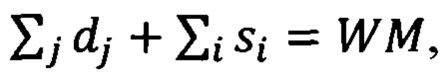 т.е. сумма числа сработавших детекторов dj и числа фотонов si, оставшихся в основных каналах, равна общему числу фотонов состояние также оказывается чистым, т.к. в этом случае точно известно, что каналы (измеренные и неизмеренные) содержат не более 1 фотона. Этот специальный случай можно отличить на практике при постселекции измерений, проводимых над вариационным состоянием
т.е. сумма числа сработавших детекторов dj и числа фотонов si, оставшихся в основных каналах, равна общему числу фотонов состояние также оказывается чистым, т.к. в этом случае точно известно, что каналы (измеренные и неизмеренные) содержат не более 1 фотона. Этот специальный случай можно отличить на практике при постселекции измерений, проводимых над вариационным состоянием  при расчете средних.
при расчете средних.
Например, при кодировке кубитов в однорельсовый базис интерес представляют только состояния в разложении (9), содержащие 0 и 1 фотон в одной моде. При кодировке кубитов в двухрельсовый базис, использующей пару каналов для одного кубита, интересуются только состояниями, для которых эти пары каналов содержат ровно 1 фотон. Без ограничения общности, полагая, что кубит закодирован в два следующих друг за другом канала, интерес представляют состояния, которые в фоковском базисе в каналах с индексами 2n+1 и 2n+2 принимают вид:  и
и  где n - номер кубита, а индексы обозначают номера каналов.
где n - номер кубита, а индексы обозначают номера каналов.
Вместе с тем, в общем случае вариационное состояние  получаемое на выходе из схемы, содержит компоненты, которые выходят из выбранной кодировки логических кубитов. Для того, чтобы эти компоненты не вносили пагубный вклад при измерениях средних
получаемое на выходе из схемы, содержит компоненты, которые выходят из выбранной кодировки логических кубитов. Для того, чтобы эти компоненты не вносили пагубный вклад при измерениях средних  проводится постселекция результатов измерений. При постселекции учитывают только те результаты измерений, которые отвечают выбранной кодировке кубитов. Например, для двухрельсовой кодировки накапливают только измерения, при которых на выходе двух каналов интерферометра Маха-Цендера (используются в блоках 20 и 24) имеется только один фотон. Ниже описан метод измерения вариационного состояния
проводится постселекция результатов измерений. При постселекции учитывают только те результаты измерений, которые отвечают выбранной кодировке кубитов. Например, для двухрельсовой кодировки накапливают только измерения, при которых на выходе двух каналов интерферометра Маха-Цендера (используются в блоках 20 и 24) имеется только один фотон. Ниже описан метод измерения вариационного состояния  при кодировании кубитов в двухрельсовый базис, с помощью которого можно рассчитывать средние от произведений операторов
при кодировании кубитов в двухрельсовый базис, с помощью которого можно рассчитывать средние от произведений операторов  где
где 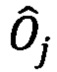 - обозначение оператора Паули из набора (4).
- обозначение оператора Паули из набора (4).
На фиг. 7а представлена оптическая схема для измерения среднего значения от одиночного оператора Паули по однокубитовому состоянию. Схема представляет собой двухканальный интерферометр Маха-Цендера, образованный двумя делителями 30 со сбалансированным коэффициентом деления и двумя варьируемых элементами сдвига фазы 31 с фазовыми сдвигами (γ и ψ), которыми можно управлять (S.A. Fldzhyan, М. Yu. Saygin, S.P. Kulik, "Optimal design of error-tolerant reprogrammable multiport interferometers" // Optics Letters, v. 45, No 9, p. 2632-2635 (2020)). Измерение среднего  проводится накоплением статистики фотоотсчетов детекторами фотонов 32. Матрица логического преобразования кубита, соответствующая интерферометру Маха-Цендера с двумя изменяемыми фазовыми сдвигами γ и ψ принимает следующий вид:
проводится накоплением статистики фотоотсчетов детекторами фотонов 32. Матрица логического преобразования кубита, соответствующая интерферометру Маха-Цендера с двумя изменяемыми фазовыми сдвигами γ и ψ принимает следующий вид:

Действие интерферометра Маха-Цендера на однокубитовое состояние  в двухрельсовой кодировке описывается умножением матрицы (10) на столбец амплитуд вероятности
в двухрельсовой кодировке описывается умножением матрицы (10) на столбец амплитуд вероятности  В качестве простейшей иллюстрации рассмотрим случай 1 кубита в двухрельсовой кодировке с состоянием
В качестве простейшей иллюстрации рассмотрим случай 1 кубита в двухрельсовой кодировке с состоянием  где базисное состояние
где базисное состояние  отвечает фотону в первом оптическом канале, а базисное состояние
отвечает фотону в первом оптическом канале, а базисное состояние  - фотону во втором оптическом канале. Для того, чтобы найти значения параметров γ и ψ интерферометра Маха-Цендера, отвечающие измерению операторов Паули, воспользуемся матричным представлением этих операторов (4). Имеем следующую связь средних значений операторов Паули от амплитуд вероятности кубита
- фотону во втором оптическом канале. Для того, чтобы найти значения параметров γ и ψ интерферометра Маха-Цендера, отвечающие измерению операторов Паули, воспользуемся матричным представлением этих операторов (4). Имеем следующую связь средних значений операторов Паули от амплитуд вероятности кубита 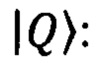

где «*» обозначает комплексное сопряжение.
На фиг. 7б представлена схема экспериментальной установки для измерения среднего от произведений Р операторов Паули  по Р-кубитовым параметризованным квантовым состояниям в двухрельсовой кодировке, которые распределены по 2Р пространственно-временным каналам. Метод использует R интерферометров Маха-Цендера, каждый из которых с помощью выставления значений разности фаз γj и ψj на каждом шаге работы схемы настраивается на измерение оператора
по Р-кубитовым параметризованным квантовым состояниям в двухрельсовой кодировке, которые распределены по 2Р пространственно-временным каналам. Метод использует R интерферометров Маха-Цендера, каждый из которых с помощью выставления значений разности фаз γj и ψj на каждом шаге работы схемы настраивается на измерение оператора  Расчет среднего от произведения операторов
Расчет среднего от произведения операторов  производится накоплением статистики с детекторов фотонов, располагаемых за интерферометрами.
производится накоплением статистики с детекторов фотонов, располагаемых за интерферометрами.
Процедура измерения Р-кубитового произведения операторов  с целью расчета его среднего
с целью расчета его среднего  проводят несколько раз, приготавливая одно и тоже параметризованное квантовое состояние в предлагаемой схеме и проводя над ним измерения, при одинаковых конфигурациях интерферометров Маха-Цендера.
проводят несколько раз, приготавливая одно и тоже параметризованное квантовое состояние в предлагаемой схеме и проводя над ним измерения, при одинаковых конфигурациях интерферометров Маха-Цендера.
При расчетах учитывают измерения только тех компонентов квантового состояния, которые не выходят из логической кодировки кубитов в двухрельсовый базис. Т.к. согласно этой кодировке в двух каналах, кодирующих кубит, всегда должен находился строго один фотон, при расчетах усредняемых величин проводят постселекцию. При постселекции в расчетах принимают во внимание только такие акты измерения, при которых срабатывает только один детектор из пары, измеряющих отдельные кубиты - таким образом гарантируется измерение компоненты состояния в логической кодировке кубитов.
Расчет среднего по параметризованному квантовому состоянию, приготовленному с помощью интерферометра, включает в себя последовательность актов измерений, т.к. за одно измерение невозможно получить всю информацию об измеряемом состоянии. Отдельный акт, для которого выполнено условие постселекции (строго один измеренный фотон в каждой паре детекторов), характеризуется набором из Р величин, которые хранят информацию о результатах измерений Р кубитов в 2Р основных каналах.
Выбор конкретного произведения операторов для измерения осуществляется конфигурированием интерферометров Маха-Цендера для каждого шага работы схемы, располагаемых на выходе из программируемого интерферометра 1 в измерительном блоке первого типа, приготавливающего параметризованное квантовое состояние, что достигается путем подбора сдвигов фаз согласно следующей процедуре:
Если в произведении операторов на j-м месте расположен оператор Паули 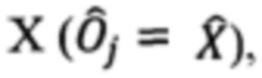 то сдвиги фаз j-м интерферометре Маха-Цендера выставляются таким образом, чтобы его передаточная матрица была:
то сдвиги фаз j-м интерферометре Маха-Цендера выставляются таким образом, чтобы его передаточная матрица была:

для этого устанавливают фазовые сдвиги  и
и  Матрица MX преобразует состояние одного кубита таким образом, что разность числа фотоотсчетов, полученных двумя детекторами, измеряющих два канала кубита, стремится к
Матрица MX преобразует состояние одного кубита таким образом, что разность числа фотоотсчетов, полученных двумя детекторами, измеряющих два канала кубита, стремится к  из (11). Таким образом, если в акте детектирования срабатывает детектор, «говорящий» о наличии фотона в первом оптическом канале кубита
из (11). Таким образом, если в акте детектирования срабатывает детектор, «говорящий» о наличии фотона в первом оптическом канале кубита  то в вектор измерений в элемент с индексом j добавляется 1. Если срабатывает детектор, «говорящий» о наличии фотона во втором канале
то в вектор измерений в элемент с индексом j добавляется 1. Если срабатывает детектор, «говорящий» о наличии фотона во втором канале 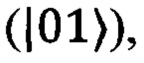 то из элемента вектора измерений с индексом j вычитается 1.
то из элемента вектора измерений с индексом j вычитается 1.
Если в произведении операторов на j-м месте расположен оператор Паули 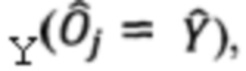 то сдвиги фаз в j-м интерферометре Маха-Цендера выставляются таким образом, чтобы его передаточная матрица была:
то сдвиги фаз в j-м интерферометре Маха-Цендера выставляются таким образом, чтобы его передаточная матрица была:

для этого устанавливают фазовые сдвиги  и
и  Матрица MY преобразует состояние одного кубита таким образом, что разность числа фотоотсчетов, полученных в измерении двумя детекторами, измеряющих два канала кубита, стремиться к
Матрица MY преобразует состояние одного кубита таким образом, что разность числа фотоотсчетов, полученных в измерении двумя детекторами, измеряющих два канала кубита, стремиться к 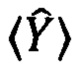 из (8). Таким образом, если в акте детектирования срабатывает детектор, «говорящий» о наличии фотона в первом оптическом канале кубита
из (8). Таким образом, если в акте детектирования срабатывает детектор, «говорящий» о наличии фотона в первом оптическом канале кубита 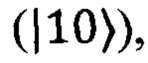 то в вектор измерений в элемент с индексом j добавляется 1. Если срабатывает детектор, «говорящий» о наличии фотона во втором канале
то в вектор измерений в элемент с индексом j добавляется 1. Если срабатывает детектор, «говорящий» о наличии фотона во втором канале 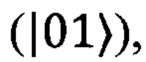 то из элемента вектора измерений с индексом j вычитается 1.
то из элемента вектора измерений с индексом j вычитается 1.
Если в произведении операторов на j-м месте расположен оператор Паули  то сдвиги фаз j-м интерферометре Маха-Цендера выставляются таким образом, чтобы его передаточная матрица была:
то сдвиги фаз j-м интерферометре Маха-Цендера выставляются таким образом, чтобы его передаточная матрица была:

для этого устанавливают фазовые сдвиги  и
и  Матрица MZ преобразует состояние одного кубита таким образом, что разность числа фототсчетов, полученных двумя детекторами, измеряющих два канала кубита, стремится к
Матрица MZ преобразует состояние одного кубита таким образом, что разность числа фототсчетов, полученных двумя детекторами, измеряющих два канала кубита, стремится к 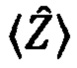 из (8). Таким образом, если в акте детектирования срабатывает детектор, «говорящий» о наличии фотона в первом оптическом канале кубита
из (8). Таким образом, если в акте детектирования срабатывает детектор, «говорящий» о наличии фотона в первом оптическом канале кубита  то в вектор измерений в элемент с индексом j добавляется 1. Если срабатывает детектор, «говорящий» о наличии фотона во втором канале
то в вектор измерений в элемент с индексом j добавляется 1. Если срабатывает детектор, «говорящий» о наличии фотона во втором канале  то из элемента вектора измерений с индексом j вычитается 1.
то из элемента вектора измерений с индексом j вычитается 1.
Если в произведении операторов на j-месте расположен оператор Паули I  то проводить измерение кубита не требуется. В этом случае усредняемое значение всегда берется равным 1.
то проводить измерение кубита не требуется. В этом случае усредняемое значение всегда берется равным 1.
После актов измерений, для которых сработала постселекция (все измеренные состояния были в логической двухрельсовой кодировке), в количестве  все элементы вектора измерений делятся на число измерений:
все элементы вектора измерений делятся на число измерений:  Рассчитанное значение среднего
Рассчитанное значение среднего 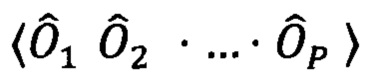 получают перемножением элементов вектора измерений.
получают перемножением элементов вектора измерений.
Ниже представлена последовательность шагов, необходимых для выполнения вариационного квантового алгоритма с использованием предложенных способа и системы приготовления параметризованных состояний фотонов.
1. Формулируют задачу в виде комбинации (суммы) произведений однокубитовых операторов и весовых коэффициентов:  где
где  - весовые коэффициенты при соответствующих произведениях операторов,
- весовые коэффициенты при соответствующих произведениях операторов, 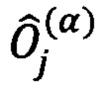 однокубитовый оператор, действующий на кубит с индексом j, S - число слагаемых в сумме. Дальнейшее решение с помощью квантового вариационного алгоритма, реализуемого с использованием перепрограммируемого интерферометра, сводится к поиску глобального минимума оптимизируемой функции
однокубитовый оператор, действующий на кубит с индексом j, S - число слагаемых в сумме. Дальнейшее решение с помощью квантового вариационного алгоритма, реализуемого с использованием перепрограммируемого интерферометра, сводится к поиску глобального минимума оптимизируемой функции 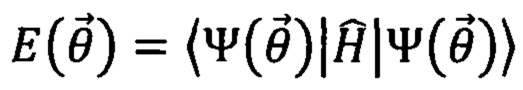 по пространству управляющих параметров
по пространству управляющих параметров  задающих преобразование интерферометра, где
задающих преобразование интерферометра, где  - параметризованное квантовое состояние, получаемое на выходе интерферометра при для набора параметров
- параметризованное квантовое состояние, получаемое на выходе интерферометра при для набора параметров 
2. Выбирают кодировку, в которую будут кодировать логические состояния кубитов приготавливаемого состояния. Например, однорельсовая кодировка кубитов с одним каналом и не более чем 1 фотоном и двухрельсовая кодировка, в которой для кодирования одного кубита используют 2 канала и 1 фотон.
3. Определяют максимальное число кубитов Р приготавливаемого состояния основных каналов. Оно задается максимальной длиной произведения однокубитовых операторов 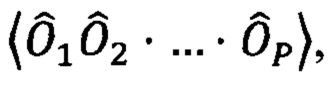 которое необходимо рассчитывать при решении задачи квантовым симулятором. Необходимое число фотонов MS также определяют из числа кубитов в приготавливаемом параметризованном состоянии. Например, при двухрельсовой кодировке число фотонов должно быть строго равно числу кубитов, тогда как при однорельсовой кодировке число фотонов, кодирующих кубитовое состояние, может принимать значения от 0 до Р - предельные значения для состояний
которое необходимо рассчитывать при решении задачи квантовым симулятором. Необходимое число фотонов MS также определяют из числа кубитов в приготавливаемом параметризованном состоянии. Например, при двухрельсовой кодировке число фотонов должно быть строго равно числу кубитов, тогда как при однорельсовой кодировке число фотонов, кодирующих кубитовое состояние, может принимать значения от 0 до Р - предельные значения для состояний  и
и 
4. Выбирают оптимизационный алгоритм, который будет выполнять поиск экстремума оптимизируемой функции 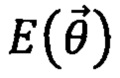 с помощью расчета этой функции на квантовом оптическом устройстве. Оптимизационные алгоритмы используются во многих областях науки и техники, поэтому существует большой выбор таких алгоритмов (R.K. Arora, Optimization algorithms and applications // CRC Press, 1st edition, 2015).
с помощью расчета этой функции на квантовом оптическом устройстве. Оптимизационные алгоритмы используются во многих областях науки и техники, поэтому существует большой выбор таких алгоритмов (R.K. Arora, Optimization algorithms and applications // CRC Press, 1st edition, 2015).
5. Задают число каналов L интерферометра, для которых будет осуществляться связь между выходными и входными каналами с помощью оптических линий обратной связи 4. Задают число выходных каналов J, сигналы с которых будут измеряться детекторами фотонов. Задают число пространственно-временных каналов 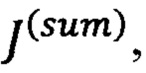 которые будут измеряться детекторами фотонов на каждом шаге выполнения алгоритма. Задают число фотонов
которые будут измеряться детекторами фотонов на каждом шаге выполнения алгоритма. Задают число фотонов  и число пространственно-временных каналов
и число пространственно-временных каналов  из которого должны состоять приготавливаемые состояния. Для числа шагов алгоритма W общее число каналов, которые будут подвергнуты измерению, должно удовлетворять равенству
из которого должны состоять приготавливаемые состояния. Для числа шагов алгоритма W общее число каналов, которые будут подвергнуты измерению, должно удовлетворять равенству  Число пространственно-временных каналов состояния для W шагов
Число пространственно-временных каналов состояния для W шагов  где N - число пространственных каналов программируемого интерферометра 1. Число каналов физического интерферометра N равно сумме числа основных каналов R, кодирующих приготавливаемое состояние на одном шаге, числа измеряемых каналов J и числа каналов L, используемых для оптических линий обратной связи 4. Также задают паттерн или паттерны фотонов, которые были измерены на всех W шагах работы схемы. Общее число фотонов, которые должны поступить на схему за все W шагов дается сложением
где N - число пространственных каналов программируемого интерферометра 1. Число каналов физического интерферометра N равно сумме числа основных каналов R, кодирующих приготавливаемое состояние на одном шаге, числа измеряемых каналов J и числа каналов L, используемых для оптических линий обратной связи 4. Также задают паттерн или паттерны фотонов, которые были измерены на всех W шагах работы схемы. Общее число фотонов, которые должны поступить на схему за все W шагов дается сложением 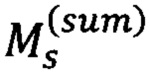 и числа фотонов в каждом выбранном(-ых) паттерне(-ах) измерений. Т.к. на каждом шаге в схему попадает одинаковое число фотонов М от источников, то общее число фотонов должно быть кратно WM. После предпоследнего шага W-1 производят переключение переключателя 15 линий 4 для вывода сигналов, выходящих из каналов 10, на измерительный блок второго типа 24 для использования этих пространственно-временных каналов в оценке среднего наравне с другими. Это осуществляется до достижения сигналов, преобразуемых интерферометром на последнем шаге W, выходных каналов.
и числа фотонов в каждом выбранном(-ых) паттерне(-ах) измерений. Т.к. на каждом шаге в схему попадает одинаковое число фотонов М от источников, то общее число фотонов должно быть кратно WM. После предпоследнего шага W-1 производят переключение переключателя 15 линий 4 для вывода сигналов, выходящих из каналов 10, на измерительный блок второго типа 24 для использования этих пространственно-временных каналов в оценке среднего наравне с другими. Это осуществляется до достижения сигналов, преобразуемых интерферометром на последнем шаге W, выходных каналов.
6. При фиксированных значениях параметров  подающихся на входы 14, управляющих передаточной матрицей интерферометра 1, производят расчет всех средних
подающихся на входы 14, управляющих передаточной матрицей интерферометра 1, производят расчет всех средних  по параметризованным квантовым состояниям
по параметризованным квантовым состояниям  приготавливаемым в устройстве симуляторе. Для приготовления параметризованного квантового состояния
приготавливаемым в устройстве симуляторе. Для приготовления параметризованного квантового состояния  с нужной размерностью, определяемой выбранными до этого числе фотонов и каналов, на интерферометр периодически подают фотоны W раз по М фотонов. На каждом шаге на выходе из каналов 9 производят детектирование. По результатам измерений на всех шагах формируют вектор измерений
с нужной размерностью, определяемой выбранными до этого числе фотонов и каналов, на интерферометр периодически подают фотоны W раз по М фотонов. На каждом шаге на выходе из каналов 9 производят детектирование. По результатам измерений на всех шагах формируют вектор измерений  Если вектор измерений соответствует выбранному(-ым) паттерну(-ам), то с помощью приготовленного состояния проводят измерение среднего от произведения однокубитовых операторов
Если вектор измерений соответствует выбранному(-ым) паттерну(-ам), то с помощью приготовленного состояния проводят измерение среднего от произведения однокубитовых операторов 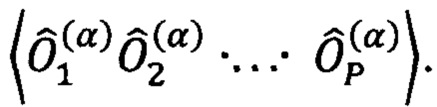 Расчет одного среднего по квантовому состоянию требует проведения нескольких измерений
Расчет одного среднего по квантовому состоянию требует проведения нескольких измерений  число которых продиктовано скоростью схождения множества измерений одной величины с неопределенностью к статистическому среднему, рассчитываемому как
число которых продиктовано скоростью схождения множества измерений одной величины с неопределенностью к статистическому среднему, рассчитываемому как 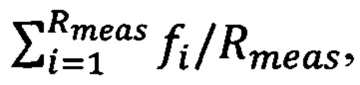 где
где  - результат i-го измерения.
- результат i-го измерения.
7. Рассчитанные средние значения от операторов входят в расчет оптимизируемой величины  который выполняется на классическом компьютере простым сложением с весовыми коэффициентами.
который выполняется на классическом компьютере простым сложением с весовыми коэффициентами.
8. По рассчитанному значению оптимизируемой функции  при заданном наборе варьируемых параметров
при заданном наборе варьируемых параметров  классический оптимизационный алгоритм, работающий на классическом компьютере, дает новые значения набора параметров
классический оптимизационный алгоритм, работающий на классическом компьютере, дает новые значения набора параметров  Управление от классического компьютера обновляет параметры перепрограммируемого интерферометра на
Управление от классического компьютера обновляет параметры перепрограммируемого интерферометра на 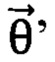 и последовательность шагов, описанная в п. 5-7 повторяется. Таким образом, набор параметров
и последовательность шагов, описанная в п. 5-7 повторяется. Таким образом, набор параметров 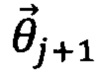 на шаге j+1 связан с набором параметров на предыдущем шаге j посредством соотношения:
на шаге j+1 связан с набором параметров на предыдущем шаге j посредством соотношения: 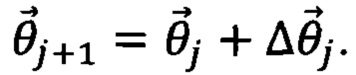 Оптимизация прекращается, если текущее значение
Оптимизация прекращается, если текущее значение  удовлетворяет условию остановки используемого оптимизационного алгоритма.
удовлетворяет условию остановки используемого оптимизационного алгоритма.
9. Часто интерес представляет расчет не одиночных значений гамильтонианов, а также их зависимость от параметров. Например, энергетические уровни основных состояний молекул в зависимости от геометрической конфигурации составляющих атомов (расстояния между атомами). В этом случае весовые коэффициенты 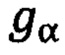 в операторе задачи
в операторе задачи  зависят от параметров. В таких случаях оптимизация, описанная в п. 4-7 производится для серии значений параметров, которые достаточны для получения требуемой зависимости.
зависят от параметров. В таких случаях оптимизация, описанная в п. 4-7 производится для серии значений параметров, которые достаточны для получения требуемой зависимости.
10. Решение задачи может быть продолжено также повторением шагов, описанных в п. 5-9, с разным числом вспомогательных каналов и фотонов и паттерном измерений, использующихся при условном приготовлении параметризованного состояния. В таком случае эти параметры - число вспомогательных каналов, число вспомогательных фотонов и паттерны измерений - могут рассматриваться как варьируемые параметры  вместе с управляющими параметрами перепрограммируемого интерферометра.
вместе с управляющими параметрами перепрограммируемого интерферометра.
Основными элементами оптических схем, реализующих предлагаемое изобретение, являются: 1) источники фотонов, 2) детекторы фотонов, 3) многоканальные перепрограммируемые интерферометры и 4) оптические линии задержки. Все эти элементы доступны для изготовления по-отдельности с последующим соединением в одну схему. Технологический уровень также позволяет интегрировать часть этих элементов в одной интегрально-оптической схеме и в будущем возможно ожидать полную интеграцию элементов на одном чипе. Высокий уровень интеграции разнородных оптических элементов, необходимых для конструирования предлагаемой схемы, на одном чипе позволяет снизить уровень потерь и повысить степень масштабирования квантового вычислителя. Вместе с тем квантовый вычислитель может быть реализован и без монолитной интеграции элементов на одном чипе.
Предложенные способ и система реализации квантовых вычислений на основе фотонных чипов с приготовлением параметризованных квантовых состояний можно реализовать в интерферометрах, где в качестве канала может выступать волновод или пространственная мода свободного пространства. В оптике волноводные структуры, которые лежат в основе схем с пространственным кодированием, могут быть выполнены в виде интегральных оптических схем. Интегральные оптические схемы можно изготовить по планарной технологии литографии (L. Chrostowski, М. Hochberg, "Silicon Photonics design: from devices to systems" // Cambridge Univ. Press, 2015) или по трехмерной технологии, например, с помощью технологии лазерной печати (I.V. Dyakonov et al., Reconfigurable photonics on a glass chip // Phys. Rev. Applied, vol. 10, 044048 (2018)). В качестве элементов фазового сдвига в таких схемах могут применяться 1) термо-оптические элементы, которые меняют фазы, которые набегают на оптические сигналы, распространяющиеся по участкам волноводов, при пропускании через них электрического тока за счет его нагрева, 2) электро-оптические элементы, которые меняют фазы при приложении напряжения за счет изменения концентрации электронов и/или дырок на участке волновода, и 3) пьезо-оптические элементы, изменяющие фазы распространяющегося в волноводе сигнала под действием электрического напряжения, которое вызывает механическое напряжение на участке волновода, что меняет его показатель преломления.
Существуют источники одиночных фотонов, основанные на квантовых точках. При возбуждении квантовой точки лазерным импульсом квантовая точка излучает одиночный фотон (R. Uppu et al., "Scalable integrated single-photon source" // Science, vol. 6, No 50, eabc8268 (2020)). Данный тип источников позволяет генерировать одиночные фотоны с высокой вероятностью генерации и чистотой. Источники фотонов на основе квантовых точек могут быть использованы в интегральных оптических схемах (Y. Arakawa, M.J. Holmes, "Progress in quantum-dot single photon sources for quantum information technologies: a broad spectrum overview" // Appl. Phys. Reviews, vol. 7, 021309 (2020)). Существуют также источники пар фотонов, основанные на нелинейно-оптических процессах. Такие источники могут быть изготовлены одновременно с процессом изготовления интегрально-оптических схем (S. Paesani et al. "Near-ideal spontaneous photon sources in silicon quantum photonics " // Nat. commun., vol. 11, 2505 (2020)). Таким образом, их можно интегрировать непосредственно в схемы с программируемыми интерферометрами.
Существуют сверхпроводниковые детекторы одиночных фотонов, обладающие высокой эффективностью детектирования и низким уровнем добавляемого шума (J. Chang et al., "Detecting telecom single photons with 99.5% system detection efficiency and high time resolution" // APL Photonics, vol. 6, No 3, 036114 (2021)). Сверхпроводниковые детекторы могут быть интегрированы непосредственно в интегрально-оптические волноводы (О. Kahl et al., "Waveguide integrated superconducting single-photon detectors with high internal quantum efficiency at telecom wavelengths" // Sci. Reps., vol. 5, 10941 (2015)). Были продемонстрированы способы создания программируемых оптических интерферометров на одном чипе со сверхпроводниковыми детекторами (S. Gyger et al., "Reconfigurable photonics with on-chip single-photon detectors" // Nat. Commun., vol. 12, 1408 (2021)).
Типичные частоты, с которыми можно генерировать одиночные фотоны, составляют 10 МГц - 1 ГГц и в основном определяются скоростью, с которой можно генерировать лазерные импульсы, используемые для возбуждения источников. Для задержки оптических сигналов на периоды следования, соответствующие таким частотам, перенаправляющие оптические линии (включая длину распространения в интерферометре) должны иметь длину 20 м - 0,2 м. Такие оптические линии можно реализовать с помощью волокон, которые присоединяются к программируемому интерферометру или же они могут быть изготовлены на одном интегральном чипе непосредственно с программируемым интерферометром (L. Zhou et al., "Integrated optical delay lines: a review and perspective" // Chinese Optics Letters, vol. 16 (10), 101301 (2018)).
Существуют быстрые модуляторы фазы оптических сигналов со временем переключения ~10 пс и скоростью переключения, превышающей 10 ГГц. Значения этих времен намного превышает характерное время задержки между двумя последовательными шагами работы схемы. Таким образом, это позволяет переключать характеристики преобразования оптических элементов схемы - интерферометров и переключателей. Существуют интегрально-оптические версии модуляторов фазы с такими характеристиками (S. Ummethala et al., "Hybrid electro-optic modulator combining silicon photonic slot waveguides with high-k radio-frequency slotlines" // Optica, vol. 8, No 4, 511 (2021)).
Помимо схем с интерферометрами с пространственными каналами - волноводами, заявляемое изобретение может быть также реализовано с использованием перепрограммируемых интерферометров с частотным кодированием каналов. В таком случае в качестве каналов выступают неперекрывающиеся частотные линии спектра электромагнитного поля. Каждой из линий ставят в соответствие номер канала, таким образом, набор из N линий образует множество каналов всего преобразования. В качестве амплитуды сигнала, распространяющегося по частотному каналу, выступает амплитуда с соответствующей спектральной компонентой. Стоит заметить, что использование частотной кодировки каналов многоканального преобразования позволяет использовать для передачи и преобразования один пространственный канал - один волновод, одну пространственную моду свободного пространства. Для осуществления взаимодействия между частотными каналами предложено использовать набор преобразований модуляции частотных каналов, которая наводит на каналы зависящую от времени фазу, профиль которой можно подбирать, и формирователь импульсов.
Перепрограммируемые интерферометры, использующиеся в предлагаемом изобретении, могут быть реализованы по аналогии с системой, описанной в работе Н.-Н. Lu et al., "Electro-optic frequency beam splitters and tritters for high-fidelity photonic quantum information processing" // Phys. Rev. Lett., vol. 120, 030502, 2018), в которой продемонстрировано на практике осуществление ряда линейных преобразований для трех частотных каналов. Для реализации изобретения может быть использовано оптоволоконное оборудование, которое является стандартным для телекоммуникационного диапазона длин волн в районе 1550 нм. Для осуществления модуляции могут быть применены электрооптические модуляторы и формирователь импульсов, которые являются стандартными компонентами телекоммуникационного оборудования. Помимо оптоволоконных телекоммуникационных компонент, весь их набор можно также реализовать с помощью интегрально-оптических схем, т.к. все необходимые элементы были продемонстрированы. Например, интегрально-оптический формировать импульсов продемонстрирован в работе K.A. McKinzie et al. "InP integrated pulse shaper with 48 channel, 50 GHz spacing amplitude and phase control", 2017 IEEE Photonics Conference (IPC), 197-198 (2017). Интегрально-оптические модуляторы на протяжении долгого времени являются доступными для изготовления в интегрально-оптическом исполнении (K. Ogawa, Integrated silicon-based optical modulators: 100 Gb/s and beyond, SPIE Press, ISBN: 9781510625815, 2019).
В случае использования частотной кодировки каналов источники должны генерировать фотоны на разных несущих частотах, которые соответствуют частотным каналам. Этого можно добиться индивидуальной подстройкой частот источников, например, электрическим полем или локальным нагревом (R. Katsumi et al., "In situ wavelength tuning of quantum-dot single-photon sources integrated on a CMOS-processes silicon waveguide" // Applied Phys. Lett., vol. 116, 041103 (2020)).
Примеры конкретного выполнения
Для проверки осуществимости изобретения с достижением технического результата был изготовлен оптический квантовый симулятор, использующий предложенное приготовление параметризованных квантовых состояний фотонов. В качестве конкретной реализации была рассмотрена квантовая схема, приготавливающая двухкубитовые состояния фотонов в двухрельсовой кодировке. В общем виде, состояние произвольной двухкубитовой системы имеет следующий вид: 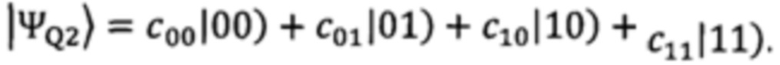 Здесь Q2 - это индекс, обозначающий 2-кубитовое состояние. При кодировании в двухрельсовый базис
Здесь Q2 - это индекс, обозначающий 2-кубитовое состояние. При кодировании в двухрельсовый базис  эти состояния принимают следующий вид:
эти состояния принимают следующий вид: 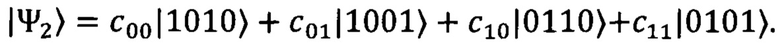 Возможность приготавливать двухкубитовые параметризованные квантовые состояния демонстрируется возможностью изменять коэффициенты разложения с00, с01, с10 и с11.
Возможность приготавливать двухкубитовые параметризованные квантовые состояния демонстрируется возможностью изменять коэффициенты разложения с00, с01, с10 и с11.
Необходимое число пространственно-временных каналов, которые кодируют логические состояний двух кубитов, NS=4, а число основных фотонов для кодировки MS=2. Вместе с тем, известно, что для линейно-оптической генерации перепутанных двухкубитовых состояний необходимо минимум М=4 фотона (S. Stanisic et al., "Generating entanglement with linear optics" // Phys. Rev. A, vol. 96, 043861 (2017)).
Для генерации двухкубитовых параметризованных состояний была использована схема с W=2 шагами, на каждом шаге которой в интерферометр подавалась пара фотонов. Перенаправление и задержка сигналов осуществлялась с L=1 выхода интерферометра. Число пространственных каналов, в которых на каждом шаге приготавливается состояние одного кубита параметризованного квантового состояния R=2; числом каналов, подвергающихся измерению сразу после интерферометра J=2. Таким образом, программируемый интерферометр 1 имел 5 входных и выходных пространственных каналов.
На Фиг. 8а представлена схема оптической установки, которая использовалась для приготовления и измерения двухкубитовых состояний. Каждый из блоков 3 и 20 содержал по два детектора одиночных фотонов - 33 и 34, соответственно. Сигналы с пар детекторов фотонов 33 и 34 поступали на компьютер 22 по электрическим линиям 35 и 36. В качестве программируемого интерферометра использовался интегрально-оптический чип, созданный с помощью технологии фемтосекундной лазерной печати, которая позволяет изготавливать как планарные, так и трехмерные интегрально-оптические схемы. Для создания интегрального чипа оптической схемы использовалась кварцевая заготовка в форме прямоугольника с длиной 10 см, шириной 5 см и толщиной 0,5 см. Схема интегрального чипа представлена на Фиг. 8б. На первом этапе изготовления чипа в объеме заготовки создавались пассивные волноводные структуры, формирующие статическую оптическую схему, представляющую собой пучок из пяти волноводов, которые сводились близко друг к другу для формирования области взаимодействия 37, где энергии оптических сигналов переходят из волновода в волновод за счет эванесцентного взаимодействия между ними, и разносились на удаление для предотвращения взаимодействия и внесения сдвигов фаз программируемым образом. Начала и концы волноводов доводились до противоположных торцов стеклянной заготовки для обеспечения возможности заведения и выведения оптических сигналов.
Для реализации программируемости на чипе изготавливались элементы сдвига фазы 38, с помощью которых осуществлялась реконфигурация интерферометров. Элементы сдвига фазы были основаны на термо-оптическом эффекте. Элементы изменяемых фазовых сдвигов представляли собой металлические полоски, располагаемые над участками волноводов, на которых было необходимо реализовать эти элементы. При подаче напряжения на элементы 38 происходил нагрев соответствующих участков волноводов, в результате чего коэффициент преломления стекла в этой области менялся, вызывая таким образом сдвиг фазы относительно не нагретых участков. Детали использованной технологии изготовления можно найти в работе I.V. Dyakonov et al., "Reconfigurable photonics on a glass chip" //Phys. Rev. Applied, vol. 10, 044048 (2018).
Источником фотонов, поступающих на вход перепрограммируемого интерферометра 1, являлся процесс спонтанного параметрического рассеяния, протекающий в нелинейном кристалле бета-бората бария. В процессе спонтанного параметрического рассеяния рождались пары фотонов, каждый из которых выходил из кристалла под своим углом, что давало возможность собирать фотоны в волокна и заводить в интерферометр. В качестве накачки использовался лазер, генерирующий импульсы на центральной длине волны 816 нм длительностью ~100 фс и частотой следования  Излучение накачки поступало на удвоитель частоты, где его длина волны становилось в 2 раза меньше изначальной, после чего оно поступало на нелинейный кристалл. Импульс накачки в нелинейном кристалле недетерминистическим образом рождал пару одиночных фотонов на длине волны 816 нм в разных пространственных модах. Через оптоволоконный ввод пары фотонов поступали на два канала интерферометра. Т.к. длина волны накачки, поступающая в нелинейный кристалл, намного отличается от длин волн генерируемых пар фотонов, и направления распространения фотонов отличается от направления распространения волны накачки, частотных фильтров не требовалось.
Излучение накачки поступало на удвоитель частоты, где его длина волны становилось в 2 раза меньше изначальной, после чего оно поступало на нелинейный кристалл. Импульс накачки в нелинейном кристалле недетерминистическим образом рождал пару одиночных фотонов на длине волны 816 нм в разных пространственных модах. Через оптоволоконный ввод пары фотонов поступали на два канала интерферометра. Т.к. длина волны накачки, поступающая в нелинейный кристалл, намного отличается от длин волн генерируемых пар фотонов, и направления распространения фотонов отличается от направления распространения волны накачки, частотных фильтров не требовалось.
В качестве линии задержки использовалось волокно, концы которого соединялись с входным и выходным каналом интегрального чипа. Длина волокна, составляющая ≈ 2,4 м, подгонялась чтобы с высокой степенью точности (не хуже ОД мм) давать время полного обхода оптических сигналов, равное периоду следования импульсов накачки  Для этой цели несколько раз проводилось укорачивание/сошлифовывание волокна (предварительно волокно бралось заведомо длиннее, чем необходимо). После каждого раза волокно соединялось с чипом и изучалась возможность наблюдения эффекта квантовой интерференции при поступлении на чип одиночных фотонов с частотой
Для этой цели несколько раз проводилось укорачивание/сошлифовывание волокна (предварительно волокно бралось заведомо длиннее, чем необходимо). После каждого раза волокно соединялось с чипом и изучалась возможность наблюдения эффекта квантовой интерференции при поступлении на чип одиночных фотонов с частотой  который возможен только, если задержанный фотон или волокна поступает в интерферометр одновременно с заново сгенерированным. Укорачивание волокна продолжалось до наблюдения эффекта. Также проводился контроль поляризации сигналов, выходящих из волокна - она всегда должна совпадать с поляризацией фотонов, поступающих на интерферометр. Нужная поляризация подбиралась контроллером поляризации.
который возможен только, если задержанный фотон или волокна поступает в интерферометр одновременно с заново сгенерированным. Укорачивание волокна продолжалось до наблюдения эффекта. Также проводился контроль поляризации сигналов, выходящих из волокна - она всегда должна совпадать с поляризацией фотонов, поступающих на интерферометр. Нужная поляризация подбиралась контроллером поляризации.
Для детектирования использовались сверхпроводниковые детекторы. Сигналы с выхода интерферометра заводились в криостат, в котором располагались детекторы, с помощью волокон. Эффективность детектирования одиночных фотонов составляла ~85%. Электрические сигналы с электронной системы считывания фотоотсчетов поступали на персональный компьютер 22, через электрические линии 35 и 36. Компьютерная программа обрабатывала сигналы, поступающие на компьютер от детекторов.
Для генерации двухкубитовых состояний 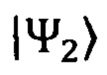 учитывались только те приготавливаемые состояния, которые получаются при паттерне измерений, выполняемые измерительным блоком 3,
учитывались только те приготавливаемые состояния, которые получаются при паттерне измерений, выполняемые измерительным блоком 3, 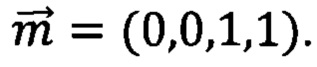 Т.е. принимаются только те состояния, для которых на последнем - втором - временном шаге были измерены по 1 фотону в каждом из детекторов 34. При выполнении этого условия, проводилась также постселекция результатов измерения приготавливаемых состояний, выполняемых измерительным блоком 20. При постселекции учитывались только такие результаты измерений, которые на каждом временном шаге детектировали по одному фотону. Данное условие постселекции гарантирует измерение только логических двухрельсовых компонент приготавливаемых состояний, т.е. учитывались только измерения с фотонами из разных пар каналов, кодирующих разные кубиты: 1010, 0101, 1001 и 0110. Таким образом, за два временных шага на вход схемы поступало четыре фотона. Также на этих шагах измерялись четыре фотона. Такая реализация позволила обойтись без использования переключателей 15 для вывода сигналов на последнем шаге, т.к. все вошедшие фотоны были уже измерены блоками 3 и 20.
Т.е. принимаются только те состояния, для которых на последнем - втором - временном шаге были измерены по 1 фотону в каждом из детекторов 34. При выполнении этого условия, проводилась также постселекция результатов измерения приготавливаемых состояний, выполняемых измерительным блоком 20. При постселекции учитывались только такие результаты измерений, которые на каждом временном шаге детектировали по одному фотону. Данное условие постселекции гарантирует измерение только логических двухрельсовых компонент приготавливаемых состояний, т.е. учитывались только измерения с фотонами из разных пар каналов, кодирующих разные кубиты: 1010, 0101, 1001 и 0110. Таким образом, за два временных шага на вход схемы поступало четыре фотона. Также на этих шагах измерялись четыре фотона. Такая реализация позволила обойтись без использования переключателей 15 для вывода сигналов на последнем шаге, т.к. все вошедшие фотоны были уже измерены блоками 3 и 20.
Стоит отметить, что выбранный паттерн измерений и требование наличия одного фотона в каналах, кодирующих кубит, не может реализоваться ни при каких условиях, если в схеме нет линий обратной связи 4. Действительно, на каждом шаге на схему поступает по два фотона. При этом без линии обратной связи фотоны из предыдущего шага не могут попасть на следующий. Таким образом, детектирование двух фотонов в блоке 3 на втором шаге может быть реализовано только если в каналах, кодирующих кубит, нет ни одного фотона. Таким образом, успешное экспериментальное приготовление квантовых состояний с выбранным паттерном измерений демонстрирует важную роль линии обратной связи.
В эксперименте установка работала непрерывно - не было необходимости включать и выключать лазер для выполнения W=2 временных шагов. Вместо этого, управляющий компьютер 22 выделял последовательные пары временных отсчетов, на которых происходят детектирования детекторами 33 и 34, и проводил постселекцию результатов измерений согласно процедуре, описанной выше. Частота измерений с учетом требований постселекции составляла 0,2-4 кГц, и отличалась для разных приготавливаемых состояний.
Приготавливаемое двухкубитовое состояние перед постселекцией по измерениям блока 20 описывается следующим выражением:

где р - компонента состояния, которая представляет собой суперпозицию двух кубитов в двухрельсовой кодировке с коэффициентами  - вектор состояния, содержащий двухфотонные базисные векторы, выходящие из двухрельсовой кодировки кубитов:
- вектор состояния, содержащий двухфотонные базисные векторы, выходящие из двухрельсовой кодировки кубитов: 
Для анализа способности схемы приготавливать двухкубитовые состояния компьютер генерировал случайные значения коэффициентов разложения (с сохранением условия нормировки:  Т.к. схема, изображенная на фиг. 8а, дает возможность получения информации только об абсолютных значениях коэффициентов разложения приготавливаемого состояния с00, с10, с01 и с11, в качестве меры, характеризующей точность реализации требуемого состояния, использовалось скалярное произведение двух векторов - одного вектора, составленного из модулей коэффициентов требуемого состояния
Т.к. схема, изображенная на фиг. 8а, дает возможность получения информации только об абсолютных значениях коэффициентов разложения приготавливаемого состояния с00, с10, с01 и с11, в качестве меры, характеризующей точность реализации требуемого состояния, использовалось скалярное произведение двух векторов - одного вектора, составленного из модулей коэффициентов требуемого состояния  и вектора, составленного из модулей коэффициентов разложения измеряемого состояния
и вектора, составленного из модулей коэффициентов разложения измеряемого состояния  Значение скалярного произведения равное 1 отвечает идеальному соответствию двух состояний. Оптимизационный алгоритм стохастической аппроксимации с одновременным возбуждением (в англоязычной литературе - Simultaneous perturbation stochastic approximation (SPSA)) на компьютере выполнял поиск максимума скалярного произведения двух векторов в зависимости от параметров
Значение скалярного произведения равное 1 отвечает идеальному соответствию двух состояний. Оптимизационный алгоритм стохастической аппроксимации с одновременным возбуждением (в англоязычной литературе - Simultaneous perturbation stochastic approximation (SPSA)) на компьютере выполнял поиск максимума скалярного произведения двух векторов в зависимости от параметров  на входе 14, задающих передаточную матрицу интерферометра 1.
на входе 14, задающих передаточную матрицу интерферометра 1.
В эксперименте по приготовлению двухкубитовых квантовых состояний в двухрельсовой кодировке со схемой, изображенной на фиг. 8, генерировался набор из 100 квантовых состояний - коэффициентов с00, с10, с01 и с11 - случайным образом из равномерного распределения. Для каждого набора коэффициентов запускалась оптическая схема, которая оптимизировала интерферометр таким образом, чтобы наилучшим образом приготовить требуемое квантовое состояние. На фиг. 9 представлена гистограмма, иллюстрирующая распределение точности приготовления целевых состояний (скалярного произведения модулей коэффициентов двух векторов - требуемого и получаемого в эксперименте). Как видно из гистограммы, точность приготовления всех состояний превышала 0,9.
Для проверки оптимальности использования 4-х фотонов для генерации двухкубитовых состояний в двухрельсовой кодировке была выполнена экспериментальная проверка возможности приготовления этих состояний с W=1 шагом и двумя фотонами. В таком случае детекторы 33 и 34, блоков 20 и 3, соответственно, играли равнозначную роль и учитывались только измерения из пар этих детекторов, которые отвечали кубитам в двухрельсовой кодировке: 1010, 0101, 1001 и 0110. Был выполнен эксперимент, аналогичный проделанному для схемы с W=2 шагами и различающейся ролью пар детекторов 33 и 34. Ни одного случая из 100 заново случайно сгенерированных целевых наборов коэффициентов с00, с10, с01 и с11 не было приготовлено с точностью, превышающей 0,4, что свидетельствует о невозможности приготовления произвольных двухкубитовых состояний с высоким качеством, подходящим для применения в квантовых вариационных алгоритмах.
Заявляемое изобретение продемонстрировало повышение эффективности использования физических ресурсов линейно-оптических интерферометров, детекторов и источников фотонов, снижение времени, затрачиваемого на выполнение квантовых вариационных алгоритмов на линейно-оптической платформе в том числе за счет повторного использования ресурсов - источников и детекторов фотонов и интерферометров, повышающего размерность приготавливаемых квантовых состояний по сравнению с известными до этого времени способами с таким же количеством ресурсов. Время, затрачиваемое на однократную генерацию квантового состояния, было обратно пропорционально вероятности генерации нужного числа фотонов, из которого это состояние получают линейно-оптическим преобразованием. При реализации предложенного способа была осуществлена генерация параметризованного двухкубитного состояния с помощью двух пар фотонов, получаемых от одного источника в разные отрезки времени. В то же время, известно, что для приготовления двухкубитовых квантовых состояний в традиционных схемах с одновременной генерацией всех фотонов, необходимо использовать 6-канальный интерферометр и одновременно генерировать 4 фотона (S. Stanisic et al., "Generating entanglement with linear optics" // Phys. Rev. A, vol. 96, 043861 (2017)), т.е. более затратно, т.к. требует в 2 раза больше источников и более крупных интерферометров.
Имея в наличии только один источник пар фотонов гораздо легче осуществить генерацию двух пар фотонов, которые посылаются на линейно-оптическую схему в разные отрезки времени, чем сгенерировать две пары фотонов, которые посылаются одновременно на 4 входных канала линейно-оптической схемы. Для получения одновременно четырех фотонов в один отрезок времени из двух пар фотонов, задержанных друг относительно друга, необходимо внести временную задержку в пару фотонов, которая была сгенерирована раньше. Это можно осуществить только с помощью оптической схемы с активными переключателями. Детали работы схем с активным переключением можно найти, например, в работе (Е. Lee, S.M. Lee, H.S. Park, "Relative time multiplexing of heralded telecom-band single-photon sources using switchable optical fiber delays" // Opt. Express, vol. 27, No 17, 24545 (2019)). Такая схема перенаправляет фотоны первой пары в петли временной задержки и выводят ее в нужный пространственный канал, тогда как фотоны второй пары, полученные позже, перенаправляется переключателями в другой канал. Следовательно, наличие активной схемы для получения одновременных четырех фотонов от одного источника будет вносит потери, и тем самым, снижать вероятность генерации четырех фотонов. Таким образом, для одного и того же источника генерация одновременно четырех фотонов менее выгодна по сравнению с генерацией двух пар фотонов в разные отрезки времени. С ростом размерностей квантовых состояний, которые необходимо приготовить для реализации квантовых вариационных алгоритмов, схемы с активными переключателями усложняются и вносимые потери растут, что усугубляет использование стандартных линейно-оптических схем, основанных на одном многоканальном интерферометре.
Схема, изображенная на фиг. 8, была также использована для расчета энергии основного состояния молекулы водорода - примера задачи из области материаловедения - квантовым вариационным алгоритмом. Для расчета использовался базис функции «sto-3g», известный из квантовой химии (D. Young, "Computational chemistry: a practical guide for applying techniques to real world problems", Wiley, 2004). В таком случае гамильтониан, описывающий энергию молекулы водорода, принимает следующий вид:

где весовые коэффициенты  зависят от базисных функций
зависят от базисных функций  Эти коэффициенты также зависят от расстояния между атомами водорода
Эти коэффициенты также зависят от расстояния между атомами водорода  т.е. разным
т.е. разным  отвечают разные значения энергии основного состояния гамильтониана (16). Для расчета коэффициентов
отвечают разные значения энергии основного состояния гамильтониана (16). Для расчета коэффициентов  в выбранном базисе использовался программный пакет OpenFermion (J.R. McClean et al. "OpenFermion: The electronic structure package for quantum computers" // arxiv:1710.07629 (2017)).
в выбранном базисе использовался программный пакет OpenFermion (J.R. McClean et al. "OpenFermion: The electronic structure package for quantum computers" // arxiv:1710.07629 (2017)).
В эксперименте рассчитывалась энергия основного состояния гамильтониана (16) для одного значения 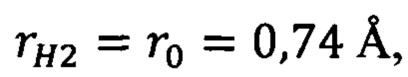 которое отвечает равновесному значению расстояния между атомами, т.е. минимуму энергии основного состояния:
которое отвечает равновесному значению расстояния между атомами, т.е. минимуму энергии основного состояния: 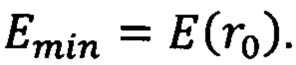 Для этого расстояния рассчитывались коэффициенты
Для этого расстояния рассчитывались коэффициенты  При этом для расчета средних от произведений двух операторов в гамильтониане (16) использовалось дополнение к схеме, нарисованной на фиг. 8. В измерительный блок 3 было добавлено два интерферометра Маха-Цендера, в соответствии с фиг. 7б. Для этого на одном интегральном чипе с программируемым интерферометром, изображенном на фиг. 8б, были изготовлены программируемые интерферометры Маха-Цендера. Измерение средних от операторов проводилось реконфигурированием интерферометров Маха-Цендера в соответствии с процедурой, описанной в тексте выше. Полученное значение энергии основного состояния составило -1,06 Хартри. Величина энергии основного состояния молекулы водорода, рассчитанная на классическом компьютере в этом же базисе «sto-3g» методом Хартри-Фока, есть -1,117 Хартри (см., например, базу данных https://cccbdb.nist.gov). Таким образом, относительная ошибка составила 5%.
При этом для расчета средних от произведений двух операторов в гамильтониане (16) использовалось дополнение к схеме, нарисованной на фиг. 8. В измерительный блок 3 было добавлено два интерферометра Маха-Цендера, в соответствии с фиг. 7б. Для этого на одном интегральном чипе с программируемым интерферометром, изображенном на фиг. 8б, были изготовлены программируемые интерферометры Маха-Цендера. Измерение средних от операторов проводилось реконфигурированием интерферометров Маха-Цендера в соответствии с процедурой, описанной в тексте выше. Полученное значение энергии основного состояния составило -1,06 Хартри. Величина энергии основного состояния молекулы водорода, рассчитанная на классическом компьютере в этом же базисе «sto-3g» методом Хартри-Фока, есть -1,117 Хартри (см., например, базу данных https://cccbdb.nist.gov). Таким образом, относительная ошибка составила 5%.
Таким образом, изобретение решает проблему высокого уровня временных затрат, требуемых для приготовления многокубитных квантовых состояний для квантовых вариационных алгоритмов, низкой вероятности приготовления параметризованных квантовых состояний фотонов и большого количества физических ресурсов, необходимых для приготовления этих состояний в квантовом вариационном алгоритме. Изобретение позволяет повысить размерность параметризованных квантовых состояний, снизить время, затрачиваемое на их приготовление, снизить объем физических ресурсов, необходимых для реализации квантовых вариационных алгоритмов, повторно использовать одни и те же физические ресурсы: источники и детекторы фотонов, и программируемый интерферометр для приготовления многокубитовых параметризованных состояний.
| название | год | авторы | номер документа |
|---|---|---|---|
| Квантовая вычислительная система на основе фотонных чипов | 2023 |
|
RU2806840C1 |
| Архитектура квантовых вычислительных устройств для решения прикладных задач в области материаловедения | 2023 |
|
RU2821360C1 |
| Управляющая система для квантовых вычислительных устройств | 2023 |
|
RU2814936C1 |
| ВОЛОКОННО-ОПТИЧЕСКИЙ КВАНТОВЫЙ КОМПЬЮТЕР (ВАРИАНТЫ) | 2023 |
|
RU2813708C1 |
| Устройство формирования квантовых состояний для систем квантовых коммуникаций на чипе | 2023 |
|
RU2814193C1 |
| Устройство формирования квантовых состояний для систем квантовых коммуникаций с оценкой качества приготовления состояний для протоколов квантовой генерации ключа на чипе | 2023 |
|
RU2806904C1 |
| СПОСОБ ФИЛЬТРАЦИИ ФОТОНОВ ОТ ОСТАТОЧНОГО ИЗЛУЧЕНИЯ КОГЕРЕНТНОЙ НАКАЧКИ | 2021 |
|
RU2783222C1 |
| СПОСОБ ПОЛУЧЕНИЯ УПРАВЛЯЮЩИХ ПАРАМЕТРОВ ДЛЯ КВАНТОВЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ НА ОСНОВЕ ИОНОВ В ЛОВУШКЕ, КОТОРЫЕ ЗАСТАВЛЯЮТ СИСТЕМУ МЕНЯТЬ СОСТОЯНИЯ, ЗАДАННЫЕ СОБСТВЕННЫМ ГАМИЛЬТОНИАНОМ, ТАК, ЧТО ЭВОЛЮЦИЯ В СИСТЕМЕ СООТВЕТСТВУЕТ ПРИМЕНЕНИЮ (ПОСЛЕДОВАТЕЛЬНОСТИ) ЛОГИЧЕСКИХ ОПЕРАЦИЙ | 2022 |
|
RU2830094C2 |
| Способ формирования сигналов управления квантовыми вентилями для выполнения квантовых вычислений при помощи вариационного алгоритма нахождения собственных значений операторов | 2023 |
|
RU2825968C1 |
| ДЕМОНСТРАЦИОННЫЙ СИМУЛЯТОР СИСТЕМЫ КВАНТОВОГО РАСПРЕДЕЛЕНИЯ КЛЮЧА | 2021 |
|
RU2795245C1 |

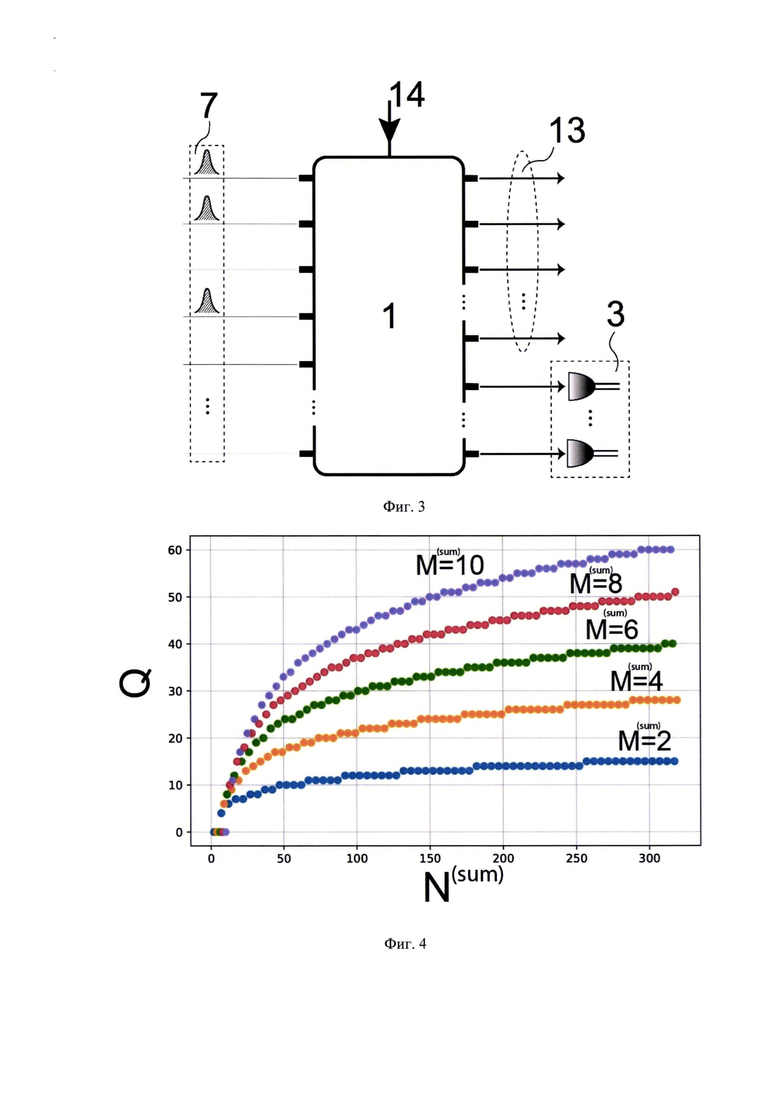



Изобретение относится к области квантовой оптики и квантовой информации, а именно к методам реализации квантовых вычислительных алгоритмов с помощью линейно-оптических устройств. Система и способ решения прикладных задач материаловедения с помощью сопряжения квантовых и классических устройств основаны на использовании интерферометра для выполнения линейно-оптических преобразований над квантовыми состояниями фотонов, снабженного линиями обратной связи, соединенного с измерительным блоком первого типа для измерения состояний фотонов и с измерительным блоком второго типа, выполненным с возможностью измерения средних значений произведения однокубитовых операторов по квантовым состояниям фотонов, изменения измерительного базиса по сигналу с управляющего входа измерительного блока второго типа; к измерительным блокам первого и второго типа, к интерферометру подключен компьютер, выполненный с возможностью вычисления результата шага квантового вариационного алгоритма и интерферометра. Изобретение позволяет снизить время, затрачиваемое на решение задач с помощью квантовых вариационных алгоритмов на линейно-оптической платформе. 2 н. и 2 з.п. ф-лы, 9 ил.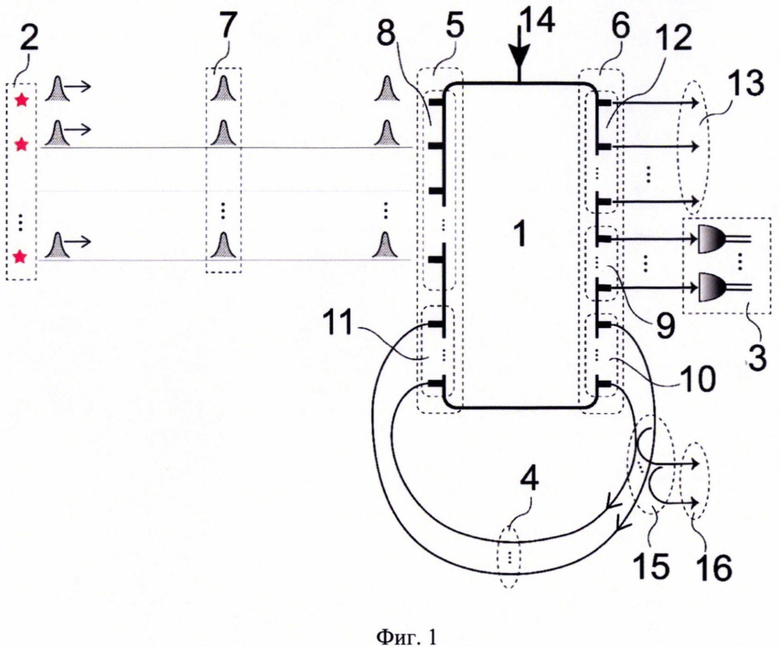
1. Система, реализующая квантовый вариационный алгоритм, включающая:
М источников одиночных фотонов;
интерферометр для выполнения линейно-оптических преобразований над квантовыми состояниями фотонов, снабженный управляющим входом для управления линейным преобразованием, N входами, из которых М входов предназначены для приема одиночных фотонов, L входов - для линий обратной связи, где  а также N выходами, из которых L выходов предназначены для подключения линий обратной связи, J выходов - для соединения с измерительным блоком первого типа, R выходов - для соединения с измерительным блоком второго типа, при этом
а также N выходами, из которых L выходов предназначены для подключения линий обратной связи, J выходов - для соединения с измерительным блоком первого типа, R выходов - для соединения с измерительным блоком второго типа, при этом 
L линий обратной связи, соединяющих соответствующие выходы и входы интерферометра;
измерительный блок первого типа для измерения состояний фотонов, снабженный J входами и включающий J детекторов фотонов, каждый из которых выполнен с возможностью измерения сигналов с выхода одного канала интерферометра;
измерительный блок второго типа, снабженный R входами, управляющим входом измерительного блока второго типа и выходом, предназначенным для подключения к компьютеру, выполненный с возможностью измерения средних значений произведения однокубитовых операторов по квантовым состояниям фотонов, и изменения измерительного базиса по сигналу с управляющего входа измерительного блока второго типа;
компьютер для вычисления результата шага квантового вариационного алгоритма, снабженный входами для подключения измерительного блока первого типа и для подключения измерительного блока второго типа, управляющими выходами для подключения к управляющим входам измерительного блока второго типа и интерферометра;
при этом:
линии обратной связи выбраны с обеспечением возможности синхронного поступления сигналов на входы для фотонов и на входы для линий обратной связи интерферометра с сохранением поляризации сигналов;
выход измерительного блока первого типа соединен со входом компьютера для измерительного блока первого типа; выход измерительного блока второго типа соединен со входом компьютера для измерительного блока второго типа;
М источников фотонов выполнены с возможностью генерации одиночных фотонов с обеспечением одновременного поступления на соответствующие входы интерферометра.
2. Система по п. 1, характеризующаяся тем, что М источников одиночных фотонов реализованы с помощью лазера, выполненного с возможностью генерации периодических последовательностей импульсов когерентного излучения, снабженного управляющим входом для управления генерацией, соединенным с компьютером, при этом компьютер снабжен соответствующим управляющим выходом;
при этом система содержит блок делителей для формирования разделенных на М каналов последовательностей импульсов когерентного излучения, снабженный входом и М выходами для вывода разделенных последовательностей импульсов, а также М фильтров для отсечения остаточной мощности импульсов когерентного излучения от одиночных фотонов, каждый из М фильтров снабжен входом и выходом для вывода одиночных фотонов, очищенных от остаточной мощности импульсов когерентного излучения.
3. Система по п. 1, характеризующаяся тем, что она снабжена блоком переключателей для вывода сигналов обратной связи интерферометра, снабженным управляющим входом для управления выводом сигналов обратной связи, L входами, L выходами обратной связи и L выходами для подключения к блоку измерения части приготавливаемого состояния, снабженному L соответствующими входами, управляющим входом, соединенным с соответствующим управляющим выходом компьютера для управления параметрами блока и выходом для вывода сигнала измерения, соединенным со входом компьютера для блока измерения приготавливаемого состояния.
4. Способ реализации квантовых вычислений с использованием системы по п. 1, включающий следующие этапы:
1) представление вычислительной задачи в виде суммы произведений операторов с весовыми коэффициентами для каждого слагаемого;
2) определение максимального числа кубитов Q, необходимого для расчетов средних значений от произведений операторов;
3) выбор числа шагов работы схемы  с округлением до наибольшего целого значения;
с округлением до наибольшего целого значения;
4) формирование произвольных значений фазовых сдвигов интерферометра путем подачи электромагнитных сигналов на его управляющие входы;
5) выбор вектора измерений фотонов для измерительного блока первого типа (на протяжении W шагов работы схемы по подэтапам а-d этапа 6);
6) выбор слагаемого в сумме произведений операторов, для которого производят следующие подэтапы:
a) генерация фотонов и подача их на вход интерферометра,
b) конфигурирование измерительного блока второго типа с обеспечением соответствия передаточной матрицы по меньшей мере одного интерферометра Маха-Цендера соответствующему множителю произведений операторов,
c) проведение измерений фотонов на выходе из блока первого типа с проверкой соответствия заданному вектору, соответствующих пятому этапу, и измерений фотонов на выходе из блока второго типа с проверкой соответствия кодировке кубитов,
d) в случае, если результаты измерений фотонов с выхода блоков первого и второго типов соответствуют заданному вектору и кодировке кубитов, то этапы b) и с) повторяют, с конфигурированием измерительного блока второго типа в соответствии с измеряемым на данном шаге произведением однокубитовых операторов и элементов вектора измерений блока первого типа, а в случае несоответствия - возвращаются к подэтапу а),
e) определение среднего значения измеренных чисел фотонов на выходах интерферометров в измерительном блоке второго типа для попыток, прошедших все W шагов,
f) повтор подэтапов а)-е) до выполнения критерия статистической сходимости применительно к среднему значению измерения числа фотонов на выходах измерительного блока второго типа;
7) повтор этапа 6) для каждого слагаемого в сумме произведений операторов с суммированием средних значений измерений числа фотонов с весовым коэффициентом, соответствующим выбранному слагаемому;
8) применение оптимизационного алгоритма к полученной на этапе 7) сумме с соответствующим изменением параметров интерферометра и числом повторений этапов 6) и 7), обеспечивающим решение оптимизационной задачи.
| US 2020150511 A1, 14.05.2020 | |||
| WO 2021262519 A1, 30.12.2021 | |||
| WO 2022246715 A1, 01.12.2022. |
Авторы
Даты
2024-03-07—Публикация
2023-04-06—Подача