Область техники, к которой относится изобретение
Изобретение относится к области помехоустойчивого кодирования, в частности к применению скрученного полярного кода (Twisted Polar code) в кодировании и декодировании данных.
Уровень техники
Полярные коды, предложенные в работе E. Arikan (Е. Арикан) "Channel polarization: A method for constructing capacity achieving codes for symmetric binary-input memoryless channels", опубликованной в журнале IEEE Transactions On Information Theory, том 55, номер 7, страницы 3051-3073, июль 2009 [1], представляют собой первый класс корректирующих кодов, которые достигают пропускной способности широкого класса каналов передачи информации. Полярные коды являются линейными блоковыми кодами, порождаемыми некоторой подматрицей матрицы 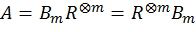 , где
, где 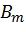 - перестановочная матрица обращения битов,
- перестановочная матрица обращения битов, 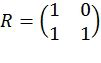 и
и 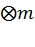 обозначает m-кратное Кронекеровское произведение матрицы с собой. Таким образом, кодовое слово полярного кода равно
обозначает m-кратное Кронекеровское произведение матрицы с собой. Таким образом, кодовое слово полярного кода равно 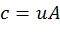 ,
, 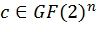 ,
, 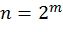 , где
, где 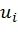 ,
, 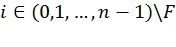 равны кодируемым информационным символам, а
равны кодируемым информационным символам, а 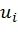 ,
, 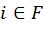 полагаются равными 0 (замороженные символы, то есть символы, значения которых никогда не меняются). Классическим методом декодирования
полагаются равными 0 (замороженные символы, то есть символы, значения которых никогда не меняются). Классическим методом декодирования 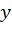 , полученного в результате передачи
, полученного в результате передачи  по симметричному по выходу каналу без памяти, является метод последовательного исключения (ПИ). Он состоит в последовательном нахождении наиболее вероятных апостериорных значений
по симметричному по выходу каналу без памяти, является метод последовательного исключения (ПИ). Он состоит в последовательном нахождении наиболее вероятных апостериорных значений 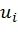 с использованием значений
с использованием значений 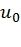 ,...,
,..., 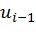 ,
, 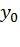 ,...,
,..., 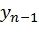 . Найденное значение
. Найденное значение 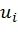 используется на последующих шагах алгоритма декодирования. Можно показать, что сочетание линейного преобразования, задаваемого матрицей
используется на последующих шагах алгоритма декодирования. Можно показать, что сочетание линейного преобразования, задаваемого матрицей 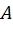 , физического канала передачи данных и декодера ПИ (при условии правильности промежуточных решений) может быть представлено как совокупность
, физического канала передачи данных и декодера ПИ (при условии правильности промежуточных решений) может быть представлено как совокупность 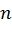 битовых подканалов различного качества, т.е. можно считать, что каждый
битовых подканалов различного качества, т.е. можно считать, что каждый 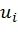 передается по i-му подканалу. Качество (например, пропускная способность, вероятность ошибки на бит) этих подканалов может быть проанализировано с помощью метода эволюции плотностей, состоящего в вычислении плотностей распределения логарифмических отношений правдоподобия, вычисляемых на различных этапах метода ПИ (раскрыт в работе I. Tal и A. Vardy "How to construct polar codes", опубликованной в журнале IEEE Transactions On Information Theory, том 59, номер 10, октябрь 2013 [2]) или его гауссовской аппроксимации (раскрыто в работе P. Trifonov "Efficient design and decoding of polar codes", опубликованной в журнале IEEE Transactions on Communications, том 60, номер 11, страницы 3221-3227, ноябрь 2012 [3]). Одним из возможных способов построения полярного кода длины
передается по i-му подканалу. Качество (например, пропускная способность, вероятность ошибки на бит) этих подканалов может быть проанализировано с помощью метода эволюции плотностей, состоящего в вычислении плотностей распределения логарифмических отношений правдоподобия, вычисляемых на различных этапах метода ПИ (раскрыт в работе I. Tal и A. Vardy "How to construct polar codes", опубликованной в журнале IEEE Transactions On Information Theory, том 59, номер 10, октябрь 2013 [2]) или его гауссовской аппроксимации (раскрыто в работе P. Trifonov "Efficient design and decoding of polar codes", опубликованной в журнале IEEE Transactions on Communications, том 60, номер 11, страницы 3221-3227, ноябрь 2012 [3]). Одним из возможных способов построения полярного кода длины 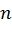 и размерности
и размерности 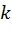 является выбор
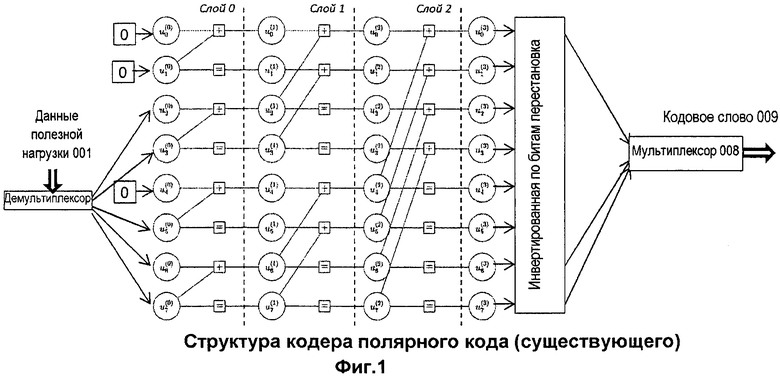
является выбор 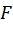 как множества индексов наихудших битовых подканалов. Фиг.1 иллюстрирует структуру кодера полярного кода. Операция кодирования разбивается на
как множества индексов наихудших битовых подканалов. Фиг.1 иллюстрирует структуру кодера полярного кода. Операция кодирования разбивается на 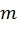 слоев. На слое
слоев. На слое  промежуточный вектор
промежуточный вектор 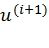 получается путем применения преобразования, задаваемого матрицей
получается путем применения преобразования, задаваемого матрицей 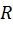 , к подвекторам
, к подвекторам  . Символы на слое 0 инициализируются символами полезных данных (для незамороженных символов) или нулями (замороженные символы). Кодовое слово получается на последнем слое.
. Символы на слое 0 инициализируются символами полезных данных (для незамороженных символов) или нулями (замороженные символы). Кодовое слово получается на последнем слое.
Заметим, что полярный код может быть представлен в виде дерева, листьями которого являются его кодовые слова, а пути из корня к листьям определяются возможными значениями символов 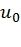 ,...,
,..., 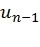 . Оптимальный декодер должен найти наиболее вероятный путь в дереве, соответствующий принятому вектору
. Оптимальный декодер должен найти наиболее вероятный путь в дереве, соответствующий принятому вектору 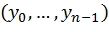 . Вышеописанный подход может быть использован для построения кодов, достигающих пропускной способности канала при
. Вышеописанный подход может быть использован для построения кодов, достигающих пропускной способности канала при 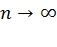 . Однако корректирующая способность полярных кодов средней длины при их декодировании методом ПИ оказывается достаточно плохой. В работе I. Tal и A. Vardy "List decoding of polar codes", опубликованной в материалах симпозиума IEEE International Symposium on Information Theory, 2011 [4], было показано, что списочное ПИ-декодирование позволяет решить эту проблему. Т.е. вместо принятия единственного решения относительно
. Однако корректирующая способность полярных кодов средней длины при их декодировании методом ПИ оказывается достаточно плохой. В работе I. Tal и A. Vardy "List decoding of polar codes", опубликованной в материалах симпозиума IEEE International Symposium on Information Theory, 2011 [4], было показано, что списочное ПИ-декодирование позволяет решить эту проблему. Т.е. вместо принятия единственного решения относительно 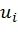 на каждом шаге ПИ-декодера могут быть рассмотрены два пути, соответствующие различным значениям незамороженного символа
на каждом шаге ПИ-декодера могут быть рассмотрены два пути, соответствующие различным значениям незамороженного символа 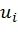 . В результате число путей
. В результате число путей 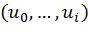 , отслеживаемых декодером, удваивается на каждом шаге
, отслеживаемых декодером, удваивается на каждом шаге 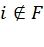 . Для предотвращения экспоненциального роста сложности и потребления памяти в [4] было предложено на каждом шаге сохранять не более чем
. Для предотвращения экспоненциального роста сложности и потребления памяти в [4] было предложено на каждом шаге сохранять не более чем  наиболее вероятных путей. Вероятность пути
наиболее вероятных путей. Вероятность пути 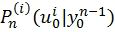 вычисляется согласно
вычисляется согласно
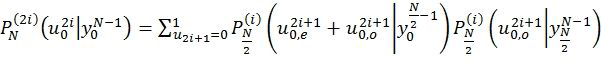 (1)
(1)
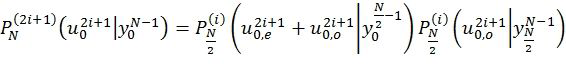 (2)
(2)
где 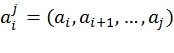 ,
, 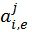 и
и 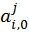 обозначают подвекторы
обозначают подвекторы 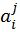 с четными и нечетными номерами компонентов, соответственно, и
с четными и нечетными номерами компонентов, соответственно, и 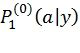 обозначает вероятность того, что был передан символ
обозначает вероятность того, что был передан символ 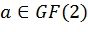 при условии того, что на выходе канала получен символ
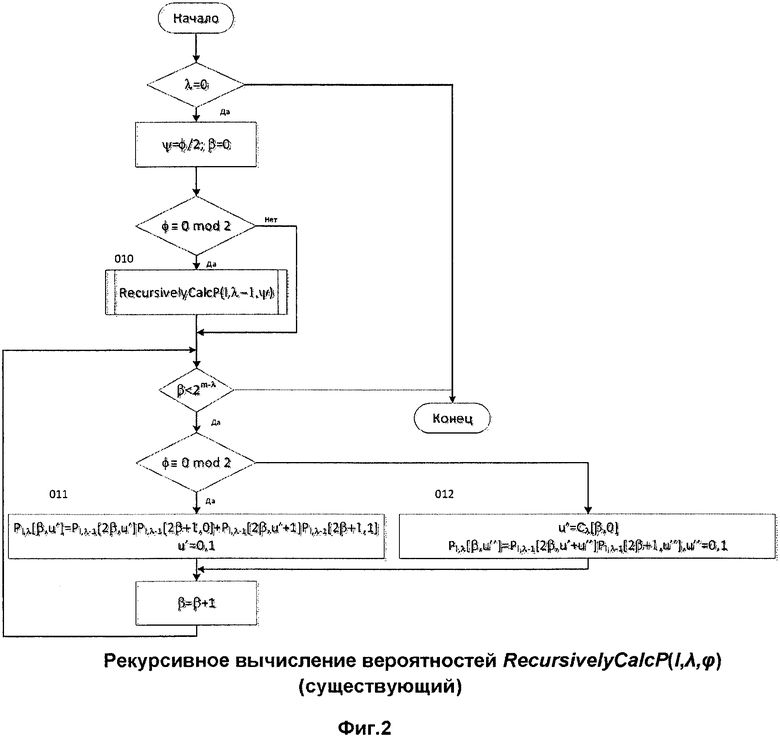
при условии того, что на выходе канала получен символ 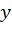 . Эффективный метод реализации этих вычислений был описан в [4]. Фиг.2 представляет блок-схему рекурсивной функции RecursivelyCalcP(l,λ,φ), которая вычисляет эти вероятности для l-го пути
. Эффективный метод реализации этих вычислений был описан в [4]. Фиг.2 представляет блок-схему рекурсивной функции RecursivelyCalcP(l,λ,φ), которая вычисляет эти вероятности для l-го пути 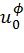 , для случая
, для случая 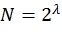 , в соответствии с [4]. Заметим, что для четных
, в соответствии с [4]. Заметим, что для четных 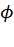 она производит рекурсивный вызов для нахождения значений, фигурирующих в правой части вышеприведенных уравнений. Непосредственные вычисления производятся в блоках, которые реализуют уравнения (1) и (2). Результаты сохраняются в переменных
она производит рекурсивный вызов для нахождения значений, фигурирующих в правой части вышеприведенных уравнений. Непосредственные вычисления производятся в блоках, которые реализуют уравнения (1) и (2). Результаты сохраняются в переменных 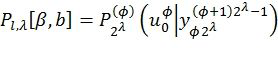 , где
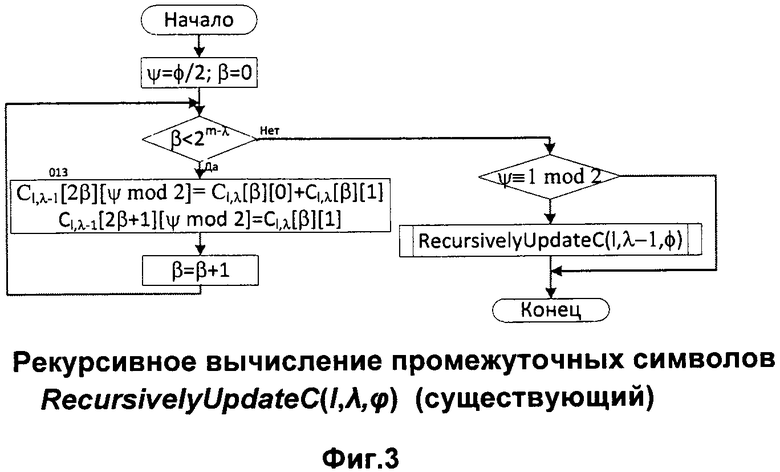
, где 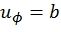 . Кроме того, декодер последовательного исключения должен хранить значения промежуточных символов, соответствующих каждому пути. Фиг.3 представляет блок-схему рекурсивной функции RecursivelyCalcC(l,λ,φ), решающей эту задачу в соответствии с [4]. Для l-го пути
. Кроме того, декодер последовательного исключения должен хранить значения промежуточных символов, соответствующих каждому пути. Фиг.3 представляет блок-схему рекурсивной функции RecursivelyCalcC(l,λ,φ), решающей эту задачу в соответствии с [4]. Для l-го пути 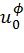 посредством блок-схемы находят значения
посредством блок-схемы находят значения 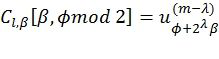 , которые используются при вычислении уравнений (1) и (2). Вычисления производятся в блоке, который соответствует структуре кодера, показанной на фиг.1.
, которые используются при вычислении уравнений (1) и (2). Вычисления производятся в блоке, который соответствует структуре кодера, показанной на фиг.1.
Описанный подход позволяет значительно повысить корректирующую способность полярных кодов в области малых отношений сигнал/шум. Вместе с тем, классические полярные коды демонстрируют эффект "насыщения" вероятности ошибки на достаточно высоком уровне, т.к. их минимальное расстояние Хэмминга равно 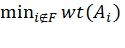 , где
, где 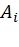 обозначает i-ю строку матрицы
обозначает i-ю строку матрицы 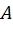 , и
, и 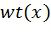 - вес Хемминга вектора
- вес Хемминга вектора  . В [4] было предложено закодировать данные кодом CRC обнаружения ошибок перед кодированием полярным кодом. Тогда из L путей в кодовом дереве, найденных с помощью вышеописанного алгоритма, можно выбрать те, которые имеют правильную контрольную сумму CRC. Было экспериментально показано, что этот подход обеспечивает достаточно хорошую корректирующую способность, хотя какие-либо нетривиальные оценки минимального расстояния найдены не были.
. В [4] было предложено закодировать данные кодом CRC обнаружения ошибок перед кодированием полярным кодом. Тогда из L путей в кодовом дереве, найденных с помощью вышеописанного алгоритма, можно выбрать те, которые имеют правильную контрольную сумму CRC. Было экспериментально показано, что этот подход обеспечивает достаточно хорошую корректирующую способность, хотя какие-либо нетривиальные оценки минимального расстояния найдены не были.
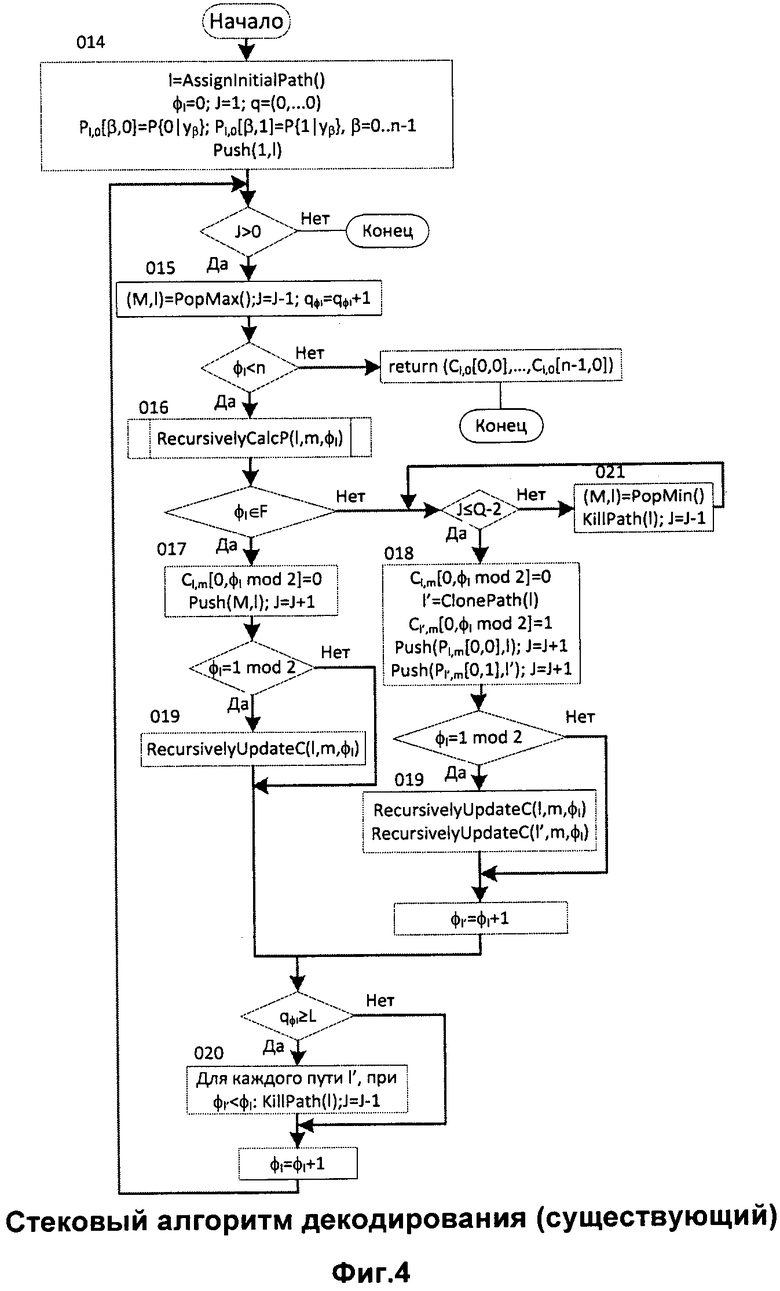
Для снижения сложности декодирования в работе K. Niu и K. Chen "CRC-aided decoding of polar codes", опубликованной в IEEE Communications Letters, том 16, номер 10, октябрь 2012 [5], было предложено выбирать на каждом шаге декодера ПИ для дальнейшего раскрытия наиболее вероятный путь, т.е. путь с наибольшим значением 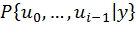 . Таким образом, декодер должен поддерживать стек (на самом деле приоритетную очередь), содержащий пути различной длины, так чтобы была возможность эффективного выбора наиболее вероятного из них. Этот подход (стековое декодирование ПИ) обеспечивает 2-3-кратное снижение сложности по сравнению со списочным декодированием ПИ без какой-либо потери корректирующей способности. Фиг.4 иллюстрирует блок-схему алгоритма, реализующего этот подход. Алгоритм использует структуры данных и вспомогательные функции, предложенные в [4]. Он использует стек (на самом деле, приоритетную очередь), поддерживающий операции Push(s,l), которая сохраняет в стеке целое число l вместе с его метрикой s, PopMax() и PopMin(), которые извлекают из стека элементы с наибольшей и наименьшей метриками соответственно. Затем создается начальный путь, идентифицируемый целым числом l. Для этого пути вычисляются вероятности символов кодового слова с помощью функции переходных вероятностей канала
. Таким образом, декодер должен поддерживать стек (на самом деле приоритетную очередь), содержащий пути различной длины, так чтобы была возможность эффективного выбора наиболее вероятного из них. Этот подход (стековое декодирование ПИ) обеспечивает 2-3-кратное снижение сложности по сравнению со списочным декодированием ПИ без какой-либо потери корректирующей способности. Фиг.4 иллюстрирует блок-схему алгоритма, реализующего этот подход. Алгоритм использует структуры данных и вспомогательные функции, предложенные в [4]. Он использует стек (на самом деле, приоритетную очередь), поддерживающий операции Push(s,l), которая сохраняет в стеке целое число l вместе с его метрикой s, PopMax() и PopMin(), которые извлекают из стека элементы с наибольшей и наименьшей метриками соответственно. Затем создается начальный путь, идентифицируемый целым числом l. Для этого пути вычисляются вероятности символов кодового слова с помощью функции переходных вероятностей канала 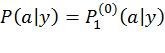 . Затем этот путь помещается в стек. На каждой итерации алгоритма наиболее вероятный путь l, соответствующий некоторой последовательности символов
. Затем этот путь помещается в стек. На каждой итерации алгоритма наиболее вероятный путь l, соответствующий некоторой последовательности символов 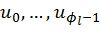 , где
, где 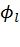 - фаза пути, извлекается из стека вместе со своей метрикой M. Затем вычисляются вероятности
- фаза пути, извлекается из стека вместе со своей метрикой M. Затем вычисляются вероятности 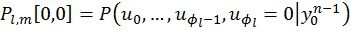 и
и 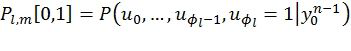 с использованием функции RecursivelyCalcP(l,m,φl). Если символ
с использованием функции RecursivelyCalcP(l,m,φl). Если символ 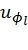 заморожен, его значение полагается равным 0, а идентификатор l помещается в стек с прежним значением метрики M. В противном случае, путь клонируется (т.е. соответствующие промежуточные данные выборочно дублируются, как описано в [4]) в новый путь, идентифицируемый числом l′. Исходный путь соответствует
заморожен, его значение полагается равным 0, а идентификатор l помещается в стек с прежним значением метрики M. В противном случае, путь клонируется (т.е. соответствующие промежуточные данные выборочно дублируются, как описано в [4]) в новый путь, идентифицируемый числом l′. Исходный путь соответствует 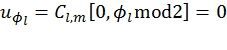 , а клонированный -
, а клонированный - 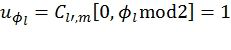 . Эти пути помещаются в стек вместе с соответствующими вероятностями. Перед этой операцией проверяется, не превысит ли число путей в стеке J его максимальной емкости Q после операции клонирования. В этом случае наименее вероятные пути удаляются из стека. В обоих случаях, если
. Эти пути помещаются в стек вместе с соответствующими вероятностями. Перед этой операцией проверяется, не превысит ли число путей в стеке J его максимальной емкости Q после операции клонирования. В этом случае наименее вероятные пути удаляются из стека. В обоих случаях, если 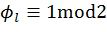 , значения промежуточных символов для путей, помещенных в стек, обновляются с помощью функции RecursivelyUpdateC. Кроме того, если число
, значения промежуточных символов для путей, помещенных в стек, обновляются с помощью функции RecursivelyUpdateC. Кроме того, если число 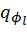 возврата декодера на фазу
возврата декодера на фазу 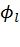 превышает некоторый порог L, все пути короче
превышает некоторый порог L, все пути короче 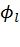 удаляются с целью недопущения обхода декодером коротких неправильных путей. Основным недостатком этого подхода является то, что декодер вынужден сравнивать вероятности
удаляются с целью недопущения обхода декодером коротких неправильных путей. Основным недостатком этого подхода является то, что декодер вынужден сравнивать вероятности 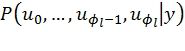 путей различной длины. Можно заметить, что
путей различной длины. Можно заметить, что 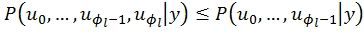 . Таким образом, вероятность длинного правильного пути может оказаться меньше вероятностей коротких неправильных путей. В результате декодеру часто приходится выполнять переключения между правильным и неправильными путями, производя таким образом большой объем бесполезных вычислений.
. Таким образом, вероятность длинного правильного пути может оказаться меньше вероятностей коротких неправильных путей. В результате декодеру часто приходится выполнять переключения между правильным и неправильными путями, производя таким образом большой объем бесполезных вычислений.
Еще одна реализация этого подхода в случае полярных кодов с внешним CRC была представлена в работе B. Li, H. Shen, D. Tse "An Adaptive Successive Cancellation List Decoder for Polar Codes with Cyclic Redundancy Check", опубликованной в IEEE Communications Letters, 16(12), декабрь 2012 [6], и в работе B. Li, H. Shen "Decoding method and decoding apparatus for polar code concatenated with cyclic redundancy check, patent application" (публикация WO2013107140) [7]. Она сводится к применению алгоритма Тала-Варди списочного декодирования с некоторым размером списка L, поиску среди найденных кодовых слов слова с правильным значением CRC и, в случае отсутствия такового, повторному запуску списочного декодера с удвоенным размером списка. Эти действия повторяются до тех пор, пока не будет найдено кодовое слово с правильным значением CRC или размер списка не превысит заданную величину. Основным недостатком этого подхода является его высокая вычислительная сложность, которая пропорциональна максимальному размеру списка.
Проблема декодирования полярных кодов была также рассмотрена в работе W. Gross, G. Sarkis, A. Raymond, C. Leroux, I. Tal, A. Vardy "Methods and Systems for Decoding Polar Codes" (US20130117344) [8], где были предложены некоторые методы снижения сложности несписочного декодера ПИ. Они, однако, не обеспечивают повышения корректирующей способности. Метод кодирования данных, предлагаемый в настоящей заявке, обеспечивает намного меньшую вероятность ошибки декодирования на кодовое слово по сравнению с [8].
Метод, предлагаемый в настоящей патентной заявке, позволяет получить регулярную структуру кодера и декодера, как и многие современные конструкции LDPC кодов, например, описанные в патенте RU2395902 авторов Т. Ричардсон, Х. Цзинь "Способы и устройство LDPC-кодирования" [9]. Однако, корректирующая способность предложенной кодовой конструкции оказывается намного лучше.
Сущность изобретения
Помехоустойчивое кодирование широко используется в современных системах передачи и хранения информации. Предметом изобретения является новая конструкция корректирующих кодов и соответствующие способы кодирования и декодирования данных. Предлагаемые коды являются обобщением недавно предложенных полярных кодов. Предлагаемый подход позволяет решить проблему малого минимального расстояния, из-за которой корректирующая способность существующих полярных кодов оказывается значительно хуже, чем у LDPC и турбокодов. В результате, предлагаемые коды обеспечивают меньшую вероятность ошибки в области «водопада» и более низкий уровень «насыщения» вероятности ошибки, чем LDPC и турбокоды. Предлагаемый способ декодирования основан на стековом алгоритме последовательного исключения и улучшает его за счет использования методов ориентированного поиска. Он также учитывает структуру предложенных скрученных полярных кодов. Использование данного способа декодирования в случае скрученных полярных кодов обеспечивает некоторое снижение сложности декодирования по сравнению с классическими полярными кодами.
В одном аспекте изобретения раскрыт способ кодирования данных, включающий в себя этапы, на которых: предварительно кодируют, посредством модуля предварительного кодирования, данные, представленные в виде k-мерного двоичного вектора x, причем кодирование состоит в вычислении u(0)=xW, где W - матрица размерности k×2m и m - параметр кода; осуществляют, посредством модуля предварительного кодирования, m-слойное скрученное поляризующее преобразование вектора u(0), причем i-й слой преобразования состоит в разбиении вектора u(i-1) на 2m-1 подвекторов длины 2, в умножении этих подвекторов на матрицу 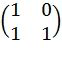 , в слиянии полученных подвекторов в один вектор размерности 2m и в перестановке элементов полученного вектора, результатом чего является вектор u(i), в результате на m-м слое получают вектор u(m), причем перестановки выбирают из общей аффинной группы; получают посредством мультиплексора кодирующего устройства закодированные посредством скрученного полярного кода данные путем мультиплексирования элементов вектора u(m). Использование матрицы W позволяет представить некоторые элементы (символы) вектора u(0), число которых равно n-k, как линейные функции от других его элементов (символов). Такие символы называются динамически замороженными. Отметим, что классические полярные коды являются частным случаем этой конструкции, в которой все эти линейные функции тождественно равны 0 и соответствующие символы называются (статически) замороженными.
, в слиянии полученных подвекторов в один вектор размерности 2m и в перестановке элементов полученного вектора, результатом чего является вектор u(i), в результате на m-м слое получают вектор u(m), причем перестановки выбирают из общей аффинной группы; получают посредством мультиплексора кодирующего устройства закодированные посредством скрученного полярного кода данные путем мультиплексирования элементов вектора u(m). Использование матрицы W позволяет представить некоторые элементы (символы) вектора u(0), число которых равно n-k, как линейные функции от других его элементов (символов). Такие символы называются динамически замороженными. Отметим, что классические полярные коды являются частным случаем этой конструкции, в которой все эти линейные функции тождественно равны 0 и соответствующие символы называются (статически) замороженными.
В дополнительных аспектах раскрыто, что матрицу W выбирают таким образом, что получаемые кодовые слова являются кодовыми словами базового расширенного кода БЧХ (Боуза-Чоудхури-Хоквингема); перестановки задают для подвекторов вектора u(i), состоящих из 2i смежных элементов, путем индексирования элементов этих подвекторов двоичными векторами длины i и задания базисов i-мерных линейных пространств для каждого из этих векторов, так что выходной индекс получается как произведение входного индекса на матрицу, соответствующую этому базису.
В другом аспекте изобретения раскрыт способ декодирования данных, закодированных в соответствии с вышеуказанным способом кодирования, причем декодированные данные получают в декодирующем устройстве, используя метод последовательного исключения, причем вычисление вероятностей путей в кодовом дереве выполняется рекурсивно в m слоев, и вероятности на слое i-1 вычисляются из переставленных вероятностей на слое i, причем используемая перестановка та же, что использована в вышеупомянутом способе кодирования, и декодирующее устройство выбирает пути с учетом значений динамически замороженных символов.
В дополнительных аспектах раскрыто, что значения динамически замороженных символов получают из уравнения 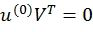 , где
, где 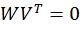 ; матрица V имеет такой вид, что не более чем одна строка начинается в каждом из столбцов и не более чем одна строка заканчивается в каждом столбце; значения динамически замороженных символов находят с использованием символьных выражений из промежуточных данных декодирующего устройства; декодирующее устройство хранит несколько путей, соответствующих последовательностям
; матрица V имеет такой вид, что не более чем одна строка начинается в каждом из столбцов и не более чем одна строка заканчивается в каждом столбце; значения динамически замороженных символов находят с использованием символьных выражений из промежуточных данных декодирующего устройства; декодирующее устройство хранит несколько путей, соответствующих последовательностям 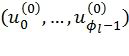 , и итеративно выбирает для расширения один из них, чтобы получить один или два пути
, и итеративно выбирает для расширения один из них, чтобы получить один или два пути 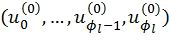 ,
, 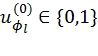 , так что выполняются ограничения динамической заморозки символов, причем выбираемый путь соответствует наибольшему значению
, так что выполняются ограничения динамической заморозки символов, причем выбираемый путь соответствует наибольшему значению 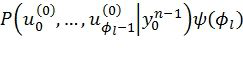 , где
, где 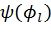 - эвристическая функция, определяемая выражением
- эвристическая функция, определяемая выражением 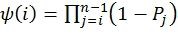 , причем
, причем 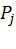 - вероятность ошибки на бит в j-м битовом подканале, задаваемом поляризующим преобразованием.
- вероятность ошибки на бит в j-м битовом подканале, задаваемом поляризующим преобразованием.
В другом аспекте раскрыто кодирующее устройство, содержащее: модуль предварительного кодирования данных, представленных в виде k-мерного двоичного вектора x, выполненный с возможностью вычисления u(0)=xW, где W - матрица размерности k×2m и m - параметр кода; модуль, выполненный с возможностью осуществления логической функции «исключающее или», и модуль, выполненный с возможностью передачи данных без изменения, которые соединены в m слоев так, что обеспечена возможность реализовать m-слойное скрученное поляризующее преобразование вектора u(0) и получать вектор u(m), причем i-й слой преобразования состоит в разбиении вектора u(i-1) на 2m-1 подвекторов длины 2, в умножении этих подвекторов на матрицу 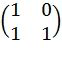 , в слиянии полученных подвекторов в один вектор размерности 2m и в перестановке элементов полученного вектора, результатом чего является вектор u(i), причем перестановки выбирают из общей аффинной группы; мультиплексор, выполненный с возможностью получения закодированного кодового слова скрученного кода из вектора u(m), полученного на m-м слое преобразования из вектора u(i).
, в слиянии полученных подвекторов в один вектор размерности 2m и в перестановке элементов полученного вектора, результатом чего является вектор u(i), причем перестановки выбирают из общей аффинной группы; мультиплексор, выполненный с возможностью получения закодированного кодового слова скрученного кода из вектора u(m), полученного на m-м слое преобразования из вектора u(i).
В другом аспекте раскрыто декодирующее устройство, содержащее: модуль вычисления вероятностей, выполненный с возможностью вычисления вероятностей промежуточных символов на m слоях, причем вероятности на (i-1)-м слое получаются из переставленных вероятностей на слое i, причем используемая перестановка та же, что и в вышеупомянутом способе кодирования, причем модуль вычисления вероятностей передает вычисленную вероятность в модуль последовательной обработки; модуль последовательной обработки, выполненный с возможностью итеративно строить пути в кодовом дереве посредством извлечения пути с наибольшей метрикой из стека, с возможностью расширения пути, с возможностью сохранения полученных путей в стеке и выполненный с возможностью определения значений декодированных символов; стек, выполненный с возможностью хранения идентификаторов путей и их метрики, соединенный с возможностью обмена данными с модулем последовательной обработки; модуль обновления значений промежуточных символов, выполненный с возможностью рекурсивно вычислять значения промежуточных символов на m слоях таким же способом, что и вышеуказанное кодирующее устройство, причем модуль обновления значений промежуточных символов выполнен с возможностью передавать вычисленные значения промежуточных символов на запоминающее устройство; запоминающее устройство, выполненное с возможностью хранения значений промежуточных символов u(i) и с возможностью передачи значений промежуточных символов на модуль последовательной обработки и на модуль вычисления вероятностей.
Предлагаемое изобретение представляет собой кодовую конструкцию и соответствующие способы и устройства кодирования и декодирования, которые обеспечивают большую корректирующую способность и меньшую сложность декодирования по сравнению с классическими полярными кодами и их улучшениями, рассмотренными выше. Численные результаты показывают, что скрученные полярные коды обеспечивают энергетический выигрыш до 0,5 дБ по сравнению с LDPC и турбокодами и лучшую корректирующую способность по сравнению с нескрученными и классическими полярными кодами с внешним CRC. Скрученные полярные коды позволяют также понизить уровень, на котором происходит «насыщение» вероятности ошибки, явление, наблюдаемое в случае турбокодов и нескрученных полярных кодов. Кроме того, предлагаемый метод декодирования использует эвристическую функцию, использование которой позволяет значительно снизить число итераций, выполняемых стековым алгоритмом декодирования.
Технический результат, достигаемый настоящим изобретением, заключается в повышении быстродействия кодирования/декодирования за счет снижения числа осуществляемых итераций.
Краткое описание чертежей
Фиг.1. Структура кодера полярного кода (существующего).
Фиг.2. Рекурсивное вычисление вероятностей RecursivelyCalcP(l,λ,φ) (существующий).
Фиг.3. Рекурсивное вычисление промежуточных символов RecursivelyUpdateC(l,λ,φ) (существующий).
Фиг.4. Стековый алгоритм декодирования (существующий).
Фиг.5. Кодер скрученного полярного кода.
Фиг.6. Система цифровой связи.
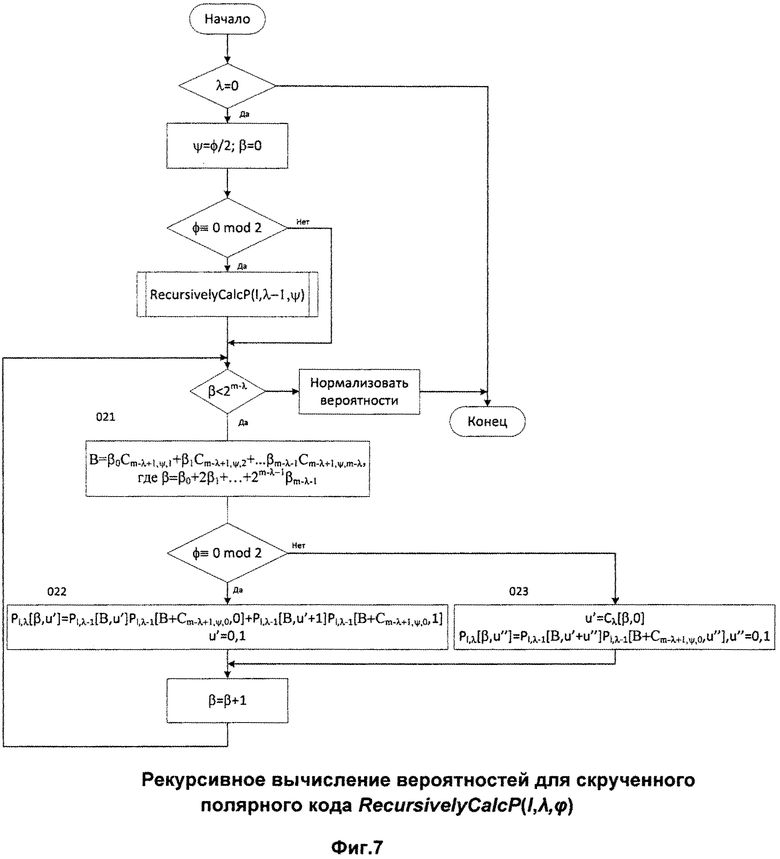
Фиг.7. Рекурсивное вычисление вероятностей для скрученного полярного кода RecursivelyCalcP(l,λ,φ).
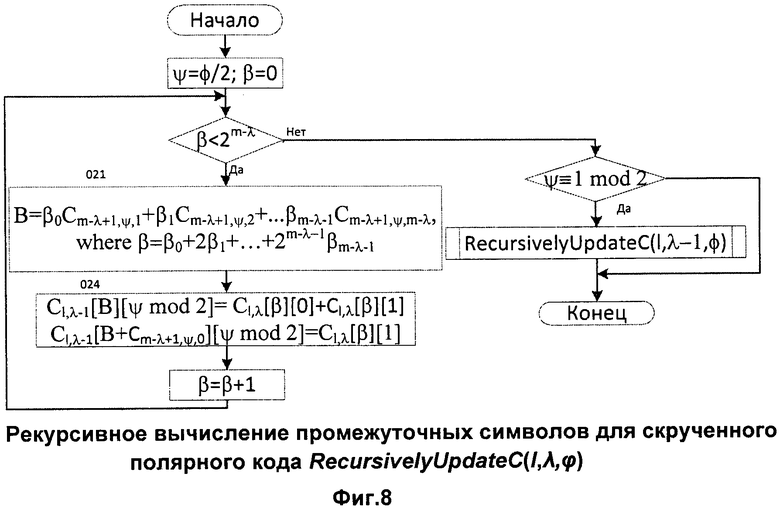
Фиг.8. Рекурсивное вычисление значений промежуточных символов для скрученного полярного кода RecursivelyUpdateC(l,λ,φ).
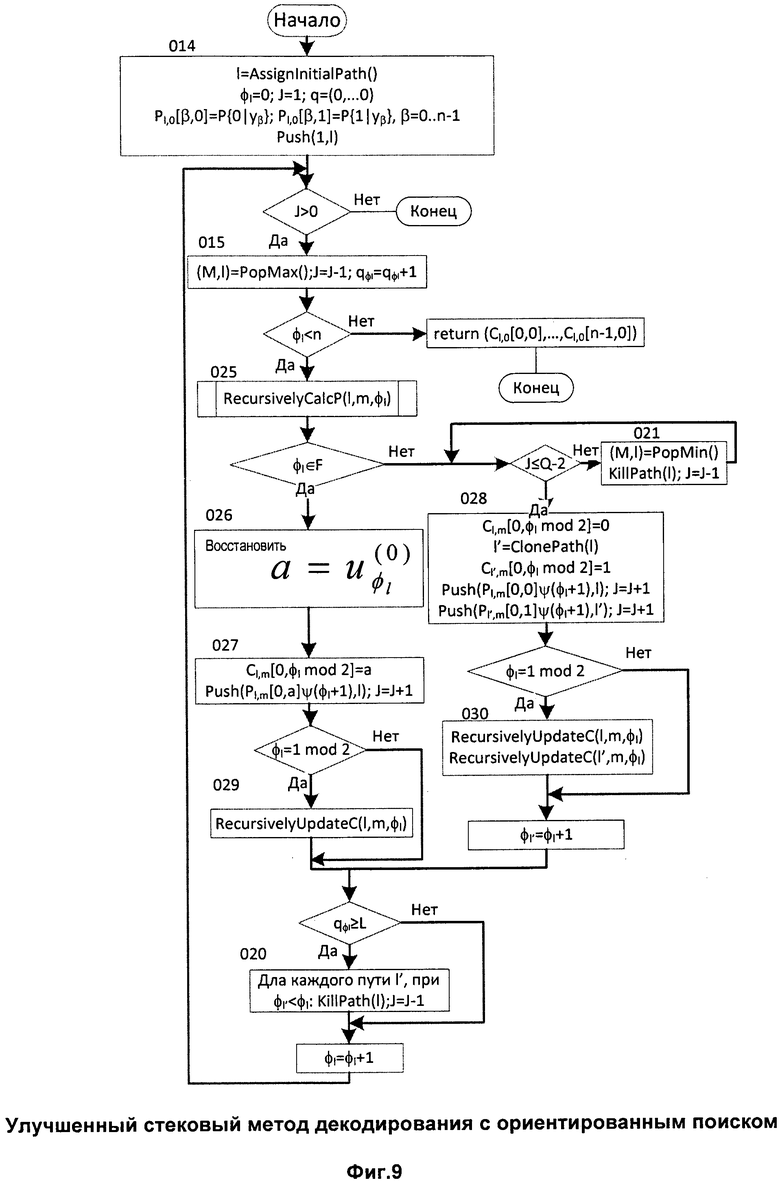
Фиг.9. Улучшенный стековый метод декодирования с ориентированным поиском.
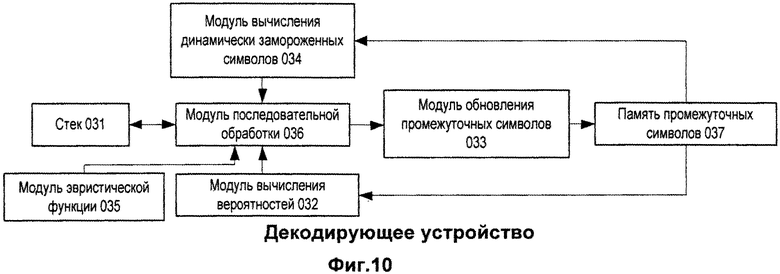
Фиг.10. Декодирующее устройство.
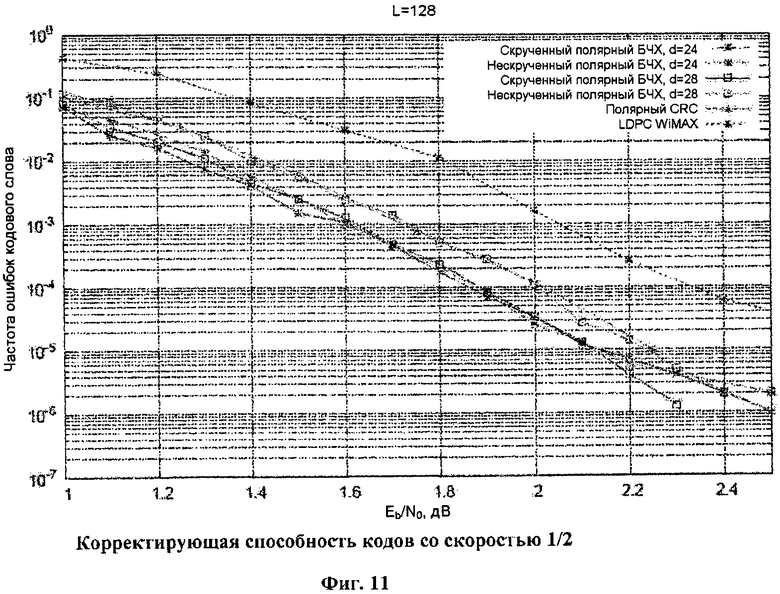
Фиг.11. Корректирующая способность кодов со скоростью 1/2.
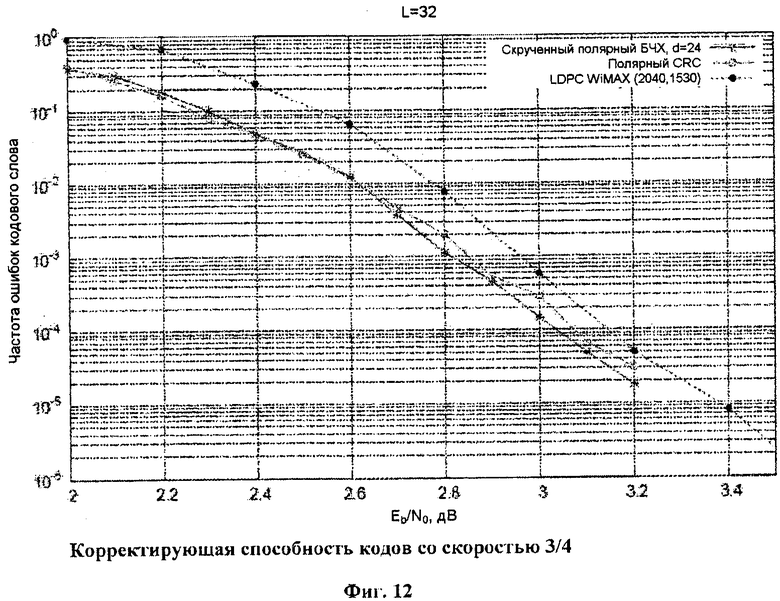
Фиг.12. Корректирующая способность кодов со скоростью 3/4.
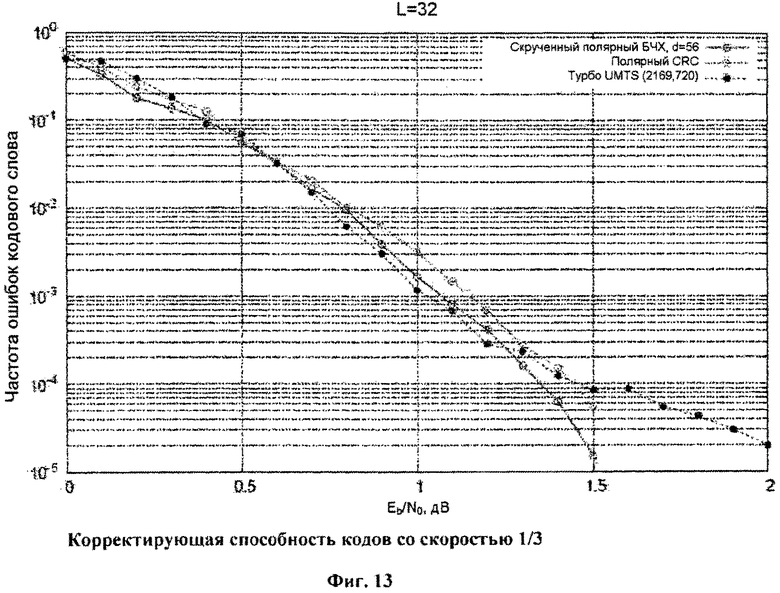
Фиг.13. Корректирующая способность кодов со скоростью 1/3.
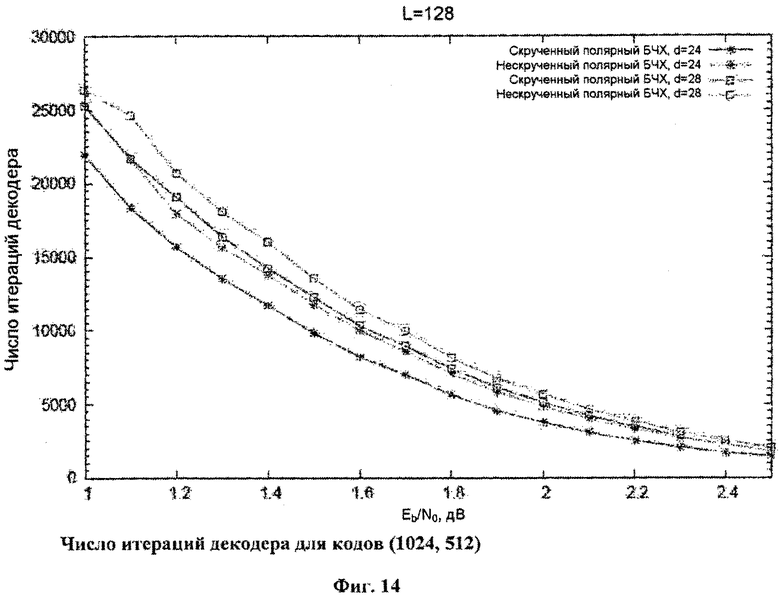
Фиг.14. Число итераций декодера для кодов (1024, 512).
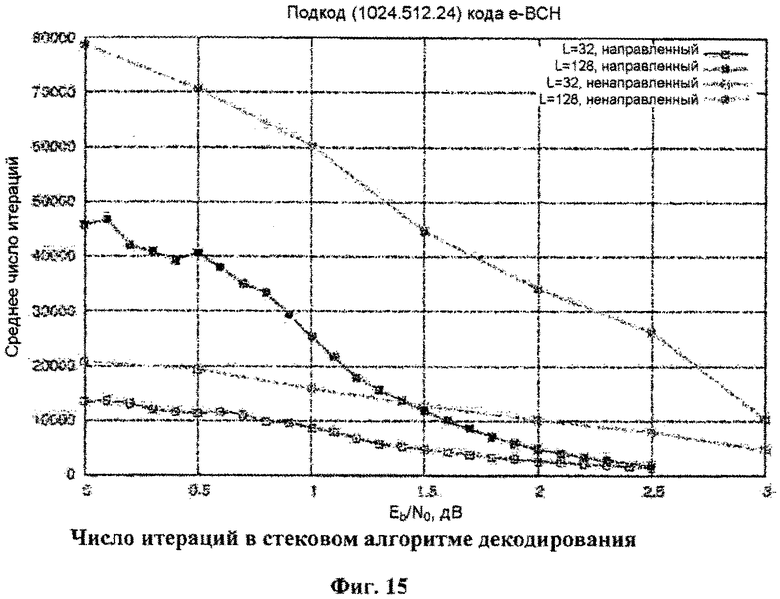
Фиг.15. Число итераций в стековом алгоритме декодирования.
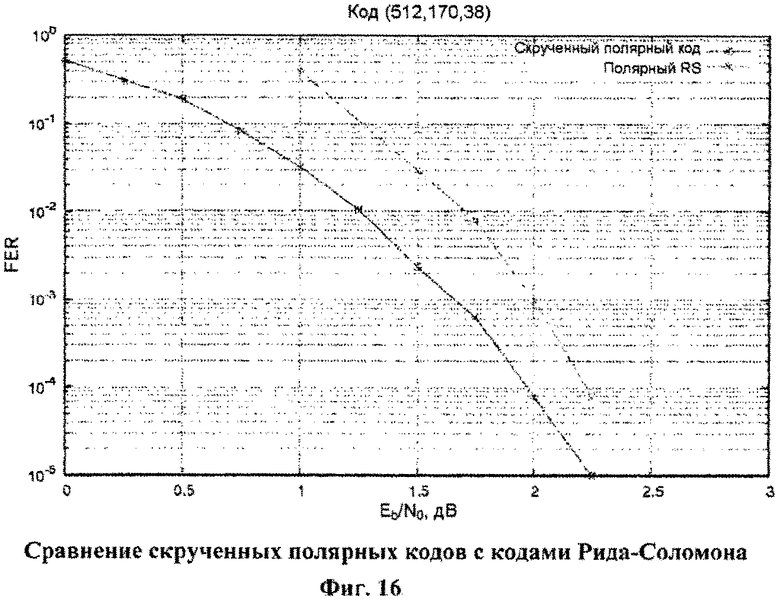
Фиг.16. Сравнение скрученных полярных и каскадных кодов с внешними кодами Рида-Соломона и внутренними полярными.
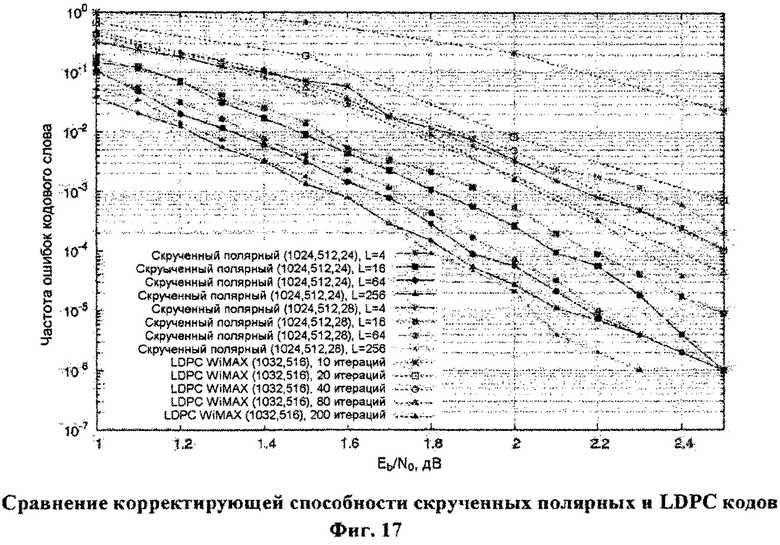
Фиг.17. Сравнение корректирующей способности скрученных полярных и LDPC кодов.
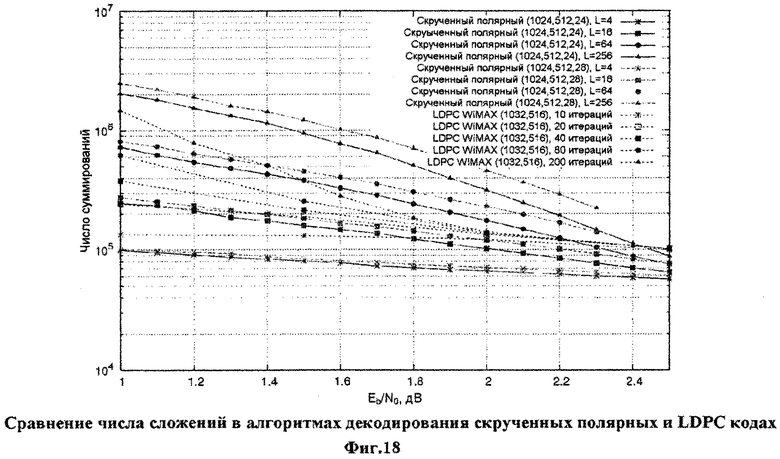
Фиг.18. Сравнение числа сложений в алгоритмах декодирования скрученных полярных и LDPC кодов.
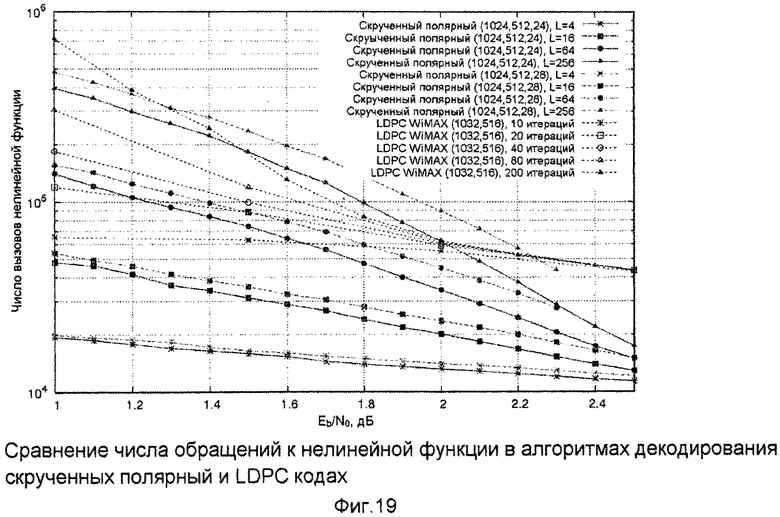
Фиг.19. Сравнение числа обращений к нелинейной функции в алгоритмах декодирования скрученных полярных и LDPC кодов.
Варианты осуществления изобретения
Основной идеей предлагаемого подхода, которая отражена в соответствующих методах кодирования и декодирования, является введение перестановки промежуточных символов, возникающих в поляризационном преобразовании, перед их передачей на следующий слой поляризационного преобразования. Это позволяет произвести динамическое замораживание символов, обеспечивающее достижение достаточно большого минимального расстояния кода, причем все достаточно плохие битовые подканалы замораживаются. Ограничения динамической заморозки могут быть получены с использованием некоторого родительского расширенного кода БЧХ (Боуза-Чоудхури-Хоквингема), а перестановки выбираются из общей аффинной группы, которая является группой автоморфизмов подкодов Рида-Маллера этого кода (см. работу авторов F. J. MacWilliams и N. J. A. Sloane «The Theory of Error-Correcting Codes», 1977 [10]). Более конкретно, элементы подблоков промежуточных векторов поляризующего преобразования индексируются двоичными векторами, которые могут эквивалентно рассматриваться как целые числа. Для каждого слоя и каждого подблока указывается базис Ci,j,0,…,Ci,j,i-1 соответствующего l-мерного линейного подпространства, так что выходной индекс x вычисляется из входного 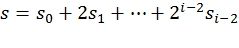 ,
, 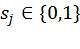 как
как 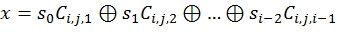 .
.
Это задает перестановку элементов вектора. Например, матрица 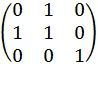 соответствует перестановке
соответствует перестановке  ,
, 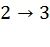 ,
, 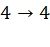 ,
, 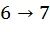 ,
, 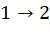 ,
, 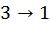 ,
, 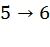 ,
,  . Формально, предлагаемый метод кодирования для кода длины n=2m состоит из следующих шагов:
. Формально, предлагаемый метод кодирования для кода длины n=2m состоит из следующих шагов:
1. Построить двоичный вектор u(0) так, что выполняются динамические ограничения заморозки, задаваемые некоторой матрицей V, т.е. 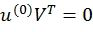 .
.
2. Пусть i=1.
3. Пусть 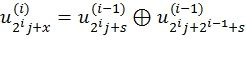 ,
, 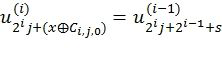 ,
, 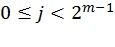 ,
, 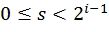 , где
, где 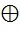 обозначает побитовую операцию «исключающее или»,
обозначает побитовую операцию «исключающее или», 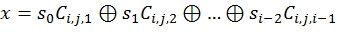 ,
, 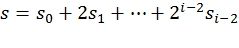 ,
, 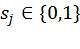 , и
, и 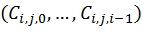 - множество линейно независимых двоичных векторов длины i, которые могут эквивалентно рассматриваться как целые числа.
- множество линейно независимых двоичных векторов длины i, которые могут эквивалентно рассматриваться как целые числа.
4. Пусть i=i+1. Если i≤m, перейти к шагу 3.
Можно заметить, что структура кодера, описанная на шаге 3, схожа со структурой, используемой в кодере классических полярных кодов Арикана. Заметим, что последние получаются путем выбора 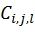 , равным l-му единичному вектору и использованию исключительно статически замороженных символов. Это позволяет воспользоваться декодером ПИ и его модификациями с учетом предложенных изменений. В частности, возможно использование эффективной реализации списочного декодера ПИ, описанного в [4], или его стекового варианта (фиг.4). Т.к. предлагаемая конструкция использует динамически замороженные символы, при декодировании возникает необходимость восстановления их значений на шагах
, равным l-му единичному вектору и использованию исключительно статически замороженных символов. Это позволяет воспользоваться декодером ПИ и его модификациями с учетом предложенных изменений. В частности, возможно использование эффективной реализации списочного декодера ПИ, описанного в [4], или его стекового варианта (фиг.4). Т.к. предлагаемая конструкция использует динамически замороженные символы, при декодировании возникает необходимость восстановления их значений на шагах 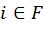 , используя значения
, используя значения 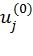 , j<i. Однако реализация, предложенная в [4], не сохраняет эти значения. В связи с этим, предлагается метод их восстановления из промежуточных переменных алгоритма, предложенного в [4].
, j<i. Однако реализация, предложенная в [4], не сохраняет эти значения. В связи с этим, предлагается метод их восстановления из промежуточных переменных алгоритма, предложенного в [4].
Пусть A′ - n×n матриц, соответствующая преобразованию, задаваемому шагами 2-4 вышеописанного алгоритма. Для того чтобы обеспечить достаточно большое минимальное расстояние получаемого кода, может быть наложено дополнительное ограничение, состоящее в том, что получаемые вышеописанным образом кодовые слова u(0)A′ принадлежат некоторому другому коду (в настоящей заявке полагается, что этот код является расширенным кодом БЧХ) с проверочной матрицей H, т.е. u(0)A′HT=0. Тогда матрица V, используемая на шаге 1 алгоритма кодирования, может быть получена как VT=A′HTQ, где Q - обратимая матрица. Предлагается выбирать матрицу Q таким образом, чтобы сложность восстановления промежуточных символов при обработке ограничений динамической заморозки была минимальной.
Для снижения сложности стекового алгоритма декодирования предлагается использование величин 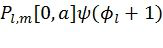 вместо
вместо 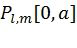 ,
, 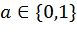 в качестве метрик путей, где
в качестве метрик путей, где 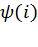 - эвристическая функция, характеризующая среднюю вероятность правильных решений после фазы i. Это позволяет декодеру избежать частых переключений между короткими и длинными путями, что обеспечивает снижение общего числа итераций.
- эвристическая функция, характеризующая среднюю вероятность правильных решений после фазы i. Это позволяет декодеру избежать частых переключений между короткими и длинными путями, что обеспечивает снижение общего числа итераций.
Фиг.5 иллюстрирует предлагаемый метод кодирования для m=4. Кодируемые данные 001, представленные в виде двоичного вектора x длины k, подаются на вход прекодера 002, который вычисляет u(0)=xW, так что 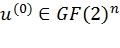 , n=2m, u(0)VT=0, где W и V - двоичные матрицы, удовлетворяющие WVT=0. Полученный начальный вектор 003, обозначаемый u(0), подвергается скрученному поляризующему преобразованию. Оно строится путем рекурсивного применения преобразования, задаваемого
, n=2m, u(0)VT=0, где W и V - двоичные матрицы, удовлетворяющие WVT=0. Полученный начальный вектор 003, обозначаемый u(0), подвергается скрученному поляризующему преобразованию. Оно строится путем рекурсивного применения преобразования, задаваемого 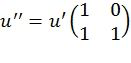 . Это преобразование реализуется с помощью узла 004 «исключающее или», который вычисляет сумму по модулю 2 входных значений, и проходного узла 005, который выдает входное значение без изменений. Это дает вектор u(1), который обрабатывается далее аналогичным образом. Модуль, выполненный с возможностью осуществления функции исключающее ИЛИ, и проходной модуль (модуль выполненный с возможностью передачи данных без изменения) организованы в m слоев. На слое i промежуточный вектор u(i+1) представляется как 2m-i-1 подвекторов длины 2i+1. Перед передачей промежуточного вектора на следующий слой его компоненты переставляются, причем компоненты различных подвекторов могут переставляться различным образом. Вектор c=u(4), полученный таким образом, обозначается заключительным вектором 007. Его элементы мультиплексируются в кодовое слово 009 скрученного полярного кода. Это кодовое слово может быть далее передано по каналу связи или сохранено на записывающем устройстве. Отметим, что выполнение перестановки на последнем слое не является обязательным. Эта перестановка показана здесь исключительно для иллюстрации конкретной перестановочной конструкции, описываемой ниже.
. Это преобразование реализуется с помощью узла 004 «исключающее или», который вычисляет сумму по модулю 2 входных значений, и проходного узла 005, который выдает входное значение без изменений. Это дает вектор u(1), который обрабатывается далее аналогичным образом. Модуль, выполненный с возможностью осуществления функции исключающее ИЛИ, и проходной модуль (модуль выполненный с возможностью передачи данных без изменения) организованы в m слоев. На слое i промежуточный вектор u(i+1) представляется как 2m-i-1 подвекторов длины 2i+1. Перед передачей промежуточного вектора на следующий слой его компоненты переставляются, причем компоненты различных подвекторов могут переставляться различным образом. Вектор c=u(4), полученный таким образом, обозначается заключительным вектором 007. Его элементы мультиплексируются в кодовое слово 009 скрученного полярного кода. Это кодовое слово может быть далее передано по каналу связи или сохранено на записывающем устройстве. Отметим, что выполнение перестановки на последнем слое не является обязательным. Эта перестановка показана здесь исключительно для иллюстрации конкретной перестановочной конструкции, описываемой ниже.
Следует понимать, что скрученный полярный код является линейным блоковым кодом. Вышеописанный метод кодирования соответствует вычислению
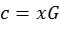 (3)
(3)
где G=WA′ - k×n некоторая порождающая матрица кода и A′ задает скрученное поляризующее преобразование. Но тот же самый код может быть получен путем замены в уравнении (3) G на G′=QG, где Q - обратимая k×k матрица. В частности, в некоторых приложениях целесообразно использовать систематическое кодирование, т.е. выбрать G′=(I|S)P, где I - единичная матрица, S - некоторая k×(n-k) матрица и P - перестановочная матрица. В этом случае получаемое кодовое слово содержит вектор полезных данных x как подвектор. Хотя структура систематического (или любого другого) кодера может отличаться от описанной выше (см. фиг.5), он все равно порождает тот же самый код. В частности, метод, описанный в [11], может быть использован для построения эффективного систематического кодера для скрученных полярных кодов. Кроме того, могут использоваться стандартные приемы укорочения и выкалывания кодов для получения кодов различной длины из вышеописанного скрученного полярного кода.
Матрица V используется для обеспечения достаточно большого минимального расстояния d≥d0 получаемого кода. Она строится следующим образом. Пусть H - проверочная матрица базового кода длины n с минимальным расстоянием d0. Пусть A′ - n×n матрица, соответствующая скрученному поляризующему преобразованию. Вектор u(0) должен быть построен таким образом, чтобы соответствующее кодовое слово cо скрученного полярного также являлось кодовым словом базового кода, т.е. u(0)A′HT=0. Таким образом, получим V=QTHA′T, где Q - произвольная обратимая матрица. Для повышения корректирующей способности получаемая таким образом матрица V может быть дополнена строками веса 1. Конкретные добавляемые строки могут быть определены с учетом вероятности ошибки в битовых подканалах, задаваемых поляризующим преобразованием A′. Пусть 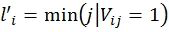 и
и 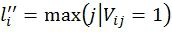 - начальная и конечная позиции строки i соответственно. Выполняя элементарные операции над строками матрица HAT, можно получить такое V, что не более чем одна строка начинается и не более чем одна строка заканчивается в позиции i, 0≤i<n. Последнее свойство означает, что
- начальная и конечная позиции строки i соответственно. Выполняя элементарные операции над строками матрица HAT, можно получить такое V, что не более чем одна строка начинается и не более чем одна строка заканчивается в позиции i, 0≤i<n. Последнее свойство означает, что
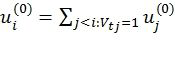 ,
, 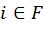 (4)
(4)
где t - индекс строки, заканчивающейся в позиции i,  , и вычисляется сумма по модулю 2. Первое свойство, как правило, уменьшает число членов в (4) и упрощает вычисление этого выражения. Символы
, и вычисляется сумма по модулю 2. Первое свойство, как правило, уменьшает число членов в (4) и упрощает вычисление этого выражения. Символы 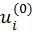 ,
, 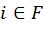 называются замороженными. Замороженные символы, такие, что
называются замороженными. Замороженные символы, такие, что 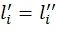 (т.е.
(т.е. 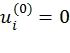 ), называются статически замороженными символами, а такие, для которых
), называются статически замороженными символами, а такие, для которых 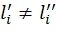 , называются динамически замороженными.
, называются динамически замороженными.
Преимущественно расширенный код БЧХ может использоваться в качестве базового в описываемой конструкции. При этом число позиций i, для которых (4) содержит нетривиальную сумму, оказывается небольшим, что упрощает декодирование. Кроме того, это позволяет использовать особую структуру перестановок, которая может быть компактно задана. Эти перестановки определяются путем индексирования элементов подвекторов длины 2i векторов u(i) двоичными векторами длины i и заданием различных базисов соответствующих i-мерных линейных пространств. Для каждого слоя i и каждого подвектора 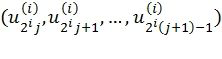 длины 2i вектора u(i) задается базис
длины 2i вектора u(i) задается базис 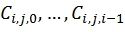 (который может быть представлен в виде i×i матрицы со строками
(который может быть представлен в виде i×i матрицы со строками 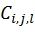 ), соответствующего i-мерного линейного подпространства, так что выходной индекс x в пределах j-го блока получается из входного индекса
), соответствующего i-мерного линейного подпространства, так что выходной индекс x в пределах j-го блока получается из входного индекса 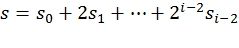 ,
, 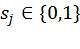 как
как 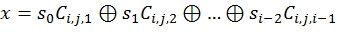 . Это задает некоторую перестановку элементов вектора. Более конкретно, кодер может быть реализован следующим образом:
. Это задает некоторую перестановку элементов вектора. Более конкретно, кодер может быть реализован следующим образом:
1. Положить 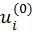 ,
, 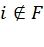 равными элементам вектора полезных данных x и вычислить оставшиеся элементы
равными элементам вектора полезных данных x и вычислить оставшиеся элементы 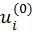 согласно (2). Заметим, что это эквивалентно вычислению u(0)=xW для соответствующей матрицы W.
согласно (2). Заметим, что это эквивалентно вычислению u(0)=xW для соответствующей матрицы W.
2. Пусть i=1.
3. Вычислить 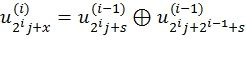 ,
, 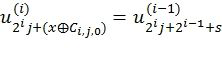 ,
, 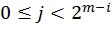 ,
, 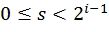 , где
, где 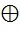 обозначает побитовую операцию «исключающее или»,
обозначает побитовую операцию «исключающее или», 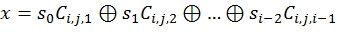 ,
, 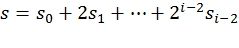 ,
, 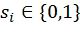 , и
, и 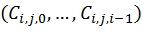 - набор линейно независимых векторов длины i, которые могут быть эквивалентно представлены как целые числа.
- набор линейно независимых векторов длины i, которые могут быть эквивалентно представлены как целые числа.
4. Пусть i=i+1. Если i≤m, перейти к шагу 3.
5. Кодовое слово получается как u(m).
Следует понимать, что существуют и другие эквивалентные методы кодирования, которые порождают то же самое множество кодовых слов. Все эти методы получаются путем замены матрицы W на W′=QW в вышеприведенном алгоритме, где Q - обратимая k×k матрица.
Например, фиг.5 соответствует следующим базисным векторам, задающим перестановки:
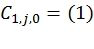 ,
, 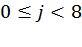 ,
,
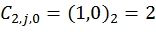 ,
, 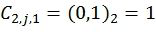 ,
, 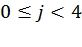 ,
,
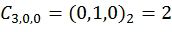 ,
, 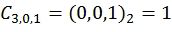 ,
, 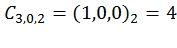 ,
,
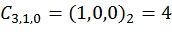 ,
, 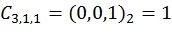 ,
, 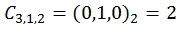 ,
,
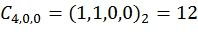 ,
, 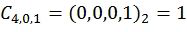 ,
, 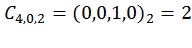 ,
, 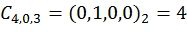
Можно заметить, что существуют два отличия от классического полярного кодера (см. фиг.1): имеется прекодер 002, и ребра, соединяющие последовательные слои, переставлены.
Заметим, что достаточно указать только 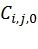 и задать некоторый детерминированный алгоритм нахождения линейно независимых векторов
и задать некоторый детерминированный алгоритм нахождения линейно независимых векторов 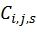 ,
, 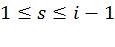 . Таким образом, каждая перестановка может быть задана с помощью всего i битов, что значительно меньше, чем
. Таким образом, каждая перестановка может быть задана с помощью всего i битов, что значительно меньше, чем 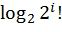 битов для случая произвольной перестановки.
битов для случая произвольной перестановки.
Конкретный вид используемых перестановок должен быть определен исходя из условия минимизации вероятности ошибки в получаемых битовых подканалах. Это может быть реализовано, например, путем полного перебора (или рандомизированного поиска) всех возможных перестановок, задаваемых невырожденными m×m двоичными матрицами и вычисления вероятности ошибки в соответствующих незамороженных битовых подканалах с помощью эволюции плотностей.
Предложенный кодер может быть использован в системах передачи или хранения данных. Фиг.6 представляет пример такой системы. Соответствующий декодер должен учитывать конкретную структуру перестановок и ограничений (2) для того, чтобы найти наиболее вероятное кодовое слово, соответствующее принятому зашумленному вектору. Декодер последовательного исключения и его списочный [4] или стековый варианты [5] должны вычислять вероятности путей аналогично тому, как это делается в случае классических полярных кодов. Фиг.7 представляет блок-схему модифицированной функции RecursivelyCalcP для вычисления этих вероятностей с использованием того же подхода, что и в [4], которая учитывает вышеописанную перестановочную структуру. Видно, что она совпадает с функцией, представленной на фиг.2, за исключением нового блока 021, который вычисляет входные индексы в соответствии с вышеописанным методом перестановки, в то время как блоки 011 и 012 заменены блоками 022 и 023, которые используют индекс, вычисленный в блоке 021. Кроме того, декодер ПИ должен учитывать значения промежуточных символов 006, соответствующих каждому пути. Это может быть реализовано с помощью соответствующим образом модифицированного алгоритма RecursivelyCalcC (см. фиг.8). Он также содержит блок вычисления индекса 021 и выполняет те же шаги, что и в блоке 013.
Декодер ПИ, его списочный [4] и стековый [5] варианты должны принимать решение относительно каждого символа 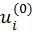 . В случае динамически замороженных символов эти решения принимаются с учетом значений символов, найденных на предыдущих фазах алгоритма. Однако реализация, описанная в [4], не сохраняет эти значения в явном виде. В связи с этим предлагается восстановить их из промежуточных значений, сохраняемых в массиве C, заполняемом функцией RecursivelyCalcC (см. фиг.8). Это может быть выполнено следующим образом. Пусть
. В случае динамически замороженных символов эти решения принимаются с учетом значений символов, найденных на предыдущих фазах алгоритма. Однако реализация, описанная в [4], не сохраняет эти значения в явном виде. В связи с этим предлагается восстановить их из промежуточных значений, сохраняемых в массиве C, заполняемом функцией RecursivelyCalcC (см. фиг.8). Это может быть выполнено следующим образом. Пусть 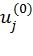 ,
, 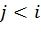 - один из членов правой части (2). Для того чтобы восстановить его на фазе i пути l, можно вычислить
- один из членов правой части (2). Для того чтобы восстановить его на фазе i пути l, можно вычислить 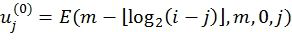 , где
, где
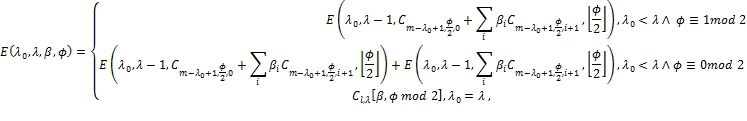
и 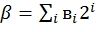 . Это выражение может быть построено в символьном виде при проектировании декодера, так что (4) выражается в терминах
. Это выражение может быть построено в символьном виде при проектировании декодера, так что (4) выражается в терминах 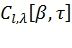 . Можно заметить, что число членов в получаемом таким образом выражении для
. Можно заметить, что число членов в получаемом таким образом выражении для 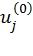 , т.е. сложность его вычисления, увеличивается с ростом
, т.е. сложность его вычисления, увеличивается с ростом 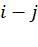 . Это обосновывает необходимость использования матрицы V, такой, что не более чем одна строка начинается и заканчивается в каждой позиции, т.к. при этом, как правило, минимизируется
. Это обосновывает необходимость использования матрицы V, такой, что не более чем одна строка начинается и заканчивается в каждой позиции, т.к. при этом, как правило, минимизируется 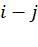 .
.
Кроме того, предлагается следующий способ снижения сложности стекового декодирования, который может быть использован как в случае скрученных, так и обычных полярных кодов. Отметим, что декодер MAP должен найти вектор 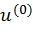 , такой, что значение
, такой, что значение
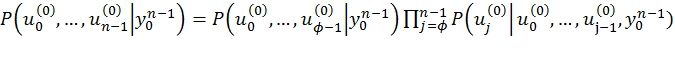 (5)
(5)
максимально. Оригинальный стековый алгоритм работает локально на кодовом дереве, выбирая на каждом шаге путь, максимизирующий первый член в выражении (3), т.к. оставшиеся члены неизвестны. Предполагая, что 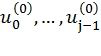 - правильные значения информационных символов, получим, что каждый из оставшихся членов представляет собой вероятность правильного нахождения
- правильные значения информационных символов, получим, что каждый из оставшихся членов представляет собой вероятность правильного нахождения 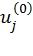 декодером ПИ [1] для заданного вектора
декодером ПИ [1] для заданного вектора 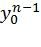 . Можно легко вычислить средние по
. Можно легко вычислить средние по 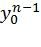 значения этих вероятностей с использованием метода эволюции плотностей или его аппроксимаций [2], [3]. Тогда вместо максимизации
значения этих вероятностей с использованием метода эволюции плотностей или его аппроксимаций [2], [3]. Тогда вместо максимизации 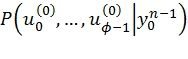 на каждом шаге стекового алгоритма можно максимизировать
на каждом шаге стекового алгоритма можно максимизировать

(6)
Вводя эвристическую функцию 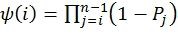 , где
, где 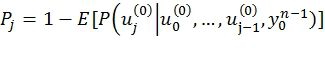 - вероятность ошибки в j-м битовом подканале, задаваемом поляризующим преобразованием, можно получить улучшенный стековый алгоритм декодирования (см. фиг.9). Его отличиями по сравнению с исходным вариантом (фиг.4) являются:
- вероятность ошибки в j-м битовом подканале, задаваемом поляризующим преобразованием, можно получить улучшенный стековый алгоритм декодирования (см. фиг.9). Его отличиями по сравнению с исходным вариантом (фиг.4) являются:
- 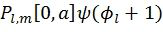 используется вместо
используется вместо 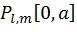 в качестве метрики пути в блоках 027 и 028.
в качестве метрики пути в блоках 027 и 028.
- Вычисление динамически замороженных символов 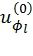 производится в блоке 026 в соответствии с (2) и вышеописанным быстрым алгоритмом для
производится в блоке 026 в соответствии с (2) и вышеописанным быстрым алгоритмом для 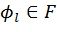 , что необходимо при декодировании скрученных полярных кодов с динамически замороженными символами. Однако предлагаемый метод может использоваться и для полярных кодов исключительно со статически замороженными символами.
, что необходимо при декодировании скрученных полярных кодов с динамически замороженными символами. Однако предлагаемый метод может использоваться и для полярных кодов исключительно со статически замороженными символами.
- Модифицированные алгоритмы RecursivelyCalcP и RecursivelyCalcC (фиг.7, фиг.8) должны использоваться для учета структуры скрученного поляризующего преобразования в блоках 025, 029, 030. Исходные их версии (см. фиг.2, фиг.3) являются частным случаем модифицированных.
Следует понимать, что специалисты в данной области могут реализовать предлагаемый способ многими путями. В частности, вместо вероятностей путей могут использоваться их логарифмы, вероятности могут вычисляться приближенно, вычисление некоторых из них, соответствующих замороженным символами, может быть пропущено. Кроме того, могут использоваться более точные эвристические функции 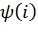 . Например, такая функция может учитывать начальную часть пути в кодовом дереве для оценки вероятности оставшихся символов. В общем случае, повышение точности оценки вероятности оставшихся символов, задаваемой функцией
. Например, такая функция может учитывать начальную часть пути в кодовом дереве для оценки вероятности оставшихся символов. В общем случае, повышение точности оценки вероятности оставшихся символов, задаваемой функцией 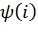 , позволяет сократить число итераций в декодер.
, позволяет сократить число итераций в декодер.
Описанные выше способы кодирования и декодирования могут быть реализованы аппаратно (например, в виде специализированной микросхемы) или программно, что позволяет построить кодирующее и декодирующее устройства. Предлагаемое кодирующее устройство состоит из следующих модулей:
1. Прекодер, реализующий вычисление 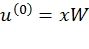 .
.
2. Преобразующие узлы, в том числе узел «исключающее или» и проходной (см. фиг.5).
3. Соединительные ребра, реализующие некоторую перестановку.
Предлагаемое декодирующее устройство состоит из следующих модулей, показанных на фиг.10:
1. Стек 031, который хранит идентификаторы путей l вместе с их метриками M и поддерживает извлечение записей с наибольшим и наименьшим M, а также удаление произвольной записи.
2. Модуль 032 вычисления вероятностей (см. фиг.7).
3. Модуль 033 обновления промежуточных символов (см. фиг.8).
4. Запоминающее устройство 037, в котором хранятся значения 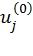 .
.
5. Модуль 036 последовательной обработки, реализующий вычисления в соответствии с блок-схемой на фиг.9.
6. Модуль 035, хранящий или вычисляющий значения эвристической функции 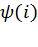 .
.
7. Модуль 034 вычисления динамически замороженных символов, который вычисляет 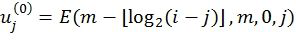 .
.
Заметим, что модули 035 и 034 не являются обязательными. С другой стороны, модули 032, 033, 037 могут быть использованы для реализации списочного декодера скрученных полярных кодов.
Предлагаемые способы кодирования и декодирования могут использоваться в беспроводных и кабельных системах связи, магнитных и оптических системах хранения данных. Фиг.11, фиг.12 и фиг.13 показывают корректирующую способность скрученных и нескрученных полярных кодов, основанных на расширенных кодах БЧХ, по сравнению с полярными кодами с внешним CRC [4], LDPC и турбокодами различной длины и скорости. Можно заметить, что скрученные полярные коды обеспечивают энергетический выигрыш до 0,5 дБ по сравнению с LDPC и турбокодами и имеют большую корректирующую способность, чем классические полярные коды с внешним CRC. Можно также заметить, что скрученные полярные коды позволяют понизить уровень «насыщения» вероятности ошибки по сравнению с турбокодами и нескрученными полярными кодами. На фиг.16 представлено сравнение корректирующей способности скрученных полярных кодов и обобщенного каскадного кода с внешними кодами Рида-Соломона и внутренними полярными кодами, предложенного в [12]. Можно заметить, что скрученные полярные коды обеспечивают значительно лучшую корректирующую способность.
Кроме того, как видно на фиг.14, скрученные коды требуют меньшего числа итераций в улучшенном стековом алгоритме декодирования, т.е. они могут быть подвергнуты декодированию с меньшей сложностью. На фиг.15 приведено сравнение среднего числа итераций, необходимого для декодирования (1024, 512) нескрученного полярного кода с динамически замороженными символами с использованием неориентированного стекового алгоритма [5] (см. фиг.4) и предложенного стекового алгоритма с ориентированным поиском (см. фиг.9). Видно, что использование ориентированного поиска позволяет значительно сократить число итераций, в особенности в области больших отношений сигнал/шум. На фиг.17 представлено более подробное сравнение корректирующей способности скрученных полярных и LDPC кодов. Представлены вероятность ошибки для различных значений параметра L (для полярных кодов) и максимального числа итераций в алгоритме распространения доверия. Оба параметра определяют сложность декодирования. Можно заметить, что снижение сложности декодирования приводит к менее значительному ухудшению корректирующей способности в случае скрученных полярных кодов по сравнению с LDPC. Кроме того, увеличение сложности декодирования позволяет получить большую корректирующую способность в случае скрученных полярных кодов, в то время как в случае LDPC увеличение максимального числа итераций с 80 до 200 практически не дает результата.
На фиг.18 и фиг.19 представлено число сложений и вычислений нелинейной функции в max-log-MAP реализации предложенного алгоритма декодирования, а также в реализации алгоритма распространения доверия в логарифмической области, используемого для декодирования LDPC кодов. Можно заметить, что скрученные полярные коды требуют меньшего числа операций, в особенности в области больших отношений сигнал/шум. Max-Log-Map реализация алгоритма декодирования предполагает вычисление величин 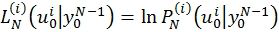 вместо
вместо 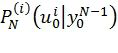 . В этом случае выражения (1) и (2) сводятся к
. В этом случае выражения (1) и (2) сводятся к
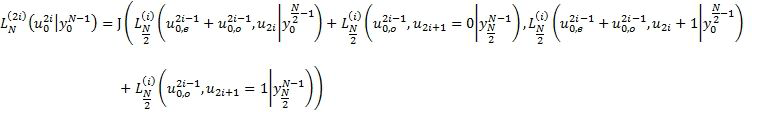
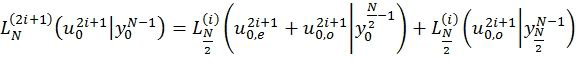 ,
,
где 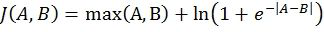 .
.
Варианты осуществления не ограничиваются описанными здесь вариантами осуществления, специалисту в данной области техники на основе информации, изложенной в описании и знаний уровня техники, станут очевидны и другие варианты осуществления изобретения, не выходящие за пределы сути и объема данного изобретения.
В заявке не указано конкретное программное и аппаратное обеспечение для реализации изобретения, но специалисту в области техники должно быть понятно, что сущность изобретения не ограничена конкретной программной или аппаратной реализацией, и поэтому для осуществления изобретения могут быть использованы любые программные и аппаратные средства известные в уровне техники. Так, аппаратные средства могут быть реализованы в одной или нескольких специализированных интегральных схемах, цифровых сигнальных процессорах, устройствах цифровой обработки сигналов, программируемых логических устройствах, программируемых пользователем вентильных матрицах, процессорах, контроллерах, микроконтроллерах, микропроцессорах, электронных устройствах, других электронных модулях, выполненных с возможностью осуществлять описанные в данном документе функции, компьютер либо комбинации вышеозначенного.
Хотя отдельно не упомянуто, но очевидно, что, когда речь идет о хранении данных, программ и т.п., подразумевается наличие машиночитаемого носителя данных, примеры машиночитаемых носителей данных включают в себя постоянное запоминающее устройство, оперативное запоминающее устройство, регистр, кэш-память, полупроводниковые запоминающие устройства, магнитные носители, такие как внутренние жесткие диски и съемные диски, магнитооптические носители и оптические носители, такие как диски CD-ROM и цифровые универсальные диски (DVD), а также любые другие известные в уровне техники носители данных.

Группа изобретений относится к области помехоустойчивого кодирования, в частности к применению скрученного полярного кода в кодировании и декодировании данных. Техническим результатом является повышение быстродействия кодирования/декодирования за счет снижения числа осуществляемых итераций. Способ содержит этапы, на которых предварительно кодируют, посредством модуля предварительного кодирования, данные, представленные в виде k-мерного двоичного вектора x, причем кодирование состоит в вычислении u(0)=xW, где W - матрица размерности k×2m и m - параметр кода; осуществляют, посредством модуля предварительного кодирования, m-слойное скрученное поляризующее преобразование вектора u(0), причем i-й слой преобразования состоит в разбиении вектора u(i-1) на 2m-1 подвекторов длины 2, в умножении этих подвекторов на матрицу, в слиянии полученных подвекторов в один вектор размерности 2m и в перестановке элементов полученного вектора, результатом чего является вектор u(i), в результате на m-м слое получают вектор u(m), причем перестановки выбирают из общей аффинной группы; получают посредством мультиплексора кодирующего устройства закодированные посредством скрученного полярного кода данные путем мультиплексирования элементов вектора u(m). 4 н. и 7 з.п. ф-лы, 19 ил.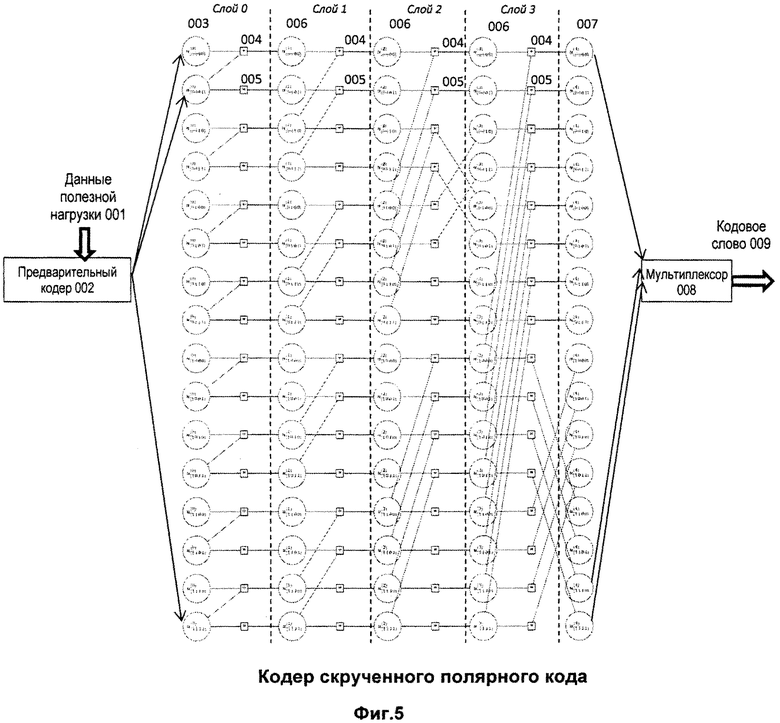
1. Способ кодирования данных, включающий в себя этапы, на которых:
а) предварительно кодируют, посредством модуля предварительного кодирования, данные, представленные в виде k-мерного двоичного вектора x, причем кодирование состоит в вычислении u(0)=xW, где W - матрица размерности k×2m и m - параметр кода;
b) осуществляют, посредством модуля предварительного кодирования, m-слойное скрученное поляризующее преобразование вектора u(0), причем i-й слой преобразования состоит в разбиении вектора u(i-1) на 2m-1 подвекторов длины 2, в умножении этих подвекторов на матрицу 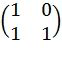 , в слиянии полученных подвекторов в один вектор размерности 2m и в перестановке элементов полученного вектора, результатом чего является вектор u(i), в результате на m-м слое получают вектор u(m), причем перестановки выбирают из общей аффинной группы;
, в слиянии полученных подвекторов в один вектор размерности 2m и в перестановке элементов полученного вектора, результатом чего является вектор u(i), в результате на m-м слое получают вектор u(m), причем перестановки выбирают из общей аффинной группы;
c) получают посредством мультиплексора кодирующего устройства закодированные посредством скрученного полярного кода данные путем мультиплексирования элементов вектора u(m).
2. Способ по п. 1, причем матрицу W выбирают таким образом, что получаемые кодовые слова являются кодовыми словами базового расширенного кода БЧХ (Боуза-Чоудхури-Хоквингема).
3. Способ по п. 1, причем перестановки задают для подвекторов вектора u(i), состоящих из 2i смежных элементов, путем индексирования элементов этих подвекторов двоичными векторами длины i и задания базисов i-мерных линейных пространств для каждого из этих векторов, так что выходной индекс получается как произведение входного индекса на матрицу, соответствующую этому базису.
4. Способ декодирования данных, закодированных в соответствии с п. 1, причем декодированные данные получают в декодирующем устройстве, используя метод последовательного исключения, причем вычисление вероятностей путей в кодовом дереве выполняется рекурсивно в m слоев, и вероятности на слое i-1 вычисляются из переставленных вероятностей на слое i, причем используемая перестановка та же, что использована в способе по п. 1, и декодирующее устройство выбирает пути с учетом значений динамически замороженных символов.
5. Способ по п. 4, в котором значения динамически замороженных символов получают из уравнения u(0)VT=0, где WVT=0.
6. Способ по п. 5, в котором матрица V имеет такой вид, что не более чем одна строка начинается в каждом из столбцов и не более чем одна строка заканчивается в каждом столбце.
7. Способ из п. 5, в котором значения динамически замороженных символов находят с использованием символьных выражений из промежуточных данных декодирующего устройства.
8. Способ по п. 4, в котором декодирующее устройство хранит несколько путей, причем начальный путь соответствует последовательности 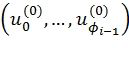 , и итеративно выбирает для расширения один из них, чтобы получить один или два пути
, и итеративно выбирает для расширения один из них, чтобы получить один или два пути 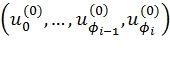 ,
, 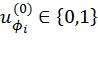 , так что выполняются ограничения динамической заморозки символов, причем выбираемый путь соответствует наибольшему значению
, так что выполняются ограничения динамической заморозки символов, причем выбираемый путь соответствует наибольшему значению 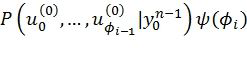 , где ψ(ϕi) - эвристическая функция.
, где ψ(ϕi) - эвристическая функция.
9. Способ по п. 8, в котором 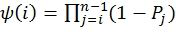 , причем Pj - вероятность ошибки на бит в j-м битовом подканале, задаваемом поляризующим преобразованием.
, причем Pj - вероятность ошибки на бит в j-м битовом подканале, задаваемом поляризующим преобразованием.
10. Кодирующее устройство, содержащее:
a) модуль предварительного кодирования данных, представленных в виде k-мерного двоичного вектора x, выполненный с возможностью вычисления u(0)=xW, где W - матрица размерности k×2m и m - параметр кода;
b) модуль, выполненный с возможностью осуществления логической функции «исключающее или», и модуль, выполненный с возможностью передачи данных без изменения, которые соединены в m слоев так, что обеспечена возможность реализовать m-слойное скрученное поляризующее преобразование вектора u(0) и получать вектор u(m), причем i-й слой преобразования состоит в разбиении вектора u(i-1) на 2m-1 подвекторов длины 2, в умножении этих подвекторов на матрицу 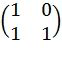 , в слиянии полученных подвекторов в один вектор размерности 2m, и в перестановке элементов полученного вектора, результатом чего является вектор u(i), причем перестановки выбирают из общей аффинной группы;
, в слиянии полученных подвекторов в один вектор размерности 2m, и в перестановке элементов полученного вектора, результатом чего является вектор u(i), причем перестановки выбирают из общей аффинной группы;
c) мультиплексор, выполненный с возможностью получения закодированного кодового слова скрученного кода из вектора u(m), полученного на m-м слое преобразования из вектора u(0).
11. Декодирующее устройство, содержащее:
a) модуль вычисления вероятностей, выполненный с возможностью вычисления вероятностей промежуточных символов на m слоях, причем вероятности на (i-1)-м слое получаются из переставленных вероятностей на слое i, причем используемая перестановка та же, что и в способе по п. 1, причем модуль вычисления вероятностей передает вычисленную вероятность в модуль последовательной обработки;
b) модуль последовательной обработки, выполненный с возможностью итеративно строить пути в кодовом дереве посредством извлечения пути с наибольшей метрикой из стека, с возможностью расширения пути, с возможностью сохранения полученных путей в стеке, выполненный с возможностью определения значений декодированных символов на основе рекурсивного алгоритма на основе путей с наибольшей метрикой и вычисленной вероятности промежуточных символов, выполненный с возможностью итеративного вычисления значений промежуточных символов и передачи их в модуль обновления промежуточных символов;
c) стек, выполненный с возможностью хранения идентификаторов путей и их метрик, соединенный с возможностью обмена данными с модулем последовательной обработки;
d) модуль обновления промежуточных символов, выполненный с возможностью рекурсивно вычислять значения промежуточных символов на m слоях таким же способом, что и кодирующее устройство по п. 10, причем модуль обновления промежуточных символов выполнен с возможностью передавать вычисленные значения промежуточных символов на запоминающее устройство промежуточных символов;
e) запоминающее устройство промежуточных символов, выполненное с возможностью хранения значений промежуточных символов u(i) и с возможностью передачи значений промежуточных символов на модуль последовательной обработки и на модуль вычисления вероятностей.
| WO 2013107140 A1, 25.07.2013 | |||
| US 2013117344 A1, 09.05.2013 | |||
| US 2014019820 A1, 16.01.2014 | |||
| СПОСОБЫ И УСТРОЙСТВО LDPC-КОДИРОВАНИЯ | 2005 |
|
RU2395902C2 |
Авторы
Даты
2015-12-20—Публикация
2014-04-10—Подача