ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Изобретение относится к вычислительному устройству, вычислительному способу, компьютерной программе и машиночитаемому носителю.
УРОВЕНЬ ТЕХНИКИ
В модели "белого ящика" взломщик может получить полное управление над программным обеспечением, которое работает на вычислительном устройстве, например, смартфоне или ПК. Цель криптографии типа "белого ящика" - защищать программную реализацию от такого взломщика.
Когда в модели "белого ящика" нужно защитить криптографическую схему, задействующую ключи, это обычно подразумевает, что атакующий, у которого есть доступ и полное управление защитным программным обеспечением и его средой исполнения, не должен извлечь никакую ценную информацию о ключах.
Одним из способов избежать получения атакующим доступа к ключам в информации является реализация части или всего чувствительного алгоритма в виде сети таблиц. Таблицы оперируют кодированными переменными. Атакующему будет трудно определить, какую операцию выполняет таблица, так как у него нет сведений о кодировании. Замена операций обращениями к таблице обычно увеличивает размер кода. Кроме того, некоторые контрмеры для дополнительной защиты таблиц приводят к дополнительному увеличению размера кода.
Например, одной возможной атакой для получения информации о ключах, когда у атакующего есть доступ к работающей реализации, является так называемая коллизионная атака, где атакующий измеряет зависящую от ключа переменную в разных прогонах на разных входных данных. Атакующий собирает статистику о коллизиях, то есть переменных, принимающих одинаковое значение в разных прогонах на разных сообщениях. В конечном счете атакующий может собрать достаточно информации для извлечения ключа. Примером такой атаки является Анализ взаимной информации (MIA).
Чтобы защититься от коллизионной атаки, можно представить переменную w с помощью n долей  , чтобы коллизию на w можно было обнаружить только из коллизий на полном наборе
, чтобы коллизию на w можно было обнаружить только из коллизий на полном наборе 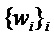 . Так как последнее будет обладать меньшей вероятностью, коллизионные атаки становятся труднее. Вычисление долей приводит к тому, что размер таблицы опять значительно увеличивается.
. Так как последнее будет обладать меньшей вероятностью, коллизионные атаки становятся труднее. Вычисление долей приводит к тому, что размер таблицы опять значительно увеличивается.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Предоставляется вычислительное устройство, выполненное с возможностью оценивания функции данных, отображающей некоторое количество входных переменных в некоторое количество выходных переменных. Функция данных организована в вычислительном устройстве в виде вычисления, содержащего функции выбора и функции оценки. Входные переменные разбиваются на одну или несколько переменных выбора и одну или несколько переменных оценки. Для каждой конкретной комбинации значений переменных выбора задается соответствующая функция выбора и функция оценки.
Вычислительное устройство содержит
- механизм выбора, выполненный с возможностью приема одной или нескольких переменных выбора и оценивания функций выбора по принятым переменным выбора; при этом функция выбора в качестве входа принимает переменные выбора, а выход функции выбора указывает, равны ли переменные выбора, принятые в функции выбора, конкретной комбинации значений, соответствующих функции выбора,
- механизм оценки, выполненный с возможностью приема одной или нескольких переменных оценки и оценивания функций оценки по принятым переменным оценки, при этом функция оценки в качестве входа принимает переменные оценки, а выход функции оценки представляет собой выход функции данных, у которой входом является объединение переменных оценки и конкретной комбинации значений переменных выбора, соответствующих функции оценки, и
- комбинационный механизм, выполненный с возможностью комбинации выходов механизма выбора и механизма оценки в выход функции данных для входных переменных.
Обе функции оценки и выбора принимают в качестве входа меньше входных данных, чем функция данных. В результате уменьшается размер кода для реализации функций оценки и выбора. Это особенно важно в реализации "белого ящика", в которой функции оценки и/или выбора реализуются в виде таблиц или сетей таблиц, потому что это требует меньших таблиц. Хотя может увеличиться размер схемы в результате разделения в переменных оценки и выбора, размер кода уменьшается. Кроме того, функции выбора являются очень простыми функциями, которые легко осуществить в реализации на основе многочлена, например, они могут использоваться, когда переменные представляются в виде нескольких кодированных долей. Поскольку функции выбора одинаковы для разных функций данных, их можно повторно использовать для нескольких функций данных; это дополнительно уменьшает размер кода.
В варианте осуществления переменные выбора дополнительно разбиваются на несколько групп переменных выбора, при этом функция выбора организована в вычислительном устройстве в виде произведения нескольких подфункций выбора, причем каждая соответствует группе из нескольких групп переменных выбора, при этом подфункция выбора в качестве входа принимает переменные выбора в группе, а выход подфункции выбора указывает, равны ли принятые переменные выбора конкретной комбинации значений в группе, соответствующей функции выбора.
Дальнейшее подразделение переменных выбора дополнительно уменьшает размер кода для реализации механизма выбора.
Механизм выбора побуждает выбор правильной функции оценки на основе переменных выбора. Механизм оценки оценивает результат функции данных по разным возможным значениям переменных выбора и переменных оценки. Функция оценки требует в качестве входа только переменные оценки. Переменные оценки дополняются в функции оценки конкретной комбинацией значений переменной выбора, которые соответствуют функции оценки. Хотя это увеличит количество функций оценки, это уменьшит размер таких функций.
Механизм выбора можно реализовать в виде системы выбора; например, в виде схемы и/или подходящего программного обеспечения, работающего в процессоре. Механизм оценки можно реализовать в виде системы оценки; например, в виде схемы и/или подходящего программного обеспечения, работающего в процессоре. Например, упомянутое программное обеспечение может содержать несколько операций табличного поиска в сети таблиц.
В варианте осуществления одна или несколько входных переменных кодируются. Фактически можно кодировать все переменные выбора и оценки. Оперирование кодированными переменными может проводиться с помощью таблиц, которые кодируются для одинакового кодирования.
Важным способом кодирования переменных, в частности, переменных выбора и оценки является кодирование переменных в виде множества кодированных долей. Операции могут исполняться над кодированными таким образом переменными путем представления операции в виде многочлена в конечном поле. Многочлен может оцениваться с использованием таблиц, которые представляют операции вроде сложения и умножения. Преимуществом этого типа кодирования является то, что таблицы для сложения и умножения могут повторно использоваться на всем протяжении оценки многочлена. Это дополнительно уменьшает размер кода.
Вычислительное устройство является электронным устройством, например, мобильным электронным устройством, например, мобильным телефоном. Вычислительное устройство может быть телевизионной приставкой, смарт-картой, компьютером и т. п.
Описанный в этом документе способ вычисления может применяться в широком диапазоне практических применений. Такие практические применения включают в себя криптографические применения. Например, подписание, дешифрование и шифрование и т.п. информации могут осуществляться в программном обеспечении без разглашения ключа, используемого для выполнения криптографической операции. Например, вычислительное устройство может использоваться для чувствительных приложений, например, использующих собственный алгоритм. Увеличивается трудность обратной разработки программного обеспечения для атакующего.
Способ в соответствии с изобретением можно реализовать на компьютере в виде реализуемого компьютером способа, или в специализированных аппаратных средствах, либо в их сочетании. Исполняемый код для способа в соответствии с изобретением можно сохранить в компьютерном программном продукте. Примеры компьютерных программных продуктов включают в себя запоминающие устройства, оптические запоминающие устройства, интегральные схемы, серверы, онлайновое программное обеспечение и т. п. Предпочтительно, чтобы компьютерный программный продукт был выполнен в виде программного кода в неизменяемой со временем форме, сохраненного на машиночитаемом носителе, для выполнения способа в соответствии с изобретением, когда упомянутый программный продукт исполняется на компьютере.
В предпочтительном варианте осуществления компьютерная программа выполнена в виде кода компьютерной программы, приспособленного для выполнения всех этапов способа в соответствии с изобретением, когда компьютерную программу прогоняют на компьютере. Предпочтительно, чтобы компьютерная программа была воплощена на машиночитаемом носителе.
Другой аспект изобретения предоставляет способ обеспечения загрузки компьютерной программы. Этот аспект используется, когда компьютерная программа отправляется, например, в App Store от Apple, Play Store от Google или Windows Store от Microsoft, и когда компьютерная программа доступна для загрузки из такого магазина.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Дополнительные подробности, аспекты и варианты осуществления изобретения только в качестве примера будут описываться со ссылкой на чертежи. Элементы на фигурах иллюстрируются для простоты и ясности и необязательно нарисованы в масштабе. На фигурах элементы, которые соответствуют уже описанным элементам, могут иметь одинаковые номера ссылок. На чертежах
Фиг. 1 схематически показывает пример функции данных,
Фиг. 2a схематически показывает пример варианта осуществления вычислительного устройства,
Фиг. 2b схематически показывает пример варианта осуществления механизма оценки,
Фиг. 2c схематически показывает пример варианта осуществления механизма выбора,
Фиг. 2d схематически показывает пример варианта осуществления механизма выбора,
Фиг. 2e схематически показывает пример варианта осуществления вычислительного устройства,
Фиг. 3 схематически иллюстрирует пример кодирования переменной,
Фиг. 4a схематически показывает пример варианта осуществления сети таблиц,
Фиг. 4b схематически показывает пример варианта осуществления сети таблиц,
Фиг. 5a схематически показывает блок-схему последовательности операций для вычислительного способа,
Фиг. 5b схематически показывает блок-схему последовательности операций для вычислительного способа,
Фиг. 6a схематически показывает пример варианта осуществления блочного шифра DES,
Фиг. 6b схематически показывает пример варианта осуществления цикловой функции DES,
Фиг. 7a схематически показывает машиночитаемый носитель с записываемой частью, содержащей компьютерную программу в соответствии с вариантом осуществления,
Фиг. 7b схематически показывает представление процессорной системы в соответствии с вариантом осуществления.
ПОДРОБНОЕ ОПИСАНИЕ ПРЕДПОЧТИТЕЛЬНЫХ ВАРИАНТОВ ОСУЩЕСТВЛЕНИЯ
Хотя данное изобретение допускает вариант осуществления во многих разных видах, один или несколько конкретных вариантов осуществления показаны на чертежах и будут подробно описаны в этом документе с пониманием того, что настоящее раскрытие изобретения нужно рассматривать как пример принципов изобретения, и оно не имеет целью ограничить изобретение показанными и описанными конкретными вариантами осуществления.
В дальнейшем элементы вариантов осуществления для понимания описываются в действии. Однако станет очевидно, что соответствующие элементы выполнены с возможностью выполнения функций, описываемых как выполняемые ими.
Кроме того, изобретение не ограничивается вариантами осуществления, и изобретение заключено в каждом без исключения новом признаке или комбинации признаков, описанных выше или перечисленных во взаимно разных зависимых пунктах формулы изобретения.
Фиг. 6a, которая скопирована из FIPS 46-3, иллюстрирует, в частности, блочный шифр DES и блочные шифры вообще. Блочный шифр принимает вход 610 блочного шифра, на который действует последовательность циклов блочного шифра; в случае DES проводится 16 циклов для тройного DES 48. Первый цикл блочного шифра действует на вход 610 блочного шифра, каждый из следующих циклов действует на выход предыдущих циклов. В цикле блочного шифра цикловая функция f применяется к части выхода предыдущего цикла. Вход блочного шифра обладает неким размером данных, в случае DES - 64 разряда. Каждый цикл блочного шифра изменяет свой вход цикла блочного шифра для создания выхода цикла блочного шифра. Вход и выход цикла блочного шифра обладают одинаковым размером данных. Отметим, что DES содержит начальную перестановку и обратную начальную перестановку в начале и конце блочного шифра. Они не имеют криптографической значимости, поскольку не зависят от ключа.
Стандарт шифрования данных описывает блочное кодирование с ключом 64-разрядного блока. Ключ формально содержит 64 разряда, но только 56 его разрядов фактически используются в шифровании. Шифрование и дешифрование использует 16 итераций, называемых циклами. В цикле r, 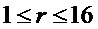 , используется 48-разрядный ключ цикла
, используется 48-разрядный ключ цикла 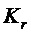 , разряды которого являются (зависящим от цикла) подмножеством 56 разрядов ключа.
, разряды которого являются (зависящим от цикла) подмножеством 56 разрядов ключа.
Цикловая функция f DES иллюстрируется на фиг. 6b и имеет вид: 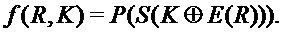 Здесь P является перестановкой 32 разрядов, а E является картой расширения, которая отображает строки разрядов с длиной 32 в строки разрядов с длиной 48 путем дублирования половины разрядов. S-блок S отображает строки разрядов с длиной 48 в строки разрядов с длиной 32, действуя по группам на 6-разрядные подстроки:
Здесь P является перестановкой 32 разрядов, а E является картой расширения, которая отображает строки разрядов с длиной 32 в строки разрядов с длиной 48 путем дублирования половины разрядов. S-блок S отображает строки разрядов с длиной 48 в строки разрядов с длиной 32, действуя по группам на 6-разрядные подстроки:
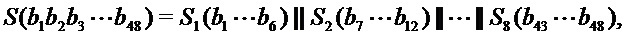 где каждый S-блок
где каждый S-блок 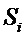 отображает строки разрядов с длиной 6 в строки разрядов с длиной 4, а || обозначает сцепление. На фиг. 6b вход S-блока
отображает строки разрядов с длиной 6 в строки разрядов с длиной 4, а || обозначает сцепление. На фиг. 6b вход S-блока 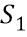 обозначен ссылкой 611, выход обозначен ссылкой 612.
обозначен ссылкой 611, выход обозначен ссылкой 612.
S-блоки (блоки подстановок) широко применяются в блочных шифрах для увеличения запутывания Шеннона в блочном шифре. S-блок особенно подходит для его кодирования в виде функции данных в соответствии с вариантом осуществления. Дешифрование выполняется путем обратного хода, то есть снизу вверх. Обратная цикловая функция имеет вид
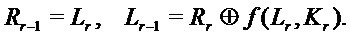
Так как DES использует ключ только из 56 разрядов, возможен поиск по всему ключевому пространству; однако восстановление ключей с использованием атаки дифференциальных искажений, особенно на программную реализацию, будет на порядки быстрее. Тройной DES использует три 56-разрядных ключа 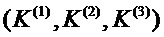 и шифрует путем выполнения сначала шифрования DES с ключом
и шифрует путем выполнения сначала шифрования DES с ключом 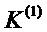 , с последующим дешифрованием DES с ключом
, с последующим дешифрованием DES с ключом  , с последующим шифрованием DES с ключом
, с последующим шифрованием DES с ключом 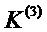 .
.
DES будет использоваться в этом документе в качестве основного примера блочного шифра, а S-блоки DES - в качестве главного примера функции данных. Конечно, варианты осуществления на основе DES всесторонне проверены, и было обнаружено, что кодирования типа "белого ящика" в DES значительно меньше в варианте осуществления, как дополнительно задается ниже. Результаты по DES прямо переносятся на тройной DES, так как S-блоки являются такими же, как в DES. Другие варианты осуществления применяются к другим блочным шифрам, например к AES, и в частности к их S-блоку (блокам). AES не относится к типу Фейстеля, как DES, но является блочным шифром подстановочно-перестановочной сети (SPN). S-блок DES имеет больше входов, чем выходов (6 против 4), тогда как S-блок в AES имеет равное количество входов и выходов.
Вообще, варианты осуществления объясняемой ниже системы также могут использоваться для других функций, например, которые требуют защищенную реализацию. Например, с использованием варианта осуществления можно реализовать базисные элементы типа хэшей или кодов аутентификации сообщений и т. п.
Фиг. 1 схематически показывает пример функции 100 данных. Функция S данных отображает некоторое количество (n) входных переменных 110 в некоторое количество (m) выходных переменных 120. Например, функция данных может быть S-блоком вроде S-блока в DES. Входами функции 100 данных могут быть разряды, например, в случае S-блока DES может быть 6 входных разрядов и 4 выходных разряда. В случае S-блока AES может быть 8 входных и выходных разрядов. Количество разрядов может быть разным, например, 8 входных разрядов и 4 выходных разряда, и т. п.
Ниже представим функцию 100 данных как функцию вида  . То есть из математического поля с
. То есть из математического поля с 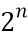 элементами в поле с
элементами в поле с 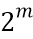 элементами. Может быть n=m, например, как в S-блоке AES. Особенно выгодны варианты осуществления, в которых m<n, поскольку они допускают выполнение всех вычислений в меньшем поле
элементами. Может быть n=m, например, как в S-блоке AES. Особенно выгодны варианты осуществления, в которых m<n, поскольку они допускают выполнение всех вычислений в меньшем поле 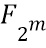 ; на функции с m<n будем ссылаться как на "конические" функции, поскольку диапазон строго меньше области определения. Если используются не разряды, а, скажем, переменные, которые принимают больше 2 разных значений, то соответственно может использоваться большее поле для выполнения в нем вычислений.
; на функции с m<n будем ссылаться как на "конические" функции, поскольку диапазон строго меньше области определения. Если используются не разряды, а, скажем, переменные, которые принимают больше 2 разных значений, то соответственно может использоваться большее поле для выполнения в нем вычислений.
Фиг. 2a схематически показывает пример варианта осуществления вычислительного устройства 200. Реализация функции данных из фиг. 1 может потребовать много памяти, особенно если используется кодирование входа и/или выходов. Например, в реализации типа "белого ящика" функцию данных из фиг. 1 можно реализовать в виде единой таблицы. Однако даже для случая S-блока DES объем данных в такой таблице может быстро увеличиваться. Например, если каждый разряд кодируется как 16 долей, и каждая доля дополнительно имеет разряд состояния, насчитывая в итоге 16 разрядов состояния (больше информации о возможных кодированиях см. ниже), входной размера S-блока раздувается до 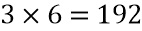 разрядов. Это означает, что единая таблица была бы невозможно большой, содержащей
разрядов. Это означает, что единая таблица была бы невозможно большой, содержащей 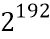 записей. Соответственно, есть потребность в другом способе кодировать функцию данных, которая может надежно кодироваться в "белом ящике" и помимо этого требует меньше пространства хранения.
записей. Соответственно, есть потребность в другом способе кодировать функцию данных, которая может надежно кодироваться в "белом ящике" и помимо этого требует меньше пространства хранения.
Вычислительное устройство 200 выполнено с возможностью приема входных данных 211. Входные данные 211 могут быть вроде входов функции 100 данных. Входы могут кодироваться. Входные данные 211 могут быть многоразрядными. Входные данные 211 также можно брать из некоторого другого поля, скажем 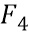 (поле с 4 элементами), вместо разрядов. Входные переменные разбиваются на одну или несколько переменных выбора и одну или несколько переменных оценки. В принципе, возможно любое разбиение, но разные выборы будут обладать разным компромиссом. Вообще говоря, увеличение количества разрядов выбора приведет к меньшему размеру реализации, тогда как выбор меньшего количества разрядов выбора приведет к быстрой реализации. Размер реализации относится к размеру хранения реализации, в частности, к общему размеру таблицы, используемому в реализации типа "белого ящика". В свою очередь, большие таблицы приведут к промахам кэша и, соответственно, также к медленному исполнению. Функция 100 данных организована в вычислительном устройстве 200 в виде вычисления, содержащего функции выбора и функции оценки. Для каждой конкретной комбинации значений переменных выбора (v) задается соответствующая функция
(поле с 4 элементами), вместо разрядов. Входные переменные разбиваются на одну или несколько переменных выбора и одну или несколько переменных оценки. В принципе, возможно любое разбиение, но разные выборы будут обладать разным компромиссом. Вообще говоря, увеличение количества разрядов выбора приведет к меньшему размеру реализации, тогда как выбор меньшего количества разрядов выбора приведет к быстрой реализации. Размер реализации относится к размеру хранения реализации, в частности, к общему размеру таблицы, используемому в реализации типа "белого ящика". В свою очередь, большие таблицы приведут к промахам кэша и, соответственно, также к медленному исполнению. Функция 100 данных организована в вычислительном устройстве 200 в виде вычисления, содержащего функции выбора и функции оценки. Для каждой конкретной комбинации значений переменных выбора (v) задается соответствующая функция 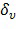 выбора и функция
выбора и функция 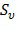 оценки. Чтобы избежать путаницы, отметим, что функция
оценки. Чтобы избежать путаницы, отметим, что функция 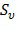 оценки не обязательно должна относиться к любому из S-блоков DES; кроме того, индекс v здесь относится к переменным выбора.
оценки не обязательно должна относиться к любому из S-блоков DES; кроме того, индекс v здесь относится к переменным выбора.
Вычислительное устройство 200 содержит механизм 220 выбора. Механизм 220 выбора выполнен с возможностью приема одной или нескольких переменных 222 выбора. Входные переменные из входных переменных 211, которые являются переменными выбора, указываются ссылкой 222. Механизм 222 выбора выполнен с возможностью оценивания функций 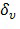 выбора по принятым переменным выбора. Например, механизм 220 выбора может оценивать каждую из функций
выбора по принятым переменным выбора. Например, механизм 220 выбора может оценивать каждую из функций 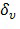 выбора по каждой конкретной комбинации значений переменных выбора (v) для переменных выбора. Функция
выбора по каждой конкретной комбинации значений переменных выбора (v) для переменных выбора. Функция 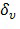 выбора в качестве входа принимает переменные выбора, а выход функции выбора указывает, равны ли переменные выбора, принятые в функции выбора, конкретной комбинации значений (v), соответствующих функции выбора. Выход механизма выбора указывается ссылкой 224.
выбора в качестве входа принимает переменные выбора, а выход функции выбора указывает, равны ли переменные выбора, принятые в функции выбора, конкретной комбинации значений (v), соответствующих функции выбора. Выход механизма выбора указывается ссылкой 224.
Функция выбора может быть дельта-функциями Кронекера за исключением того, что они могут иметь несколько входов. В математическом обозначении  обозначает:
обозначает:
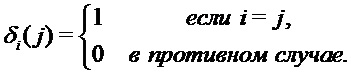
В вышеприведенном примере i и j могут представлять несколько входов, например, для всех переменных выбора. Кроме того, функция выбора не обязательно должна возвращать результаты 0 и 1, хотя они удобны, но может использовать другие значения, в принципе можно использовать любые два разных значения, и размещаться где-нибудь еще в вычислительном устройстве 200.
Вычислительное устройство 200 содержит механизм 210 оценки. Механизм 210 оценки выполнен с возможностью приема одной или нескольких переменных 212 оценки и оценивания функций оценки по принятым переменным оценки. Входные переменные из входных переменных 211, которые являются переменными оценки, указываются ссылкой 212.
Функция оценки в качестве входа принимает переменные оценки, а выход функции оценки представляет собой выход функции данных, входом которой является объединение переменных оценки и конкретной комбинации значений переменных выбора, соответствующих функции оценки. Другими словами, функция оценки выдает результат, который выдала бы функция данных, если бы функция данных приняла в качестве входа переменные оценки вместе с конкретными значениями переменных выбора, которым соответствует функция оценки.
Идея в вариантах осуществления состоит в том, что функции выбора выбирают, какая конкретная комбинация значений переменных выбора присутствует на входе, и в определенном смысле выбирают правильную функцию оценки. Функции выбора являются очень простыми функциями для реализации. Функции выбора зависят только от количества разрядов выбора и могут быть одинаковыми для разных функций данных. Соответственно, функцию выбора можно повторно использовать для разных функций данных в одном и том же вычислительном устройстве.
Механизм оценки и механизм выбора также могут называться блоком оценки и блоком выбора.
Вычислительное устройство 200 содержит комбинационный механизм, выполненный с возможностью комбинации выходов механизма выбора и механизма оценки в выход функции данных для входных переменных. Например, комбинационный механизм может суммировать произведения (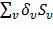 ) функции выбора (
) функции выбора (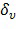 ) и функции оценки (
) и функции оценки (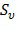 ), соответствующие одной и той же конкретной комбинации значений. Если функция выбора дает значения 0 и 1, то это точно идентифицирует правильные функции оценки. Если функция выбора дает некоторые другие значения помимо 0 и 1, то может использоваться некоторая другая линейная комбинация функций выбора.
), соответствующие одной и той же конкретной комбинации значений. Если функция выбора дает значения 0 и 1, то это точно идентифицирует правильные функции оценки. Если функция выбора дает некоторые другие значения помимо 0 и 1, то может использоваться некоторая другая линейная комбинация функций выбора.
В варианте осуществления сумма берется по всем комбинациям значений переменных выбора (v). Таким образом, функция данных будет правильно эмулироваться для всех входных переменных. Однако если известно, что не может возникнуть некоторая комбинация переменных выбора, то сумму нужно взять только по возможным комбинациям переменных выбора. Это дополнительно уменьшит размер вычислительного устройства.
Ниже приводится математическое описание варианта осуществления для дополнительного разъяснения и пояснения примером.
Рассматриваемая функция данных является функцией  ; отметим, что можно принять m<n. Выбираем положения
; отметим, что можно принять m<n. Выбираем положения 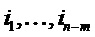 в качестве переменных выбора из набора входных положений (или переменных)
в качестве переменных выбора из набора входных положений (или переменных) 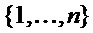 ; пусть m оставшихся положений
; пусть m оставшихся положений 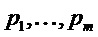 содержат переменные оценки. Теперь для каждого
содержат переменные оценки. Теперь для каждого  задаем функцию
задаем функцию  , полагая
, полагая  , где
, где 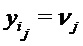 для
для 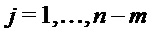 и
и 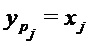 для
для 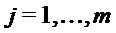 . Другими словами, для каждого
. Другими словами, для каждого  функция
функция 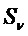 получается из S путем установки выбора n-m из входов в значения, заданные v. Чтобы вычислить S(x), рассмотрим значения входа x в n-m выбранных положениях; если тем значением является v, то применяем функцию
получается из S путем установки выбора n-m из входов в значения, заданные v. Чтобы вычислить S(x), рассмотрим значения входа x в n-m выбранных положениях; если тем значением является v, то применяем функцию 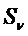 к оставшимся входным символам.
к оставшимся входным символам.
В защищенной, типа "белого ящика", оценке S(x) механизм выбора выбирает  , а затем возвращает результат
, а затем возвращает результат  без раскрытия информации о входе x и выходе S(x). Комбинационный механизм 230 может использовать следующее тождество:
без раскрытия информации о входе x и выходе S(x). Комбинационный механизм 230 может использовать следующее тождество:
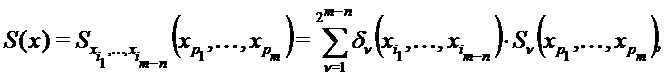
где  удовлетворяет
удовлетворяет
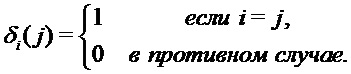
Фиг. 2b схематически показывает пример варианта осуществления механизма 210 оценки. Механизм 210 оценки может содержать несколько блоков оценки, реализующих функции оценки; показаны блоки 215 и 216 оценки. Блок оценки можно реализовать в виде таблицы, например, справочной таблицы, или в виде сети таблиц. Например, механизм оценки из фиг. 2b может оценивать каждую из функций оценки, включая функции 215 и 216, по переменным оценки, принятым в механизме 210 оценки. Правильный результат обязан быть включенным в функции оценки, если функции оценки включаются для каждой возможной комбинации значений функций выбора. Выбор правильного результата среди нескольких результатов нескольких функций оценки выполняется с помощью механизма выбора.
Фиг. 2c схематически показывает пример варианта осуществления механизма 220 выбора. Механизм 220 выбора может содержать несколько блоков выбора, реализующих функции выбора; показаны блоки 225 и 226 выбора. Блок выбора можно реализовать в виде таблицы, например, справочной таблицы, или в виде сети таблиц.
Фиг. 2d схематически показывает пример варианта осуществления механизма 220 выбора. В варианте осуществления переменные выбора могут дополнительно разбиваться на несколько групп переменных выбора. Тогда функцию выбора можно организовать в вычислительном устройстве 200 в виде произведения нескольких подфункций выбора, причем каждая соответствует группе из нескольких групп переменных выбора, при этом подфункция выбора в качестве входа принимает переменные выбора в группе, а выход подфункции выбора указывает, равны ли принятые переменные выбора конкретной комбинации значений в группе, соответствующей функции выбора.
Например, в механизме 220 выбора из фиг. 2d блок 225.1 выбора и блок 226.1 выбора могут принимать первую группу переменных выбора, тогда как блок 225.2 выбора и блок 226.2 выбора могут принимать вторую группу переменных выбора. Может быть больше 2 групп. При желании количество переменных выбора можно заполнить фиктивными переменными, скажем нулями (0), пока количество переменных выбора и фиктивных переменных кратно количеству групп; в последнем случае количество входов в блоке выбора может быть таким же. Комбинационный блок 227 выполнен с возможностью комбинации выходов блоков выбора, соответствующих одной и той же комбинации значений. Например, комбинационный блок 227 может комбинировать выходы комбинационных блоков 225.1 и 225.2, например, путем умножения или операции логического И.
Например, в варианте осуществления функция данных является конической функцией с n входными переменными и m выходными переменными (m<n). В варианте осуществления количество переменных оценки может выбираться как m, а количество переменных выбора как n-m. Количество групп переменных выбора выбирается как  . Эти выборы позволяют выполнять все вычисления в
. Эти выборы позволяют выполнять все вычисления в  , последнее, в свою очередь, позволяет чаще повторно использовать кодированные таблицы умножения и сложения, чем если бы вычисления требовались в нескольких разных полях. Например, если n=8 и m=3, то можно использовать две группы разрядов выбора с одним разрядом заполнения.
, последнее, в свою очередь, позволяет чаще повторно использовать кодированные таблицы умножения и сложения, чем если бы вычисления требовались в нескольких разных полях. Например, если n=8 и m=3, то можно использовать две группы разрядов выбора с одним разрядом заполнения.
Ниже приводится математическое описание варианта осуществления для дополнительного разъяснения и пояснения примером. Чтобы обеспечить вычисление только на меньшем выходном поле 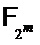 , разделим разряды выбора
, разделим разряды выбора 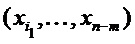 на порции из m разрядов, например
на порции из m разрядов, например
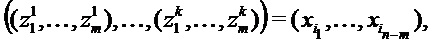
где 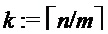 и каждое
и каждое 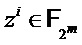 . Если n-m не делится на m, то заполняем разряды выбора ведущими нулями до тех пор, пока результирующее количество разрядов не поделится на m перед разделением. Если вместо разряда используются q-значные переменные, то
. Если n-m не делится на m, то заполняем разряды выбора ведущими нулями до тех пор, пока результирующее количество разрядов не поделится на m перед разделением. Если вместо разряда используются q-значные переменные, то 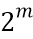 выше можно заменить
выше можно заменить 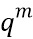 .
.
Из 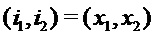 , тогда и только тогда, когда оба
, тогда и только тогда, когда оба 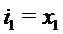 и
и 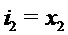 , получаем
, получаем

Последний результат также можно указать как добавление логического сравнения: 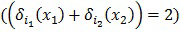 . В этом уравнении операция "=" интерпретируется как логическая операция типа символа Кронекера, например, возвращающая 0 в случае неравенства и 1 в случае равенства. Логическое сравнение с тем же успехом может выполняться над кодированными переменными с использованием сети таблиц. Если используется больше 2 групп, то "2" в формуле можно заменить количеством групп.
. В этом уравнении операция "=" интерпретируется как логическая операция типа символа Кронекера, например, возвращающая 0 в случае неравенства и 1 в случае равенства. Логическое сравнение с тем же успехом может выполняться над кодированными переменными с использованием сети таблиц. Если используется больше 2 групп, то "2" в формуле можно заменить количеством групп.
В варианте осуществления механизм 220 выбора из фиг. 2d содержит функцию выбора для всех комбинаций значений для каждой из нескольких групп переменных выбора. Например, если имеется 8 переменных выбора, разделенных на две группы A и B переменных выбора, то механизм 220 выбора может содержать функции выбора для всех возможных комбинаций значений для группы A и функции выбора для всех возможных комбинаций значений для группы B. Чтобы эмулировать функцию выбора для конкретной комбинации значений для полного набора функций выбора, комбинационный блок 227 может быть выполнен с возможностью комбинации правильной функции выбора из группы A и из группы B. Функции выбора на группе переменных также могут выводить 0 и 1 для указания отсутствия или наличия совпадения. Эти значения можно легко комбинировать с умножением или сложением и т. п.
Механизм выбора может содержать несколько блоков выбора, реализующих функции выбора, например, несколько блоков выбора могут непосредственно представлять функции выбора либо могут представлять функцию выбора на группах переменных выбора.
Блоки выбора и/или блоки оценки можно реализовать в виде таблиц или сетей таблиц.
В варианте осуществления количество входных переменных (n) больше количества выходных переменных (m), при этом количество переменных оценки равно количеству выходных переменных. Количество переменных выбора может быть равно разности (n-m) между количеством входных переменных и количеством выходных переменных. Это позволяет выполнять все вычисления с использованием меньшего количества переменных, например, в поле 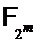 .
.
Существуют несколько способов кодировать переменную w. Переменная w может непосредственно соответствовать переменной выбора или оценки. Однако переменная w также может собирать несколько переменных. Например, вычислительное устройство 200 может быть выполнено с возможностью оперирования несколькими переменными. Например, в варианте осуществления переменные выбора, оценки и выходные переменные являются разрядными переменными, представляющими один разряд. В варианте осуществления несколько разрядных переменных можно комбинировать в более крупные переменные.
Например, в варианте осуществления переменная 310 может представлять 2 или 4 переменные выбора или оценки. Например, для конической функции большая переменная может содержать такое же количество разрядов, как и выходные переменные (m). (n-m) переменных выбора собираются в одну или несколько групп из (m) переменных, каждая из которых представляется в большей переменной.
Например, S-блок DES содержит 4 выходных разрядных переменных и 6 входных разрядных переменных. В этом случае большая переменная w может представлять 4 разряда. Входные разряды можно разбить на 4 разряда оценки, представленные одной большой 4-разрядной переменной, и 2 переменные выбора, которые также представляются одной (большой) 4-разрядной переменной.
Например, S-блок AES содержит 8 выходных разрядных переменных и 8 входных разрядных переменных. В этом случае большая переменная w также может представлять 4 разряда. Входные разряды можно разбить на 4 разряда оценки, представленные одной большей 4-разрядной переменной, и 4 переменные выбора, также представленные одной (большей) 4-разрядной переменной. Выход можно представить двумя большими 4-разрядными переменными. Ниже объясняется, как можно представить, является ли переменная w разрядной переменной или большей переменной.
Переменная w может кодироваться посредством отображения 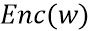 . Кодирование является криптографическим кодированием и может выбираться случайно либо может быть шифрованием с использованием секретного ключа, и т. п. Атакующему неизвестно используемое кодирование. Когда обрабатывается переменная w, неявно предполагается кодирование в устройстве. Переменная также может кодироваться вместе с переменной s состояния,
. Кодирование является криптографическим кодированием и может выбираться случайно либо может быть шифрованием с использованием секретного ключа, и т. п. Атакующему неизвестно используемое кодирование. Когда обрабатывается переменная w, неявно предполагается кодирование в устройстве. Переменная также может кодироваться вместе с переменной s состояния, 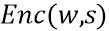 , это дополнительно запутывает связь между w и кодированием. Более надежное кодирование разделяет переменную на несколько долей и кодирует каждую долю, предпочтительно вместе с переменной состояния. Хотя последний тип кодирования наиболее защищен, в этом типе кодирования особенно трудно комбинировать с представлением функции данных в виде сети таблиц. Фиг. 3 иллюстрирует способ кодирования переменной w, который использует несколько долей. Фиг. 3 показывает переменную 310 w и иллюстрирует, как w может кодироваться для использования в криптографическом устройстве, например криптографическом устройстве 200, чтобы избегать коллизий на w. Переменная 310 w распределяется по нескольким долям
, это дополнительно запутывает связь между w и кодированием. Более надежное кодирование разделяет переменную на несколько долей и кодирует каждую долю, предпочтительно вместе с переменной состояния. Хотя последний тип кодирования наиболее защищен, в этом типе кодирования особенно трудно комбинировать с представлением функции данных в виде сети таблиц. Фиг. 3 иллюстрирует способ кодирования переменной w, который использует несколько долей. Фиг. 3 показывает переменную 310 w и иллюстрирует, как w может кодироваться для использования в криптографическом устройстве, например криптографическом устройстве 200, чтобы избегать коллизий на w. Переменная 310 w распределяется по нескольким долям 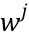 . Разрядный размер w будем называть k. В варианте осуществления разрядный размер доли
. Разрядный размер w будем называть k. В варианте осуществления разрядный размер доли 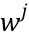 равен разрядному размеру w. Разные переменные могут обладать разными разрядными размерами. Например, k может быть 1, 2, 4 или больше. В варианте осуществления k=1, 2, 3, 4, 5, 6, 7, 8 или больше. Показаны доли 321, 322 и 323.
равен разрядному размеру w. Разные переменные могут обладать разными разрядными размерами. Например, k может быть 1, 2, 4 или больше. В варианте осуществления k=1, 2, 3, 4, 5, 6, 7, 8 или больше. Показаны доли 321, 322 и 323.
Доли могут выбираться так, что 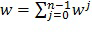 . В варианте осуществления эта сумма использует функцию XOR для суммирования, однако возможны и другие выборы. Например, сумма может использовать арифметическое сложение по модулю
. В варианте осуществления эта сумма использует функцию XOR для суммирования, однако возможны и другие выборы. Например, сумма может использовать арифметическое сложение по модулю 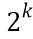 .
.
В более общем виде может задаваться комбинирующая функция (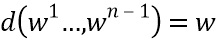 ), которая отображает доли (
), которая отображает доли (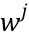 ) в переменную (w). Комбинирующая функция может быть XOR или арифметическим сложением, упомянутым выше. Комбинирующая функция обладает свойством, что отображение из любой одиночной доли (
) в переменную (w). Комбинирующая функция может быть XOR или арифметическим сложением, упомянутым выше. Комбинирующая функция обладает свойством, что отображение из любой одиночной доли (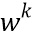 ) в переменную (w), полученную путем фиксирования значений других долей (
) в переменную (w), полученную путем фиксирования значений других долей ( ), является биекцией. То есть функция
), является биекцией. То есть функция 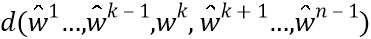 является биекцией; элементы
является биекцией; элементы  обозначают статическое значение. Это свойство гарантирует, что никакое подмножество долей не дает информацию о w. Существует много таких комбинирующих функций. Например, d может быть любой линейной комбинацией долей
обозначают статическое значение. Это свойство гарантирует, что никакое подмножество долей не дает информацию о w. Существует много таких комбинирующих функций. Например, d может быть любой линейной комбинацией долей 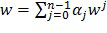 , в которой коэффициенты
, в которой коэффициенты  являются нечетными; сумма использует арифметическое сложение по модулю
являются нечетными; сумма использует арифметическое сложение по модулю 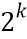 . Комбинирующая функция может быть многочленом.
. Комбинирующая функция может быть многочленом.
Фиг. 3 дополнительно показывает несколько состояний 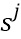 . Показаны состояния 331, 332 и 333. Количество долей 321-323 такое же, как количество состояний 331-333. Состояния являются избыточными данными, которые вносят избыточность в кодирование переменной. Каждая из долей согласована с одним из состояний и кодируется в кодированную долю:
. Показаны состояния 331, 332 и 333. Количество долей 321-323 такое же, как количество состояний 331-333. Состояния являются избыточными данными, которые вносят избыточность в кодирование переменной. Каждая из долей согласована с одним из состояний и кодируется в кодированную долю: 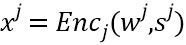 . В варианте осуществления кодирования
. В варианте осуществления кодирования 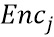 отличаются. Например, кодирования
отличаются. Например, кодирования 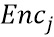 могут случайно выбираться во время компиляции. Не является строго необходимым, чтобы кодирование было биективным, при условии, что оно обратимо по отношению к
могут случайно выбираться во время компиляции. Не является строго необходимым, чтобы кодирование было биективным, при условии, что оно обратимо по отношению к 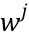 , то есть с помощью сведений о
, то есть с помощью сведений о 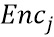 и
и 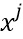 можно восстановить долю
можно восстановить долю 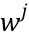 . Тем не менее, в вариантах осуществления кодирования
. Тем не менее, в вариантах осуществления кодирования 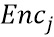 являются биективными. Последнее является более практичным выбором при реализации и упрощает анализ. Как только решено, какие переменные будут кодироваться с какими кодированиями в какой момент, таблицы можно просто приспособить для учета кодирования. Использование состояний необязательно, но предпочтительно, так как состояния увеличивают запутывание, поскольку они допускают несколько представлений для одного и того же значения данных.
являются биективными. Последнее является более практичным выбором при реализации и упрощает анализ. Как только решено, какие переменные будут кодироваться с какими кодированиями в какой момент, таблицы можно просто приспособить для учета кодирования. Использование состояний необязательно, но предпочтительно, так как состояния увеличивают запутывание, поскольку они допускают несколько представлений для одного и того же значения данных.
Фиг. 3 показывает, что доля 321 и состояние 331 кодируются посредством кодирования 361 в кодированную долю 341. Также доля 322 и состояние 332 кодируются посредством кодирования 362 в кодированную долю 342; доля 323 и состояние 333 кодируются посредством кодирования 363 в кодированную долю 343. Будем ссылаться на состояния и доли, которые кодируются вместе для представления переменной w, как на соответствующие той переменной.
Результатом являются несколько кодированных долей, из которых показаны кодированные доли 341, 342 и 343. В варианте осуществления переменная w представляется в криптографическом устройстве 200 в виде нескольких кодированных долей. В криптографическом устройстве не должны возникать ни некодированные доли 321-323, ни состояния 331-333.
Состояния сначала могут просто выбираться случайно, а позже обновляться посредством таких же процессов, которые обновляют переменную w. В варианте осуществления несколько состояний 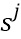 , соответствующих одной и той же переменной w, выбираются так, что существует инъективное отображение 352, обозначенное как
, соответствующих одной и той же переменной w, выбираются так, что существует инъективное отображение 352, обозначенное как 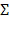 , из входного сообщения M 310 в несколько состояний (
, из входного сообщения M 310 в несколько состояний (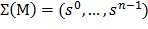 ). Инъективное отображение обладает свойством, что
). Инъективное отображение обладает свойством, что 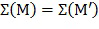 тогда и только тогда, когда
тогда и только тогда, когда  . В частности,
. В частности, 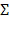 можно выбрать биективным, так как это более строгое условие подразумевает инъективность. Фиг. 3 показывает, как несколько состояний 331-333 зависят от входного сообщения 300 M, и инъективного отображения
можно выбрать биективным, так как это более строгое условие подразумевает инъективность. Фиг. 3 показывает, как несколько состояний 331-333 зависят от входного сообщения 300 M, и инъективного отображения 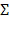 352. Например, входное сообщение 300 может быть входным сообщением 610. Входное сообщение 300 может быть, например, входным сообщением, принятым извне устройства 200, например, входом в блочный шифр. Так как состояния кодируют входное сообщение M 300, разные M приведут к разным кодированным переменным:
352. Например, входное сообщение 300 может быть входным сообщением 610. Входное сообщение 300 может быть, например, входным сообщением, принятым извне устройства 200, например, входом в блочный шифр. Так как состояния кодируют входное сообщение M 300, разные M приведут к разным кодированным переменным: 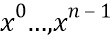 .
.
Отображение 352 не должно быть явным при реализации криптографической функции для большинства или для всех переменных. Например, как только у кодированной переменной есть необходимая инъективная связь с входным сообщением, операции, выполняемые над частями долей 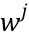 кодированной переменной, могут одновременно выполнять избыточные операции над частями состояний, которые сохраняют инъективную связь. Так как вычисления осуществляются в кодированной области определения, вычисления над состояниями нельзя отделить от вычислений над долями. Например, рассмотрим, что первая и вторая переменные
кодированной переменной, могут одновременно выполнять избыточные операции над частями состояний, которые сохраняют инъективную связь. Так как вычисления осуществляются в кодированной области определения, вычисления над состояниями нельзя отделить от вычислений над долями. Например, рассмотрим, что первая и вторая переменные 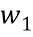 и
и 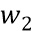 кодируются, как указано выше, в виде нескольких кодированных долей
кодируются, как указано выше, в виде нескольких кодированных долей 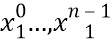 и
и  . Предположим, что операция g над
. Предположим, что операция g над 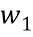 и
и 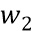 вычисляет третью переменную
вычисляет третью переменную 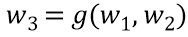 . Переменная
. Переменная 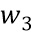 представляется в виде кодированных долей
представляется в виде кодированных долей 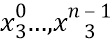 . В варианте осуществления состояния, кодированные в
. В варианте осуществления состояния, кодированные в 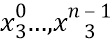 равны состояниям, кодированным в
равны состояниям, кодированным в 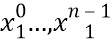 или в
или в  . В этом случае, если у входов есть необходимая связь со входным сообщением M, то таким будет и выход
. В этом случае, если у входов есть необходимая связь со входным сообщением M, то таким будет и выход 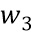 . Таким образом, необходимую связь можно сохранить во всем вычислении. Операцию можно реализовать в виде сети таблиц для выполнения операции, которая, в свою очередь, может быть подсетью сети таблиц, реализующей криптографическую функцию.
. Таким образом, необходимую связь можно сохранить во всем вычислении. Операцию можно реализовать в виде сети таблиц для выполнения операции, которая, в свою очередь, может быть подсетью сети таблиц, реализующей криптографическую функцию.
Начальные переменные, например, которые непосредственно получаются из входного сообщения, могут быть приняты криптографическим устройством 200 в правильной кодированной форме. В качестве альтернативы устройство 200 может содержать кодирующее устройство, выполненное с возможностью кодирования входа.
Кодирование переменной w вместе с состоянием и/или в виде нескольких долей делает менее вероятным то, что есть коллизия на кодированном значении во время исполнения криптографической функции. Соответственно, здесь не возможна никакая коллизионная атака.
В практическом варианте осуществления не будет других представлений w помимо представления посредством кодированных долей. Кроме того, защита эффективнее, если таким образом защищается больше чувствительных переменных. Все переменные, которые зависят от ключа и от входного сообщения, предпочтительно защищаются. Чтобы предотвратить коллизионные атаки, не требуется, чтобы входные сообщения представлялись в виде кодированных долей перед тем, как выполняется операция с ключом. Однако гарантия того, что инъективное отображение существует и поддерживается, упрощается наличием входного сообщения, кодированного в виде нескольких наборов кодированных долей даже перед тем, как используется ключ.
Сети таблиц сами по себе известны из криптографии "белого ящика". См., например, "White-box cryptography and an AES implementation" под авторством Chow и др. Пример сети 420 таблиц показан на фиг. 4a, в этом случае - сеть таблиц для вычисления векторных произведений.
Сеть таблиц принимает один или несколько входов, например, входов 410, и создает один или несколько выходов, например, выходов 430. В сети 420 таблиц показано несколько справочных таблиц; показаны таблицы 421-424. Таблицы получают входы непосредственно из входов 410 и/или выходов других таблиц. Таблица может получать одиночный вход, два входа или больше двух входов.
Удобным способом преобразования вычисления над некодированными переменными w в вычисление над переменными w, кодированными в виде нескольких долей, предоставляется в "Higher-Order Masking Schemes for S-boxes" под авторством Carlet и др. Этот документ не обсуждает коллизионные атаки или кодирование с состояниями. Документ дальше называется как "Carlet". Carlet не предотвращает коллизию на переменной, кодированной в виде нескольких долей.
Ниже объясняется, как вычисление над переменной w, например, для вычисления значения D(w) функции, можно преобразовать в вычисление над переменной w, кодированной в несколько долей. Функция D может быть функцией данных, но такой же способ может использоваться для любого внутреннего этапа вычисления криптографической функции, например, сложения, умножения и т. п. Покажем, как создать сеть таблиц, которая вычисляет D(w) на долях. Сначала рассмотрим случай, в котором у D есть один вход w. Несколько состояний можно обрабатывать аналогично. Также сначала будем игнорировать состояния, позже покажем, как можно добавить состояния.
Если w представляется n долями 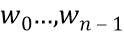 , то с тем же успехом хотим представить D(w) с помощью n долей, чтобы обеспечить результирующую переменную такой же защитой, как и w. Это возможно для любой функции путем использования следующих фактов.
, то с тем же успехом хотим представить D(w) с помощью n долей, чтобы обеспечить результирующую переменную такой же защитой, как и w. Это возможно для любой функции путем использования следующих фактов.
Для демонстрации сначала предполагаем, что значение D(w), как и w, также является k-разрядным числом. k-разрядные числа можно считать элементами конечного поля Галуа 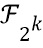 , а функцию D - функцией от
, а функцию D - функцией от 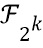 . Все функции в конечных полях являются многочленами, соответственно, для любой функции D от
. Все функции в конечных полях являются многочленами, соответственно, для любой функции D от 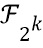 существуют коэффициенты
существуют коэффициенты 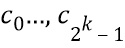 , так что для любого w
, так что для любого w
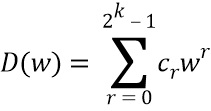
Также функцию S(x) данных можно представить в виде многочлена от нескольких переменных:
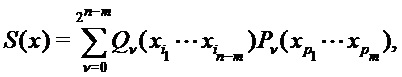
где 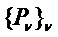 обозначает набор многочленов, представляющий функции оценки
обозначает набор многочленов, представляющий функции оценки 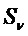 на
на 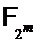 , а
, а  - многочлены выбора, то есть набор многочленов, представляющий дельты
- многочлены выбора, то есть набор многочленов, представляющий дельты 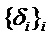 на
на 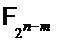 .
.
Многочлен D и многочлены 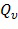 и
и 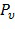 также можно выразить в виде вычисления над долями следующим образом. Пусть доли задаются
также можно выразить в виде вычисления над долями следующим образом. Пусть доли задаются 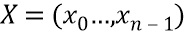 и
и 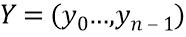 . Для простоты предположим, что сумма долей равна некодированным переменным. Сумма X и Y может кодироваться с долями
. Для простоты предположим, что сумма долей равна некодированным переменным. Сумма X и Y может кодироваться с долями 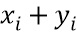 . Скалярное кратное
. Скалярное кратное 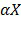 может кодироваться с долями
может кодироваться с долями 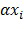 . В конечном счете пусть Z будет произведением X и Y. Зададим для
. В конечном счете пусть Z будет произведением X и Y. Зададим для 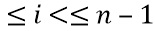 значения
значения 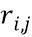 и
и 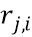 .Возьмем для
.Возьмем для 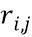 случайный элемент из
случайный элемент из 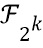 , например, путем выбора случайной k-разрядной строки. В варианте осуществления случайное число для
, например, путем выбора случайной k-разрядной строки. В варианте осуществления случайное число для 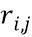 получается путем выбора во время компиляции функция рандомизации
получается путем выбора во время компиляции функция рандомизации 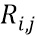 из входного сообщения M к
из входного сообщения M к 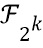 и задания
и задания 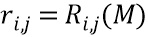 . Последнее обладает преимуществом в том, что избегают доверия к генератору случайных чисел во время исполнения. Только когда создается сеть таблиц, называемое временем компиляции, нужен источник случайности. Отметим, что Carlet опирается на случайность во время исполнения. Это открывает Carlet для манипуляции источником случайных чисел во время исполнения. В частности, генератор случайных чисел можно перехватить и заменить постоянными значениями.
. Последнее обладает преимуществом в том, что избегают доверия к генератору случайных чисел во время исполнения. Только когда создается сеть таблиц, называемое временем компиляции, нужен источник случайности. Отметим, что Carlet опирается на случайность во время исполнения. Это открывает Carlet для манипуляции источником случайных чисел во время исполнения. В частности, генератор случайных чисел можно перехватить и заменить постоянными значениями.
Примем 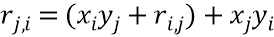 ; здесь порядок вычислений важен и указывается скобками. Теперь для
; здесь порядок вычислений важен и указывается скобками. Теперь для 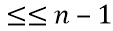 примем
примем  .
.
Подсеть таблиц векторных произведений может вычислить 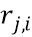 . Эти таблицы вычисляют два векторных произведения
. Эти таблицы вычисляют два векторных произведения 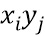 и
и 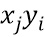 .
.
В варианте осуществления функция 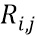 рандомизации для вычисления
рандомизации для вычисления 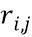 реализуется в виде сети таблиц, принимающей в качестве входа входные сообщения. Это устраняет потребность в источнике случайных чисел во время исполнения.
реализуется в виде сети таблиц, принимающей в качестве входа входные сообщения. Это устраняет потребность в источнике случайных чисел во время исполнения.
Доли 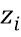 теперь представляют произведение X и Y. Используя операции сложения, скалярного умножения и умножения, многочленное представление для S может быть выражено в виде операции над долями. Операцию над долями, в свою очередь, можно реализовать в виде справочной таблицы, принимающей в качестве входа одну или несколько долей и/или случайные числа.
теперь представляют произведение X и Y. Используя операции сложения, скалярного умножения и умножения, многочленное представление для S может быть выражено в виде операции над долями. Операцию над долями, в свою очередь, можно реализовать в виде справочной таблицы, принимающей в качестве входа одну или несколько долей и/или случайные числа.
Возможная сеть 420 таблиц для вычисления 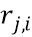 иллюстрируется на фиг. 4a. Таблицы 421-424 взаимодействуют для вычисления
иллюстрируется на фиг. 4a. Таблицы 421-424 взаимодействуют для вычисления 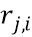 . Входы в сеть 420 таблиц показаны ссылкой 410. Выход сети 420 таблиц показан ссылкой 430.
. Входы в сеть 420 таблиц показаны ссылкой 410. Выход сети 420 таблиц показан ссылкой 430.
Например, таблицы 421 и 422 могут быть выполнены с возможностью умножения своих входов, тогда как таблицы 423 и 424 могут быть выполнен с возможностью сложения своих входов. Отметим, что каждая из таблиц может использовать разные кодирования.
Фиг. 4b схематически показывает пример варианта осуществления сети 440 таблиц с умножением. Сеть 440 таблиц с умножением может создаваться с использованием приведенных выше формул для вычисления  . Сеть 440 таблиц с умножением выполнена с возможностью умножения переменной X, представленной в вычислительном устройстве 200, скажем, в его хранилище данных, в виде первого кратного кодированных долей (
. Сеть 440 таблиц с умножением выполнена с возможностью умножения переменной X, представленной в вычислительном устройстве 200, скажем, в его хранилище данных, в виде первого кратного кодированных долей (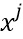 ), и второй переменной Y, представленной в виде второго кратного кодированных долей (
), и второй переменной Y, представленной в виде второго кратного кодированных долей (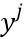 ). Сеть таблиц с умножением действует на первое и второе кратное кодированных долей (
). Сеть таблиц с умножением действует на первое и второе кратное кодированных долей (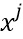 ,
, 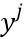 ) и получает третье кратное кодированных долей (
) и получает третье кратное кодированных долей ( ), представляющее собой произведение первой и второй переменной. Отметим, что здесь верхние индексы относятся к долям, а не степени. Сеть 440 таблиц с умножением может быть частью сети таблиц для вычисления криптографической функции.
), представляющее собой произведение первой и второй переменной. Отметим, что здесь верхние индексы относятся к долям, а не степени. Сеть 440 таблиц с умножением может быть частью сети таблиц для вычисления криптографической функции.
Сеть 440 таблиц с умножением может содержать подсети таблиц векторных произведений для вычисления векторных произведений, 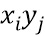 . В варианте осуществления векторные произведения вычисляются парами
. В варианте осуществления векторные произведения вычисляются парами 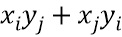 . Например, сеть 440 таблиц с умножением может содержать сеть 420 таблиц. Сеть 440 таблиц с умножением также может содержать сеть 450 таблиц для вычисления одной или нескольких функций
. Например, сеть 440 таблиц с умножением может содержать сеть 420 таблиц. Сеть 440 таблиц с умножением также может содержать сеть 450 таблиц для вычисления одной или нескольких функций 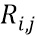 рандомизации. На фиг. 4b сеть 450 таблиц зависит от входного сообщения 110. Эта зависимость указана пунктирной линией для указания, что зависимость можно получить через посредника, например, переменные, сохраненные в хранилище данных. Сеть 440 таблиц может получать свои входы и хранить свои выходы в хранилище данных вычислительного устройства 200.
рандомизации. На фиг. 4b сеть 450 таблиц зависит от входного сообщения 110. Эта зависимость указана пунктирной линией для указания, что зависимость можно получить через посредника, например, переменные, сохраненные в хранилище данных. Сеть 440 таблиц может получать свои входы и хранить свои выходы в хранилище данных вычислительного устройства 200.
Таблицу, действующую на доли, можно преобразовать в таблицу, действующую на кодированные доли. Задаем s и t так, что для кодированной доли x имеем 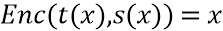 . Функции s и t получают состояние и долю из x соответственно. Пусть задана таблица T для t(x). Тогда
. Функции s и t получают состояние и долю из x соответственно. Пусть задана таблица T для t(x). Тогда  задает таблицу для x, которая реализует таблицу T для части доли x и функцию P для части состояния. Функция P избыточна и может выбираться при создании сети таблиц, например, во время компиляции. Например, P может быть функцией тождества. Аналогичные построения возможны для нескольких входов. Используемое здесь кодирование
задает таблицу для x, которая реализует таблицу T для части доли x и функцию P для части состояния. Функция P избыточна и может выбираться при создании сети таблиц, например, во время компиляции. Например, P может быть функцией тождества. Аналогичные построения возможны для нескольких входов. Используемое здесь кодирование 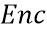 также называется входным кодированием. Кодирование Enc' называется выходным кодированием. Входное и выходное кодирования таблицы не должны быть одинаковыми при условии, что выходное кодирование, используемое для выхода таблицы, такое же, как входное кодирование следующей таблицы, которая использует упомянутый выход в качестве входа.
также называется входным кодированием. Кодирование Enc' называется выходным кодированием. Входное и выходное кодирования таблицы не должны быть одинаковыми при условии, что выходное кодирование, используемое для выхода таблицы, такое же, как входное кодирование следующей таблицы, которая использует упомянутый выход в качестве входа.
Фиг. 2e показывает вариант осуществления вычислительного устройства 200, например, которое описано в отношении фиг. 2a, содержащего хранилище 242 данных и хранилище 244 таблиц. Хранилище 242 данных выполнено с возможностью хранения переменных, на которые действует вычислительное устройство 200. В частности, хранилище 242 данных может хранить кодированные переменные, например несколько кодированных долей. Хранилище 242 таблиц выполнено с возможностью хранения одной или нескольких сетей таблиц для реализации механизма 220 выбора и механизма 230 оценки. Хранилище 242 данных и хранилище 244 таблиц могут быть электронным запоминающим устройством. Они могут быть двумя частями одного и того же запоминающего устройства. Хранилище 244 таблиц может быть энергонезависимым хранилищем. Хранилище 242 данных может быть энергозависимым хранилищем.
Вычислительное устройство 200 может содержать блок 243 управления, сконфигурированный для применения функции данных, например, как часть блочного шифра, к входному сообщению путем применения нескольких справочных таблиц в хранилище 244 таблиц к переменным, представленным в хранилище 242 данных. Например, хранилище 244 таблиц может дополнительно содержать команды, которые указывают порядок, в котором нужно применять таблицы к каким переменным.
Вычислительное устройство 200 может содержать сетевой интерфейс 250. Сетевой интерфейс 250 может быть выполнен с возможностью приема кодированных данных по компьютерной сети. Например, вычислительное устройство 200 может принимать зашифрованные данные, например, зашифрованное содержимое, которое дешифруется криптографическим устройством 200. Входные данные, принятые по сетевому интерфейсу 250, можно представить как кодированные доли, например, как описано выше. Это не является необходимым, так как кодирование может выполняться внутри устройства 200.
Как правило, устройство 200 содержит микропроцессор (не показан отдельно), который исполняет подходящее программное обеспечение, сохраненное в устройстве 200; например, это программное обеспечение может быть загружено и/или сохранено в соответствующем запоминающем устройстве, например, энергозависимом запоминающем устройстве, таком как RAM, или энергонезависимом запоминающем устройстве, таком как флэш-память (не показано отдельно). В качестве альтернативы устройства 200 можно полностью или частично реализовать в программируемой логике, например, в виде программируемой пользователем вентильной матрицы (FPGA). Устройства 200 можно полностью или частично реализовать в виде так называемой специализированной интегральной схемы (ASIC), то есть интегральной схемы (IC), настроенной на конкретное использование. Например, схемы можно реализовать в CMOS, например, с использованием языка описания аппаратных средств, такого как Verilog, VHDL и т. п.
В варианте осуществления устройство 200 содержит схему выбора, схему оценки и комбинационную схему. Устройство 200 может содержать дополнительные схемы, например схему выбора для групп переменных выбора, и т. п. Схемы реализуют соответствующие блоки и механизмы, описанные в этом документе. Схемы могут быть схемой процессора и схемой хранения, при этом схема процессора исполняет команды, представленные электронно в схемах хранения. Схемы также могут быть FPGA, ASIC или т. п.
Ниже обсуждаются влияния на размер кода для S-блоков DES после вышеупомянутого разбиения на разряды выбора и оценки. Сравнение выполняется со способом, раскрытым в "Higher-Order Masking Schemes for S-Boxes" под авторством Goubin и др.; дополнительно называемым Goubin, и на способ, раскрытый в "Fast evaluation of polynomials over binary finite fields and application to side-channel countermeasures" под авторством Coron и др.; дополнительно называемый Coron.
В Таблице 1 перечисляем три способа: прямой циклотомический способ от Goubin-а на 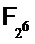 , способ CRV от Coron-а на
, способ CRV от Coron-а на 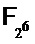 и решение в соответствии с вариантом осуществления на
и решение в соответствии с вариантом осуществления на 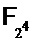 , использующее 2 разряда выбора. Здесь k обозначает количество долей, используемое для представления переменной.
, использующее 2 разряда выбора. Здесь k обозначает количество долей, используемое для представления переменной.
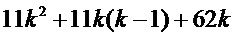
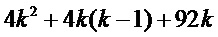
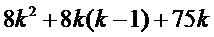
Таблица 1: Подсчет табличных поисков в трех способах.
В Таблице 2 подсчитывается количество байт, используемых для трех способов при применении к DES, где k=16 и каждая n-разрядная доля сопровождается 4-разрядным состоянием, означая, что каждая переменная на 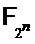 представляется 16 долями с разрядным размером n+4. Из этого следует, что размер таблиц для сложения и умножения содержит
представляется 16 долями с разрядным размером n+4. Из этого следует, что размер таблиц для сложения и умножения содержит 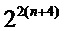 записей по (n+4) разрядов. Приводим результат как для реализации DES, в которой используются разные таблицы на основе разных кодирований для каждого табличного поиска, так и реализации, в которой таблицы и кодирования повторно используются. Здесь получаем n=6 для подхода Goubin и Coron, но n=4 в соответствии с вариантом осуществления, который разделяет 6-разрядный вход на два разряда выбора и четыре разряда оценки.
записей по (n+4) разрядов. Приводим результат как для реализации DES, в которой используются разные таблицы на основе разных кодирований для каждого табличного поиска, так и реализации, в которой таблицы и кодирования повторно используются. Здесь получаем n=6 для подхода Goubin и Coron, но n=4 в соответствии с вариантом осуществления, который разделяет 6-разрядный вход на два разряда выбора и четыре разряда оценки.
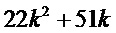
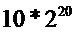 разрядов
разрядов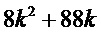
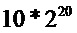 разрядов
разрядов
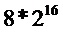 разрядов
разрядов
Таблица 2: Подсчет количества байт, необходимых для хранения таблиц, используемых в реализации типа "белого ящика" на долях, когда k=16.
Отметим, что решение в соответствии с вариантом осуществления требует менее 10% памяти по сравнению с другими решениями. Результаты нижней строки следуют из приведенного выше обсуждения; ниже подробно объясняется, как общая теория может применяться к DES.
Стандарт шифрования данных содержит 8 S-блоков ( ), отображающих 6-разрядные входы в 4-разрядные выходы. Ниже показываем, как создать арифметическую схему на
), отображающих 6-разрядные входы в 4-разрядные выходы. Ниже показываем, как создать арифметическую схему на 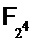 для оценивания каждого S-блока DES. Затем эта арифметическая схема может оцениваться с помощью арифметики долей, как объяснялось выше. Отметим, что v имеет размер 6-4=2 разряда. Поэтому его можно представить одиночным элементом в
для оценивания каждого S-блока DES. Затем эта арифметическая схема может оцениваться с помощью арифметики долей, как объяснялось выше. Отметим, что v имеет размер 6-4=2 разряда. Поэтому его можно представить одиночным элементом в 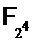 , обозначенным как [v]. Количество разных значений на
, обозначенным как [v]. Количество разных значений на  у [v] равно
у [v] равно  . После заполнения они равны
. После заполнения они равны
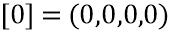

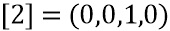
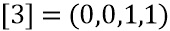
4 многочлена выбора 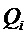 на
на 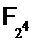 могут вычисляться следующим образом. Вычисляем
могут вычисляться следующим образом. Вычисляем 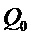 ,
,  ,
, 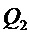 ,
,  на
на 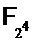 с помощью
с помощью
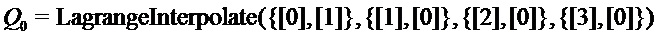
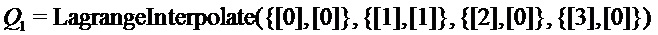
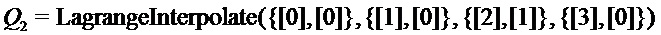
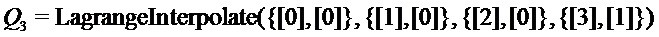
Затем для каждого S-блока  выбираем первый и последний входные разряды в качестве переменных выбора, чтобы задать v, то есть на входе
выбираем первый и последний входные разряды в качестве переменных выбора, чтобы задать v, то есть на входе 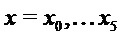 задаем
задаем 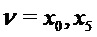 . Затем вычисляем многочлены оценки
. Затем вычисляем многочлены оценки  следующим образом:
следующим образом:
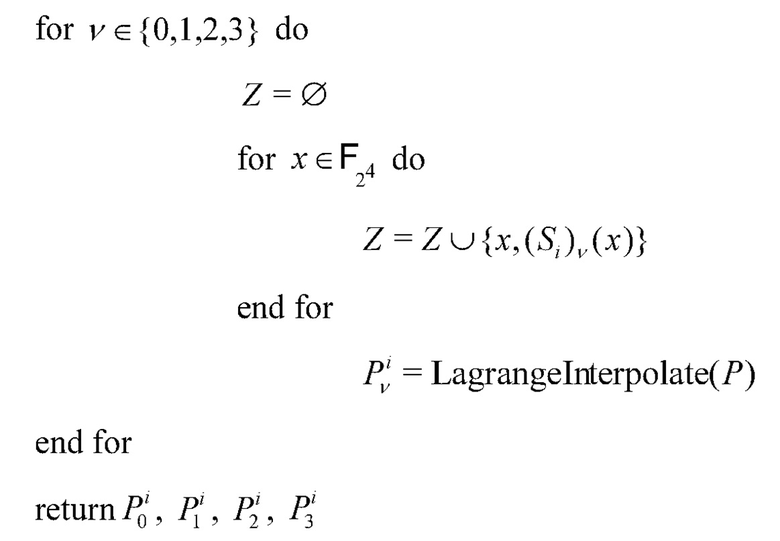
В конечном счете для надежного вычисления 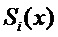 оценивается уравнение
оценивается уравнение
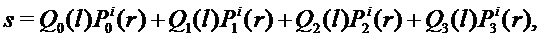
где каждый многочлен оценивается на долях. Здесь 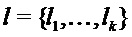 представляет
представляет 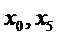 ,
, 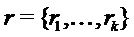 представляет
представляет 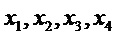 , и
, и  представляет результат
представляет результат 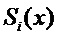 .
.
Это решение требует 4 умножения на  для вычисления всех степеней r, необходимых
для вычисления всех степеней r, необходимых 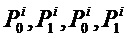 , с использованием циклотомического способа и 1 умножение для вычисления степеней l, необходимых для оценивания многочленов степени 3
, с использованием циклотомического способа и 1 умножение для вычисления степеней l, необходимых для оценивания многочленов степени 3 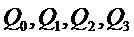 . Затем необходимо 4 умножения для вычисления произведений
. Затем необходимо 4 умножения для вычисления произведений  . В заключение это решение требует 9 умножений на
. В заключение это решение требует 9 умножений на  . Многочлены
. Многочлены 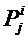 требуют 15 сложений каждый, а многочлены
требуют 15 сложений каждый, а многочлены 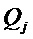 требуют 3 сложения каждый. Поэтому наше решение требует 4*15+4*3+3=75 сложений.
требуют 3 сложения каждый. Поэтому наше решение требует 4*15+4*3+3=75 сложений.
Фиг. 5a схематически показывает блок-схему последовательности операций для вычислительного способа 500. Вычислительный способ 500 выполнен с возможностью оценивания функции данных (S), отображающей некоторое количество (n) входных переменных в некоторое количество выходных переменных (m), при этом функция данных организована в вычислительном способе в виде вычисления, содержащего функции выбора и функции оценки, причем входные переменные разбиваются на одну или несколько переменных выбора и одну или несколько переменных оценки, для каждой конкретной комбинации значений переменных выбора (v) задается соответствующая функция выбора (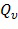 ) и функция оценки (
) и функция оценки (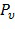 ). Вычислительный способ 500 содержит
). Вычислительный способ 500 содержит
часть 510 выбора, содержащую
- прием одной или нескольких переменных выбора, и
- оценивание функций выбора по принятым переменным выбора, при этом функция выбора в качестве входа принимает переменные выбора, а выход функции выбора указывает, равны ли переменные выбора, принятые в функции выбора, конкретной комбинации значений, соответствующих функции выбора,
часть 520 оценки, содержащую
- прием одной или нескольких переменных оценки, и
- оценивание функций оценки по принятым переменным оценки, при этом функция оценки в качестве входа принимает переменные оценки, а выход функции оценки представляет собой выход функции данных, входом которой является объединение переменных оценки и конкретной комбинации значений переменных выбора, соответствующих функции оценки, и
комбинационную часть 530, выполненную с возможностью комбинации выходов механизма выбора и механизма оценки в выход функции данных для входных переменных.
Дополнительный вариант осуществления вычислительного способа 550 содержит
- прием 560 входных переменных, предпочтительно кодированных в виде нескольких кодированных долей
- оценивание 570 многочленов выбора для каждой комбинации значений переменных выбора, со входом виде фактических принятых переменных выбора из принятых входных переменных,
- оценивание 580 многочленов оценки для каждой комбинации значений переменных выбора, со входом виде фактических принятых переменных оценки из принятых входных переменных,
- вычисление 590 комбинации многочленов выбора и оценки, например, путем умножения результатов многочленов выбора на результат соответствующих многочленов оценки и сложения результатов умножений.
Оценки 570 и 580 и вычисление 590 могут выполняться с помощью сети таблиц, оперирующей кодированными переменными.
Возможны многие разные способы исполнения способов 500 и 550, что будет очевидно специалисту в данной области техники. Например, может меняться порядок этапов, или некоторые этапы могут исполняться параллельно. Кроме того, между этапами можно вставить другие этапы способа. Вставленные этапы могут представлять собой уточнения способа, например описанные в этом документе, или могут быть не связаны со способом. Например, этапы 570 и 580 могут исполняться параллельно, по меньшей мере частично. Кроме того, заданный этап может быть не завершен полностью перед тем, как начинается следующий этап.
Способ в соответствии с изобретением может исполняться с использованием программного обеспечения, которое содержит команды для побуждения процессорной системы выполнить способ 500 и/или 550. Программное обеспечение может включать в себя только те этапы, которые выполняются конкретным подобъектом системы. Программное обеспечение может храниться на подходящем носителе информации, например жестком диске, дискете, запоминающем устройстве, оптическом диске и т. п. Программное обеспечение можно отправить в виде сигнала по проводу, или беспроводным способом, или с использованием сети передачи данных, например Интернета. Программное обеспечение можно сделать доступным для загрузки и/или для удаленного использования на сервере. Способ в соответствии с изобретением может исполняться с использованием потока двоичных сигналов, выполненного с возможностью конфигурирования программируемой логики, например программируемой пользователем вентильной матрицы (FPGA), для выполнения способа.
Станет понятно, что изобретение также распространяется на компьютерные программы, особенно на компьютерные программы на некотором носителе, приспособленном для применения изобретения на практике. Программа может быть в виде исходного кода, объектного кода, переходного кода между исходным и объектным кодом, например, в частично компилированном виде, или в любом другом виде, подходящем для использования в реализации способа в соответствии с изобретением. Вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером команды, соответствующие каждому из этапов обработки по меньшей мере в одном из изложенных способов. Эти команды могут подразделяться на подпрограммы и/или храниться в одном или нескольких файлах, которые могут быть связаны статически или динамически. Другой вариант осуществления, относящийся к компьютерному программному продукту, содержит исполняемые компьютером команды, соответствующие каждому из средств по меньшей мере в одной из изложенных систем и/или продуктов.
Фиг. 7a показывает машиночитаемый носитель 1000 с записываемой частью 1010, содержащей компьютерную программу 1020, при этом компьютерная программа 1020 содержит команды для побуждения процессорной системы выполнить способ вычисления в соответствии с вариантом осуществления. Компьютерную программу 1020 можно воплотить на машиночитаемом носителе 1000 в виде физических меток или посредством намагничивания машиночитаемого носителя 1000. Однако с тем же успехом возможен любой другой подходящий вариант осуществления. Кроме того, станет понятно, что хотя машиночитаемый носитель 1000 показан здесь в виде оптического диска, машиночитаемый носитель 1000 может быть любым подходящим машиночитаемым носителем, например жестким диском, твердотельным запоминающим устройством, флэш-памятью и т. п., и может быть незаписываемым либо записываемым. Компьютерная программа 1020 содержит команды для побуждения процессорной системы выполнить упомянутый способ вычисления.
Фиг. 7b показывает на схематическом представлении процессорную систему 1140 в соответствии с вариантом осуществления. Процессорная система содержит одну или несколько интегральных схем 1110. Архитектура одной или нескольких интегральных схем 1110 схематически показана на фиг. 7b. Схема 1110 содержит блок 1120 обработки, например CPU, для выполнения компонентов компьютерной программы, чтобы исполнить способ в соответствии с вариантом осуществления и/или реализовать его модули или блоки. Схема 1110 содержит запоминающее устройство 1122 для хранения программного кода, данных и т. п. Часть запоминающего устройства 1122 может быть только для чтения. Схема 1110 может содержать элемент 1126 связи, например антенну, соединители или то и другое, и т. п. Схема 1110 может содержать специальную интегральную схему 1124 для выполнения части или всей обработки, заданной в способе. Процессор 1120, запоминающее устройство 1122, специальная ИС 1124 и элемент 1126 связи могут быть подключены друг к другу через межсоединение 1130, например шину. Процессорная система 1110 может быть выполнена с возможностью контактной и/или бесконтактной связи с использованием антенны и/или соединителей соответственно.
Следует отметить, что вышеупомянутые варианты осуществления скорее иллюстрируют, а не ограничивают изобретение, и специалисты в данной области техники смогут спроектировать многие альтернативные варианты осуществления.
В формуле изобретения любые знаки ссылок, помещенные в круглые скобки, не следует толковать как ограничивающие формулу изобретения. Использование глагола "содержать" и его спряжений не исключает наличия элементов или этапов помимо заявленных в формуле изобретения. Употребление элемента в единственном числе не исключает наличия множества таких элементов. Изобретение может быть реализовано посредством аппаратных средств, содержащих несколько отдельных элементов, и посредством соответствующим образом запрограммированного компьютера. В пункте формулы на устройство, перечисляющем несколько средств, некоторые из этих средств могут быть воплощены с помощью одного и того же элемента аппаратных средств. Сам факт, что некоторые критерии перечисляются во взаимно разных зависимых пунктах формулы изобретения, не указывает на то, что сочетание этих критериев не может использоваться с пользой.
В формуле изобретения ссылки в круглых скобках относятся к знакам ссылок на чертежах в вариантах осуществления или к формулам вариантов осуществления, соответственно повышая понятность формулы изобретения. Эти ссылки не следует толковать как ограничивающие формулу изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| КРИПТОГРАФИЧЕСКОЕ УСТРОЙСТВО И КОДИРУЮЩЕЕ УСТРОЙСТВО | 2016 |
|
RU2692419C1 |
| КРИПТОГРАФИЧЕСКОЕ УСТРОЙСТВО, ПРИСПОСОБЛЕННОЕ ДЛЯ ВЫЧИСЛЕНИЯ ЦЕЛЕВОГО БЛОЧНОГО ШИФРА | 2016 |
|
RU2711193C2 |
| УСТРОЙСТВО И СПОСОБ ВЫЧИСЛЕНИЯ БЛОЧНОГО ШИФРА | 2018 |
|
RU2696334C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, КОНФИГУРИРУЕМОЕ С ПОМОЩЬЮ ТАБЛИЧНОЙ СЕТИ | 2013 |
|
RU2661308C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, СОДЕРЖАЩЕЕ СЕТЬ ТАБЛИЦ | 2013 |
|
RU2676454C2 |
| ЭЛЕКТРОННОЕ УСТРОЙСТВО БЛОЧНОГО ШИФРОВАНИЯ, ПОДХОДЯЩЕЕ ДЛЯ ОБФУСКАЦИИ | 2014 |
|
RU2666281C2 |
| УСТРОЙСТВО ВИРТУАЛЬНОЙ МАШИНЫ, ИМЕЮЩЕЕ УПРАВЛЯЕМУЮ КЛЮЧОМ ОБФУСКАЦИЮ, И СПОСОБ | 2012 |
|
RU2620712C2 |
| АДАПТИВНОЕ УПРАВЛЕНИЕ РАЗРЕШЕНИЕМ НА БЛОЧНОЙ ОСНОВЕ | 2020 |
|
RU2836360C2 |
| ЭФФЕКТИВНОЕ ПО ИСПОЛЬЗОВАНИЮ ПАМЯТИ АДАПТИВНОЕ БЛОЧНОЕ КОДИРОВАНИЕ | 2007 |
|
RU2413360C1 |
| СПОСОБ СКРЫТОЙ ПЕРЕДАЧИ ЗАШИФРОВАННОЙ ИНФОРМАЦИИ ПО МНОЖЕСТВУ КАНАЛОВ СВЯЗИ | 2011 |
|
RU2462825C1 |
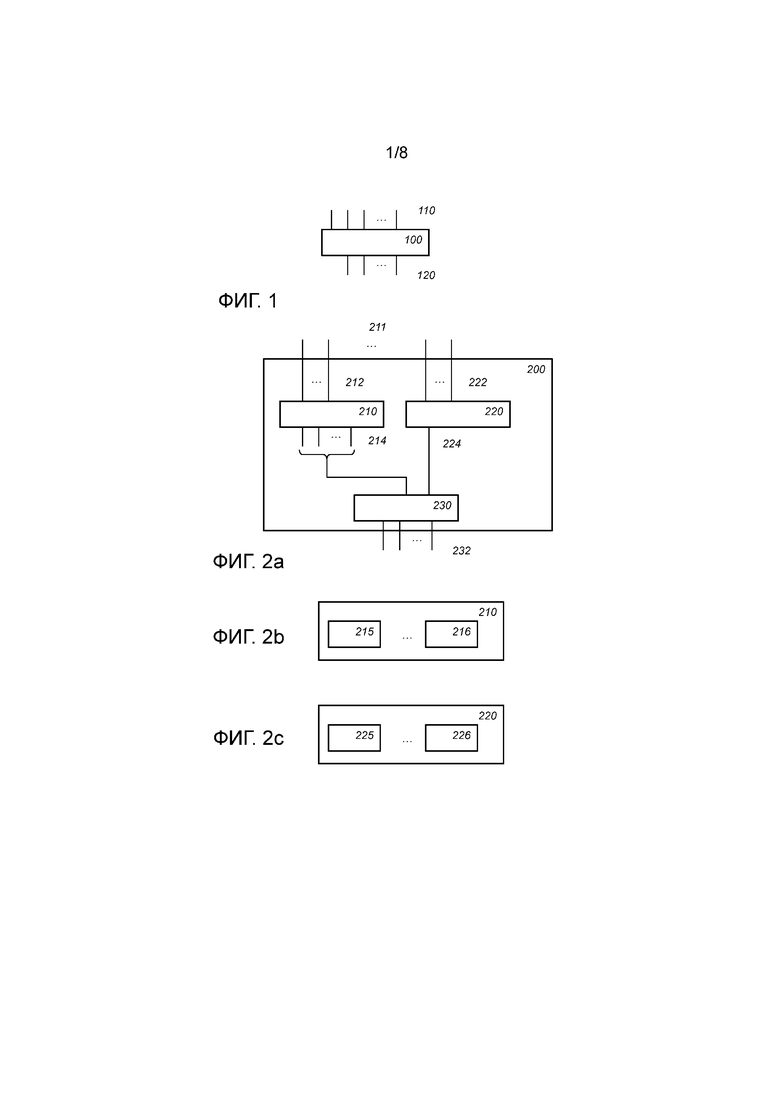
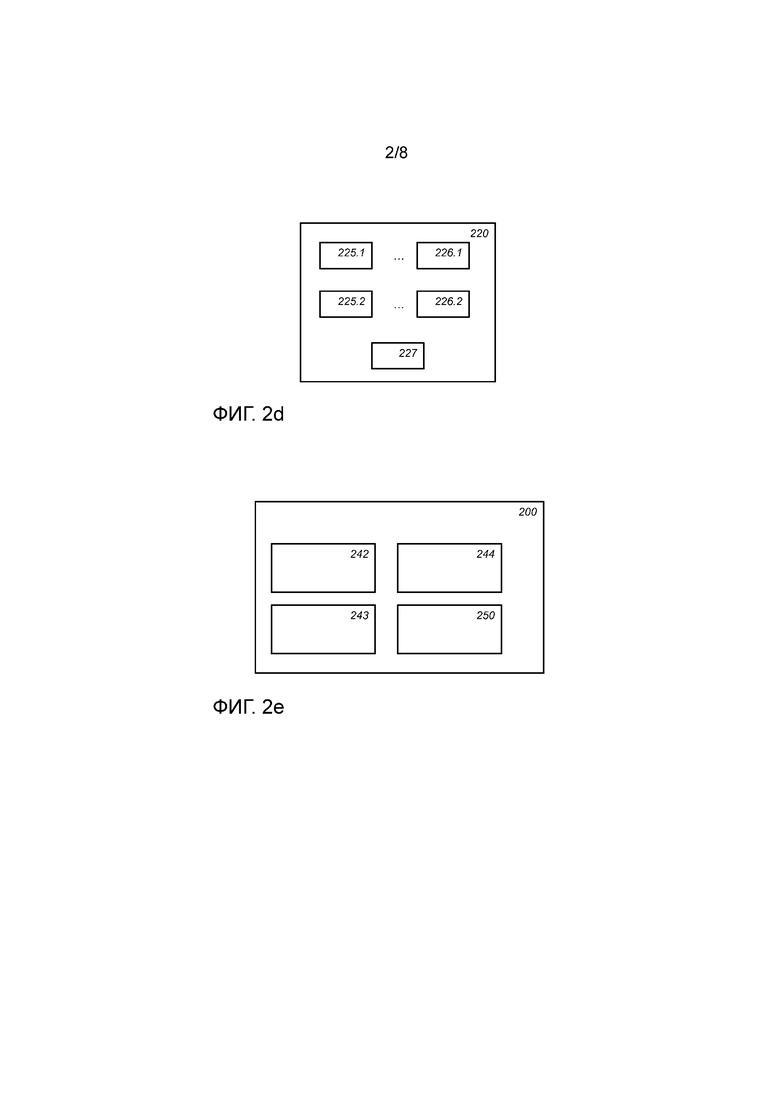

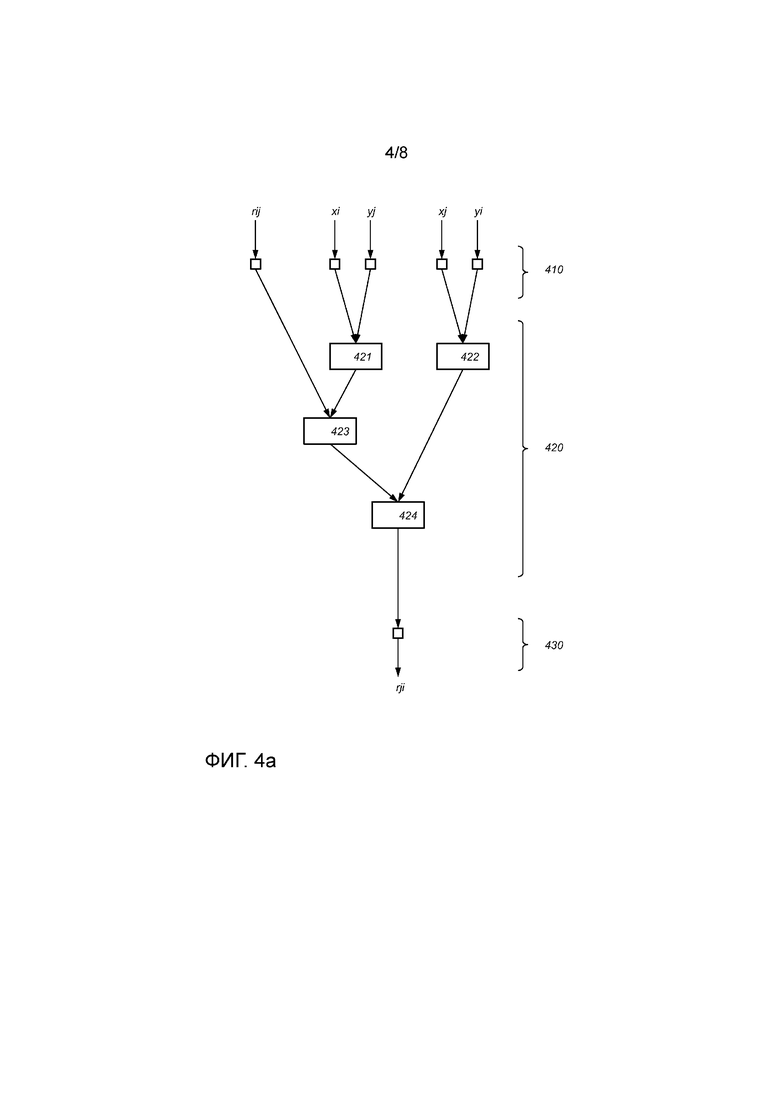
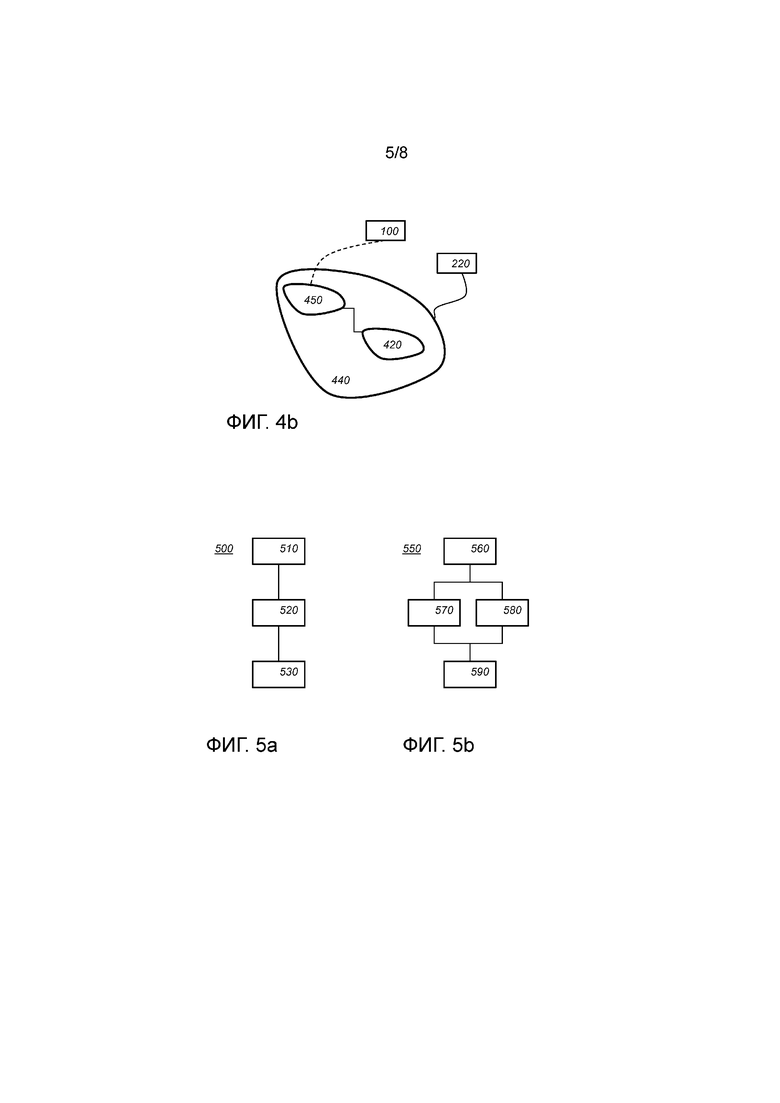
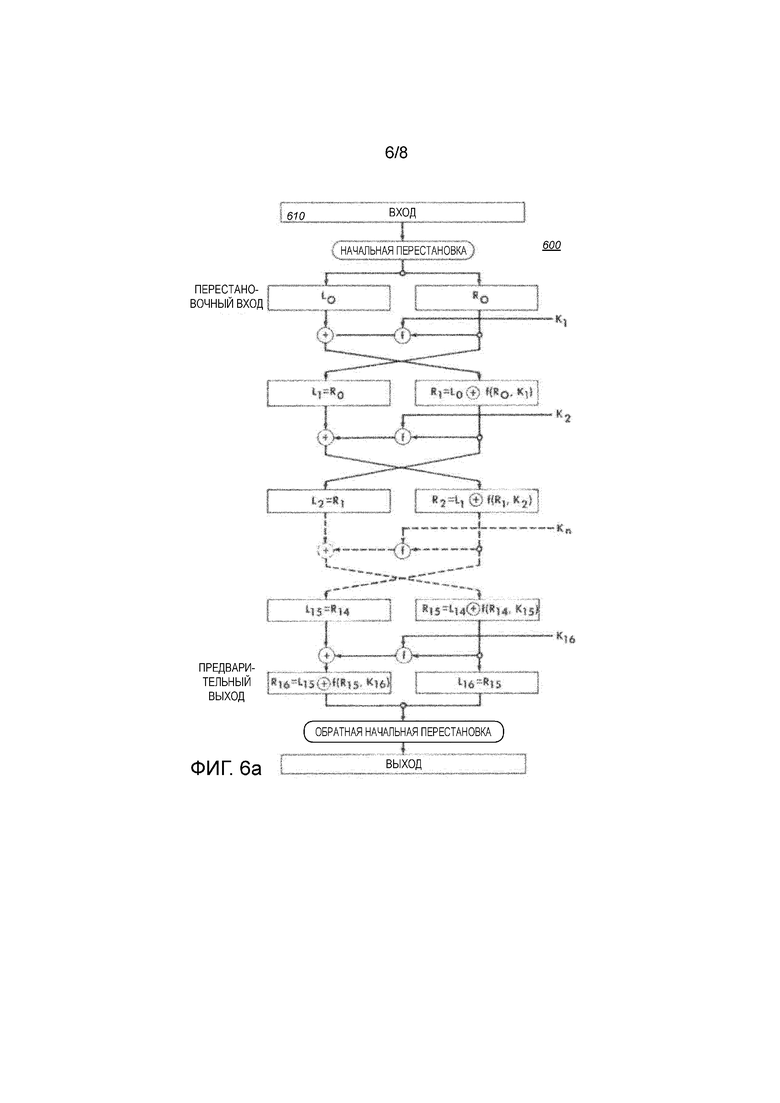
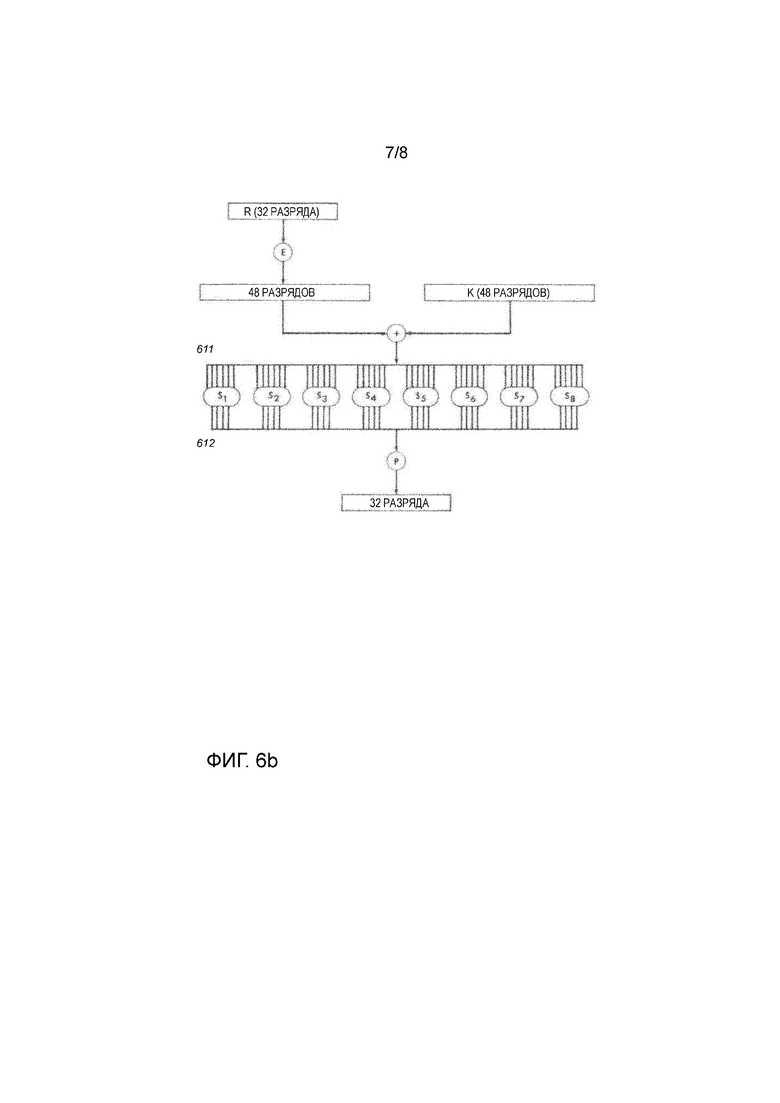
Группа изобретений относится к области вычислительной техники и может быть использована для защиты программного обеспечения от взлома. Техническим результатом является повышение защищенности. Вычислительное устройство (200) выполнено с возможностью оценивания функции данных (S), отображающей некоторое количество (n) входных переменных в некоторое количество выходных переменных (m). Вычислительное устройство содержит механизм выбора (220), в качестве входа принимающий переменные выбора, и механизм оценки (210), выполненный с возможностью приема одной или нескольких переменных оценки и оценивания функций оценки по принятым переменным оценки, при этом функция оценки в качестве входа принимает переменные оценки. 3 н. и 11 з.п. ф-лы, 15 ил., 2 табл.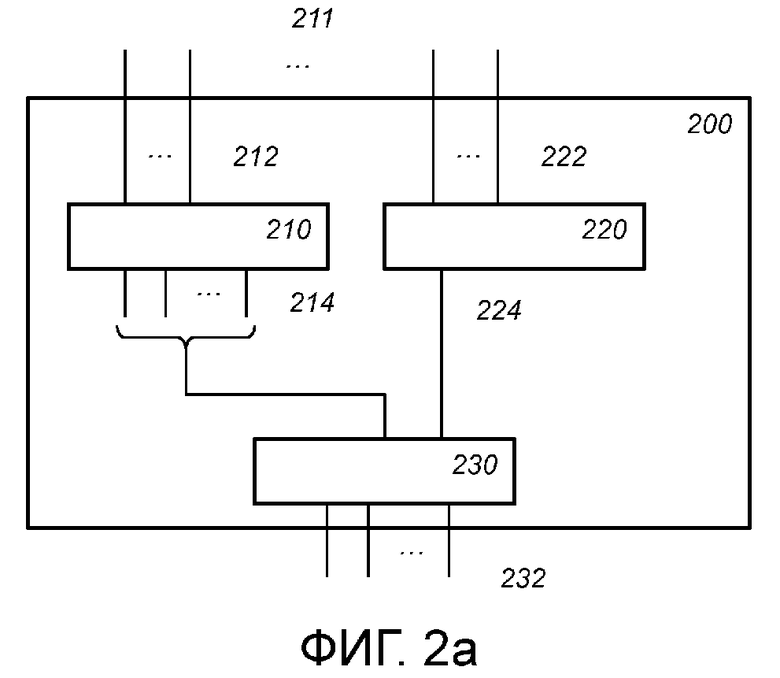
1. Вычислительное устройство (200), выполненное с возможностью оценивания функции данных (S), отображающей некоторое количество (n) входных переменных в некоторое количество выходных переменных (m), при этом функция данных организована в вычислительном устройстве в виде вычисления, содержащего функции выбора и функции оценки, причем входные переменные разбиваются на одну или несколько переменных выбора и одну или несколько переменных оценки, для каждой конкретной комбинации значений переменных выбора (v) задается соответствующая функция выбора ( ) и функция оценки (
) и функция оценки (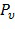 ),
),
при этом вычислительное устройство содержит
- механизм выбора (220), выполненный с возможностью приема одной или нескольких переменных выбора и оценивания функций выбора по принятым переменным выбора, при этом функция выбора в качестве входа принимает переменные выбора, а выход функции выбора указывает, равны ли переменные выбора, принятые в функции выбора, конкретной комбинации значений, соответствующих функции выбора,
- механизм оценки (210), выполненный с возможностью приема одной или нескольких переменных оценки и оценивания функций оценки по принятым переменным оценки, при этом функция оценки в качестве входа принимает переменные оценки, а выход функции оценки представляет собой выход функции данных, у которой входом является объединение переменных оценки и конкретной комбинации значений переменных выбора, соответствующих функции оценки, и
- комбинационный механизм (230), выполненный с возможностью комбинации выходов механизма выбора и механизма оценки в выход функции данных для входных переменных, при этом комбинационный механизм суммирует произведения (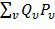 ) функции выбора (
) функции выбора ( ) и функции оценки (
) и функции оценки (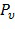 ), соответствующие одной и той же конкретной комбинации значений, причем упомянутое суммирование проводится по всем комбинациям значений переменных выбора (v).
), соответствующие одной и той же конкретной комбинации значений, причем упомянутое суммирование проводится по всем комбинациям значений переменных выбора (v).
2. Вычислительное устройство по п.1, в котором механизм выбора содержит несколько блоков выбора, реализующих функции выбора, и/или в котором механизм оценки содержит несколько блоков оценки, реализующих функции оценки.
3. Вычислительное устройство по любому из предшествующих пунктов, в котором переменные выбора дополнительно разбиваются на несколько групп переменных выбора, при этом функция выбора организована в вычислительном устройстве в виде произведения нескольких подфункций выбора, причем каждая соответствует группе из нескольких групп переменных выбора, при этом подфункция выбора в качестве входа принимает переменные выбора в группе, а выход подфункции выбора указывает, равны ли принятые переменные выбора конкретной комбинации значений в группе, соответствующей функции выбора.
4. Вычислительное устройство по п. 1, в котором входные переменные и/или выходные переменные являются разрядами.
5. Вычислительное устройство по п. 1, организованное в виде блочного шифра, где функция данных является S-блоком блочного шифра.
6. Вычислительное устройство по п. 5, в котором блочный шифр является блочным шифром DES или тройного DES и в котором S-блок является одним из S-блоков DES.
7. Вычислительное устройство по п. 1, в котором количество входных переменных (n) больше количества выходных переменных (m), при этом количество переменных оценки равно количеству выходных переменных.
8. Вычислительное устройство по п. 1, в котором одна или несколько входных переменных кодируются.
9. Вычислительное устройство по п. 8, в котором кодированная входная переменная (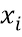 ) кодируется в виде множества долей (
) кодируется в виде множества долей ( ), в частности при этом кодированная входная переменная (
), в частности при этом кодированная входная переменная (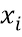 ) кодируется в виде множества кодированных долей (
) кодируется в виде множества кодированных долей ( ), точнее при этом множество долей (
), точнее при этом множество долей ( ) кодируются вместе с множеством состояний (
) кодируются вместе с множеством состояний ( ).
).
10. Вычислительное устройство по п. 1, в котором функция выбора реализуется в виде многочлена выбора и/или функция оценки реализуется в виде многочлена оценки.
11. Вычислительное устройство по п. 1, в котором функции выбора используются для нескольких функций данных.
12. Вычислительное устройство по п. 1, в котором механизм выбора, механизм оценки и/или комбинационный механизм реализуется в виде сети таблиц.
13. Вычислительный способ, выполненный с возможностью оценивания функции данных (S), отображающей некоторое количество (n) входных переменных в некоторое количество выходных переменных (m), при этом функция данных организована в вычислительном способе в виде вычисления, содержащего функции выбора и функции оценки, причем входные переменные разбиваются на одну или несколько переменных выбора и одну или несколько переменных оценки, для каждой конкретной комбинации значений переменных выбора (v) задается соответствующая функция выбора ( ) и функция оценки (
) и функция оценки (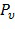 ),
),
при этом вычислительный способ содержит
- этап выбора, на котором принимают одну или несколько переменных выбора и оценивают функции выбора по принятым переменным выбора, при этом функция выбора в качестве входа принимает переменные выбора, а выход функции выбора указывает, равны ли переменные выбора, принятые в функции выбора, конкретной комбинации значений, соответствующих функции выбора,
- этап оценки, на котором принимают одну или несколько переменных оценки и оценивают функции оценки по принятым переменным оценки, при этом функция оценки в качестве входа принимает переменные оценки, а выход функции оценки представляет собой выход функции данных, у которой входом является объединение переменных оценки и конкретной комбинации значений переменных выбора, соответствующих функции оценки, и
- комбинационный этап, на котором комбинируют выходы механизма выбора и механизма оценки в выход функции данных для входных переменных, при этом комбинационный этап содержит этап, на котором суммируют произведения (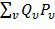 ) функции выбора (
) функции выбора ( ) и функции оценки (
) и функции оценки (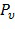 ), соответствующие одной и той же конкретной комбинации значений, причем упомянутое суммирование проводится по всем комбинациям значений переменных выбора (v).
), соответствующие одной и той же конкретной комбинации значений, причем упомянутое суммирование проводится по всем комбинациям значений переменных выбора (v).
14. Машиночитаемый носитель (1000), содержащий команды компьютерной программы (1020), выполненные с возможностью выполнения способа по п. 13, когда компьютерная программа выполняется на компьютере.
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
| US 5442306 A, 15.08.1995 | |||
| СИСТЕМА БЛОЧНОЙ КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ, ИСПОЛЬЗУЮЩАЯ ПРЕОБРАЗОВАНИЯ ДЛЯ СОКРЫТИЯ ОСНОВНОЙ ФУНКЦИИ КРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫ КАЖДОГО ЦИКЛА ШИФРОВАНИЯ | 2004 |
|
RU2370897C2 |
Авторы
Даты
2019-12-06—Публикация
2016-12-14—Подача