ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ
Настоящее изобретение относится к криптографическому устройству, кодирующему устройству, криптографическому способу, способу кодирования, компьютерной программе и компьютерно-читаемому носителю данных.
УРОВЕНЬ ТЕХНИКИ
При создании криптографического устройства нужно беспокоиться не только о выборе звуковых криптографических примитивов, но и о предотвращении побочных каналов. Через побочный канал атакующий получает информацию о криптографических вычислениях, которые выходят за пределы нормального поведения ввода/вывода. Атака по побочным каналам является атакой на основе информации, получаемой из физической реализации криптосистемы, а не только на основе анализа криптографического алгоритма и/или метода грубой силы.
Особенно существенным побочным каналом является так называемая модель атаки методом «белого ящика». В модели атаки методом «белого ящика» атакующий имеет полный доступ к внутренней организации алгоритма во время его выполнения. В частности, атакующий может наблюдать за переменными и может даже модифицировать данные во время выполнения. Защита секретной информации, такой как секретные ключи, является особенно трудной при модели атаки методом «белого ящика».
В работе ʺDES and the Differential Power Analysis, The ʺDuplicationʺ methodʺ за авторством Goubin и Patarin выдвинуто предложение о том, как предотвратить некоторые атаки по побочным каналам. В этой работе переменную v представляют k переменными v1,…,vk таким образом, что v=∑vi. Побочным каналом, рассматриваемым в этой работе, является потребление электроэнергии микроконтроллером.
Авторы изобретения обнаружили, что это решение не является адекватным модели «белого ящика» и может быть взломано. Таким образом, задача состоит в улучшении стойкости реализаций криптографических функций при модели атаки методом «белого ящика».
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
Обеспечено криптографическое устройство, выполненное с возможностью вычисления зависящей от ключа криптографической функции для входного сообщения. Криптографическое устройство содержит
- хранилище данных, выполненное с возможностью хранения множественных переменных, на которые криптографическое устройство воздействует для вычисления криптографической функции, причем переменная распределена по множественным долям и представлена в хранилище данных в виде множественных кодированных долей, причем кодированная доля является кодированием доли вместе с состоянием, причем множественные состояния, соответствующие одной и той же переменной, имеют соотношение с входным сообщением, так что существует инъективное отображение из входного сообщения во множественные состояния,
- хранилище таблиц, хранящее множественные справочные таблицы, причем справочная таблица принимает в качестве входных данных одну или более кодированных долей одной или более переменных, причем множественные справочные таблицы вместе образуют сеть таблиц, реализующую криптографическую функцию,
- блок управления, выполненный с возможностью применения криптографической функции к входному сообщению посредством применения множественных справочных таблиц к переменным, представленным в хранилище данных.
Как будет объяснено более полно в данном описании, возможной атакой на реализацию криптографической функции является конфликтная атака. В конфликтной атаке атакующий старается найти такие два разных входных сообщения, чтобы некоторая внутренняя переменная имела одно и то же значение для них обоих. Такой случай может дать информацию о ключе.
Кодированные доли представляют как доли переменной, так и множественные состояния. Поскольку существует инъективное отображение из входного сообщения во множественные состояния, не может быть таких двух разных входных сообщений, чтобы соответствующие два набора множественных состояний были одними и теми же. Поскольку состояния являются частью кодированных долей, не может быть таких двух разных входных сообщений, чтобы соответствующие кодированные доли были одними и теми же. Соответственно, предотвращаются конфликтные атаки на кодированные доли. Результирующее криптографическое устройство является более устойчивым к атакам по модели «белого ящика».
Криптографическое устройство также обеспечивает механизм защиты от дифференциального анализа энергопотребления. Несмотря на то, что случайные кодирования блокируют успешный статистический анализ отношений между разными возникающими значениями, они все же могут позволить успешно получить статистические данные на основе конфликтов. Поскольку последнее предотвращается, нарушается статистический анализ, используемый атаками на основе дифференциального анализа энергопотребления.
В одном варианте осуществления,
- хранилище таблиц хранит сеть таблиц умножения для умножения первой переменной, распределенной по первому множеству долей и представленной в хранилище данных в виде первого множества кодированных долей, и второй переменной, распределенной по второму множеству долей, представленной в хранилище данных в виде второго множества кодированных долей, причем сеть таблиц умножения воздействует на первое и второе множество кодированных долей и получает третье множество кодированных долей, представляющее произведение первой и второй переменной,
- причем сеть таблиц умножения содержит одну или более подсетей таблиц прямых произведений для вычисления произведения первой доли первого множества долей и второй доли второго множества долей, причем подсети таблиц прямых произведений вычисляют сумму произведения первой доли и второй доли на основе соответствующих кодированных долей плюс функции рандомизации от входного сообщения.
Как будет объяснено в данном описании, вычисление на основе переменных может быть преобразовано в вычисление на основе кодированных долей. В частности, две переменные, представленные в виде кодированных долей, могут быть умножены. В одном варианте осуществления умножения, требуются прямые произведения, а именно, произведение доли первой переменной (например, представленной в виде xi) и доли второй переменной (например, представленной в виде yj). Для запутывания этого вычисления может быть использован источник случайности. Авторы изобретения обнаружили, что генераторы случайных чисел в программном обеспечении легко идентифицируются и обходятся, в результате чего это запутывание аннулируется. Эта проблема может быть предотвращена посредством использования функции рандомизации от входного сообщения. Функция рандомизации от входного сообщения может быть определена в криптографическом устройстве. Функция рандомизации может быть определена при создании криптографического устройства, в случае программной реализации, во время компиляции программного средства. Поскольку функция рандомизации определена, она не может быть легко идентифицирована в других сетях таблиц. Если одни и те же входные данные будет использоваться дважды, функция рандомизации будет вырабатывать одни и те же результаты; таким образом, эта функция не выделяется в сети таблиц.
Одним путем обеспечения того, чтобы существовало инъективное отображение, является кодирование входного сообщения даже до использования ключа. Инъективное отображение может затем сохраняться на протяжении всего вычисления вплоть до момента создания переменной w. Кодирование входного сообщения может быть выполнено компьютером, внешним по отношению к криптографическому устройству. Например, входное сообщение может представлять контент, который создается для дешифрования в криптографическом устройстве. Входное сообщение может быть принято криптографическим устройством в форме множественных наборов кодированных долей. Однако кодирование может быть также выполнено в криптографическом устройстве, например, для защиты от раскрытия ключа посредством конфликтной атаки.
Обеспечено кодирующее устройство для кодирования входного сообщения, для использования вместе с криптографическим устройством по п. 1 формулы изобретения. Кодирующее устройство содержит
- принимающий блок для приема входного сообщения, причем входное сообщение содержит множественные входные части,
- кодирующий блок, выполненный с возможностью, для каждой части входного сообщения,
- распределять часть входного сообщения по множественным долям посредством применения множественных функций распределения к входному сообщению для получения множественных долей, причем объединяющая функция, применяемая к функциям распределения, равняется части входного сообщения
- применять инъективное отображение из входного сообщения для получения множественных состояний, причем число множественных долей и множественных состояний является одинаковым
- кодировать каждую долю из множественных долей вместе с соответствующим состоянием из множественных состояний и получать множественные кодированные доли, представляющие данную часть.
Кодирующее устройство может, но не обязательно, содержаться в криптографическом устройстве.
Криптографическое и кодирующее устройства являются электронными устройствами. Например, они могут быть мобильным электронным устройством, таким как телефон или планшет. Они могут быть телевизионной приставкой, компьютером, проигрывателем мультимедиа, телевизором и т.п.
Способ криптографической обработки и кодирования, описанный здесь, может быть применен в разнообразных практических применениях. Такие практические применения включают в себя управление цифровым контентом, защищенные банковские операции, управление доступом, защита электронных хранилищ и т.п.
Способ согласно настоящему изобретению может быть реализован на компьютере в виде компьютерно-реализуемого способа, или в специальном аппаратном средстве, или в их комбинации. Выполняемый код для способа согласно настоящему изобретению может храниться в компьютерном программном продукте. Примеры компьютерных программных продуктов включают в себя запоминающие устройства, оптические запоминающие устройства, интегральные схемы, серверы, онлайновые программные средства и т.д. Предпочтительно, компьютерный программный продукт содержит энергонезависимое программное кодовое средство, хранимое на компьютерно-читаемом носителе данных, для выполнения способа согласно настоящему изобретению при выполнении на компьютере упомянутого программного продукта.
В предпочтительном варианте осуществления, компьютерная программа содержит компьютерное программное кодовое средство, выполненное с возможностью выполнения всех этапов способа согласно настоящему изобретению при выполнении компьютерной программы на компьютере. Предпочтительно, компьютерная программа реализуется на компьютерно-читаемом носителе данных.
Другой аспект настоящего изобретения обеспечивает способ создания компьютерной программы, доступной для загрузки. Этот аспект используется, когда компьютерная программа загружается, например, в хранилище Apple's App Store, хранилище Google's Play Store, или хранилище Microsoft's Windows Store, и когда компьютерная программа является доступной для загрузки из такого хранилища.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Дополнительные подробности, аспекты и варианты осуществления настоящего изобретения будут описаны, только в качестве примера, со ссылкой на чертежи. Элементы на фигурах показаны для простоты и ясности и не обязательно приведены в масштабе. На фигурах, элементы, которые соответствуют уже описанным элементам, могут иметь те же самые ссылочные позиции. В чертежах,
Фиг. 1 схематично показывает пример кодирования переменной,
Фиг. 2 схематично показывает пример варианта осуществления криптографического устройства,
Фиг. 3 схематично показывает пример варианта осуществления кодирующего устройства,
Фиг. 4а схематично показывает пример варианта осуществления сети таблиц,
Фиг. 4b схематично показывает пример варианта осуществления сети таблиц,
Фиг. 5а схематично показывает блок-схему последовательности операций криптографического способа,
Фиг. 5b схематично показывает блок-схему последовательности операций способа кодирования,
Фиг. 6 схематично показывает блок-схему последовательности операций блочного шифра DES,
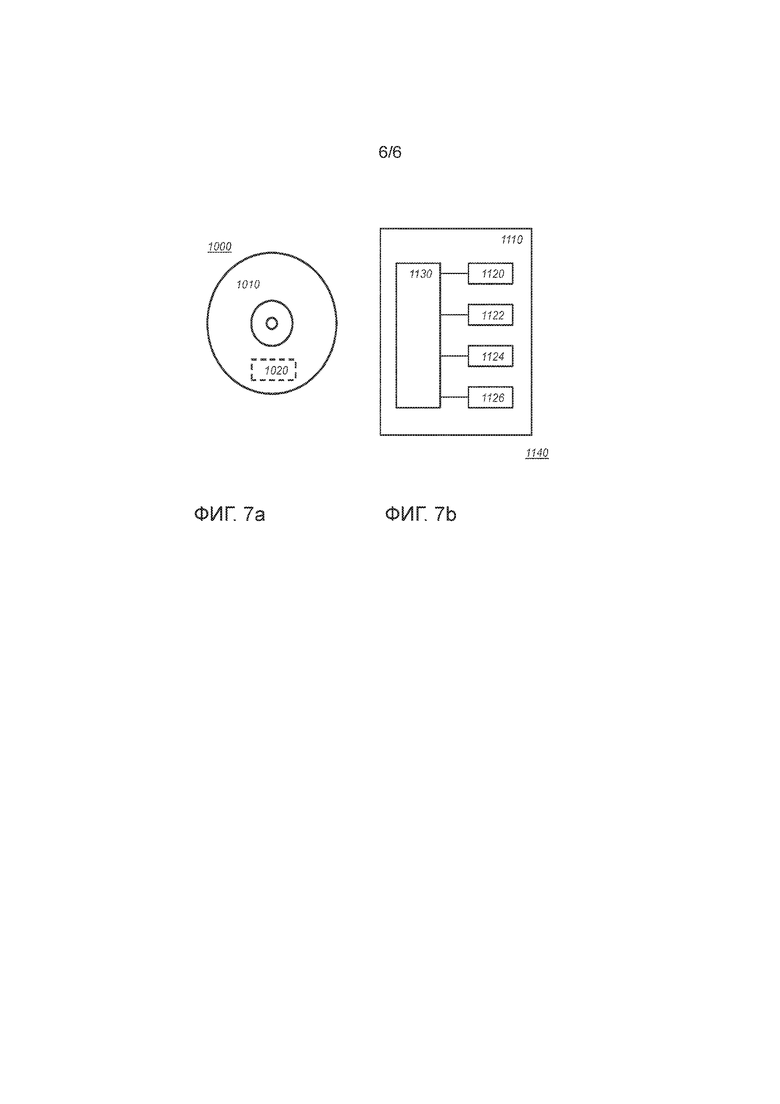
Фиг. 7а схематично показывает компьютерно-читаемый носитель данных, имеющий записываемую часть, содержащую компьютерную программу согласно одному варианту осуществления,
Фиг. 7b схематично показывает представление процессорной системы согласно одному варианту осуществления.
ПОДРОБНОЕ ОПИСАНИЕ ПРЕДПОЧТИТЕЛЬНЫХ ВАРИАНТОВ ОСУЩЕСТВЛЕНИЯ
В то время как это изобретение допускает варианты осуществления во многих других формах, в чертежах показаны и будут подробно описаны здесь один или более конкретных вариантов осуществления, причем следует понимать, что настоящее раскрытие следует считать примером реализации принципов настоящего изобретения, и оно не предназначено для ограничения настоящего изобретения показанными и описанными конкретными вариантами осуществления.
Далее, для легкости понимания, элементы вариантов осуществления описаны в ходе операций. Однако будет очевидно, что соответствующие элементы выполнены с возможностью выполнения функций, которые, как описано, выполняются ими.
Дополнительно, настоящее изобретение не ограничено данными вариантами осуществления, и настоящее изобретение заключается в каждом новом признаке или комбинации признаков, описанных выше или приведенных во взаимно отличающихся зависимых пунктах формулы изобретения.
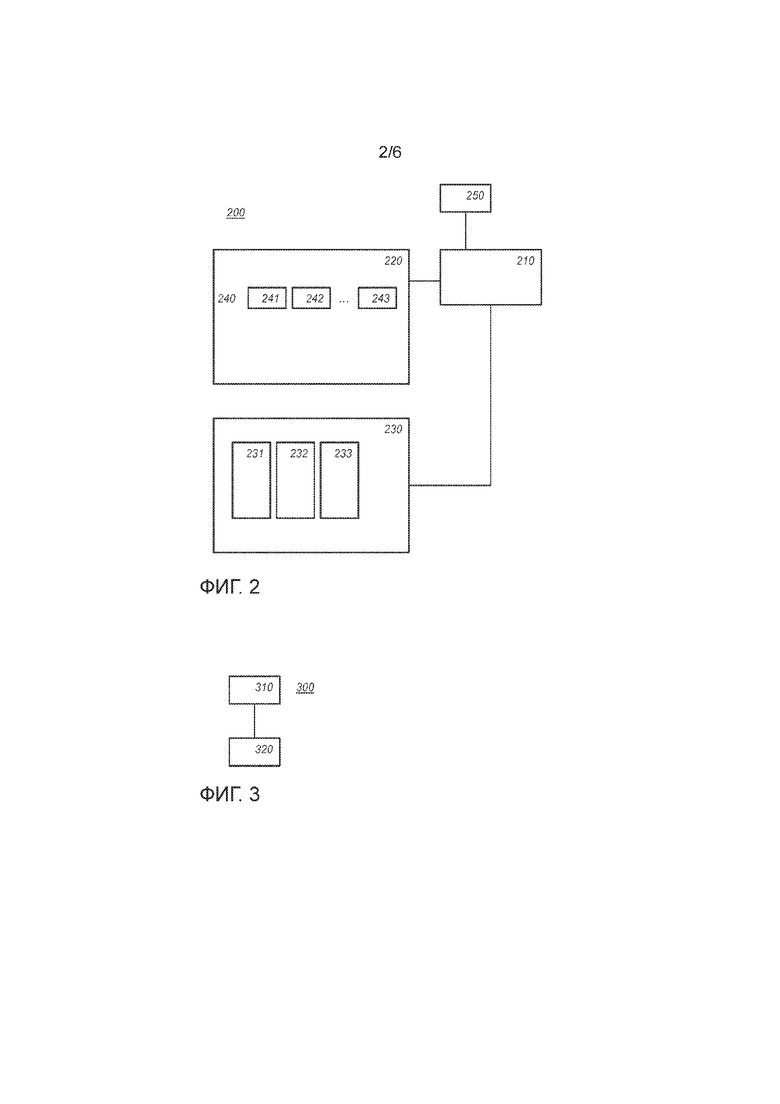
Фиг. 2 схематично показывает пример варианта осуществления криптографического устройства 200. Возможные варианты осуществления аспектов криптографического устройства 200 показаны со ссылкой на фиг. 1-4.
Криптографическое устройство 200 выполнено с возможностью вычисления зависящей от ключа K криптографической функции для входного сообщения М. Криптографическая функция может быть обозначена как fK. Результатом вычисления является выходное сообщение fK(M). Следует отметить, что ключ не обязательно должен быть явными входными данными функции, а может быть также встроен в нее, например, с использованием частичного вычисления.
Зависящие от ключа криптографические функции являются уязвимыми для так называемых конфликтных атак. В такой атаке, атакующий старается найти два разных входных сообщения M и M', для которых некоторая внутренняя зависящая от ключа переменная w имеет одно и то же значение в некоторый момент времени во время вычисления криптографической функции f.
Рассмотрим внутреннюю переменную w, которая зависит как от входного сообщения, так и от ключа. Обозначим соотношение между входным сообщением, ключом и переменной как w=gK(M). Предположим, что атакующий нашел два сообщения M и M', для которых gK(M)=gK(M'). Эта информация может быть использована при использовании корреляционных атак на основе, например, Анализа взаимной информации. В частности, атакующий теперь имеет уравнение gK(M)=gK(M'); никакой K, который не удовлетворяет этому уравнению, не может быть ключом. Кроме того, поскольку неизвестен только ключ K, нахождение K может прямо обеспечить информацию о секретном ключе. Еще более опасной эту атаку делает то, что многие блочные шифры имеют переменные, особенно в ранних раундах, которые зависят от относительно немногих битов секретного ключа K.
Внутренние переменные, которые имеют одно и то же значение для разных входных сообщений, могут быть обнаружены с использованием побочного канала. Например, это может быть обеспечено посредством исследования аппаратного средства, на котором выполняется вычисление. Конфликтные атаки являются особенно мощными, если криптографическая функция выполняется в программном средстве, поскольку атакующий может легко проверить, имеет ли или нет некоторая внутренняя переменная одно и то же значение. Атакующий может быть способен получить полный контроль над программным средством, которое выполняется на вычислительном устройстве, например, на смартфоне или на настольном компьютере, и т.д.
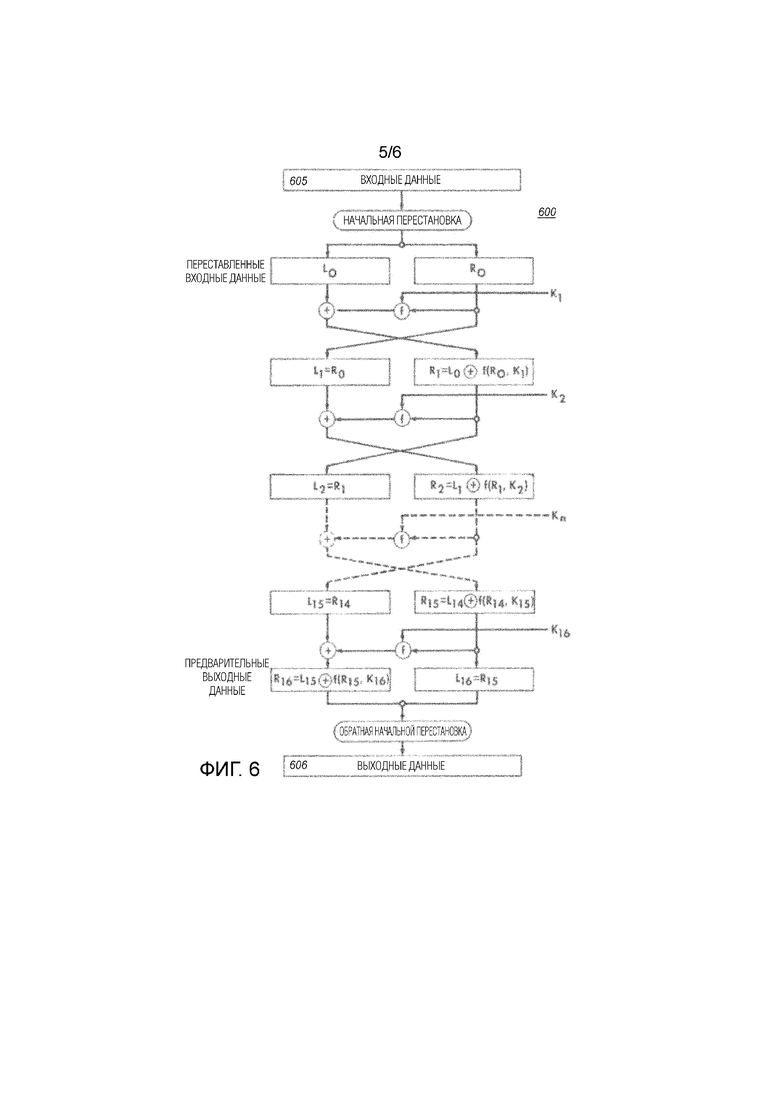
Зависящая от ключа криптографическая функция может быть, например, блочным шифром для шифрования или дешифрования входного сообщения M. Другие примеры включают в себя хэш-функции с ключами, функции аутентификации сообщений, потоковые шифры и т.п. Один пример блочного шифра приведен на фиг. 6.
Фиг. 6, которая скопирована из документа FIPS 46-3 (включенного в данный документ по ссылке), показывает блочный шифр DES, в частности, и блочные шифры Feistel, в общем. Блочный шифр принимает входные данные 605 блочного шифра, на которые воздействует последовательность раундов блочного шифра; в случае DES, имеется 16 раундов, для тройного DES 48. Первый раунд блочного шифра воздействует на входные данные 605 блочного шифра, каждый из следующих раундов воздействует на выходные данные предыдущих раундов. В раунде блочного шифра, функция раунда применяется к части выходных данных предыдущего раунда. Входные данные блочного шифра имеют размер данных, равный 64 битам в случае DES. Каждый раунд блочного шифра модифицирует свои входные данные раунда блочного шифра для создания выходных данных раунда блочного шифра. Все входные и выходные данные раундов блочного шифра имеют один и тот же размер данных. Стандарт шифрования данных описывает блочное кодирование с ключами 64-битового блока. Ключ официально имеет 64 бита, но только 56 его битов фактически используются в шифровании, от которого зависят ключи K1-K16 раундов. Следует отметить, что значительная часть промежуточных данных зависит как от входного сообщения, так и от ключа, что может быть использовано способом, описанным выше. Например, выходные данные S-блока являются уязвимыми для конфликтной атаки (S-блоки отдельно не показаны на фиг. 6). Например, переменные, которые представляют выходные данные функции раунда (показанной на фиг. 6 как 'f'), являются уязвимыми для конфликтной атаки.
Потенциальное улучшение по сравнению с упрощенной реализацией блочного шифра фиг. 6 состоит в кодировании переменной w, возможно, вместе с переменной s состояния. Вместо вычисления прямо на основе w, такая реализация может работать на основе значения x=Enc(w,s). Однако кодирование на основе самого себя не предотвращает конфликты. Два входных сообщения M и M', для которых кодированная переменная x является одинаковой, все же приводят к тому же самому уравнению gK(M)=gK(M').
Другое потенциальное улучшение состоит в распределении переменной w по множественным долям wj, например, таким образом, что 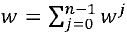 . Однако одновременный конфликт в отношении долей wj все же будет приводить к конфликту для w, который обеспечивает утечку того же самого количества информации. Хотя конфликты могут стать более редкими, они не будут устранены.
. Однако одновременный конфликт в отношении долей wj все же будет приводить к конфликту для w, который обеспечивает утечку того же самого количества информации. Хотя конфликты могут стать более редкими, они не будут устранены.
Следует отметить, что для того, чтобы конфликтная атака достигла цели, неважно, зашифрован ли ключ или только явно присутствует в реализации, например, встроен посредством частичного вычисления. Поскольку конфликтные атаки обходят кодирование данных, они особенно опасны для криптографии методом «белого ящика», поскольку они часто основаны на кодировании внутренних данных, например, переменных, ключей, и постоянных.
Авторы изобретения поняли, что существует значительная дополнительная проблема. В программной реализации некто может быть склонен к использованию псевдо-генератора случайных чисел (RNG) для создания некоторых долей w, но это не рекомендуется. Атакующий может быть способен устранить случайность посредством замены выходных данных RNG неслучайным значением. Даже если программная реализация осуществит вызов истинного генератора случайных чисел, этот вызов может быть перехвачен. В принципе, эта атака может быть выполнена на основе аппаратной реализации, хотя это значительно труднее.
Нижеследующий пример иллюстрирует эту проблему. Предположим, что реализация зависящей от ключа криптографической функции распределяет переменную w по n долям, но использует случайные значения для большинства долей. Например, предположим, что доли от w0 до wn-2 генерируются генератором случайных чисел в программном средстве, и 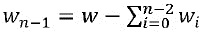 . Хотя теоретически переменная w может казаться идеально распределенной по n долям - никакой поднабор n долей не дает никакой информации о w, этот выбор все же является уязвимым для конфликтной атаки. Атакующий может определить генератор случайных чисел таким образом, чтобы он выдавал постоянные значения для долей от w0 до wn-2. После этого изменения, конфликт в отношении wn-1 будет достаточным для получения информации о ключе. Наличие конфликта только в отношении wn-1 является гораздо менее редким, чем одновременный конфликт в отношении всех долей.
. Хотя теоретически переменная w может казаться идеально распределенной по n долям - никакой поднабор n долей не дает никакой информации о w, этот выбор все же является уязвимым для конфликтной атаки. Атакующий может определить генератор случайных чисел таким образом, чтобы он выдавал постоянные значения для долей от w0 до wn-2. После этого изменения, конфликт в отношении wn-1 будет достаточным для получения информации о ключе. Наличие конфликта только в отношении wn-1 является гораздо менее редким, чем одновременный конфликт в отношении всех долей.
Следует отметить, что источник случайных чисел может быть легко распознан в программном средстве посредством многократного выполнения программного средства с одними и теми же входными данными. Дивергентное выполнение указывает на генератор случайных чисел. Такой анализ программного средства может быть также автоматизирован.
Фиг. 1 показывает путь для кодирования переменной w, который может устранить конфликты для этой переменной. Фиг. 1 показывает переменную 110 w, и показывает, как w может быть закодирована для использования в криптографическом устройстве, таком как криптографическое устройство 200, таким образом, чтобы конфликты в отношении w были предотвращены.
Переменная 110 w распределена по множественным долям wj. Обозначим размер w в битах как k. В одном варианте осуществления размер части wj в битах равняется размеру w в битах. Другие переменные могут иметь другие размеры в битах. Например, k может быть равен 4 или более. В одном варианте осуществления k=4,5,6,7,8, или более. Показаны доли 121, 122 и 123.
Доли могут быть выбраны таким образом, что 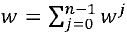 . В одном варианте осуществления эта сумма использует функцию XOR для суммирования, однако возможны и другие альтернативы. Например, эта сумма может использовать арифметическое сложение по модулю 2k.
. В одном варианте осуществления эта сумма использует функцию XOR для суммирования, однако возможны и другие альтернативы. Например, эта сумма может использовать арифметическое сложение по модулю 2k.
В общем, может быть определена объединяющая функция (d(w0,…,wn-1)=w), которая отображает доли (wj) в переменную (w). Объединяющая функция может быть функцией XOR или функцией арифметического сложения, упомянутыми выше. Объединяющая функция имеет свойство, состоящее в том, что отображение из любой единственной доли (wk) в переменную (w), получаемое посредством определения значений других долей (w0,…,wk-1,wk+1,…,wn-1), является биективным отображением. А именно, функция 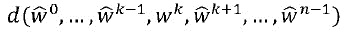 является биективным отображением; причем элементы
является биективным отображением; причем элементы 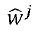 обозначают определенное значение. Это свойство обеспечивает то, что никакой поднабор долей не дает информацию о w. Существует много таких объединяющих функций. Например, d может быть любой линейной комбинацией долей
обозначают определенное значение. Это свойство обеспечивает то, что никакой поднабор долей не дает информацию о w. Существует много таких объединяющих функций. Например, d может быть любой линейной комбинацией долей 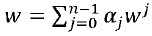 , в которой коэффициенты αj являются нечетными; причем эта сумма использует арифметическое сложение по модулю 2k. Объединяющая функция может быть многочленом.
, в которой коэффициенты αj являются нечетными; причем эта сумма использует арифметическое сложение по модулю 2k. Объединяющая функция может быть многочленом.
Фиг. 1 дополнительно показывает множественные состояния sj. Показаны состояния 131, 132 и 133. Число долей 121-123 является таким же, как число состояний 131-133. Состояния являются избыточными данными, которые вводят избыточность в кодирование переменной. Каждая из долей скомпонована с одним из состояний и закодирована в кодированной доле: xj=Encj(wj,sj). В одном варианте осуществления, кодирования Encj являются разными. Например, кодирования Encj могут быть случайным образом выбраны во время компиляции. Нет строгой необходимости в том, чтобы кодирование было биективным, поскольку оно является обратимым в отношении wj, а именно, если знать Encj и xj, то можно восстановить долю wj. Тем не менее, в вариантах осуществления кодирования Encj являются биективными. При этом последнее является более практическим выбором в реализации и упрощает анализ. После принятия решения о том, какие переменные будут закодированы какими кодированиями в какие моменты времени, таблицы могут быть просто выполнены с возможностью учета этих кодирований.
Фиг. 1 показывает, что доля 121 и состояние 131 закодированы посредством кодирования 161 в кодированной доле 141. Также, доля 122 и состояние 132 закодированы посредством кодирования 162 в кодированной доле 142; доля 123 и состояние 133 закодированы посредством кодирования 163 в кодированной доле 143. Назовем состояния и доли, которые закодированы вместе для представления переменной w, состояниями и долями, соответствующими этой переменной.
Результатом являются множественные кодированные доли, из которых показаны кодированные доли 141, 142, и 143. Переменная w представляется в криптографическом устройстве 200 в виде множественных кодированных долей. Ни некодированные доли 121-123, ни состояния 131-133 не должны возникать в криптографическом устройстве.
Авторы изобретения поняли, что посредством выбора состояний специальным образом, конфликты в отношении w могут быть предотвращены. А именно, не будет существовать таких двух разных сообщений M и M', чтобы все кодированные доли 141-143 были одними и теми же.
Множественные состояния sj, соответствующие одной и той же переменной w, выбирают таким образом, чтобы существовало инъективное отображение 152, обозначаемое как ∑, из входного сообщения M во множественные состояния (∑(M)=(s0,…,sn-1). Инъективное отображение имеет свойство, состоящее в том, что ∑(M)=∑(M'), если и только если M=M'. В частности, ∑ может быть выбрано таким образом, чтобы оно было биективным, поскольку это более жесткое условие предполагает инъективность. Фиг. 1 показывает, как множественные состояния 131-133 зависят от входного сообщения 100 M и от инъективного отображения 152 ∑.
Поскольку состояния кодируют входное сообщение 100 M, другое M будет приводить к другим кодированным переменным: x0,…,xn-1. Это может быть обеспечено следующим образом: выбирают целое l таким образом, чтобы удовлетворялось n*l≥«размер(M) в битах». Здесь n обозначает число состояний, l является размером состояния в битах. Число долей также равно n. Таким образом, общий размер в битах множественных состояний sj, соответствующих одной и той же переменной w, имеет величину по меньшей мере вплоть до размера в битах входного сообщения M. Кодирования Encj выбирают, например, случайным образом, из биективных функций 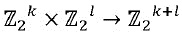 . Размер состояний в битах не обязательно должен быть равен размеру долей в битах.
. Размер состояний в битах не обязательно должен быть равен размеру долей в битах.
Возьмем DES в качестве первого примера. В DES входное сообщение имеет размер 64 бита. Предположим, что внутренние переменные имеют размер 4 бита и распределены по 6 долям. В этом случае, размер состояний должен составлять, по меньшей мере, 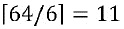 битов. В этом случае, переменная может быть закодирована 6 кодированными долями, каждая из которых содержит 4+11=15 битов. В этом случае, общий размер состояний в битах будет составлять 6*11=66 битов. Поскольку 66 больше, чем размер входного сообщения в битах, равный 64, отображение ∑ будет инъективным, но не биективным.
битов. В этом случае, переменная может быть закодирована 6 кодированными долями, каждая из которых содержит 4+11=15 битов. В этом случае, общий размер состояний в битах будет составлять 6*11=66 битов. Поскольку 66 больше, чем размер входного сообщения в битах, равный 64, отображение ∑ будет инъективным, но не биективным.
Предположим, также с использованием DES в качестве примера, что внутренние переменные имеют размер 4 бита и распределены по 16 долям. В этом случае, размер состояний должен составлять по меньшей мере 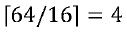 бита. С использованием битов для состояния, в этом случае кодированная доля будет иметь размер 4+4=8 битов. Общий размер в битах состояний, соответствующих одной и той же переменной, составляет 16*4=64 бита. Поскольку это равно размеру входного сообщения в битах, инъективное отображение является биективным. В общем, если общий размер долей в битах, например, nk равен размеру входного сообщения M в битах, то размер долей в битах может быть равен этому размеру долей в битах.
бита. С использованием битов для состояния, в этом случае кодированная доля будет иметь размер 4+4=8 битов. Общий размер в битах состояний, соответствующих одной и той же переменной, составляет 16*4=64 бита. Поскольку это равно размеру входного сообщения в битах, инъективное отображение является биективным. В общем, если общий размер долей в битах, например, nk равен размеру входного сообщения M в битах, то размер долей в битах может быть равен этому размеру долей в битах.
В качестве дополнительного примера, рассмотрим блочный шифр AES с размером входного сообщения, равным 128 битов. Если переменные распределены по 16 долям, то состояния могут иметь размер 128/16=8 битов. Если доли также имеют размер 8 битов, то кодированная доля будет иметь размер 16 битов.
Отображение 152 не обязательно должно быть явным в реализации криптографической функции для большинства или всех переменных. Например, поскольку кодированная переменная имеет требуемое инъективное соотношение с входным сообщением, операции, выполняемые в отношении частей долей wj кодированной переменной, могут одновременно выполнять избыточные операции в отношении частей состояний, которые сохраняют инъективное отображение. Поскольку вычисления выполняются в кодированной области, вычисления в отношении состояний не могут быть отделены от вычислений в отношении долей.
Например, предположим, что первая и вторая переменные w1 и w2 обе закодированы, как указано выше, в виде множественных кодированных долей 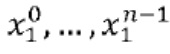 и
и 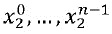 . Предположим, что операция g в отношении w1 и w2 вычисляет третью переменную w3=g(w1,w2). Переменную w3 представляют в виде кодированных долей
. Предположим, что операция g в отношении w1 и w2 вычисляет третью переменную w3=g(w1,w2). Переменную w3 представляют в виде кодированных долей 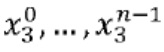 . В одном варианте осуществления, состояния, закодированные в
. В одном варианте осуществления, состояния, закодированные в 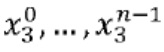 , равняются состояниям, закодированным в
, равняются состояниям, закодированным в 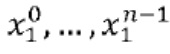 или в
или в 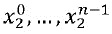 . В этом случае, если входные данные имеют требуемое соотношение с входным сообщением M, то тогда w3 будет иметь требуемое соотношение с входным сообщением M. Таким образом, требуемое соотношение может быть сохранено на всем протяжении вычислений. Операции могут быть реализованы в виде сети таблиц для выполнения операций, которая в свою очередь может быть подсетью сети таблиц, реализующей криптографическую функцию.
. В этом случае, если входные данные имеют требуемое соотношение с входным сообщением M, то тогда w3 будет иметь требуемое соотношение с входным сообщением M. Таким образом, требуемое соотношение может быть сохранено на всем протяжении вычислений. Операции могут быть реализованы в виде сети таблиц для выполнения операций, которая в свою очередь может быть подсетью сети таблиц, реализующей криптографическую функцию.
Вместо выбора состояний третьей переменной равными состояниям одних из входных данных, также может быть применено дополнительное инъективное отображение ∑2, например, 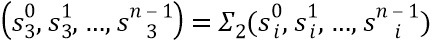 , где i обозначает одну из входных переменных, например, i=1 или 2. Посредством создания ∑2 в виде множества из n биективных отображений, которые управляют только одним состоянием, это не увеличивает сеть таблиц, поскольку отображение может быть объединено с существующими таблицами.
, где i обозначает одну из входных переменных, например, i=1 или 2. Посредством создания ∑2 в виде множества из n биективных отображений, которые управляют только одним состоянием, это не увеличивает сеть таблиц, поскольку отображение может быть объединено с существующими таблицами.
Таким образом, в одном варианте осуществления избыточные операции могут быть биективными операциями. Биективные функции могут быть выбраны случайным образом, например, во время компиляции. В одном варианте осуществления, для переменных, которые зависят только от входного сообщения, состояния могут быть получены в виде инъективной функции входного сообщения. Для переменной, которая зависит от кодированной переменной, для которой доли имеют инъективное соотношение с входным сообщением, новые доли 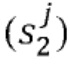 могут быть получены посредством применения множества биективных функций (gj) к соответствующей доле кодированной переменной
могут быть получены посредством применения множества биективных функций (gj) к соответствующей доле кодированной переменной 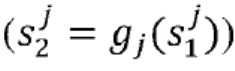 . Можно сделать состояния третьей переменной зависимыми от состояний входных переменных и все же сохранить требуемое соотношение с входным сообщением. Однако это может увеличить сеть таблиц.
. Можно сделать состояния третьей переменной зависимыми от состояний входных переменных и все же сохранить требуемое соотношение с входным сообщением. Однако это может увеличить сеть таблиц.
Начальные переменные, например, переменные, которые прямо получены из входного сообщения, могут быть приняты криптографическим устройством 200 в корректной кодированной форме. Альтернативно, устройство 200 может содержать кодирующее устройство, описанное ниже.
Кодирование переменной w обеспечивает то, что не может быть конфликта в отношении кодированного значения во время выполнения криптографической функции. Соответственно, никакие конфликтные атаки не являются возможными в это время. Если все переменные, которые зависят от входного сообщения, а также от ключа, будут кодироваться таким образом на всем протяжении вычисления криптографической функции, то тогда конфликты могут быть полностью предотвращены. Кроме того, эта система является простой, эффективной, доказуемой и изящной.
В практической варианте осуществления, не будет никаких других представлений w, кроме представления посредством кодированных долей. Дополнительно, защита будет более эффективной, если большее число чувствительных переменных будет защищено таким образом. Предпочтительно, защищают все переменные, которые зависят как от ключа, так и от входного сообщения. Для предотвращения конфликтных атак не требуется, чтобы входные сообщения были представлены в виде кодированных долей до того, как будет выполнена операция с ключом. Однако обеспечение того, чтобы существовало и сохранялось инъективное отображение, упрощается посредством обеспечения кодирования входного сообщения в виде множественных наборов кодированных долей даже до использования ключа.
Возвращаясь к фиг. 2; криптографическое устройство 200 содержит хранилище 220 данных, выполненное с возможностью хранения множественных переменных, на которые криптографическое устройство воздействует для вычисления криптографической функции. Переменная 240 представлена в хранилище 220 данных в виде множественных кодированных долей. Показаны кодированные доли 241, 242, и 243. Переменная распределена по множественным долям, и каждая доля закодирована вместе с состоянием. Существует инъективное отображение (∑) из входного сообщения (M) во множественные состояния, как объяснено со ссылкой на фиг. 1.
Криптографическое устройство 200 содержит хранилище 230 таблиц, хранящее множественные справочные таблицы. На фиг. 2 показаны таблицы 231, 232 и 233. По меньшей мере некоторые из справочных таблиц принимают в качестве входных данных одну или более кодированных долей одной или более переменных. В одном варианте осуществления справочная таблица принимает в качестве входных данных по меньшей мере одну кодированную долю из двух разных переменных. Множественные справочные таблицы вместе образуют сеть таблиц, реализующую криптографическую функцию.
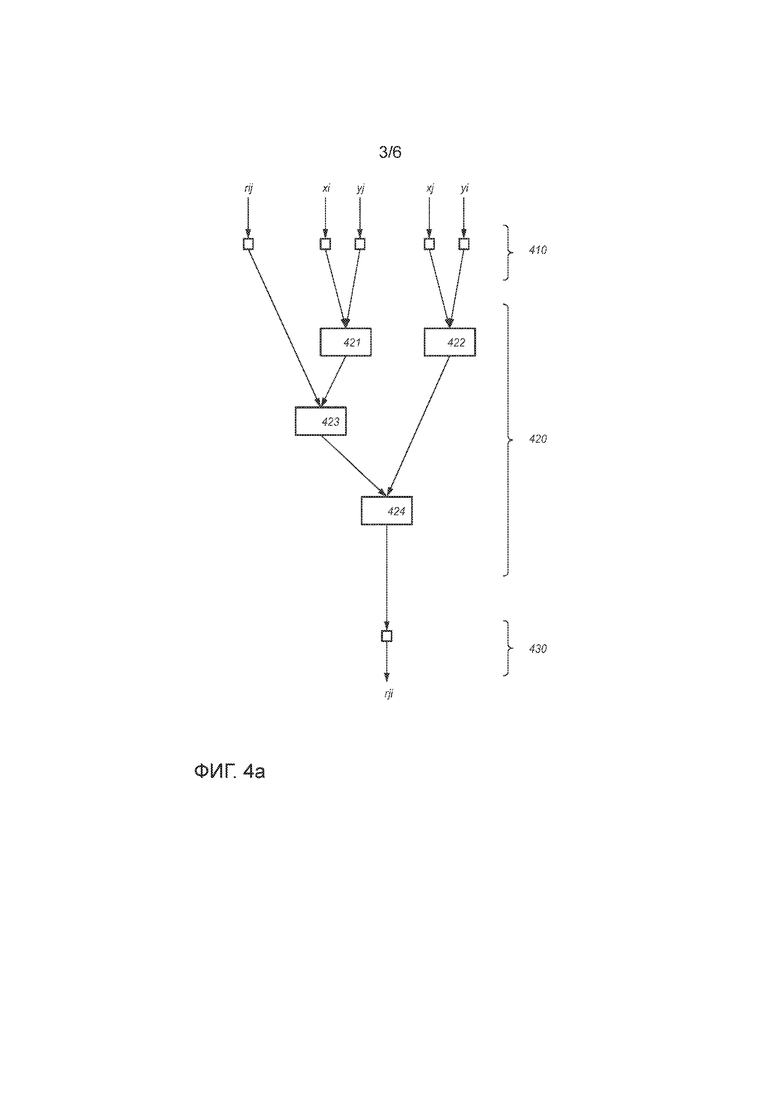
Сами по себе сети таблиц известны из криптографии методом «белого ящика». См. например, работу ʺWhite-box cryptography and an AES implementationʺ, за авторством Chow и др. Пример сети 420 таблиц показан на фиг. 4а, в этом случае это сеть таблиц для вычисления прямых произведений.
Сеть таблиц принимает один или более элементов входных данных, например, входные данные 410, и создает один или более элементов выходных данных, например, выходные данные 430. В сети 420 таблиц показаны множественные справочные таблицы; конкретно, показаны таблицы 421-421. Таблицы принимают входные данные прямо из входных данных 410 и/или выходных данных других таблиц. Таблица может принимать единственный элемент входных данных, два элемента входных данных, или более двух элементов входных данных.
Удобный способ преобразования вычисления на основе некодированных переменных w в вычисление на основе переменных w, кодированных в виде множественных долей, обеспечен в работе ʺHigher-Order Masking Schemes for S-boxesʺ, за авторством Carlet и др. В этой работе не обсуждаются конфликтные атаки и кодирование с использованием состояний. Эта работа также называется Carlet. Carlet не предотвращает конфликты в отношении переменной, кодированной в виде множественных долей.
Ниже объяснено, как вычисление на основе переменной w, например, для вычисления значения функции S(w), может быть преобразовано в вычисление на основе переменной w, закодированной во множественных долях. Функция S может быть любым внутренним этапом вычисления криптографической функции, например, сложением, умножением, S-блоком и т.д. Мы покажем, как создать сеть таблиц, которая вычисляет S(w) на основе долей. Сначала, мы рассмотрим здесь случай, в котором S имеет единственную входную w. Множественные состояния могут быть обработаны аналогично. Мы будем также сначала игнорировать состояния, затем мы покажем, как состояния могут быть добавлены.
Если w представлена n долями w0,…,wn-1, то тогда мы также хотим представить S(w) n долями, чтобы обеспечить результирующей переменной такую же защиту, как у w. Это возможно для любой функции с использованием следующих фактов.
Для демонстрации, мы сначала предположим, что значение S(w), подобно w, также является k-битовым числом. k-битовые числа могут считаться элементами конечного поля Галуа 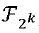 , а функция S может считаться функцией от
, а функция S может считаться функцией от 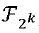 . Все функции в конечных полях являются многочленами, таким образом, для любой функции S от
. Все функции в конечных полях являются многочленами, таким образом, для любой функции S от 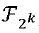 , существуют такие коэффициенты
, существуют такие коэффициенты 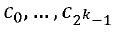 , что для любой w, которую это поле содержит,
, что для любой w, которую это поле содержит,
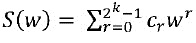
Многочлен может быть выражен в виде вычисления на основе долей следующим образом. Пусть доли заданы в виде X=(x0,…,xn-1) и Y=(y0,…,yn-1). Для простоты предположим, что сумма долей равняется некодированным переменным. Сумма X и Y может быть закодирована долями xi+yi. Скалярное умножение αX может быть закодировано долями αxi. Наконец, пусть Z будет произведением X и Y. Определим для 0≤i<j≤n-1 значения ri,j и rj,i.
Возьмем для ri,j случайный элемент 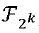 , например, с помощью выбора случайной k-битовой строки. В одном варианте осуществления, случайное число для ri,j получают с помощью выбора во время компиляции функции Ri,j рандомизации от входного сообщения M в отношении
, например, с помощью выбора случайной k-битовой строки. В одном варианте осуществления, случайное число для ri,j получают с помощью выбора во время компиляции функции Ri,j рандомизации от входного сообщения M в отношении 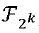 и установления ri,j=Ri,j(M). Последнее имеет преимущество, состоящее в том, что во время выполнения можно избежать зависимости от генератора случайных чисел. Источник случайности необходим только тогда, когда создается сеть таблиц, т.е. во время компиляции. Следует отметить, что метод Carlet основан на случайности во время выполнения. Это открывает Carlet для управления источником случайных чисел во время выполнения. В частности, генератор случайных чисел может быть перехвачен и заменен постоянными значениями.
и установления ri,j=Ri,j(M). Последнее имеет преимущество, состоящее в том, что во время выполнения можно избежать зависимости от генератора случайных чисел. Источник случайности необходим только тогда, когда создается сеть таблиц, т.е. во время компиляции. Следует отметить, что метод Carlet основан на случайности во время выполнения. Это открывает Carlet для управления источником случайных чисел во время выполнения. В частности, генератор случайных чисел может быть перехвачен и заменен постоянными значениями.
Возьмем rj,i=(xiyj+ri,j)+xjyi; порядок вычислений здесь важен и указан скобками. Теперь для 0≤i≤n-1 возьмем 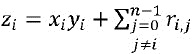 .
.
Подсеть таблиц прямых произведений может вычислить rj,i. Эти таблицы вычисляют два прямых произведения xiyj и xjyi.
В одном варианте осуществления функция Ri,j рандомизации для вычисления rj,i реализована в виде сети таблиц, принимающей входные сообщения в качестве входных данных. Это устраняет потребность в источнике случайных чисел во время выполнения.
Доли zi теперь представляют произведение X и Y. С использованием операций сложения, скалярного умножения и умножения, многочленное представление для S может быть выражено в виде операции на основе долей. Операция на основе долей в свою очередь может быть реализована в виде справочной таблицы, принимающей в качестве входных данных одну или более долей и/или случайных чисел.
Возможная сеть 420 таблиц для вычисления rj,i показана на фиг. 4а. Таблицы 421-424 взаимодействуют для вычисления rj,i. Входные данные сети 420 таблиц показаны ссылочной позицией 410. Выходные данные сети 420 таблиц показаны ссылочной позицией 430.
Например, таблицы 421 и 422 могут быть выполнены с возможностью умножения их входных данных, тогда как таблицы 423 и 424 могут быть выполнены с возможностью сложения их входных данных. Следует отметить, что каждая из таблиц может использовать отличные кодирования.
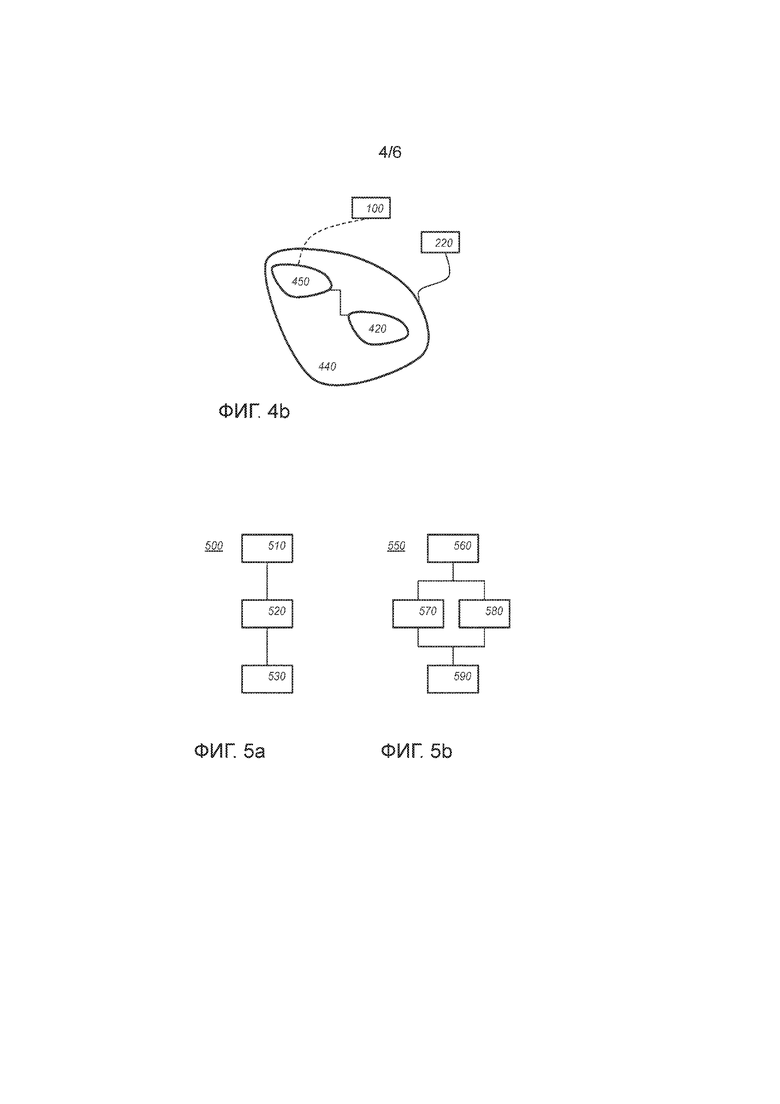
Фиг. 4b схематично показывает пример варианта осуществления сети 440 таблиц умножения. Сеть 440 таблиц умножения может быть создана с использованием формул, приведенных выше, для вычисления Z=(z0,…,zn-1). Сеть 440 таблиц умножения выполнена с возможностью умножения переменной X, представленной в хранилище 220 данных в виде первого множества кодированных долей (xj), на вторую переменную Y, представленную в хранилище 220 данных в виде второго множества кодированных долей (yj). Сеть таблиц умножения воздействует на первое и второе множество кодированных долей (xj,yj) и получает третье множество кодированных долей (zj), представляющее произведение первой и второй переменной. Сеть 440 таблиц умножения может быть частью сети таблиц для вычисления криптографической функции.
Сеть 440 таблиц умножения может содержать подсети таблиц прямых произведений для вычисления прямых произведений xiyj. В одном варианте осуществления прямые произведения вычисляют в парах xiyj+xjyi. Например, сеть 440 таблиц умножения может содержать сеть 420 таблиц. Сеть 440 таблиц умножения может также содержать сеть 450 таблиц для вычисления одной или более функций Ri,j рандомизации. На фиг. 4b, сеть 450 таблиц зависит от входного сообщения 110. Эта зависимость указана пунктирной линией, чтобы указать на то, что эта зависимость может быть получена через промежуточный элемент, например, переменные, хранимые в хранилище 220 данных. Сеть 440 таблиц может получать свои входные данные и хранить свои выходные данные в хранилище 220 данных.
Таблица, воздействующая на доли, может быть преобразована в таблицу, воздействующую на кодированные доли. Определим s и t таким образом, чтобы для кодированной доли x мы имели Enc(t(x),s(x))=x. Функции s и t получают состояние и долю из x, соответственно. Пусть определена таблица Т для t(x). Тогда Enc'(T(t(x)),P(s(x))) определяет таблицу для x, которая реализует таблицу Т для части доли x и функцию P для части состояния. Функция P является избыточной и может быть выбрана при создании сети таблиц, например, во время компиляции. Например, P может быть функцией идентичности. Подобные конструкции возможны для множественных входных данных. Кодирование Enc, используемое здесь, также называется кодированием входных данных. Кодирование Enc' называется кодированием выходных данных. Кодирования входных данных и выходных данных таблицы не обязательно должны быть одними и теми же, поскольку кодирование выходных данных, используемое для выходных данных таблицы, является таким же, как кодирование входных данных следующей таблицы, которая использует упомянутые выходные данные в качестве входных данных.
Хранилище 220 данных и хранилище 230 таблиц могут быть электронной памятью. Они могут быть двумя частями одной и той же памяти. Хранилище 230 таблиц может быть энергонезависимым хранилищем. Хранилище 220 данных может быть энергозависимым хранилищем.
Криптографическое устройство 200 содержит блок 210 управления, выполненный с возможностью применения криптографических функций к входному сообщению посредством применения множественных справочных таблиц к переменным, представленным в хранилище данных. Например, хранилище 230 таблиц может содержать команды, которые указывают порядок, в котором таблицы должны быть применены к разным переменным.
Криптографическое устройство 200 может содержать сетевой интерфейс 250. Сетевой интерфейс 250 может быть выполнен с возможностью приема кодированных данных через компьютерную сеть. Например, криптографическое устройство 200 может принимать зашифрованные данные, например, зашифрованный контент, который дешифруется криптографическим устройством 200. Входные данные, принимаемые через сетевой интерфейс 250, могут быть представлены в виде кодированных долей, например, описанных выше. Кодирование не обязательно должно выполняться внутри устройства 200.
Фиг. 3 показывает пример кодирующего устройства 300. Кодирующее устройство 300 выполнено с возможностью кодирования входного сообщения M для использования его вместе с криптографическим устройством по п. 1 формулы изобретения. Кодирующее устройство 300 содержит принимающий блок для приема входного сообщения M. Входное сообщение содержит множественные входные части M=(m0,m1,…). Например, множественные части могут быть полубайтами или байтами. В одном варианте осуществления размер частей в битах находится между 4 и 8 (включительно). Сообщение M может быть конкатенацией частей сообщения.
Кодирующее устройство 300 содержит кодирующий блок 320, который выполняет кодирование. Кодирующий блок 320 кодирует каждую часть входного сообщения M отдельно. Таким образом, для каждой части mi входного сообщения M, кодирующий блок выполняет следующее:
Часть mi входного сообщения M распределяется по множественным долям посредством применения множественных функций 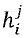 распределения к входному сообщению для получения множественных долей
распределения к входному сообщению для получения множественных долей 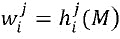 . Объединяющая функция, применяемая к функциям
. Объединяющая функция, применяемая к функциям 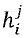 распределения, применяемым к M, равняется части mi входного сообщения:
распределения, применяемым к M, равняется части mi входного сообщения: 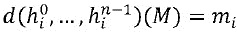 . В частности, если объединяющая функция является функцией XOR или функцией арифметической суммы, то тогда сумма функций
. В частности, если объединяющая функция является функцией XOR или функцией арифметической суммы, то тогда сумма функций 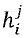 распределения равняется части mi входного сообщения M, так что
распределения равняется части mi входного сообщения M, так что 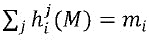 .
.
Например, в случае, если имеется четное число долей, функции распределения могут быть выбраны в виде 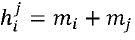 для i≠j и
для i≠j и 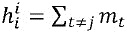 . В этом примере, сложение является операцией XOR. Возможны многие другие возможности. Например, все кроме одной функции распределения для данной части могут быть выбраны случайно, а последняя может быть вычислена в виде поправочного члена, например, функции проекции M на mi минус другие функции распределения.
. В этом примере, сложение является операцией XOR. Возможны многие другие возможности. Например, все кроме одной функции распределения для данной части могут быть выбраны случайно, а последняя может быть вычислена в виде поправочного члена, например, функции проекции M на mi минус другие функции распределения.
Кодирующий блок 320 также применяет инъективное отображение ∑i из входного сообщения M для получения множественных состояний 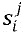 , причем число множественных долей и множественных состояний является одинаковым. В одном варианте осуществления
, причем число множественных долей и множественных состояний является одинаковым. В одном варианте осуществления 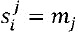 ; этот выбор ясно гарантирует, что входное сообщение M закодировано в состояниях. Конкатенация всех долей является инъективным отображением на основе входного сообщения M.
; этот выбор ясно гарантирует, что входное сообщение M закодировано в состояниях. Конкатенация всех долей является инъективным отображением на основе входного сообщения M.
Наконец, каждую долю из множественных долей кодируют вместе с соответствующим состоянием из множественных состояний, при этом получают множественные кодированные доли 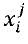 , представляющие часть mi. Например, кодирующий блок 320 может вычислить
, представляющие часть mi. Например, кодирующий блок 320 может вычислить 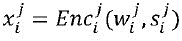 .
.
После этого этапа часть mi кодируют во множественных кодированных долях 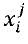 , так что все входное сообщение кодируют как часть состояний в кодированных долях.
, так что все входное сообщение кодируют как часть состояний в кодированных долях.
Сеть таблиц, реализующая криптографическую функцию, выполнена с возможностью сохранения соотношения между входным сообщением и состояниями кодированных долей, которые соответствуют переменной. Поскольку конфликт в отношении набора кодированных переменных предполагает конфликт в отношении состояния, это означает, что конфликт с разными вводимыми сообщениями является невозможным.
В качестве дополнительного примера, инъективное отображение ∑i, используемое для отображения M в состояния в кодирующем блоке, может быть составлено из множественных меньших биективных функций. Например, инъективное отображение ∑i может содержать множественные функции 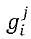 состояний. Этап получения множественных состояний
состояний. Этап получения множественных состояний 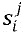 содержит этап применения множественных функций
содержит этап применения множественных функций 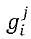 состояний к соответствующим множественным входным частям
состояний к соответствующим множественным входным частям 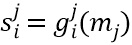 , причем множественные функции состояний являются биективными. Например,
, причем множественные функции состояний являются биективными. Например, 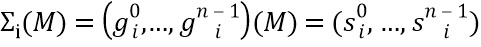 . Это является особенно легким путем для создания биективного отображения и, таким образом, также инъективной функции. Если необходимо заполнить больше состояний, то может быть добавлено больше функций состояний, причем в этом случае функция ∑i становится строго инъективной, а не биективной.
. Это является особенно легким путем для создания биективного отображения и, таким образом, также инъективной функции. Если необходимо заполнить больше состояний, то может быть добавлено больше функций состояний, причем в этом случае функция ∑i становится строго инъективной, а не биективной.
Обычно, каждое из устройств 200 и 300 содержит микропроцессор (не показан на фиг. 1-4), который выполняет соответствующее программное средство, хранимое в устройстве 200 и 300; например, это программное средство могло быть загружено в соответствующую память и/или может храниться в соответствующей памяти, например, энергозависимой памяти, такой как RAM, или энергонезависимой памяти, такой как флэш-память (не показана на фиг. 1-4). Альтернативно, устройства 200 и 300 могут быть реализованы, целиком или частично, в программируемых логических схемах, например, в виде матрицы программируемых логических вентилей (FPGA). Устройства 200 и 300 могут быть реализованы, целиком или частично, в виде так называемой специализированной интегральной схемы (ASIC), т.е. интегральной схемы (IC), приспособленной к ее конкретному применению. Например, схемы могут быть реализованы в CMOS, например, с использованием языка описания аппаратных средств, такого как Verilog, VHDL и т.д.
В одном варианте осуществления устройство 200 содержит схему хранения данных и схему хранения таблиц, например, электронные запоминающие устройства, и схему блока управления. Эти схемы реализуют соответствующие блоки, описанные здесь. Эти схемы могут быть схемой процессора и схемой хранилища, причем схема процессора выполняет команды, представленные электронным способом в схемах хранилищ. Эти схемы могут также быть FPGA, ASIC и т.п. Система может содержать дополнительные схемы, например, схему сетевого интерфейса, и т.д.
Фиг. 5а показывает блок-схему последовательности операций, которая иллюстрирует криптографический способ 500, выполненный с возможностью вычисления fK(M) зависящей от ключа K криптографической функции f для входного сообщения M. Криптографический способ 500 содержит
- этап 510 сохранения множественных переменных w, на которые криптографическое устройство воздействует для вычисления криптографической функции, причем переменную w распределяют по множественным долям wj и представляют в хранилище данных в виде множественных кодированных долей xj, причем кодированная доля является кодированием xj=Encj(wj,sj) доли wj вместе с состоянием sj, причем множественные состояния sj, соответствующие одной и той же переменной w, имеют соотношение с входным сообщением M, так что существует инъективное отображение ∑ из входного сообщения M во множественные состояния ∑(M)=(s0,…,sn-1),
- этап 520 сохранения множественных справочных таблиц, причем справочная таблица принимает в качестве входных данных одну или более кодированных долей одной или более переменных, причем множественные справочные таблицы вместе образует сеть таблиц, реализующую криптографическую функцию,
- этап 530 применения криптографической функции к входному сообщению посредством применения множественных справочных таблиц к переменным, представленным в хранилище данных.
Фиг. 5b показывает блок-схему последовательности операций, которая иллюстрирует способ 550 кодирования для кодирования входного сообщения M, для использования вместе с криптографическим устройством по п. 1 формулы изобретения, причем способ кодирования содержит:
- этап 560 приема входного сообщения M, причем входное сообщение содержит множественные входные части M=(m0,m1,…),
- для каждой части mi входного сообщения M,
- этап 570 распределения части mi входного сообщения M во множественные доли посредством применения множественных функций 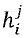 распределения к входному сообщению для получения множественных долей
распределения к входному сообщению для получения множественных долей 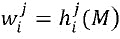 , причем объединяющая функция, применяемая к функциям
, причем объединяющая функция, применяемая к функциям 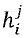 распределения, равняется части mi входного сообщения:
распределения, равняется части mi входного сообщения: 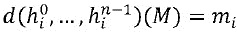 ,
, 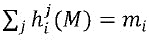
- этап 580 применения инъективного отображения ∑i из входного сообщения M для получения множественных состояний 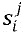 , причем число множественных долей и множественных состояний является одинаковым
, причем число множественных долей и множественных состояний является одинаковым
- этап 590 кодирования каждой доли из множественных долей вместе с соответствующим состоянием из множественных состояний, при этом получают множественные кодированные доли 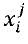 , представляющие часть mi.
, представляющие часть mi.
Способ 550 имеет несколько возможностей для распределения воздействия на каждую часть входного сообщения. Например, способ 550 может сначала вычислить доли для всех частей, затем вычислить состояния для всех частей, и наконец, выполнить кодирование для всех частей. Однако способ 550 может также вычислить доли, состояния, и кодирование для одной части одномоментно. Возможны другие комбинации.
Специалистам в данной области техники будет понятно, что возможны многие другие пути выполнения способов. Например, порядок этапов может быть изменен, или некоторые этапы могут быть выполнены параллельно. Кроме того, между этапами могут быть вставлены другие этапы способа. Вставленные этапы могут представлять улучшения способа, описанного здесь, или могут быть этапами, не связанными с данным способом. Например, этапы 570 и 580 могут быть выполнены, по меньшей мере частично, параллельно. Кроме того, данный этап может не заканчиваться до начала следующего этапа.
Способ согласно настоящему изобретению может быть выполнен с использованием программного средства, которое содержит команды для предписания процессорной системе выполнять способ 500 или 550. Программное средство может включать в себя только те этапы, которые осуществляются конкретным подобъектом системы. Программное средство может храниться в пригодном запоминающем носителе, таком как жесткий диск, гибкий диск, память, оптический диск и т.д. Программное средство может быть отправлено в виде сигнала по проводу, или беспроводным способом, или с использованием сети передачи данных, например, сети Интернет. Программное средство может быть выполнено доступным для загрузки и/или для удаленного использования на сервере. Способ согласно настоящему изобретению может быть выполнен с использованием битового потока, выполненного с возможностью конфигурировать программируемые логические схемы, например, матрицу программируемых логических вентилей (FPGA), для выполнения способа.
Следует понимать, что настоящее изобретение также распространяется на компьютерные программы, особенно на компьютерные программы, находящиеся на или в носителе, выполненные с возможностью осуществления на практике настоящего изобретения. Программа может быть в форме исходного кода, объектного кода, промежуточного источника кода, и объектного кода, такого как частично скомпилированная форма, или в любой другой форме, пригодной для использования в реализации способа согласно настоящему изобретению. Вариант осуществления, относящийся к компьютерному программному продукту, содержит компьютерно-выполняемые команды, соответствующие каждому из этапов обработки по меньшей мере одного из перечисленных способов. Эти команды могут подразделяться на подпрограммы и/или могут храниться в одном или более файлах, которые могут быть связаны статически или динамически. Другой вариант осуществления, относящийся к компьютерному программному продукту, содержит компьютерно-выполняемые команды, соответствующие каждому из средств по меньшей мере одной из перечисленных систем и/или продуктов.
Фиг. 7а показывает компьютерно-читаемый носитель 1000 данных, имеющие записываемую часть 1010, содержащую компьютерную программу 1020, причем компьютерная программа 1020 содержит команды для предписания процессорной системе выполнить криптографический способ или способ кодирования, согласно одному варианту осуществления. Компьютерная программа 1020 может быть реализована на компьютерно-читаемом носителе 1000 данных в виде физических масок или посредством намагничивания компьютерно-читаемого носителя 1000 данных. Однако также возможны любые другие пригодные варианты осуществления. Дополнительно следует понимать, что хотя компьютерно-читаемый носитель 1000 данных показан здесь в виде оптического диска, компьютерно-читаемый носитель 1000 данных может быть любым пригодным компьютерно-читаемым носителем данных, таким как жесткий диск, твердотельная память, флэш-память и т.д., и может быть незаписываемым или записываемым. Компьютерная программа 1020 содержит команды для предписания процессорной системе выполнять упомянутый криптографический способ или способ кодирования, согласно варианту осуществления.
Фиг. 7b показывает схематичное представление процессорной системы 1140 согласно одному варианту осуществления. Процессорная система содержит одну или более интегральных схем 1110. Архитектура одной или более интегральных схем 1110 схематично показана на фиг. 7b. Схема 1110 содержит обрабатывающий блок 1120, например, CPU, для выполнения компонентов компьютерной программы для выполнения способа согласно одному варианту осуществления и/или реализации ее модулей или блоков. Схема 1110 содержит память 1122 для хранения кода программирования, данных и т.д. Часть памяти 1122 может быть предназначена только для считывания. Схема 1110 может содержать коммуникационный элемент 1126, например, антенну, соединители или и то, и другое, и т.п. Схема 1110 может содержать специальную интегральную схему 1124 для выполнения части или всей обработки, определенной в способе. Процессор 1120, память 1122, специальная IC 1124 и коммуникационный элемент 1126 могут быть соединены друг с другом через межсоединение 1130, например, шину. Процессорная система 1110 может быть выполнена с возможностью обеспечения контактной и/или бесконтактной связи, с использованием антенны и/или соединителей, соответственно.
Следует отметить, что вышеупомянутые варианты осуществления иллюстрируют, а не ограничивают настоящее изобретение, и что специалисты в данной области техники могут разработать многие альтернативные варианты осуществления.
В формуле изобретения, никакие ссылочные позиции, помещенные в скобки, не должны толковаться как ограничение формулы изобретения. Использование глагола «содержать» и его спряжений не исключает наличия элементов или этапов, отличных от элементов или этапов, заявленных в формуле изобретения. Элемент в единственном числе не исключает наличия множества таких элементов. Настоящее изобретение может быть реализовано посредством аппаратного средства, содержащего некоторые отдельные элементы, и посредством соответствующим образом запрограммированного компьютера. В пункте формулы изобретения на устройство, в котором перечислены некоторые средства, некоторые из этих средств могут быть реализованы одним и тем же элементом аппаратного средства. Тот факт, что некоторые меры приведены во взаимно отличающихся зависимых пунктах формулы изобретения, не указывает на то, что комбинация этих мер не может быть использована с преимуществом.
В формуле изобретения ссылочные позиции, помещенные в скобки, относятся к ссылочным обозначениям на чертежах вариантов осуществления или к формулам вариантов осуществления, таким образом, увеличивается ясность формулы изобретения. Ссылочные позиции не должны толковаться как ограничения формулы изобретения.
Список ссылочных позиций фиг. 1-4b, и 6:
100 - M - входное сообщение
110 - w - переменная
121, 122, 123 - w0,w1,…,wn-1 - доля
131, 132, 133 - s0,s1,…,sn-1 - доля
141, 142, 143 - x0,x1,…,xn-1 - кодированная доля
151 - h - распределяющее отображение
152 - ∑ - инъективное отображение
161, 162, 163 - Enc1, Enc2, Enc3 - кодирование
200 - криптографическое устройство
210 - блок управления
220 - хранилище данных
230 - хранилище таблиц
231, 232, 233 - таблица
240 - переменная
250 - сетевой интерфейс
300 - кодирующее устройство
310 - принимающий блок
320 - кодирующий блок
410 - входные данные сети таблиц
420 - сеть таблиц
421-424 - таблица
430 - выходные данные сети таблиц
440 - сеть таблиц
450 - сеть таблиц
600 - блок-схема последовательности операций для блочного шифра DES
605 - входное сообщение
606 - выходное сообщение
| название | год | авторы | номер документа |
|---|---|---|---|
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО И СПОСОБ | 2016 |
|
RU2708439C1 |
| КРИПТОГРАФИЧЕСКОЕ УСТРОЙСТВО, ПРИСПОСОБЛЕННОЕ ДЛЯ ВЫЧИСЛЕНИЯ ЦЕЛЕВОГО БЛОЧНОГО ШИФРА | 2016 |
|
RU2711193C2 |
| УСТРОЙСТВО И СПОСОБ ВЫЧИСЛЕНИЯ БЛОЧНОГО ШИФРА | 2018 |
|
RU2696334C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, КОНФИГУРИРУЕМОЕ С ПОМОЩЬЮ ТАБЛИЧНОЙ СЕТИ | 2013 |
|
RU2661308C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, СОДЕРЖАЩЕЕ СЕТЬ ТАБЛИЦ | 2013 |
|
RU2676454C2 |
| ЭЛЕКТРОННОЕ УСТРОЙСТВО БЛОЧНОГО ШИФРОВАНИЯ, ПОДХОДЯЩЕЕ ДЛЯ ОБФУСКАЦИИ | 2014 |
|
RU2666281C2 |
| УСТРОЙСТВО ВИРТУАЛЬНОЙ МАШИНЫ, ИМЕЮЩЕЕ УПРАВЛЯЕМУЮ КЛЮЧОМ ОБФУСКАЦИЮ, И СПОСОБ | 2012 |
|
RU2620712C2 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО, ХРАНЯЩЕЕ ТАБЛИЦЫ СООТВЕТСТВИЯ ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИИ | 2013 |
|
RU2657178C2 |
| ЭЛЕКТРОННОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ АРИФМЕТИКИ С ОБФУСКАЦИЕЙ | 2015 |
|
RU2701716C2 |
| ЭЛЕКТРОННОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ ЗАМАСКИРОВАННЫХ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ | 2015 |
|
RU2698764C2 |
Изобретение относится к криптографическому и кодирующему устройствам, способам и машиночитаемому носителю для кодирования входного сообщения. Технический результат заключается в повышении надежности криптографических функций. Криптографическое устройство содержит хранилище данных для хранения множественных переменных, распределенных по множественным долям и представленных в виде множественных кодированных долей, являющихся кодированием доли вместе с состоянием, имеющим соотношение с входным сообщением, так что существует инъективное отображение из входного сообщения во множественные состояния, хранилище таблиц, хранящее множественные справочные таблицы, принимающие в качестве входных данных кодированные доли переменных и образующие сеть таблиц, реализующую криптографическую функцию, и выполняющую операции в отношении множественных долей кодированной переменной и выполняющую избыточные операции в отношении множественных состояний, сохраняющие инъективное отображение из входного сообщения во множественные состояния, блок управления для применения криптографической функции к входному сообщению посредством применения множественных справочных таблиц к переменным, представленным в хранилище данных. 5 н. и 8 з.п. ф-лы, 10 ил.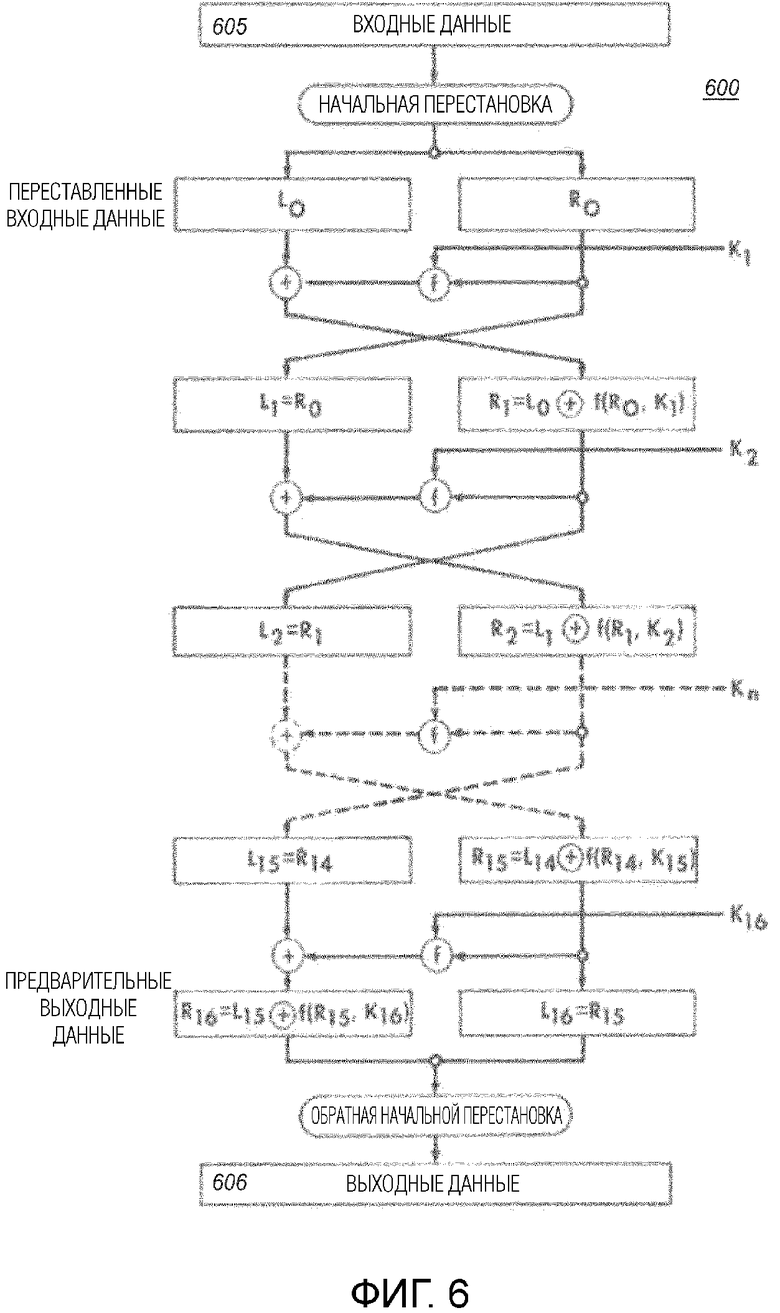
1. Криптографическое устройство (200), выполненное с возможностью вычисления (fK(M)) зависящей от ключа (K) криптографической функции (f) для входного сообщения (M), причем криптографическое устройство содержит:
хранилище (220) данных, выполненное с возможностью хранения множественных переменных (w), на которые криптографическое устройство воздействует для вычисления криптографической функции, причем переменная (w) распределена по множественным долям (wj) и представлена в хранилище данных в виде множественных кодированных долей (xj), при этом кодированная доля является кодированием (xj=Encj(wj,sj)) доли (wj) вместе с состоянием (sj), причем множественные состояния (sj), соответствующие одной и той же переменной (w), имеют соотношение с входным сообщением (M), так что существует инъективное отображение (∑) из входного сообщения (M) во множественные состояния (∑(M)=(s0,s1,…,sn-1)),
хранилище (230) таблиц, хранящее множественные справочные таблицы, причем справочная таблица принимает в качестве входных данных одну или более кодированных долей одной или более переменных, причем множественные справочные таблицы вместе образуют сеть таблиц, реализующую криптографическую функцию, причем сеть таблиц выполняет операции в отношении множественных долей (wj) кодированной переменной (w) и одновременно выполняет избыточные операции в отношении множественных состояний (sj), сохраняющие инъективное отображение из входного сообщения (M) во множественные состояния,
блок (210) управления, выполненный с возможностью применения криптографической функции к входному сообщению посредством применения множественных справочных таблиц к переменным, представленным в хранилище данных.
2. Криптографическое устройство по п.1, в котором общий размер в битах множественных состояний (sj), соответствующих одной и той же переменной (w), имеет величину, по меньшей мере, вплоть до размера в битах входного сообщения (M).
3. Криптографическое устройство по любому из предшествующих пунктов, в котором упомянутое кодирование является биективным отображением.
4. Криптографическое устройство по любому из предшествующих пунктов, в котором объединяющая функция (d(w0,…,wn-1)=w) отображает доли (wj) в переменную (w), причем объединяющая функция имеет свойство, состоящее в том, что отображение из любой одной доли (wk) в переменную (w), получаемое посредством определения значений других долей (w0,…,wk-1,wk+1,…,wn-1), является биективным отображением.
5. Криптографическое устройство по любому из предшествующих пунктов, в котором сумма множественных долей (wj) равняется соответствующей переменной (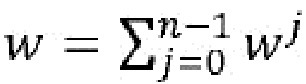 ).
).
6. Криптографическое устройство по любому из предшествующих пунктов, в котором
хранилище (230) таблиц хранит сеть таблиц умножения для умножения первой переменной (w), распределенной по первому множеству долей (wj) и представленной в хранилище данных в виде первого множества кодированных долей (xj), и второй переменной (v), распределенной по второму множеству долей (vj), представленной в хранилище данных в виде второго множества кодированных долей (yj), причем сеть таблиц умножения воздействует на первое и второе множество кодированных долей (xj,yj) и получает третье множество кодированных долей (zj), представляющее произведение первой и второй переменной,
причем сеть таблиц умножения содержит одну или более подсетей таблиц прямых произведений для вычисления произведения первой доли (w1) первого множества долей и второй доли (v2) второго множества долей, причем подсети таблиц прямых произведений вычисляют сумму произведения первой доли и второй доли из соответствующих кодированных долей и функции (R1,2) рандомизации от входного сообщения (M).
7. Криптографическое устройство по любому из предшествующих пунктов, в котором хранилище (230) таблиц хранит сеть таблиц для выполнения операции, принимающей в качестве входных данных первую кодированную переменную (w1) и вторую кодированную переменную (w2) и создающей в качестве выходных данных третью кодированную переменную (w3), причем сеть таблиц выполнена таким образом, что множественные состояния, закодированные в третьей кодированной переменной (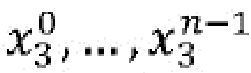 ), зависят только от состояний, закодированных в одной из первой кодированной переменной (
), зависят только от состояний, закодированных в одной из первой кодированной переменной (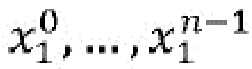 ) и второй кодированной переменной (
) и второй кодированной переменной (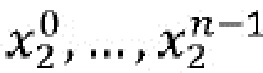 ).
).
8. Кодирующее устройство для кодирования входного сообщения (M), причем кодирующее устройство содержит
принимающий блок (310) для приема входного сообщения (M), причем входное сообщение содержит множественные входные части (M=(m0,m1,…)),
кодирующий блок (320), выполненный с возможностью, для каждой части (mi) входного сообщения (M),
- распределять часть (mi) входного сообщения (M) по множественным долям посредством применения множественных функций (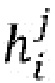 ) распределения к входному сообщению для получения множественных долей (
) распределения к входному сообщению для получения множественных долей (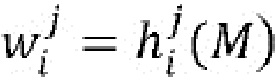 ), причем функция объединения, применяемая к функциям (
), причем функция объединения, применяемая к функциям (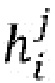 ) распределения, равняется части (mi) входного сообщения (M): (
) распределения, равняется части (mi) входного сообщения (M): (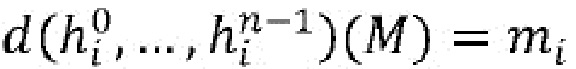 ;
;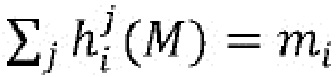 ),
),
- применять инъективное отображение (∑i) из входного сообщения (M) для получения множественных состояний (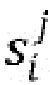 ), причем число множественных долей и множественных состояний является одинаковым,
), причем число множественных долей и множественных состояний является одинаковым,
- кодировать каждую долю из множественных долей вместе с соответствующим состоянием из множественных состояний и получать множественные кодированные доли (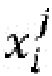 ), представляющие часть (mi).
), представляющие часть (mi).
9. Кодирующее устройство по п. 8, при этом инъективное отображение (∑i) содержит множественные функции (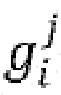 ) состояний, причем получение множественных состояний (
) состояний, причем получение множественных состояний (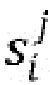 ) содержит применение множественных функций (
) содержит применение множественных функций (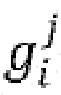 ) состояний к соответствующим множественным входным частям
) состояний к соответствующим множественным входным частям 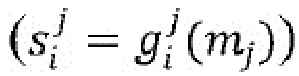 , при этом множественные функции состояний являются биективными.
, при этом множественные функции состояний являются биективными.
10. Криптографическое устройство по п. 1, содержащее кодирующее устройство по п.8 или 9.
11. Реализуемый в криптографическом устройстве по п.1 криптографический способ (500), приспособленный для вычисления (fK(M)) зависящей от ключа (K) криптографической функции (f) для входного сообщения (M), причем криптографический способ содержит этапы, на которых:
сохраняют (510) множественные переменные (w), на которые криптографическое устройство воздействует для вычисления криптографической функции, причем переменную (w) распределяют по множественным долям (wj) и представляют в хранилище данных в виде множественных кодированных долей (xj), при этом кодированная доля является кодированием (xj=Encj(wj,sj)) доли (wj) вместе с состоянием (sj), причем множественные состояния (sj), соответствующие одной и той же переменной (w), имеют соотношение с входным сообщением (M), так что существует инъективное отображение (∑) из входного сообщения (M) во множественные состояния (∑(M)=(s0,…,sn-1)),
сохраняют (520) множественные справочные таблицы, причем справочная таблица принимает в качестве входных данных одну или более кодированных долей одной или более переменных, при этом множественные справочные таблицы вместе образуют сеть таблиц, реализующую криптографическую функцию, причем таблица выполняет операции в отношении множественных долей (wj) кодированной переменной (w) и одновременно выполняет избыточные операции в отношении множественных состояний (sj), сохраняющие инъективное отображение из входного сообщения (M) во множественные состояния,
применяют (530) криптографическую функцию к входному сообщению посредством применения множественных справочных таблиц к переменным, представленным в хранилище данных.
12. Реализуемый в кодирующем устройстве по п.8 способ (550) кодирования для кодирования входного сообщения (M), причем способ кодирования содержит этапы, на которых:
принимают (560) входное сообщение (M), причем входное сообщение содержит множественные входные части (M=(m0,m1,…)),
для каждой части (mi) входного сообщения (M),
- распределяют (570) часть (mi) входного сообщения (M) во множественные доли посредством применения множественных функций (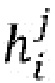 ) распределения к входному сообщению для получения множественных долей (
) распределения к входному сообщению для получения множественных долей (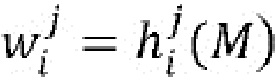 ), причем объединяющая функция, применяемая к функциям (
), причем объединяющая функция, применяемая к функциям (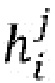 ) распределения, равняется части (mi) входного сообщения (M): (
) распределения, равняется части (mi) входного сообщения (M): (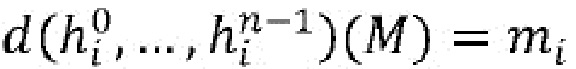 ;
;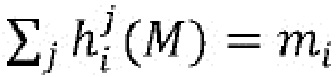 ),
),
- применяют (580) инъективное отображение (∑i) из входного сообщения (M) для получения множественных состояний (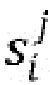 ), причем число множественных долей и множественных состояний являются одинаковым,
), причем число множественных долей и множественных состояний являются одинаковым,
- кодируют (590) каждую долю из множественных долей вместе с соответствующим состоянием из множественных состояний, при этом получают множественные кодированные доли (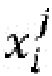 ), представляющие часть (mi).
), представляющие часть (mi).
13. Машиночитаемый носитель (1000) данных, содержащий машиноисполняемые команды для предписания процессорной системе выполнять способ по п.11 или 12.
| Способ защиты переносных электрических установок от опасностей, связанных с заземлением одной из фаз | 1924 |
|
SU2014A1 |
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ КРИПТОГРАФИЧЕСКОГО ВЫЧИСЛЕНИЯ | 2005 |
|
RU2357365C2 |
| СПОСОБ КОДИРОВАНИЯ И ПЕРЕДАЧИ КРИПТОГРАФИЧЕСКИХ КЛЮЧЕЙ | 2005 |
|
RU2302085C1 |
Авторы
Даты
2019-06-24—Публикация
2016-10-10—Подача