Область техники
[0001] Настоящее раскрытие относится к устройству моделирования форм материалов, способу моделирования форм материалов и способу изготовления трехмерных плетеных волокнистых компонентов и подходит для использования, например, в трехмерном плетеном волокнистом материале.
Предпосылки изобретения
[0002] В последние годы армированные волокнами композиционные материалы применяются в различных областях. Армированный волокнами композиционный материал представляет собой композиционный материал, изготовленный путем объединения волокон с материалом-основой; и поскольку армированные волокнами композиционные материалы имеют превосходные свойства, т.е. небольшой вес и высокую прочность по сравнению с однокомпонентными материалами, армированные волокнами композиционные материалы привлекают внимание, так как они могут использоваться для изготовления компонентов, например, летательных аппаратов и транспортных средств. Примеры армированных волокнами композиционных материалов включают в себя композиты с керамической матрицей (CMC) и армированные волокнами пластики (FRP), и различные типы армированных волокнами композиционных материалов выбираются и применяются надлежащим образом в зависимости, например, от среды эксплуатации и назначения.
[0003] Такие армированные волокнами композиционные материалы имеют особенно высокую прочность в отношении усилия в направлении волокон, так что формы компонентов и т.п. зачастую образуются гибкой армированных волокнами композиционных материалов без выполнения такой обработки, как резание, чтобы использовать вышеописанные свойства. Следовательно, форма материала в виде плоской пластины для образования намеченной трехмерно спроектированной формы посредством гибки моделируется и прогнозируется посредством численного расчета.
[0004] PTL 1 раскрывает способ моделирования поверхностного эффекта плетеной ткани после плетения с использованием схемы плетения плетеной ткани. PTL 2 раскрывает систему анализа простых плетеных пленочных материалов, в которой форма плетения основной пряжи и уточной пряжи выражается как коэффициент волнистости, и деформирование этой плетеной ткани выражается как непрерывная функция относительно пространства. PTL 3 раскрывает способ проектирования, включающий в себя: этап получения данных формы, представляющих внешнюю поверхность компонента; этап определения, относительно каждой точки из набора точек на внешней поверхности, расстояния между точкой и проекцией точки на целевую поверхность; и этап определения структуры трехмерной плетеной заготовки согласно определенному расстоянию.
Список библиографических ссылок
[0005] Патентные документы
PTL 1. Публикация заявки на патент Японии номер 2004-292976
PTL 2. Публикация заявки на патент Японии номер 2004-009543
PTL 3. Публикация заявки на патент Японии номер 2015-506007
[0006] Непатентные документы
NPL 1. A. Hertzmann, D. Zorin, Illustrating smooth surfaces, in: Proceedings of the 27th annual conference on Computer graphics and interactive techniques, 2002.
NPL 2. K. Hormann, G. Greiner, Mips: An efficient global parameterization method, in: P. P. L. Schumaker (Ed.), Composites Part A: Applied Science and Manufacturing: Saint-Malo 1999 год, Vanderbilt University Press, 2000.
NPL 3. P. V. Sander, J. Snyder, S. J. Gortler, H. Hoppe, Texture mapping progressive meshes, in: Proceedings of ACM SIGGRAPH, ACM, 2001.
NPL 4. M. Desbrun, M. Meyer, P. Alliez, Intrinsic parameterizations of surface meshes, in: Computer Graphics Forum, издание 21(3), 2002.
NPL 5. B. Levy, S. Petitjean, N. Ray, J. Maillot, Least squares conformal maps for automatic texture atlas generation, in: ACM SIGGRAPH conference proceedings, 2002.
NPL 6. M. Nieser, U. Reitebuch, K. Polthier, Cube cover - parameterization of 3d volumes, in: Computer Graphics Forum, издание 30, 2011.
NPL 7. Y. Li, Y. Liu, W. Xu, W. Wang, B. Cuo, All-hex meshing using singularity-restricted field, in: ACM Transactions on Graphics - Proceddings of ACM SIGGRAPH Asia 2012, издание 31(6), 2012.
NPL 8. J. Nocedal, S. J. Wright, Numerical Optimization, 2nd Edition, Springer Series in Operations Research, Springer Science+Business Media, LLC, 2006.
Сущность изобретения
Задачи, решаемые изобретением
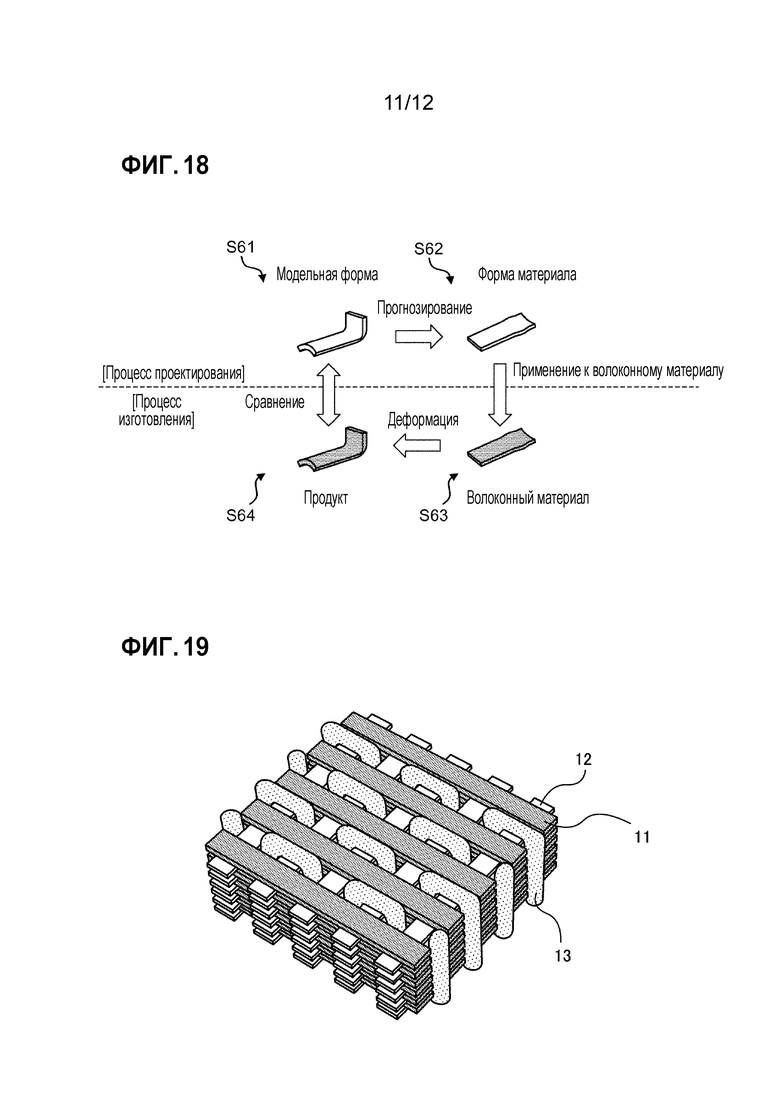
[0007] Фиг. 18 является схемой, иллюстрирующей пример процесса изготовления армированных волокнами композиционных материалов. Что касается процесса изготовления, проиллюстрированного на этом рисунке, то сначала определяют (S61) трехмерную форму модели и ее направления волокон, например компонента, и вычисляют (S62) форму материала, которая должна формироваться и изгибаться в форму модели, например, посредством моделирования. Затем применяют (S63) вычисленную форму материала к волокнистому материалу и деформируют волокнистый материал, например, посредством его гибки, и тем самым придают ему форму продукта (S64). Наконец, сравнивают и оценивают форму модели и форму продукта. Моделирование, используемое на этапе S61 для того, чтобы вычислить форму материала для формирования трехмерной формы модели, зачастую проектируется с возможностью моделировать каждый из двумерных плетеных волокнистых материалов для передней поверхности и задней поверхности формы модели в двух измерениях и прогнозировать плоскую пластинчатую форму посредством задания смоделированных передней и задней поверхностей соответствующими друг другу.
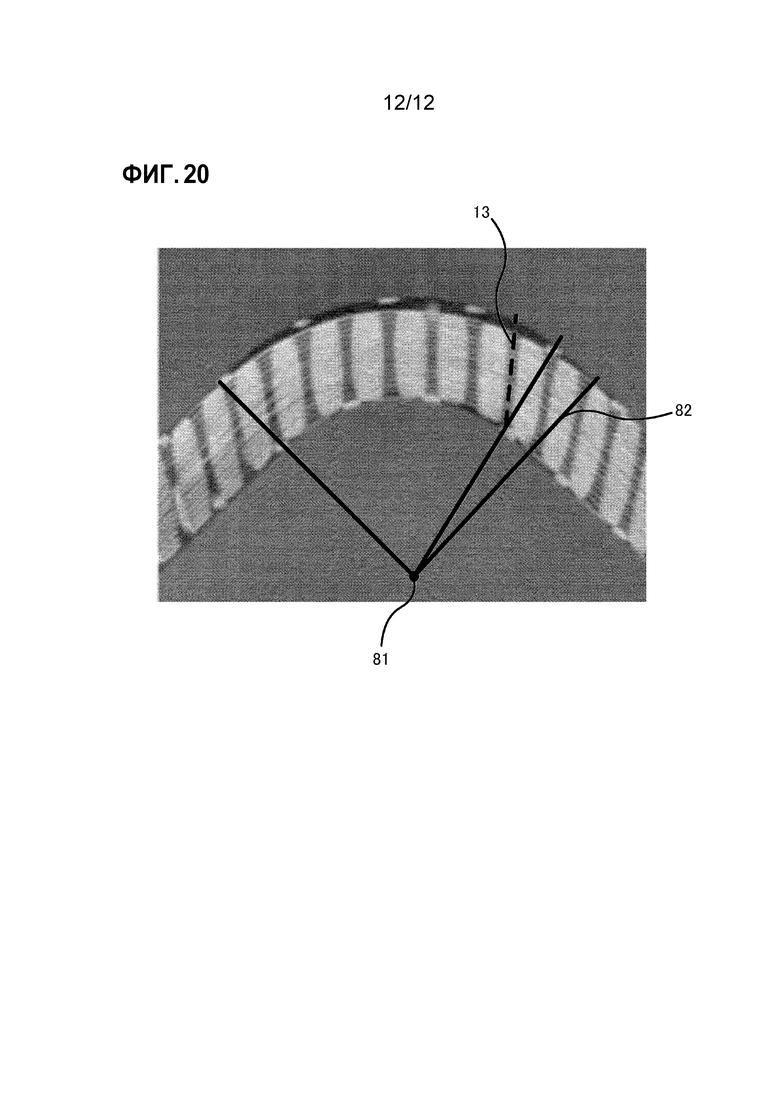
[0008] Однако трехмерный плетеный волокнистый материал формируется посредством укладки поверх друг друга тонких листов из простых плетеных волокон, изготовленных из X-пряжи 11 и Y-пряжи 12, и связывания множества тонких листов Z-пряжей 13, как проиллюстрировано на фиг. 19, так что трехмерный плетеный волокнистый материал показывает различные направления волокон и имеет анизотропное структурное свойство. Фиг. 20 является схемой, показывающей изображение компьютерной томографии (КТ) сечения трехмерного плетеного волокнистого материала, который деформируется. Волокнистый материал из этого изображения деформируется вдоль дуги вокруг центральной точки 81. Секции, указываемые белым цветом, представляют собой секции, в которых X-пряжа и Y-пряжа пересекаются друг с другом, и можно видеть, что эти секции перемещаются в направлении Z-пряжи 13. Если этот материал является изотропным, Z-пряжа 13 должна совпасть с радиальными линиями 82, проходящими из центральной точки 81. Однако Z-пряжа 13 не соответствует направлениям деформирования и является наклонной. Соответственно, X-пряжа и Y-пряжа показывают деформационные свойства, отличающиеся от деформационных свойств простых плетеных волокон, вследствие Z-пряжи. Поэтому затруднительно точно смоделировать деформирование трехмерного плетеного волокнистого материала путем использования моделирования двумерного плетеного волокнистого материала.
[0009] Настоящее раскрытие разработано с учетом вышеописанных обстоятельств и направлено на предоставление устройства и способа более точного моделирования формы материала, которые моделируют деформирование трехмерного плетеного волокнистого материала.
Средства решения задач
[0010] Чтобы решать вышеописанную задачу, устройство моделирования форм материалов согласно настоящему раскрытию включает в себя: блок формирования поля векторов ориентации, который формирует поле векторов ориентации формы модели на трехмерных сетках формы модели трехмерного плетеного волокнистого материала, который получается укладкой друг на друга множества листов двумерной плетеной ткани, изготовленной из X-пряжи, проходящей в направлении Х, и Y-пряжи, проходящей в направлении Y, и связыванием их Z-пряжей, проходящей в направлении Z; блок параметризации, который выполняет поиск вектора градиента для вычисления поля векторов ориентации формы материала, которое представляет собой поле векторов ориентации формы материала перед деформированием формы модели, из поля векторов ориентации формы модели; и блок обновления векторов ориентации, который обновляет поле векторов ориентации формы модели посредством применения условия сохранения объема между полем векторов ориентации формы модели и полем векторов ориентации формы материала и условия, что ни X-пряжа, ни Y-пряжа не растягивается и не сжимается.
[0011] Кроме того, способ моделирования форм материалов согласно настоящему раскрытию включает в себя: формирование поля векторов ориентации формы модели на трехмерных сетках формы модели трехмерного плетеного волокнистого материала, который получается укладкой друг на друга множества листов двумерной плетеной ткани, изготовленной из X-пряжи, проходящей в направлении Х, и Y-пряжи, проходящей в направлении Y, и связыванием их Z-пряжей, проходящей в направлении Z; поиск вектора градиента для вычисления поля векторов ориентации формы материала, которое представляет собой поле векторов ориентации формы материала перед деформированием формы модели, из поля векторов ориентации формы модели; и обновление поля векторов ориентации формы модели посредством применения условия сохранения объема между полем векторов ориентации формы модели и полем векторов ориентации формы материала и условия, что ни X-пряжа, ни Y-пряжа не растягивается и не сжимается.
[0012] Кроме того, способ изготовления трехмерных плетеных волокнистых компонентов согласно настоящему раскрытию включает в себя: вычисление формы материала вышеописанным способом моделирования форм материалов; создание трехмерного плетеного волокнистого материала с вычисленной формой материала; и формирование трехмерного плетеного волокнистого компонента деформированием трехмерного плетеного волокнистого материала.
Преимущественные эффекты изобретения
[0013] Согласно настоящему раскрытию, деформирование трехмерного плетеного волокнистого материала может моделироваться более точно.
Краткое описание чертежей
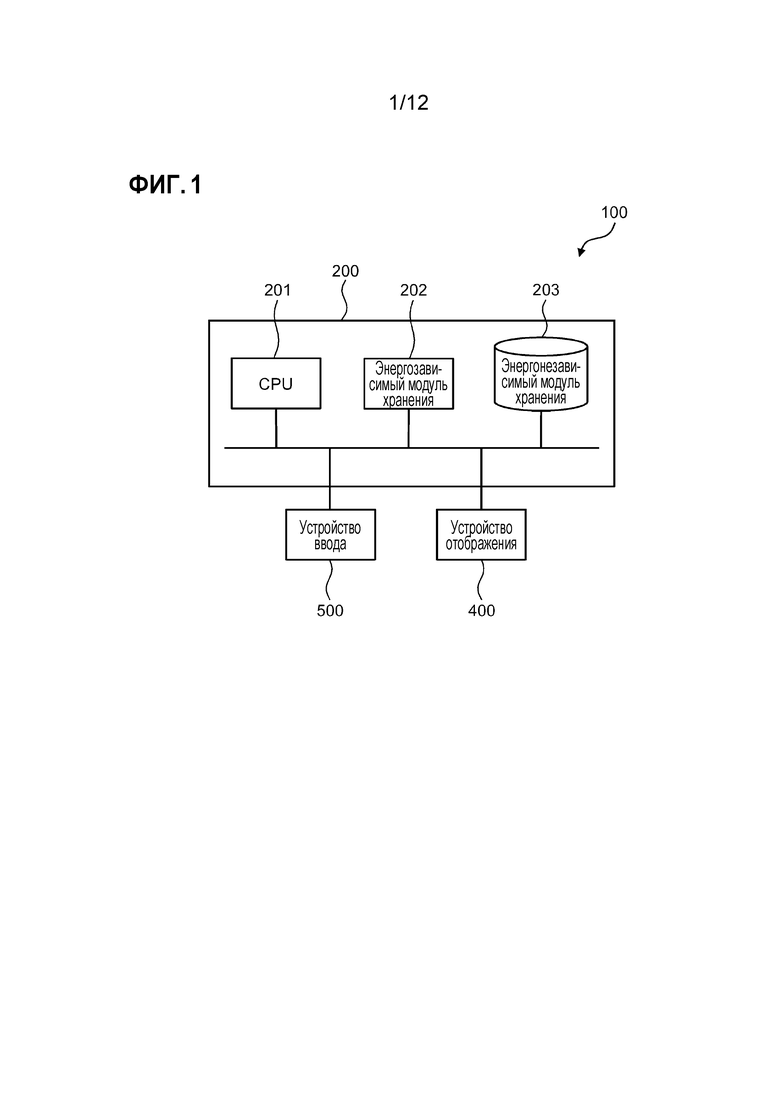
[0014] Фиг. 1 является схемой, иллюстрирующей конфигурацию аппаратных средств устройства моделирования форм материалов согласно варианту осуществления настоящего раскрытия;
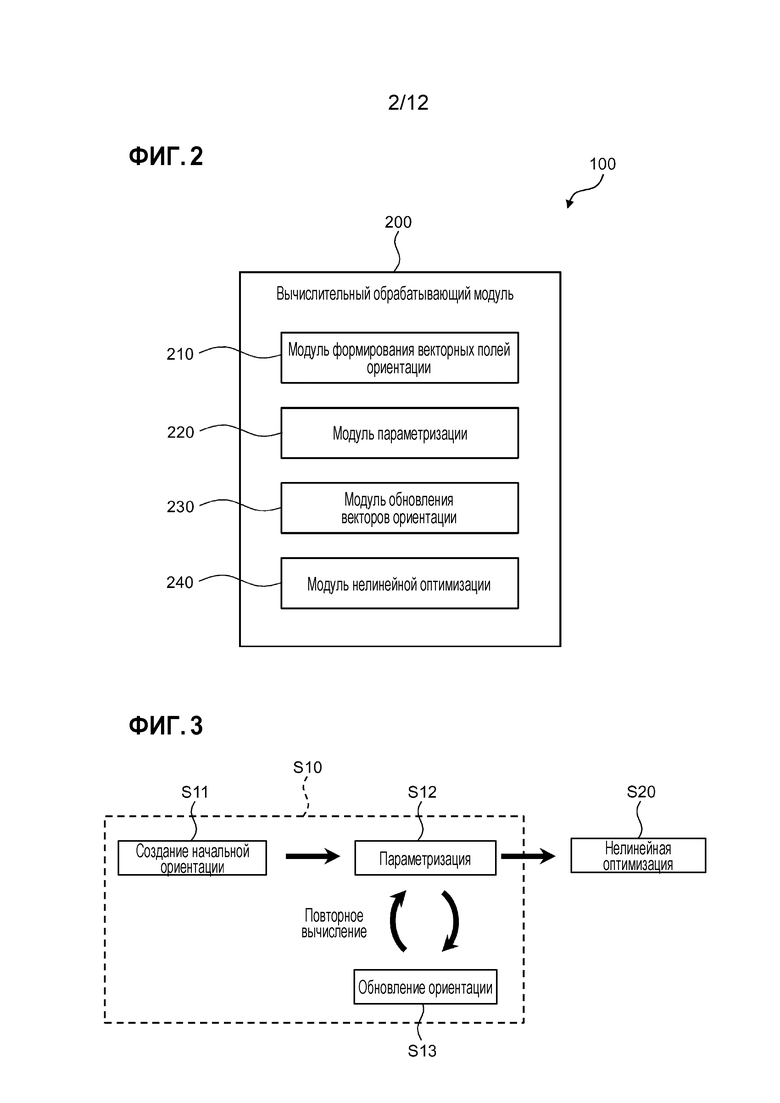
Фиг. 2 является блок-схемой, иллюстрирующей функциональную конфигурацию вычислительного блока обработки для устройства моделирования форм материалов;
Фиг. 3 является блок-схемой, иллюстрирующей общее представление обработки моделированием посредством устройства моделирования форм материалов;
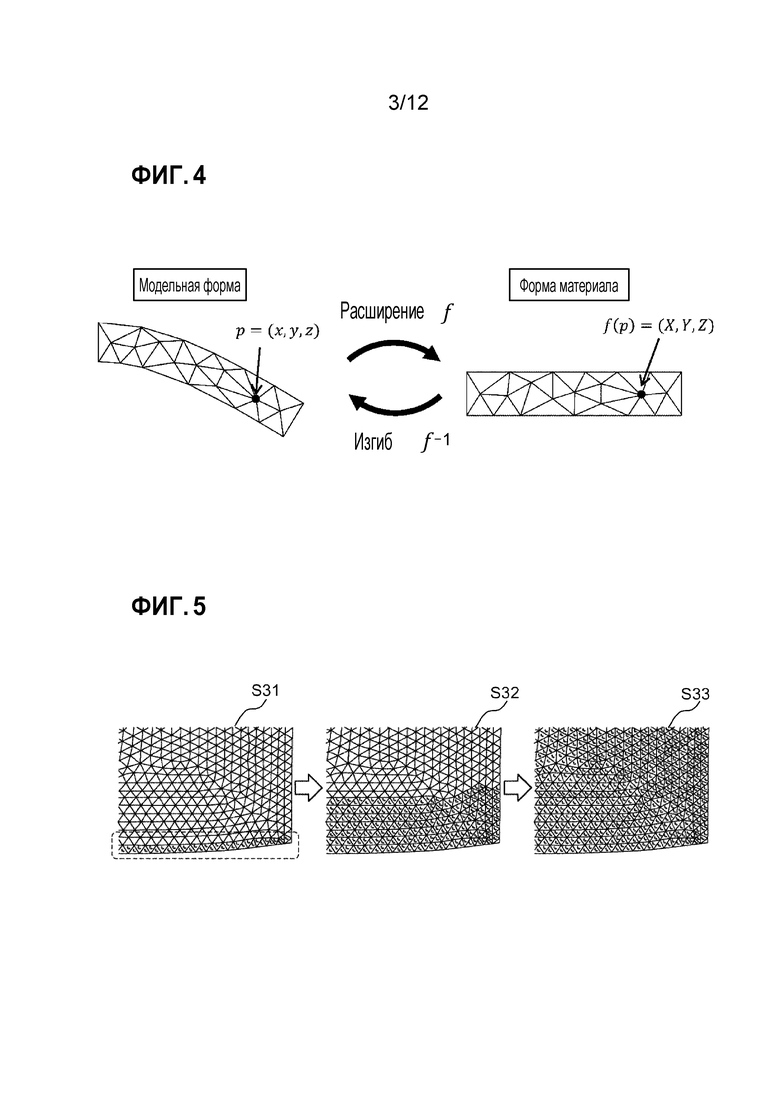
Фиг. 4 является схемой, принципиально иллюстрирующей взаимосвязь между координатами на форме модели и форме материала при обработке моделированием;
Фиг. 5 является схемой, иллюстрирующей то, как векторы направления волокон распространяются на искривленной поверхности из краевой области, где заданы граничные условия;
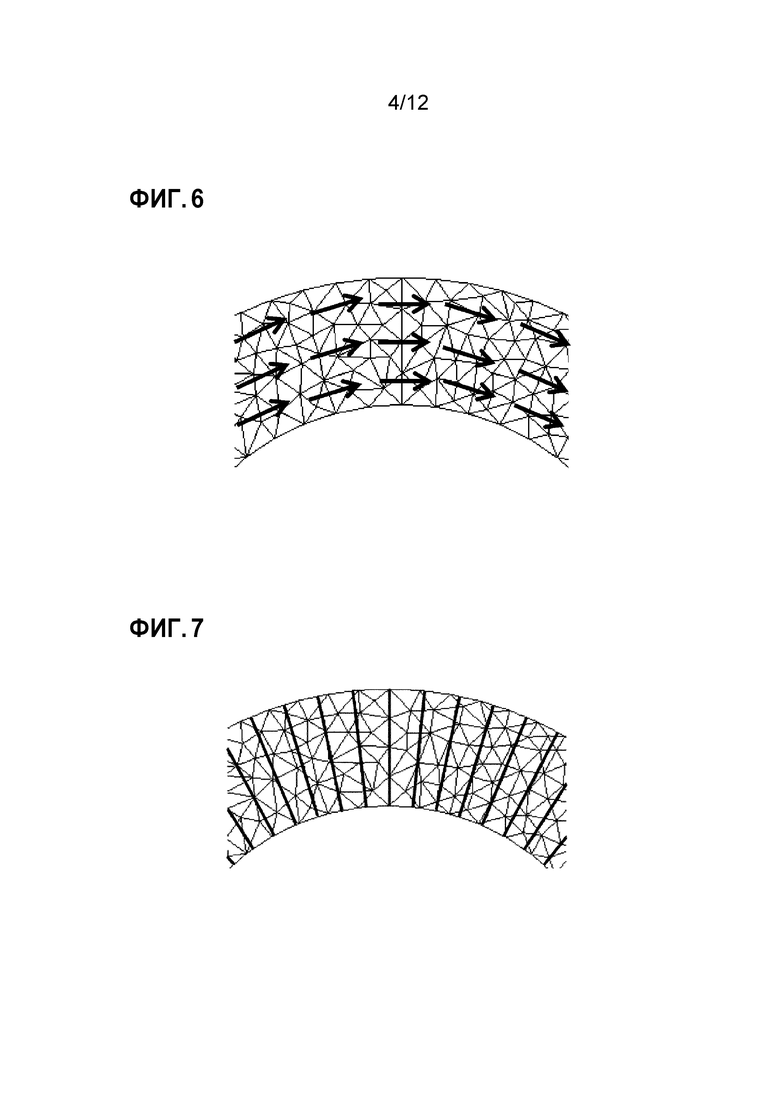
Фиг. 6 является схемой, иллюстрирующей пример распределения поля векторов ориентации;
Фиг. 7 является схемой, иллюстрирующей пример параметризации в распределении по фиг. 6;
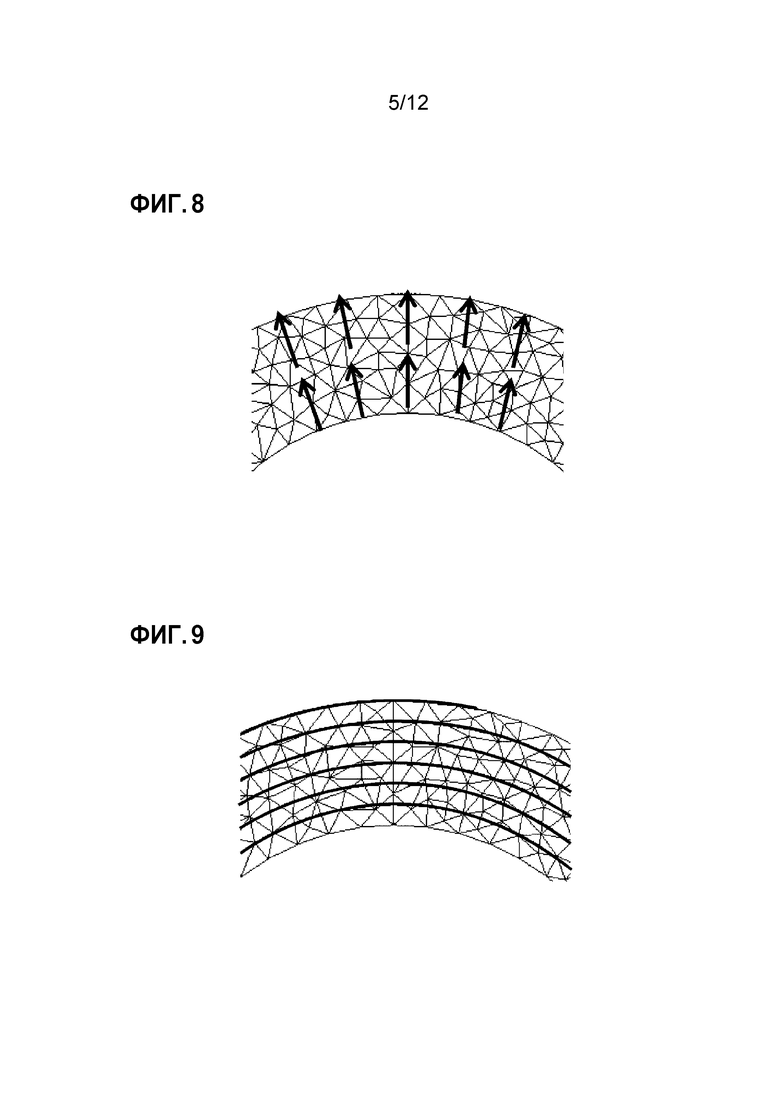
Фиг. 8 является схемой, иллюстрирующей пример распределения поля векторов ориентации;
Фиг. 9 является схемой, иллюстрирующей пример параметризации в распределении по фиг. 8;
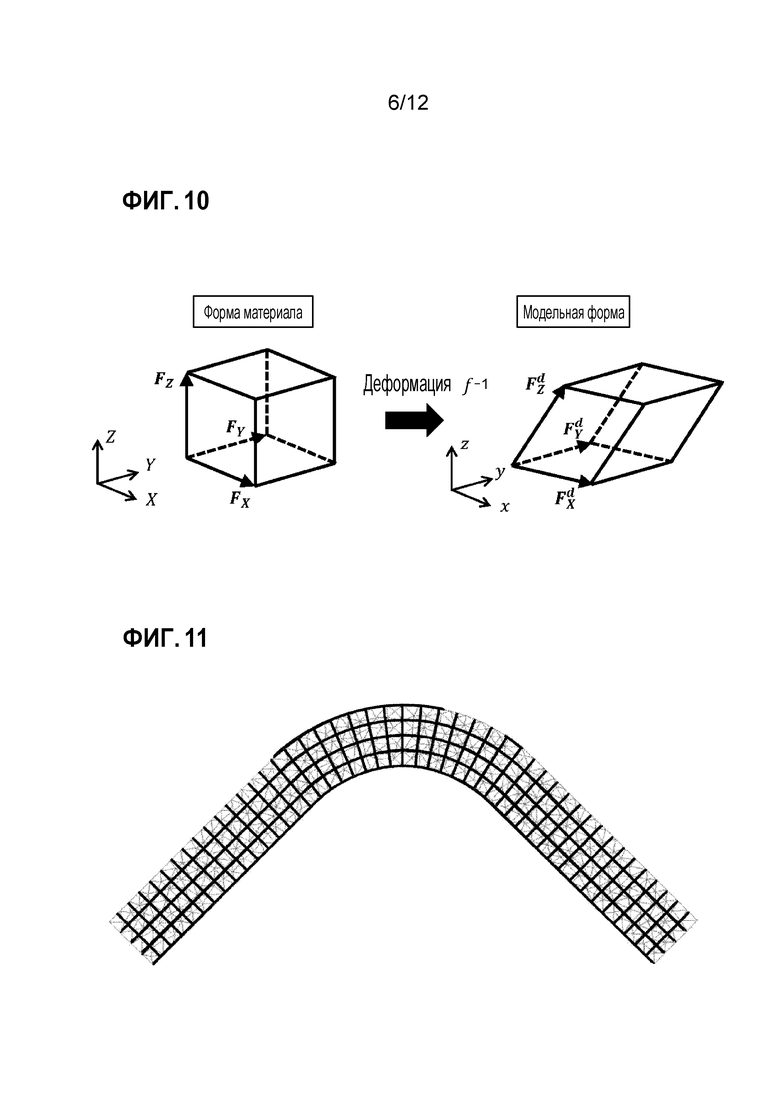
Фиг. 10 является схемой для пояснения обработки обновления векторов ориентации;
Фиг. 11 является схемой, иллюстрирующей результат первой повторяющейся обработки из обработки параметризации и обработки обновления векторов ориентации в случае двух измерений;
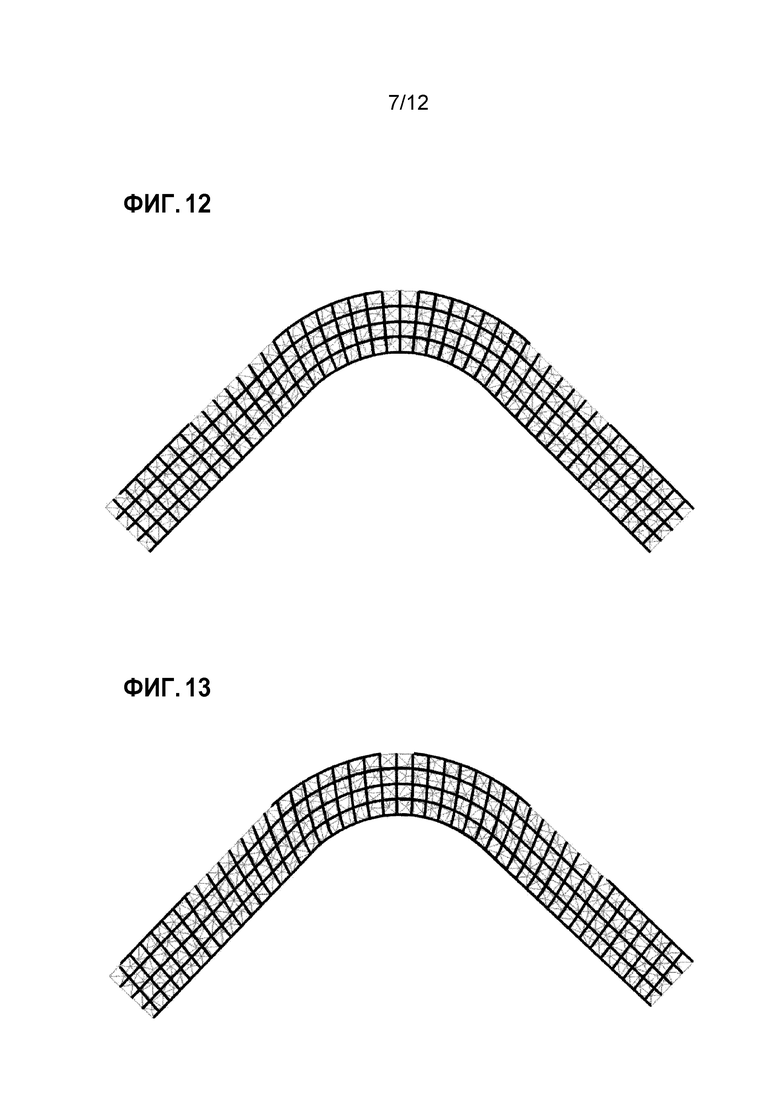
Фиг. 12 является схемой, иллюстрирующей результат седьмой повторяющейся обработки из обработки параметризации и обработки обновления векторов ориентации в случае двух измерений;
Фиг. 13 является схемой, иллюстрирующей результат 20-й повторяющейся обработки из обработки параметризации и обработки обновления векторов ориентации в случае двух измерений;
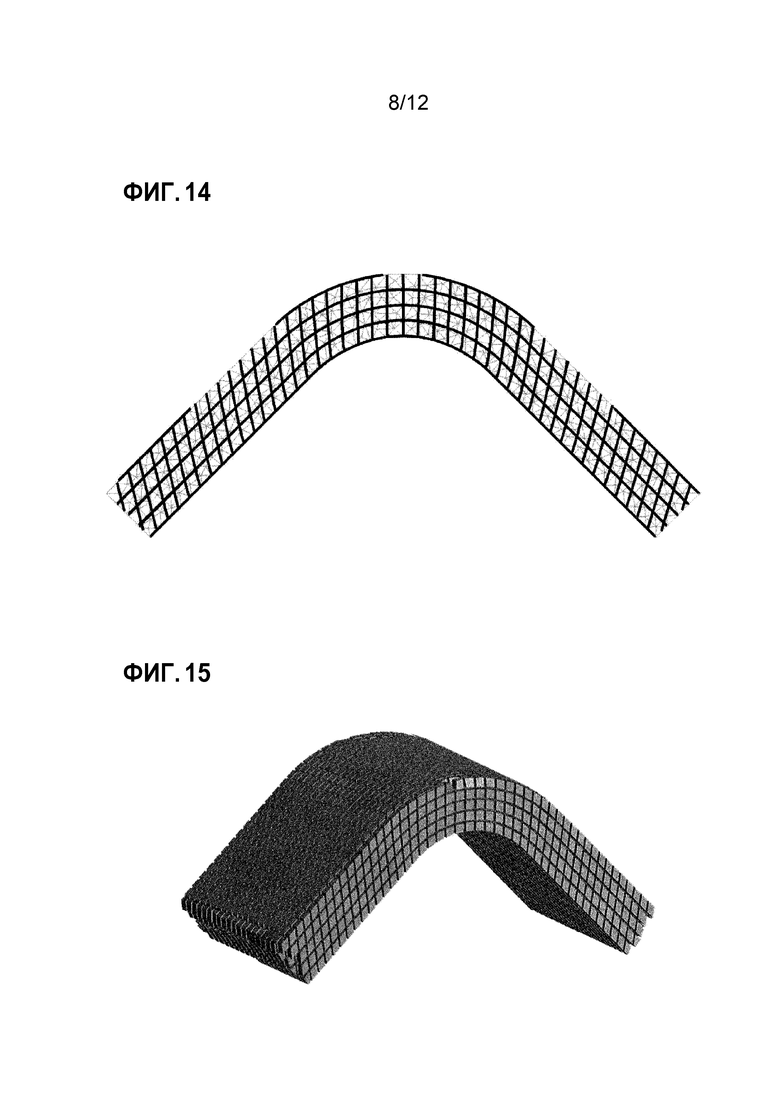
Фиг. 14 является схемой, иллюстрирующей результат 87-й повторяющейся обработки из обработки параметризации и обработки обновления векторов ориентации в случае двух измерений;
Фиг. 15 является схемой, иллюстрирующей результат моделирования формы модели относительно примера детали машины;
Фиг. 16 является схемой, иллюстрирующей результат моделирования формы материала относительно примера детали машины по фиг. 15;
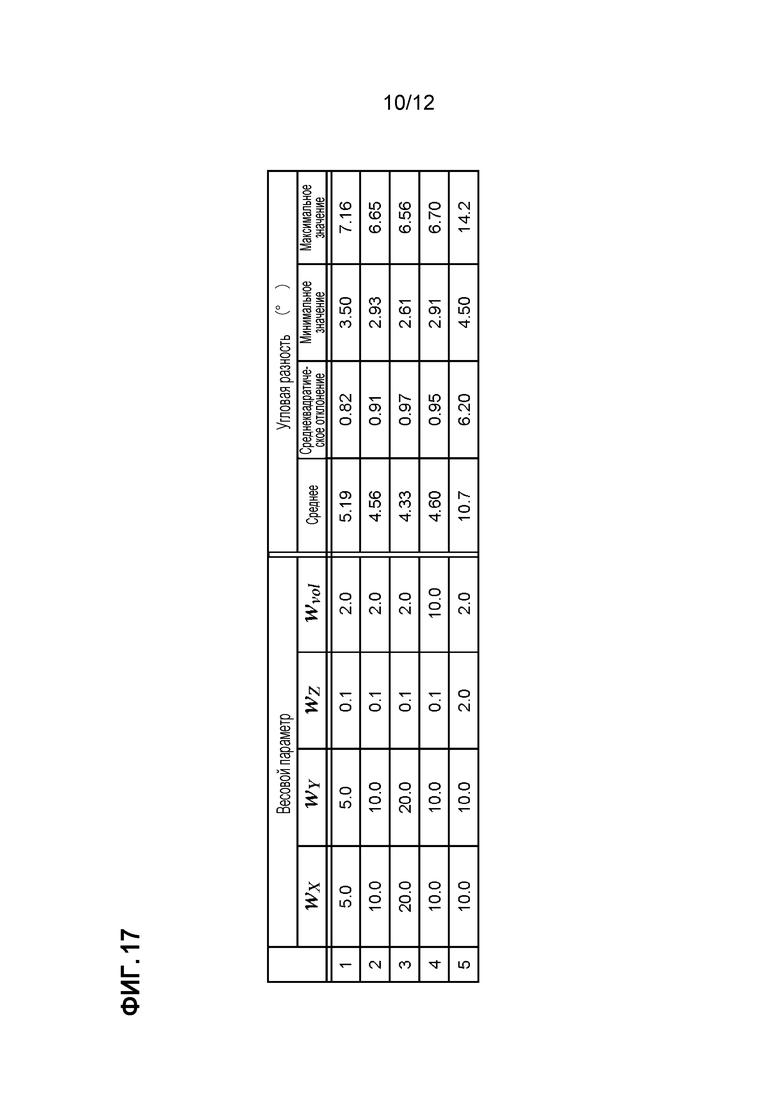
Фиг. 17 является таблицей, указывающей разности ошибок, вызываемые различиями весовых параметров функции энергии деформации;
Фиг. 18 является схемой, иллюстрирующей пример процесса изготовления армированных волокнами композиционных материалов;
Фиг. 19 является схемой, принципиально иллюстрирующей плетеную структуру трехмерного плетеного волокнистого материала; и
Фиг. 20 является схемой, иллюстрирующей пример поперечного сечения трехмерного плетеного волокнистого материала, который деформируется.
Подробное описание вариантов осуществления
[0015] Ниже подробно поясняется вариант осуществления настоящего раскрытия со ссылкой на чертежи. В нижеприведенном пояснении идентичные ссылочные номера присвоены аналогичным элементам, и какие-либо дублированные пояснения опускаются.
(1) Конфигурация устройства моделирования форм материалов согласно этому варианту осуществления
[0016] Фиг. 1 является схемой, иллюстрирующей конфигурацию аппаратных средств устройства 100 моделирования форм материалов согласно этому варианту осуществления. Устройство 100 моделирования форм материалов может быть выполнено из центрального процессора (ЦП) 201, энергозависимого блока 202 хранения, такого как оперативное запоминающее устройство (ОЗУ), энергонезависимого блока 203 хранения, такого как жесткий диск и флэш-память, устройства 500 ввода, такого как клавиатура и мышь, и устройства 400 отображения, включающего в себя, например, жидкокристаллический экран отображения, как проиллюстрировано на этом чертеже. При этом ЦП 201, энергозависимый блок 202 хранения и энергонезависимый блок 203 хранения составляют вычислительный блок 200 обработки, который работает посредством программного обеспечения. В этой связи, устройство 100 моделирования форм материалов может быть выполнено из компьютерной системы, с которой компьютерное устройство с проиллюстрированной на фиг. 1 конфигурацией аппаратных средств соединяется по сети.
[0017] Фиг. 2 является блок-схемой, иллюстрирующей функциональную конфигурацию вычислительного блока 200 обработки устройства 100 моделирования форм материалов. Вычислительный блок 200 обработки устройства 100 моделирования форм материалов, как проиллюстрировано на этом чертеже, включает в себя: блок 210 формирования поля векторов ориентации, который формирует поле векторов ориентации формы модели на трехмерных сетках формы модели трехмерного плетеного волокнистого материала, который получается укладкой друг на друга множества листов двумерной плетеной ткани, изготовленной из X-пряжи, проходящей в направлении Х, и Y-пряжи, проходящей в направлении Y, и связыванием их Z-пряжей, проходящей в направлении Z; блок 220 параметризации, который выполняет поиск вектора градиента для вычисления поля векторов ориентации формы материала, которое представляет собой поле векторов ориентации формы материала перед деформированием формы модели, из поля векторов ориентации формы модели; блок 230 обновления векторов ориентации, который обновляет поле векторов ориентации формы модели посредством применения условия сохранения объема между полем векторов ориентации формы модели и полем векторов ориентации формы материала и того условия, что ни X-пряжа, ни Y-пряжа не растягивается и не сжимается; и блок 240 нелинейной оптимизации, который дополнительно обновляет поле векторов ориентации формы модели при минимизации энергии деформации формы модели. При этих блок 240 нелинейной оптимизации включен в этот вариант осуществления; тем не менее, также может использоваться конфигурация, которая не включает в себя блока 240 нелинейной оптимизации.
[0018] Фиг. 3 является блок-схемой, иллюстрирующей общее представление обработки моделированием посредством устройства 100 моделирования форм материалов. Сначала блок 210 формирования поля векторов ориентации заставляют определять вектор направления волокон для элемента четырехгранника, который представляет собой сетку формы модели, и он создает начальный вектор ориентации (этап S11), как проиллюстрировано на этом чертеже. Затем блок 220 параметризации выполняет поиск преобразования f из формы модели в форму материала (этап S12). Когда это происходит, поиск преобразования f может выполняться посредством выполнения параметризации, такой как разложение в ряд Тейлора. Затем блок 230 обновления векторов ориентации вынуждают обновлять полученную параметризацией форму материала в пространство модели посредством использования установленных условий (этап S13). Этап S12 и этап S13 повторяют. Наконец, блок 240 нелинейной оптимизации заставляют выполнять оптимизацию, минимизируя энергию деформации в направлении волоконного жгута и объемной деформации (этап S20). Когда блок 240 нелинейной оптимизации не включен, обработка завершается в результате повторения обработки параметризации и обработки обновления векторов ориентации. Ниже подробно поясняется обработка каждым блоком обработки.
(2) Обработка блоком формирования поля векторов ориентации
[0019] Фиг. 4 является схемой, принципиально иллюстрирующей взаимосвязь между координатами на форме модели и форме материала при обработке моделированием. Когда вершина pi сетки пространства модели (x, y, z) преобразуется в вершину f(pi) пространства (X, Y, Z) материала посредством функции f преобразования, как проиллюстрировано на этом чертеже, вектор ориентации известен как идеальный вектор градиента функции f преобразования. Когда функция f преобразования выражена формулой (1), векторы градиента функции f преобразования выражаются формулой (2).
[Математическое выражение 1]
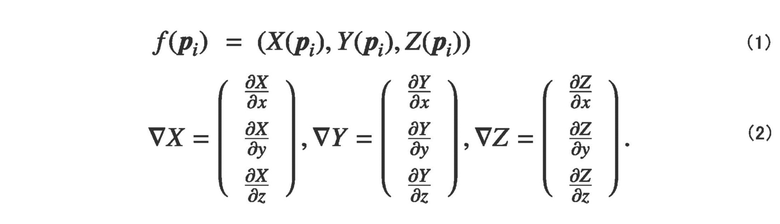
Идеальный вектор градиента оценивается при каждой повторяющейся обработке, и полученные идеальные векторы градиента называются "векторами ориентации". Каждый набор из трех векторов ориентации присваивается четырехграннику, и поле векторов ориентации используется в качестве направляющего поля во время обработки параметризации.
[0020] Эти векторы ориентации непосредственно связаны с направлениями волокон через четкие правила деформирования. Чтобы показать это, формула (3) выражается матрицами Якоби функций f и f-1 преобразования.
[Математическое выражение 2]
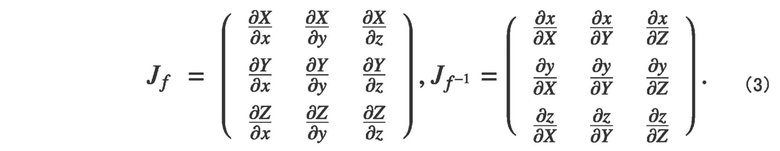
Эти матрицы Якоби имеют следующую очевидную взаимосвязь, как указано в виде нижеприведенной формулы (4).
[Математическое выражение 3]

[0021] Поскольку трехмерный плетеный волокнистый материал образован нитями волокон, которые пересекаются друг с другом под прямыми углами, X-пряжа, Y-пряжа и Z-пряжа пространства материала ориентированы параллельно базовым направлениям пространства XYZ. Кроме того, с учетом того факта, что нити волокон в пространстве материала не растягиваются и не сжимаются, X-пряжа, Y-пряжа и Z-пряжа в этом пространстве выражаются соответственно в виде нижеприведенной формулы (5).
[Математическое выражение 4]

Направления волокон в пространстве модели заданы как Fdx, Fdy, Fdy, и они явно выражаются нижеприведенной формулой (6) посредством применения матрицы Якоби Jf-1 к Fx, Fy, Fy.
[Математическое выражение 5]
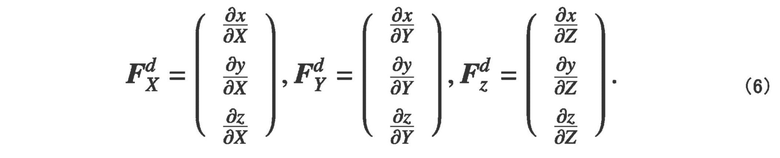
Следующая формула (7) выводится посредством сопоставления формул (2) и (6) с формулой (3).
[Математическое выражение 6]
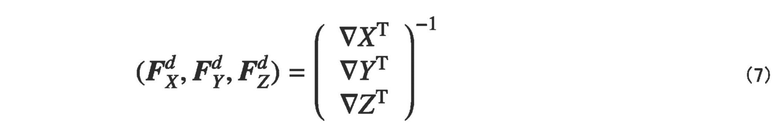
Формула (7) показывает взаимосвязь между векторами ориентации и направлениями волокон в пространстве модели. Набор этих векторов может взаимно деформироваться с использованием формулы (7).
[0022] В дальнейшем поясняется обработка блоком 210 формирования поля векторов ориентации для формирования поля векторов ориентации формы модели в каждой сетке. Векторы направления волокон присваиваются на границе искривленной поверхности формы модели. Эти векторы направления волокон определяются касательным пространством искривленной поверхности и устанавливаются на треугольной площади граничной поверхности. Чтобы формировать начальное поле векторов ориентации, векторы направления волокон вычисляются относительно каждого четырехгранника формы модели и деформируются в поле векторов ориентации формы модели с использованием формулы (7). Поле направления волокон вычисляется на основе конкретных направлений волокон посредством использования следующих этапов 1 и 2.
Этап 1. Векторы направления волокон искривленной поверхности на границе формы модели распространяют.
Этап 2. Векторы направления волокон распространяют вовнутрь формы модели.
При этом можно использовать способы, отличные от описанных выше способов, для того, чтобы распространять векторы направления волокон. Векторы распространяют посредством повторного вычисления их среднего по смежным треугольникам или четырехгранникам. При этих обстоятельствах может использоваться метод Херцмана из NPL 1.
[0023] На этапе 1 необходимо выполнять глобальную минимизацию изменений векторов смежных треугольников с тем, чтобы получать сглаженное векторное поле; и это становится нелинейной задачей. При этих обстоятельствах нелинейная задача может решаться; тем не менее, этот вариант осуществления рассчитан на повторение локальной минимизации с использованием среднего значения угловых разностей векторов смежных треугольников. Фиг. 5 иллюстрирует то, как векторы направления волокон распространяются на искривленной поверхности из краевой области, где граничные условия заданы на этапе 1. Сначала, как проиллюстрировано на этом чертеже, векторы направления волокон в пограничной области задают (этап S31) и распространяют (этап S32), тем самым формируя поле векторов направления волокон (этап S33). На этапе 2 сглаженное векторное поле может быть получено с использованием среднего значения полярных координат смежных четырехгранников таким же самым образом. Векторы направления волокон могут быть расположены в каждой сетке вышеописанным методом. К полученным векторам направления волокон применяют формулу (7), тем самым деформируя их в векторы ориентации формы модели.
(3) Обработка блоком параметризации
[0024] Что касается параметризации, то способы задания трехмерной искривленной поверхности соответствующей двумерному евклидову пространству описаны в NPL 2 - NPL 5. В этом варианте осуществления применяется способ, аналогичный NPL 6 и NPL 7, чтобы использовать направляющее векторное поле, в котором тройное многообразие задается соответствующим трехмерному евклидову пространству.
[0025] Набор векторов ориентации на краю определяется по следующей формуле (8), а координаты (pi, pj) преобразованной вершины выражаются следующей формулой (9).
[Математическое выражение 7]
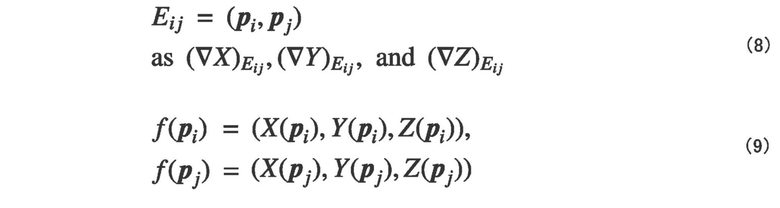
Условия преобразования выражаются следующей формулой (10).
[Математическое выражение 8]
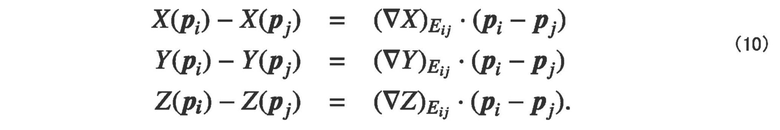
Когда формула (10) удовлетворяется, векторы градиента совпадают с конкретными векторами ориентации. При этих обстоятельствах создают следующую формулу (11), которая представляет собой функцию минимизации, суммируя квадратические ошибки формулы (10) относительно всех краев.
[Математическое выражение 9]
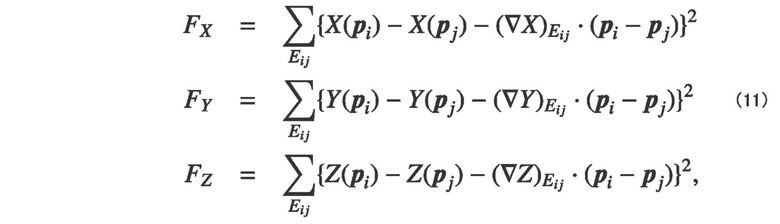
[0026] (∇X)Eij, (∇Y)Eij, (∇Z)Eij могут вычисляться посредством получения среднего векторов ориентации (∇X)Tk, (∇Y)Tk, (∇Z)Tk относительно всех четырехгранников Tk. Каждое уравнение этой формулы (11) минимизируется. Когда это происходит, минимизация этой формулы представляет собой линейную задачу, и может применяться метод сопряженных градиентов. В результате могут быть найдены векторы градиента для преобразования из формы модели в форму материала.
[0027] Фиг. 6-9 являются схемами, иллюстрирующими примеры двумерной параметризации с использованием поля векторов ориентации формы модели. Фиг. 6 и фиг. 8 представляют распределение поля векторов ориентации формы модели, а фиг. 7 и фиг. 9 являются схемой, показывающей результаты параметризации, соответствующей фиг. 6 и 8 соответственно, как указано изоплетическими линиями. Что касается этих результатов, то формула (10) обязательно удовлетворяется, и векторы направления волокон, вычисленные из векторов градиента преобразования, отличаются от требуемых результатов, а значения энергии деформации становятся высокими. Обработка блоком обновления векторов ориентации в следующем разделе заключается в том, чтобы улучшать поле векторов ориентации на основе результатов этой параметризации.
(4) Обработка блоком обновления векторов ориентации
[0028] Обработка блоком 230 обновления векторов ориентации заключается в том, чтобы обновлять поле векторов ориентации на основе поля градиентов. Фиг. 10 является схемой для пояснения обработки обновления векторов ориентации. Деформирование шестигранника с его сторонами, сформированными из направлений волокон, выражается так, как проиллюстрировано на этом чертеже, и для того, чтобы пояснять локальное деформирование, используется величина деформации континуума. Ссылаясь на фиг. 19, наклон и растяжение Z-пряжи возникают проще, чем перемещения скольжением X-пряжи и Y-пряжи относительно друг друга на пересечениях между X-пряжей и Y-пряжей. Говоря конкретнее, сдвиговая деформация между X/Y-пряжей и Z-пряжей и деформация Z-пряжи возникают проще, чем деформация между X-пряжей и Y-пряжей. Следовательно, можно предполагать, что деформация между X-пряжей и Y-пряжей не возникает, а возникает только сдвиговая деформация между X/Y-пряжей и Z-пряжей. Поскольку норма деформирования в XY-направлении волокон пространства модели близка к норме деформирования в XY-направлении волокон пространства материала, и растяжение/сжатие Z-пряжи может считаться вызываемым в результате принудительных изменений объема, следует уделять внимание сохранению объема. Следовательно, применяется следующая формула (12).
[Математическое выражение 10]
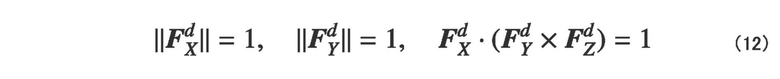
При этих обстоятельствах, когда формулы (5) и (7) применяются к формуле (12), можно получить условия следующей формулы (13).
[Математическое выражение 11]
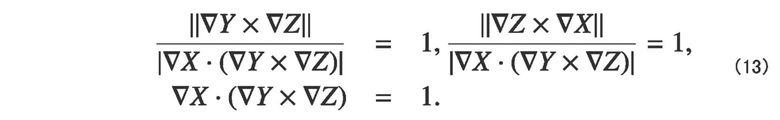
[0029] Векторы градиента (∇X)f, (∇Y)f и (∇Z)f, полученные посредством обработки блоком параметризации, используются для того, чтобы получать формулу (13) для обновления векторов ориентации. В частности, направления векторов градиента (∇X)f, (∇Y)f и (∇Z)f приспосабливаются в качестве направлений векторов ∇X, ∇Y и ∇Z ориентации, и формула (13) используется для того, чтобы определить норму векторов градиента. Поскольку градиент преобразования может деформироваться в направлениях волокон с использованием формулы (7), норма векторов может корректироваться с использованием полученных параметризацией направлений волокон, так что эта корректировка будет отражаться в фактическом явлении деформирования волокнистого материала. В этом варианте осуществления применяется вышеуказанная формула (12) или (13); тем не менее, без ограничения этими формулами, можно применять формулу, означающую такое допущение, что деформация между X-пряжей и Y-пряжей не возникает, а возникает только сдвиговая деформация между X/Y-пряжей и Z-пряжей.
[0030] Фиг. 11-14 являются схемами, показывающими результаты применения обработки для повторения обработки параметризации и обработки обновления векторов ориентации в случае двух измерений. Фиг. 11 является результатом первой повторяющейся обработки; фиг. 12 является результатом 7-ой повторяющейся обработки; фиг. 13 является результатом 20-й повторяющейся обработки; и фиг. 14 является результатом 87-й повторяющейся обработки. Сплошные линии представляют координатные линии, преобразованные в пространство материала, и соответствуют направлениям волокон в пространстве модели. Что касается результата первой повторяющейся обработки, проиллюстрированной на фиг. 11, то X-пряжа значительно растягивается, а сдвиговая деформация возникает редко. Соответственно, результат первого повторения, как проиллюстрировано на фиг. 11, отличается от фактического явления деформирования. По мере того, как повторяющаяся обработка продолжается, вытягивание X-пряжи снижается, а сдвиговая деформация между X-пряжей и Y-пряжей увеличивается, как проиллюстрировано в результатах повторения по фиг. 12-14. Поэтому ориентация каждой пряжи, в частности, Z-пряжи, для формы модели и формы материала может точно моделироваться при таком допущении, что деформация между X-пряжей и Y-пряжей не возникает, а возникает только сдвиговая деформация между X/Y-пряжей и Z-пряжей.
(5) Обработка блоком нелинейной оптимизации
[0031] Вышеописанное повторение обработки параметризации и обработки для обновления векторов ориентации позволяет косвенно минимизировать функцию энергии и грубо оценить соответствие между формой модели и формой материала. Обработка этим блоком 240 нелинейной оптимизации может использоваться для того, чтобы точно оценивать форму материала, и представляет собой обработку для непосредственной минимизации функции энергии деформации. Функция энергии деформации с учетом режима деформирования трехмерного плетеного волокнистого материала может выражаться следующей формулой (14).
[Математическое выражение 12]
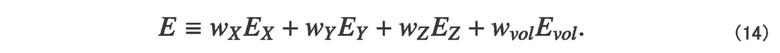
Что касается этой формулы, то EX, EY и EZ являются энергией деформации X, Y и Z соответственно, а Evol является энергией объемной деформации. При этих обстоятельствах, можно предполагать континуум для вычисления каждой энергии, и для такого вычисления может использоваться модуль Юнга. Каждый из wX, wY, wZ и wvol представляет собой весовой параметр и может определяться на основе экспериментальных результатов деформирования трехмерного плетеного волокнистого материала. Эта формула может использоваться для того, чтобы оценить энергию деформации, и использоваться в качестве условия завершения повторения обработки параметризации и обработки обновления векторов ориентации. Тем не менее, могут использоваться и другие условия завершения, такие как установленное число раз или какие-либо изменения, возникающие в результатах, а функция энергии деформации может не использоваться. Поскольку энергия деформации формы модели может уменьшаться посредством выполнения обработки нелинейной оптимизации, ориентация каждой пряжи, в частности, Z-пряжи, формы модели может моделироваться более точно.
[0032] Чтобы минимизировать эту нелинейную функцию, можно использовать, например, способ линейного поиска согласно нижеприведенной формуле (15), которая выражает k-ое повторение в случае, когда начальным решением является x0.
[Математическое выражение 13]

Что касается вышеприведенной формулы, то pk и αk являются направлением поиска и размером шага для k-ого повторения. При этих обстоятельствах, направление градиента энергии E деформации может использоваться для того, чтобы определить направление P поиска. Кроме того, NPL 8 может использоваться для того, чтобы найти размер шага αk.
[0033] Фиг. 15 и фиг. 16 являются схемами, иллюстрирующими результаты моделирования деформирования формы детали машины с использованием устройства моделирования форм материалов согласно этому варианту осуществления. Фиг. 15 показывает форму модели, а фиг. 16 показывает форму материала; и, как проиллюстрировано на этих чертежах, можно видеть, что ориентация волокон, обозначенных в форме модели, моделирует ориентацию волокон формы материала с учетом толщины. Фиг. 17 является таблицей, указывающей угловые ошибки Z-пряжи между фактическими объектами и результатами моделирования вследствие различий в весовых параметрах. Согласно этой таблице, третий пример имеет минимальную ошибку. Предпочтительно, как указано в этой таблице, что весовой параметр wZ должен задаваться равным или меньшим одной сотой (1/100) весового параметра wX или wY, либо, более предпочтительно, равным или меньшим одной двухсотой (1/200) весового параметра wX или wY. Кроме того, предпочтительно, что весовой параметр wvol должен быть равным или меньшим одной пятой (1/5) весового параметра wX или wY, либо, более предпочтительно, равным или меньшим одной десятой (1/10) весового параметра wX или wY. Моделирование может выполняться более точно также и в количественном смысле посредством определения весовых параметров, как описано выше.
(6) Эффекты этого варианта осуществления
[0034] Устройство 100 моделирования форм материалов согласно этому варианту осуществления включает в себя: блок 210 формирования поля векторов ориентации, который формирует поле векторов ориентации формы модели на трехмерных сетках формы модели трехмерного плетеного волокнистого материала, который получается укладкой друг на друга множества листов двумерной плетеной ткани, изготовленной из X-пряжи, проходящей в направлении Х, и Y-пряжи, проходящей в направлении Y, и связыванием их Z-пряжей, проходящей в направлении Z; блок 220 параметризации, который выполняет поиск вектора градиента для вычисления поля векторов ориентации формы материала, которое представляет собой поле векторов ориентации формы материала перед деформированием формы модели, из поля векторов ориентации формы модели; и блок 230 обновления векторов ориентации, который обновляет поле векторов ориентации формы модели посредством применения условия сохранения объема между полем векторов ориентации формы модели и полем векторов ориентации формы материала и условия, что ни X-пряжа, ни Y-пряжа не растягивается и не сжимается. Следовательно, устройство 100 моделирования форм материалов может более точно моделировать деформирование трехмерного плетеного волокнистого материала и вычислять форму материала.
Промышленная применимость
[0035] Настоящее раскрытие может применяться к деформированию трехмерного плетеного волокнистого материала.
[0036] Список ссылочных обозначений
100 - устройство моделирования форм материалов
200 - вычислительный блок обработки
202 - энергозависимый блок хранения
203 - энергонезависимый блок хранения
210 - блок формирования поля векторов ориентации
220 - блок параметризации
230 - блок обновления векторов ориентации
240 - блок нелинейной оптимизации
400 - устройство отображения
500 - устройство ввода.
| название | год | авторы | номер документа |
|---|---|---|---|
| МАШИНА ДЛЯ ФОРМИРОВАНИЯ КОМПОЗИТНЫХ МАТЕРИАЛОВ ПУТЕМ МНОГОМЕРНОГО ПЛЕТЕНИЯ | 2012 |
|
RU2590809C2 |
| СПОСОБ МОДЕЛИРОВАНИЯ ТРЕХМЕРНОГО ПРОСТРАНСТВА | 2016 |
|
RU2713611C2 |
| СИСТЕМА И СПОСОБ ИЗГОТОВЛЕНИЯ | 2000 |
|
RU2305864C2 |
| СПОСОБ ТРЕХМЕРНОГО МОДЕЛИРОВАНИЯ ПЕРСОНИФИЦИРОВАННЫХ ЧЕЛЮСТНО-ЛИЦЕВЫХ ИМПЛАНТАТОВ ДЛЯ МОДЕЛИРОВАНИЯ ФОРМЫ ПОДБОРОДКА | 2021 |
|
RU2797494C1 |
| НЕПАРАМЕТРИЧЕСКИЕ МИКРОФАСЕТОЧНЫЕ ФАКТОРНЫЕ МОДЕЛИ ДЛЯ ИЗОТРОПНЫХ ФУНКЦИЙ ДВУНАПРАВЛЕННОГО РАСПРЕДЕЛЕНИЯ ОТРАЖАТЕЛЬНОЙ СПОСОБНОСТИ | 2015 |
|
RU2684480C2 |
| Способ автоматического построения модели гетерогенной волокнистой внутренней структуры композиционного материала | 2017 |
|
RU2670922C9 |
| СИСТЕМА И СПОСОБ МОДЕЛИРОВАНИЯ И КАЛИБРОВКИ УСТРОЙСТВА ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЯ | 2014 |
|
RU2677562C2 |
| Способ автоматизированного построения трехмерной модели гетерогенной структуры композиционного материала с волокнами | 2018 |
|
RU2689803C1 |
| УСТРОЙСТВО ДЛЯ ПРОИЗВОДСТВА ДВУМЕРНЫХ ИЛИ ТРЕХМЕРНЫХ ВОЛОКНИСТЫХ МАТЕРИАЛОВ ИЗ МИКРОВОЛОКОН И НАНОВОЛОКОН | 2011 |
|
RU2547638C2 |
| СПОСОБ УПРАВЛЕНИЯ ТРЕЩИНООБРАЗОВАНИЕМ В МАТЕРИАЛЕ И СООТВЕТСТВУЮЩЕЕ УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2682583C1 |

Изобретение относится к устройству и способу моделирования форм материалов и способу изготовления трехмерных плетеных волокнистых компонентов. Технический результат заключается в автоматизации моделирования форм материалов. Устройство содержит: блок формирования поля векторов ориентации, который формирует поле векторов ориентации формы модели на трехмерных сетках формы модели трехмерного плетеного волокнистого материала, который получается укладкой друг на друга множества листов двумерной плетеной ткани, изготовленной из X-пряжи, проходящей в направлении Х, и Y-пряжи, проходящей в направлении Y, и связыванием их Z-пряжей, проходящей в направлении Z; блок параметризации, который выполняет поиск вектора градиента для вычисления поля векторов ориентации формы материала, которое представляет собой поле векторов ориентации формы материала перед деформированием формы модели, из поля векторов ориентации формы модели; и блок обновления векторов ориентации, который обновляет поле векторов ориентации формы модели посредством применения условия сохранения объема между полем векторов ориентации формы модели и полем векторов ориентации формы материала и условия, что ни X-пряжа, ни Y-пряжа не растягивается и не сжимается. 3 н. и 10 з.п. ф-лы, 20 ил.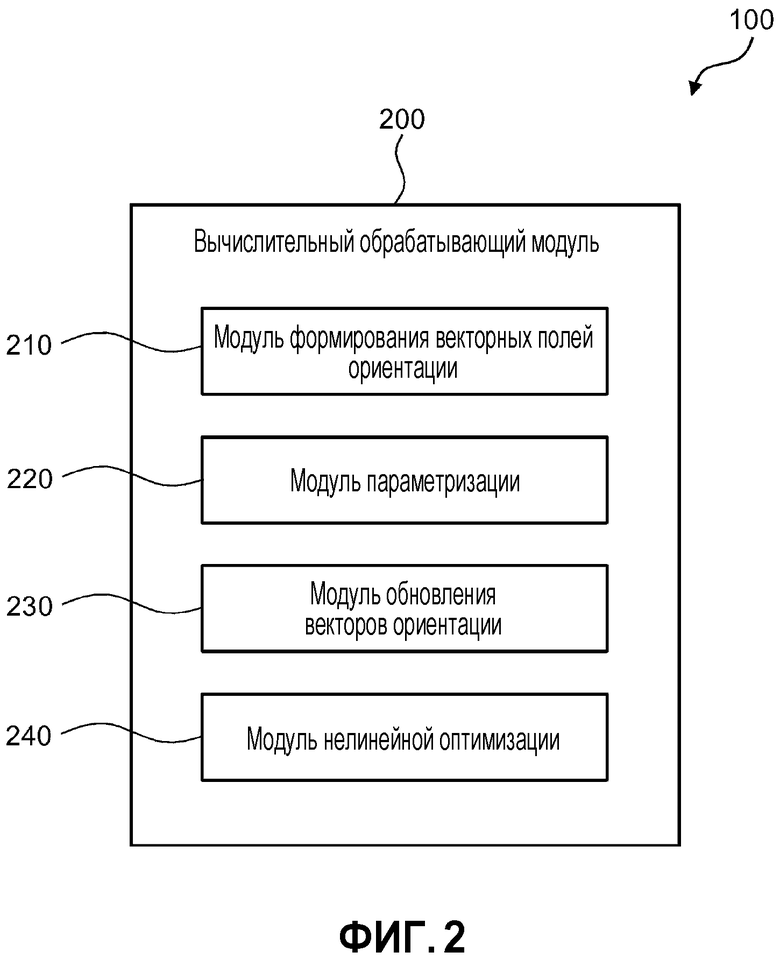
1. Устройство моделирования форм материалов, содержащее:
блок формирования поля векторов ориентации, который формирует поле векторов ориентации формы модели на трехмерных сетках формы модели трехмерного плетеного волокнистого материала, который получается укладкой друг на друга множества листов двумерной плетеной ткани, изготовленной из X-пряжи, проходящей в направлении Х, и Y-пряжи, проходящей в направлении Y, и связыванием их Z-пряжей, проходящей в направлении Z;
блок параметризации, который выполняет поиск вектора градиента для вычисления поля векторов ориентации формы материала, которое представляет собой поле векторов ориентации формы материала перед деформированием формы модели, из поля векторов ориентации формы модели; и
блок обновления векторов ориентации, который обновляет поле векторов ориентации формы модели посредством применения условия сохранения объема между полем векторов ориентации формы модели и полем векторов ориентации формы материала и условия, что ни X-пряжа, ни Y-пряжа не растягивается и не сжимается.
2. Устройство моделирования форм материалов по п. 1, причем блок параметризации выполняет поиск вектора градиента посредством задания вектора градиента согласно нижеприведенной формуле (1) относительно пространства модели (x, y, z) и пространства материала (X, Y, Z):
[Математическое выражение 1]
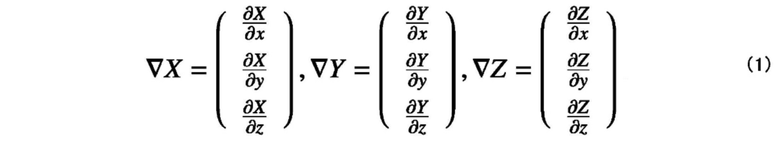
и посредством задания направлений волокон пространства модели согласно нижеприведенной формуле (2):
[Математическое выражение 2]
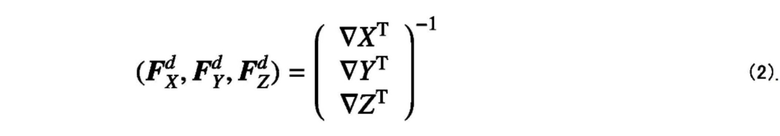
3. Устройство моделирования форм материалов по п. 2, причем, когда направления волокон пространства материала задаются как FX=(1, 0, 0), FY=(0, 1, 0) и FZ=(0, 0, 1), блок обновления векторов ориентации обновляет поле векторов ориентации формы модели с применением нижеприведенной формулы (3):
[Математическое выражение 3]
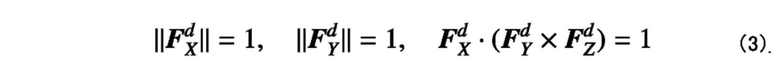
4. Устройство моделирования форм материалов по любому из пп. 1-3, причем блок формирования поля векторов ориентации задает вектор направления волокон на границе формы модели, распространяет вектор направления волокон на искривленную поверхность формы модели на основе упомянутого вектора направления волокон на границе и распространяет вектор направления волокон вовнутрь формы модели на основе вектора направления волокон искривленной поверхности.
5. Устройство моделирования форм материалов по любому из пп. 1-4, причем, когда вектор градиента для вектора ориентации Eij=(pi, pj) на краю трехмерных сеток задается как ((X)Eij, (Y)Eij, (Z)Eij), блок параметризации выполняет поиск вектора градиента так, что значения правой и левой сторон нижеприведенной формулы (4) становятся как можно более близкими друг к другу:
[Математическое выражение 4]
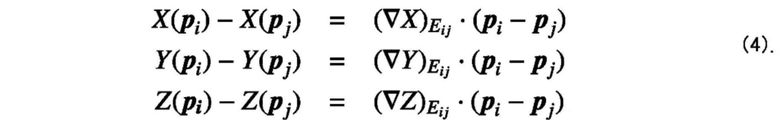
6. Устройство моделирования форм материалов по п. 5, причем поиск вектора градиента выполняется посредством минимизации каждого значения, вычисленного согласно нижеприведенной формуле (5):
[Математическое выражение 5]
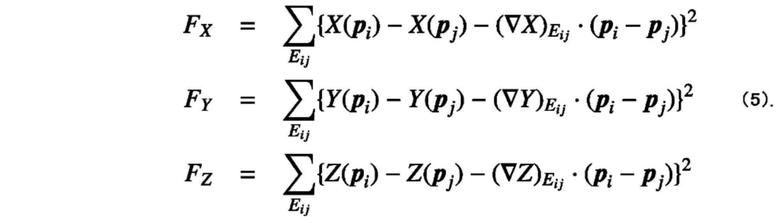
7. Устройство моделирования форм материалов по любому из пп. 1-6, дополнительно содержащее блок нелинейной оптимизации, который дополнительно обновляет поле векторов ориентации формы модели при минимизации энергии деформации формы модели.
8. Устройство моделирования форм материалов по п. 7, причем, когда EX, EY и EZ - энергия деформации X, Y и Z соответственно, Evol - энергия объемной деформации, а wX, wY и wZ - весовые значения, блок нелинейной оптимизации дополнительно обновляет поле векторов ориентации формы модели при минимизации значения нижеприведенной формулы (6):
[Математическое выражение 6]
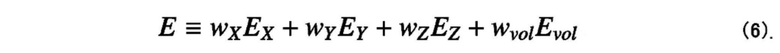
9. Устройство моделирования форм материалов по п. 8, причем весовой параметр wZ равен или меньше одной сотой (1/100) весового параметра wX или wY.
10. Устройство моделирования форм материалов по п. 8 или 9, причем весовой параметр wvol равен или меньше одной пятой (1/5) весового параметра wX или wY.
11. Устройство моделирования форм материалов по любому из пп. 1-10, причем каждая из трехмерных сеток представляет собой четырехгранник.
12. Способ моделирования форм материалов, реализуемый устройством моделирования форм материалов по любому из пп. 1-11, содержащий:
формирование поля векторов ориентации формы модели на трехмерных сетках формы модели трехмерного плетеного волокнистого материала, который получается укладкой друг на друга множества листов двумерной плетеной ткани, изготовленной из X-пряжи, проходящей в направлении Х, и Y-пряжи, проходящей в направлении Y, и связыванием их Z-пряжей, проходящей в направлении Z;
выполнение поиска вектора градиента для вычисления поля векторов ориентации формы материала, которое представляет собой поле векторов ориентации формы материала перед деформированием формы модели, из поля векторов ориентации формы модели; и
обновление поля векторов ориентации формы модели посредством применения условия сохранения объема между полем векторов ориентации формы модели и полем векторов ориентации формы материала и условия, что ни X-пряжа, ни Y-пряжа не растягивается и не сжимается.
13. Способ изготовления трехмерных плетеных волокнистых компонентов, содержащий:
вычисление формы материала способом моделирования форм материалов, указанным в п. 12;
создание трехмерного плетеного волокнистого материала с вычисленной формой материала; и
формирование трехмерного плетеного волокнистого компонента деформированием трехмерного плетеного волокнистого материала.
| JP 8338795 A, 24.12.1996 | |||
| JP 2006272928 A, 12.10.2006 | |||
| JP 2013011504 A, 17.01.2013 | |||
| RU 2007103231 A, 20.10.2008 | |||
| СИСТЕМА И СПОСОБ ДЛЯ УЛУЧШЕННОГО ПАРАМЕТРИЧЕСКОГО ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ | 1994 |
|
RU2127449C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ПОСТРОЕНИЯ ТРЕХМЕРНОЙ ГЕОМЕТРИЧЕСКОЙ МОДЕЛИ ИЗДЕЛИЯ В СИСТЕМЕ ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ | 2005 |
|
RU2308763C2 |
| RU 2014125774 A, 27.12.2015. | |||
Авторы
Даты
2020-02-07—Публикация
2017-02-06—Подача