Изобретение относится к технической кибернетике и предназначено для использования в качестве способа текущей (в реальном масштабе времени), либо после заранее проведенной серии экспериментов (постфактум), идентификации моделей объектов (динамических систем). Техническим результатом является обеспечение структурно-параметрической идентификации модели не линеаризованного объекта по известным значениям измеренных входных и выходных сигналов, позволяющей автоматизированно определять структуру и неизвестные параметры математической модели объекта при одновременном улучшении качества и достоверности результатов.
Задача построения модели системы по некоторым данным, подаваемым на вход и считываемым с ее выхода, известна как задача идентификации модели системы [8]. Существует много частных постановок задач идентификации применительно к различным целям построения моделей систем. При построении модели системы в задаче идентификации часто предполагается, что физическая теория работы системы (объекта) отсутствует или по тем или иным причинам не может быть использована. Объект идентификации представляет собой так называемый «черный ящик» с некоторым числом доступных (или, по крайней мере, измеряемых) входов X и одним или несколькими наблюдаемыми (непосредственно измеряемыми) выходами U.
Общий принцип изоморфизма может служить единой методологической и формально-математической основой для решения многих задач теории систем [1-6]. Одной из таких задач является классическая задача реализации системы [7], рассматриваемой в качестве «черного ящика», подразумевающая построение модели системы по некоторым данным о ней, то есть идентификацию модели. Задача не имела формально строгого решения, так как не удавалось, как указано в [7], не только доказать, но и сформулировать «теорему о реализации». Введение общего принципа изоморфизма позволило сформировать новую парадигму в теории систем [1, 6], основанную на этом единственном принципе, в рамках которой не только сформулирована и доказана теорема о реализации [6], но и формализованы и взаимоувязаны все основные свойства систем: наблюдаемость, управляемость, контролируемость, идентифицируемость, разделимость задач синтеза регуляторов и наблюдателей и их комплексируемость в интегрированную информационно-управляющую систему [1-6].
Модель (функцию преобразования) большинства применяемых на практике скалярных (один вход-один выход) и векторных (много входов - много выходов) систем как правило стремятся получить в линейной параметрической форме вида
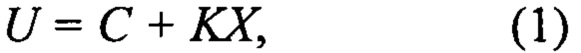
где X - вектор входных сигналов системы, т.е. измеряемая векторная физическая величина, воздействующая на систему; U - вектор сигналов на выходе системы, соответствующий (пропорциональный) вектору входных сигналов, K - матричный коэффициент пропорциональности векторов выходных и входных сигналов системы, называемый масштабным коэффициентом, С - вектор «нулевых сигналов», называемых «смещением нуля», измеряемых на выходе системы при отсутствии векторного сигнала на его входе, точнее, при заведомо известном нулевом векторе сигналов на входе системы. Такая модель, по сути, представляет собой полином минимальной (первой) степени для аппроксимации значений векторного выходного сигнала и требует идентификации лишь двух параметров - С и К. Следует иметь в виду, что для случая векторной системы матрицы С и К могут быть не обязательно диагональными.
Простота линейной модели позволяет определять (идентифицировать) ее параметры с использованием достаточно простой процедуры калибровки и даже надежно и с известной точностью предсказывать (на основе паспортных данных) значения выходных сигналов системы вообще без калибровки, если требования к точности предсказания выходных сигналов системы не высоки и лежат в пределах погрешностей, характерных для множества систем данного типа. Характерным примером идентифицируемых систем (объектов) могут служить датчики различных физических величин. В этом случае еще одним достоинством линейной функции преобразования вида (1) является то, что восстановление и предсказание значений измеряемой датчиком физической величины осуществляется по весьма просто получаемой из (1) обратной функции преобразования датчика
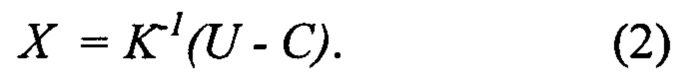
Однако, линейность модели, как указывалось выше, достигается, в прямом смысле, дорогой ценой, которую приходится платить за сложные конструкторские ухищрения (специально направленные на обеспечение линейности датчика) и высокий коэффициент отбраковки датчиков. Это является недостатком подавляющего большинства всех современных датчиков, измеряющих самые разные физические величины. Достаточно простые способы избавления датчиков от этого недостатка до настоящего времени практически не известны. В случае датчиков, идентификация их моделей, как правило, осуществляется не в реальном времени, а постфактум - после серии заранее проведенных калибровочных экспериментов, в результате которых формируются множества входных и выходных сигналов.
Известен патент №2256950 Способ идентификации линеаризованного динамического объекта МПК7 G06F 17/18, G05B 17/02, опубликованы 20.07.2005 г., бюл. №20.
В известном изобретении на основе дискретных измерений входного x(t) и выходного y(t) сигналов объекта с шагом дискретизации Δt определяют интервалы согласно выражениям [x(nΔt)-εx, x(nΔt)+εx], [y(nΔt)-εy, y(Δt)+εy], где n=0, 1, 2, …, a εx, εy - значения предельных допускаемых погрешностей применяемых средств измерения, подают интервальные значения входного и выходного сигналов на идентификатор непрерывной дроби, в котором получают непрерывную дробь с несколькими интервальными коэффициентами, по которым производят восстановление интервальной дискретной передаточной функции и прогнозирующей модели, и определяют интервальные модельные значения выходного сигнала объекта.
Недостатком данного способа является то, что при построении дискретных моделей объекта не учитываются погрешности, присущие единичным исходным измеренным значениям вход-выходных сигналов. Измерения дискретных вход-выходных сигналов производят, начиная с единичного округленного исходного значения, и линейные интервалы между дискретными значениями сигналов выполняют по одной кривой. Ошибки измерения, моделирования, округления вносят наиболее существенные искажения в значения вход-выходных величин, и, следовательно, использование описанного метода может привести как к неверным оценкам параметров модели, так и к подмене (искажению) структуры прогнозирующей модели объекта. Так, способ идентификации не учитывает точности измерительной аппаратуры.
Известен также патент №2189622 Способ идентификации линейного объекта, МПК7 G05B 23/02, G05B 17/02, опубликован 20.09.2002, бюл. №26. Изобретение относится к технической кибернетике и предназначено для идентификации линейных динамических объектов со случайным стационарным или нестационарным входным воздействием. В приведенном изобретении измеряют значения вход-выходных сигналов объекта, вычисляют структурные функции сигналов, сглаживают значения структурных функций с помощью фильтра низких частот, аппроксимируют непрерывной дробью модели структурных функций вход-выходных сигналов и определяют с помощью полученных моделей стационарность каждого из сигналов, подают значения вход-выходных сигналов на идентификатор непрерывной дроби с последующим восстановлением прогнозирующей модели идентифицируемого объекта и определяют по ней модельные значения выходного сигнала объекта идентификации.
Практически все применяемые на практике способы идентификации динамических систем применяются для линейных или линеаризованных динамических объектов.
Целью предлагаемого способа является разработка способа идентификации моделей динамических объектов, исключающего требование линеаризации их моделей приемами конструирования и позволяющего создавать, например, «интеллектуальные датчики» с заданной точностью восстановления измеряемой физической величины в ожидаемых условиях функционирования, обладающие свойством избирательного повышения чувствительности в интересующих диапазонах.
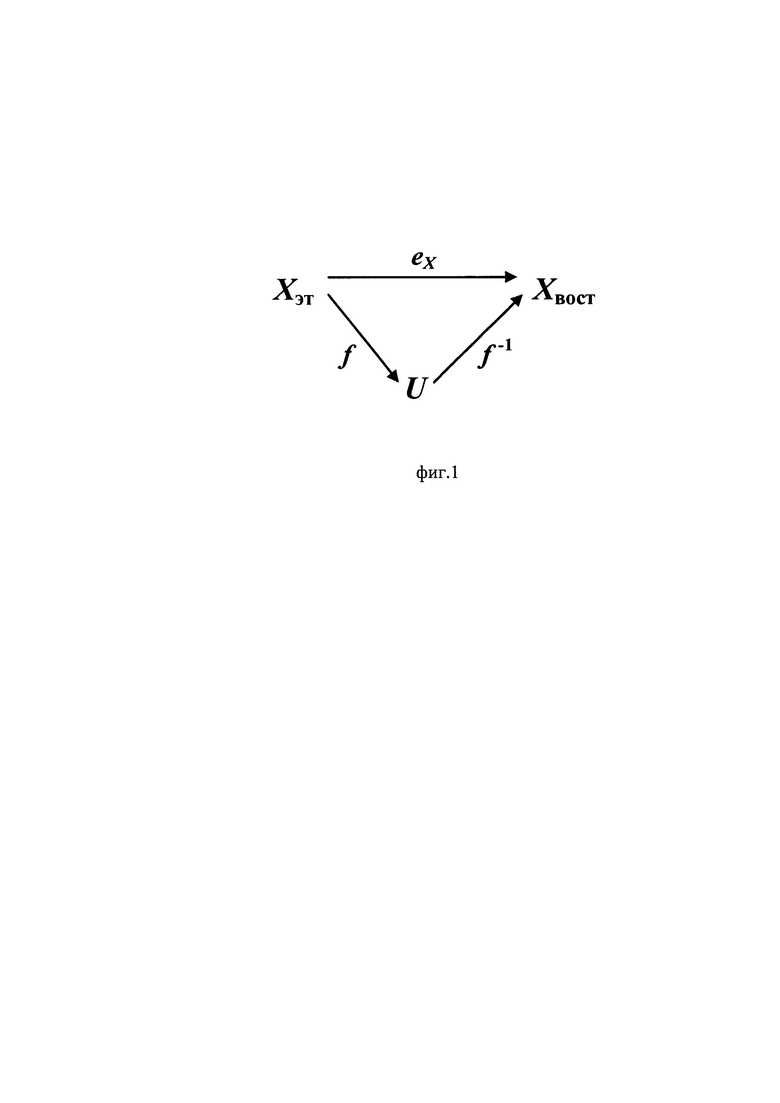
Поставленная цель достигается предлагаемым Способом идентификации нелинейных систем путем подачи на вход множества известных сигналов и наблюдения множества выходных сигналов, отличающийся тем что, для непараметрической текущей в реальном масштабе времени, либо после проведения серии экспериментов, идентификации используют коммутативную диаграмму, показанную на фиг. 1, в которой должны выполняться условия
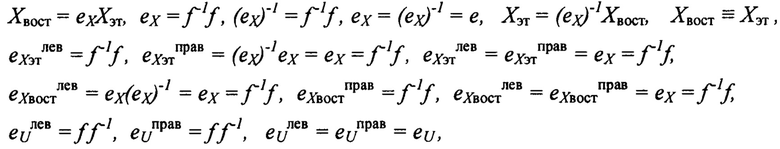
где eX - изоморфное отображение, характеризующее желаемое тождество между известным (эталонным) сигналом Хэт на входе идентифицируемой системы или на входе калибруемого датчика и восстановленным сигналом Хвост, полученным после преобразования выходного сигнала U системы обратной моделью ƒ-1; ƒ - неизвестная модель (функция преобразования) системы, отображающая сигнал Хэт в сигнал U на выходе идентифицируемой системы; ƒ-1 - обратное с точностью до изоморфизма eX отображение к отображению ƒ характеризующее функцию восстановления измеряемой физической величины Хвост для датчика или обратную модель для идентифицируемой системы; eXэтлев, eXэтправ, eXвостлев, eXвостправ, eUлев, eUправ - соответственно левая и правая единицы на множествах сигналов Хэт, Хвост, U; дополнительно в качестве универсального аппроксиматора (интерполятора) неизвестной обратной модели ƒ-1 используют некоторую искусственную нейронную сеть, обучая которую с точностью до изоморфизма eX:Xэт→Хвост, получают модель ƒ-1 идентифицируемой системы, либо, в случае датчика, используя искусственную нейронную сеть, осуществляют обучение интеллектуального датчика в процессе непараметрической идентификации его модели для формирования обратной функции преобразования ƒ-1 с точностью до изоморфного отображения eX:Xэт→Xвост, и обеспечивающего существование этой обратной функции, позволяющей восстанавливать с заданной точностью реальные значения физической величины, действующей на вход нелинейной системы; непараметрическую идентификацию неизвестной модели системы ƒ осуществляют посредством обучения той же, либо другой нейронной сети на тех же известных множествах входных и выходных сигналов идентифицируемой системы с точностью до изоморфного отображения eU:Uвост→U, реализующего тождество Uвост≡U. (2-ил.)
Сущность изобретения поясняется чертежами, где на фиг. 1 представлена Коммутативная диаграмма отображений в задаче калибровки, на фиг. 2 представлена примерная структура реализации способа.
В основном, в задачах теории и практики (калибровка и обучение интеллектуальных датчиков, синтез регуляторов, наблюдателей и устройств контроля) достаточно идентификации (восстановления) именно неизвестной обратной модели ƒ-1 идентифицируемой системы. Если же необходима и «прямая» модель ƒ, то для ее идентификации можно использовать ту же самую или другую дополнительную искусственную нейронную сеть, обучаемую на тех же известных множествах ее входных сигналов Хэт и выходных сигналов U с точностью до изоморфизма еU: Uвост→U, обеспечивающего восстановление с заданной точностью известного обучающего множества сигналов U, сравниваемых с восстановленными на выходе нейронной сети сигналами из множества Uвост.
Описание изобретения
В отличие от подхода к идентификации систем и к конструированию датчиков, обусловливающего необходимость обеспечения линейности их моделей и порождающего соответствующие проблемы, общий принцип изоморфизма [1, 6] позволяет исходить из того, что создаваемые системы (объекты) и датчики в производстве не отбраковываются, их модели существенно индивидуальны (уникальны), нелинейны, а в наиболее общем случае и вообще не известны. Это требует ставить задачу непараметрической идентификации модели системы и модели датчика, как системы, по известным данным на их входе и выходе. Такая задача идентификации может быть решена на основе теоремы о реализации [7], сформулированной и доказанной в [6] в форме основной (фундаментальной) леммы, используемой применительно к анализу всех свойств систем. На основе леммы применительно к общей задаче идентификации систем, можно построить коммутативную диаграмму, показанную на фиг. 1.
В соответствии с теоремой о реализации (основной леммой), доказанной в [6], в самках коммутативной диаграммы на фиг. 1 должны выполняться условия:
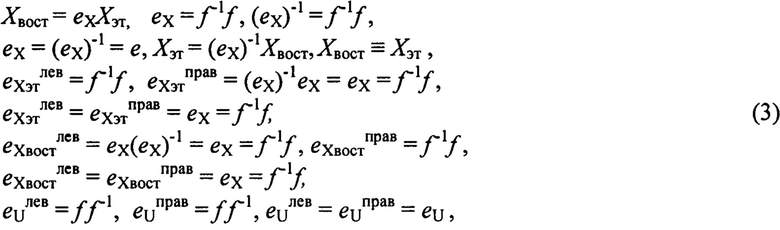
где eX - изоморфное отображение, характеризующее желаемое тождество между известным (эталонным) сигналом Хэт на входе идентифицируемой системы или на входе калибруемого датчика и восстановленным сигналом Хвост, полученным после преобразования выходного сигнала U системы обратной моделью ƒ-1; ƒ - неизвестная функция преобразования (модель) системы, отображающая сигнал Хэт в сигнал U на выходе идентифицируемой системы; ƒ-1 - обратное с точностью до изоморфизма eX отображение к отображению ƒ характеризующее функцию восстановления измеряемой физической величины Хвост для датчика или обратную модель для идентифицируемой системы; eXэтлев, eXэтправ, eXвостлев, eXвостправ, eUлев, eUправ - соответственно левая и правая единицы на множествах сигналов Хэт, Хвост, U. Причем, в соответствии с условиями и результатами доказательства основной леммы [6], матричные единицы еUлев=еUправ=еU, определяемые на множестве U в рамках коммутативной диаграммы, не обязательно должны быть обычными единичными матрицами. Отметим важность понимания этого, доказанного в [6] утверждения. Определение матричных единиц еUлев=еUправ=еU в процессе идентификации не требуется.
Кроме того, следует иметь в виду, что в отличие от применяемых систем и датчиков, у которых функция преобразования часто линейна и обязательно обратима, у систем и датчиков, идентифицируемых на основе общего принципа изоморфизма, векторная функция преобразования ƒ может быть не только нелинейной, но и необратимой в обычном смысле. На ƒ накладывается лишь одно требование-ограничение [6] - она должна быть мономорфным отображением ƒ: Xэт→U. Это условие легко выполнить при накоплении информации об идентифицируемой системе: каждому эталонному сигналу из Хэт должен строго соответствовать один единственный выходной сигнал из U и, наоборот, в множестве сигналов U должно существовать подмножество U*⊂U таких сигналов, каждому из которых обязательно отвечает единственный сигнал из множества Хэт. Тогда обязательно будет существовать эпиморфное отображение ƒ-1: U→Хвост, восстанавливающее сигналы из множества Хвост, точно и взаимно однозначно соответствующие сигналам из Хэт. Как следует из основной леммы [6], отображение ƒ есть изоморфизм с точностью до изоморфизма eX: Хэт→Хвост, т.е. внутри коммутативной диаграммы. Доказательство утверждения о существовании эпиморфного отображения ƒ-1 аналогично доказательству основной леммы, подробно изложенному в [6].
Условия (3) позволяют решить задачу идентификации отображений ƒ и ƒ-1 как прямо после формирования множеств Хэт≡Хвост и U в результате проведения калибровочных экспериментов, так и опосредованно - путем решения оптимизационной задачи, предполагающей минимизацию с заданной точностью «невязки» между множествами Хэт и Хвост при условии удовлетворения уравнений связи (3). Такой подход, опирающийся на основную лемму [6], позволяет решать в общей постановке задачи идентификации моделей любых систем, удовлетворяющих условиям мономорфности соответствующих отображений и рассматриваемых как «черный ящик». Причем часто достаточно идентифицировать обратную модель ƒ-1. Модель ƒ может оставаться неизвестной, так как во многих задачах используется именно обратная модель ƒ-1. Это относится, например, к задачам синтеза регуляторов и наблюдателей [2-5]. При необходимости этим же способом может быть идентифицирована и модель ƒ, но уже с точностью до изоморфизма еU: Uвост→U.
На практике, например, при калибровке датчиков не нужно решать выражения (3). Действительно, под обратной функцией ƒ-l может подразумеваться некоторый алгоритм «интеллектуальной» обработки выходных сигналов U, который может быть сформирован в результате процедуры обучения представленного на фиг. 1 в виде коммутативной диаграммы «интеллектуального датчика». Обучение реализуется на примерах сигналов из множеств Хэт и U с учетом тождества Хвост≡Хэт. Аналогично в общем случае идентификации систем формирование обратной модели ƒ-1 может осуществляться в форме «интеллектуального алгоритма», обучаемого на примерах сигналов из множеств Хэт и U с учетом удовлетворения тождества Хвост≡Хэт. При необходимости идентификации «прямой» модели ƒ ее формирование может осуществляться в форме «интеллектуального алгоритма», обучаемого на тех же примерах сигналов из множеств Хэт и U, но с учетом удовлетворения тождества Uвост≡U.
Из приведенных утверждений и рассуждений следуют выводы:
- во-первых, на множестве выходных сигналов U датчика допускается существование «зашумленных» сигналов, ни один из которых не отвечает какому-либо эталонному сигналу из множества Хэт. Тем не менее «интеллектуальная» обработка зашумленных сигналов посредством обратной функции ƒ-1: U→Хвост позволит восстановить точные сигналы из Хвост, однозначно отвечающие соответствующим сигналам из Хэт посредством выделения в U указанного выше подмножества U*⊂U;
- во-вторых, предложенный подход позволяет решать задачу идентификации систем с шумами в выходном сигнале, которую изначально ставили в классической литературе [7];
- в-третьих, утверждение о существовании и единственности ƒ-1 и его доказательство справедливы в том случае, когда требование изоморфизма отображения eX: Хэт→Хвост заявлено заранее и реализовано, например, путем «обучения» интеллектуального датчика в процессе идентификации. Процесс обучения позволяет сформировать обратную с точностью до изоморфизма eX: Хэт→Хвост функцию преобразования ƒ-l датчика, то есть решить задачу непараметрической идентификации его модели. Аналогично, при необходимости, процесс обучения позволяет сформировать и «прямую» функцию преобразования (модель) ƒ системы с точностью до изоморфизма eU:Uвост→U, то есть решить задачу непараметрической идентификации системы (модели датчика).
Технологию обучения интеллектуального датчика можно описать следующим образом. Ставятся эксперименты, позволяющие получить для каждого эталонного сигнала из Хэт единственный сигнал из множества U выходных сигналов датчика (например, некоторый уникальный цифровой код). Множества эталонных (тестовых) входных сигналов Xэт и выходных сигналов U могут быть сформированы и в реальном времени функционирования системы, например, в «фоновом» режиме «встроенного» контроля, реализуемом периодически при решении системой основной функциональной задачи. Далее, в качестве модели обратной функции преобразования ƒ-1 выбирается, например, искусственная нейронная сеть, обучаемая на полученных примерах таким образом, чтобы каждому уникальному выходному сигналу из U строго отвечало единственное восстановленное значение физической величины из множества Хвост, точно соответствующее тому значению входной физической величины из Xэт, которому точно соответствует сигнал из U, вызвавший указанный отклик нейронной сети (сигнал из множества Хвост). После обучения нейронной сети на всем множестве идентифицирующих сигналов-примеров для проверки точности модели ƒ-1 может быть проведена серия контрольных экспериментов с подачей на вход системы таких сигналов, которые не вошли в множество обучающих эталонных сигналов Хэт. При необходимости для повышения точности интеллектуального датчика нейронная сеть может быть дообучена на результатах дополнительных экспериментов, позволяющих сформировать промежуточные обучающие точки-сигналы. Такая процедура обучения опирается на изоморфное отображение eX: Хэт→Хвост и в неявной форме (в форме нейронной сети) позволяет получить обратную функцию преобразования ƒ-1, восстанавливающую с заданной точностью реальные значения физической величины, действующей на вход датчика. Аналогично в неявной форме (в форме нейронной сети) может быть получена и модель ƒ, моделирующая с заданной точностью значения выходного сигнала U на выходе рассматриваемой системы.
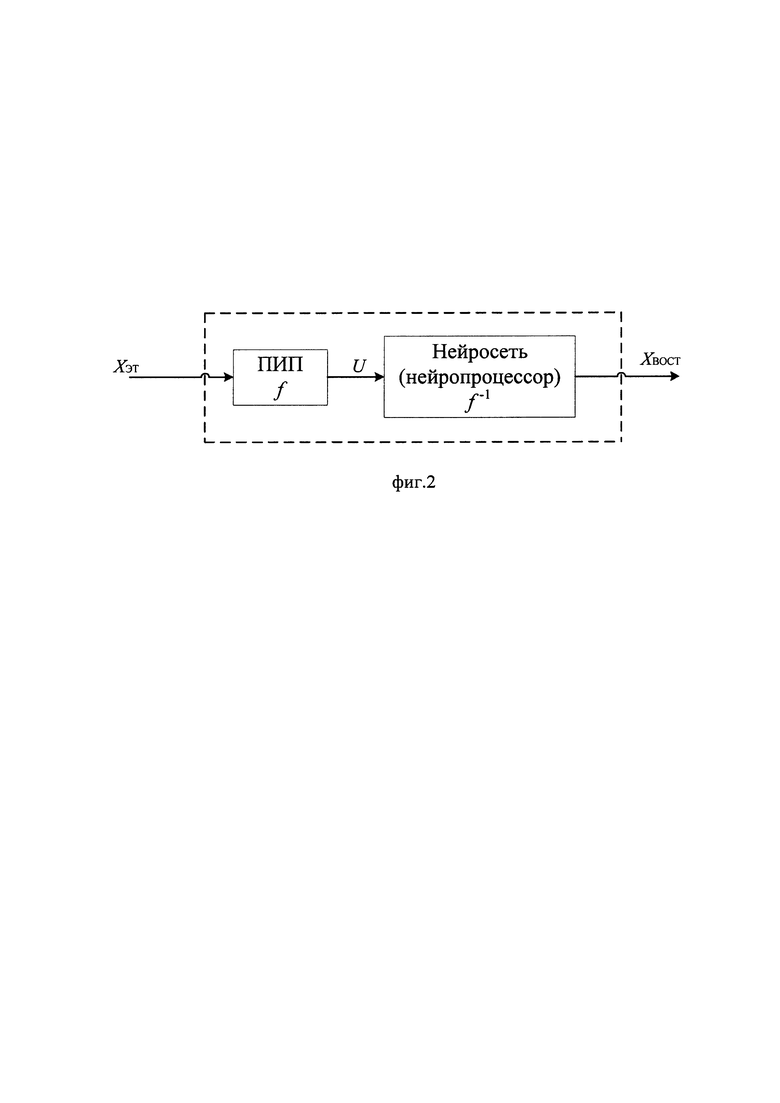
Нейронная сеть (обратная функция ƒ-1), сформированная и обученная в процессе экспериментов, должна записываться в память интеллектуального датчика и в дальнейшем использоваться при его рабочем функционировании (см. фиг. 2, где ПИП - первичный измерительный преобразователь датчика). Обратим внимание на то, что необходимость идентификации самой функции преобразования ƒ, а также необходимость решения системы алгебраических уравнений (3) для определения обратной функции ƒ-1 в случае датчика при рассмотренном подходе отсутствует. Функция ƒ может оставаться вообще неизвестной. К ней предъявляется лишь обычное и для «линейного» датчика требование - высокая стабильность характеристик при длительных сроках эксплуатации. При этом ƒ может изменяться (трансформироваться) при изменении в широких пределах ожидаемых условий эксплуатации датчика. В этом случае нейронная сеть должна быть обучена применительно ко всем этим условиям путем проведения дополнительных экспериментов. Кроме того, у конструкторов, в отличие от традиционного подхода, связанного с необходимостью обеспечения линейности функции ƒ, появляется свобода выбора таких ее видов, которые обеспечивают, например, избирательное повышение чувствительности датчика в некоторых, интересующих разработчика, диапазонах измерения физической величины. Если таких требований нет, конструктор может вообще не задаваться каким-либо видом функции ƒ, ориентируясь лишь на приемлемую чувствительность датчика во всем диапазоне измерения физической величины.
Аналогичная процедура аппроксимации функции ƒ-1 нейронной сетью может применяться и в общем случае идентификации систем, в том числе и динамических. В последнем случае может быть применена обучаемая в реальном времени (в темпе функционирования системы) нейронная сеть, либо рассмотрена задача аппроксимации амплитудно-фазовой частотной характеристики системы нейронной сетью, либо могут использоваться динамические нейронные сети [11].
Применение многих известных видов искусственных нейронных сетей [11], потенциально отвечающих целям обучения интеллектуальных датчиков и идентификации систем, в практических приложениях может встретить трудности, так как алгоритмы их обучения сложны и, как правило, итерационны. Возникнет необходимость проведения заранее неизвестного числа эпох обучения, что увеличит сроки идентификации и потребует повышения квалификации персонала. Исходя из практически значимых критериев, нужно использовать такие нейронные сети, которые легко обучаются персоналом обычной квалификации, допускают высокий уровень автоматизации и имеют предсказуемое время обучения, не приводящее к увеличению обычных сроков идентификации. Таким требованиям удовлетворяют, например, искусственные нейробионические сети, рассмотренные в [12].
Таким образом предложен способ идентификации, опирающейся на общий эффект от применения двух технологий - технологии идентификации систем на основе общего принципа изоморфизма [1-6] и технологии разработки и обучения искусственных нейронных сетей [12].
Способ идентификации моделей нелинейных систем исключает требование линеаризации их моделей приемами конструирования. Применение метода позволит создавать «интеллектуальные датчики» с заданной точностью восстановления измеряемой физической величины в ожидаемых условиях функционирования, обладающие свойством избирательного повышения чувствительности в интересующих диапазонах. Полученные результаты обеспечивают возможность реализации принципиально новых способов идентификации нелинейных систем, конструирования и калибровки датчиков различного назначения.
Литература
1. Кулабухов B.C. Принцип изоморфности в задаче реализации и его приложения к анализу свойств систем управления // В сборнике: XII Всероссийское совещание по проблемам управления ВСПУ-2014. Институт проблем управления им. В.А. Трапезникова РАН. 2014. С.438-448. URL: http://vspu2014.ipu.ru/prcdngs.
2. Кулабухов B.C. Изоморфные наблюдатели состояния и робастная фильтрация сигналов систем // Радиотехника. 2017. №8. С.50-55.
3. Кулабухов B.C. Синтез регуляторов для следящих систем на основе принципа изоморфности // Мехатроника, автоматизация, управление. 2017. Том 18, №8. С.507-515.
4. Kulabukhov V. Linear Isomorphic Regulators // CMTAI2016. MATEC Web of Conf. 2017. T. 99. C. 03008.(doi:10.1051/matecconf/20179903008).
URL:https://www.matec-
conferences.org/articles/matecconf/pdf/2017/13/matecconf cmtai2017 03008.pdf.
5. Kulabukhov V. S. Isomorphic observers of the linear systems state // Workshop on Materials and Engineering in Aeronautics (MEA2017) 15-16 November 2017, Moscow, Russian Federation. doi:10.1088/1757-899X/312/l/012016. p.012016. URL: http://iopscience.iop.org/issue/1757-899X/312/1.
6. Кулабухов B.C. Общий принцип изоморфизма в теории систем // Cloud of Science. 2018. Т.5. №3. С.400-472. URL: https://cloudofscience.ru/sites/default/files/pdf/CoS 5 400.pdf
7. Калман Р.Е. Идентификация систем с шумами // УМН. 1985. Т. 40. Вып.4 (244). С.27-41.
8. Цыпкин ЯЗ. Информационная теория идентификации. - М.: Наука. Физматлит, 1995. - 336 с.
9. URL: https://search.rsl.ru/ru/record/011006744194.
10. ГОСТ Р 8.879-2014 Государственная система обеспечения единства измерений. Методики калибровки средств измерений. Общие требования к содержанию и изложению.
П. Хайкин С.Нейронные сети. Полный курс.2-е изд. Пер. с англ. - М.: Издательский дом «Вильяме», 2006. - 1104 с.
12. Кулабухов B.C. Модель нейробионической сети для бортовых систем искусственного интеллекта // В сборнике: III Всероссийская научно-техническая конференция «Моделирование авиационных систем». Сборник тезисов докладов. ФГУП «ГосНИИАС», 21-22 ноября 2018 г., г. Москва. С.339-341.
13. Патент RU №2256950 // Способ идентификации линеаризованного динамического объекта МПК 7 G06F17/18, G05B17/02, опубликован 20.07.2005 г., бюл. №20.
14. Патент RU №2189622// Способ идентификации линейного объекта, МПК 7 G05B23/02, G05B17/02, опубликован 20.09.2002, бюл №26.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ калибровки интеллектуальных датчиков | 2019 |
|
RU2730367C1 |
| Система для разработки интеллектуального датчика | 2019 |
|
RU2714039C1 |
| СПОСОБ И УСТРОЙСТВО ТЕХНИЧЕСКОЙ ДИАГНОСТКИ СЛОЖНОГО ТЕХНОЛОГИЧЕСКОГО ОБОРУДОВАНИЯ НА ОСНОВЕ НЕЙРОННЫХ СЕТЕЙ | 2013 |
|
RU2563161C2 |
| СИСТЕМА ИНТЕГРИРОВАННОГО КОНТРОЛЯ РАБОТЫ БОРТОВОГО ОБОРУДОВАНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА | 2010 |
|
RU2431175C1 |
| СПОСОБ ДИАГНОСТИКИ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ЭЛЕКТРОПРИВОДА ПО ОЦЕНКЕ ДИНАМИКИ ЕГО ПАРАМЕТРОВ | 2013 |
|
RU2546993C1 |
| СПОСОБ КАРТОГРАФИРОВАНИЯ ЛЕДНИКОВОЙ ГЕОМОРФОЛОГИИ | 2014 |
|
RU2570334C1 |
| СПОСОБ ИНТЕЛЛЕКТУАЛЬНОГО АНАЛИЗА ОЦЕНКИ УСТОЙЧИВОСТИ ИНФОКОММУНИКАЦИОННОЙ СИСТЕМЫ К ДЕСТРУКТИВНОМУ ВОЗДЕЙСТВИЮ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ | 2014 |
|
RU2560803C1 |
| Система оперативной идентификации морских целей по их информационным полям на базе нейро-нечетких моделей | 2021 |
|
RU2763384C1 |
| МЕТОД РЕЗЕРВИРОВАНИЯ КАНАЛОВ КОНСТРУКТИВНО-ФУНКЦИОНАЛЬНЫХ МОДУЛЕЙ БОРТОВЫХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЕЙ ЛЕТАТЕЛЬНЫХ АППАРАТОВ НА ОСНОВЕ ИНТЕЛЛЕКТУАЛЬНОЙ ДИАГНОСТИЧЕСКОЙ СИСТЕМЫ В УСЛОВИЯХ ИНТЕГРИРОВАННОЙ МОДУЛЬНОЙ АВИОНИКИ | 2021 |
|
RU2778366C1 |
| СПОСОБ ОБНАРУЖЕНИЯ И ИДЕНТИФИКАЦИИ ВЗРЫВЧАТЫХ, БОЕВЫХ ОТРАВЛЯЮЩИХ И НАРКОТИЧЕСКИХ ВЕЩЕСТВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2023 |
|
RU2823893C1 |
Изобретение относится к вычислительной технике. Технический результат заключается в обеспечении автоматизированной структурно-параметрической, либо непараметрической идентификации модели объекта по известным на основе измерений значениям входных и выходных сигналов. Технический результат достигается за счет способа идентификации нелинейных систем путем подачи на их вход множества известных сигналов, наблюдения множества выходных сигналов и использования искусственной нейронной сети для аппроксимации (интерполяции) идентифицируемой модели, которая должна удовлетворять определенным условиям в соответствии с коммутативной диаграммой, соответствующей принципу изоморфизма. 2 ил.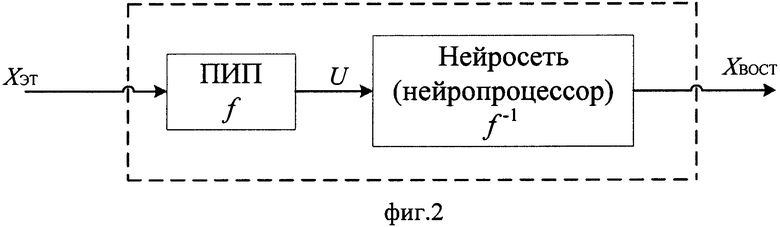
Способ идентификации нелинейных систем путем подачи на вход множества известных сигналов и наблюдения множества выходных сигналов, отличающийся тем, что дополнительно для непараметрической текущей в реальном масштабе времени, либо после проведения серии экспериментов, идентификации используют коммутативную диаграмму, в которой должны выполняться условия
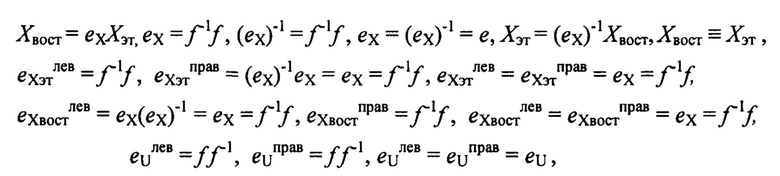
где eX - изоморфное отображение, характеризующее желаемое тождество между известным (эталонным) сигналом Хэт на входе идентифицируемой системы или на входе калибруемого датчика и восстановленным сигналом Хвост, полученным после преобразования выходного сигнала U системы (датчика) обратной моделью ƒ-1; ƒ - неизвестная модель (функция преобразования) системы, отображающая сигнал Xэт в сигнал U на выходе идентифицируемой системы; ƒ-1 - обратное с точностью до изоморфизма eX отображение к отображению ƒ, характеризующее функцию восстановления измеряемой физической величины Хвост для датчика или обратную модель для идентифицируемой системы; еХэтлев, еХэтправ, еXвостлев, еXвостправ, еUлев, еUправ - соответственно левая и правая единицы на множествах сигналов Хэт, Хвост, U, и для формирования обратной модели (обратной функции преобразования) ƒ-1 системы дополнительно используют искусственную нейронную сеть, обучаемую с точностью до изоморфного отображения eX: Хэт→Хвост, реализующего тождество Xвост≡Хэт и обеспечивающего существование этой обратной функции, позволяющей восстанавливать с заданной точностью реальные значения физической величины, действующей на вход нелинейной системы; непараметрическую идентификацию неизвестной модели системы ƒ осуществляют посредством обучения той же, либо другой нейронной сети на тех же известных множествах входных и выходных сигналов идентифицируемой системы с точностью до изоморфного отображения eU:Uвост→U, реализующего тождество Uвост≡U.
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕАРИЗОВАННОГО ДИНАМИЧЕСКОГО ОБЪЕКТА | 2003 |
|
RU2256950C2 |
| СПОСОБ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ МАТЕМАТИЧЕСКОЙ МОДЕЛИ СУДНА | 2010 |
|
RU2444043C1 |
| Беспоршневая отсадочная машина | 1959 |
|
SU127957A1 |
| ОБЪЕКТНО-ОРИЕНТИРУЕМЫЕ СПОСОБЫ И МУЛЬТИАГЕНТНЫЕ АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ КОМПЛЕКСНОЙ БЕЗОПАСНОСТИ-ЗАЩИЩЕННОСТИ ТЕРРИТОРИАЛЬНО РАСПРЕДЕЛЕННОГО ПРОМЫШЛЕННОГО КОМПЛЕКСА | 2012 |
|
RU2569810C2 |
| US 7813822 B1, 12.10.2010. | |||
Авторы
Даты
2020-02-18—Публикация
2019-06-10—Подача