Изобретение относится к судовождению и предназначено для оперативной идентификации математической модели судна в реальном масштабе времени.
Известным методом идентификации параметров математической модели является метод дифференциальной аппроксимации, основанный на непосредственном измерении всех компонент вектора состояния динамического объекта, судна, и вычислении их производных [9].
Существует ряд недостатков, свойственных данному методу. Причем эти недостатки ярко проявляются при выполнении идентификации параметров математической модели судна в судовых условиях. В частности:
- в том случае, когда производные вектора состояния судна не могут быть измерены непосредственно, что характерно для судовых условий, приходится прибегать к численному дифференцированию. Дифференцирование при наличии погрешностей в измерениях представляет самостоятельную трудную проблему. В то же время метод не может быть применим в том случае, когда не могут быть измерены все компоненты вектора состояний судна;
- при большом количестве параметров математической модели судна реализация метода связана с большими математическими трудностями. Для уменьшения этих трудностей прибегают к декомпозиции - уменьшению количества идентифицируемых параметров разбиением исходной задачи на ряд подзадач с меньшим количеством идентифицируемых параметров, например:
- понижение порядка системы дифференциальных уравнений, т.е. упрощение самой математической модели;
- ограничения в выборе управлений динамическим объектом с целью искусственного уменьшения зависимости выходных переменных от некоторых идентифицируемых параметров математической модели.
Использование декомпозиции при параметрической идентификации снижает точность конечных результатов;
- незначительные изменения значений входных параметров могут привести к большим изменениям результатов идентификации. При вычислениях указанная неустойчивость приводит к неоднозначности решения в рамках требуемой для прогнозирования точности результатов, а часто к физически бессмысленным результатам [10];
- представленный метод типичен для математически некорректных задач. Известно, что результат решения некорректно поставленной задачи является практически не однозначным [8], что противоречит цели решения рассматриваемой здесь задачи.
Предложенный авторами [4], [10] способ идентификации по векторному критерию при максимальном использовании априорной информации [3], обеспечиваемый комплексом взаимодействующих между собой программ и системой проведения и обработки большого количества натурных (модельных) испытаний, также не может быть признан оптимальным, поскольку кроме отдельных из указанных недостатков, свойственных выше представленному способу идентификации, имеет свой существенный недостаток, а именно способ не может быть использован оперативно в судовых условиях, т.к. требует проведения большого количества натурных экспериментов за рамками условий эксплуатации судна. Результаты идентификации при этом будут точечными и потребуют обновления при изменении условий плавания.
Известен способ идентификации линейного объекта, предназначенный для определения математической модели объекта (А.с. СССР №361456, опубл. 07.12.1972), включающий подачу входного сигнала на объект идентификации и модель объекта, сравнение выходного сигнала с объекта идентификации и модели объекта с получением разности сигналов, вычисление настроечных коэффициентов, которые суммируют и получают вектор параметров модели, процесс многократно повторяют, пока разность выходных сигналов будет равна нулю. Способ прост, но обладает недостаточной точностью и быстродействием.
Известен способ идентификации линейного объекта (Пат. РФ №2146063, опубл. 27.02.2000), включающий подачу на объект идентификации случайного сигнала, определение значений входного и выходного сигналов объекта, подачу их на идентификатор напрерывной дроби, в котором эти значения преобразуют в детерминированные характеристики корреляции значений входного и вход-выходного сигналов объекта с последующей их обработкой, получение прогнозирующей модели объекта и определение модельных значений выходного сигнала объекта идентификации. Способ предназначен для определения математической модели объекта. Способ недостаточно точен и не исключает искажение прогнозирующей модели объекта, что обусловлено многократным уменьшением шага дискретизации, производимым с целью повышения точности.
Известен способ идентификации линейного объекта (Пат. РФ №2233480, опубл. 27.07.2004), предназначенный для автоматического определения структуры и параметров математической модели динамического объекта в реальном масштабе времени. Способ включает определение значений входного и выходного сигналов объекта, подачу их на идентификатор непрерывной дроби с последующим восстановлением дискретной математической модели объекта и переходом к непрерывной математической модели объекта, в которой определяют дискретные модельные значения выходного сигнала, из множества которых определяют параметры нелинейной статической характеристики объекта, эти данные запасают в блоке хранения, многократно изменяют амплитуду подаваемого входного сигнала и повторяют весь процесс.
Известен способ идентификации линеаризованного динамического объекта (Пат. РФ №2256950, опубл. 20.07.2005). Способ включает измерение входного и выходного сигналов объекта с шагом дискретизации Δt, последовательную подачу интервальных значений этих сигналов на идентификатор непрерывной дроби, восстановление дискретной передаточной функции и прогнозирующей модели объекта, определение интервальных модельных значений выходного сигнала. Способ позволяет автоматически определять структуру и неизвестные параметры математической модели динамического объекта, улучшая качество и достоверность результатов моделирования объекта управления. Данный способ наиболее близок к предлагаемому способу и принят за прототип.
Задачей изобретения является устранение указанных недостатков существующих методов и способов параметрической идентификации математических моделей именно судов за счет определенным образом рассчитанных априорных значений входных параметров и измеренных выходных сигналов объекта, позволяющих автоматически определять структуру и параметры математической модели судна, улучшая качество и достоверность результатов моделирования управления судном, и на их основании прогнозирование развития процессов управления судном.
Технический результат, на достижение которого направлено заявляемое изобретение, состоит в обеспечении автоматического определения параметров математической модели судна, повышении качества и достоверности результатов моделирования движения судна как объекта управления и на их основании прогнозировании развития процессов управления судном.
Для достижения указанного технического результата в способе параметрической идентификации математической модели судна, включающем определение входных и выходных сигналов судна, осуществляемое с шагом дискретизации Δt, определение параметров математической модели судна и на их основе построение прогнозирующей модели, математическая модель судна представляет собой систему дифференциальных уравнений, входные сигналы рассчитывают, а выходные сигналы измеряют, при этом измеряют линейные продольное, поперечное и угловое ускорения судна N раз за цикл обработки продолжительностью Т, по измеренным значениям ускорений находят соответствующие значения линейных и угловой скоростей, рассчитывают невязки (разности) между левой и правой частями дифференциальных уравнений, определяют взвешенную сумму квадратов невязок и осуществляют минимизацию последней, находят значения параметров математической модели судна и осуществляют повторение цикла измерений и идентификации. При этом измерение линейных продольного, поперечного и углового ускорений производят в процессе движения судна с помощью судовой инерциальной системы в реальном масштабе времени. Минимизацию суммы квадратов невязок осуществляют путем ее дифференцирования по идентифицируемым параметрам, частные производные которых приравнивают к нулю, при этом получают систему нормальных уравнений. Количество уравнений в системе нормальных уравнений равно количеству идентифицируемых параметров. Систему нормальных уравнений решают методом последовательных приближений или методом Зейделя, если она линейная.
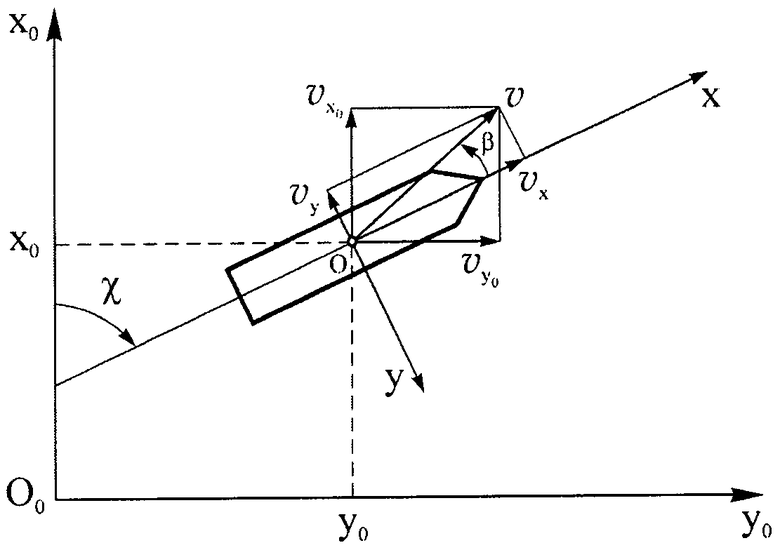
Предлагаемый способ иллюстрируется чертежом.
Способ заключается в следующем.
Математическая модель судна, используемая для компьютерного моделирования при прогнозировании движения судна в процессе маневрирования, представляет собой систему дифференциальных уравнений, общий вид которых в соответствии с данными, представленными в работах [1], [2], [3], [6], [7], следующий:
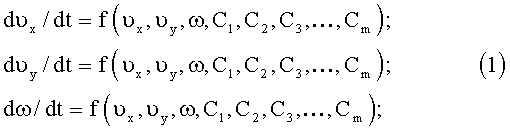
где υx, υу - проекции вектора линейной скорости в центре тяжести (ЦТ) судна на продольную 0Х и поперечную 0Y оси, соответственно (см. чертеж);
ω - угловая скорость судна;
С1, С2, С3, …, Cm - параметры математической модели [1], [2], [3], [6], [7].
Способ параметрической идентификации математической модели судна отличается тем, что в процессе движения судна с помощью судовой инерциальной системы в реальном масштабе времени измеряют линейные продольное 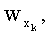 поперечное
поперечное 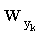 и угловое εk ускорения судна N раз за цикл обработки продолжительностью Т и шагом дискретизации Δt, так что
и угловое εk ускорения судна N раз за цикл обработки продолжительностью Т и шагом дискретизации Δt, так что
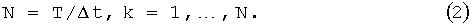
По измеренным значениям ускорений находят соответствующие значения линейных и угловой скоростей:
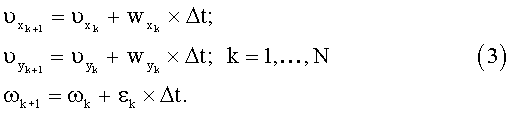
Началом процесса идентификации следует считать момент начала движения судна, поэтому начальные значения линейных (υx0, υу0) и угловой (ω0) скоростей принимают равными нулю. В ином случае начальные значения линейных и угловой скоростей устанавливают в соответствии с показаниями приборов измерения скорости объекта (на судне это лаг) и измерителя угловой скорости.
Рассчитывают невязки Δk, т.е. разности между левой и правой частями дифференциальных уравнений движения судна (1) в момент k-го измерения:
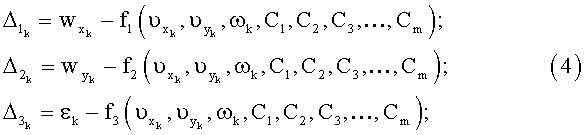
k=1,…,N.
Как следует из уравнений (1), (4), количество идентифицируемых параметров равно m.
Для определения значений параметров математической модели судна С1, С2, С3, …, Cm строят взвешенную сумму квадратов невязок:
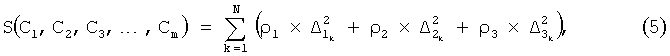
здесь ρ - вес уравнения в системе (1) (0≤ρ≤1,0), устанавливается по приоритету оператором в соответствии со степенью важности уравнения при моделировании с использованием идентифицированной математической модели судна и его конкретного маневра. В случае равнозначности уравнений в системе (1) значения ρ1, ρ2, ρ3 можно принимать равными 1,0.
Сумму квадратов невязок минимизируют. Для этого сумму дифференцируют по идентифицируемым параметрам Cq (q=1,…,m) и частные производные приравнивают к нулю, тем самым образуется система нормальных уравнений, состоящая из m уравнений, по количеству идентифицируемых параметров:
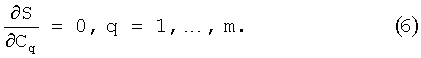
Систему уравнений (6) решают методом последовательных приближений или Зейделя [5], если она линейная. Результатом решения системы уравнений (6) будут значения параметров уравнений (1).
Далее цикл измерений и идентификацию параметров повторяют, что обеспечивает их постоянное обновление. Постоянно обновляющиеся параметры модели используют для построения прогнозирующей модели судна как объекта управления при маневрировании.
Литература
1. Басин A.M. Ходкость и управляемость судов / A.M.Басин. - М.: Транспорт, 1967. - 255 с.
2. Васильев А.В. Управляемость судов: учеб. пособие / А.В.Васильев. - Л.: Судостроение, 1989. - 328 с.
3. Гофман А.Д. Движительно-рулевой комплекс и маневрирование судна: справочник / А.Д.Гофман. - Л.: Судостроение, 1988. - 360 с.
4. Зильман Г.И., Тер-Захарянц А.А. Идентификации гидродинамических коэффициентов уравнений управляемости как задача многокритериальной оптимизации // Навигация и управление судном. - М.: Транспорт, 1986, вып.433.
5. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). - М.: Наука. 1974. с.831.
6. Соболев Г.В. Управляемость корабля и автоматизация судовождения / Г.В.Соболев. - Л.: Судостроение, 1976. - 478 с.
7. Справочник по теории корабля. В 3-x т. Т.3. Управляемость водоизмещающих судов. Гидродинамика судов с динамическими принципами поддержания / под ред. Я.И.Войткунского. - Л.: Судостроение, 1985. - 544 с.
8. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1974.
9. Эйкрофт П. Основы идентификации систем управления. - М.: Мир, 1975.
10. Zilman G., Ter-Zakhariantz A. Parameter identification of ships steering dynamics as a problem of multiobjective optimization. // 14-th Scientific and methodological seminar on ship hydrodynamics. Vama, 1986, V.2.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НАСТРОЙКИ СИСТЕМЫ УПРАВЛЕНИЯ СУДНОМ ПО КУРСУ | 2024 |
|
RU2828164C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ ОБЪЕКТА ШВАРТОВКИ | 2011 |
|
RU2459742C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2001 |
|
RU2189622C1 |
| Способ коррекции математической модели жидкостного ракетного двигателя | 2022 |
|
RU2820905C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 1999 |
|
RU2146063C1 |
| Способ коррекции математической модели жидкостного ракетного двигателя | 2020 |
|
RU2749497C1 |
| СИСТЕМА ОПРЕДЕЛЕНИЯ ГИДРОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДВИЖЕНИЯ СУДНА | 2013 |
|
RU2537080C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ХАРАКТЕРИСТИК И ВОЗМУЩЕНИЙ ДИНАМИЧЕСКИХ ОБЪЕКТОВ В СТОХАСТИЧЕСКИХ СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ | 2015 |
|
RU2623464C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕЙНОГО ОБЪЕКТА | 2002 |
|
RU2233480C1 |
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕАРИЗОВАННОГО ДИНАМИЧЕСКОГО ОБЪЕКТА | 2003 |
|
RU2256950C2 |
Изобретение относится к судовождению и предназначено для оперативной идентификации математической модели судна в реальном масштабе времени. Технический результат состоит в обеспечении автоматического определения параметров математической модели судна, повышении качества и достоверности результатов моделирования движения судна как объекта управления и на их основании прогнозировании развития процессов управления судном. Измеряют линейные продольное, поперечное и угловое ускорения судна N раз за цикл обработки продолжительностью Т с шагом дискретизации Δt, по измеренным значениям ускорений находят значения линейных и угловой скоростей, рассчитывают невязки, определяют взвешенную сумму квадратов невязок и минимизируют их, находят значения параметров математической модели судна, строят прогнозирующую модель судна и повторяют весь цикл измерений и идентификации. 4 з.п. ф-лы, 1 ил.
1. Способ параметрической идентификации математической модели судна, включающий определение входных и выходных сигналов судна, осуществляемое с шагом дискретизации Δt, определение параметров математической модели судна и на их основе построение прогнозирующей модели, отличающийся тем, что математическая модель судна представляет собой систему дифференциальных уравнений, входные сигналы рассчитывают, а выходные сигналы измеряют, при этом измеряют линейные продольное, поперечное и угловое ускорения судна N раз за цикл обработки продолжительностью Т, по измеренным значениям ускорений находят соответствующие значения линейных и угловой скоростей, рассчитывают невязки (разности) между левой и правой частями дифференциальных уравнений, определяют взвешенную сумму квадратов невязок и осуществляют минимизацию последней, находят значения параметров математической модели судна и осуществляют повторение цикла измерений и идентификации.
2. Способ по п.1, отличающийся тем, что измерение линейных продольного, поперечного и углового ускорений производят в процессе движения судна с помощью судовой инерциальной системы в реальном масштабе времени.
3. Способ по п.1, отличающийся тем, что минимизацию суммы квадратов невязок осуществляют путем ее дифференцирования по идентифицируемым параметрам, частные производные которых приравнивают к нулю, при этом получают систему нормальных уравнений.
4. Способ по п.3, отличающийся тем, что количество уравнений в системе нормальных уравнений равно количеству идентифицируемых параметров.
5. Способ по п.3, отличающийся тем, что систему нормальных уравнений решают методом последовательных приближений или методом Зейделя, если она линейная.
| СПОСОБ ИДЕНТИФИКАЦИИ ЛИНЕАРИЗОВАННОГО ДИНАМИЧЕСКОГО ОБЪЕКТА | 2003 |
|
RU2256950C2 |
| УСТРОЙСТВО ДЛЯ НАХОЖДЕНИЯ ЭКСТРЕМУМА ФУНКЦИИ МЕТОДОМ ДИХОТОМИИ | 2002 |
|
RU2229742C2 |
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ | 1998 |
|
RU2143729C1 |
| Прибор для очистки паром от сажи дымогарных трубок в паровозных котлах | 1913 |
|
SU95A1 |
| US 20050276275 A1, 15.12.2005. | |||
Авторы
Даты
2012-02-27—Публикация
2010-10-11—Подача