Изобретение относится к способам цифровой обработки изображений и может быть использовано в интеллектуальных системах классификации рентгеновских снимков. При построении интеллектуальных систем дифференциальной диагностики онкологических заболеваний используются искусственные нейронные сети (ИНС). ИНС - это компьютерные модели, которые способны дублировать способности человеческого интеллекта посредством использования вычислительной мощности компьютеров, и, обрабатывая большие объемы информации, обучаться на аннотированных примерах.
Существует два подхода использования ИНС для интерпретации рентгеновских снимков. Первый подход заключается в выделении вектора информативных признаков из изображения или его сегмента, а затем построения классифицирующей модели с учетом вектора информативных признаков: обучаемого или не обучаемого классификатора. Второй подход предполагает применение классификатора непосредственно к данным изображения или области интереса.
Первый подход назовем попиксельной классификацией. Это значит, что классификация осуществляется путем отнесения каждого пикселя изображения к определенному классу. Как правило, это бинарная классификация, в результате которой на выходе классификатора получаем бинарное изображение с исходным растром, в котором пикселям искомого класса присваивается код 255, а пикселям, не относящихся к искомому классу – код 0. В качестве реализации способа классификации, основанного на таком подходе, рассмотрим автоматизированную систему обнаружения микрокальцификаций в цифровых маммограммах [Computer aided detection system for microcalcifications in digital mammograms/Hayat Mohameda, Mai S. Mabroukb, Amr Sharawy //Computer methods and programs in biomedicine 116 (2014) 226–235, https://doi.org/10.1016/j.cmpb.2014.04.010]. Способ классификации состоит из четырех этапов: 1- этап предварительной обработки изображения, который может быть реализован посредством известных способов повышения контрастности изображения за счет видоизменения гистограмм, и удаление шумов на изображении, например, посредством медианной фильтрации или посредством морфологической фильтрации; 2 – этап сегментации или выделения областей интереса на изображении, который может быть осуществлен посредством пороговой обработки, или более сложными способами, например, [Патент 2629629 Российская Федерация, МПК G06K 9/34. Заявка - № 2016132680; заявл. 09.08.16; опубл. 30.08.17, Бюл. № 25]; 3 – этап выделения информативных признаков, способы выделения которых основаны на анализе текстурных, спектральных, статистических или геометрических характеристик сегмента; 4 – этап классификации, который предусматривает построение обучаемого или не обучаемого классификаторов, в качестве которого могут быть использованы ИНС, машина опорных векторов, метод k - ближайших соседей и т.д.
Для реализации второго подхода используется технология сверточных нейронных сетей (СНС) [Aksenov S.V., Kostin K.A., Ivanova A.V., Liang J., Zamyatin A.V. An ensemble of convolutional neural networks for the use in video endoscopy. Sovremennye tehnologii v medicine 2018; 10(2): 7–19, https://doi.org/10.17691/stm2018.10.2.01]. Задача построения архитектуры СНС сводится к «сворачиванию» размеров входного изображения к трехмерным слоям с размерами 2×2 или 1×1 таким образом, чтобы получить выходные сигналы в виде вероятности принадлежности входного изображения к одному из представленных классов. Архитектура СНС разделяется на несколько блоков (слоев) с определенными значениями характеристик, чередование которых позволяет сформировать наиболее эффективную архитектуру СНС. Как и в случае с многослойными НС прямого распространения, при проектировании архитектуры СНС увеличение количества слоев и связей внутри сети дает возможность строить более сложные модели, позволяющие оперировать более сложными образами.
Известна автоматизированная система диагностики медицинских изображений с использованием глубоких СНС (патент США 9,589,374 B1, 07.03.2017). Данное изобретение раскрывает методы применения глубоких СНС к анализу медицинских изображений для диагностики в режиме реального времени. В приведенном изобретении применяется анализ КТ и МРТ снимков, которые обрабатываются с применением двух СНС и других программных модулей, для получения отклика с вероятностью наличия областей интереса на снимках пациента, которые необходимы для дальнейшего анализа лечащим врачом.
В статье «Automatic Liver and Tumor Segmentation of CT and MRI Volumes Using Cascaded Fully Convolutional Neural Networks» (Patrick Ferdinand Christ et al. Computer Vision and Pattern Recognition (cs.CV); Artificial Intelligence (cs.AI). 20.02.2017) рассматриваются подходы к автоматизированному анализу КТ и МРТ снимков для и выявления патологий печени, при этом используется сверточная нейронная сеть U-NET типа.
Недостаток вышеперечисленных технических решений заключается в том, что СНС настраивается на решение конкретной задачи. Отсутствие универсальности затрудняет ее использование в рентгеновской диагностике. Для преодоления этого недостатка в структуре СНС используют распараллеливание каналов анализа данных таким образом, чтобы каждый канал был настроен на определенный класс изображений.
В работе [Анохина О.А., Шустова М.В. Методы нейросетевой обработки биомедицинских данных МРТ. – Сборник научных трудов по итогам V Международной научно-практической конференции «Актуальные проблемы медицины в России и за рубежом» (г. Новосибирск, 11 февраля 2018 г.), 2018, С.37-46.] предлагается решение задачи автоматической сегментации снимков МРТ головного мозга на разные классы тканей с помощью набора СНС. Для каждого класса входное изображение разбивается на некоторое число фрагментов разного размера. Каждая СНС обучается классифицированию фрагментов определенного размера. Качество классификации оказывается выше, чем в случае использования только одной сети. Это объясняется тем, что отдельная нейронная сеть лучше настраивается на извлечение признаков из фрагмента конкретного размера. Количество выходных классов N задается пользователем. В проведенных экспериментах для обработки снимков новорожденных N задавалось равным 9 (8 классов тканей и фон), для снимков пожилых взрослых N=8 (7 классов тканей и фон), для снимков молодых взрослых N=7 (6 классов тканей и фон). Сегментация снимков с помощью СНС показывает хорошие результаты.
Однако увеличение каналов анализа данных приводит к необоснованному увеличению схемы принятия решения, к неприемлемым экономическим и временным затратам. Оперативность принятия решений важно при массовых скрининг-обследованиях или обследовании реанимационных больных.
В классификаторах часто применяют предварительную обработку входных данных. Для предобработки последовательно применяются метод «winsorizing», удаляющий выбросы яркости, и метод нормализации яркости изображения N4ITK [Nicholas J. Tustison, Brian B. Avants, Philip A. Cook N4ITK: Improved N3 Bias Correction // IEEE Transactions on Medical Imaging (Volume: 29, Issue: 6, June 2010)], которые статистически значимо улучшают качество сегментации. После этого изображение преобразуется так, чтобы математическое ожидание и дисперсия яркости составляли 0 и 1 соответственно.
Качество сегментации улучшается за счет увеличения количества размеченных изображений с помощью поворотов на углы, кратные 90º. В архитектуре СНС, используемой в работе [Sérgio Pereira, Adriano Pinto, Victor Alves, and Carlos A. Silva. Brain Tumor Segmentation Using Convolutional Neural Networks in MRI Images // IEEE Transactions on Medical Imaging (Volume: 35, Issue: 5, May 2016)], задействованы следующие слои:
– сверточные (Conv. – Convolutional layer);
– субдискретизирующие слои, выбирающие максимум (Max-pool.);
– полносвязные (FC – Fully-Connected layer).
Переход от обработки последовательности двухмерных изображений к трехмерным позволяет получить больше информации об исследуемом объекте. Эффективность использования 3D-сверточных нейронных сетей при сегментации областей интереса продемонстрирована в [Konstantinos Kamnitsas, Christian Ledig, Virginia F.J. Newcombe, Joanna P. Simpson, Andrew D. Kane, David K. Menon, Daniel Rueckert, Ben Glocker. Efficient Multi-Scale 3D CNN with fully connected CRF for Accurate Brain Lesion Segmentation. // Medical Image Analysis, Volume 36, pages 61-78. URL: https://arxiv.org/pdf/1603.05959.pdf (дата обращения: 25.01.2018)]. Структура используемой многомасштабной трехмерной СНС выделяется использованием «двух путей» (dual pathway multi-scale 3D Convolutional Neural Network) – на одном пути сеть обучается определению местоположения зоны интереса внутри мозга, на другом фиксируется внешний вид структур.
Данное решение является, по своей технической сути, наиболее близким аналогом. Основным недостатком данного решения является такая настройка СНС, которая не подразумевает разделения откликов по весомым коэффициентам с их последующим перевзешиванием в слоях каждой СНС и разделением обучающей выборке по типу патологий в процессе обучения ансамбля, что приводит к достаточно высокой степени появления ошибок в ходе распознавания изменений структур на рентгеновских снимках. При этом данное решение, как таковое, не используется для анализа рентгеновских снимков.
Технической задачей предлагаемого способа является минимизация ошибки ложных срабатываний ансамбля СНС и, соответственно, увеличение точности распознавания областей интереса при анализе графический информации за счет новой архитектуры СНС.
Поставленная задача достигается тем, что в известном способе автоматической классификации рентгеновских снимков, предусматривающем формирование рентгеновского цифрового изображения в виде матрицы оптических плотностей объекта, получение слоев изображения (размерность по глубине) путем обработки исходного цифрового изображения локальными фильтрами, уникальными для каждого слоя, последующим снижением размерности изображений в глубинных слоях посредством технологии пулинга (субдискретизаии), формирование пространства информативных признаков для обучаемой полносвязной нейронной сети разверткой глубинных слоев, обучение полносвязной нейронной сети на примерах рентгеновских снимков с заданными морфологическими образованиями; входное цифровое изображение дополняется маской прозрачности, локальные фильтры реализуются в виде тождественных операторов, которые формируют глубинные слои посредством индексации масштаба маски фильтра. При этом технология пулинга осуществляется путем формирования трехмерных тензоров по два на каждый глубинный слой путем обработки глубинных слоев двумя дифференциальными операторами, число элементов которых определяется масштабом глубинного слоя, с бинарными выходами и пороговой функцией активации, при этом каждый масштаб будет характеризоваться трехмерными мегапикселями, число которых определяется масштабной маской соответствующего глубинного слоя.
В качестве субдискретизаторов используются маска прозрачности и однослойные персептроны. Маска прозрачности прореживает трехмерные тензоры информативных признаков таким образом, что на выходе остаются только информативные признаки, принадлежащие к одному сегменту. Однослойные персептроны обучены на классификацию определенного класса патологии при условии, что на их вход поступает вектор информативных признаков, соответствующий мегапикселю сегмента определённого масштаба, следовательно, их структура не зависит от структуры сегмента, а зависит только от глубины трехмерного тензора информативных признаков. Однослойный персептрон агрегирует решение по всем мегапикселям данного прореженного трехмерного тензора классифицируемого сегмента. Результаты классификации мегасегментов с однослойных персептронов поступают на интеллектуальный анализатор, в котором происходит агрегация результатов классификации по всему сегменту с выявлением выбросов в каждом однослойном персептроне и анализом выбросов по всем однослойным персептронам. Агрегированные результаты классификации однослойных персептронов формируют входы полносвязной нейронной сети, настроенной на классификацию сегмента с заданной патологией.
На фиг.1 представлена структурная схема устройства, осуществляющего предлагаемый способ.
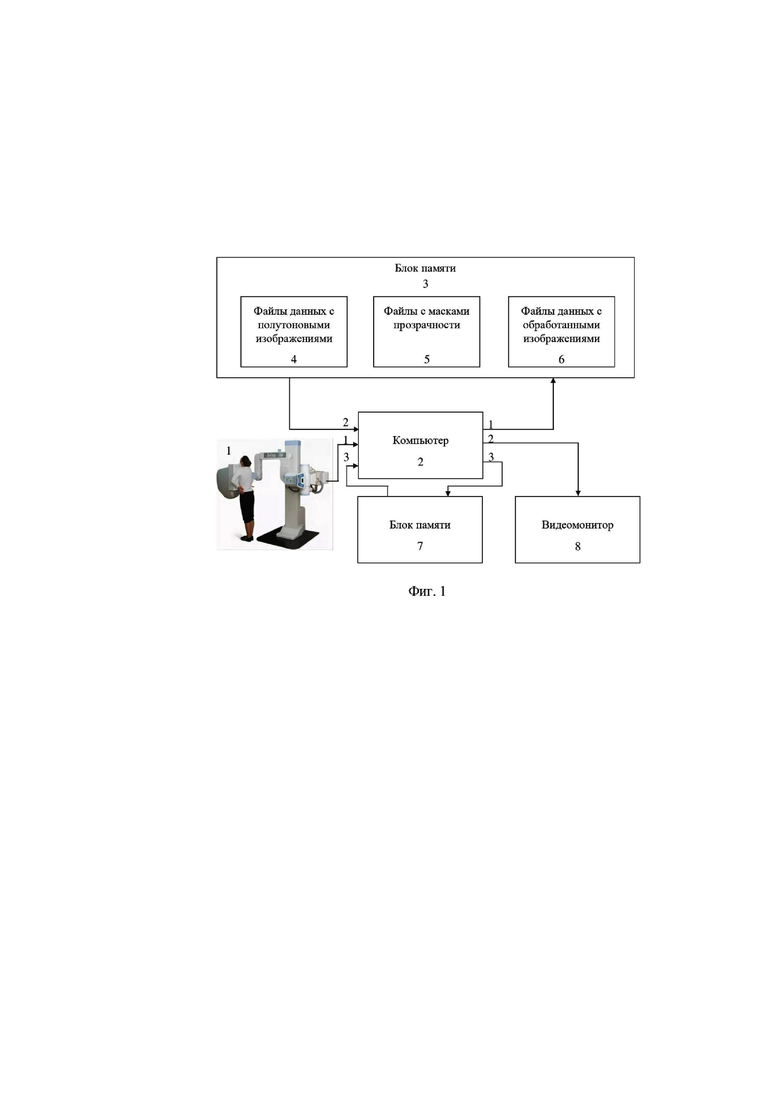
На фиг.2 представлена укрупненная схема алгоритма, реализующего предлагаемый способ.
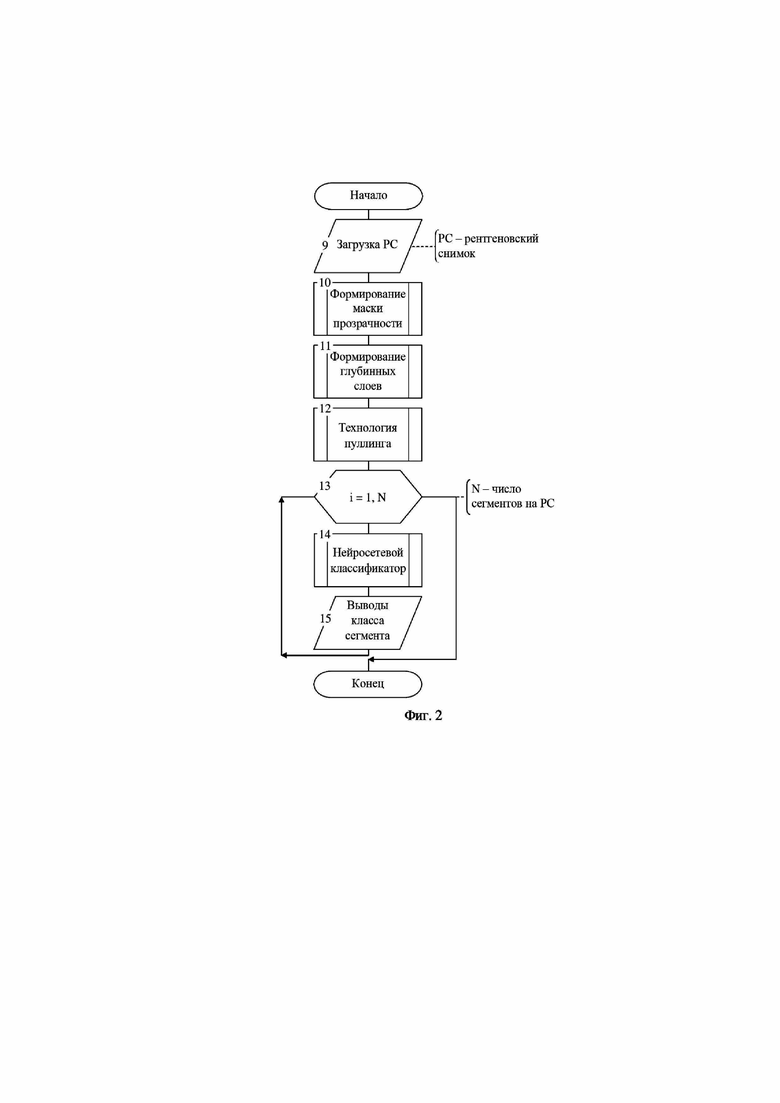
На фиг. 3 представлены примеры масок прозрачности, определяемых на первом этапе классификации изображения рентгеновского снимка.
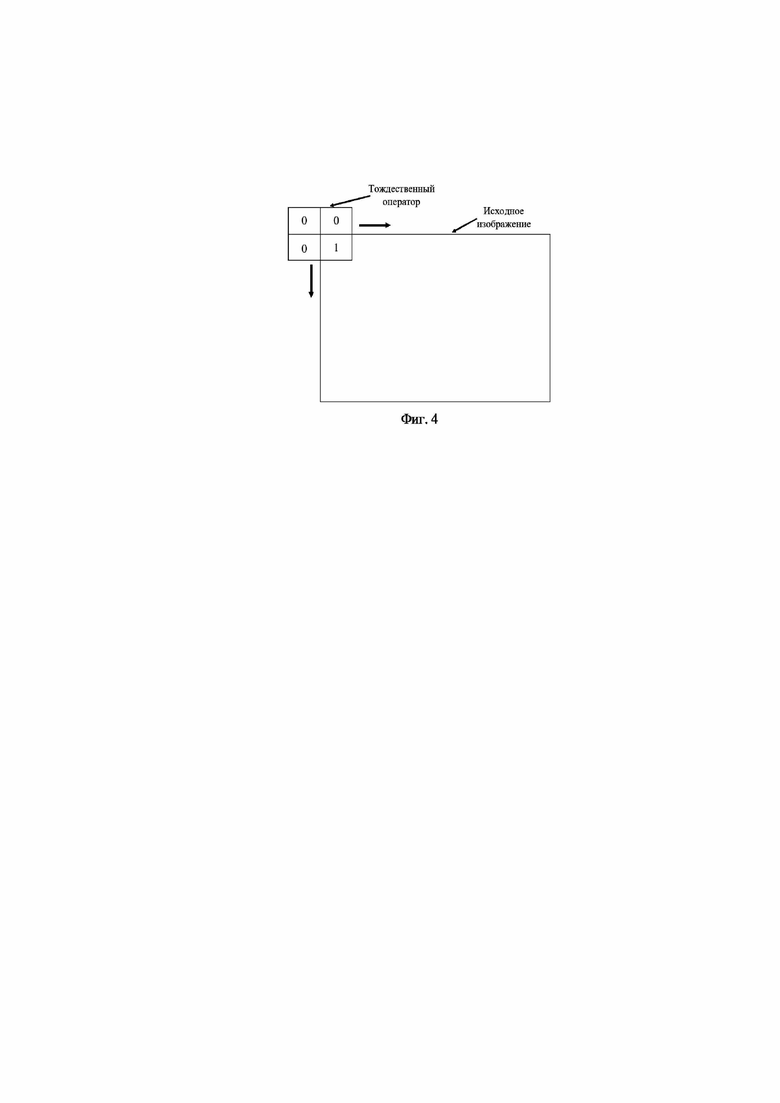
На фиг.4 представлена схема взаимодействия тождественного оператора и исходного изображения для тождественного оператора с матрицей свертки 2 х 2.
На фиг. 5 представлена иллюстрация технологии классического пулинга.
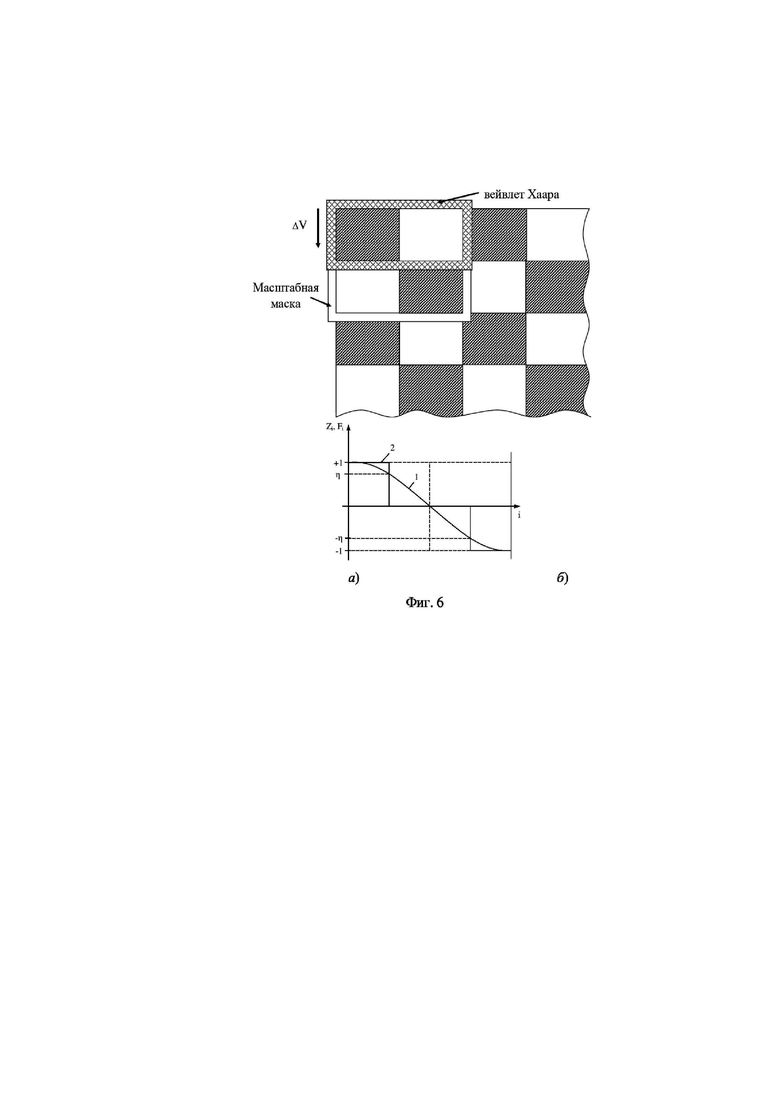
На фиг. 6 представлена иллюстрация взаимодействия горизонтального вельвета Хаара с масштабной маской глубинного изображения (а) и формирование третьего измерения у тензора информативных признаков (б).
На фиг. 7 показан фрагмент рентгеновского снимка с наложенной масштабной маской.
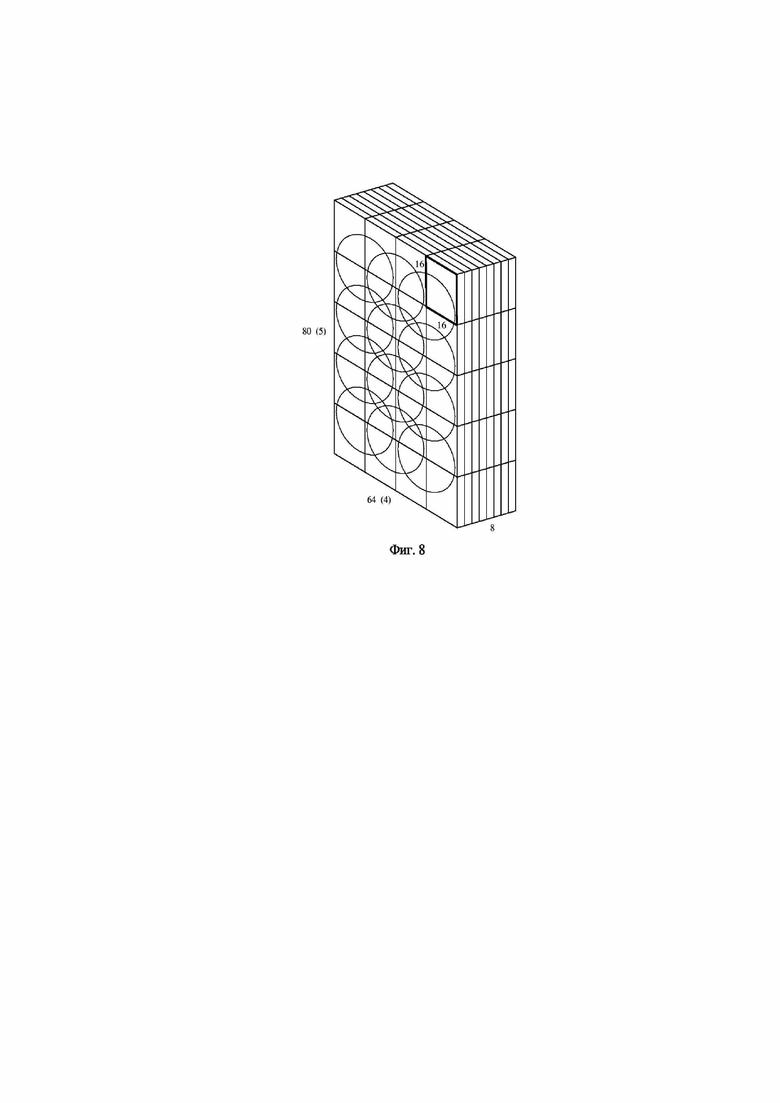
На фиг. 8 представлен пример трехмерного тензора информативных признаков для сегмента размером 80 х 64 пикселя и маски (мегапикселя) 16 х 16 пикселей, используемого для формирования пространства информативных признаков для однослойного персептрона (слабого классификатора).
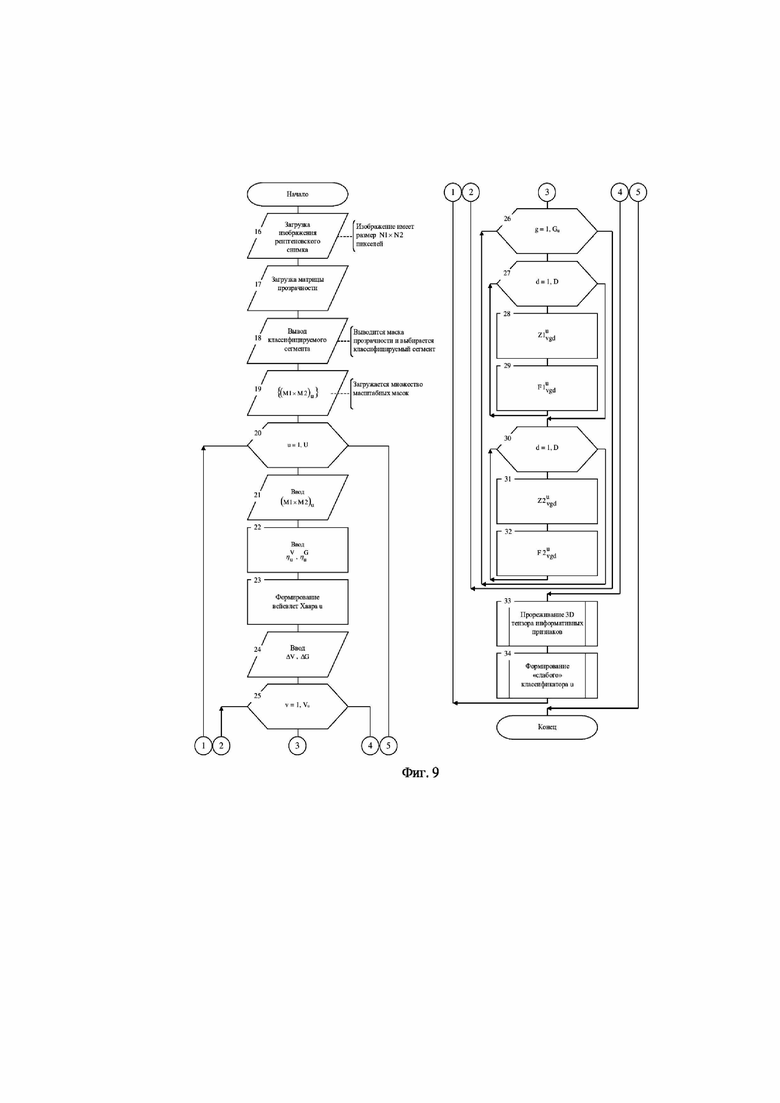
На фиг. 9 показана схема алгоритма пулинга.
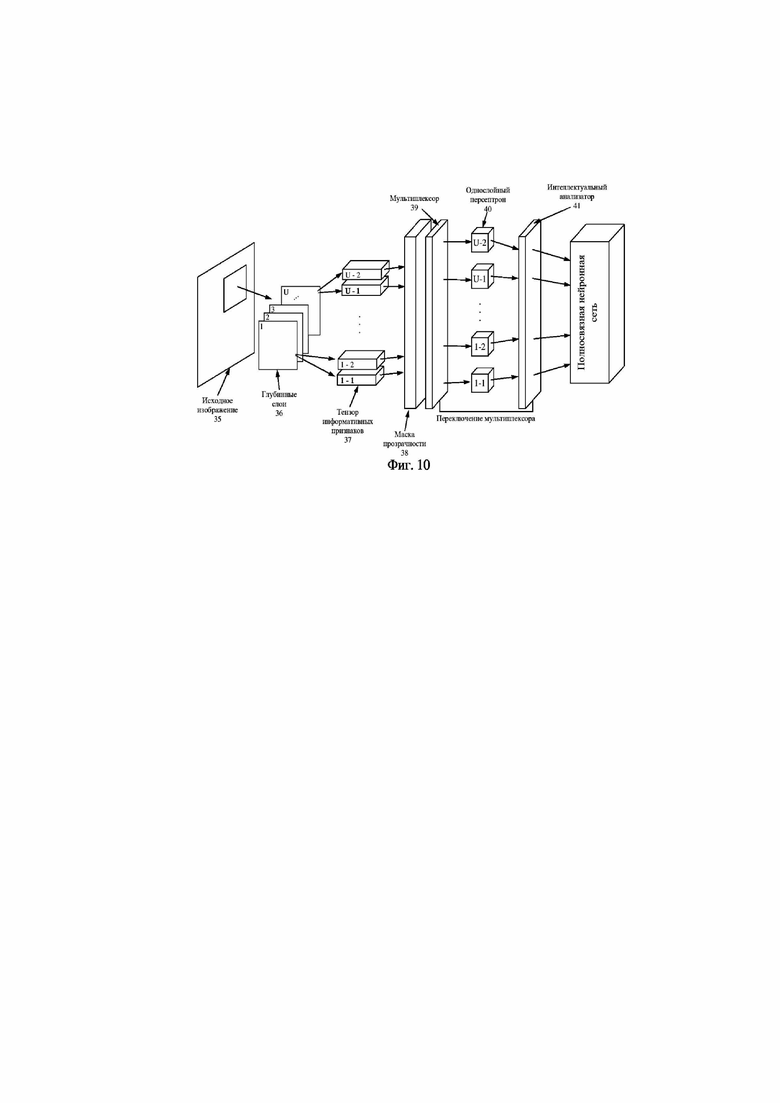
На фиг. 10 представлена структурная схема классификатора, реализующего предлагаемый способ.
На фиг. 11 представлена структура полносвязной нейронной сети, используемой на четвертом этапе классификации сегментов изображения рентгеновского снимка.
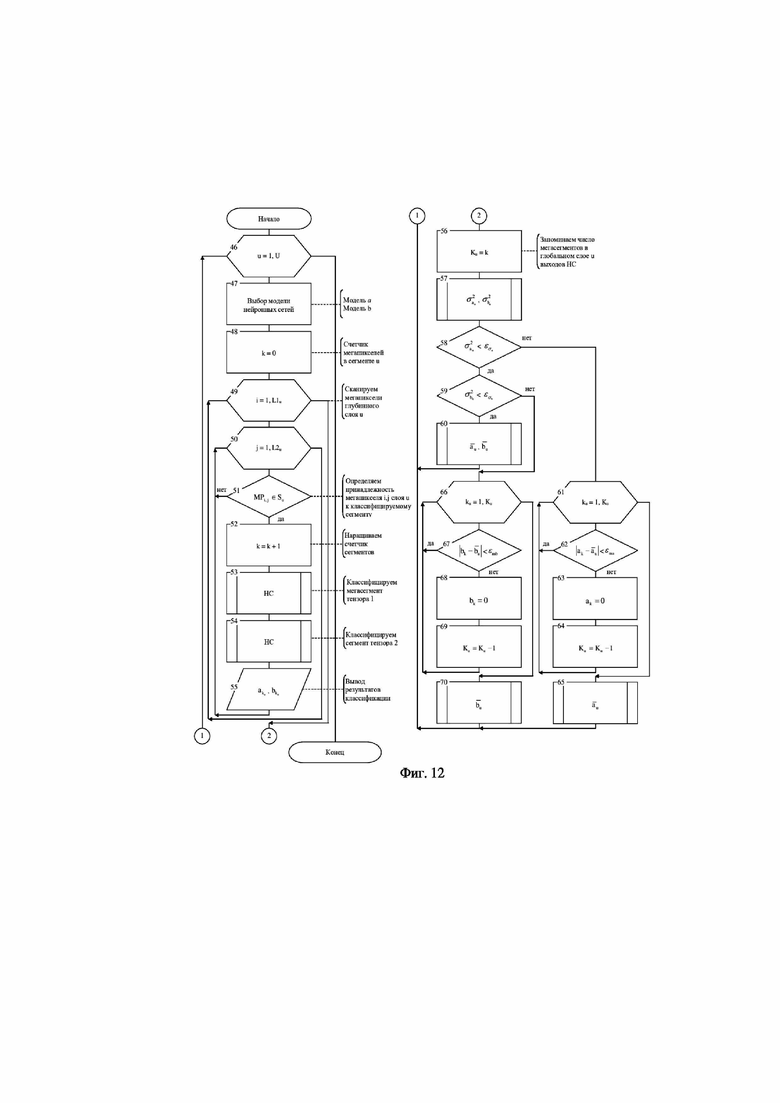
На фиг. 12 показана схема алгоритма работы интеллектуального анализатора.
Устройство фиг. 1 состоит из цифрового рентгеновского аппарата 1, компьютера 2; первым входом подключённого к выходу рентгеновского аппарата 1, блока памяти 3, предназначенного для хранения рентгеновских снимков, входом подключенного к первому выходу компьютера 2, а выходом – ко второму входу компьютера 2, который включает файлы данных 4 с полутоновыми растровыми изображениями рентгеновских снимков, файлы с масками прозрачности 5 и файлы с обработанными (классифицированными) изображениями рентгеновских снимков 6; блока памяти 7, входы подключенного к третьему выходу компьютера 3, а выходы – к третьему входу компьютера 3, предназначенного для хранения рабочих программ и моделей сверточных нейронных сетей, и видеомонитора 8, подключенного ко второму выходу компьютера 2.
Способ реализуется посредством последовательности программных модулей 9…15 (фиг.2) включающих технологию пуллинга.
Технология пуллинга реализуется посредством выполнения последовательности программных модулей 16…34, представленных на фиг. 9.
Классификатор фиг. 10 включает последовательные процедуры преобразования рентгеновского снимка 35 в глубинные слои 36, глубинные слои 36 в трехмерные тензоры информативных признаков 37, прореживание тензоров информативных признаков 37 посредством маски прозрачности 38, последовательное подключение мегапикселей тензоров 37 посредством блока мультиплексоров 39 к однослойным персептронам 40, классификацию вектора размерностью 2U, где U – число глубинных слоев, интеллектуальным анализатором 41, и классификацию области интереса посредством полносвязной нейронной сети 42. Выход (2U + 1) интеллектуального анализатора 41 подключен к входу (2U + 1) блока мультиплексоров 39.
Полносвязная нейронная сеть 42 фиг. 11 состоит из последовательно соединенных входного слоя 43, скрытого слоя 44 и выходного слоя 45.
Способ реализуется согласно алгоритму, схема которого представлена на фиг. 2. Посредством рентгеновского аппарата 1 получают рентгеновский снимок. Это изображение с помощью компьютера 2 фиг. 1 загружается в файлы данных 4 блока памяти 3 фиг. 1. После этого компьютер приступает к его обработке, включающей четыре этапа.
На первом этапе формируется матрица прозрачности (блок 10 фиг. 2). Размер матрицы прозрачности соответствует размеру матрицы рентгеновского снимка. Элементы матрицы прозрачности принимают значения нуля или единицы, то есть она является бинарной матрицей. Значение единицы принимают те пиксели матрицы прозрачности, которые принадлежат области интереса рентгеновского снимка (сегменты). Следовательно, формирователь матрицы прозрачности является двух альтернативным классификатором, позволяющим выделить на рентгеновском снимке области интереса, которые классифицируются на следующих этапах более «тонкими» классификаторами, позволяющими определить, к какому заболеванию может быть отнесена соответствующая область интереса. Процедура выделения зон интереса, соответствующая первому этапу обработки, и представленная на схеме алгоритма фиг.2 блоком 10, подробно описана в работе [Метод каскадной сегментации рентгенограмм молочной железы / Дабагов А.Р. и др. // Известия ЮЗГУ. Серия Управление, вычислительная техника, информатика. Медицинское приборостроение. – 2019. – Т.9. № 1(30) – С.49-61]. Маски прозрачности хранятся в файлах 3 фиг. 1.
На фиг. 3а представлена маска прозрачности для сегментов, образованных тенями ребер на рентгенограмме грудной клетке, на фиг. 3б представлена маска прозрачности для пикселей попавших в область легочных полей на рентгенограмме грудной клетки, на фиг. 3в показана маска прозрачности для зоны интереса-пневмония, на фиг. 3г показана маска прозрачности для рентгеновской маммограммы с зоной интереса-рак.
На втором этапе осуществляется формирование глубинных слоев (блок 11 фиг. 2). За основу формирования глубинных слоев взята технология формирования сверточных слоев в сверточных нейронных сетях (СНС). Но в отличие от архитектуры СНС в данном способе используются тождественные операторы. Тождественные операторы имеют такую же масочную структуру, что и операторы свертки, то есть результат их работы (яркость пикселя с координатами i, j) можно представить выражением
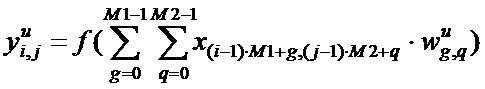
где u - идентификатор свертки (идентификатор масштаба), M1 x M2 – размер матрицы свертки, 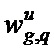
Особенностью тождественного оператора является то, что у него отличен от нуля (равен единице) только один весовой коэффициент, координата которого совпадает с координатой активного пикселя на изображении.
Этому условию соответствует следующее правило продукционного типа
Если ((g=M1-1)И(q=M2-1)) ТО 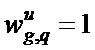
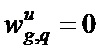
Пример тождественного оператора для размера матрицы свертки (масштаба) 2 × 2 и схема его взаимодействие с исходным изображением при получении глубинного слоя с этим масштабом показаны на фиг. 4.
Таким образом, тождественный оператор транслирует исходное изображение в глубинный слой с присвоением ему определенного масштаба (размечает исходное изображение на мегапиксели). Масштабы глубинных слоев выбираются из ряда: 2×2; 4×4; 8×8 …, то есть из ряда 2n+1, где n принимает значения ряда натуральных чисел. При этом размерность изображения в глубинном слое сокращается и принимает значение (N1-M1/2) x (N2-M2/2), где N1 × N2 – размер исходного изображения, а M1 × M1 – размер мегапикселя.
На третьем этапе осуществляется сокращения размерности глубинных слоев, которая в технологии СНС называется пулингом или субдискретизациией (блок 12 фиг. 2).
Задача пулинга – сократить карты признаков, то есть сократить число признаков в глубинных слоях. На фиг. 5 представлена иллюстрация классического пулинга, используемого в СНС. Для его реализации необходима матрица весовых коэффициентов, также как и при реализации сверточного слоя. На фиг. 5 представлен пример пулинга с матрицей размером 2 × 2, который позволяет сократить размерность глубинного слоя с 24 × 24 до 12 × 12. В результате пулинга каждые четыре элемента из исходного изображения, попавшие в матрицу пулинга размером 2 × 2, заменены одним элементом в выходном изображении, который является максимальным из четырех. В литературе описаны и другие способы выбора элемента выходного изображения и шага перемещения матрицы пулинга.
В данном способе используется технология пуллинга, отличная от классической. Сущность технологии состоит в том, что элементам глубинного слоя (1), находящимся в области масштабной маски, соответствующей этому глубинному слою, ставится в соответствии некоторый функционал Z. При формировании этого функционала учитываем то, что в результате сегментации первого этапа сегменты уже селектированы по показателям яркости и текстуры. Поэтому дальнейшая обработка изображения сегмента направлена только на его классификацию. Каждая масштабная маска глубинного слоя может быть описана вектором информативных признаков, число элементов в котором должно быть меньше, чем в масштабной маске (как в классическом пулинге фиг. 5). За основу формирования такого вектора взят метод Виолы-Джонса. В этом методе для описания текстуры в масштабном окне используются множество вейвлетов (примитивов) Хаара. В предлагаемой технологии пулинга для каждого масштабного окна используем только два вейвлета Хаара: вертикальный и горизонтальный. Размер вертикального вейлета равен M2/2 × M1, а размер горизонтального вейвлета равен М1/2 × М2. Горизонтальный вейвлет Хаара перемещается по маске в вертикальном направлении с шагом ΔV, а вертикальный вейвлет Хаара перемещается по маске в горизонтальном направлении с шагом ΔG. При каждом i-м положении вейвлета вычисляется разность
Zi=Wi – Bi, (3)
где Wi – сумма яркостей пикселей, находящихся под «белой» частью вейвлета Хаара, Bi – сумма яркостей пикселей, находящихся под «черной» частью вейвлета Хаара.
При этом получаем два вариационных ряда, число элементов в которых определяется как int(M1/(2 ΔV) и int(M2/(2 ΔG). Если выбрать М1=М2, то число элементов в вариационных рядах одинаково и их можем принять за элементы комплексного ряда с соответствующей действительной (первый ряд) и мнимой (второй ряд) составляющими.
При классификации сегмента необходимо учитывать, что на рентгеновском снимке он может быть не прямоугольной формы, причем допускаются самые разнообразные конфигурации его контура. Таким образом, формируем первое требование к пространству информативных признаков: вектор информативных признаков не должен зависеть от масштаба глубинного слоя и от количества масштабных окон в сегменте. Это первое требование к технологии пулинга. Вторым требованием является инвариантность информативных признаков к динамическому диапазону яркости пикселей на рентгеновском снимке.
Для реализации второго требования к пространству информативных признаков полагаем, что (3) может принимать только значения -1, 0 и +1. С этой целью введем пороговый параметр η и преобразуем результат взаимодействия маскированных пикселей с вейвлетом Хаара следующим образом:

На фиг. 6 показан пример определения вектора информативных признаков масштабного окна. Для простоты иллюстрации в качестве примера глубинного слоя взято изображение «шахматное поле». Масштабная маска выбрана 2 × 2 элемента с горизонтальным вейвлетом Хаара 1 × 2. Это иллюстрирует фиг. 6а. В результате продвижения вейвлета Хаара по масштабной маске получаем отсчеты согласно (3), аппроксимация которых представлена кривой 1 на фиг. 6б. Кривая 2 на фиг. 6б иллюстрирует отсчеты, полученные согласно (4).
На фиг. 7 показан фрагмент изображения реального рентгеновского снимка с масштабной маской, образующей мегапиксель, при сканировании которой вейвлетами Хаара формируется вектор информативных признаков (4).
Перейдем к процедуре пулинга, позволяющей удовлетворить первое требование. Функционал Z должен быть выбран таким образом, чтобы его значение не зависело от размера сегмента, а зависело только от его текстуры. Это требование обусловлено тем, что субдискретизированное глубинное изображение представляет из себя множество 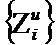
Так как нейронная сеть должна ответить на вопрос, принадлежит ли элемент сегмента глубинного изображения, определенный масштабной маской, к заданному известному классу, то однослойный персептрон обучен под известный класс с известной масштабной маской, поэтому его структура не зависит от числа масштабных масок (мегапикселей), включенных в классифицируемый сегмент. Этот однослойный персептрон является слабым классификатором. Слабые классификаторы формируют входной вектор для полносвязной нейронной сети.
Алгоритм, реализующий технологию пулинга, представлен на фиг. 9. Целью алгоритма является формирование информативных признаков по результатам анализа глубинных слоев для полносвязной нейронной сети, реализующий четвертый этап классификации сегментов изображения рентгеновского снимка, поэтому алгоритм включает глобальный цикл анализа U глубинных изображений рентгеновского снимка (блок 20). Идентификатор U определяет количество масштабных окон (масштабов), используемых для классификации сегментов изображения рентгеновского снимка, которые определяются в блоке 11 фиг. 2.
В блоке 16 осуществляется загрузка рентгеновского снимка, изображение которого имеет размер N1 × N2 пикселей. В блоке 17 загружается маска прозрачности, изображение которой определено на первом этапе классификации. В блоке 18 выбирается классифицируемый сегмент. В блоке 18 загружаются масштабные маски, которые используются при формировании глубинных слоев. Полагаем, что для формирования глубинных слоев используется U масштабных масок. В блоке 21 вводится соответствующая масштабная маска, которая форматирует изображение рентгеновского снимка в соответствии со своим размером (M1×M2)u. В блоке 22 вводятся значения порогов 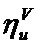
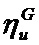
Непосредственно тензор информативных признаков для "слабых" классификаторов вычисляется в цикле, который организован посредством блока 25. Цикл предусматривает сканирование изображения рентгеновского снимка согласно правилу строчной развертки. При этом анализируется группа пикселей, попавшая в масштабную маску. Каждой группе пикселей ставится в соответствие комплексный вектор размером D, который формирует третье измерение. Первая компонента комплексного вектора формируется блоками 27-29, а вторая - блоками 30-32. Блоки 25 и 26 организуют сканирование псевдоматрицы глубинного слоя. Элементы этой матрицы составляют пиксели изображения рентгеновского снимка, попавшие в масштабную маску - мегапиксели. Число мегапикселей в u-ом глубинном слое определяется как Vu x Gu, где Vu=int(N1/M1u), Gu=int(N2/M2u).
Блоки 27-29 и 30-32 представлены, с целью упрощения описания алгоритма, для случая ΔV= ΔG и М1=М2. В этом случае число компонент вектора, соответствующих координате d, полученных сканированием мегапикселя горизонтальным и вертикальным вейвлетами Хаара одинаково и определяется как D=M1/(2 ΔV)=M2/(2 ΔG).
После получения двух тензоров, один из которых представлен на фиг. 8, для каждого глубинного слоя осуществляется их прореживание в блоке 33 согласно матрицы прозрачности и выбранному в блоке 18 сегменту. Каждый из оставшихся после прореживания мегапикселей будет формировать слабый классификатор, на выходе которого присутствуют две компоненты, характеризующие принадлежность анализируемого сегмента к заданному классу. "Слабый" классификатор формируется однослойным персептроном, который реализуется в блоке 34. На его вход поступают элементы не только слоя D, соответствующие мегапикселю этого "слабого" классификатора, но и элементы слоев D смежных мегапикселей (на фигуре 8 обведены окружностью). Однослойный персептрон настраивается на один класс, поэтому для всех мегасегментов глубинного слоя u используются два однослойных персептрона, которые обучаются на примерах D-слоев, полученных в результате горизонтального и вертикального сканирования вейвлетами Хаара соответствующего мегапикселя.
На четвертом этапе осуществляется классификация сегмента посредством многослойного персептрона. Полносвязный слой выполнен в виде двух нейронных сетей блочного типа, скрытые слои которых обучены на векторах, полученных в результате вертикального и горизонтального сканирования вейвлетом Хаара соответствующего мегапикселя. Последние слои полносвязной нейронной сети агрегируют результаты автономной классификации нейронных сетей блочного типа.
На фиг. 10 показана полная структурная схема классификатора, реализующая предлагаемый способ.
Входными данными для классификатора является матрица отчетов пикселей рентгеновского снимка 35, из которой формируется глубинные слои 36 используя технологию пулинга из глубинных слоев 36 получают тензоры информативных признаков 37, которые прореживаются посредством маски прозрачности 38. Мультиплексор 39 подключает Д - слои тензоров 37 к входам однослойным персептронам 40, что обеспечивает интеллектуальный анализатор 41, который также формирует входные данные для полносвязной нейронной сети 42.
Полносвязная нейронная сеть 42 (фиг. 11) включает входной слой 43, который является выходом интеллектуального анализатора 41, скрытые слои 44 и выходной слой 45.
На фиг. 12 представлена схема алгоритма работы интеллектуального анализатора 41 (фиг. 10). Исходными данными для него является выходы однослойный персептронов 40 (фиг. 10). На выходы однослойных персептронов последовательно поступает информация о каждом мегапикселе глубинного слоя U. Интеллектуальный анализатор должен хранить эти данные, которые на схеме алгоритма обозначенный как 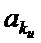
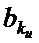
Посредством блоков 49 и 50 осуществляется сканирование глубинного слоя U. Сканирование ведется по мегапикселям. Размер рентгеновского снимка в мегапикселях в глубинном слое U определяется как:
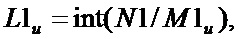
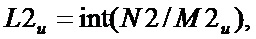
где - (M1×M2)u где размер масштабной маски.
Координаты мегапикселя (i, j) сравниваются с координатами сегмента и на маске прозрачности, если мегапиксель попадает в сегмент, то из соответствующих слоев D тензора на однослойные персептроны поступают входные данные, что реализуется блоками 51, 53, 54. При этом срабатывает счётчик сегментов в слое U (блок 52) и выходные данные с однослойных персептронов 40 запоминается в блоке 55.
После просмотра мегапикселей глубинного слоя U и в блоке 56 запоминаются число пикселей Ku, принадлежащих классифицируемому сегменту.
Сущность интеллектуального анализатора данных 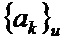
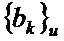
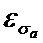
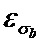
Если эти условия не соблюдаются (блоки 58 и 59), то необходимо искать выбросы в данных, я и при формировании соответствующего входа полносвязные нейронные сети 42 выбросы не учитывать.
Выбросы для множества 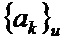
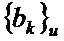
Таким образом, для решения задач классификации морфологических структур с патологическими образованиями на растровых полутоновых изображениях рентгеновских снимков предложено разделить исходное изображение на части (сегменты), различающиеся по своему семантическому содержанию, и затем классифицировать эти сегменты. При сегментации изображений рентгеновских снимков на них выделяются зоны интереса произвольной формы (не растровые изображения). Поэтому ставится вопрос не о классификации исходного изображения, а о классификации его сегментов. Компьютерные программы классификации работают, как правило, с «матричными» изображениями, представленными прямоугольными или квадратными растрами. Для преобразования не растрового изображения (сегмента) в растровое к нему присоединяется маска (изображение) прозрачности, размер которой совпадает с размером исходного изображения. Пиксели маски, принимающие значение единица, формируют массив обрабатываемых пикселей исходного изображения, принадлежащих к выделенному сегменту, а пиксели маски, принимающие значение ноль - преобразуют яркость соответствующих пикселей исходного изображения в яркость фона.
Классификация выделенного сегмента осуществляется модифицированной сверточной нейронной сетью, в которой из классической сверточной сети используются слои пулинга и слои полносвязной нейронной сети. Для того, чтобы использовать формальные процедуры обработки изображений с прямоугольным растром, взаимодействие с маской прозрачности осуществляется после выполнения пулинга. В отличие от классической сверточной сети в предложенном техническом решении после слоя пулинга вставлен слой слабых классификаторов, выполненный на однослойных персептронах. Число слабых классификаторов не зависит от структуры и размеров мегасегмета (масштаба глубинного слоя). Каждый слабый классификатор настроен на определенный класс сегмента и на определенный размер масштабной маски. Следовательно, число слабых классификаторов, участвующих в классификации сегмента равно числу используемых масштабов (глубинных слоев) в сверточной нейронной сети умноженному на два. Для агрегирования решений каждого из слабых классификаторов по всем мегапикселям сегмента используется слой «интеллектуальный анализатор», который и формирует пространство информативных признаков для полносвязной нейронной сети. Каждый слабый классификатор выдает решение о принадлежности мегапикселя анализируемого сегмента к заданному классу, но на полносвязную нейронную сеть поступает информация, усредненная по всем сегментам.
Процедуру усреднения осуществляет интеллектуальный анализатор с учетом выбросов. Если результат классификации мегасегмента слабым классификатором отнесен к выбросам значения, резко отличающиеся от других значений в собранном наборе данных, то он не участвует в формирование входных данных для полносвязной нейронной сети.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ распознавания речевых эмоций при помощи 3D сверточной нейронной сети | 2023 |
|
RU2816680C1 |
| Способ выявления объектов на изображении плана-схемы объекта строительства | 2022 |
|
RU2785821C1 |
| СИСТЕМА МОНИТОРИНГА РЕЖИМОВ ГОРЕНИЯ ТОПЛИВА ПУТЕМ АНАЛИЗА ИЗОБРАЖЕНИЙ ФАКЕЛА ПРИ ПОМОЩИ КЛАССИФИКАТОРА НА ОСНОВЕ СВЁРТОЧНОЙ НЕЙРОННОЙ СЕТИ | 2018 |
|
RU2713850C1 |
| Устройство создания многомерных виртуальных изображений органов дыхания человека и способ создания объёмных изображений с применением устройства | 2021 |
|
RU2783364C1 |
| ОБРАБОТКА И АНАЛИЗ ДАННЫХ НА ИЗОБРАЖЕНИЯХ КОМПЬЮТЕРНОЙ ТОМОГРАФИИ | 2017 |
|
RU2667879C1 |
| СИСТЕМА СЖАТИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ НА ОСНОВЕ ИТЕРАТИВНОГО ПРИМЕНЕНИЯ ТЕНЗОРНЫХ АППРОКСИМАЦИЙ | 2019 |
|
RU2734579C1 |
| СИСТЕМА ИДЕНТИФИКАЦИИ СВЕЖИХ ПРОДУКТОВ ДЛЯ КАССОВОГО ТЕРМИНАЛА РОЗНИЧНОЙ ТОРГОВЛИ | 2018 |
|
RU2769888C2 |
| ОБУЧЕНИЕ GAN (ГЕНЕРАТИВНО-СОСТЯЗАТЕЛЬНЫХ СЕТЕЙ) СОЗДАНИЮ ПОПИКСЕЛЬНОЙ АННОТАЦИИ | 2019 |
|
RU2735148C1 |
| ГЕНЕРАТОРЫ ИЗОБРАЖЕНИЙ С УСЛОВНО НЕЗАВИСИМЫМ СИНТЕЗОМ ПИКСЕЛЕЙ | 2021 |
|
RU2770132C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ОПРЕДЕЛЕНИЯ ПРАВИЛЬНОСТИ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ НА ЖИДКОКРИСТАЛЛИЧЕСКОМ ИНДИКАТОРЕ | 2007 |
|
RU2346331C1 |



Изобретение относится к способам цифровой обработки изображений и может быть использовано в интеллектуальных системах классификации рентгеновских снимков. Технический результат заключается в увеличении точности распознавания областей интереса при анализе графический информации. Такой результат достигается способом автоматической классификации рентгеновских изображений с использованием масок прозрачности, который предусматривает формирование рентгеновского цифрового изображения в виде матрицы оптических плотностей объекта, получение глубинных слоев изображения путем обработки исходного цифрового изображения локальными фильтрами, уникальными для каждого слоя, снижение размерности изображений в глубинных слоях посредством технологии пулинга (субдискретизации), формирование пространства информативных признаков для обучаемой полносвязной нейронной сети из субдискретизированных глубинных слоев и классификацию полученного вектора информативных признаков посредством полносвязной нейронной сети. 7 з.п. ф-лы, 12 ил.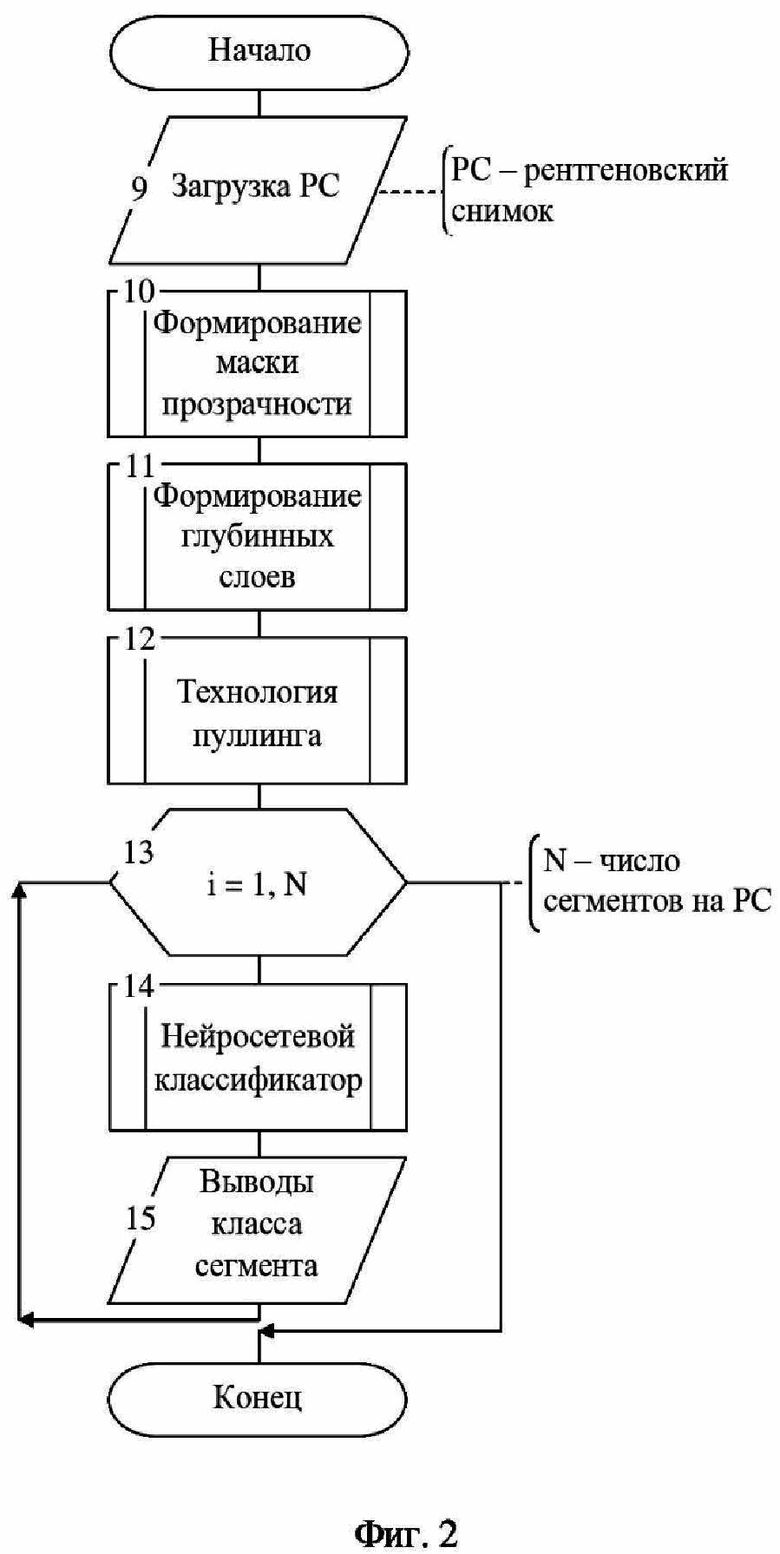
1. Способ автоматической классификации рентгеновских изображений с использованием масок прозрачности, предусматривающий формирование рентгеновского цифрового изображения в виде матрицы оптических плотностей объекта, получение глубинных слоев изображения путем обработки исходного цифрового изображения локальными фильтрами, уникальными для каждого слоя, снижение размерности изображений в глубинных слоях посредством технологии пулинга (субдискретизации), формирование пространства информативных признаков для обучаемой полносвязной нейронной сети из субдискретизированных глубинных слоев и классификацию полученного вектора информативных признаков посредством полносвязной нейронной сети, отличающийся тем, что входное цифровое изображение дополняется маской прозрачности, полученной путем предварительной сегментации изображения рентгеновского снимка, а классифицируемый вектор признаков формируется не по всем пикселям изображения, а только по тем пикселям, которые не маскированы маской прозрачности.
2. Способ по п.1, отличающийся тем, что локальные фильтры реализуются в виде тождественных операторов с различными масштабными масками, которые формируют глубинные слои посредством индексации масштаба маски фильтра, которая преобразует пиксели исходного изображения в мегапиксели - множество пикселей исходного изображения, попавших в границы маски фильтра.
3. Способ по п.1, отличающийся тем, что пулинг состоит из четырех этапов: на первом этапе каждый мегапиксель глубинного слоя изображения представляется в виде двух векторов, получаемых посредством двух дифференциальных операторов адаптированных к горизонтальному и вертикальному направлениям; на втором этапе на маске прозрачности выбирается классифицируемый сегмент и из полученных двух трехмерных тензоров удаляются векторы, мегапиксели которых не принадлежат классифицируемому сегменту; на третьем этапе из четырех смежных векторов каждого мегапикселя формируется вектор информативных признаков для "слабого" классификатора; на четвертом этапе каждый слабый классификатор каждого глубинного слоя определяет степень принадлежности данного мегапикселя к заданному классу.
4. Способ по п.3, отличающийся тем, что на первом этапе пулинга результаты дифференцирования Zi сравниваются с порогом η, в результате чего компоненты вектора информативных признаков принимают значение
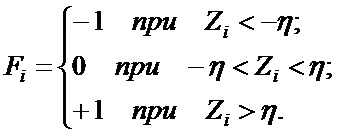
5. Способ по п.3, отличающийся тем, что в качестве дифференциальных операторов используются вейвлеты Хаара с размерами M2/2xM1 и М1/2хМ2, где М1 х М2 - размер масштабной маски соответствующего глубинного слоя.
6. Способ по п.3, отличающийся тем, что в качестве "слабых" классификаторов используются однослойные персептроны.
7. Способ по п.1, отличающийся тем, что полносвязная нейронная сеть включает две блочных полносвязных сети, входы первой из которых подключены к выходам слабых классификаторов, информативные признаки которых сформированы из векторов мегапикселей первого тензора, а входы второй блочной нейронной сети подключены к выходам слабых классификаторов, информативные признаки которых сформированы из векторов мегапикселей второго тензора.
8. Способ по п.7, отличающийся тем, что входы полносвязной нейронной сети формируются посредством интеллектуального анализа результатов классификации однослойными персептронами мегапикселей глобального слоя и при наличии «выбросов» у классификатора мегапикселя, результаты его классификации не участвуют при формировании соответствующего входа полносвязной нейронной сети.
| US 9589374 B1, 07.03.2017 | |||
| CN 110110776 A, 09.08.2019 | |||
| WO 2019010470 A1, 10.01.2019 | |||
| WO 2019135234 A1, 11.07.2019 | |||
| US 20190130575 A1, 02.05.2019 | |||
| RU 2016138608 A, 30.03.2018 | |||
| НЕЙРОННАЯ СЕТЬ ДЛЯ ГЕНЕРАЦИИ СИНТЕТИЧЕСКИХ МЕДИЦИНСКИХ ИЗОБРАЖЕНИЙ | 2017 |
|
RU2698997C1 |
Авторы
Даты
2020-03-17—Публикация
2019-10-22—Подача