Область техники, к которой относится изобретение
Предлагаемое изобретение относится к области вычислительной техники, в к использованию регистров сдвига с линейной обратной связью на вычислительных платформах с SIMD-архитектурой.
Уровень техники
Регистры сдвига с линейной обратной связью (РСЛОС) используются в различных сферах информационных технологий, в том числе в криптографии, сетевых технологиях и цифровой передаче данных. РСЛОС позволяют генерировать линейные рекуррентные последовательности и могут применяться, например, для выработки псевдослучайных последовательностей, вычисления линейных отображений или получения множества различных значений определенной длины.
РСЛОС определяется полем, которому принадлежат элементы входной и выходной последовательности регистра, а также линейной функцией над этим полем, которая задает обратную связь РСЛОС. Различают два типа РСЛОС: РСЛОС в конфигурации Галуа и РСЛОС в конфигурации Фибоначчи. Два этих типа являются эквивалентными, то есть для каждого РСЛОС в конфигурации Галуа может быть построен РСЛОС в конфигурации Фибоначчи (и наоборот), порождающий ту же самую линейную рекуррентную последовательность, возможно, с некоторым сдвигом. В дальнейшем будем рассматривать только РСЛОС в конфигурации Фибоначчи.
Рассмотрим принцип работы РСЛОС, определенного над конечным полем Р и имеющего линейную функцию обратной связи РСЛОС ƒ : Pn → Р вида
ƒ(xn-1, xn-2, …, х0) = (cn-1 ⊗ хп-1) ⊕ (cn-2 ⊗ xn-2) ⊕…⊕ (c0 ⊗ x0),
где n - натуральное число,
ci; ∈ Р, i=0, 1, …, n-1, - константные элементы поля Р,
xi ∈ P, i=0, 1, …, n-1, - аргументы функции,
«⊗» и «⊕» - операции умножения и сложения в поле Р:
• в качестве входной последовательности РСЛОС берут последовательность из n элементов:
a 0, a1, …, an-1, ai ∈ P, i=0, 1, …, n-1;
• формируют начальное состояние РСЛОС, представляющее собой вектор длины n:
(qn-1, qn-2, …, q0),
где qi ∈ Р, i=0, 1, …, n-1,
в виде:
qi=ai, i=0, 1, …, n-1;
• задают количество тактов работы РСЛОС - m, где m - натуральное число;
• выполняют m тактов работы РСЛОС, причем на s-м такте, 1 ≤ s ≤ m:
 вычисляют новое состояние РСЛОС, представляющее собой вектор длины n:
вычисляют новое состояние РСЛОС, представляющее собой вектор длины n:
(qn+s-1, qn+s-2, …, qs),
где qn+s-1=ƒ(qn+s-2, qn+s-3, …, qs-1)∈P,
 вычисляют элемент выходной последовательности РСЛОС
вычисляют элемент выходной последовательности РСЛОС
bs-1 = qs-1 ∈ P:
• в качестве выходной последовательности РСЛОС берут последовательность из m элементов:
b0, b1, …, bm-1.
Повсеместное использование РСЛОС делает актуальной задачу получения его высокопроизводительных реализаций. Одним из базовых способов повышения производительности программных и аппаратных реализаций является использование параллельных вычислений.
Обозначим класс линейных функций, определенных над полем Р и имеющих n переменных, через Ln:
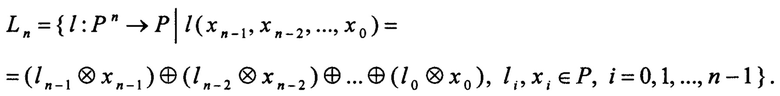
Рассмотрим вычислительную систему, выполненную с возможностью для любой линейной функции h ∈ Ln и любых элементов xr,i ∈ P, r=0, 1, …, k-1, i=0, 1, n-1, осуществлять параллельное вычисление k значений h(x0, n-1, x0, n-2, …, x0, 0), h(x1, n-1, x1, n-2, …, x1, 0), …, h(xk-1, n-1, xk-1, n-2, …, xk-1, 0), где k - натуральное число. Обозначим эту вычислительную систему через Sk.
Согласно своему свойству, система Sk позволяет вычислять одновременно k одинаковых линейных функций от разных аргументов. Данное требование является более слабым по сравнению с требованием о возможности параллельного вычисления k произвольных линейных функций от разных аргументов. Это позволяет использовать в качестве вычислительной системы Sk не только системы с возможностью параллельного вычисления k произвольных линейных функций, но и системы, не имеющие данной возможности, но допускающие параллельное вычисление k одинаковых линейных функций.
Примером вычислительной системы Sk может являться вычислительная система с поддержкой SIMD-технологий (Single Instruction, Multiple Data - одна инструкция, несколько блоков данных). В основе SIMD-технологий лежит возможность одновременного выполнения одного и того же преобразования сразу для нескольких фрагментов данных. Таким образом, вычислительная система с поддержкой SIMD-технологий, позволяющая выполнять каждую операцию, применяющуюся при вычислении функции из Ln, одновременно для k фрагментов данных, обеспечивает возможность параллельного вычисления k одинаковых функций из Ln. При этом, в общем случае, такая система не обязана обеспечивать возможность параллельного вычисления k произвольных функций из Ln, поскольку преобразования, используемые при вычислении различных функций, могут отличаться друг от друга, что не позволит или крайне затруднит использование SIMD-технологий для одновременного вычисления этих функций.
Известен способ работы РСЛОС в конфигурации Фибоначчи (патент РФ №2598781, приоритет от 31.07.2015 г.), предусматривающий использование вспомогательных таблиц. Данный способ позволяет на каждом шаге вычислять сразу несколько новых элементов состояния РСЛОС.
Недостатком данного способа является необходимость хранения и использования таблиц, размер которых пропорционален количеству одновременно вычисляемых элементов состояния.
Известен способ работы РСЛОС в конфигурации Фибоначчи в соответствии с традиционным определением РСЛОС, приведенным выше (Алферов А.П., Зубов А.Ю., Кузьмин А.С., Черемушкин А.В. Основы криптографии. 2-е изд., М., Гелиос АРВ, 2002). Способ позволяет на каждом шаге вычислять один новый элемент состояния РСЛОС посредством вычисления одной линейной функции.
Известный способ принят за прототип.
Недостатком данного способа является неэффективное использование возможностей вычислительной системы Sk, выражающееся в том, что способ подразумевает вычисление только одной линейной функции в произвольный момент времени. В результате, производительность способа на вычислительной системе Sk не зависит от значения k, соответствующего количеству линейных функций, которые могут быть вычислены параллельно на этой системе, и равна производительности способа на вычислительной системе S1, то есть системе без возможности осуществления параллельных вычислений.
Раскрытие изобретения
Техническим результатом является повышение производительности работы РСЛОС типа Фибоначчи при использовании вычислительной системы, позволяющей параллельно вычислять k одинаковых линейных функций от разных аргументов. При этом предлагаемый способ не требует хранения и использования вспомогательных таблиц.
Предлагаемый способ работы регистра сдвига с линейной обратной связью (РСЛОС) в вычислительной системе, заключается в том, что
• задают конечное поле Р с операцией сложения ⊕, операцией умножения ⊗, нулевым элементом θ и единичным элементом е;
• выбирают вычислительную систему, имеющую процессор с SIMD-архитектурой и выполненную с возможностью
 преобразования элементов поля Р в интерпретируемый вычислительной системой вид и обратного преобразования элементов вида, интерпретируемого вычислительной системой, в элементы поля Р;
преобразования элементов поля Р в интерпретируемый вычислительной системой вид и обратного преобразования элементов вида, интерпретируемого вычислительной системой, в элементы поля Р;
 выполнения операций с преобразованными элементами поля Р, эквивалентных операциям сложения и умножения в поле Р;
выполнения операций с преобразованными элементами поля Р, эквивалентных операциям сложения и умножения в поле Р;
• задают натуральное число n;
• задают натуральное число k, k≤n;
• задают РСЛОС в конфигурации Фибоначчи, в котором
 входные и выходные элементы РСЛОС являются элементами поля Р;
входные и выходные элементы РСЛОС являются элементами поля Р;
 количество элементов вектора состояний РСЛОС равно n;
количество элементов вектора состояний РСЛОС равно n;
 линейная функция обратной связи РСЛОС ƒ : Pn → Р имеет вид
линейная функция обратной связи РСЛОС ƒ : Pn → Р имеет вид
ƒ(xn-1, xn-2, …, x0) = (cn-1 ⊗ xn-1) ⊕ (cn-2 ⊗ xn-2) ⊕…⊕ (c0 ⊗ x0),
где ci ∈ Р, i=0, 1, …, n-1, - константные элементы поля Р,
xi ∈ Р, i=0, 1, …, n-1;
причем
 при подаче на вход РСЛОС последовательности из n элементов
при подаче на вход РСЛОС последовательности из n элементов
а 0, а1, …, an-1, где ai ∈ Р, i=0, 1, …, n-1,
начальное состояние РСЛОС, представляющее собой вектор длины n:
(qn-1, qn-2, …, q0), где qi ∈ P, i=0, 1, …, n-1,
формируется в виде:
qi=ai, i=0, 1, …, n-1;
 в результате выполнения s-го такта работы РСЛОС, s≥1:
в результате выполнения s-го такта работы РСЛОС, s≥1:
 новым состоянием РСЛОС становится вектор длины n:
новым состоянием РСЛОС становится вектор длины n:
(qn+s-1, qn+s-2, …, qs),
где qn+s-1=ƒ(qn+s-2, qn+s-3, …, qs-1)∈Р,
 выходным элементом РСЛОС становится элемент
выходным элементом РСЛОС становится элемент
bs-1=qs-1 ∈ P;
• задают входную последовательность РСЛОС, состоящую из n элементов поля Р:
а'0, а'1, a'n-1, где а'i ∈ Р, i=0, 1, …, n-1;
• задают количество тактов работы РСЛОС - m, где m≥1, m=kν+w, где ν, w - целые неотрицательные числа, 0 ≤ w ≤ k-1;
• осуществляют m тактов работы РСЛОС, выполняя следующие действия
 формируют начальное состояние РСЛОС, представляющее собой вектор длины n:
формируют начальное состояние РСЛОС, представляющее собой вектор длины n:
(q'n-1, q'n-2, …, q's), где q'i ∈ P, i=0, 1, …, n-1,
в виде:
q'i=а'i, i=0, 1, …, n-1;
 вычисляют j=0;
вычисляют j=0;
 если ν=0, то переходят к этапу (В);
если ν=0, то переходят к этапу (В);
 (А) вычисляют с использованием SIMD-инструкций процессора параллельно k элементов un+jk, un+jk+1, …, un+jk+k-1 ∈ P:
(А) вычисляют с использованием SIMD-инструкций процессора параллельно k элементов un+jk, un+jk+1, …, un+jk+k-1 ∈ P:
un+jk+t=ƒ(θ, θ, …, θ, q'n+jk-1, q'n+jk-2, …, q'jk+t), t=0, 1, …, k-1;
 вычисляют с использованием SIMD-инструкций процессора параллельно k элементов q'n+jk, q'n+jk+1, …, q'n+jk+k-1 ∈ P:
вычисляют с использованием SIMD-инструкций процессора параллельно k элементов q'n+jk, q'n+jk+1, …, q'n+jk+k-1 ∈ P:
q'n+jk+t=g(θ, θ, …, θ, u'n+jk, un+jk+1, …, u'n+jk+t), t=0, 1, …, k-1;
где функция g : Pk → Р имеет вид
g(xk-1, xk-2, …, x0) = (dk-1 ⊗ xk-1) ⊕ (dk-2 ⊗ xk-2) ⊕…⊕ (d0 ⊗ x0),
где di ∈ Р, i=0, 1, …, k-1, - константные элементы поля Р, для которых справедливо соотношение
di=Fn-1+i (е, θ, θ, …, θ), i=0, 1, …, k-1,
где функции Fi : Pn → Р, i=0, 1, …, имеют вид
Fi(xn-1, xn-2, …, x0)=xi, i=0, 1, …, n-1;
Fi((xn-1, xn-2, …, x0)=Fi-1(ƒ(xn-1, xn-2, …, x0), xn-1, xn-2, …, x1), i=n, n+1, …;
 формируют новое состояние РСЛОС, представляющее собой вектор длины n:
формируют новое состояние РСЛОС, представляющее собой вектор длины n:
(q'n+jk+k-1,q'n+jk+k-2, …, q'n+jk, q'n+jk+-1, …, q' jk+k);
 вычисляют k элементов выходной последовательности РСЛОС
вычисляют k элементов выходной последовательности РСЛОС
b'jk, b'jk+1, …, b'jk+k-1 ∈ P:
b'i=q'i, i=jk, jk+1, …, jk+k-1;
 вычисляют j=j+1;
вычисляют j=j+1;
 если j<ν, то переходят к этапу (A);
если j<ν, то переходят к этапу (A);
 если w=0, то переходят к этапу (С);
если w=0, то переходят к этапу (С);
 (В) вычисляют с использованием SIMD-инструкций процессора параллельно w элементов un+jk, un+jk+1, …, un+jk+w-1 ∈ Р:
(В) вычисляют с использованием SIMD-инструкций процессора параллельно w элементов un+jk, un+jk+1, …, un+jk+w-1 ∈ Р:
un+jk+t=ƒ(θ, θ, …, θ, q'n+jk-1, q'n+jk-2, …, q'jk+t), t=0, 1, …, w-1;
 вычисляют с использованием SIMD-инструкций процессора параллельно w элементов q'n+jk, q'n+jk+1, …, q'n+jk+w-1 ∈ Р:
вычисляют с использованием SIMD-инструкций процессора параллельно w элементов q'n+jk, q'n+jk+1, …, q'n+jk+w-1 ∈ Р:
q'n+jk+t=g(θ, θ, …, θ, un+jk, un+jk+1, …, un+jk+t), t=0, 1, …, w-1;
 формируют новое состояние РСЛОС, представляющее собой вектор длины n:
формируют новое состояние РСЛОС, представляющее собой вектор длины n:
(q'n+jk+w-1, q'n+jk+w-2, …, q'n+jk, q'n+jk-1, …, q'jk+w);
 вычисляют w элементов выходной последовательности РСЛОС
вычисляют w элементов выходной последовательности РСЛОС
b'jk, b'jk+1, …, b'jk+w-1 ∈ P:
b'i=q'i, i=jk, jk+1, …, jk+w-1;
• (С) получают выходную последовательность РСЛОС за m тактов работы:
b'0, b'1, …, b'm-1 ∈ Р.
Результат достигается за счет изменения хода вычисления элементов состояния РСЛОС с целью организации возможности их параллельного вычисления.
Рассмотрим вопросы корректности предлагаемого способа. Заметим, что процедура формирования выходных элементов РСЛОС из элементов состояния РСЛОС в предлагаемом способе идентична соответствующей процедуре в способе, выбранном в качестве прототипа. Таким образом, для обоснования корректности предлагаемого способа достаточно показать, что для одной и той же входной последовательности РСЛОС справедливы равенства:
q'i=qi, i=0, 1, …, n+m-1,
где q'i - элементы состояния РСЛОС при использовании предлагаемого способа,
qi - элементы состояния РСЛОС при использовании способа, выбранного в качестве прототипа.
Используемые в предлагаемом способе функции Fi, i=0, 1, …, определяются через композицию функций из Ln и, следовательно, сами принадлежат Ln. Это значит, что для любых xj, yj, c ∈ Р, j=0, 1, …, n-1, справедливы следующие тождества:
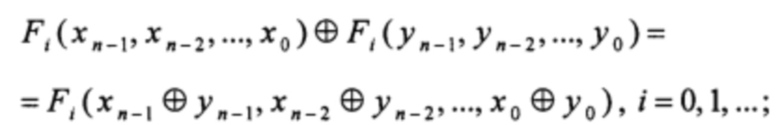
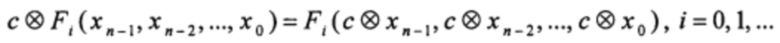
Кроме того, для любых qn+s-1, qn+s-2, …, qs ∈ P - элементов состояния РСЛОС при использовании способа, выбранного в качестве прототипа, и любых неотрицательных целочисленных значений s, i, таких что i+s ≤ n+m-1, выполняется:

Заметим, что процедура формирования начального состояния РСЛОС из входных элементов РСЛОС в предлагаемом способе идентична соответствующей процедуре в способе, выбранном в качестве прототипа. Отсюда следует, что для одной и той же входной последовательности РСЛОС справедливы равенства:
q'i=qi, i=0, 1, …, n-1.
Примем данный факт за базу индукции. Осуществим шаг индукции, показав, что если для некоторого j, 0 ≤ j< ν, выполняется
q'i=qi, i=0, 1, …, n+jk-1,
то справедливы равенства:
q'i=qi, i=n+jk, n+jk+1, n+jk+k-1.
Для этого заметим, что любого t=0, 1, …, k-1 выполняется:
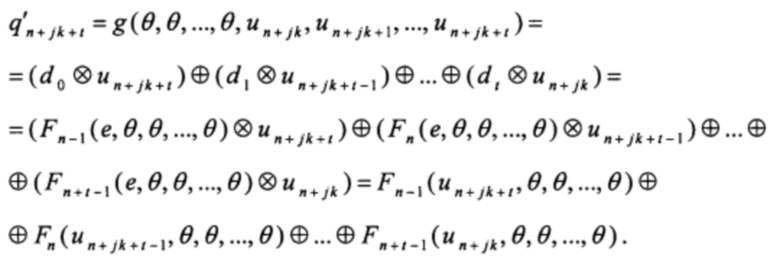
Первое слагаемое данной суммы можно представить в виде
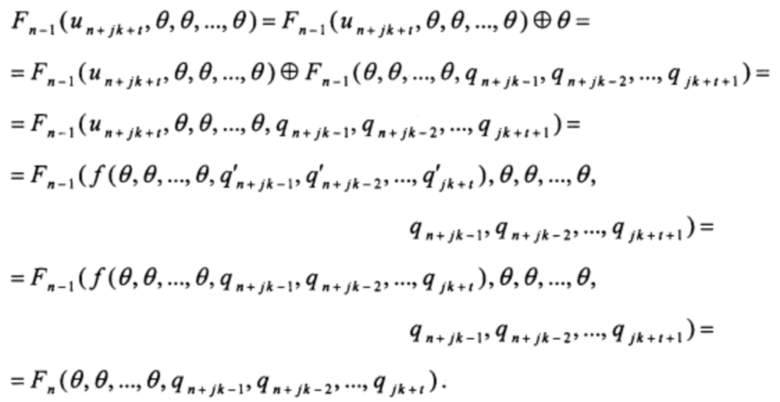
Прибавляя к полученному значению второе слагаемое, имеем
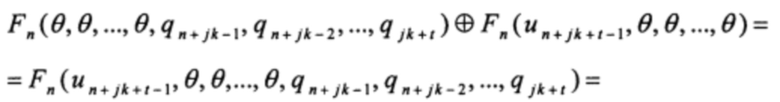
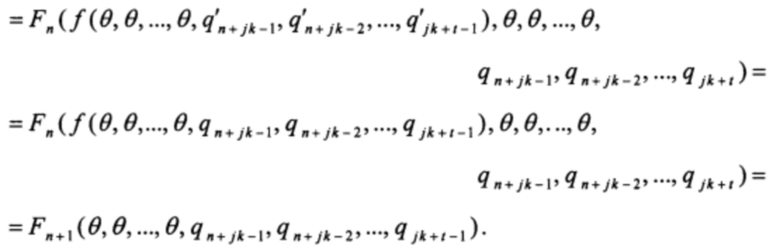
Прибавляя к полученному значению третье слагаемое, имеем
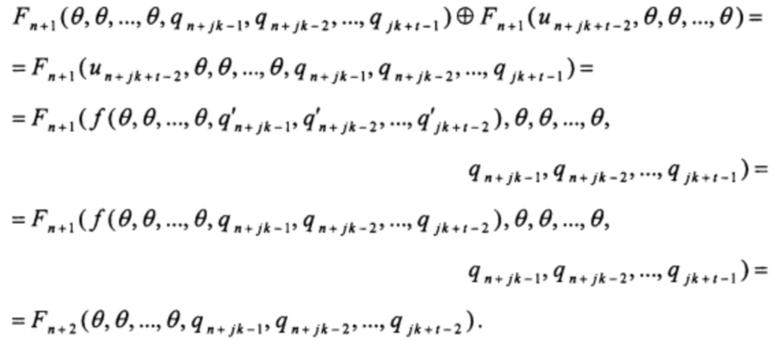
Действуя аналогичным образом, на этапе прибавления последнего слагаемого получаем:
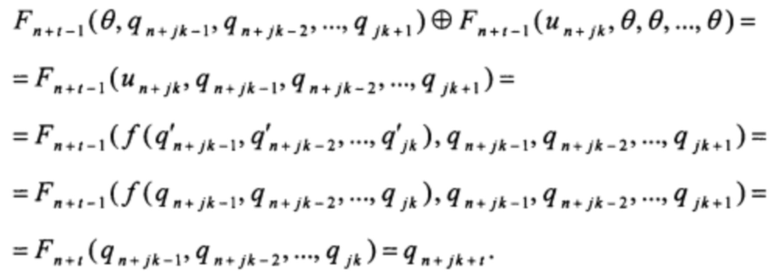
Таким образом, для любого t=0, 1, …, k-1:
q'n+jk+t=qn+jk+t,
то есть
q'i=qi, i=n+jk, n+jk+1, …, n+jk+k-1.
Последовательно осуществляя приведенный шаг индукции для всех j, 0 ≤ j ≤ ν, получаем, что
q'i=qi, i=0, 1, …, n+νk-1.
Обоснование равенства оставшихся w элементов состояния РСЛОС
q'i=qi, i=n+νk, n+ν+1, …, n+νk+w-1.
выполняется аналогично очередному шагу индукции с тем отличием, что вместо k элементов состояния рассматриваются w элементов состояния.
В результате имеем, что все элементы состояния, получающиеся в процессе работы РСЛОС при использовании предлагаемого способа, равны соответствующим элементам состояния, получающимся в процессе работы РСЛОС при использовании способа, выбранного в качестве прототипа. С учетом идентичности алгоритмов вычисления выходных значений из элементов состояния в рассматриваемых способах, это доказывает корректность предлагаемого способа работы РСЛОС.
Рассмотрим вопросы эффективности предлагаемого способа.
Выберем вычислительную систему, выполненную с возможностью для любой линейной функции h∈Ln и любых элементов xr,i ∈ P, r=0, 1, k-1,
i=0, 1, n-1, осуществлять параллельное вычисление k значений
h(x0, n-1, x0, n-2, …, x0, 0), h(x1, n-1, x1, n-2, …, x1, 0), …h(xk-1,n-1, xk-1, n-2, …, xk-1, 0),
где k - натуральное число.
Возможность параллельного вычисления k функций h подразумевает, что для любого р, 1 ≤ р ≤ k, время параллельного вычисления р функций h равно времени вычисления одной функции h. Обозначим это время через Т. Необходимо отметить, что описанная вычислительная система, в том числе, позволяет осуществлять параллельное вычисление k функций h* ∈ Ls, 1 ≤ s ≤ n-1, ввиду возможности представления функции h* как функции из Ln путем добавления n-s несущественных переменных.
Оценим время выполнения m последовательных тактов работы РСЛОС, m ≥ 1, на данной вычислительной системе в случае использования способа, выбранного в качестве прототипа, и в случае использования предлагаемого способа. При использовании способа, выбранного в качестве прототипа, данное время составит
Told=mT,
поскольку в этом случае выполнение каждого такта работы РСЛОС потребует одного вычисления функции ƒ.
При использовании предлагаемого способа рассмотрим три возможных варианта значений параметров:
• k=1;
• k ≥ 2, w=1;
• k ≥ 2, w≠1,
где m=kν+w.
При k=1 время выполнения m последовательных тактов работы РСЛОС составит
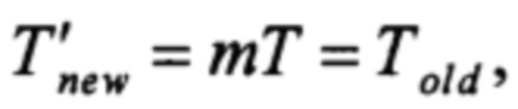
поскольку в этом случае для вычисления каждого нового элемента состояния РСЛОС согласно предлагаемому способу достаточно одного вычисления функции ƒ:
q'n+jk = g(θ, θ, …, θ, un+jk) = d0 ⊗ un+jk = un+jk = ƒ(q'n+jk-1, q'n+jk-2, …, q'jk),
так как d0=Fn-1(е, θ, θ, …, θ)=е.
При k ≥ 2, w=1 время выполнения m последовательных тактов работы РСЛОС составит:
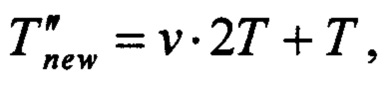
поскольку в этом случае для вычисления последнего элемента состояния РСЛОС согласно предлагаемому способу достаточно одного вычисления функции ƒ:
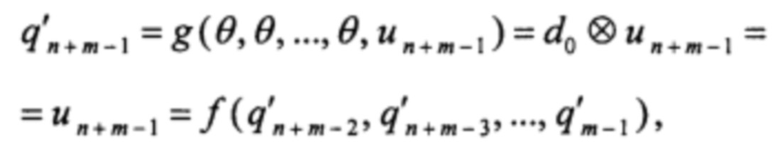
а для вычисления остальных элементов состояния потребуется вычисление функций ƒ и g на каждые k элементов. В результате, при k ≥ 2, w=1:
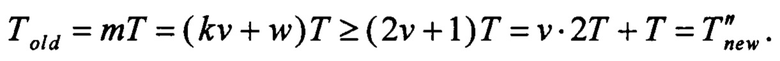
При k ≥ 2, w ≠ 1 время выполнения m последовательных тактов работы РСЛОС составит:
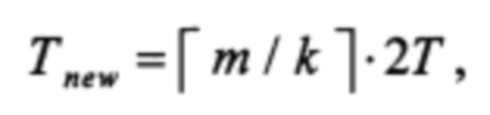
поскольку для вычисления каждых k элементов состояния (w элементов состояния на последнем шаге) потребуется вычисление функций ƒ и g. Причем, если w=0, то
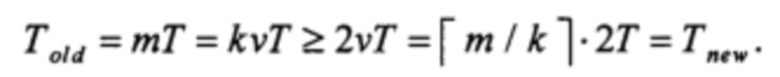
В случае же w ≥ 2, имеем
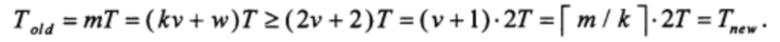
Таким образом, производительность предлагаемого способа больше или равна производительности способа, выбранного в качестве прототипа во всех трех рассмотренных случаях. Более того, при k ≥ 2 и достаточно больших значениях m предлагаемый способ позволяет увеличить производительность работы РСЛОС приблизительно в 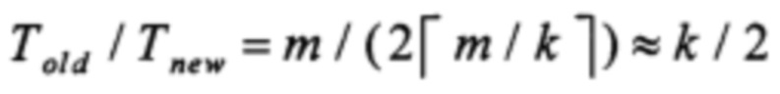 раз по сравнению со способом, выбранным в качестве прототипа.
раз по сравнению со способом, выбранным в качестве прототипа.
На практике весьма вероятна ситуация, при которой вычисление линейной функции g, зависящей от k аргументов, k ≤ n, может оказаться быстрее вычисления линейной функции ƒ, зависящей от n аргументов. В этом случае разница в производительности способов лишь увеличится.
Обозначим время вычисления функции от k переменных через Tk, а время вычисления функции от n переменных через Tn, Tk ≤ Tn.
Рассмотрим в данных обозначениях третий вариант значений параметров: k ≥ 2, w ≠ 1, как наиболее общий из всех. В этом случае время выполнения m последовательных тактов работы РСЛОС, m ≥ 1,
• при использовании способа, выбранного в качестве прототипа, составит
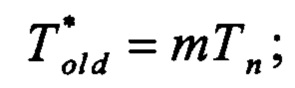
• при использовании предлагаемого способа составит:
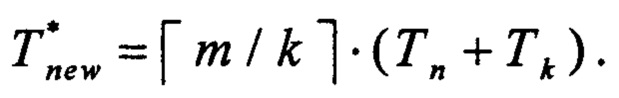
Таким образом, при k ≥ 2 и достаточно больших значениях m производительность предлагаемого способа превысит производительность способа, выбранного в качестве прототипа, приблизительно в
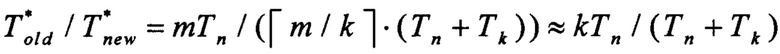 раз.
раз.
Сделаем еще одно практическое предположение о том, что Tk/Tn=k/n. Тогда отношение производительностей способов примет следующий вид:
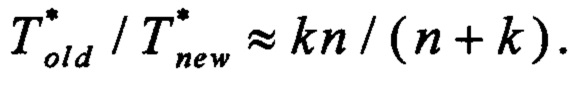
Рассмотрим несколько вариантов значений k и соответствующих значений отношения производительности способов:
• при k ≤ n:
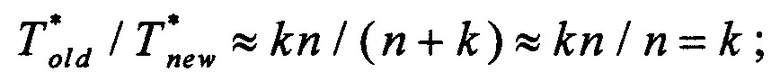
• при k=n/t, где t - натуральное число:
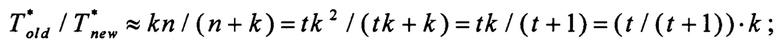
• при k=n:
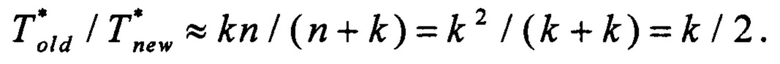
В рамках сделанных предположений, производительность предлагаемого способа превысит производительность способа, выбранного в качестве прототипа, в приблизительно от k/2 до k раз. При этом эффективность повышения производительности будет определяться тем, насколько близко значение k к значению n:
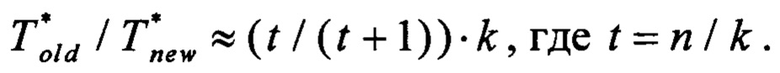
Осуществление изобретения
Рассмотрим пример реализации предлагаемого способа.
Предлагаемый способ может быть реализован в виде прикладной программы, предназначенной для выполнения на вычислительной системе. В качестве вычислительной системы может использоваться компьютер с процессором, поддерживающим SIMD-вычисления, например, процессор Intel Core i7-2600 с поддержкой SSE-инструкций (Streaming SIMD Extensions) [статья по адресу: https://ark.intel.com/content/www/ru/ru/ark/products/52213/intel-core-i7-2600-processor-8m-cache-up-to-3-80-ghz.html].
Прикладная программа, реализующая работу РСЛОС в конфигурации Фибоначчи согласно предлагаемому способу, может быть составлена специалистом по программированию (программистом).
Рассмотрим поле Р с операциями умножения ⊗ и сложения ⊕, состоящее из 16 элементов и заданное над неприводимым многочленом Х4 ⊕ Х ⊕ 1, X ∈ {0, 1}: Р = GF(24) = GF(2)[X] / (X4 ⊕ X ⊕ 1). Для удобства записи будем обозначать элементы поля Р целыми числами, предполагая, что элементу поля (z3 ⊗ X3) ⊕ (z2 ⊗ X2) ⊕ (z1 ⊗ X) ⊕ z0 ∈ Р, zi ∈ {0, 1}, i=0, 1, 2, 3, соответствует целое число z3 ⋅23+z2 ⋅22+z1 ⋅2+z0 ∈ Z.
Для возможности представления элементов поля Р в виде, интерпретируемом вычислительной системой, можно использовать взаимно однозначное преобразование элементов поля в двоичные строки, которое сопоставляет элементу поля (z3 ⊗ X3) ⊕ (z2 ⊗ X2) ⊕ (z1 ⊗ X) ⊕ z0 ∈ Р, zi ∈{0, 1}, i=0, 1, 2, 3, двоичную строку 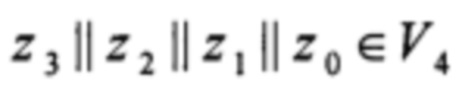 , где Vs - множество всех двоичных строк длины s,
, где Vs - множество всех двоичных строк длины s, 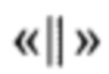 - операция конкатенации двоичных строк.
- операция конкатенации двоичных строк.
Для реализации на вычислительной системе операции сложения в поле Р можно использовать SSE-инструкцию «pxor», предназначенную для выполнения побитовой операции «исключающее ИЛИ» двух двоичных строк длиной 128. Для реализации на вычислительной системе операции умножения в поле Р можно использовать, например, классический алгоритм умножения в столбик без переноса значимого бита с последующим приведением результата умножения по модулю поля X4 ⊕ X ⊕ 1, или алгоритм, основанный на табличном задании результатов умножения и осуществлении поиска по этим таблицам. В первом случае можно использовать SSE-инструкции «pxor», «pand», предназначенные для выполнения побитовых операций «исключающее ИЛИ», «И» двух двоичных строк длиной 128, и SSE-инструкции «psrlw», «psllw», предназначенные для выполнения битовых сдвигов двоичных строк длиной 128 вправо и влево. Во втором случае можно использовать SSE-инструкцию «pshufb», предназначенную для осуществления поиска по заранее вычисленным таблицам.
Зададим значения параметров n=8 и k=4.
Вычисление значения h(x7, x6, …, x0), где h ∈ L8 - произвольная линейная функция вида:
h(x7, x6, …, x0) = (h7 ⊗ x7) ⊕ (h6 ⊗ x6) ⊕ … ⊕ (h0 ⊗ x0),
hi, xi ∈ Р, i=0, 1, …, 7,
на вычислительной системе можно осуществлять с использованием упомянутых выше реализаций операций сложения и умножения в поле Р посредством SSE-инструкций. Параллельное вычисление четырех значений h(x0, 7, x0, 6, …, x0, 0), h(x1, 7, x1, 6, …, x1, 0), …, h(х3, 7, х3, 6, …, х3, 0), где xr, i ∈ P, r=0, 1, 2, 3, i=0, 1, …, 7, на вычислительной системе можно осуществлять аналогично вычислению одного значения h(x7, x6, …, x0) с предварительной группировкой элементов x0, i, x1, i, x2, i, x3, i на одном 128-битном SSE-регистре с целью одновременного выполнения операций, требуемых при вычислении функции h, сразу для четырех этих элементов.
Рассмотрим РСЛОС в конфигурации Фибоначчи, входные и выходные элементы которого принадлежат конечному полю Р, а линейная функция обратной связи ƒ:Р8 →Р задается в виде
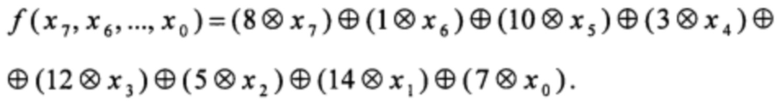
Заданные РСЛОС и значение k однозначно определяют функцию g:Р4 →Р:
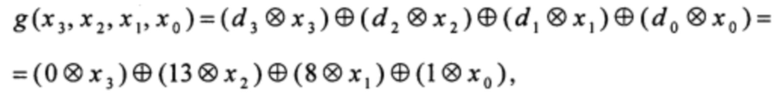
где элементы di ∈ P, i=0, 1, …, 3, вычисляются следующим образом
d0 = F7(1, 0, 0, …, 0) = 1,
d1 = F8(1, 0, 0, …, 0) = F7(ƒ(1, 0, 0, …, 0), 1, 0, 0, 0) = ƒ(1, 0, 0, …, 0) = 8 ⊗ 1 = 8,
d2 = F9(1, 0, 0, …, 0) = F8(ƒ(1, 0, 0, …, 0), 1, 0, 0, …, 0) = F8(8, 1, 0, 0, …, 0) = F7(ƒ(8, 1, 0, 0, …, 0), 8, 1, 0, 0, …, 0) = ƒ(8, 1, 0, 0, …, 0) = (8 ⊗ 8) ⊕ (1 ⊗ 1) = 12 ⊕ 1 = 13,
d3 = F10(1, 0, 0, …, 0) = F9(ƒ(1, 0, 0, …, 0), 1, 0, 0, …, 0) = F9(8, 1, 0, 0, …, 0) = F8(ƒ(8, 1, 0, 0, …, 0), 8, 1, 0, 0, …, 0) = F8 (13, 8, 1, 0, 0, …, 0) = = F7 (ƒ(13, 8, 1, 0, 0…, 0), 13, 8, 1, 0, 0, …, 0) = ƒ(13, 8, 1, 0, 0, …, 0) = (8 ⊗ 13) ⊕ (1 ⊗ 8) ⊕ (10 ⊗ 1) = 2 ⊕ 8 ⊕ 10 = 0.
Зададим входную последовательность РСЛОС, состоящую из 8 элементов а'0, а'1, …, а'7, где а'i ∈ Р, i=0, 1, …, 7:
а'0=0, а'1=2, a'2=4, a'3=6,
а'4=9, а'5=11, а'6=13, а'7=15.
Зададим количество тактов работы РСЛОС m=11. Тогда m=kν+w=4⋅2+3, то есть ν=2, w=3.
Осуществим 11 тактов работы РСЛОС, для чего выполним следующие действия:
• сформируем начальное состояние РСЛОС, представляющее собой вектор длины 8:
(q'7, q'6, …, q'0), где q'i ∈ Р, i=0, 1, …, 7,
в виде
(q'7, q'6, …, q'0) = (а'7, а'6, …, а'0) = (15, 13, 11, 9, 6, 4, 2, 0);
• вычислим j=0; поскольку ν=2 ≠ 0, то
 вычислим с помощью SIMD-инструкций параллельно 4 элемента
вычислим с помощью SIMD-инструкций параллельно 4 элемента
u8, u9, u11, ∈ P:
u8 = ƒ(q'7, q'6, …, q'0) = ƒ(15, 13, 11, 9, 6, 4, 2, 0) = 0,
u9 = ƒ(0, q'7, q'6, …, q'1) = ƒ(0, 15, 13, 11, 9, 6, 4, 2) = 2,
u10 = ƒ(0, 0, q'7, q'6, …, q'2) = ƒ(0, 0, 15, 13, 11, 9, 6, 4) = 3,
u11 = ƒ(0, 0, 0, q'7, q'6, …, q'0) = ƒ(0, 0, 0, 15, 13, 11, 9, 6) = 6;
 вычислим с помощью SIMD-инструкций параллельно 4 элемента
вычислим с помощью SIMD-инструкций параллельно 4 элемента
q'8, q'9, q'10, q'11, ∈ P
q'8 = g(0, 0, 0, u8) = g(0, 0, 0, 0) = 0,
q'9 = g(0, 0, u8, u9) = g(0, 0, 0, 2) = 2,
q'10 = g(0, u8, u9, u10) = g(0, 0, 2, 3) = 0,
q'11 = g(u8, u9, u10, u11) = g(0, 2, 3, 6) = 4;
 сформируем новое состояние РСЛОС, представляющее собой вектор длины 8:
сформируем новое состояние РСЛОС, представляющее собой вектор длины 8:
(q'11, q'10, …, q'8, q'7, q'4) = (4, 0, 2, 0, 15, 13, 11, 9);
 вычислим 4 выходных элемента РСЛОС b'0, b'1, b'2, b'3 ∈ P:
вычислим 4 выходных элемента РСЛОС b'0, b'1, b'2, b'3 ∈ P:
b'0=q'0=0, b'1=q'1=2, b'2=q'2=4, b'3=q'3=6;
• вычислим j=j+1=1; поскольку j=1<2=ν, то
 вычислим с помощью SSE-инструкций параллельно 4 элемента
вычислим с помощью SSE-инструкций параллельно 4 элемента
u12, u13, u14, u15 ∈ P:
u12 = ƒ(q'11, q'10, …, q'4) = ƒ(4, 0, 2, 0, 15, 13, 11, 9) = 7,
u13 = ƒ(0, q'11, q'10, …, q'5) = ƒ(0, 4, 0, 2, 0, 15, 13, 11) = 10,
u11 = ƒ(0, 0, q'11, q'10, …, q'6) = ƒ(0, 0, 4, 0, 2, 0, 15, 13) = 5,
u15 = ƒ(0 , 0, 0, q'11, q'10, …, q'7) = ƒ(0, 0, 0, 4, 0, 2, 0, 15) = 13;
 вычислим с помощью SSE-инструкций параллельно 4 элемента
вычислим с помощью SSE-инструкций параллельно 4 элемента
q'12, q'13, q'14, q'15, ∈ P
q'12 = g(0, 0, 0, u12) = g(0, 0, 0, 7) = 7,
q'13 = g(0, 0, u12, u13) = g(0, 0, 7, 10) = 7,
q'14 = g(0, u12, u13, u14) = g(0, 7, 10, 5) = 15,
q'15 = g(u12, u13, u14, u15) = g(7, 10, 5, 13) = 8;
 сформируем новое состояние РСЛОС, представляющее собой вектор длины 8:
сформируем новое состояние РСЛОС, представляющее собой вектор длины 8:
(q'15, q'14, …, q'12, q'11, …, q'8) = (8, 15, 7, 7, 4, 0, 2, 0);
 вычислим 4 выходных элемента РСЛОС b'4, b'5, b'6, b'7 ∈ P:
вычислим 4 выходных элемента РСЛОС b'4, b'5, b'6, b'7 ∈ P:
b'4=q'4=9, b'5=q'5=11, b'6=q'6=13, b'7=q'7=15;
• вычислим j=j+1=2; поскольку j=2 ≥ 2=ν, то проверим равенство w=0; поскольку w=3 ≠ 0, то
 вычислим с помощью SSE-инструкций параллельно 3 элемента
вычислим с помощью SSE-инструкций параллельно 3 элемента
u16, u17, u18 ∈ P:
u16 = ƒ(q'15, q'14, …, q'8) = ƒ(8, 15, 7, 7, 4, 0, 2, 0) = 3,
u17 = ƒ(0, q'15, q'14, …, q'9) = ƒ(0, 8, 15, 7, 7, 4, 0, 2) = 6,
u18 = ƒ(0, 0, q'15, q'14, …, q'10) = ƒ(0, 0, 8, 15, 7, 7, 4, 0) = 10;
 вычислим с помощью SSE-инструкций параллельно 3 элемента
вычислим с помощью SSE-инструкций параллельно 3 элемента
q'126 q'17, q'18, ∈ P
q'16 = g(0, 0, 0, u16) = g(0, 0, 0, 3) = 3,
q'17 = g(0, 0, u16, u17) = g(0, 0, 3, 6) = 13,
q'18 = g(0, u16, u17, u18) = g(0, 3, 6, 10) = 11;
 сформируем новое состояние РСЛОС, представляющее собой вектор длины 8:
сформируем новое состояние РСЛОС, представляющее собой вектор длины 8:
(q'18, q'17, q'16, q'15, …, q'11)=(11, 13, 3, 8, 15, 7, 7, 4);
 вычислим 3 выходных элемента РСЛОС b'8, b'9, b'10 ∈ Р:
вычислим 3 выходных элемента РСЛОС b'8, b'9, b'10 ∈ Р:
b'8=q'8=0, b'9=q'9=2, b'10=q'10=0.
В результате получим выходную последовательность РСЛОС за 11 тактов работы b'0, b'1, …, b'10 ∈Р : 0, 2, 4, 6, 9, 11, 13, 15, 0, 2, 0.
Практическое измерение производительности работы рассмотренного РСЛОС, выполненное при больших значениях m (m≈107) в одном потоке одного ядра процессора Intel Core i7-2600, показало, что
• в случае осуществления работы РСЛОС согласно способу, выбранному в качестве прототипа, производительность работы РСЛОС составляет порядка 85⋅106 тактов работы РСЛОС в секунду;
• в случае осуществления работы РСЛОС согласно предлагаемому способу, производительность работы РСЛОС составляет порядка 185⋅106 тактов работы РСЛОС в секунду.
Таким образом, производительностей способов отличается приблизительно в 2,18 раз, что соответствует приведенным теоретическим оценкам, согласно которым предлагаемый способ позволяет увеличить производительность работы РСЛОС в приблизительно от k/2 до k раз.
Рассмотренный РСЛОС и используемые значения параметров выбраны для наглядной демонстрации работы предлагаемого способа. Следует отметить, что предлагаемый способ может быть по аналогии осуществлен и при реализации других РСЛОС в конфигурации Фибоначчи, в том числе РСЛОС, используемых на практике, например, при выработке псевдослучайных последовательностей, вычислении линейных отображений или получении множества различных значений определенной длины.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ (ВАРИАНТЫ) | 2015 |
|
RU2598781C1 |
| Способ защиты информации в облачных вычислениях с использованием гомоморфного шифрования | 2017 |
|
RU2691874C2 |
| СПОСОБ ДЛЯ ГЕНЕРИРОВАНИЯ ПСЕВДОСЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ И СПОСОБ ДЛЯ КОДИРОВАНИЯ ИЛИ ДЕКОДИРОВАНИЯ ПОТОКА ДАННЫХ | 2013 |
|
RU2609098C2 |
| СПОСОБ И УСТРОЙСТВО СОГЛАСОВАНИЯ СКОРОСТИ ПОЛЯРНОГО КОДА И УСТРОЙСТВО БЕСПРОВОДНОЙ СВЯЗИ | 2014 |
|
RU2663351C1 |
| Устройство для полиномиального разложения логических функций | 1988 |
|
SU1559335A1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ДИСКРЕТНЫХ ПОЛИНОМИАЛЬНЫХ ПРЕОБРАЗОВАНИЙ | 2012 |
|
RU2517694C1 |
| Устройство для вычисления булевых дифференциалов | 1989 |
|
SU1777132A1 |
| СПОСОБ ПУСКА РАКЕТ ДЛЯ ПОДВИЖНЫХ ПУСКОВЫХ УСТАНОВОК | 2012 |
|
RU2504725C2 |
| СПОСОБ МОДЕЛИРОВАНИЯ ГАРМОНИЧЕСКИХ ОДНОМЕРНЫХ АКУСТИЧЕСКИХ ПОЛЕЙ В ПРОТЯЖЕННОЙ УЗКОЙ ЗАМКНУТОЙ ГИДРОКАМЕРЕ | 2005 |
|
RU2297734C1 |
| Способ шифрования данных | 2018 |
|
RU2710669C1 |
Изобретение относится к области вычислительной техники. Технический результат заключается в повышении производительности работы РСЛОС типа Фибоначчи при использовании вычислительной системы, позволяющей параллельно вычислять k одинаковых линейных функций от разных аргументов. Технический результат достигается за счет способа работы регистра сдвига с линейной обратной связью (РСЛОС) в вычислительной системе, включающего задание конечного поля Р с операцией сложения ⊕, операцией умножения ⊗, нулевым элементом θ и единичным элементом е; выбор вычислительной системы, имеющей процессор с SIMD-архитектурой, задание натурального числа n; задание натурального числа k, k ≤ n; задания РСЛОС в конфигурации Фибоначчи, задания количества тактов работы РСЛОС - m, где m ≥ 1, m=kν+w, где ν, w - целые неотрицательные числа, 0 ≤ w ≤ k-1; осуществление m тактов работы РСЛОС.
Способ работы регистра сдвига с линейной обратной связью (РСЛОС) в вычислительной системе, заключающийся в том, что
• задают конечное поле Р с операцией сложения ⊕, операцией умножения ⊗, нулевым элементом θ и единичным элементом е;
• выбирают вычислительную систему, имеющую процессор с SIMD-архитектурой и выполненную с возможностью
 преобразования элементов поля Р в интерпретируемый вычислительной системой вид и обратного преобразования элементов вида, интерпретируемого вычислительной системой, в элементы поля Р;
преобразования элементов поля Р в интерпретируемый вычислительной системой вид и обратного преобразования элементов вида, интерпретируемого вычислительной системой, в элементы поля Р;
 выполнения операций с преобразованными элементами поля Р, эквивалентных операциям сложения и умножения в поле Р;
выполнения операций с преобразованными элементами поля Р, эквивалентных операциям сложения и умножения в поле Р;
• задают натуральное число n;
• задают натуральное число k, k ≤ n;
• задают РСЛОС в конфигурации Фибоначчи, в котором
 входные и выходные элементы РСЛОС являются элементами поля Р;
входные и выходные элементы РСЛОС являются элементами поля Р;
 количество элементов вектора состояний РСЛОС равно n;
количество элементов вектора состояний РСЛОС равно n;
 линейная функция обратной связи РСЛОС ƒ : Pn → Р имеет вид
линейная функция обратной связи РСЛОС ƒ : Pn → Р имеет вид
ƒ(xn-1, xn-2, …, х0) = (cn-1 ⊗ xn-1) ⊕ (cn-2 ⊗ xn-2) ⊕…⊕ (c0 ⊗ x0),
где ci ∈ P, i=0, 1, …, n-1, - константные элементы поля Р,
xi ∈ P, i=0, 1 …, n-1;
причем
 при подаче на вход РСЛОС последовательности из n элементов
при подаче на вход РСЛОС последовательности из n элементов
a 0, a1, …, an-1, где ai ∈ P, i=0, 1, …, n-1,
начальное состояние РСЛОС, представляющее собой вектор длины n:
(qn-1, qn-2, …, q0), где qi ∈ Р, i=0, 1, …, n-1,
формируется в виде:
qi=ai, i=0, 1, …, n-1;
 в результате выполнения s-го такта работы РСЛОС, s≥1:
в результате выполнения s-го такта работы РСЛОС, s≥1:
 новым состоянием РСЛОС становится вектор длины n:
новым состоянием РСЛОС становится вектор длины n:
(qn+s-1, qn+s-2, …, qs),
где qn+s-1=ƒ(qn+s-2, qn+s-3, …, qs-1)∈P,
 выходным элементом РСЛОС становится элемент
выходным элементом РСЛОС становится элемент
bs-1=qs-1 ∈ P;
• задают входную последовательность РСЛОС, состоящую из n элементов поля Р:
а'0, а'1, …, a'n-1, где а'i ∈Р, i=0, 1, …, n-1;
• задают количество тактов работы РСЛОС - m, где m ≥ 1, m=kν+w, где ν, w - целые неотрицательные числа, 0 ≤ w ≤ k-1;
• осуществляют m тактов работы РСЛОС, выполняя следующие действия:
 формируют начальное состояние РСЛОС, представляющее собой вектор длины n:
формируют начальное состояние РСЛОС, представляющее собой вектор длины n:
(q'n-1, q'n-2, …, q'0), где q'i ∈ P, i=0, 1, …, n-1,
в виде:
q'i=а'i, i=0, 1, …, n-1;
 вычисляют j=0;
вычисляют j=0;
 если ν=0, то переходят к этапу (В);
если ν=0, то переходят к этапу (В);
 (А) вычисляют с использованием SIMD-инструкций процессора параллельно k элементов un+jk, un+jk+1, …, un+jk+k-1 ∈ P:
(А) вычисляют с использованием SIMD-инструкций процессора параллельно k элементов un+jk, un+jk+1, …, un+jk+k-1 ∈ P:
un+jk+t=ƒ(θ, θ, …, θ, q'n+jk-1, q'n+jk-2, …, q'jk+t), t=0, 1, …, k-1;
 вычисляют с использованием SIMD-инструкций процессора параллельно k элементов q'n+jk, q'n+jk+1, …, q'n+jk+k-1 ∈ P:
вычисляют с использованием SIMD-инструкций процессора параллельно k элементов q'n+jk, q'n+jk+1, …, q'n+jk+k-1 ∈ P:
q'n+jk+t=g(θ, θ, …, θ, un+jk, un+jk+1, …, un+jk+t), t=0, 1, …, k-1,
где функция g : Pk → Р имеет вид
g(xk-1, xk-2, …, x0) = (dk-1 ⊗ xk-1) ⊕ (dk-2 ⊗ xk-2) ⊕…⊕ (d0 ⊗ x0),
где di ∈ P, i=0, 1, …, k-1, - константные элементы поля Р, для которых справедливо соотношение
di=Fn-1+i (е, θ, θ, …, θ), i=0, 1, …, k-1,
где функции Fi : Pn → Р, i=0, 1, …, имеют вид
Fi(xn-1, xn-2, …, x0)=xi, i=0, 1, …, n-1;
Fi(xn-1, xn-2, …, x0)=Fi-1(ƒ(xn-1, xn-2, …, x0), xn-1, xn-2, …, x1), i=n, n+1, …;
 формируют новое состояние РСЛОС, представляющее собой вектор длины n:
формируют новое состояние РСЛОС, представляющее собой вектор длины n:
(q'n+jk+k-1, q'n+jk+k-2, …, q'n+jk, q'n+jk-1, …, q'jk+k);
 вычисляют k элементов выходной последовательности РСЛОС
вычисляют k элементов выходной последовательности РСЛОС
b'jk, b'jk+1, …, b'jk+k-1 ∈ P:
b'i=q'i, i=jk, jk+1, …, jk+k-1;
 вычисляют j=j+1;
вычисляют j=j+1;
 если j<ν, то переходят к этапу (А);
если j<ν, то переходят к этапу (А);
 если w=0, то переходят к этапу (С);
если w=0, то переходят к этапу (С);
 (В) вычисляют с использованием SIMD-инструкций процессора параллельно w элементов un+jk, un+jk+1, …, un+jk+w-1 ∈ Р:
(В) вычисляют с использованием SIMD-инструкций процессора параллельно w элементов un+jk, un+jk+1, …, un+jk+w-1 ∈ Р:
un+jk+t=ƒ(θ, θ, …, θ, q'n+jk-1, q'n+jk-2,…, q'jk+t), t=0, 1, …, w-1;
 вычисляют с использованием SIMD-инструкций процессора параллельно w элементов q'n+jk, q'n+jk+1, …, q'n+jk+w-1 ∈ Р:
вычисляют с использованием SIMD-инструкций процессора параллельно w элементов q'n+jk, q'n+jk+1, …, q'n+jk+w-1 ∈ Р:
q'n+jk+t=g(θ, θ, …, θ, un+jk, un+jk+1, …, un+jk+t), t=0, 1, …, w-1;
 формируют новое состояние РСЛОС, представляющее собой вектор длины n:
формируют новое состояние РСЛОС, представляющее собой вектор длины n:
(q'n+jk+w-1, q'n+jk+w-2, …, q'n+jk, q'n+jk-1, …, q'jk+w);
 вычисляют w элементов выходной последовательности РСЛОС
вычисляют w элементов выходной последовательности РСЛОС
b'jk, b'jk+1, …, b'jk+w-1 ∈ P:
b'i=q'i, i=jk, jk+1, …, jk+w-1;
• (С) получают выходную последовательность РСЛОС за m тактов работы:
b'0, b'1, …, b'm-1 ∈ Р.
| СПОСОБ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ (ВАРИАНТЫ) | 2015 |
|
RU2598781C1 |
| РЕГИСТР СДВИГА | 2002 |
|
RU2219597C1 |
| US 9177666 B2, 03.11.2015 | |||
| US 7499519 B1, 03.03.2009 | |||
| Способ приготовления мыла | 1923 |
|
SU2004A1 |
Авторы
Даты
2020-07-10—Публикация
2020-02-20—Подача