Изобретение относится к технике преобразования электрических сигналов, в частности, к преобразованию цифровой информации в аналоговый сигнал.
Известны два основных способа цифроаналогового преобразования:
в одном из которых производят суммирование единичных эталонных сигналов, а в другом - суммирование эталонных сигналов, веса которых отличаются.
В первом способе при формировании выходного аналогового сигнала и при использовании двоичного кода управления используется только одна эталонная величина весом в один квант (см. [1. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. Пер. с нем. - М. Мир, 1982, - 512 с. стр. 444, рис. 24.1 и стр. 245 рис. 24.2]).
Во втором способе применяются эталонные сигналы с весами, зависящими от номера разряда, и в суммировании участвуют только те эталонные сигналы, для которых в соответствующем разряде входного кода имеется единица при использовании двоичного кода управления или значащая цифра, отличная от нуля при недвоичном коде управления, например, от 1 до 9 при декадном коде управления (см. [2. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. Пер. с нем. - М. Мир, 1982, - 512 с. стр. 446, рис. 24.3, стр. 446, рис. 24.5]).
В упомянутых цифроаналоговых преобразователях из опорного сигнала Y формируют эталонные величины, соответствующие значениям разрядов входного кода управления X, которые суммируют и образуют дискретные значения выходной аналоговой величины Z.
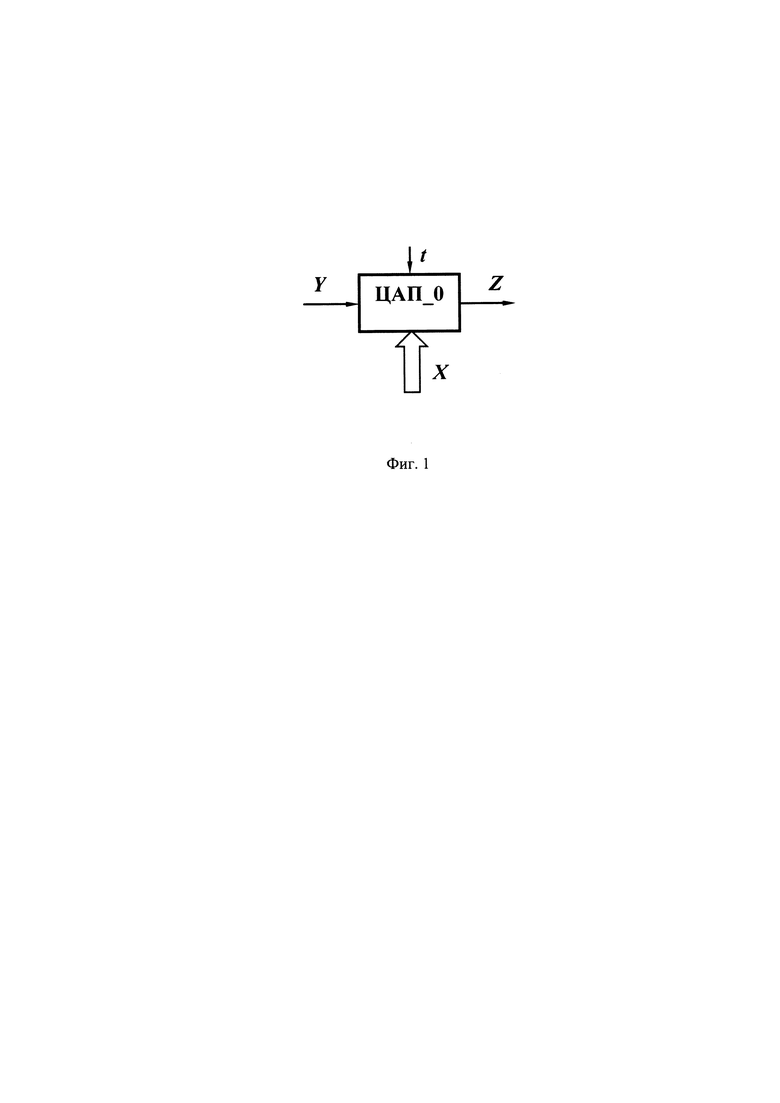
Принцип способа цифроаналогового преобразования можно представить в виде, показанном на фиг. 1
Рассмотрим параллельный цифро-аналоговый преобразователь (ЦАП), представленный на фиг. 1, который имеет вход единственного аналогового (опорного) сигнала Y - тока или напряжения, цифровые входы управления X, тактируемые во времени с интервалом t и выход аналогового сигнала Z - тока или напряжения, причем опорный Y и выходной Z сигналы могут быть как одинаковыми (ток или напряжение на входе и ток или напряжение на выходе), так и разными (напряжение или ток на входе - ток или напряжение на выходе).
Преобразование цифрового кода управления X в выходной аналоговый сигнал Z осуществляется за один или несколько тактов времени t, т.е. в предельном случае за один такт в аналоговую величину Z преобразуются все разряды управляющего слова X. Поэтому ЦАП_0, реализующий такой способ преобразования, называют параллельным.
Будем считать, что цифровой код управления позиционный, а система счисления с основанием а непринципиальна - она может быть двоичной (а=2), десятичной (а=10), шестнадцатеричной (а=16) или любой другой.
Например, цифровой двоичный код числа (слово) X, отнормированный к единице:
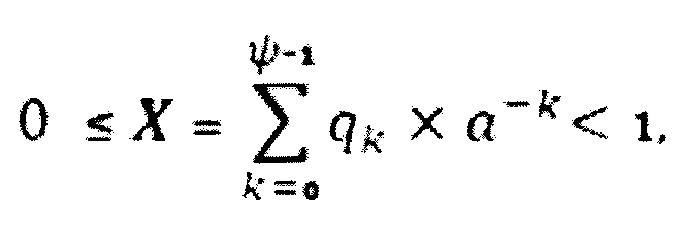
где a=2; qk ∈ [0,1]; ψ - число двоичных разрядов в слове X.
Для двоичного ЦАП выходной сигнал определяется следующим образом:
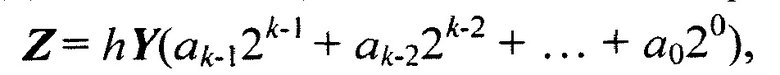
где Y - опорный (эталонный) сигнал; 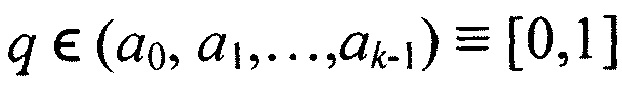 , - коэффициенты двоичных разрядов, принимающие значения «0» или «1»;
, - коэффициенты двоичных разрядов, принимающие значения «0» или «1»;
k=0, 1, … ψ-1 - номер двоичного разряда;
h - коэффициент пропорциональности.
В случае цифрового десятичного управляющего кода числа X, отнормированного к единице:
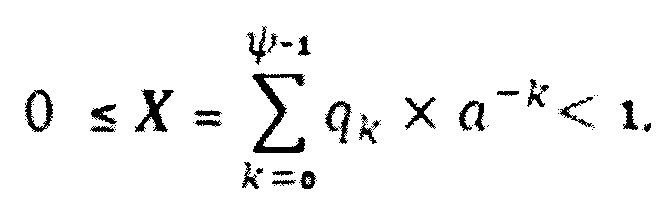
где а=10; qk ∈ [0, 1, …, 9]: ψ - число десятичных разрядов в слове X.
В цифроаналоговых преобразователях из опорного сигнала Y формируют эталонные сигналы, соответствующие значениям разрядов входного управляющего кода X, которые суммируют и образуют дискретные значения выходной аналоговой величины Z.
Внутреннее содержание ЦАП_0 и алгоритм его работы (внутреннего функционирования) для дальнейшего рассмотрения не имеет принципиального значения.
Аналоговый сигнал Z на выходе ЦАП_0 образуется из опорного аналогового сигнала Y на его входе с помощью управления ЦАП_0 цифровым кодом X длины ψ разрядов; при этом опорный сигнал Y - основа аналоговой мерной шкалы. Величина ступеньки (шага квантования) на выходе такого ЦАП_0 равна
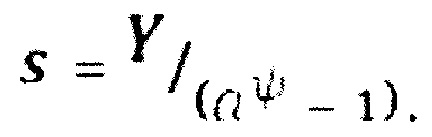
В этом случае Z=Y×X и имеет место "классическое" преобразование X ⇒ z, причем точность преобразования является линейной функцией точности элементарных электронных компонентов ЦАП_0 - резистивных (конденсаторных) матриц, ключей тока (напряжения) и т.д., т.е. определена технологией изготовления конкретной микросхемы ЦАП_0 и конечной точностью (разбросом) номинальных значений его внутренних элементов.
При рассмотренном преобразовании, как в первом, так и во втором способе возникают погрешности, вызванные изготовлением элементов ЦАП_0. Основными факторами погрешностей элементов являются:
технологический разброс параметров (точность изготовления);
влияние изменений окружающей среды (в основном температуры) - температурная стабильность;
изменение параметров во времени (старение);
воздействия внешних и внутренних шумов и помех.
Поэтому характеристики преобразования реальных ЦАП_0 отличаются от идеальных формой, значением ступеней и их расположением относительно осей координат.
Для увеличения точности преобразования можно усложнять внутреннюю структуру ЦАП_0, увеличивать точность и стабильность параметров используемых элементов, но только в пределах возможностей производства.
Указанные причины, а это, в конечном счете, технологические возможности производства, ограничивают максимально достижимую точность параллельного ЦАП_0, которая в настоящее время не превышает 20…22 двоичных разрядов (бит) кода управления X.
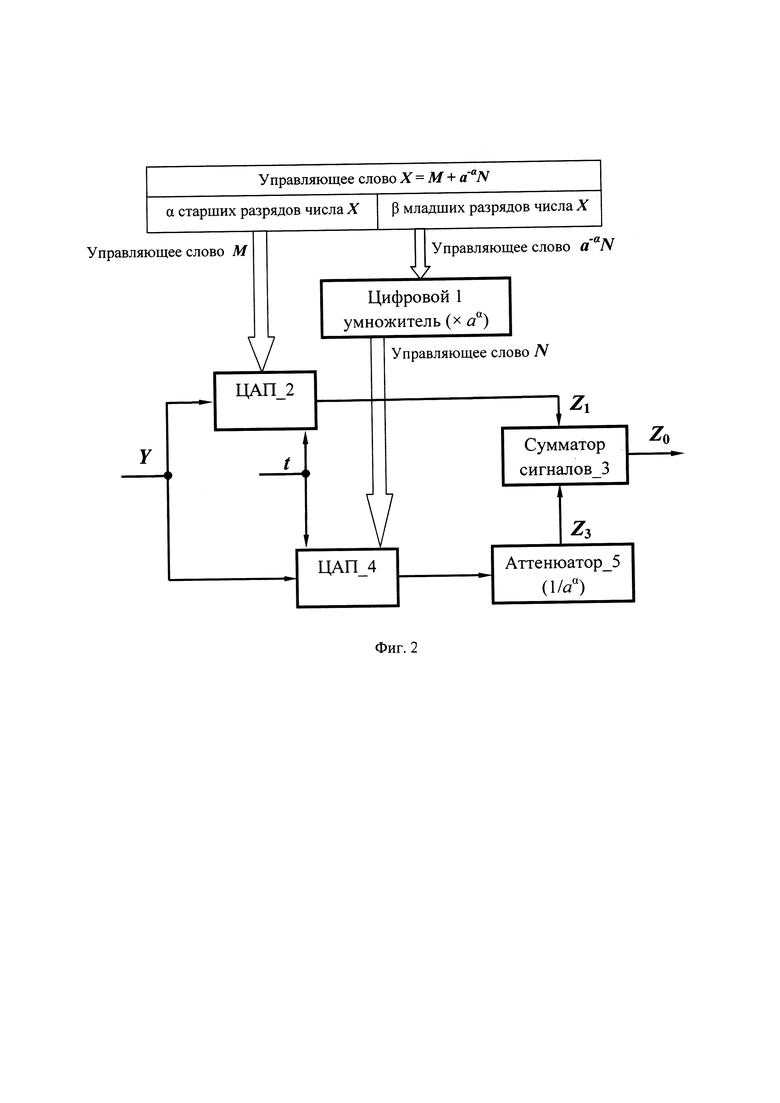
Известен способ цифроаналогового преобразования, пример реализации которого приведен на фиг. 2, при этом используется исходный ЦАП_0, показанный на фиг. 1 (см. [3. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. Пер. с нем., М. Мир, 1982. - 512 с. стр. 447, рис. 24.7]).
На фиг. 2 показаны: ЦАП_2, сумматор 3 сигналов, ЦАП_4, на соответствующие входы ЦАП_2 и ЦАП_4 подается опорный сигнал Y и тактирующий сигнал t, а на их входные шины поступают соответственно управляющие слова М длиной α разрядов и a-αN длиной β разрядов. Выход ЦАП_4 подключен ко входу аттенюатора 5, выход которого соединен с первым входом сумматора 3 сигналов, ко второму входу которого подключен выход ЦАП 2. На выходе сумматора 3 сигналов имеем результирующий аналоговый сигнал Z0.
В этом способе преобразования цифровое слово управления X=M+a-αN длины ψ разрядов делится на два слова управления М и a-αN (желательно половинной длины ψ/2, но не обязательно): ψ=α+β, где α - число старших разрядов кода управления X, а β - число младших разрядов кода управления X. Тактируются оба ЦАП в одни и те же моменты времени t.
При данном преобразовании, как и у предыдущих аналогов, используется единственный опорный сигнал (мерная шкала) Y.
Младшие a-αN разряды длины β кода управления X умножаются в цифровом 1 умножителе в аα раз, образуя управляющее слово N длины β разрядов.
Первый ЦАП_2 преобразует управляющее слово М длины α разрядов в аналоговый сигнал Z1, второй ЦАП_4 преобразует управляющее слово N длины β разрядов в аналоговый сигнал Z2.
Величина ступеньки (шага квантования) на выходе ЦАП_2 равна 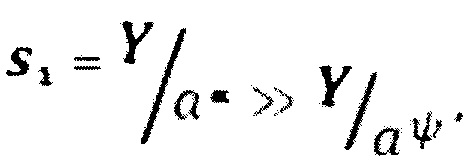 а величина ступеньки (шага квантования) на выходе ЦАП_4 равна
а величина ступеньки (шага квантования) на выходе ЦАП_4 равна 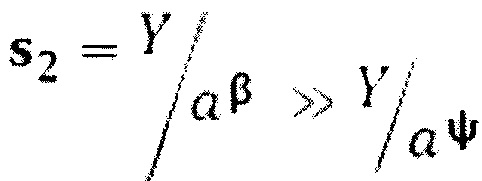 . В случае α≈β величины ступенек s1≈s2.
. В случае α≈β величины ступенек s1≈s2.
При этом изменения величин (размах) выходного сигнала Z1 при изменении отнормированного к единице кода управления М от 0 до (1-а-α) на выходе ЦАП_2 будет равным Y(1-а-α) размах выходного сигнала Z2 при изменении отнормированного к единице кода управления N от 0 до (1-а-β) на выходе ЦАП_4 будет равным Y(1-a-β).
Для того, чтобы уменьшить величину ступеньки выходного сигнала Z0 до исходного значения необходимо уменьшить размах выходного сигнала Z2 на выходе ЦАП_4 в аα раз с помощью аналогового 5 аттенюатора и сложить полученный сигнал 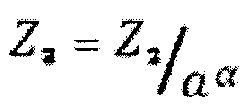 с выходным сигналом ЦАП 2 Z1 (у которого величина ступеньки
с выходным сигналом ЦАП 2 Z1 (у которого величина ступеньки 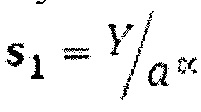 ) в сумматоре 3 сигналов.
) в сумматоре 3 сигналов.
На выходе сумматора 3 сигналов (фиг. 2) получим выходной сигнал Z0=Z1+Z3, который может изменяться от 0 до Y(1-а-ψ) с требуемым шагом квантования 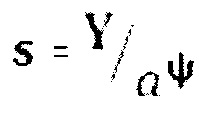 .
.
Точность преобразования опорного сигнала Y в аналоговую величину Z0 будет такой же, как у аналога, показанного на фиг. 1, но требования к точности ЦАП_4 будут уменьшены в аα раз.
Однако в рассмотренном способе цифроаналогового преобразования необходимо обеспечить высокую точность ЦАП_2 и аналогового аттенюатора 5, помещенного между выходом ЦАП_4 и входом сумматора 3 сигналов.
К этим двум аналоговым узлам структуры, показанным на фиг. 2, предъявляются такие же жесткие требования по точности, как и к ЦАП_0, показанному на фиг. 1. Точность ЦАП_2 и аттенюатора 5 будут ограничивать результирующую точность всего ЦАП, показанного на фиг. 2.
Заметим также, что точность аналогового аттенюатора 5 зависит не только от его собственной точности, но и от выходного сопротивления ЦАП_4 и входного сопротивления сумматора 3 сигналов, которые могут изменяться в диапазоне рабочих частот.
Способ преобразования, реализуемый в структуре параллельного ЦАП, приведенной на фиг. 2, примем за прототип.
Техническим результатом изобретения является повышение точности преобразования аналоговой величины с помощью цифровой обработки кода управления и использования, по меньшей мере, двух разных мерных шкал Y.
Достижение технического результата обеспечивается в предлагаемом способе нониусного цифроаналогового преобразования, при котором преобразуют опорный сигнал Y с помощью управляющего слова Х=М+a-αN длины ψ=α+β разрядов, где М - старшие разряды управляющего слова X длины α, a-αN - младшие разряды управляющего слова X длины β, причем α≈β,
а над аналоговым сигналом Z осуществляют два параллельных преобразования, причем при первом преобразовании первый выходной аналоговый сигнал Z1 пропорционален старшим М разрядам управляющего слова X длины α, и опорному сигналу Y1, т.е Z1=Y1×M, при втором преобразовании второй выходной аналоговый сигнал Z2 пропорционален младшим N разрядам управляющего слова X длины β и опорному сигналу Y1, т.е Z2=Y1×N, при этом перед упомянутыми параллельными преобразованиями осуществляют цифровое умножение младших a-αN разрядов управляющего слова X в аα раз (сдвиг влево на α разрядов), а также производят суммирование преобразованных аналоговых сигналов Z1, Z2, отличающемся тем, что над аналоговым сигналом Z осуществляют третье параллельное преобразование, при котором третий выходной аналоговый сигнал Z3 пропорционален младшим N разрядам управляющего слова X длины β и опорному сигналу Y2, т.е Z3=Y2×N, при этом опорные сигналы Y1 и Y2 связаны соотношением
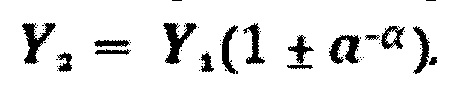
где а - основание системы счисления, α - число разрядов, на которое сдвинут код управления a-αN, после чего производят суммирование преобразованных аналоговых сигналов Z1, Z2 и Z3, получая выходной сигнал Z0.
При этом при параллельных преобразованиях аналоговых сигналов Z1, Z2 и Z3 в выходной сигнал Z0 масштаб преобразований выбран одинаковым.
Причем, если опорный сигнал Y2 формируют в соответствии с выражением
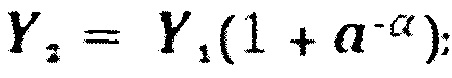
то аналоговое преобразование выходных сигналов Z1, Z2 и Z3 производят путем их алгебраического сложения по формуле:

Если опорный сигнал Y2 формируют в соответствии с выражением
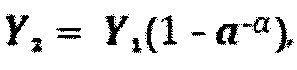
то аналоговое преобразование выходных сигналов Z1, Z2 и Z3 производят путем их алгебраического сложения по формуле:

Поясним достижение технического результата в предлагаемом способе указанными выше отличиями.
В основу предлагаемого способа положен принцип нониусного преобразования - использование, как минимум, двух мерных шкал, находящихся в дробно-кратном соотношении, т.е. осуществление трех преобразований:
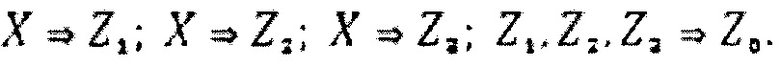
Иными словами, присутствует пара мерных шкал (опорных сигналов Y), связанных зависимостью:
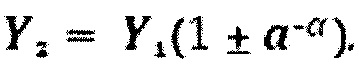
при этом структуру числа X представляют в виде (разбиение искусственное):
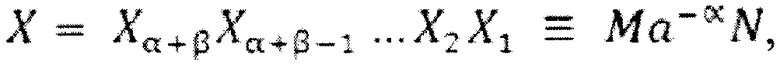
где М группа старших разрядов длины α и a-αN группа младших разрядов длины β числа X в выбранной системе счисления. Практически, число N есть результат умножения числа a-αN в аα раз, (сдвинутое на α разрядов влево), т.е. умноженное цифровым способом в аα раз. Тогда можно записать:
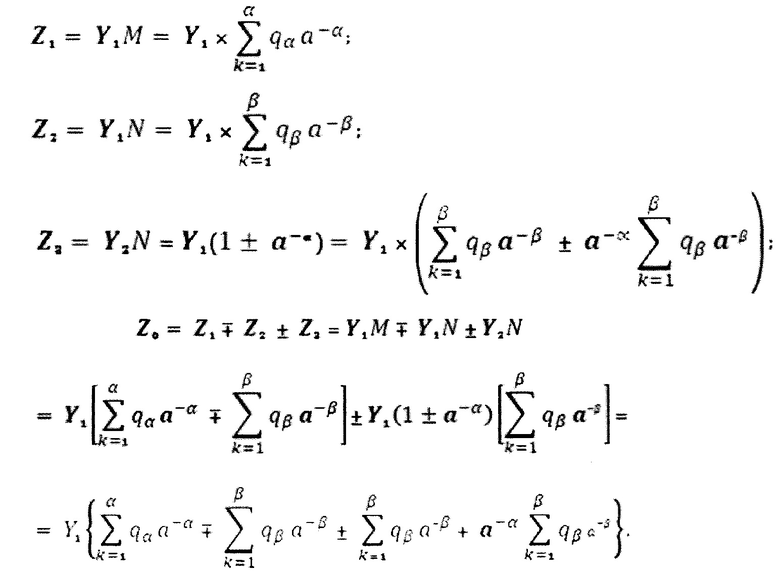
При этом должны соблюдаться условия:
при алгебраическом суммировании сигналов Z1, Z2 и Z3 в выходном аналоговом сумматоре, сигнал Z3 должен вычитаться из сигнала Z2, как и второй опорный сигнал Y2=Y1(1-а-α) в соответствии с выражением:
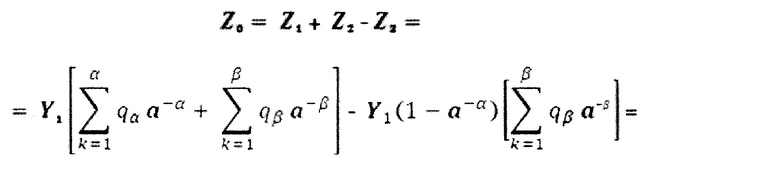
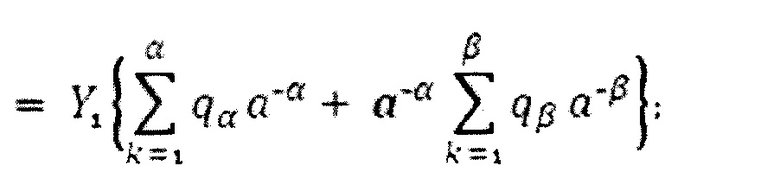
при алгебраическом суммировании сигналов Z1, Z2 и Z3 в выходном аналоговом сумматоре, сигнал Z2 должен вычитаться из сигнала Z3 в соответствии с выражением:
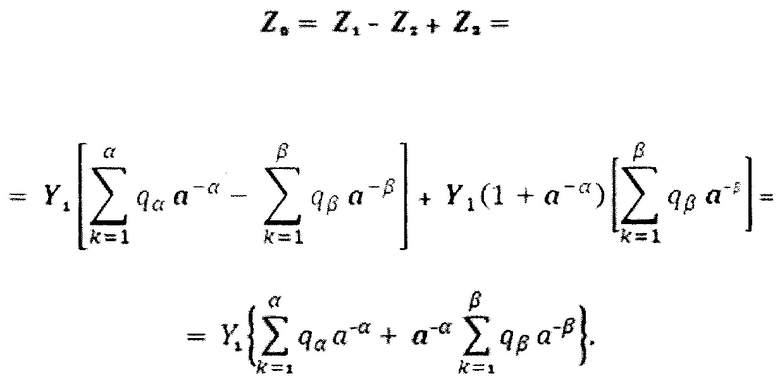
но при этом второй опорный сигнал Y2=Y1(1+а-α).
Как следует из приведенных формул данные преобразования приводят к одинаковому результату, что обеспечивает требуемую точность преобразования цифрового кода управления X в аналоговую величину Z0:
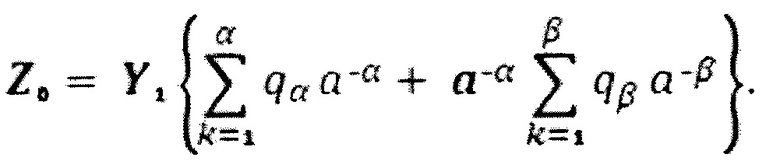
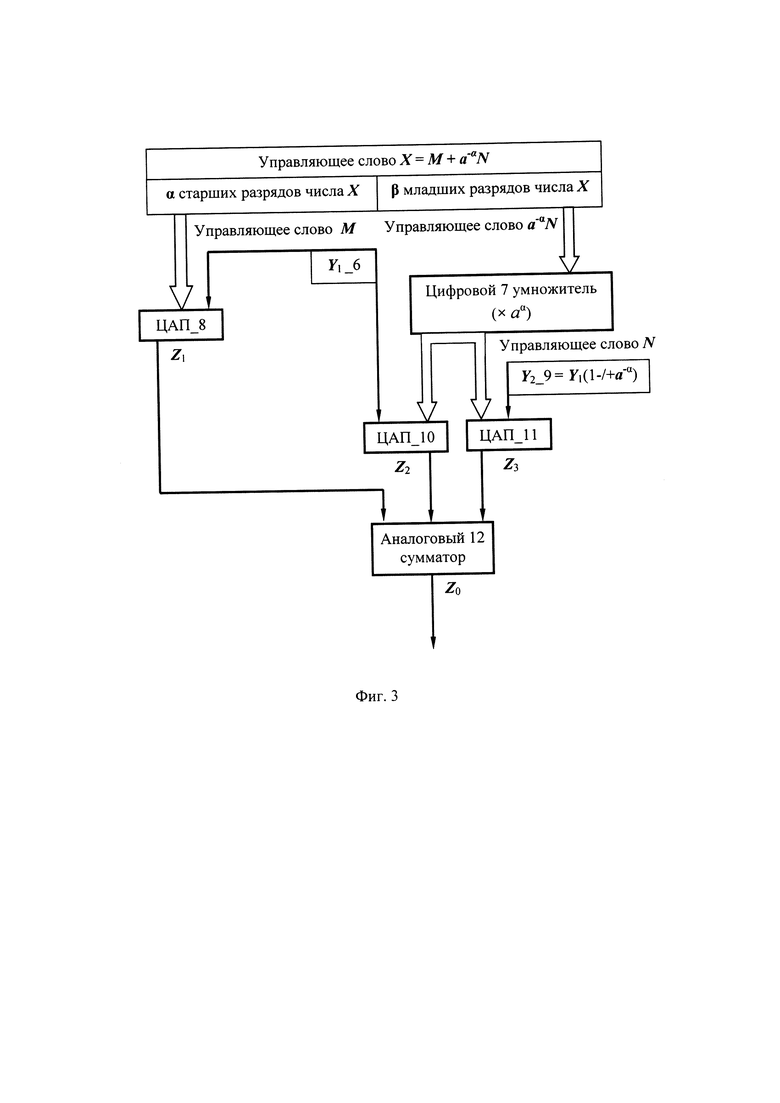
Структурная схема одного из возможных вариантов построения нониусного цифроаналогового преобразователя (ЦАП), реализующего предлагаемый способ, приведена на фиг. 3, на которой показаны:
Источник 6 опорного сигнала Y1.
Цифровой умножитель 7,
Первый ЦАП_8,
Источник 9 опорного сигнала Y2,
Второй ЦАП_10,
Третий ЦАП_11,
Аналоговый сумматор 12.
В цифровом умножителе 7 младшие β a-αN разрядов управляющего слова a-αN подвергаются цифровому умножению в аα раз (сдвиг влево на α разрядов). При этом выходная шина α старших разрядов управляющего слова М подключена к соответствующей входной шине управления ЦАП_8, к другому входу которого подключен выход источника 6 опорного сигнала Y1. Выход ЦАП_8 соединен с соответствующим входом аналогового 12 сумматора, к другим входам которого подключены выход ЦАП_10 и выход ЦАП_11, а на входную шину управления ЦАП_10 и ЦАП_11 поданы β младших разрядов управляющего слова N (управляющее слово a-αN, подвергшееся цифровому умножению в аα раз (сдвиг влево на α разрядов), другой вход ЦАП 10 соединен с выходом источника 6 опорного сигнала Y1, а соответствующий вход ЦАП_11 соединен с выходом источника 9 опорного сигнала Y2, причем мерные шкалы (опорные сигналы) Y1 и Y2 связанных зависимостью:
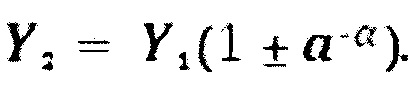
На выходе аналогового сумматора 12 имеем выходной аналоговый сигнал Z0.
В качестве числового примера рассмотрим вариант нониусного преобразования десятичного числа 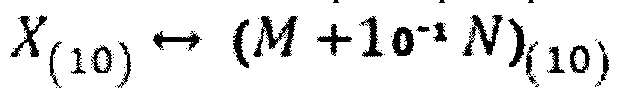 в абстрактный аналоговый параметр Z.
в абстрактный аналоговый параметр Z.
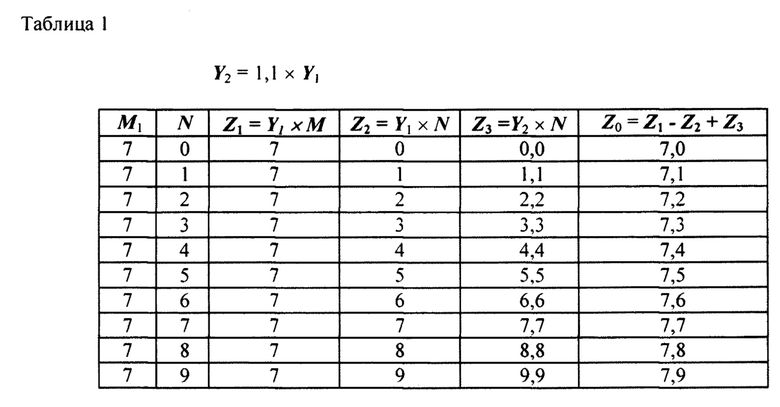
Поскольку система счисления десятичная, двухразрядное цифровое слово Х(10) разбиваем на два одноразрядных - М и N, а опорные сигналы Y примут вид: Y1=1,0; Y2=1,1×Y1.
Характерных вариантов будет два: для случая М1>N и для случая М2<N. Пусть М1=7 и М2=3, а N принимает значения от 0 до 9. Сведем этапы вычислений и преобразований в табл. 1 и табл. 2.
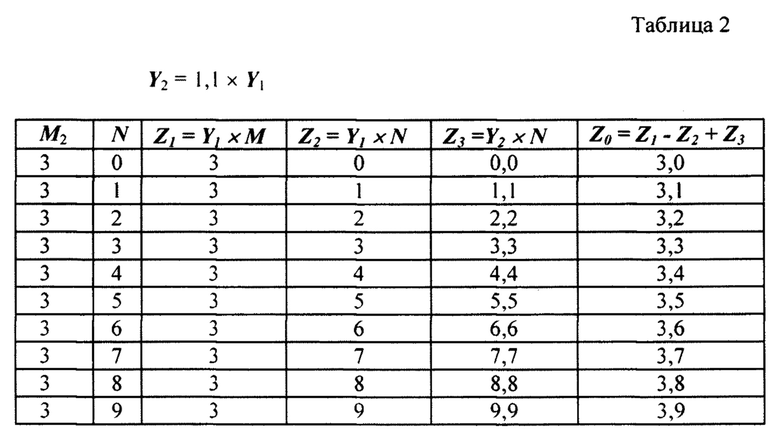
Единственными узлами нониусного ЦАП (фиг. 3), к которым следует предъявить жесткие требования по обеспечению точности, являются выходной аналоговый сумматор 12 и источники опорных сигналов Y1_8 и Y2_9, причем трудности по их реализации не являются непреодолимыми, более того, стандартными для (высоко) прецизионной электроники.
Так, например, при двадцатиразрядном входном двоичном слове (α=β=10) и Y1=10 В, требуемая относительная точность аналогового сумматора и источника Y1 δа≤2-20≈10-6 (абсолютная точность 9,5 мкВ), что вполне реализуемо на современной микроэлектронной элементной базе.
В случае Y2=0,9×Y1 и при тех же числовых параметрах, получим:
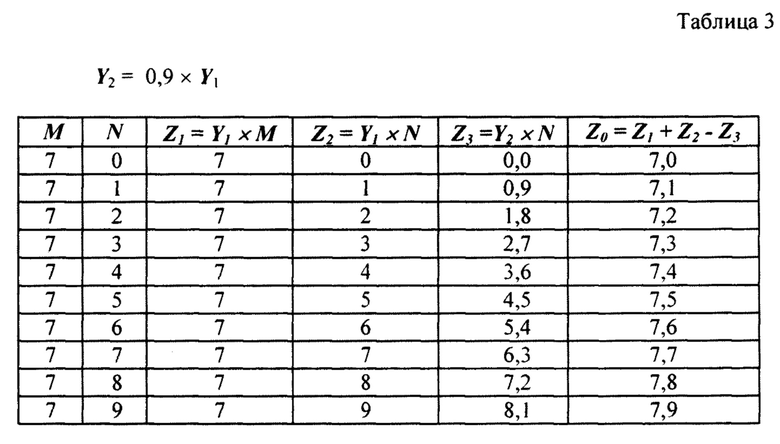
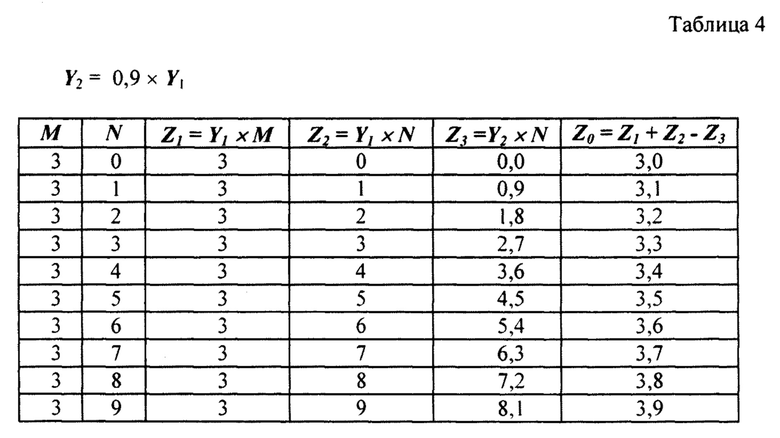
В предлагаемом способе преобразования при любом соотношении чисел N и М не происходит потери разрядов при росте точности цифроаналогового преобразования в ≈ аα раз, т.к. происходит значительное уменьшение погрешности, а, значит, увеличение точности параллельного цифроаналогового преобразования без ужесточения требований к технологии изготовления элементов ЦАП.
Выигрыш в точности преобразования связан с тем, что при аналоговом суммировании, при прочих равных условиях, требования к точности узла сумматора менее жесткие, чем требования к точности аналогового аттенюатора при аналоговом делении сигнала Z.
Кроме того, обеспечить точность опорных сигналов (мерных шкал) Y1, Y2 и их соотношение необходимо в одной точке и на постоянном токе (при постоянных значениях тока или напряжения), что значительно проще, чем во всем диапазоне выходных уровней Z и рабочих частот.
Еще раз обратим внимание на следующее обстоятельство: при использовании любого метода цифроаналогового преобразования (двойного и более интегрирования, сигма-дельта, конвейерного, последовательного приближения, нониусного и т.д.) требования к точности аналоговых узлов определены только требуемой точностью преобразования.
Весовой вклад отдельных аналоговых элементов цифроаналогового преобразователя, реализующего предлагаемый способ, в бюджет допустимых погрешностей устройства в целом зависит от конкретной схемотехнической реализации. И, разумеется, действует известное правило:
чем жестче требования к точности преобразования, тем (как минимум, линейно) жестче требования к аналоговым узлам.
Требования к точности и стабильности источников опорных напряжений (токов) и аналоговых алгебраических сумматоров входных/выходных напряжений (токов) инвариантны выбранному методу преобразования, а их вклад невелик.
Основной вклад в бюджет погрешностей вносит собственно ЦАП (который присутствует в структуре нониусного цифроаналогового преобразования в явном или неявном виде) посредством погрешностей ключей тока/напряжения и R (С) - матриц.
Применение одинаковых резисторов позволяет существенно улучшить точность по сравнению с обычным взвешивающим ЦАП, так как сравнительно просто изготовить набор прецизионных элементов с одинаковыми параметрами. ЦАП типа R-2R позволяют отодвинуть, но не снять, ограничения по разрядности. С лазерной подгонкой пленочных резисторов, расположенных на одной подложке гибридной микросхемы, можно достигнуть точности ЦАП 20-22 бита.
Поэтому ослабление требований к ЦАП в виде уменьшения требуемого числа разрядов ψ=α+β управляющего слова X при сохранении конечной точности преобразования так важно для практики.
Рассмотрим пример выполнения элементов в структурной схеме при реализации предлагаемого способа преобразования.
В качестве ЦАП 8, 10 и 11 могут быть использованы микросхемы двойного ЦАП AD5763, одиночного ЦАП К594ПА1, К1108ПА1 или аналогичные. Источники 6 и 9 опорных сигналов могут быть выполнены на микросхемах LT6657 (прецизионный источник напряжения) или L13092 (прецизионный источник тока).
Для осуществления цифрового умножения в α раз N младших разрядов управляющего слова X (сдвиг влево на α разрядов) можно использовать микросхемы регистров сдвига - универсальных регистров КР1533ИР8 (SN74HC164).
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ нониусного цифроаналогового преобразования | 2019 |
|
RU2703228C1 |
| СПОСОБ И УСТРОЙСТВО КОРРЕКЦИИ ПОГРЕШНОСТЕЙ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ | 2007 |
|
RU2352060C1 |
| АНАЛОГО-ЦИФРОВОЕ ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО | 1997 |
|
RU2123720C1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ИЗ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ В ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2409840C2 |
| РЕЛЯТОРНЫЙ ПРОЦЕССОР ДЛЯ АДРЕСНО-РАНГОВОЙ ИДЕНТИФИКАЦИИ, СЕЛЕКЦИИ И РАНЖИРОВАНИЯ ТРЕХ АНАЛОГОВЫХ СИГНАЛОВ | 1999 |
|
RU2149450C1 |
| СПОСОБ КАЛИБРОВКИ ПЕРЕДАТОЧНОЙ ХАРАКТЕРИСТИКИ ЦИФРОАНАЛОГОВОГО ПРЕОБРАЗОВАТЕЛЯ | 1991 |
|
RU2022464C1 |
| ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ УГЛА | 2013 |
|
RU2541856C2 |
| Устройство для сравнения двоичных чисел | 1990 |
|
SU1805463A1 |
| ИЗМЕРИТЕЛЬ КУРСА ПОДВИЖНОГО ОБЪЕКТА | 2003 |
|
RU2241208C1 |
| СПОСОБ КОРРЕКЦИИ ПОГРЕШНОСТЕЙ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2007 |
|
RU2326494C1 |
Изобретение относится к технике преобразования электрических сигналов. Технический результат заключается в повышении точности преобразования аналоговой величины. Технический результат достигается за счет того, что с помощью цифровой обработки кода управления и использования двух разных мерных шкал Y преобразуют опорный сигнал Y с помощью управляющего слова X=М+a-αN длины ψ=α+β разрядов, где М - старшие разряды управляющего слова X длины α, a-αN - младшие разряды управляющего слова X длины β, причем α≈β, а над аналоговым сигналом Z осуществляют три параллельных преобразования, причем при первом преобразовании первый выходной аналоговый сигнал Z1 пропорционален старшим М разрядам управляющего слова X длины α и опорному сигналу Y1, т.е Z1=Y1×М, при втором и третьем преобразованиях второй выходной аналоговый сигнал Z2 и третий выходной аналоговый сигнал Z3 пропорциональны младшим N разрядам управляющего слова X длины β и опорному сигналу Y1 и Y2 соответственно, т.е. Z2=Y1×N, a Z3=Y2×N, при этом перед упомянутыми параллельными преобразованиями осуществляют цифровое умножение младших a-αN разрядов управляющего слова X в аα раз, а также производят суммирование преобразованных аналоговых сигналов Z1, Z2, Z3, получая выходной сигнал Zo. 3 з.п. ф-лы, 3 ил., 4 табл.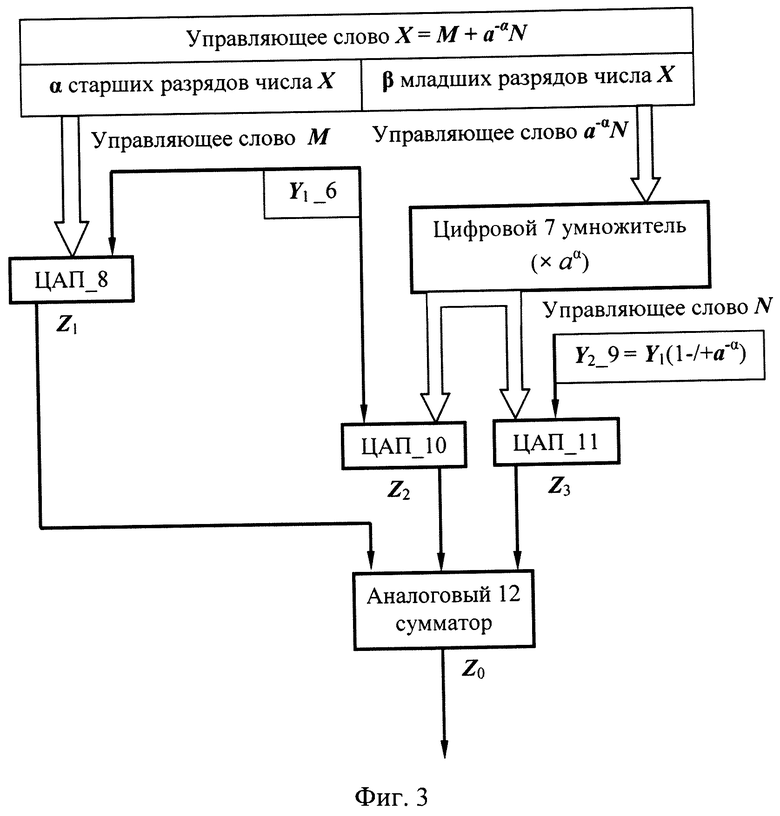
1. Способ нониусного цифроаналогового преобразования, при котором преобразуют опорный сигнал Y с помощью управляющего слова X=М+a-αN длины ψ=α+β разрядов, где М старшие разряды управляющего слова X длины α, a-αN младшие разряды управляющего слова X длины β, причем α≈β, а над аналоговым сигналом Z осуществляют два параллельных преобразования, причем при первом преобразовании первый выходной аналоговый сигнал Z1 пропорционален старшим М разрядам управляющего слова X длины α и опорному сигналу Y1, т.е Z1=Y1×M, при втором преобразовании второй выходной аналоговый сигнал Z2 пропорционален младшим N разрядам управляющего слова X длины β и опорному сигналу Y1, т.е Z2=Y1×N, при этом перед упомянутыми параллельными преобразованиями осуществляют цифровое умножение младших a-αN разрядов управляющего слова X в аα раз, а также производят суммирование преобразованных аналоговых сигналов Z1, Z2, отличающийся тем, что над аналоговым сигналом Z осуществляют третье параллельное преобразование, при котором третий выходной аналоговый сигнал Z3 пропорционален младшим N разрядам управляющего слова X длины β и опорному сигналу Y2, т.е Z3=Y2×N, при этом опорные сигналы Y1 и Y2 связаны соотношением
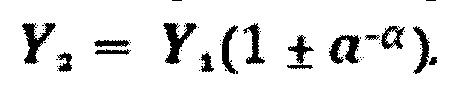
где а - основание системы счисления, α - число разрядов, на которое сдвинут код управления a-αN, после чего производят суммирование преобразованных аналоговых сигналов Z1, Z2 и Z3, получая выходной сигнал Z0.
2. Способ по п. 1, отличающийся тем, что при параллельных преобразованиях аналоговых сигналов Z1, Z2 и Z3 в выходной сигнал Z0 масштаб преобразований выбран одинаковым.
3. Способ по п. 1, отличающийся тем, что при формировании опорного сигнала Y2 в соответствии с выражением
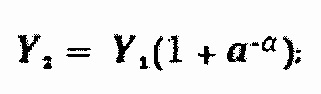
аналоговое преобразование выходных сигналов Z1, Z2 и Z3 производят путем их алгебраического сложения по формуле:

4. Способ по п. 1, отличающийся тем, что при формировании опорного сигнала Y2 в соответствии с выражением
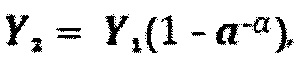
аналоговое преобразование выходных сигналов Z1, Z2 и Z3 производят путем их алгебраического сложения по формуле:

| ФУНКЦИОНАЛЬНЫЙ ЦИФРОАНАЛОГОВЫЙ ПРЕОБРАЗОВАТЕЛЬ | 2007 |
|
RU2339159C1 |
| СПОСОБ ЦИФРОАНАЛОГОВОГО ПРЕОБРАЗОВАНИЯ | 2009 |
|
RU2420867C2 |
| АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ И СПОСОБ ЕГО КАЛИБРОВКИ | 2010 |
|
RU2442279C1 |
| СПОСОБ КОРРЕКЦИИ ПОГРЕШНОСТЕЙ АНАЛОГО-ЦИФРОВОГО ПРЕОБРАЗОВАНИЯ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2007 |
|
RU2326494C1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
Авторы
Даты
2020-07-16—Публикация
2019-07-02—Подача