Область техники
Изобретение относится к области селекции растений, в частности к созданию предикативных математических моделей для оценки качества селекционного материала по геномным данным. Такую математическая модель можно использовать, в частности, для оценки распределения селекционного материала сразу же по нескольким признакам интереса в потомстве от скрещивания родительских пар и для отбора желательных пар.
Уровень техники
Оценка селекционного материала производится на основании данных полногеномного секвенирования или генотипирования путем оценки селекционной ценности сорта, которая рассчитываeтся с помощью предварительно построенной предиктивной модели, связывающей генетическую вариабельность (однонуклеотидные полиморфизмы, ОНП) с фенотипической (признаковой). Селекционный материал оценивается по качеству признака интереса, т.е. на основании оценки фенотипа. Среди значимых фенотипических признаков можно отметить, например, следующие: высота растений, устойчивость к полеганию, группа спелости, количество семян на растении, урожайность семян, процентное содержание масла или белка в семенах, процентное содержание жирных кислот определенного типа (определяет качество масла) и другие. Способ геномной селекции растений, который может использоваться в качестве прототипа, состоит из следующих шагов: (1) в исследуемой популяции выделяется обучающая выборка, состоящая из набора линий/сортов, которые генотипированы и фенотипированы; (2) обучающая выборка используется для создания предиктивной математической модели; (3) для селекции другие линии или сорта только генотипируются и оцениваются их значения селекционной ценности для каждого признака по‒отдельности согласно модели, тем самым уменьшая количество экспериментов по фенотипированию. Далее селекция проводится на основе значений селекционной ценности без фенотипирования растений (Crossa, J., Pérez-Rodríguez, P., Cuevas,J et al. (2017) Genomic Selection in Plant Breeding: Methods, Models, and Perspectives, Trends in Plant Science, 22, 11: 961-975).
Существующие предикативные модели геномной селекции для предсказания фенотипов используют в основном различные модификации линейной модели со смешанными эффектами - гребневая регрессия (RR-BLUP), Лассо-регрессия (Usai et al.,2009), методы, основанные на использовании Гильбертова пространства с воспроизводящим ядром (RKHS) (Endelman, J. B. 2011. Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP. Plant Genome 4:250-255), либо Байесовские методы BayesB (Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps, T. H. E. Meuwissen, B. J. Hayes and M. E. Goddard, GENETICS, April 1, 2001 vol. 157 no. 4 1819-1829). Эти модели связывают фенотипические признаки с эффектами однонуклеотидных полиморфизмов (SNP). При этом не учитывается, что фенотипические признаки могут быть скоррелированы. Корреляция может быть обусловлена тем, что SNP действует на несколько признаков одновременно, что называется плейотропным действием. Таким образом эффекты ОНП могут быть плейотропными и одно-фенотипными, что необходимо учитывать при построении моделей геномной селекции.
Таким образом, несмотря на известность ряда способов геномной селекции растений, существует потребность в новых способах, позволяющих осуществлять выбор родительских пар таким образом, чтобы получить у потомков этих пар сразу несколько желаемых фенотипических признаков.
Сущность изобретения
Задачей настоящего изобретения является создание нового способа оценки селекционного материала по генотипу для подбора желательных родительских пар, идентификации желательных генотипов из популяций и оценки селекционных линий, позволяющего осуществлять отбор родительских пар таким образом, чтобы получить у потомков этих пар сразу несколько желаемых фенотипических признаков.
Указанная задача решается путем создания способа идентификации родительских пар из набора растений, содержащего растения одного или разных сортов или линий, но при этом содержащего растения одного вида или одной сельскохозяйственной культуры, позволяющего получить у потомков этих пар желаемые значения для двух или более выбранных фенотипических признаков, включающего следующие стадии:
(а) выбирают два или более количественных фенотипических признака и определяют выбранные фенотипические признаки для всех растений из набора растений;
(б) проводят генотипирование для всех растений из набора растений, заключающееся в идентификации однонуклеотидных полиморфизмов (ОНП) в геномной ДНК этих растений, при этом выделяют не менее 1000 ОНП, различающихся хотя бы у двух растений набора;
(в) при помощи факторного анализа определяют латентные факторы, которые влияют на несколько скоррелированных фенотипических признаков;
(г) строят математическую модель, связывающую латентные факторы, фенотипические признаки и выделенные ОНП в направленный ациклический граф, поочередно добавляя ОНП в модель как переменные, влияющие на латентные факторы или на фенотипические признаки, при этом добавление ОНП в модель происходит следующим образом:
тестируют все ОНП и выбирают один, наибольшим образом увеличивающий значение функции правдоподобия выборочной ковариационной матрицы фенотипических признаков,
тестируют все оставшиеся ОНП таким же образом и выбирают следующий ОНП, наибольшим образом увеличивающий значение функции правдоподобия выборочной ковариационной матрицы фенотипических признаков,
добавляют ОНП поочередно до тех пор, пока добавление ОНП увеличивает значение функции правдоподобия выборочной ковариационной матрицы фенотипических признаков;
(д) отбирают родительскую пару из набора растений, содержащую такие ОНП, чтобы у всех возможных потомков этой пары значения всех выбранных фенотипических признаков, предсказанные по построенной математической модели, отвечали желаемым значениям.
В некоторых вариантах изобретения данный способ характеризуется тем, что в качестве желаемых значений для всех выбранных фенотипических признаков указывают значения выше среднего по популяции, где популяция включает в себя растения одного вида или сельскохозяйственной культуры с указанным набором растений.
В некоторых вариантах изобретения данный способ характеризуется тем, что в качестве фенотипических признаков выбирают по меньшей мере один из следующих: высота растений, количество семян на растении, урожайность, процентное содержание масла в семенах, процентное содержание белка в семенах, процентное содержание жирных кислот определенного типа.
Таким образом, указанная задача решается с помощью построения предикативной модели, которая описывает связь между несколькими фенотипическими признаками и однонуклеотидными полиморфизмами (ОНП), которые в рамках модели разделяются на ОНП плейотропного и прямого эффекта.
Техническим результатом настоящего изобретения является расширение возможностей геномной селекции растений для получения потомков, имеющих сразу несколько желаемых фенотипических признаков.
Краткое описание рисунков
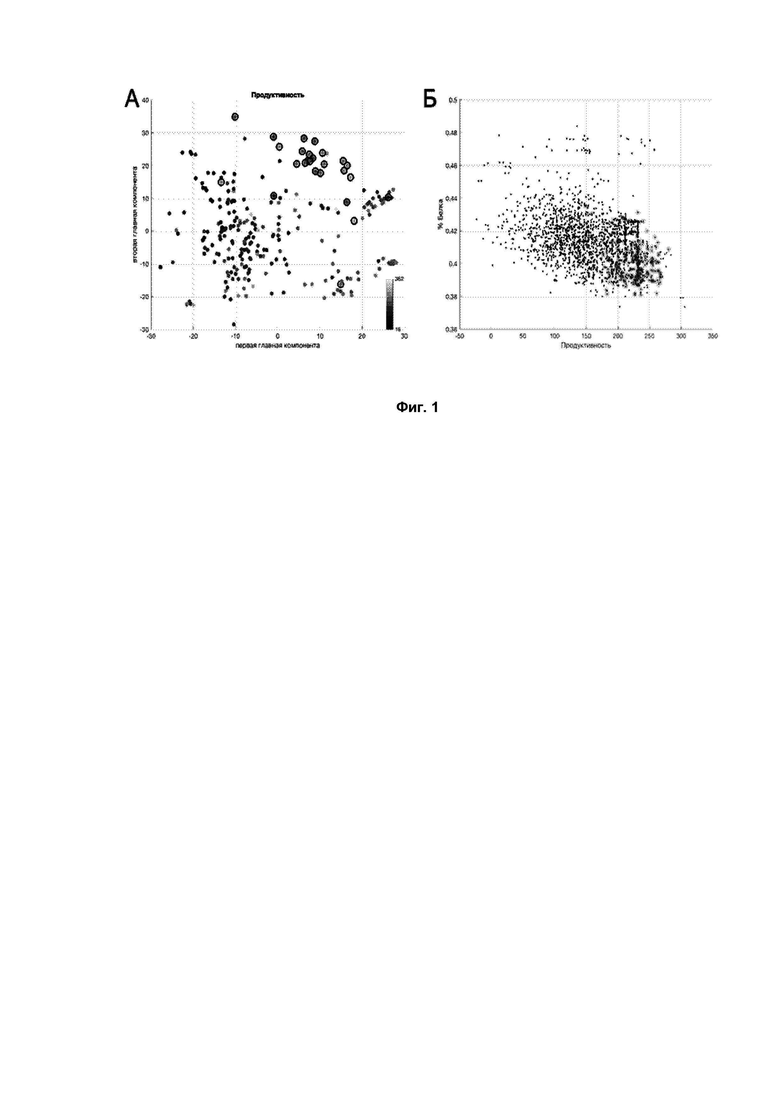
Фиг. 1 – А: Представление сортов сои в первых двух главных компонентах, построенных на полногеномных данных. Цвет отражает значение продуктивности. Черные кружки маркируют желательные родительские линии. Б: связь продуктивности и процентного содержания белка в семенах для всех возможных потомков, кружками обозначены потомки выбранных родительских пар.
Фиг. 2 – (слева) Представление образцов сои в первых двух главных компонентах, построенных на основании полных генетических данных. Черные кружки показывают образцы, которые желательны для образования родительских пар. Цвет точек отражает значение признака “урожайность”. (справа) Сопоставление процентного содержания белка и масла в семенах сои. Треугольниками отмечены желательные родительские образцы; серые кружочки – остальные образцы. Черные линии отражают средние значения фенотипических признаков.
Подробное раскрытие изобретения
В описании данного изобретения термины «включает» и «включающий» интерпретируются как означающие «включает, помимо всего прочего». Указанные термины не предназначены для того, чтобы их истолковывали как «состоит только из». Если не определено отдельно, технические и научные термины в данной заявке имеют стандартные значения, общепринятые в научной и технической литературе.
Одной из задач настоящего изобретения является разработка нового способа селекции по генотипу для подбора желательных родительских пар, позволяющих получить потомков, имеющих сразу несколько желаемых фенотипических признаков.
Отличие предлагаемого способа от других известных способов заключается в следующем:
1. Предикативная модель разработана с использованием техники моделирования структурными уравнениями и является расширением классической модели LISREL.
2. Структура модели конструируется автоматически путем объединения скоррелированных фенотипических признаков в латентные факторы и добавления ОНП к этим факторам и фенотипам, причем на каждом этапе происходит автоматический выбор наилучшей модели с помощью критерия максимального правдоподобия.
3. Используется оригинальный, не описанный ранее аналитический вид формул апостериорных распределений вероятностей.
4. Получаемые апостериорные распределения принадлежат известным классам, что обеспечивает возможность применения эффективных оптимизационных процедур для нахождения параметров моделей.
Нижеследующие примеры осуществления способа приведены в целях раскрытия характеристик настоящего изобретения и их не следует рассматривать как каким-либо образом ограничивающие объем изобретения.
Определение фенотипа и генотипа набора растений
Способ идентификации родительских пар из набора растений по настоящему изобретению позволяет работать с набором растений, содержащим растения одного или разных сортов или линий, но при этом содержащим растения одного вида или одной сельскохозяйственной культуры (то есть способных скрещиваться и давать плодовитое потомство). Предпочтительно, этот набор, или выборка, выращена стандартным образом в условиях, приближенных к реальным полевым условиям, и далее стандартным образом фенотипирована (например, см. Shin et al., Multi-trait analysis of domestication genes in Cicer arietinum - Cicer reticulatum hybrids with a multidimensional approach: Modeling wide crosses for crop improvement. Plant Sci. 2019 Aug; 285:122-131.). Фенотипирование ‒ стандартная процедура оценки количественных и качественных признаков сорта/линии. Стандартными методами (вычисление коэффициента корреляции) может быть установлено, что между некоторыми признаками имеется статистически достоверная корреляция.
Предпочтительно, каждый сорт/линия также генотипирован стандартным образом. Метод генотипирования может быть либо GBS (DePristo et al., A framework for variation discovery and genotyping using next-generation DNA sequencing data (2011), NATURE GENETICS 43:491-498; van der Auwera et al., From FastQ Data to High-Confidence Variant Calls: The Genome Analysis Toolkit Best Practices Pipeline, (2013) CURRENT PROTOCOLS IN BIOINFORMATICS 43:11.10.1-11.10.33), либо DArTSeq (метод запатентованный компанией Diversity Array technologies, www.diversityarrays.com), либо любой другой метод. ОНП, полученные в результате генотипирования по методу GBS, фильтруются стандартным образом, как описано, например, в (Shin et al., Multi-trait analysis of domestication genes in Cicer arietinum - Cicer reticulatum hybrids with a multidimensional approach: Modeling wide crosses for crop improvement. Plant Sci. 2019), с тем, чтобы убрать позиции с большим числом пропусков ОНП в сортах, а также убрать низкочастотные полиморфизмы.
Таким образом в результате этой процедуры, каждый сорт/линия оказывается охарактеризованным по фенотипическим признакам интереса, часть из которых коррелирована, и также охарактеризованным по ОНП (т.е. по позициям генома, в которых в данной выборке есть различия между сортами). Предпочтительно, выделяют не менее 1000 ОНП внутри выборки/набора растений, то есть такие ОНП, которые присутствуют в геномной ДНК некоторых растений набора, но отсутствуют в геномной ДНК у других растений набора.
Для реализации способа по настоящему изобретению, сорта должны различаться по крайней мере по нескольким сотням полиморфизмов (предпочтительно по 1000 и более полиморфизмов), а признаков должно быть несколько (не менее двух) и корреляция должна быть по крайней мере между парой признаков.
Описание построения математической модели с использованием техники моделирования структурными уравнениями.
Математическая модель, используемая в настоящем изобретении, принадлежит к классу моделей SEM (Structural equation modeling, моделирование структурными уравнениями) и состоит из системы линейных уравнений. Традиционной моделью SEM является модель в нотации LISREL (Kline, Rex B. 2011. Principles and Practice of Structural Equation Modeling. Guilford Publications.) Модель LISREL состоит из двух частей: структурной (взаимодействия между латентными переменными) и измерительной (влияния латентных переменных на наблюдаемые переменные). Предлагаемая авторами модель SEM является расширением LISREL и также состоит из двух частей – структурной и измерительной. Структурная части модели описывает влияние ОНП с плейотропным эффектом на латентную переменную, имеющую смысл общей дисперсии скоррелированных признаков. Измерительная часть описывает то, как латентная переменная и ОНП прямого эффекта влияют на наблюдаемые фенотипические признаки. Таким образом, модель имеет следующий вид:
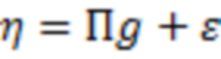
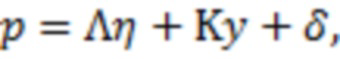
где  is – латентная переменная,
is – латентная переменная,  – вектор значений фенотипических признаков,
– вектор значений фенотипических признаков,  – вектор плейотропных ОНП,
– вектор плейотропных ОНП,  – вектор ОНП, влияющих на признаки напрямую;
– вектор ОНП, влияющих на признаки напрямую;  ,
, 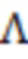 и
и  - матрицы линейных эффектов,
- матрицы линейных эффектов,  и
и  – независимые случайные ошибки, имеющие нормальные распределения с ковариационными матрицами
– независимые случайные ошибки, имеющие нормальные распределения с ковариационными матрицами 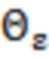 и
и 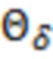 , соответственно.
, соответственно.
Взаимодействия между переменными в модели соответствуют направленному ациклическому графу, в котором узлы – переменные, ребра – взаимодействия между двумя переменными, направленные от влияющей переменной на зависимую переменную.
Построение модели заключается в связывании фенотипических признаков и ОНП в направленный ациклический граф так, что ОНП являются внешними узлами графа, а фенотипические признаки – стоками. Связи между ОНП и фенотипическими признаками могут быть прямыми и опосредованными через дополнительные(скрытые/латентные) узлы, играющие роль общей дисперсии у нескольких фенотипических признаков. На первом этапе построения модели происходит факторный анализ фенотипических признаков с целью нахождения латентных факторов, которые влияют на несколько фенотипических признаков. Определение количества факторов может быть проведено любым способом, например, с помощью параллельного анализа (Horn, John L. A rationale and test for the number of factors in factor analysis (1965) Psychometrika. 30 (2): 179–185). После того, как определены латентные факторы, структура модели соответствует ациклическому двудольному графу (доли соответствуют латентным фактора и фенотипическим признакам). Направления ребер идут от латентных переменных к фенотипическим признакам.
ОНП могут принимать только значения 0, 1 и 2, поэтому их нельзя описывать с помощью переменных, имеющих нормальное распределение. Для описания ОНП авторы вводят в модель вспомогательные нормально распределенные латентные переменные  и
и  , имитирующие
, имитирующие  и
и  следующим образом. Пусть
следующим образом. Пусть 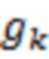 – ординальная переменная, описывающая
– ординальная переменная, описывающая 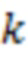 -й ОНП, и пусть этот полиморфизм принимает значения 0, 1 или 2 с частотами
-й ОНП, и пусть этот полиморфизм принимает значения 0, 1 или 2 с частотами 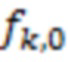 ,
, 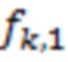 и
и 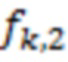 , соответственно. Тогда, значения соответствующих латентных переменных
, соответственно. Тогда, значения соответствующих латентных переменных 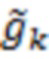 связаны с
связаны с  следующим образом:
следующим образом:
Если 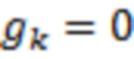 , то
, то 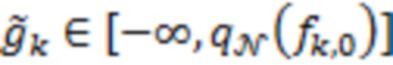 ,
,
Если 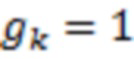 , то
, то 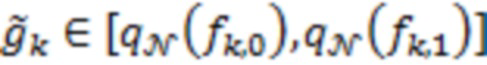 ,
,
Если 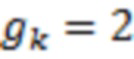 , то
, то 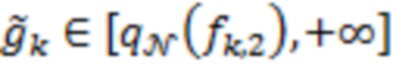 .
.
После замены переменных, модель примет следующий вид:

Алгоритм добавления ОНП в модель
На втором этапе построения модели, в модель добавляются ОНП как переменные, влияющие как на латентные факторы так и на фенотипические признаки. ОНП добавляются в модель по одному, каждый раз увеличивая значение функции правдоподобности фенотипических признаков. Чтобы добавить один ОНП как влияющий на конкретный латентный фактор или фенотипический признак, необходимо протестировать все ОНП и выбрать один, наибольшим образом увеличивающий значение правдоподобия. После того, как ОНП добавлены как влияющие переменные на латентные факторы и фенотипические признаки, структурам модели выглядит искомым образом. ОНП, влияющие на латентные факторы имеют смысл плейотропных ОНП, остальные ОНП – индивидуального эффекта.
Для того, чтобы добавить в модель ОНП, авторы реализовали итеративный алгоритм, который вначале находит значимые плейотропные ОНП, а затем те ОНП, которые действуют на признаки напрямую. Процедура добавления ОНП к интересующей нас переменной ( или
или  ) включает в себя следующую последовательность шагов. Вначале необходимо найти и зафиксировать значения элементов матрицы
) включает в себя следующую последовательность шагов. Вначале необходимо найти и зафиксировать значения элементов матрицы 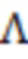 (2). После этого каждый полиморфизм проверяется на наличие эффекта на интересующую нас переменную. Затем, параметры модели оцениваются методом максимального правдоподобия, с учетом значений, зафиксированных ранее. Таким образом, находится тот ОНП, который соответствует наибольшему значению функции правдоподобия. После этого, найденный ОНП добавляется в модель и фиксируется линейный эффект его влияния на интересующую нас переменную. Процедура продолжается до тех пор, пока добавление нового ОНП увеличивает значение функции правдоподобия модели.
(2). После этого каждый полиморфизм проверяется на наличие эффекта на интересующую нас переменную. Затем, параметры модели оцениваются методом максимального правдоподобия, с учетом значений, зафиксированных ранее. Таким образом, находится тот ОНП, который соответствует наибольшему значению функции правдоподобия. После этого, найденный ОНП добавляется в модель и фиксируется линейный эффект его влияния на интересующую нас переменную. Процедура продолжается до тех пор, пока добавление нового ОНП увеличивает значение функции правдоподобия модели.
Аналитический вид формул апостериорных распределений вероятностей
Для того, чтобы оценить параметры модели был использован Байесовский подход: нахождение значений параметров, которые дают максимум произведения функции правдоподобия и априорных распределений параметров. В качестве априорных распределений параметров можно использовать любые распределения, однако для того, чтобы реализовать схему Гиббса, необходимо использовать априорные распределения для дисперсий случайных ошибок из класса обратных Гамма распределений, а априорные распределения для параметров линейных взаимодействий – из многомерного нормального распределения.
Для тестирования работы модели рекомендуется проводить кросс-валидацию в любой схеме, и в случае успешного тестирования использовать все полученные модели для оценки фенотипических признаков у потенциальных потомков родительских пар.
Байесовский вывод для нахождения распределений параметров структурной и измерительной части модели был реализован схожим образом: все уравнения рассматривались по-отдельности и для каждой группы параметров выбиралось свое сопряженное априорное распределение. В качестве распределений для математического ожидания и дисперсии нормального распределения были взяты нормальное и обратное гамма распределения, соответственно.
Обозначим объем рассматриваемой выборки как  , а длины векторов, соответствующих переменным
, а длины векторов, соответствующих переменным  ,
,  ,
,  и
и  как
как  ,
,  ,
, 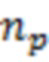 и
и 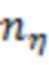 . Значения, соответствующие переменным
. Значения, соответствующие переменным  ,
,  ,
,  и
и  запишем в матрицы
запишем в матрицы 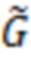 ,
, 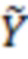 ,
,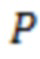 и
и 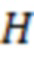 размерности
размерности 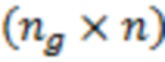 ,
, 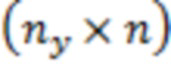 ,
, 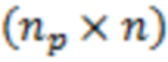 и
и 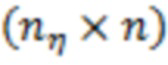 , соответственно. Рассмотрим уравнение структурной части, соответствующее
, соответственно. Рассмотрим уравнение структурной части, соответствующее  -й латентной переменной
-й латентной переменной 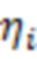 :
:
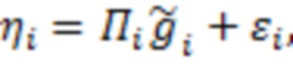
где 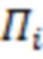 -
-  -я строка матрицы
-я строка матрицы 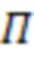 ;
; 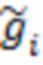 содержит значения
содержит значения  соответствующее
соответствующее  -й строке
-й строке 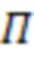 ;
; 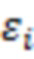 -
-  -й элемент случайного вектора ошибок, имеющий нормальное распределение с нулевым средним и дисперсией
-й элемент случайного вектора ошибок, имеющий нормальное распределение с нулевым средним и дисперсией 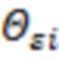 .
.
Для параметров 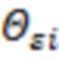 и
и 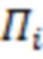 в качестве априорных распределений были взяты обратное Гамма распределение и нормальное распределение, соответственно:
в качестве априорных распределений были взяты обратное Гамма распределение и нормальное распределение, соответственно:
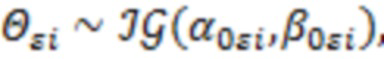
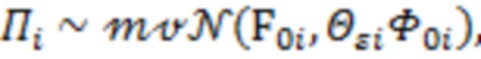
где  оценка параметра
оценка параметра  , полученная методом максимального правдоподобия, а
, полученная методом максимального правдоподобия, а 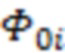 – единичная матрица; параметры обратного Гамма распределения были взяты по аналогии с тем как это предложено в (Lee, Sik-Yum. 2007. Structural Equation Modeling: A Bayesian Approach. John Wiley & Sons Ltd. https://doi.org/10.1002/9780470024737) на с. 76:
– единичная матрица; параметры обратного Гамма распределения были взяты по аналогии с тем как это предложено в (Lee, Sik-Yum. 2007. Structural Equation Modeling: A Bayesian Approach. John Wiley & Sons Ltd. https://doi.org/10.1002/9780470024737) на с. 76: 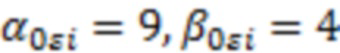 . Запишем значения переменной
. Запишем значения переменной 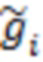 в матрицу
в матрицу 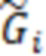 размерности
размерности 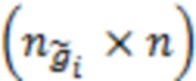 ; запишем значения переменной
; запишем значения переменной 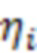 в горизонтальный вектор
в горизонтальный вектор 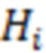 длины
длины  . Тогда апостериорная оценка параметров
. Тогда апостериорная оценка параметров 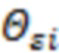 и
и 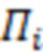 выражается следующим образом:
выражается следующим образом:

где
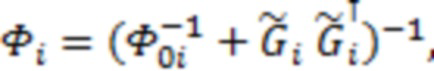
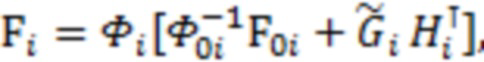
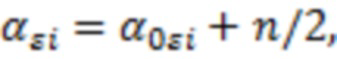
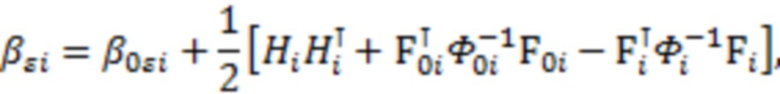
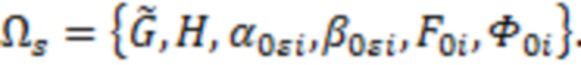
Байесовский вывод для нахождения апостериорных распределений параметров измерительной части модели реализуется по аналогии с тем, как это было сделано для структурной части. Рассмотрим уравнение измерительной части, соответствующее  -му фенотипическому признаку
-му фенотипическому признаку 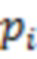 :
:
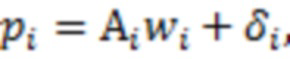
где 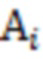 - горизонтальный вектор, в который записаны значения из
- горизонтальный вектор, в который записаны значения из  -х строк матриц
-х строк матриц 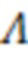 и
и  ;
; 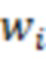 - вектор, в который записаны значения переменных
- вектор, в который записаны значения переменных  и
и  , соответствующие
, соответствующие  -м строка матриц
-м строка матриц 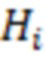 and
and 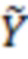 ;
; 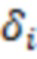 -
-  -й элемент вектора случайных ошибок, распределенного по нормальному закону с нулевым математическим ожиданием и дисперсией равной
-й элемент вектора случайных ошибок, распределенного по нормальному закону с нулевым математическим ожиданием и дисперсией равной 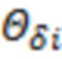 .
.
Для параметров 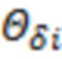 и
и 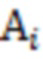 в качестве априорных распределений были взяты обратное гамма распределение и нормальное распределение, соответственно:
в качестве априорных распределений были взяты обратное гамма распределение и нормальное распределение, соответственно:
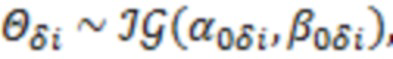
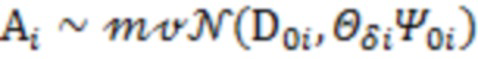
где 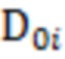 - оценка
- оценка 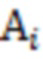 , полученная методом максимального правдоподобия,
, полученная методом максимального правдоподобия, 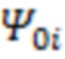 - единичная матрица; параметры обратного Гамма распределения были взяты аналогично тому, как это предложено в (Lee 2007) на с. 76:
- единичная матрица; параметры обратного Гамма распределения были взяты аналогично тому, как это предложено в (Lee 2007) на с. 76: 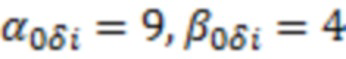 . Значения
. Значения 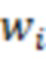 запишем в матрицу
запишем в матрицу 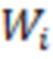 размерности
размерности 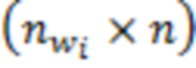 ; значения
; значения 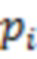 запишем в горизонтальный вектор
запишем в горизонтальный вектор 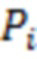 длины
длины  . Тогда апостериорное распределение параметров
. Тогда апостериорное распределение параметров 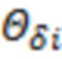 и
и 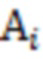 будет иметь следующий вид:
будет иметь следующий вид:

где
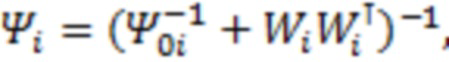
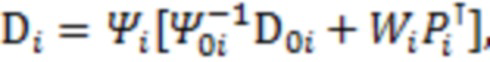
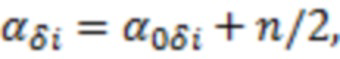
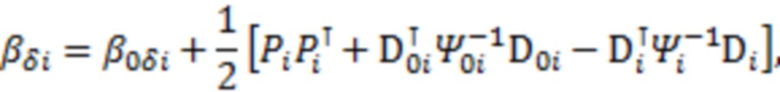
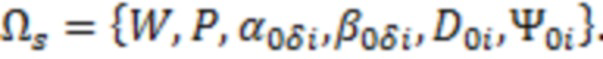
Эффективный метод оптимизации: Сэмплирование по Гиббсу
В модели содержатся переменные трех типов: наблюдаемые значения фенотипических признаков ( ), значения латентных переменных (
), значения латентных переменных ( ) и значения латентных переменных имитирующих ОНП (
) и значения латентных переменных имитирующих ОНП (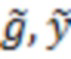 ). Так как значения латентных переменных не заданы, их необходимо генерировать в начале каждого цикла алгоритма MCMC (Markov Chain Monte Carlo, Монте-Kaрло по схеме марковской цепи).
). Так как значения латентных переменных не заданы, их необходимо генерировать в начале каждого цикла алгоритма MCMC (Markov Chain Monte Carlo, Монте-Kaрло по схеме марковской цепи).
Обозначим объем рассматриваемой выборки как  . Запишем значения наблюдений, соответствующих переменным
. Запишем значения наблюдений, соответствующих переменным  ,
,  и
и  в матрицы
в матрицы 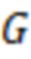 размерности
размерности 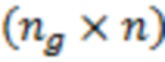 ,
, 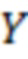 размерности
размерности 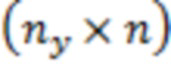 и
и 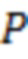 размерности
размерности 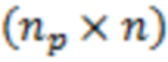 . Матрицы значений латентных переменных
. Матрицы значений латентных переменных 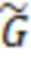 для
для  и
и 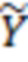 для
для  будут генерироваться схожим образом. Например, элемент
будут генерироваться схожим образом. Например, элемент  -й строки
-й строки 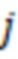 -го столбца матрицы
-го столбца матрицы 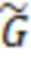 получается случайным образом из усеченного нормального распределения
получается случайным образом из усеченного нормального распределения 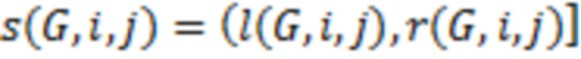 :
:
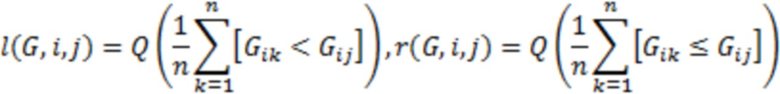
где 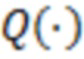 - квантиль функция, ассоциированная со стандартным нормальным распределением,
- квантиль функция, ассоциированная со стандартным нормальным распределением,  - скобки Айверсона (Kenneth E. Iverson (1962). A Programming Language. Wiley. p. 11).
- скобки Айверсона (Kenneth E. Iverson (1962). A Programming Language. Wiley. p. 11).
Таким образом, первые два шага одного цикла MCMC - это сэмплирование значений 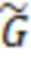 и
и 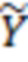 из усеченных нормальных распределений:
из усеченных нормальных распределений:
(i) 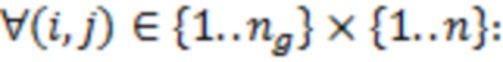 получаем
получаем 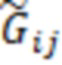 из
из 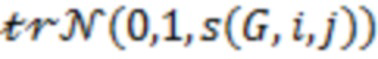 ;
;
(ii) 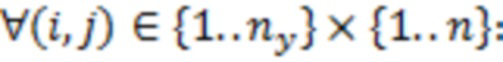 получаем
получаем 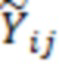 из
из 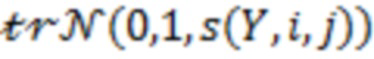 .
.
Для получения значений латентной переменной  , авторы реализуют подход предложенный в (Lee S-Y. Structural Equation Modeling: A Bayesian approach [Internet]. Structural Equation Modeling: A Multidisciplinary Journal. Chichester, UK: John Wiley & Sons, Ltd; 2007. 432 p) на с.83. Обозначим вектор значений латентной переменной
, авторы реализуют подход предложенный в (Lee S-Y. Structural Equation Modeling: A Bayesian approach [Internet]. Structural Equation Modeling: A Multidisciplinary Journal. Chichester, UK: John Wiley & Sons, Ltd; 2007. 432 p) на с.83. Обозначим вектор значений латентной переменной  для
для 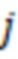 -го образца как
-го образца как 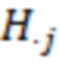 . Тогда третий шаг цикла МСМС будет выглядеть следующим образом:
. Тогда третий шаг цикла МСМС будет выглядеть следующим образом:
(iii) 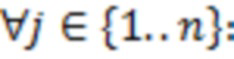 получаем
получаем 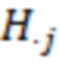 из
из 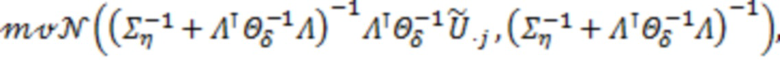
где 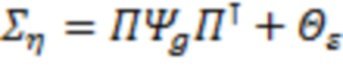 и
и 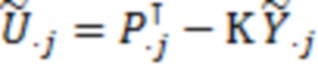 .
.
После того как были получены значения для всех латентных переменных, можно преступить к сэмплированию параметров модели, со следующими шагами:
(iv) получаем 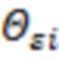 из
из 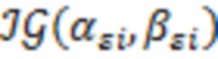 ,
,
(v) получаем 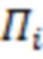 из
из 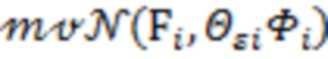 .
.
(vi) получаем 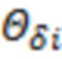 из
из 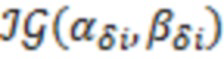 ,
,
(vii) получаем 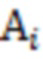 из
из 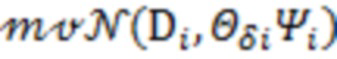 .
.
Таким образом, каждый цикл алгоритма MCMC состоит из семи шагов сэмплирования по Гиббсу, наиболее быстрого алгоритма оптимизации апостериорных вероятностей.
Программная реализация
Алгоритм автоматического добавления ОНП в модель реализован на языке программирования Python. В алгоритме используется метод максимального правдоподобия для моделей SEM, реализованный в пакете SEMOPY. Алгоритм сэмплирования по Гиббсу для значений латентных переменных и значений параметров реализован на языке программирования Python.
Результат применения модели на соевых данных и определение оптимальных родительских пар
Примеры работы способа продемонстрированы на выборке из 280 сортов сои которая состояла из 121 образца сои коллекции ВИР (114 сортов G.max, 2 образца G.gracilis и 5 образцов мутантов и гибридов G.soja) и 160 образцов сои G.max коллекции компании «СоКо» (79 современных сортов и 80 линий из предварительного сортоиспытания).
Посев и фенотипирование сортов и линий сои были произведены стандартно в Краснодарском крае (ЮФО) в соответствии с (Shin et al., Multi-trait analysis of domestication genes in Cicer arietinum - Cicer reticulatum hybrids with a multidimensional approach: Modeling wide crosses for crop improvement. Plant Sci. 2019). Были определены процентное содержание белка и масла в семенах и произведена оценка продуктивности растений выборки, эти признаки скоррелированы, причем между продуктивностью и маслом была обнаружена отрицательная корреляция. Продуктивность оценивали как массу семян растений на кв. м площади.
Для оценки селекционной ценности растений была построена модель, которая описывала связь между этими признаками и ОНП.
Чтобы проверить предикативную силу разработанной модели, было проведено ее тестирование с помощью стандартного метода кросс-валидации. При построении моделей геномной селекции, обучающая выборка оптимизируется путем стратификации (Isidro et al., 2015), так, что количество генотипов в ней, выбранных из каждой популяции, пропорционально размеру популяции. Для сравнения моделей используется метод кросс-валидации, при котором выборка делится на несколько подвыборок, из которых все, кроме одной, используются для обучения модели, а оставшаяся выборка ‒ для проверки аккуратности предсказаний. Для того чтобы избежать переобучения (ситуации, когда модель хорошо предсказывает фенотипические признаки только на обучающей выборке), рекомендуется, чтобы объем тестовой выборки равнялся бы одной пятой или одной десятой от общего количества образцов. Для оценки аккуратности предсказаний обычно проводят 50 раундов кросс-валидации, при которой все кроме одной подвыборки из общей выборки используются для обучения, а оставшаяся - для предсказания фенотипов. Оценка качества предсказаний фенотипов моделью производится путем вычисления коэффициента корреляции Пирсона.
В примере выборка разбивалась на 10 частей, однако такое разбиение нефиксировано и определяется конкретной ситуацией с тем, чтобы затем можно было бы достоверно посчитать значение коэффициента корреляции между предсказаниями модели и данными. Результаты кросс-валидации показали значение корреляции между оценками и реальными значениями рассматриваемых фенотипических признаков равным 0.4 (Таблица 1). Это значение является достаточно высоким, так как рассматриваемые фенотипические признаки имеют высокую зависимость от факторов окружающей среды.
Для выбора оптимальных родительских пар проводилась следующая процедура. Для каждой пары образцов сои были сгенерированы все возможные генетические комбинации потомков, и для каждого потомка было проведено предсказание трех признаков интереса в 10 моделях. Количество моделей строго не фиксировано, но не меньше 5. Родительская пара считалась оптимальной, если для всех потомков во всех моделях значения всех фенотипов были больше соответствующих средних значений. С помощью такого подхода были определены образцы сои, которые могут выступать в качестве желательных родительских пар при селекции по рассмотренным признакам.
Таблица 1. Коэффициент корреляции Пирсона между измеренными и предсказанными значениями признаков в рамках модели
Выбор родительских пар на основании показателя “продуктивность”
Сначала, авторы применили разработанную модель для подбора желательных родительских пар по признаку продуктивность. Для этого авторы разработали следующий критерий отбора: пара сортов является желательной, если значение продуктивности у всех ее потомков будет превышать среднее значение по популяции в 1.3 раза, это соотношение не фиксировано, определяется вариабельностью признака.
Отобранные таким образом родительские сорта тоже обладали высоким значением продуктивности (Фиг. 1А), однако, процентное содержание белка у возможных потомков пар, образованных ими, было ниже среднего, так как признаки продуктивность и процентное содержание белка в семенах отрицательно зависимы (Фиг. 1Б).
Выбор родительских пар на основании совокупности признаков - продуктивности и признаков, связанных с составом семян сои - содержанием белка и масла в семенах
Разработанная авторами модель позволяет получать совместное распределение значений фенотипических признаков для потенциальных потомков. Авторы использовали это свойство для того, чтобы оценить желательные родительские пары по целому ряду признаков одновременно: продуктивность, процентное содержание масла и процентное содержание белка. Авторы использовали следующий критерий: пара сортов является перспективной, если значения всех трех фенотипических признаков у всех ее возможных потомков во всех 10 моделях будут выше среднего по популяции. Количество моделей строго не фиксировано, но должно быть не меньше 5. Родительские сорта, участвующие в отобранных парах, представлены на Фиг. 2 (слева). У этих сортов помимо высокого значения продуктивности также присутствует высокое процентное содержание масла и белка, так что суммарно на белок и масло в родительских линиях в среднем приходится более 65% от композиционного состава семян. Стоит отметить, что родительские линии, оцененные на основании трех признаков, не совпадают с таковыми, отобранными на основании оценки одного признака. Таким образом, применение данной модели с использованием совместного распределения значений нескольких признаков у потенциальных потомков является предпочтительным перед селекцией по одному признаку.
Таким образом, главным преимуществом разработанной модели по сравнению с аналогичными моделями геномной селекции является то, что она оценивает селекционную ценность сорта сразу же по нескольким признакам, что важно в случае отрицательно скоррелированных признаков. Модель позволяет отделить прямые эффекты ОНП от плейотропных, обусловленных корреляционными связями между признаками
Несмотря на то, что изобретение описано со ссылкой на раскрываемые варианты воплощения, для специалистов в данной области должно быть очевидно, что конкретные подробно описанные случаи приведены лишь в целях иллюстрирования настоящего изобретения, и их не следует рассматривать как каким-либо образом ограничивающие объем изобретения. Должно быть, понятно, что возможно осуществление различных модификаций без отступления от сути настоящего изобретения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОТБОРА ЖИВОТНЫХ ПО ПРИЗНАКАМ, НАСЛЕДУЕМЫМ ПО МЕХАНИЗМУ РОДИТЕЛЬСКОГО ИМПРИНТИНГА | 1999 |
|
RU2262229C2 |
| СПОСОБ ОЦЕНКИ ЭФФЕКТИВНОСТИ СЕЛЕКЦИОННОЙ РАБОТЫ НА ОСНОВЕ ПОЛИЛОКУСНОГО ГЕНОТИПИРОВАНИЯ СЕЛЬСКОХОЗЯЙСТВЕННЫХ ЖИВОТНЫХ | 2020 |
|
RU2756922C2 |
| Способ отбора растений по генотипу | 1989 |
|
SU1741673A1 |
| РАСТЕНИЯ ОГУРЦА, УСТОЙЧИВЫЕ К ЗАБОЛЕВАНИЯМ | 2006 |
|
RU2418405C2 |
| СПОСОБ ПОЛУЧЕНИЯ ВЫСОКОПРОДУКТИВНЫХ РАСТЕНИЙ- САМООПЫЛИТЕЛЕЙ НА ОСНОВЕ ЭФФЕКТА ЗАКРЕПЛЕННОГО ГЕТЕРОЗИСА | 2003 |
|
RU2254709C1 |
| Способ оценки и отбора высокоурожайных генотипов сои по устьичной проводимости паров воды | 2017 |
|
RU2685151C1 |
| МОЛЕКУЛЯРНЫЕ МАРКЕРЫ НИЗКОГО СОДЕРЖАНИЯ ПАЛЬМИТИНОВОЙ КИСЛОТЫ В ПОДСОЛНЕЧНИКЕ (HELIANTHUS ANNUS) И СПОСОБЫ ИХ ПРИМЕНЕНИЯ | 2013 |
|
RU2670517C2 |
| СПОСОБ ОТБОРА ВЫСОКОПРОДУКТИВНЫХ ГЕНОТИПОВ КОНОПЛИ С ОПТИМАЛЬНЫМ СООТНОШЕНИЕМ ПЕРВИЧНОГО И ВТОРИЧНОГО ВОЛОКОН | 1991 |
|
RU2013044C1 |
| Маркеры для маркерной селекции сои по хозяйственно-полезным признакам | 2019 |
|
RU2740798C1 |
| СПОСОБ СЕЛЕКЦИИ УНИСЕКСУАЛЬНОЙ КОНОПЛИ | 1994 |
|
RU2077191C1 |
Изобретение относится к области селекции растений, в частности к способу идентификации родительских пар из набора растений, содержащего растения одного или разных сортов или линий, но при этом содержащего растения одного вида или одной сельскохозяйственной культуры, позволяющему получить у потомков этих пар желаемые значения для двух или более выбранных фенотипических признаков. Изобретение позволяет эффективно осуществлять геномную селекцию растений для получения потомков, имеющих сразу несколько желаемых фенотипических признаков. 2 з.п. ф-лы, 1 табл., 1 ил.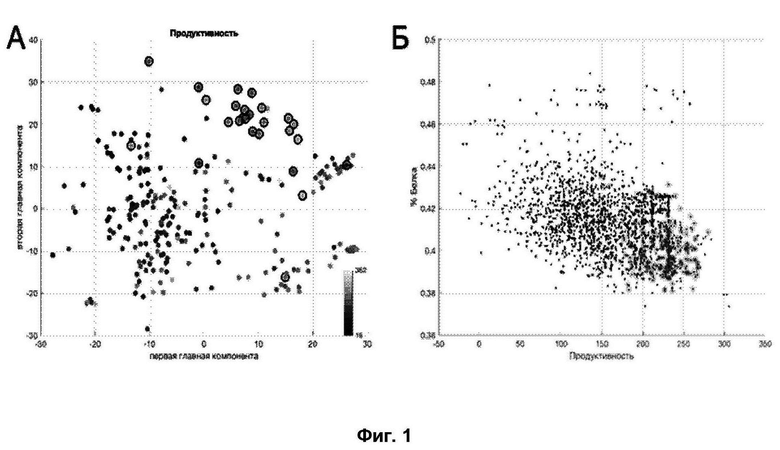
1. Способ идентификации родительских пар из набора растений, содержащего растения одного или разных сортов или линий, но при этом содержащего растения одного вида или одной сельскохозяйственной культуры, позволяющий получить у потомков этих пар желаемые значения для двух или более выбранных фенотипических признаков, включающий следующие стадии:
(а) выбирают два или более количественных фенотипических признака и определяют выбранные фенотипические признаки для всех растений из набора растений;
(б) проводят генотипирование для всех растений из набора растений, заключающееся в идентификации однонуклеотидных полиморфизмов (ОНП) в геномной ДНК этих растений, при этом выделяют не менее 1000 ОНП, различающихся хотя бы у двух растений набора;
(в) осуществляют факторный анализ выбранных фенотипических признаков и определяют латентные факторы, которые влияют на несколько скоррелированных фенотипических признаков;
(г) строят математическую модель, связывающую латентные факторы, фенотипические признаки и выделенные ОНП в направленный ациклический граф, поочередно добавляя ОНП в модель как переменные, влияющие на латентные факторы или на фенотипические признаки, при этом добавление ОНП в модель происходит следующим образом:
тестируют все ОНП и выбирают один, наибольшим образом увеличивающий значение функции правдоподобия выборочной ковариационной матрицы фенотипических признаков,
тестируют все оставшиеся ОНП таким же образом и выбирают следующий ОНП, наибольшим образом увеличивающий значение функции правдоподобия выборочной ковариационной матрицы фенотипических признаков,
добавляют ОНП поочередно до тех пор, пока добавление ОНП увеличивает значение функции правдоподобия выборочной ковариационной матрицы фенотипических признаков;
(д) отбирают родительскую пару из набора растений, содержащую такие ОНП, чтобы у всех возможных потомков этой пары значения всех выбранных фенотипических признаков, предсказанные по построенной математической модели, отвечали желаемым значениям.
2. Способ по п. 1, характеризующийся тем, что в качестве желаемых значений для всех выбранных фенотипических признаков указывают значения выше среднего по популяции, где популяция включает в себя растения одного вида или сельскохозяйственной культуры с указанным набором растений.
3. Способ по п. 1, характеризующийся тем, что в качестве фенотипических признаков выбирают по меньшей мере один из следующих: высота растений, количество семян на растение, урожайность семян, процентное содержание масла в семенах, процентное содержание белка в семенах, процентное содержание жирных кислот определенного типа.
| JOSE CROSSA et al., Genomic Selection in Plant Breeding: Methods, Models, and Perspectives, Trends in Plant Science, 2017, Vol | |||
| Машина для добывания торфа и т.п. | 1922 |
|
SU22A1 |
| Походная разборная печь для варки пищи и печения хлеба | 1920 |
|
SU11A1 |
| JEFFREY B | |||
| ENDELMAN, Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP, The Plant Genome, 2011, Vol.4, pp.250-255 | |||
| T.H.E.MEUWISSEN et al., Prediction of Total Genetic | |||
Авторы
Даты
2020-08-06—Публикация
2019-12-05—Подача