Изобретение относится к измерительной технике и может быть использовано для определения параметров избыточного шума изделий электронной техники при контроле их качества и прогнозировании отказов, а также в научных исследованиях.
Известен способ определения спектральной плотности мощности шума, в соответствии с которым шумовой сигнал пропускают через узкополосный фильтр, настроенный на частоту ω0, измеряют среднюю мощность на выходе фильтра, определяют среднюю спектральную плотность мощности шумового сигнала, для чего измеренную среднюю мощность шума делят на ширину Δω эффективной полосы пропускания фильтра. При этом средняя частота, которой соответствует средняя спектральная плотность мощности, остается неизвестной, но если полоса частот фильтра Δω значительно меньше, чем сама частота ω0, т.е. если Δω<<ω0, и изменение спектральной плотности на протяжении всей полосы значительно меньше величины средней спектральной плотности, то за среднюю частоту без особого ущерба для точности измерения можно принять частоту настройки ω0, а среднюю спектральную плотность принять за "истинную" спектральную плотность мощности на частоте ω0 (Ф.В. Кушнир, В.Г. Савенко. Электрорадиоизмерения "Энергия" Ленинградское отделение, 1975 г., стр. 346).
Если измеряемый шум является избыточным, или "розовым", как часто его еще называют, то данный способ позволяет определить все его параметры. Для этого достаточно измерить спектральные плотности мощности на двух разных частотах ω01 и ω02 с помощью фильтров, настроенных на эти частоты. Действительно, известно, что спектральная плотность мощности избыточного шума следующим образом зависит от частоты

где Sизб - спектральная плотность мощности избыточного шума;
ω - круговая частота;
γ - частотный индекс, который может принимать значения от 0,1 до 2,5;
В - размерный коэффициент пропорциональности, зависящий от тока, текущего через измеряемый объект.
Считается, что величины γ и В от частоты не зависят. Если измерены Sизб1 и и Sизб2 соответственно на частотах ω01 и ω02, то параметры γ и В можно определить из системы двух уравнений с двумя неизвестными, которая легко решается путем логарифмирования уравнений.
Недостатком рассматриваемого способа является то, что измерение мощности шума в очень узкой полосе частот сопряжено с длительным временем измерения, и чем уже полоса пропускания фильтров, тем более длительное время требуется для измерений с заданной степенью точности. Более того, чтобы измеренное значение средней мощности шума соответствовало именно избыточному шуму, необходимо, чтобы спектральная плотность мощности избыточного шума значительно превосходила спектральную плотность мощности "белых" шумов, которые всегда присутствуют, а для этого приходится вести измерения на низких и очень низких частотах, обеспечивая при этом условия, о которых говорилось выше. Построение фильтров, удовлетворяющих этим условиям на низких частотах встречает большие трудности, а продолжительность измерений катастрофически растет.
Наиболее близким к заявленному как раз и является способ определения параметров избыточного шума, в котором, руководствуясь известной зависимостью спектральной плотности мощности избыточного шума от частоты, определяют эту спектральную плотность вкупе с другими параметрами, характеризующими избыточный шум и используют при этом фильтры с не очень узкими эффективными полосами пропускания, лежащими в не слишком глубокой низкочастотной области (А.Л. Андреев и др. Способ определения параметров избыточного шума А.С. №1481694 G01R-29/26,1989 г.).
В этом способе измерения ведут на нескольких частотах ω1, ω2, …, ωn, …, а исследуемый шумовой сигнал усиливают и пропускают через фильтры с номерами 1, 2, …, n, …, настроенными определенным образом на эти частоты, причем эффективные полосы пропускания фильтров пропорциональны выбранным частотам, а сами эти частоты считают расположенными в определенных положениях в пределах соответствующих им полос пропускания. Первоначально в способе используют три частоты ω1, ω2 и ω3, измеряют средние мощности P1, Р2 и Р3 шумового напряжения на выходах фильтров 1, 2 и 3 путем квадратичного детектирования этого напряжения с последующим усреднением (интегрированием в течение того или иного фиксированного промежутка времени), определяют средние спектральные плотности мощности, для чего делят измеренные средние мощности P1, Р2 и Р3 на соответствующие эффективные полосы пропускания Δω1, Δω2 и Δω3. Затем, используя результаты определения средних спектральных плотностей мощности шума на выходах двух из трех задействованных фильтров, например, первого и третьего и рассматривая их как предполагаемые значения "истинных" спектральных плотностей на частотах ω1 и ω3, а сам измеряемый шум считая избыточным, определяют предполагаемые значения частотного индекса γ и коэффициента пропорциональности «В» по формулам, полученным в результате решения системы уравнений, о которой говорилось выше. Используя полученные предполагаемые значения параметров γ и «В», вычисляют предполагаемую спектральную плотность мощности шума на выходе второго фильтра по формуле (1) и сравнивают ее со значением 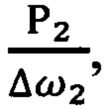 полученным в результате измерения. Если эти значения не совпадают, то проводят аналогичный цикл операций, но уже с использованием другой совокупности фильтров с другими частотами настройки и полосами пропускания. И эти циклы операций повторяют до тех пор, пока результаты вычислений и измерений не совпадут друг с другом (или, наверное, будут отличаться в пределах допустимой погрешности). Таким образом, в рассматриваемом способе предпринята попытка своего рода тестирования шума исследуемого объекта на соответствие избыточному шуму в надежде на то, что закон изменения спектральной плотности мощности с частотой, характерный для избыточного шума, как бы «узнает» себя в совпадении результатов измерений и вычислений, о которых говорилось выше.
полученным в результате измерения. Если эти значения не совпадают, то проводят аналогичный цикл операций, но уже с использованием другой совокупности фильтров с другими частотами настройки и полосами пропускания. И эти циклы операций повторяют до тех пор, пока результаты вычислений и измерений не совпадут друг с другом (или, наверное, будут отличаться в пределах допустимой погрешности). Таким образом, в рассматриваемом способе предпринята попытка своего рода тестирования шума исследуемого объекта на соответствие избыточному шуму в надежде на то, что закон изменения спектральной плотности мощности с частотой, характерный для избыточного шума, как бы «узнает» себя в совпадении результатов измерений и вычислений, о которых говорилось выше.
Значительное преобладание избыточного шума над шумами других типов (а таковыми являются «белые» шумы) может иметь место лишь при низких, а то и очень низких частотах, так как с уменьшением частоты спектральная плотность мощности избыточного шума растет, в то время как спектральная плотность мощности «белых» шумов остается неизменной. И если при последовательной смене совокупности трех частот соответствующие им полосы пропускания постепенно смещаются в низкочастотную область, то может наступить момент, когда степень преобладания избыточного шума над «белыми» шумами окажется достаточной для того, чтобы в пределах точности измерений вычисленные и измеренные значения спектральной плотности совпали друг с другом. Это позволило бы в процессе измерения вовремя остановиться и не проводить измерения на еще более низких частотах, на которых такое совпадение должно было бы наблюдаться и подавно, и избежать тем самым трудностей, связанных с измерениями на чрезмерно низких частотах.
Достоинством данного способа является то, что он позволяет двигаться в сторону низких частот не «вслепую», а руководствуясь сравнением результатов вычислений и измерений. Кроме того, в силу наличия такой возможности сам способ претендует на то, что результаты, полученные с его помощью, могли бы считаться надежными.
Одним из недостатков способа является то, что он содержит большое количество операций, а устройства, необходимые для реализации способа, сложны и громоздки. Действительно, для того, чтобы как можно раньше зафиксировать совпадение результатов измерений и вычислений и тем самым сполна использовать идею способа измерения желательно начинать «исподволь», на не очень низких частотах, а к более низким частотам переходить постепенно, причем заранее не известно, когда произойдет указанное совпадение и сколько понадобиться фильтров для его своевременной фиксации. Значит количество фильтров должно быть таким, чтобы обеспечить необходимый запас. При этом сами фильтры желательно выбирать с приблизительно прямоугольной амплитудно-частотной характеристикой (т.е. с достаточно крутыми фронтами и пологой вершиной), чтобы четко фиксировать ширину полосы пропускания и ее границы, а также и положения выбранных частот в пределах соответствующих им полос пропускания. Такие фильтры громоздки по конструкции и сложны в настройке. При использовании же более «ходовых» полосовых фильтров приходится оперировать понятием эффективной полосы пропускания, т.е. заменять реальную амплитудно-частотную характеристику воображаемым «прямоугольником». Это понятие весьма полезно при измерении «белых» шумов с их равномерной по частоте спектральной плотностью мощности, на него же уместно ориентироваться, например, при оценке необходимого времени усреднения квадрата шумового напряжения на выходе фильтра и т.д. Но при измерении избыточного шума с существенно неравномерной зависимостью его спектральной плотности мощности от частоты замена реальной передаточной функции фильтра прямоугольной ведет к увеличению погрешности в определении его параметров. Да и в случае достаточно прямоугольной характеристики фильтров в рассматриваемом способе содержатся неопределенности и нестыковки. Например, средняя спектральная плотность мощности, фигурирующая в способе, оставляет неопределенной частоту, которой она соответствует, а эта частота может и не совпадать с заданными частотами ω1 и ω3, которые используются в формуле для вычисления параметров избыточного шума. Правда, в способе эти частоты ω1, ω2, ω3, …, используемые при расчетах, все время обновляют (в зависимости от их номеров) свои положения в пределах соответствующих им полосах пропускания, возможно, как бы «сканируя» «истинные» средние частоты. Так или иначе, неопределенности этим не снимаются, и лишь только в процессе сужения полос пропускания они становятся не столь существенными. Невозможно избежать сужения полос пропускания в известном способе еще и потому, что для достижения достаточного превалирования избыточного шума над «белыми» шумами эти полосы и соответствующие им частоты все более и более должны «спускаться» в низкочастотную область, в которой эти полосы неизбежно сужаются. И если не брать в расчет уж слишком грубые измерения, то скорее всего, полосы пропускания, при которых произойдет совпадение результатов вычислений и измерений, окажутся все еще слишком узкими, а время проведения измерительных операций соответственно слишком большим. Словом, стремление повысить точность измерения параметров избыточного шума в известном способе все еще вступает в противоречие со стремлением уменьшить время проведения измерительных операций.
Задача изобретения состоит в том, чтобы обеспечить измерение параметров избыточного шума в условиях отсутствия значительного превалирования этого шума над «белыми» шумами, используя при этом простые по конструкции и удобные в настройке фильтры с не обязательно слишком узкими полосами пропускания, существенно уменьшив зависимость точности измерений от ширины этих полос, что позволило бы значительно сократить время проведения измерительных операций и упростить конструкцию измерительных устройств, необходимых для реализации способа.
Для решения поставленной задачи в способе определения параметров избыточного шума, в котором определение этих параметров ведут с использованием нескольких частот, а исследуемый шумовой сигнал усиливают и пропускают через фильтры, настроенные определенным образом на эти частоты, причем эффективные полосы пропускания фильтров пропорциональны выбранным частотам, а сами эти частоты считают расположенными в определенных положениях в пределах соответствующих им полос пропускания, измеряют средние мощности шумового напряжения на выходах фильтров путем его квадратичного детектирования с последующим усреднением (интегрированием в течение того или иного фиксированного промежутка времени) и, руководствуясь известной зависимостью спектральной плотности мощности избыточного шума от частоты, используют с помощью определенных вычислительных операций результаты этих измерений для определения параметров этой зависимости - частотного индекса γ, коэффициента пропорциональности «В», а также и самой спектральной плотности мощности, которую определяют по формуле (1), выбирают три частоты ω1, ω2 и ω3, а в качестве фильтров, настраиваемых на эти частоты, используют трехполосники, передаточная по напряжению функция которых может быть приведена к виду
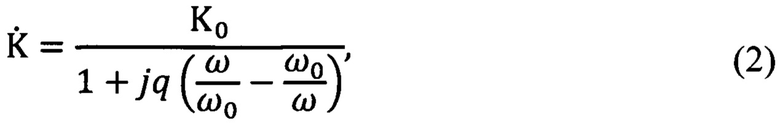
где 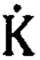 - комплексный коэффициент передачи фильтра;
- комплексный коэффициент передачи фильтра;
К0 - коэффициент передачи фильтра на частоте ω, равной ω0,
j - мнимая единица;
q - добротность (эквивалентная добротность) фильтра;
ω - текущая круговая частота;
ω0 - величина, имеющая размерность частоты, равная резонансной (квазирезонансной) частоте фильтра, и зависящая, как и безразмерные величины К0 и q, от параметров элементов конструкции фильтра,
причем значения резонансных частот ω01, ω02 и ω03, на которые настраивают фильтры 1, 2 и 3 совпадают с выбранными частотами ω1, ω2 и ω3, чем и определяется положение последних в пределах эффективных полос пропускания фильтров, а саму настройку фильтров на эти различные частоты осуществляют таким образом, что значения величин К0 и q у всех трех фильтров остаются одинаковыми, нумеруют для определенности частоты ω01, ω02 и ω03 таким образом, что выполняется соотношение

и проводят следующие вычислительные операции:
среднюю мощность напряжения шума, измеренную на выходе первого фильтра умножают на отношение частот настройки второго и первого фильтров и из полученного результата вычитают среднюю мощность, измеренную на выходе второго фильтра, в свою очередь мощность шума на выходе второго фильтра умножают на отношение частот настройки третьего и второго фильтров и из полученного результата умножения вычитают мощность шума, измеренную на выходе третьего фильтра, затем первую разность делят на вторую, а частотный индекс γ определяют в общем случае как решение трансцендентного уравнения
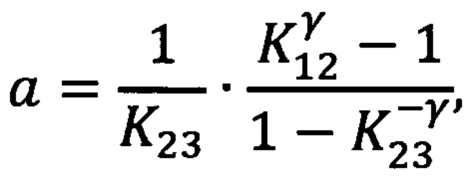
где 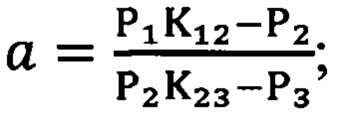
P1, Р2 и Р3 - средние мощности шума, измеренные на выходах соответственно первого, второго и третьего фильтров;
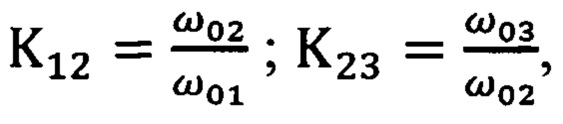
причем, если частоты ω01, ω02, ω03 выбирают такими, что выполняется соотношение

то частотный индекс γ определяют просто по формуле
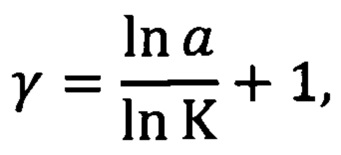
а полученное значение частотного индекса γ используют для определения коэффициента пропорциональности «В», для чего вычисляют интеграл
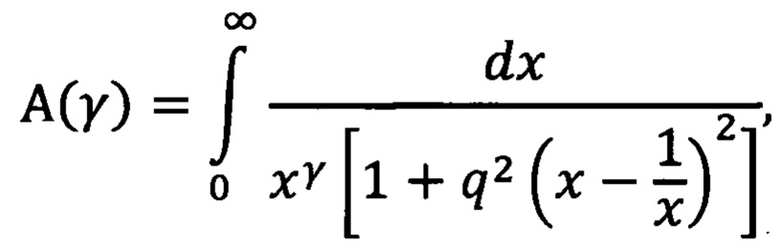
где х - отвлеченные действительные числа;
после чего коэффициент «В» вычисляют по любой из формул
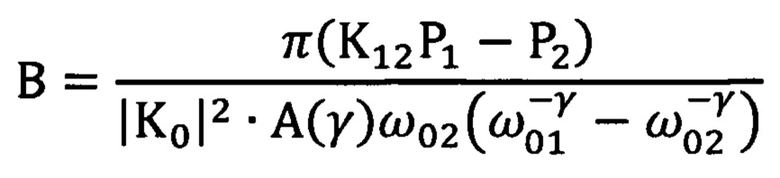
или
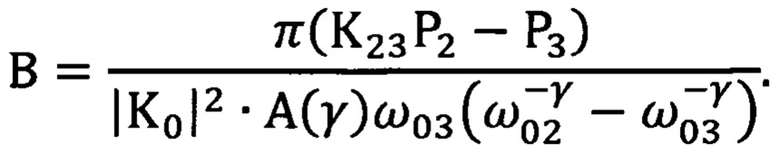
Измерение параметров избыточного шума в условиях отсутствия значительного его преобладания над белыми шумами в предложенном способе достигается за счет того, что как будет показано ниже, разности P1K12 - P2 и P2K23 - P3 не содержат параметра, характеризующего «белый» шум, а определяются только параметрами γ и «В» избыточного шума и выбранными частотами настройки фильтров. Отношение же указанных разностей не содержит и неизвестного параметра «В» и зависит только от отношений между выбранными частотами и от частотного индекса γ. Получающееся при этом трансцендентное уравнение для определения частотного индекса не зависит от добротности q фильтров и его можно использовать не только в случае узких полос пропускания, но и в довольно широких. В общем случае уравнение это довольно сложно для решения, но если частоты ω01, ω02 и ω03 выбраны специальным образом, о котором говорилось выше, то оно сильно упрощается. Определение коэффициента пропорциональности «В» оказалось связанным с вычислением интеграла А(γ). Замечательно, что этот интеграл сходится при любом возможном значении параметра γ. Это обстоятельство явилось одной из причин, по которой авторы остановились на выборе фильтров с передаточной функцией вида (2). К тому же эти фильтры удобны в настройке и значительно проще фильтров с прямоугольной характеристикой. Предложенный способ свободен от использования понятия «средняя спектральная плотность мощности». Использование этого понятия было бы не совсем уместным при измерения в не слишком узких полосах пропускания, поскольку, как мы уже неоднократно подчеркивали, остается неизвестной средняя частота, соответствующая средней спектральной плотности мощности. В способе измеряют лишь средние мощности шума на выходах фильтров и этого в нем вполне достаточно для определения параметров избыточного шума. При этом в отличие от известного способа, в котором формулы для расчета параметров избыточного шума γ и «В» предполагают знание спектральных плотностей мощности на выбранных частотах, в качестве которых в действительности выступают лишь средние спектральные плотности на этих частотах, предложенный способ позволяет подойти к определению спектральной плотности мощности на любой частоте через параметры избыточного шума γ и «В», так сказать, более «окольным» путем в том смысле, что само определение параметров γ и «В» не связано в нем с непосредственным определением спектральной плотности на тех или иных конкретных частотах. Предложенный способ позволяет, таким образом, освободиться от непосредственного определения спектральной плотности на конкретных частотах через среднюю спектральную плотность, неизбежно связанного с измерением мощности шума в очень узких полосах пропускания и открыть тем самым дорогу к использованию более широких полос пропускания и, как следствие, к сокращению времени проведения измерительных операций.
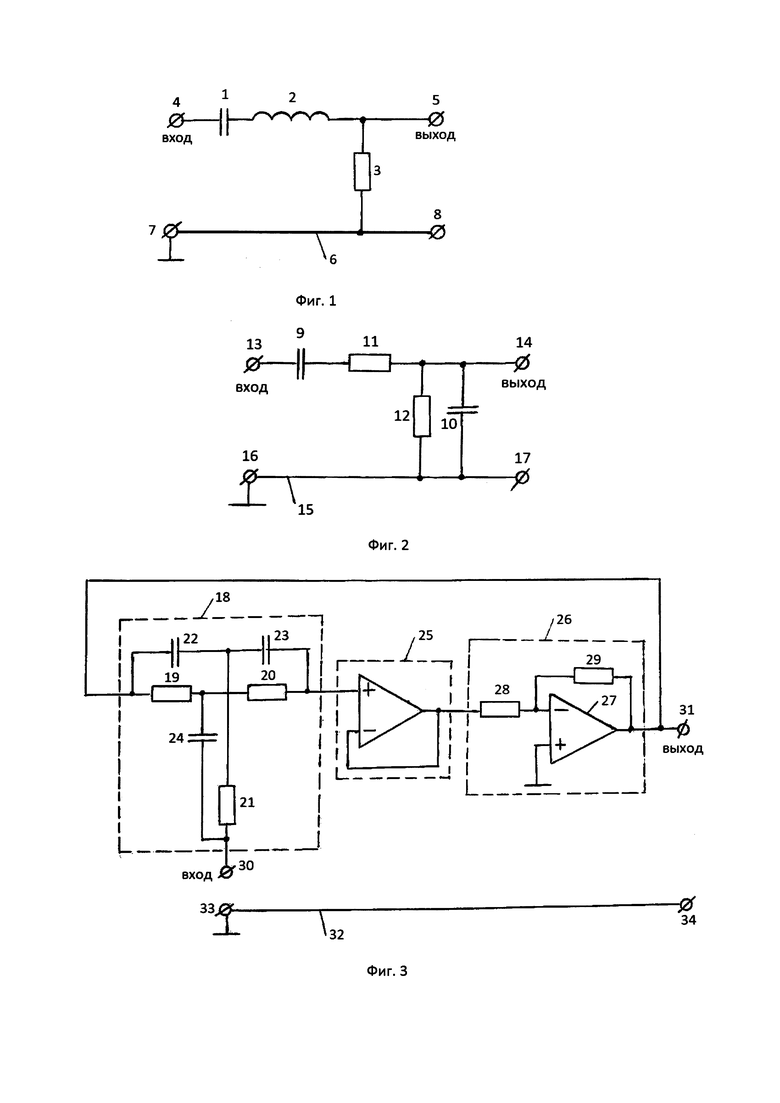
Фильтры с передаточной функцией вида (2) широко распространены в измерительной технике. Они могут быть как пассивными, так и активными. На фигурах 1, 2 и 3 приведены примеры таких фильтров, не исчерпывающие, конечно, всех возможных вариантов их исполнения. Проиллюстрированы также возможности их настройки на разные резонансные частоты при неизменных и одинаковых для всех трех фильтров параметрах q и К0. На фиг. 1 представлен пассивный RZC-фильтр. Он содержит конденсатор 1, катушку индуктивности 2, резистор 3, входной зажим 4, выходной зажим 5 и общую шину 6 с зажимами 7 и 8. На фиг. 2 изображен пассивный RC-фильтр, содержащий конденсаторы 9 и 10, резисторы 11 и 12, входной зажим 13, выходной зажим 14, общую шину 15 с зажимами 16 и 17.
Наконец, на фиг. 3 приведен пример активного RC-фильтра, содержащего двойной Т-образный мост 18 с резисторами 19, 20 и 21 и конденсаторами 22, 23 и 24, повторитель напряжения 25, инвертирующий усилитель 26, выполненный на базе операционного усилителя 27 с масштабными резисторами 28 и 29, входной зажим 30, выходной зажим 31, общую шину 32 с зажимами 33 и 34.
Каждый из этих фильтров настраивают на разные частоты ω0 таким образом, что величины К0 и q у них остаются одинаковыми. Осуществить это несложно, но частоту настройки, зависящую от параметров входящих в фильтр элементов, необходимо в каждом конкретном случае изменять определенным образом, чтобы сохранить неизменными К0 и q, которые также зависят от параметров элементов фильтров. Это можно проиллюстрировать на примерах.
Передаточная функция фильтра, изображенного на фиг. 1 имеет вид
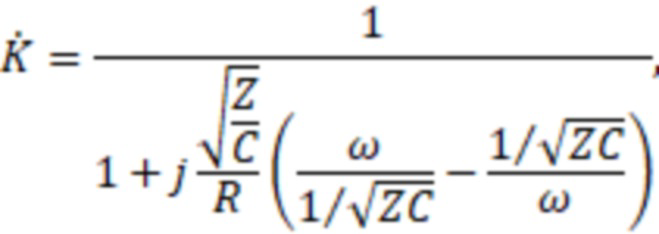
где Z, С и R - соответственно индуктивность катушки индуктивности 2, емкость конденсатора 1 и сопротивление резистора 3.
Она соответствует виду (2). Стало быть у этого фильтра 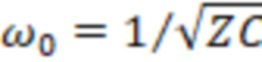 ; К0=1 и ни от чего не зависит;
; К0=1 и ни от чего не зависит; 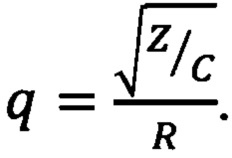 И для сохранения добротности неизменной при перестройке частоты достаточно Z и С увеличивать или уменьшать в одинаковое число раз. Если при этом сопротивление резистора 3 у всех трех фильтров одинаково, то одинаковы будут и добротности всех фильтров.
И для сохранения добротности неизменной при перестройке частоты достаточно Z и С увеличивать или уменьшать в одинаковое число раз. Если при этом сопротивление резистора 3 у всех трех фильтров одинаково, то одинаковы будут и добротности всех фильтров.
В случае фильтра, изображенного на фиг. 2, можно показать, что его передаточная функция тоже имеет вид (2), в котором
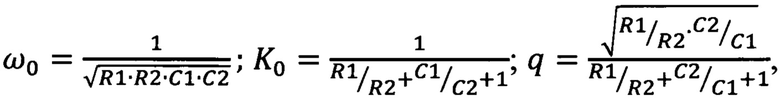
Где R1 и R2 - соответственно сопротивления резисторов 11 и 12;
С1 и С2 - соответственно емкости конденсаторов 9 и 10.
Из этих соотношений видно, что изменяя сопротивления R1 и R2 в одинаковое число раз можно регулировать частоту ω0, оставляя неизменными значения величин К0 и q. Обычно в таких фильтрах выбирают
R1=R2=R; С1=С2=С,
тогда
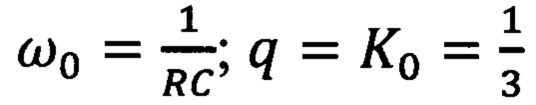
Несколько более сложным оказывается процесс перестройки частоты у активного фильтра, изображенного на фиг. 3. Можно показать, что если, например, выполняются соотношения
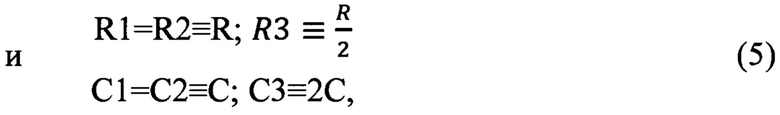
где R1, R2 и R3 - сопротивления резисторов 19, 20 и 21 Т-образного моста 18;
C1, С2 и С3 - емкости конденсаторов 22, 23 и 24 моста 18, то коэффициент передачи фильтра может быть представлен в виде
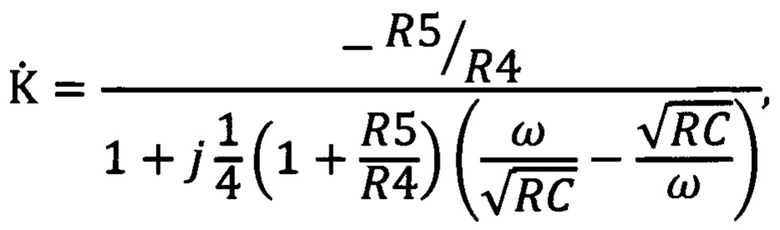
где R5 и R4 - сопротивления масштабных резисторов 29 и 28 инвертирующего усилителя 26.
Сравнивая это выражение с соотношением (2), приходим к выводу, что
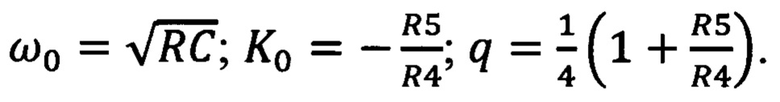
И перестройку частоты можно вести путем изменения R1, R2 и R3 таким образом, чтобы соотношения (5) оставались в силе. Добротность у этого фильтра можно изменять регулировкой отношения 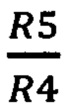 в широких пределах. С изменением добротности будет изменяться и К0. То, что величина К0 у этого фильтра оказалась отрицательной, свидетельствует о том, что на частоте квазирезонанса ω0 входное и выходное напряжения фильтра колеблются в противофазах.
в широких пределах. С изменением добротности будет изменяться и К0. То, что величина К0 у этого фильтра оказалась отрицательной, свидетельствует о том, что на частоте квазирезонанса ω0 входное и выходное напряжения фильтра колеблются в противофазах.
В вычислительных операциях в предложенном способе фигурирует интеграл
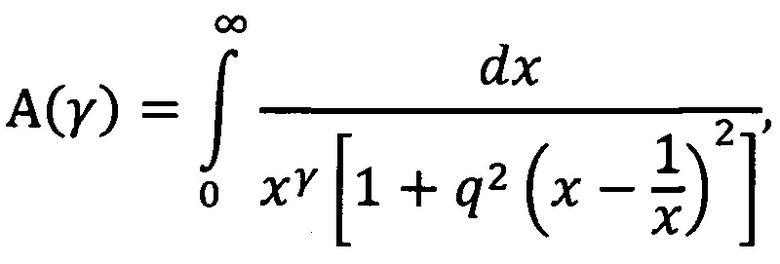
который при уже выбранном значении добротности q фильтров можно считать функцией параметра γ. Этот интеграл является несобственным по верхнему пределу. Более того, при значениях γ больших 2 он является несобственным и по нижнему пределу, поскольку при этих значениях γ подынтегральная функция при стремлении х к нулю обращается в бесконечность. Но можно показать, что этот несобственный интеграл при любых значениях добротности q, больших нуля, сходится, если значение параметра γ меньше, чем 3, что с запасом перекрывает все возможные значения частотного индекса γ. Довольно любопытные свойства этого интеграла и вопросы, связанные с его вычислением, рассмотрены в Приложении к тесту описания данной заявки.
Сущность способа поясняется следующим образом.
Пусть на входы фильтров поступает аддитивная смесь «белого» шума и избыточного шума. Спектральная плотность мощности S(ω) этой смеси есть
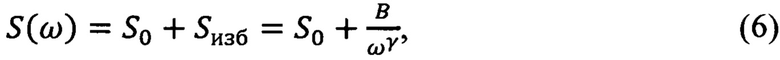
где S(ω) - спектральная плотность мощности смеси;
S0 - спектральная плотность мощности «белого» шума, которая от частоты не зависит.
При этом средняя мощность шума (т.е. средний квадрат напряжения шума) на выходе линейного фильтра выражается, как известно, соотношением
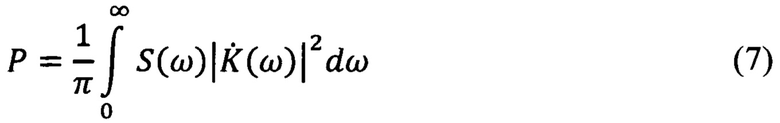
где Р - средняя мощность шума на выходе фильтра, которая в способе измеряется;
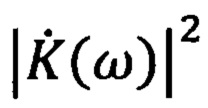 - квадрат модуля комплексного коэффициента передачи фильтра.
- квадрат модуля комплексного коэффициента передачи фильтра.
Используя формулы (2) и (6) и обозначив через «n» номер фильтра, напишем выражение (7) для фильтра с номером n в виде

или
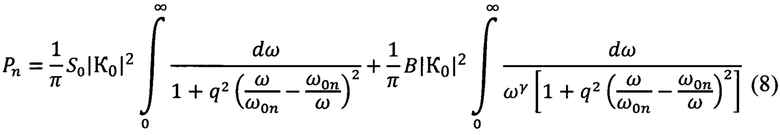
В этих формулах индекс «n» у величин K0 и q отсутствует, поскольку эти величины у всех трех фильтров одинаковы. Можно показать, что оба несобственных интеграла в формуле (8) сходятся при любых возможных значениях параметра γ и любых значениях добротности q, отличных от нуля.
Проведем в последней формуле замену переменной

тогда
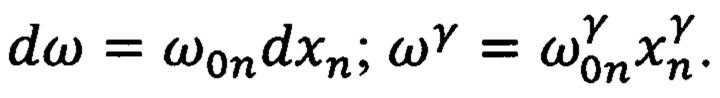
Очевидно, что пределы интегрирования при этом не изменятся, а выражение (8) примет следующий вид
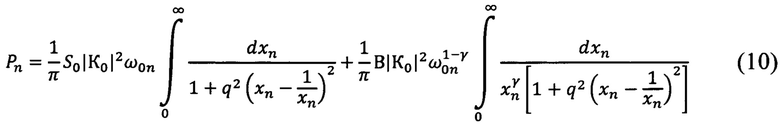
Подынтегральные выражения в этом соотношении зависят от номера n фильтра, ибо переменные xn у них различны, как явствует из формулы (9). Но так как сами интегралы берутся от одних и тех же функций этих переменных и в одних и тех же пределах интегрирования, они не зависят от номера n, так что значок «n» у этих переменных можно опустить.
Введем обозначения
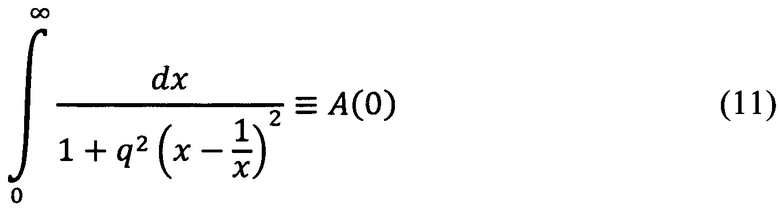
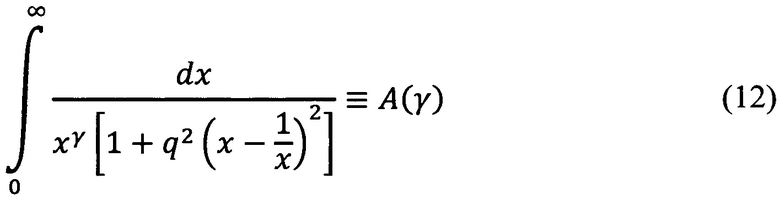
Между прочим, нетрудно усмотреть, что интеграл A(0) есть коэффициент пропорциональности между частотами настройки фильтров ω0n и их эффективными полосами пропускания Δω0n, т.е. имеет место соотношение
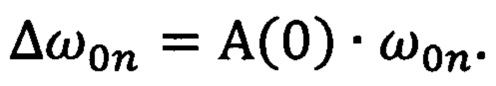
Отметим, что, как показывают вычисления, 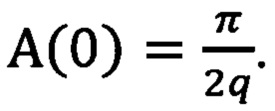
С учетом обозначений (11) и (12) выражение (10) можно переписать в виде
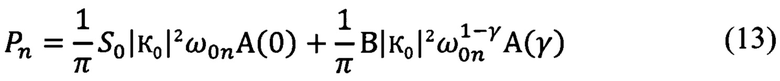
А придавая индексу «n» значения 1, 2 и 3, получим выражения для средних мощностей шума на выходах фильтров 1, 2 и 3, которые измеряют в способе путем аппаратурного возведения напряжения шума в квадрат с последующим усреднением (интегрированием в течение того или иного фиксированного промежутка времени)
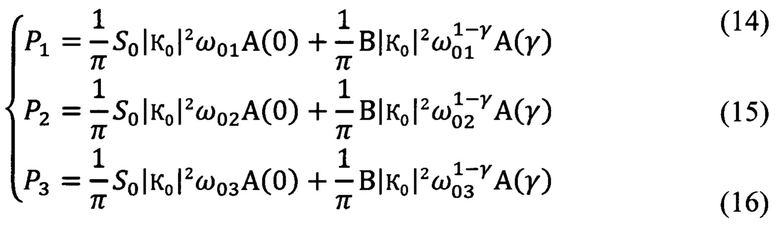
В способе умножают среднюю мощность на выходе первого фильтра на отношение частот настройки второго и первого фильтров. Из соотношения (14) следует, что
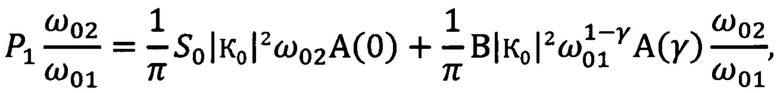
определяют разность 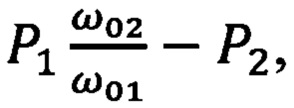 которая с учетом соотношения (15) равна
которая с учетом соотношения (15) равна
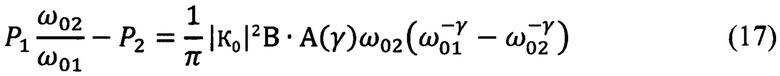
Затем умножают среднюю мощность Р2 на выходе второго фильтра на отношение 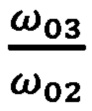 частот настройки третьего и второго фильтров и вычитают из полученного произведения мощность Р3 на выходе третьего фильтра. Из соотношений (15) и (16) следует:
частот настройки третьего и второго фильтров и вычитают из полученного произведения мощность Р3 на выходе третьего фильтра. Из соотношений (15) и (16) следует:
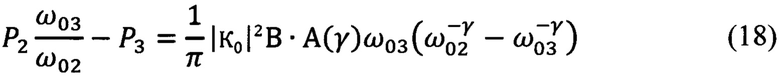
Далее делят одну разность на другую, например, первую (17) на вторую (18):
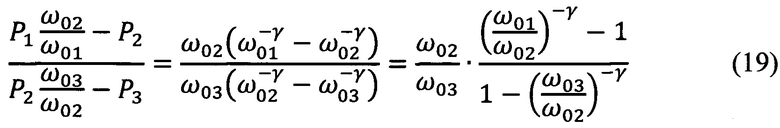
Обозначим:

Подставив эти обозначения в соотношение (19), получим:
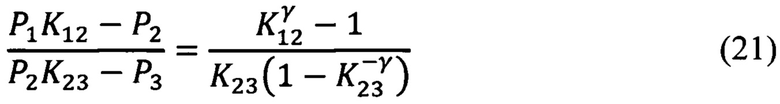
Обозначим еще
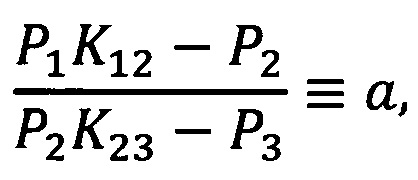
тогда выражение (21) запишется в виде

Очевидно, К12<1 и К23<1 ввиду неравенства (3). Величина а, полученная в результате измерения мощностей на выходах фильтров, должна оказаться положительной, поскольку положительна правая часть выражения (22), в которой числитель и знаменатель отрицательны.
Для определения частотного индекса γ решают трансцендентное уравнение (22). Можно показать, что правая часть уравнения (22) монотонно изменяется (убывает) с увеличением γ, поэтому решение этого уравнения может быть только единственным. Для решения уравнения, например, заблаговременно составляют таблицы зависимости его правой части от γ, строят соответствующий график, по которому по результатам определения величины а находят искомое значение γ или решают уравнение с применением процессорной техники.
Впрочем, если выбирают частоты настройки ω01, ω02 и ω03 фильтров такими, что выполняется соотношение

то уравнение (22) сильно упрощается и дело сводится, как нетрудно проверить, к вычислению γ по формуле

Нетрудно видеть также, что соотношение (23) окажется выполненным, если частота ω02 будет равной среднему геометрическому частот ω01 и ω03, т.е. если
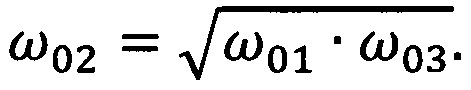
Измеренное значение γ используют для определения коэффициента пропорциональности В, для чего вычисляют интеграл
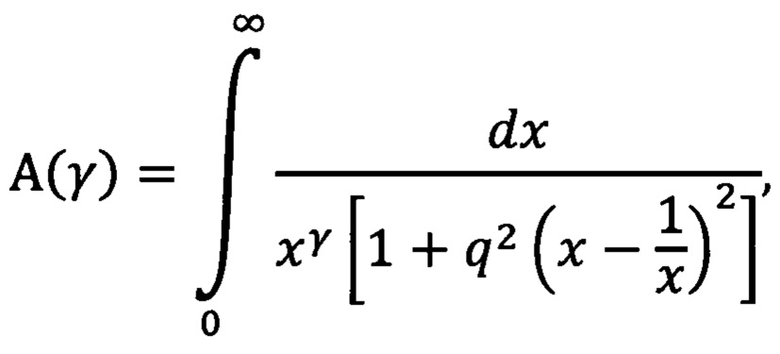
а значение коэффициента «В» вычисляют, используя соотношение (17) или (18). Например, из соотношения (17) следует, что
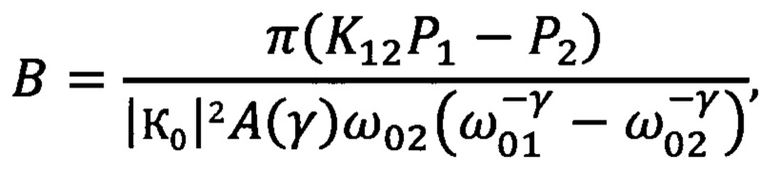
а из соотношения (18) -
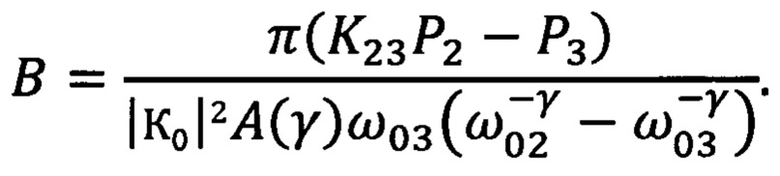
И по результатам определения параметров γ и «В» вычисляют спектральную плотность мощности избыточного шума на любой частоте его спектра по формуле (1).
Таким образом, предложенный способ действительно позволяет с использованием известной зависимости спектральной плотности мощности избыточного шума от частоты определить параметры этой зависимости - частотный индекс γ и коэффициент пропорциональности В, а через них и саму спектральную плотность мощности на любой частоте, не прибегая, в отличие от известного способа, к непосредственному определению спектральной плотности мощности на тех или иных различных частотах, которое непременно было бы связано с измерениями мощности шума в очень узких полосах пропускания. При этом в предложенном способе преодолено влияние «белых» шумов на результат определения параметров γ и В, не прибегая для этого использования частот, лежащих в глубокой низкочастотной области, в котором избыточные шумы значительно преобладали бы над «белыми» шумами, что также влекло бы за собой сужение полос пропускания.
Поэтому предложенный способ действительно позволяет определить параметры избыточного шума в отсутствии значительного его превалирования над «белыми» шумами и с использованием не слишком узких полос пропускания, за счет чего значительно уменьшить время проведения измерительных операций.
Приложение. О некоторых свойствах интеграла А(γ) и вопросах, связанных с его вычислением.
Рассматриваемый интеграл
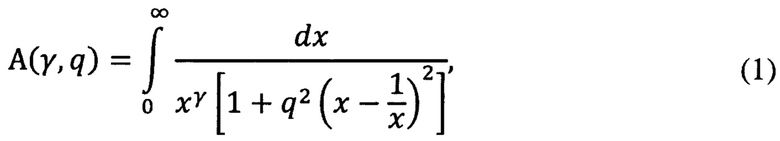
поскольку он сходится, является функцией двух параметров γ и q. Параметр q зависит от используемых в способе фильтров, а значение параметра γ становится известным в результате измерений и вычислений, проводимых с помощью данного способа. Однако для упрощения записи мы будем часто, как и в тексте Описания, обозначать этот интеграл в виде функции одного аргумента, т.е. через А(γ).
К сожалению, вряд ли интеграл А(γ, q) может быть в общем случае выражен с помощью элементарных функций от γ и q. Даже при фиксированном значении q, зависимость А(γ) скорее всего непредставима в общем случае в виде совокупности элементарных функций, так же, как и при фиксированном значении γ зависимость A(q) непредставима в общем случае в виде конечного числа элементарных функций от q. Правда, при некоторых значениях γ, таких, например, как 0; 0,5; 1; 1,5; 2; 2,5 интеграл может быть вычислен точно в виде функции от q, ибо первообразные от подынтегральной функции в этих случаях выражаются с помощью конечного числа элементарных функций. При вычислении таких интегралов полезно представить интеграл (1) в виде
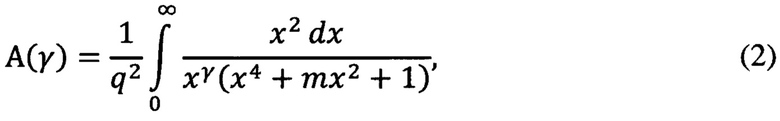
где 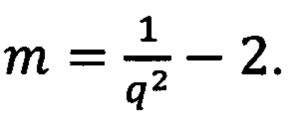
При этом дело сводится к определению первообразных от дробно-рациональной функции от х или от какой-либо другой переменной, зависящей от х. После подстановки в эти первообразные пределов интегрирования результат выражается в виде функции от q. Кроме того, эти первообразные могли бы служить ориентирами для выбора подходящего конечного верхнего предела интегрирования х0, которым можно было бы заменить бесконечность при интегрированиях приближенными численными методами, а также и для выбора нижнего, отличного от нуля, предела интегрирования в тех случаях, когда подынтегральная функция при стремлении х к нулю обращается в бесконечность. Отметим в этой связи, что по верхнему пределу интегралы А(γ) сходятся равномерно относительно параметра γ при всех возможных его значениях. Они сходятся равномерно также и по нижнему пределу относительно значений γ, лежащих в пределах 2<γ<3, т.е. при тех его значениях, при которых интеграл является несобственным по нижнему пределу. Это обстоятельство позволяет при заданной точности приближенных вычислений выбрать верхний предел интегрирования, отличный от бесконечности, общим для всех значений γ, лежащих в пределах того или иного диапазона (или поддиапазона). Это же можно сказать и о выборе нижнего, отличного от нуля предела интегрирования в тех случаях, когда такой выбор необходим. Использование этой возможности может упростить процесс приближенных вычислений и разработку программы для их проведения.
Можно было указать еще на ряд значений параметра γ, при которых подынтегральное выражение представляло бы дробно-рациональную функцию, но определение первообразной в этих случаях оказались бы уже слишком громоздкими (хотя любителей алгебраических вычислений это обстоятельства, возможно, и не смутило бы).
Так что, при произвольных возможных значениях параметра γ следует заменить верхний предел интегрирования, равный бесконечности, на подходящий конечный предел х0 и при фиксированном значении добротности q прибегнуть к приближенным численным методам интегрирования, используя процессорную вычислительную технику. Верхний предел х0 может быть различным для разных поддиапазонов изменений параметра γ, но одним и тем же в пределах одного поддиапазона. Что касается нижнего, отличного от нуля, предела интегрирования, то на его выборе мы пока внимания не заостряем, тем более, что, как выяснится из дальнейшего, при желании можно вообще избежать в нем необходимости.
Вычисления можно проводить прямо «по ходу дела» в процессе измерительного цикла.
Но лучше, пожалуй, поступить по-другому - провести эти вычисления заблаговременно для различных значений параметра γ и составить таблицы, которые можно было бы использовать в процессе измерения, в том числе и опять-таки прибегнув к помощи процессорной техники (выбор этих вариантов - на усмотрение разработчиков конкретного устройства, реализующего способ, и программы проведения вычислительных операций).
Численное интегрирование можно осуществить, например, методом прямоугольников, в котором интервал интегрирования разбивают на мелкие части, берут значение х в середине каждого частичного интервала, умножают соответствующее ему значение подынтегральной функции на длину частичного интервала и суммируют все эти произведения (См., например, М.Я. Выгодский. Справочник по высшей математике, 1956 г., стр. 478-480).
Главным вопросом во всех этих приближенных численных интегрированиях является выбор интервала интегрирования, т.е. значения конечного верхнего предела интегрирования х0, при котором отличие интеграла, вычисленного в пределах 0 - x0 от интеграла, вычисленного в пределах 0 - ∞ не превышало бы по абсолютной величине заданного значения.
Но прежде, чем обсуждать этот вопрос, полезно обратить внимание на одно, замеченное авторами данной заявки, довольно любопытное свойство, присущее рассматриваемым интегралам. Можно показать в самом общем виде и не прибегая даже к вычислению самих интегралов, что при фиксированных значениях добротности q интегралы А(γ) при любых возможных значениях γ, равноотстоящих по обе стороны от значения γ=1, равны друг другу. Например, значения интеграла А(γ) при γ=0,5 и при γ=1,5 равны между собой, т.е. A(0,5)=A(1,5). Точно также равны, например, интегралы A(0,3) и А(1,7) и т.д. Иными словами, значение γ=1 является средним между значениями γ1 и γ2, при которых интегралы равны, т.е. сами эти значения удовлетворяют соотношению

в пределах возможных значений γ.
Под возможными значениями γ здесь мы понимаем те его значения, при которых интегралы А(γ) сходятся. Но, оказывается, что они сходятся и при отрицательных значениях γ, если они по абсолютной величине меньше единицы. В действительности γ не могут быть отрицательными, но воображаемые отрицательные его значения, имеющие в нашем случае лишь формальный смысл, могут тем не менее пригодиться, как будет видно из дальнейшего, при вычислении интегралов с «нормальными» положительными значениями γ. Например, интегралу А(2,5) соответствует равный ему интеграл А(-0,5), что следует из соотношения (3).
Характер зависимости А(γ) изображен на фиг. 1. На нем кривая 1 соответствует 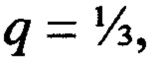 кривая 2 - добротности q=1, а кривая 3, которая больше напоминает прямую - добротности q=10. Продолжение левого относительно γ=1 участка зависимости для воображаемых отрицательных значений γ изображено на фигуре пунктиром. Кривые симметричны относительно перпендикуляра γ=1 и имеют по нашим прикидкам минимум при γ=1 с равной нулю производной
кривая 2 - добротности q=1, а кривая 3, которая больше напоминает прямую - добротности q=10. Продолжение левого относительно γ=1 участка зависимости для воображаемых отрицательных значений γ изображено на фигуре пунктиром. Кривые симметричны относительно перпендикуляра γ=1 и имеют по нашим прикидкам минимум при γ=1 с равной нулю производной 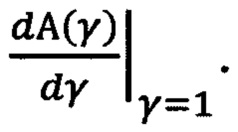
Только что отмеченное свойство интеграла A(γ) может быть использовано для уменьшения количества вычислительных операций. Действительно, пусть для каждого возможного значения параметра γ1, взятого из области значений γ, больших единицы, известен интеграл А(γ1), тогда значение интеграла А(γ2) при γ2, взятого из области значений переменной γ меньших единицы, будет просто равно значению интеграла А(γ1) при γ1=2-γ2, как явствует из соотношения (3). И наоборот, если известен интеграл А(γ2) для каждого возможного значения γ2, взятого из области значений γ, меньших единицы, то значение интеграла А(γ1) при γ1, взятого из области значений γ 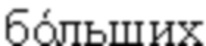 единицы, будет равно значению интеграла А(γ2) при γ2=2-γ1.
единицы, будет равно значению интеграла А(γ2) при γ2=2-γ1.
Однако области со значениями γ, 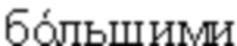 единицы и меньшими единицы кажутся не вполне равноценными с точки зрения выбора верхнего конечного предела интегрирования х0, обеспечивающего степень отличия вычисленного интеграла с верхним пределом х0 от его истинного значения, не превышаемую требуемой величины. Дело в том, что подынтегральные функции интегралов А(γ) и А(2-γ) сильно отличаются друг от друга. Отличаются и первообразные этих функций, несмотря на то, что интегралы в пределах 0 - ∞ равны между собой. Фиг. 2 иллюстрирует сказанное. На ней изображены графики трех подынтегральных функций при
единицы и меньшими единицы кажутся не вполне равноценными с точки зрения выбора верхнего конечного предела интегрирования х0, обеспечивающего степень отличия вычисленного интеграла с верхним пределом х0 от его истинного значения, не превышаемую требуемой величины. Дело в том, что подынтегральные функции интегралов А(γ) и А(2-γ) сильно отличаются друг от друга. Отличаются и первообразные этих функций, несмотря на то, что интегралы в пределах 0 - ∞ равны между собой. Фиг. 2 иллюстрирует сказанное. На ней изображены графики трех подынтегральных функций при 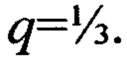 Кривая 1 - подынтегральная функция интеграла
Кривая 1 - подынтегральная функция интеграла
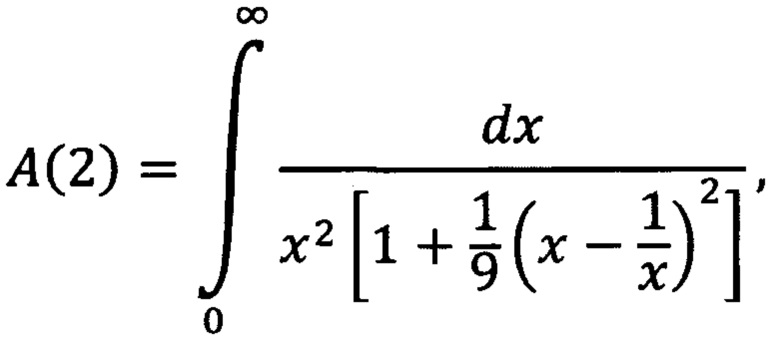
кривая 2 - подынтегральная функция интеграла
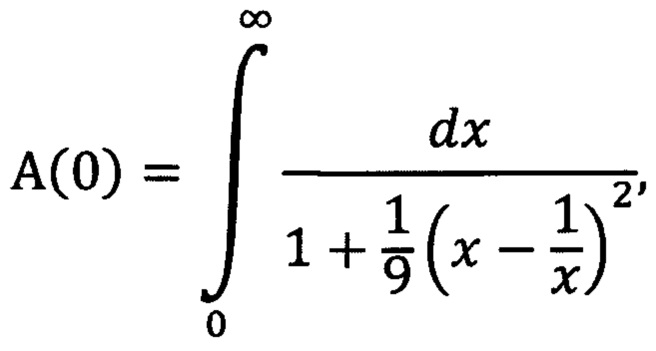
кривая 3 - подынтегральная функция интеграла
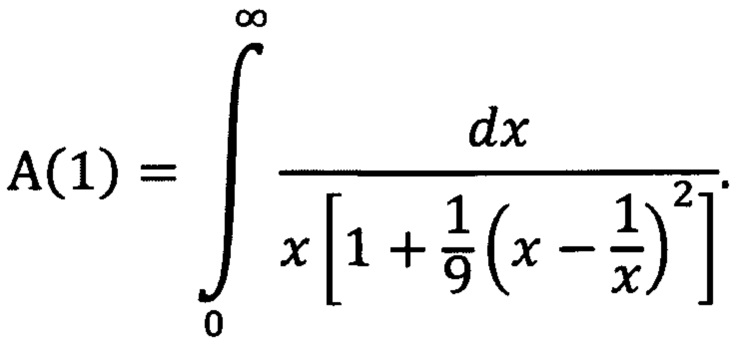
Интегралы А(2) и А(0) равны друг другу. Между тем их подынтегральные функции (кривые 1 и 2) сильно отличаются, хотя площади под этими кривыми в пределе одинаковы. Из графиков видно, что основная часть всей «массы» интеграла А(2) сосредоточена в пределах 0-10 изменения независимой переменной х, в то время как эта основная часть равного ему интеграла А(0) распределена вдоль оси х гораздо более равномерно. В результате, как показывают конкретные расчеты, при γ=2 интеграл 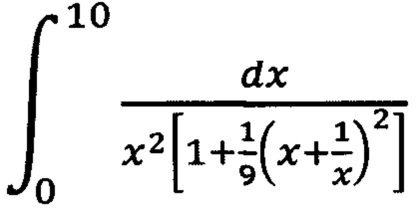 с верхним пределом х0=10 отличается от интеграла от той же подынтегральной функции, но с верхним пределом, равным бесконечности, не более, чем на десятые доли процента. Но для того, чтобы при γ=0 достигнуть такой же достаточно малой степени отличия интегралов
с верхним пределом х0=10 отличается от интеграла от той же подынтегральной функции, но с верхним пределом, равным бесконечности, не более, чем на десятые доли процента. Но для того, чтобы при γ=0 достигнуть такой же достаточно малой степени отличия интегралов 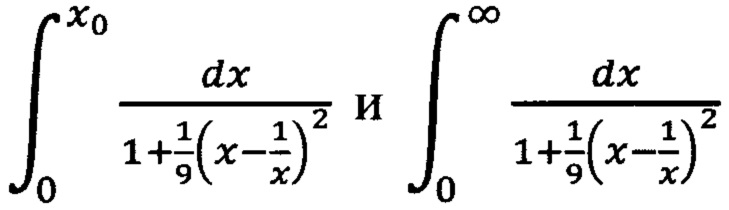 необходимо, как оказалось, верхний предел х0 выбрать равным ~500!
необходимо, как оказалось, верхний предел х0 выбрать равным ~500!
Это обстоятельство необходимо учитывать при конкретной разработке программы приближенного вычисления интегралов.
Точкой разграничения областей 1 и 2, в которых значения γ соответственно больше и меньше единицы является, естественно γ=1. Из графика подынтегральной функции, соответствующей А(1) (кривая 3 на фиг. 2) видно, что, возможно, требуемое значение верхнего предела интегрирования х0 равно ~20, но только путем конкретного расчета можно определить каким оно будет именно, причем нетрудно усмотреть, что для других значений γ, больших единицы оно было бы таким и подавно. Первообразная подынтегральной функции интеграла А(1) сравнительно легко вычисляется и определяется в виде функции х и добротности q. Следовательно, есть прямая возможность сравнить интегралы 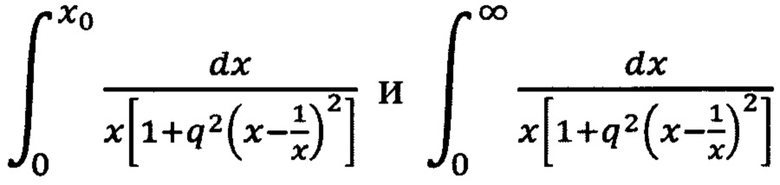 и при выбранной добротности фильтров выбрать подходящее значение х0 и использовать его для приближенных вычислений интегралов со значениями γ1,
и при выбранной добротности фильтров выбрать подходящее значение х0 и использовать его для приближенных вычислений интегралов со значениями γ1, 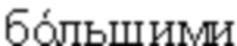 единицы, или со значениями γ2 меньшими единицы, «приведенными» к значениям γ1
единицы, или со значениями γ2 меньшими единицы, «приведенными» к значениям γ1 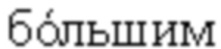 единицы, в соответствии с формулой (3).
единицы, в соответствии с формулой (3).
При вычислениях методом прямоугольников интервал 0 - х0 следует разбить на ряд частичных интервалов, которые могут отличаться не только протяженностью, но и степенью дробления на «элементарные» интервалы. При вычислениях в области, в которой γ>1 смутить может то обстоятельство, что при γ>2 дробление участка вблизи нуля должно быть очень мелким, поскольку подынтегральная функция в этом случае изменяется на этом участке очень круто (стремится к бесконечности при х→0). Начальный интервал 0-0,1 в этом случае следует разбить предположительно хотя бы на 10 частей, а «самый начальный» интервал 0-0,01 при этом в свою очередь желательно разбить еще на 10 или даже на 20 частей. Однако определить, какова именно должна быть степень дробления можно лишь в том случае, если известен нижний, отличный от нуля, предел интегрирования, обеспечивающий требуемую точность вычислений. Для его определения в области значений γ, лежащих в пределах 2<γ≤2,5, можно воспользоваться интегралом А(2,5), первообразная подынтегральной функции которого определяется аналитическими методами. Если необходимость такого мелкого дробления приведет разработчика программы в замешательство (хотя и напрасно), то можно для вычислений использовать область в которой γ<1, поскольку в этой области подынтегральные функции изменяются гораздо медленнее. Верхний предел х0 при этом сильно возрастет, но и продвигаться к нему можно будет, начиная с некоторых значений переменной х, гораздо более крупными «шагами» ввиду большой плавности изменения подынтегральной функции.
Но для определения конкретной величины х0 в этом случае необходимо использовать не точку γ=1, а точку γ=-0,5, которая является точкой γ=2,5, «приведенной» к области, в которой γ<1. Первообразная подынтегральной функции интеграла А(-0,5) тоже может быть найдена путем не слишком громоздких выкладок, что позволяет, сравнивая интегралы 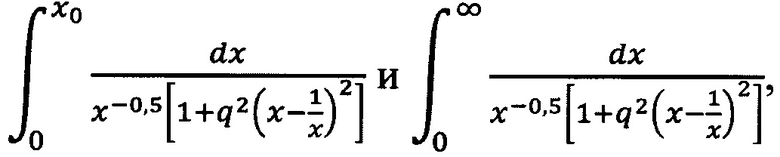 подобрать подходящее значение x0.
подобрать подходящее значение x0.
Таким образом, разработчик программы приближенных вычислений интеграла А(γ) может по своему усмотрению использовать как область, в которой γ>1, так и область, в которой γ<1. Но область, в которой γ<1, привлекательна тем, что при ее использовании исчезает необходимость в определении нижнего, отличного от нуля, предела интегрирования, поскольку подынтегральные функции интегралов со значениями γ, лежащих в пределах 2<γ<3, «приведенных» к области γ<1, не обращаются в бесконечность при стремлении х к нулю, в чем нетрудно убедиться, рассматривая формулу (2).
В заключение хотелось бы отметить, что существует еще и совсем простой и незатейливый путь определения значений интегралов А(γ), избавляющий от всех хлопот по выбору и нижнего, и верхнего пределов интегрирования и от приближенных численных методов вычисления вообще. Он состоит в использовании значений γ, при которых интегралы вычисляются точно, для построения графика зависимости А(γ) от γ, подобного графикам, представленным на фиг. 1 Описания. Ранее мы указали на ряд точек (значений параметра γ), в которых интегралы А(γ) вычисляются точно через первообразные своих подынтегральных функций и выражаются в виде функций от добротности q выбранных фильтров. Этих точек, пожалуй, маловато для построения графика, но число их можно увеличить, если добавить к ним еще несколько точек, таких как 1,25 (или 0,75), 1,75 (или 0,25), 2,25 (или - 0,25), 2,75 (или - 0,75). К сожалению, недоступной является точка 3 (или - 1), поскольку интегралы А(3) и А(-1) уже расходятся: первый из них по нижнему пределу интегрирования, а второй в точке (-1), симметричной точке 3, - по верхнему. Интегралы А(γ) при этих «новых» значениях γ тоже вычисляются точно через первообразные своих подынтегральных функций. Правда, находятся эти первообразные путем довольно громоздких, хотя в принципе и несложных математических выкладок. Эти «новые» точки мы не принимали во внимание в начале повествования, предпочитая сосредоточиться на проблемах численного интегрирования. Но вычислив интегралы в эквидистантных точках, расположенных «справа» от точки γ=1, в которой А(γ) имеет минимум, мы получим 8 точек для построения правой ветви графика зависимости А(γ) от γ. Такими точками будут являться 1; 1,25; 1,5; 1,75; 2; 2,25; 2,5; 2,75.
Этих точек, на наш взгляд, вполне достаточно для построения графика, интерполирующего промежуточные точки, причем в этот график войдет и точка со значением γ, равным 2,75, принадлежащим аномальной области значений γ, т.е. области, в которой 2,5<γ<3. Такие значения γ очень редко, но все же встречаются время от времени.
В «левую» ветвь графика войдут точки со значениями γ, равными 0,75; 0,5; 0,25; 0, симметричные точкам 1,25; 1,5; 1,75; 2 правой ветви и вычислять интеграл в них уже не нужно.
Итак, для построения графика достаточно всего лишь на всего вычислить 8 интегралов. По построенному графику, соответствующему уже выбранным значениям добротности q фильтров, можно составить таблицы соответствия значений интегралов А(γ) различным промежуточным значениям γ, при этом вполне достаточным было бы разбиение эквидистантных интервалов изменения этих значений протяженностью 0,25 на 5 частей. Процесс использования полученной таблицы можно автоматизировать с помощью процессорной техники.
Именно только что описанный графический путь определения значений интегралов А(γ) нам и хотелось бы рекомендовать для использования. А все остальное, о чем говорилось ранее, предназначалось в основном лишь для того, чтобы описать свойства интегралов А(γ), сразу не очевидные, а также чтобы нарисовать общую картину вариантов возможностей вычисления интегралов.

| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ И ИЗМЕРЕНИЯ МАЛОГО СИНУСОИДАЛЬНОГО НАПРЯЖЕНИЯ | 2006 |
|
RU2340906C2 |
| ПОРОГОВЫЙ БИНАРНЫЙ ОБНАРУЖИТЕЛЬ | 2000 |
|
RU2185638C2 |
| СПОСОБ КОНТРОЛЯ ИЗМЕРИТЕЛЯ АЭРОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ЛЕТАТЕЛЬНОГО АППАРАТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1993 |
|
RU2079142C1 |
| УСТРОЙСТВО ПРИЕМА ЧАСТОТНО-МОДУЛИРОВАННЫХ СИГНАЛОВ | 1999 |
|
RU2179786C2 |
| Способ определения параметров избыточного шума | 1987 |
|
SU1481694A1 |
| Способ регулирования выхода по току алюминиевого электролизера | 1984 |
|
SU1225881A1 |
| СПОСОБ ОПТИМАЛЬНОГО ОБНАРУЖЕНИЯ ИМПУЛЬСНЫХ СИГНАЛОВ С НЕМОДУЛИРОВАННОЙ НЕСУЩЕЙ ЧАСТОТОЙ | 1993 |
|
RU2082988C1 |
| СПОСОБ ШИФРОВАНИЯ АДАПТИВНЫМ МЕТОДОМ МНОГОАЛФАВИТНОЙ ЗАМЕНЫ | 2010 |
|
RU2469484C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СТОЙКОСТИ ПОЛУПРОВОДНИКОВЫХ ПРИБОРОВ СВЧ К ВОЗДЕЙСТВИЮ ИОНИЗИРУЮЩИХ ИЗЛУЧЕНИЙ | 2015 |
|
RU2602416C1 |
| Способ идентификации энергетического спектра сигнала | 1987 |
|
SU1483467A1 |
Изобретение относится к измерительной технике и может быть использовано для определения параметров избыточного шума изделий электронной техники при контроле их качества и прогнозировании отказов, а также в научных исследованиях. Способ определения параметров избыточного шума заключается в том, что определение этих параметров проводят с использованием нескольких частот, а исследуемый шумовой сигнал усиливают и пропускают через фильтры, настроенные определенным образом на эти частоты. При этом эффективные полосы пропускания фильтров пропорциональны выбранным частотам, а сами эти частоты располагают в определенных положениях в пределах соответствующим им полосах пропускания. Далее измеряют средние мощности шумового напряжения на выходах фильтров путем его квадратичного детектирования и усреднения (интегрирования в течение того или иного фиксированного промежутка времени) и, руководствуясь известной зависимостью спектральной плотности мощности избыточного шума от частоты, используют с помощью определенных вычислительных операций результаты этих измерений для определения параметров этой зависимости - частотного индекса γ, коэффициента пропорциональности «В», а также и самой спектральной плотности мощности, которую на любой частоте определяют по формуле

где Sизб - спектральная плотность мощности избыточного шума;
В - коэффициент пропорциональности;
ω - круговая частота;
γ - частотный индекс,
При этом выбирают три частоты ω1, ω2, ω3, которые нумеруют для определенности таким образом, что выполняется соотношение ω1>ω2>ω3. Резонансные частоты полосовых фильтров ω01, ω02 и ω03 равны выбранным частотам ω1, ω2 и ω3. Каждый из фильтров, имеющих одинаковую структуру соединений своих элементов, выполнен в виде линейного пассивного или активного трехполюсника с передаточной по напряжению функцией, заданной раскрытым в описании изобретения математическим выражением. При этом фильтры настраивают на выбранные резонансные частоты ω01, ω02 и ω03 таким образом, что их добротности q и коэффициенты передачи K0 на своих резонансных частотах остаются одинаковыми. Измеряют средние мощности шума P1, Р2 и Р3 на выходах фильтров 1, 2 и 3. По результатам этих измерений определяют один из параметров избыточного шума - частотный индекс γ, при при заданном соотношении частоты настройки ω01, ω02 и ω03. После этого вычисляют коэффициент пропорциональности «В», а также спектральную плотность мощности избыточного шума Sизб. Способ позволяет определять параметры избыточного шума в условиях отсутствия значительного превалирования его над «белыми» шумами, используя при этом простые по конструкции и удобные в настройке фильтры с не обязательно очень узкими эффективными полосами пропускания и с резонансными частотами, расположенными в не обязательно слишком глубокой низкочастотной области, и за счет этого дает возможность существенно уменьшить время проведения измерительных операций. 3 ил.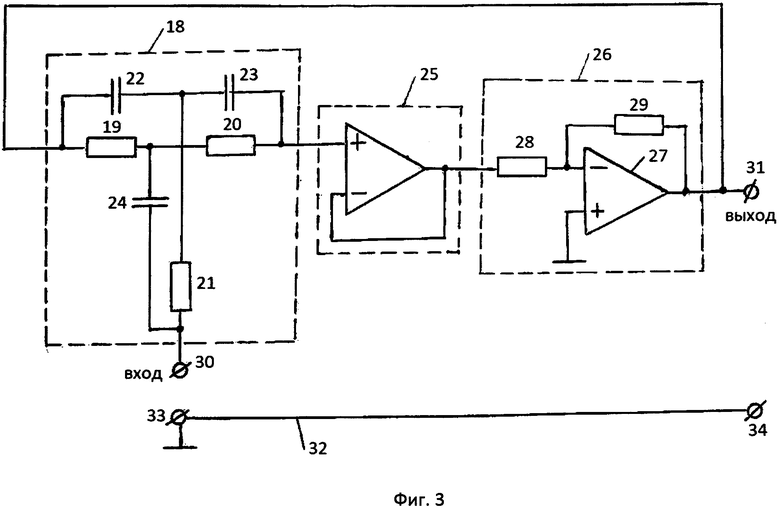
Способ определения параметров избыточного шума, в котором определение этих параметров проводят с использованием нескольких частот, а исследуемый шумовой сигнал усиливают и пропускают через фильтры, настроенные определенным образом на эти частоты, причем эффективные полосы пропускания фильтров пропорциональны выбранным частотам, а сами эти частоты располагают в определенных положениях в пределах соответствующих им полосах пропускания, измеряют средние мощности шумового напряжения на выходах фильтров путем его квадратичного детектирования и усреднения (интегрирования в течение того или иного фиксированного промежутка времени) и, руководствуясь известной зависимостью спектральной плотности мощности избыточного шума от частоты, используют с помощью определенных вычислительных операций результаты этих измерений для определения параметров этой зависимости - частотного индекса γ, коэффициента пропорциональности «В», а также и самой спектральной плотности мощности, которую на любой частоте определяют по формуле
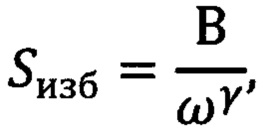
где Sизб - спектральная плотность мощности избыточного шума;
В - коэффициент пропорциональности;
ω - круговая частота;
γ - частотный индекс,
отличающийся тем, что выбирают три частоты ω1, ω2 и ω3, а в качестве фильтров, настраиваемых на эти частоты, используют трехполюсники, передаточная по напряжению функция которых может быть приведена к виду
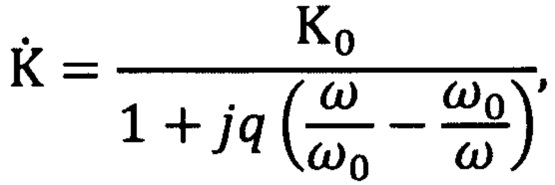
где 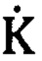 - комплексный коэффициент передачи фильтра;
- комплексный коэффициент передачи фильтра;
К0 - коэффициент передачи фильтра на частоте ω, равной ω0;
j - мнимая единица;
q - добротность (эквивалентная добротность) фильтра;
ω - текущая круговая частота;
ω0 - величина, имеющая размерность частоты, равная резонансной (квазирезонансной) частоте фильтра, и зависящая, как и безразмерные величины К0 и q, от параметров элементов конструкции фильтра,
причем значения резонансных частот ω01, ω02, ω03, на которые настраивают фильтры 1, 2 и 3, совпадают с выбранными частотами ω1, ω2, ω3, а саму настройку фильтров на эти различные частоты осуществляют таким образом, что значения К0 и q у всех трех фильтров остаются одинаковыми, нумеруют для определенности частоты ω01, ω02 и ω03 таким образом, что выполняется соотношение
ω01>ω02>ω03,
и проводят следующие вычислительные операции:
среднюю мощность напряжения шума, измеренную на выходе первого фильтра, умножают на отношение частот настройки второго и первого фильтров и из полученного результата вычитают среднюю мощность шума, измеренную на выходе второго фильтра, в свою очередь мощность шума на выходе второго фильтра умножают на отношение частот настройки третьего и второго фильтров и из полученного результата умножения вычитают мощность шума, измеренную на выходе третьего фильтра, затем первую разность делят на вторую, а частотный индекс γ определяют в общем случае как решение трансцендентного уравнения
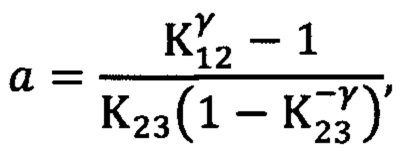
где 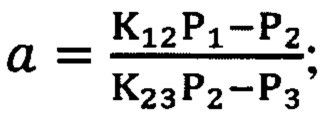
P1, Р2 и Р3 - средние мощности шума, измеренные на выходах соответственно первого, второго и третьего фильтров;

причем частоты ω01, ω02, ω03 выбирают такими, что выполняется соотношение
К12=К23≡К,
при этом частотный индекс γ определяют просто по формуле
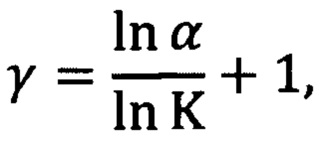
а полученное значение частотного индекса γ используют для определения коэффициента пропорциональности «В», для чего вычисляют интеграл
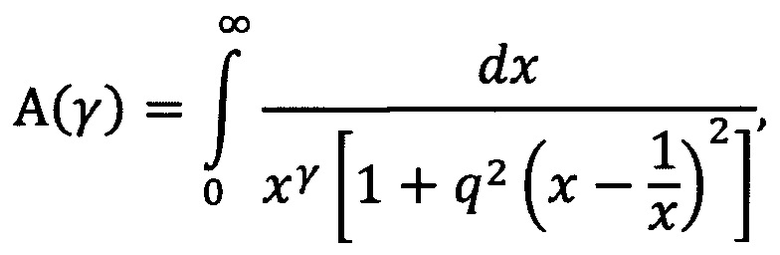
где х - отвлеченные действительные числа, после чего коэффициент «В» вычисляют по любой из формул
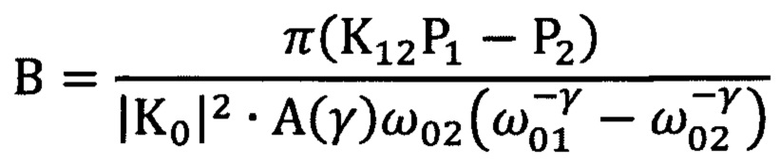
или
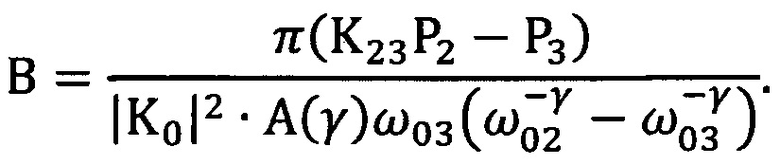
| Способ определения параметров избыточного шума | 1987 |
|
SU1481694A1 |
| СПОСОБ ИЗМЕРЕНИЯ ОТНОШЕНИЯ СИГНАЛ-ШУМ | 2009 |
|
RU2414718C2 |
| УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ШУМОВЫХ ПАРАМЕТРОВ ЧЕТЫРЕХПОЛЮСНИКА СВЧ | 2012 |
|
RU2499274C1 |
| Устройство для измерения отношения сигнал/помеха и мощностей сигнала и шума | 1986 |
|
SU1359759A1 |
| Способ определения коэффициента шума при воздействии помехи | 1988 |
|
SU1659918A1 |
| US 7747403 B2, 29.06.2010. | |||
Авторы
Даты
2020-08-17—Публикация
2019-08-08—Подача