ОБЛАСТЬ ПРИМЕНЕНИЯ ИЗОБРЕТЕНИЯ
[0001] Настоящее изобретение относится к подъемной системе вертикальной шахты, в частности, к способу управления пространственным расположением подъемного контейнера в подъемной системе двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте, а также относится к технической области осуществления подъемных работ в вертикальной шахте.
ОПИСАНИЕ ПРЕДШЕСТВУЮЩЕГО УРОВНЯ ТЕХНИКИ
[0002] Подъемная система в сверхглубокой вертикальной шахте представляет собой подъемную систему в вертикальной шахте, глубина разработки которой составляет более 1500 м. Из-за большой глубины разработки подъемной системы сверхглубокой вертикальной шахты общая жесткая направляющая клети подъемного контейнера подвержена возникновению повреждений, таких как деформация направляющей клети в шахте, повреждение балки направляющей клети, ослабление соединения балки и нестабильность работы при высокой скорости работы и большой нагрузке подъемного контейнера, поэтому в подъемных работах в сверхглубокой вертикальной шахте не может использоваться общая жесткая направляющая клети подъемного контейнера. Однако в случае если для подъема используется канатная направляющая клети, то различия в диаметрах барабанов для намотки, различия установки двух стальных канатов, расхождения в модулях упругости этих двух стальных канатов и прочие факторы могут стать причиной несинхронного движения заднего конца двух стальных канатов подъемной системы, что приводит к наклону подъемного контейнера, а также к дополнительной несогласованности в натяжении двух стальных канатов. В случае если стальные канаты будут работать в таких условиях в течение длительного времени, то вполне вероятно, что может возникнуть состояние, при котором напряжение одного стального каната будет превышать его же напряжение безопасного использования, вследствие чего возникшее разрушение каната может привести к серьезным и опасным для жизни аварийным ситуациям. Во избежание таких аварий требуется активное регулирование угла подъемного контейнера с тем, чтобы подъемный контейнер сохранял сбалансированное состояние, а натяжение двух стальных канатов было согласованным.
[0003] В предшествующем уровне техники обычно используется способ разработки регулятора на основе алгоритма бэкстеппинга, но для такого способа управления необходимо выполнение вывода переменной на основе переменных состояния системы, что делает процесс разработки регулятора более сложным. Кроме того, если регулятор применяется в практической системе сверхглубокой вертикальной шахты, при этом учитывая, что подъемная система сверхглубокой вертикальной шахты представляет собой сложную многоструктурную механико-электрогидравлическую систему, и даже несмотря на то, что многие практические факторы рассматриваются в процессе моделирования, то очень трудно реализовать согласованность работы с этой практической системой. Следовательно, в процессе разработки регулятора вывод переменных состояния системы, несомненно, увеличит уровень шума, измеряемый датчиком, и данные, находящиеся за пределами модели системы, а также приведет к большим погрешностям отслеживания и увеличит время выравнивания.
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
[0004] В целях устранения различных дефектов в предшествующем уровне техники, настоящее изобретение предлагает способ управления пространственным расположением подъемного контейнера в подъемной системе двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте. Процесс разработки достаточно прост. Обеспечивается эффективное осуществление контроля. Своевременное срабатывание предоставляет возможность быстрого выравнивания подъемной системы. Малая вероятность возникновения ошибок.
[0005] С целью достижения цели изобретения, в настоящем предлагается способ управления пространственным расположением подъемного контейнера в подъемной системе двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте. Способ включает в себя следующие этапы:
[0006] этап 1 - построение математической модели подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте;
[0007] этап 2 - построение математической модели расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления;
[0008] этап 3 - вывод данных плоскостности нелинейной системы;
[0009] этап 4 - разработка регулятора плоскостности для выравнивания расположения подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте; а также
[0010] этап 5 - разработка регулятора плоскостности для установки расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления.
[0011] Кроме того, на этапе 1 математическая модель подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте заключается в следующем:
[0012] 1) Параметры, используемые в процессе моделирования, определяются следующим образом:
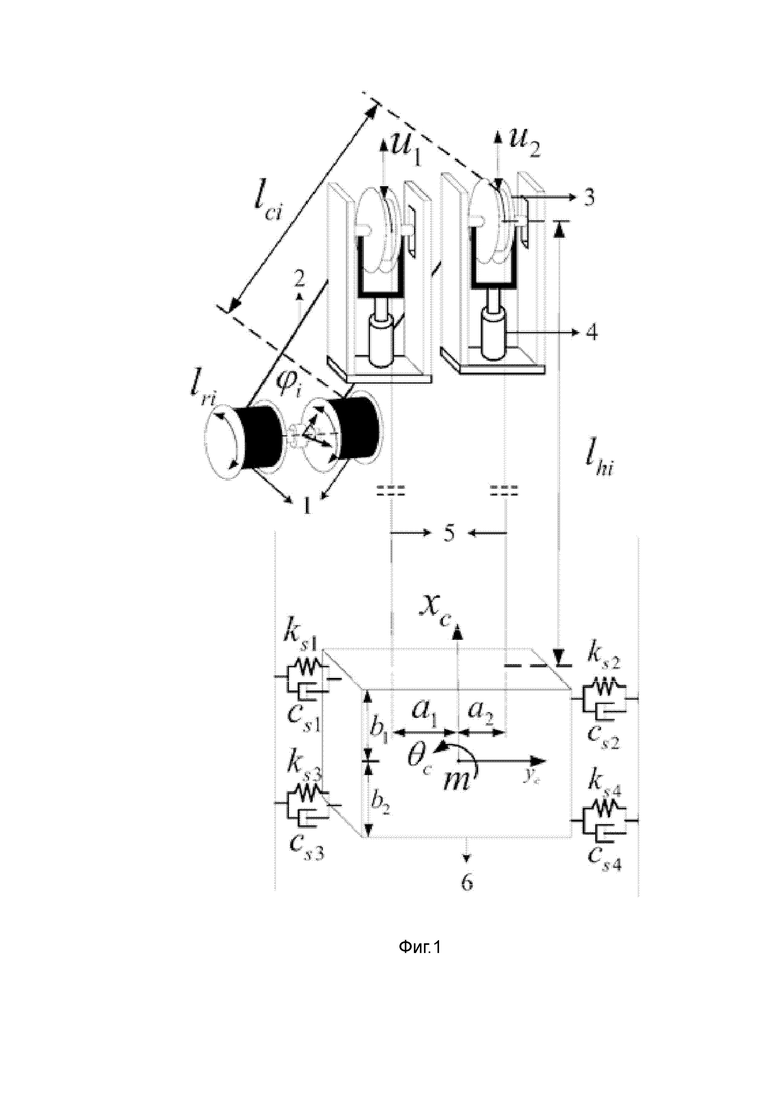
[0013] Iri (i=1,2) - длина намотки барабана для двойной намотки;
[0014] Ici (i=1,2) - длина двух одиночных канатов во время подъема или спуска подъемного контейнера;
[0015] Ihi (i=1,2) - длина двух вертикальных участков стальных канатов во время подъема или спуска подъемного контейнера;
[0016] ui (i=1,2) - смещение двух подвижных канатных шкивов;
[0017] ϕi - внутренний угол между двумя одиночными канатами и горизонтальной плоскостью;
[0018] ai (i=1,2) - расстояние по горизонтали между точкой соединения двух вертикальных участков стальных канатов на подъемном контейнере и центром тяжести подъемного контейнера;
[0019] bi (i=1,2) - расстояние по вертикали между верхней и нижней поверхностями подъемного контейнера и центром тяжести подъемного контейнера;
[0020] ksi (i=1,2,3,4) - поперечная эквивалентная жесткость четырех пар упругодемпфирующих моделей; а также
[0021] csi (i=1,2,3,4) - коэффициент поперечного эквивалентного демпфирования четырех пар упругодемпфирующих моделей.
[0022] 2) Процесс подъема определяется как положительное направление, а во время подъема или опускания подъемного контейнера длины двух вертикальных участков стальных проволочных канатов 5 представлены следующим образом:
[0023]  ; и
; и
[0024] 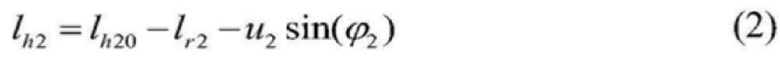 , где
, где
[0025] lh10 и lh20 - первоначальные длины двух вертикальных участков стальных канатов.
[0026] 3) Определяется обобщенный вектор подсистемы подъема q=[xc,yc,θ], где xc и yc являются вертикальным смещением и горизонтальным смещением центра тяжести подъемного контейнера 6 соответственно, θ - это угол поворота против часовой стрелки подъемного контейнера 6, а динамическое уравнение Лагранжа подсистемы подъема представлено следующим образом:
[0027] 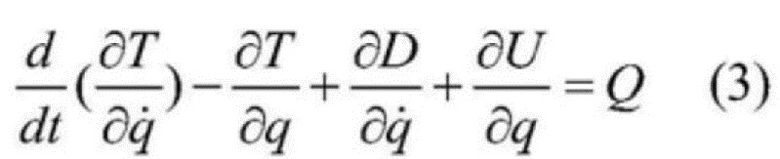 , где
, где
[0028] T, U и D являются кинетической энергией, потенциальной энергией и диссипативной функцией Рэлея подъемной системы соответственно, а Q - это непотенциальная обобщенная сила подсистемы подъема без учета демпфирования.
[0029] 4) Смещение в точке касательной между подвижным канатным шкивом и левым одиночным канатом равно 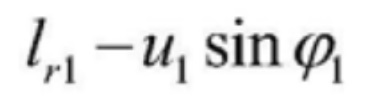 , а смещение в точке касательной между подвижным канатным шкивом и вертикальным участком левого стального каната равно
, а смещение в точке касательной между подвижным канатным шкивом и вертикальным участком левого стального каната равно  .
.
[0030] Смещение левого каната в позицию на расстояние длиной s представлено следующим образом:
[0031] 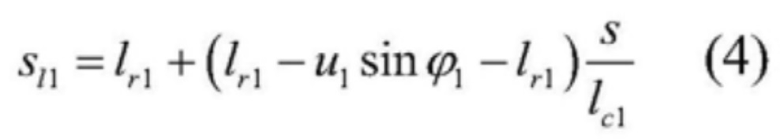 .
.
[0032] Аналогичным образом, смещение вертикального участка левого каната в позицию на расстояние длиной y представлено следующим образом:
[0033] 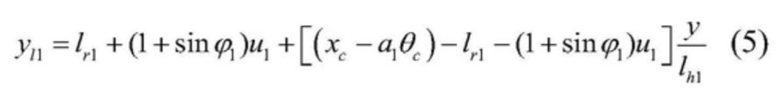 .
.
[0034] 5) В соответствии с формулами (4) и (5) ниже приводятся формулы кинетической энергии левого одиночного каната и вертикального участка левого стального каната соответственно:
[0035] 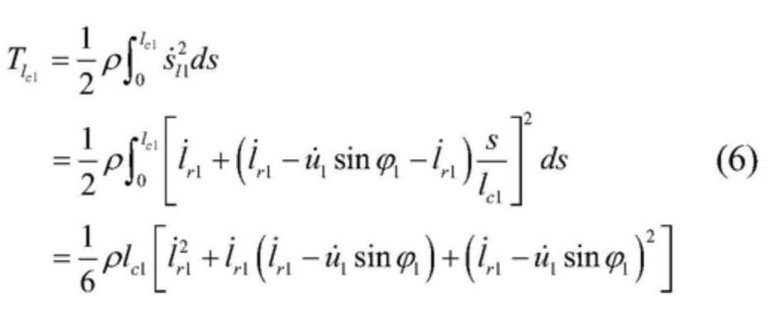 , и
, и
[0036] 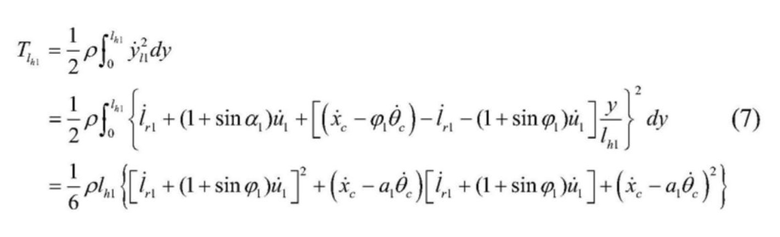 , где
, где
[0037] в формулах: ρ - единица массы стального каната.
[0038] 6) Смещение в точке касательной между подвижным канатным шкивом и правым одиночным канатом равно  , а смещение правого одиночного каната в позиции на расстояние длиной s показано следующим образом:
, а смещение правого одиночного каната в позиции на расстояние длиной s показано следующим образом:
[0039] 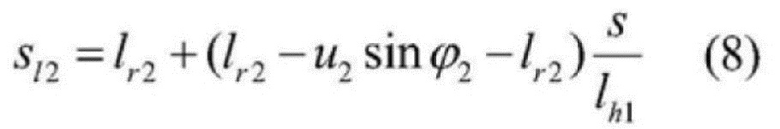 .
.
[0040] Смещение в точке касательной между подвижным канатным шкивом и вертикальным участком правого стального каната равно  , а смещение вертикального участка правого стального каната в позиции на расстояние длиной y представлено следующим образом:
, а смещение вертикального участка правого стального каната в позиции на расстояние длиной y представлено следующим образом:
[0041] 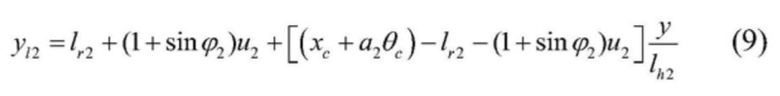 .
.
[0042] 7) В соответствии с формулами (8) и (9) ниже приводятся формулы кинетической энергии правого одиночного каната и вертикального участка правого стального каната соответственно:
[0043] 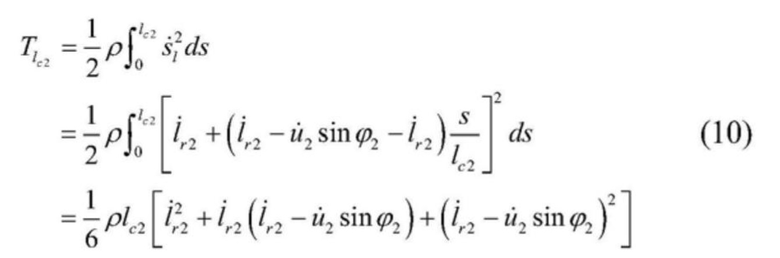 , и
, и
[0044] 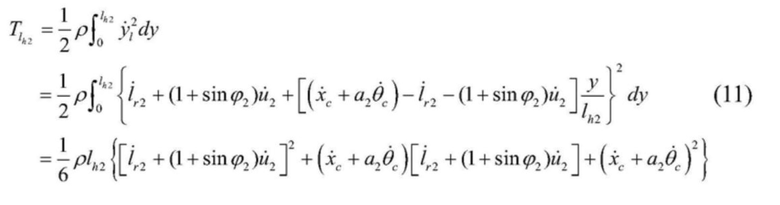 .
.
[0045] 8) Ниже приводятся формулы кинетической энергии левого и правого подвижных канатных шкивов:
[0046] 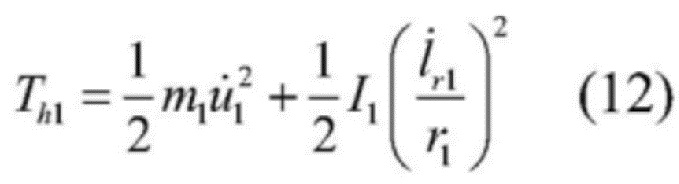 , и
, и
[0047] 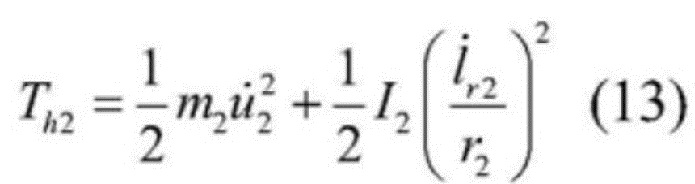 , где
, где
[0048] в формулах: m1 и m2 - массы левого и правого подвижных канатных шкивов соответственно, r1 и r2 - радиусы левого и правого подвижных канатных шкивов соответственно, а I1 и I2 - моменты инерции левого и правого подвижных канатных шкивов соответственно.
[0049] Ниже приводится формула кинетической энергии подъемного контейнера:
[0050] 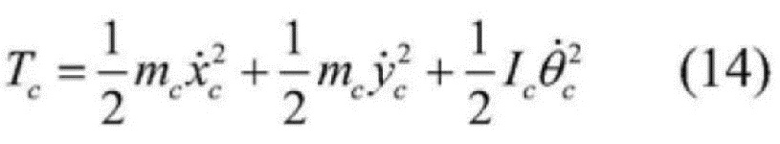 , где
, где
[0051]в формуле: mc - масса подъемного контейнера, а Ic - момент инерции подъемного контейнера.
[0052] 9) Ниже приводится формула потенциальной энергии левого стального каната:
[0053] 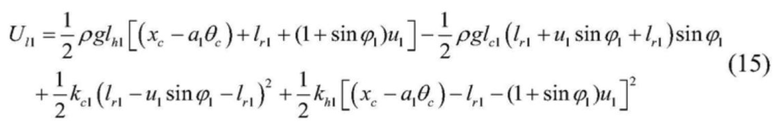 ; и
; и
[0054] формула потенциальной энергии правого стального каната представлена следующим образом:
[0055] 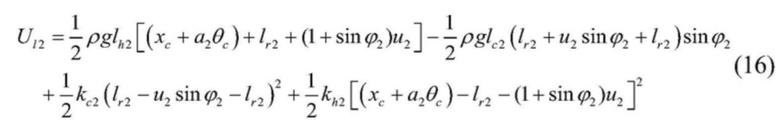 , где
, где
[0056] в формуле: kc1 и kh1 - жесткости левого одиночного каната и вертикального участка левого стального каната соответственно, а kc2 и kh2 - жесткости правого одиночного каната и вертикального участка правого стального каната соответственно.
[0057] Ниже приводятся формулы потенциальной энергии левого и правого подвижных канатных шкивов соответственно:
[0058] Uh1=m1gu1 (17), и
[0059] Uh2=m2gu2 (18).
[0060] Потенциальная энергия системы подъемного контейнера включает в себя потенциальную энергию подъемного контейнера и потенциальную энергию канатной направляющей клети, а формула представлена следующим образом:
[0061] 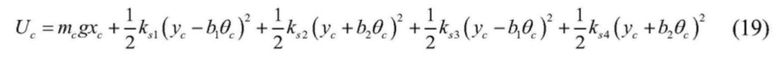 .
.
[0062] 10) Ниже приводятся формулы диссипации энергии по Рэлею левого и правого одиночных канатов соответственно:
[0063] 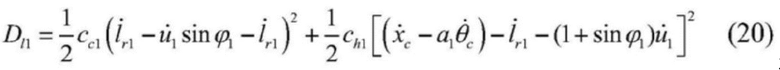 ; и
; и
[0064] 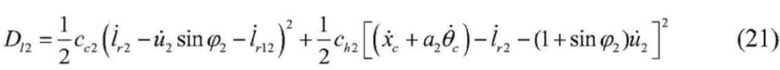 , где
, где
[0065] в формулах: cc1 и cc2 являются коэффициентами демпфирования левого одиночного каната и вертикального участка левого стального каната соответственно, а cc2 и ch2 - коэффициенты демпфирования правого одиночного каната и вертикального участка правого стального каната соответственно.
[0066] 10) Ниже приводится формула диссипации энергии по Рэлею системы подъемного контейнера:
[0067]  .
.
[0068] С учетом вышеизложенного, ниже показаны кинетическая энергия, потенциальная энергия и диссипация энергии по Рэлею подсистемы подъема соответственно:
[0069] 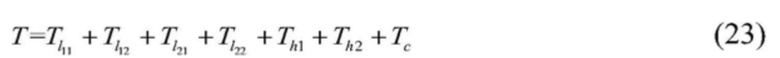 ,
,
[0070]  и
и
[0071] 
[0072] 11) Вышеприведенные формулы подставляются в общее уравнение:
[0073]  , где
, где
[0074] в формуле: 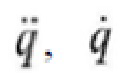 и q являются обобщенным ускорением, скоростью и смещением соответственно, а M, C, K и F - матрица массы, матрица демпфирования, матрица жесткости и непотенциальная сила подсистемы подъема соответственно, вследствие чего получаются следующие формулы:
и q являются обобщенным ускорением, скоростью и смещением соответственно, а M, C, K и F - матрица массы, матрица демпфирования, матрица жесткости и непотенциальная сила подсистемы подъема соответственно, вследствие чего получаются следующие формулы:
[0075] 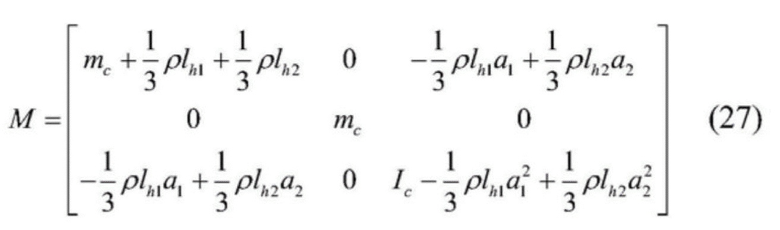 ,
,
[0076] 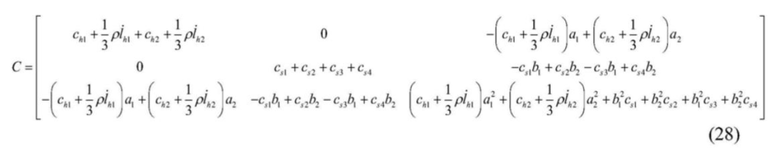 ,
,
[0077] 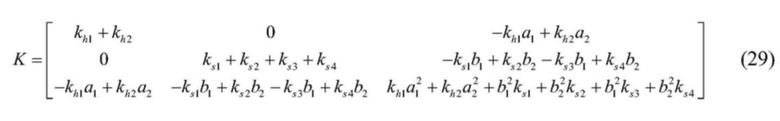 ,и
,и
[0078] 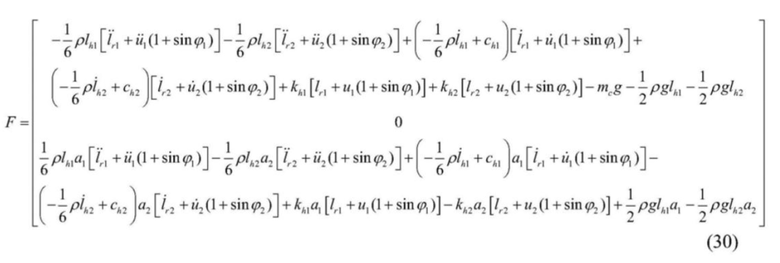 .
.
[0079] 12) Тем самым уравнение упрощается. Если в процессе моделирования подсистемы подъема не предполагается смещение нагрузки, то есть a1=a2, и, кроме того, если угол поворота против часовой стрелки подъемного контейнера равен 0, то натяжение двух стальных канатов будет согласованным; и, следовательно, формула (30) может быть упрощена и выглядеть таким образом
[0080] 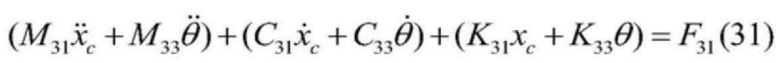 , где
, где
[0081] в формуле: Mij, Cij, Kij и Fij являются элементами матрицы массы, матрицы демпфирования, матрицы жесткости и непотенциальной силы соответственно (i=1,2,3 и j=1,2,3).
[0082] Выравнивание расположения подъемного контейнера регулируется двумя гидравлическими контролерами, тем самым u1=u=-u2, угол наклона θ подъемного контейнера является регулируемой величиной, а формула (31) может быть дополнительно упрощена в виде:
[0083] 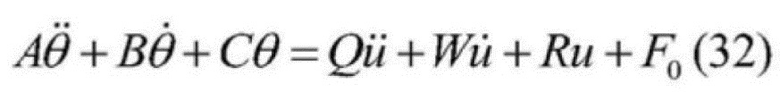 , где
, где
[0084] в формуле:
[0085] 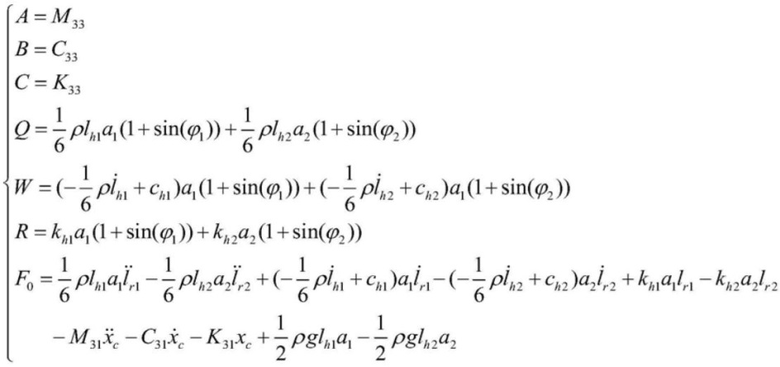 .
.
[0086] kh1 и kh2 намного больше ch1 и ch2, что дает возможность еще больше упростить формулу (32) до следующего вида:
[0087] 
[0088] Для подсистемы подъема переменная состояния выбирается таким образом 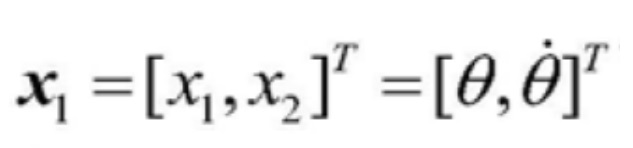 , чтобы динамическую модель подсистемы подъема можно было преобразовать в форму пространственного состояния:
, чтобы динамическую модель подсистемы подъема можно было преобразовать в форму пространственного состояния:
[0089] 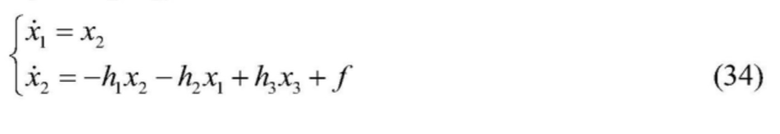 , и
, и
[0090] y1=x1, где
[0091] в формулах:, h1=B/A, h2=C/A, h3=R/A, а f=F0/A.
[0092] Создание условия для вышеупомянутой модели заключается в следующем: для подсистемы подъема оба угла θ и 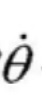 ограничены.
ограничены.
[0093] Кроме того, на этапе 2 математическая модель подсистемы автоматического электрогидравлического управления заключается в следующем.
[0094] Подсистема автоматического электрогидравлического управления включает в себя пропорциональный клапан гидроусилителя в системе подвижного канатного шкива и в гидравлическом цилиндре со штоком двустороннего действия.
Предполагается, что для подсистемы автоматического электрогидравлического управления исходный сигнал смещения xp, скорость 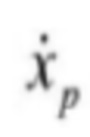 , ускорение
, ускорение 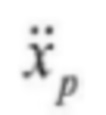 и резкое движение
и резкое движение 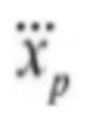 гидравлического цилиндра ограничены.
гидравлического цилиндра ограничены.
[0095] Уравнение непрерывности скорости подачи гидравлического цилиндра со штоком двустороннего действия выглядит следующим образом:
[0096] 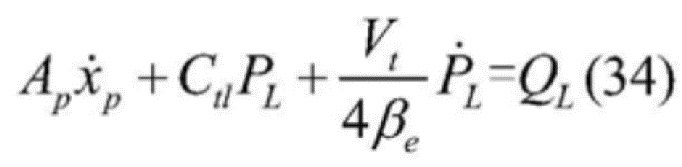 , где
, где
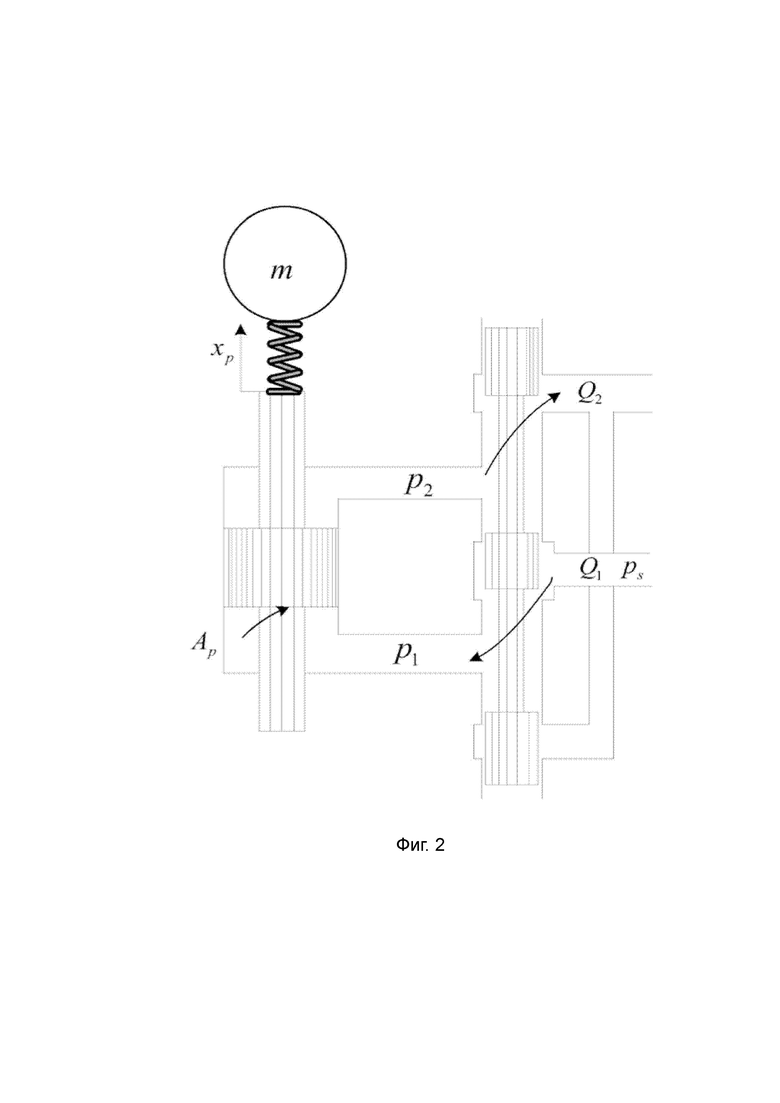
[0097] в формуле: Ap является эффективной рабочей площадью поршня гидравлического цилиндра, Ct1 является общим коэффициентом рассеяния гидравлического цилиндра, xp - смещение штока поршня гидравлического цилиндра, Vt - общий объем полости для вброса и выброса гидравлического масла, βe - эффективный объем модуля упругости гидравлического масла в гидравлическом цилиндре, PL=p1-p2 - падение давления нагрузки гидравлического цилиндра, где p1 - напорное движение в гидравлический цилиндр, p2 - напорное движение из гидравлического цилиндра, QL=Q1-Q2 - скорость подачи нагрузки, где Q1 - скорость подачи, направленной вовнутрь гидравлического цилиндра, а Q2 - скорость подачи, направленной извне гидравлического цилиндра.
[0098] Согласно второму закону Ньютона уравнение равновесия силы нагрузки системы автоматического электрогидравлического управления выглядит следующим образом:
[0099]  ,
,
[0100] где FL является силой гидравлических цилиндров со штоком двустороннего действия, с которой они воздействуют на подвижные канатные шкивы, m является общей массой подвижных канатных шкивов, а Bp - коэффициент демпфирования за счет вязкого трения гидравлического цилиндра.
[0101] Для подсистемы автоматического электрогидравлического управления, переменная состояния выбирается таким образом  , чтобы кинетическую модель подсистемы автоматического электрогидравлического управления можно было преобразовать в форму пространственного состояния:
, чтобы кинетическую модель подсистемы автоматического электрогидравлического управления можно было преобразовать в форму пространственного состояния:
[0102]  , и
, и
[0103] y2=x3, где
[0104] в формулах: a1=Ap/m, a2=Bp/m, a3=1/m, a4=4βeAp/Vt, a5=4βeCtl/Vt, а a6=4βe/Vt, с возможностью получения ввода сигнала управления u в формуле (33).
[0105] Кроме того, на этапе 3 разработка конкретного вывода данных плоскостности нелинейной системы заключается в следующем.
[0106] Предлагается к рассмотрению следующая нелинейная система:
[0107] 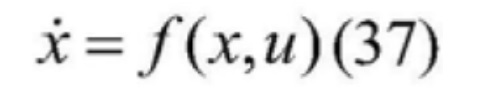 , где
, где
[0108] в формуле: x - переменная состояния системы, а u - ввод сигнала управления с тем же значением что и у вывода сигнала системы y.
[0109] В случае если имеется следующий вывод сигнала системы
[0110] 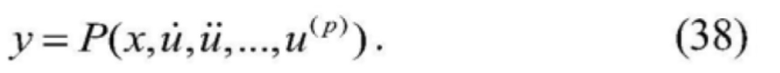 ,
,
[0111] переменная состояния системы x и ввод сигнала управления системы u могут быть выражены в виде уравнения вывода сигнала системы и его конечного дифференциала:
[0112]  , и
, и
[0113] 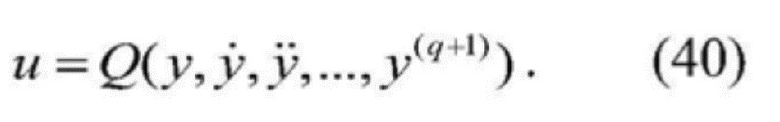 .
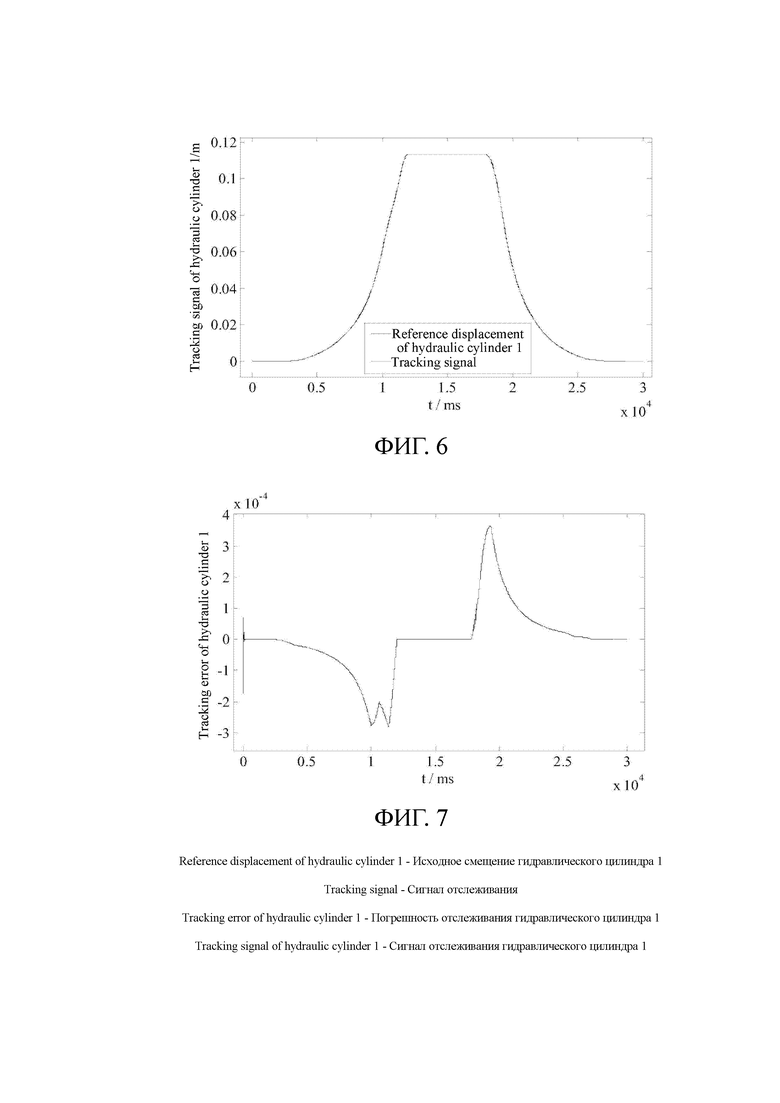
.
[0114] Формула (37) является так называемой плоскостностью. Вывод сигнала этой системы является выводом сигнала плоскостности.
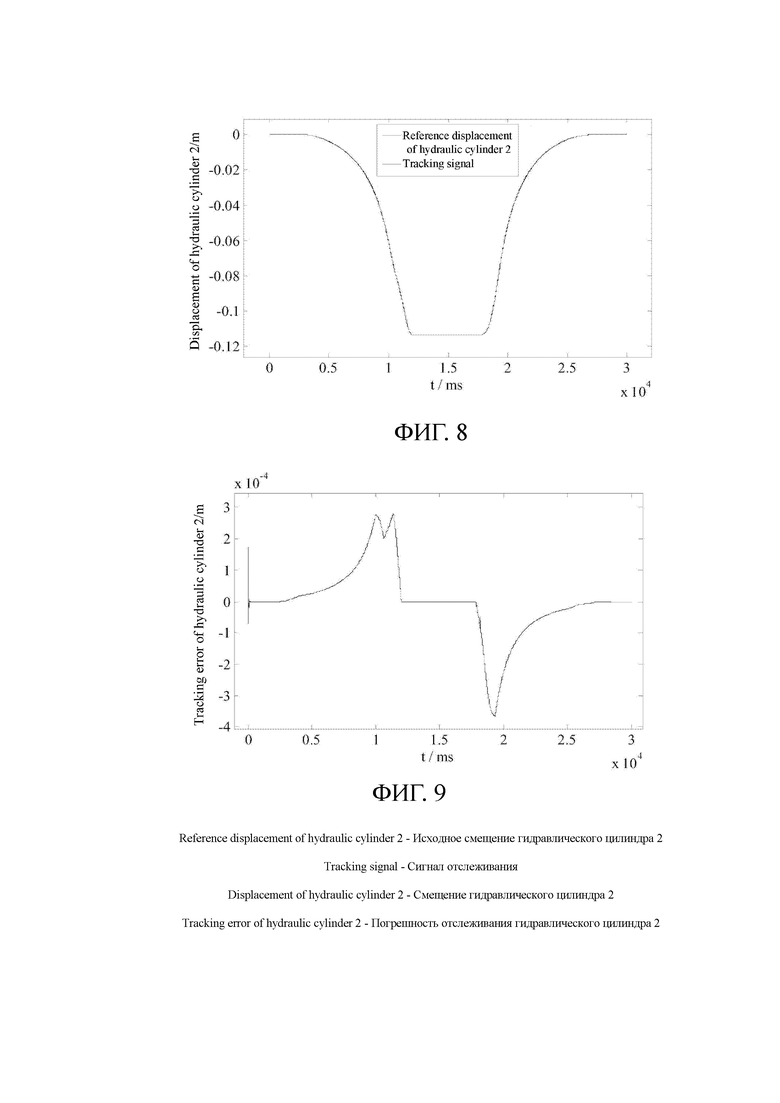
[0115] Кроме того, на этапе 4 разработка регулятора плоскостности для выравнивания расположения подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте заключается в следующем.
[0116] Согласно способу разработки регулятора плоскостности в подсистеме подъема (34), вывод сигнала управления системы представлен в виде y1=x1, а ввод сигнала управления системы представлен в виде uh=x3.
[0117] Для подсистемы подъема, уравнение плоскостности, полученное из y1, и для определения переменной состояния системы x1 и вывода сигнала управления системы uh, выглядит следующим образом:
[0118] 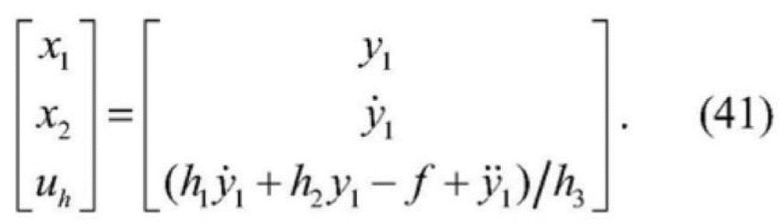 .
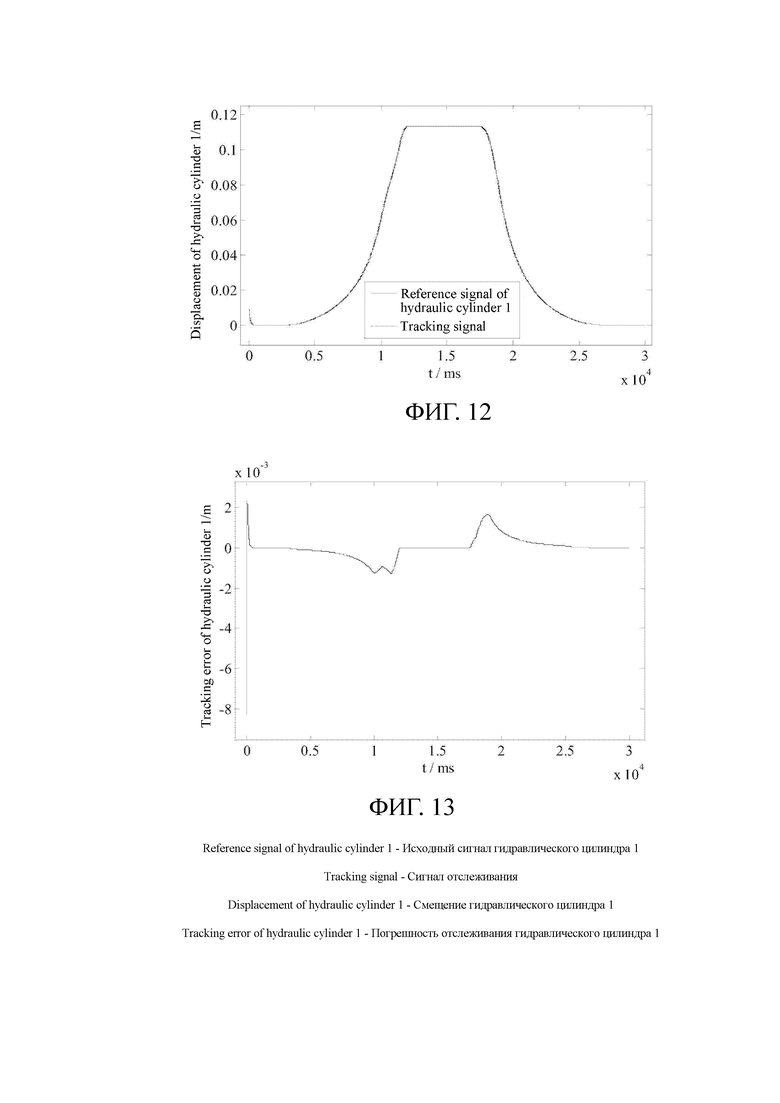
.
[0119] Переменная предполагаемого состояния подсистемы подъема определяется в соответствии с формулой 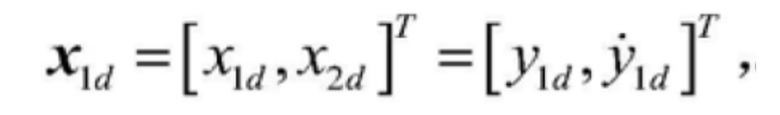 y1d отображает предполагаемый вывод сигнала системы, то есть исходный сигнал, а динамическое уравнение переменной предполагаемого состояния системы x1d выглядит следующим образом:
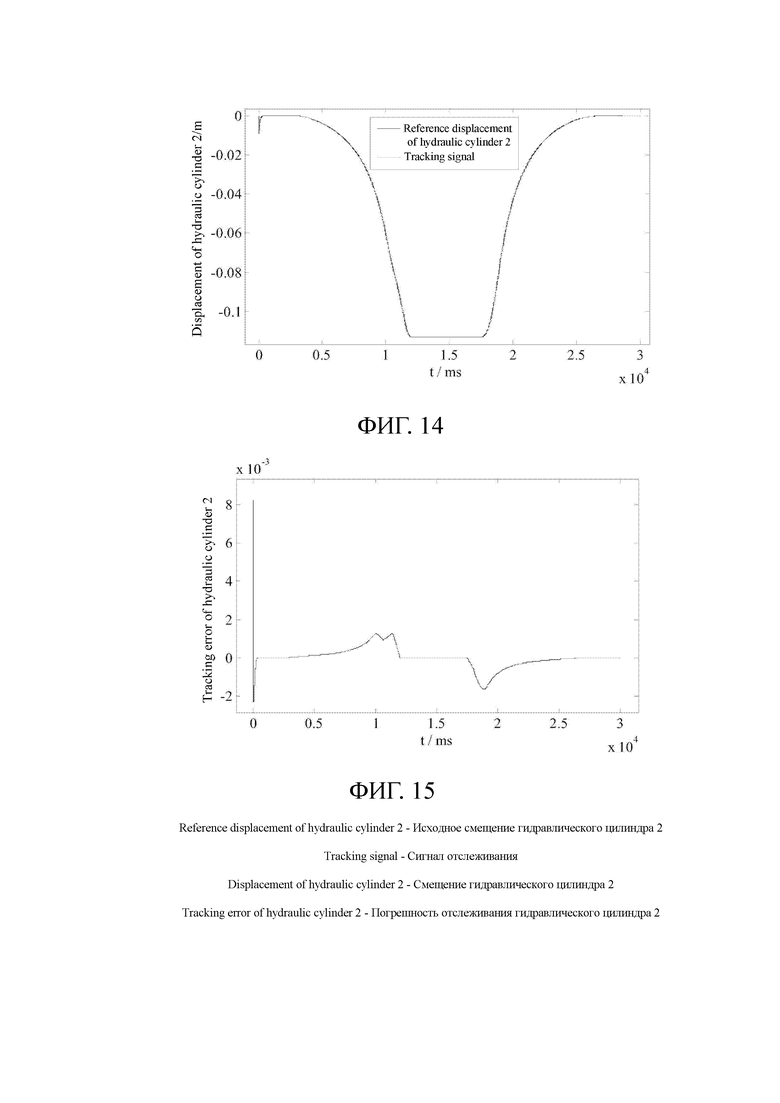
y1d отображает предполагаемый вывод сигнала системы, то есть исходный сигнал, а динамическое уравнение переменной предполагаемого состояния системы x1d выглядит следующим образом:
[0120] 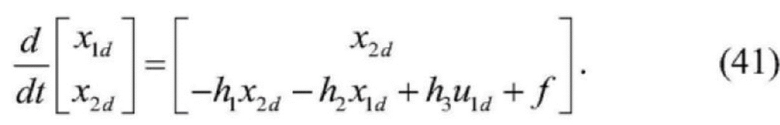 .
.
[0121] Ввод сигнала разомкнутой цепи uhd выглядит следующим образом:
[0122] 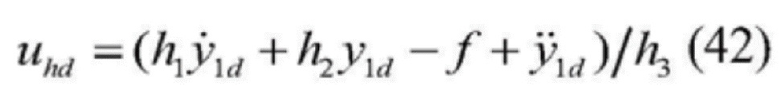 .
.
[0123] Ошибка отслеживания состояния системы определяется в виде 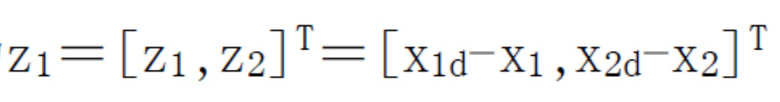 , а динамическое уравнение ошибки отслеживания системы выглядит следующим образом:
, а динамическое уравнение ошибки отслеживания системы выглядит следующим образом:
[0124] 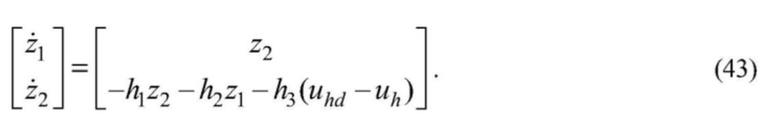 .
.
[0125] Если uhd=uh, то получаем
[0126]  .
.
[0127] Согласно формуле, представленной в виде матрицы, это будет выглядеть так:
[0128] 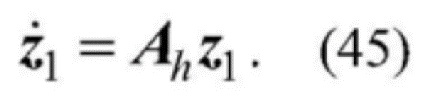 , где
, где
[0129] в формуле:  .
.
[0130] Ah является матрицей Гурвица, а погрешность z1 экспоненциально приближается к 0. Скорость при приближении может быть согласующейся не только с вводом сигнала управления системы разомкнутой цепи, что определяет ввод управления с обратной связью ее состояния в виде
[0131]  , где
, где
[0132] в формуле: K1=[k1, k2], таким образом динамическое уравнение ошибки отслеживания системы с обратной связью ее состояния выглядит следующим образом:
[0133]  , где
, где
[0134] в формуле: 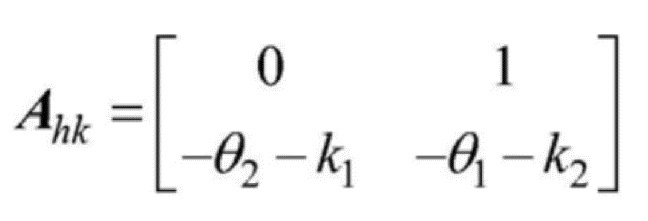 .
.
[0135] При правильном выборе матрицы коэффициентов усиления системы управления K1 матрица Ahk становится матрицей Гурвица. В настоящий момент ошибка отслеживания системы z1 может экспоненциально приближаться к 0.
[0136] Правило управления подсистемой подъема можно резюмировать следующим образом:
[0137] 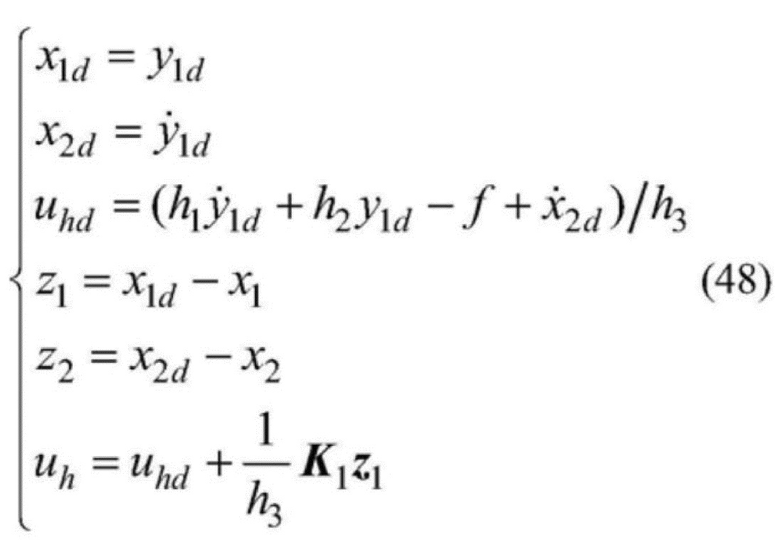 .
.
[0138] Кроме того, на этапе 5 разработка регулятора плоскостности для установки расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления заключается в следующем.
[0139] В соответствии с подсистемой автоматического электрогидравлического управления (36), вывод данных системы равен y2=y3, а ввод сигнала управления системы равен uL=QL, что дает возможность получить уравнение нижеприведенной плоскостности ввода сигнала uL, которое выглядит следующим образом:
[0140] 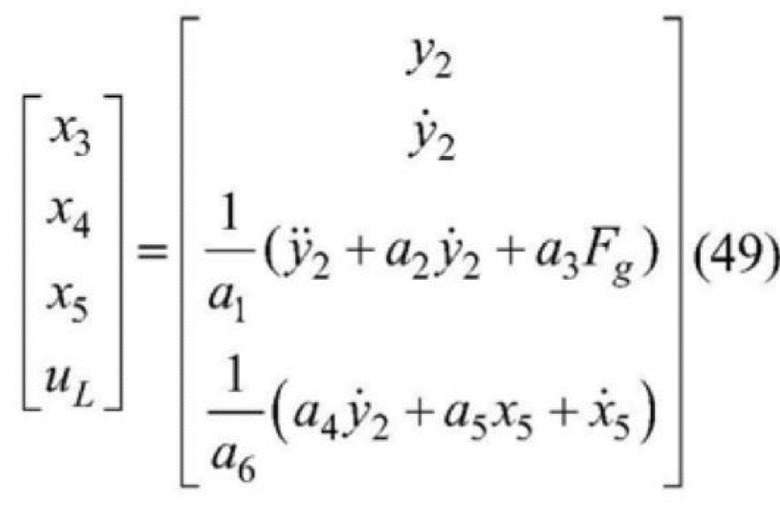 .
.
[0141] Определяется переменная предполагаемого состояния системы. В формуле: y2d является предполагаемым выводом данных системы, то есть исходным сигналом. То есть динамика погрешности предполагаемой переменной 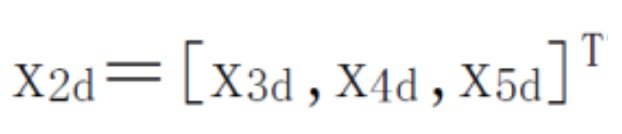 представлена следующим образом:
представлена следующим образом:
[0142]  .
.
[0143] Таким образом, ввод сигнала разомкнутой цепи uLd может быть получен следующим образом:
[0144] 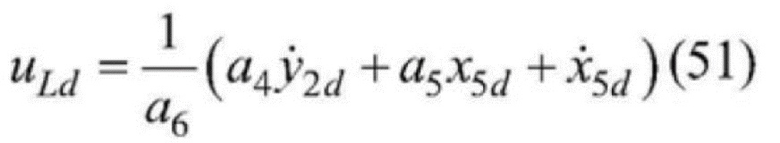 .
.
[0145] Определяется ошибка отслеживания системы 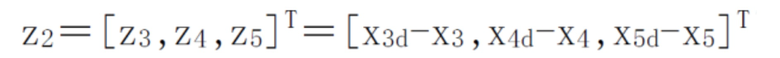 . Следовательно, динамика погрешности отслеживания системы будет представлена следующим образом:
. Следовательно, динамика погрешности отслеживания системы будет представлена следующим образом:
[0146] 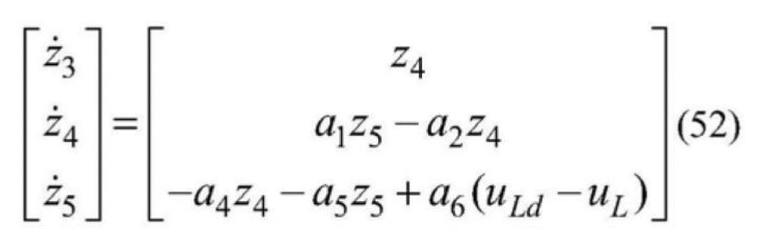 .
.
[0147] В случае если uLd=uL, то получаем
[0148] 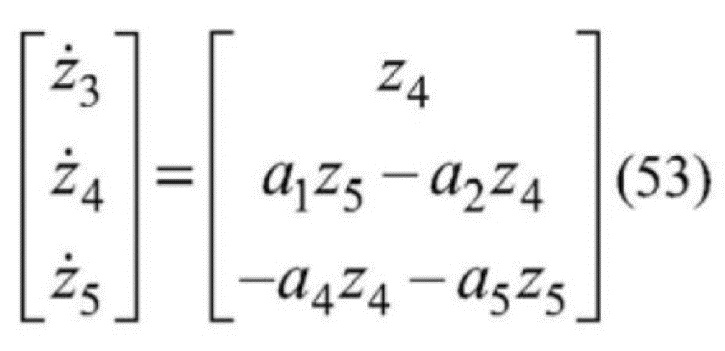 .
.
[0149] Согласно формуле, представленной в виде матрицы, это будет выглядеть так:
[0150] 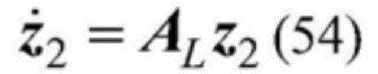 , где
, где
[0151] в формуле:  .
.
[0152] Кроме того, ввод сигнала управления с обратной связью ее состояния определяется в виде
[0153] 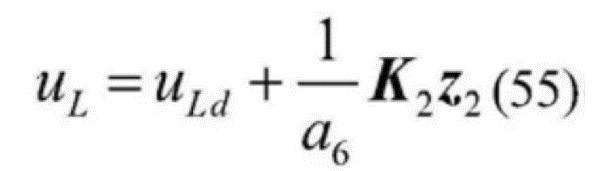 , где
, где
[0154] в формуле: K2=[k3,k4,k5]T. Динамическое уравнение ошибки отслеживания системы с обратной связью ее состояния выглядит следующим образом:
[0155] 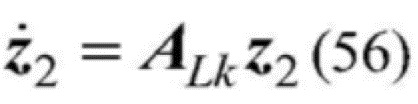 , где
, где
[0156] в формуле: 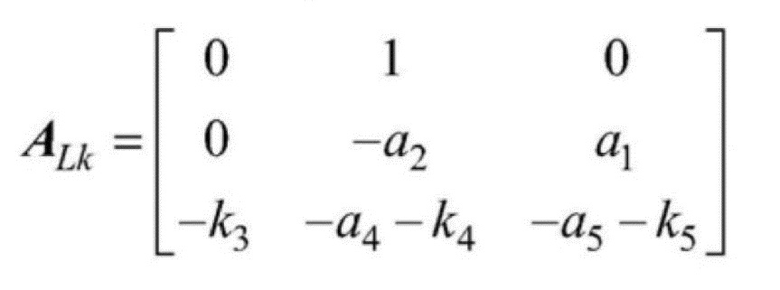 .
.
[0157] Выбирается собственно ортогональная матрица коэффициента усиления системы управления K2 , что представляет матрицу ALK в виде матрицы Гурвица, а ошибка отслеживания системы z2 экспоненциально приближается к 0. Следовательно, получается следующая формула подсистемы автоматического электрогидравлического управления:
[0158] 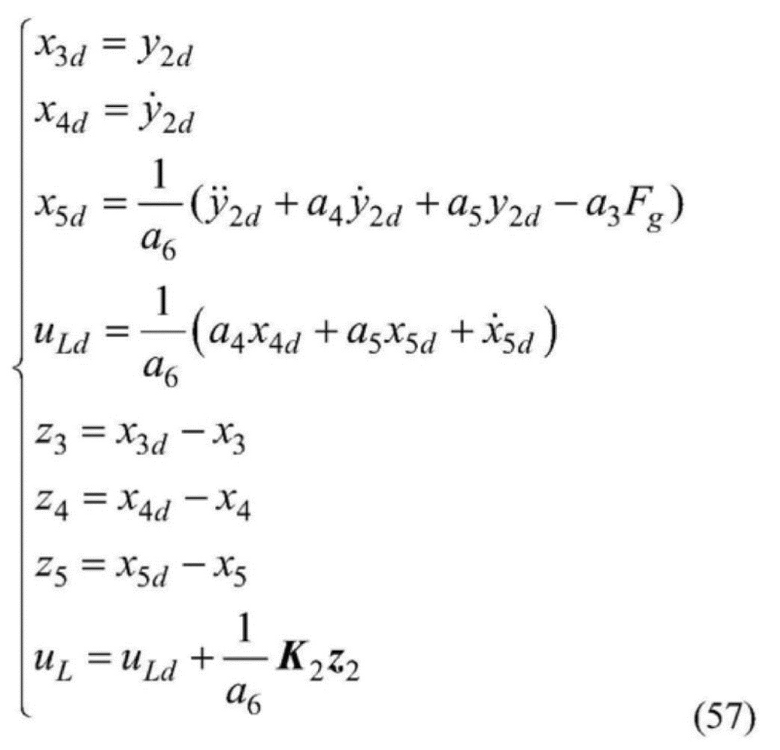 .
.
[0159] По сравнению с существующим популярным способом разработки регулятора на основе алгоритма бэкстеппинга настоящее изобретение имеет преимущества, заключающиеся в том, что процесс вывода переменных состояния системы опускается, таким образом, что процесс разработки регулятора значительно упрощается; время срабатывания регулятора может быть сокращено, а выравнивание расположения подъемного контейнера может осуществляться быстрее; в процессе применения системы уровень шума, измеряемый датчиком, и данные, находящиеся за пределами модели системы, могут быть увеличены посредством вывода переменной состояния самой системы, таким образом, может быть снижена вероятность возникновения ошибок отслеживания при помощи разработки регулятора плоскостности; данный процесс контроля является более точным, при этом также обеспечивается эффективность осуществления этого контроля.
КРАТКОЕ ОПИСАНИЕ СХЕМ
[0160] Фиг. 1 представляет собой схематическое структурное изображение подъемной системы настоящего изобретения.
[0161] Фиг. 2 представляет собой схему кинетической модели гидравлического цилиндра со штоком двустороннего действия.
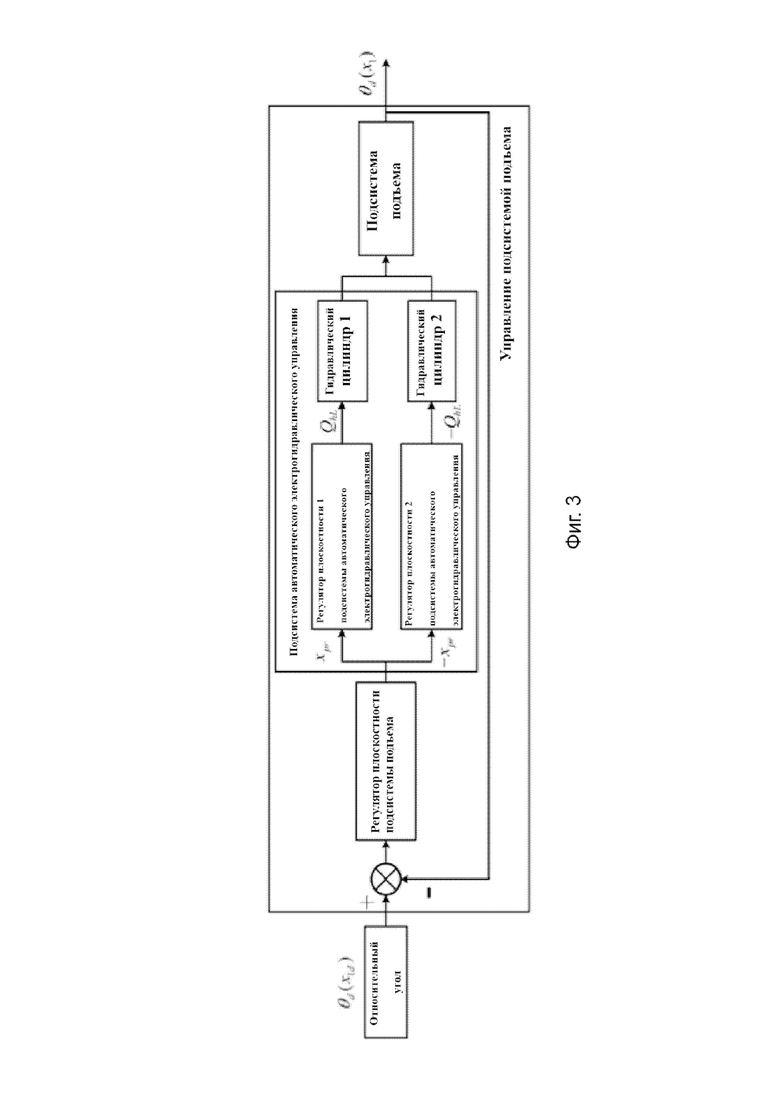
[0162] Фиг. 3 представляет собой пространственную диаграмму системы управления настоящего изобретения.
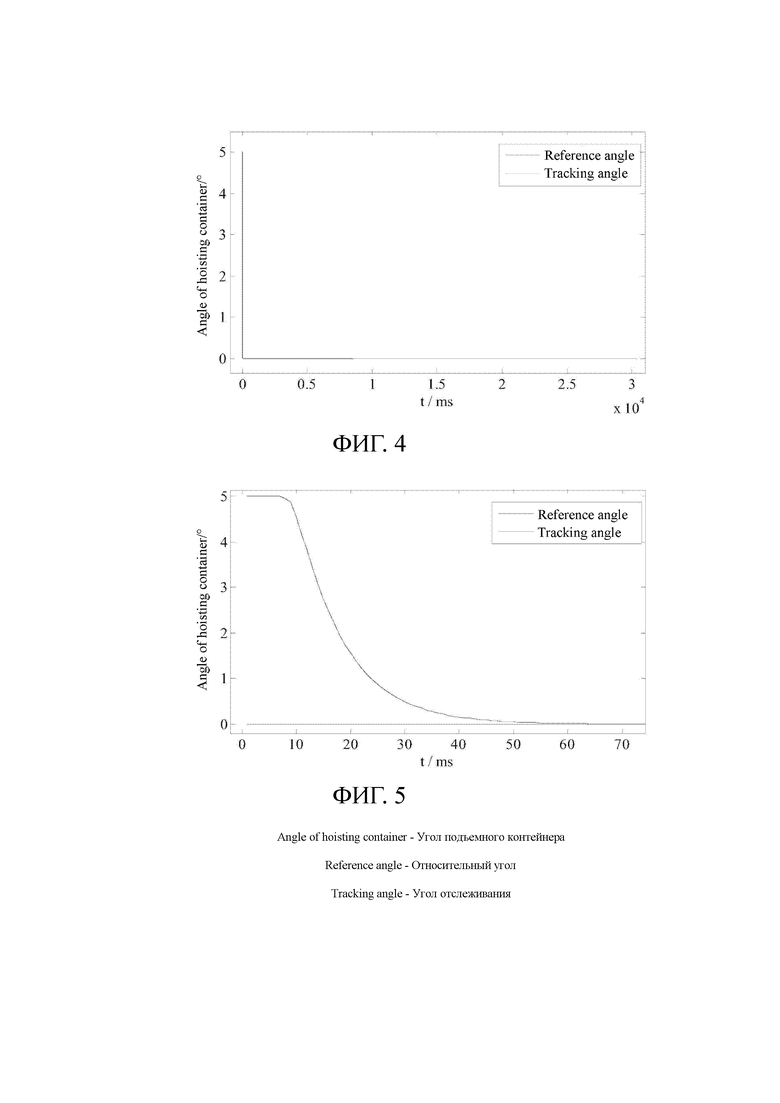
[0163] Фиг. 4 представляет собой сравнительную диаграмму сигналов отслеживания угла подъемного контейнера регулятором плоскостности в конкретном варианте осуществления настоящего изобретения.
[0164] Фиг. 5 представляет собой увеличенное схематическое изображение отдельно взятого участка сигналов отслеживания угла подъемного контейнера регулятором плоскостности в конкретном варианте осуществления настоящего изобретения.
[0165] Фиг. 6 представляет собой сравнительную диаграмму сигналов отслеживания гидравлического цилиндра 1 регулятором плоскостности в конкретном варианте осуществления настоящего изобретения.
[0166] Фиг. 7 представляет собой схематическое изображение ошибки отслеживания гидравлического цилиндра 1 регулятором плоскостности в конкретном варианте осуществления настоящего изобретения.
[0167] Фиг. 8 представляет собой сравнительную диаграмму сигналов отслеживания гидравлического цилиндра 2 регулятором плоскостности в конкретном варианте осуществления настоящего изобретения.
[0168] Фиг. 9 представляет собой схематическое изображение ошибки отслеживания гидравлического цилиндра 2 регулятором плоскостности в конкретном варианте осуществления настоящего изобретения.
[0169] Фиг.10 представляет собой сравнительную диаграмму сигналов отслеживания угла подъемного контейнера регулятором на основе алгоритма бэкстеппинга в конкретном варианте осуществления настоящего изобретения.
[0170] Фиг. 11 представляет собой увеличенное схематическое изображение отдельно взятого участка сигналов отслеживания угла подъемного контейнера регулятором на основе алгоритма бэкстеппинга.
[0171] Фиг. 12 представляет собой сравнительную диаграмму сигналов отслеживания гидравлического цилиндра 1 регулятором на основе алгоритма бэкстеппинга.
[0172] Фиг. 13 представляет собой схематическое изображение ошибки отслеживания гидравлического цилиндра 1 регулятором на основе алгоритма бэкстеппинга в конкретном варианте осуществления.
[0173] Фиг. 14 представляет собой сравнительную диаграмму сигналов отслеживания гидравлического цилиндра 2 регулятором на основе алгоритма бэкстеппинга на основе конкретного варианта осуществления.
[0174] Фиг. 15 представляет собой диаграмму погрешностей отслеживания гидравлического цилиндра 2 регулятором на основе алгоритма бэкстеппинга на основе конкретного варианта осуществления.
[0175] Цифрами на фигурах обозначены: 1 - барабан для двойной намотки; 2 - одиночный канат; 3 - подвижный канатный шкив; 4 - гидравлический цилиндр со штоком двустороннего действия; 5 - вертикальный участок стального каната; а также 6 - подъемный контейнер.
ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ
[0176] Настоящее изобретение более подробно описывается ниже со ссылкой на прилагаемые схемы, а также на конкретный вариант его осуществления.
[0177] Как показано на Фиг. 1 и Фиг. 2, для источника давления гидравлического масла Ps гидравлической системы, Ps=15·106 Па. Для эффективной рабочей площади Ap гидравлического цилиндра со штоком двустороннего действия 4 Ap=1,88·10-3 м2. Для массы груза m гидравлической системы, m=200 кг. Для коэффициента демпфирования Bp за счет вязкого трения гидравлического цилиндра, Bp=25000 Н (м/с). Для общего объема Vt вброса и выброса гидравлического масла гидравлического цилиндра, Vt=0,96·10-3 м3. Для общего коэффициента рассеяния Ct1 гидравлической системы, Ct1=9,2·10-13 м3/(с/Па). Для объема модуля упругости βe гидравлического масла, βe=6,9·108 Па. Для расстояний по вертикали b1 и b2 от верхней и нижней поверхности подъемного контейнера 6 к центру тяжести подъемного контейнера, b1=b2=0,0625 м. Для расстояний по горизонтали a1 и a2 от точки соединения двух вертикальных участков стальных канатов 5 на подъемном канате 6 к центру тяжести подъемного контейнера, a1=a2=0,1575 м. Для первоначальных длин lh20 и lh20 вертикальных участков стальных канатов 5, lh20=lh20=6 м. Для момента инерции Ic подъемного контейнера 6, Ic=3,307 кг·м2. Для единицы длины к массе ρ стального каната ρ = 0,417 кг/м. Для углов наклона a1 и a2 левого и правого одиночных канатов 2, a1=a2=64,5°. Для радиусов r1 и r2 двух подвижных канатный шкивов 3, r1=r2=0,2 м. Для масс m1 и m2 двух подвижных канатных шкивов 3, m1=m2= 10 кг. Для массы mc подъемного контейнера 6, mc=120 кг. Для коэффициентов поперечного эквивалентного демпфирования cs1, cs2, cs3 и cs4 четырех пар упругодемпфирующих моделей, cs1=cs2=cs3=cs4=10 Н/(м/с). Для поперечной эквивалентной жесткости ks1, ks2, ks3 и ks4 четырех пар упругодемпфирующих моделей, ks1=ks2=ks3=ks4=1000 Па.
[0178] Для параметров управления регулятора плоскостности, K1=[k1,k2]=[20,10] и K2=[k3,k4,k5]=[3·1014,2·1012,2].
[0179] Для параметров управления регулятора на основе алгоритма бэкстеппинга, k1=20, k2=20, k3=300, k4=280 и k5=260.
[0180] Устанавливается угол наклона луча подъемного контейнера в 5°.
[0181] Как показано на Фиг. 3, этапы выравнивания расположения подъемного контейнера регулятора плоскостности заключаются в следующем:
[0182] 1) Форма пространственного состояния кинетической модели подсистемы подъема выглядит следующим образом:
[0183] 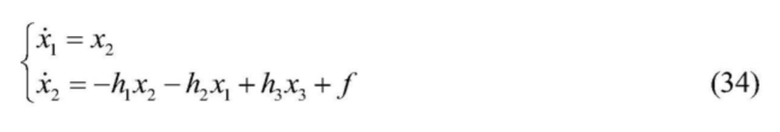 , и
, и
[0184] y1=x1, где
[0185]в формуле: h1=B/A, h2=C/A, h3=R/A, а f=F0/A.
[0186] 2) Форма пространственного состояния кинетической модели подсистемы автоматического электрогидравлического управления выглядит следующим образом:
[0187] 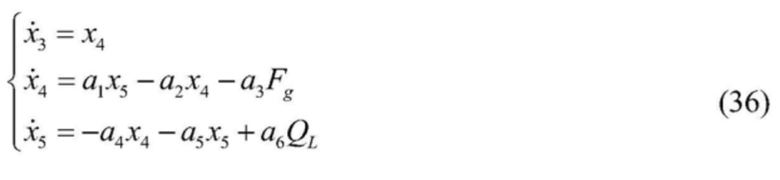 , и
, и
[0188] y2=x3, где
[0189] в формуле: a1=Ap/m, a2=Bp/m, a3=1/m, a4=4βeAp/Vt, a5=4βeCtl/Vt, а a6=4βe/Vt.
[0190] 3) Переменная состояния системы x и ввод сигнала управления системы u могут быть выражены в виде нижеприведенного уравнения вывода сигнала данных плоскостности системы и его конечного дифференциала:
[0191]  , и
, и
[0192] 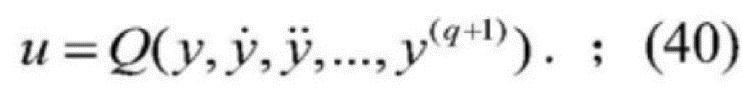 .
.
[0193] 4) Разработка конкретного регулятора плоскостности для выравнивания расположения подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте выглядит следующим образом:
[0194]  .
.
[0195] 5) Разработка регулятора плоскостности для установки расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления выглядит следующим образом:
[0196] 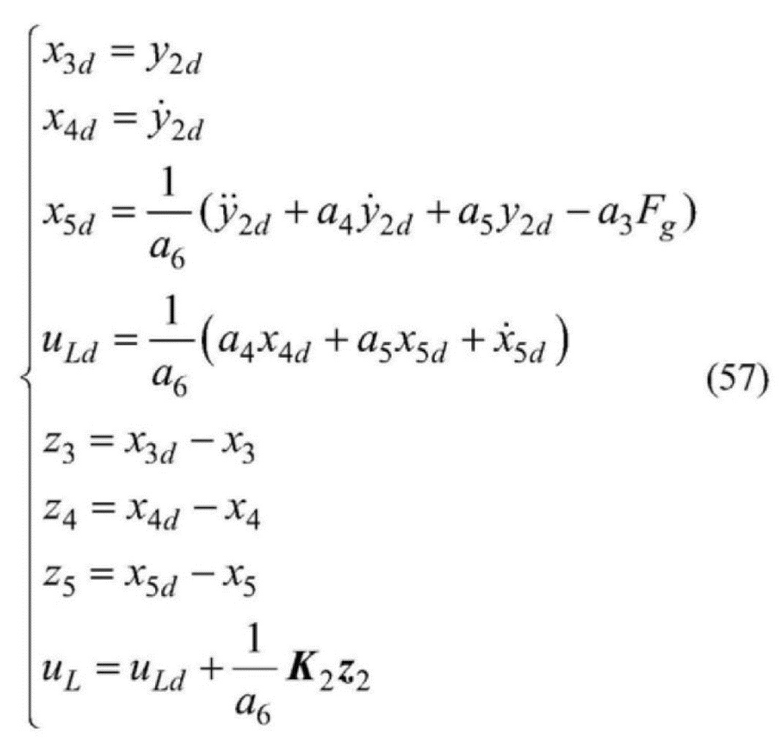 .
.
[0197] Согласно вводному параметру конкретного варианта осуществления изобретения, полученные характеристики выравнивания подъемного контейнера регулятором плоскостности показаны на Фигурах с 4 по 9.
[0198] Расчет системы управления выравнивания расположения регулятора на основе алгоритма бэкстеппинга выглядит следующим образом:
[0199] 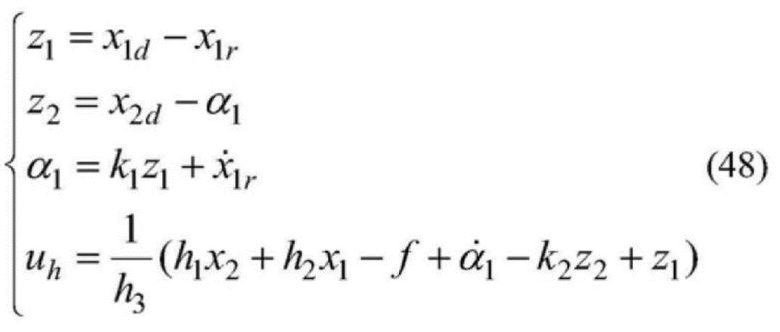 .
.
[0200] Процесс управления расположением замкнутой цепи движения подсистемы автоматического электрогидравлического управления регулятором на основе алгоритма бэкстеппинга выглядит следующим образом:
[0201] 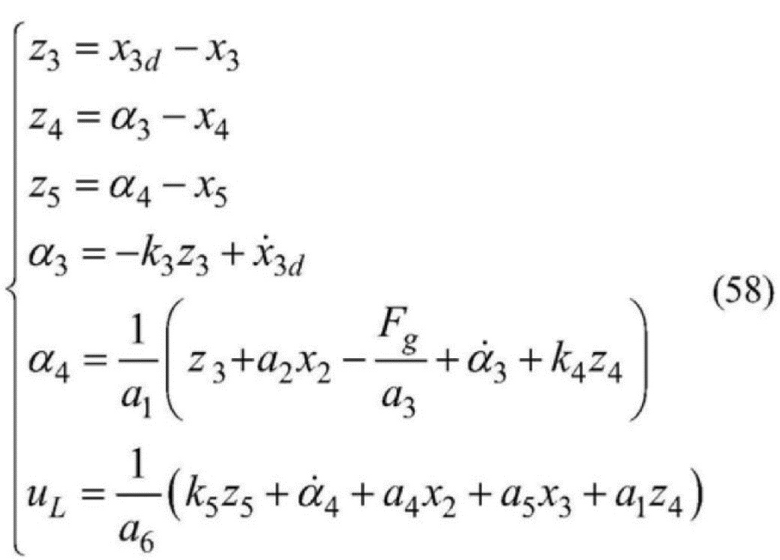 .
.
[0202] Согласно вводному параметру конкретного варианта осуществления изобретения, результативность выравнивания подъемного контейнера регулятором на основе алгоритма бэкстеппинга показаны на Фигурах с 10 по 15.
[0203] Исходя из характеристики отслеживания угла подъемных контейнеров двумя регуляторами, подъемные контейнеры могут быть выровнены за определенное время, но в тоже время регулятор плоскостности дает возможность выровняться подъемному контейнеру за 70 мс, а регулятор на основе алгоритма бэкстеппинга позволяет подъемному контейнеру достичь стабильного состояния за 450 мс. Исходя из характеристики отслеживания расположения двух гидравлических цилиндров, ошибка отслеживания регулятора на основе алгоритма бэкстеппинга является большей, чем у регулятора плоскостности. Основываясь на вышеизложенное, контрольная результативность регулятора плоскостности превосходит результативность регулятора на основе алгоритма бэкстеппинга.

Изобретение относится к подъемной системе вертикальной шахты, в частности к способу управления пространственным расположением подъемного контейнера в подъемной системе двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте. Для осуществления способа на первом этапе осуществляют построение математической модели подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте. На втором этапе выполняют построение математической модели расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления. На третьем этапе осуществляют вывод данных плоскостности нелинейной системы. На четвертом этапе выполняют разработку регулятора плоскостности для выравнивания расположения подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте. На пятом этапе выполняют разработку регулятора плоскостности для установки расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления. Достигается технический результат – повышение эффективности управления пространственным расположением подъемного контейнера за счет снижения времени срабатывания регуляторов, позволяющего ускорить выравнивание контейнера, снижения вероятности возникновения ошибок отслеживания и повышения точности процесса контроля. 9 з.п. ф-лы, 15 ил.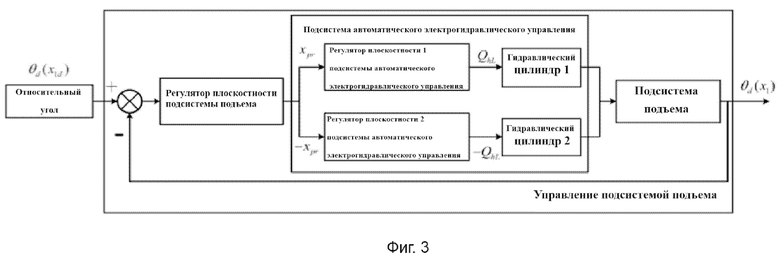
1. Способ управления пространственным расположением подъемного контейнера в подъемной системе двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте включает в себя следующее:
этап 1 - построение математической модели подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте;
этап 2 - построение математической модели расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления;
этап 3 - вывод данных плоскостности нелинейной системы;
этап 4 - разработка регулятора плоскостности для выравнивания расположения подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте; а также
этап 5 - разработка регулятора плоскостности для установки расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления.
2. Способ по п. 1, отличающийся тем, что на этапе 1 математическая модель подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте выглядит следующим образом:
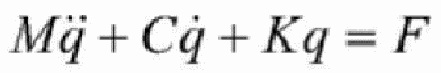 , где
, где
в формуле:  , и q являются обобщенным ускорением, скоростью и смещением соответственно, q=[xc,yc,θ], xc и yc являются вертикальным смещением и горизонтальным смещением центра тяжести подъемного контейнера соответственно, θc - это угол поворота против часовой стрелки подъемного контейнера, а M, C, K и F являются матрицей массы, матрицей демпфирования, матрицей жесткости и непотенциальной силой подсистемы подъема соответственно, где
, и q являются обобщенным ускорением, скоростью и смещением соответственно, q=[xc,yc,θ], xc и yc являются вертикальным смещением и горизонтальным смещением центра тяжести подъемного контейнера соответственно, θc - это угол поворота против часовой стрелки подъемного контейнера, а M, C, K и F являются матрицей массы, матрицей демпфирования, матрицей жесткости и непотенциальной силой подсистемы подъема соответственно, где
 , где
, где
mc - масса подъемного контейнера; ρ - единица массы стального каната; lhi - длина стального каната; ai - расстояние по горизонтали между точкой соединения двух вертикальных участков стальных канатов на подъемном контейнере и центром тяжести подъемного контейнера; Ic - момент инерции подъемного контейнера;
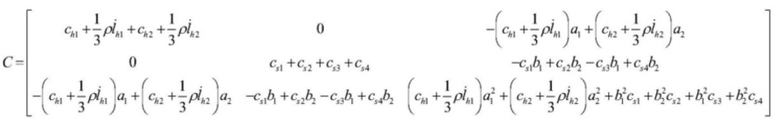 , где
, где
сhi - коэффициент демпфирования вертикального участка правого стального каната; csi - коэффициент поперечного эквивалентного демпфирования; bi - расстояние по вертикали между верхней и нижней поверхностями подъемного контейнера и центром тяжести подъемного контейнера;
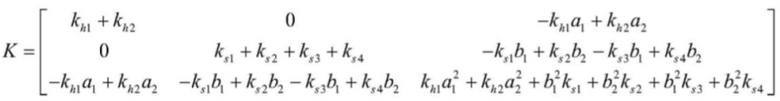 , где
, где
khi - жесткость вертикальных участков стального каната; ksi - поперечная эквивалентная жесткость четырех пар упругодемпфирующих моделей; kc1 и kh1 - жесткости левого одиночного каната и вертикального участка левого стального каната соответственно, а kc2 и kh2 - жесткости правого одиночного каната и вертикального участка правого стального каната соответственно и 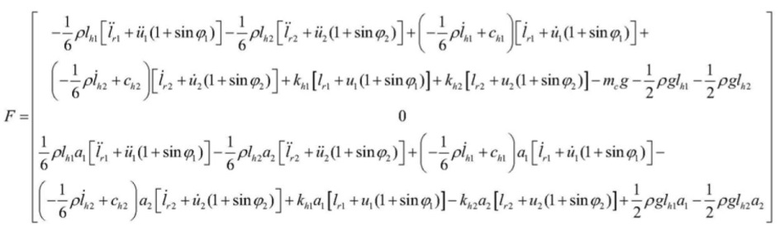 , где
, где
lri - длина намотки барабана для двойной намотки; ui - смещение двух подвижных канатных шкивов; ϕi - внутренний угол между двумя одиночными канатами и горизонтальной плоскостью; g – ускорение свободного падения.
3. Способ по п. 2, отличающийся тем, что если в процессе моделирования подсистемы подъема не предполагается смещение нагрузки, то есть a1=a2, и, кроме того, если угол поворота против часовой стрелки подъемного контейнера равен 0, то натяжение двух стальных канатов будет согласованным; и, следовательно, математическая модель подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте может быть упрощена и выглядеть следующим образом:
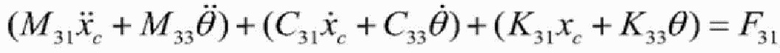 , где
, где
в формуле: Mij, Cij, Kij и Fij являются элементами матрицы массы, матрицы демпфирования, матрицы жесткости и непотенциальной силы соответственно (i=1,2,3 и j=1,2,3); xc – вертикальное смещение центра тяжести подъемного контейнера; θ - угол наклона подъемного контейнера.
4. Способ по п. 3, отличающийся тем, что выравнивание расположения подъемного контейнера регулируется двумя гидравлическими контролерами, тем самым u1=u=-u2, угол наклона θ подъемного контейнера является регулируемой величиной, а математическая модель подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте может быть дополнительно упрощена и выглядеть следующим образом:
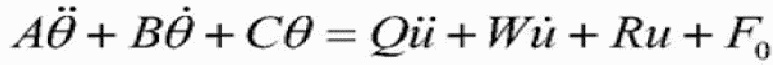 , где
, где
в формуле:
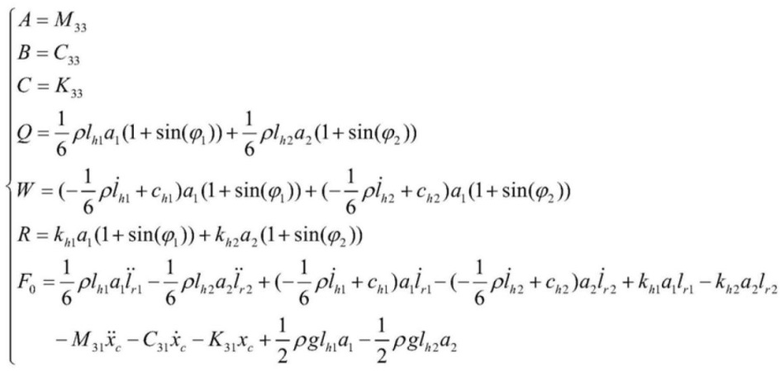 , и
, и
kh1 и kh2 намного больше ch1 и ch2, что еще больше упрощает формулу до следующего вида:
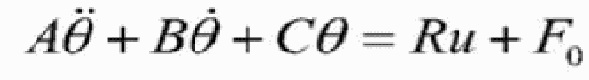 .
.
5. Способ по п. 3, отличающийся тем, что переменная состояния выбирается таким образом 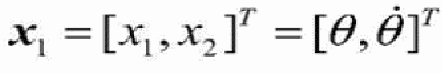 , чтобы динамическую модель подсистемы подъема можно было преобразовать в форму пространственного состояния:
, чтобы динамическую модель подсистемы подъема можно было преобразовать в форму пространственного состояния:
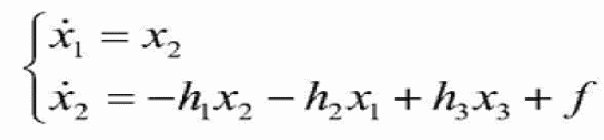 , и
, и
y1=x1, где
в формуле: h1=B/A, h2=C/A, h3=R/A, а f=F0/A.
6. Способ по п. 1, отличающийся тем, что на этапе 2 математическая модель подсистемы автоматического электрогидравлического управления выглядит следующим образом:
 , где
, где
в формуле: Ap является эффективной рабочей площадью поршня гидравлического цилиндра, Ctl является общим коэффициентом рассеяния гидравлического цилиндра, xp - смещение штока поршня гидравлического цилиндра, Vt - общий объем полости для вброса и выброса гидравлического масла, а βe - эффективный объем модуля упругости гидравлической масла в гидравлическом цилиндре; PL=p1-p2 - падение давления нагрузки гидравлического цилиндра, где p1 - напорное движение в гидравлический цилиндр, p2 - напорное движение из гидравлического цилиндра; QL = Q1-Q2 – скорость подачи нагрузки, где Q1 - скорость подачи, направленной внутрь гидравлического цилиндра, а Q2 - скорость подачи, направленной извне гидравлического цилиндра; а также
согласно второму закону Ньютона уравнение равновесия силы нагрузки системы автоматического электрогидравлического управления представлено следующим образом:
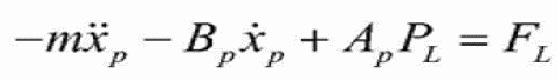 ,
,
где FL является силой гидравлических цилиндров со штоком двустороннего действия, с которой они воздействуют на подвижные канатные шкивы, m является общей массой подвижных канатных шкивов, а Bp - коэффициент демпфирования за счет вязкого трения гидравлического цилиндра.
7. Способ по п. 5, отличающийся тем, что переменная состояния выбирается таким образом 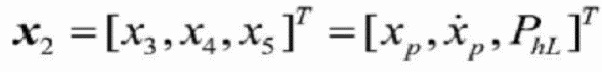 , чтобы кинетическую модель подсистемы автоматического электрогидравлического управления можно было преобразовать в форму пространственного состояния:
, чтобы кинетическую модель подсистемы автоматического электрогидравлического управления можно было преобразовать в форму пространственного состояния:
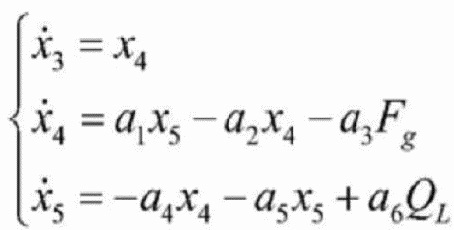 , и
, и
y2=x3, где
в формуле: a1=Ap/m, a2=Bp/m, a3=1/m, a4=4βeAp/Vt, a5=4βeCtl/Vt, а a6=4βe/Vt.
8. Способ по п. 1, отличающийся тем, что на этапе 3 разработка конкретного вывода данных плоскостности нелинейной системы выглядит следующим образом:
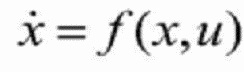 , где
, где
в формуле: x - переменная состояния системы, а u - ввод сигнала управления с тем же значением, что и у вывода сигнала системы y;
а в случае если имеется следующий вывод сигнала системы:
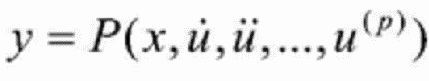 ,
,
переменная состояния системы x и ввод сигнала управления системы u могут быть выражены в виде уравнения вывода сигнала системы и его конечного дифференциала:
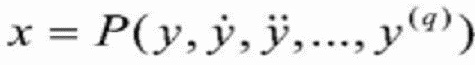 , и
, и
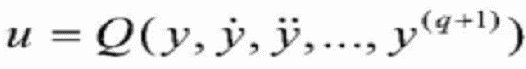 .
.
9. Способ по п. 1, отличающийся тем, что на этапе 4 разработка регулятора плоскостности для выравнивания расположения подсистемы подъема двойного типа намотки канатов для работы в сверхглубокой вертикальной шахте выглядит следующим образом:
 , где
, где
x1d - переменная предполагаемого состояния подсистемы подъема; y1d - предполагаемый вывод сигнала системы, то есть исходный сигнал; x2d - динамика погрешности предполагаемой переменной; uhd - вывод сигнала разомкнутой цепи; z1 - ошибка отслеживания состояния системы; x1 – переменная состояния системы; uh – вывод сигнала управления системы; K1 – матрица коэффициентов усиления системы управления.
10. Способ по п. 1, отличающийся тем, что на этапе 5 разработка регулятора плоскостности для установки расположения замкнутой цепи движения в подсистеме автоматического электрогидравлического управления выглядит следующим образом:
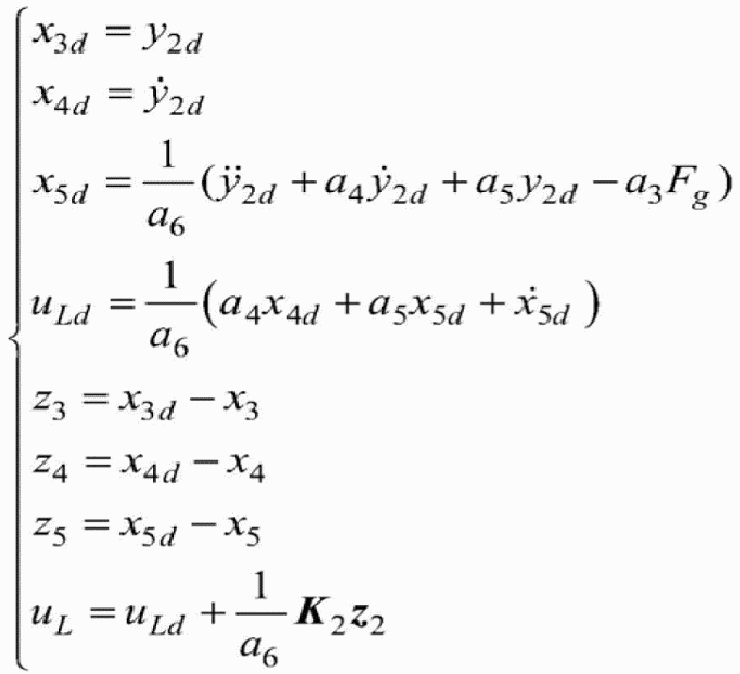 , где
, где
y2d - предполагаемый вывод данных системы, то есть исходный сигнал; uLd – ввод сигнала разомкнутой цепи; z2 - ошибка отслеживания системы; uL – ввод сигнала управления с обратной связью; K2 - ортогональная матрица коэффициентов усиления системы управления.
| CN 102602838 A, 25.07.2012 | |||
| Устройство для транспортировки длинномеров в шахтах | 1983 |
|
SU1153088A1 |
| КОМПЛЕКС ДЛЯ ПОДЗЕМНОГО СБОРА И ХРАНЕНИЯ ТВЕРДЫХ БЫТОВЫХ ОТХОДОВ | 2009 |
|
RU2408516C1 |
| УСТРОЙСТВО И СПОСОБ СБОРА ЭНЕРГИИ ДЛЯ КЛЕТИ С НАПРАВЛЯЮЩИМИ ТРОСАМИ | 2015 |
|
RU2662765C2 |
| СПОСОБ И УСТРОЙСТВО УПРАВЛЕНИЯ ГРУЗОПОДЪЕМНОЙ МАШИНОЙ, ЗАПОМИНАЮЩАЯ СРЕДА И СИСТЕМА ГРУЗОПОДЪЕМНОЙ МАШИНЫ | 2012 |
|
RU2597052C2 |
| СПОСОБ ЗАЩИТЫ ШАХТНОЙ ПОДЪЕМНОЙ УСТАНОВКИ ОТ НАПУСКА ТЯГОВЫХ КАНАТОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1992 |
|
RU2031830C1 |
Авторы
Даты
2021-02-09—Публикация
2019-09-12—Подача