Изобретение относится к областям радиотехники и измерительной техники и может быть использовано в устройствах аппаратуры управления и передачи информации для измерения коэффициента корреляции случайного сигнала и оценки параметров случайного сигнала.
Известны [1, 2] устройства измерения коэффициента корреляции случайных процессов, принцип действия которых основан на усреднении произведения текущего и смещенного во времени сигналов, оценке их дисперсий и вычислении коэффициента корреляции на основе теории вероятностей [3, 4] и метолов эмпирического определения характеристик случайных процессов [5]. К их недостаткам следует отнести аналоговую обработку и приближенные нелинейные преобразования сигналов, что приводит к погрешностям измерения.
Известны [6, 7] цифровые корреляторы, состоящие из блоков аналого-цифрового преобразования, регистров, сумматоров и умножителей.
Близким к предлагаемому техническому решению является цифровой коррелятор [8], содержащий аналого-цифровые преобразователи, регистры, блоки памяти и умножения и суммирования мантисс.
К недостаткам известных цифровых корреляторов следует отнести сложность реализации и низкую скорость обработки отсчетов сигнала. Кроме того, для определения коэффициента корреляции необходимо дополнительно определять среднее значение и дисперсию случайного сигнала. Еще одним недостатком известных цифровых устройств является прерывистый характер измерительной процедуры: сигнал обрабатывается на заданном интервале времени, формируется результат, а затем начинается новый цикл измерения.
Наиболее близким по технической сущности к предлагаемому цифровому устройству является цифровой измеритель статистических характеристик случайных сигналов [9], содержащий аналого-цифровой преобразователь (АЦП), регистры, каналы формирования среднего значения (ФСЗ) и среднего квадрата (ФСК), квадратичные преобразователи, вычитатель и генератор тактовых импульсов (ГТИ), формирующий оценки среднего значения и дисперсии входного сигнала. Его недостатком является отсутствие возможности измерения коэффициента корреляции.
Задачей предлагаемого технического решения является обеспечение непрерывного цифрового измерения коэффициента корреляции с высокой точностью при минимальном числе необходимых арифметических операций.
Поставленная задача решается тем, что цифровой измеритель коэффициента корреляции случайного сигнала, содержащий аналого-цифровой преобразователь (АЦП), последовательно соединенный с ним регистр (РГ), к выходу которого подключены канал формирования среднего значения (ФСЗ) и первый квадратичный преобразователь (КП), канал формирования среднего квадрата (ФСК), вход которого подключен к выходу первого КП, второй КП, вход которого соединен с выходом ФСЗ, а выход подключен к первому входу первого вычитателя (В1), второй вход вычитателя подключен к выходу ФСК, генератор тактовых импульсов (ГТИ), каналы ФСЗ и ФСК содержат по n каскадно соединенных накопителей отсчетов (НО) (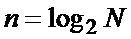 ,
, 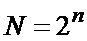 - объем выборки, по которой проводится усреднение), каждый НО содержит сумматор и регистр сдвига многоразрядных кодов, первый вход сумматора и вход регистра соединены вместе и образуют общий вход НО, выход регистра сдвига соединен со вторым входом сумматора, а выход сумматора является выходом НО, вход первого НО канала ФСЗ является входом ФСЗ, а выход его n-го НО - выходом ФСЗ, вход первого НО канала ФСК является входом ФСК, а выход его n-го НО - выходом ФСК, дополнительно содержит цифровую линию задержки (ЦЛЗ) и умножитель (УМ), входы ЦЛЗ и первый вход УМ соединены с выходом РГ, управляющий вход ЦЛЗ соединен с выходом блока управления сдвигом (БУС), а выход ЦЛЗ подключен ко второму входу УМ, канал формирования корреляционной функции (ФКФ), содержащий n каскадно соединенных накопителей отсчетов (НО), вход первого НО канала ФКФ является входом ФКФ, а выход его n-го НО - выходом ФКФ, вход ФКФ соединен с выходом УМ, второй вычитатель (В2), первый вход которого подключен к выходу второго КП, а второй вход - к выходу ФКФ, и формирователь результата (ФР), первый вход которого подключен к выходу первого вычитателя, а второй вход - к выходу второго вычитателя, выход ФР является выходом измерителя, сигналы ГТИ подаются на тактовые входы АЦП, РГ, ФСЗ, ФСК, ЦЛЗ, ФКФ и ФР.
- объем выборки, по которой проводится усреднение), каждый НО содержит сумматор и регистр сдвига многоразрядных кодов, первый вход сумматора и вход регистра соединены вместе и образуют общий вход НО, выход регистра сдвига соединен со вторым входом сумматора, а выход сумматора является выходом НО, вход первого НО канала ФСЗ является входом ФСЗ, а выход его n-го НО - выходом ФСЗ, вход первого НО канала ФСК является входом ФСК, а выход его n-го НО - выходом ФСК, дополнительно содержит цифровую линию задержки (ЦЛЗ) и умножитель (УМ), входы ЦЛЗ и первый вход УМ соединены с выходом РГ, управляющий вход ЦЛЗ соединен с выходом блока управления сдвигом (БУС), а выход ЦЛЗ подключен ко второму входу УМ, канал формирования корреляционной функции (ФКФ), содержащий n каскадно соединенных накопителей отсчетов (НО), вход первого НО канала ФКФ является входом ФКФ, а выход его n-го НО - выходом ФКФ, вход ФКФ соединен с выходом УМ, второй вычитатель (В2), первый вход которого подключен к выходу второго КП, а второй вход - к выходу ФКФ, и формирователь результата (ФР), первый вход которого подключен к выходу первого вычитателя, а второй вход - к выходу второго вычитателя, выход ФР является выходом измерителя, сигналы ГТИ подаются на тактовые входы АЦП, РГ, ФСЗ, ФСК, ЦЛЗ, ФКФ и ФР.
Предлагаемое техническое решение поясняется чертежами.
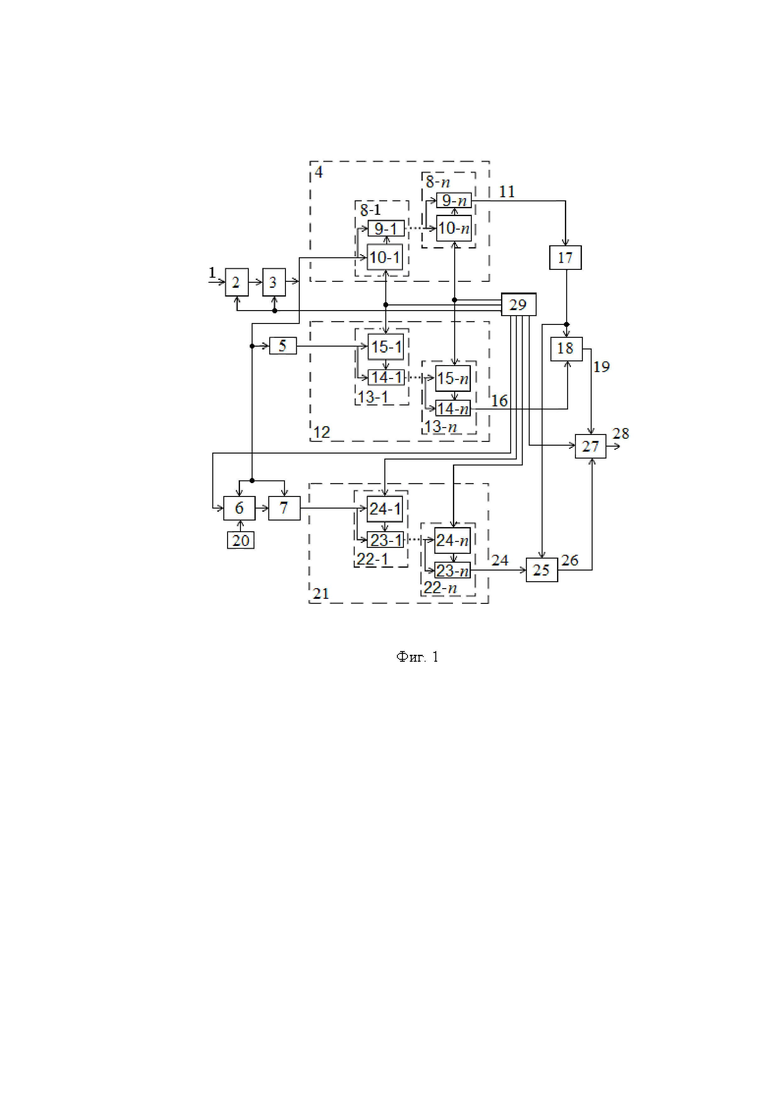
На фиг. 1 представлена структурная схема предлагаемого устройства, на фиг. 2 - временная диаграмма отсчетов случайного сигнала (фиг. 2а) и его коэффициент корреляции (фиг. 2б), на фиг. 3 - пример реализации формирователя результата, на фиг. 4 - структурная схема цифровой линии задержки, на фиг. 5 - результаты статистического имитационного моделирования работы устройства, на фиг. 6 - зависимости оценки коэффициента корреляции от номера текущего отсчета, а на фиг. 7 - результаты оценки погрешности измерения.
Принимаемый случайный сигнал 1 поступает на вход АЦП 2. Формируемые АЦП 2 отсчеты сигнала записываются в РГ 3, а с его выхода параллельно поступают на входы ФСЗ 4, первого КП 5, ЦЛЗ 6 и на первый вход умножителя 7. Блок ФСЗ 4 содержит 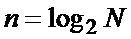 каскадно соединенных модулей НО 8-1,…,8-n, каждый из которых содержит сумматоры 9-1, …, 9-n и регистры 10-1, …, 10-n сдвига многоразрядных кодов соответственно. В каждом НО 8 первый вход сумматора 9 соединен с первым входом регистра 10 и является входом НО 8. Второй вход сумматора 9 соединен с выходом регистра сдвига 10, выход сумматора 9 является выходом блока 8 накопления отсчетов. Вход НО 8-1 является входом ФСЗ 4, а выход НО 8-n соответственно выходом ФСЗ 4, на котором формируется число, пропорциональное среднему значению 11 входного сигнала.
каскадно соединенных модулей НО 8-1,…,8-n, каждый из которых содержит сумматоры 9-1, …, 9-n и регистры 10-1, …, 10-n сдвига многоразрядных кодов соответственно. В каждом НО 8 первый вход сумматора 9 соединен с первым входом регистра 10 и является входом НО 8. Второй вход сумматора 9 соединен с выходом регистра сдвига 10, выход сумматора 9 является выходом блока 8 накопления отсчетов. Вход НО 8-1 является входом ФСЗ 4, а выход НО 8-n соответственно выходом ФСЗ 4, на котором формируется число, пропорциональное среднему значению 11 входного сигнала.
Блок ФСК 12 содержит n каскадно соединенных модулей НО 13-1, …,13-n, каждый из НО 13 содержит сумматоры 14-1, …, 14-n и регистры 15-1, …, 15-n сдвига многоразрядных кодов соответственно. В каждом НО 13 первый вход сумматора 14 соединен с первым входом регистра 15 и является входом НО 13. Второй вход сумматора 14 соединен с выходом регистра сдвига 15, выход сумматора 14 является выходом блока НО 13. Вход НО 13-1 является входом ФСК 12, а выход НО 13-n - соответственно выходом ФСК 12, на котором формируется число 16, пропорциональное среднему квадрату входного сигнала. Выход 11 ФСЗ 4 соединен с входом второго КП 17, выход которого подключен к первому входу первого вычитателя В1 18. Второй вход первого вычитателя В1 18 подключен к выходу 16 ФСК 12, а на выходе вычитателя В 16 формируется значение 19 дисперсии сигнала.
С выхода ЦЛЗ 6 на второй вход умножителя 7 поступает последовательность отсчетов сигнала, задержанная во времени на заданное число k значений, которое устанавливается в блоке управления сдвигом 20. С выхода умножителя 7 произведения сдвинутых во времени отсчетов поступают на вход ФКФ 21, который содержит n каскадно соединенных модулей НО 22-1, …,22-n, каждый из НО 22 содержит сумматоры 23-1, …, 23-n и регистры 24-1, …, 24-n сдвига многоразрядных кодов соответственно. В каждом НО 22 первый вход сумматора 23 соединен с первым входом регистра 24 и является входом НО 22. Второй вход сумматора 23 соединен с выходом регистра сдвига 24, выход сумматора 23 является выходом блока НО 22. Вход НО 22-1 является входом ФКФ 21, а выход НО 22-n - соответственно выходом ФКФ 21, на котором формируется число 24, пропорциональное ковариационной функции входного сигнала, поступающее на первый вход второго вычитателя В2 25, а на его второй вход поступает квадрат среднего значения сигнала с выхода второго КП 17. При этом на выходе В2 25 формируется значение 26 корреляционной функции, поступающее на первый вход формирователя результата ФР 26. На второй вход ФР 26 подается значение 19 дисперсии сигнала с выхода первого вычитателя 18, и на выходе ФР 26 путем деления значений 26 на 19 и преобразования результата в требуемую форму (например, в двоично-десятичный код с отображением на семисегментных индикаторах) формируется результат измерения коэффициента корреляции 28.
На управляющие входы АЦП 1, РГ 3, ФСЗ 4, ФСК 12, ЦЛЗ 6, ФКФ 21 и ФР 27 подаются импульсы от ГТИ 29.
Устройство работает следующим образом.
Входной случайный сигнал 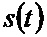 1, поступает на вход АЦП 2, который в моменты времени
1, поступает на вход АЦП 2, который в моменты времени 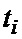 , определяемые импульсами ГТИ 29 (i - порядковый номер), формирует отсчеты
, определяемые импульсами ГТИ 29 (i - порядковый номер), формирует отсчеты 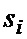 входного случайного сигнала. В текущий момент времени
входного случайного сигнала. В текущий момент времени 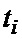 (
(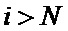 ) обрабатывается выборка отсчетов объемом
) обрабатывается выборка отсчетов объемом 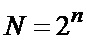 (n - целое число), по которой согласно [3-5] определяются текущие экспериментальные оценки среднего значения сигнала
(n - целое число), по которой согласно [3-5] определяются текущие экспериментальные оценки среднего значения сигнала
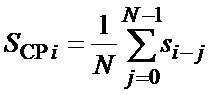 (1)
(1)
и его среднего квадрата
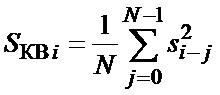 . (2)
. (2)
Оценка дисперсии входного сигнала может быть найдена как [3-5]
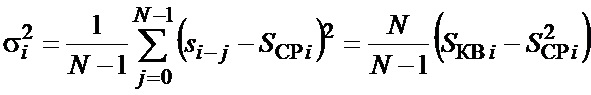 . (3)
. (3)
Поскольку на практике обычно выполняется соотношение 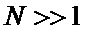 , то без заметной потери в точности вместо (3) используем оценку
, то без заметной потери в точности вместо (3) используем оценку
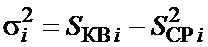 . (4)
. (4)
Текущее значение ковариационной функции оценивается посредством выражения [4]
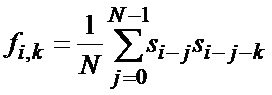 , (5)
, (5)
где k - величина смещения отсчетов.
На основе соотношений (1)-(5) для оценки текущего значения корреляционной функции формируется величина
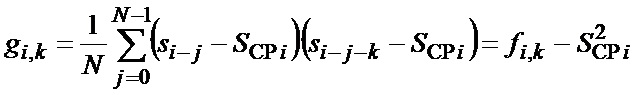 , (6)
, (6)
а для оценки текущего значения коэффициента корреляции - величина
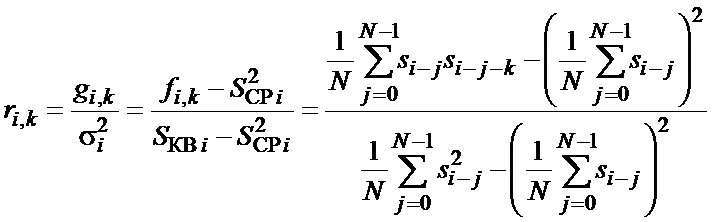 . (7)
. (7)
Согласно [3-5] относительные погрешности оценок статистических характеристик при независимых отсчетах сигнала, подчиняющегося гауссовскому распределению, уменьшаются с ростом N обратно пропорционально 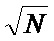 . При больших N (
. При больших N (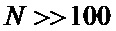 ) актуальным является использование быстрых вычислительных алгоритмов усреднения, требующих выполнения минимального числа операций сложения, что позволяет расширить рабочий частотный диапазон измерителя и упростить его аппаратную реализацию.
) актуальным является использование быстрых вычислительных алгоритмов усреднения, требующих выполнения минимального числа операций сложения, что позволяет расширить рабочий частотный диапазон измерителя и упростить его аппаратную реализацию.
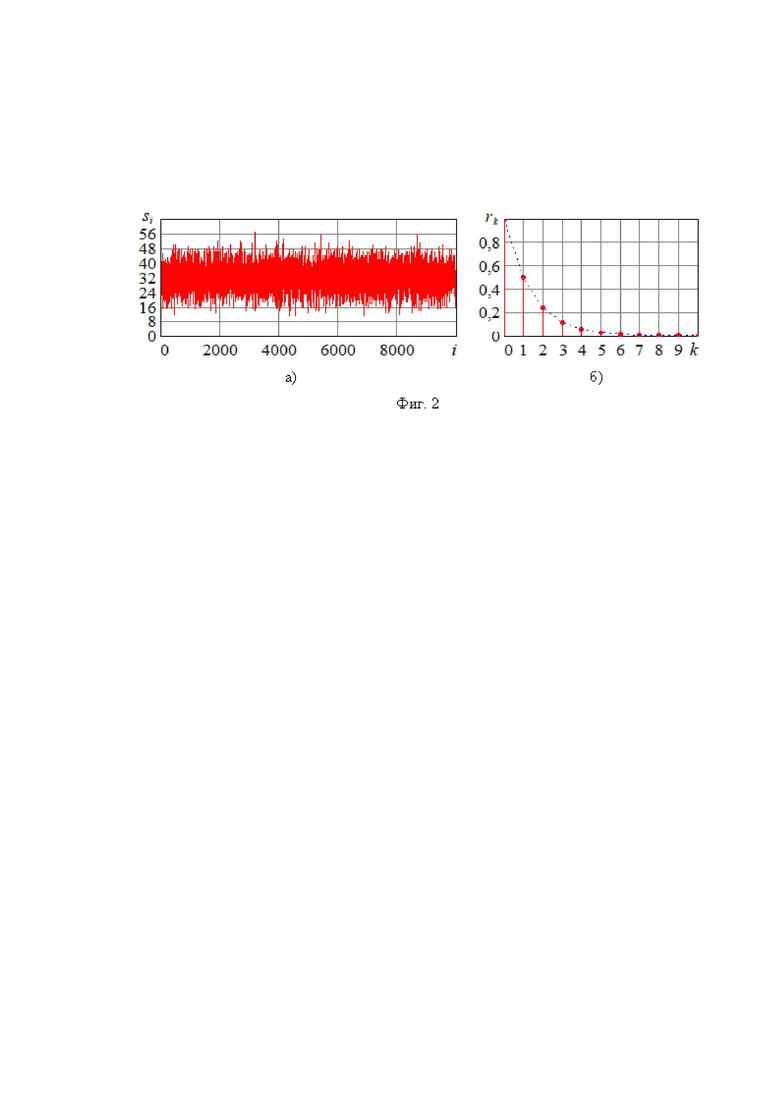
В качестве примера возможного входного воздействия на фиг. 2а показана реализация гауссовского случайного процесса 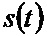 с нулевым средним, среднеквадратическим значением
с нулевым средним, среднеквадратическим значением 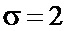 и коэффициентом корреляции между соседними отсчетами
и коэффициентом корреляции между соседними отсчетами 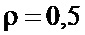 , при дискретизации шестиразрядным АЦП (64 интервала) с раствором
, при дискретизации шестиразрядным АЦП (64 интервала) с раствором 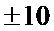 . Нормированная корреляционная функция (коэффициент корреляции) такого дискретного процесса приведена на фиг. 2б.
. Нормированная корреляционная функция (коэффициент корреляции) такого дискретного процесса приведена на фиг. 2б.
В момент времени 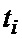 отсчет
отсчет 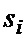 , записанный в регистре РГ 3, подается в ФСЗ 4 на вход первого НО 8-1. В сумматоре 9-1 он складывается с предшествующим значением
, записанный в регистре РГ 3, подается в ФСЗ 4 на вход первого НО 8-1. В сумматоре 9-1 он складывается с предшествующим значением 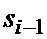 из регистра 10-1 емкостью в одну ячейку памяти, которое было записано в него на предшествующем шаге. Таким образом, на выходе сумматора 9-1 формируется сумма отсчетов
из регистра 10-1 емкостью в одну ячейку памяти, которое было записано в него на предшествующем шаге. Таким образом, на выходе сумматора 9-1 формируется сумма отсчетов 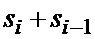 , после чего новое значение
, после чего новое значение 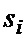 записывается в регистр 10-1. Полученная сумма подается во второй НО 8-2, в сумматоре 9-2 которого она складывается со значением
записывается в регистр 10-1. Полученная сумма подается во второй НО 8-2, в сумматоре 9-2 которого она складывается со значением 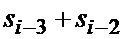 на выходе регистра сдвига 10-2 на две ячейки памяти, после чего содержимое регистра сдвигается и в освободившуюся ячейку записывается новое значение
на выходе регистра сдвига 10-2 на две ячейки памяти, после чего содержимое регистра сдвигается и в освободившуюся ячейку записывается новое значение 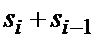 . В результате на выходе сумматора 9-2 получим сумму четырех отсчетов
. В результате на выходе сумматора 9-2 получим сумму четырех отсчетов 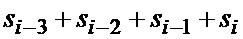 . Далее вычисления проводятся аналогично, и на вход последнего НО 8-n подается сумма
. Далее вычисления проводятся аналогично, и на вход последнего НО 8-n подается сумма
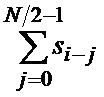 , (8)
, (8)
которая складывается в сумматоре 9-n с суммой
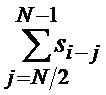 ,
,
ранее записанной в регистре сдвига 10-n на 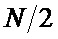 ячеек. На выходе сумматора 9-n формируется искомая сумма
ячеек. На выходе сумматора 9-n формируется искомая сумма
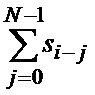 , (9)
, (9)
после чего содержимое регистра 10-n сдвигается и в освободившуюся ячейку записывается величина (8).
Нетрудно видеть, что для вычисления полной суммы (9) требуется 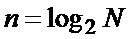 блоков НО. Например, при
блоков НО. Например, при 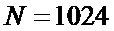 отсчета имеем
отсчета имеем 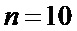 . Полученное на выходе ФСЗ 4 число пропорционально среднему значению (1) входного сигнала. Операция его деления на
. Полученное на выходе ФСЗ 4 число пропорционально среднему значению (1) входного сигнала. Операция его деления на 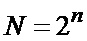 , как требуется согласно (1), выполняется отбрасыванием n младших двоичных разрядов.
, как требуется согласно (1), выполняется отбрасыванием n младших двоичных разрядов.
Блок ФСК 12 функционирует аналогично за исключением того, что накапливаются квадраты отсчетов 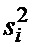 . В результате на выходе НО 14-n генерируется сумма
. В результате на выходе НО 14-n генерируется сумма
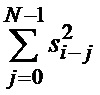 . (10)
. (10)
Для получения среднего квадрата 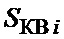 согласно (2) необходимо разделить результат (10) на N, что достигается отбрасыванием n младших разрядов.
согласно (2) необходимо разделить результат (10) на N, что достигается отбрасыванием n младших разрядов.
Число на выходе ФСЗ 4 является измеренным средним значением сигнала 11. Для вычисления дисперсии данное среднее значение подается на вход второго КП 17, который формирует значение 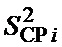 . В первом вычитателе 18 полученное значение
. В первом вычитателе 18 полученное значение 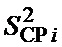 вычитается из среднего квадрата
вычитается из среднего квадрата 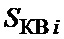 , поступающего с выхода 16 ФСК 12, так что на выходе первого вычитателя 16 формируется значение
, поступающего с выхода 16 ФСК 12, так что на выходе первого вычитателя 16 формируется значение 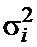 дисперсии сигнала 19 в соответствии с (4).
дисперсии сигнала 19 в соответствии с (4).
Отсчеты входного сигнала с выхода регистра 3 поступают на вход ЦЛЗ 6 и первый вход умножителя 7. С выхода ЦЛЗ 6 задержанные на k тактов отсчеты поступают на второй вход умножителя 7, на выходе которого получим произведение отсчетов 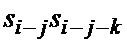 . Блок ФКФ 21 функционирует аналогично ФСЗ и ФСК, но в нем накапливаются произведения отсчетов
. Блок ФКФ 21 функционирует аналогично ФСЗ и ФСК, но в нем накапливаются произведения отсчетов 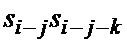 . В результате на выходе НО 22-n получим сумму
. В результате на выходе НО 22-n получим сумму
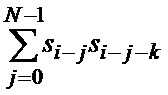 ,
,
которая затем поступает на второй вход второго вычитателя 25. На первый вход второго вычитателя 25 поступает величина 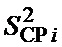 с выхода второго квадратичного преобразователя 17, и на выходе В2 после деления на N формируется величина
с выхода второго квадратичного преобразователя 17, и на выходе В2 после деления на N формируется величина 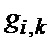 (6).
(6).
Текущее значение коэффициента корреляции 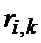 , определяемое согласно (7), рассчитывается в формирователе результата ФР 27, который производит код значения
, определяемое согласно (7), рассчитывается в формирователе результата ФР 27, который производит код значения 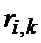 . Деление двоичных чисел может выполняться известными методами [10], например, «в столбик». Аппаратная реализация данной операции может быть выполнена согласно [11], однако при этом возникают трудности преобразования результата в двоично-десятичный код (например, при необходимости его отображения на цифровом индикаторе).
. Деление двоичных чисел может выполняться известными методами [10], например, «в столбик». Аппаратная реализация данной операции может быть выполнена согласно [11], однако при этом возникают трудности преобразования результата в двоично-десятичный код (например, при необходимости его отображения на цифровом индикаторе).
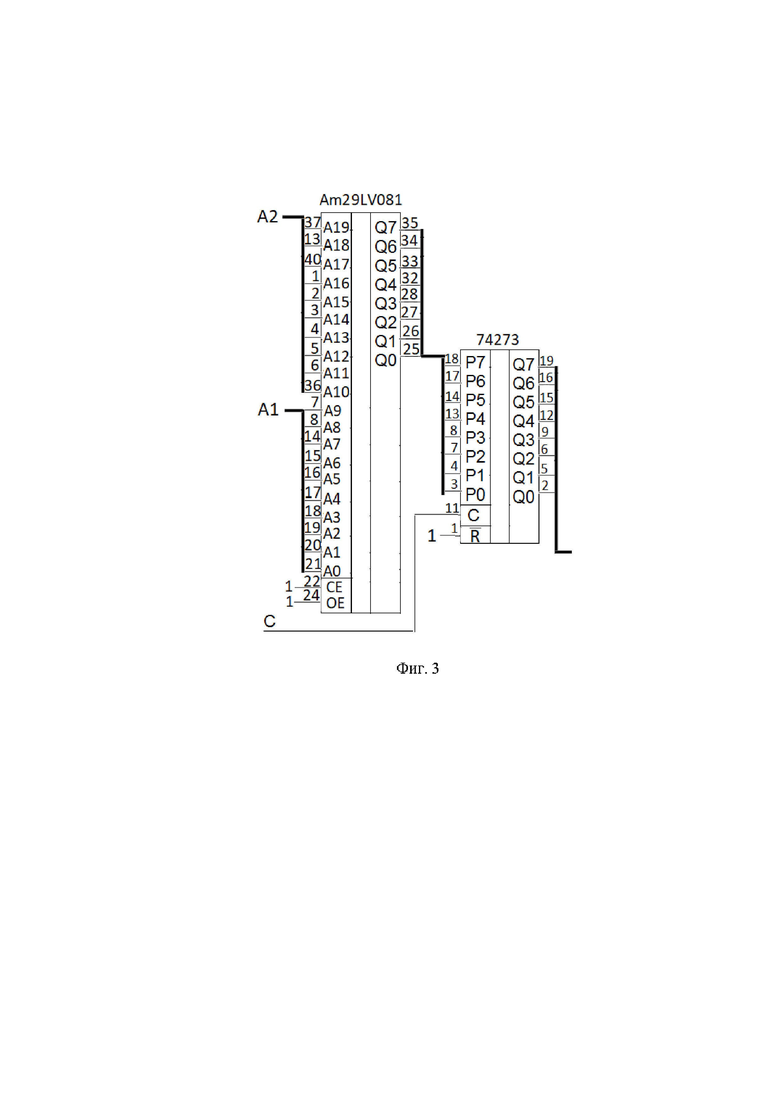
Наиболее эффективно ФР 27 может быть реализован на основе постоянного запоминающего устройства (ПЗУ), например, Am29LV081 емкостью 1М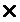 8 бит или S29JL032J емкостью 4М
8 бит или S29JL032J емкостью 4М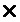 8 бит и регистра. Один из вариантов такой схемы показан на фиг. 3. Здесь шина адреса разделена на две части (десятиразрядные шины A1 и A2), которые образуют первый и второй входы ФР 27. В результате код адреса равен
8 бит и регистра. Один из вариантов такой схемы показан на фиг. 3. Здесь шина адреса разделена на две части (десятиразрядные шины A1 и A2), которые образуют первый и второй входы ФР 27. В результате код адреса равен
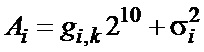 ,
,
а в соответствующей ячейке ПЗУ заранее записан требуемый (двоичный или двоично-десятичный) код значения 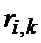 , равного (7).
, равного (7).
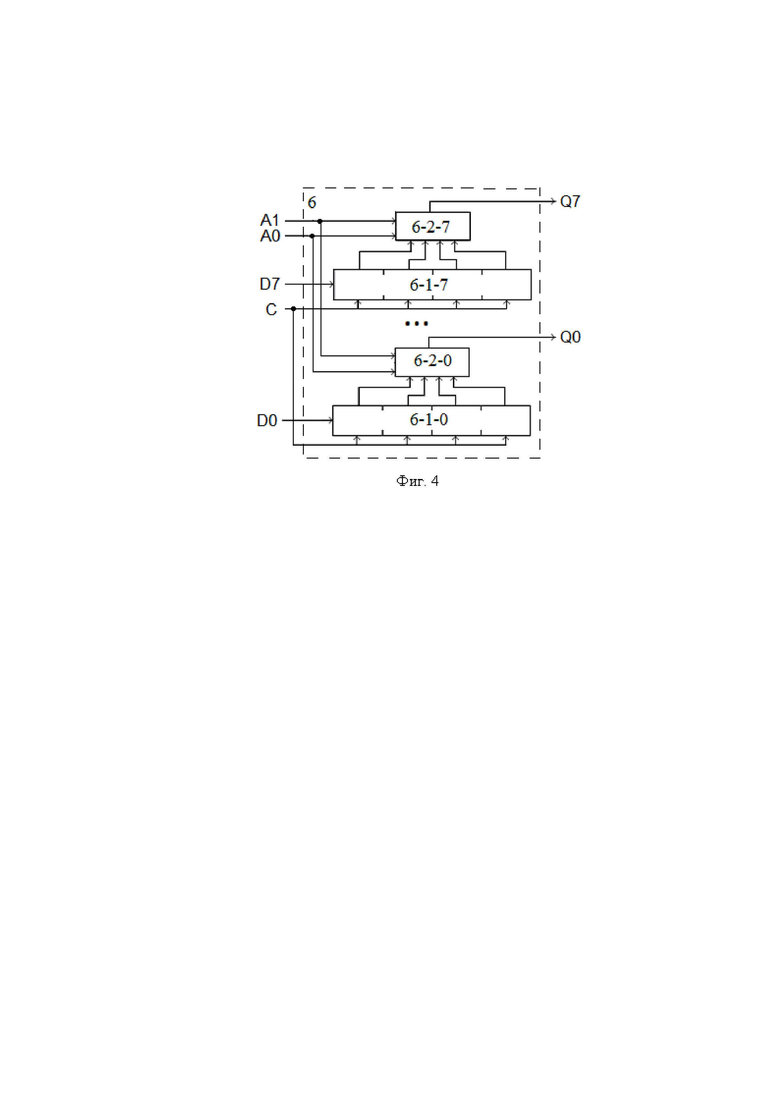
Цифровая линия задержки 6 может быть реализована на регистрах сдвига и мультиплексорах. Пример структурной схемы ЦЛЗ 6 на четыре байтовых ячейки показан на фиг. 4. Здесь входной восьмиразрядный код подается на входы D7…D0 четырехразрядных регистров сдвига 6-1-7 … 6-1-0, к выходам которых подключены мультиплексоры 6-2-7 … 6-2-0, управляемые двоичным кодом A1, A0 от БУС 20 (например, от наборного поля). В результате получим задержку отсчетов сигнала на 1, 2, 3 или 4 отсчета.
В предлагаемом устройстве на один отсчет сигнала необходимо выполнить минимальное число операций сложения. Технически устройство наиболее целесообразно реализовать на базе программируемых логических интегральных схем (ПЛИС). Так, современные ПЛИС средней сложности, например фирмы Xilinx серии Spartan-6, позволяют реализовать предлагаемое устройство при 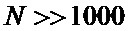 с рабочими частотами до 50-100 МГц.
с рабочими частотами до 50-100 МГц.
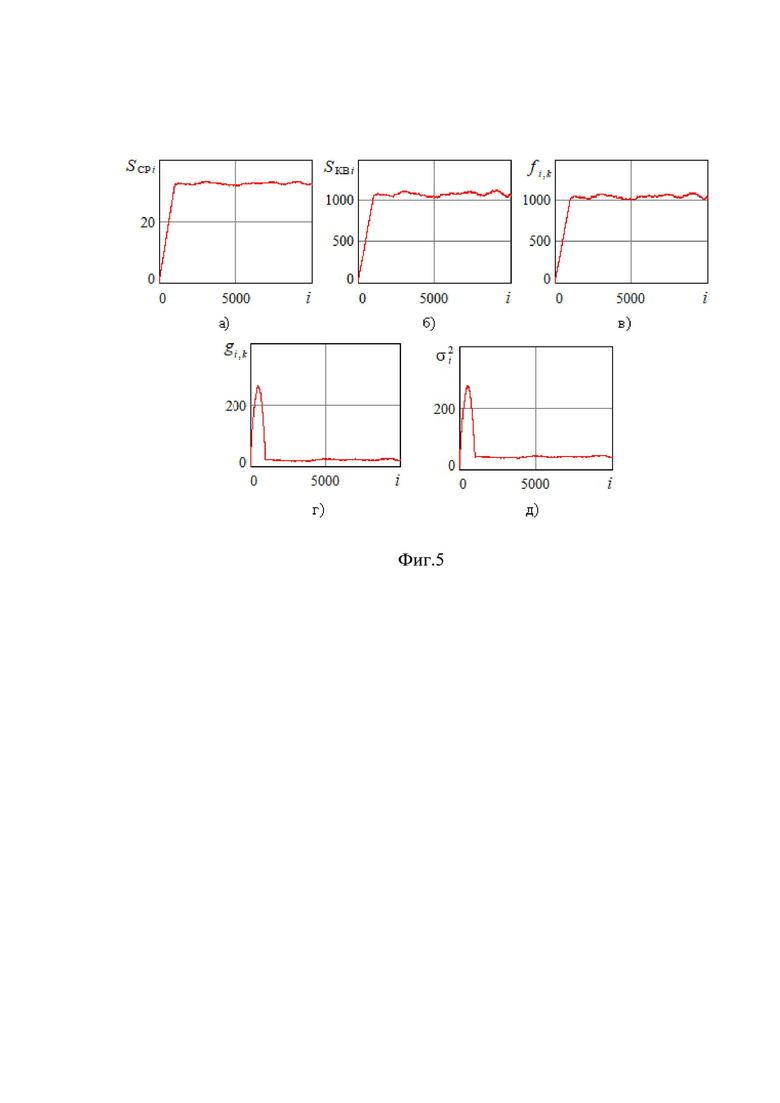
На фиг. 5 для входного воздействия в виде реализации гауссовского случайного процесса с коэффициентом корреляции между соседними отсчетами 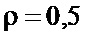 , показанного на фиг. 2, при
, показанного на фиг. 2, при 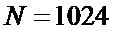 и разрядности АЦП 6 (целочисленных значениях сигнала от 0 до 63) приведены зависимости от номера отсчета i оценок среднего значения
и разрядности АЦП 6 (целочисленных значениях сигнала от 0 до 63) приведены зависимости от номера отсчета i оценок среднего значения 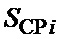 (1) измеряемого сигнала на выходе ФСЗ (фиг. 5а), среднего квадрата
(1) измеряемого сигнала на выходе ФСЗ (фиг. 5а), среднего квадрата 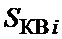 (2) (фиг. 5б), ковариационной функции
(2) (фиг. 5б), ковариационной функции 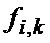 (5) (фиг. 5в), корреляционной функции
(5) (фиг. 5в), корреляционной функции 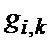 (6) (фиг. 5г), дисперсии сигнала
(6) (фиг. 5г), дисперсии сигнала 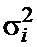 (4) (фиг. 5д). Отметим, что на начальном этапе при
(4) (фиг. 5д). Отметим, что на начальном этапе при 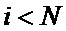 для всех формируемых оценок наблюдается переходной процесс, обусловленный начальной инициализацией (заполнением) многоразрядных регистров сдвига.
для всех формируемых оценок наблюдается переходной процесс, обусловленный начальной инициализацией (заполнением) многоразрядных регистров сдвига.
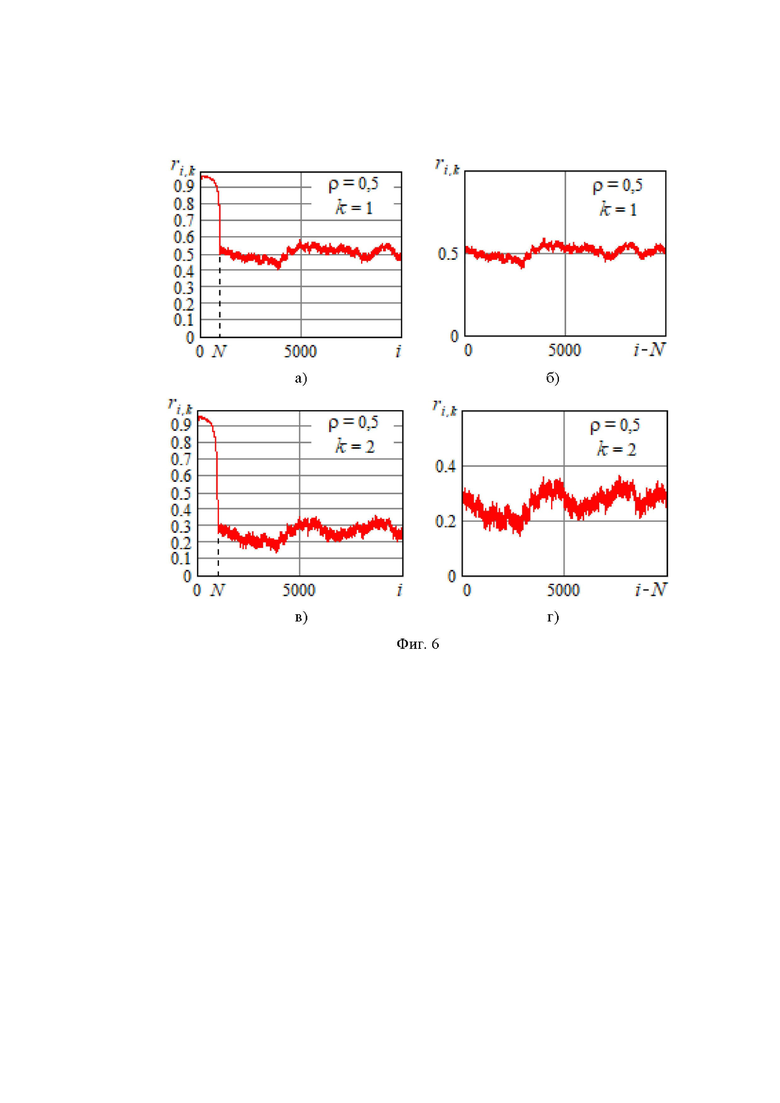
На фиг. 6а представлена зависимость оценки коэффициента корреляции от номера текущего отсчета i при тех же условиях и смещении 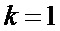 , а на фиг. 6б - ее часть после завершения переходного процесса, обусловленного начальным заполнением многоразрядных регистров сдвига. На фиг. 6в и фиг. 6г показаны аналогичные зависимости при
, а на фиг. 6б - ее часть после завершения переходного процесса, обусловленного начальным заполнением многоразрядных регистров сдвига. На фиг. 6в и фиг. 6г показаны аналогичные зависимости при 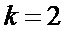 , когда соответствующий коэффициент корреляции равен 0,25 (фиг. 2б). Приведенные зависимости свидетельствуют о работоспособности устройства, однако погрешность измерения при
, когда соответствующий коэффициент корреляции равен 0,25 (фиг. 2б). Приведенные зависимости свидетельствуют о работоспособности устройства, однако погрешность измерения при 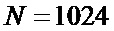 достаточно велика.
достаточно велика.
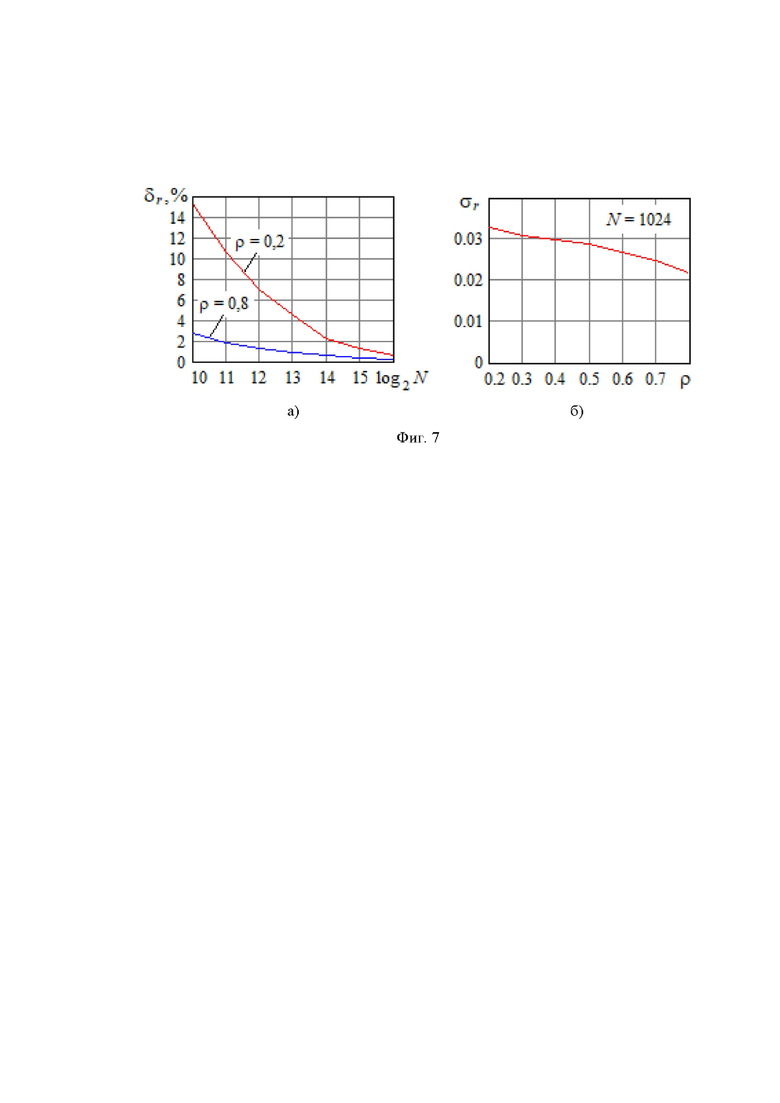
На фиг. 7а в логарифмическим масштабе представлена зависимость относительной погрешности (в процентах) измерения коэффициента корреляции вида
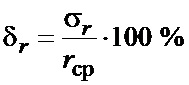 ,
,
где 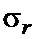 - среднеквадратическое отклонение оценки коэффициента корреляции от его среднего значения
- среднеквадратическое отклонение оценки коэффициента корреляции от его среднего значения 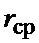 , для различных объемов выборки отсчетов N. Нетрудно видеть, что с ростом N погрешность измерения уменьшается. При этом, чем меньше коэффициент корреляции, тем больше относительная погрешность измерения. Это обусловлено тем, что среднеквадратическое отклонение оценки
, для различных объемов выборки отсчетов N. Нетрудно видеть, что с ростом N погрешность измерения уменьшается. При этом, чем меньше коэффициент корреляции, тем больше относительная погрешность измерения. Это обусловлено тем, что среднеквадратическое отклонение оценки 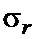 (абсолютная погрешность), как показано на фиг. 7б, не снижается при уменьшении ρ. В целом устройство обеспечивает оценку коэффициента корреляции с приемлемой точностью при
(абсолютная погрешность), как показано на фиг. 7б, не снижается при уменьшении ρ. В целом устройство обеспечивает оценку коэффициента корреляции с приемлемой точностью при 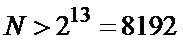 .
.
Литература
1. Баранов П.Е., Муранов А.С., Муранова Е.В. Измеритель модуля коэффициента корреляции случайных процессов // АС SU 1205091А, МПК G01S7/30 от 15.01.86 (Бюл. № 2).
2. Муранов А.С. Измеритель модуля междупериодного коэффициента корреляции пассивных помех // АС SU 1218357А, МПК G01S7/30 от 15.03.86 (Бюл. № 10).
3. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1969. - 576 с.
4. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1970. - 720 с.
5. Мирский Г.Я. Аппаратурное определение характеристик случайных процессов. - М.: Энергия, 1972. - 456 с.
6. Бритин С.Н., Ипатов В.П., Коломенский Ю.А., Корниевский В.И. Цифровой коррелятор // Авторское свидетельство SU 739544, МПК G06F15/34 от 05.06.80 (Бюл. № 21).
7. Кожемяко В.П., Кутаев Ю.Ф., Гайда В.Б., Мартынюк Т.Б., Могилевец А.В. Цифровой коррелятор // АС SU 1566368А1, МПК G06F15/336 от 23.05.90 (Бюл. № 19).
8. Долгов А.И., Джус В.С. Цифровой коррелятор // Авторское свидетельство SU 842768, МПК G06F15/336 от 30.06.81 (Бюл. № 24).
9. Чернояров О.В., Макаров А.А., Глушков А.Н., Литвиненко В.П., Литвиненко Ю.В., Матвеев Б.В. Цифровой измеритель статистических характеристик случайных сигналов // Патент № 2662412 C1, МПК G06F17/18, G01R19/25, G01R19/255, G01R19/02, H03K25/00 от 25.07.2018 (Бюл. № 21); заявка № 2017141798 от 30.11.2017.
10. Вашкевич Н.П., Калиниченко Е.И. Основы арифметики цифровых процессоров: Учебное пособие. - Пенза: Изд-во ПГУ, 2010. - 160 с.
11. Громов С.В., Жуков В.А. Устройство для деления // Авторское свидетельство SU 602944, МПК G06F7/52 от 15.04.78 (Бюл. № 14).
| название | год | авторы | номер документа |
|---|---|---|---|
| ЦИФРОВОЙ ИЗМЕРИТЕЛЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ | 2017 |
|
RU2662412C1 |
| Цифровой измеритель отношения сигнал/шум сигналов с фазовой манипуляцией | 2023 |
|
RU2799234C1 |
| Цифровой измеритель отношения сигнал/шум сигналов с фазовой манипуляцией | 2024 |
|
RU2827313C1 |
| Цифровой измеритель параметров случайных процессов с распределением Накагами | 2020 |
|
RU2742695C1 |
| Цифровой обнаружитель фазоманипулированных сигналов | 2015 |
|
RU2634382C2 |
| ЦИФРОВОЙ ДЕМОДУЛЯТОР ДВОИЧНЫХ СИГНАЛОВ С ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ ВТОРОГО ПОРЯДКА | 2018 |
|
RU2690959C1 |
| ЦИФРОВОЙ ДЕМОДУЛЯТОР СИГНАЛОВ С АМПЛИТУДНО-ФАЗОВОЙ МАНИПУЛЯЦИЕЙ | 2022 |
|
RU2786159C1 |
| ЦИФРОВОЙ ДЕМОДУЛЯТОР СИГНАЛОВ С ОТНОСИТЕЛЬНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ | 2011 |
|
RU2505922C2 |
| Цифровой демодулятор сигналов с двухуровневой амплитудно-фазовой манипуляцией и относительной оценкой амплитуды символа | 2022 |
|
RU2790140C1 |
| ЦИФРОВОЙ ОБНАРУЖИТЕЛЬ ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ | 2018 |
|
RU2693930C1 |
Изобретение относится к областям радиотехники и измерительной техники и может быть использовано в устройствах измерения коэффициента корреляции случайного сигнала в устройствах оценки параметров случайного сигнала аппаратуры управления и передачи информации. Технический результат заключается в обеспечении непрерывного цифрового измерения коэффициента корреляции с высокой точностью при минимальном числе необходимых арифметических операций. Такой результат достигается за счет цифрового измерителя коэффициента корреляции случайного сигнала, содержащего аналого-цифровой преобразователь, регистр, канал формирования среднего значения (ФСЗ), первый квадратичный преобразователь, канал формирования среднего квадрата (ФСК), канал формирования корреляционной функции (ФКФ), второй квадратичный преобразователь, первый вычитатель, генератор тактовых импульсов, цифровую линию задержки, умножитель, блок управления сдвигом, второй вычитатель, и формирователь результата, каналы ФСЗ, ФСК и ФКФ содержат по n каскадно соединенных накопителей отсчетов (НО), каждый НО содержит сумматор и регистр сдвига многоразрядных кодов. 7 ил.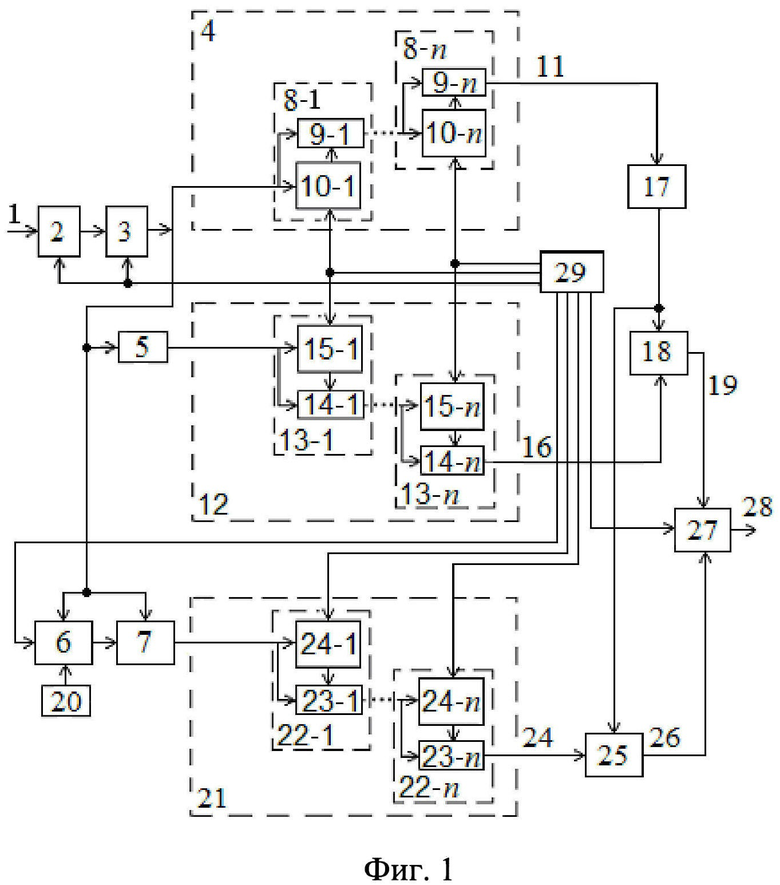
Цифровой измеритель коэффициента корреляции случайного сигнала, содержащий аналого-цифровой преобразователь (АЦП), последовательно соединенный с ним регистр (РГ), к выходу которого подключены канал формирования среднего значения (ФСЗ) и первый квадратичный преобразователь (КП), канал формирования среднего квадрата (ФСК), вход которого подключен к выходу первого КП, второй КП, вход которого соединен с выходом ФСЗ, а выход подключен к первому входу первого вычитателя (В1), второй вход первого вычитателя подключен к выходу ФСК, генератор тактовых импульсов (ГТИ), каналы ФСЗ и ФСК содержат по n каскадно соединенных накопителей отсчетов (НО) (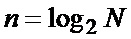
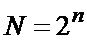
| ЦИФРОВОЙ ИЗМЕРИТЕЛЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ СИГНАЛОВ | 2017 |
|
RU2662412C1 |
| US 5550766 A, 27.08.1996 | |||
| US 3469187 A, 23.09.1969 | |||
| US 20180285079 A1, 04.10.2018. | |||
Авторы
Даты
2021-05-13—Публикация
2020-07-17—Подача