Изобретение относится к области техники связи и может быть использовано для декодирования линейных помехоустойчивых кодов с исправлением стираний в канале связи.
Важнейшим направлением повышения помехоустойчивости передачи сообщений по каналам связи является использование помехоустойчивых кодов. Декодирование помехоустойчивых кодов может выполняться с исправлением ошибок и с исправлением стираний. Декодирование кодов с исправлением стираний существенно проще, чем декодирование с исправлением ошибок, а по помехоустойчивости декодирование с исправлением стираний не хуже, чем декодирование с исправлением ошибок, а во многих случаях, лучше, поскольку число исправляемых стираний примерно вдвое больше, чем число исправляемых ошибок. Однако, эффективное декодирование с исправлением стираний возможно только в стирающем канале связи, в котором имеются признаки достоверности символов, обеспечивающие надежное стирание ошибочных символов кода. Ведь даже небольшое число ошибок, остающееся после стирания недостоверных символов, при декодировании с исправлением стираний приводит к ошибочному декодированию помехоустойчивого кода. В стирающем канале помимо двух обычных решений о значении символа 0 либо 1 принимается третье решение, заключающееся в стирании символа кода. При этом вероятность стирания символа с ошибкой должна быть близка к 1, например, равна 0,99 и более.
В предлагаемом способе исправление стираний выполняется на основе ортогональных контрольных соотношений, в которые входит только одно стирание, а остальные символы известны, что позволяет исправить это стирание. Вместо последовательного выбора и проверки контрольных соотношений помехоустойчивого кода на ортогональность применяется регулярная процедура построения ортогональных контрольных соотношений, что упрощает способ и повышает его помехоустойчивость. Способ декодирования помехоустойчивого кода является универсальным и может использоваться для декодирования произвольных линейных помехоустойчивых кодов: Хемминга, Голея, Боуза-Чоудхури-Хоквинхема (БЧХ), Рида-Маллера, квадратично-вычетных, Рида-Соломона и многих других кодов.
Известен способ декодирования линейных помехоустойчивых кодов с исправлением стираний, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода, из которых s символов являются стертыми. В декодирующем устройстве выбирают одно из контрольных соотношений помехоустойчивого кода и проверяют число стираний, входящих в это контрольное соотношение. При числе стираний в контрольном соотношении, равном 1, вычисляют стертый символ помехоустойчивого кода, исправляют это стирание и число стираний s уменьшают на единицу и так далее, пока не будут выбраны и проверены все контрольные соотношения помехоустойчивого кода. (Колесник В.Д., Мирончиков Е.Т. Декодирование циклических кодов. - Связь. - 1968. - с. 105-109).
Недостатком этого способа является высокая сложность декодирования, поскольку число контрольных соотношений помехоустойчивого кода может быть чрезвычайно большим и выбор и проверка всех контрольных соотношений потребует большого времени, а также недостаточно высокая помехоустойчивость из-за того, что контрольные соотношения помехоустойчивого кода с исправленными стираниями повторно не выбирают и не проверяют.
Наиболее близким к предлагаемому способу является способ (прототип) декодирования линейных помехоустойчивых кодов с исправлением стираний, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода, из которых s символов являются стертыми. В декодирующем устройстве выбирают одно из контрольных соотношений помехоустойчивого кода и проверяют число стираний, входящих в это контрольное соотношение. При числе стираний в контрольном соотношении, равном 1, вычисляют стертый символ кода, исправляют это стирание, и число стираний s уменьшают на единицу. После этого заменяют стирание на вычисленный символ кода во всех контрольных соотношениях помехоустойчивого кода. Далее выбирают одно из следующих контрольных соотношений помехоустойчивого кода и оценивают число стираний, входящих в это контрольное соотношение. При числе стираний в контрольном соотношении, равном 1, вычисляют стертый символ кода, исправляют это стирание, и число стираний s опять уменьшают на единицу. (Патент РФ №2611235 МПК H004L 1/2 Золотарев В.В. Способ обнаружения и исправления стираний при приеме дискретной информации. - Приор. 24.11.2015. - Опубл. 21.02.2017. - Бюл. №6).
Недостатком этого способа является высокая сложность декодирования, поскольку число контрольных соотношений помехоустойчивого кода может быть очень большой величиной и для выбора и проверки всех контрольных соотношений требуется большое время.
Целью изобретения является снижение сложности декодирования за счет того, что контрольные соотношения, содержащие только одно стирание, вычисляют с помощью ортогонализации Грама-Шмидта проверочной матрицы помехоустойчивого кода относительно позиций стертых символов, что проще, чем выбор и проверка всех контрольных соотношений помехоустойчивого кода, число которых может быть очень большим.
Для достижения цели предложен способ декодирования линейных помехоустойчивых кодов с исправлением стираний, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода, из которых s символов являются стертыми. В декодирующем устройстве выбирают и проверяют одно из контрольных соотношений помехоустойчивого кода и оценивают число стираний, входящих в это контрольное соотношение. При числе стираний в контрольном соотношении, равном 1, вычисляют стертый символ кода, исправляют это стирание, и число стираний s уменьшают на единицу. После этого заменяют исправленное стирание на вычисленный символ кода во всех контрольных соотношениях помехоустойчивого кода. Далее выбирают одно из следующих контрольных соотношений помехоустойчивого кода и оценивают число стираний, входящих в это контрольное соотношение. При числе стираний в контрольном соотношении, равном 1, вычисляют стертый символ кода, исправляют это стирание, и число стираний s опять уменьшают на единицу. Новым является то, что после приема помехоустойчивого кода и определения позиций s стертых символов, выполняют ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода относительно позиций стертых символов. Затем, используя контрольные ортогональные соотношения проверочной матрицы помехоустойчивого кода, вычисляют стертые символы помехоустойчивого кода и исправляют стирания. Причем ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода выполняют путем тождественных преобразований строк проверочной матрицы над полем Галуа помехоустойчивого кода. При этом ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода выполняют при числе стираний символов, равном или меньше d-1, а при числе стираний символов больше d-1 ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода выполняют, если ранг матрицы, составленной из столбцов проверочной матрицы, соответствующих позициям стертых символов, не меньше числа стираний в помехоустойчивом коде, а при ранге соответствующей матрицы меньше числа стираний в помехоустойчивом коде, ортогонализацию Грама-Шмидта не выполняют, и происходит отказ от декодирования помехоустойчивого кода.
Рассмотрим осуществление способа декодирования линейных помехоустойчивых кодов с исправлением стираний.
При декодировании помехоустойчивого кода с исправлением стираний помимо жестких решений о значении каждого символа оценивают также достоверности символов. Для формирования достоверностей символов можно использовать первичные статистические характеристики канала связи, например, амплитуду сигнала на выходе интегратора демодулятора, уровень фонового шума (за пределами полосы частот передачи сигнала), искажения пилот-сигнала по частоте и фазе, отклонения спектра принятого сигнала от ожидаемого спектра и так далее. Для формирования достоверностей символов можно также использовать вторичные статистические характеристики канала связи в виде дроблений и искажений краев посылок на выходе устройства тактовой цифровой синхронизации. Достоверности символов можно также формировать на выходе декодирующего устройства внутреннего кода каскадного помехоустойчивого кода в зависимости от числа ошибок, корректируемых внутренним кодом. Наиболее достоверными будут символы, полученные при декодировании кодов, в которых не было исправлено ни одной ошибки, менее достоверными - с исправлением одиночной ошибки, затем - двойной ошибки и так далее. Оценки достоверностей символов затем используют для декодирования внешнего кода каскадного кода с исправлением стираний.
Для стирания символов помехоустойчивого кода достоверности символов подают на пороговый элемент, который при величине достоверности символа меньше некоторого порогового значения формирует признак стирания символа кода. В результате с порогового элемента на декодирующее устройство подают n символов принятого помехоустойчивого кода, из которых s символов являются стертыми.
Декодирование помехоустойчивого кода выполняют с использованием контрольных соотношений кода. Контрольные соотношения помехоустойчивого кода образуются как линейные комбинации строк проверочной матрицы кода. Запишем проверочную матрицу помехоустойчивого кода в виде

где hi - строки проверочной матрицы кода.
Линейная комбинация строк проверочной матрицы кода
r=a0h0+alhl+…+an_k-1hn_k-1,
где коэффициенты а0, a1, …, an-k-1 ∈GF(pm),
Число контрольных соотношений кода, например, для наиболее простого двоичного поля будет равно
N=2n-k,
что даже для небольших n-k≥20 дает N≥106. Выбрать и проверить столь большое число контрольных соотношений помехоустойчивого кода весьма сложно и требует большого времени.
При выборе контрольного соотношения выполняется его проверка на ортогональность. Контрольное соотношение кода называется ортогональным, если в это соотношение входит только одно стирание, а остальные символы кода, входящие в контрольное соотношение, известны. Контрольное соотношение позволяет выразить стирание через известные символы кода, то есть исправить стирание. Однако, выбор всех контрольных соотношений кода и проверка их на ортогональность является задачей экспоненциальной сложности. Упростить декодирование до полиномиальной сложности позволяет формирование контрольных ортогональных соотношений на основе проверочной матрицы помехоустойчивого кода. Для этого выполняют ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода относительно позиций стертых символов. Ортогонализацию выполняют путем тождественных преобразований строк матрицы, при этом линейно независимые столбцы матрицы приводят к виду, при котором в этих столбцах будет только одна 1, а остальные элементы равны 0. Тождественными преобразованиями называют операции сложения строк между собой, умножения строк матрицы на постоянный элемент поля Галуа и перестановки строк матрицы.
Запишем проверочную матрицу (1) кода в виде
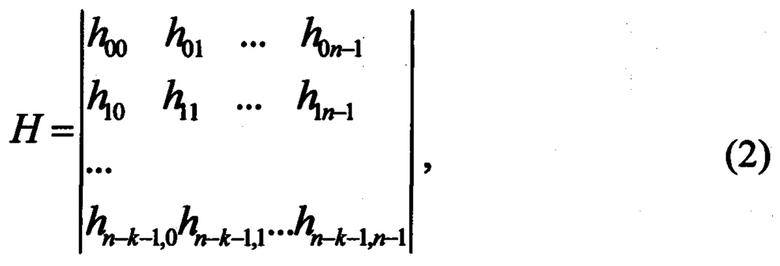
где hij - элемент поля Галуа GF(pm).
Сначала рассмотрим процедуру ортогонализации для первого стирания. Пусть позиция первого стирания есть j, тогда
Шаг 1. Выбирают j столбец проверочной матрицы (2), а в этом столбце выделяют первый элемент, отличный от нуля, например hij.
Шаг 2. Делят все элементы i строки на hij.
Шаг 3. Для всех w=0…n-k-1, w≠i умножают i строку матрицы (2) на hwj и складывают ее поэлементно с w строкой.
Шаг 4. Переставляют между собой 1 строку и i строку матрицы.
После выполнения этой процедуры 1-ый элемент j-го столбца проверочной матрицы будет равен 1, а остальные элементы этого столбца будут равны 0. Аналогичным образом выполняют ортогонализацию для других стираний помехоустойчивого кода. Все операции с элементами матрицы (2) выполняют над полем Галуа GF(pm) помехоустойчивого кода. В результате ортогонализации Грама-Шмидта s первых строк проверочной матрицы будут представлять собой контрольные ортогональные соотношения для исправления стираний. Примером ортогонализации проверочной матрицы относительно позиций проверочных символов является представление проверочной матрицы в систематической форме

где Р - некоторая матрица размера (n-k)×k, а I - единичная матрица размера (n-k)×(n-k). Проверочную матрицу в систематической форме используют для вычисления проверочных символов кода через информационные символы.
Ортогонализация Грама-Шмидта всегда может быть выполнена для s столбцов проверочной матрицы, если эти s столбцов линейно независимы. Поскольку любые d-1 столбцов проверочной матрицы помехоустойчивого кода линейно независимы, то помехоустойчивый код всегда исправляет d-1 и меньшее число стираний символов кода. Если s>d-1 столбцов проверочной матрицы линейно независимы, то возможно исправление и большего числа стираний, вплоть до максимального значения, равного n-k стираний. Примером исправления n-k стираний является исправление стираний всех n-k проверочных символов при условии приема всех k информационных символов кода. После ортогонализации будет получена проверочная матрица в систематической форме (3), которая позволяет исправить стирания всех проверочных символов кода, а для циклических кодов и циклические сдвиги стираний всех проверочных символов кода.
При линейной независимости столбцов проверочной матрицы, соответствующих стертым символам кода, ранг матрицы, составленной из этих столбцов, будет равен числу стираний в помехоустойчивом коде. Поэтому для упрощения вычислений можно сначала определить ранг матрицы из столбцов проверочной матрицы стертых символов. Если ранг этой матрицы меньше числа стертых символов, можно не выполнять ортогонализацию Грама-Шмидта, поскольку она приведет к нулевой строке матрицы, из которой нельзя определить стертый символ. Ранг матрицы определяют вычислением определителя и сравнением его значения с нулем. Для некоторых кодов, например кодов БЧХ и Рида-Соломона, бывает проще вычислить определитель из столбцов проверочной матрицы кода.
В качестве примера рассмотрим декодирование с исправлением стираний двоичного помехоустойчивого кода БЧХ (15,7,5), блоковая длина которого n=15, информационная длина k=7, а минимальное кодовое расстояние d=5, что гарантированно позволяет исправлять не менее 4 стираний. Проверочная матрица кода
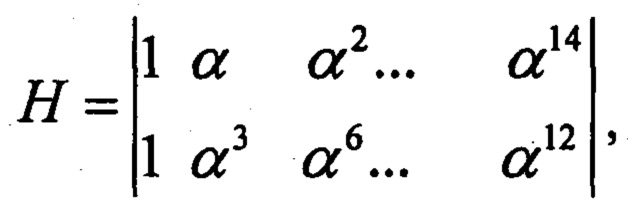
где α - примитивный элемент поля GF(24) с генераторным многочленом х4+х+1. Любые 4 столбца проверочной матрицы линейно независимы.
Пусть передавался код БЧХ B=100110111000010, а принят код A=100a1110a8110a4001a0, где ai обозначены стирания на i=11,8,4,0 позициях кода. Проверочная матрица кода в двоичной форме

Выполним ортогонализацию матрицы относительно позиций стертых символов и выпишем контрольные проверки для восстановления стираний

Отсюда значения стертых символов
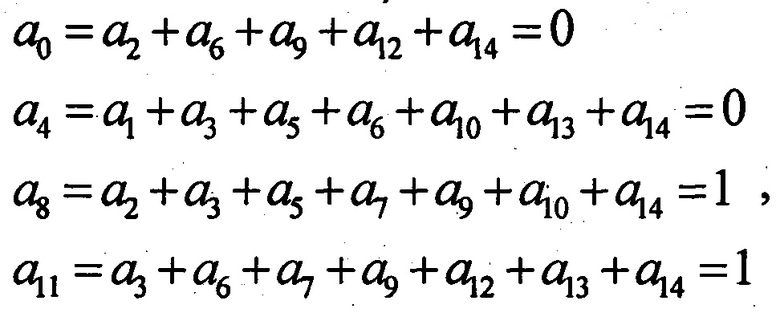
что совпадает с исходным кодом БЧХ.
В примере при небольшом числе вычислений удалось исправить 4 стирания символов кода БЧХ(15,7,5), что в два раза больше, чем число исправляемых этим кодом ошибок.
Обеспечить небольшую сложность декодирования с исправлением стираний при высокой помехоустойчивости стало возможным за счет ортогонализации Грама-Шмидта проверочной матрицы относительно позиций стираний символов кода. Способ может применяться для произвольных линейных помехоустойчивых кодов. Число исправляемых стираний лежит в диапазоне значений d-1≤s≤n-k. Исправление стираний за пределами минимального кодового расстояния кода s>d-1 возможно, если ранг матрицы из столбцов проверочной матрицы, соответствующих стертым символам, не меньше числа стираний. Причем сложность исправления стираний за пределами минимального кодового расстояния кода соизмерима со сложностью исправления стираний в пределах минимального кодового расстояния. Способ полностью реализует возможности помехоустойчивого кода по исправлению стираний, в том числе за пределами минимального кодового расстояния.
Достигаемым техническим результатом способа декодирования линейных помехоустойчивых кодов с исправлением стираний является уменьшение сложности декодирования при его высокой помехоустойчивости.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ мягкого декодирования помехоустойчивого кода | 2023 |
|
RU2812043C1 |
| Способ передачи сообщений с использованием стохастических помехоустойчивых кодов | 2022 |
|
RU2804323C1 |
| Способ мягкого декодирования помехоустойчивого кода | 2019 |
|
RU2725699C1 |
| Способ мягкого декодирования помехоустойчивого кода | 2020 |
|
RU2738724C1 |
| СПОСОБ ПАКЕТНОЙ ПЕРЕДАЧИ СООБЩЕНИЙ В СЕТЯХ СВЯЗИ С МНОГОМЕРНОЙ МАРШРУТИЗАЦИЕЙ | 2006 |
|
RU2313187C1 |
| Способ передачи многоблочных сообщений каскадным кодом [PC (32, 16, 17), БЧХ (31, 16, 7)] | 2020 |
|
RU2755055C1 |
| СПОСОБ ПЕРЕДАЧИ СООБЩЕНИЙ В СИСТЕМАХ С ОБРАТНОЙ СВЯЗЬЮ И ГИБРИДНЫМ АВТОМАТИЧЕСКИМ ЗАПРОСОМ НА ПОВТОРЕНИЕ | 2022 |
|
RU2786023C1 |
| Способ передачи многоблочных сообщений в комплексах телекодовой связи | 2018 |
|
RU2669069C1 |
| СИСТЕМА ДЛЯ КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ С ИСПРАВЛЕНИЕМ ОШИБОК | 1991 |
|
RU2007042C1 |
| ДЕКОДЕР С ПОВЫШЕННОЙ КОРРЕКТИРУЮЩЕЙ СПОСОБНОСТЬЮ | 2010 |
|
RU2438252C1 |
Изобретение относится к области техники связи. Технический результат заключается в уменьшении сложности декодирования при его высокой помехоустойчивости. Такой результат достигается тем, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода, из которых s символов являются стертыми. В декодирующем устройстве выполняют ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода относительно позиций стертых символов, затем, используя контрольные ортогональные соотношения проверочной матрицы помехоустойчивого кода, вычисляют стертые символы помехоустойчивого кода и исправляют стирания. Причем ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода выполняют путем тождественных преобразований строк проверочной матрицы над полем Галуа помехоустойчивого кода. При этом ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода выполняют при числе стираний символов, равном или меньше d-1, а при числе стираний символов больше d-1 ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода выполняют, если ранг матрицы, составленной из столбцов проверочной матрицы, соответствующих позициям стертых символов, не меньше числа стираний в помехоустойчивом коде, а при ранге соответствующей матрицы меньше числа стираний в помехоустойчивом коде ортогонализацию Грама-Шмидта не выполняют, и происходит отказ от декодирования помехоустойчивого кода. 2 з.п. ф-лы.
1. Способ декодирования линейных помехоустойчивых кодов с исправлением стираний, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода, из которых s символов являются стертыми, в декодирующем устройстве выбирают и проверяют одно из контрольных соотношений помехоустойчивого кода и оценивают число стираний, входящих в это контрольное соотношение, при числе стираний в контрольном соотношении, равном 1, вычисляют стертый символ кода, исправляют это стирание и число стираний s уменьшают на единицу, после этого заменяют исправленное стирание на вычисленный символ кода во всех контрольных соотношениях помехоустойчивого кода, далее выбирают одно из следующих контрольных соотношений помехоустойчивого кода и оценивают число стираний, входящих в это контрольное соотношение, при числе стираний в контрольном соотношении, равном 1, вычисляют стертый символ кода, исправляют это стирание и число стираний s опять уменьшают на единицу, отличающийся тем, что после приема помехоустойчивого кода и определения позиций s стертых символов выполняют ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода относительно позиций стертых символов, затем, используя контрольные ортогональные соотношения проверочной матрицы помехоустойчивого кода, вычисляют стертые символы помехоустойчивого кода и исправляют стирания.
2. Способ по п. 1, отличающийся тем, что ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода выполняют путем тождественных преобразований строк проверочной матрицы над полем Галуа помехоустойчивого кода.
3. Способ по п. 1, отличающийся тем, что ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода всегда выполняют при числе стираний символов, равном или меньше d-1, при числе стираний символов больше d-1 ортогонализацию Грама-Шмидта проверочной матрицы помехоустойчивого кода выполняют, если ранг матрицы, составленной из столбцов проверочной матрицы, соответствующих позициям стертых символов, не меньше числа стираний в помехоустойчивом коде, а при ранге соответствующей матрицы меньше числа стираний в помехоустойчивом коде ортогонализацию Грама-Шмидта не выполняют, и происходит отказ от декодирования помехоустойчивого кода.
| Способ обнаружения и исправления стираний при приеме дискретной информации | 2015 |
|
RU2611235C1 |
| Способ декодирования помехоустойчивого кода | 2020 |
|
RU2721937C1 |
| Способ мягкого декодирования помехоустойчивого кода | 2019 |
|
RU2725699C1 |
| СПОСОБ КОДИРОВАНИЯ-ДЕКОДИРОВАНИЯ ИНФОРМАЦИИ В СИСТЕМАХ ПЕРЕДАЧИ ДАННЫХ | 2005 |
|
RU2310273C2 |
| Устройство для закрепления лыж на раме мотоциклов и велосипедов взамен переднего колеса | 1924 |
|
SU2015A1 |
Авторы
Даты
2021-04-21—Публикация
2020-11-03—Подача