Изобретение относится к области техники связи и может быть использовано для мягкого декодирования помехоустойчивых кодов в каналах связи с высоким уровнем помех.
Важнейшим направлением совершенствования систем связи является повышение помехоустойчивости при минимальных затратах энергетических и частотных ресурсов канала связи. Немаловажное значение имеет также сокращение сложности и стоимости технической реализации систем связи. Одним из основных методов повышения помехоустойчивости систем связи является применение помехоустойчивого кодирования. Помехоустойчивое кодирование позволяет обеспечить сколь угодно малую вероятность ошибки при скорости передачи меньше пропускной способности канала связи и отличается от других методов тем, что полностью реализуется на элементах цифровой техники: микроконтроллерах, программируемых логических интегральных схемах (ПЛИС), микросхемах различной степени интеграции с жесткой логикой. Это делает кодовые методы повышения помехоустойчивости менее энергоемкими, менее габаритными и более дешевыми, чем методы, использующие ресурсы канала связи.
Помехоустойчивость в значительной степени определяется выбором способа декодирования кода. Мягкое декодирование учитывает оценки достоверностей принятых символов и обеспечивает большую помехоустойчивость, поскольку позволяет корректировать примерно вдвое большее количество ошибок по сравнению с жестким декодированием. Однако, для мягкого декодирования требуется выполнять большой объем вычислений, что значительно усложняет декодирование кода по сравнению с жестким декодированием. Уменьшить сложность мягкого декодирования кода возможно за счет того, что наименее достоверные символы можно выразить через наиболее достоверные символы и восстановить все информационные символы кода. При этом используют контрольные соотношения кода, вычисление которых не вызывает затруднений. Помехоустойчивость способа также повышается за счет итеративного декодирования кода. Сначала вычисляют первый символ кода, который получают из контрольного соотношения, в которое входят наиболее достоверные символы, второй символ определяют с учетом не только наиболее достоверных символов, но и вновь вычисленного первого символа и его новой достоверности, третий символ - с учетом двух ранее вычисленных символов и так далее.
Предлагаемый способ мягкого декодирования помехоустойчивого кода является универсальным и может использоваться для декодирования произвольных линейных помехоустойчивых кодов: Хемминга, Боуза-Чоудхури-Хоквинхема (БЧХ), Рида-Маллера, Голея, Рида-Соломона и многих других.
Известен способ мягкого декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства поступают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов. В декодирующем устройстве помехоустойчивого кода эти символы сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода, где s есть число наименее достоверных символов помехоустойчивого кода. Затем формируют 2s вариантов помехоустойчивого кода, в каждом из которых s наименее достоверных символов помехоустойчивого кода принимают всевозможные двоичные комбинации, начиная с комбинации из множества 0 и заканчивая комбинацией из множества 1, a n-s наиболее достоверных символов помехоустойчивого кода не изменяют. Далее выполняют жесткое декодирование всех 2s вариантов помехоустойчивого кода и корректируют ошибки в каждом из этих вариантов. Затем каждый из 2s вариантов декодированного помехоустойчивого кода сравнивают по расстоянию Хемминга с принятым помехоустойчивым кодом и получают совокупность 2s расстояний Хемминга. На выход декодирующего устройства подается помехоустойчивым код, соответствующий минимальному кодовому расстоянию Хемминга из совокупности 2s расстояний Хемминга. (Кларк Дж., мл. Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. - Пер. с англ. - Радио и связь. - 1987. - с. 160-165).
Недостатком этого способа является чрезмерно большая сложность, поскольку жесткое декодирование 2s вариантов помехоустойчивого кода с исправлением ошибок в каждом из вариантов помехоустойчивого кода требует большого числа вычислений.
Известен также способ мягкого декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства поступают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов. В декодирующем устройстве помехоустойчивого кода эти символы сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода, где s есть число наименее достоверных символов помехоустойчивого кода. Затем по n-s наиболее достоверным символам восстанавливают помехоустойчивый код. При однозначном восстановлении кода декодирование заканчивается, в противном случае к n-s наиболее достоверным символам добавляют еще один символ и делают еще одну попытку восстановления помехоустойчивого кода и так далее до тех пор, пока помехоустойчивый код не будет восстановлен однозначно. (Бородин Л.Ф. Введение в теорию помехоустойчивого кодирования. - Советское радио. - М. - 1968. - с. 281-284).
Недостатком этого способа является недостаточная помехоустойчивость, поскольку помехоустойчивый код восстанавливают по всем наиболее достоверным символам кода, а в этих символах возможны ошибки.
Наиболее близким к предлагаемому способу является способ (прототип) мягкого декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов. В декодирующем устройстве помехоустойчивого кода сначала оценивают величину s числа наименее достоверных символов помехоустойчивого кода. Затем символы помехоустойчивого кода сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода. Далее выполняют декодирование помехоустойчивого кода с использованием n-s наиболее достоверных символов кода. В результате определяют s наименее вероятных символов кода и восстанавливают информационные символы кода. (Патент РФ №2546070 МПК Н03М 13/00 Ква-шенников В.В., Сосин П. А. Способ мягкого декодирования помехоустойчивого кода. - Приор. 12.11.2013. - Опубл. 10.04.2015. - Бюл. №10).
Недостатком этого способа также является большая сложность, поскольку декодирование помехоустойчивого кода с исправлением ошибок требует выполнения большого числа вычислений, а также недостаточная помехоустойчивость из-за декодирования по всем наиболее достоверным символам кода.
Целью изобретения является снижение сложности декодирования за счет того, что наименее достоверные символы помехоустойчивого кода вычисляют через наиболее достоверные символы с использованием простых контрольных соотношений проверочной матрицы кода, что требует меньшего объема вычислений, чем декодирование помехоустойчивого кода с исправлением ошибок, также целью является повышение помехоустойчивости за счет итеративного декодирования, при котором используется только часть наиболее достоверных символов кода.
Для достижения цели предложен способ мягкого итеративного декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов. В декодирующем устройстве помехоустойчивого кода сначала оценивают величину 5 числа наименее достоверных символов помехоустойчивого кода. Затем символы помехоустойчивого кода сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода. Далее выполняют декодирование помехоустойчивого кода с использованием n-s наиболее достоверных символов кода. В результате определяют s наименее достоверных символов кода и восстанавливают информационные символы кода. Новым является то, что после определения s наименее достоверных символов кода сначала выполняют ортогонализацию проверочной матрицы кода относительно позиций этих s наименее достоверных символов кода. Затем умножают полученное слово на проверочную матрицу кода и при получении нулевого вектора декодирование считают успешным, в противном случае выбирают проверочное соотношение для одного из s наименее достоверных символов кода, такое, что другие символы кода входят в него с наибольшей достоверностью по сравнению с проверочными соотношениями для других наименее вероятных символов кода. После этого вычисляют выбранный наименее достоверный символ и определяют его новую достоверность. Далее символы кода снова сортируют по достоверности с учетом новой достоверности вновь вычисленного символа кода. Затем опять выполняют ортогонализацию проверочной матрицы кода относительно позиций уже s-1 наименее достоверных символов кода и вычисляют эти s-1 символов. Далее умножают полученное слово на проверочную матрицу кода и при получении нулевого вектора декодирование считают успешным, в противном случае в полученной проверочной матрице снова выбирают проверочное соотношение для одного из s-1 наименее достоверных символов кода, такое, что другие символы кода входят в него с наибольшей достоверностью. После этого вычисляют выбранный наименее достоверный символ и определяют его новую достоверность и так далее до тех пор, пока не будут вычислены все s наименее достоверных символов кода. При этом новую достоверность наименее достоверного символа определяют как наименьшую достоверность наиболее достоверных символов, входящих в его контрольную проверку, причем ортогонализацию проверочной матрицы кода выполняют путем тождественных преобразований над строками проверочной матрицы, при этом величину s числа наименее достоверных символов помехоустойчивого кода определяют из условия s=d-1, где d - минимальное кодовое расстояние кода.
Рассмотрим осуществление предлагаемого способа мягкого декодирования помехоустойчивого кода.
При мягком декодировании помехоустойчивого кода помимо жестких решений о значении каждого символа (0 либо 1) оценивают также достоверности символов. Для формирования достоверностей символов можно использовать первичные статистические характеристики канала связи, например амплитуду сигнала на выходе интегратора демодулятора, уровень фонового шума (за пределами полосы частот передачи сигнала), искажения пилот-сигнала по частоте и фазе, отклонения спектра принятого сигнала от ожидаемого спектра и так далее. Для формирования достоверностей символов можно также использовать вторичные статистические характеристики канала связи в виде дроблений и искажений краев посылок на выходе устройства тактовой цифровой синхронизации. Достоверности символов можно также формировать на выходе декодирующего устройства внутреннего кода каскадного помехоустойчивого кода в зависимости от числа ошибок, корректируемых внутренним кодом. Наиболее достоверными будут символы, полученные при декодировании кодов, в которых не было исправлено ни одной ошибки, менее достоверными - с исправлением одиночной ошибки, затем - двойной ошибки и так далее. Оценки достоверностей символов тогда используют для мягкого декодирования внешнего кода каскадного кода. На основе частных достоверностей символов от различных источников формируют интегральные достоверности символов, которые учитывают весовые коэффициенты надежности различных источников достоверности символов.
Величину s числа наименее достоверных символов помехоустойчивого кода, в которых наиболее вероятно возникновение ошибок, определяют в зависимости от корректирующей способности кода. При мягком декодировании помехоустойчивый код способен корректировать d-1 и менее ошибок, где d - минимальное кодовое расстояние кода. Поэтому, число s наименее достоверных символов помехоустойчивого кода, которые корректируются, целесообразно также определять из условия s=d-1.
Затем символы помехоустойчивого кода сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода. Оставшиеся s=d-1 символов кода будут наименее достоверными.
Проверочную матрицу помехоустойчивого кода запишем в виде

где hi - столбцы проверочной матрицы кода.
В проверочной матрице помехоустойчивого линейного кода любые d-1 столбцов являются линейно независимыми. Поэтому, и s=d-1 наименее достоверных символов кода будут соответствовать линейно независимым столбцам проверочной матрицы кода.
Проверочную матрицу помехоустойчивого кода запишем также в виде

где gi - строки проверочной матрицы кода.
Линейно независимые столбцы матрицы можно путем тождественных преобразований строк матрицы ортогонализировать, то есть привести к виду, при котором в этих столбцах будет только одна 1, а остальные - 0. Тождественными преобразованиями называют операции сложения строк между собой и перестановки строк матрицы.
Примером ортогонализации проверочной матрицы относительно позиций проверочных символов является представление проверочной матрицы в систематической форме

где Р - некоторая матрица размера (n-k)×k, а I - единичная матрица размера (n-k)×(n-k). Проверочная матрица в систематической форме используется для вычисления проверочных символов кода через информационные символы.
Теперь выполним ортогонализацию проверочной матрицы кода относительно позиций s наименее достоверных символов кода. После ортогонализации матрицы s наименее достоверных символов можно выразить через наиболее достоверные символы кода. Для помехоустойчивого кода A=a0a1…an-1 справедливо

Умножим полученное слово на проверочную матрицу кода. При получении нулевого вектора декодирование считают успешным, в противном случае в проверочной матрице кода выбирают проверочное соотношение для одного из s наименее достоверных символов кода, такое, что в него входят другие символы кода с наибольшими достоверностями по сравнению с проверочными соотношениями для других наименее достоверных символов кода. После этого вычислим выбранный наименее достоверный символ и определим его новую достоверность. Новую достоверность наименее достоверного символа определяют как наименьшую достоверность наиболее достоверных символов, входящих в его контрольную проверку. Тем самым наименее достоверный символ переводится в область наиболее достоверных символов. Далее выполняют итеративное декодирование. Символы кода снова сортируют по достоверности с учетом новой достоверности вновь вычисленного символа кода. Затем опять выполняют ортогонализацию проверочной матрицы кода относительно позиций уже s-1 наименее достоверных символов кода и вычисляют эти символы. Полученное слово опять проверяют путем умножения на проверочную матрицу. В случае получения нулевого вектора декодирование считается законченным, в противном случае в полученной проверочной матрице снова выбирают проверочное соотношение для одного из s-1 наименее достоверных символов кода, такое, что в него входят другие символы кода с наибольшими достоверностями. После этого вычисляют выбранный наименее достоверный символ и определяют его новую достоверность и так далее до тех пор, пока не будут вычислены все s наименее достоверных символов кода, что позволяет восстановить все информационные символы кода. В результате получаем множество символов помехоустойчивого кода, все достоверности которых будут находиться в области достоверностей наиболее достоверных символов.
Достоверности символов кода определяют степень доверия принятым символам, которая оценивается вероятностью трансформации этих символов. Поэтому, вероятность трансформации символа р связана некоторой монотонно убывающей функцией с его достоверностью ν

Вероятность ошибки декодирования кода для биномиального канала

где pi - вероятности трансформации символов кода.
При восстановлении наименее вероятных символов кода через наиболее вероятные символы вероятности трансформации символов уменьшаются и согласно (5) вероятность ошибки декодирования также уменьшается. Обычно при выборе помехоустойчивого кода и алгоритмов его декодирования задают предельно допустимую вероятность ошибки декодирования Рtm, достаточно близкую к 1, например 0,99. Сравнение Рt с требуемым значением Рtm показывает выполнение технических требований на помехоустойчивое кодирование.
Например, для помехоустойчивого кода Хемминга (15,11), блоковая длина которого n=15, информационная длина кода k=11, а минимальное кодовое расстояние d=3, проверочная матрица запишется

Столбцы проверочной матрицы кода Хемминга представляют собой различные ненулевые двоичные комбинации символов. Любые два столбца проверочной матрицы линейно независимы. Число наименее достоверных символов помехоустойчивого кода будет s=d-1=2.
Поскольку s=2, то будем исправлять 2 наименее достоверных символа кода Хемминга. Пусть передавался код Хемминга B=001100110010110, а принят код Хемминга A=011100111010110 с соответствующими достоверностями
D=0,8; 0,1; 0,6; 0,7; 0,8; 0,6; 0,7; 0,8; 0,2; 0,7; 0,8; 0,5; 0,7; 0,8; 0,6
Множество индексов наименее достоверных символов j∈(1,8). Достоверности этих символов соответственно будут равны 0,1 и 0,2. Первая и третья строки матрицы ортогональны относительно позиций наименее достоверных символов. Отсюда, наименее достоверные символы через наиболее достоверные символы запишутся
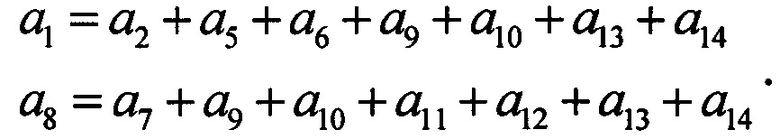
Новая достоверность вычисляется как минимальная достоверность наиболее достоверных символов, входящих в проверку. Поэтому, достоверность a1 будет 0,6, а достоверность a8 будет 0,5. Выбираем проверку для a1, которая дает a1=0. Вторая проверка дает а8=0. Умножение полученного слова на проверочную матрицу дает нулевой вектор, что свидетельствует об успешном декодировании.
В данном примере при небольшом объеме вычислений удалось исправить 2 ошибки, хотя при жестком декодировании код Хемминга исправляет только 1 ошибку. Причем для декодирования оказалось достаточным выполнение всего 1 шага итеративного декодирования.
Обеспечить высокую помехоустойчивость при небольшой сложности декодирования стало возможным за счет ортогонализации проверочной матрицы относительно наименее достоверных символов кода и итеративного декодирования.
Достигаемым техническим результатом способа мягкого декодирования помехоустойчивого кода является уменьшение сложности при его высокой помехоустойчивости.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ мягкого декодирования помехоустойчивого кода | 2023 |
|
RU2812043C1 |
| Способ мягкого декодирования помехоустойчивого кода | 2019 |
|
RU2725699C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ ПОМЕХОУСТОЙЧИВОГО КОДА | 2013 |
|
RU2546070C1 |
| Способ декодирования линейных помехоустойчивых кодов с исправлением стираний | 2020 |
|
RU2746797C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ПОМЕХОУСТОЙЧИВЫХ КАСКАДНЫХ КОДОВ ПО НАИБОЛЕЕ ДОСТОВЕРНЫМ СИМВОЛАМ ВНЕШНЕГО КОДА | 2009 |
|
RU2419966C2 |
| Способ передачи сообщений с использованием стохастических помехоустойчивых кодов | 2022 |
|
RU2804323C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ С МЯГКИМИ РЕШЕНИЯМИ | 2012 |
|
RU2500074C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ ПОСЛЕДОВАТЕЛЬНОГО КАСКАДНОГО КОДА (ВАРИАНТЫ) | 2006 |
|
RU2340091C2 |
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ В СКРУЧЕННОМ ПОЛЯРНОМ КОДЕ | 2014 |
|
RU2571587C2 |
| Способ декодирования линейного каскадного кода | 2017 |
|
RU2667370C1 |
Изобретение относится к области техники связи и может быть использовано для мягкого декодирования помехоустойчивого кода в каналах связи с высоким уровнем помех. Технический результат заключается в повышении эффективности декодирования при сохранении высокой помехоустойчивости. Для этого на вход декодирующего устройства подают n символов принятого помехоустойчивого кода с оценками достоверностей символов. В декодирующем устройстве помехоустойчивого кода сначала оценивают величину s числа наименее достоверных символов помехоустойчивого кода, затем символы помехоустойчивого кода сортируют по достоверности и выделяют s наименее достоверных символов и n-s наиболее достоверных символов кода. Используя проверочную матрицу кода, вычисляют наименее достоверные символы через наиболее достоверные символы кода. Декодирование заканчивается, если все проверочные соотношения кода выполняются, в противном случае в проверочной матрице выбирают проверку, в которую входят более достоверные символы по сравнению с символами других проверок и вычисляют наименее достоверный символ и его новую достоверность. Во все проверки проверочной матрицы подставляют вновь вычисленный символ с учетом новой достоверности и вычисляют заново s-1 наименее достоверных символов. 3 з.п. ф-лы.
1. Способ мягкого декодирования помехоустойчивого кода, заключающийся в том, что на вход декодирующего устройства подают n символов принятого помехоустойчивого кода с оценками достоверностей этих символов, в декодирующем устройстве помехоустойчивого кода сначала оценивают величину s числа наименее достоверных символов помехоустойчивого кода, затем символы помехоустойчивого кода сортируют по достоверности, выбирая сначала символы с наибольшей достоверностью, затем символы с меньшей, но следующей по величине достоверностью и так далее, пока не будет набрано n-s наиболее достоверных символов помехоустойчивого кода, далее выполняют декодирование помехоустойчивого кода с использованием n-s наиболее достоверных символов кода, в результате определяют s наименее достоверных символов кода и восстанавливают информационные символы кода, отличающийся тем, что после определения s наименее достоверных символов кода сначала выполняют ортогонализацию проверочной матрицы кода относительно позиций этих s наименее достоверных символов кода, затем умножают полученное слово на проверочную матрицу кода и при получении нулевого вектора декодирование считают успешным, в противном случае выбирают проверочное соотношение для одного из s наименее достоверных символов кода, такое, что в него входят другие символы кода с наибольшей достоверностью по сравнению с проверочными соотношениями для других наименее достоверных символов кода, после этого вычисляют выбранный наименее достоверный символ и определяют его новую достоверность, далее символы кода снова сортируют по достоверности с учетом новой достоверности вновь вычисленного символа кода, затем опять выполняют ортогонализацию проверочной матрицы кода относительно позиций уже s-1 наименее достоверных символов кода и вычисляют эти s-1 символов, далее умножают полученное слово на проверочную матрицу кода и при получении нулевого вектора декодирование считают успешным, в противном случае в полученной проверочной матрице снова выбирают проверочное соотношение для одного из s-1 наименее достоверных символов кода, такое что в него входят другие символы кода с наибольшей достоверностью, после этого вычисляют выбранный наименее достоверный символ и определяют его новую достоверность и так далее до тех пор, пока не будут вычислены все s наименее достоверных символов кода.
2. Способ по п. 1, отличающийся тем, что новую достоверность наименее достоверного символа определяют как наименьшую достоверность наиболее достоверных символов, входящих в проверочное соотношение.
3. Способ по п. 1, отличающийся тем, что ортогонализацию проверочной матрицы кода выполняют путем тождественных преобразований над строками проверочной матрицы.
4. Способ по п. 1, отличающийся тем, что величину s числа наименее достоверных символов помехоустойчивого кода определяют из условия равенства числа наименее достоверных символов s величине d-1, где d - минимальное кодовое расстояние кода.
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ ПОМЕХОУСТОЙЧИВОГО КОДА | 2013 |
|
RU2546070C1 |
| RU 2002116722 A, 10.02.2004 | |||
| СПОСОБ ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ СО СТИРАНИЯМИ ЭЛЕМЕНТОВ | 2006 |
|
RU2327297C2 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ СИСТЕМАТИЧЕСКИХ БЛОКОВЫХ КОДОВ | 2010 |
|
RU2444127C1 |
| СПОСОБ МЯГКОГО ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ | 2015 |
|
RU2580797C1 |
| US 6654926 B1, 25.11.2003 | |||
| Способ обработки целлюлозных материалов, с целью тонкого измельчения или переведения в коллоидальный раствор | 1923 |
|
SU2005A1 |
Авторы
Даты
2020-12-16—Публикация
2020-06-02—Подача