Область техники, к которой относится изобретение
Заявляемое изобретение относится к области компьютерных технологий, а именно, к сетевым компьютерным технологиям, позволяющим объединять и использовать вычислительные ресурсы различных видов для проведения междисциплинарных исследований, например, в области биоинформатики, биоинженерии, космических исследований, в медицине, физике и др. Разные направления исследования зачастую требуют применения вычислителей различных типов, в результате чего задача объединения вычислительных ресурсов в единую систему, работающую над решением одной задачи, становится чрезвычайно актуальной. Выбор вычислителей для формирования такой системы представляет собой нетривиальный процесс, требующий использования специализированных аппаратно-программных решений.
Уровень техники
На данном этапе развитие многих высокотехнологичных отраслей науки и техники подразумевает использование высокопроизводительных систем обработки данных. Для таких задач используют модульные вычислительные системы, состоящие из отдельных серверов, вычислительные ресурсы которых объединены в единое целое посредством специального программного обеспечения. Благодаря специально разработанным диспетчерским системам пакетной обработки данных, каждая задача может быть распределена на все узлы объединения, в результате чего для решения каждой задачи могут быть использованы ресурсы всей системы. Существенное влияние на общую производительность и эффективность использования такого объединения вычислительных ресурсов (вычислительного комплекса) оказывает принцип объединения вычислителей в комплекс, а также выбранный подход к реализации каналов межузлового взаимодействия.
В качестве вычислителей, объединяемых в такие вычислительные системы, могут быть использованы, например, персональные компьютеры, рабочие станции, серверы, мэйнфреймы, кластеры, представляющие собой распределённые системы компьютеров, суперкомпьютеры или облачные IT- ресурсы.
Известные из уровня техники способы формирования вычислительных комплексов (объединения вычислителей) имеют целью, в основном, обеспечение снижения энергозатрат или экономическое преимущество.
Так, например, из публикации US9342376B2 « Способ, система и устройство для динамического энергоэффективного планирования заданий в среде облачных вычислений» («Method, system, and device for dynamic energy efficient job scheduling in a cloud computing environment», Intel Corp - https://patents.google.com/patent/US9342376B2 ) известны способ, система и устройство для энергосберегающего планирования заданий в вычислительной среде центра обработки данных, включающего в себя главный узел. Главный узел может периодически принимать энергетические данные от подчиненных узлов и динамически назначать вычислительные задачи, которые должны выполняться подчиненными узлами, на основе энергетических данных. В качестве вычислителей в известном техническом решении используют вычислительные узлы, а в качестве вычислительного комплекса - центр обработки данных.
Из публикации US20100111105, « Центр обработки данных и дизайн центра данных» («Data center and data center design», Hewlett Packard Enterprise Development LP - https://patents.google.com/patent/US20100111105) известен центр обработки данных, содержащий: множество секций центра обработки данных, причем каждая секция имеет различный предварительно определенный уровень надежности; и множество наборов приложений, причем каждый набор приложений заполняется на одном из множества участков центра обработки данных. В качестве вычислителей в известном техническом решении используют секции с разным уровнем надёжности (разные уровни надёжности имеют разную стоимость), а в качестве вычислительного комплекса - центр обработки данных.
Как отмечено выше, известные способы основаны на применении отборочного критерия, не обеспечивающего формирования вычислительного комплекса, имеющего оптимальную загрузку, как по времени выполнения отдельных задач, так и по затрачиваемым ресурсам.
Наиболее близким по технической сущности к заявляемому способу является способ определения состава вычислительного комплекса, обеспечивающий оптимальное энергопотребление набора вычислителей (US8225119, Energy-aware server management, Microsoft Technology Licensing LLC, https://patents.google.com/patent/US8225119). При таком подходе производится управление энергопотреблением в ферме серверов путем переключения отдельных серверов между активным и неактивным состояниями, с сохранением времени отклика для фермы серверов на предварительно определенном уровне. Для этого при реализации способа в зависимости от ожидаемой нагрузки определяли, какие вычислители должны быть включены (остальные вычислители при этом выключены). Таким образом, производили выбор подмножества вычислителей, определяющих состав вычислительного комплекса для состояния системы в определенный момент времени. Для определения состава вычислительного комплекса прогнозируют будущую рабочую нагрузку для набора серверов, включаемых в вычислительный комплекс. Отдельные серверы имеют, по крайней мере, два энергетических состояния: включено и выключено. Энергетические состояния отдельных серверов корректируются в зависимости от прогнозируемой будущей рабочей нагрузки.
Недостатком известного способа является тот факт, что такой подход не обеспечивает формирование вычислительного комплекса, обеспечивающего максимальное покрытие типов решаемых задач с помощью минимального количества вычислителей, то есть формирование вычислительного комплекса максимальной полноты или производительности.
В общем случае, для каждой программы в отдельности наиболее оптимальным способом ее исполнения является направление её для выполнения на вычислитель, обеспечивающий наиболее быстрое исполнение программы данного типа, без учета характеристики временных классов вычислителей, в результате чего состав вычислительного комплекса в известном решении формируют различные представители всех временных классов, что может приводить к избыточному включению в комплекс вычислителей одних и тех же временных классов, то есть к избыточному количеству вычислителей в вычислительном комплексе в целом, что соответствует понятию «недостаточности полноты вычислительного комплекса», а также снижению эффективности инвестиций в её функционирование в дальнейшем. В результате, известный способ формирования вычислительного комплекса не обеспечивает формирование оптимального состава вычислительного комплекса с точки зрения максимального покрытия типов решаемых задач (максимально возможного количества выполняемых программ разных типов) при минимальном количестве включенных в комплекс вычислителей.
Таким образом, известные вычислительные комплексы не обеспечивают возможности группировки входящих в них вычислителей по временным классам, в результате чего отсутствует возможность приоритетного выполнения той или иной программы вычислителем соответствующего временного класса, то есть все вычислители всех временных классов имеют равный приоритет для задач любого типа.
Между тем, следует отметить, что более рациональным представляется подход, когда для выполнения программы используют вычислители определенных временных классов.
Временной класс - последовательность временных интервалов фиксированного размера, задающая измерительную шкалу времени выполнения программы на вычислителе. Размер интервала является единицей измерения времени выполнения программы на вычислителе в данном временном классе. Временные классы могут формировать интервалы времени, например, 10 секунд (тогда измерительная шкала данного временного класса выглядит как 0, 10, 20, 30 и т.д.) или 15 секунд (тогда измерительная шкала данного временного класса выглядит как 0, 15, 30, 45 и т.д.). По аналогии временные классы могут быть определены и для других интервалов времени. Соответственно, если программа выполняется на определенном вычислителе за 40 секунд, то полагают, что данная программ относится к первому временному классу вычислителей (где измерительная шкала сформирована как 0, 10, 20, 30 и т.д.) и не относится ко второму (где измерительная шкала сформирована как 0, 15, 30, 45 и т.д.).
Таким образом, на каждом вычислителе вычислительного комплекса возможно осуществить запуск программы любого временного класса. При этом выполненные тем или иным вычислителем программы не соотносятся с определенным временным классом, поскольку после получения результатов выполнения программы информация о временном классе программы становится излишней, так как её повторные запуски маловероятны. Между тем на эффективности использования вычислительного комплекса несвязанность программы при ее запуске с определенным временным классом вычислителя сказывается, поскольку при отсутствии корреляции программ временным классам вычислителей, могут быть выявлены простои отдельных вычислителей или, наоборот, слишком длительное выполнение программы при возможности ее более быстрого завершения на другом вычислителе. При отсутствии такой группировки вычислителей по временным классам выполняемых программ также может уменьшиться полнота вычислительного комплекса, поскольку не будут исключены вычислители, дублирующие одинаковые временные классы.
Техническая проблема, решаемая посредством заявляемого изобретения, заключается в необходимости преодоления недостатков, присущих известным способам формирования вычислительного комплекса, за счет создания способа определения такого состава вычислительного комплекса, который позволит обеспечить формирование вычислительного комплекса, обеспечивающего максимальное покрытие классов решаемых задач с помощью минимального количества вычислителей.
Краткое раскрытие сущности изобретения
Технический результат, достигаемый при использовании заявляемого изобретения, заключается в обеспечении оптимального покрытия типов решаемых задач с помощью минимального количества вычислителей за счет, в том числе, устранения дублирования вычислителей в составе вычислительного комплекса, что обеспечивает формирование вычислительного комплекса оптимальной полноты.
Количество выбранных для формирования вычислительного комплекса вычислителей в соответствии с заявляемым способом является минимально возможным (необходимым и достаточным) для решения задач разной степени сложности, при этом вычислительный комплекс формируется таким образом, что в результате применения характеристики временного класса не допускается простоя или перегрузки отдельных вычислителей комплекса, что способствует экономии как потребляемых энергоресурсов, так и затрачиваемых мощностей и машинного времени.
Заявляемый способ обеспечивает выбор подмножества вычислителей из множества вычислителей таким образом, что выбирается состав вычислительного комплекса, оптимальный по соотношению числа участников вычислительного комплекса к количеству различных временных классов, т.е. обеспечивается максимальное покрытие временных классов минимальным количеством вычислителей.
Заявляемый технический результат достигается тем, что способ формирования вычислительного комплекса оптимального состава включает следующие этапы:
1) формирование множества вычислителей, являющихся кандидатами в состав вычислительного комплекса,
2) формирование набора бенчмарков, предназначенных к выполнению на каждом вычислителе из множества вычислителей, сформированного на этапе 1),
3) серийное выполнение на каждом вычислителе набора бенчмарков с определением и фиксацией времени выполнения каждого бенчмарка из набора,
4) определение среднего времени выполнения в серии каждого бенчмарка отдельно и всего набора бенчмарков в целом на каждом вычислителе из множества вычислителей,
5) составление всех возможных пар вычислителей из множества, сформированного на шаге 1) и определение модуля попарного коэффициента корреляции Пирсона (ккП) для каждой пары на основании данных, полученных на этапах 3) и 4),
для каждого из полученных значений модуля (ккП) из диапазона от 0,1 до 1 с шагом от 0,01 до 0,05 выполняют этапы 6)-9):
6) выделение групп вычислителей, включающих пары вычислителей, имеющих значение модуля попарного коэффициента корреляции Пирсона (ккП) больше заданного значения,
7) определение множества вычислителей из вычислителей, вошедших в группы, сформированные на шаге 6), включающего по одному вычислителю из всех групп, выделенных на шаге 6),
8) формирование вычислительного комплекса из вычислителей, определенных на шаге 7), с исключением повторных включений одного и того же вычислителя в комплекс,
9) определение полноты сформированного вычислительного комплекса, для чего для каждого сформированного на шаге 8) вычислительного комплекса определяют отношение количества групп, полученных на шаге 6), к количеству вычислителей, составляющих множество на шаге 1),
10) выбирают наиболее оптимальный вычислительный комплекс по наибольшему значению его полноты, определенной на этапе 9).
При формировании набора бенчмарков для выполнения этапа 2) выбирают бенчмарки в количестве не менее 5 штук: а) принадлежащие различным временным классам, то есть бенчмарки, время выполнения которых на одном и том же вычислителе находится в разных измерительных временных шкалах, б) характеризующиеся минимальным и максимальным временем выполнения, в) характеризующиеся различными значениями требуемых машинных ресурсов для выполнения.
Серийное выполнение набора бенчмарков на каждом вычислителе включает, по меньшей мере, три последовательных запуска набора. На этапе 6) для формирования групп вычислителей используют алгоритм формирования клик. В качестве такого алгоритма может быть использован алгоритм Брона-Кербоша.
Краткое описание чертежей
Заявляемое изобретение поясняется следующими чертежами, где:
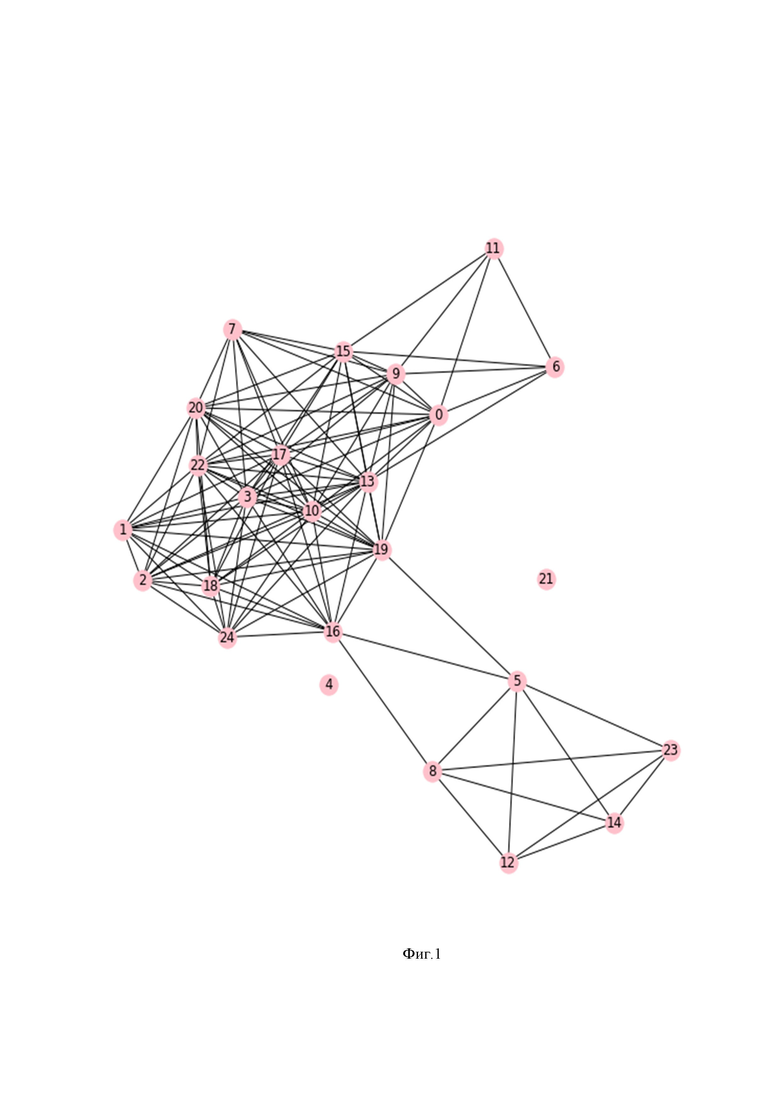
На фиг. 1 схематично представлена часть графа, вершины которого представляют собой вычислители, являющиеся кандидатами в создаваемый вычислительный комплекс, а рёбрами соединены вычислители, ккП между которыми превышает заранее заданное пороговое значение (в примере равное 0.75).
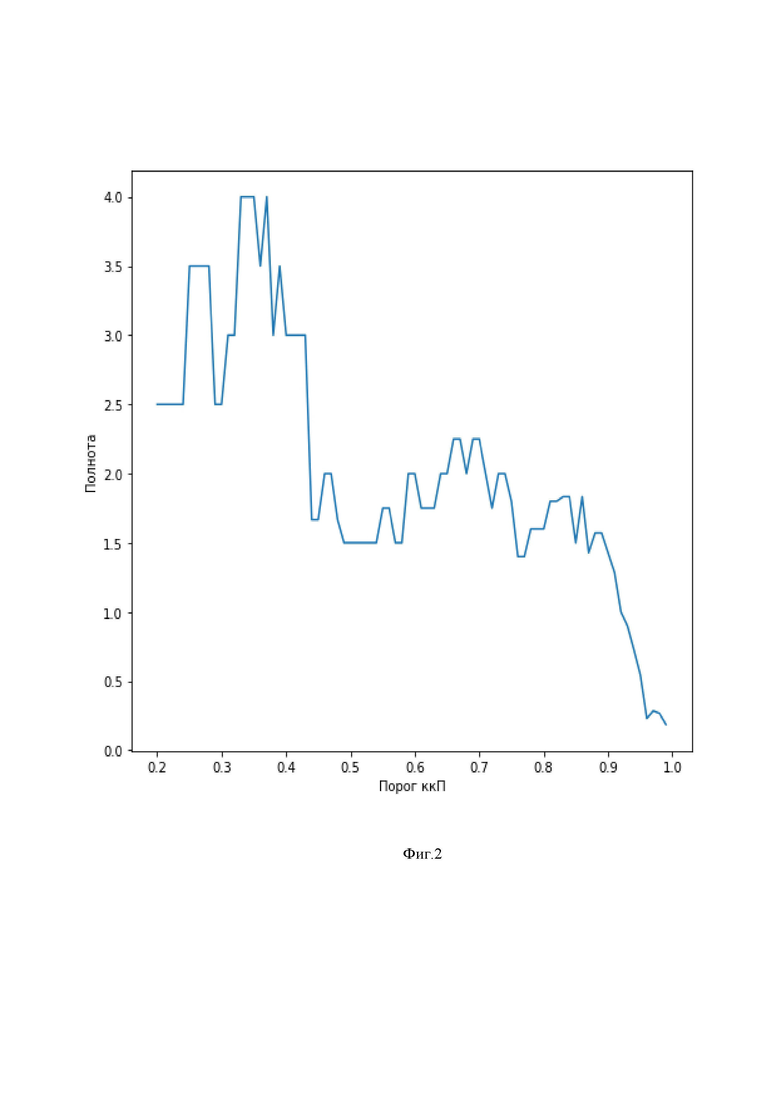
На фиг. 2 представлен график зависимости полноты формируемого вычислительного комплекса от порогового значения ккП при минимальном размере группы, равном трём.
Используемая терминология
Для наилучшего понимания заявляемой сущности изобретения ниже приведены основные термины и определения, используемые в дальнейшем описании.
Вычислительный комплекс - вычислительная среда, в которой все участники могут делиться и/или использовать вычислительные ресурсы друг друга.
Вычислитель - участник вычислительного комплекса.
Кандидат в состав вычислительного комплекса - потенциальный участник вычислительного комплекса.
Бенчмарк - эталонный тест производительности компьютерной системы (программа).
Коэффициент корреляции Пирсона [ http://www.machinelearning.ru/wiki/index.php?title=Коэффициент_корреляции_Пирсона ] характеризует существование линейной зависимости между двумя величинами.
Пусть даны две выборки размера m: 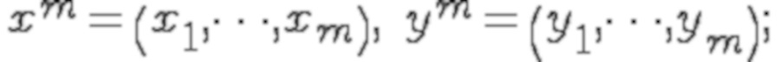 ,
,
коэффициент корреляции Пирсона рассчитывается по формуле:
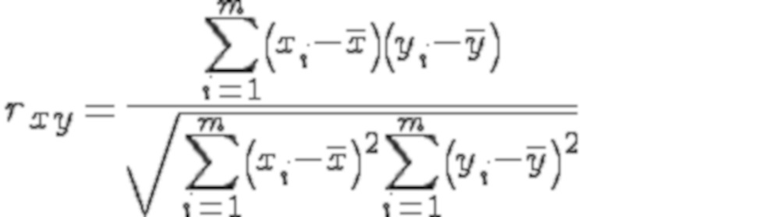
где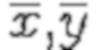 - выборочные средние
- выборочные средние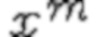 и
и 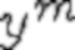 ,
, 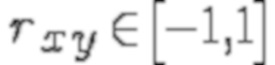 .
.
Коэффициент корреляции Пирсона называют также теснотой линейной связи:
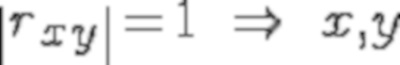 линейно зависимы,
линейно зависимы,
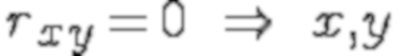 линейно независимы.
линейно независимы.
Алгоритм формирования клик - алгоритм, определяющий в неориентированном графе все максимальные по включению полные подграфы.
Таких алгоритмов известно несколько, возможен выбор любого из них, на сущность изобретения это не влияет. Одним из самых эффективных алгоритмов формирования клик является алгоритм Брона-Кербоша (https://ru.wikipedia.org/wiki/Алгоритм_Брона_-_Кербоша).
Алгоритм оперирует тремя множествами вершин графа:
• Множество compsub - множество, содержащее на каждом шаге рекурсии полный подграф для данного шага. Строится рекурсивно.
• Множество candidates - множество вершин, которые могут увеличить compsub
• Множество not - множество вершин, которые уже использовались для расширения compsub на предыдущих шагах алгоритма.
Алгоритм является рекурсивной процедурой, применяемой к этим трем множествам.
ПРОЦЕДУРА extend (candidates, not):
ПОКА candidates НЕ пусто И not НЕ содержит вершины, СОЕДИНЕННОЙ СО ВСЕМИ вершинами из candidates,
ВЫПОЛНЯТЬ:
1 Выбираем вершину v из candidates и добавляем её в compsub
2 Формируем new_candidates и new_not, удаляя из candidates и not вершины, не СОЕДИНЕННЫЕ с v
3 ЕСЛИ new_candidates и new_not пусты
4 ТО compsub - клика
5 ИНАЧЕ рекурсивно вызываем extend (new_candidates, new_not)
6 Удаляем v из compsub и candidates, и помещаем в not
Алгоритм формирования состава вычислительного комплекса - алгоритм, определяющий минимальный состав представителей заданного набора множеств (минимальное покрытие).
Таких алгоритмов может быть предложено несколько, возможен выбор любого из них, на сущность изобретения выбор не влияет. Одним из самых простых алгоритмов является жадный алгоритм.
Алгоритм оперирует двумя множествами и словарём:
• Множество memb - множество, содержащее текущий состав вычислительного комплекса для данной итерации цикла. Строится последовательно. Изначально множество memb пустое.
• Множество rem_cliques - набор множеств, которые ещё не использовались для расширения memb на предыдущих шагах алгоритма (среди элементов этого набора множеств отсутствуют элементы из memb). Изначально rem_cliques равен исходному набору множеств.
• Словарь comp - словарь, в котором по элементу хранится величина, определяющая, в какое количество множеств входит этот элемент для известного набора элементов(COMP_SET) и заданного набора множеств(rem_cliques).
Алгоритм является последовательной процедурой, применяемой к этим трем объектам.
ПРОЦЕДУРА cover (rem_cliques):
ПОКА rem_cliques НЕ пусто,
ВЫПОЛНЯТЬ:
1 Формируем comp по rem_cliques и COMP_SET(задаётся извне)
2 Определяем new_memb, выбирая из comp элемент, входящий в максимальное количество множеств(если таких элементов несколько, выбирается любой из них)
3 Добавляем в memb значение new_memb
4 Формируем new_rem_cliques, добавляя в него те множества из rem_cliques, в которые не входит new_memb
5 Заменяем rem_cliques на new_rem_cliques
Полнота вычислительного комплекса - соотношение количества групп, имеющих размер более заданного к общему количеству вычислителей, составляющих вычислительный комплекс.
Временной класс - последовательность временных интервалов заданной ширины, задающая измерительную шкалу, в которой размер интервала является единицей измерения.
Осуществление изобретения
Для реализации заявляемого изобретения на первом этапе выполнения способа определяют множество вычислителей, которые являются кандидатами в состав вычислительного комплекса. В качестве таких вычислителей могут быть использованы, например, персональные компьютеры, рабочие станции, серверы, мэйнфреймы, кластеры, представляющие собой распределённые системы компьютеров, суперкомпьютеры или облачные IT- ресурсы. Каждому вычислителю присваивают идентификационный номер, а также фиксируют его основные характеристики: конфигурацию процессора, объём оперативной и дисковой памяти, операционную систему, компилятор, файловую систему, сетевой интерфейс.
Затем из определенного известного множества бенчмарков определяют набор бенчмарков, которые планируют запускать на каждом из вычислителей сформированного выше множества. Как правило, набор бенчмарков включает от 10 до 20 тестирующих программ. Рассматриваются популярные бенчмарки, состоящие из программ различных предметных областей https://www.spec.org/auto/accel/Docs/]. Например, часто используемыми и характерными для своих областей являются бенчмарки, представленные в Таблице 1.
В результате каждый бенчмарк из сформированного набора запускают на каждом вычислителе и фиксируют время его выполнения и соотносят с идентификационным номером вычислителя. На каждом вычислителе из множества вычислителей производят серию, по меньшей мере, из трёх запусков сформированного набора бенчмарков.
Результаты выполнения бенчмарков направляют архитектору вычислительного комплекса, который формирует таблицу результатов запусков бенчмарков на вычислителях. Таблица представляет собой матрицу с усреднёнными результатами запусков, в столбцах которой располагаются идентификационные номера вычислителей, в строках - порядковые номера бенчмарков. Каждая ячейка матрицы с результатами содержит среднее время выполнения бенчмарка на вычислителе (сек.) (см. Таблицу 2, раскрывающую данный этап изобретения на примере конкретного выполнения, где строки 1..10 соответствуют номерам бенчмарков из Таблицы 1, а столбцы 0..24 соответствуют идентификационным номерам вычислителей - кандидатов в вычислительный комплекс).
Таким образом, в результате выполнения данного этапа получают данные о среднем времени выполнения того или иного теста на каждом вычислителе из выбранного множества.
Проводят группировку вычислителей в соответствии со следующим критерием:
Для всего множества вычислителей, являющихся кандидатами в вычислительный комплекс, сформированного на шаге 1), образуют всевозможные пары вычислителей, для чего формируют квадратную матрицу (Таблица 3), строки и столбцы которой представляют собой идентификационные номера кандидатов. Для каждой пары вычислителей определяют коэффициент корреляции Пирсона (к.к.П.) по столбцам с соответствующими временами выполнения бенчмарков (см. Таблицу 3). В случае, если к.к.П. превышает заранее установленное пороговое значение, это означает, что между вычислителями существует линейная зависимость по времени выполнения на них заданного набора бенчмарков. Соответственно, ячейки матрицы содержат значение ккП, определенного для каждой пары вычислителей. КкП может принимать значения от 1 до -1. Отрицательные значения также характеризуют наличие линейной зависимости, поэтому анализируется значение модуля ккП - чем оно ближе к 1, тем больше теснота линейной связи.
Далее процесс ведут для каждого значения ккП, больше 0,1. Задают минимальное пороговое значение ккП в диапазоне от 0,1 до 1 с шагом 0,05, и для каждого такого порогового значения выполняют следующие действия по формированию вычислительного комплекса:
Формируют граф, в качестве вершин которого используют вычислители (их идентификационные номера), при этом рёбрами соединяют пары вычислителей с ккП, превышающим заранее заданное пороговое значение ккП (см. Фиг. 1).
К построенному таким образом графу применяют алгоритм формирования клик (например, алгоритм Брона-Кербоша), в результате применения которого выделяют полные подграфы, представляющие собой группы вычислителей, попарный модуль значения к.к.П. внутри которых больше заранее заданного порогового значения, например, 0.75. Меняя величину порогового значения ккП при формировании графа вычислителей, можно влиять на количество выделяемых групп вычислителей, и, следовательно, на размер вычислительного комплекса. Таким образом, если величина порогового значения мала, например, 0.2, количество групп в вычислительном комплексе также будет мало, например, 6, что в свою очередь означает незначительное покрытие временных классов программ. Если же порог велик, например, 0.99, то количество групп в вычислительном комплексе также будет велико, например, 17, что в свою очередь означает значительное покрытие временных классов выполняемых программ, однако также может приводить к значительному размеру вычислительного комплекса, что не всегда целесообразно с точки зрения энергозатрат, например. Поэтому для получения оптимального по соотношению число участников/покрытие типов программ вычислительного комплекса необходимо подобрать такое пороговое значение ккП, при котором максимальна величина, равная отношению количества групп более заданного размера к размеру вычислительного комплекса - за счет чего достигается полнота вычислительного комплекса. Однако если выбрать пороговое значение ккП меньше 0.75, то группы могут формироваться случайным образом и не определять временной класс программ. Минимальный размер групп также является значимой величиной, поскольку, например, группа, состоящая из одного узла, может быть аномалией и не определять временной класс.
После группировки вычислителей описанным выше образом, для каждого вычислителя определяют, в какое количество групп он входит. Выбирают вычислитель, входящий в состав максимального количества групп. Затем группы, в которые входит выбранный вычислитель, исключают из рассмотрения, а выбранный вычислитель фиксируют в составе создаваемого вычислительного комплекса. Для оставшихся групп вновь выбирают вычислитель, входящий в состав максимального количества групп. После чего состав групп вновь уменьшается. Процедуру повторяют до тех пор, пока состав групп не исчерпан. В случае если на некотором шаге есть несколько вычислителей, входящих в максимальное количество групп, выбирается любой из них. Выбранные в результате описанной процедуры вычислители объединяют в вычислительный комплекс, который имеет оптимальный состав. Для получения оптимального состава вычислительного комплекса применяют алгоритм формирования состава вычислительного комплекса (например, «жадный» алгоритм).
Для каждого полученного вышеописанным способом вычислительного комплекса проводят оценку его полноты с целью выбора вычислительного комплекса оптимального состава по наибольшему значению полноты, для чего
- определяют минимально возможное количество групп в множестве кандидатов в вычислительный комплекс,
- значение количества групп делят на количество вычислителей сформированного вычислительного комплекса.
Пример конкретного выполнения
В качестве примера конкретной реализации заявляемый способ воплощен в режиме опытной эксплуатации для вычислителей, представленных в [https://www.spec.org/accel/results/accel_omp.html].
Для реализации заявляемого способа сформировано множество кандидатов в состав вычислительного комплекса, состоящее из 25 вычислителей (идентификационные номера 0..24), характеризующихся конфигурацией процессора, объёмом оперативной и дисковой памяти, операционной системой, компилятором, файловой системой, сетевым интерфейсом (см. например, Таблицу 4 в качестве примера параметров вычислителя).
Для оценки возможности включения указанных вычислителей в вычислительный комплекс сформирован набор, включающий все бенчмарки, описанные ранее. Данный набор считается достаточным, поскольку в нём представлены программы различных предметных областей.
На каждом вычислителе из сформированного множества каждый из выбранных бенчмарков был запущен троекратно, при этом после каждого запуска фиксировали время его выполнения, а также определяли среднее время выполнения каждого теста за три запуска.
Полученные результаты фиксировали на сервере, управляющем формированием вычислительного комплекса. В Таблице 2 представлен пример матрицы результатов выполнения программ на вычислителях, представленных в https://www.spec.org/accel/results/accel_omp.html, и бенчмарков, описанных ранее.
Для полученных результатов измерений определяли коэффициент корреляции Пирсона - попарно, в отношении всех пар вычислителей. В Таблице 3 представлен пример матрицы попарных корреляций. Для дальнейшей группировки вычислителей задавали различные пороговые значения ккП, равного от 0.20 до 0.99 (с шагом 0.01), и определяли состав вычислительного комплекса в зависимости от предустановленного порогового значения.
На фиг. 1 представлен граф вычислителей, в котором рёбрами соединены вычислители, ккП между которыми превышает 0.75 (данное значение выбрано исключительно с иллюстративной целью). В Таблице 5 приведены результаты реализации заявляемого способа для различных пороговых значений ккП. В результате группировки с различными ккП (см. 1 столбец Таблицы 5) выделены группы вычислителей (см. 2 столбец Таблицы 5), попарный ккП которых больше соответствующего заданного порогового значения. Так, для значения ккП 0.2 в графе выделяют 6 групп, а для значения ккП равного 0.99 выделяют 17 групп.
К каждому набору групп применяется алгоритм определения состава вычислительного комплекса, в результате которого определяется состав вычислительного комплекса (см. 3 столбец Таблицы 5).

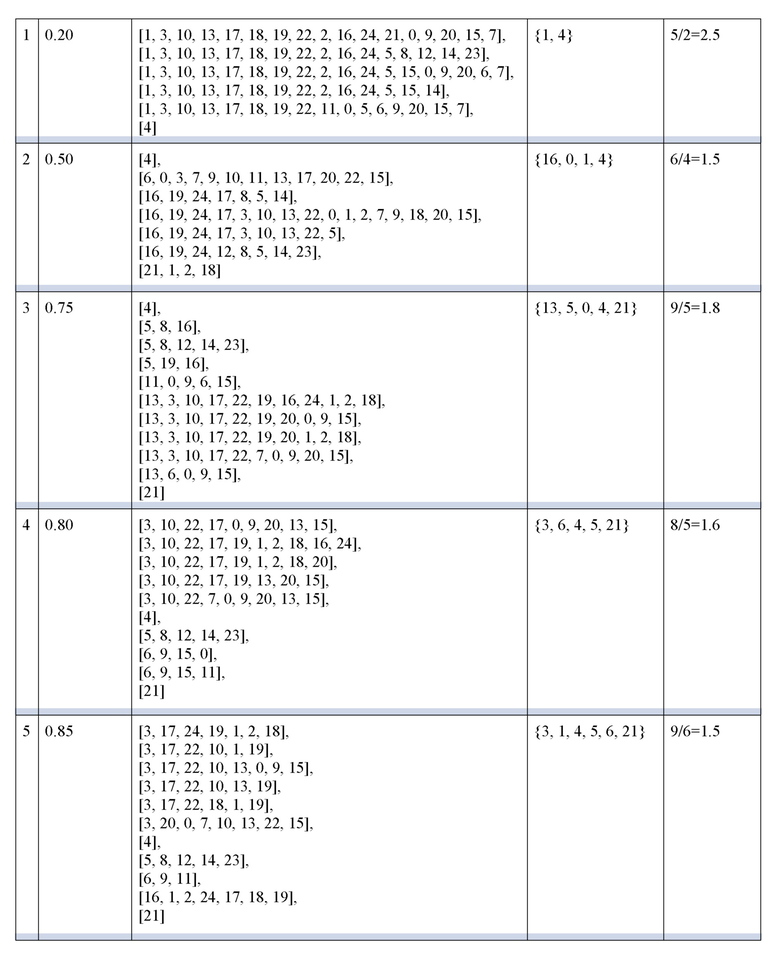
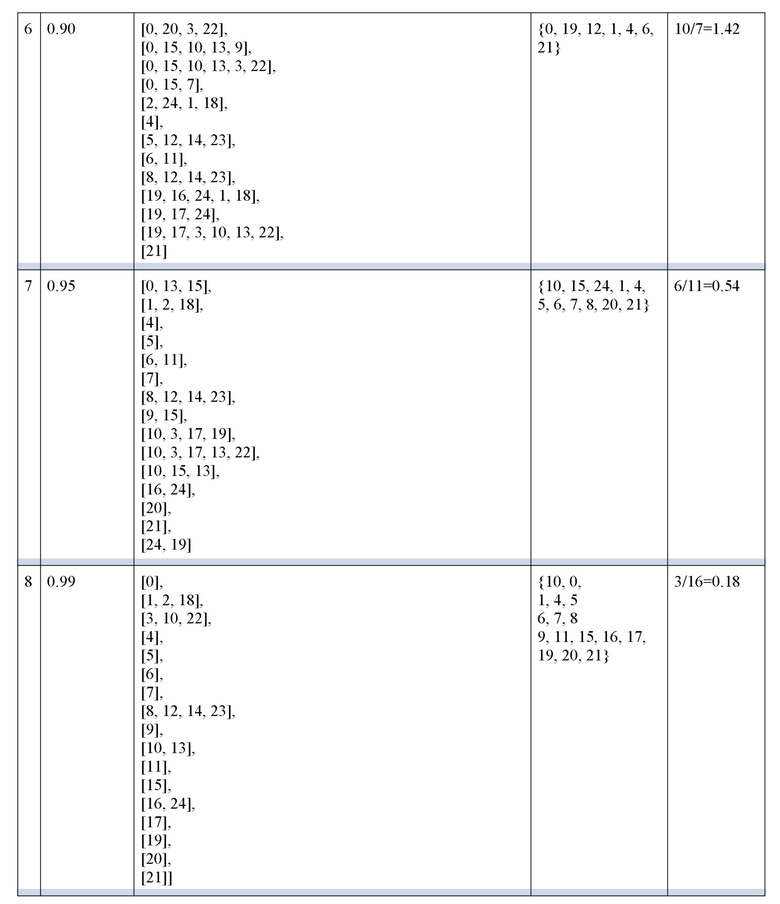
Была получена оценка полноты каждого сформированного вычислительного комплекса, для чего было поделено значение количества групп, размером более заданного, на количество вычислителей полученного вычислительного комплекса. Наибольшая полнота является характеристикой формирования вычислительного комплекса оптимального состава.
При минимальном размере группы 3 оптимальным порогом ккП среди рассмотренных ккП (от 0.2 до 0.99 с шагом 0.01 - см. фиг. 2) является порог ккП 0.86, поскольку при этом пороге достигается максимальная оценка полноты - 1.83. Такое же значение полноты также достигается при порогах ккП 0.83 и 0.84, однако значение полноты, полученное для более высокого порога 0.86, является более достоверным.
Таким образом, регулируя пороговое значение ккП можно для множества кандидатов в состав вычислительного комплекса сформировать вычислительный комплекс оптимального состава с максимальной полнотой, то есть вычислительный комплекс, обеспечивающий максимальное покрытие временных классов решаемых задач с помощью минимального количества вычислителей.
СПОСОБ ФОРМИРОВАНИЯ ВЫЧИСЛИТЕЛЬНОГО КОМПЛЕКСА

СПОСОБ ФОРМИРОВАНИЯ ВЫЧИСЛИТЕЛЬНОГО КОМПЛЕКСА
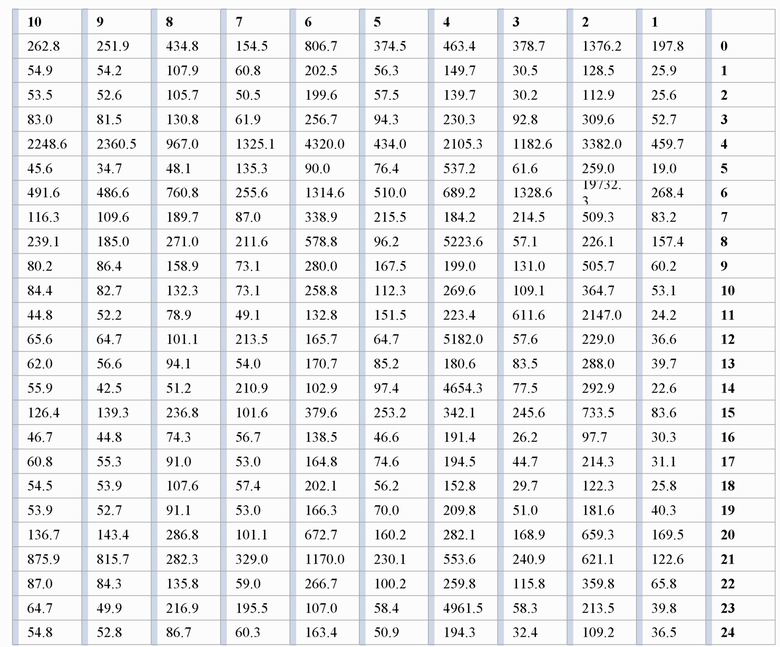
Таблица 2
СПОСОБ ФОРМИРОВАНИЯ ВЫЧИСЛИТЕЛЬНОГО КОМПЛЕКСА
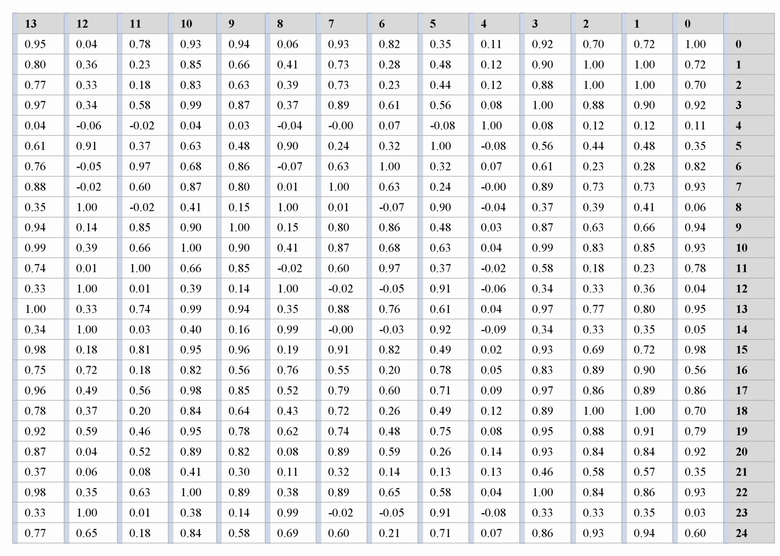
Таблица 3
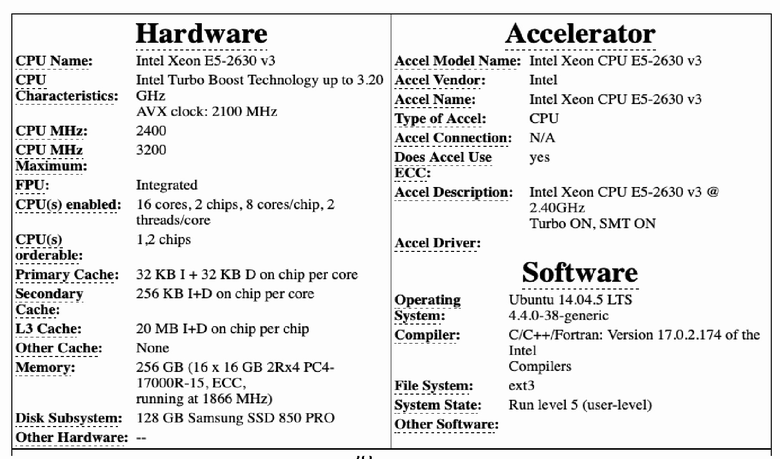
Таблица 4
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ ФЕДЕРАЦИИ ВЫЧИСЛИТЕЛЕЙ | 2020 |
|
RU2749336C1 |
| СПОСОБ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ СИСТЕМЫ УПРАВЛЕНИЯ МНОГОПАРАМЕТРИЧЕСКИМ ОБЪЕКТОМ И ПРОГРАММНО-АППАРАТНЫЙ КОМПЛЕКС ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2019 |
|
RU2730387C2 |
| СИСТЕМА И СПОСОБ ИДЕНТИФИКАЦИИ ЖЕЛЕЗНОДОРОЖНЫХ НОМЕРНЫХ ДЕТАЛЕЙ ПО ИЗОБРАЖЕНИЮ ИХ ПОВЕРХНОСТЕЙ С КЛЕЙМАМИ И ЗНАКАМИ МАРКИРОВКИ | 2019 |
|
RU2702965C1 |
| ИЗВЛЕЧЕНИЕ ИНФОРМАЦИОННЫХ ОБЪЕКТОВ С ИСПОЛЬЗОВАНИЕМ КОМБИНАЦИИ КЛАССИФИКАТОРОВ, АНАЛИЗИРУЮЩИХ ЛОКАЛЬНЫЕ И НЕЛОКАЛЬНЫЕ ПРИЗНАКИ | 2018 |
|
RU2686000C1 |
| ИТЕРАТИВНОЕ ПОПОЛНЕНИЕ ЭЛЕКТРОННОГО СЛОВНИКА | 2013 |
|
RU2549118C2 |
| ВЕРОЯТНОСТНЫЙ АВТОМАТ | 2021 |
|
RU2777531C1 |
| ГЕНЕРАТОР СЛУЧАЙНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ | 2022 |
|
RU2797406C1 |
| СПОСОБ ЭВОЛЮЦИОННОГО МОДЕЛИРОВАНИЯ ЭПИДЕМИЧЕСКОЙ ДИНАМИКИ ВИЧ-ИНФЕКЦИИ | 2017 |
|
RU2677002C1 |
| Способы и системы для определения компьютером наличия объектов | 2018 |
|
RU2743895C2 |
| СПОСОБЫ И СЕРВЕРЫ ДЛЯ ОПРЕДЕЛЕНИЯ ЗАВИСЯЩИХ ОТ МЕТРИКИ ПОРОГОВ, ИСПОЛЬЗУЕМЫХ СО МНОЖЕСТВОМ ВЛОЖЕННЫХ МЕТРИК ДЛЯ БИНАРНОЙ КЛАССИФИКАЦИИ ЦИФРОВОГО ОБЪЕКТА | 2020 |
|
RU2795202C2 |
Предложенное изобретение относится к области компьютерных технологий. Технический результат, достигаемый при использовании предложенного изобретения, заключается в обеспечении оптимального покрытия типов решаемых задач с помощью минимального количества вычислителей за счет, в том числе, устранения дублирования вычислителей в составе вычислительного комплекса, что обеспечивает формирование вычислительного комплекса оптимальной полноты. Способ формирования вычислительного комплекса оптимального состава включает следующие этапы: формирование множества вычислителей, являющихся кандидатами в состав вычислительного комплекса, серийное выполнение на каждом вычислителе набора бенчмарков с определением и фиксацией времени выполнения каждого бенчмарка из набора, составление всех возможных пар вычислителей и определение модуля попарного коэффициента корреляции Пирсона (ккП) для каждой пары, формирование вычислительного комплекса с исключением повторных включений одного и того же вычислителя в комплекс. 4 з.п. ф-лы, 2 ил., 5 табл.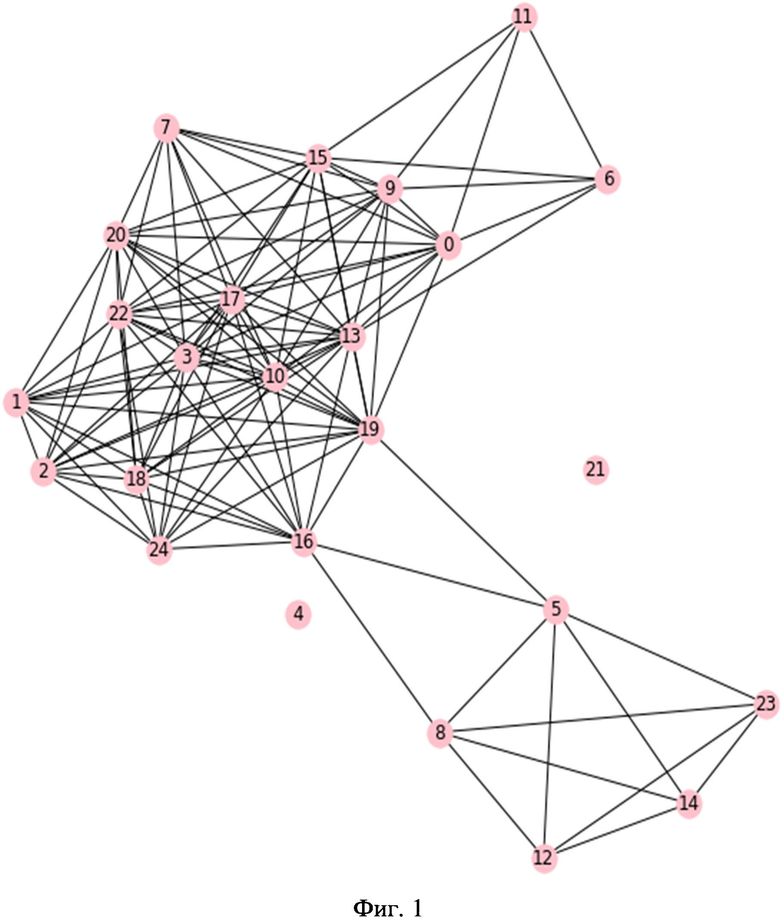
1. Способ формирования вычислительного комплекса, включающий следующие этапы:
1) формирование множества вычислителей, являющихся кандидатами в состав вычислительного комплекса,
2) формирование набора бенчмарков, предназначенных к выполнению на каждом вычислителе из множества вычислителей, сформированного на этапе 1),
3) серийное выполнение на каждом вычислителе набора бенчмарков с определением и фиксацией времени выполнения каждого бенчмарка из набора,
4) определение среднего времени выполнения в серии каждого бенчмарка отдельно и всего набора бенчмарков в целом на каждом вычислителе из множества вычислителей,
5) составление всех возможных пар вычислителей из множества, сформированного на шаге 1) и определение модуля попарного коэффициента корреляции Пирсона (ккП) для каждой пары на основании данных, полученных на этапах 3) и 4),
и выполнение этапов 6)-9) для каждого из полученных значений модуля (ккП) из диапазона от 0,1 до 1 с шагом от 0,01 до 0,05:
6) выделение групп вычислителей, включающих пары вычислителей, имеющих значение модуля попарного коэффициента корреляции Пирсона (ккП) больше заданного значения,
7) определение множества вычислителей из вычислителей, вошедших в группы, сформированные на шаге 6), включающего по одному вычислителю из всех групп, выделенных на шаге 6),
8) формирование вычислительного комплекса из вычислителей, определенных на шаге 7), с исключением повторных включений одного и того же вычислителя в комплекс,
9) определение полноты сформированного вычислительного комплекса, для чего для каждого сформированного на шаге 8) вычислительного комплекса определяют отношение количества групп, полученных на шаге 6), к количеству вычислителей, составляющих множество на шаге 1),
после чего выбирают наиболее оптимальный вычислительный комплекс по наибольшему значению его полноты, определенной на этапе 9).
2. Способ по п.1, отличающийся тем, что при формировании набора бенчмарков для выполнения этапа 2) выбирают бенчмарки в количестве не менее 5 штук: а) принадлежащие различным временным классам, то есть бенчмарки, время выполнения которых на одном и том же вычислителе находится в разных измерительных временных шкалах, б) характеризующиеся минимальным и максимальным временем выполнения, в) характеризующиеся различными значениями требуемых машинных ресурсов для выполнения.
3. Способ по п.1, отличающийся тем, что серийное выполнение набора бенчмарков на каждом вычислителе включает, по меньшей мере, три последовательных запуска набора.
4. Способ по п.1, отличающийся тем, что на этапе 6) для формирования групп вычислителей используют алгоритм формирования клик.
5. Способ по п.4, отличающийся тем, что при этом в качестве алгоритма формирования клик используют алгоритм Брона-Кербоша.
| US 8225119 B, 17.07.2012 | |||
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
| CN 107729338 A, 23.02.2018 | |||
| СПОСОБ ВЫПОЛНЕНИЯ ЗАДАЧ В КРИТИЧЕСКОЙ СИСТЕМЕ РЕАЛЬНОГО ВРЕМЕНИ | 2014 |
|
RU2660614C2 |
| СПОСОБ ОБРАБОТКИ ДЛЯ МНОГОЯДЕРНОГО ПРОЦЕССОРА И МНОГОЯДЕРНЫЙ ПРОЦЕССОР | 2012 |
|
RU2630753C2 |
Авторы
Даты
2021-07-13—Публикация
2020-09-11—Подача