СПОСОБ ФОРМИРОВАНИЯ ФЕДЕРАЦИИ ВЫЧИСЛИТЕЛЕЙ Российский патент 2021 года по МПК G06F7/60 G06F11/36 

Область техники, к которой относится изобретение

Заявляемое изобретение относится к области компьютерных технологий, а именно к сетевым компьютерным технологиям, позволяющим объединять и использовать вычислительные ресурсы различных видов для проведения междисциплинарных исследований, например, в области биоинформатики, биоинженерии, космических исследований, медицине, физике и др. Разные направления исследования зачастую требуют применения вычислителей различных типов, в результате чего задача объединения вычислительных ресурсов в единую систему, работающую над решением одной задачи, становится чрезвычайно актуальной. Выбор вычислителей для формирования такой системы (федерации) представляет собой нетривиальный процесс, требующий использования специализированных аппаратно-программных решений.

Уровень техники

На данном этапе развитие многих высокотехнологичных отраслей науки и техники подразумевает использование высокопроизводительных систем обработки данных. Для таких задач используют модульные вычислительные системы (федерации), состоящие из отдельных серверов, вычислительные ресурсы которых объединены в единое целое посредством специального программного обеспечения. Из уровня техники известны следующие федерации вычислителей:

1) GENI [Hwang, T. (2017, March). NSF GENI cloud enabled architecture for distributed scientific computing. In 2017 IEEE Aerospace Conference (pp. 1-8). IEEE.] - представляет собой открытую инфраструктуру для масштабных сетевых и распределенных систем исследований и образования, которая охватывает США. Проект позволяет получать вычислительные ресурсы из мест по всей территории Соединенных Штатов;

2) Федерация облачных вычислений EGI (ЕС, Голландия) - инфраструктура для проведения научных междисциплинарных исследований на основе принципов федерации путем объединения вычислительных мощностей, ИКТ ресурсов;

Известные федерации не обеспечивают возможности группировки входящих в них федератов (вычислителей) по классам выполняемых программ, в результате чего отсутствует возможность приоритетного выполнения той или иной программы вычислителем соответствующего класса, то есть все федераты имеют равный приоритет для задач любого класса. Таким образом, на каждом вычислителе федерации возможно осуществить запуск программы любого класса. При этом выполненные тем или иным федератом программы не сопоставляются определенным классам, поскольку после получения результатов выполнения программы информация о классе программы становится излишней, ее повторные запуски маловероятны. Однако при отсутствии такой группировки федератов по классам выполняемых программ может уменьшаться полнота федерации, в результате чего работа федерации будет менее эффективной.

Известен способ определения состава федерации, обеспечивающий оптимальное энергопотребление набора вычислителей (US8225119, Energy-aware server management, Microsoft Technology Licensing LLC, https://patents.google.com/patent/US8225119). При таком подходе производится управление энергопотреблением в ферме серверов путем переключения отдельных серверов между активным и неактивным состояниями, с сохранением времени отклика для фермы серверов на предварительно определенном уровне. Для этого при реализации способа в зависимости от ожидаемой нагрузки определяли, какие вычислители должны быть включены (остальные вычислители при этом выключены). Таким образом производили выбор подмножества вычислителей, определяющих состав вычислительного комплекса для состояния системы в определенный момент времени. Для определения состава федерации прогнозируют будущую рабочую нагрузку для набора серверов, включаемых в нее.

Наиболее близким по технической сущности к заявляемому способу является способ определения оптимального состава федерации вычислителей, исходя из информации о текущей загруженности и мощности вычислителей. При таком подходе производится классификация программ по их ожидаемой длительности выполнения, после чего программы, требующие большей продолжительности времени для реализации, направляют на выполнение на наиболее мощные из наименее загруженных вычислителей федерации. При таком подходе вычислители группируют по мощности, а классы программ соответствуют уровням длительности выполнения программ.

Однако недостатком данного способа является тот факт, что такой подход не обеспечивает достижения полноты федерации, то есть отношение количества групп вычислителей, предназначенных для решения определенных классов задач и имеющих размер более заданного к общему количеству вычислителей, составляющих федерацию, поскольку для каждой программы в отдельности оптимальным является направление её для выполнения на наиболее мощный из наименее загруженных вычислителей своего класса, в результате чего состав федерации формируют из наиболее мощных вычислителей, что может приводить к дублированию классов вычислителей, и, в результате, к снижению полноты федерации, а также эффективности ее функционирования в дальнейшем. Таким образом, программы некоторых классов не могут быть выполнены в такой федерации, в случае, когда этим классам соответствуют менее мощные вычислители, которые не войдут в состав федерации. В результате, известный способ формирования федерации вычислителей не обеспечивает оптимальности ее состава и, соответственно, не покрывает возможность выполнения программ из максимально возможного количества классов.

Техническая проблема, решаемая посредством заявляемого изобретения, заключается в необходимости преодоления недостатков, присущих известным способам формирования федераций вычислителей за счет создания способа определения такого состава федерации вычислителей, который позволит обеспечить представительство как можно большего числа классов программ при наименьшем количестве вычислителей, с учетом того, что один вычислитель может относиться к нескольким классам.

Краткое раскрытие сущности изобретения

Технический результат, достигаемый при использовании заявляемого изобретения, заключается в обеспечении возможности максимального покрытия классов решаемых задач (максимально возможного количества выполняемых программ разных классов) при минимальном количестве включенных в комплекс вычислителей, что соответствует увеличению полноты федерации за счет устранения дублирования вычислителей, предназначенных для решения задач из различных классов, при создании федерации, и добавления новых вычислителей, обеспечивающих возможность решения задач из новых классов (дополнительное покрытие классов). Заявляемый способ обеспечивает выбор подмножества вычислителей из множества вычислителей таким образом, что выбирается состав федерации вычислителей, оптимальный по соотношению числа участников федерации к количеству различных классов, т.е. обеспечивается максимальное покрытие классов программ минимальным количеством вычислителей. Увеличение полноты достигается тем, что в состав федерации не включаются дублирующих существующие классы вычислители и включаются вычислители, определяющие новые классы.

Заявляемый технический результат достигается тем, способ формирования федерации вычислителей оптимального состава включает следующие этапы:

1) предоставление множества вычислителей, являющихся кандидатами в федераты,

2) формирование набора бенчмарков, предназначенных к выполнению на каждом вычислителе из множества вычислителей, сформированного на этапе 1),

3) серийное выполнение на каждом вычислителе набора бенчмарков с определением и фиксацией времени выполнения каждого бенчмарка из набора,

4) определение среднего времени выполнения в серии каждого бенчмарка отдельно и всего набора бенчмарков в целом на каждом вычислителе из множества вычислителей,

5) определение коэффициента корреляции Пирсона для всех пар вычислителей, составляющих множество на шаге 1),

6) формирование групп вычислителей, включающих все пары вычислителей, имеющих коэффициент корреляции Пирсона (ккП) больше заранее заданного значения,

7) определение в каждой группе вычислителей, сформированной на шаге 6), вычислителя, характеризующегося минимальным средним временем выполнения набора бенчмарков, определенным на шаге 4),

8) формирование федерации из вычислителей, определенных на шаге 7) с исключением их дублирования. При формировании набора бенчмарков на этапе 2) выбирают бенчмарки, принадлежащие различным классам программ. Серия запуска бенчмарков подразумевает, по меньшей мере, по три запуска набора бенчмарков на каждом тестируемом вычистлителе. На этапе 6) для формирования групп вычислителей используют алгоритм формирования клик. В качестве алгоритма формирования клик может быть использован алгоритм Брона-Кербоша. Пороговое значение коэффициента корреляции Пирсона находится в диапазоне от 0,5 до 0,99.

Краткое описание чертежей

Заявляемое изобретение поясняется следующими чертежами, где

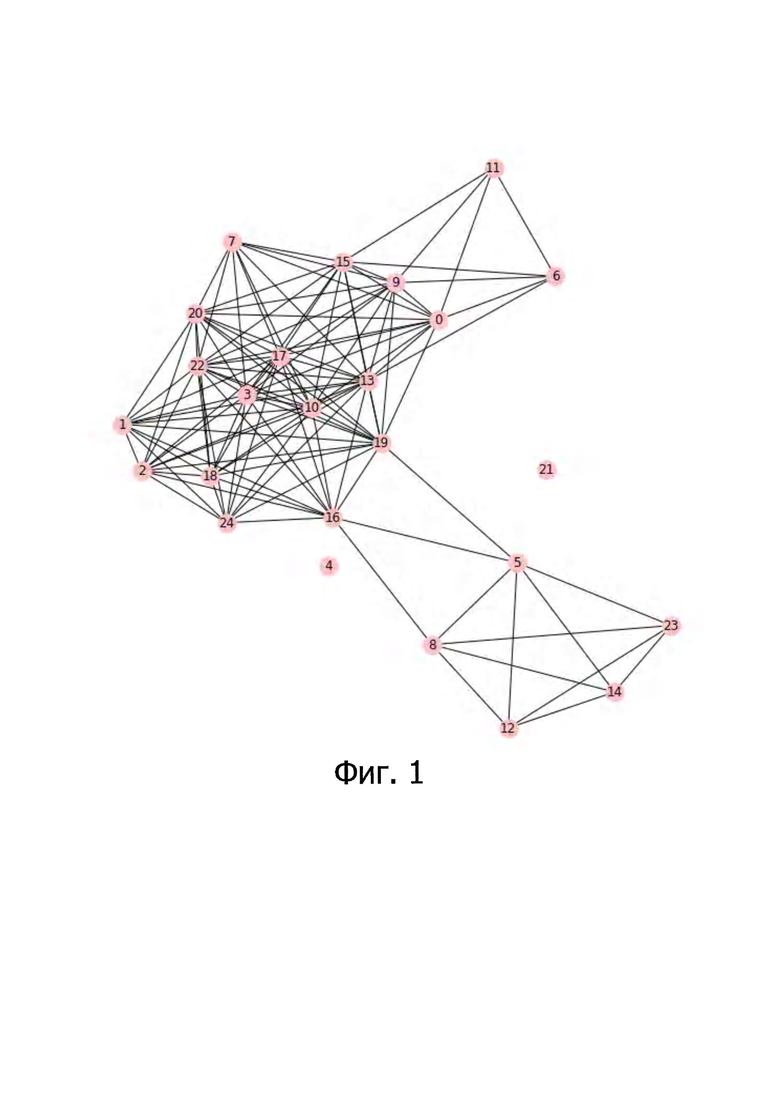
На фиг. 1 представлен граф, вершины которого представляют собой вычислители, являющиеся кандидатами в создаваемую федерацию, а рёбрами соединены вычислители, ккП между которыми превышает заранее заданное пороговое значение (в примере равное 0.75).

Используемая терминология

Для наилучшего понимания заявляемой сущности изобретения ниже приведены основные термины и определения, используемые в дальнейшем описании.

Федерация - вычислительная среда, в которой все участники могут делиться и/или использовать вычислительные ресурсы друг друга.

Федераты - участники федерации.

Кандидат в федераты - потенциальный участник федерации.

Бенчмарк - эталонный тест производительности компьютерной системы (программа).

Коэффициент корреляции Пирсона [http://www.machinelearning.ru/wiki/index.php?title=%D0%9A%D0%BE%D1%8D%D1%84%D1%84%D0%B8%D1%86%D0%B8%D0%B5%D0%BD%D1%82_%D0%BA%D0%BE%D1%80%D1%80%D0%B5%D0%BB%D1%8F%D1%86%D0%B8%D0%B8_%D0%9F%D0%B8%D1%80%D1%81%D0%BE%D0%BD%D0%B0] характеризует существование линейной зависимости между двумя величинами.

Пусть даны две выборки размера m: ,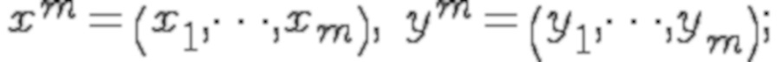

коэффициент корреляции Пирсона рассчитывается по формуле:

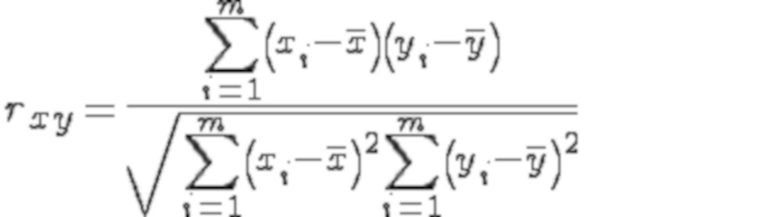
где 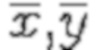- выборочные средние 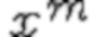и , .

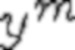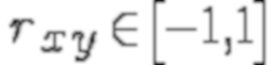Коэффициент корреляции Пирсона называют также теснотой линейной связи:

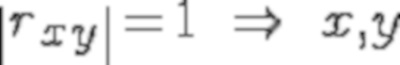линейно зависимы,

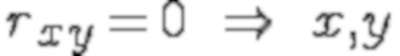линейно независимы.

Алгоритм формирования клик - алгоритм, определяющий в неориентированном графе все максимальные по включению полные подграфы.

Таких алгоритмов известно несколько, возможен выбор любого из них, на сущность изобретения это не влияет. Одним из самых эффективных алгоритмов формирования клик является алгоритм Брона-Кербоша (https://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D0%91%D1%80%D0%BE%D0%BD%D0%B0_%E2%80%94_%D0%9A%D0%B5%D1%80%D0%B1%D0%BE%D1%88%D0%B0).

Алгоритм оперирует тремя множествами вершин графа:

• Множество compsub - множество, содержащее на каждом шаге рекурсии полный подграф для данного шага. Строится рекурсивно.

• Множество candidates - множество вершин, которые могут увеличить compsub.

• Множество not - множество вершин, которые уже использовались для расширения compsub на предыдущих шагах алгоритма.

Алгоритм является рекурсивной процедурой, применяемой к этим трем множествам.

ПРОЦЕДУРА extend (candidates, not):

ПОКА candidates НЕ пусто И not НЕ содержит вершины, СОЕДИНЕННОЙ СО ВСЕМИ вершинами из candidates,

ВЫПОЛНЯТЬ:

1 Выбираем вершину v из candidates и добавляем её в compsub

2 Формируем new_candidates и new_not, удаляя из candidates и not вершины, не СОЕДИНЕННЫЕ с v

3 ЕСЛИ new_candidates и new_not пусты

4 ТО compsub - клика

5 ИНАЧЕ рекурсивно вызываем extend (new_candidates, new_not)

6 Удаляем v из compsub и candidates, и помещаем в not.

Полнота федерации - соотношение количества клик, имеющих размер более заданного к количеству вычислителей, составляющих федерацию.

Класс - последовательность временных интервалов заданной ширины, задающая измерительную шкалу, в которой размер интервала является единицей измерения.

Содержательно заявляемый способ сводится к отбору федератов из множества кандидатов в федераты с целью максимизировать полноту федерации либо к получению оценки полноты для существующей федерации.

Осуществление изобретения

1. Для реализации заявляемого изобретения на первом этапе выполнения способа формируют множество вычислителей, которые являются кандидатами в федераты. В качестве вычислителей, объединяемых в такие федерации, могут быть использованы, например, кластеры, представляющие собой распределённые системы компьютеров, суперкомпьютеры или облачные IT- ресурсы. Каждому вычислителю присваивают идентификационный номер, а также фиксируют его основные характеристики (скорость процессора, объем памяти и т.д.).

2. Затем из определенного известного множества бенчмарков определяют набор бенчмарков, которые планируют запускать на каждом из вычислителей сформированного выше множества. Как правило, набор бенчмарков включает до 15 тестирующих программ. Рассматриваются популярные бенчмарки, состоящие из программ различных предметных областей [https://www.spec.org/auto/accel/Docs/#Benchmark%20Documentation]. Например, часто используемыми и характерными для своих областей являются:

• 503.postencil - Термодинамика (https://www.spec.org/auto/accel/Docs/503.postencil.html)

• 504.polbm - Вычислительная гидродинамика, метод решеточных уравнений Больцмана (https://www.spec.org/auto/accel/Docs/504.polbm.html)

• 514.pomriq - Медицина (https://www.spec.org/auto/accel/Docs/514.pomriq.html)

• 550.pmd - Молекулярная динамика (https://www.spec.org/auto/accel/Docs/550.pmd.html)

• 551.ppalm - Моделирование больших вихрей, атмосферная турбулентность (https://www.spec.org/auto/accel/Docs/551.ppalm.html)

• 552.pep - Чрезвычайная параллельность (https://www.spec.org/auto/accel/Docs/552.pep.html)

• 553.pclvrleaf - Точная гидродинамика (https://www.spec.org/auto/accel/Docs/553.pclvrleaf.html)

• 554.pcg - Сопряженный градиент (https://www.spec.org/auto/accel/Docs/554.pcg.html)

• 555.pseismic - Моделирование сейсмических волн (https://www.spec.org/auto/accel/Docs/555.pseismic.html)

• 556.psp - Скалярный Пента-Диагональный решатель (https://www.spec.org/auto/accel/Docs/556.psp.html)

• 557.pcsp - Скалярный Пента-Диагональный решатель (https://www.spec.org/auto/accel/Docs/557.pcsp.html)

• 559.pmniGhost - Конечные разности (https://www.spec.org/auto/accel/Docs/559.pmniGhost.html)

• 560.pilbdc - Жидкостная механика (https://www.spec.org/auto/accel/Docs/560.pilbdc.html)

• 563.pswim - Погода(https://www.spec.org/auto/accel/Docs/563.pswim.html)

• 570.pbt - Блочно-Трёхдиагональный решатель для 3D PDE (https://www.spec.org/auto/accel/Docs/570.pbt.html).

3. В результате запуска на каждом вычислителе каждого бенчмарка из набора фиксируют время его выполнения и соотносят с идентификационным номером вычислителя. На каждом вычислителе из множества вычислителей производят серию, по меньшей мере, из трёх запусков сформированного набора бенчмарков.

4. Результаты выполнения бенчмарков направляют архитектору федерации, который формирует таблицу результатов запусков бенчмарков на вычислителях, представляющую собой матрицу с усреднёнными результатами запусков, в столбцах которой располагаются идентификационные номера вычислителей, в строках - порядковые номера бенчмарков. Каждая ячейка матрицы с результатами содержит среднее время выполнения бенчмарка на вычислителе (сек.) (см. Таблицу 1).

Таблица 1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 288.9 15.4 14.5 72.0 2333.8 27.3 520.8 106.8 154.4 64.2 73.0 41.9 53.7 48.2 43.9 114.6 29.8 47.6 15.4 44.7 243.0 107.3 63.9 48.6 35.1 1 197.8 25.9 25.6 52.7 459.7 19.0 268.4 83.2 157.4 60.2 53.1 24.2 36.6 39.7 22.6 83.6 30.3 31.1 25.8 40.3 169.5 122.6 65.8 39.8 36.5 2 1376.2 128.5 112.9 309.6 3382.0 259.0 19732.3 509.3 226.1 505.7 364.7 2147.0 229.0 288.0 292.9 733.5 97.7 214.3 122.3 181.6 659.3 621.1 359.8 213.5 109.2 3 378.7 30.5 30.2 92.8 1182.6 61.6 1328.6 214.5 57.1 131.0 109.1 611.6 57.6 83.5 77.5 245.6 26.2 44.7 29.7 51.0 168.9 240.9 115.8 58.3 32.4 4 463.4 149.7 139.7 230.3 2105.3 537.2 689.2 184.2 5223.6 199.0 269.6 223.4 5182.0 180.6 4654.3 342.1 191.4 194.5 152.8 209.8 282.1 553.6 259.8 4961.5 194.3 5 374.5 56.3 57.5 94.3 434.0 76.4 510.0 215.5 96.2 167.5 112.3 151.5 64.7 85.2 97.4 253.2 46.6 74.6 56.2 70.0 160.2 230.1 100.2 58.4 50.9 6 806.7 202.5 199.6 256.7 4320.0 90.0 1314.6 338.9 578.8 280.0 258.8 132.8 165.7 170.7 102.9 379.6 138.5 164.8 202.1 166.3 672.7 1170.0 266.7 107.0 163.4 7 154.5 60.8 50.5 61.9 1325.1 135.3 255.6 87.0 211.6 73.1 73.1 49.1 213.5 54.0 210.9 101.6 56.7 53.0 57.4 53.0 101.1 329.0 59.0 195.5 60.3 8 434.8 107.9 105.7 130.8 967.0 48.1 760.8 189.7 271.0 158.9 132.3 78.9 101.1 94.1 51.2 236.8 74.3 91.0 107.6 91.1 286.8 282.3 135.8 216.9 86.7 9 251.9 54.2 52.6 81.5 2360.5 34.7 486.6 109.6 185.0 86.4 82.7 52.2 64.7 56.6 42.5 139.3 44.8 55.3 53.9 52.7 143.4 815.7 84.3 49.9 52.8 10 262.8 54.9 53.5 83.0 2248.6 45.6 491.6 116.3 239.1 80.2 84.4 44.8 65.6 62.0 55.9 126.4 46.7 60.8 54.5 53.9 136.7 875.9 87.0 64.7 54.8 11 469.9 90.6 87.3 126.3 12351.9 57.7 1468.0 187.0 402.1 118.6 126.6 67.0 210.1 94.1 68.0 221.3 70.0 94.1 90.1 93.4 304.7 398.5 127.3 98.0 79.5 12 879.0 165.5 162.6 265.5 1722.9 64.9 1818.3 547.8 344.4 182.8 266.2 120.4 80.0 183.5 76.8 441.7 119.8 157.7 165.1 154.7 585.2 663.4 287.4 79.8 140.3 13 244.6 42.4 41.8 75.2 5674.1 29.5 552.9 106.6 170.6 99.4 74.8 31.8 58.1 48.8 32.8 99.2 37.7 46.0 42.5 47.3 122.0 173.3 80.2 64.1 46.9 14 177.7 28.7 28.0 51.1 4054.0 26.2 555.7 67.1 79.0 42.0 52.6 55.0 51.4 35.4 30.8 101.7 25.3 32.7 28.7 32.2 77.4 781.8 47.7 55.5 29.7

Таким образом, в результате выполнения данного этапа получают данные о среднем времени выполнения того или иного теста на каждом вычислителе из выбранного множества, а также среднее время выполнения каждой тестирующей программы на каждом вычислителе.

5. Проводят группировку вычислителей в соответствии со следующим критерием:

Все вычислители, составляющие множество, сформированное на шаге 1) попарно объединяют и для каждой пары вычислителей определяют коэффициент корреляции Пирсона (ккП) по столбцам с соответствующими временами выполнения бенчмарков (см. Таблицу 2). В случае если ккП превышает заранее установленное пороговое значение, это означает, что между вычислителями существует линейная зависимость по времени выполнения на них заданного набора бенчмарков. В Таблице 2 столбцы и строки представляют собой идентификационные номера вычислителей - кандидатов в федераты. Соответственно, ячейки содержат значение ккП, определенного для каждой пары вычислителей.

Таблица 2

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0 1.00 0.72 0.70 0.92 0.11 0.35 0.82 0.93 0.06 0.94 0.93 0.78 0.04 0.95 0.05 0.98 0.56 0.86 0.70 0.79 0.92 0.35 0.93 0.03 0.60 1 0.72 1.00 1.00 0.90 0.12 0.48 0.28 0.73 0.41 0.66 0.85 0.23 0.36 0.80 0.35 0.72 0.90 0.89 1.00 0.91 0.84 0.57 0.86 0.35 0.94 2 0.70 1.00 1.00 0.88 0.12 0.44 0.23 0.73 0.39 0.63 0.83 0.18 0.33 0.77 0.33 0.69 0.89 0.86 1.00 0.88 0.84 0.58 0.84 0.33 0.93 3 0.92 0.90 0.88 1.00 0.08 0.56 0.61 0.89 0.37 0.87 0.99 0.58 0.34 0.97 0.34 0.93 0.83 0.97 0.89 0.95 0.93 0.46 1.00 0.33 0.86 4 0.11 0.12 0.12 0.08 1.00 -0.08 0.07 -0.00 -0.04 0.03 0.04 -0.02 -0.06 0.04 -0.09 0.02 0.05 0.09 0.12 0.08 0.14 0.13 0.04 -0.08 0.07 5 0.35 0.48 0.44 0.56 -0.08 1.00 0.32 0.24 0.90 0.48 0.63 0.37 0.91 0.61 0.92 0.49 0.78 0.71 0.49 0.75 0.26 0.13 0.58 0.91 0.71 6 0.82 0.28 0.23 0.61 0.07 0.32 1.00 0.63 -0.07 0.86 0.68 0.97 -0.05 0.76 -0.03 0.82 0.20 0.60 0.26 0.48 0.59 0.14 0.65 -0.05 0.21 7 0.93 0.73 0.73 0.89 -0.00 0.24 0.63 1.00 0.01 0.80 0.87 0.60 -0.02 0.88 -0.00 0.91 0.55 0.79 0.72 0.74 0.89 0.32 0.89 -0.02 0.60 8 0.06 0.41 0.39 0.37 -0.04 0.90 -0.07 0.01 1.00 0.15 0.41 -0.02 1.00 0.35 0.99 0.19 0.76 0.52 0.43 0.62 0.08 0.11 0.38 0.99 0.69 9 0.94 0.66 0.63 0.87 0.03 0.48 0.86 0.80 0.15 1.00 0.90 0.85 0.14 0.94 0.16 0.96 0.56 0.85 0.64 0.78 0.82 0.30 0.89 0.14 0.58 10 0.93 0.85 0.83 0.99 0.04 0.63 0.68 0.87 0.41 0.90 1.00 0.66 0.39 0.99 0.40 0.95 0.82 0.98 0.84 0.95 0.89 0.41 1.00 0.38 0.84 11 0.78 0.23 0.18 0.58 -0.02 0.37 0.97 0.60 -0.02 0.85 0.66 1.00 0.01 0.74 0.03 0.81 0.18 0.56 0.20 0.46 0.52 0.08 0.63 0.01 0.18 12 0.04 0.36 0.33 0.34 -0.06 0.91 -0.05 -0.02 1.00 0.14 0.39 0.01 1.00 0.33 1.00 0.18 0.72 0.49 0.37 0.59 0.04 0.06 0.35 1.00 0.65 13 0.95 0.80 0.77 0.97 0.04 0.61 0.76 0.88 0.35 0.94 0.99 0.74 0.33 1.00 0.34 0.98 0.75 0.96 0.78 0.92 0.87 0.37 0.98 0.33 0.77 14 0.05 0.35 0.33 0.34 -0.09 0.92 -0.03 -0.00 0.99 0.16 0.40 0.03 1.00 0.34 1.00 0.20 0.72 0.50 0.37 0.59 0.04 0.06 0.36 1.00 0.64 15 0.98 0.72 0.69 0.93 0.02 0.49 0.82 0.91 0.19 0.96 0.95 0.81 0.18 0.98 0.20 1.00 0.62 0.90 0.70 0.83 0.86 0.32 0.95 0.18 0.64 16 0.56 0.90 0.89 0.83 0.05 0.78 0.20 0.55 0.76 0.56 0.82 0.18 0.72 0.75 0.72 0.62 1.00 0.89 0.91 0.95 0.66 0.44 0.81 0.72 0.99 17 0.86 0.89 0.86 0.97 0.09 0.71 0.60 0.79 0.52 0.85 0.98 0.56 0.49 0.96 0.50 0.90 0.89 1.00 0.88 0.99 0.85 0.43 0.97 0.49 0.90 18 0.70 1.00 1.00 0.89 0.12 0.49 0.26 0.72 0.43 0.64 0.84 0.20 0.37 0.78 0.37 0.70 0.91 0.88 1.00 0.91 0.83 0.57 0.86 0.37 0.95 19 0.79 0.91 0.88 0.95 0.08 0.75 0.48 0.74 0.62 0.78 0.95 0.46 0.59 0.92 0.59 0.83 0.95 0.99 0.91 1.00 0.81 0.41 0.95 0.59 0.95 20 0.92 0.84 0.84 0.93 0.14 0.26 0.59 0.89 0.08 0.82 0.89 0.52 0.04 0.87 0.04 0.86 0.66 0.85 0.83 0.81 1.00 0.44 0.91 0.03 0.72 21 0.35 0.57 0.58 0.46 0.13 0.13 0.14 0.32 0.11 0.30 0.41 0.08 0.06 0.37 0.06 0.32 0.44 0.43 0.57 0.41 0.44 1.00 0.42 0.06 0.48 22 0.93 0.86 0.84 1.00 0.04 0.58 0.65 0.89 0.38 0.89 1.00 0.63 0.35 0.98 0.36 0.95 0.81 0.97 0.86 0.95 0.91 0.42 1.00 0.35 0.83 23 0.03 0.35 0.33 0.33 -0.08 0.91 -0.05 -0.02 0.99 0.14 0.38 0.01 1.00 0.33 1.00 0.18 0.72 0.49 0.37 0.59 0.03 0.06 0.35 1.00 0.64 24 0.60 0.94 0.93 0.86 0.07 0.71 0.21 0.60 0.69 0.58 0.84 0.18 0.65 0.77 0.64 0.64 0.99 0.90 0.95 0.95 0.72 0.48 0.83 0.64 1.00

6. Затем формируют граф, в качестве вершин которого используют вычислители (их идентификационные номера), при этом ребрами соединяют пары вычислителей с ккП, превышающим заранее заданное пороговое значение (см. Фиг. 1).

7. К построенному таким образом графу применяют алгоритм формирования клик (например, алгоритм Брона-Кербоша), в результате применения которого выделяют полные подграфы (клики), представляющие собой группы вычислителей, попарный модуль значения ккП внутри которых больше заранее заданного порогового значения, например, 0.75. Меняя величину порогового значения ккП при формировании графа вычислителей, можно влиять на количество выделяемых групп вычислителей, а следовательно, и на размер федерации. Таким образом, если величина порогового значения мала, например, 0.2, количество групп в федерации также будет мало, например, 6, что в свою очередь означает незначительное покрытие классов программ. Если же порог велик, например, 0.99, то количество групп в федерации также будет велико, например, 17, что в свою очередь означает значительное покрытие классов программ, однако также приводит к значительному размеру федерации. Поэтому для получения оптимальной по соотношению число участников/покрытие классов программ федерации вычислителей необходимо подобрать такое пороговое значение ккП, при котором максимальна величина, равная отношению количества групп более заданного размера к размеру федерации - полнота федерации. Минимальный размер групп является значимой величиной, поскольку, например, группа, состоящая из одного узла, может быть аномалией и не определять класс программ.

8. После группировки вычислителей описанным выше образом из каждой группы выбирают самый эффективный по времени выполнения бенчмарков вычислитель. Уровень эффективности в данном случае устанавливают по значению среднего времени выполнения набора бенчмарков. Минимальное значение среднего времени соответствует наибольшей эффективности. Выбранные таким образом вычислители из каждой группы объединяют в федерацию, которая имеет оптимальный состав.

Важным является понятие класса. Поскольку фактически строится сопоставление программ и вычислителей, это понятие должно быть универсальным и применимым как для вычислителей, так и для программ. Учитывая это, классом называется единица измерения. У каждого вычислителя есть некоторая шкала, в которой определён шаг. А у каждой программы есть результат её измерения в каждой такой шкале (содержательно это время выполнения). Если программа укладывается в близкое к целому число шагов, считается, что она относится к классу соответствующей шкалы. Поскольку все вычислители, относящиеся к одной группе, имеют линейную зависимость времён выполнения, возможно выбрать такую шкалу, в которую войдут все шаги (содержательно это наименьшее общее кратное, НОК). Таким образом, каждой группе соответствует своя шкала, определяющая класс программ, которые могут быть измерены близким к целому числом шагов такой шкалы. Это означает, что чем больше групп представлено в федерации, тем выше покрытие классов программ.

Пример конкретного выполнения

В качестве примера конкретной реализации заявляемый способ воплощен в режиме опытной эксплуатации.

1. Для реализации заявляемого способа сформировано множество кандидатов в федераты, состоящее из 25 вычислителей (идентификационные номера 0..24).

2. Для оценки возможности включения указанных вычислителей в федерацию сформирован набор бенчмарков, описанных выше.

3. На каждом вычислителе из сформированного множества каждый из выбранных бенчмарков был запущен троекратно, при этом после каждого запуска фиксировали время его выполнения, а также определяли среднее время выполнения каждого теста за три запуска (серию запусков).

4. Полученные результаты фиксировали на сервере, управляющем формированием федерации. В Таблице 1 представлен пример матрицы результатов выполнения программ на вычислителях, представленных в https://www.spec.org/accel/results/accel_omp.html и бенчмарков, описанных ранее.

5. Для полученных результатов измерений определяли коэффициент корреляции Пирсона - попарно, в отношении всех пар вычислителей. В Таблице 2 представлен пример матрицы попарных корреляций. Для дальнейшей группировки вычислителей задавали различные пороговые значения ккП, равные от 0,20 до 0,99, и определяли федерацию вычислителей в зависимости от предустановленного порогового значения.

6. На фиг. 1 представлен граф вычислителей, в котором рёбрами соединены вычислители, ккП между которыми превышает 0.75 (данное значение выбрано исключительно с иллюстративной целью). В Таблице 3 приведены результаты реализации заявляемого способа для различных пороговых значений ккП. В результате группировки с различными ккП (см. 1 столбец Таблицы 3) выделены группы вычислителей (см. 2 столбец Таблицы 3), попарный ккП которых больше соответствующего заданного порогового значения. Так, для значения ккП 0,2 в графе выделяют 6 клик, а для значения ккП, равного 0,99, выделяют 17 клик.

7. В каждой группе (клике) вычислителей по наименьшему среднему времени выполнения набора бенчмарков выделяют наиболее мощный вычислитель (см. 3 столбец Таблицы 3).

8. Из выделенных наиболее мощных вычислителей формируют федерацию оптимального состава, при этом учитывают (исключают) дублирование вычислителей, вошедших в качестве выбранных наиболее мощных представителей из различных групп (см. 4 столбец Таблицы 3). Так, в строке 3 Таблицы 3 видно, что при формировании федерации устранено дублирование вычислителей 0, 6, 8.

Таблица 3

Пороговое значение ккП Клики Выбранные представители клик Состав федерации Полнота федерации 1 0.20 [1, 3, 10, 13, 17, 18, 19, 22, 2, 16, 24, 21, 0, 9, 20, 15, 7],
[1, 3, 10, 13, 17, 18, 19, 22, 2, 16, 24, 5, 8, 12, 14, 23],
[1, 3, 10, 13, 17, 18, 19, 22, 2, 16, 24, 5, 15, 0, 9, 20, 6, 7],
[1, 3, 10, 13, 17, 18, 19, 22, 2, 16, 24, 5, 15, 14],
[1, 3, 10, 13, 17, 18, 19, 22, 11, 0, 5, 6, 9, 20, 15, 7],
[4] 21
8
6
14
6
4 {4, 6, 8, 14, 21} 5/5=1. 2 0.50 [4],
[6, 0, 3, 7, 9, 10, 11, 13, 17, 20, 22, 15],
[16, 19, 24, 17, 8, 5, 14],
[16, 19, 24, 17, 3, 10, 13, 22, 0, 1, 2, 7, 9, 18, 20, 15],
[16, 19, 24, 17, 3, 10, 13, 22, 5],
[16, 19, 24, 12, 8, 5, 14, 23],
[21, 1, 2, 18] 4
6
8
0
22
8
21 {0, 4, 6, 8, 21, 22} 6/6=1. 3 0.75 [4],
[5, 8, 16],
[5, 8, 12, 14, 23],
[5, 19, 16],
[11, 0, 9, 6, 15],
[13, 3, 10, 17, 22, 19, 16, 24, 1, 2, 18],
[13, 3, 10, 17, 22, 19, 20, 0, 9, 15],
[13, 3, 10, 17, 22, 19, 20, 1, 2, 18],
[13, 3, 10, 17, 22, 7, 0, 9, 20, 15],
[13, 6, 0, 9, 15],
[21] 4
8
8
5
6
22
0
20
0
6
21 {0, 4, 5, 6, 8, 20, 21, 22} 9/8=1.125 4 0.80 [3, 10, 22, 17, 0, 9, 20, 13, 15],
[3, 10, 22, 17, 19, 1, 2, 18, 16, 24],
[3, 10, 22, 17, 19, 1, 2, 18, 20],
[3, 10, 22, 17, 19, 13, 20, 15],
[3, 10, 22, 7, 0, 9, 20, 13, 15],
[4],
[5, 8, 12, 14, 23],
[6, 9, 15, 0],
[6, 9, 15, 11],
[21] 0
22
20
20
0
4
8
6
6
21 {0, 4, 6, 8, 20, 21, 22} 8/7=1.142 5 0.85 [3, 17, 24, 19, 1, 2, 18],
[3, 17, 22, 10, 1, 19],
[3, 17, 22, 10, 13, 0, 9, 15],
[3, 17, 22, 10, 13, 19],
[3, 17, 22, 18, 1, 19],
[3, 20, 0, 7, 10, 13, 22, 15],
[4],
[5, 8, 12, 14, 23],
[6, 9, 11],
[16, 1, 2, 24, 17, 18, 19],
[21] 3
22
0
22
22
0
4
8
6
17
21 {0, 3, 4, 6, 8, 17, 21, 22} 9/8=1.125 6 0.90 [0, 20, 3, 22],
[0, 15, 10, 13, 9],
[0, 15, 10, 13, 3, 22],
[0, 15, 7],
[2, 24, 1, 18],
[4],
[5, 12, 14, 23],
[6, 11],
[8, 12, 14, 23],
[19, 16, 24, 1, 18],
[19, 17, 24],
[19, 17, 3, 10, 13, 22],
[21] 0
0
0
0
1
4
12
6
8
19
17
22
21 {0, 1, 4, 6, 8, 12, 17, 19, 21, 22} 10/10=1 7 0.95 [0, 13, 15],
[1, 2, 18],
[4],
[5],
[6, 11],
[7],
[8, 12, 14, 23],
[9, 15],
[10, 3, 17, 19],
[10, 3, 17, 13, 22],
[10, 15, 13],
[16, 24],
[20],
[21],
[24, 19] 0
1
4
5
6
7
8
15
10
22
15
24
20
21
19 {0, 1, 4, 5, 6, 7, 8, 10, 15, 19, 20, 21, 22, 24} 6/14=0.428 8 0.99 [0],
[1, 2, 18],
[3, 10, 22],
[4],
[5],
[6],
[7],
[8, 12, 14, 23],
[9],
[10, 13],
[11],
[15],
[16, 24],
[17],
[19],
[20],
[21]] 0
1
22
4
5
6
7
8
9
10
11
15
24
17
19
20
21 {0, 1, 4, 5, 6, 7, 8, 9, 10, 11, 15, 17, 19, 20, 21, 22, 24} 3/17=0.176

При минимальном размере группы 3 оптимальным порогом ккП среди рассмотренных примеров является порог ккП 0.8, поскольку при этом пороге достигается максимальная оценка полноты - 1.142.

Таким образом, регулируя пороговое значение ккП, можно для множества кандидатов в федерацию сформировать федерацию оптимального состава с максимальной полнотой, то есть федерацию, обеспечивающую максимальное покрытие классов решаемых задач.

Изобретение относится к области компьютерных технологий. Технический результат заключается в обеспечении возможности максимального покрытия классов решаемых задач при минимальном количестве включенных в комплекс вычислителей. Технический результат достигается тем, что способ формирования федерации вычислителей включает следующие этапы: 1) предоставление множества вычислителей, являющихся кандидатами в федераты, 2) формирование набора бенчмарков, предназначенных к выполнению на каждом вычислителе из множества вычислителей, сформированного на этапе 1), 3) серийное выполнение на каждом вычислителе набора бенчмарков с определением и фиксацией времени выполнения каждого бенчмарка из набора, 4) определение среднего времени выполнения в серии каждого бенчмарка отдельно и всего набора бенчмарков в целом на каждом вычислителе из множества вычислителей, 5) определение коэффициента корреляции Пирсона для всех пар вычислителей, составляющих множество на шаге 1), 6) формирование групп вычислителей, включающих все пары вычислителей, имеющих коэффициент корреляции Пирсона (ккП) больше заранее заданного значения, 7) определение в каждой группе вычислителей, сформированной на шаге 6), вычислителя, характеризующегося минимальным средним временем выполнения набора бенчмарков, определенным на шаге 4), 8) формирование федерации из вычислителей, определенных на шаге 7) с исключением их дублирования. 5 з.п. ф-лы, 3 табл., 1 ил.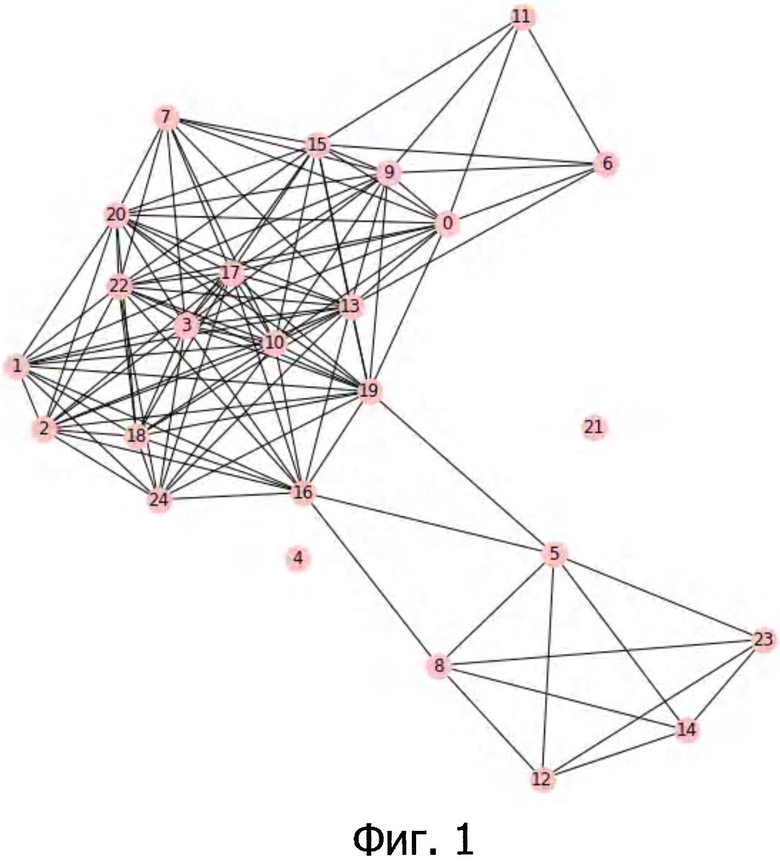

1. Способ формирования федерации вычислителей, включающий следующие этапы:

1) предоставление множества вычислителей, являющихся кандидатами в федераты,

2) формирование набора бенчмарков, предназначенных к выполнению на каждом вычислителе из множества вычислителей, сформированного на этапе 1),

3) серийное выполнение на каждом вычислителе набора бенчмарков с определением и фиксацией времени выполнения каждого бенчмарка из набора,

4) определение среднего времени выполнения в серии каждого бенчмарка отдельно и всего набора бенчмарков в целом на каждом вычислителе из множества вычислителей,

5) определение коэффициента корреляции Пирсона для всех пар вычислителей, составляющих множество на шаге 1),

6) формирование групп вычислителей, включающих все пары вычислителей, имеющих коэффициент корреляции Пирсона (ккП) больше заранее заданного значения,

7) определение в каждой группе вычислителей, сформированной на шаге 6), вычислителя, характеризующегося минимальным средним временем выполнения набора бенчмарков, определенным на шаге 4),

8) формирование федерации из вычислителей, определенных на шаге 7) с исключением их дублирования.

2. Способ по п.1, отличающийся тем, что при формировании набора бенчмарков на этапе 2) выбирают бенчмарки, принадлежащие различным классам программ.

3. Способ по п.1, отличающийся тем, что серия запуска бенчмарков представляет собой, по меньшей мере, три запуска каждого бенчмарка.

4. Способ по п.1, отличающийся тем, что на этапе 6) для формирования групп вычислителей используют алгоритм формирования клик.

5. Способ по п.4, отличающийся тем, что в качестве алгоритма формирования клик используют алгоритм Брона-Кербоша.

6. Способ по п.1, отличающийся тем, что пороговое значение коэффициента корреляции Пирсона находится в диапазоне от 0,5 до 0,99.