Область техники.
Изобретение относится к обработке сигналов расходомера Кориолиса, а именно к способу определения фазового сдвига сигналов расходомера и к определению массового расхода. Изобретение может быть использовано также в других областях, в которых требуется измерение сдвига фаз сигналов, описывающих колебательные процессы.
Расходомер Кориолиса (также существуют варианты названий - кориолисов расходомер, кориолисовый расходомер) является средством измерения массового расхода жидкости, широко востребованным в различных областях применения. В настоящее время первичный измерительный сигнал преобразователя расходомера Кориолиса в большинстве случаев представляет собой два гармонических или близких к гармоническим сигнала напряжения или тока, снимаемые с катушек, размещенных на колеблющихся участках трубок расходомера. Сдвиг фаз между этими двумя сигналами несет основную информацию об измеряемом расходе жидкости. Указанный сдвиг фаз пропорционален массовому расходу жидкости. Коэффициент пропорциональности между расходом и сдвигом фаз определяется при градуировке прибора. Таким образом, задача измерения массового расхода по первичным сигналам расходомера Кориолиса сводится к задаче измерения сдвига фаз двух сигналов.
Уровень техники.
Предшествующий уровень техники в области обработки сигналов расходомера Кориолиса обусловлен особенностями этих сигналов. Среди этих особенностей, осложняющих обработку и приводящих к росту погрешности измерения, можно отметить следующие:
- высокий уровень шумов;
- частота сигнала от нескольких десятков герц до нескольких килогерц в зависимости от модели и типоразмера расходомера, от плотности заполняющей жидкости;
- малая амплитуда сигналов, обусловленная малой амплитудой колебаний трубок;
- весьма малые величины сдвига фаз, подлежащего измерению - сдвиг фаз для верхнего предела измерения расходомера не превышает величины нескольких градусов.
Отсюда вытекают требования к обработке таких сигналов. Результат измерения должен быть нечувствителен к шумам, должен обеспечиваться за счет обработки слабого или усиленного сигнала. Фильтрация сигнала не должна способствовать ухудшению точности измерения. Чувствительность и разрешающая способность обработки должна быть не грубее 0,001-0,01 угловых градуса. Также результат измерения должен сохранять необходимые параметры точности в широком диапазоне частот колебаний сигналов от нескольких десятков до нескольких тысяч герц.
Следует сказать также о частоте выдачи результата измерения. Поскольку в большинстве практических применений измерение расхода осуществляется при режимах течения, близких к стационарному режиму, отсюда следует, что необходимая частота выдачи результата измерения лежит в диапазоне от 1 до 10 герц. Следовательно, для практических целей достаточно, чтобы прибор осуществлял измерение расхода от 1 до 10 раз в секунду. С целью увеличения экономической эффективности и снижения стоимости расходомера способ измерения должен быть реализуемым с помощью оборудования, имеющего минимально необходимые и достаточные параметры производительности.
Рассмотрим некоторые применяемые в настоящее время подходы к решению представленной задачи об определении малого сдвига фаз сигналов.
Известен метод преобразования фазового сдвига в интервал времени, описанный в учебном пособии Электронные средства измерений электрических величин: [учеб. пособие] / А.С. Волегов, Д.С. Незнахин, Е.А. Степанова; М-во образования и науки Рос. Федерации, Урал, федер. ун-т. - Екатеринбург: Изд-во Урал, ун-та, 2014. - 104 с. ([1], с. 40). Данный способ определения фазового сдвига основан на измерении временной задержки между двумя сигналами при прохождении ими некоторого уровня. Однако указанный способ обладает некоторыми недостатками. Так, точность указанного способа резко ухудшается при наличии шума анализируемых сигналов. Кроме того, помимо измерения временной задержки, требуется осуществлять измерение периода или частоты колебаний сигналов. При измерении малого сдвига фаз, характерного для сигналов расходомера Кориолиса, резко возрастают требования к точности измерения малых отрезков времени. В результате указанный способ имеет высокую погрешность в применении к расходомеру Кориолиса.
Для преодоления негативного влияния шума сигналов на точность измерения разработаны различные способы фильтрации исходных сигналов. Так, известен патент RU 2159410 С2, МПК G01F 1/84. Устройство и способ обработки сигнала для определения фазового сдвига, опубликован 20.11.2000 ([2]). Указанный способ включает в себя создание фильтрационной системы снижения шумов для расходомера Кориолиса. Принцип измерения угла сдвига фаз в этом способе такой же, как описан в упомянутой выше работе ([1], с. 40). Улучшение точности достигается за счет лучшей фильтрации исходных сигналов. Однако указанный способ также обладает определенным недостатком. При отклонении частоты или формы сигнала, вызванном флуктуациями плотности или расхода измеряемой жидкости, возможно возникновение дополнительной погрешности измерения угла сдвига фаз, поскольку указанный способ основан на замере временного сдвига между пересечениями определенного уровня двух сигналов, и упускает из рассмотрения все остальные моменты и форму сигналов. Кроме того, для измерения малого сдвига фаз сигналов требуется аппаратура, способная обеспечить высокую точность измерения малых отрезков времени, что ведет к увеличению стоимости расходомера.
Известен также способ, описанный в патентном документе Патент RU 2456548 С2, МПК G01F 1/84. Способ обработки сигналов, устройство обработки сигналов и Кориолисов расходомер, опубликован 20.07.2012 ([3]). Данный способ включает в себя для определения разности фаз сигналов дискретное преобразование Фурье (DFT) или быстрое преобразование Фурье (FFT). Указанный способ позволяет получить технический результат - выполнение измерений с постоянной точностью и возможность измерения фазы с высокой производительностью фильтрации. Однако для реализации указанного способа требуется высокопроизводительное и высокоточное электронно-вычислительное оборудование, обладающее высокой точностью измерения отсчетов времени. Как следствие, применение этого способа приводит к усложнению и удорожанию измерительной схемы и расходомера в целом.
Известен также способ, описанный в патентном документе Патент RU 2371678 С2, МПК G01F 1/84. Высокоскоростная оценка частоты и фазы расходомеров, опубликован 27.10.2009 ([4]). Согласно данному способу, определение сдвига фаз сигналов осуществляют путем формирования девяностоградусного сдвига фаз одного из сигналов при помощи преобразования Гилберта. Вычисление разности фаз выполняют из сигналов первого и второго датчиков и сформированного сигнала девяностоградусного сдвига фаз. Однако, как указано в рассмотренном далее документе [5], этот метод также имеет недостатки, связанные с погрешностями, возникающими при изменениях частоты колебаний трубок вследствие скачков плотности измеряемого вещества, проходящего через расходомер, а также вследствие наличия газовых включений в измеряемой жидкости. В этом способе также используется фильтрация сигнала, вследствие чего ухудшается быстродействие способа. В патентном документе [5] также указано, что данный способ, так же как и способы измерения фазы при помощи преобразования Фурье, относится к так называемым непараметрическим методам, которые имеют принципиальное ограничение на разрешение частот, согласно которому разрешающая способность по частоте А со обратно пропорциональна времени наблюдения ΔТ.
Известен также способ, описанный в патентном документе Патент RU 2707576 С1, МПК G01F 1/84. Способ вычисления текущей разности фаз и частоты сигналов кориолисовых расходомеров (варианты). А.С. Семенов, О.Л. Ибряева, опубликован 28.11.2019 ([5]). Согласно данному способу, сигнал от датчиков положения расходомерных трубок представляют в виде суммы комплексных экспонент с неизвестными параметрами. Получают набор дискретных отсчетов, затем проводят обработку этого набора методом матричных пучков или векторным методом матричных пучков, вычисляют частоту и сдвиг фаз сигналов. Технический результат данного способа - повышение точности измерения массового и объемного расхода жидкой среды при наличии возмущающей газовой или твердой фазы, сокращение времени измерения за счет уменьшения количества отсчетов. Данный способ является быстродействующим, результат измерения выдается через каждый шаг дискретизации. Однако для реализации указанного способа требуется высокопроизводительное и высокоточное вычислительное оборудование, обладающее высокой точностью по каналу измерения отсчетов времени. Получение результата измерения частоты и фазы (а следовательно, плотности и массового расхода) за каждый шаг дискретизации является избыточным для большинства практических применений. Как следствие, применение этого высокопроизводительного способа приводит к усложнению и удорожанию измерительной схемы и расходомера в целом, при этом частота выдачи результата измерения существенно превосходит практические потребности.
В книге [1] приведен также метод эллипса ([1], с. 52). Этот метод относится к группе осциллографических методов измерения фазового сдвига. Данный метод наиболее близок к рассматриваемому изобретению, поэтому он является прототипом. Согласно этому методу, для определения фазового сдвига между двумя сигналами используется осциллограф, причем один из сигналов подается на вход канала горизонтального отклонения, а другой - на вход канала вертикального отклонения. В результате на экране осциллографа наблюдают фигуру Лиссажу в виде эллипса. Геометрические параметры эллипса зависят от амплитуд анализируемых сигналов и от угла сдвига фаз между ними. Искомый угол сдвига фаз определяют по известным формулам ([1], с. 52), исходя из параметров фигуры Лиссажу (эллипса), наблюдаемой на экране осциллографа. К преимуществам данного метода измерения угла фазового сдвига относится простота и независимость точности метода от частоты сигналов, поскольку анализируют взаимное соотношение сигналов без переменной времени. К недостаткам данного метода относится невозможность его автоматизации, поскольку для его осуществления требуется участие оператора. Другие недостатки данного метода - низкая точность при измерении малого сдвига фаз сигналов, а также низкая точность при наличии шума сигналов, поскольку для расчета сдвига фаз используют геометрические координаты отдельных точек фигуры Лиссажу, имеющие значительные случайные отклонения вследствие зашумленности анализируемых сигналов. Предлагаемое изобретение позволяет преодолеть указанные недостатки данного метода при сохранении его преимуществ. Раскрытие сущности изобретения.
Рассмотрим сущность способа. Заданы два гармонических сигнала тока или напряжения равной частоты и амплитуды, имеющие взаимный сдвиг фаз Δϕ:


где AS - амплитуда сигналов, мА или мВ;
t - время, с;
ω - угловая частота, с-1;
Δϕ - сдвиг фаз, рад.
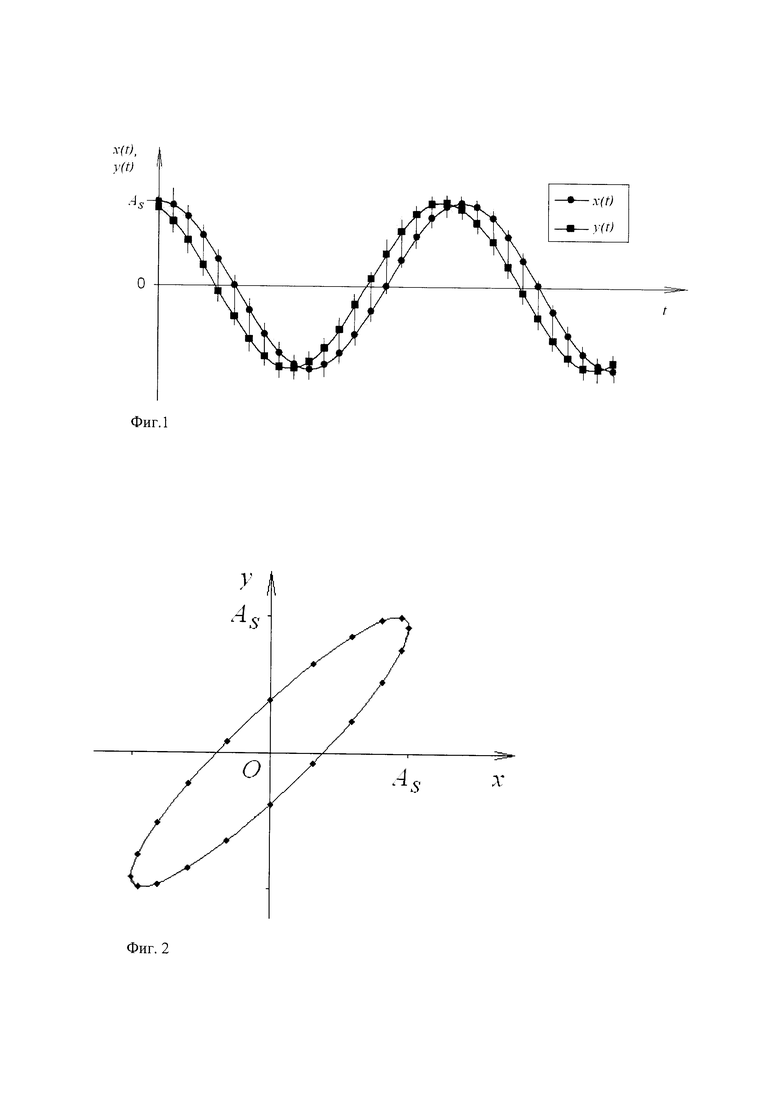
Сигналы регистрируют аналого-цифровым преобразователем в виде периодических отсчетов xi=f(ti) и yi=f(ti) для моментов времени ti. График изменения сигналов во времени показан на рисунке фиг. 1. В виде маркеров показаны значения дискретных отсчетов сигналов x(t) и y(t), полученные при аналого-цифровом преобразовании. Для наглядности изложения случайной составляющей шумов пока пренебрегаем. Требуется найти сдвиг фаз Δϕ.
Для минимизации погрешности, связанной с неопределенностью измерения моментов времени отсчетов ti, исключим время из рассмотрения сигналов x(t) и y(t). Будем рассматривать фигуры Лиссажу, образующиеся на экране осциллографа при подключении сигналов x(t) и y(t) на входы каналов горизонтального и вертикального отклонения соответственно, как указано в методе ([1], с. 52). Сигнал x(t), подаваемый на вход горизонтального отклонения, принимаем в качестве опорного, то есть относительно него будем определять сдвиг фаз Δϕ. В результате на экране осциллографа можно наблюдать фигуру эллипса, главные оси которого наклонены к горизонтальной оси экрана. Вид наблюдаемой фигуры при отсутствии шумов приведен на рисунке фиг. 2. В процессе прохождения сигналов x(t), y(t) точка, соответствующая мгновенному значению этих сигналов в каждый момент времени, движется вдоль линии эллипса либо по часовой стрелке, либо против часовой стрелки в зависимости от знака сдвига фаз сигналов. Таким образом, путем исключения параметра времени вместо двух исходных функций x(t) и y(t) получаем одну функцию y=f(x).
Как указано в методе ([1], с. 52), искомый сдвиг фаз однозначно определяется геометрическими параметрами полученной фигуры, изображающей график функции y=f(x). Однако, для увеличения точности, для создания возможности автоматизации процесса измерения, для уменьшения погрешности, вызванной шумами сигналов, проведем усовершенствование метода, указанного в ([1], с. 52). Вместо определения координат граничных точек фигуры и координат точек пересечения графика у=f(х) с осями координат и расчета по этим координатам угла сдвига фаз определяем площадь фигуры Лиссажу, с учетом знака, соответствующего направлению обхода контура фигуры. Полученная площадь пропорциональна искомому сдвигу фаз, знак, соответствующий направлению обхода, соответствует знаку искомого сдвига фаз, а коэффициент пропорциональности между площадью и сдвигом фаз может быть получен либо при градуировке, либо расчетным путем. Таким образом, основная идея предлагаемого способа заключается в исключении параметра времени из анализа сигналов и в определении площади фигуры Лиссажу, очерчиваемой на координатной плоскости точкой, координаты которой в каждый момент времени пропорциональны мгновенному значению анализируемых сигналов. Вместо использования осциллографа в предлагаемом способе используем значения одновременных дискретных отсчетов анализируемых сигналов, полученные при аналого-цифровом преобразовании. Поскольку при аналого-цифровом преобразовании непрерывный сигнал преобразуется к множеству дискретных отсчетов, то будем определять площадь фигуры, равновеликой площади указанной фигуры Лиссажу или ее части. Особенностью предлагаемого способа является отсутствие высоких требований к точности измерения отсчетов времени и отсутствие требований к фильтрации шума исходных сигналов, а также вычисление среднего сдвига фаз для одного или нескольких периодов колебаний исходных сигналов.
Изложим последовательность действий описываемого способа.
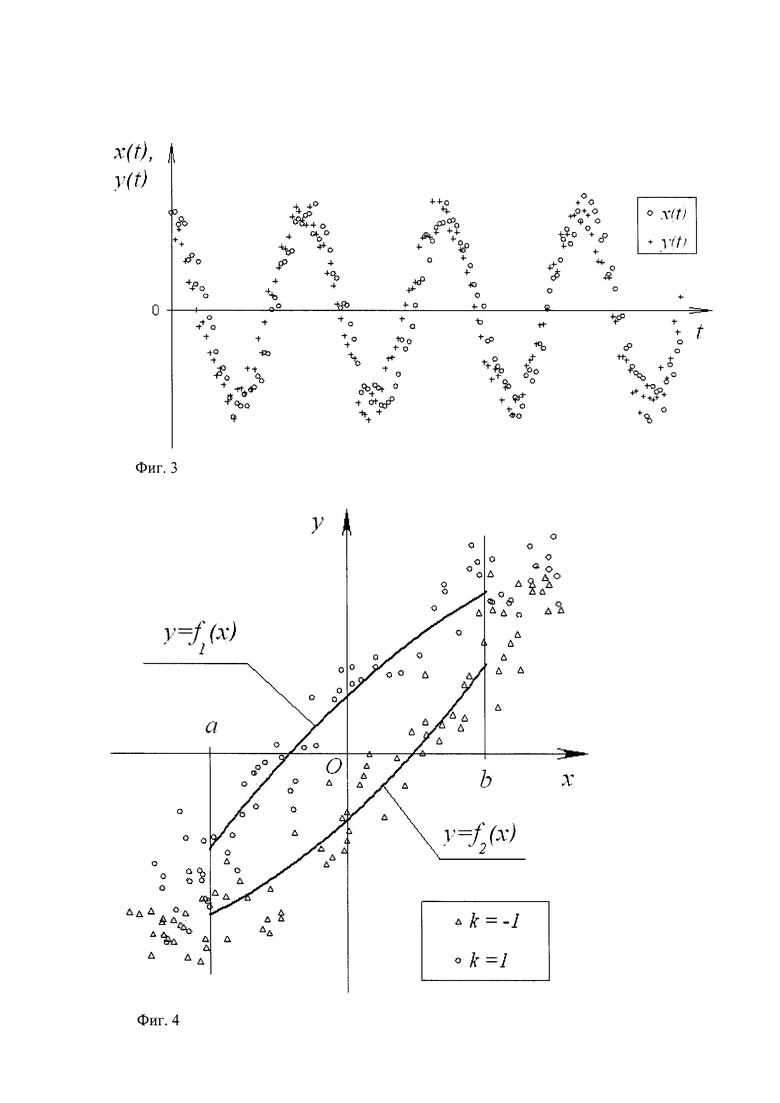
Дальнейшее изложение будем вести для сигналов, имеющих, помимо основной гармонической составляющей, также случайную составляющую и шум. Вид сигналов с наличием случайной составляющей и шума представлен на рисунке фиг. 3.
Последовательность действий заключается в следующих операциях.
1. Выполняют аналого-цифровое преобразование двух сигналов, получают множество дискретных одновременных отсчетов сигналов xi(ti) и yi(ti) за время не менее одного периода колебаний одного из сигналов (фиг. 3). Объем указанного множества, то есть ширина окна сбора данных, влияет на степень усреднения результата измерения. При необходимости получения более сглаженного результата измерения следует увеличить ширину окна до нескольких периодов колебаний одного из сигналов, а при необходимости получить результат с более резкой реакцией на изменения следует уменьшить ширину окна, но до величины, соответствующей не менее чем одному периоду колебаний одного из сигналов.
2. При выполнении аналого-цифрового преобразования каждый дискретный отсчет с индексом i маркируют специальной меткой, например ki=1 или ki=-1 (минус 1), в зависимости от того, принадлежит ли данный отсчет участку возрастания или участку убывания одного из сигналов, например сигналах x(t):
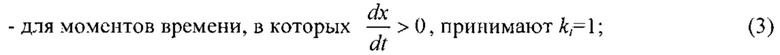
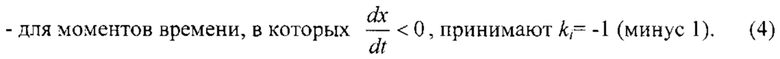
В результате все точки множества дискретных одновременных отсчетов делятся на две группы - имеющие значение метки k=1 и имеющие значение метки k=-1 (минус 1). То или иное значение метки характеризует принадлежность каждой из точек верхней либо нижней ветви фигуры Лиссажу.
3. Множество дискретных одновременных отсчетов рассматривают в качестве координат точек на координатной плоскости Оху, оси координат которой изображают анализируемые сигналы. Вследствие того, что значения отсчетов получены дискретно в последовательные моменты времени в результате аналого-цифрового преобразования, множество дискретных одновременных отсчетов рассматривают как облако точек на плоскости Оху, причем форма этого облака представляет собой при отсутствии шумов и при равной амплитуде сигналов эллипс, главные оси которого наклонены к осям координат Оху на 45 градусов. Однако, вследствие малой величины сдвига фаз сигналов расходомера Кориолиса, указанный эллипс оказывается сильно сжатым вдоль одной из главных осей, в результате точки облака точек занимают область, весьма близкую к отрезку прямой, наклоненной под углом 45 градусов к осям координат. Далее, вследствие наличия случайной составляющей погрешности и шума сигналов x(t), y(t), имеется рассеяние координат xi, yi для каждого дискретного отсчета, поэтому облако точек имеет рассеяние, искажающее форму эллипса. Вид облака точек при наличии шума сигналов показан на рисунке фиг. 4. Каждая из точек указанного облака помимо присущих ей координат xi, yi, представляющих собой значения дискретных отсчетов сигналов xi(ti) и yi(ti), несет присущее ей значение метки ki=1 или ki=-1. На рисунке фиг. 4 точки с разными значениями меток показаны в виде маркеров различного вида.
4. Выбирают вид функций, описывающих границы фигуры, которая будет повторять форму облака точек или его части. Границы указанной фигуры должны очерчивать форму облака или выбранной части с наименьшей погрешностью, причем одна из границ проходит через область облака с точками, имеющими метку ki=1, а другая - через область с точками, имеющими метку ki=-1. Например, может быть выбран вид фигуры, в которой две наклонные границы описываются полиномами второго порядка y(x)=f1(x) и y(x)=f2(x), а две вертикальные границы очерчиваются прямыми, проведенными через заранее выбранные точки с абсциссами а и b (фиг. 4).
5. Для каждой из неизвестных функций выбранного вида, описывающих границы фигуры, выполняют одним из известных способов процедуру наилучшего приближения функций, с тем, чтобы получить функции, описывающие с наименьшей погрешностью форму облака точек или его части. Например, может быть выбран метод наименьших квадратов для определения неизвестных коэффициентов функций (в частности, полиномов второго порядка) f1(x) и f2(x). При определении функций наилучшего приближения включают в расчет для одной из функций точки, имеющие значение метки ki=1, для другой функции - точки, имеющие значение метки ki=-1 (фиг. 4). В зависимости от того, повторяет ли фигура форму всего облака точек или его части, включают в расчет или все точки облака с соответствующим значением метки, или те точки, абсциссы которых лежат внутри выбранной области [а; b].
6. Определяют площадь фигуры одним из известных способов. Например, в случае, если в качестве функций выбран полином второго порядка, для определения площади может быть выбран способ вычисления определенного интеграла с пределами интегрирования, соответствующими абсциссам крайних точек облака или выбранной части облака точек. В этом случае площадь фигуры вычисляют по формуле

где S - площадь фигуры;
а, b - пределы интегрирования.
7. Определяют искомый сдвиг фаз сигналов по полученному значению площади S, причем знак сдвига фаз соответствует знаку вычисленного значения площади. Полученная площадь S, равная разности двух указанных определенных интегралов, является однозначной мерой искомой разности фаз сигналов расходомера Кориолиса, а следовательно, и однозначной мерой массового расхода. Сдвиг фаз и массовый расход вычисляют по формулам


где kS, kϕ - коэффициенты;
K=kS⋅kϕ - произведение коэффициентов.
Коэффициенты kS, kϕ или их произведение K определяют при градуировке прибора.
Описанный способ обеспечивает получение нескольких технических результатов. Первый результат способа - это обеспечение возможности автоматизации измерений за счет аналого-цифрового преобразования. Второй результат способа - увеличение точности измерений углового сдвига фаз при отсутствии высоких требований к точности измерения отсчетов времени. Этот результат достигается за счет исключения параметра времени из процесса определения сдвига фаз. Третий результат способа - увеличение точности измерения при минимизации требований к фильтрации сигнала. Этот результат достигается за счет определения сдвига фаз через площадь фигуры. Четвертый результат - это сохранение точности измерения при изменении частоты колебаний, вызванных флуктуациями расхода или плотности жидкости или наличием газовой или твердой фазы в потоке. Этот результат обусловлен также исключением параметра времени из процесса определения сдвига фаз. Пятый результат - увеличение экономической эффективности обработки. Этот результат достигается за счет получения усредненного результата измерения для выборки данных, соответствующей ширине окна сбора данных, причем ширину окна сбора данных целесообразно выбирать, исходя из условий практической задачи, в которой будет применяться расходомер, работающий по описанному способу. Как следствие, для большинства практических применений, где не требуется высокая частота выдачи результата измерения, применение способа приводит к снижению требований по производительности и к снижению стоимости электронной аппаратуры и расходомера в целом.
В частных случаях применения расходомера возможны ситуации, когда амплитуда колебаний сигналов является величиной переменной - например, при изменении плотности измеряемой жидкости. В этих случаях требуется для обеспечения точности измерения сдвига фаз учитывать также и амплитуду сигналов. Для этого в описанный способ включают дополнительные этапы обработки, согласно пункту 2 формулы изобретения. Опишем эти дополнительные этапы обработки.
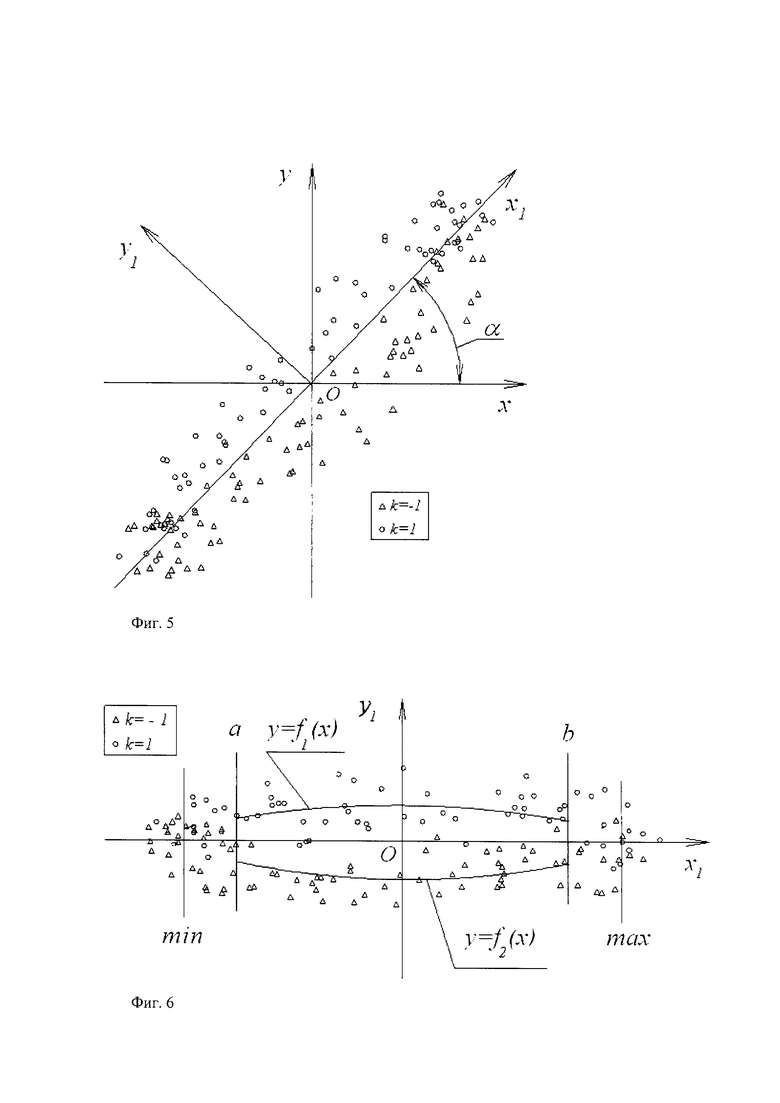
1. После выполнения аналого-цифрового преобразования и получения множества дискретных одновременных отсчетов и изображающего его облака точек выполняют линейное преобразование координат точек, аналогичное повороту осей координат. Вводят систему координат Ox1y1, повернутую относительно системы Оху на угол 45 градусов, как показано на рисунке фиг. 5. Определяют для каждой точки облака точек (xi, yi, ki) координаты в системе координат Ox1y1 по формулам


где α=45°.
Параметр ki не изменяется.
Для величины угла α=45° существует возможность упрощения выражений (8) и (9). Вынося множитель 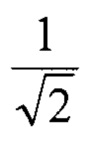 в итоговый коэффициент преобразования, приходим к выражению
в итоговый коэффициент преобразования, приходим к выражению


Вид облака точек в повернутой системе координат показан на рисунке фиг. 6.
2. Определяют тем или иным известным способом средние значения минимумов и максимумов координат точек вдоль повернутой координатной оси Ох1. В частности, среднее значение минимумов может быть вычислено по формуле

где min - среднее значение минимумов;
j - индекс суммирования по точкам, удовлетворяющим условию 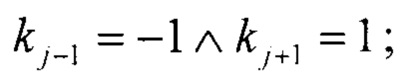
L1 - количество точек, удовлетворяющих условию 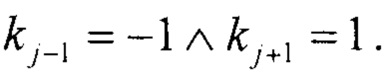
Суммирование проводят для всех точек облака точек, удовлетворяющих условию 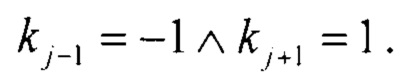 Формула (12) означает, что проводят вычисление средней координаты х1 таких точек, для которых удовлетворяется условие локального минимума
Формула (12) означает, что проводят вычисление средней координаты х1 таких точек, для которых удовлетворяется условие локального минимума 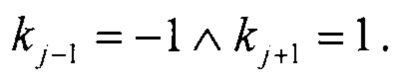
Аналогично, среднее значение максимумов может быть вычислено по формуле

где max - среднее значение максимумов;
j - индекс суммирования по точкам, удовлетворяющим условию 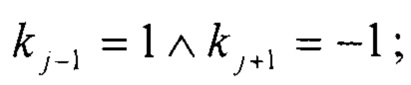
L2 - количество точек, удовлетворяющих условию 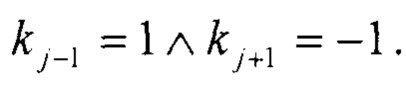
Суммирование проводят для всех точек облака точек, удовлетворяющих условию 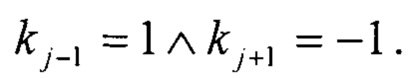 Формула (13) означает, что проводят вычисление средней координаты x1 таких точек, для которых удовлетворяется условие локального максимума
Формула (13) означает, что проводят вычисление средней координаты x1 таких точек, для которых удовлетворяется условие локального максимума 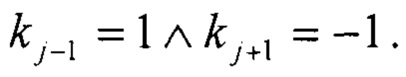
3. Определяют границы а и b анализируемого участка облака точек вдоль координатной оси Ох1, повернутой относительно оси Ох на 45 градусов. Границы анализируемого участка определяют таким образом, чтобы максимально включить в расчет среднюю часть облака точек, поскольку она является наиболее информативной с точки зрения вычисления площади фигуры, соответствующей искомому углу сдвига фаз. Краевые зоны облака точек, соответствующие экстремумам сигналов x(t), y(t), целесообразно исключить из анализируемого участка, с целью снижения погрешности результата и с целью упрощения дальнейшего подбора аппроксимирующей функции. В частности, положение границ а и b может быть определено через средние значения минимумов min и максимумов max. Примерное расположение границ анализируемого участка показано на рисунке фиг. 6.
4. Выбирают вид функции наилучшего приближения y=f(x), которая устанавливает зависимость между координатами x1i и y1i облака точек на анализируемом участке. В частности, в качестве функции наилучшего приближения может быть выбран полином второго порядка.
5. Выполняют одним из известных способов для каждой группы точек, принадлежащих верхней и нижней ветви фигуры Лиссажу, то есть имеющей одинаковое значение метки процедуру наилучшего приближения функций для функции выбранного вида y=f(x). В частности, может быть использован известный метод наименьших квадратов. При определении функции наилучшего приближения включают в расчет те точки, абсциссы которых лежат внутри области [а; b]. Находят численные значения коэффициентов функции, таким образом, находят две функции:
- для точек, имеющих значение метки ki=1 (верхняя ветвь) - функция f1(x);
- для точек, имеющих значение метки ki=-1 (нижняя ветвь) - функция f2(х). Примерный вид графиков функций f1(x) и f2(x) показан на рисунке фиг. 6.
6. Вычисляют значения определенных интегралов функций f1(x) и f2(х) на анализируемом участке и их разность, соответствующую площади S фигуры, повторяющей форму облака точек или его части:

7. Вычисляют сдвиг фаз сигналов с использованием полученных значений площади S, средних значений минимумов min и максимумов max. В частности, сдвиг фаз может быть вычислен по формуле

где Δϕ - искомый сдвиг фаз;
kS - градуировочный коэффициент, определяемый при градуировке.
Краткое описание чертежей.
Фиг. 1 - вид сигналов расходомера Кориолиса при отсутствии случайных погрешностей и шума. Значения дискретных одновременных отсчетов показаны в виде маркеров, имеющих одинаковое значение момента времени отсчета для двух сигналов.
Фиг. 2 - вид фигуры Лиссажу, построенной на сигналах расходомера Кориолиса.
Фиг. 3 - вид сигналов расходомера Кориолиса при наличии случайной составляющей и шума. Значения дискретных отсчетов показаны в виде маркеров.
Фиг. 4 - вид облака точек дискретных одновременных отсчетов сигналов расходомера Кориолиса. Показаны границы фигуры, повторяющей форму части облака точек.
Фиг. 5 - вид облака точек дискретных одновременных отсчетов сигналов расходомера Кориолиса. Показана новая система координат, повернутая относительно исходной системы координат на угол α.
Фиг. 6 - вид облака точек дискретных одновременных отсчетов сигналов расходомера Кориолиса в повернутой системе координат. Показаны границы фигуры, повторяющей форму части облака точек.
Осуществление изобретения.
Осуществление изобретения выполняют средствами электронно-вычислительной техники, входящими в состав расходомера, таким образом, чтобы выполнялись этапы обработки, приведенные в раскрытии изобретения.
Для осуществления изобретения по пункту 1 формулы изобретения выполняют следующие этапы обработки.
1. Выполняют аналого-цифровое преобразование сигналов тока или напряжения датчиков положения трубок расходомера. Путем выполнения одновременных (синхронных) опросов датчиков сигналов x(t), y(t) формируют массив отсчетов А=[xi, yi, ki] для i=1…N, где N - глубина (емкость) массива, ki - значение метки отсчета с индексом i. Емкость массива должна быть такой, чтобы заполнение всего массива происходило с течением времени, соответствующим ширине окна сбора данных, при этом ширину окна сбора данных выбирают такой, чтобы она соответствовала необходимой частоте выдачи результата измерения. Таким образом, массив А представляет собой одномерный массив векторов 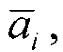 каждый из которых имеет компоненты, равные мгновенным значениям отсчетов xi, yi и значению метки ki. После заполнения массива А индекс записи массива i обнуляется, выполняется запись новых отсчетов поверх наиболее старых. Формируется круговая схема заполнения массива А по принципу «первый вошел, первый вышел». Все векторы
каждый из которых имеет компоненты, равные мгновенным значениям отсчетов xi, yi и значению метки ki. После заполнения массива А индекс записи массива i обнуляется, выполняется запись новых отсчетов поверх наиболее старых. Формируется круговая схема заполнения массива А по принципу «первый вошел, первый вышел». Все векторы 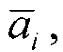 содержащиеся в массиве А, рассматривают как координаты точек на плоскости Оху, составляющие облако точек и снабженные метками ki. Полученный массив соответствует фигуре Лиссажу, которая может быть построена на координатной плоскости Оху, оси координат которой соответствуют значениям анализируемых сигналов, а каждая точка фигуры соответствует определенному вектору массива А и изображает значения дискретных отсчетов сигналов в определенные моменты времени.
содержащиеся в массиве А, рассматривают как координаты точек на плоскости Оху, составляющие облако точек и снабженные метками ki. Полученный массив соответствует фигуре Лиссажу, которая может быть построена на координатной плоскости Оху, оси координат которой соответствуют значениям анализируемых сигналов, а каждая точка фигуры соответствует определенному вектору массива А и изображает значения дискретных отсчетов сигналов в определенные моменты времени.
2. При заполнении массива отсчетов А значения меток отсчетов определяют по формулам (3) и (4).
3. Выполняют методом наименьших квадратов процедуру наилучшего приближения для функций заранее выбранного вида, например для полиномов второго порядка, определяют коэффициенты полиномов. В случае использования фигуры, повторяющей форму всего облака точек, определяют функции наилучшего приближения для всех точек облака, имеющих соответствующие значения метки ki. В случае использования фигуры, повторяющей форму некоторой части облака точек, назначают границы а, b этой части облака, как показано на рисунке фиг. 4, затем определяют функции наилучшего приближения для тех точек облака, которые попадают в интервал, определенный указанными границами, и имеют соответствующее значение метки.
4. Вычисляют определенные интегралы и площадь по формуле (5). В случае использования фигуры, повторяющей форму всего облака, пределы интегрирования а, b принимают в соответствии с абсциссами крайних точек облака точек. В случае использования фигуры, повторяющей форму части облака точек, пределы интегрирования а, b принимают равными назначенным выше границам а, b.
5. Вычисляют сдвиг фаз и массовый расход по формулам (6) и (7). В результате полученные значения площади S, сдвига фаз Δϕ и массового расхода Qm являются усредненными значениями, полученными при обработке множества отсчетов исходных сигналов, содержащихся в исходном массиве А[xi, yi, ki].
6. Повторяют приведенные этапы обработки для выполнения измерений сдвига фаз и массового расхода в последующие моменты времени с той частотой выдачи результата, которая необходима по условиям применения расходомера.
Для осуществления изобретения по пункту 2 формулы изобретения выполняют следующие этапы обработки.
1. Выполняют аналого-цифровое преобразование сигналов тока или напряжения датчиков положения трубок расходомера. Путем выполнения одновременных (синхронных) опросов датчиков сигналов x(t), y(t) формируют массив отсчетов А=[xi, yi, ki] для i=1…N, где N - глубина (емкость) массива, ki - значение метки отсчета с индексом i. Емкость массива должна быть такой, чтобы заполнение всего массива происходило с течением времени, соответствующим ширине окна сбора данных, при этом ширину окна сбора данных выбирают такой, чтобы она соответствовала необходимой частоте выдачи результата измерения. Таким образом, массив А представляет собой одномерный массив векторов 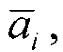 каждый из которых имеет компоненты, равные мгновенным значениям отсчетов xi, yi и значению метки ki. После заполнения массива А индекс записи массива i обнуляется, выполняется запись новых отсчетов поверх наиболее старых. Формируется круговая схема заполнения массива А по принципу «первый вошел, первый вышел». Все векторы
каждый из которых имеет компоненты, равные мгновенным значениям отсчетов xi, yi и значению метки ki. После заполнения массива А индекс записи массива i обнуляется, выполняется запись новых отсчетов поверх наиболее старых. Формируется круговая схема заполнения массива А по принципу «первый вошел, первый вышел». Все векторы 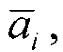 содержащиеся в массиве А, рассматривают как координаты точек на плоскости Оху, составляющие облако точек и снабженные метками Полученный массив соответствует фигуре Лиссажу, которая может быть построена на координатной плоскости Оху, оси координат которой соответствуют значениям анализируемых сигналов, а каждая точка фигуры соответствует определенному вектору массива А и изображает значения дискретных отсчетов сигналов в определенные моменты времени.
содержащиеся в массиве А, рассматривают как координаты точек на плоскости Оху, составляющие облако точек и снабженные метками Полученный массив соответствует фигуре Лиссажу, которая может быть построена на координатной плоскости Оху, оси координат которой соответствуют значениям анализируемых сигналов, а каждая точка фигуры соответствует определенному вектору массива А и изображает значения дискретных отсчетов сигналов в определенные моменты времени.
2. При заполнении массива отсчетов А значения меток отсчетов определяют по формулам (3) и (4).
3. Выполняют линейное преобразование координат точек, аналогичное повороту осей координат на 45 градусов. Линейное преобразование координат выполняют по формулам (10), (11). Полученные новые значения координат (xi, yi, ki) заносят в другой массив А1(x1i, y1i, ki). Дальнейшие преобразования выполняют над данными массива A1.
4. Определяют средние значения минимумов и максимумов координат точек массива A1 вдоль повернутой координатной оси Ох1 по формулам (12) и (13).
5. Определяют границы а и b анализируемого участка. Для фигуры, повторяющей форму всего облака, границы назначают равными абсциссам крайних точек облака точек. Для фигуры, повторяющей форму части облака точек, границы определяют, исходя из средних значений минимумов и максимумов
6. Выполняют методом наименьших квадратов процедуру наилучшего приближения на участке [а; b] для функций заранее выбранного вида, например, для полиномов второго порядка. В расчет каждой функции включают точки, имеющие одинаковое значение метки ki, и попадающие в границы анализируемого участка [а; b].
7. Вычисляют определенные интегралы и площадь S по формуле (14).
8. Вычисляют сдвиг фаз сигналов и массовый расход по формулам (15) и (7).
9. Повторяют приведенные этапы обработки для выполнения измерений сдвига фаз и массового расхода в последующие моменты времени с той частотой выдачи результата, которая необходима по условиям применения расходомера.
Перечень документов.
1. Электронные средства измерений электрических величин: [учеб. пособие] / А.С. Волегов, Д.С. Незнахин, Е.А. Степанова; М-во образования и науки Рос. Федерации, Урал. федер. ун-т. - Екатеринбург: Изд-во Урал. ун-та, 2014. - 104 с.
2. Патент RU 2159410 С2, МПК G01F 1/84, опубликован 20.11.2000. Устройство и способ обработки сигнала для определения фазового сдвига.
3. Патент RU 2456548 С2, МПК G01F 1/84, опубликован 20.07.2012. Способ обработки сигналов, устройство обработки сигналов и Кориолисов расходомер.
4. Патент RU 2371678 С2, МПК G01F 1/84, опубликован 27.10.2009. Высокоскоростная оценка частоты и фазы расходомеров.
5. Патент RU 2707576 С1, МПК G01F 1/84, опубликован 28.11.2019. Способ вычисления текущей разности фаз и частоты сигналов кориолисовых расходомеров (варианты). А.С. Семенов, О.Л. Ибряева.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДИ РЕЛЬЕФА | 2004 |
|
RU2255357C1 |
| Способ вычисления текущей разности фаз и частоты сигналов кориолисовых расходомеров (варианты) | 2019 |
|
RU2707576C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО ОБНАРУЖЕНИЯ ПЕРИОДИЧНОСТИ В ЦИФРОВОМ ПОТОКЕ | 2006 |
|
RU2308811C1 |
| Способ вычисления текущей разности фаз и частоты сигналов кориолисовых расходомеров | 2017 |
|
RU2687803C1 |
| СПОСОБ РАННЕЙ ЛЕСОПАТОЛОГИЧЕСКОЙ ДИАГНОСТИКИ | 2010 |
|
RU2436291C1 |
| СПОСОБ И УСТРОЙСТВО ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2005 |
|
RU2283505C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОЩАДИ РЕЛЬЕФА | 2004 |
|
RU2251075C1 |
| СПОСОБ ИЗМЕРЕНИЯ КООРДИНАТ МИКРОСЕЙСМИЧЕСКИХ ИСТОЧНИКОВ ПРИ ВОЗДЕЙСТВИИ ПОМЕХ | 2011 |
|
RU2451308C1 |
| СПОСОБ ПЕЛЕНГОВАНИЯ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2015 |
|
RU2603356C1 |
| Способ контроля положения и дыхания пациента с применением набора инфракрасных датчиков глубины | 2019 |
|
RU2732735C1 |
Изобретение относится к способу измерения сдвига фаз сигналов расходомера Кориолиса. Для определения сдвига фаз выполняют аналого-цифровое преобразование сигналов тока или напряжения расходомера, получают значения одновременных дискретных отсчетов сигналов в последовательные моменты времени. Полученные значения рассматривают как точки на плоскости в системе координат, оси которой соответствуют двум анализируемым сигналам, а множество таких значений, полученных за время не менее одного периода колебаний одного из сигналов, рассматривают как облако точек на указанной плоскости. Определяют фигуру, границы которой с наименьшей погрешностью повторяют форму указанного облака точек или его части, причем указанные границы определяют с учетом принадлежности того или иного дискретного отсчета участку возрастания или участку убывания одного из сигналов. Определяют площадь указанной фигуры, затем на основе полученной площади определяют сдвиг фаз. Технический результат способа - обеспечение автоматизации измерений, увеличение точности измерений при минимизации требований к точности измерения времени и к фильтрации сигнала, сохранение точности измерения при изменении частоты колебаний, увеличение экономической эффективности обработки. 1 з.п. ф-лы, 6 ил.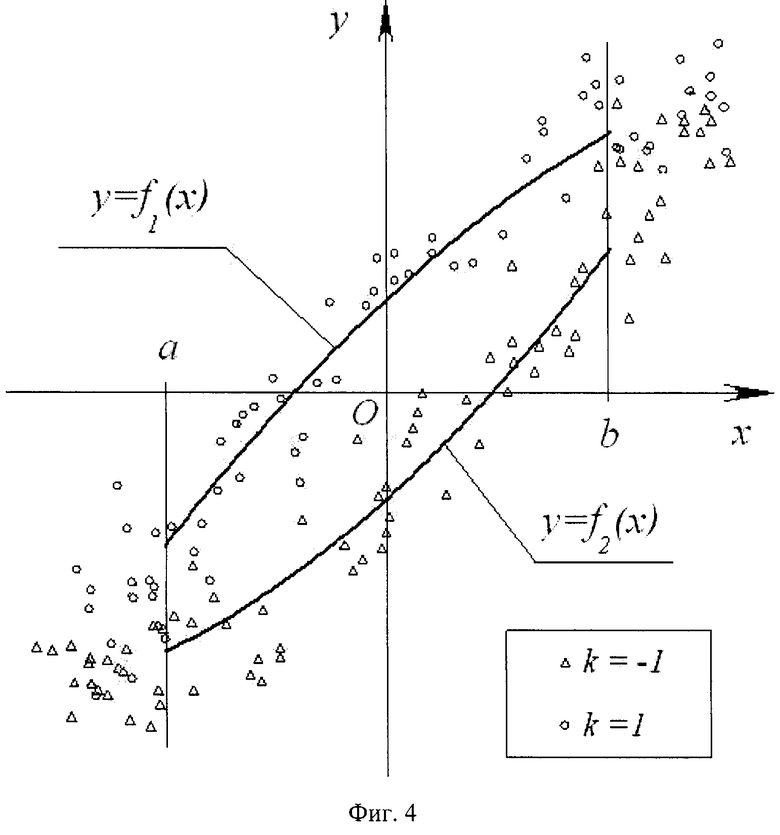
1. Способ измерения сдвига фаз сигналов расходомера Кориолиса, включающий в себя определение параметров фигуры, получаемой на координатной плоскости при отображении одного из сигналов на одной координатной оси, а другого сигнала на второй координатной оси, отличающийся тем, что анализируемые сигналы подвергают аналого-цифровому преобразованию, получают значения дискретных одновременных отсчетов двух сигналов за время не менее одного периода колебаний одного из сигналов, полученные значения отсчетов рассматривают в качестве координат точек на плоскости, оси координат которой изображают анализируемые сигналы, а множество дискретных одновременных отсчетов двух сигналов за время не менее одного периода колебаний одного из сигналов рассматривают как облако точек на указанной плоскости, далее одним из известных способов определяют фигуру, границы которой с наименьшей погрешностью повторяют форму указанного облака точек или его части, причем указанные границы определяют с учетом принадлежности того или иного дискретного отсчета участку возрастания или участку убывания одного из сигналов, затем вычисляют одним из известных способов площадь указанной фигуры, далее на основе полученной площади определяют сдвиг фаз сигналов.
2. Способ измерения сдвига фаз по п. 1, отличающийся тем, что для снижения погрешности измерения и увеличения эффективности обработки в случае измерения сигналов с переменной амплитудой в него дополнительно включают этапы обработки, а именно выполняют линейное преобразование координат облака точек, аналогичное повороту системы координат на 45 градусов, определяют средние значения максимумов и минимумов координат облака точек вдоль повернутой на 45 градусов координатной оси, на основе полученной согласно п. 1 площади фигуры и на основе средних значений максимумов и минимумов координат определяют искомый сдвиг фаз сигналов.
| Способ вычисления текущей разности фаз и частоты сигналов кориолисовых расходомеров (варианты) | 2019 |
|
RU2707576C1 |
| US 6748813 B1, 15.06.2004 | |||
| DE 69607756 T2, 10.08.2000 | |||
| Способ вычисления текущей разности фаз и частоты сигналов кориолисовых расходомеров (варианты) | 2019 |
|
RU2707576C1 |
| Электронные средства измерений электрических величин : учебное пособие / А | |||
| С | |||
| Волегов, Д | |||
| С | |||
| Незнахин, Е | |||
| А | |||
| Степанова | |||
| — Екатеринбург : УрФУ, 2014 | |||
| Счетная таблица | 1919 |
|
SU104A1 |
Авторы
Даты
2021-12-16—Публикация
2021-01-11—Подача