Область техники
Изобретение относится к компьютерным системам, основанным на биологических моделях, а именно к моделированию программно-аппаратной реализации (активных) биологических нейронов и может быть использовано в нейрокомпьютерах, технических системах на основе нейронных сетей, распознании образов, анализе и обработке изображений, и искусственном интеллекте.
Уровень техники
История искусственных и математических моделей нейронов началась с изобретения искусственного нейрона МакКаллока-Питса, который явился исторической вехой в нейроинформатике [1]. Нейрон МакКаллока-Питса или формальный нейрон-базовый элемент искусственных нейронных сетей, применение которых привело к бурному развитию направления нейроинформатики.
Формальный нейрон - это абстрактный логический элемент, в котором отражены лишь те свойства реального нейрона, которые связаны с переработкой информации, блок-схема которого показана на фиг. 1, где x1, x2, …, xN - входные сигналы, заданные в виде бинарных кодов; w1, w2, wN - весовые коэффициенты; ∑ - сумматор; F - пороговая функция; U - выходной сигнал.
Математически искусственный нейрон обычно представляется как некоторая нелинейная функция от линейной комбинации всех входных сигналов. Полученный результат подается на пороговую функцию или функцию активации, обеспечивающую единственный выход нейрона. Таким образом, линейная комбинация входных сигналов с определенными весами подается на вход нейрона. На входе сумматора получают сигнал S

где x=(xl, …, xN), w=wl, …, wN, ( ,
,  ) - скалярное произведение векторов
) - скалярное произведение векторов  ,
,  ; N - число входов нейрона. После прохождения порогового устройства и преобразования пороговой функцией F(S) с порогом θ получают на выходе
; N - число входов нейрона. После прохождения порогового устройства и преобразования пороговой функцией F(S) с порогом θ получают на выходе
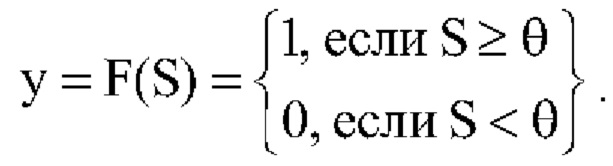
К основным компонентам формального нейрона относятся перемножители, сумматор, пороговое устройство, реализующее функцию активации нейрона, которая может иметь различную форму [1-2].
Известны недостатки искусственного нейрона МакКаллока-Питса. В работах [3-5] показано, что суммация стимулов на нейроне не имеет биологического смысла, кроме того, нейрон не является проводящей единицей, а является активным элементом. В противовес суммации, для преодоления недостатков искусственного нейрона МакКаллока-Питса предлагается придерживаться активной парадигмы поведения нейрона, согласно которой «нейрон обеспечивает «потребности» своего метаболизма, объединяясь с другими элементами организма в функциональную систему и формирование подобных объединений выступает как метаболическая кооперация нейронов» [4].
Искусственный нейрон МакКаллока-Питса неадекватен биологическому нейрону ввиду того, что 1) основан на суммации приходящих сигналов; 2) рассматривается как проводящий элемент; 3) в искусственных нейронных сетях известна ошибка «катастрофическое забывание», которая относится к сложности обучения системы новым навыкам без потери ранее изученных функций, например, если сеть, первоначально обученная различать фотографии собак и кошек, затем переучивается, чтобы различать лошадей, она теряет свои прежние способности; 4) результат работы искусственного нейрона и нейронных сетей, основанных на таких нейронах, является «черным ящиком» и необъясним, что делает невозможным их применение в таких ответственных областях как медицина, военные приложения и финансы. Требование объяснимости принимаемого решения системами искусственного интеллекта является в настоящее время одним из ключевых. Об этом, в частности, говорится в УКАЗЕ ПРЕЗИДЕНТА РОССИЙСКОЙ ФЕДЕРАЦИИ (№490) «О развитии искусственного интеллекта в Российской Федерации» в разделе III «Основные принципы развития и использования технологий искусственного интеллекта …, соблюдение которых обязательно для реализации настоящей Стратегии, являются … в) прозрачность: объяснимость работы искусственного интеллекта и процесса достижения им результатов».
Ранее в патентах [6-9] отмечалась важная роль дендритов в процессе получения выходного сигнала. Отмечалось, что в реальных нейронах формирование паттернов-синдромов происходит естественным образом за счет подкармливания работающих дендритов и уничтожения неработающих дендритов путем прекращения питания. Подкармливание дендритов происходит при прохождении по ним электрических импульсов. При этом в дендрит поступают строительные материалы в виде белков, АТФ, обеспечивающих дендриты энергетическими ресурсами. Если электрические нервные импульсы не проходят по дендриту, то питание не подается, и он отмирает [6-9]. Делается вывод об адаптации к входной информации не за счет весовых коэффициентов, а за счет кластеризации дендритов, изменения их количества и качества. В результате автором этих патентов было введено понятие избирательного нейрона: в каждом нейроне создаются кластеры специализированных каналов связи, настроенные на соответствующие характеристические кодовые комбинации входных сигналов. Однако в этих работах и патентах кодовые комбинации распознаваемых классов предполагаются известными, что обычно не верно. Постановка задачи классификации не предполагает знания кодовых комбинаций классов.
В дальнейших работах были более точно описаны возможности дендритов и их узлов в обработке поступающих сигналов и были введены понятия дендритной пластичности и дендритных вычислений [10-14], которые позволяют определить автоматическое формирование кодов-синдромов, которого нет в патентах [6-9].
В качестве ближайшего аналога выбран нейрон, моделирующий свойства реального нейрона, по патенту РФ на изобретение №2597495 (МПК G06N 3/06, опубликован 10.09.2016). Известная модель характеризуется тем, что содержит входы для сигналов от объектов, внутренние каналы связи от входов, из части которых формируют кластер, в которых осуществляют умножение входных сигналов на весовые коэффициенты, далее полученные сигналы суммируют и производят их нелинейное пороговое преобразование, которое используют как выходной сигнал, при этом формирование кластера осуществляют в соответствии с кодовой комбинацией входного сигнала; кластер связывают с сумматором, после чего производят нелинейное пороговое преобразование сигнала, которое используют как выходной сигнал.
Как было отмечено ранее, в такой модели кодовые комбинации распознаваемых классов предполагаются известными, что не соответствует реальному биологическому нейрону.
В отличии от известного нейрона, предлагаемая модель активного нейрона основана на том, что нейрон в кооперации с другими нейронами формирует нейронные сети, представляющие собой функциональные системы для достижения заданных целей и удовлетворения заданных потребностей и, таким образом, имеет информацию о том достигнута цель в результате его собственной активности или нет. Данная информация о результативности нейрона в виде сигнала обратной связи поступает обратно к нейрону через входы для сигналов обратной связи и учитывается при оценке результативности дендритов, а также при формировании кластеров.
Раскрытие изобретения
Предлагаемая модель нейрона основана на активности нейрона, на дендритной пластичности и дендритных вычислениях, которые автоматически формируют паттерны-синдромы, опираясь на знании о достижении нейроном результата. Паттерны-синдромы не суммируются и поэтому дают ответ нейрона, который понятен и формулируем в терминах входных стимулов. Таким образом результат работы нейрона объясним в противовес искусственным нейронам МакКаллока-Питса.
В [3] активность нейрона «представляется не как реакция на синаптический приток, обеспечивающая проведение возбуждения, а как средство изменения соотношения со средой, «действие», направленное в будущее, которое обусловливает устранение рассогласования между «потребностями» нейрона и его микросредой. Сам же нейрон предстает не как «проводник» или «сумматор», а как организм в организме, обеспечивающий свои «потребности» за счет метаболитов, поступающих от других элементов». Действия нейрона обеспечивают «потребности» в его метаболизме, объединяясь с другими элементами организма в функциональную систему. В этом случае нейрон «знает» удовлетворил ли он свою потребность за счет своей активности или нет, т.е. он всегда знает, правильно ли (будем говорить результативно ли) он сработал или нет. По данным работы [3] в этом процессе участвуют глиальные клетки: «Современные данные подтверждают участие глии в снабжении нейронов питательными веществами (лактат, кислород, глюкоза). Глиальные клетки включены во все процессы мозга, требующие пластических перестроек нейронных сетей: эмбриогенез и прижизненный нейрогенез, формирование следов памяти».
Дендритная пластичность - это характерный для ЦНС фундаментальный механизм, который лежит в основе синаптической потенциации и является ключевым для формирования памяти, обучения и когнитивных способностей, для нормального функционирования мозга. В основе дендритной пластичности лежит динамическая природа дендритов, которые могут быть смоделированы через изменение их объема, наклона, с потерей или добавлением других дендритов и дендритных шипиков, изменениями длины шеи шипиков, действием на дендритные потенциал-зависимые ионные каналы. Все эти формы дендритной пластичности связаны с обучением и памятью и являются основой уникальных биологических, вычислительных функций одиночных нейронов [9].
Дендритные ветви способны активно выявлять специфические свойства входных сигналов, например, их синхронность. А поскольку пространственно локализованные синаптические входные импульсы имеют большую вероятность вызвать локальные дендритные спайки, из этого следует важный вывод, что аксоны пресинаптических нейронов с коррелированной активностью образуют синаптические кластеры в дендритном дереве, к которому посылают импульсы. Подобная синаптическая кластеризация (т.н. «гипотеза кластерной пластичности») дает эффективный способ обработки и хранения информации нейроном. При одновременной стимуляции кластеров синапсов на дендритной ветке, их повторная активация приводит к постепенным изменениям в ответе мембраны на стимулы и «слабые» ветви превращаются в ветви с сильной спаечной активностью путем сочетания синаптического возбуждения с постсинаптическим потенциалом действия. Такое превращение слабой дендритной ветви дает новую форму пластичности - «branch-strength potentiations, (потенциация силы ветви, BSP). Нейроны, благодаря дендритным спайкам и сочетанию классической (зависящей от времени спайка (англ. spike-timing dependent plasticity, STDP) и неклассической (BSP) пластичности, способны выполнять сложные нелинейные вычисления путем самоорганизации. Оба механизма пластичности могут породить конкуренцию между дендритными ветвями, что позволяет одному нейрону, на клеточном уровне, выполнять такие нелинейные вычисления, которые ранее считались возможными только для нейронных сетей, например, способность связывать множество входных признаков (т.н. «проблема связывания», англ. binding problem). Таким образом, активность дендритных шипиков часто синхронизируется в пределах группы шипиков, которые находятся близко друг к другу и объединены общими синаптическими входными сигналами от синхронизированных пресинаптических нейронов. Кластерная синхронизация, которая возникнет в результате этого, может служить основой ассоциативного обучения на клеточном уровне [9]. Поскольку синапсы могут быть как возбуждающие, так и тормозные, то, соответственно, кластерная синхронизация может быть, как возбуждающей, так и тормозной.
Дендритные вычисления основываются на исследованиях Bartlett Mel и его коллег, которые более тщательно исследовали способность нейрона управлять несколькими входами, используя лишь отдельные дендриты. То, что они обнаружили, удивило их: дендриты оказались способными генерировать локальные всплески, иметь собственные нелинейные кривые ввода-вывода и собственные пороги активации, отличные от порогов нейрона. Сами дендриты могут действовать как логические вентили «И» или как хост других вычислительных устройств. Из этого они сделали вывод, что отдельный нейрон можно рассматривать как двухслойную сеть. Дендриты служат в ней нелинейными вычислительными субъединицами, собирающими входные данные и выдающими промежуточные выходные данные. Затем эти сигналы объединяются в клеточном теле, и там формируется реакция нейрона в целом [10-13].
Задачей заявленного изобретения является создание модели активного биологического нейрона, способного к избирательному распознаванию входных объектов без использования суммации и пороговой функции, с возможностью автоматического создания максимально информативных паттернов-синдромов, распознающих объекты.
Техническим результатом является повышение точности, объяснимости результата и снижение противоречивости распознавания.
Поставленная задача решается и заявленный технический результат достигается тем, что модель нейрона, основанная на дендритных вычислениях, которая включает информационные входы, информационный выход, дендриты, синапсы которых внутренними каналами связи соединены с информационными входами и формируют кластеры, и вычислительное ядро для формирования выходного сигнала нейрона, дополнительно включает вход для сигнала обратной связи, посредством которого сигнал о результативности нейрона подается на дендриты для учета их результативности, а синапсы формируют кластеры в соответствии с их результативностью. Дендритные вычисления могут быть выполнены, в частности, в вычислительных блоках дендритов, а для передачи сигнала о результативности нейрона могут быть использованы глиальные клетки.
Благодаря тому, что нейрон получает информацию о своей результативности через сигнал обратной связи о достижении заданного результата в результате его активности и взаимодействия с другими нейронами, появляется возможность учитывать данную информацию о результативности нейрона при оценке результативности дендритов, а также при формировании кластеров синапсов. Что в конечном итоге приводит к повышению точности и объяснимости вычислений, а также позволяет снизить противоречивость распознавания.
Краткое описание чертежей
Заявленное техническое решение поясняется с помощью фигур.
На фиг. 1 представлена схема формального нейрона МакКаллока-Питса
На фиг. 2 представлена схема дендрита
На фиг. 3 представлена заявленная модель нейрона
На фиг. 4. представлена структурная схема устройства, реализующего заявленную модель нейрона
На фигурах обозначены: 1 - возбуждающие синапсы дендритов; 2 - тормозные синапсы дендритов; 3 - ветви дендритов; 4 - глиальные клетки, 5 -вычислительное ядро; 6 - дендрит с ветвлениями; 7 - входы для сигнала обратной связи, 8 - шина данных, X1, Х2, Х3, XN-1, XN - входные сигналы, поступающие на информационные входы; U - выходной сигнал нейрона, формируемый на информационном выходе, Z - сигнал обратной связи.
Осуществление изобретения
Входной сигнал X1 - XN, заданный в виде бинарного кода, подают на информационные входы устройства. Каждая переменная X имеет значение 0 или 1 в комбинации, представляющей бинарный код входного сигнала.
Эта комбинация бинарного кода по одноименным внутренним каналам связи, передается на возбуждающие (1), либо тормозные (2) синапсы дендритов (6). В частном случае, представленном на фигурах, каждый дендрит (6) включает по 3-5 ветвей (3) перед каждым дендритным узлом. Следует отметить, что схема дендрита (6) и нейрона, представленные на фигурах, являются условными, служащими целям пояснения заявляемого технического решения, и количество ветвей (3) дендрита (6), и их конфигурация не ограничены представленными вариантами.
Значения бинарного кода, поступающие на синапсы (1, 2), не суммируются, но они либо «учитываются», либо нет в зависимости от того, увеличивают ли они вероятность правильной (результативной) реакции нейрона или нет. Процесс «учета» синапсов (1, 2) при формировании синхронизированного кластера описан далее.
Значение на выходе каждого дендрита (6) складывается из возбуждений и торможений «учтенных» синапсов (1, 2), формирующих синхронизированный кластер, находящийся ближе к телу нейрона и выше. Синхронизация осуществляется вдоль дендрита (6). Если все учитываемые синапсы возбуждающие (1), то дендрит (6) выдаст возбуждение, если все учитываемые синапсы тормозные (2), то торможение.
Значение выходного сигнала U нейрона определяется в вычислительном ядре (5) нейрона исходя из импульсов, поступающих от дендритов (6):
а) нейрон не возбуждается и не тормозится, т.е. не активен и его значение не определено, если (I) нет ни одного возбуждающего импульса от какого-то из дендритов (6) и нет тормозных импульсов от дендритов (6), (II) есть как возбуждающие импульсы от какого-то из дендритов (6), так и тормозные импульсы от какого-то из дендритов (6);
б) нейрон возбуждается, если есть возбуждающие импульсы от дендритов (6) и при этом нет тормозных импульсов от дендритов (6). В этом случае возбуждение нейрона объясняется возбуждением соответствующих кластеров дендритов (6), которое фиксируется в терминах возбуждающих импульсов этих кластеров;
в) нейрон тормозится, если есть тормозные импульсы от дендритов (6) и при этом нет возбуждающих импульсов от дендритов (6). В этом случае торможение нейрона объясняется торможением соответствующих кластеров дендритов (6), которое фиксируется в терминах тормозных импульсов этих кластеров.
Нейрон, согласно заявленной модели, формирует нейронные сети с другими нейронами для достижения заданных целей (удовлетворения заданных потребностей). Таким образом, после того, как цель достигнута или нет (потребность удовлетворена или нет), формируется информация о результативности нейрона в результате его активности (возбуждения или торможения). Данная информация о результативности нейрона в виде сигнала Z обратной связи поступает обратно к нейрону через вход (7) для сигнала обратной связи и далее, например, через глиальные клетки (4), к дендритам (6) для учета результативности дендритов (6), а также при формировании кластеров. Следует отметить, что на фиг. 4 представлено два входа (7) обратной связи. Однако такая конфигурация устройства является лишь частным случаем. В зависимости от задач, условий работы и прочих факторов вход (7) может быть один, либо более двух. Глиальные клетки (4), соединенные с входом (7) для сигнала обратной связи, могут быть соединены с одним, несколькими или и с каждым дендритом (6) нейрона.
Далее раскрыт один из возможных вариантов учета синапсов (1, 2) при формировании синхронизированного кластера. Данный вариант характерен тем, что он обеспечивает непротиворечивость возбуждений и полученных по ним предсказаний (доказано в [19]). Это принципиально важно для данной модели, т.к. обеспечивает, либо одновременное возбуждение, либо одновременное торможение дендритов (6). Для этого в вычислительных блоках дендритов (6) (на фигурах не показаны) производятся вычисления в соответствии с «семантическим вероятностным выводом», описанным в [18-20]. Применительно к данной формальной модели нейрона он определяется следующим образом.
Пусть {y1, …, yk} - некоторое подмножество {y1, …, yk}⊂{x1, x2, …, xN} из всех приходящих на вход нейрона сигналов {x1, x2, …, xN}, которые приходят на дендрит (6). В отличии от нейрона МакКаллока-Питса, у которого сигналы {x1, x2, …, xN} - непрерывные величины, в заявляемой модели нейрона входные сигналы ближе к биологической форме и состоят из импульсов yj, которые идут по аксонам. Если в момент времени t сигнал приходит на возбуждающий синапс (1) i-го дендрита, то он обозначается предикатом Yi(t), если на тормозной (2), то он обозначается отрицанием предиката ¬Yi(t). На один и тот же дендрит (6) от некоторого импульса yj может приходить сигнал, как через возбуждающий синапс (1), так и через тормозной (2). Возбуждение и торможение i-го дендрита (6) обозначено соответственно через Дi(t) и ¬Дi(t). Сигнал Z обратной связи о результативности нейрона, поступающий на входы (7), передается далее к дендритам (6), в частности, через глиальные клетки (4). Поэтому, когда нейрон возбуждается, а это значит, что получены возбуждающие импульсы от каких-то дендритов (6), и работа нейрона оказалась результативной, то результативной оказалось и возбуждение этих дендритов (6). Если же нейрон затормозился, что означает наличие тормозных импульсов от некоторых дендритов (6), и работа нейрона оказалась результативной, то результативным оказалось и данное торможение этих дендритов (6). Для описания возбуждающих и тормозных синхронизированных кластеров, формируемых на дендритах (6), определены возбуждающие и тормозные правила:

Условную вероятность их результативности определим следующим образом. Пусть общее число возбуждений нейрона будет N, а результативных из них будет M<N. Тогда безусловная (частотная) вероятность результативности возбуждений нейрона будет M/N. Если i-ый дендрит возбудился по правилу  , что привело к возбуждению нейрона в n из N случаев и из них результативными были только m, то вероятность результативности этого правила будет равна
, что привело к возбуждению нейрона в n из N случаев и из них результативными были только m, то вероятность результативности этого правила будет равна 
Аналогично можно определить результативность тормозного правила. Пусть общее число торможений нейрона будет N, а результативных из них будет M<N. Тогда безусловная (частотная) вероятность результативности торможения нейрона будет M/N. Если i-ый дендрит затормозился по правилу  , что привело к торможению нейрона в n из N случаев и из них результативными были только m, то вероятность результативности этого правила будет равна
, что привело к торможению нейрона в n из N случаев и из них результативными были только m, то вероятность результативности этого правила будет равна 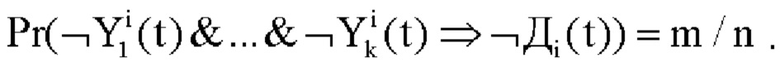
Формирование возбуждающих и тормозных правил и, тем самым, учет возбуждений от синапсов (1, 2) i-го дендрита (6) начинается с ближайших к соме нейрона синапсов дендрита (6) и осуществляется по следующим правилам:
1. Если синапс  i-го дендрита по правилу
i-го дендрита по правилу  с вероятностью m/n строго увеличивает безусловную вероятность результативности возбуждения нейрона M/N, т.е. m/n>M/N, то данный синапс учитывается при возбуждении дендрита.
с вероятностью m/n строго увеличивает безусловную вероятность результативности возбуждения нейрона M/N, т.е. m/n>M/N, то данный синапс учитывается при возбуждении дендрита.
2. Другой синапс также начнет учитываться в возбуждении дендрита, если условная вероятность правила  будет строго больше условной вероятности правила
будет строго больше условной вероятности правила  , т.е.
, т.е. 
3. Далее по индукции синапс  начнет учитываться в возбуждении дендрита, если условная вероятность правила
начнет учитываться в возбуждении дендрита, если условная вероятность правила  будет строго больше условной вероятности правила
будет строго больше условной вероятности правила  т.е.
т.е. 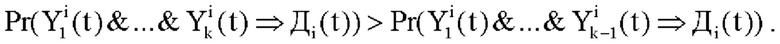
4. Если среди учитываемых в возбуждении дендрита синапсов  найдется синапс
найдется синапс  , возбуждение которого будет перекрыто другими синапсами, в том смысле, что его возбуждение уже не нужно для максимально вероятного (и значит максимально быстрого) возбуждения дендрита (известно, что максимально вероятные условные связи срабатывают быстрее по времени), то такой синапс перестает учитываться. В терминах вероятности это означает, что
, возбуждение которого будет перекрыто другими синапсами, в том смысле, что его возбуждение уже не нужно для максимально вероятного (и значит максимально быстрого) возбуждения дендрита (известно, что максимально вероятные условные связи срабатывают быстрее по времени), то такой синапс перестает учитываться. В терминах вероятности это означает, что

5. Аналогичные условия 1-4 должны быть выполнены для учета тормозных синапсов при торможении дендрита и нейрона.
Аппаратная реализация заявляемой модели нейрона может быть осуществлена, в частности, следующим образом. На информационные входы X1, Х2, Х3, …, XN поступают бинарные электрические импульсы, которые далее по внутренним каналам передаются в вычислительные блоки дендритов (6), где производят обработку данных сигналов, например, по описанной выше схеме, формируют кластеры, определяющие выходной сигнал дендрита (6), далее сигнал из вычислительного блока каждого из дендритов (6) поступает на шину (8), по которой эти сигналы поступают в вычислительное ядро (5) нейрона, которое формирует выходной сигнал U нейрона. По результатам активности нейрона и при взаимодействии с другими нейронами формируется сигнал Z о результативности нейрона, который поступает на вход (7) для сигнала обратной связи, передается в вычислительные блоки дендритов (6) и учитывается в дальнейшем при вычислениях при формировании кластеров.
Благодаря тому, что формирование кластеров осуществляют в соответствии с результативностью нейрона на основании сигнала обратной связи о его результативности, поступающем на вход (7) обратной связи и далее к дендритам (6), они порождают объяснимое возбуждение/торможение нейрона, при этом система «учета» синапсов происходит в соответствии с описанным выше «семантическим вероятностным выводом», который обеспечивает точность и непротиворечивость распознавания. Заявленная модель нейрона характеризуется большей адекватностью реальному биологическому нейрону и позволяет выполнить сжатие входной информации, так как используется только та информация об объектах, которая эффективно приводит к результату.
Эффективность предлагаемого нейрона продемонстрирована в следующих результатах применения данной модели, реализованной программной системой Discovery, осуществляющей «семантический вероятностный вывод»:
1. Финансового прогнозирования [15];
2. Распознавания рака груди [16];
3. Распознавания регуляторных районов генов [17];
Промышленная применимость.
Изобретение может быть использовано для моделирования активных биологических нейронов, достигающих своих целей, основанных на дендритных вычислениях, в качестве элементов нейронных сетей и нейрокомпьютеров, технических систем на основе нейронных сетей, для распознания образов, анализа изображений и задачах искусственного интеллекта.
Изобретение позволяет расширить области применения нейронных сетей, основным элементом которых является нейрон, нейросетевых технологий и систем искусственного интеллекта.
СПИСОК ЛИТЕРАТУРЫ
1. Мак-Каллок У., Питтс В. Логическое исчисление идей, относящихся к нервной активности // Нейрокомпьютер. - 1992. - №3/4. - Р. 40-50.
2. Хайкин Саймон. Нейронные сети: полный курс. М.: «Вильяме», 2006. - С. 1104.
3. Нейрон. Обработка сигналов. Пластичность. Моделирование. Фундаментальное руководство. ООО «Компания Мир», 2008.
4. Ю.И. Александров. Закономерности актуализации индивидуального опыта и реорганизации его системной структуры: комплексное исследование // Методологические проблемы системного анализа. Труды ИСА РАН. Том 61. 3/2011
5. Системный анализ интегративной деятельности нейрона / ред. П.К. Анохин. - Москва: Наука, 1974. - 157 с.
6. Мазуров М.Е. Обучение избирательных нейронных сетей без математики и без учителя на основе самоорганизации // Доклады Международной конференции "Математическая биология и биоинформатика". Под ред. В.Д. Лахно. Том 7. Пущино: ИМПБ РАН, 2018. Статья № е32.
7. Мазуров М.Е. НЕЙРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО НЕЙРОНА. ПАТЕНТ RU 2597495.
8. Мазуров М.Е. ИМПУЛЬСНЫЙ НЕЙРОН, БЛИЗКИЙ К РЕАЛЬНОМУ. ПАТЕНТ RU 2598298.
9. Мазуров М.Е. Инструментальный способ обучения избирательной нейронной сети без математики и без учителя с использованием самоорганизации. ПАТЕНТ 2729878.
10. Дендритная пластичность. Материал из Википедии.
11. Panayiota Poirazi, Terrence Brannon and Bartlett W. Mel. Pyramidal Neuron as Two-Layer Neural Network. Neuron, Vol. 37, 989-999, March 27, 2003.
12. Jordana Cepelewicz. Hidden Computational Power Found in the Arms of Neurons. NEUROSCIENCE, JANUARY 14, 2020.
13. Albert Gidon, Timothy Adam Zolnik, Pawel Fidzinski, Felix Bolduan, Athanasia Papoutsi, Panayiota Poirazi, Martin Holtkamp, Imre Vida, Matthew Evan Larkum. Dendritic action potentials and computation in human layer 2/3 cortical neurons. Science 367, 83-87 (2020) Русский перевод: Вычислительная мощь дендритных ветвей отдельных нейронов оказалась неожиданно высокой, https://22century.ru/popular-science-publications/hidden-computational-power-found-in-the-arms-of-neurons
14. Bartlett W. Me. Information Processing in Dendritic Trees. Neural Computation 6,1031-1085 (1994).
15. Boris Kovalerchuk and Evgenii Vityaev. Data Mining in Finance: Advances in Relational and Hybrid Methods, Kluwer Acad. Pub., 2000.
16. Kovalerchuk, В., Vityaev E., Ruiz J.F. Consistent and Complete Data and "Expert" Mining in Medicine // Medical Data Mining and Knowledge Discovery, Springer, 2001, pp. 238-280.
17. Y.Y. Vaskin, I.V. Khomicheva, E.V. Ignatieva, E.E. Vityaev. ExpertDiscovery and UGENE integrated system for intelligent analysis of regulatory regions of genes. In Silico Biology v.11 (2011/2012), IOS Press, pp.97-108.
18. Витяев E.E. Семантический подход к созданию баз знаний. Семантический вероятностный вывод наилучших для предсказания ПРОЛОГ-программ по вероятностной модели данных. // Логика и семантическое программирование (Вычислительные системы, вып. 146), Новосибирск, 1992, с. 19-49.
19. Vityaev, E., Odintsov, S. How to predict consistently? Trends in Mathematics and Computational Intelligence In: Studies in Computational Intelligence, 796, Maria Eugenia Cornejo (ed), 2019, 35-41.
20. Витяев E.E. Семантический вероятностный вывод предсказаний ИЗВЕСТИЯ ИРКУТСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА", Серия "Математика". 2017. Том 21. С. 33-50.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИМПУЛЬСНЫЙ НЕЙРОН, БЛИЗКИЙ К РЕАЛЬНОМУ | 2015 |
|
RU2598298C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН НА ОСНОВЕ ИЗБИРАТЕЛЬНЫХ НЕЙРОНОВ | 2015 |
|
RU2597497C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО ПЕРЦЕПТРОНА | 2015 |
|
RU2597496C1 |
| НЕЙРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО НЕЙРОНА | 2014 |
|
RU2597495C2 |
| УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ НЕЙРОНА | 1991 |
|
RU2028669C1 |
| Устройство для моделирования нейрона | 1987 |
|
SU1501101A1 |
| Устройство для морфодинамического моделирования нейрона | 1991 |
|
SU1815658A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ НЕЙРОННОГО ВРЕМЕННОГО КОДИРОВАНИЯ, ОБУЧЕНИЯ И РАСПОЗНАВАНИЯ | 2012 |
|
RU2597504C2 |
| Устройство для моделирования нейрона высших отделов | 1988 |
|
SU1561076A1 |
| Устройство для моделирования нейрона | 1988 |
|
SU1585811A1 |



Изобретение относится к компьютерным системам, основанным на биологических моделях, и может быть использовано в нейрокомпьютерах, технических системах на основе нейронных сетей, в распознании образов, анализе и обработке изображений и искусственном интеллекте. Техническим результатом является избирательное распознавание входных объектов с возможностью автоматического создания максимально информативных паттернов-синдромов, распознающих объекты. Технический результат заявленного решения достигается тем, что модель нейрона основана на дендритных вычислениях и включает информационные входы, информационный выход, дендриты, синапсы которых формируют кластеры, и вычислительное ядро для формирования выходного сигнала нейрона, также предусмотрен вход для сигнала обратной связи, посредством которого сигнал о результативности нейрона подается на дендриты для учета их результативности. 2 з.п. ф-лы, 4 ил.
1. Модель нейрона, основанная на дендритных вычислениях, которая включает информационные входы, информационный выход, дендриты, синапсы которых внутренними каналами связи соединены с информационными входами и формируют кластеры, и вычислительное ядро для формирования выходного сигнала нейрона, отличающаяся тем, что дополнительно включает вход для сигнала обратной связи, посредством которого сигнал о результативности нейрона подается на дендриты для учета их результативности, а синапсы формируют кластеры в соответствии с их результативностью.
2. Модель нейрона по п.1, отличающаяся тем, что содержит вычислительные блоки дендритов для выполнения дендритных вычислений.
3. Модель нейрона по п.1, отличающаяся тем, что содержит глиальные клетки для передачи сигнала о результативности нейрона на дендриты.
| НЕЙРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО НЕЙРОНА | 2014 |
|
RU2597495C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН НА ОСНОВЕ ИЗБИРАТЕЛЬНЫХ НЕЙРОНОВ | 2015 |
|
RU2597497C2 |
| УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ НЕЙРОНА | 1991 |
|
RU2028669C1 |
| US 20140074761 A1, 13.03.2014 | |||
| US 20140156574 A1, 05.06.2014 | |||
| US 20140317035 A1, 23.10.2014. | |||
Авторы
Даты
2022-08-01—Публикация
2021-04-29—Подача