Изобретение относится к моделированию нейронов в качестве элемента нейронных сетей, к нейрокибернетике и может найти применение при разработке нейрокомпьютеров, технических систем на основе нейронных сетей, для распознания образов, анализа и обработки изображений и многих других приложений. Целью изобретения является расширение области применения нейронных сетей, основным элементом которых является нейрон, нейросетевых технологий, создания искусственного интеллекта.
История искусственных и математических моделей нейронов началась с изобретения искусственного нейрона МакКаллока-Питса, который явился исторической вехой в нейроинформатике [8]. Нейрон МакКаллока-Питса или формальный нейрон - базовый элемент искусственных нейронных сетей, применение которых привело к бурному развитию нового направления в нейроинформатике, созданию нейрокомпьютеров, позволило значительно продвинуться к пониманию и познанию процессов в головном мозге.
Формальный нейрон - это абстрактный логический элемент, в котором отражены лишь те свойства реального, живого нейрона, которые связаны с переработкой информации, блок-схема которого показана на фиг. 1.
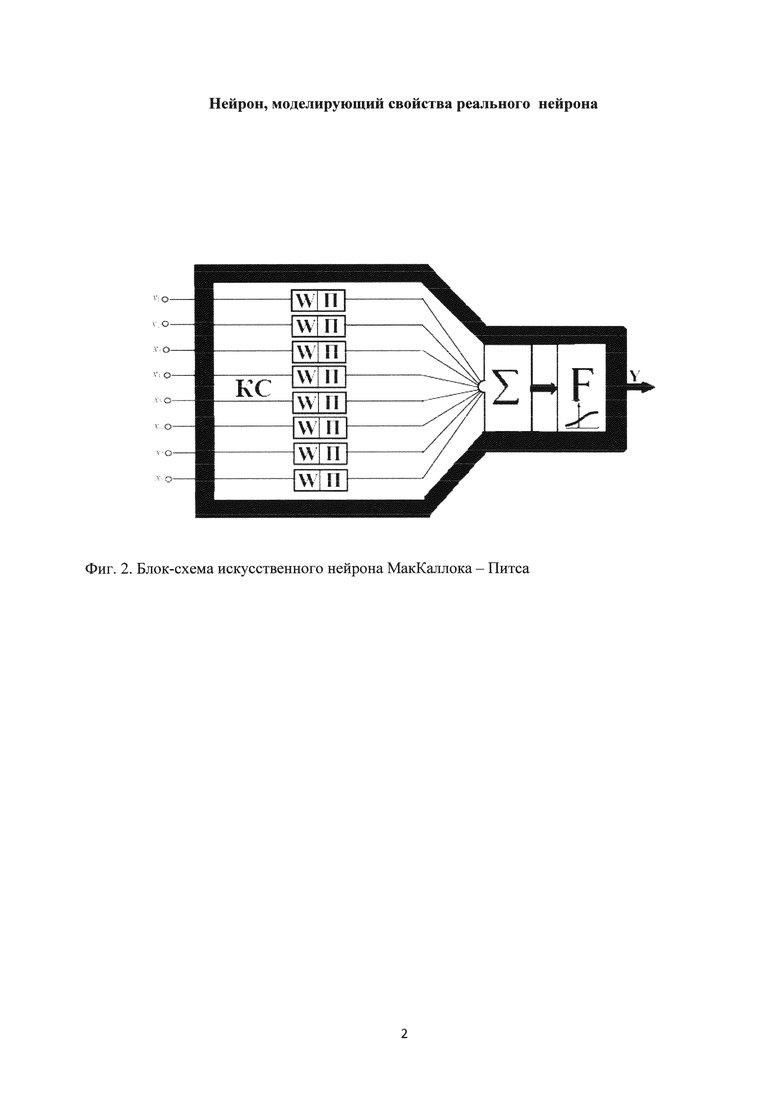
На фиг. 1 приняты обозначения: x1, x2, …, xN - входные сигналы, заданные в виде бинарных кодов; w1, w2, …, wN - весовые коэффициенты; Σ - сумматор; F - пороговая функция; Y - выходной сигнал. В дальнейшем мы будем использовать блок-схему нейрона МакКаллока-Питса, как показано на фиг. 2.
На фиг. 2 приняты обозначения: КС - каналы связи; W - устройства памяти, где сохраняются весовые коэффициенты, П - перемножители входных сигналов на весовые коэффициенты; Σ - устройство суммирования входных воздействий с весовыми коэффициентами; F - пороговая функция; Y - выходной сигнал.
Рассмотрим математическую теорию искусственного нейрона МакКаллока-Питса. Математически искусственный нейрон обычно представляют как некоторую нелинейную функцию от единственного аргумента - линейной комбинации всех входных сигналов. Полученный результат подается на пороговую функцию или функцию активации, обеспечивающую единственный выход нейрона. Таким образом, линейная комбинация входных сигналов с определенными весами подается на вход нейрона. На входе сумматора получаем сигнал S

где x=(xl,…,xN), w=(w1,…,wN), (w, x) - скалярное произведение векторов w, x; N - число входов нейрона. После прохождения порогового устройства и преобразования пороговой функцией F(S) получаем выходной ответ, равный

Взвешенную сумму иногда представляют в виде  , где θ - смещение. К основным компонентам искусственного нейрона относятся перемножители, сумматор, пороговое устройство, реализующее функцию активации нейрона, которая может иметь различную форму [1-4, 8-10].
, где θ - смещение. К основным компонентам искусственного нейрона относятся перемножители, сумматор, пороговое устройство, реализующее функцию активации нейрона, которая может иметь различную форму [1-4, 8-10].
Известны недостатки искусственного нейрона МакКаллока-Питса: 1) искусственный нейрон МакКаллока-Питса неадекватен реальному биологическому нейрону; 2) входными и выходными сигналами реального биологического нейрона являются кодовые комбинации в бинарном представлении; 3) в реальном биологическом нейроне весовой градации входных сигналов не производится; 4) нейросетевые алгоритмы с нейроном МакКаллока-Питса при большом количестве входных сигналов неустойчивы и ненадежны, увеличение входных сигналов даже на один требует полного перерасчета процессов в системе, такое недопустимо в реальной биологической системе [1-4, 8-10]. Список недостатков можно продолжить.
Раскрытие изобретения
Наиболее близким техническим решением к заявляемой модели является модель нейрона, рассматриваемого как устройство с взвешенным суммированием входных сигналов, реализуемым с помощью перемножителя и блока памяти, где хранятся весовые коэффициенты, и последующим преобразованием с помощью порогового устройства.
Основное предназначение нейрона - участвовать в составе нейронной сети в качестве базового функционального элемента и реализовывать в составе нейронной сети следующие основные функции: 1. Способность к обучению; 2. Избирательность; 3. Устранение избыточности информации; 4. Кодирование номером канала. Можно отметить и ряд других желательных свойств искусственного нейрона, более детально они изложены в статьях и монографиях [1-4, 6-17]. Обзор патентов по моделям нейронов приведен, например, в работе [10].
Избирательность абстрактно можно сравнить с избирательностью колебательного контура - базового элемента радиоэлектроники, телевидения. Колебательный контур или полосовой фильтр частот позволяет выделить из всего множества частот объект, расположенный в заданной полосе частот. При этом естественным образом устраняется избыточность всего входного сигнала в целом. Естественным образом может быть организовано кодирование сигнала номером каната, поскольку выделение сигнала происходят конкретным нейроном путем установления близости кодовой комбинации сигнала кодовой комбинации сформированной в нейронном кластере.
Определенными преимуществами перед искусственными нейронами МакКаллока-Питса и описанными выше нейронами обладает предлагаемый в данной работе нейрон, близкий по своим свойствам к реальному нейрону. Он основан на использовании управляемой кластеризации входных каналов связи нейрона и последующей кластеризации возбуждающих и тормозных каналов связи после проведения кластеризации. Экспериментально установлено, что в реальном биологическом нейроне решение основных информационных задач в нейроне достигается изменением конфигурации-кластеризации входных и числа возбуждающих и тормозных дендритов. Решение основной задачи нейрона: сжатие сенсорной или промежуточной информации, распознавание стимулов, распределительные функции, такие как кодирование информации номером канала и др., достигается за счет изменения конфигурации-кластеризации и числа дендритов на входе нейрона, возбуждающих и тормозных. Надобность в регулировании весовых функций дендритов отпадает.
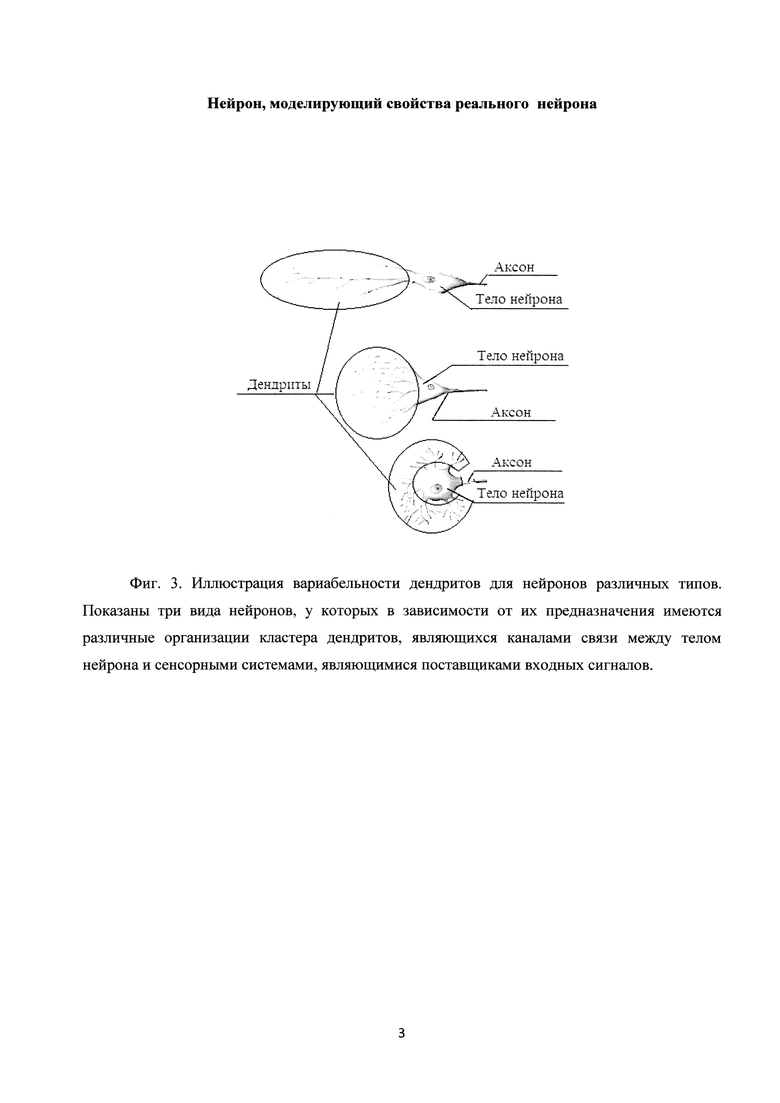
Вариабельность организации входных каналов связи нейрона - дендритов, широко представлена для различных типов биологических нейронов. Иллюстрация такой вариабельности дендритов для нейронов различных типов представлена на фиг. 3.
На фиг. 3 показаны три вида нейронов, у которых в зависимости от их предназначения имеются различные организации кластера дендритов, являющихся входными каналами связи между телом нейрона и сенсорными системами, являющимися поставщиками входных сигналов.
Может ли система дендритов на входе нейрона быть столь пластичной и лабильной, чтобы адекватным образом отражать входную информацию за счет изменения числа возбуждающих и тормозных дендритов. Ранее этот вопрос был изучен недостаточно. Однако в последнее время были сделаны ряд открытий, показавших наличие у дендритов совершенно необычных возможностей их роста, изменения количества и качества с помощью специальной системы шипиков [5]. Установлено также наличие у дендритов активных свойств, похожих на свойства аксонов [5]. Все это вместе взятое доказывает возможность адаптации к отражению любой входной информации не за счет весовых функций дендритов, а за счет кластеризации дендритов, изменения их количества и качества. Под различным качеством дендритов понимается их свойства: дендриты возбуждающие и тормозные, различные по диаметру и электрической мощности и т.д.; возможность самоорганизации путем роста и гибели отдельных дендритов. В реальных условиях в организме человека или животного формирование эффективных связей в кластере происходит естественным образом за счет подкармливания работающих дендритов и уничтожения неработающих дендритов путем прекращения питания. Подкармливание дендритов происходит при прохождении по ним электрических импульсов. При этом в дендрит поступают строительные материалы в виде белков, АТФ, обеспечивающих дендриты энергетическими ресурсами, и других органелл. Регулирование питания происходит за счет снабжения АТФ и белковыми компонентами при прохождении электрических нервных импульсов. Если электрические нервные импульсы не проходят по дендриту, то питание не подается, и он отмирает.
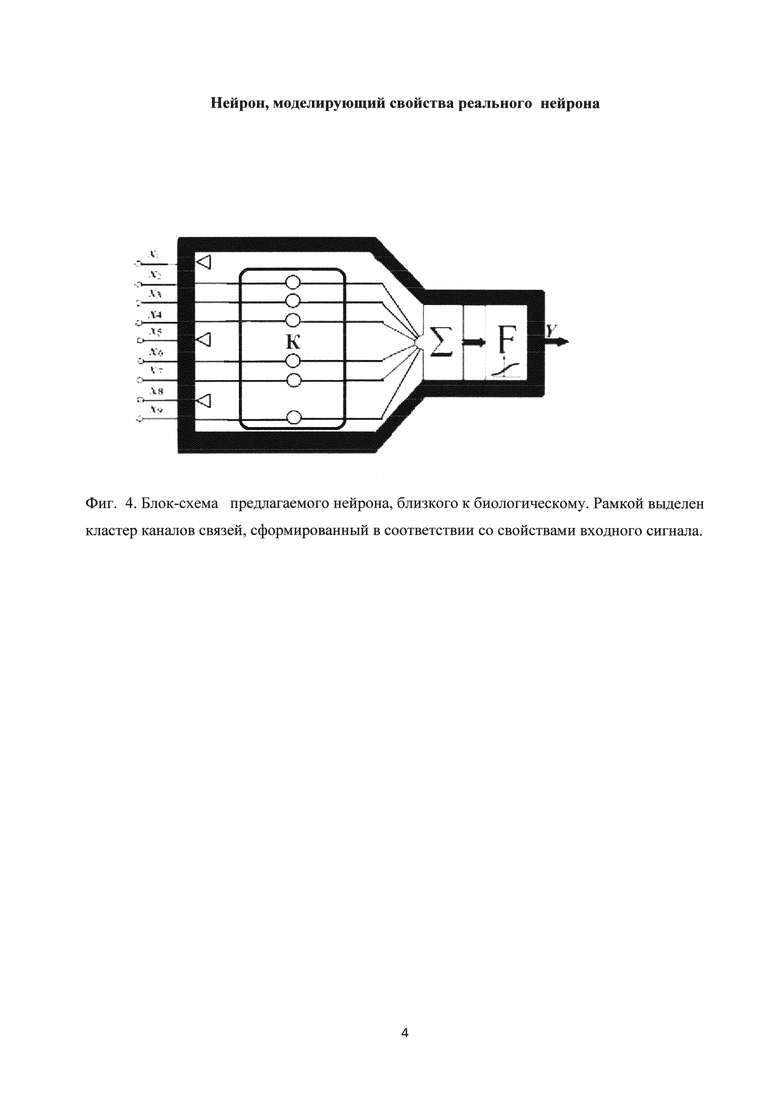
В связи со всем сказанным выше предлагается модель нейрона, представляющая устройство, более адекватно отражающее устройство и функции реального нейрона, блок-схема которого показана на фиг. 4.
На фиг. 4 приняты следующие обозначения: К - сформированный кластер каналов связи; Σ - сумматор, F - пороговый преобразователь. Треугольниками отмечены заблокированные каналы связи из числа входных, не являющихся существенными для выделения входной информации.
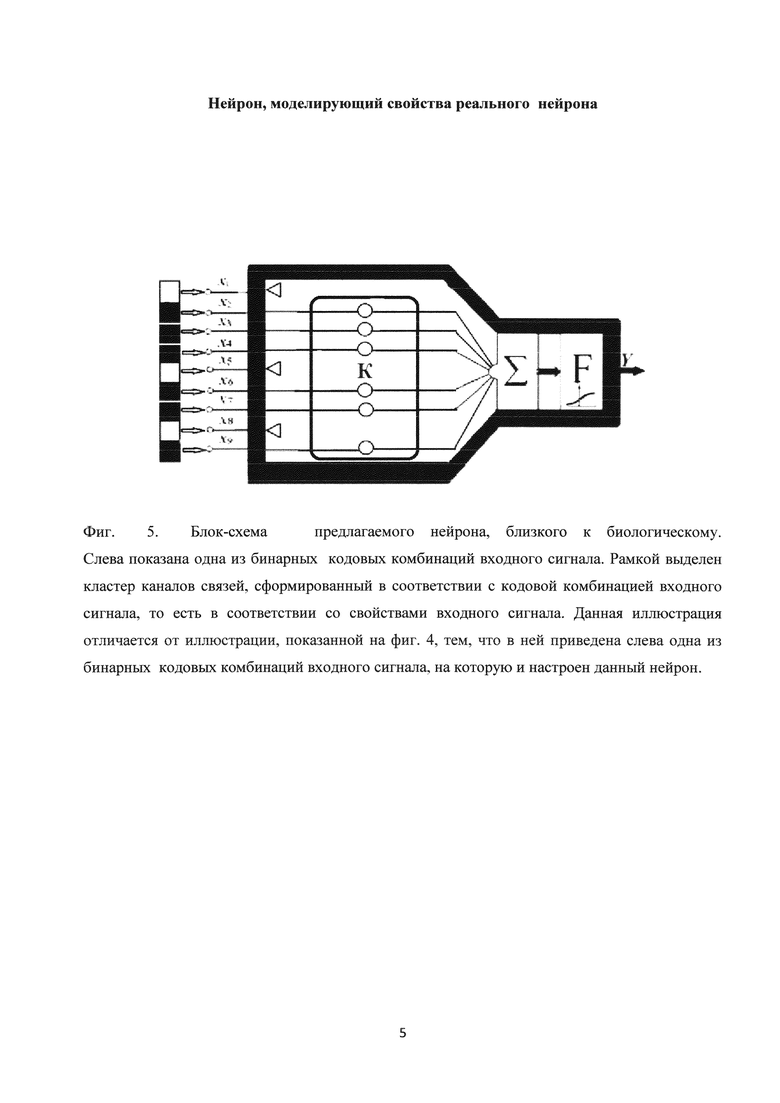
Пояснение формирования кластера каналов связей в зависимости от свойств входного сигнала иллюстрируется фиг. 5.
Фиг. 5. Блок-схема предлагаемого нейрона, близкого к биологическому. Слева показана одна из бинарных кодовых комбинаций входного сигнала. Рамкой выделен кластер каналов связей, сформированный в соответствии с кодовой комбинацией входного сигнала, то есть в соответствии со свойствами входного сигнала. Данная иллюстрация отличается от иллюстрации, показанной на фиг. 4, тем, что в ней приведена слева одна из бинарных кодовых комбинаций входного сигнала, на которую и настроен данный нейрон.
В связи с вышеизложенным предлагается следующая формула изобретения.
Нейрон, который имеет: входы для сигналов от объектов, внутренние каналы связи от входов, в которых осуществляют умножение входных сигналов на весовые коэффициенты, далее полученные сигналы суммируют и производят их нелинейное пороговое преобразование, которое используют как выходной сигнал, отличающийся кластером, который формируют из части внутренних каналов связи; формирование кластера осуществляют в соответствии с кодовой комбинацией входного сигнала; кластер связывают с сумматором, после чего производят нелинейное пороговое преобразование сигнала, которое используют как выходной сигнал.
Технические результаты, на достижение которых направлено изобретение
Технические результаты, на достижение которых направлено изобретение следующие:
1. достижение избирательного распознавания входных объектов без использования весового взвешивания входных сигналов;
2. достижение возможности кодирования предлагаемым нейроном входного объекта определенного типа номером канала или номером регистрирующего нейрона;
3. сжатие входной информации, благодаря сохранению только той информации об объектах, которая попадают в заданный канал или регистрирующий нейрон;
4. повышение быстродействия работы предлагаемого нейрона;
5. повышение надежности распознавания объектов при их большом количестве;
6. достижение значительно большей адекватности предлагаемого нейрона реальному биологическому нейрону.
Совокупность достигаемых технических результатов, указанных в пп. 1-6, достигается за счет следующей совокупности признаков, содержащихся в независимом пункте формулы:
1. индивидуальными кластерами; 2. формирование кластеров осуществляют в соответствии с кодовыми комбинациями входных сигналов; 3. кластеры из части каналов связи связывают с сумматорами.
Эффективность предлагаемого нейрона реально доказана в разработанных нами нейросетевых системах для распознавания:
1. Распознавание цифр;
2. Распознавание букв русского алфавита;
3. Распознавание текстов художественных произведений;
4. Распознавание автомобильных номеров;
5. Распознавание электрокардиограмм (ЭКГ);
6. Распознавание черно-белых портретов известных русских писателей и поэтов.
Системы, указанные в пп. 3, 5, 6, разработаны впервые и не имеют аналогов.
Раскрытие математической теории предлагаемого нейрона.
Рассмотрим математическую теорию предлагаемого избирательного нейрона. Обозначим возможные характеристические кодовые комбинации объектов на входе нейрона в виде векторов
x1=(xl1,…,x1n); …; wm=(wm1,…,wmn),
где: n - число элементов кодовой комбинации; m-число возможных объектов. Таким образом, имеется m векторов xi=(xi1,…,xin) с размерностью n. В предлагаемом нейроне кластер связей представляет собой одну из этих кодовых комбинаций. Вообще говоря, все возможные кодовые комбинации образуют матрицу А, которую можно представить в виде

Пусть конкретный рассматриваемый нами нейрон содержит кластер связей, характеризуемый кодовой комбинацией в виде
xi=(xi1,…,xin)
При подаче на вход данного нейрона с номером i кодовой комбинации xk=(xk1,…,xkn) (из совокупности возможных объектов на входе нейрона) получаем сумму

Всего мы получим очевидно m сумм Sik k=(1,…,m). Наибольшей будет сумма Sii

где Ni - число единиц в кодовой комбинации xi=(xi1,…,xin). Отметим следующее свойство сумм Sik
Sik<Sii.
Это строгое неравенство справедливо, поскольку сумма Sik содержит в своем составе большее количество слагаемых, равных произведениям 1·0, чем сумма Sii. Это свойство можно качественно сравнить со свойством ортогональных векторов или ортогональных функций. Оно не является строгой ортогональностью, ее можно считать ортогональностью в качественном смысле. Свойство может быть полезным при использовании предлагаемого динамического нейрона для распознавания объектов, кодировании номером канала и ряде других приложений. Вообще все возможные значения сумм Sij равны элементам матрицы В, равной
В=А*AT,
где AT - транспонированная матрица к А.
Принципиальным отличием предлагаемого нейрона от искусственного нейрона МакКаллока-Питса и от нейрона на основе математической модели Ходжкина-Хаксли, Ижикевича и других моделей подобного рода является: полное отсутствие весовых коэффициентов для входных воздействий и отсутствие всех недостатков нейронных сетей, связанных с наличием весового суммирования [11-17].
Рассмотрим процесс формирования кластера в предлагаемом нейроне в вычислительном эксперименте.
Примеры формирования кластеров в предлагаемом нейроне
Рассмотрим 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. На телевизионном экране с растром 4×6 располагаются цифры. Для цифр взята система Euclid. Система Euclid позволяет получить приемлемое кодирование цифр с помощью символов 0 и 1. Изображение цифр в системе Euclid приведено на фиг. 6.
Фиг. 6. Изображение цифр в системе Euclid
Кодировка цифр, то есть значения входных сигналов-векторов x1=(x11,…,x1n); …; xm=(xm1,…,xmn), приведена в таблице 1.


Таблица кодовых комбинаций при распознавании цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 при их расположении в двумерном поле 4×6.
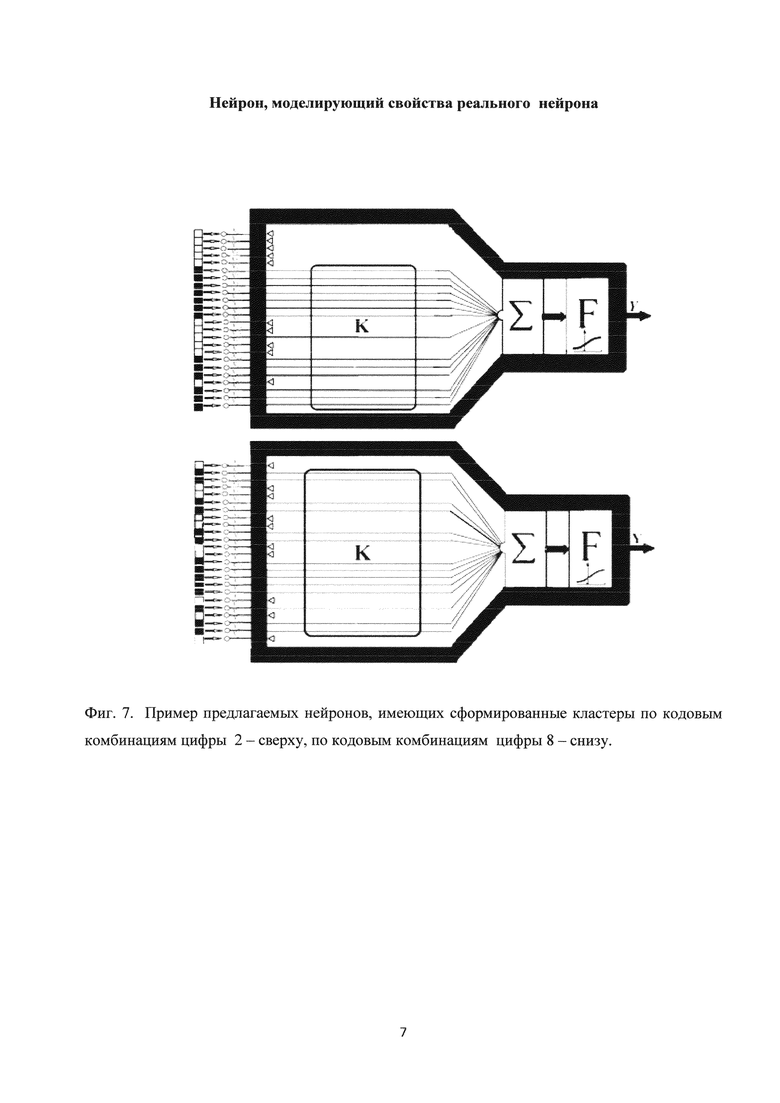
Рассмотрим два примера нейронов, у которых сформированы кластеры, настроенные на цифры 2 и 8. Более подробно описание формирования кластеров приведено ниже. Нейроны со сформированными кластерами показаны на фиг. 7. С левой стороны от изображения нейронов приведены бинарные кодовые комбинации цифр 2 и 8, в соответствии с которыми и формируется кластер каналов связи каждого нейрона.
Фиг. 7. Пример предлагаемых нейронов, имеющих сформированные кластеры по кодовым комбинациям цифры 2 - сверху, по кодовым комбинациям цифры 8 - снизу.
Отметим, что для кодовых комбинаций цифры 2 и цифры 8 справедливы соотношения


Таким образом, если порог Uпор=14, то нейрон, кластер которого сформирован по кодовым комбинациям цифры 2, идентифицирует эту цифру и не реагирует на кодовую комбинацию цифры 8, поскольку S28<S22, или 9<14.
Заключение
Предлагаемый нейрон обладает рядом существенных преимуществ перед искусственным нейроном МакКаллока-Питса. Ввиду отсутствия необходимости взвешивания входных сигналов достигается значительное повышение эффективности нейронных сетей, где предлагаемый нейрон может быть использован. Предлагаемый нейрон дает эффективные возможности при его использовании в приложениях: 1. повышение эффективности распознавания объектов; 2) возможность кодирования номером канала; 3) сжатие входной информации; 4)повышение быстродействия и др.
Предлагаемый нейрон в значительно большей степени адекватен реальному нейрону по сравнению с искусственным нейроном МакКаллока-Питса. Это достигается благодаря использованию кластеризации входных каналов связи вместо их весового взвешивания, что как установлено в последнее время, является фундаментальным свойством дендритной системы связи входов нейрона с его телом (сомой) [5].
СПИСОК ЛИТЕРАТУРЫ
1. Александров Ю.И., Анохин К.В., Соколов Е.Н., Греченко Т.Н. и др. Нейрон. Обработка сигналов. Пластичность. Моделирование. Фундаментальное руководство // Изд-во Тюменского государственного университета. 2008. 548 с.
2. Анохин К.В., Бурцев М.С., Ильин В.А., Киселев И.И., Кукин К.А., Лахман К.В., Параскевов А.В., Рыбка Р.Б., Сбоев А.Г., Твердохлебов Н.В. Современные подходы к моделированию активности культур нейронов in vitro / Математическая биология и биоинформатика. 2012. Т. 7. №2. С. 372-397.
3. Борисов В.В. Модель нейрона. Патент №RU 2034332. G06G 7/60, 1995.
4. Вассерман Ф. Нейрокомпьютерная техника: Теория и практика. // М.: «Мир», 1992.
5. Гутман А. Дендриты нервных клеток: теория электрофизиология, функция. 1984.
6. Мазуров М.Е. Решение диофантовых неравенств в задачах о синхронизации релаксационных колебаний // ЖВМ и МФ АН СССР. 1991. Т. 31. №11. С. 1619-1636.
7. Мазуров М. Е. Идентификация математических моделей нелинейных динамических систем // М.: - Ижевск. РХД. 2008. 284 с.
8. Мак-Каллок У., Питтс В. Логическое исчисление идей, относящихся к нервной активности // Нейрокомпьютер. - 1992. - №3/4. - Р. 40-50.
9. Самойлин Е.А. Способ моделирования нейрона. Патент RU 2402813. G06N 3/06. - 2010.
10. Субботин С.А. Аналитический обзор изобретений и патентов. Нейрокибернетика в СССР-СНГ. Запорожский национальный технический университет.
11. Сэломон Д. Сжатие данных, изображений и звука. Москва: Техносфера, 2004. 368 с.
12. Хайкин Саймон. Нейронные сети: полный курс = Neural Networks: A Comprehensive Foundation. - 2-е изд. - М.: «Вильяме», 2006. - С. 1104. - ISBN 0-13-273350-1.
13. Fitzhugh R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. // Biophysical journal. 1961. V. 1, №6. P. 445-466.
14. Hindmarsh J.L., Rose R.M. A model of the nerve impulse using two first-order differential equations. // Nature. Nature Publishing Group, 1982. V. 296, №5853. P. 162-164.
15. Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve // The J. of physiology. 1952. V. 117, №4. P. 500-544.
16. Izhikevich E.M. Simple model of spiking neurons. // IEEE transactions on neural networks / a publication of the IEEE Neural Networks Council. 2003. V. 14, №6. P. 1569-1572.
17. Morris C., Lecar H. Voltage oscillations in the barnacle giant muscle fiber. // Biophysical journal. 1981. V. 35, №1. P. 193-213.
| название | год | авторы | номер документа |
|---|---|---|---|
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН НА ОСНОВЕ ИЗБИРАТЕЛЬНЫХ НЕЙРОНОВ | 2015 |
|
RU2597497C2 |
| ИМПУЛЬСНЫЙ НЕЙРОН, БЛИЗКИЙ К РЕАЛЬНОМУ | 2015 |
|
RU2598298C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО ПЕРЦЕПТРОНА | 2015 |
|
RU2597496C1 |
| Инструментальный способ обучения избирательной нейронной сети без математики и без учителя с использованием самоорганизации | 2019 |
|
RU2729878C2 |
| Способ кодирования информации в импульсных нейронных сетях | 2019 |
|
RU2748257C2 |
| Модель нейрона, основанная на дендритных вычислениях | 2021 |
|
RU2777262C1 |
| Эффективный перцептрон на основе нейронов МакКаллока-Питтса с использованием компараторов | 2019 |
|
RU2729554C1 |
| МОДЕЛЬ НЕЙРОНА, РЕАЛИЗУЮЩАЯ ЛОГИЧЕСКУЮ ФУНКЦИЮ НЕРАВНОЗНАЧНОСТИ | 2003 |
|
RU2269155C2 |
| ИСКУССТВЕННЫЙ НЕЙРОН (ВАРИАНТЫ) | 2014 |
|
RU2604331C2 |
| ИСКУССТВЕННАЯ НЕЙРОННАЯ СЕТЬ | 2014 |
|
RU2573766C1 |


Изобретение относится к моделированию нейронов и может быть использовано в нейрокомпьютерах, технических системах на основе нейронных сетей для распознания образов, анализа и обработки изображений. Техническим результатом является обеспечение возможности достижения избирательного распознавания входных объектов без использования весового взвешивания входных сигналов, возможности кодирования входного объекта определенного типа номером канала или номером регистрирующего нейрона, сжатие входной информации, повышение быстродействия, повышение надежности распознавания объектов. Устройство содержит входы для сигналов от объектов, внутренние каналы связи от входов, кластер, который формируют из части внутренних каналов связи в соответствии с кодовой комбинацией входного сигнала, кластер связывают с сумматором, после чего производят нелинейное пороговое преобразование сигнала, которое используют как выходной сигнал. 7 ил., 1 табл.
Нейрон, который имеет: входы для сигналов от объектов, внутренние каналы связи от входов, в которых осуществляют умножение входных сигналов на весовые коэффициенты, далее полученные сигналы суммируют и производят их нелинейное пороговое преобразование, которое используют как выходной сигнал, отличающийся кластером, который формируют из части внутренних каналов связи; формирование кластера осуществляют в соответствии с кодовой комбинацией входного сигнала; кластер связывают с сумматором, после чего производят нелинейное пороговое преобразование сигнала, которое используют как выходной сигнал.
| МОДЕЛЬ НЕЙРОНА | 1992 |
|
RU2034332C1 |
| МОДЕЛЬ НЕЙРОНА, РЕАЛИЗУЮЩАЯ ЛОГИЧЕСКУЮ ФУНКЦИЮ НЕРАВНОЗНАЧНОСТИ | 2003 |
|
RU2269155C2 |
| US 2014156574 A1, 05.06.2014 | |||
| US 2014317035 A1, 23.10.2014. | |||
Авторы
Даты
2016-09-10—Публикация
2014-11-07—Подача