Изобретение относится к моделированию нейронных структур и может найти применение при разработке нейрокомпьютеров, технических систем на основе нейронных сетей для распознания образов, анализа и обработки изображений и многих других приложений. Целью изобретения является расширение области применения нейронных сетей, основным элементом которых является однослойный перцептрон, нейросетевых технологий, создания искусственного интеллекта.
Типовая блок-схема известного однослойного перцептрона на основе нейронов МакКаллока-Питса показана на фиг. 1 [1, 2, 4, 9-11, 16, 17].
На фиг. 1 приняты обозначения: (х1, х2,…, xn) - вектор входных сигналов, заданный в виде бинарного кода из 0 и 1; W - блок весовых коэффициентов; Р - перемножитель входных сигналов на весовые коэффициенты; Σ - сумматор; 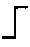 - пороговая функция; Y - выходной сигнал.
- пороговая функция; Y - выходной сигнал.
Блок-схема нейрона МакКаллока-Питса показана на фиг. 2.
На фиг. 2 приняты обозначения: (х1, х2,…, xn) - вектор входных сигналов, заданный в виде бинарного кода из 0 и 1; W - блок весовых коэффициентов; Р - перемножитель входных сигналов на весовые коэффициенты; Σ - сумматор; 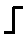 - пороговая функция; Y - выходной сигнал.
- пороговая функция; Y - выходной сигнал.
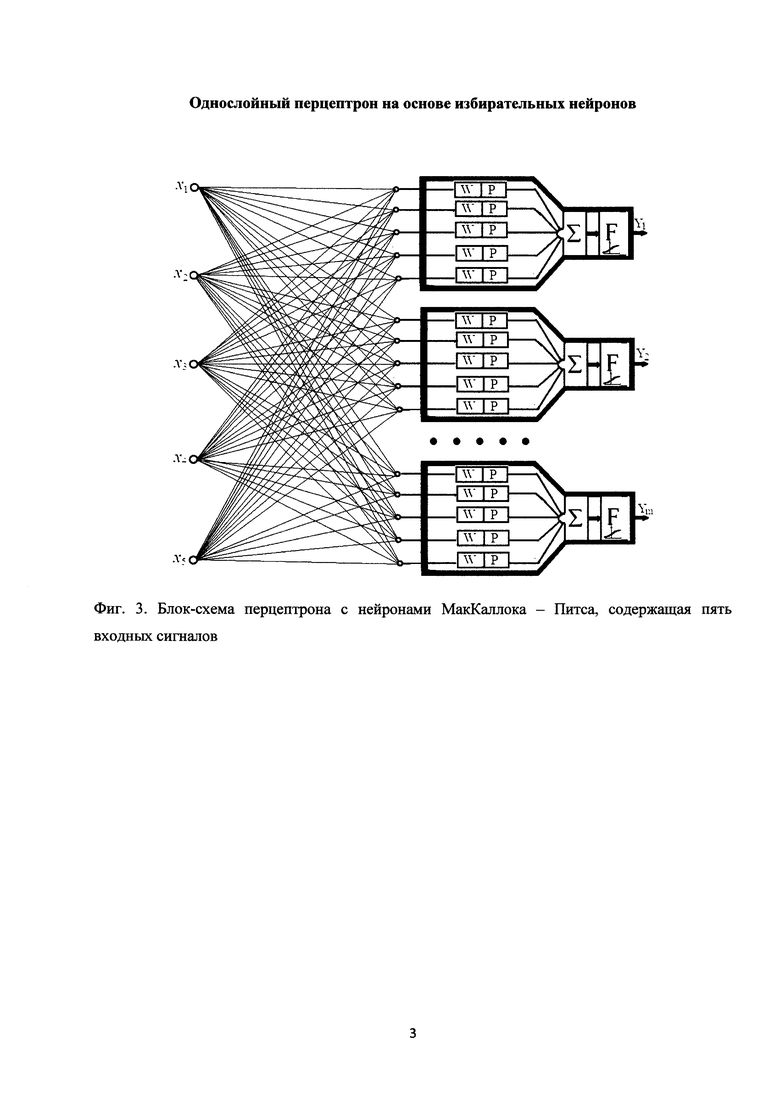
В дальнейшем мы будем использовать блок-схему перцептрона с нейронами МакКаллока-Питса, показанную, на примере пяти входных сигналов, на фиг. 3.
Свойства, недостатки однослойных перцептронов.
Перечислим свойства однослойных перцептронов [1, 4, 16, 17]: 1. Тип входных сигналов: бинарные; 2. Размерности входа и выхода ограничены при программной
реализации возможностями вычислительной системы, на которой моделируется нейронная сеть, при аппаратной реализации - технологическими возможностями; 3. Области применения: распознавание образов, классификация, использование в многослойных нейронных сетях в качестве одного слоя.
Известны недостатки однослойного перцептрона на основе искусственного нейрона МакКаллока-Питса [1, 4, 16, 17]: 1) однослойный перцептрон на основе искусственного нейрона МакКаллока-Питса неадекватен реальному биологическому перцептрону; 2) входными и выходными сигналами реального биологического нейрона являются кодовые комбинации в бинарном представлении; 3) в реальном биологическом нейроне весовой градации входных сигналов не производится, весовая градация искуственный прием, придуманный инженерами; 4) нейросетевые алгоритмы при использовании однослойного перцептрона на основе искусственного нейрона МакКаллока-Питса при большом количестве входных сигналов неустойчивы, увеличение входных сигналов даже на один требует полного перерасчета процессов в системе, такое недопустимо в реальной биологической системе [1, 2, 4, 16, 17]. Список недостатков можно продолжить.
Раскрытие изобретения.
Наиболее близким техническим решением к заявляемой модели однослойного перцептрона является модель однослойного перцептрона на основе искусственного нейрона МакКаллока-Питса, показанная на фиг. 1.
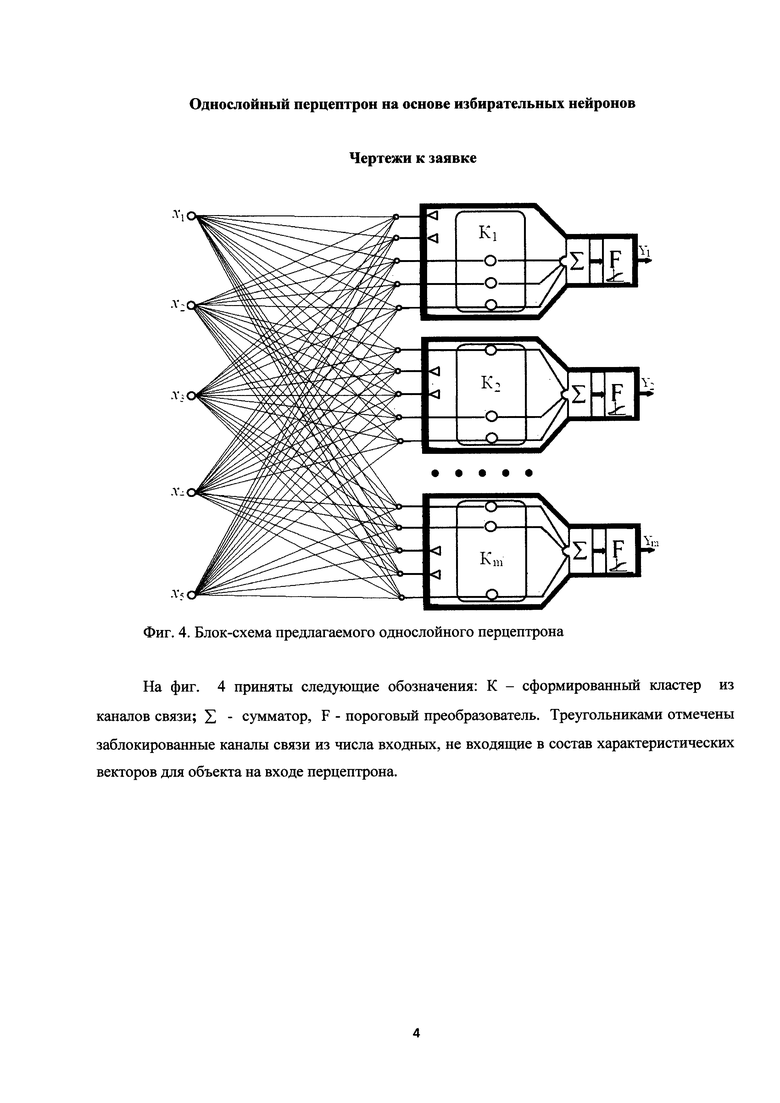
В связи с недостатками однослойного перцептрона на основе искусственного нейрона МакКаллока-Питса предлагается модель однослойного перцептрона, представляющая устройство, более адекватно отражающее функции реального однослойного перцептрона, блок-схема которого показана на фиг. 4.
На фиг. 4 приняты следующие обозначения: К - сформированный кластер из каналов связи; Σ - сумматор, F - пороговый преобразователь. Треугольниками отмечены заблокированные каналы связи из числа входных, не входящие в состав характеристических векторов для объекта на входе перцептрона.
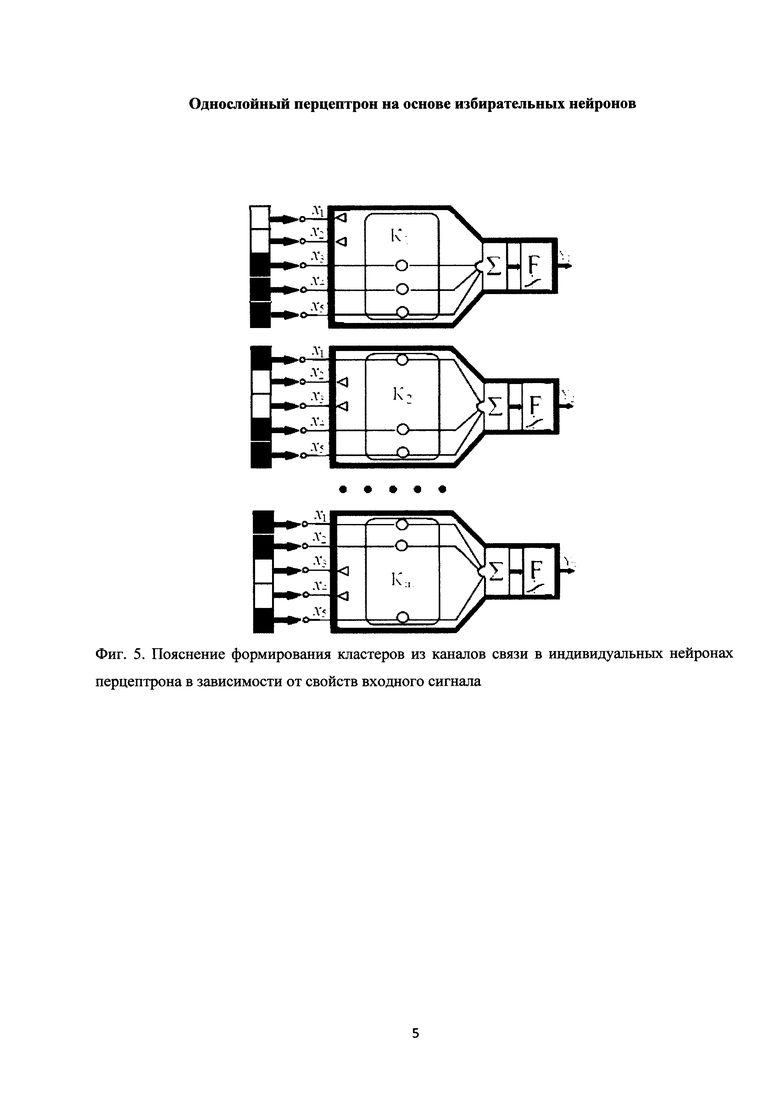
Пояснение формирования кластера из каналов связи в зависимости от свойств входного сигнала иллюстрируется фиг. 5.
Слева на фиг. 5 показаны три бинарные кодовые комбинации входного сигнала. Рамкой выделены кластеры из каналов связи, сформированные в соответствии с тремя характеристическими кодовыми комбинациями входного сигнала, то есть в соответствии со свойствами входного сигнала. Черной информативной ячейке кодовой комбинации соответствует цифра 1, белой не информативной ячейке соответствует цифра 0. Каналы
связи нейрона, соответствующие не информативным ячейкам, заблокированы символом треугольник, как показано на фиг. 5. Таким образом, предлагаемый однослойный перцептрон оказывается настроенным на три бинарные кодовые комбинации входного сигнала, приведенные слева.
В результате предложена следующая формула изобретения.
Перцептрон однослойный, включающий несколько регистрирующих нейронов, входы для сигналов от объектов, внутренние каналы связи от входов, в которых осуществляют умножение входных сигналов на весовые коэффициенты, далее полученные сигналы суммируют и производят их нелинейные пороговые преобразования; которые используют как выходные сигналы, отличающийся индивидуальными кластерами в каждом из регистрирующих нейронов перцептрона; кластеры формируют из части входных каналов связи отдельных нейронов; формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями входных сигналов; кластеры из каналов связи связывают с сумматорами; после сумматоров производят нелинейные пороговые преобразования сигналов; преобразованные сигналы используют как выходные сигналы.
Технические результаты, на достижение которых направлено изобретение
Технические результаты, на достижение которых направлено изобретение, следующие:
1. достижение избирательного распознавания входных объектов без использования весового взвешивания входных сигналов;
2. достижение возможности кодирования входного объекта определенного типа номером канала или номером регистрирующего нейрона;
3. сжатие входной информации, благодаря сохранению только той информации об объектах, которая попадают в заданный канал или регистрирующий нейрон;
4. повышение быстродействия работы предлагаемого однослойного перцептрона;
5. повышение надежности распознавания объектов при их большом количестве;
6. достижение значительно большей адекватности предлагаемого однослойного перцептрона реальному биологическому однослойному перцептрону.
Совокупность достигаемых технических результатов, указанных в пп. 1-6, достигается за счет следующей совокупности признаков, содержащихся в независимом пункте формулы:
1. индивидуальными кластерами из каналов связи в каждом из регистрирующих нейронов, кластеры формируют из части входных каналов связи отдельных нейронов; 2. формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями входных сигналов; 3. кластеры из части каналов связи связывают с сумматорами.
Эффективность предлагаемого перцептрона реально доказана в разработанных нами нейросетевых системах для распознавания:
1. Распознавание цифр;
2. Распознавание букв русского алфавита;
3. Распознавание текстов художественных произведений;
4. Распознавание автомобильных номеров;
5. Распознавание электрокардиограмм (ЭКГ);
6. Распознавание черно-белых портретов известных русских писателей и поэтов.
Системы, указанные в пп. 3, 5, 6, разработаны впервые и не имеют аналогов.
Раскрытие изобретения на биологическом уровне.
Может ли система дендритов на входе нейрона быть столь пластичной и лабильной, чтобы адекватным образом отражать входную информацию за счет изменения числа возбуждающих и тормозных дендритов. Ранее этот вопрос был изучен недостаточно. Однако в последнее время были сделаны ряд открытий, показавших наличие у дендритов совершенно необычных возможностей их роста, изменения количества и качества с помощью специальной системы шипиков [1-3, 5]. Установлено также наличие у дендритов активных свойств, похожих на свойства аксонов [5]. Все это вместе взятое доказывает возможность адаптации к отражению любой входной информации не за счет весовых функций дендритов, а за счет кластеризации дендритов, изменения их количества и качества. Под различным качеством дендритов понимается их свойства: дендриты возбуждающие и тормозные, различные по диаметру и электрической мощности и т.д.; возможность самоорганизации путем роста и гибели отдельных дендритов. В реальных условиях в организме человека или животного формирование эффективных связей в кластере происходит естественным образом за счет подкармливания работающих дендритов и уничтожения неработающих дендритов путем прекращения питания. Подкармливание дендритов происходит при прохождении по ним электрических импульсов. При этом в дендрит поступают строительные материалы в виде белков, АТФ, обеспечивающих дендриты энергетическими ресурсами, и других органелл. Регулирование питания происходит за счет снабжения АТФ и белковыми компонентами при прохождении электрических нервных импульсов. Если электрические нервные импульсы не проходят по дендриту, то питание не подается и он отмирает.
В связи с вышеизложенным предлагается следующая формула изобретения.
Перцептрон однослойный, включающий несколько регистрирующих нейронов, входы для сигналов от объектов, внутренние каналы связи от входов, в которых осуществляют умножение входных сигналов на весовые коэффициенты, далее полученные сигналы суммируют и производят их нелинейные пороговые преобразования; которые используют как выходные сигналы, отличающийся индивидуальными кластерами в каждом из регистрирующих нейронов перцептрона; кластеры формируют из части входных каналов связи отдельных нейронов; формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями входных сигналов; кластеры из каналов связи связывают с сумматорами; после сумматоров производят нелинейные пороговые преобразования сигналов; преобразованные сигналы используют как выходные сигналы.
Косвенное обоснование эффективности предлагаемого однослойного перцептрона следует из замечательной работы выдающегося нейрофизиолога и нейропсихолога проф. Е.Н. Соколова, разработавшего векторную теорию восприятия сенсорной информации и памяти головного мозга [7, 8, 12-15].
Рассмотрим базовые положения векторной теории восприятия, сформулированные в работе Е.Н. Соколова, достойные для подтверждения эффективности предлагаемого однослойного перцептрона. Отметим, что в работах Е.Н. Соколова в качестве входных объектов выступают слой нейронов, называемый Е.Н. Соколовым слоем предетектором. Предетекторы расположены в предшествующем нейронном слое. Сигналы от нейронов предетекторного слоя подаются на входы в слое нейронов, который следует считать однослойным перцептроном. Приведем дословно первые 10 пунктов из его работы, где содержатся основные результаты, полученные Е.Н. Соколовым и его школой [12-15].
1. Вектор возбуждения - это комбинация возбуждений ограниченного числа нейронов предетекторов, образующих нейронный ансамбль.
2. Вектор возбуждения предетекторов характеризуется постоянством своей длины при всех стимулах, воздействующих на данный ансамбль предетекторов.
3. Вектор возбуждения предетекторов воздействует параллельно на множество нейронов-предетекторов, образующих детекторную карту, на которой отображаются стимулы, воздействующие на ансамбль предетекторов.
4. Отображение стимулов на детекторной карте достигается синаптической специализацией детекторов: каждый детектор характеризуется особым набором разных по весу синапсов, образующих уникальный вектор синаптических контактов данного детектора.
5. Все векторы синаптических связей детекторов, получающих входы от данного ансамбля предетекторов, равны по своей длине.
6. Каждый детектор умножает пресинаптическое возбуждение на вес соответствующего синапса и суммирует эти произведения, выполняя формально операцию вычисления скалярного произведения вектора предетекторов и вектора синаптических связей данного детектора.
7. Скалярное произведение равных по длине векторов зависит только от угла между ними и достигает максимума, когда векторы совпадают по направлению.
8. Вектор синаптических связей данного детектора определяет его избирательную чувствительность в отношении определенного вектора возбуждения предетекторов, а, следовательно, и в отношении того стимула, который этот вектор возбуждения порождает.
9. Постоянство длины векторов синаптических связей детекторов означает, что детекторная карта представляет собой сферическую поверхность в пространстве, размерность которого определяется числом синапсов, связывающих детектор с предетекторами.
10. Максимальное возбуждение определенного детектора как элемента детекторной карты соответствует специфическому ощущению.
Теория векторного восприятия Е.Н. Соколова подкреплена серией нейрофизиологических экспериментов, реализованной учениками проф. Е.Н. Соколова [12-15]. Отметим некоторые базовые сходства и отличия положений векторной теории восприятия для подтверждения эффективности предлагаемого материального однослойного перцептрона.
1. Наличие характеристических свойств входного объекта в виде векторов возбуждения (п. 1). Вектор возбуждения - это комбинация возбуждений ограниченного числа нейронов предетекторов, образующих нейронный ансамбль и расположенных в слое, предшествующем слою, в котором расположен рассматриваемый однослойный перцептрон. Таким образом, проф. Е.Н. Соколовым утверждается наличие для объекта на входе однослойного перцептрона отдельных характеристических векторов. В
предлагаемом однослойном перцептроне характеристическими векторами можно считать характеристические кодовые комбинации входных объектов, что иллюстрируется фиг. 5.
2. Постоянство длины характеристических векторов возбуждения (пп. 2, 5). В предлагаемом однослойном перцептроне равенство длины характеристических векторов возбуждения отражено равенством числа каналов в специфических кластерах каждого из нейронов однослойного перцептрона.
3. Максимальное возбуждение определенного входного вектора соответствует специфическому ощущению (п. 10).
4. Существенным элементом новизны предлагаемого однослойного перцептрона является в отличие от нейронных сетей, изучаемых в работах Е.Н. Соколова, формирование в нейронах перцептрона не векторов возбуждения, а кластеров из каналов связи, которыми являются в реальных нейронах дендриты, связывающие входы нейрона с его сомой (телом нейрона). Кластеры из каналов связи в однослойном перцептроне формируются в соответствии с выходными характеристическими кластерами объекта на входе.
Существенно, что в целях нормирования интенсивности входных воздействий должно выполняться условие постоянства или практического равенства числа каналов связи в индивидуальных кластерах предлагаемого однослойного перцептрона.
Таким образом, можно сказать, что предлагаемый однослойный перцептрон является специфическим оригинальным устройством, представляющим материальное воплощение векторной теории проф. Е.Н. Соколова
Раскрытие математической теории предлагаемого изобретения.
Рассмотрим математическую теорию предлагаемого однослойного перцептрона. Обозначим возможные характеристические кодовые комбинации объектов на входе нейрона в виде векторов [6, 9, 10]
x1=(x11,…, x1n), x2=(х21,…, x2n);…; xm=(xm1,…, xmn),
где n - число элементов характеристической входной кодовой комбинации; m - число возможных входных объектов. Таким образом, имеется m векторов xi=(xi1,…, xin) размерностью n. В предлагаемом однослойном перцептроне кластеры из каналов связи представляет собой совокупность этих кодовых комбинаций. Вообще говоря, все возможные кодовые комбинации входных сигналов можно собрать в матрицу А, которую можно представить в виде
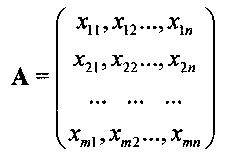
Пусть конкретный рассматриваемый нами нейрон содержит кластер связей, характеризуемый кодовой комбинацией в виде
xi=(xi1,…, xin)
При подаче на вход данного нейрона с номером i кодовой комбинации xk=(xk1,…, xkn) (из совокупности возможных объектов на входе нейрона) получаем сумму
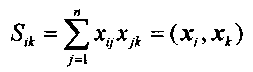
Сумму Sjk можно представить в виде
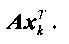
где 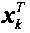 - транспонированный вектор-столбец из вектор-строки вектора xk.
- транспонированный вектор-столбец из вектор-строки вектора xk.
Все возможные суммы Sik (i=1,…, m; k=1,…, m) равны элементам матрицы В, равной
В=А*АТ,
где AT - транспонированная матрица к А.
Всего мы получим, очевидно, m2 сумм Sik (i=1,…, m; k=1,…, m). Наибольшими будут суммы Sii
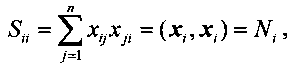
где Ni - число единиц в кодовой комбинации xi=(xi1,…, xin). Отметим следующее свойство сумм Sik при i≠k
Sik<Sii.
Это строгое неравенство справедливо, поскольку сумма Sik содержит в своем составе большее количество слагаемых, равных произведениям 1·0, чем сумма Sii. Это свойство можно качественно сравнить со свойством ортогональных векторов или ортогональных функций. Оно не является строгой ортогональностью, ее можно считать ортогональностью в качественном смысле. Свойства
Sii=Ni; Sik<Sii
как раз являются базовыми свойствами для распознавания входных объектов однослойным перцептроном, кодирования номером канала и ряда других приложений.
Рассмотрим приложение предлагаемого однослойного перцептрона для распознавания цифр.
Раскрытие предлагаемого изобретения в эксперименте при распознавании цифр
Рассмотрим пример распознавания 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Используются кодовые представления цифр, показанные ниже. На телевизионном экране с растром 4×6 располагаются цифры, взятые в системе Euclid. Система Euclid позволяет получить приемлемое кодирование цифр с помощью символов 0 и 1. Изображение цифр в системе Euclid приведено на фиг. 6.
Кодировка цифр, то есть их кодовые комбинации, приведены в таблице ниже.

Таблица кодовых комбинаций при распознавании цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 при их расположении в двумерном поле 4×6.
Кодовые комбинации объектов представляем в виде векторов
x1=(x11,…,x1n); x2=(x21,…,x2n); …; xm=(xm1,…,xmn),
где: n - число элементов кодовой комбинации; m - число объектов (цифр, m=10). Всего имеется m векторов с размерностью n (n=24). Ниже предполагается исследование в вычислительном эксперименте распознавание 10 объектов (цифр), на экране с числом пикселей в изображении 4×6, n=24. Кодовые комбинации образуют матрицу А 10×24, которую можно представить в виде
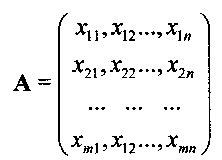
Транспонированная к А матрица равна
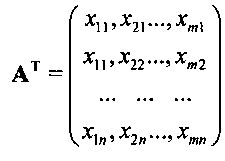
Получим скалярные произведения строк кодовой матрицы. Обозначим А матрицу кодов. Скалярные произведения равны строкам матрицы В
В=А*АТ,
где AT - транспонированная матрица к А. Программная реализация распознавания, написанная на языке Matlab-7, имеет вид

В=А.′;
С=А*В;
End
В результате работы программы получаем матрицу, позволяющую вычислить суммы на входе сумматора для каждого объекта (цифры).

Например, для объекта 3 - цифры 2 получаем столбец, в котором на третьей позиции сверху - диагональном члене матрицы стоит сумма цифр кодовой комбинации цифры 2 равная 14. На других позициях стоят цифры, равные сумме цифр от кодовых комбинаций других кластеров. Чтобы распознавание имело место, требуется, чтобы все эти суммы были меньше порогового значения U=14. Это как раз имеет место. Все сказанное имеет место для всех остальных объектов (цифр), что следует из приведенной
выше таблицы. Таким образом, с помощью предлагаемого однослойного перцептрона можно решать достаточно сложные задачи распознавания без использования сложных вычислений весовых коэффициентов. Приведенный пример иллюстрирует технологию формирования кластеров индивидуальных нейронов предлагаемого однослойного перцептрона и технологию распознавания.
Предлагаемый однослойный перцептрон был использован также для решения более сложных задач, например, для распознавания букв русского и английского алфавитов на экране с размерностью 300×200. Предлагаемый однослойный перцептрон также был успешно использован для распознавания слов с любым числом букв в слове, для распознавания трехсловных фраз из (5-7) буквенных слов и ряда других задач.
Заключение
Предлагаемый однослойный перцептрон обладает рядом существенных преимуществ перед однослойным перцептроном на основе искусственных нейронов МакКаллока-Питса. Предлагаемый однослойный перцептрон в значительно большей степени адекватен реальному однослойному перцептрону, если он является реальной частью нейронной сети. Это достигается благодаря использованию кластеризации входных каналов связи вместо их весового взвешивания, что как установлено в последнее время, является фундаментальным свойством дендритной системы связи входов нейрона с его телом (сомой) [1, 2].
Полезным свойством предлагаемого перцептрона в отличие от перцептрона Розенблатта, основанного на искусственном нейроне МакКаллока-Питса, является то, что при добавлении нового объекта или регистрирующего нейрона на выходе имеющиеся ранее кластеры не изменяются, добавляется лишь новый кластер в новом нейроне; при этом требуется минимальная коррекция возбуждающих и тормозных связей, обусловленных всей совокупностью объектов и нейронов.
Литература
1. Александров Ю.И., Анохин К.В., Соколов Е.Н., Греченко Т.Н. и др. Нейрон. Обработка сигналов. Пластичность. Моделирование. Фундаментальное руководство // Изд-во Тюменского государственного университета. 2008. 548 с.
2. Анохин К.В., Бурцев М.С., Ильин В.А., Киселев И.И., Кукин К.А., Лахман К.В., Параскевов А.В., Рыбка Р.Б., Сбоев А.Г., Твердохлебов Н.В. Современные подходы к моделированию активности культур нейронов in vitro / Математическая биология и биоинформатика. 2012. Т. 7. №2. С. 372-397.
3. Вызов А.Л. Электрофизиологические исследования сетчатки. М., Наука 1966 г., 196 с.
4. Вассерман Ф. Нейрокомпьютерная техника: Теория и практика. - М.: «Мир», 1992.
5. Гутман А. Дендриты нервных клеток: теория электрофизиология, функция. 1984.
6. Левитан Б.М. Почти-периодические функции. // ГИТТЛ. 1953. 396 с.
7. Лебедев А.Н. Константа М.Н. Ливанова в количественном описании психологических явлений. // Психологический журнал, 1997, выпуск 6. С. 96-105.
8. Лебедев А.Н. Психофизиология памяти. // Психофизиология. 2-е издание / под ред. Ю.И. Александрова / М.: из-во «Инфра-М», 2001. С. 128-141.
9. Мазуров М.Е. Решение диофантовых неравенств в задачах о синхронизации релаксационных колебаний / ЖВМ и МФ АН СССР. 1991. Т. 31. №11. С. 1619-1636.
10. Мазуров М. Е. Идентификация математических моделей нелинейных динамических систем // М.: - Ижевск. РХД. 2008. 284 с.
11. Минский М., Пейперт С. Персептроны = Perceptrons. М.: «Мир», 1971.
12. Соколов Е.Н. Принцип векторного кодирования в психлфизиологии. Вестник МГУ. Серия 14. Психология, 1995, №4.
13. Соколов Е.Н., Вайткявичус Г.Г. Нейроинтеллект: от нейрона к нейрокомпьютеру. М.: Наука, 1989.
14. Соколов Е.Н. Нейронные механизмы памяти и обучения. М., 1981.
15. Соколов Е.Н. Восприятие и условный рефлекс: новый взгляд. М., 2003.
16. Розенблатт Ф. Принципы нейродинамики: перцептроны и теория механизмов мозга. Principles of Neurodynamic: perceptrons and the theory of brain mechanisms. M.: «Мир», 1965.
17. Хайкин Саймон Нейронные сети: полный курс = Neural Networks: A Comprehensive Foundation. - 2-е изд. - М.: «Вильяме», 2006. - С. 1104. - ISBN 0-13-273350-1.



Изобретение относится к моделированию нейронных структур и может быть использовано в нейрокомпьютерах, технических системах на основе нейронных сетей для распознания образов, анализа и обработки изображений. Техническим результатом является обеспечение возможности достижения избирательного распознавания входных объектов без использования весового взвешивания входных сигналов, возможности кодирования входного объекта определенного типа номером канала или номером регистрирующего нейрона, сжатие входной информации, повышение быстродействия, повышение надежности распознавания объектов. Устройство содержит несколько регистрирующих нейронов, входы для сигналов от объектов, внутренние каналы связи от входов, индивидуальные кластеры в каждом из регистрирующих нейронов перцептрона, которые формируют из части входных каналов связи отдельных нейронов, формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями входных сигналов, кластеры из каналов связи связывают с сумматорами, после сумматоров производят нелинейные пороговые преобразования сигналов; преобразованные сигналы используют как выходные сигналы. 6 ил., 1 табл.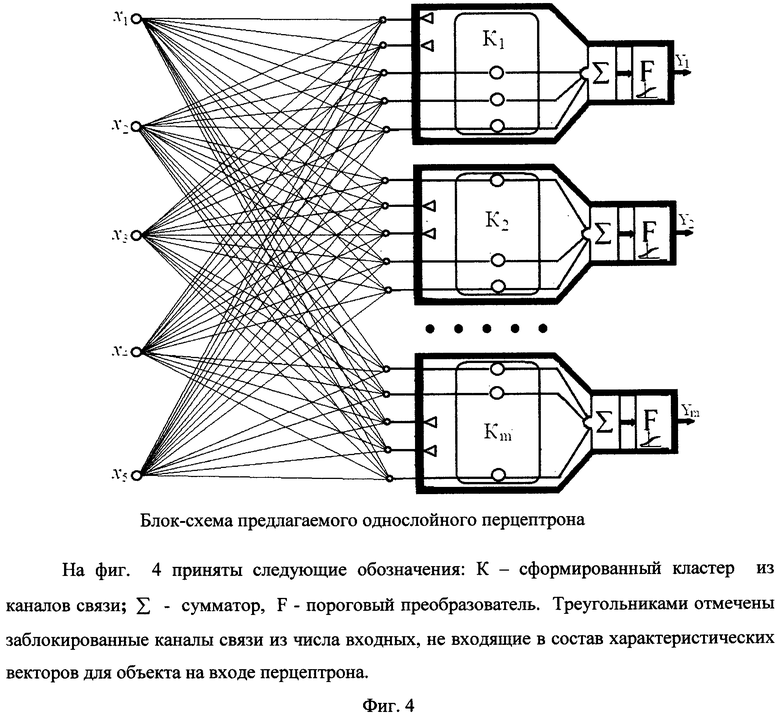
Перцептрон однослойный, включающий несколько регистрирующих нейронов, входы для сигналов от объектов, внутренние каналы связи от входов, в которых осуществляют умножение входных сигналов на весовые коэффициенты, далее полученные сигналы суммируют и производят их нелинейные пороговые преобразования; которые используют как выходные сигналы, отличающийся индивидуальными кластерами в каждом из регистрирующих нейронов перцептрона; кластеры формируют из части входных каналов связи отдельных нейронов; формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями входных сигналов; кластеры из каналов связи связывают с сумматорами; после сумматоров производят нелинейные пороговые преобразования сигналов; преобразованные сигналы используют как выходные сигналы.
| МОДЕЛЬ НЕЙРОНА | 1992 |
|
RU2034332C1 |
| МОДЕЛЬ НЕЙРОНА, РЕАЛИЗУЮЩАЯ ЛОГИЧЕСКУЮ ФУНКЦИЮ НЕРАВНОЗНАЧНОСТИ | 2003 |
|
RU2269155C2 |
| US 2014156574 A1, 05.06.2014 | |||
| US 2014317035 A1, 23.10.2014. | |||
Авторы
Даты
2016-09-10—Публикация
2015-01-13—Подача