Изобретение относится к моделированию нейронных структур и может найти применение при разработке нейрокомпьютеров, технических систем на основе нейронных сетей для распознания образов, создания искусственного интеллекта, анализа и обработки изображений и многих других приложений. Целью изобретения является расширение области применения нейронных сетей, основным элементом которых является однослойный перцептрон, нейросетевых технологий, создания искусственного интеллекта.
Типовая блок-схема известного однослойного импульсного перцептрона на примере пяти входных сигналов показана на фиг. 1 [1, 2, 4, 5, 9, 14, 17, 22, 28, 29].
Фиг. 1. Блок-схема известного однослойного импульсного перцептрона на примере пяти входных сигналов.
Требования к импульсному или спайковому нейрону, используемому в известном однослойном импульсном перцептроне
Сформулируем требования к импульсному или спайковому нейрону, используемому в известном однослойном импульсном перцептроне. В известном однослойном импульсном перцептроне используется импульсный или спайковый нейрон, более адекватный реальному биологическому нейрону, чем нейрон МакКаллока-Питса, блок-схема которого показана на фиг. 2 [1, 2, 3, 5, 7, 10, 11, 13, 15, 16, 18, 26-36].
Фиг. 2. Блок-схема известного импульсного (спайкового) нейрона.
На фиг. 2 приняты обозначения: (х1, х2,…, xn) - вектор входных сигналов, заданный в виде импульсных потоков; w1, w2, …, wN - весовые коэффициенты; Σ - синоптическое устройство для суммирования входных воздействий с весовыми коэффициентами; F - пороговый возбудимый элемент, генерирующий выходную импульсную последовательность или одиночный импульс при превышении сигналом на выходе сумматора порогового значения; Y - выходной сигнал. Механизм синаптического суммирования условно отражается общепринятым в нейробиологии символом для отображения синапса под знаком суммы Σ. Механизм генерирования выходной импульсной последовательности или одиночного импульса при превышении сигналом на выходе сумматора порогового значения условно отражается общепринятым в нейробиологии символом для отображения нейронного импульса. В дальнейшем мы будем использовать блок-схему импульсного нейрона в виде, показанном на фиг. 3
Фиг. 3. Блок-схема известного импульсного (спайкового) нейрона и выполняемые им функции.
На фиг. 3 приняты обозначения: КС - каналы связи (дендриты); W - устройства памяти, где сохраняются весовые коэффициенты, П - перемножители входных сигналов на весовые коэффициенты; Σ - синаптическое устройство для суммирования входных воздействий с весовыми коэффициентами; F - пороговый возбудимый элемент, генерирующий выходную импульсную последовательность или одиночный импульс при превышении сигналом на выходе сумматора порогового значения; Y - выходной сигнал.
В известном однослойном импульсном перцептроне используется известная модель импульсного нейрона. Рассмотрим более детально свойства и недостатки этой модели нейрона. На данный момент разработано большое количество моделей единичных нейронов: от пороговых моделей до биологоправдоподобных моделей [1, 2, 3, 5, 7, 10, 11, 13, 15, 16, 18, 26-36]. Известная модель нейрона состоит из следующих основных блоков: 1) блока для хранения или генерации весовых коэффициентов; 2) перемножителя; 3) синаптического устройства для суммирования импульсных потоков воздействий с весовыми коэффициентами; F - пороговый возбудимый элемент, генерирующий выходную импульсную последовательность или одиночный импульс при превышении сигналом на выходе сумматора порогового значения; Y - выходной сигнал.
Для изучения феноменов, наблюдаемых в нейронных сетях, необходимо понимание принципов функционирования нейронов. Нейроны являются с точки зрения реализации сложными генераторами импульсных сигналов, механизмы работы которых к настоящему моменту в определенной степени изучены.
Импульсный нейрон как элемент нейронной сети должен отвечать ряду требований [1, 2]. Основные из них: 1) способность генерирования потенциала действия, близкого по форме к потенциалу действия реального биологического нейрона; 2) способность генерирования пачек нейронов, близких по характеристикам (частоте, структуре и т.д.) пачкам реального биологического нейрона; 3) должен обладать пороговыми свойствами, свойством рефрактерности, как у реального биологического нейрона; 4) должен суммировать приходящие на вход импульсы от других нейронов, т.е. нейрон должен включать в себя устройство, называемое синапсом; 5) сами синапсы могут быть возбуждающими и тормозными и могут заметно отличаться по другим свойствам; 6) обладать способностью к адаптации по отношению к внешним воздействиям или пластичностью; 7) обладать рядом других свойств, менее значимых в первом приближении, но могущих быть существенными в приложениях.
Обычно выполнением указанных требований не задаются, а сразу используют математическую модель нейрона, подходящую с точки зрения пользователя. Например, математические модели нейрона Ходжкина-Хаксли, Ван дер Поля-Фитцхью, Хиндемарша-Розе и т.д. [29-36]. Второй немаловажный критерий - преодолимая сложность вычислений при использовании выбранной модели. Краткий список используемых в настоящее время математических моделей нейронов приведен в таблице [1, 2, 7, 11, 15, 29-36].

Ограниченность вычислительного ресурса породила множество упрощенных моделей, позволяющих, с одной стороны, удовлетворительно моделировать динамику единичных элементов, а с другой, эффективно использовать вычислительный ресурс. Эти модели стали называть феноменологическими.
Механизмы суммирования импульсных потоков в импульсном нейроне принципиально отличаются от суммирования бинарных сигналов в искусственном нейроне МакКаллока-Питса. Рассмотрим этот процесс более подробно.
Методы суммирования импульсных потоков в импульсном нейроне
Сравнительное пространственное распределение дендритов для нейронов различных типов по данным нейробиологических исследований иллюстрируется фиг. 4.
Фиг. 4. Сравнительное пространственное распределение дендритов для нейронов различных типов по данным нейробиологических исследований
На фиг. 4 показаны три вида нейронов, у которых в зависимости от их предназначения имеются различные организации кластера дендритов, являющихся входными каналами связи между телом нейрона и сенсорными системами, являющимися поставщиками входных сигналов. Суммирование импульсных потоков, выходящих из каналов связи, в реальном нейроне происходит специфическим образом, а именно, как пространственно-временное суммирование. Оно принципиальным образом отличается от интегрального синаптического суммирования в известном импульсном спайковом нейроне. Специфика следует из реального экспериментально известного устройства дендритов. Дендриты в виде тонких волокон по мере сближения с телом нейрона объединяются путем присоединения к более толстому волокну или друг с другом. В результате тонкие множественные волокна дендритов эволюционируют в меньшее количество (вплоть до одного) более толстых дендритов [19, 20].
Более толстые волокна могут опять объединяться в еще более толстые, образуя электрически мощные проводники токов от импульсных потоков.
При объединении дендритов происходит суммирование токов импульсных потоков в исходных волокнах дендритов. Таким образом, происходит безынерционное суммирование токов всех исходных импульсных потоков. При этом образуются иерархические дендритные деревья. Анализ функциональных свойств дендритов в связи с их структурой был изучен в основополагающей работе [19, 20]. В работе изучены: входное сопротивление дендритов, возникающие на них потенциалы при протекании в них импульсных потоков электрического тока, конвергенция дендритов. Конвергенция дендритов особенно представлена в нейронах головного мозга человека и животных. Конвергенция дендритов в звездчатой клетке коры мозжечка кошки изучена в работе В.В. Смолянинова [19, 20].
Роль синапсов в суммировании импульсных потоков
Импульсные потоки поступают в нейрон непосредственно от дендритов за счет соединения их биологических мембран, то есть возникает общая биологическая мембрана для дендритов и сомы нейрона [1, 2]. Другая часть импульсных потоков поступает в сому нейрона через синапсы, соединяющие дендрит с сомом нейрона. Синапс служит преобразователем электрического потенциала дендрита в химический медиатор и далее снова в электрический потенциал [1, 2]. Замечательной особенностью химических синапсов является их односторонняя проводимость. Они могут проводить электрический ток от дендрита к телу нейрона только в одном направлении. В обратном направлении электрический ток и потенциал не проводятся. Суммирование электрических потенциалов импульсных потоков после преобразования их синапсами происходит в соме нейрона. Таким образом, сами синапсы фактически не участвуют в суммировании импульсных потоков. Синапсы осуществляют одностороннюю проводимость от дендритов к соме. Таким образом, они защищают слабые электрические потенциалы дендритов от воздействия потенциала, возникающего в триггерной зоне вблизи аксона. Есть аргументированная гипотеза, что импульсные потоки, попадающие через химические синапсы, играют тонкую управляющую роль в генерации импульсного ответа нейрона.
В реальном биологическом нейроне количество синапсов на соме нейрона, как правило, значительно меньше, чем число дендритов, оканчивающихся на соме за счет общих мембран. Количество синапсов на теле нейрона варьирует от единиц до многих тысяч. Они присоединены к соме наряду с основаниями дендритов. Нейробиологические исследования свойств синапсов показывают, что в общей картине пространственно-временного суммирования импульсных последовательностей синапсы играют роль практически безынерционных преобразователей электрических импульсных последовательностей в химические и затем снова в электрические.
Фундаментальным свойством и предназначением синапсов является, по-видимому, их односторонняя проводимость по отношению к приходящим импульсным последовательностям. Временная константа синапсов при воздействии прямоугольных импульсов при их преобразовании заднего фронта по закону

имеет порядок 10 (1/мсек). Поэтому такие импульсы при суммировании можно считать безынерционными односторонними преобразователями.
Зачастую синапсы расположены не только на соме нейрона, но и на самих дендритах и импульсные потоки от них поступают к телу нейрона вместе с импульсными последовательностями от дендритов. Это иллюстрируется фиг. 5. В реальном биологическом нейроне количество синапсов на соме нейрона, как правило, значительно меньше, чем число дендритов, оканчивающихся на соме за счет общих мембран. Число синапсов на соме нейрона варьирует от единиц до сотен тысяч, что также иллюстрируется фиг. 5.
Фиг. 5. Расположение основных видов синапсов на теле нейрона: 1 - аксодендритический синапс; 2 - аксосоматический синапс; 3 - аксоаксонный синапс; 4 - дендрит; 5 - сома; 6 - аксонный холмик; 7 - аксон. На фиг. 5 вверху справа и на фиг.5 внизу показаны нейроны с большим количеством синапсов
Общие выводы по методам суммирования импульсных потоков в нейроне
Изложенное выше позволяет утверждать, что в большинстве случаев импульсные потоки суммируются безынерционным образом:
1) В самих дендритах в зонах их конвергенции или в соме нейрона при естественном слиянии дендрита с сомой при общей мембране. Это суммирование происходит последовательно путем конвергенции за счет все большего утолщения дендритов в распределенной области, где расположено дендритное дерево. Поскольку суммирование происходит на самих дендритах, представляющих из себя электрически проводящие резистивные каналы, то это суммирование является безынерционным практически мгновенным суммированием на резистивной нагрузке. Это свойство является принципиально необходимым для выделения максимальных значений оконечных импульсных потоков, подходящих к соме нейрона;
2) Часть импульсных потоков поступает в сому нейрона через синапсы, соединяющие дендрит с сомом нейрона. Синапс служит преобразователем электрического потенциала дендрита в химический медиатор и далее снова в электрический потенциал [1, 2]. Суммирование электрических потенциалов импульсных потоков после преобразования их синапсами происходит в соме нейрона. Таким образом, сами синапсы фактически не участвуют в суммировании импульсных потоков. Синапсы осуществляют одностороннюю проводимость от дендритов к соме. Таким образом, они защищают слабые электрические потенциалы дендритов от воздействия потенциала, возникающего в триггерной зоне вблизи аксона. Описанные выше механизмы суммирования импульсных потоков отражены в предлагаемом изобретении.
Раскрытие изобретения
Наиболее близким техническим решением к заявляемой модели однослойного перцептрона является однослойный перцептрон на основе импульсных нейронов, показанный на фиг. 1. Достаточно подробно известны недостатки однослойного перцептрона на основе искусственного импульсного нейрона [1, 2, 29-36]: 1) однослойный перцептрон на основе искусственных импульсных нейронов неадекватен реальному биологическому перцептрону; 2) в реальном биологическом нейроне весовой градации входных сигналов не производится, весовая градация - искусственный прием, придуманный инженерами; 3) нейросетевые алгоритмы при использовании однослойных перцептронов на основе искусственного импульсного нейрона при большом количестве входных сигналов требуют значительных вычислительных ресурсов; 4) увеличение входных сигналов даже на один требует полного перерасчета весовых коэффициентов. Список недостатков можно продолжить.
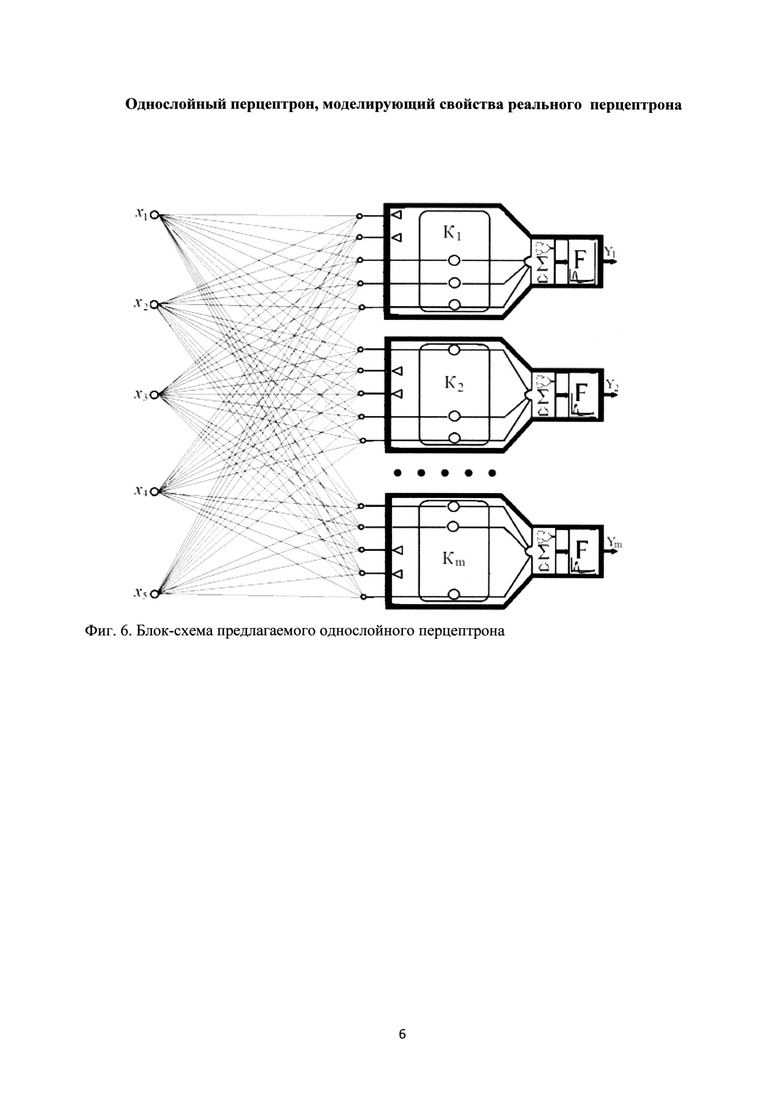
В связи с недостатками однослойного перцептрона на основе искусственных импульсных нейронов предлагается модель однослойного перцептрона, представляющая устройство на основе импульсных нейронов, содержащих кластеры из каналов связи, более адекватно отражающее функции реального однослойного перцептрона, блок-схема которого показана на фиг. 6.
Фиг. 6. Блок-схема предлагаемого однослойного перцептрона.
На фиг. 6 приняты следующие обозначения: К - сформированный кластер каналов связи; Σ - сумматор, F - пороговый преобразователь. Треугольниками отмечены заблокированные каналы связи из числа входных, не являющихся существенными характеристическими векторами для объекта на входе перцептрона.
Блок-схема импульсного нейрона, используемого в предлагаемом однослойном перцептроне, содержащего кластеры из каналов связи, более адекватно отражающего функции реального нейрона, показана на фиг. 7.
Фиг. 7. Блок-схема импульсного нейрона, используемого в предлагаемом однослойном перцептроне. Нейрон содержит кластеры из каналов связи, согласованные с входным объектом. Данный нейрон более адекватно отражает функции реального нейрона.
Поясним технологию формирования кластеров из каналов связи. Дадим пример однослойного перцептрона с импульсными нейронами, имеющими сформированные кластеры. Пояснение формирования кластеров каналов связей в зависимости от свойств входного сигнала иллюстрируется фиг. 8.
Фиг. 8. Пояснение формирования кластеров из каналов связи в индивидуальных нейронах перцептрона в зависимости от свойств входного сигнала.
Слева показаны три кодовые комбинации входного сигнала, в соответствии с которыми и формируется кластер каналов связи каждого нейрона. Черному цвету на кодовой комбинации соответствуют различные, произвольные периоды парциальных импульсных потоков, а белому цвету - отсутствие парциальных импульсных потоков. Рамкой выделены кластеры каналов связи, сформированные в соответствии с тремя характеристическими кодовыми комбинациями входного сигнала, то есть в соответствии со свойствами входного сигнала.
Каналы связи нейрона, соответствующие неинформативным ячейкам, заблокированы символом треугольник, как показано на фиг. 8. Таким образом, предлагаемый однослойный перцептрон оказывается настроенным на характеристические кодовые комбинации входного сигнала, приведенные слева.
Может ли система дендритов на входе нейрона быть столь пластичной и лабильной, чтобы адекватным образом отражать входную информацию за счет изменения числа возбуждающих и тормозных дендритов. Ранее этот вопрос был изучен недостаточно. Однако в последнее время был сделан ряд открытий, показавших наличие у дендритов совершенно необычных возможностей их роста, изменения количества и качества с помощью специальной системы шипиков [1, 2, 6]. Установлено также наличие у дендритов активных свойств, похожих на свойства аксонов [1, 2, 6]. Все это вместе взятое доказывает возможность адаптации к отражению любой входной информации не за счет весовых функций дендритов, а за счет кластеризации дендритов, изменения их количества и качества. Под различным качеством дендритов понимаются их свойства: дендриты возбуждающие и тормозные, различные по диаметру и электрической мощности и т.д.; возможность самоорганизации путем роста и гибели отдельных дендритов. В реальных условиях в организме человека или животного формирование эффективных связей в кластере происходит естественным образом за счет подкармливания работающих дендритов и уничтожения неработающих дендритов путем прекращения питания. Подкармливание дендритов происходит при прохождении по ним электрических импульсов. При этом в дендрит поступают строительные материалы в виде белков, АТФ, обеспечивающих дендриты энергетическими ресурсами, и других органелл. Регулирование питания происходит за счет снабжения АТФ и белковыми компонентами при прохождении электрических нервных импульсов. Если электрические нервные импульсы не проходят по дендриту, то питание не подается, и он отмирает.
В связи с вышеизложенным предлагается следующая формула изобретения.
Перцептрон однослойный, включающий несколько регистрирующих импульсных нейронов, входы для входных сигналов-импульсных потоков, внутренние каналы связи от входов, в которых производят умножение входных сигналов на весовые коэффициенты и отправляют на сумматоры, связанные с пороговыми нелинейными возбудимыми элементами, генерирующими выходные одиночные импульсы или импульсные последовательности при превышении сигналами на выходах сумматоров порогового значения возбудимого нелинейного элемента, которые используют как выходные сигналы;
Отличающийся индивидуальными кластерами из части каналов связи в каждом из регистрирующих нейронов, которые пропускают часть входных сигналов; формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями и структурой периодов парциальных составляющих входных импульсных потоков; далее производят безынерционное суммирование всех парциальных импульсных потоков на выходах кластеров; это реализуется для сигнала в виде суммарных импульсных потоков на выходах кластеров ε-почти-периодов с максимальной суммой амплитуд всех парциальных импульсных потоков; после безынерционного суммирования производят преобразование полученного сигнала пороговыми возбудимыми элементами, которые генерируют одиночные импульсы или импульсные последовательности при превышении максимальной суммой амплитуд импульсных потоков порогового значения возбудимых элементов, которые используют как выходные сигналы.
Технические результаты, на достижение которых направлено изобретение
Технические результаты, на достижение которых направлено изобретение, следующие:
1) достижение избирательного распознавания входных объектов без использования весового взвешивания входных сигналов;
2) достижение возможности кодирования предлагаемым избирательным однослойным перцептроном входного объекта определенного типа номером канала или номером регистрирующего нейрона;
3) сжатие входной информации благодаря сохранению только той информации об объектах, которая попадает в заданный канал или регистрирующий нейрон;
4) повышение быстродействия работы предлагаемого однослойного перцептрона;
5) повышение надежности распознавания объектов при их большом количестве;
6) достижение значительно большей адекватности предлагаемого однослойного перцептрона реальному биологическому однослойному перцептрону.
Совокупность достигаемых технических результатов, указанных в п. 1-6, достигается за счет следующей совокупности признаков, содержащихся в независимом пункте формулы:
1) индивидуальными кластерами из каналов связи в каждом из регистрирующих нейронов, кластеры формируют из части входных каналов связи отдельных нейронов;
2) формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями входных сигналов;
3) кластеры из части каналов связи связывают с сумматорами.
Эффективность предлагаемого перцептрона реально доказана в разработанных нейросетевых системах для распознавания:
1. Распознавание цифр;
2. Распознавание букв русского алфавита;
3. Распознавание текстов художественных произведений;
4. Распознавание автомобильных номеров;
5. Распознавание электрокардиограмм (ЭКГ);
6. Распознавание черно-белых портретов известных русских писателей и поэтов.
Системы, указанные в п. 3, 5, 6, разработаны впервые и не имеют аналогов.
Еще одно обоснование эффективности предлагаемого однослойного перцептрона
Косвенное обоснование эффективности предлагаемого однослойного перцептрона следует из замечательной работы выдающегося нейрофизиолога и нейропсихолога профессора Е.Н. Соколова, разработавшего векторную теорию восприятия сенсорной информации и памяти головного мозга [9, 21-24].
Рассмотрим базовые положения векторной теории восприятия, сформулированные в работе Е.Н. Соколова, которые можно использовать для подтверждения эффективности предлагаемого однослойного перцептрона. В работах Е.Н. Соколова в качестве входных объектов выступают предшествующий слой нейронов, называемый Е.Н. Соколовым предетектором. Сигналы от нейронов предетекторного слоя подаются на входы в слое нейронов, который следует считать однослойным перцептроном. Приведем некоторые из пунктов работы, где содержатся основные результаты, полученные Е.Н. Соколовым и его школой [9, 21-24].
1. Вектор возбуждения - это комбинация возбуждений ограниченного числа нейронов предетекторов, образующих нейронный ансамбль.
2. Вектор возбуждения предетекторов характеризуется постоянством своей длины при всех стимулах, воздействующих на данный ансамбль предетекторов.
5. Все векторы синаптических связей детекторов, получающих входы от данного ансамбля предетекторов, равны по своей длине.
10. Максимальное возбуждение определенного детектора как элемента детекторной карты соответствует специфическому ощущению.
Теория векторного восприятия Е.Н. Соколова подкреплена серией нейрофизиологических экспериментов, реализованной учениками проф. Е.Н. Соколова [9, 21-24]. Отметим некоторые базовые сходства и отличия положений векторной теории восприятия для подтверждения эффективности предлагаемого материального однослойного перцептрона.
1. Наличие характеристических свойств, векторов входного объекта (п. 1). Вектор возбуждения - это комбинация возбуждений ограниченного числа нейронов предетекторов, образующих нейронный ансамбль и расположенных в слое, предшествующем слою, в котором расположен рассматриваемый однослойный перцептрон. Таким образом, проф. Е.Н. Соколовым утверждается наличие для объекта на входе однослойного перцептрона отдельных характеристических векторов. В предлагаемом однослойном перцептроне характеристическими векторами можно считать характеристические кодовые комбинации входных объектов.
2. Постоянство длины характеристических векторов возбуждения (п.п. 2, 5). В предлагаемом однослойном перцептроне равенство длины характеристических векторов возбуждения отражено равенством числа каналов в специфических кластерах каждого из нейронов однослойного перцептрона.
3. Максимальное возбуждение определенного входного вектора соответствует специфическому ощущению (п. 10).
Существенным элементом новизны предлагаемого однослойного перцептрона является в отличие от нейронных сетей, изучаемых в работах Е.Н. Соколова, формирование в нейронах перцептрона не векторов возбуждения, а кластеров из каналов связи, которыми являются в реальных нейронах дендриты, связывающие входы нейрона с его сомой (телом нейрона). Кластеры из каналов связи в однослойном перцептроне формируются в соответствии с выходными характеристическими кластерами объекта на входе. Существенно, что в целях нормирования интенсивности входных воздействий должно выполняться условие постоянства или практического равенства числа каналов связи в индивидуальных кластерах предлагаемого однослойного перцептрона.
Таким образом, можно сказать, что предлагаемый однослойный перцептрон является специфическим оригинальным устройством, представляющим материальное воплощение векторной теории проф. Е.Н. Соколова.
Раскрытие математической теории изобретения. Первая математическая теория изобретения
Рассмотрим математическую теорию предлагаемого однослойного перцептрона. Обозначим возможные характеристические кодовые комбинации объектов на входе нейрона в виде векторов
x1=(xl1,…,x1n); …; xm=(xm1, …, xmn),
где n - число элементов кодовой комбинации; m-число возможных объектов. Все компоненты векторов считаем равными xij=А, либо xij=0. Таким образом, имеется m векторов xi=(xi1, …, xin) с размерностью n. В предлагаемом нейроне кластер связей представляет собой одну из этих кодовых комбинаций. Вообще говоря, все возможные кодовые комбинации образуют матрицу А, которую можно представить в виде

Пусть конкретный рассматриваемый нами нейрон содержит кластер связей, характеризуемый кодовой комбинацией в виде
xi=(xi1, …, xin).
При подаче на вход данного нейрона с номером i кодовой комбинации входного паттерна xk=(xk1, …, xkn) (из совокупности возможных на входе нейрона) получаем сумму

Всего мы получим m сумм Sik k=(1, …, m). Наибольшей будет сумма Sii
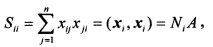
где NiA - число единиц в кодовой комбинации xi=(xi1, …, xin). Значение NiA принимается пороговым значением нейронов. Превышение этого значения приводит к появлению на выходе нейрона импульса или последовательности импульсов. Отметим следующее свойство сумм Sik
Sik<Sii.
Это строгое неравенство справедливо, поскольку сумма Sik содержат в своем составе большее количество слагаемых, равных произведениям 1·0, чем сумма Sii. Это свойство можно качественно сравнить со свойством ортогональных векторов или ортогональных функций. Оно не является строгой ортогональностью, ее можно считать ортогональностью в качественном смысле. Свойство может быть полезным при использовании предлагаемого динамического нейрона для распознавания объектов, кодировании номером канала и ряде других приложений. Вообще все возможные значения сумм Sij равны элементам матрицы В, равной
B=AAT,
где AT - транспонированная матрица к А.
Как следует из приведенного математического анализа предлагаемого однослойного импульсного перцептрона, кластеризация каналов связи в нейронах перцептрона обеспечивает следующие фундаментальные функции перцептрона: 1) избирательность к определенным свойствам паттернам входного объекта; 2) избирательное распределение паттернов по каналам на выходе перцептрона или то, что называют кодированием номером канала.
Таким образом, первая математическая теория, применяемая для раскрытия изобретения, позволяет: 1) описать избирательные свойства однослойного паттерна; 2) произвести нормирование кластеров из каналов связи за счет уравнивания числа каналов в кластере; 3) оценить величину артефактов при выделении конкретных каналов; 4) осуществить кодирование по номеру канала; 5) удалять избыточную входную информацию путем отсеивания информации, на которую кластеры каналов не настроены. Отметим сразу, что фундаментальные свойства почти-периодических функций (о чем подробнее будет сказано далее) не позволяют осуществить избирательное выделение входных паттернов и избирательное распределение по каналам на выходе однослойного перцептрона, то есть осуществить кодирование номером канала. Все перечисленные выше свойства могут быть достигнуты именно благодаря управляемой кластеризации каналов связи каждого из нейронов, входящих в состав однослойного перцептрона.
Раскрытие второй математической теории изобретения в части математической теории преобразования импульсных потоков нейроном с помощью фундаментальных свойств почти-периодических функций
Импульсная электрическая активность нейронов создает в нервной системе импульсные потоки. В первом приближении эти потоки представляют суммы периодических импульсных функций. Периодическая импульсная функция задана на интервале [0,∞), имеет период Tt, то есть 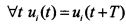 . Импульсные последовательности нейронов для исследования процессов суммации в первом приближении можно аппроксимировать последовательностями прямоугольных импульсов ν(t) с периодом Т=1/ƒ (ƒ - частота). На интервале периода
. Импульсные последовательности нейронов для исследования процессов суммации в первом приближении можно аппроксимировать последовательностями прямоугольных импульсов ν(t) с периодом Т=1/ƒ (ƒ - частота). На интервале периода
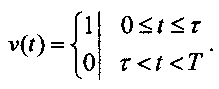
Общий импульсный поток равен сумме парциальных импульсных потоков, являющихся периодическими функциями

где ui(t) - отдельные парциальные импульсные потоки (i=1, …, N) с периодами Ti. Результирующий импульсный поток является равномерной почти-периодической функцией [7-9]. Основным свойством равномерных почти-периодических функций является существование для любого сколь угодно малого числа ε, соответствующего ε-почти-периода Tε, обладающих свойством
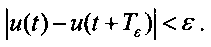
Другое фундаментальное свойство почти-периодической функции: ε-почти-периоды лежат на оси времени [0,∞) всюду плотно. Множество Е действительных чисел называется всюду плотным, если существует такое число l>0, что в каждом интервале действительной оси длины l (α<x<α+l) найдется хотя бы одно число множества Е [7-9]. Рассмотрим теорему Кронекера, являющуюся следствием базовой теоремы для теории почти-периодической функции [8, 10, 11].
Теорема. Пусть T1, Т2, …, TN - произвольные действительные числа. Каково бы ни было число положительное число ε, можно указать такое положительное число L=L(ε), что в каждом интервале длины L найдется по крайней мере одно число τ, удовлетворяющее системе неравенств

где ni - натуральные числа. Согласно теореме Кронекера существует ε-почти-период почти-периодической функции, удовлетворяющей соотношению (1). Согласно фундаментальному свойству почти-периодических функций существует t, такое что
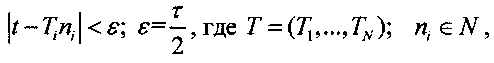
то  ; t-ε<t<t+ε.
; t-ε<t<t+ε.
При этом существует ε-почти-период функции
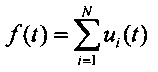
такой, что 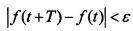 . После прохождения нелинейного преобразователя с характеристикой F получим на его выходе импульсную последовательность
. После прохождения нелинейного преобразователя с характеристикой F получим на его выходе импульсную последовательность
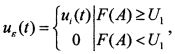
при этом |uε(t+Tε)-uε(t)|<ε.
Сумма нескольких импульсных последовательностей представляет собой равномерную почти-периодическую функцию [8, 10, 11]. Согласно теореме Кронекера такая функция имеет сгущения и разряжения импульсов, следующие с интервалами ε-почти-периодов. Рассмотрим иллюстрацию ε-почти-периодов. Сигналы на входах и на выходах нейронов можно представить в виде суммы почти-периодических функций, как показано на фиг. 9 слева, суммарный импульсный поток показан выше оси времени на фиг. 9 справа.
Фиг. 9. Схематическое изображение последовательности электрических импульсов нейрона в виде прямоугольных импульсов слева. Четыре импульсные последовательности с периодами T1-T4, ε-почти-период приблизительно равен Tε=8T1=4T2=3T3=2T4. ε-почти-период заключен между двумя максимумами. Сгущения и разрежения для импульсных потоков с несоизмеримыми периодами следования импульсов 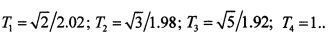 показаны справа.
показаны справа.
Максимальная амплитуда суммы импульсов достигается через ε-почти-период и равна 4А=2, где А - амплитуда импульса, равная 0,5. В пределах 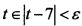 происходит суммирование амплитуд импульсов, происходящее через каждые ε-почти-периоды. Следствие из теоремы аппроксимации показывает возможность использования почти периодических функций в задачах нейроинформатики. Известно, что для возбуждения нейрона необходимо, чтобы сумма импульсов, пришедших по дендритам, превышала порог возбуждения. Специфическое свойство почти-периодических функций - существование ε-почти-периодов - позволяет осуществить это требование.
происходит суммирование амплитуд импульсов, происходящее через каждые ε-почти-периоды. Следствие из теоремы аппроксимации показывает возможность использования почти периодических функций в задачах нейроинформатики. Известно, что для возбуждения нейрона необходимо, чтобы сумма импульсов, пришедших по дендритам, превышала порог возбуждения. Специфическое свойство почти-периодических функций - существование ε-почти-периодов - позволяет осуществить это требование.
Для раскрытия изобретения из приведенной выше второй математической теории следует, что фундаментальные свойства почти-периодических функций позволяют осуществить безынерционное суммирование парциальных импульсных потоков и образование максимальных значений амплитуд, следующих через почти-периоды почти-периодической функции, которой является результирующий импульсный поток.
Вторая математическая теория, применяемая для раскрытия изобретения, позволяет описать механизмы безынерционного суммирования импульсных потоков, приходящих в сому нейрона для последующего порогового возбуждения генератора отдельных импульсов или последовательностей. Очень важно, что другого эффективного механизма суммирования максимальных значений импульсных потоков не существует в биологии, физике, математике. Нет также другого более эффективного носителя информации в нейробиологии, кроме импульсных потоков. Имеется естественный способ генерирования импульсных потоков с помощью возбудимой ткани, реагирующей на превышение порога возбуждения одним или серией импульсов. Совокупность таких возбуждений образует импульсный поток.
Инженеры, специалисты, ученые знают, что бинарные последовательности хороши для анализа работы нейронных сетей на быстродействующих ЭВМ, но категорически непригодны в качестве носителей информации в нейробиологии.
На основании экспериментальных фактов в нейробиологии установлено в первом приближении одинаковое значение импульсных потоков, приходящих непосредственно от дендритов и импульсных потоков, приходящих через синапсы. Установлено, что величина максимального значения импульсного потока на основании фундаментальных свойств почти-периодических функций обусловлена максимальным значением суммы импульсных потоков, приходящих непосредственно по дендритам и через синапсы. Естественно учитывается роль возбуждающих (положительных) и тормозных (отрицательных) синапсов.
Механизмы безынерционного суммирования импульсных потоков, приходящих в сому нейрона для последующего порогового возбуждения генератора отдельных импульсов или последовательностей, обладают свойствами инвариантности, позволяющими реализовать безынерционное суммирование устойчиво и надежно.
Существенно, что различие периодов парциальных импульсных потоков, поступающих на входы, в первом приближении не оказывает влияния на максимальное значение их суммы, автоматически получаемое благодаря фундаментальным свойствам почти-периодических функций. Это обусловлено тем, что максимальные значения почти-периодической функции, представляющей результирующий импульсный поток, не зависят от того, какая часть периодов парциальных импульсных потоков, составляющих весь импульсный поток, имеет те или иные периоды. То есть максимальное значение не зависит от структуры периодов составляющих импульсного потока. Это базовое свойство почти-периодических функций делает механизм образования максимального значения устойчивым, а саму систему безынерционного суммирования на основе фундаментальных свойств почти-периодических функций надежной в реальных условиях. Вывод такой: все составляющие парциальные потоки могут иметь либо один и тот же период следования, либо различные периоды, в крайнем случае, все парциальные импульсные потоки могут иметь различные периоды следования, образуя как бы мозаику периодов. Общее максимальное значение суммы максимальных значений парциальных периодов, следующее через ε-почти период будет одно и то же, оно равно

где Ai, Bj - максимальные значения амплитуд возбуждающих и тормозных парциальных импульсных потоков.
Рассмотрим более подробно свойства инвариантности безынерционного суммирования парциальных импульсных потоков. Инвариантность общего импульсного потока имеет место по двум основным параметрам импульсного потока: по мозаике периодов парциальных импульсных потоков и по количеству отдельных парциальных составляющих в общем потоке. Покажем это математически. Значение максимальной суммы общего импульсного потока в случае парциальных импульсных потоков с периодами T1, T2, …, Tl равно
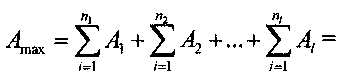
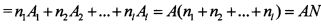
где N - общее количество парциальных импульсных потоков. Независимость максимальной амплитуды общего импульсного потока от мозаики периодов парциальных импульсных потоков следует из фундаментальных свойств почти-периодических функций, а именно, от парциальных периодов зависит ε-почти-период, а величина Amax от ε-почти-периода не зависит. Отсюда и следует инвариантность Amax от мозаики периодов парциальных импульсных потоков.
Раскрытие изобретения в вычислительном эксперименте
Рассмотрим процесс формирования кластеров в предлагаемом однослойном перцептроне в вычислительном эксперименте. Рассмотрим 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. На телевизионном экране с растром 4×6 располагаются цифры. Для цифр взята система Euclid. Система Euclid позволяет получить приемлемое кодирование цифр с помощью символов 0 и 1. Изображение цифр в системе Euclid приведено на фиг. 10.
Фиг. 10. Изображение цифр в системе Euclid.
Кодировка цифр, то есть значения входных сигналов - векторов x1=(xl1, …, xln); …; xm=(xm1, …, xmn), приведена в таблице 1. В дальнейшем полагаем, что значению единица соответствует период импульсной последовательности Т1=0.8, значению ноль - Т2=1.2

Таблица кодовых комбинаций при распознавании цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 при их расположении в двумерном поле 4×6.
Рассмотрим однослойный перцептрон, у которого в 2-х нейронах на выходе сформированы кластеры, настроенные на цифры 2 и 8. Более подробно описание формирования кластеров приведено ниже. Нейроны со сформированными кластерами показаны на фиг. 11. С левой стороны от изображения нейронов приведены бинарные кодовые комбинации цифр 2 и 8, в соответствии с которыми и формируется кластер каналов связи каждого нейрона. Каждая черная клетка отражает парциальный импульсный поток с определенным периодом следования. Совокупность черных клеток отражает результирующий импульсный поток.
Фиг. 11. Пример предлагаемых импульсных нейронов, имеющих сформированные кластеры по кодовым комбинациям цифры 2 - сверху, по кодовым комбинациям цифры 8 - снизу. Каждая черная клетка отражает парциальный импульсный поток с определенным периодом следования. Совокупность черных клеток отражает результирующий импульсный поток. Белому цвету соответствует отсутствие парциальных импульсных потоков.
Полагаем, что черному цвету соответствуют парциальные импульсные потоки с периодами 0.8, количество этих потоков равно 7, и импульсные потоки с периодами 1.2, количество этих потоков равно 7. Общее количество потоков равно 14, амплитуда каждого из парциальных потоков А=1. Взаимодействие импульсных последовательностей с периодами T1=0.8 и Т2=1.2 иллюстрируется фиг. 12 сверху. На фиг. 12 снизу показано взаимодействие импульсных последовательностей с периодами T1=0.9 и T2=1.2.
Фиг. 12. Иллюстрация инвариантности безынерционного суммирования, основанного на фундаментальных свойствах почти-периодических функций, относительно периодов парциальных импульсных потоков. Показано на рисунке сверху взаимодействие 7-ми импульсных последовательностей с периодами Т1=0.8 и амплитудами A=1 и 7-ми импульсных последовательностей с периодами T2=1.2 и амплитудами А=1 ε-почти-период равен 2.4. На фиг. 12 снизу показано взаимодействие 7-ми импульсных последовательностей с периодами T1=0.9 и амплитудами А=1 и 7-ми импульсных последовательностей с периодами Т2=1.2 и амплитудами А=1; ε-почти-период равен 3.6.
Фиг. 12 иллюстрирует свойства инвариантности безынерционного суммирования, основанного на фундаментальных свойствах почти-периодических функций, относительно периодов парциальных импульсных потоков. Видно, что максимальное значение суммы парциальных импульсных потоков остается неизменным и равным 14.
Инвариантность безынерционного суммирования, основанного на фундаментальных свойствах почти-периодических функций, относительно количества импульсов в парциальных импульсных потоках иллюстрируется фиг. 13.
Фиг. 13. Иллюстрация инвариантности безынерционного суммирования, основанного на фундаментальных свойствах почти-периодических функций, относительно количества импульсов в парциальных импульсных потоках. На фиг.13 слева показано взаимодействие 7-ми импульсных последовательностей с периодами Т1=0.8 и амплитудами А=1 и 7-ми импульсных последовательностей с периодами Т2-1.2 и амплитудами А=1. ε-почти-период равен 2.4. Импульсные потоки с периодом 0.8 показаны пунктирной линией, импульсные потоки с периодом 1.2 показаны сплошной линией. На фиг.13 справа показано взаимодействие 9-ти импульсных последовательностей с периодами Т1=0.8 и амплитудами А=1 и 5-ти импульсных последовательностей с периодами Т2=1.2 и амплитудами А=1. ε-почти-период равен 2.4.
Полагаем, что общее количество импульсов, характеризующих входной паттерн, равно 14. Импульсы с меньшим периодом следования показаны пунктирной линией. На фиг.13 слева показано взаимодействие 7-ми импульсных последовательностей с периодами T1=0.8 и амплитудами А=1 и 7-ми импульсных последовательностей с периодами T2=1.2 и амплитудами А=1. ε-почти-период равен 2.4. На фиг.13 справа показано взаимодействие 9-ти импульсных последовательностей с периодами Т1=0.8 и амплитудами А=1 и 5-ти импульсных последовательностей с периодами T2=1.2 амплитудами А=1. ε-почти-период равен 2.4. Видно, что максимальное значение суммы парциальных импульсных потоков остается неизменным и равным 14.
В заключение рассмотрим на примере, как происходит распознавание цифры 2 из 10-ти возможных цифр импульсным нейроном, кластер из каналов связи которого настроен на цифру 2. Импульсный нейрон, кластер из каналов связи которого настроен на цифру 2, реагирует на цифру 2, как показано на фиг. 12 сверху. При этом происходит взаимодействие 7-ми импульсных последовательностей с периодами Т1=0.8 и амплитудами А=1 и 7-ми импульсных последовательностей с периодами Т2=1.2 и амплитудами А=1, при этом ε-почти-период равен 2.4. Отметим, что для кодовых комбинаций цифры 2 и цифры 8 справедливы соотношения
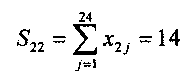
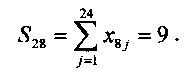
Таким образом, если порог Uпор=14, то нейрон, кластер которого сформирован по кодовым комбинациям цифры 2, идентифицирует эту цифру и не реагирует на кодовую комбинацию цифры 8, поскольку S28<S22 или 9<10. С другой стороны, когда нейрон, настроенный на цифру 2, реагирует на эту цифру, другие нейроны, общее число которых равно 10, на эту цифру не реагируют, поскольку для них S2i<14(i≠2). Мы привели простейший пример использования предлагаемого однослойного перцептрона для распознавания цифр. Предлагаемый однослойный перцептрон был использован для решения более сложных задач, например для распознавания букв русского алфавита, распознавания слов, распознавания фраз. Предлагаемый однослойный перцептрон может быть использован также для решения и различных других прикладных задач.
Заключение
Можно сделать заключение, что два механизма обработки импульсных потоков на основе управляемой кластеризации входных каналов связи и на основе фундаментальных свойств почти-периодических функций позволяют в целом реализовать основные функции однослойного перцептрона: 1) избирательность к определенным свойствам или паттернам входного объекта; 2) избирательное распределение паттернов по каналам на выходе перцептрона или то, что называют кодированием номером канала. Предлагаемый однослойный перцептрон позволяет осуществить безынерционное устойчивое, независимое от периодов парциальных импульсных потоков суммирование амплитуд парциальных импульсных потоков и образование максимальных значений амплитуд, следующих через почти-периоды почти-периодической функции, поскольку результирующий импульсный поток является почти-периодической функцией.
ЛИТЕРАТУРА
1. Александров Ю.И., Анохин К.В., Соколов Е.Н., Греченко Т.Н. и др. Нейрон. Обработка сигналов. Пластичность. Моделирование. Фундаментальное руководство // Изд-во Тюменского государственного университета. 2008. 548 с.
2. Анохин К.В., Бурцев М.С., Ильин В.А., Киселев И.И., Кукин К.А., Лахман К.В., Параскевов А.В., Рыбка Р.Б., Сбоев А.Г., Твердохлебов Н.В. Современные подходы к моделированию активности культур нейронов in vitro / Математическая биология и биоинформатика. 2012. Т. 7. №2. С. 372-397.
3. Борисов В. В. Модель нейрона. Патент № RU 2034332, G06G 7/60 1995.
4. Бызов А.Л. Электрофизиологические исследования сетчатки. - М.: Наука 1966 г. 196 с.
5. Вассерман Ф. Нейрокомпьютерная техника: Теория и практика // М.: «Мир», 1992.
6. Гутман А. Дендриты нервных клеток: теория электрофизиология, функция. 1984
7. Казанцев В.Б., Некоркин, В.И., Велардэ М.Г. Модель нейрона с осцилляторной активностью ниже порога возбуждения // Известия вузов. Радиофизика. 1998. №. 41. С. 1623-1635.
8. Левитан Б.М. Почти-периодические функции.// ГИТТЛ. 1953,396 с.
9. Лебедев А.Н. Психофизиология памяти. // Психофизиология. 2-е издание / под ред. Ю.И. Александрова / М.: «Инфра-М», 2001. С. 128-141.
10. Мазуров М.Е. Решение диофантовых неравенств в задачах о синхронизации релаксационных колебаний // ЖВМ и МФ АН СССР. 1991. Т. 31. №11. С. 1619-1636.
11. Мазуров М. Е. Идентификация математических моделей нелинейных динамических систем // М.: - Ижевск. РХД. 2008. 284 с.
12. Мак-Каллок У., Питтс В. Логическое исчисление идей, относящихся к нервной активности // Нейрокомпьютер. -1992. - №3/4. - С. 40-50.
13. Маркин В.С, Пастушенко В.Ф., Чизмаджев Ю.А. Теория возбудимых сред // М.: Наука. 1981. 276 с.
14. Минский М., Пейперт С. Персептроны = Perceptions. - М.: «Мир», 1971.
15. Некоркин, В.И., Дмитричев, А.С., Щапин, Д.С., Казанцев В.Б. Динамика модели нейрона со сложно-пороговым возбуждением // Математическое моделирование 2005. №6. С. 75-91.
16. Прокин И.С., Казанцев В.Б. Анализ передачи импульсных сигналов в системе взаимодействующих нейронных генераторов с частотно-зависимыми связями // Известия ВУЗов. Радиофизика. 2011. V. 54, №11. С. 848-858.
17. Розенблатг Ф. Принципы нейродинамики: перцептроны и теория механизмов мозга. Principles of Neurodynamic: perceptions and the theory of brain mechanisms. M: «Мир», 1965.
18. Самойлин E. А. Способ моделирования нейрона. Патент RU 2402813, G06N 3/06 -2010.
19. Смолянинов В.В. О некоторых особенностях организации коры мозжечка. Статья в сборнике «Модели структурно-функциональной организации некоторых биологических систем» // М.: Наука, 1966, с. 203-262.
20. Смолянинов В.В. Математические модели биологических тканей. // М: Наука, 1980, 368 с.
21. Соколов Е.Н. Принцип векторного кодирования в психофизиологии. Вестник МГУ. Серия 14. Психология, 1995, №4.
22. Соколов Е.Н., Вайткявичус Г.Г. Нейроинтеллект: от нейрона к нейрокомпьютеру. М.: Наука, 1989.
23. Соколов Е.Н. Нейронные механизмы памяти и обучения. М., 1981.
24. Соколов Е.Н. Восприятие и условный рефлекс: новый взгляд. М., 2003.
25. Субботин С.А. Аналитический обзор изобретений и патентов. Нейрокибернетика в СССР-СНГ. Запорожский национальный технический университет.
26. Тикиджи-Хамбурьян Р.А. Анализ влияния генератора спайков на динамические свойства модифицированного импульсного нейрона // Тез. док. 5-ой Всероссийской научно-технической конференции Нейроинформатика. 2003, М.: МИФИ, 2003, с. 134-141.
27. Тикиджи-Хамбурьян Р.А. Модифицированный импульсный нейрон как базовая модель для реалистичных нейронных сетей // Нейрокомпьютеры: разработка и применение, №7, 2002.
28. Хайкин Саймон. Нейронные сети: полный курс = Neural Networks: A Comprehensive Foundation. - 2-е изд. - М.: «Вильяме», 2006. - С. 1104. - ISBN 0-13-273350-1
29. Шепард Г. Нейробиология. В 2-х т.Т. 1. Пер. с англ. // М.: Мир, 1987. 454 с.
30. Fitzhugh R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. // Biophysical journal. 1961. V. 1, №6. P. 445-466.
31. Hindmarsh J.L., Rose R.M. A model of the nerve impulse using two first-order differential equations. // Nature. Nature Publishing Group, 1982. V. 296, №5853. P. 162-164.
32. Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve // The J. of physiology. 1952. V. 117, №4. P. 500-544.
33. Izhikevich E.M. Simple model of spiking neurons. // IEEE transactions on neural networks / a publication of the IEEE Neural Networks Council. 2003. V. 14, №6. P. 1569-1572.
34. Izhikevich E.M., FitzHugh R. FitzHugh-Nagumo model // Scholarpedia, 3193, 2006.
35. Lapicque M.L. Recherches quantitatives sur l′excitation  des Nerfs
des Nerfs  comme une Polarisation [Quantitative studies on electric excitation of nerves treated as polarization] // Journal de Physiologie et Pathologie General. 1907. V. 9. P. 620-635.
comme une Polarisation [Quantitative studies on electric excitation of nerves treated as polarization] // Journal de Physiologie et Pathologie General. 1907. V. 9. P. 620-635.
36. Morris C., Lecar H. Voltage oscillations in the barnacle giant muscle fiber. // Biophysical journal. 1981. V. 35, №1. P. 193-213.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИМПУЛЬСНЫЙ НЕЙРОН, БЛИЗКИЙ К РЕАЛЬНОМУ | 2015 |
|
RU2598298C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН НА ОСНОВЕ ИЗБИРАТЕЛЬНЫХ НЕЙРОНОВ | 2015 |
|
RU2597497C2 |
| Способ кодирования информации в импульсных нейронных сетях | 2019 |
|
RU2748257C2 |
| Инструментальный способ обучения избирательной нейронной сети без математики и без учителя с использованием самоорганизации | 2019 |
|
RU2729878C2 |
| НЕЙРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО НЕЙРОНА | 2014 |
|
RU2597495C2 |
| Эффективный перцептрон на основе нейронов МакКаллока-Питтса с использованием компараторов | 2019 |
|
RU2729554C1 |
| Модель нейрона, основанная на дендритных вычислениях | 2021 |
|
RU2777262C1 |
| Устройство для моделирования нейрона | 1988 |
|
SU1585811A1 |
| ОПТОЭЛЕКТРОННАЯ МОДЕЛЬ НЕЙРОННОЙ СЕТИ | 1992 |
|
RU2070334C1 |
| Устройство для моделирования нейрона | 1987 |
|
SU1501101A1 |












Изобретение относится к области моделирования нейронных структур и может быть использовано в нейрокомпьютерах, технических системах на основе нейронных сетей для распознания образов, анализа и обработки изображений. Техническим результатом является обеспечение возможности достижения избирательного распознавания входных объектов без использования весового взвешивания входных сигналов, возможности кодирования входного объекта определенного типа номером канала или номером регистрирующего нейрона, сжатие входной информации, повышение быстродействия, повышение надежности распознавания объектов. Устройство содержит регистрирующие импульсные нейроны, входы для входных сигналов - импульсных потоков, внутренние каналы связи от входов, индивидуальные кластеры из части каналов связи в каждом из регистрирующих нейронов, которые пропускают часть входных сигналов; формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями и структурой периодов парциальных составляющих входных импульсных потоков; производят безынерционное суммирование всех парциальных импульсных потоков на выходах кластеров; производят преобразование полученного сигнала пороговыми возбудимыми элементами, которые генерируют одиночные импульсы или импульсные последовательности при превышении максимальной суммой амплитуд импульсных потоков порогового значения возбудимых элементов, которые используют как выходные сигналы. 13 ил., 2 табл.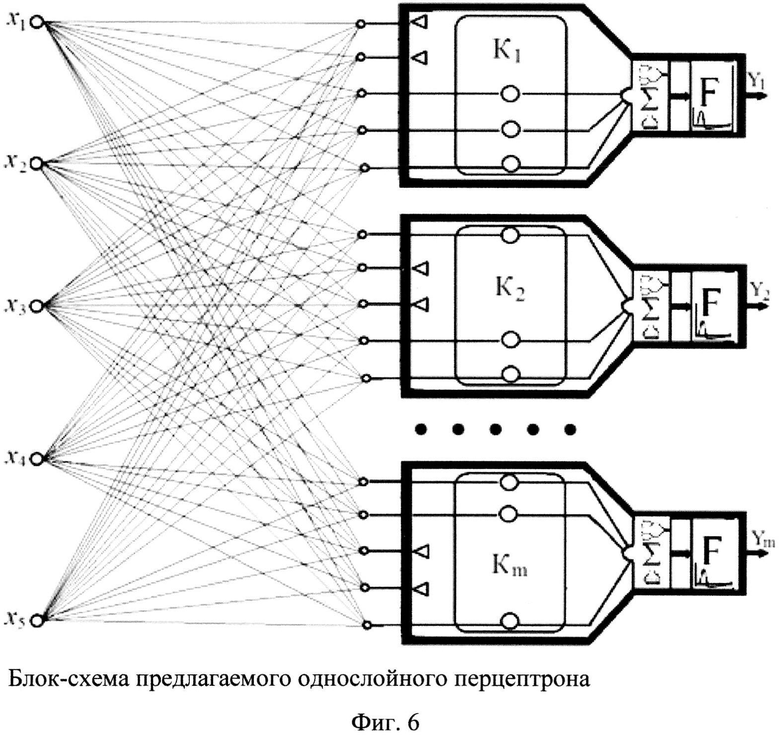
Перцептрон однослойный, включающий несколько регистрирующих импульсных нейронов, входы для входных сигналов - импульсных потоков, внутренние каналы связи от входов, в которых производят умножение входных сигналов на весовые коэффициенты и отправляют на сумматоры, связанные с пороговыми нелинейными возбудимыми элементами, генерирующими выходные одиночные импульсы или импульсные последовательности при превышении сигналами на выходах сумматоров порогового значения возбудимого нелинейного элемента, которые используют как выходные сигналы; отличающийся индивидуальными кластерами из части каналов связи в каждом из регистрирующих нейронов, которые пропускают часть входных сигналов; формирование кластеров и уравнивание количества каналов в кластерах осуществляют в соответствии с кодовыми комбинациями и структурой периодов парциальных составляющих входных импульсных потоков; далее производят безынерционное суммирование всех парциальных импульсных потоков на выходах кластеров; это реализует для сигнала в виде суммарных импульсных потоков на выходах кластеров ε-почти-периодов с максимальной суммой амплитуд всех парциальных импульсных потоков; после безынерционного суммирования производят преобразование полученного сигнала пороговыми возбудимыми элементами, которые генерируют одиночные импульсы или импульсные последовательности при превышении максимальной суммой амплитуд импульсных потоков порогового значения возбудимых элементов, которые используют как выходные сигналы.
| МОДЕЛЬ НЕЙРОНА | 1992 |
|
RU2034332C1 |
| МОДЕЛЬ НЕЙРОНА, РЕАЛИЗУЮЩАЯ ЛОГИЧЕСКУЮ ФУНКЦИЮ НЕРАВНОЗНАЧНОСТИ | 2003 |
|
RU2269155C2 |
| US 2014156574 A1, 05.06.2014 | |||
| US 2014317035 A1, 23.10.2014. | |||
Авторы
Даты
2016-09-10—Публикация
2015-02-24—Подача