Изобретение относится к вычислительной технике, в частности к способам идентификации объектов на изображении.
Известны способ и устройство для распознавания изображений объектов (см. патент на изобретения РФ №2361273, М.кл. G06K 9/62, опубл. 10.07.2009 г.). Способ заключается в следующем: эталонные изображения хранят в виде векторной трехмерной модели, для каждой модели фиксируют набор параметров для аффинных преобразований: углы поворота по осям X, Y, Z, масштаб, с учетом сложности формы модели, далее получают векторную трехмерную модель эталонного объекта путем геометрического построения и, изменяя ее положение в пространстве (поворот, отражение, масштабирование), получают вышеуказанные параметры, которые сохраняют и используют в дальнейшем при распознавании для воссоздания соответствующего ракурса эталона объекта, плоское изображение представляют в виде двумерного массива, элементами которого являются значения от 0 до 255- градации серого цвета, в набор параметров дополнительно включают соотношение сторон габаритного изображения контейнера объекта и кодированное представление объекта, которое позволяет определить его положение внутри габаритного контейнера. При этом под габаритным контейнером подразумевают минимальную прямоугольную область на плоскости, в которую вписывается изображение объекта, а кодирование производят путем разбиения габаритного контейнера на 25 одинаковых областей и определением наличия части объекта в каждой из них, получая, таким образом, 25-битный код данного ракурса объекта в двоичном виде: если часть изображения находится в области, то ее получают перебором значений меток в областях слева направо, сверху вниз; на вход распознавателя подают изображение, представленное массивом пикселей в градациях серого, т.е. каждый элемент массива имеет значение от 0 до 255, размерность массива зависит от параметров дискретизации изображения, распознавание производят следующим образом: определяют габаритный контейнер входного изображения объекта, затем кодируют вышеуказанным способом, исходя из отношения сторон габаритного контейнера и полученного кода, выбирают набор параметров из базы эталонов, после чего выполняют преобразование векторной модели эталонного объекта соответственно установленным ранее параметрам: поворот и масштабирование, после этого строят плоское изображение модели эталона, которое сравнивают с поданным на вход изображением посредством нейронной сети типа персептрон, сравнение производят путем анализа градаций серого для каждой дискретной области изображения, причем производят попиксельное сравнение, затем находят модуль разности для каждой пары пикселей изображения, поданного на вход распознавателя и полученной проекции векторной модели эталонного объекта и сравнивают его с пороговым значением, полученные данные подают на вход нейросети персептрон и, в зависимости от значения ее функции активации принимают решение о схожести проекции векторной модели эталонного объекта и входного изображения.
Данный способ предполагает достаточно сложную обработку изображения объекта, что снижает точность распознавания из-за влияния суточных и сезонных изменений яркости выделяемых объектов, а так же требует огромного временного ресурса для компьютерной реализации.
Известен способ получения изображения объекта (см. патент на изобретение РФ №2243591, М.кл. G06T 5/50, опубл. 27.12.2004 г.), включающий предобработку сигналов представленной временной последовательности изображений сцены, на которой возможно появление объекта, запоминание опорных, характеризующих изображение сцены сигналов, вычисление взаимно-корреляционной функции опорного и текущих изображений, измерение параметров взаимно-корреляционной функции, получение в каждый момент времени полной информации о координатах и перемещениях объекта и измерение параметров объекта и сцены, отличиями способа являются разделение на фрагменты изображения рассматриваемой последовательности изображений, вычисление взаимно-корреляционной функции опорного и последующих текущих изображений, после чего получают сигналы, соответствующие, например, средней и максимальной величине амплитуды сигнала взаимно-корреляционной функции и сравнивают их, например, вычитают из максимальной величины амплитуды сигнала взаимно-корреляционной функции среднее значение величины амплитуды, полученный разностный сигнал сравнивают с заданной пороговой величиной сигнала, а затем формируют управляющие сигналы, с помощью которых осуществляют фрагментарную фильтрацию временной последовательности текущих изображений, причем для фрагментов, разностные сигналы которых превышают пороговое значение, формируют управляющие сигналы, блокирующие сигналы изображения, а для фрагментов, разностные сигналы которых меньше или равны пороговому значению, формируют управляющие сигналы, пропускающие сигналы соответствующих фрагментов.
При этом фрагменты изображения могут быть выбраны одинаковыми по конфигурации и равными по площади, с размерностью К пикселей, где 2 ≤ К ≤ N, причем N - число пикселей в изображении, или различными по конфигурации и по площади с размерностью К1 пикселей на каждом фрагменте, где К1 = 2, … nj1, причем nj1 ≤ N/2.
Причем на фрагменты могут быть разделены либо опорное, либо текущее изображения.
Кроме того, сигналы, принадлежащие выделенному изображению объекта, записывают в качестве опорного изображения.
А при выполнении операции вычитания сигналов взаимно-корреляционной функции из сигналов взаимно-корреляционной функции для фрагментов предыдущего кадра вычитают сигналы взаимно-корреляционной функции соответствующих фрагментов последующих кадров.
В данном способе изображение представляется в видеосигнальном виде, например, в виде телевизионного сигнала.
В известном способе по патенту №2243591 также, как в предыдущем аналоге, осуществляется обработка изображений сцены в целом, без выделения их контуров и локализации объектов на изображении, поэтому корреляционная обработка, проводимая в способе, зависит в значительной мере от освещенности, погодных условий, что повышает вероятность ложного обнаружения объектов.
Данный способ выбран в качестве прототипа.
Проблемой, которую необходимо решить, является то, что обработка изображений сцены в целом и локализации объектов на изображении требует значительного времени и ресурсов для обработки изображений, а также то, что обработка зависит в значительной мере от освещенности, погодных условий, которые увеличивают вероятность ложного обнаружения объектов на изображении.
Техническим результатом предлагаемого изобретения является уменьшение времени и ресурсов, требуемых для осуществления обработки изображений, а также повышение вероятности обнаружения объектов на изображении.
Достижение технического результата обеспечивается в предлагаемом способе автоматического распознавания сцен и объектов на изображении, при котором формируют и запоминают эталонные изображения, осуществляют обработку потока входных изображений, для нахождения на них интересующего объекта, используя эталонные изображения, согласно предлагаемому изобретению, выделяют на эталонном изображении ключевые точки и участки вокруг них (окрестности ключевых точек), размеры которых выбирают в пределах необходимых для вычисления градиентов яркости, в которых происходит максимальное изменение градиента яркости и которые представляют собой, например, края линий, небольшие круги, резкие перепады освещенности, углы, после чего осуществляют поиск на входном изображении соответствующих ключевых точек эталонного изображения, при этом выделение ключевых точек на изображении осуществляют с помощью матрицы Гессе, определяя ее детерминанты, называемые гессианами, достигающими экстремума в точках максимального изменения градиента яркости, причем определение гессианов для каждой ключевой точки производят с помощью разномасштабных фильтров Хаара, далее создают дескрипторы ключевых точек, в виде чисел, отображающих флуктуации градиента яркости вокруг ключевой точки, полученные числа инвариантны к масштабу и вращению, причем флуктуации градиента окрестностей ключевой точки вычисляют относительно направления градиента по всей окрестности ключевой точки, после этого для каждой ключевой точки эталонного изображения по признаку максимальной близости дескрипторов определяют соответствующую ключевую точку на текущем изображении, и, если размер близости меньше заданного порога, соответствующую ключевую точку на текущем изображении запоминают, при этом заданный порог определяют экспериментально по результатам оценки среднего значения сумм разностей дескрипторов по всем ключевым точкам эталонного и текущего изображений, и, когда количество соответствующих ключевых точек на текущем изображении превысит половину ключевых точек на эталонном изображении, объект сцены на изображении считают распознанным.
Выделение на изображении ключевых точек с участками вокруг них, в которых происходит максимальное изменение градиента яркости, обеспечивает получение информации о локальных изменениях яркости в анализируемом изображении. При этом применяемая обработка ключевых точек с помощью матриц Гессе и фильтров Хаара, последующее создание дескрипторов ключевых точек, инвариантных к масштабу и вращению, и использование максимальной близости дескрипторов при сравнении с заданным порогом позволяют при обнаружении на текущем изображении половины количества ключевых точек эталонного изображения обеспечить высокую вероятность правильного обнаружения объектов интереса. При этом количество ключевых точек значительно меньше пикселов во всем анализируемом изображении, что значительно ускоряет процесс обработки потока входных изображений и уменьшает объем обрабатываемой информации.
Кроме того, поскольку применяемые при выделении ключевых точек на изображении с помощью матрицы Гессе детерминанты, называемые гессианами, являются производными и зависят только от перепада яркости, но не от абсолютного ее уровня, то они инвариантны по отношению к сдвигу яркости изображения, поэтому изменение уровня освещения образца не влияет на обнаружение ключевых точек, т.е. значительно уменьшаются зависимость от освещенности, погодных условий, вероятность ложного обнаружения объектов.
Предлагаемый способ поясняется чертежами, где на фиг. 1 показаны ключевые точки изображения на эталоне(справа) и на сцене(слева). При этом, несмотря на то, что сцена имеет другой масштаб, угол обзора и частично заслонена другим объектом, ключевые точки достаточно точно идентифицируются.
На фиг. 2 показаны ключевые точки изображения здания, найденные с помощью матрицы Гессе. Диаметр круга показывает масштаб ключевой точки. Прямая линия - направление градиента яркости.
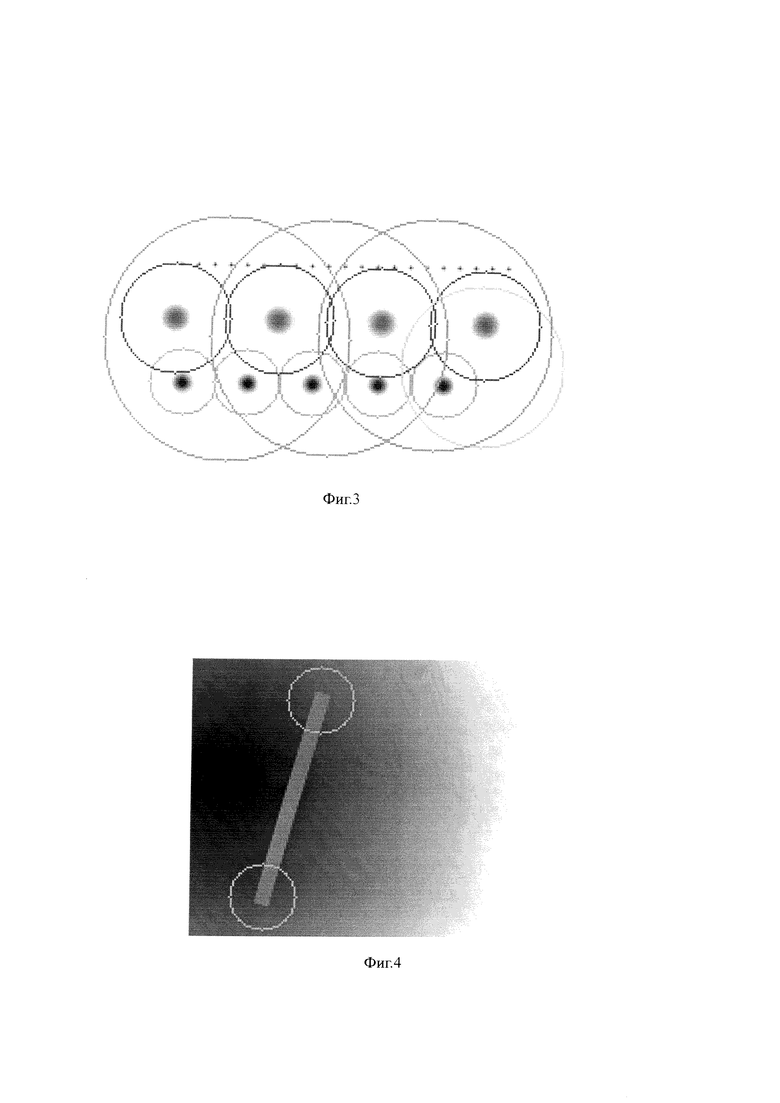
На фиг. 3 показаны экстремумы гессиана.
На фиг. 4 приведен пример распознавания ключевых точек, где показаны концы отрезка, распознанные как ключевые точки, с помощью матрицы Гессе.
На фиг. 5 изображены дискретизированные фильтры для нахождения четырех элементов матрицы Гессе (четвертый - совпадает с третьим, поскольку матрица Гессе симметрична). Фильтры имеют пространственный масштаб 9×9 пикселов. Темные участки соответствуют отрицательным значениям фильтра, светлые - положительным.
На фиг. 6 изображены фильтры, используемые для нахождения матрицы Гессе. Белые области соответствуют значению +1, черные -2 (на третьем фильтре - 1), серые - нулевые. Пространственный масштаб - 9×9 пикселов.
На фиг. 7 поясняется использование гессиана в предлагаемом способе для распознавания как светлых точек на темном фоне, так и темных точек на светлом фоне.
На фиг. 8 показаны две ключевые точки разного масштаба в одной точке изображения.
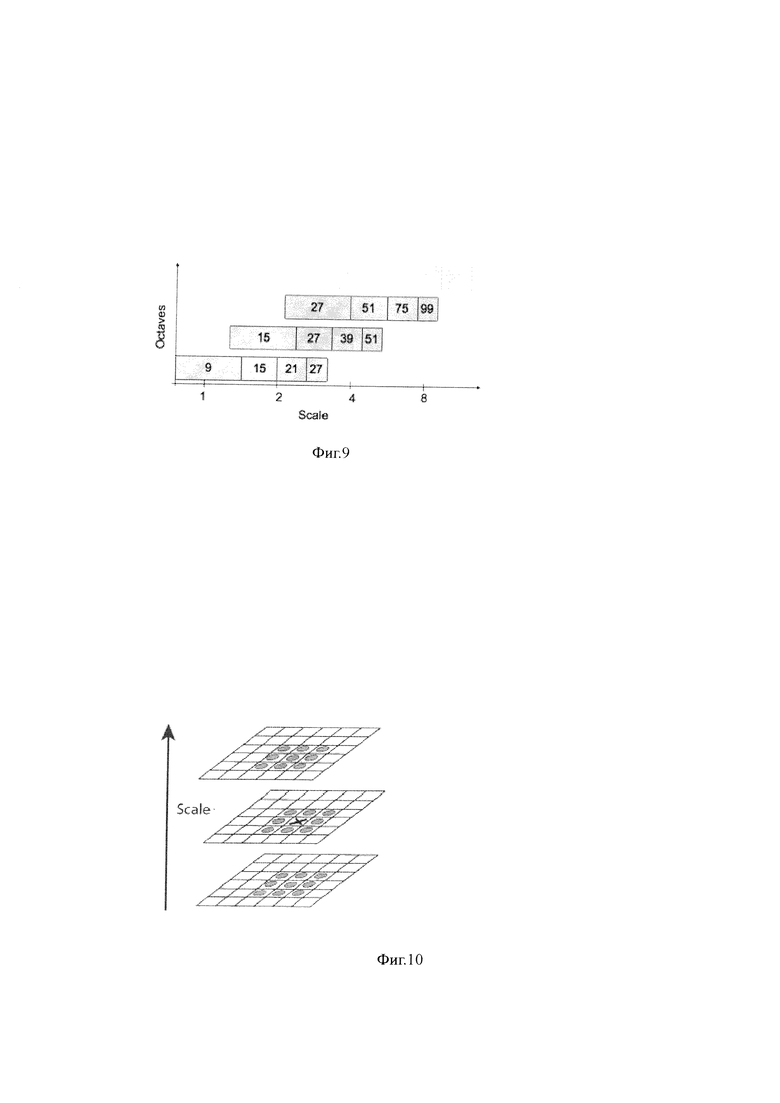
На фиг. 9 показано разбиение всех множеств масштабов фильтров Fast-Hessian на октавы, показаны первые три октавы. Цифры в прямоугольниках показывают размер фильтра Fast-Hessian. Логарифмическая шкала снизу - показывает масштабы, покрываемые октавами.
На фиг. 10 поясняется поиск локального максимума, где пиксел, помеченный крестиком, считается локальным максимумом, если его гессиан больше чем у любого соседнего пиксела в его масштабе, а также больше любого из соседних пикселов масштабом меньше и масштабом больше (всего 26 соседей).
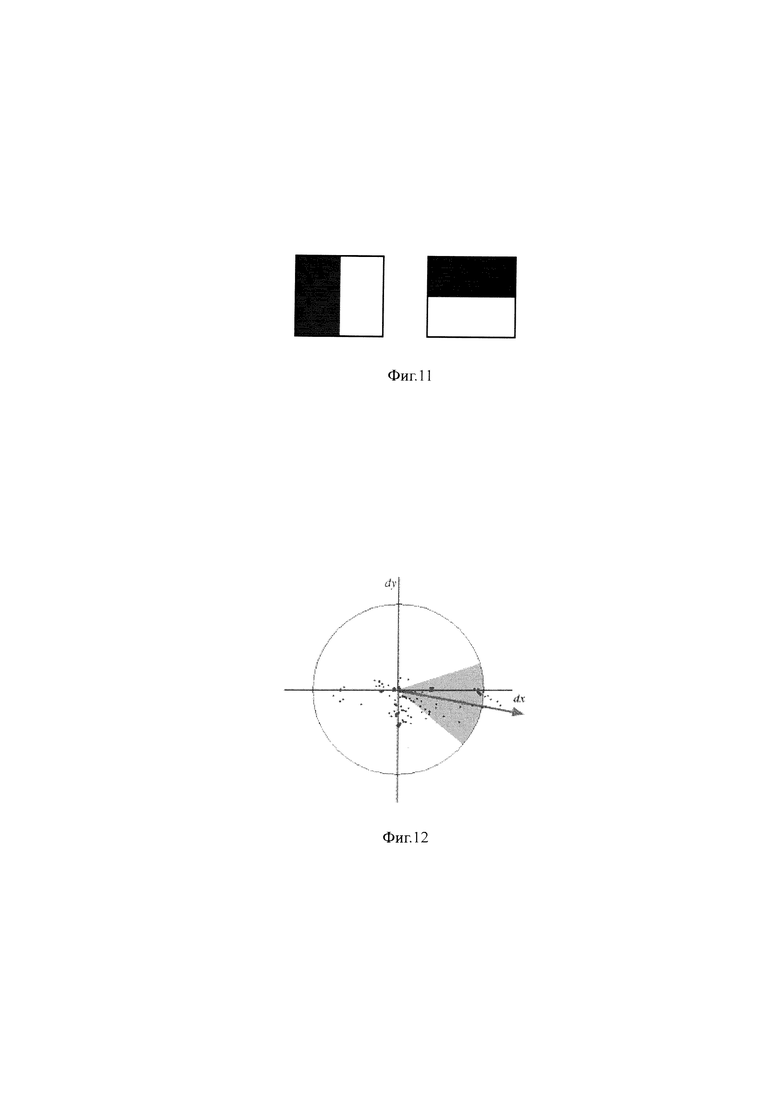
На фиг. 11 приведен вид фильтров Хаара, где черные области имеют значения -1, белые +1.
На фиг. 12 показаны все найденные значения градиентов вейвлета Хаара dX и dY в виде точек в пространстве dX и dY.
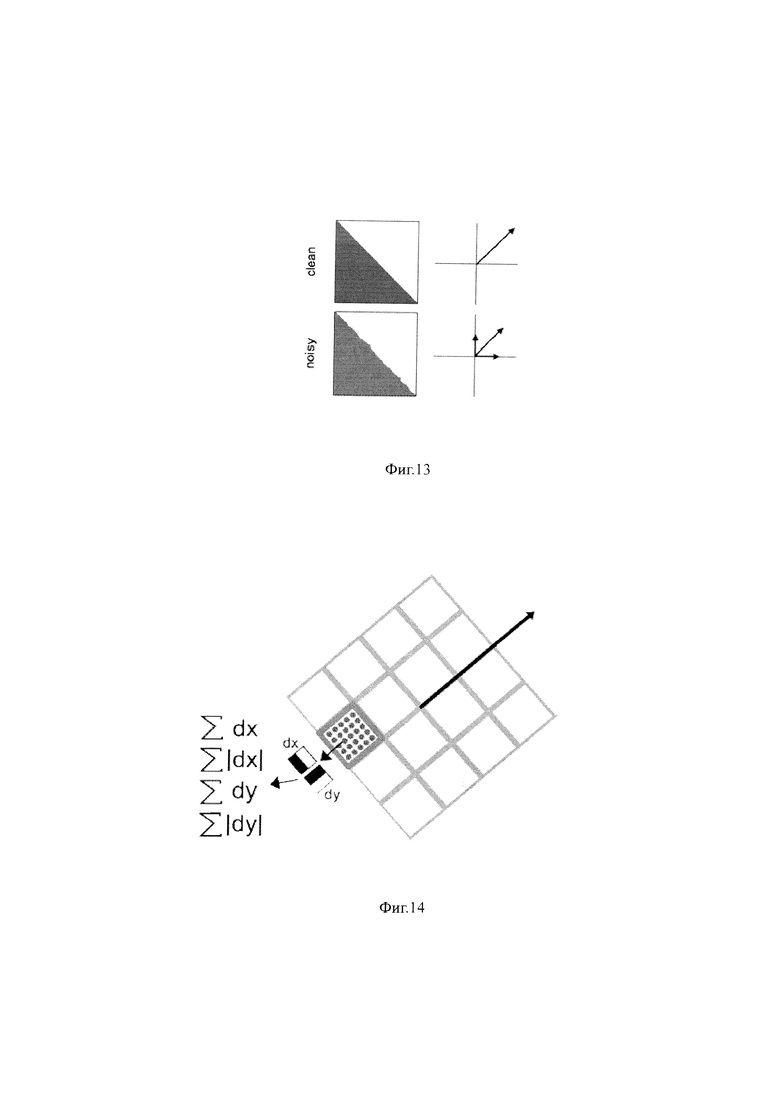
На фиг. 13 приведен пример градиента при идеальном крае, и при крае с шумом.
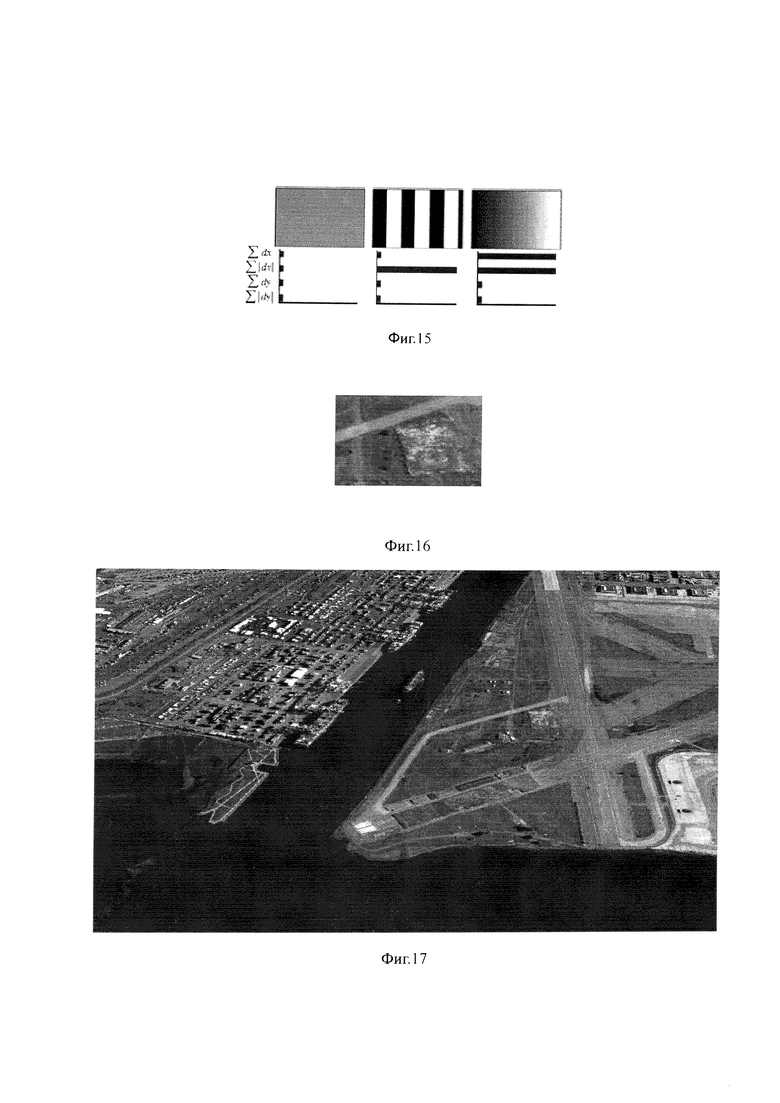
На фиг. 14 иллюстрируется вычисление компонентов дескриптора в прямоугольной области, имеющей размер 20s.
На фиг. 15 приведены примеры дескрипторов для изображений, где показано поведение дескриптора для разных изображений. Для равномерных областей - все значения близки к нулю. Для повторяющихся вертикальных полосок - все величины, кроме второй близки к нулю. При увеличении яркости в направлении оси X, две первые компоненты имеют большие значения.
На фиг. 16 изображено эталонное изображение.
На фиг. 17 - приведено изображение сцены.
На фиг. 18 - показаны ключевые точки эталонного изображения.
На фиг. 19 приведен результат распознавания по ключевым точкам.
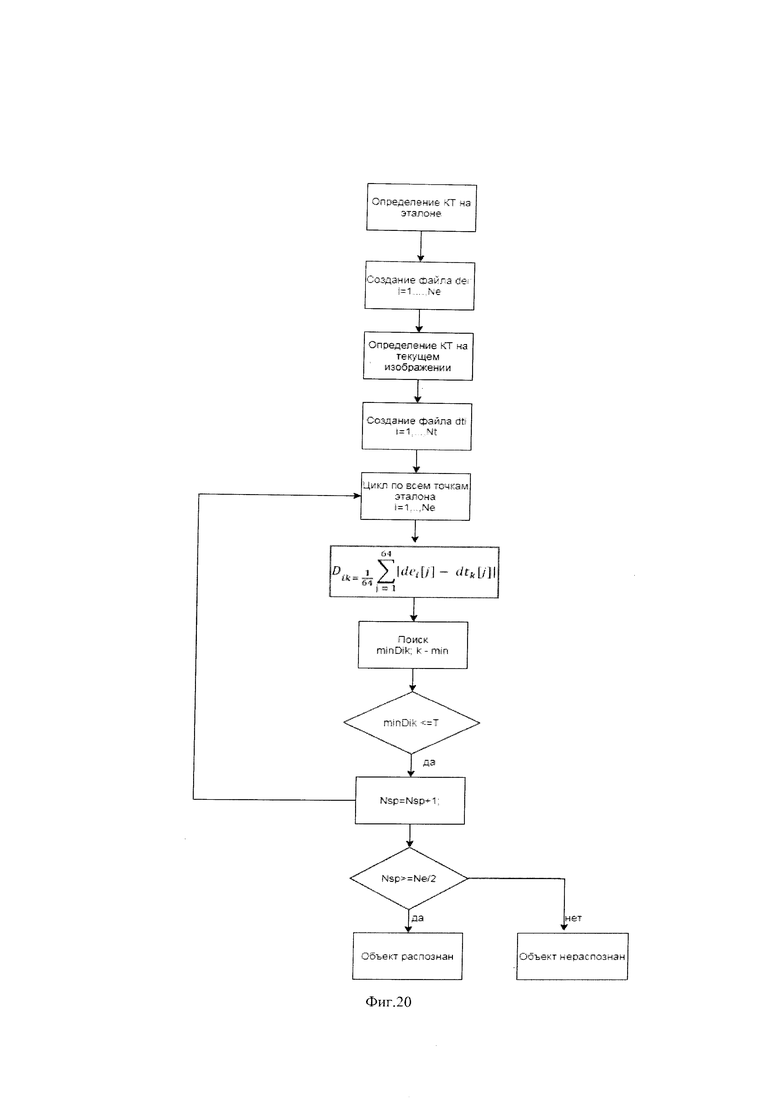
На фиг. 20 приведена блок-схема алгоритма реализации предлагаемого способа.
Рассмотрим пример осуществления предлагаемого способа.
Предварим собственно описание предлагаемого способа следующими пояснениями.
Современные компьютеры могут хранить огромные объемы информации в виде изображений, и видео-файлов. Для распознавания объектов на текущем изображении, получаемом с приемной камеры, препятствует ряд моментов:
1. Изображения имеют разный масштаб. Одинаковые объекты на самом деле занимают разную площадь на разных изображениях.
2. Интересующий нас объект может находиться в разных местах изображения.
3. Объект, который мы воспринимаем как что-то отдельное, на изображении никак не выделен, и находится на фоне других предметов и объектов. Кроме того, изображение не идеально и может быть подвержено всякого рода искажениям и помехам.
4. Изображение является лишь двумерной проекцией трехмерного мира. Поэтому поворот объекта и изменение угла обзора кардинальным образом влияют на его двумерную проекцию - изображение. Один и тот же объект может давать совершенно разную картину, в зависимости от поворота или расстояния до него.
Итак, даны два изображения, одно из них будем считать эталонным изображением (образцом), другое - сценой. Задача сводится к определению факта наличия образца на сцене, и к его локализации.
При этом образец на сцене может:
а) иметь другой масштаб
б) быть повернут в плоскости изображения
в) быть в произвольном месте сцены
г) может быть зашумлен, виден не полностью, частично заслонен другими предметами
д) может иметь отличную от образца яркость и контраст
е) его может не быть совсем.
Метод корреляции, использованный в прототипе, предлагает получить образец в разных масштабах, повернуть его на всевозможные углы, перебрать все возможные места на сцене, и все эти эталоны попиксельно сравнить со сценой. Однако данное решение практически трудно реализовать. Действительно, если образец и сцена имеют типичные размеры - порядка сотен пикселов по вертикали и горизонтали, то посчитав общее число всевозможных эталонов, их поворотов, масштабов и локализации, а также умножив на число операций попиксельного (корреляционного) сравнения, получим около триллиона операций для поиска и локализации эталона на сцене.
Кроме того, непосредственное сравнение образца со сценой может дать плохой результат, из-за шумов, искажений, заслонения, объектов фона.
В заявляемом способе предлагается выделить на образце некие ключевые точки и небольшие участки вокруг них. Ключевой точкой будем считать такую точку, которая имеет некие признаки, существенно отличающие ее от основной массы точек. Например, это могут быть края линий, небольшие круги, резкие перепады освещенности, углы и т.д. Предполагая, что ключевые точки присутствуют на образце всегда, то можно поиск образца свести к поиску на сцене ключевых точек образца. А поскольку ключевые точки сильно отличаются от основной массы точек, то их число будет существенно меньше, чем общее число точек эталона.
Главное то, что их не слишком много и они присутствуют на изображении эталона всегда. Вокруг точек выделяют малые участки. Чем меньше участок, тем меньше на него влияют крупномасштабные искажения. Так, если объект в целом, подвержен эффекту перспективы (то есть ближний край объекта имеет больший видимый размер, чем дальний), то для малого его участка явлением перспективы можно пренебречь и заменить на изменение масштаба. Аналогично, небольшой поворот объекта вокруг некоторой оси может сильно изменить картинку объекта в целом, но малые участки изменятся незначительно. Кроме того, если часть объекта выходит за край изображения или заслонена, то небольшие участки вокруг части ключевых точек будут видны целиком, что также позволяет их легче идентифицировать. А еще, если малые области лежат целиком внутри искомого объекта, то на них не оказывают никакого влияния объекты фона. С другой стороны, участок вокруг ключевой точки не должен быть слишком мал. Очень малые участки несут слишком мало информации об изображении и с большей вероятностью могут случайно совпадать между собой.
На фиг. 1 изображены ключевые точки изображения на эталоне(справа) и на сцене(слева).
С другой стороны, участок вокруг ключевой точки не должен быть слишком мал. Очень малые участки несут слишком мало информации об изображении и с большей вероятностью могут случайно совпадать между собой.
Предлагаемый способ решает две задачи - поиск ключевых точек изображения и создание их дескрипторов, инвариантных к масштабу и вращению. Это значит, что описание ключевой точки будет одинаково, даже если образец изменит размер и будет повернут (здесь и далее мы будем говорить только о вращении в плоскости изображения). Кроме того, сам поиск ключевых точек тоже должен обладать инвариантностью. Так, что бы повернутый объект сцены имел тот же набор ключевых точек, что и образец.
В способе выделяют ключевые точки с помощью матрицы Гессе. Детерминант матрицы Гессе (т.н. гессиан) достигает экстремума в точках максимального изменения градиента яркости. Он хорошо детектирует пятна, углы и края линий.
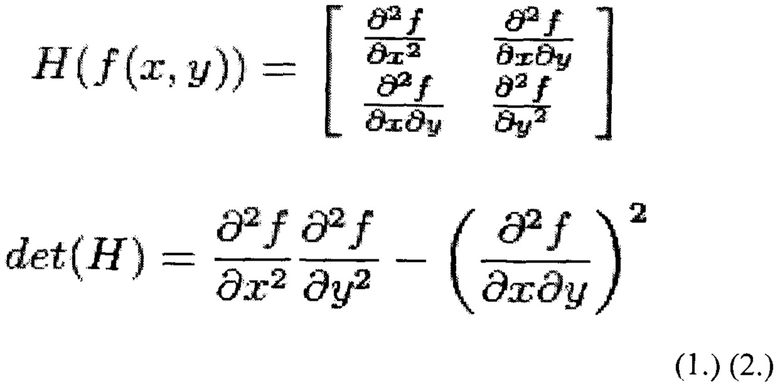
Выше приведены формулы для матрицы Гессе (1.) и Гессиана (детерминанта) (2.), достигающего максимума в точке максимального изменения градиента яркости.
Гессиан инвариантен относительно вращения. Но не инвариантен масштабу. Поэтому в способе используют разномасштабные фильтры для нахождения гессианов. Для каждой ключевой точки рассчитывают направление максимального изменения яркости (градиент) и масштаб, взятый из масштабного коэффициента матрицы Гессе. Градиент в точке вычисляется с помощью фильтров Хаара.
После нахождения ключевых точек, в способе формируют их дескрипторы. Дескриптор представляет собой набор из 64 (либо 128) чисел для каждой ключевой точки. Эти числа отображают флуктуации градиента вокруг ключевой точки (что понимается под флуктуацией - рассмотрим ниже). Поскольку ключевая точка представляет собой максимум гессиана, то это гарантирует, что в окрестности точки должны быть участки с разными градиентами. Таким образом, обеспечивается дисперсия (различие) дескрипторов для разных ключевых точек.
Флуктуации градиента окрестностей ключевой точки считаются относительно направления градиента вокруг точки в целом (по всей окрестности ключевой точки). Таким образом, достигается инвариантность дескриптора относительно вращения. Размер же области, на которой считается дескриптор, определяется масштабом матрицы Гессе, что обеспечивает инвариантность относительно масштаба. Флуктуации градиента также считаются с помощью фильтра Хаара.
Значение гессиана используется для нахождения локального минимума или максимума яркости изображения. В этих точках значение гессиана достигает экстремума. На фиг. 3 видно, что особые точки (очерченные цветными кругами) представляют собой локальные экстремумы яркости изображения. Мелкие точки не распознаны как особые, из-за порогового отсечения по величине гессиана.
На Фиг. 4 показаны концы отрезка, распознанные как ключевые точки, с помощью матрицы Гессе.
Теоретически, вычисление матрицы Гессе сводится к нахождению Лапласиана Гауссиан. По сути, элементы матрицы Гессе вычисляются как свертка (сумма произведений) пикселов изображения на фильтры, изображенные на фиг. 5.
На Фиг. 5 изображены дискретизированные фильтры для нахождения четырех элементов матрицы Гессе (четвертый - совпадает с третьим, поскольку матрица Гессе симметрична). Фильтры имеют пространственный масштаб 9×9 пикселов. Темные участки соответствуют отрицательным значениям фильтра, светлые - положительным. Однако, предлагаемый способ не использует лапласиан гауссиан в том виде, который изображен на фиг. 5. Во-первых, дискретизированный лапласиан гауссиан имеет довольно большой разброс значений детерминанта, при вращении образца (в идеале гессиан должен быть инвариантен к вращению). Особенно детерминант «проседает» в районе поворота на 45 градусов. А во-вторых, и это главное, фильтр для лапласиана гауссианы имеет непрерывный характер. Почти все пикселы фильтра имеют разные величины яркости. А это не позволяет использовать быстрый механизм расчета. Поэтому используется бинаризированная аппроксимация лапласиана гауссиан. (Fast-Hessian): На Фиг. 6 изображены бинаризированные фильтры, используемые для нахождения матрицы Гессе. Белые области соответствуют значению +1, черные -2 (на третьем фильтре -1), серые - нулевые. Пространственный масштаб - 9×9 пикселов. Этот фильтр более устойчив к вращению, и его можно эффективно вычислить. Таким образом, гессиан вычисляется так (3.):
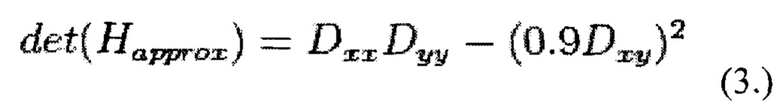
Где Dxx, Dyy, Dxy - свертки по фильтрам, изображенным на фиг. 6. Коэффициент 0.9 имеет теоретическое обоснование, и корректирует приближенный характер вычислений.
Итак, для нахождения ключевых точек, анализируют точки изображения и определяют максимум гессиана. В способе задается пороговое значение гессиана. Если вычисленное значение для анализируемой точки выше порога - точка рассматривается как кандидат на ключевую точку.
Следует заметить, что поскольку гессиан является производной, и зависит только от перепада яркости, но не от абсолютного ее уровня, то он инвариантен по отношению к сдвигу яркости изображения. Таким образом, изменение уровня освещения образца не влияет на обнаружение ключевых точек.
Кроме того, свойства гессиана таковы, что он достигает максимума, как в точке белого пятна на черном фоне, так и черного пятна на белом фоне. Таким образом, способ обнаруживает и темные, и светлые особенности изображения.(Фиг. 7). Однако, гессиан не инвариантен относительно масштаба. Это значит, что для одного и того же пиксела, гессиан может меняться при изменении масштаба фильтра. Решение этой проблемы только одно - перебирать различные масштабы фильтров и поочередно их применять к данному пикселу.
Из соображений симметрии и дискретизации, размер фильтра Fast-Hessian не может принимать произвольные значения. Допустимые размеры этого фильтра таковы (начиная с минимального): 9, 15, 21, 27 и так далее, с шагом 6. Однако, на практике, постепенно увеличивать размер фильтра на 6 - не выгодно, потому что для крупных масштабов шаг 6 оказывается слишком мелким, а фильтры - избыточными. Поэтому (и по некоторым другим причинам), разбивается все множество масштабов на так называемые октавы. Каждая октава покрывает определенный интервал масштабов, и имеет свой характерный размер фильтра.
При этом если бы на октаву приходился только один фильтр, это было бы слишком грубым приближением. Кроме того, мы бы не могли найти локальный максимум гессиана, среди разных масштабов, в разных октавах. Ведь одна и та же точка может иметь несколько локальных максимумов гессиана, в разных масштабах. Это хорошо видно на фиг.8, где рассмотрены две ключевые точки разного масштаба в одной точке изображения Если искать максимум среди всех гессианов, по всем масштабам, то нашелся бы только один из максимумов, в то время как их может быть несколько. Один - в одном масштабе, другой - в другом.
Исходя из перечисленного, октава содержит не один фильтр, а четыре фильтра, которые хорошо покрывают характерный масштаб октавы:
На фиг. 9 показаны первые три октавы Цифры в прямоугольниках показывают размер фильтра Fast-Hessian. Логарифмическая шкала снизу - показывает масштабы, покрываемые октавами.
Шаг размера фильтра в первой октаве - составляет 6, во второй - 12, в третьей - 24 и так далее.
Как видим, октавы значительно перекрываются друг другом. Это увеличивает надежность нахождения локальных максимумов. Почему в октаве именно четыре фильтра станет ясно из следующих пояснений.
Возникает вопрос, а сколько собственно октав достаточно для покрытия множества ключевых точек разных масштабов? Теоретически, масштабы бесконечны, однако в реальных изображениях, они вполне конечны, и основная масса сосредоточена в интервале от 1 до 10 (по данным анализа множества изображений). Для покрытия этого диапазона достаточно четырех октав. Плюс добавляется одна или две октавы для покрытия больших масштабов. Итого, используется 5-6 октав. Теоретически, этого вполне достаточно для покрытия всевозможных масштабов на изображении 1024×768 пикселов.
Для нахождения локального максимума гессиана, используется так называемый метод соседних точек 3×3×3.
Его смысл понятен из фиг. 10, где изображен поиск локального максимума. Пиксел, помеченный крестиком считается локальным максимумом, если его гессиан больше чем у любого его соседа в его масштабе, а также больше любого из соседей масштабом меньше и масштабом больше (всего 26 соседей).
Исходя из такого определения локального максимума, понятно, что октава должна содержать не менее трех фильтров, иначе мы не сможем определить факт нахождения локального максимума гессиана внутри октавы.
Отметим, что фильтры октавы вычисляют не для всех пикселов подряд. Первая октава считается для каждого второго пиксела изображения. Вторая - для каждого четвертого, третья - для каждого восьмого и так далее. Смысл понятен - две точки с расстоянием 2 не могут содержать более одного максимума масштаба 2, 3 или более высоких масштабов. Поэтому нет смысла перебирать все точки изображения, для нахождения максимума масштаба 3, например.
Удвоение шага пикселов для октав позволяет экономить при расчете фильтров. Размеры фильтров в октавах повторяются. Так, например, фильтр размером 27 присутствует в трех октавах, при вычислениях, этот фильтр будет считаться только для первой октавы. Вторая и третья - просто используют расчеты первой октавы. А удвоение шага пикселов гарантирует, что точки в которых нужно вычислять гессиан, уже были просчитаны предыдущей октавой.
Поэтому, несмотря на то, что октава содержит четыре фильтра, на самом деле каждая октава (кроме первой) считает только два характерных для нее размера, два других - всегда можно взять из предыдущих октав. Первая же октава вынуждена вычислять все четыре своих фильтра.
Итак, после нахождения максимального гессиана методом соседних точек 3×3×3, мы нашли пиксел, в котором этот максимум достигается. Однако, поскольку, октава перебирает не все точки изображения, то истинный максимум может не совпадать с найденным пикселом, а лежать где-то рядом, в соседних пикселах.
Для нахождения точки истинного максимума, используется интерполирование найденных гессианов куба 3×3×3 квадратичной функцией. Далее, вычисляется производная (методом конечных разностей соседних точек). Если она близка к нулю - мы в точке истинного максимума. Если производная велика - сдвигаемся в сторону ее уменьшения, и повторяем итерацию, до тех пор пока производная не станет меньше заданного порога. Если в процессе итераций мы отходим от начальной точки слишком далеко, то это считается ложным максимумом, и точка больше не считается ключевой.
Для инвариантности вычисления дескрипторов особой точки, которые будут рассмотрены ниже, требуется определить преобладающую ориентацию перепадов яркости в ключевой точке. Это понятие близко к понятию градиента, но здесь используется немного другой алгоритм нахождения вектора ориентации.
Сначала, вычисляются точечные градиенты в пикселах, соседних с ключевой точкой. Для рассмотрения берутся пикселы в окружности радиуса 6s вокруг особой точки. Где s - масштаб особой точки. Для первой октавы берутся точки из окрестности радиусом 12.
Для вычисления градиента, используется фильтр Хаара. Размер фильтра берется равным 4s, где s - масштаб особой точки. Вид фильтров Хаара показан на фиг. 11. Черные области имеют значения -1, белые +1.
Фильтры Хаара дают точечное значение перепада яркости по оси X и Y соответственно. Поскольку фильтры Хаара имеют прямоугольную форму, их значения легко вычисляются. Значения вейвлета Хаара dX и dY для каждой точки умножаются на вес и запоминаются в массиве. Вес определяется как значение гауссианы с центром в особой точке и сигмой равной 2s. Взвешивание на гауссиане необходимо для отсечения случайных помех на далеких от ключевой точки расстояниях.
Далее, все найденные значения dX и dY, условно наносятся в виде точек на плоскость, как показано на фиг. 12:
На фиг. 12 показаны все найденные градиенты в виде точек в пространстве dXdY.
Далее, берется угловое окно (показано серым на фиг. 12) размером π/3, и вращается вокруг центра координат. Выбирается такое положение окна, при котором длина суммарного вектора для попавших в окно точек - максимальна. Вычисленный таким образом вектор нормируется и принимается как приоритетное направление в области ключевой точки.
Манипуляции с окном нужны для уменьшения влияния шумовых точек. На фиг. 13 приведен пример градиента при идеальном крае, и при крае с шумом:
Как видим, шум дает дополнительные градиенты в направлениях, не совпадающих с направлением основного градиента. Использование окна позволяет отсечь такие шумовые точки, и более точно вычислить истинный градиент.
Дескриптор ключевой точки представляют собой массив из 64 (в расширенной версии 128) чисел, позволяющих идентифицировать особую точку. Дескрипторы одной и той же ключевой точки на образце и на сцене должны примерно совпадать. Метод расчета дескриптора таков, что он не зависит от вращения и масштаба.
Для вычисления дескриптора, вокруг ключевой точки формируется прямоугольная область, имеющая размер 20s, где s - масштаб в котором была найдена ключевая точка (фиг. 14). Для первой октавы, область имеет размер 40×40 пикселов. Квадрат ориентируется вдоль приоритетного направления, вычисленного для ключевой точки. Дескриптор считается как описание градиента для 16 квадратов вокруг ключевой точки. Далее, квадрат разбивается на 16 более мелких квадратов, как показано на фиг. 14. В каждом квадрате берется регулярная сетка 5×5 и для точки сетки ищется градиент, с помощью фильтра Хаара. Размер фильтра Хаара берется равным 2s, и для первой октавы составляет 4×4.
Следует отметить, что при расчете фильтра Хаара, изображение не поворачивается, фильтр считается в обычных координатах изображения. А вот полученные координаты градиента (dX, dY) поворачиваются на угол, соответствующий ориентации квадрата.
Итого, для вычисления дескриптора ключевой точки, нужно вычислить 25 фильтров Хаара, каждый из 16 квадрантов. Итого, 400 фильтров Хаара. Учитывая, что на фильтр нужно 6 операций, выходит, что дескриптор обойдется минимум в 2400 операций.
После нахождения 25 точечных градиентов квадранта, вычисляются четыре величины, которые собственно и являются компонентами дескриптора:
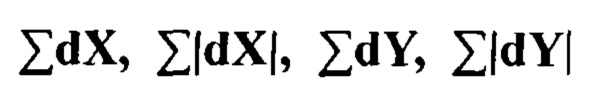
Две из них есть просто суммарный градиент по квадранту, а две других - сумма модулей точечных градиентов.
На фиг. 15 показано поведение этих величин для разных участков изображений. Рисунок на фиг. 15 показывает поведение дескриптора для разных изображений. Для равномерных областей - все значения близки к нулю. Для повторяющихся вертикальных полосок - все величины, кроме второй близки к нулю. При увеличении яркости в направлении оси X, две первые компоненты имеют большие значения.
Четыре компонента на каждый квадрант, и 16 квадрантов, дают 64 компонента дескриптора для всей области ключевой точки. При занесении в массив, значения дескрипторов взвешиваются на гауссиану, с центром в ключевой точке и с сигмой 3.3s. Это нужно для большей устойчивости дескриптора к шумам в удаленных от ключевой точки областях.
Плюс к дескриптору, для описания ключевой точки используется знак следа матрицы Гессе, то есть величина sign(Dxx + Dyy). Для светлых точек на темном фоне, след отрицателен, для темных точек на светлом фоне - положителен. Таким образом различаются светлые и темные пятна.
Таким образом для каждой ключевой точки размер дескриптора 4*16=64
Имея дескрипторы всех ключевых точек эталона и дескрипторы всех ключевых точек изображения сцены, для каждой точки эталона определяется самая близкая (по дескриптору) точка на изображении сцены.
PE(i)(j) - j-ый элемент дескриптора для i-той ключевой точки эталона.
PI(k)(j) - j-ый элемент дескриптора для k-той ключевой точки сцены
Имея дескрипторы всех ключевых точек эталона и дескрипторы всех ключевых точек изображения сцены, для каждой точки эталона ищется самая близкая (по дескриптору) точка на изображении сцены.
Критерий близости точек определяется как минимум суммы модулей разности значений дескрипторов для всех точек эталона с точками текущего изображения.
Для каждой i-ой точки эталона ищется такая точка к на текущем изображении, для которой сумма модулей разности значений дескрипторов минимальна.
Таким образом на изображении сцены определяются точки, соответствующие эталонному изображению. Если эта сумма меньше заданного порога, то эта точка определяется как точка, соответствующая точке на эталонном изображении. Заданный порог определяется экспериментально по результатам оценки среднего значения сумм разностей дескрипторов по всем точкам эталонного и текущего изображений.
Таким образом определенные точки на изображении сцены соответствуют точкам эталонного изображения.
Количество соответственных точек должно превышать половину точек эталона. Если это условие выполнено, то считается, что объект распознан на изображении сцены. На фиг. 16 представлен пример эталона для изображения сцены на фиг. 17.
На фиг. 18 показаны ключевые точки, определенные на эталонном изображении. На фиг. 19 показан результат распознавания объекта по ключевым точкам изображения сцены.
На фиг. 20 Изображена блок-схема алгоритма автоматического распознавания объектов на изображении сцены. На блок-схеме приняты следующие сокращенные обозначения:
КТ - ключевая точка.
Nt- число КТ текущего изображения.
Ne- число КТ эталонного изображения.
Nsp- номер КТ эталона, для которой ищется наиболее близкая КТ текущего изображения.
dei -множество компонентов дескриптора для i-той ключевой точки эталонного изображения.
dti -множество компонентов дескриптора для i-той ключевой точки текущего изображения.
Dik- критерий близости i-ой ключевой точки эталона и k-ой ключевой точки текущего изображения.
minDik - минимальное значение близости между i-ой КТ эталона и k-ой КТ текущего изображения.
Nsp- номер текущей точки эталона.
Т - порог для распознавания объекта, определяется экспериментально по результатам оценки среднего значения сумм модулей разностей дескрипторов по всем точкам эталона и текущего изображения.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ И УСТРОЙСТВО ДЕТЕКТИРОВАНИЯ ЛОКАЛЬНЫХ ОСОБЕННОСТЕЙ НА ИЗОБРАЖЕНИИ | 2013 |
|
RU2535184C2 |
| УСТРОЙСТВО ПОИСКА ДУБЛИКАТОВ ИЗОБРАЖЕНИЙ | 2013 |
|
RU2538319C1 |
| СПОСОБ И СИСТЕМА ТОЧНОЙ ЛОКАЛИЗАЦИИ СЛАБОВИДЯЩЕГО ИЛИ СЛЕПОГО ЧЕЛОВЕКА | 2017 |
|
RU2681346C2 |
| СПОСОБ ИДЕНТИФИКАЦИИ ОПОРНЫХ ТОЧЕК НА КОСМИЧЕСКИХ ИЗОБРАЖЕНИЯХ МЕСТНОСТИ ПРИ ОТСУТСТВИИ ПАРАМЕТРОВ ГЕОГРАФИЧЕСКОЙ ПРИВЯЗКИ | 2021 |
|
RU2768219C1 |
| CПОСОБ АВТОМАТИЧЕСКОГО РАСПОЗНАВАНИЯ ОБЪЕКТОВ НА ИЗОБРАЖЕНИИ | 2013 |
|
RU2528140C1 |
| Способ идентификации опорных точек на космических изображениях местности при их трансформировании | 2018 |
|
RU2683626C1 |
| Способ нахождения соответствия особых точек цифровых изображений | 2015 |
|
RU2614494C2 |
| СПОСОБ ИНТЕЛЛЕКТУАЛЬНОЙ ОБРАБОТКИ МАССИВА НЕОДНОРОДНЫХ ИЗОБРАЖЕНИЙ | 2021 |
|
RU2767281C1 |
| АВТОМАТИЗИРОВАННЫЕ СПОСОБЫ И СИСТЕМЫ ВЫЯВЛЕНИЯ НА ИЗОБРАЖЕНИЯХ, СОДЕРЖАЩИХ ДОКУМЕНТЫ, ФРАГМЕНТОВ ИЗОБРАЖЕНИЙ ДЛЯ ОБЛЕГЧЕНИЯ ИЗВЛЕЧЕНИЯ ИНФОРМАЦИИ ИЗ ВЫЯВЛЕННЫХ СОДЕРЖАЩИХ ДОКУМЕНТЫ ФРАГМЕНТОВ ИЗОБРАЖЕНИЙ | 2016 |
|
RU2647670C1 |
| СПОСОБ РАСПОЗНАВАНИЯ ОБЪЕКТОВ | 2010 |
|
RU2438174C1 |




Изобретение относится к области идентификации объектов на изображении. Технический результат заключается в уменьшении времени и ресурсов, требуемых для осуществления обработки изображений, а также повышении вероятности обнаружения объектов на изображении. Способ автоматического распознавания сцен и объектов на изображении, при котором формируют и запоминают эталонные изображения, осуществляют обработку потока входных изображений для нахождения на них интересующего объекта, используя эталонные изображения, отличающийся тем, что выделяют на эталонном изображении ключевые точки и участки вокруг них, после чего осуществляют поиск на входном изображении соответствующих ключевых точек эталонного изображения, далее создают дескрипторы ключевых точек, после этого для каждой ключевой точки эталонного изображения по признаку максимальной близости дескрипторов определяют соответствующую ключевую точку на текущем изображении и, если размер близости меньше заданного порога, соответствующую ключевую точку на текущем изображении запоминают, и когда количество соответствующих ключевых точек на текущем изображении превысит половину ключевых точек на эталонном изображении, объект сцены на изображении считают распознанным. 20 ил.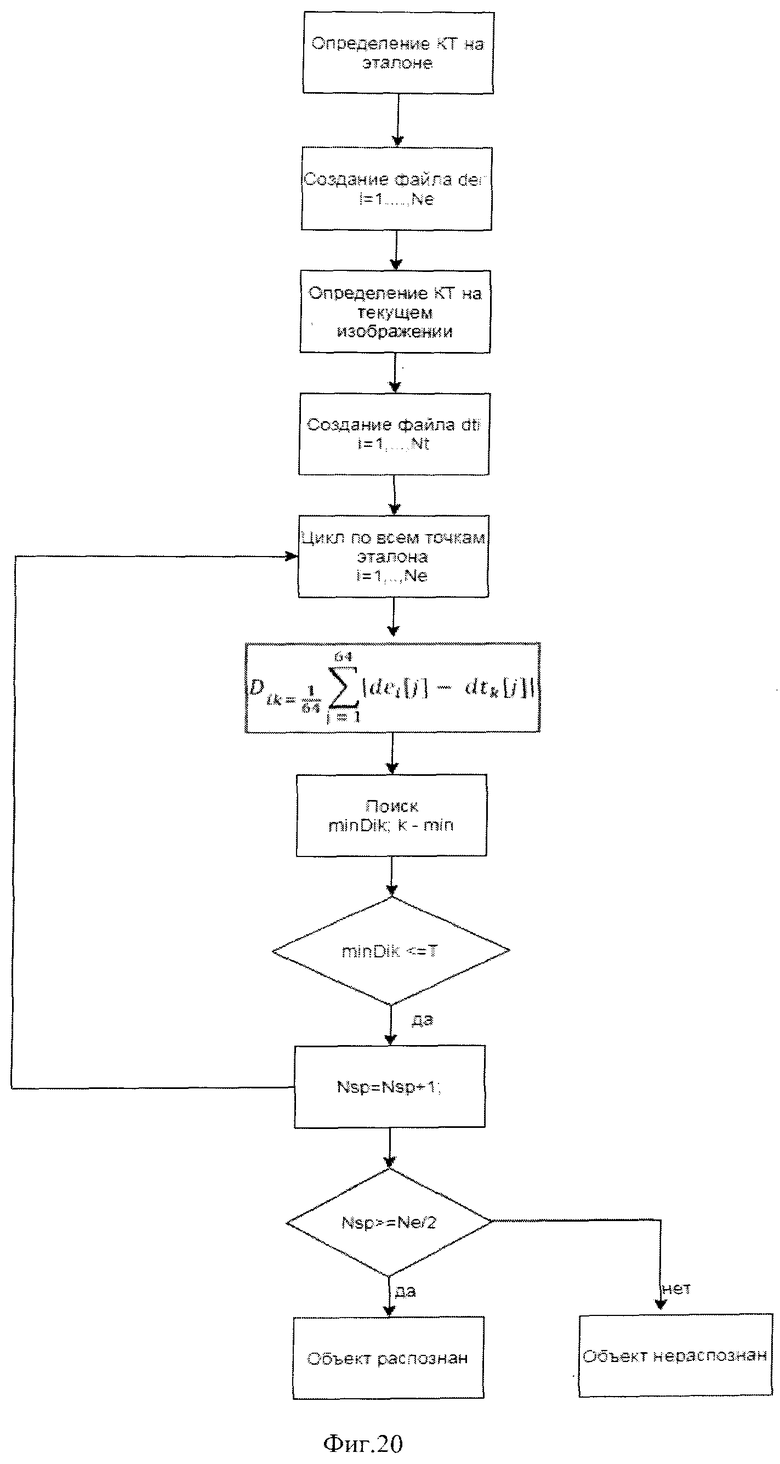
Способ автоматического распознавания сцен и объектов на изображении, при котором формируют и запоминают эталонные изображения, осуществляют обработку потока входных изображений для нахождения на них интересующего объекта, используя эталонные изображения, отличающийся тем, что выделяют на эталонном изображении ключевые точки и участки вокруг них, размеры которых выбирают в пределах, необходимых для вычисления градиентов яркости, в которых происходит максимальное изменение градиента яркости и которые представляют собой, например, края линий, небольшие круги, резкие перепады освещенности, углы, после чего осуществляют поиск на входном изображении соответствующих ключевых точек эталонного изображения, при этом выделение ключевых точек на изображении осуществляют с помощью матрицы Гессе, определяя ее детерминанты, называемые гессианами, достигающими экстремума в точках максимального изменения градиента яркости, причем определение гессианов для каждой ключевой точки производят с помощью разномасштабных фильтров Хаара, далее создают дескрипторы ключевых точек в виде чисел, отображающих флуктуации градиента яркости вокруг ключевой точки и инвариантных к масштабу и вращению, причем флуктуации градиента окрестностей ключевой точки вычисляют относительно направления градиента по всей окрестности ключевой точки, после этого для каждой ключевой точки эталонного изображения по признаку максимальной близости дескрипторов определяют соответствующую ключевую точку на текущем изображении и, если размер близости меньше заданного порога, соответствующую ключевую точку на текущем изображении запоминают, при этом заданный порог определяют экспериментально по результатам оценки среднего значения сумм разностей дескрипторов по всем ключевым точкам эталонного и текущего изображений, и когда количество соответствующих ключевых точек на текущем изображении превысит половину ключевых точек на эталонном изображении, объект сцены на изображении считают распознанным.
| Способ распознавания объектов на изображении | 2018 |
|
RU2693267C1 |
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ РАСПОЗНАВАНИЯ ИЗОБРАЖЕНИЙ ОБЪЕКТОВ | 2007 |
|
RU2361273C2 |
| СПОСОБ ПОЛУЧЕНИЯ ИЗОБРАЖЕНИЯ ОБЪЕКТА | 2003 |
|
RU2243591C1 |
Авторы
Даты
2022-08-29—Публикация
2021-03-23—Подача