Область техники
Чтобы оптимизировать характеристики авиационных (газотурбинных) двигателей во всей области полета, одной из возможностей является добавление «органов с изменяемой геометрией» (разгрузочные вентили, лопатки или лопасти с регулируемым углом установки, сопловые створки переменного сечения и т.д.). В общем, органы с изменяемой геометрией представляют собой узлы, оснащенные подвижными элементами, положением которых можно управлять для изменения таких параметров, как прохождение газового потока, и которые позволяют, таким образом, получать степени свободы при управлении газотурбинным двигателем. Обычно ими управляет вычислительное устройство, и их действия должны быть согласованными, чтобы быть оптимальными с точки зрения эффективности и оставаться в допустимых пределах управляемости и безопасности работы газотурбинного двигателя (в частности, что касается давления, температуры, скоростных режимов, крутящих моментов…).
Обычно говорят о многомерной системе, когда система имеет несколько входов и/или несколько выходов. Классические одномерные стратегии архитектуры и регулирования не подходят для этих систем по причине взаимодействий между различными переменными.
Случай турбовинтового двигателя
Турбовинтовой двигатель классически содержит газогенератор (турбину), приводящий во вращение воздушный винт с изменяемым шагом.
Главной задачей системы регулирования турбовинтового двигателя является обеспечения требуемой тяги с одновременным сохранением постоянной скорости вращения воздушного винта. С точки зрения управления турбовинтовой двигатель можно рассматривать как многомерную систему, имеющую:
- две входные величины:
- расход топлива, в дальнейшем обозначаемый WF,
- шаг воздушного винта (называемый также углом установки), в дальнейшем обозначаемый β;
- две выходные величины:
- мощность воздушного винта, в дальнейшем обозначаемую SHP,
- скорость вращения воздушного винта, в дальнейшем обозначаемую XNP.
Как правило, мощностью SHP управляют за счет воздействия на расход топлива WF, тогда как скоростью вращения XNP воздушного винта управляют посредством воздействия на шаг β воздушного винта. Скорость XNP автоматически регулируется вокруг нескольких горизонтальных участков скорости, определяемых относительно условий полета и относительно состояния турбовинтового двигателя.
Основной проблемой регулирования является то, что запрос на изменение SHPref мощности приводит к нежелательному изменению скорости вращения XNP воздушного винта. Точно так же, запрос на изменение XNPref заданной скорости вращения воздушного винта затрагивает мощность SHP газогенератора. Это связано с тем, что каждая из команд действует на каждый из выходов.
Эти изменения отрицательно сказываются на турбовинтовом двигателе. В частности, они приводят к значительным превышениям крутящего момента, которые влияют на усталостный износ компонентов, в частности, редуктора.
Другие примеры применений
Все вышесказанное относится также к управлению двигателями в других примерах применений.
Например, это относится к управлению двигателем, содержащим не закрытые обтекателем сдвоенные воздушные винты с противоположным вращением (или “Open Rotor” - двигатель с открытым ротором - в терминологии, обычно используемой в данной области), который является примером, подобным турбовинтовому двигателю с точки зрения управления: система использует три входные величины (расход топлива и соответствующие шаги двух воздушных винтов с противоположным вращением), чтобы управлять тремя выходными величинами (скорость вращения камеры низкого давления и скорости вращения каждого из двух воздушных винтов).
Это относится также к случаю турбореактивных двигателей, в которых дополнительно к расходу топлива можно управлять также сечением реактивного сопла. Эта дополнительная степень свободы в основном позволяет воздействовать на скорость выброса газа и, следовательно, на тягу.
В турбореактивные двигатели можно также встроить различные элементы с изменяемой геометрией. Хотя заданные значения для изменяемых геометрий и для расхода топлива разрабатываются согласованно, их системы регулирования (токи сервоклапана) синтезируются независимо и могут влиять на некоторые общие рабочие параметры, такие как скорости вращения или кривая производительности компрессоров.
Основные задачи при синтезе правил управления
Основными задачами при синтезе правил управления для этих систем являются:
- Соблюдение спецификаций, заданных техническими требованиями (время реагирования, превышение, запасы стабильности),
- Ограничение взаимодействий между различными переменными: изменение заданного значения одной из величин должно приводить к наименьшему возможному отклонению на других величинах,
- Стойкость управления к отклонениям и к погрешностям моделирования.
Кроме задач обеспечения эффективности, правила управления должны быть легко корректируемыми и иметь разумную сложность, чтобы облегчать регулирование, коррекцию во время испытаний и применение в вычислительных устройствах.
Существующие решения многомерного управления с развязкой
В этих решениях синтезирование правил управления осуществляют на основании линейной модели, идентифицированной вокруг рабочих точек. Указанные ниже схемы известных систем представлены с линейными моделями турбовинтового двигателя. Эти модели обозначены G, если применяют форму матрицы перехода. Когда используют форму состояния, модель турбовинтового двигателя состоит из матриц состояния, управления и выхода А, В и С (при этом в рассматриваемых случаях управления двигателем матрица прямого действия D является нулевой).
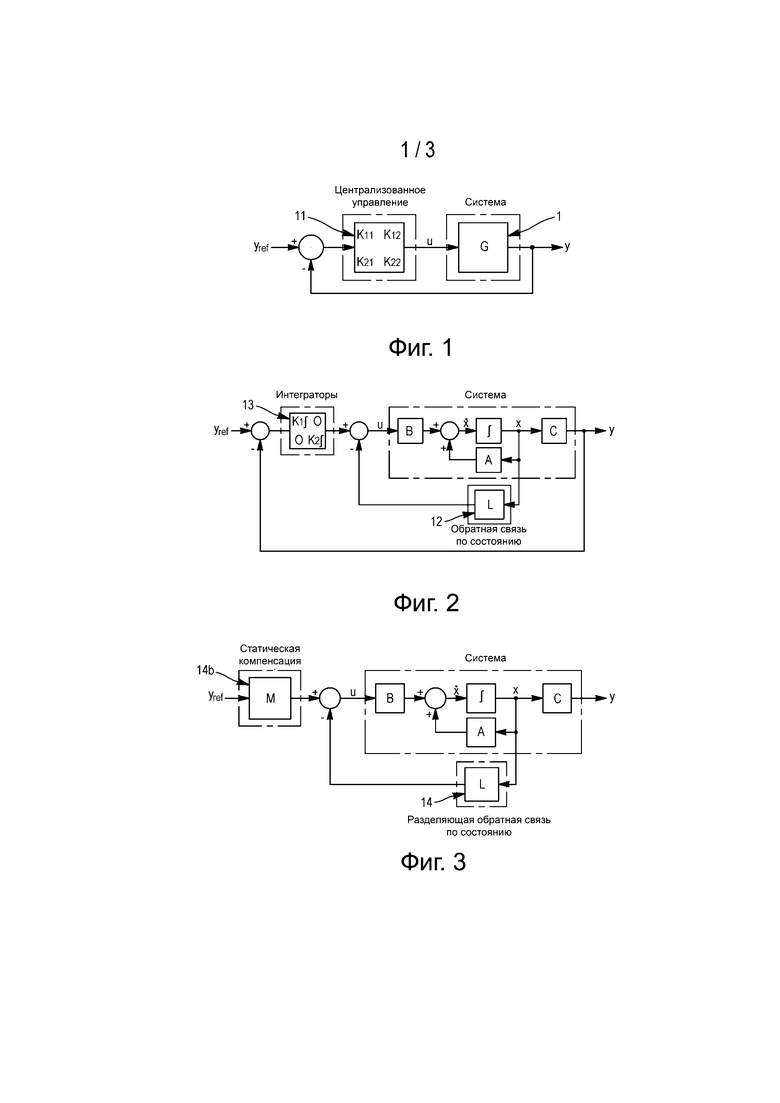
Как показано на фиг. 1, известны так называемые централизованные решения типа Н2, Н∞ (как решение, описанное в документе G. Zames, Feedback and Optimal Sensitivity Model Reference Transformations, Multiplicative Seminorms, and Approximations, IEEE Transactions on Automatic Control, vol. 26, issue n° 4, 1981).
Эти подходы позволяют синтезировать многомерный корректор 11, напрямую учитывая мощность SHP и скорость XNP воздушного винта.
Хотя эти решения являются относительно эффективными, их разработка требует сложных вычислений, и получаемые корректоры, как правило, являются сложными. Кроме того, эти правила управления не являются интуитивными, что создает очевидную проблему для коррекции регулировок во время испытаний двигателей.
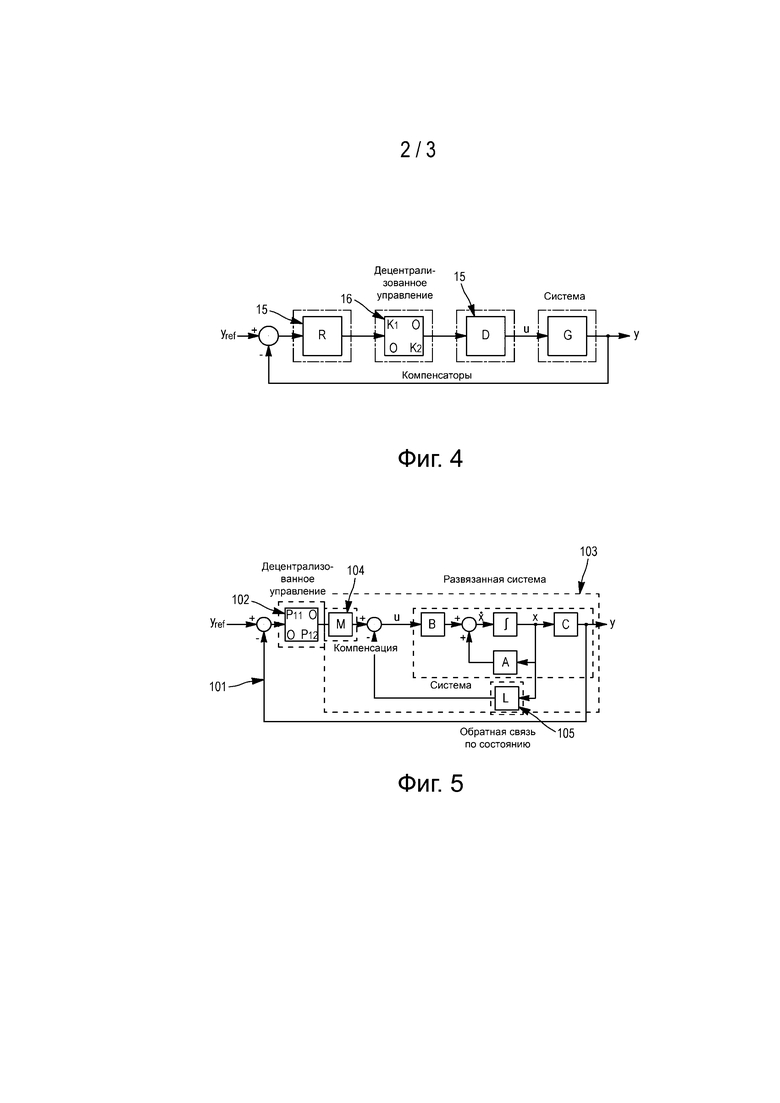
Как показано на фиг. 2, известны также варианты управления с обратной связью по состоянию (типа метода размещения полюсов, метода квадратичного линейного управления). Эти методы состоят в добавлении обратной связи, включающей в себя обратную связь по состоянию 12. Как правило, к обратной связи по состоянию 12 добавляют члены интегрального действия 13, чтобы добиться хорошей эффективности.
Поскольку эти методы не предусматривают развязку, взаимодействия между контурами мощности SНP и винта XNP остаются слишком значительными. Кроме того, управление двигателем с обратной связью по состоянию практически не поддается коррекции на испытательном стенде.
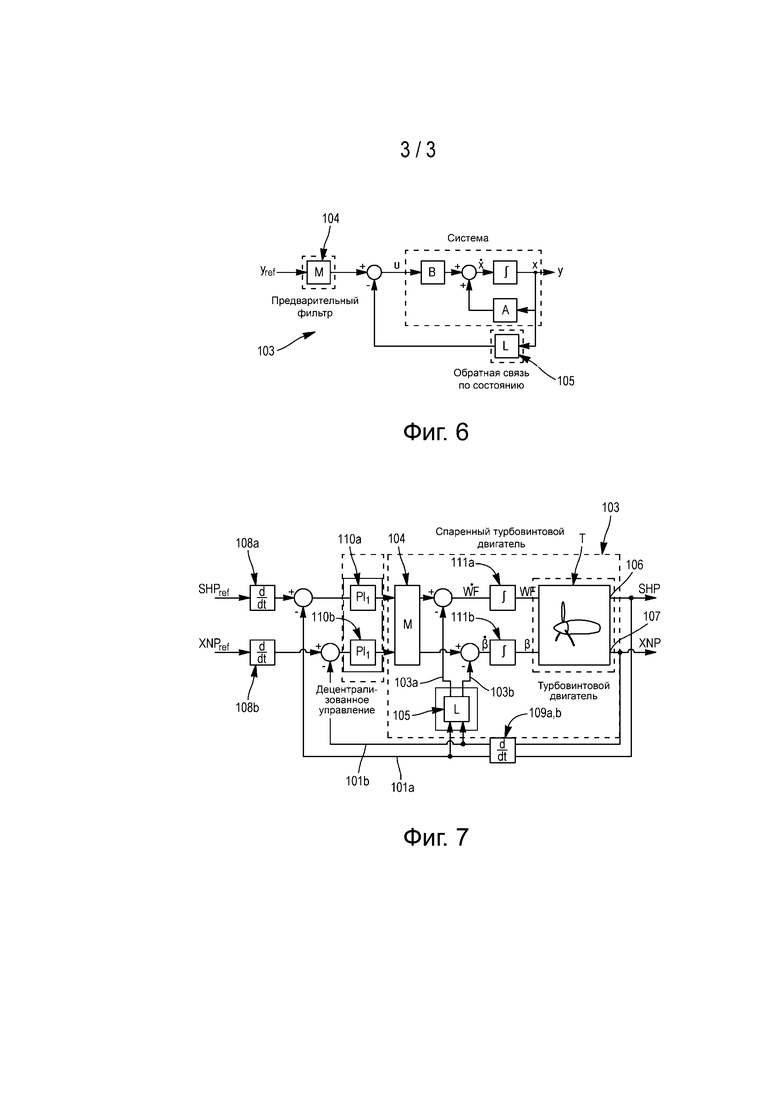
Как показано на фиг. 3, известны подходы развязки обратной связи по состоянию (например, такие как синтез Фальбе-Волович (описанный в работе «Многомерное управление и оценка», Ostertag, 2006) или полный модальный синтез). Эти методы состоят в добавлении обратной связи, включающей в себя обратную связь по состоянию 14 и статическую компенсацию М 14b для развязки системы.
Преимуществом этих методов является то, что они обеспечивают полную развязку при использовании относительно простых корректоров.
Однако эти методы не совместимы с добавлением интегральных действий. Действительно, эти методы основаны на перемещении ограниченного числа полюсов, зависящих от системы, и добавление интеграторов и, следовательно, нестабильных полюсов приводит к перемещению последних вместо полюсов системы. Достигаемая эффективность является недостаточной, в частности, с точки зрения устранения помех. Кроме того, на практике трудно корректировать системы управления с обратной связью по состоянию.
Как показано на фиг. 4, известны также частотные методы развязки (такие как метод псевдо-диагонализации, метод разложения на собственные значения и на сингулярные значения, метод упрощенной схемы развязки или идеальной схемы развязки), которые позволяют развязать систему при помощи компенсаторов 15, прежде чем использовать одномерные регуляторы 16 типа ПИД, позволяющие автоматически регулировать систему.
Преимуществом этих методов является то, что этапы синтеза компенсаторов 15 и одномерных регуляторов 16 являются раздельными. Следовательно, можно относительно просто корректировать апостериори регулировки одномерных регуляторов 16.
Проблемой является то, что, как правило, простые компенсаторы не обеспечивают удовлетворительной развязки. Надлежащей или идеальной развязки можно достичь, используя только сложные компенсаторы, которые практически не поддаются внедрению и интерполяции.
Некоторые методы состоят только в применении матрицы 15 компенсации в качестве смещений, добавляемых в команды для компенсации помех различных контуров. Проблемой этих методов является то, что смещения трудно вычислять и что они не всегда являются достаточно точными.
Вышеуказанные подходы позволяют:
- получить среднюю развязку, или
- получить правильную развязку за счет относительно сложных правил управления и методов синтеза.
Кроме того, из документа US 5274558 известна система авиационного двигателя, которая содержит:
- следящий контур, который получает на входе заданное значение крутящего момента QCMD,
- контур скорости вращения (фиг. 3 - заданное значение скорости NPSFLT).
Система содержит также блок 18, 35 развязки, который выдает сигнал, показывающий развязанный крутящий момент QDC, который позволяет отделить контур крутящего момента от контура скорости, чтобы на резкие изменения скорости вращения двигателя реагировал только контур скорости.
Здесь не предусмотрено никакого управления с обратной связью по состоянию.
В документе US 5001646 описана электрическая система управления (“fly-by-wire”) вертолета.
Эта система содержит по меньшей мере один следящий контур, который получает на входе заданные значения параметров (крен, тангаж, рыскание, вертикаль), поступающие от ручки управления.
Контур обратной связи регулирует рабочие параметры двигателя.
В этой системе тоже не предусмотрено управление с обратной связью по состоянию.
В документе US 5920478 описана общая динамическая система управления со следящим контуром.
Блок развязки обрабатывает данные MIMO и преобразует их в данные, обеспечивающие простую одномерную обработку SISO, учитывая при этом сложные взаимодействия между переменными.
Применяемая развязка не является развязкой типа обратной связи по состоянию, но соответствует развязкам, представленным выше со ссылками на фиг. 4. Как было указано выше, недостатком этих схем развязок является то, что они не обеспечивают удовлетворительной развязки, если только не использовать исключительно сложные компенсаторы.
Раскрытие изобретения
Общей задачей изобретения является обеспечение необходимой эффективности, в частности, что касается развязки, с одновременным сохранением возможности регулировать корректоры простым и интуитивным способом.
Для этого предложена система управления авиационным двигателем, которая содержит:
- по меньшей мере один следящий контур, который получает на входе заданные значения рабочих параметров двигателя и который управляет системой вместе с контуром обратной связи по этим рабочим параметрам, при этом указанный следящий контур включает в себя блок децентрализованного управления с одномерными регуляторами,
- по меньшей мере один блок управления с обратной связью по состоянию, встроенный в следящий контур, при этом указанный блок управления получает на входе выходные данные блока децентрализованного управления с одномерными регуляторами и является контуром обратной связи между рабочими параметрами двигателя и выходами указанного блока децентрализованного управления, при этом указанный контур обратной связи выдает параметры управления двигателем,
при этом блок управления c обратной связью по состоянию выполнен с возможностью развязки рабочих параметров, при этом одномерные регуляторы децентрализованного управления выполнены с возможностью автоматического регулирования рабочих параметров по заданным значениям этих параметров.
Под децентрализованным управлением в данном случае следует понимать управление, которое не является централизованным, а которое использует множество локальных и независимых правил управления для различных управляемых подсистем.
Управление с обратной связью может включать в себя статический компенсатор и контур с корректором обратной связи по состоянию, при этом указанный статический компенсатор и указанный контур с корректором обратной связи по состоянию выполнены с возможностью развязки рабочих параметров.
Такая система сочетает в себе преимущества решений развязки обратной связи по состоянию и методов частотной развязки.
В частности, схема развязки и регуляторы разделены.
Поскольку схема развязки выполнена с применением подхода развязки обратной связи по состоянию, можно обеспечить полную развязку при помощи очень простого корректора состояния и матрицы М компенсации, сохраняя при этом, в отличие от классических методов развязки, основные динамические факторы способа (что выражается в матрице значениями, равными 0, на недиагональных элементах, и ненулевыми значениями на диагональных элементах).
Таким образом, уменьшение связей является очень эффективным. Кроме того, развязывающая обратная связь по состоянию представляет собой две простые матрицы коэффициентов усиления: обратной связи по состоянию и статической компенсации.
Предпочтительно одномерные регуляторы децентрализованного управления являются пропорционально-интегральными корректорами (ПИ-корректорами).
ПИ-корректоры позволяют получить требующиеся характеристики.
Их преимущество заключается в их простоте, и их установки облегчаются благодаря развязки. Кроме того, их можно легко корректировать/переустанавливать, причем независимо от развязывающей обратной связи по состоянию. Эти корректировки/переустановки можно осуществлять во время фаз проектирования, в ходе стендовых испытаний, а также в течение эксплуатации турбовинтового двигателя. Действительно, в ходе старения системы ее поведение меняется. В этом случае ПИ-корректоры можно адаптировать с целью поддержания требующихся характеристик (в частности, что касается времени отклика и выхода за установленные пределы).
Объектом изобретения является также способ параметризации вышеупомянутой системы управления авиационного двигателя, содержащий этапы, на которых:
- определяют линейную модель двигателя, при этом модель имеет переходную функцию и представление состояния;
- определяют статический компенсатор и корректор обратной связи по состоянию таким образом, чтобы развязать состояния, образованные рабочими параметрами регулируемого двигателя;
- определяют одномерные регуляторы, так чтобы автоматически регулировать указанные рабочие параметры по заданным значениям.
Таким образом, реализуют смешанную развязку, при которой:
- осуществляют развязку посредством обратной связи по состоянию;
- синтезируют регуляторы (в частности, ПИ-регуляторы) при помощи способа, развязанного посредством обратной связи по состоянию.
В частности, корректор обратной связи по состоянию и статический компенсатор могут быть выполнены таким образом, чтобы переходная функция системы управления имела коэффициенты усиления и полюсы, соответствующие коэффициентам усиления и полюсам переходной функции модели двигателя.
Способ может дополнительно содержать этап интерполяции одномерных корректоров в зависимости от переменных условий полета.
Параметры одномерных корректоров могут быть интерполированы индивидуально посредством задания последовательности коэффициентов усиления.
Способ может также содержать этап интерполяции корректора обратной связи по состоянию и статического компенсатора в зависимости от переменных условий полета.
Изобретение относится также к применению предложенной системы для различных приложений.
Следует отметить, что предложенное изобретением решение является исключительно эффективным в случае системы, рассматривающей 2 или 3 элементов управления и выходных параметров, при этом можно предусмотреть более значительное число переменных, но, возможно, с менее точными результатами. Действительно, обычно правила управления синтезируют на номинальной линейной модели. Поскольку эта модель не является идеальной, то правила управления не обеспечивают одинаковый уровень эффективности на нелинейной модели. Это же касается и развязки, которая, как известно, является довольно чувствительной к погрешностям модели. Матрицы М и L учитывают все переходы многомерной системы и могут оказаться менее точными, когда число переменных увеличивается.
В случае управления двигателем с воздушным винтом с переменным шагом, таким как турбовинтовой двигатель, автоматически регулируемые рабочие параметры включают в себя мощность (SHP) воздушного винта и скорость его вращения (XNP), управляемыми параметрами являются расход топлива и шаг винта.
В случае управления двигателем, имеющим сдвоенные воздушные винты с противоположным вращением (сдвоенные винты противоположного вращения с переменным шагом, не закрытые обтекателем “Open Rotor” или закрытые обтекателем “Contrafan”), в котором автоматически регулируемые рабочие параметры включают в себя режим камеры низкого давления (NBP) и режим двух воздушных винтов (N1 и N2), а управляемые параметры включают в себя расход топлива (WF) и шаг винтов (β1 и β2).
Для управления турбореактивным двигателем с регулируемым сечением сопла автоматически регулируемые рабочие параметры включают в себя режим камеры низкого давления (NBP) и положение (хТ) силового цилиндра или силовых цилиндров, управляющих регулируемым сечением сопла, при этом управляемые параметры включают в себя расход топлива (WF) и ток (iTuy) сервоклапана, питающий силовой цилиндр или силовые цилиндры.
В случае управления турбореактивным двигателем с элементами с изменяемой геометрией, автоматически регулируемые рабочие параметры включают в себя режим камеры низкого давления (NBP) и положение силовых цилиндров (xVSV и xVBV) (при этом можно также предусмотреть другие рабочие параметры, такие как кривая производительности гидроусилителя), а управляемые параметры включают в себя расход топлива (WF) и токи управления (iVSV и iVBV) сервоклапанами.
Краткое описание чертежей
Другие признаки и преимущества изобретения будут более очевидны из нижеследующего описания, которое представлено исключительно в качестве иллюстративного и не ограничительного примера со ссылками на прилагаемые фигуры, на которых:
Фиг. 1 - схема известной централизованной системы регулирования.
Фиг. 2 - схема известной системы регулирования с обратной связью по состоянию.
Фиг. 3 - схема известной системы развязки с обратной связью по состоянию.
Фиг. 4 схематично иллюстрирует известный метод частотный развязки.
Фиг. 5 - система со смешанной стратегией управления согласно возможному варианту выполнения изобретения.
Фиг. 6 - управление системы, показанной на фиг. 5, с обратной связью по состоянию.
Фиг. 7 - пример применения изобретения для управления турбовинтовым двигателем.
Описание вариантов осуществления изобретения
В примере, представленном на фиг. 5, рассмотрен случай двух заданных значений, команд и выходов, причем эта архитектура и способ регулирования в дальнейшем обобщены для N заданных значений, команд и выходов.
Архитектура этой системы 100 управления включает в себя:
- децентрализованный контур 101 управления с компенсаторами;
- систему 103 развязки с обратной связью по состоянию, встроенную в указанный контур 101.
Контур 101 получает N заданных значений Yref и содержит блок 102 децентрализованного управления, выходы которого питают систему 103 развязки с обратной связью по состоянию и корректоры которого выбраны таким образом, чтобы контур 101 мог обеспечивать функцию автоматического регулирования способа.
Развязка с обратной связью по состоянию
Система развязки с обратной связью по состоянию более конкретно показана на фиг. 6 и содержит:
- статический компенсатор 104, выполненный с возможностью развязывать заданные значения на выходе децентрализованного блока управления 101 (матрица М предварительного фильтра (или матрица компенсации));
- корректор 105 обратной связи по состоянию (матрица L обратной связи по состоянию).
В дальнейшем предполагается, что соблюдены следующие гипотетические условия:
- Способ является линейным.
- Число команд равно числу регулируемых выходов. Речь идет о классической гипотезе для развязки (и в любом случае невозможно развязать систему, если не располагать необходимым числом степеней свободы).
- Матрица прямого действия является нулевой. Это является классической гипотезой, соблюдаемой большинством систем управления с обратной связью по состоянию (команды не действуют мгновенно на выходы).
- Матрица В управления является необратимой.
- Способ не содержит нестабильного нуля (как и в случае других методов развязки с обратной связью по состоянию, нестабильный ноль привел бы к нестабильному полюсу в решении).
Рассмотрим также случай, когда число состояний системы равно числу выходов (все рассматриваемые состояния измеряются). В этом случае можно корректировать А и В, чтобы рассматривать выходную матрицу С как матрицу тождества.
Вместе с тем, эту гипотезу можно обойти. В частности, в случае, когда система имеет число состояний, превышающее число входов/выходов, можно добавить алгоритм наблюдения.
С учетом вышеупомянутых гипотетических условий выходная матрица С схемы на фиг. 3 равна тождеству по предположению, поэтому:
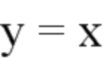 и
и 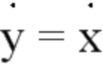
Представление состояния d можно записать следующим образом:
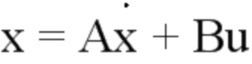
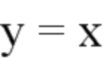
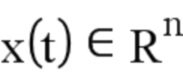 : столбец, представляющий N переменных состояния
: столбец, представляющий N переменных состояния
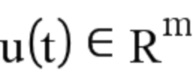 : столбец, представляющий N команд
: столбец, представляющий N команд
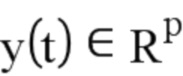 : столбец, представляющий N выходов
: столбец, представляющий N выходов
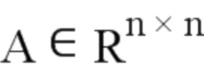 : Матрица состояния
: Матрица состояния
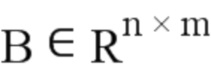 : Матрица управления
: Матрица управления
Рассматриваемую систему можно полностью представить в виде нижеследующего выражения (1). Затем можно использовать обозначения выражения (2).
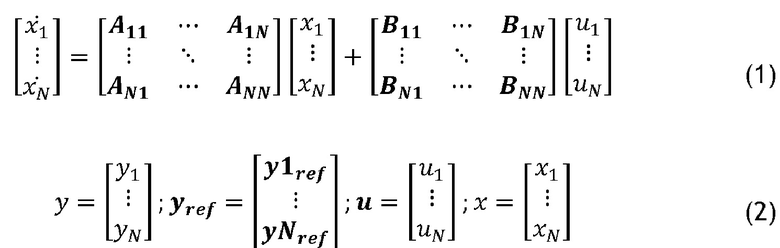
Следовательно, управление, осуществляемое системой развязки, показанной на фиг. 6, является таким, что:
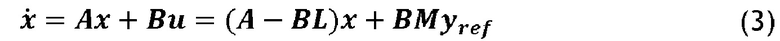
Что касается L и М, их выбирают таким образом, чтобы:
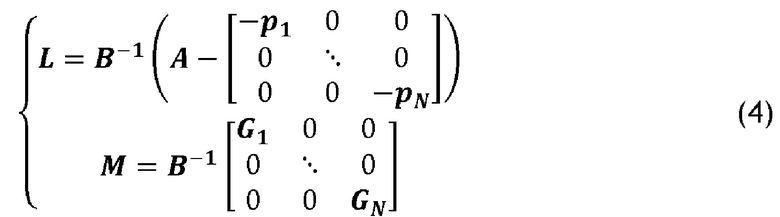
где параметры pi и Gi являются скалярными величинами.
Действительно, такое управление обеспечивает идеальную развязку:
- каждый элемент, включенный в 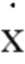 , зависит только от его соответствующего элемента в векторе х (например,
, зависит только от его соответствующего элемента в векторе х (например, 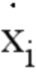 должен зависеть только от
должен зависеть только от 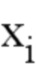 , но не от других элементов х),
, но не от других элементов х),
- на каждый элемент, включенный в 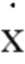 , влияет только соответствующий ему элемент в векторе u (например, на
, влияет только соответствующий ему элемент в векторе u (например, на 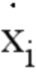 влияет только
влияет только 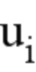 , но не другие элементы u).
, но не другие элементы u).
Действительно, с такими матрицами L и М:
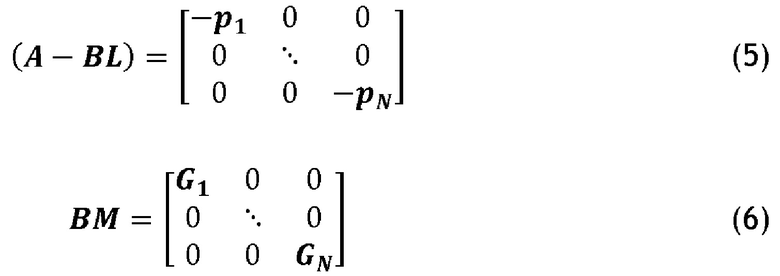
Получаем (7), комбинируя выражения (3), (5) и (6). Переход к (8) и (9) использует только тот факт, что 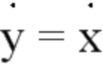 и
и 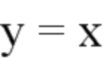 .
.
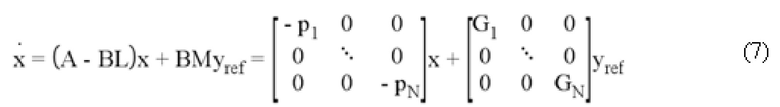
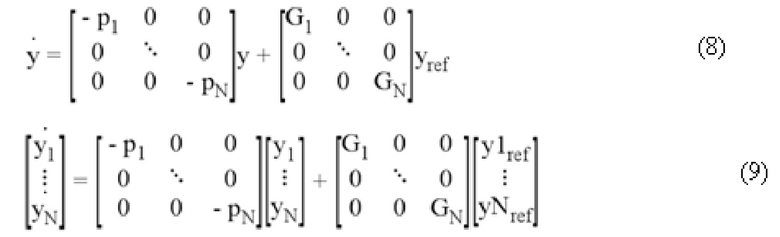
Перейдя в область Лапласа, получаем:
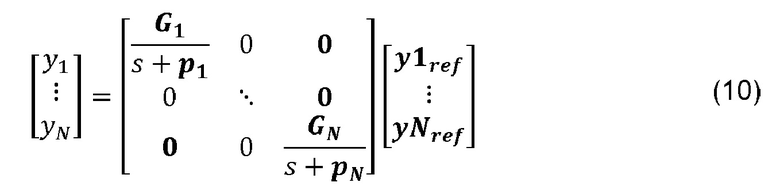
Таким образом, отклики системы развязаны и соответствуют переходным функциям первого порядка с полюсами pi и коэффициентами усиления Gi.
Значения коэффициентов усиления Gi и полюсов pi определяют, приближая диагональные члены способа при помощи первых порядков уравнения (10). Различные методы упрощения позволяют сделать выбор коэффициентов усиления Gi и полюсов pi на основании диагональных переходов системы.
Например, для этого применяют методы упрощения модели, например, такие как метод усечения, и сравнивают частотные отклики первоначальных переходов и частотные отклики уменьшенных переходов, стараясь при этом сохранить статический коэффициент усиления и частоту отсечки.
В частности, коэффициенты усиления Gi и полюсы pi можно выбрать таким образом, чтобы статические коэффициенты усиления и частоты отсечки были подобными.
Следует отметить, что с предложенной схемой управления получаемая развязка является полной, при этом установку автоматического регулирования осуществляют не на контур 103 с обратной связью по состоянию, а на корректорах/компенсаторах контура 101.
Таким образом, в отличие от так называемого метода Фальбе-Волович [Многомерные управление и оценка, Ostertag, 2006] задачей системы с обратной связью по состоянию является не способ автоматическое регулирования, а способ его развязки.
Это позволяет коэффициентам усиления корректоров (см. ниже) наилучшим образом сохранять динамику переходов.
Одномерные корректоры
Корректоры децентрализованного блока управления 102 выбирают таким образом, чтобы корректировать необходимое автоматическое регулирование на основании развязанной системы.
В частности, когда эти корректоры являются ПИ-корректорами, их относительно простая структура значительно облегчает установки параметров. Действительно, форма ПИ-корректоров позволяет сохранить определенный физический смысл, что делает установки параметров более интуитивными. Их можно корректировать независимо от развязки в ходе стендовых испытаний.
Если применяют другой метод развязки и если развязка не является полной, необходимо применять так называемые многоконтурные методы синтеза (методы “detuning”, циклические методы…). Такие методы позволяют учитывать взаимодействия между контурами SHP и XNP во время синтеза корректоров, но они являются более сложными, чем классические методы регулирования.
Поскольку развязка с обратной связью по состоянию является полной, можно применять классические методы установки параметров для настройки корректоров. Эти методы являются простыми в применении, так как настройки можно осуществлять независимо для автоматического регулирования выходов системы.
В частности, для осуществления этих настроек можно применять метод ПИД-IMC (Internal Model Control - модель внутреннего контроля) на основании переходных функций развязанного процесса и спецификаций, выраженных в виде переходных функций первого порядка. Настройки ПИ-регуляторов являются относительно простыми и могут происходить автоматически при помощи этого метода, на основании переходных функций развязанного процесса и спецификаций.
Тем не менее, вместо метода ПИД-IMC можно использовать другие одномерные корректоры и другие методы настроек.
Параметризация
Систему управления параметризуют в соответствии со способом параметризации, содержащим этапы, на которых:
- Е1 определяют модель рассматриваемой механической системы двигателя;
- Е1 определяют корректор 105 обратной связи по состоянию и статический компенсатор 104 таким образом, чтобы развязать управляемые параметры выходов, сохраняя при этом основные динамические характеристики системы;
- Е3 определяют корректоры блока 102 децентрализованного управления (например, одномерные ПИ-корректоры), чтобы автоматически регулировать выходные параметры в соответствии с выбранным правилом.
Факультативно, способ может содержать этап Е4 интерполяции корректоров блока 102 децентрализованного управления, корректора 105 обратной связи по состоянию и статического компенсатора 104.
Применение для турбовинтового двигателя
На фиг. 7 представлено применение для управления турбовинтовым двигателем Т.
Представленная на этой фигуре система управления получает на входе заданные значения мощности воздушного винта SHPref и скорости воздушного винта XNPref.
Эти заданные значения генерирует, например, блок управления (не показан), вычисляющий указанные заданные значения мощности и скорости на основании заданного значения тяги, которое поступает от устройства 18 управления, как правило, ручки управления.
Указанная система выдает на выходе мощность воздушного винта SHP и скорость вращения воздушного винта XNP турбовинтового двигателя, которые измеряются датчиком 106 мощности воздушного винта SHP и датчиком 107 скорости вращения воздушного винта XNP.
Система содержит два общих контура управления 101а и 101b, из которых один (101а) автоматически устанавливает мощность SHP по заданному значению мощности SHPref, а другой (101b) автоматически устанавливает скорость вращения воздушного винта XNP по заданному значению скорости вращения воздушного винта XNPref.
На входе общего контура мощности SHP 101а находится дифференциатор 108а, а на входе общего контура скорости вращения воздушного винта XNP 101b находится дифференциатор 108b.
Дифференциаторы 109а и 109b тоже получают на входе мощность воздушного винта SHP и скорость вращения XNP и перенаправляют их на входы обратной связи двух контуров 101а и 101b.
Каждый из этих двух контуров 101а, 101b содержит, в свою очередь, блок децентрализованного управления 110а, 110b и два контура развязки 103а, 103b, питаемые соответственно через выходы блоков децентрализованного управления 101а, 101b.
Каждый блок децентрализованного управления 101а, 101b получает на входе сигнал ошибки контура, которому он соответствует.
Блок децентрализованного управления 110а содержит одномерный корректор мощности SHP, выполненный с возможностью автоматически регулировать мощность SHP по заданному значению SHPref, тогда как блок децентрализованного управления 110b содержит одномерный корректор скорости XNP, выполненный с возможностью автоматически регулировать скорость XNP по заданному значению XNPref.
Контуры развязки 103а, 103b включают в себя корректор 105 обратной связи по состоянию, выполненный с возможностью развязывать мощность воздушного винта SHP и скорость вращения воздушного винта XNP турбовинтового двигателя 1 с точки зрения состояний системы.
Указанный корректор 105 получает на входе выходные данные дифференциаторов 109а и 109b.
Выходы корректора 105 образуют входы обратной связи указанных контуров 103а и 103b, которые получают на своем другом входе выходные данные статического компенсатора 104.
Указанные контуры 103а, 103b содержат также соответственно интегратор 111а, расположенный перед входом управления расходом топлива WF турбовинтового двигателя Т, и интегратор 111b, расположенный переход входом управления шагом воздушного винта β турбовинтового двигателя Т.
Эти два интегратора 111а и 111b генерируют соответственно команду расхода топлива WF и команду шага винта β для турбовинтового двигателя Т.
Определяют определенное число характеристических рабочих точек. Эти характеристические рабочие точки характеризуются условиями полета (число Маха, высота полета) и состояниями турбовинтового двигателя.
Во время фазы проектирования для каждой из этих характеристических рабочих точек моделируют сценарии идентификации на основании нелинейной термодинамической модели двигателя. Управление, используемое для этих сценариев идентификации, представляет собой последовательность рассинхронизованных ступеней управления с белым шумом.
Затем используют результаты этих моделирований, чтобы характеризовать поведение турбовинтового двигателя и определить линейную модель турбовинтового двигателя, которая моделирует работу турбовинтового двигателя и входными данными которой являются расход топлива WF и шаг воздушного винта β, а выходными данными - мощность воздушного винта SHP и скорость вращения воздушного винта XNP.
После анализа результатов выбирают модель порядка 2 турбовинтового двигателя. Таким образом, модель турбовинтового двигателя имеет две переменные состояния, при этом порядок системы равен числу переменных состояния.
Поскольку число переменных состояния равно одновременно числу входов и числу выходов модели турбовинтового двигателя, то можно напрямую связать переменные состояния с выходами модели турбовинтового двигателя. Таким образом, переменными состояния турбовинтового двигателя являются мощность воздушного винта SHP и скорость вращения воздушного винта XNP.
На этапах Е2 и Е3 применяют компьютерное цифровое моделирование работы турбовинтового двигателя при помощи модели турбовинтового двигателя, определенной на этапе Е1.
Анализ этих данных привел к необходимости определения моделей порядка 2 без прямого действия.
Матрицы перехода идентифицированных линейных систем имеют форму (11) в виде состояния и (12) в виде матрицы перехода. После анализа нулей и матриц В линейных систем на всех рабочих точках выясняется, что первые являются стабильными и что матрицы В является необратимыми.
Таким образом, можно применять стратегию смешанного децентрализованного управления.
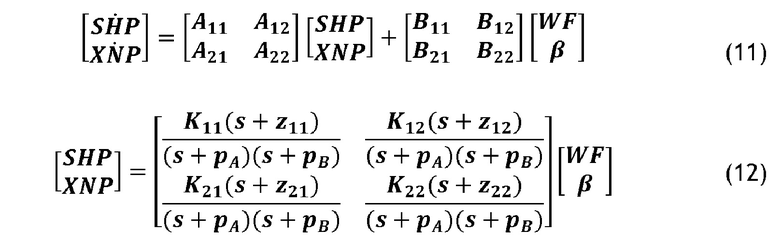
На основании этого вывода применяют описанное выше определение параметров для каждой из идентифицированных систем.
На первом этапе (Е1) происходит автоматический поиск основных динамических условий диагональных переходов турбовинтового двигателя на каждой из идентифицированных моделей. Это может происходить автоматически через определенные методы упрощения моделей, такие как усечение уравновешенного основания. Это позволяет найти переходы первого порядка, которые сближают диагональные переходы, состоящие из двух полюсов и нуля. Отсюда выводят G1, G2, p1 и р2. Предпочтительно коэффициенты усиления Gi и полюсы pi выбирают таким образом, чтобы статический коэффициент усиления частотных откликов упрощенных переходов не удалялся от статического коэффициента усиления частотных откликов первоначальных переходов и чтобы частота отсечки частотных откликов упрощенных переходов на удалялась от частоты отсечки частотных откликов первоначальных переходов.
На втором этапе (Е2) аналитическим путем определяют матрицы М и L на каждой рабочей точке, применяя (10).
На третьем этапе (Е3) производят определение ПИ-корректоров для контуров мощности SHP и режима воздушного винта XNP. Это тоже осуществляют аналитически при помощи метода ПИД-IMC.
Матрицы М, L и ПИ-корректоры изменяются в области полета, чтобы компенсировать изменчивость системы. Чтобы максимально повысить эффективность регулирования, производят интерполяцию правил управления в зависимости от условий полета (число Маха, высота полета, состояние турбовинтового двигателя).
Таким образом, производят интерполяцию ПИ-корректоров для улучшения характеристик системы (статическая ошибка, время отклика, переполнение) и матриц М и L, чтобы сохранить оптимальную развязку.
Интерполяция корректоров позволяет повысить эффективность системы управления (в частности, что касается статической ошибки, времени отклика и переполнения).
Интерполяция корректора 105 обратной связи по состоянию и статического компенсатора 104 позволяет сохранить оптимальную развязку на всей области полета.
В частности, параметры одномерных корректоров можно интерполировать индивидуально посредством упорядочения последовательности коэффициентов усиления.
Задание последовательности коэффициентов усиления состоит в определении семейства линейных систем, приближаясь к нелинейной системе в данном числе рабочих точек, и в предложении правил управления в каждой из соответствующих областей пространства состояния, чтобы в конечном итоге реализовать общее правило управления.
В частности, если одномерные корректоры являются ПИ-корректорами, интерполяция коэффициентов усиления является простой, поскольку речь идет о сумме различных действий, взвешенных коэффициентами усиления. Точно так же, корректор 105 обратной связи по состоянию и статический компенсатор 104 являются матрицами коэффициентов усиления (размером 2×2) L и М, следовательно, можно относительно просто интерполировать коэффициенты этих матриц.
Можно применить инкрементальный алгоритм, чтобы сгладить команды во время интерполяции правил управления и обеспечить более плавные переходы, когда параллельно используются несколько контуров регулирования. Таким образом, заданные значения и выходные данные дифференцируются (дифференциаторы 108а, 108b и 109a, 109b), что позволяет работать с инкрементами ошибки, при этом инкременты управления впоследствии подвергаются интегрированию.
Правила управления позволяют получить оптимальные отклики по всей области полета, при этом правила управления являются относительно простыми и легко корректируются.
Применение к другим системам
В случае других вариантов применения этапы получения решений являются такими же, как и в случае турбовинтового двигателя.
В случае силовой установки, содержащей сдвоенные воздушные винты противоположного вращения, не закрытые обтекателем “Open Rotor” или закрытые обтекателем “Contrafan”, команды включают в себя расход топлива WF и шаги воздушных винтов 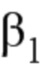 и
и 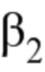 . Что касается выходных данных, то они включают в себя режим корпуса низкого давления NBP и режимы двух воздушных винтов N1 и N2, как показано ниже:
. Что касается выходных данных, то они включают в себя режим корпуса низкого давления NBP и режимы двух воздушных винтов N1 и N2, как показано ниже:

Система, линеаризованная на различных рабочих точках, выражена полной (все члены являются ненулевыми) матрицей переходов 3×3. Соблюдены различные гипотетические условия, что позволяет получить матрицы L и М, описанные в (10).
В случае турбореактивных двигателей с регулируемом сечением сопла команды управления включают в себя расход топлива WF и ток сервоклапана iTuy, питающий силовой цилиндр, позволяющий изменять регулируемое сечение сопла. Что касается выходных данных, то они включают в себя режим камеры низкого давления NBP и консолидированное положение силовых цилиндров ХTuy:

Система линеаризована на меньшем числе рабочих точек. Линеаризованная система соответствует матрице 2×2, но переход WF→xTuy является нулевым (изменение расхода топлива не оказывает прямого влияния на положение сопла). Таким образом, речь идет о минимизации другого члена связывания, а именно iTuy→NBP. Это не приводит к изменению гипотетических условий, и можно применить формулу (10).
В случае турбореактивных двигателей с элементами, имеющими изменяемую геометрию, команды управления включают в себя расход топлива WF и токи управления сервоклапанов iVSV and iVBV, обеспечивающие питание силовых цилиндров соответственно для оптимизации угла статоров (VSV от Variable Stator Vanes - регулируемые лопатки статора) компрессора высокого давления и для модулирования смещения открывания разгрузочных клапанов (VBV от Variable Bleed Valves - перепускные клапаны терминологии). Автоматически регулируемые выходы включают в себя режим корпуса низкого давления NBP и положения силовых цилиндров xVSV и xVBV. Что касается заданных значений этих приводов, то они являются идеально синхронизированными.
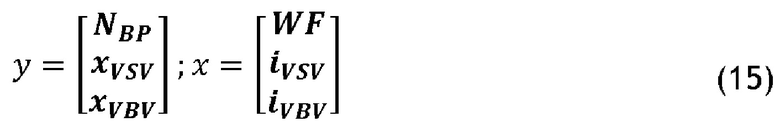
Система, линеаризованная на различных рабочих точках, описана матрицей переходов 3×3. Преобладающими членами являются диагональные члены, и переходы WF→xVSV и WF→xVBV являются нулевыми. С другой стороны, другие члены связи являются ненулевыми (действие VBV влияет на режим низкого давления напрямую, а действие VSV тоже влияет на него через режим высокого давления). Здесь тоже можно применить заявленное решение.
Настоящее техническое решение относится к области вычислительной техники для авиации. Технический результат заключается в обеспечении полной развязки с одновременным сохранением возможности простой регулировки корректоров. Технический результат достигается за счёт того, что система управления авиационным двигателем содержит - следящий контур, который получает на входе заданные значения рабочих параметров двигателя и который управляет системой вместе с контуром обратной связи по этим рабочим параметрам, при этом следящий контур содержит блок децентрализованного управления с одномерными регуляторами, блок управления с обратной связью по состоянию, встроенный в следящий контур, при этом указанный блок управления получает на входе выходные данные блока децентрализованного управления с одномерными регуляторами и является контуром обратной связи между рабочими параметрами двигателя и выходами указанного блока децентрализованного управления, при этом контур обратной связи выдает параметры управления двигателем, при этом блок управления с обратной связью по состоянию выполнен с возможностью развязки указанных рабочих параметров, при этом одномерные регуляторы блока децентрализованного управления выполнены с возможностью автоматического регулирования указанных рабочих параметров по заданным значениям этих параметров. 6 н. и 6 з.п. ф-лы, 7 ил.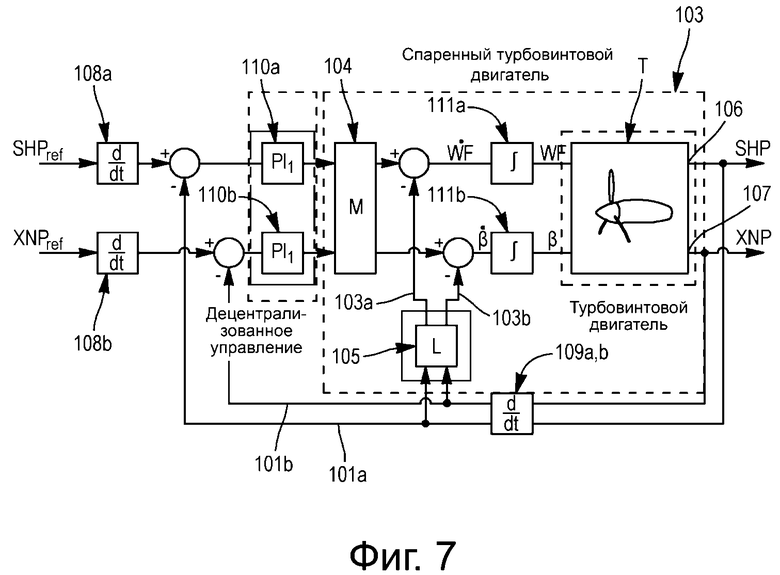
1. Система управления авиационным двигателем, характеризующаяся тем, что содержит:
- по меньшей мере один следящий контур, который получает на входе заданные значения рабочих параметров двигателя и который управляет системой вместе с контуром обратной связи по этим рабочим параметрам, при этом указанный следящий контур содержит блок децентрализованного управления с одномерными регуляторами,
- по меньшей мере один блок управления с обратной связью по состоянию, встроенный в следящий контур, при этом указанный блок управления получает на входе выходные данные блока децентрализованного управления с одномерными регуляторами и является контуром обратной связи между рабочими параметрами двигателя и выходами указанного блока децентрализованного управления, при этом указанный контур обратной связи выдает параметры управления двигателем,
при этом блок управления с обратной связью по состоянию выполнен с возможностью развязки указанных рабочих параметров, при этом одномерные регуляторы блока децентрализованного управления выполнены с возможностью автоматического регулирования указанных рабочих параметров по заданным значениям этих параметров.
2. Система по п. 1, в которой блок управления с обратной связью по состоянию содержит статический компенсатор и контур с корректором обратной связи по состоянию, при этом указанный статический компенсатор и указанный контур с корректором обратной связи по состоянию выполнены с возможностью развязки рабочих параметров.
3. Система по п. 1 или 2, в которой одномерные регуляторы блока децентрализованного управления являются пропорционально-интегральными корректорами.
4. Способ параметризации системы управления авиационным двигателем по любому из пп. 1-3, содержащий этапы, на которых:
- определяют линейную модель двигателя, при этом модель имеет переходную функцию и представление состояния;
- определяют статический компенсатор и корректор обратной связи по состоянию таким образом, чтобы развязать состояния, образованные автоматически регулируемыми рабочими параметрами двигателя;
- определяют одномерные регуляторы таким образом, чтобы автоматически регулировать указанные рабочие параметры по заданным значениям.
5. Способ параметризации системы управления по предыдущему пункту, в котором корректор обратной связи по состоянию и статический компенсатор выполнены таким образом, чтобы переходная функция системы управления имела коэффициенты усиления и полюсы, соответствующие коэффициентам усиления и полюсам переходной функции модели двигателя.
6. Способ параметризации системы управления по п. 4 или 5, дополнительно содержащий этап интерполяции одномерных корректоров в зависимости от переменных условий полета.
7. Способ параметризации системы управления по п. 6, в котором параметры одномерных корректоров интерполируют индивидуально посредством задания последовательности коэффициентов усиления.
8. Способ параметризации системы управления по любому из пп. 4-7, дополнительно содержащий этап интерполяции корректора обратной связи по состоянию и статического компенсатора в зависимости от переменных условий полета (С1, С2, С3, …).
9. Применение системы по любому из пп. 1-3 для управления двигателем с воздушным винтом переменного шага, таким как турбовинтовой двигатель, при этом автоматически регулируемые рабочие параметры включают в себя мощность (SHP) воздушного винта и скорость его вращения (XNP), при этом управляемые параметры содержат расход топлива и шаг винта.
10. Применение системы по любому из пп. 1-3 для управления двигателем, имеющим сдвоенные воздушные винты с противоположным вращением и с переменным шагом, при этом автоматически регулируемые рабочие параметры включают в себя режим камеры низкого давления (NBP) и режимы двух воздушных винтов (N1 и N2), а управляемые параметры включают в себя расход топлива (WF) и шаг винтов (β1 и β2).
11. Применение системы по любому из пп. 1-3 для управления турбореактивным двигателем с регулируемым сечением сопла, при этом регулируемые рабочие параметры включают в себя режим камеры низкого давления (NBP) и положение (хТ) силового цилиндра или силовых цилиндров, управляющих устанавливаемым сечением сопла, при этом параметры управления включают в себя расход топлива (WF) и ток (iTuy) сервоклапана, питающий силовой цилиндр или силовые цилиндры.
12. Применение системы по любому из пп. 1-3 для управления турбореактивным двигателем с элементами, имеющими изменяемую геометрию, при этом автоматически регулируемые рабочие параметры включают в себя режим камеры низкого давления (NBP) и положения силовых цилиндров (xVSV и xVBV), параметры управления включают в себя расход топлива (WF) и токи управления (iVSV и iVBV) сервоклапанами.
| US 5274558 A, 28.12.1993 | |||
| US 5001646 A, 19.03.1991 | |||
| US 5920478 A, 06.07.1999 | |||
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
| ЦИФРОВАЯ ЭЛЕКТРОННАЯ СИСТЕМА УПРАВЛЕНИЯ С ВСТРОЕННОЙ ПОЛНОЙ ТЕРМОГАЗОДИНАМИЧЕСКОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛЬЮ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ И АВИАЦИОННЫЙ ГАЗОТУРБИННЫЙ ДВИГАТЕЛЬ | 2013 |
|
RU2554544C2 |
Авторы
Даты
2022-09-05—Публикация
2018-08-09—Подача