Изобретение относится к области микропроцессоров, а именно к скалярно-векторным процессорам, и может быть использовано при построении архитектуры процессорных IP-ядер, ориентированных на решение задач цифровой обработки сигналов, включая приложения искусственного интеллекта и нейронных сетей.

Постоянное повышение сложности решаемых задач в области цифровой обработки сигналов и увеличение объемов обрабатываемых данных приводят к непрерывному росту требований к вычислительной производительности выполняющих эти задачи микропроцессорных систем. Основным методом повышения производительности вычислений является их распараллеливание. Возможность распараллеливания обеспечивают тем, что во многих задачах обработки сигналов требуется, как правило, выполнение большого объема одинаковых вычислительных процедур по отношению к большим массивам обрабатываемых данных. Массивы однотипных данных векторизуют, и дальнейшую высокопроизводительную обработку проводитят уже не над отдельными элементами, а над векторами. Архитектуры микропроцессоров, выполняющих подобную обработку, известны под названием SIMD-архитектур (SIMD - Single Instruction, Multiple Data).

Сложность, однако, заключается в том, что ни в одном реальном приложении не удается достичь стопроцентной векторизации. Известен закон Амдала, согласно которому общее ускорение, полученное в результате векторизации на векторном процессоре с Р элементами обработки, в зависимости от доли кода f, которая может быть векторизована, равно 1/(1-f+f/P). Таким образом, в реальных прикладных задачах, наряду с векторной обработкой, всегда присутствует и скалярная часть вычислений.

На практике применяют различные подходы к организации такого рода смешанных вычислений. Например, для реализации нейронных сетей широко используют гетерогенные вычислительные системы, содержащие в своем составе центральный процессор (CPU), выполняющий верхний уровень задачи и связанные с этим скалярные вычисления, и графический процессор (GPU), функцией которого является выполнение массивно-параллельной обработки данных. Недостатком такого подхода является то, что передача данных от одного процессора другому связана со значительными временными задержками, что сказывается отрицательным образом на реально достигаемой производительности.

Это привело к появлению архитектур, в которых некоторое количество скалярных и векторных вычислительных секций (ядер) объединяют в составе одного микропроцессора. Одной из главных проблем таких архитектур является организация эффективного взаимодействия между скалярным и векторным каналами микропроцессора. Дело в том, что во многих прикладных задачах, связанных с обработкой векторных данных, возникает потребность в выполнении операций, в которых скалярный канал формирует и/или потребляет скаляр, требуемый и/или формируемый векторным каналом микропроцессора. Таким образом, скалярный канал процессора может подготовить или дополнительно обработать скаляры, необходимые для векторного канала или созданные векторным каналом, гарантируя, что векторный канал может продолжать потоковую обработку векторов без лишних торможений.

Примером операций, в которые вовлечены и скалярный и векторный каналы процессора, являются операции редукции - к ним относятся, в частности, определение и вывод минимального или максимального значения вектора, сумма или произведение элементов вектора и т.п.

В задачах обработки изображений широко применяют и другие операции, выполняемые над вектором в целом - операции перестановок (shuffle), вычисление гистограмм, табличные преобразования (LUT, Look-Up Table). Известные способы реализации таких процедур имеют свои достоинства и недостатки. Программная реализация на основе стандартного набора команд не позволяет достичь высокой производительности, а аппаратная реализация в виде ускорителей требует дополнительных аппаратурных затрат и обладает ограниченной гибкостью. По указанным причинам поиск эффективных способов выполнения такого рода вычислительных процедур остается по-прежнему актуальным.

Известно решение (патент US 5659706), в котором описывается скалярно-векторный процессор с отдельной скалярным и векторным каналами. Каждый из каналов процессора разделен на функциональные блоки. Недостатком этого решения является то, что между функциональными блоками скалярного и векторного канала процессора нет тесного взаимодействия. Оба канала работают полностью независимо, и это приводит к дополнительным временным потерям при передаче данных от одной части процессора к другой, соответственно, к ухудшению быстродействия процессора.

Известно другое решение (патент US 5822606 А), в котором описана одна из первых архитектур сигнальных процессоров, содержащая одновременно функционирующие скалярное и векторные вычислительные ядра. Недостатком этой архитектуры является то, что, как и в предыдущем случае, скалярное и векторные вычислительные ядра непосредственно между собой не взаимодействуют, обмены данными между ними выполняются через внешнюю память, что связано со значительными задержками, соответственно, к ухудшению быстродействия процессора.

В патенте US 2004015677 А1 описана архитектура скалярно-векторного процессора цифровой обработки сигналов, в которой предусматривается выполнение некоторых операций редукции в последовательном стиле, путем передачи данных от одной SIMD-секции к другой. Недостатком данной архитектуры является невысокая производительность, достигаемая при последовательной организации вычислений.

Известна архитектура (патент US 2005/0240644 А1) скалярно-векторного процессора, который включает в себя набор функциональных (вычислительных) блоков, содержащих взаимодействующие между собой векторный и скалярный каналы. Недостатком этой архитектуры является то, что взаимодействие между векторным и скалярным каналами процессора ограничено рамками конкретного функционального блока. Кроме того, данное решение не предусматривает поддержку операций редукции.

В патенте US 2020/142704 А1 описана архитектура скалярно-векторного процессора, в которой наряду с SIMD-распараллеливанием, используется также параллелизм на уровне команд по принципу VLIW (Very Long Instruction Word) как в скалярном, так и в векторном канале процессора, что повышает общую производительность. Однако никаких механизмов взаимодействия между скалярным и векторным каналами процессора не предусмотрено.

Наиболее близким к заявленному изобретению является архитектурный подход, описанный в патенте US 2021/0216318 А1. В данном патенте предложено целое семейство вариантов архитектур скалярно-векторного процессора, в том числе такие, в которых поддерживается взаимодействие скалярного и векторного каналов процессора и предусмотрено выполнение операций редукции. Данные архитектуры скалярно-векторного процессора выбраны в качестве прототипов заявленного изобретения. Однако операции редукции в данном патенте реализуют на базе векторных вычислительных секций за счет дополнительных связей между секциями. Это ухудшает масштабируемость архитектуры и делает невозможным одновременное выполнение операций редукции и других векторных вычислений. Кроме того, предложенный подход не предусматривает поддержку выполнения других операций над вектором в целом - перестановки, вычисление гистограмм, табличные преобразования (LUT).

Техническим результатом изобретения является создание скалярно-векторного процессора, который обладает повышенной эффективностью, скоростью работы, функциональностью и универсальностью за счет того, что: в его составе содержится блок редукции, соединенный со скалярным и векторным каналами процессора и реализующий функции их взаимодействия в разнообразных операциях, в которых скалярный канал формирует и/или потребляет скаляр, требуемый и/или формируемый векторным каналом процессора; блок редукции выполняет, кроме того, различные операции над вектором в целом - операции перестановок (shuffle), LUT-преобразования, вычисления гистограмм; скалярный и векторный каналы процессора объединены дополнительно кольцеобразной шиной, позволяющей производить по ней обмен данными одновременно с выполнением вычислительных операций в скалярном и векторном каналах процессора и в блоке редукции.

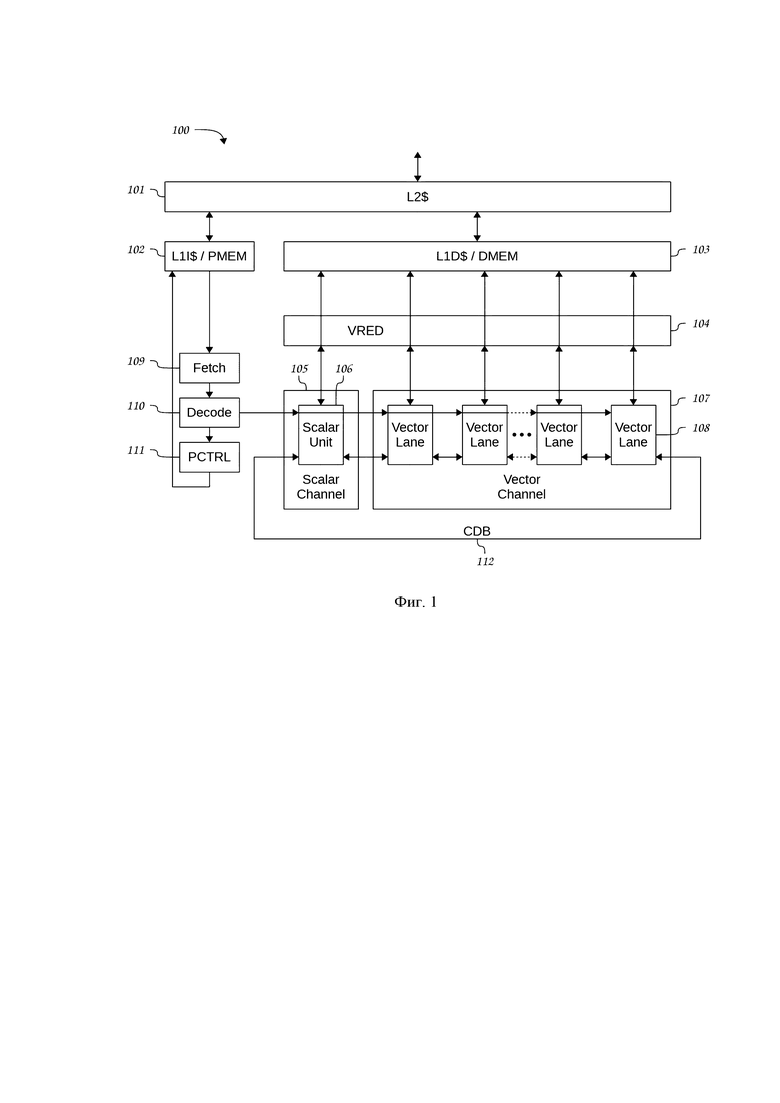
Поставленный технический результат достигнут путем создания скалярно-векторного процессора 100, содержащего соединенные кольцевой шиной CDB 112 скалярный и векторный каналы 105 и 107 обработки данных, которые соединены с блоком редукции VRED 104, а также с памятью данных первого уровня DMEM/L1D$ 103, которая соединена с кэш-памятью второго уровня L2$ 101, которая соединена с внешним интерфейсом процессора, который имеет доступ к внешней памяти вычислительной системы, а также соединена с памятью программ первого уровня РМЕМ/L1I$ 102, выход которой соединен с входом блока выборки команд FETCH 109, выход которого соединен с входом блока декодирования команд DECODE 110, первый выход которого соединен с входами скалярного и векторного каналов, а второй выход соединен с блоком программного управления PCTRL 111, выход которого соединен с входом памяти программ первого уровня РМЕМ/L1I$ 102, причем

- память программ первого уровня РМЕМ/L1I$ 102 и память данных первого уровня DMEM/L1D$ 103 выполнены с возможностью формирования обращений и передачи их в

- кэш-память второго уровня L2$ 101, которая выполнена с возможностью обслуживания обращений из памяти программ первого уровня PMEM/L1I$ 102 и памяти данных первого уровня DMEM/L1D$ 103, а также загрузки данных через внешний интерфейс из внешней памяти вычислительной системы и передачи данных в память данных первого уровня DMEM/L1D$ 103 и память программ первого уровня РМЕМ/L1I$ 102;

- блок выборки команд FETCH 109 выполнен с возможностью выборки команд из памяти программ РМЕМ/L1I$ 102 и передачи их в

- блок декодирования команд DECODE ПО, выполненный с возможностью декодирования команд и формирования команд программного управления для исполнительных устройств процессора и передачи их в

- блок PCTRL, который выполнен с возможностью выполнения команд программного управления.

В предпочтительном варианте осуществления процессора память данных первого уровня DMEM/L1D$ 103 выполнена в виде кэш-памяти первого уровня L1D$ или в виде тесно связанной ТСМ (Tightly-Coupled Memory) статической памяти DMEM.

В предпочтительном варианте осуществления процессора память программ первого уровня PMEM/L1I$ 102 выполнена в виде кэш-памяти первого уровня L1I$ или в виде тесно связанной ТСМ (Tightly-Coupled Memory) статической памяти РМЕМ.

В предпочтительном варианте осуществления процессора на уровне вычислительного ядра имеет гарвардскую архитектуру с возможностью одновременного доступа к памяти программ первого уровня PMEM/L1I$ 102 и памяти данных первого уровня DMEM/L1D$ 103 по отдельным шинам.

В предпочтительном варианте осуществления процессора кэш-память второго уровня L2$ 101 имеет фон-неймановскую архитектуру.

В предпочтительном варианте осуществления процессора команды программного управления выбраны из набора команд, содержащего команды программных переходов и команды программных циклов.

В предпочтительном варианте осуществления процессора команды объединены в инструкции, которые организованы в виде VLIW-пакета 201 (VLIW - Very Long Instruction Word).

В предпочтительном варианте осуществления процессора VLIW-пакет 201 содержит до восьми команд, из которых до четырех команд предназначены для исполнительных устройств скалярного канала обработки данных и до четырех команд предназначены для исполнительных устройств векторного канала обработки данных.

В предпочтительном варианте осуществления процессора VLIW-пакет 201 содержит до двух команд скалярных обменов данными и до двух векторных команд обмена данными с памятью данных DMEM/L1D$ 103.

В предпочтительном варианте осуществления процессор имеет систему команд, состоящую из команд программного управления, команд исполнительных устройств скалярного канала обработки данных и векторного канала обработки данных, а также команд блока редукции VRED 104.

В предпочтительном варианте осуществления процессора скалярный канал 105 содержит одну скалярную вычислительную секцию 106.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит скалярный регистровый файл RF 301, который является многопортовым и в котором хранятся обрабатываемые скалярные данные.

В предпочтительном варианте осуществления процессора скалярный регистровый файл RF 301 содержит порты, связанные со скалярным каналом 105 обработки данных и выполненные с возможностью обмена данными с памятью данных DMEM/L1D$ 103.

В предпочтительном варианте осуществления процессора скалярный регистровый файл RF 301 содержит порты, связанные с исполнительными устройствами скалярной вычислительной секции 106 скалярного канала 105 обработки данных, выполненные с возможностью передачи исходных данных для выполнения вычислительных операций и записи результатов операций обратно в скалярный регистровый файл RF 301.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит блоки обработки данных SLSE0 310, SLSE1 311, которые выполнены с возможностью обеспечения обмена данными между памятью данных DMEM/L1D$ 103 и скалярным регистровым файлом RF 301, в том числе выполнения команд пересылок данных между памятью данных DMEM/L1D$ 103 и скалярным регистровым файлом RF 301.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит блоки обработки данных ALU0 302, ALU1 303, ALU2 304, ALU3 305, выполняющие арифметические и логические операции над числами с фиксированной запятой.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит блоки обработки данных FALU0 306, FALU1 307, выполняющие арифметические и логические операции над числами с плавающей запятой.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит блоки обработки данных SMU0 308, SMU1 309, выполняющие операции умножения над числами с фиксированной и плавающей запятой.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит блок обработки данных SH 312, выполняющий операции логического и арифметического сдвига.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит блок обработки данных CONV 315, выполняющий операции преобразования типов данных.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит блок обработки данных DIV 313, выполняющий операции деления.

В предпочтительном варианте осуществления процессора скалярная вычислительная секция 106 содержит блок обработки данных MF 314, выполняющий операции вычисления трансцендентных математических функций. Базовый набор операций, выполняемых блоком MF 314, приведен в таблице 9.

В предпочтительном варианте осуществления процессора векторный канал 107 состоит из нескольких векторных вычислительных секций 108, количество которых соответствует разрядности обрабатываемого вектора.

В предпочтительном варианте осуществления процессора векторная вычислительная секция 108 содержит векторный регистровый файл VRF 401, который является многопортовым и мультиформатным, и в котором хранятся обрабатываемые векторные данные.

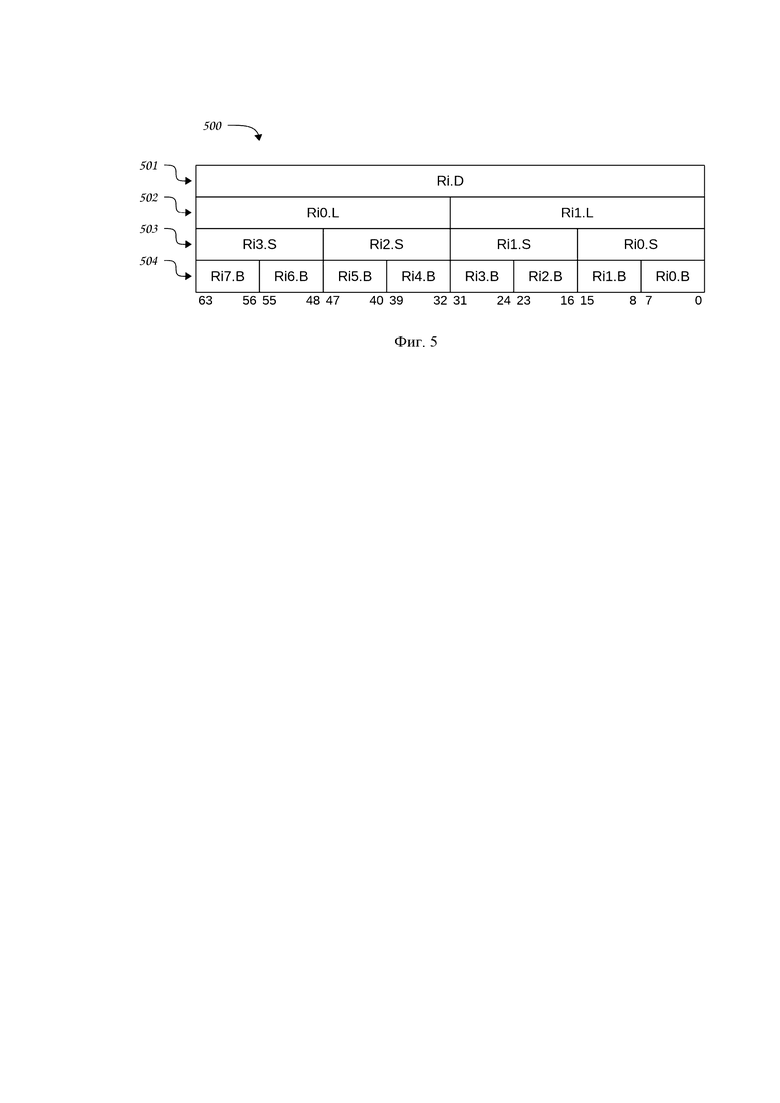
В предпочтительном варианте осуществления процессора векторный регистровый файл VRF 401 является мультиформатным, так что каждый 64-разрядный регистр 500 векторного регистрового файла VRF 401 может хранить либо одно 64-разрядное значение 501, либо два 32-разрядных значения 502, либо четыре 16-разрядных значения 503, либо восемь 8-разрядных значений 504.

В предпочтительном варианте осуществления процессора векторный регистровый файл VRF 401 содержит порты, связанные с внешним интерфейсом векторного канала 107 и выполненные с возможностью обмена данными с памятью данных DMEM/L1D$ 103.

В предпочтительном варианте осуществления процессора векторный регистровый файл VRF 401 содержит порты, связанные с исполнительными устройствами векторной вычислительной секции 108, выполненные с возможностью передачи исходных данных для выполнения вычислительных операций и записи результатов обратно.

В предпочтительном варианте осуществления процессора векторный регистровый файл VRF 401 выполнен с возможностью работы с различными форматами данных.

В предпочтительном варианте осуществления процессора векторная вычислительная секция 108 содержит блоки VLSE0 412, VLSE1 413, которые выполнены с возможностью обеспечения обмена данными между памятью данных DMEM/L1D$ 103 и векторным регистровым файлом VRF 401, в том числе и выполнения команд пересылок данных между памятью данных DMEM/L1D$ 103 и векторным регистровым файлом VRF 401.

В предпочтительном варианте осуществления процессора векторная вычислительная секция 108 содержит блоки VALU0 403, VALU1 404, VALU2 405, VALU3 406, выполненные с возможностью осуществления арифметических и логических операции над числами с фиксированной запятой.

В предпочтительном варианте осуществления процессора векторная вычислительная секция 108 содержит блоки VFALU0 407, VFALU1 408, выполненные с возможностью осуществления арифметических и логических операции над числами с плавающей запятой.

В предпочтительном варианте осуществления процессора векторная вычислительная секция 108 содержит блоки VMU0 409, VMU1 410, выполненные с возможностью осуществления операций умножения и умножения с накоплением над числами с фиксированной и плавающей запятой.

В предпочтительном варианте осуществления процессора векторная вычислительная секция 108 содержит векторный регистровый файл регистров-аккумуляторов VAC 402, выполненный с возможностью хранения данных, получаемых и используемых в результате выполнения операций умножения с накоплением, выполняемых блоками векторных умножителей VMU0 409, VMU1 410.

В предпочтительном варианте осуществления процессора векторная вычислительная секция 108 содержит блок VSH 411, выполненный с возможностью осуществления операции логического и арифметического сдвига над векторными операндами.

В предпочтительном варианте осуществления процессора векторная вычислительная секция 108 содержит блок VCONV 414, выполненный с возможностью осуществления операции преобразования типов данных над векторными операндами.

В предпочтительном варианте осуществления процессора блок редукции VRED 104 выполнен с возможностью вычисления функций редукции, и при этом обеспечения повышенной эффективности, скорости работы, функциональности и универсальности процессора.

В предпочтительном варианте осуществления процессора блок редукции VRED 104 выполнен с возможностью вычисления функций редукции, и при этом реализации функций взаимодействия скалярной и векторной частей процессора в разнообразных операциях, в которых скалярный канал 105 формирует и/или потребляет скаляр, требуемый и/или формируемый векторным каналом 107.

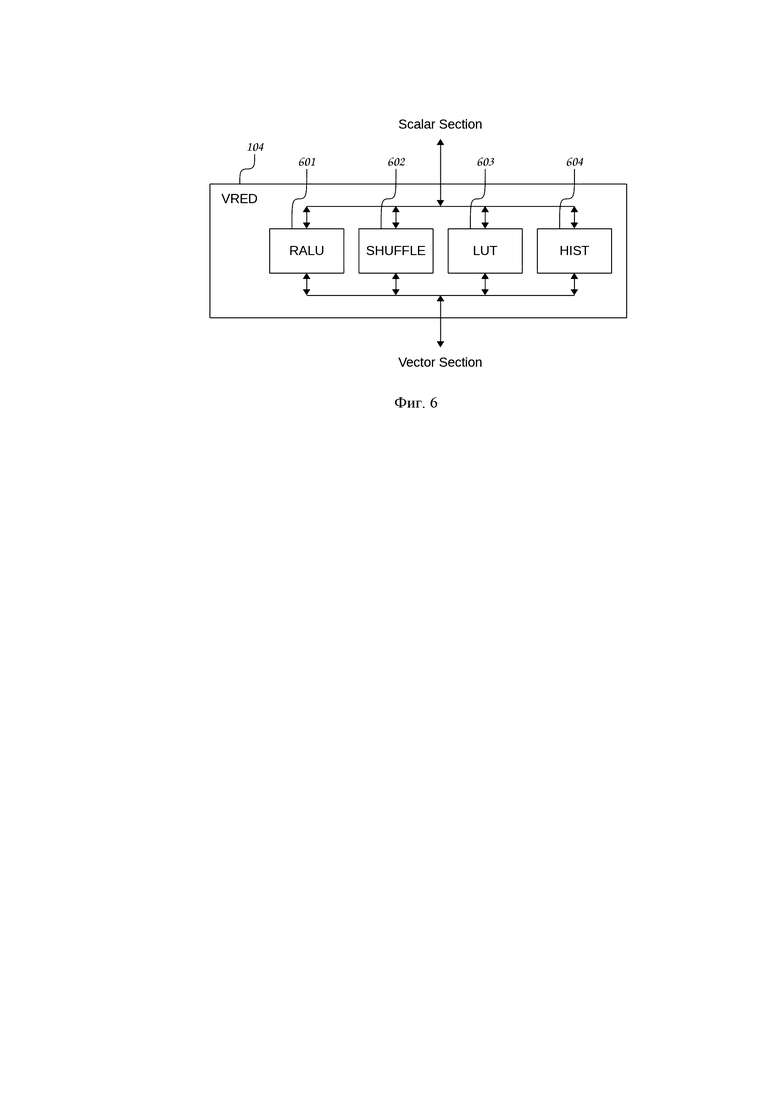
В предпочтительном варианте осуществления процессора блок редукции VRED 104 содержит блок RALU 601, выполненный с возможностью осуществления арифметико-логических межсекционных операций редукции.

В предпочтительном варианте осуществления процессора блок редукции VRED 104 содержит блок SHUFFLE 602, выполненный с возможностью осуществления операций межсекционных перестановок.

В предпочтительном варианте осуществления процессора блок редукции VRED 104 содержит блок LUT 603, выполненный с возможностью осуществления операций межсекционньгх табличных преобразований.

В предпочтительном варианте осуществления процессора блок редукции VRED 104 содержит блок HIST 604, выполненный с возможностью осуществления операций вычисления гистограмм.

В предпочтительном варианте осуществления процессора кольцевая шина CDB (Circular Data Bus) 112, выполнена с возможностью осуществления обмена данными одновременно с осуществлением вычислительных операций в скалярном и векторном каналах 105, 107 и в блоке редукции VRED 104.

В предпочтительном варианте осуществления процессора кольцевая шина CDB 112, выполнена с возможностью осуществления команд циклического сдвига, в результате выполнения которых регистр Ri скалярного регистрового файла RF 301 смещается в регистр Vj векторного регистрового файла VRF 401 нулевой векторной вычислительной секции 108: Vj.0=Ri; регистр Vj векторного регистрового файла VRF 401 старшей (N-1) векторной вычислительной секции 108 смещается в регистр Ri скалярного регистрового файла RF 301: Ri=Vj.N-1; регистры Vj векторных регистровых файлов VRF 401 остальных векторных вычислительных секций 108 смещаются на одну секцию в сторону старших секций: Vj.k=Vj.k-1, k=1,2,…,N-1.

В предпочтительном варианте осуществления процессора кольцевая шина CDB 112, выполнена с возможностью последовательного перемещения данных из векторного канала 107 в скалярный канал 105 с целью выполнения операций, имеющихся только в скалярном канале 105, с последующим возвращением преобразованных данных в векторный канал 107.

Для лучшего понимания заявленного изобретения далее приводится его подробное описание с соответствующими графическими материалами.

Фиг. 1. Структурная схема скалярно-векторного процессора, выполненная согласно изобретению.

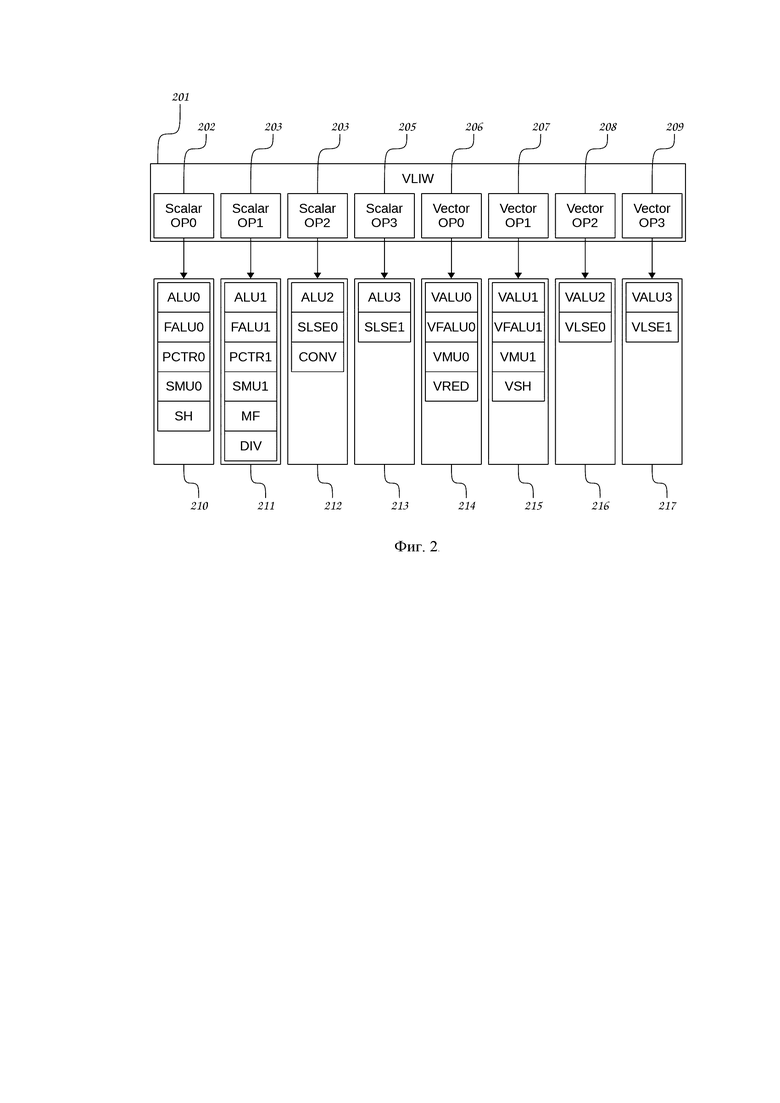
Фиг. 2. Структурная схема VLIW-инструкции скалярно-векторного процессора, выполненная согласно изобретению.

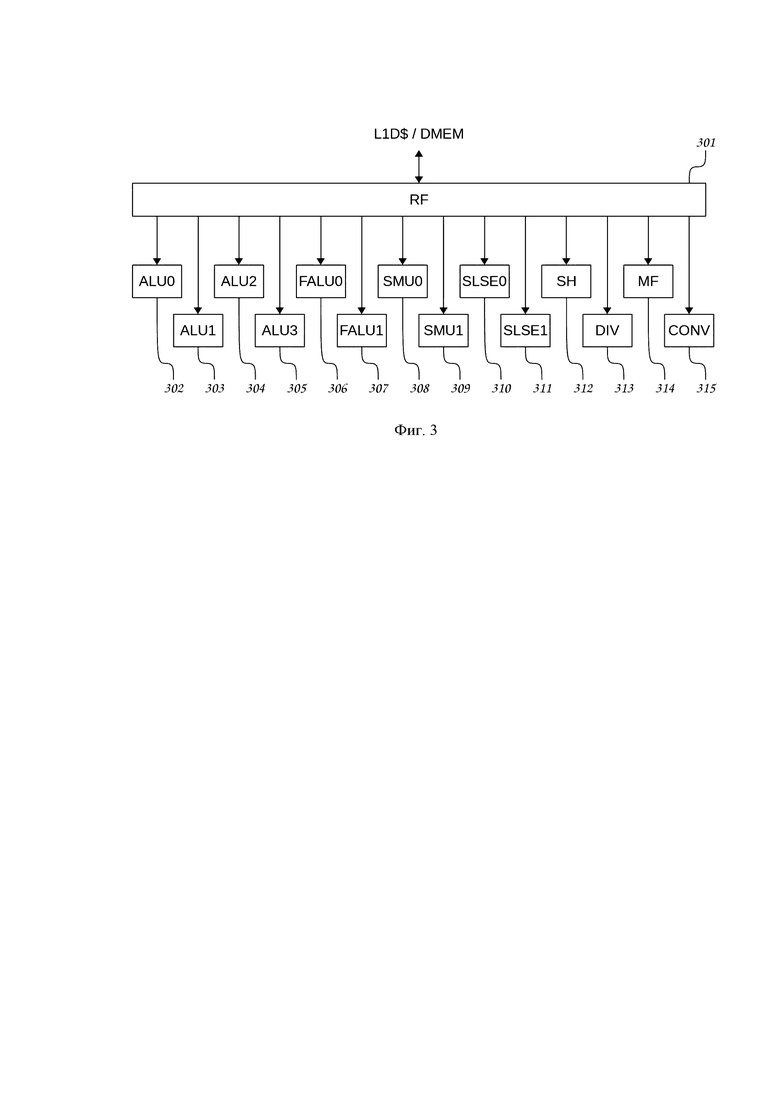
Фиг. 3. Структурная схема скалярной вычислительной секции скалярного канала скалярно-векторного процессора, выполненная согласно изобретению.

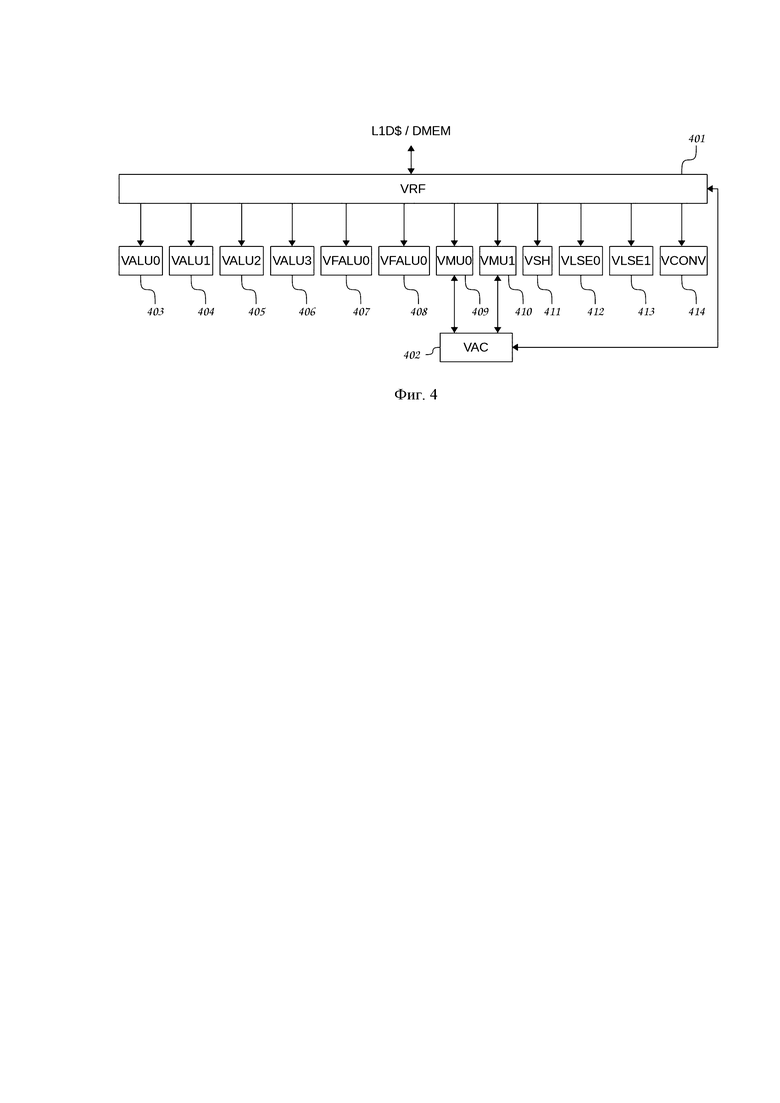
Фиг. 4. Структурная схема векторной вычислительной секции векторного канала скалярно-векторного процессора, выполненная согласно изобретению.

Фиг. 5. Структурная схема мультиформатного векторного регистрового файла в составе вычислительной секции векторного канала, выполненная согласно изобретению.

Фиг. 6. Структурная схема блока редукции, выполненная согласно изобретению.

Фиг. 7. Кольцевая шина для межсекционных скалярно-векторных обменов данными, выполненная согласно изобретению.

Табл. 1. Базовый набор команд устройства программного управления, выполненный согласно изобретению.

Табл. 2. Базовый набор команд блока обменов с памятью скалярного канала, выполненный согласно изобретению.

Табл. 3. Базовый набор команд блока арифметико-логических операций с фиксированной запятой скалярного канала, выполненный согласно изобретению.

Табл. 4. Базовый набор команд блока арифметико-логических операций с плавающей запятой скалярного канала, выполненный согласно изобретению.

Табл. 5. Базовый набор команд блока умножения с фиксированной и плавающей запятой скалярного канала, выполненный согласно изобретению.

Табл. 6. Базовый набор команд блока сдвига скалярного канала, выполненный согласно изобретению.

Табл. 7. Базовый набор команд блока преобразования типов скалярного канала, выполненный согласно изобретению.

Табл. 8. Базовый набор команд блока деления скалярного канала, выполненный согласно изобретению.

Табл. 9. Базовый набор команд блока вычисления трансцендентных функций скалярного канала, выполненный согласно изобретению.

Табл. 10. Базовый набор команд блока обменов с памятью векторного канала, выполненный согласно изобретению.

Табл. 11. Базовый набор команд блока арифметико-логических операций с фиксированной запятой векторного канала, выполненный согласно изобретению.

Табл. 12. Базовый набор команд блока арифметико-логических операций с плавающей запятой векторного канала, выполненный согласно изобретению.

Табл. 13. Базовый набор команд блока умножения с фиксированной и плавающей запятой векторного канала.

Табл. 14. Базовый набор команд блока сдвига векторного канала, выполненный согласно изобретению.

Табл. 15. Базовый набор команд блока преобразования типов векторного канала, выполненный согласно изобретению.

Табл. 16. Базовый набор команд арифметико-логического устройства межсекционной редукции.

Табл. 17. Базовый набор команд блока межсекционных перестановок, выполненный согласно изобретению.

Табл. 18. Базовый набор команд блока межсекционных табличных преобразований (LUT-преобразований), выполненный согласно изобретению.

Табл. 19. Базовый набор команд блока вычисления гистограмм, выполненный согласно изобретению.

Табл. 20. Базовый набор команд межсекционного скалярно-векторного сдвига, выполненный согласно изобретению.

Архитектура заявленного скалярно-векторного процессора ориентирована прежде всего на решение задач цифровой обработки сигналов, связанных с массивно-параллельными вычислениями, включая приложения искусственного интеллекта и нейронных сетей.

В состав процессора 100 (Фиг. 1) входит скалярный канал 105 (Scalar Channel) и векторный канал 107 (Vector Channel) обработки данных. Скалярный канал 105 включает в себя одну скалярную вычислительную секцию 106 (Scalar Unit), в то время как векторный канал включает несколько векторных вычислительных секций 108 (Vector Lane).

Взаимодействие процессора с памятью организовано традиционным способом. На уровне вычислительного ядра процессора реализуется гарвардская архитектура с возможностью одновременного доступа к памяти программ и данных по отдельным шинам. При этом память программ и данных может быть реализована как в виде кэш-памяти первого уровня (соответственно L1I$ 102 и L1D$ 103), так и в виде тесно связанной (Tightly-Coupled Memory, ТСМ) статической памяти (соответственно РМЕМ 102 и DMEM 103). На верхнем уровне реализуется фон-неймановская архитектура, в которой кэш-память второго уровня L2$ 101 обслуживает обращения кэш-памяти программ и данных первого уровня, и через внешний интерфейс имеет доступ к внешней памяти системы.

Инструкции, считываемые из программной памяти PMEM/L1I$ 102 при помощи устройства выборки FETCH 109, поступают в блок DECODE 110, который декодирует их и формирует сигналы управления для исполнительных устройств процессора.

Инструкции организованы в виде VLIW-пакетов (VLIW - Very Long Instruction Word), содержащих несколько одновременно исполняемых команд как для скалярного, так и для векторного каналов 105, 107 процессора. На Фиг. 2 показана структура VLIW-пакета 201. Для каждой команды в VLIW-пакете 201 предусмотрено место, называемое слотом. Всего в VLIW-пакете имеется четыре слота 202-205 для команд скалярного канала 105 и четыре слота 206-209 для команд векторного канала 107. Таким образом, одновременно может выполняться до восьми команд. Каждый из восьми слотов 202-209 VLIW-пакета 201 может содержать команды определенного типа, предназначенные для соответствующего набора исполнительных устройств 210-217. Состав и общее количество команд для каждого VLIW-пакета могут быть различны.

Команды программного управления, в число которых входят команды программных переходов и команды программных циклов, выполняются с помощью блока программного управления PCTRL 111.

В таблице 1 приведен базовый набор команд программного управления, выполняемых с помощью блока PCTRL 111.

К командам скалярного канала 105 процессора относятся команды скалярных обращений к памяти данных (SLSE0 310, SLSE1 311) и команды на выполнение скалярных вычислительных операций - арифметико-логических операций с фиксированной запятой (ALU0 302, ALU1 303, ALU2 304, ALU3 305), арифметико-логических операций с плавающей запятой (FALU0 306, FALU1 307), умножения с фиксированной и плавающей запятой (SMU0 308, SMU1 309), сдвига (SH 312), преобразования типов (CONV 315), деления (DIV 313), вычисления трансцендентных математических функций (MF 314).

К командам векторного канала 107 процессора относятся команды векторных обращений к памяти данных (VLSE0 412, VLSE 413) и команды на выполнение векторных вычислительных операций - арифметико-логических операций с фиксированной запятой (VALU0 403, VALU1 404, VALU2 405, VALU3 406), арифметико-логических операций с плавающей запятой (VFALU0 407, VFALU1 408), умножения с фиксированной и плавающей запятой (VMU0 409, VMU1 410), сдвига (VSH 411), преобразования типов (VCONV 414), а также операций редукции (VRED 104).

В совокупности команды программного управления, команды исполнительных устройств скалярного и векторного каналов 105, 107 процессора, а также команды блока редукции 104 формируют полную систему команд процессора.

Структура скалярной вычислительной секции 106 скалярного канала 105 процессора приведена на Фиг. 3. Центральным элементом скалярной вычислительной секции 106 является многопортовый скалярный регистровый файл RF 301, в котором хранятся обрабатываемые скалярные данные. Через порты RF 301, связанные с внешним интерфейсом скалярного канала 105 процессора с помощью контроллеров скалярных обращений к памяти данных SLSE1 311, SLSE2 происходят обмены данными между памятью данных DMEM/L1D$ 103 и скалярным каналом 105 процессора. Через порты RF 301, связанные с исполнительными устройствами скалярной вычислительной секции 106 процессора, передают исходные данные для выполняемых вычислительных операций и записываются их результаты. К числу исполнительных устройств скалярной вычислительной секции 106 процессора относятся: четыре блока арифметико-логических устройств с фиксированной запятой ALU0 302, ALU1 303, ALU2 304, ALU3 305; два блока арифметико-логических устройств с плавающей запятой FALU0 306, FALU1 307; два блока умножителей с фиксированной и плавающей запятой SMU0 308, SMU1 309; блок сдвига SH 312; блок преобразователя типов CONV 315; блок делителя DIV 313; блок вычисления трансцендентных математических функций MF 314. Каждый из указанных блоков выполняет соответствующий набор скалярных вычислительных операций. Одновременно при указанной структуре VLIW-пакета может выполняться до четырех скалярных вычислительных операций, включая две операции скалярных обменов данными с памятью данных первого уровня DMEM/L1D$ 103.

В таблице 2 приведен базовый набор команд скалярных обращений к памяти данных 103, выполняемых блоками SLSE0 310, SLSE1 311.

В таблице 3 приведен базовый набор команд скалярных арифметико-логических операций с фиксированной запятой, выполняемых блоками ALU0 302, ALU1 303, ALU2 304, ALU3 305.

В таблице 4 приведен базовый набор команд скалярных арифметико-логических операций с плавающей запятой, выполняемых блоками FALU0 306, FALU1 307.

В таблице 5 приведен базовый набор скалярных команд умножения с фиксированной и плавающей запятой, выполняемых блоками SMU0 308, SMU1 309.

В таблице 6 приведен базовый набор скалярных команд сдвига, выполняемых с помощью блока SH 312.

В таблице 7 приведен базовый набор скалярных команд преобразования типов, выполняемых с помощью блока CONV 315.

В таблице 8 приведен базовый набор скалярных команд деления, выполняемых с помощью блока DIV 313.

В таблице 9 приведен базовый набор скалярных команд вычисления трансцендентных математических функций, выполняемых с помощью блока MF 314.

В таблицах 1-20 используются следующие обозначения:

R, Ri, Ra, Rt, Rs, Rd - скалярные регистры данных;

V, Vi, Va, Vt, Vs, Vd - векторные регистры данных;

VAi - векторные регистры-аккумуляторы;

.b, .h, .l, .d - спецификаторы формата данных:

.b - byte (8 разрядов);

.h - halfword (16 разрядов);

.l - long (32 разряда);

.d - double (64 разряда);

i8, i16, i32, i64 - целочисленные знаковые 8/16/32/64-разрядные форматы;

u8, u16, u32, u64 - целочисленные беззнаковые 8/16/32/64-разрядные форматы;

#imm - непосредственное значение;

#N - непосредственное N-разрядное значение;

trunk_N - отсечение до N разрядов;

zext_N→M - расширение числа с N до М разрядов путем заполнения недостающих старших разрядов нулями;

sext_N→M - расширение числа с N до М разрядов путем заполнения недостающих старших разрядов знаковым разрядом;

{,} - конкатенация (объединение) нескольких операндов;

T[i], S[i], D[i], V[i] - элементы векторов.

Векторный канал 107 процессора включает в себя несколько векторных вычислительных секций 108, общее количество которых определяется разрядностью обрабатываемого вектора. Структура векторной вычислительной секции 108 векторного канала 107 представлена на Фиг. 4. В ее состав входит многопортовый мультиформатный векторный регистровый файл VRF 401, предназначенный для хранения обрабатываемых векторных данных. Через порты VRF 401, связанные с внешним интерфейсом векторного канала 107 процессора с помощью контроллеров векторных обращений к памяти данных VLSE0 412, VLSE1 413 производится загрузка/выгрузка данных из/в память данных DMEM/L1D$ 103. Через порты VRF 401, связанные с исполнительными устройствами векторной вычислительной секции 108 процессора, векторные данные передают исполнительным устройствам, и полученные результаты снова записывают в векторный регистровый файл VRF 401.

Особенностью векторного регистрового файла VRF 401 является возможность работы с различными форматами данных, как это показано на Фиг. 5. Каждый 64-разрядный регистр 500 из векторного регистрового файла VRF 401 может хранить либо одно 64-разрядное значение 501, либо два 32-разрядных значения 502, либо четыре 16-разрядных значения 503, либо восемь 8-разрядных значений 504.

В состав векторной вычислительной секции 108 векторного канала 107 входит также векторный регистровый файл регистров-аккумуляторов VAC 402, предназначенный для хранения данных, получаемых и используемых в результате выполнения операций умножения с накоплением, выполняемых двумя блоками векторных умножителей VMU0 409, VMU1 410.

К числу исполнительных устройств вычислительной секции 108 векторного канала 107 процессора относятся также: четыре блока векторных арифметико-логических устройств с фиксированной запятой VALU0 403, VALU1 404, VALU2 405, VALU3 406; два блока векторных арифметико-логических устройств с плавающей запятой VFALU0 407, VFALU1 408; блок векторного сдвига VSH 411; блок преобразователя типов VCONV 414; блок вычисления функций редукции VRED 104. Каждый из указанных блоков выполняет соответствующий набор векторных вычислительных операций. Одновременно при указанной структуре VLIW-пакета выполняют до четырех векторных вычислительных операций, включая две операции векторных обменов данными с памятью DMEM/L1D$ 103.

В таблице 10 приведен базовый набор команд векторных обращений к памяти данных, выполняемых блоками VLSE0 412, VLSE1 413.

В таблице 11 приведен базовый набор команд векторных арифметико-логических операций с фиксированной запятой, выполняемых блоками VALU0 403, VALU1 404, VALU2 405, VALU3 406.

В таблице 12 приведен базовый набор команд векторных арифметико-логических операций с плавающей запятой, выполняемых блоками VFALU0 407, VFALU1 408.

В таблице 13 приведен базовый набор векторных команд умножения с фиксированной и плавающей запятой, выполняемых блоками VMU0 409, VMU1 410.

В таблице 14 приведен базовый набор векторных команд сдвига, выполняемых с помощью блока VSH 411.

В таблице 15 приведен базовый набор векторных команд преобразования типов, выполняемых с помощью блока VCONV 414.

Важнейшей особенностью рассматриваемой архитектуры скалярно-векторного процессора является наличие в ее составе блока редукции VRED 104, связывающего между собой скалярный и векторный каналы 105, 107 процессора, и предназначенную как для организации обменов между ними, так и для выполнения операций, использующих и/или формирующих одновременно и скалярные, и векторные данные. Структурная схема блока редукции VRED 104 представлена на Фиг. 6. В его состав входят следующие исполнительные устройства: блок арифметико-логических межсекционных операций редукции RALU 601, блок межсекционных перестановок SHUFFLE 602, блок межсекционных табличных преобразований LUT 603, блок вычисления гистограмм HIST 604.

В таблице 16 приведен базовый набор команд арифметико-логического устройства межсекционной редукции RALU 601, входящего в состав блока редукции VRED 104.

В таблице 17 приведен базовый набор команд блока межсекционных перестановок SHUFFLE 602, входящего в состав блока редукции VRED 104.

В таблице 18 приведен базовый набор команд блока межсекционных табличных преобразований LUT 603, входящего в состав блока редукции VRED 104.

В таблице 19 приведен базовый набор команд блока вычисления гистограмм HIST 604, входящего в состав блока редукции VRED 104.

Еще одним механизмом, объединяющим скалярный и векторный каналы процессора, является кольцевая шина CDB (Circular Data Bus) 112, изображенная на Фиг. 7.

Одной из команд, выполняемой с помощью кольцевой шины CDB 112, является команда циклического сдвига VPUSHRD Ri, Vj, в результате выполнения которой скалярный регистр Ri перемещается в векторный регистр Vj нулевой векторной вычислительной секции 108: Vj.0=Ri; векторный регистр Vj старшей векторной вычислительной секции 108 перемещается в скалярный регистр Ri: Ri=Vj.N; в остальных векторных вычислительных секциях 108 данные векторных регистров смещаются на одну секцию в сторону старших секций: Vj.k=Vj.k-1, k=1,2,…,N. Этот механизм может быть использован, например, для последовательного перемещения данных из векторного канала 107 процессора в скалярный канал 105 с целью выполнения специфических операций, имеющихся только в скалярном канале 105 (например, для вычисления трансцендентных математических функций), с последующим возвращением преобразованных данных в векторный канал 107 процессора.

В таблице 20 приведен базовый набор команд межсекционного скалярно-векторного сдвига, выполняемых с помощью кольцевой шины данных CDB 112.

Таким образом, рассматриваемая архитектура, по сравнению с ранее известными архитектурами скалярно-векторных процессоров, обладает значительно более широкими возможностями для организации эффективного взаимодействия между скалярным и векторным каналами 105, 107 процессора, тем самым обеспечивая более высокую производительность выполняемых скалярно-векторных вычислений.

Состав и функциональность исполнительных устройств скалярного и векторного каналов 105, 107 процессора могут быть дополнены или сокращены в зависимости от области применения процессора.

Хотя описанный выше вариант выполнения заявленного изобретения был изложен с целью иллюстрации заявленного изобретения, специалистам ясно, что возможны различные модификации, добавления и замены, не выходящие из объема и смысла заявленного изобретения, раскрытого в прилагаемой формуле изобретения.

Мнемоника команды Описание B #16
B #32
B Ra.L Программный переход по относительному адресу #16, #32, Ra.L J #16
J #32
J Ra.L Программный переход по абсолютному адресу #16, #32, Ra.L BS #16, Ri.L
BS #32, Ri.L
BS Ra.L, Ri.L Программный переход по относительному адресу #16, #32, Ra.L с сохранением адреса возврата в регистр Ri.L (все 32 регистра RF) JS #16, Ri.L
JS #32, Ri.L
JS Ra.L, Ri.L Программный переход по абсолютному адресу #16, #32, Ra.L с сохранением адреса возврата в регистр Ri.L (все 32 регистра RF) DO #4, #16
DO #16, #32 Запуск цикла с относительным адресом окончания #16, #32 и непосредственным числом повторений DO R.L, #16
DO R.L, #32 Запуск цикла с относительным адресом окончания #16, #32 и числом повторений из регистра R.L ENDDO Останов цикла по условию. Происходит немедленное прерывание цикла и выход на инструкцию, идущую следом за последней инструкцией цикла.

Табл. 1.

Мнемоника команды Описание LDB (A), R Загрузка i8 из памяти, расширение знаком до i32 LDBU (A), R Загрузка u8 из памяти, расширение нулем до u32 LDH (A), R Загрузка i16 из памяти, расширение знаком до i32 LDHU (A), R Загрузка u16 из памяти, расширение нулем до u32 LDL (A), R Загрузка слова i32 из памяти (без преобразования) LDD (A), R Загрузка двойного слова i64 из памяти (без преобразования) STB R, (A) Сохранение u8 в память STH R, (A) Сохранение u16 в память STL R, (A) Сохранение u32 в память STD R, (A) Сохранение u64 в память

Табл. 2.

Мнемоника команды Формула Описание Скалярные операции целочисленного сложения/вычитания ADDD Rt, Rs, Rd
ADDD #imm, Rs, Rd
ADDD.SAT Rt, Rs, Rd Rd.d = (Rt.d(#imm) + Rs.d)
Rd.d = sat64(Rt.d + Rs.d) Сложение двух операндов, знаковое, с опциональной сатурацией, i64+i64→i64 ADDL Rt, Rs, Rd
ADDL #imm, Rs, Rd
ADDL.SAT Rt, Rs, Rd Rd = (Rt(#imm) + Rs)
Rd = sat32(Rt + Rd) Сложение двух операндов, знаковое, с опциональной сатурацией, i32+i32→i32 ADDL.SCL Rt, Rs, Rd
ADDL.SCL.RND Rt,Rs,Rd Rd = (Rt + Rs)>>1
Rd = (Rt + Rs + 1) >>1 Сложение со сдвигом, знаковое, с опциональным округлением, i32+i32→i32 ADDL.RND Rt, Rs, Rd Rd.l = (Rt.l + Rs.l).rnd Сложение с округлением i32+i32→i32
Округляются младшие 16 бит. SUBD Rt, Rs, Rd
SUBD #imm, Rs, Rd
SUBD.SAT Rt, Rs, Rd Rd.d = (Rs.d - Rt.d(#imm))
Rd.d = sat64(Rs.d - Rt.d) Вычитание двух операндов, знаковое, с опциональной сатурацией, i64 - i64 → i64 SUBL.SCL Rt, Rs, Rd
SUBL.SCL.RND Rt,Rs,Rd Rd = (Rs - Rt)>>1
Rd = (Rs - Rt - 1) >>1 Вычитание со сдвигом, знаковое, с опциональным округлением i32+i32→i32 SUBL.RND Rt, Rs, Rd Rd.l = (Rs.l - Rt.l).rnd Вычитание с округлением i32+i32→i32
Округляются младшие 16 бит. NEGD Rs, Rd
NEGD.SAT Rs, Rd Rd = -Rs
Rd = sat32(-Rs) Отрицание результата с опциональной сатурацией результата, i64 NEGL Rs, Rd
NEGL.SAT Rs, Rd Rd = -Rs
Rd = sat32(-Rs) Отрицание результата с опциональной сатурацией результата, i32 Скалярные операции вычисления абсолютной величины ABSD Rs, Rd
ABSD.SAT Rs, Rd Rd = |Rs|
Rd = sat64(|Rs|) Вычисление модуля 64 битного целого, знакового, с опциональной сатурацией ABSL Rs, Rd
ABSL.SAT Rs, Rd Rd = |Rs|
Rd = sat32(|Rs|) Вычисление модуля 32 битного целого, знакового, с опциональной сатурацией Скалярные операции вычисления целочисленного максимума/минимума MAXD Rt, Rs, Rd Rd = max(Rt, Rs) Максимум из двух элементов, i64 → i64 MAXDU Rt, Rs, Rd Rd = maxu(Rt, Rs) Максимум из двух элементов, u64 → u64 MAXMD Rt, Rs, Rd Rd = maxm(Rt, Rs) Выбор числа с большим модулем, i64 → i64 MIND Rt, Rs, Rd Rd = min(Rt, Rs) Минимум из двух элементов, i64 → i64 MINDU Rt, Rs, Rd Rd = minu(Rt, Rs) Минимум из двух элементов, u64 → u64 MINMD Rt, Rs, Rd Rd = minm(Rt, Rs) Выбор числа с меньшим модулем, i64 → i64 MAXL Rt, Rs, Rd Rd = max(Rt, Rs) Максимум из двух элементов, i32 → i32 MAXLU Rt, Rs, Rd Rd = maxu(Rt, Rs) Максимум из двух элементов, u32 → u32 MAXML Rt, Rs, Rd Rd = maxm(Rt, Rs) Выбор числа с большим модулем, i32 → i32 MINL Rt, Rs, Rd Rd = min(Rt, Rs) Минимум из двух элементов, i32 → i32 MINLU Rt, Rs, Rd Rd = minu(Rt, Rs) Минимум из двух элементов, u32 → u32 MINML Rt, Rs, Rd Rd = minm(Rt, Rs) Выбор числа с меньшим модулем, i32 → i32 Скалярные логические операции ANDD Rt/#imm, Rs, Rd Rd = Rt(#imm) & Rs Поэлементное логическое «И» ORD Rt/#imm, Rs, Rd Rd = Rt(#imm) | Rs Поэлементное логическое «ИЛИ» EORD Rt, Rs, Rd Rd = Rt ^ Rs Поэлементное логическое исключающее «ИЛИ» INSD Rt, Rs, Rd Rd = (~Rt & Rs) | (Rt & Rd) Объединение по маске ANDL Rt/#imm, Rs, Rd Rd = Rt(#imm) & Rs Поэлементное логическое «И» ORL Rt/#imm, Rs, Rd Rd = Rt(#imm) | Rs Поэлементное логическое «ИЛИ» EORL Rt, Rs, Rd Rd = Rt ^ Rs Поэлементное логическое исключающее «ИЛИ» INSL Rt, Rs, Rd Rd = (~Rt & Rs) | (Rt & Rd) Объединение по маске NOTL Rs, Rd Rd = ~Rs Отрицание результата

Табл. 3.

Мнемоника команды Формула Описание Скалярные операции сложения/вычитания с плавающей запятой FADD Rt, Rs, Rd Rd = Rt + Rs Сложение двух чисел, f32 + f32 → f32 DADD Rt, Rs, Rd Rd = Rt + Rs Сложение двух чисел, f64 + f64 → f64 FSUB Rt, Rs, Rd Rd = Rs - Rt Вычитание двух чисел, f32 - f32 → f32 DSUB Rt, Rs, Rd Rd = Rs - Rt Вычитание двух чисел, f64 - f64 → f64 Скалярные операции максимума/минимума с плавающей запятой FMAX Rt, Rs, Rd Rd = max(Rt, Rs) Максимум двух чисел, f32 DMAX Rt, Rs, Rd Rd = max(Rt, Rs) Максимум двух чисел, f64 FMIN Rt, Rs, Rd Rd = min(Rt, Rs) Минимум двух чисел, f32 DMIN Rt, Rs, Rd Rd.d = min(Rt, Rs) Минимум двух чисел, f64

Табл. 4.

Мнемоника команды Формула Описание Скалярные операции целочисленного умножения MPYLLO Rt, Rs, Rd
MPYLLO #imm, Rs, Rd Rd = trunk₃₂(Rs * Rt)
Rd = trunk₃₂(Rs * #imm) Умножение i32*i32→i64, использование младших 32 разрядов, i32 MPYLULO Rt, Rs, Rd
MPYLULO #imm, Rs, Rd Rd = trunk₃₂(Rs * Rt)
Rd = trunk₃₂(Rs * #imm) Умножение u32*u32→u64, использование младших 32 разрядов, u32 MPYLHI Rt, Rs, Rd
MPYLHI #imm, Rs, Rd
MPYLHI.RND Rt, Rs, Rd Rd = (Rs * Rt)>>32
Rd = (Rs * #imm)>>32
Rd = (Rs * #imm + 0x8000_0000)>>32 Умножение, использование старших 32 разрядов, i32*i32→i64, с опциональным округлением MPYLUHI Rt, Rs, Rd
MPYLUHI #imm, Rs, Rd Rd = (Rs * Rt)>>32
Rd = (Rs * #imm)>>32 Умножение, использование старших 32 разрядов, u32*u32→u32 MPYL Rt, Rs, Rdd
MPYL #imm, Rs, Rdd Rdd = Rs * Rt
Rdd = Rs * #imm Умножение, запись полного результата в парный регистр, i32*i32→i64 MPYLU Rt, Rs, Rdd
MPYLU #imm, Rs, Rdd Rdd = Rs * Rt
Rdd = Rs * #imm Умножение, запись полного результата в парный регистр, u32*u32→u64 MPYDLO Rt, Rs, Rd Rd = trunk₆₄(Rs * Rt) Умножение i64*i64→i128, использование младших 64 разрядов, i64 MPYDHI Rt, Rs, Rd Rd = (Rs * Rt)>>128 Умножение, использование старших 64 разрядов, i64*i64→i128 MPYDULO Rt, Rs, Rd Rd = trunk₆₄(Rs * Rt) Умножение u64*u64→u128, использование младших 64 разрядов, u64 MPYDUHI Rt, Rs, Rd Rd = (Rs * Rt)>>128 Умножение, использование старших 64 разрядов, u64*u64→u128 Скалярные операции умножения с плавающей запятой FMPY Rt, Rs, Rd Rd = Rt*Rs Умножение двух чисел, f32*f32 → f32 DMPY Rt, Rs, Rd Rd.d = Rt.d*Rs.d Умножение двух чисел, f64*f64 → f64 FMADD Rt, Rs, Rd
FMADD Rt, Rs, Rr, Rd Rd = Rd + Rt*Rs
Rd = Rr + Rt*Rs Сложение с произведением, f32*f32+f32→f32 FMSUB Rs, Rt, Rd Rd = Rd - Rt*Rs Вычитание произведения, f32*f32-f32→f32

Табл. 5.

Мнемоника команды Формула Описание Скалярные операции сдвига ASRD Rt,Rs, Rd
ASRD #5u, Rs, Rd
ASRD1 #5u, Rs, Rd Rd.d = Rs.d >> Rt
Rd.d = Rs.d >> #5u
Rd.d = Rs.d >> (#5u+32) Арифметический сдвиг вправо LSLD Rt,Rs, Rd
LSLD #5u,Rs, Rd
LSLD1 #5u,Rs, Rd Rd.d = Rs.d <<< Rt
Rd.d = Rs.d <<< #5u
Rd.d = Rs.d <<< (#5u+32) Логический сдвиг влево LSRD Rt,Rs, Rd
LSRD #u5,Rs, Rd
LSRD1 #u5,Rs, Rd Rd.d = Rs.d >>> Rt
Rd.d = Rs.d >>> #5u
Rd.d = Rs.d >>> (#5u+32) Логический сдвиг вправо LSLD.SAT Rt(#u5),Rs, Rd
LSLD1.SAT #u5,Rs, Rd Rd = sat64(Rs <<< (#5u))
Rd = sat64(Rs <<< (#5u+32)) Логический сдвиг влево с сатурацией. При выходе за пределы разрядной сетки любого единичного бита устанавливается максимальное беззнаковое значение. ROLD Rt/#5u, Rs, Rd Rd = (Rs <<< Rt) | (Rs>>>(64-Rt)) Циклический сдвиг влево, сетка 64 бит
Обычное поведение при #5 = 0: результат Rd = Rs. RORD Rt/#5u, Rs, Rd Rd = (Rs >>> Rt) | (Rs<<<(64-Rt)) Циклический сдвиг вправо, сетка 64 бит
Особое поведение при #5 = 0: результат Rd = {Rs.L[0], Rs.L[1]} (два слова 32-бит меняются местами). ASRL Rt(#u5),Rs, Rd Rd = Rs >> Rt Арифметический сдвиг вправо LSLL Rt(#u5),Rs, Rd Rd = Rs <<< Rt Логический сдвиг влево LSRL Rt(#u5),Rs, Rd Rd = Rs >>> Rt Логический сдвиг вправо LSLL.SAT Rt(#u5),Rs, Rd Rd = sat32(Rs <<< Rt) Логический сдвиг влево с сатурацией. При выходе за пределы разрядной сетки любого единичного бита устанавливается максимальное беззнаковое значение. ROLL Rt, Rs, Rd
ROLL #5u, Rs, Rd Rd = (Rs <<< Rt) | (Rs>>>(32-Rt)) Циклический сдвиг влево, сетка 32 бит RORL Rt, Rs, Rd
RORL #5u, Rs, Rd Rd = (Rs >>> Rt) | (Rs<<<(32-Rt)) Циклический сдвиг вправо, сетка 32 бит

Табл. 6.

Мнемоника команды Формула Описание Скалярные операции расширения целочисленных типов CVBLU Rt, Rd
CVBL Rt, Rd Rd.l = zext_8→32(Rt.b)
Rd.l = sext_8→32(Rt.b) Расширение байта до целого, i8 → i32, знаковое и беззнаковое CVHLU Rt, Rd
CVHL Rt, Rd Rd.l = zext_16→32(Rt.h)
Rd.l = sext_16→32(Rt.h) Расширение короткого целого до целого, i16 → i32, знаковое и беззнаковое CVBDU Rt, Rs
CVBD Rt, Rd Rd.d= zext_8→64(Rt.b)
Rd.d = sext_8→64(Rt.b) Расширение байта до целого, i8 → i64, знаковое и беззнаковое CVHDU Rt, Rs
CVHD Rt, Rd Rd.d= zext_16→64(Rt.h)
Rd.d = sext_16→64(Rt.h) Расширение байта до целого, i16 → i64, знаковое и беззнаковое CVLDU Rt, Rs
CVLD Rt, Rd Rd.d= zext_32→64(Rt.l)
Rd.d = sext_32→64(Rt.l) Расширение байта до целого, i32 → i64, знаковое и беззнаковое Скалярные операции усечения целочисленных типов CVLB Rt, Rd
CVLB.sat Rt, Rd
CVLBU.sat Rt, Rd
CVLH Rt, Rd
CVLH.sat Rt, Rd
CVLHU.sat Rt, Rd
CVDB Rt, Rd
CVDB.sat Rt, Rd
CVDBU.sat Rt, Rd
CVDH Rt, Rd
CVDH.sat Rt, Rd
CVDHU.sat Rt, Rd
CVDL Rt, Rd
CVDL.sat Rt, Rd
CVDLU.sat Rt, Rd (на примере CVLB)
CVLB Rt, Rd Rd=sext_8→32(trunk8(Rt))
CVLB.sat Rt, Rd
Rd=sext_8→32 (sat8(Rt))
CVLBU.sat Rt, Rd
Rd=zext_8→32 (usat8(Rt)) (на примере CVLB)
Усечение исходных данных (L) до запрашиваемой величины (B), с опциональной сатурацией. Полученное число (B) расширяется своим знаком (для знаковых расширений) или нулем (для беззнаковых расширений - с суффиксом U) до исходной величины (L) Скалярные операции преобразования типов с плавающей запятой FDCV Rt, Rd Rd = float_to_double(Rt) Преобразование float32 в float64 DFCV Rt, Rd Rd = double_to_float(Rt) Преобразование float64 в float32 FHCV Rt, Rd Rd[0].h = float_to_halffloat(Rt)
Rd[1].h = 0 Преобразование float32 в float16
Старшие 16 бит регистра Rd заполняются нулем. DHCV Rt, Rd Rd[0].h = double_to_halffloat(Rt)
Rd[1].h = 0 Преобразование float64 в float16
Старшие 16 бит регистра Rd заполняются нулем. HFCV Rt, Rd Rd = halffloat_to_float(Rt) Преобразование float16 в float32 HDCV Rt, Rd Rd = halffloat_to_doubleRt) Преобразование float16 в float64 Скалярные операции преобразования типов INT->FLT CVDF Rt, Rd Rd.f32 = int64_to_float32(Rt.d) Преобразование int64 в float32 CVDFU Rt, Rd Rd.f32 = uint64_to_float32(Rt.d) Преобразование uint64 в float32 CVDD Rt, Rd Rd.f64= int64_to_float64(Rt.d) Преобразование int64 в float64 CVDDU Rt, Rd Rd.f64 = uint64_to_float64(Rt.d) Преобразование из uint64 в float64 CVIF Rt, Rd Rd.f32 = int32_to_float32(Rt.d) Преобразование из int32 в float32 CVIFU Rt, Rd Rd.f32 = uint32_to_float32(Rt.d) Преобразование из uint32 в float32 CVID Rt, Rd Rd.f64 = int32_to_float64(Rt.d) Преобразование из int32 в float64 CVIDU Rt, Rd Rd.f64 = uint32_to_float64(Rt.d) Преобразование из uint32 в float64 CVHF Rt, Rd Rd.f32 = int16_to_float32(Rt.d) Преобразование из int16 в float32 CVHFU Rt, Rd Rd.f32 = uint16_to_float32(Rt.d) Преобразование из uint16 в float16 Скалярные операции преобразования типов FLT-> INT FCVD Rt, Rd Rd.d = float32_to_int64(Rt.d) Преобразование из float32 в int64 FCVDU Rt, Rd Rd.ud = float32_to_uint64(Rt.d) Преобразование из float32 в uint64 FCVI Rt, Rd
FCVI.floor Rt, Rd
FCVI.round Rt, Rd
FCVI.ceil Rt, Rd
FCVI.trunc Rt, Rd Rd.l = float32_to_int32(Rt.d) Преобразование из float32 в int32
Опциональное округление FCVIU Rt, Rd
FCVIU.floor Rt, Rd
FCVIU.round Rt, Rd
FCVIU.ceil Rt, Rd
FCVIU.trunc Rt, Rd Rd.ul = float32_to_uint32(Rt.d) Преобразование из float32 в uint32
Опциональное округление DCVD Rt, Rd
DCVD.floor Rt, Rd
DCVD.round Rt, Rd
DCVD.ceil Rt, Rd
DCVD.trunc Rt, Rd Rd.d = float64_to_int64(Rt.d) Преобразование из float64 в int64
Опциональное округление DCVDU Rt, Rd
DCVDU.floor Rt, Rd
DCVDU.round Rt, Rd
DCVDU.ceil Rt, Rd
DCVDU.trunc Rt, Rd Rd.ud = float64_to_uint64(Rt.d) Преобразование из float64 в uint64
Опциональное округление DCVI Rt, Rd Rd.l = float64_to_int32(Rt.d) Преобразование из float64 в int32 DCVIU Rt, Rd Rd.ul = float64_to_uint32(Rt.d) Преобразование из float64 в uint32 FCVH Rt, Rd Rd.l = float32_to_int16(Rt.d) Преобразование из float32 в int16 FCVHU Rt, Rd Rd.ul = float32_to_uint16(Rt.d) Преобразование из float32 в uint16

Табл. 7.

Мнемоника команды Формула Описание Скалярные операции целочисленного деления DIVL Rd.L = Rt.L/Rs.L Деление i32:
if (Rs == 0)
REM = 0
DIV = (Rt >= 0)? 0x7FFFFFFF: 0x80000000
else
DIV = Rt / Rs
REM = Rt % Rs
Rd = DIV REML Rd.L = Rt.L%Rs.L Остаток от деления i32:
if (Rs == 0)
REM = 0
DIV = (Rt >= 0)? 0x7FFFFFFF: 0x80000000
else
DIV = Rt / Rs
REM = Rt % Rs
Rd = REM DIVREML Rd.D = {Rt.L%Rs.L , Rt.L/Rs.L} Остаток от деления i32, деление i32:
if (Rs == 0)
REM = 0
DIV = (Rt >= 0)? 0x7FFFFFFF: 0x80000000
else
DIV = Rt / Rs
REM = Rt % Rs
Rd = {REM, DIV} DIVLU Rd.L = Rt.L/Rs.L Деление u32:
if (Rs == 0)
DIV = 0xFFFFFFFF
REM = 0
else
DIV = Rt / Rs
REM = Rt % Rs
Rd = DIV REMLU Rd.L = Rt.L%Rs.L Остаток от деления u32:
if (Rs == 0)
DIV = 0xFFFFFFFF
REM = 0
else
DIV = Rt / Rs
REM = Rt % Rs
Rd = REM DIVREMLU Rd.D = {Rt.L%Rs.L , Rt.L/Rs.L} Остаток от деления u32, деление u32:
if (Rs == 0)
DIV = 0xFFFFFFFF
REM = 0
else
DIV = Rt / Rs
REM = Rt % Rs
Rd = {REM, DIV}

Табл. 8.

Мнемоника команды Формула Описание Скалярные операции вычисления трансцендентных математических функций FEXP2 Rt, Rd Rd.L = 2.0^Rt Вычисление значения показательной функции c основанием 2: Z=2^X.
Вход (X) и выход (Z) имеют 32-разрядный формат плавающей точки: (float32)X, (float32)Z FLOG Rt, Rd Rd.L = ln(Rt) Вычисление значения натурального логарифма:
Z=Ln X.
Вход (X) и выход (Z) имеют 32-разрядный формат плавающей точки: (float32)X, (float32)Z FSQRT Rt, Rd Rd.L = sqrt_approx(Rt) Извлечение квадратного корня:
Z=√X.
Вход (X) и выход (Z) имеют 32-разрядный формат плавающей точки:
(float32)X, (float32)Z.
Ограничения и особые случаи:
FSQRT(0) = 0
FSQRT(-0) = -0
FSQRT(A) = NaN, A < 0 FISQRT Rt, Rd Rd.L = isqrt_approx(Rt) Вычисление обратной величины квадратного корня:
Z=1./√X.
Вход (X) и выход (Z) имеют 32-разрядный формат плавающей точки: (float32)X, (float32)Z FRECIP Rt, Rd Rd.L = recip_approx(Rt) Вычисление обратной величины:
Z=1./X.
Вход (X) и выход (Z) имеют 32-разрядный формат плавающей точки: (float32)X, (float32)Z

Табл. 9.

Мнемоника команды Описание VLD Загрузка без преобразования типа данных VLDBH
VLDBHU Загрузка данных с расширением типа данных знаком или нулем, i8(u8) → i16(u16) VLDBL
VLDBLU Загрузка данных с расширением типа данных знаком или нулем, i8(u8) → i32(u32) VLDHL
VLDHLU Загрузка данных с расширением типа данных знаком или нулем, i16(u16) → i32(u32) VLDLD
VLDLDU Загрузка данных с расширением типа данных знаком или нулем, i32(u32) → i64(u64) VST Сохранение без преобразования типа данных VSTHBU Сохранение с обрезкой типа данных, u16 → u8 VSTLBU Сохранение с обрезкой типа данных, u32 → u8 VSTLHU Сохранение с обрезкой типа данных, u32 → u16 VSTDLU Сохранение с обрезкой типа данных, u64 → u32

Табл. 10.

Мнемоника команды Формула Описание Векторные операции целочисленного сложения/вычитания VADDD Vt, Vs, Vd
VADDD.SAT Vt, Vs, Vd
VADDDU.SAT Vt, Vs, Vd D[i] = T[i] + S[i], i = 0
D[i] = sat32(T[i] + S[i]),i=0
D[i] = usat32(T[i] + S[i]), i = 0, unsigned Сложение i64 = i64 + i64 знаковые (беззнаковые u64+u64→u64),
Опциональная сатурация VADDD.SCL Vt, Vs, Vd
VADDD.SCL.RND Vt, Vs, Vd
VADDDU.SCL Vt, Vs, Vd
VADDDU.SCL.RND Vt, Vs, Vd D[i] = (T[i] + S[i]) >> 1, i=0
D[i] = rnd(T[i] + S[i]) >> 1, i = 0
D[i] = (T[i] + S[i]) >> 1, i = 0, unsigned
D[i] = rnd(T[i] + S[i]) >> 1, i = 0, unsigned Сложение i64 = i64 + i64 знаковые (беззнаковые u64+u64→u64),
Опциональное округление VADDL Vt, Vs, Vd
VADDL #32, Vs, Vd
VADDL.SAT Vt, Vs, Vd
VADDLU.SAT Vt, Vs, Vd D[i] = T[i] + S[i], i = 0:1
D[i] = #I2 + S[i], i = 0:1
D[i] = sat32(T[i] + S[i]), i = 0:1
D[i] = usat32(T[i] + S[i]), i = 0:1, unsigned Сложение i32 = i32 + i32 знаковые (беззнаковые u32+u32→u32),
Опциональная сатурация VADDL.SCL Vt, Vs, Vd
VADDL.SCL.RND Vt, Vs, Vd
VADDLU.SCL Vt, Vs, Vd
VADDLU.SCL.RND Vt, Vs, Vd D[i] = (T[i] + S[i]) >> 1, i = 0:1
D[i] = rnd(T[i] + S[i]) >> 1, i = 0:1
D[i] = (T[i] + S[i]) >> 1, i = 0:1, unsigned
D[i] = rnd(T[i] + S[i]) >> 1, i = 0:1, unsigned Сложение i32 = i32 + i32 знаковые (беззнаковые u32+u32→u32),
Опциональное округление VADDH Vt, Vs, Vd
VADDH #IMM16, Vs, Vd
VADDH.SAT Vt, Vs, Vd
VADDHU.SAT Vt, Vs, Vd D[i] = T[i] + S[i], i = 0:3
D[i] = #IMM16 + S[i], i = 0:3
D[i] = sat16(T[i] + S[i]), i = 0:3
D[i] = usat16(T[i] + S[i]), i = 0:3, unsigned Сложение i16 = i16 + i16 знаковые (беззнаковые u32+u32→u32),
Опциональная сатурация VADDH.SCL Vt, Vs, Vd
VADDH.SCL.RND Vt, Vs, Vd
VADDHU.SCL Vt, Vs, Vd
VADDHU.SCL.RND Vt, Vs, Vd D[i] = (T[i] + S[i]) >> 1, i = 0:3
D[i] = rnd(T[i] + S[i]) >> 1, i = 0:3
D[i] = (T[i] + S[i]) >> 1, i = 0:3, unsigned
D[i] = rnd(T[i] + S[i]) >> 1, i = 0:3, unsigned Сложение i16 = i16 + i16 знаковые (беззнаковые u32+u32→u32),
Опциональное округление VADDB Vt, Vs, Vd
VADDB #IMM8, Vs, Vd
VADDB.SAT Vt, Vs, Vd
VADDBU.SAT Vt, Vs, Vd D[i] = T[i] + S[i], i = 0:7
D[i] = #IMM8 + S[i], i = 0:7
D[i] = sat8(T[i] + S[i]), i = 0:7
D[i] = usat8(T[i] + S[i]), i = 0:7, unsigned Сложение i8 = i8 + i8 знаковые (беззнаковые u8+u8→u8),
Опциональная сатурация VADDB.SCL Vt, Vs, Vd
VADDB.SCL.RND Vt, Vs, Vd
VADDBU.SCL Vt, Vs, Vd
VADDBU.SCL.RND Vt, Vs, Vd D[i] = (T[i] + S[i]) >> 1, i = 0:7
D[i] = rnd(T[i] + S[i]) >> 1, i = 0:7
D[i] = (T[i] + S[i]) >> 1, i = 0:7, unsigned
D[i] = rnd(T[i] + S[i]) >> 1, i = 0:7, unsigned Сложение i8 = i8 + i8 знаковые (беззнаковые u8+u8→u8),
Опциональное округление VSUBD Vt, Vs, Vd
VSUBD.SAT Vt, Vs, Vd
VSUBDU.SAT Vt, Vs, Vd D[i] = S[i] - S[i], i = 0
D[i] = sat64(S[i] - T[i]), i = 0
D[i] = usat64(S[i] - T[i]), i = 0, unsigned
Vt: = {T1, T0}, i64/u64, Vs = {S0, S0}, i64/u64
Vd = {D1, D0}, i64/u64 Вычитание i64 = i64 - i64 знаковые (беззнаковые u64-u64→u64),
Опциональная сатурация VSUBL Vt, Vs, Vd
VSUBL #32, Vs, Vd
VSUBL.SAT Vt, Vs, Vd
VSUBLU.SAT Vt, Vs, Vd D[i] = S[i] - T[i], i = 0:1
D[i] = S[i] - #32, i = 0:1
D[i] = sat32(S[i] - T[i]), i = 0:1
D[i] = usat32(S[i] - T[i]), i = 0:1, unsigned Вычитание i32 = i32 - i32 знаковые (беззнаковые u32-u32→u32),
Опциональная сатурация VSUBL.SCL Vt, Vs, Vd
VSUBL.SCL.RND Vt, Vs, Vd
VSUBL.SCL.RND.SAT Vt, Vs, Vd D[i] = (S[i] - T[i]) >> 1, i = 0:1
D[i] = rnd(S[i] - T[i] + 1) >> 1, i = 0:1
D[i] = sat32(rnd(S[i] - T[i]) >> 1), i = 0:1 Вычитание i32 = i32 - i32 знаковые,
Опциональное округление и сатурация VSUBH Vt, Vs, Vd
VSUBH #IMM16, Vs, Vd
VSUBH.SAT Vt, Vs, Vd
VSUBHU.SAT Vt, Vs, Vd D[i] = S[i] - S[i], i = 0:3
D[i] = S[i] - #IMM16, i = 0:1
D[i] = sat16(S[i] - T[i]), i = 0:1
D[i] = usat16(S[i] - T[i]), i = 0:3, unsigned Вычитание i16 = i16 - i16 знаковые (беззнаковые u16-u16→u16),
Опциональная сатурация VSUBH.SCL Vt, Vs, Vd
VSUBH.SCL.RND Vt, Vs, Vd
VSUBH.SCL.RND.SAT Vt, Vs, Vd D[i] = (S[i] - T[i]) >> 1, i = 0:1
D[i] = rnd(S[i] - T[i]) >> 1, i = 0:1
D[i] = sat16(rnd(S[i] - T[i]) >> 1), i = 0:1 Вычитание i16 = i16 - i16 знаковые,
Опциональное округление и сатурация VSUBB Vt, Vs, Vd
VSUBB #IMM8, Vs, Vd
VSUBB.SAT Vt, Vs, Vd
VSUBBU.SAT Vt, Vs, Vd D[i] = S[i] - S[i], i = 0:7
D[i] = S[i] - #IMM8, i = 0:7
D[i] = sat8(S[i] - T[i]), i = 0:7
D[i] = usat8(S[i] - T[i]), i = 0:7, unsigned Вычитание i8 = i8 - i8 знаковые (беззнаковые u8-u8→u8),
Опциональная сатурация VSUBB.SCL Vt, Vs, Vd
VSUBB.SCL.RND Vt, Vs, Vd
VSUBB.SCL.RND.SAT Vt, Vs, Vd D[i] = (S[i] - T[i]) >> 1, i = 0:7
D[i] = rnd(S[i] - T[i]) >> 1, i = 0:7
D[i] = sat8(rnd(S[i] - T[i]) >> 1), i = 0:7 Вычитание i8 = i8 - i8 знаковые,
Опциональное округление и сатурация Векторные операции вычисления абсолютной величины VABSD Vs, Vd
VABSD.SAT Vs, Vd D[i] = abs(S[i]), i=0
D[i] = sat64(abs(S[i])), i=0 Модуль целого, i64, с опциональной сатурацией VABSL Vs, Vd
VABSL.SAT Vs, Vd D[i] = abs(S[i]), i=0:1
D[i] = sat32(abs(S[i])), i=0:1 Модуль целого, i32, с опциональной сатурацией VABSH Vs, Vd
VABSH.SAT Vs, Vd D[i] = abs(S[i]), i=0:3
D[i] = sat16(abs(S[i])), i=0:3 Модуль целого, i16, с опциональной сатурацией VABSB Vs, Vd
VABSB.SAT Vs, Vd D[i] = abs(S[i]), i=0:7
D[i] = sat8(abs(S[i])), i=0:7 Модуль целого, i8, с опциональной сатурацией Векторные операции вычисления целочисленного максимума/минимума VMAXD Vt, Vs, Vd
VMAXDU Vt, Vs, Vd D[i] = max(T[i], S[i]), i=0
D[i] = umax(T[i], S[i]), i=0 Поэлементный максимум, i64, u64 VMAXL Vt, Vs, Vd
VMAXLU Vt, Vs, Vd D[i] = max(T[i], S[i]), i=0:1
D[i] = umax(T[i], S[i]), i=0:1 Поэлементный максимум, i32, u32 VMAXH Vt, Vs, Vd
VMAXHU Vt, Vs, Vd D[i] = max(T[i], S[i]), i=0:3
D[i] = umax(T[i], S[i]), i=0:3 Поэлементный максимум, i16, u16 VMAXB Vt, Vs, Vd
VMAXBU Vt, Vs, Vd D[i] = max(T[i], S[i]), i=0:7
D[i] = umax(T[i], S[i]), i=0:7 Поэлементный максимум, i8, u8 VMIND Vt, Vs, Vd
VMINDU Vt, Vs, Vd D[i] = min(T[i], S[i]), i=0
D[i] = umin(T[i], S[i]), i=0 Поэлементный минимум, i64, u64 VMINL Vt, Vs, Vd
VMINLU Vt, Vs, Vd D[i] = min(T[i], S[i]), i=0:1
D[i] = umin(T[i], S[i]), i=0:1 Поэлементный минимум, i32, u32 VMINH Vt, Vs, Vd
VMINHU Vt, Vs, Vd D[i] = min(T[i], S[i]), i=0:3
D[i] = umin(T[i], S[i]), i=0:3 Поэлементный минимум, i16, u16 VMINB Vt, Vs, Vd
VMINBU Vt, Vs, Vd D[i] = min(T[i], S[i]), i=0:7
D[i] = umin(T[i], S[i]), i=0:7 Поэлементный минимум, i8, u8 VMAX2L Vt, Vs, Vd
VMAX2LU Vt, Vs, Vd D[0] = T[0]; then D[i] = max(D[0], S[i]), i=0, …, n-1
D[0] = T[0]; then D[i] = maxu(D[0], S[i]), i=0, …, n-1 Поиск текущего максимум, i32/u32, n=2 VMAX4H Vt, Vs, Vd
VMAX4HU Vt, Vs, Vd D[0] = T[0]; then D[i] = max(D[0], S[i]), i=0, …, n-1
D[0] = T[0]; then D[i] = maxu(D[0], S[i]), i=0, …, n-1 Поиск текущего максимум, i16/u16, n=4 VMAX8B Vt, Vs, Vd
VMAX8BU Vt, Vs, Vd D[0] = T[0]; then D[i] = max(D[0], S[i]), i=0, …, n-1
D[0] = T[0]; then D[i] = maxu(D[0], S[i]), i=0, …, n-1 Поиск текущего максимум, i8/u8, n=8 VMIN2L Vt, Vs, Vd
VMIN2LU Vt, Vs, Vd D[0] = T[0]; then D[i] = min(D[0], S[i]), i=0, …, n-1
D[0] = T[0]; then D[i] = minu(D[0], S[i]), i=0, …, n-1 Поиск текущего минимума, i32/u32, n=2 VMIN4H Vt, Vs, Vd
VMIN4HU Vt, Vs, Vd D[0] = T[0]; then D[i] = min(D[0], S[i]), i=0, …, n-1
D[0] = T[0]; then D[i] = minu(D[0], S[i]), i=0, …, n-1 Поиск текущего минимума, i16/u16, n=4 VMIN8B Vt, Vs, Vd
VMIN8BU Vt, Vs, Vd D[0] = T[0]; then D[i] = min(D[0], S[i]), i=0, …, n-1
D[0] = T[0]; then D[i] = minu(D[0], S[i]), i=0, …, n-1 Поиск текущего минимума, i8/u8, n=8 Векторные логические операции VAND Vt, Vs, Vd D = T & S Поэлементное логическое «И», i8 VANDC Vt, Vs, Vd
VANDI Vt, Vs, Vd D = ~T & S
D = ~ (T & S) Поэлементное логическое «И» с инверсией
одного из операндов или результата, i8 VOR Vt, Vs, Vd D= T | S Поэлементное логическое «ИЛИ», i8 VORC Vt, Vs, Vd
VORI Vt, Vs, Vd D = ~T | S
D = ~ (T | S) Поэлементное логическое «ИЛИ» с инверсией
одного из операндов или результата, i8 VEOR Vt, Vs, Vd D = T ^ S Поэлементное логическое исключающее «ИЛИ», i8 VNOT Vs, Vd D = ~S Поэлементное отрицание результата, i8

Табл. 11.

Мнемоника команды Формула Описание Векторные операции сложения/вычитания с плавающей запятой VHADD Vt, Vs, Vd VT = {T3, T2, T1, T0}
VS = {S3, S2, S1, S0}
VD = {S3 + T2, S2 + T3, S1 + T0, S0 + T1} Сложение двух чисел, f16 + f16 → f16 VFADD Vt, Vs, Vd VT = {T1, T0}
VS = {S1, S0}
Vd={S1 + T1, S0 + T0} Сложение двух чисел, f32 + f32 → f32 VDADD Vt, Vs, Vd VT = {T0}
VS = {S0}
Vd = {S0 + T0} Сложение двух чисел, f64 + f64 → f64 VHSUB Vt, Vs, Vd VT = {T3, T2, T1, T0}
VS = {S3, S2, S1, S0}
VD = {S3 - T2, S2 - T3, S1 - T0, S0 - T1} Вычитание двух чисел, f16 - f16 → f16 VFSUB Vt, Vs, Vd VT = {T1, T0}
VS = {S1, S0}
Vd = {S1 - T1, S0 - T0} Вычитание двух чисел, f32 ‒ f32 → f32 VDSUB Vt, Vs, Vd VT = {T0}
VS = {S0}
Vd = {S0 - T0} Вычитание двух чисел, f64 - f64 → f64 Векторные операции максимума/минимума с плавающей запятой VHMAX Vt, Vs, Vd Vt={T[i]}, Vs={S[i]}, Vd={D[i]}, i=0…3
D[i] = max(T[i], S[i]) Максимум двух чисел, f16 VFMAX Vt, Vs, Vd Vt={T[i]}, Vs={S[i]}, Vd={D[i]}, i=0…1
D[i] = max(T[i], S[i]) Максимум двух чисел, f32 VDMAX Vt, Vs, Vd Vt={T[i]}, Vs={S[i]}, Vd={D[i]}, i=0
D[i] = max(T[i], S[i]) Максимум двух чисел, f64 VHMIN Vt, Vs, Vd Vt={T[i]}, Vs={S[i]}, Vd={D[i]}, f16, i=0…3
D[i] = min(T[i], S[i]) Минимум двух чисел, f16 VFMIN Vt, Vs, Vd Vt={T[i]}, Vs={S[i]}, Vd={D[i]}, i=0…1
D[i] = min(T[i], S[i]) Минимум двух чисел, f32 VDMIN Vt, Vs, Vd Vt={T[i]}, Vs={S[i]}, Vd={D[i]}, i=0
D[i] = min(T[i], S[i]) Минимум двух чисел, f64

Табл. 12.

Мнемоника команды Формула Описание Векторные операции целочисленного умножения VMPYB T, S, D T = {8{i8}} = {T7,…,T0};
S = {8{i8}} = {S7,…,S0};
D = {8{i16}} = {D7,…,D0} = {D1,D0};
Di = Ti ⋅ Si; i = 0:7; Умножение, целое, со знаком.
[i16 = i8 ⋅ i8] VMPYBU T, S, D T = {8{u8}} = {T7,…,T0};
S = {8{u8}} = {S7,…,S0};
D = {8{u16}} = {D7,…,D0} = {D1,D0};
Di = Ti ⋅ Si; i = 0:7; Умножение, целое, без знака.
[u16 = u8 ⋅ u8] VMPYH T, S, D T = {4{i16}} = {T3,…,T0};
S = {4{i16}} = {S3,…,S0};
D = {4{i32}} = {D3,…,D0} = {D1,D0};
Di = Ti ⋅ Si; i = 0:3; Умножение, целое, со знаком.
[i32 = i16 ⋅ i16] VMPYHU T, S, D T = {4{u16}} = {T3,…,T0};
S = {4{u16}} = {S3,…,S0};
D = {4{u32}} = {D3,…,D0} = {D1,D0};
Di = Ti ⋅ Si; i = 0:3; Умножение, целое, без знака.
[u32 = u16 ⋅ u16] VMPYL T, S, D T = {2{i32}} = {T1,T0};
S = {2{i32}} = {S1,S0};
D = {2{i64}} = {D1,D0} = {D1,D0};
Di = Ti ⋅ Si; i = 0,1; Умножение, целое, со знаком.
[i64 = i32 ⋅ i32] VMPYLU T, S, D T = {2{u32}} = {T1,T0};
S = {2{u32}} = {S1,S0};
D = {2{u64}} = {D1,D0} = {D1,D0};
Di = Ti ⋅ Si; i = 0,1; Умножение, целое, без знака.
[u64 = u32 ⋅ u32] VMPYD T, S, D T = {i64};
S = {i64};
D = {i128} = {D1,D0};
D = T ⋅ S; Умножение, целое, со знаком.
[i128 = i64 ⋅ i64] VMPYDU T, S, D T = {u64};
S = {u64};
D = {u128} = {D1,D0};
D = T ⋅ S; Умножение, целое, без знака.
[u128 = u64 ⋅ u64] Векторные операции целочисленного умножения с накоплением в аккумуляторе VMPACBB T, S
VMPACBB T, S, VAd T = {8{i8}} = {T7,…,T0};
S = {8{i8}} = {S7,…,S0};
AC = {8{i32}} = {AC7,…,AC0};
ACi += Ti ⋅ Si; i = 0:7; Умножение с накоплением в аккумуляторе, целое, со знаком.
В двухадресной форме неявно используется VA0.
[i32 += i8 ⋅ i8] VMPACBB T, S
VMPACBB T, S, VAd T = {8{u8}} = {T7,…,T0};
S = {8{i8}} = {S7,…,S0};
AC = {8{i32}} = {AC7,…,AC0};
ACi += Ti ⋅ Si; i = 0:7; Умножение с накоплением в аккумуляторе, целое, со знаком.
В двухадресной форме неявно используется VA0.
[i32 += u8 ⋅ i8] VMPACBH T, S
VMPACBH T, S, VAd T = {4{0, i8}} = {0,T3,…,0,T0};
S = {4{i16}} = {S3,…,S0};
AC = {4{i64}} = {AC3,…,AC0};
ACi += Ti ⋅ Si; i = 0:3; Умножение с накоплением в аккумуляторе, целое, со знаком.
В двухадресной форме неявно используется VA0.
[i64 += i8 ⋅ i16] VMPACBUH T, S
VMPACBUH T, S, VAd T = {4{0,u8}} = {0,T3,…,0,T0};
S = {4{i16}} = {S3,…,S0};
AC = {4{i64}} = {AC3,…,AC0};
ACi += Ti ⋅ Si; i = 0:3; Умножение с накоплением в аккумуляторе, целое, со знаком.
В двухадресной форме неявно используется VA0.
[i64 += u8 ⋅ i16] VMPACHH T, S
VMPACHH T, S, VAd T = {4{i16}} = {T3,…,T0};
S = {4{i16}} = {S3,…,S0};
AC = {4{i64}} = {AC3,…,AC0};
ACi += Ti ⋅ Si; i = 0:3; Умножение с накоплением в аккумуляторе, целое, со знаком.
В двухадресной форме неявно используется VA0.
[i64 += i16 ⋅ i16] VMPACHUH T, S
VMPACHUH T, S, VAd T = {4{u16}} = {T3,…,T0};
S = {4{i16}} = {S3,…,S0};
AC = {4{i64}} = {AC3,…,AC0};
ACi += Ti ⋅ Si; i = 0:3; Умножение с накоплением в аккумуляторе, целое, со знаком.
В двухадресной форме неявно используется VA0.
[i64 += u16 ⋅ i16] VMPACLL T, S
VMPACLL T, S, VAd T = {2{i32}} = {T1,T0};
S = {2{i32}} = {S1,S0};
AC = {4{i64}} = {AC3,…,AC0};
ACi += Ti ⋅ Si; i = 0,2; Умножение с накоплением в аккумуляторе, целое, со знаком.
В двухадресной форме неявно используется VA0.
[i64 += i32 ⋅ i32] Векторные операции умножения с плавающей запятой VHMPY T, S, D T = {4{f16}} = {T3,…,T0};
S = {4{f16}} = {S3,…,S0};
D = {4{f16}} = {D3,…,D0};
Di = Ti ⋅ Si; i = 0:3; Умножение, числа с плавающей точкой половинной точности.
[f16 = f16 ⋅ f16] VFMPY T, S, D T = {2{f32}} = {T1,T0};
S = {2{f32}} = {S1,S0};
D = {2{f32}} = {D1,D0};
Di = Ti ⋅ Si; i = 0,1; Умножение, числа с плавающей точкой одинарной точности.
[f32 = f32 ⋅ f32] VDMPY T, S, D T = {f64};
S = {f64};
D = {f64};
D = T ⋅ S; Умножение, числа с плавающей точкой двойной точности.
[f64 = f64 ⋅ f64] Векторные операции умножения с плавающей запятой с накоплением в аккумуляторе VHMPAC T, S
VHMPAC T, S, VAd T = {4{f16}} = {T3,…,T0};
S = {4{f16}} = {S3,…,S0};
AC = {4{f32}} = {AC3,…,AC0};
ACi += Ti ⋅ Si; i = 0:3;
[f32 += f32(f16 ⋅ f16)] Умножение с накоплением, числа с плавающей точкой половинной точности. Умножение и сложение произведений производится в разрядной сетке f16, затем результат расширяется до f32 и накапливается в аккумуляторе f32.
В двухадресной форме неявно используется VA0. VFMPAC T, S
VFMPAC T, S, VAd T = {2{f32}} = {T1,T0};
S = {2{f32}} = {S1,S0};
AC = {2{f32}} = {AC1,AC0};
ACi += Ti ⋅ Si; i = 0,1; Умножение с накоплением, числа с плавающей точкой одинарной точности.
В двухадресной форме неявно используется VA0.
[f32 += f32 ⋅ f32] VFMPAC4 T, S
VFMPAC4 T, S, VAd T = {T', T} = {4{f32}} = {T3,T2,T1,T0};
S = {S', S} = {4{f32}} = {S3,S2,S1,S0};
AC = {4{f32}} = {AC3,…,AC0};
ACi += Ti ⋅ Si; i = 0,3; Умножение с накоплением, числа с плавающей точкой одинарной точности.
В двухадресной форме неявно используется VA0.
[f32 += f32 ⋅ f32]
Используются смежные входные регистры: R'[i] = R[i^1]. VDMPAC T, S
VDMPAC T, S, VAd T = {1{f64}} = {T0};
S = {1{f64}} = {S0};
AC = {1{f64}} = {AC0};
ACi += Ti ⋅ Si; i = 0; Умножение с накоплением, числа с плавающей точкой двойной точности.
В двухадресной форме неявно используется VA0.
[f64 += f64 ⋅ f64] VDMPAC2 T, S
VDMPAC2 T, S, VAd T = {T', T} = {2{f64}} = {T1, T0};
S = {S', S} = {2{f64}} = {S1, S0};
AC = {2{f64}} = {AC1,AC0};
ACi += Ti ⋅ Si; i = 0…1; Умножение с накоплением, числа с плавающей точкой двойной точности.
В двухадресной форме неявно используется VA0.
[f64 += f64 ⋅ f64]
Используются смежные входные регистры: R'[i] = R[i^1].

Табл. 13.

Мнемоника команды Формула Описание Векторные операции сдвига VASRD Vt(#u5),Vs, Vd D[i] = S[i] >> T[i], i=0
D[i] = S[i] >> #IMM5, i=0 Арифметический сдвиг вправо, i64 VLSLD Vt(#u5),Vs, Vd D[i] = S[i] << T[i], i=0
D[i] = S[i] << #IMM5, i=0 Сдвиг влево, i64 VLSRD Vt(#u5),Vs, Vd D[i] = S[i] >>> T[i], i=0
D[i] = S[i] >>> #IMM5, i=0 Логический сдвиг вправо, i64 VASRD.RND Vt(#u5),Vs, Vd If(T[i] == 0) D[i]= S[i]
Else D[i] = RND(S[i] >> T[i]) Арифметический сдвиг вправо с округлением, i64 VLSRD.RND Vt(#u5),Vs, Vd If(T[i] == 0) D[i]= S[i]
Else D[i] = RND(S[i] >>> T[i]) Логический сдвиг вправо с округлением, i64 VASRL Vt(#u5),Vs, Vd D[i] = S[i] >> T[i], i=0:1
D[i] = S[i] >> #IMM5, i=0:1 Арифметический сдвиг вправо, i32 VLSLL Vt(#u5),Vs, Vd D[i] = S[i] << T[i], i=0:1
D[i] = S[i] << #IMM5, i=0:1 Сдвиг влево, i32 VLSRL Vt(#u5),Vs, Vd D[i] = S[i] >>> T[i], i=0:1
D[i] = S[i] >>> #IMM5, i=0:1 Логический сдвиг вправо, i32 VASRL.RND Vt(#u5),Vs, Vd If(T[i] == 0) D[i]= S[i]
Else D[i] = RND(S[i] >> T[i]), i=0…1 Арифметический сдвиг вправо с округлением, i32 VLSRL.RND Vt(#u5),Vs, Vd If(T[i] == 0) D[i]= S[i]
Else D[i] = RND(S[i] >>> T[i]), i=0…1 Логический сдвиг вправо с округлением, i32 VASRH Vt(#u5),Vs, Vd D[i] = S[i] >> T[i], i=0:3
D[i] = S[i] >> #IMM5, i=0:3 Арифметический сдвиг вправо, i16 VLSLH Vt(#u5),Vs, Vd D[i] = S[i] << T[i], i=0:3
D[i] = S[i] << #IMM5, i=0:3 Сдвиг влево, i16 VLSRH Vt(#u5),Vs, Vd D[i] = S[i] >>> T[i], i=0:3
D[i] = S[i] >>> #IMM5, i=0:3 Логический сдвиг вправо, i16 VASRH.RND Vt(#u5),Vs, Vd If(T[i] == 0) D[i]= S[i]
Else D[i] = RND(S[i] >> T[i]), i=0:3 Арифметический сдвиг вправо с округлением, i16 VLSRH.RND Vt(#u5),Vs, Vd If(T[i] == 0) D[i]= S[i]
Else D[i] = RND(S[i] >>> T[i]), i=0:3 Логический сдвиг вправо с округлением, i16 VASRB Vt(#u5),Vs, Vd D[i] = S[i] >> T[i], i=0:7
D[i] = S[i] >> #IMM5, i=0:7 Арифметический сдвиг вправо, i8 VLSLB Vt(#u5),Vs, Vd D[i] = S[i] << T[i], i=0:7
D[i] = S[i] << #IMM5, i=0:7 Сдвиг влево, i8 VLSRB Vt(#u5),Vs, Vd D[i] = S[i] >>> T[i], i=0:7
D[i] = S[i] >>> #IMM5, i=0:7 Логический сдвиг вправо, i8 VASRB.RND Vt(#u5),Vs, Vd If(T[i] == 0) D[i]= S[i]
Else D[i] = RND(D[i] >> T[i]), i=0:7 Арифметический сдвиг вправо с округлением, i8 VLSRB.RND Vt(#u5),Vs, Vd If(T[i] == 0) D[i]= S[i]
Else D[i] = RND(D[i] >>> T[i]), i=0:7 Логический сдвиг вправо с округлением, i8

Табл. 14.

Мнемоника команды Формула Описание Векторные операции расширения целочисленных типов VCVBHEU Vs, Vd
VCVBHOU Vs, Vd
VCVBHE Vs, Vd
VCVBHO Vs, Vd Vs = {S7…S0}, i8
Vd = {D3…D0}, i16
D[i]=zext_8→16(S[2i+0]), i=0…3
D[i]=zext_8→16(S[2i+1]), i=0…3
D[i] = sext_8→16(S[2i+0]), i=0…3
D[i] = sext_8→16(S[2i+1]), i=0…3 Расширение знаком i8→i16 или расширение нулем u8→u16. В качестве источника используется четные или нечетные элементы первого операнда. VCVHLEU Vs, Vd
VCVHLOU Vs, Vd
VCVHLE Vs, Vd
VCVHLO Vs, Vd Vs = {S3…S0}, i16
Vd = {D1…D0}, i32
D[i]=zext_16→32(S[2i+0]), i=0…1
D[i]=zext_16→32(S[2i+1]), i=0…1
D[i]=sext_16→32(S[2i+0]), i=0…1
D[i]=sext_16→32(S[2i+1]), i=0…1 Расширение знаком i16→i32 или расширение нулем u16→u32. В качестве источника используется четные или нечетные элементы первого операнда. VCVLDEU Vs, Vd
VCVLDOU Vs, Vd
VCVLDE Vs, Vd
VCVLDO Vs, Vd Vs = {S1…S0}, i32
Vd = {D0}, i64
D[i]=zext_32→64(S[2i+0]), i=0…1
D[i]=zext_32→64(S[2i+1]), i=0…1
D[i]=sext_32→64(S[2i+0]), i=0…1
D[i]=sext_32→64(S[2i+1]), i=0…1 Расширение знаком i32→i64 или расширение нулем u32→u64. В качестве источника используется четные или нечетные элементы первого операнда. Векторные операции усечения целочисленных типов VSATDL Vt, Vs, Vd Vt = {T0}, i64
Vs = {S0}, i64
Vd = {sat32(S0), sat32(T0)}, i32 Принудительная сатурация, i64 → i32 VSATDLU Vt, Vs, Vd Vt = {T0}, i64
Vs = {S0}, i64
Vd = {usat32(S0), usat32(T0)}, u32 Принудительная сатурация, i64 → u32 VSATLH Vt, Vs, Vd Vt = {T1, T0}, i32
Vs = {S1, S0}, i32
Vd = {sat16(S1), sat16(T1), sat16(S0), sat16(T0)}, i16 Принудительная сатурация, i32 → i16 VSATLHU Vt, Vs, Vd Vt = {T1, T0}, i32
Vs = {S1, S0}, i32
Vd = {usat16(S1), usat16(T1), usat16(S0), usat16(T0)}, u16 Принудительная сатурация, i32 → u16 VSATHB Vt, Vs, Vd Vt = {T3, T2, T1, T0}, i16
Vs = {S3, S2, S1, S0}, i16
Vd = {sat8(S3), sat8(T3), …, sat8(S0), sat8(T0)}, i8 Принудительная сатурация, i16 → i8 VSATHBU Vt, Vs, Vd Vt = {T3, T2, T1, T0}, i16
Vs = {S3, S2, S1, S0}, i16
Vd = {usat8(S3), usat8(T3), …,u sat8(S0), usat8(T0)},u8 Принудительная сатурация, i16 → u8 Векторные операции преобразования типов с плавающей запятой VFDCV Vt, VVd Vt = {T1, T0}, f32
VVd = {Vd’, Vd} = {{D1}, {D0}}, f64
Di = Ti, i = 0…1 Преобразование из float32 в float64 VDFCV Vt, Vs, Vd Vt = {T0}, f64
Vs = {S0}, f64
Vd = {D1, D0}, f32
D1 = S0, D0 = T0 Преобразование из float64 в float32 VHFCV Vt, VVd Vt = {T3, T2, T1, T0}, f16
VVd = {Vd’, Vd} = {{D3, D1}, {D2, D0}}, f32
Di = Ti, i = 0…1 Преобразование из float16 в float32 VFHCV Vt, Vs, Vd Vt = {T1, T0}, f64
Vs = {S1, S0}, f64
Vd = {D3, D2, D1, D0}, f32
D3 = S1, D2 = T1, D1 = S0, D0 = T0 Преобразование из float32 в float16 Векторные операции преобразования типов INT->FLT VCVDF Vt, Vs, Vd Vt = {T0}, i64
Vs = {S0}, i64
Vd = {D1, D0}, f32
D1 = S0, D0 = T0 Преобразование из i64 в float32 VCVDFU Vt, Vs, Vd Vt = {T0}, u64
Vs = {S0}, u64
Vd = {D1, D0}, f32
D1 = S0, D0 = T0 Преобразование из u64 в float32 VCVDD Vt, Vd Vt = {T0}, i64
Vd = {D0}, f64
D0 = T0 Преобразование из i64 в float64 VCVDDU Vt, Vd Vt = {T0}, u64
Vd = {D0}, f64
D0 = T0 Преобразование из u64 в float64 VCVIF Vt, Vd Vt = {T1, T0}, i32
Vd = {D1, D0}, f32
D1 = T1, D0 = T0 Преобразование из i32 в float32 VCVIFU Vt, Vd Vt = {T1, T0}, u32
Vd = {D1, D0}, f32
D1 = T1, D0 = T0 Преобразование из u32 в float32 VCVID Vt, VVd Vt = {T1, T0}, i32
Vd = {Vd’, Vd] = {{D1}, {D0}}, f64
D1 = T1, D0 = T0 Преобразование из int32 в float64 VCVIDU Vt, VVd Vt = {T1, T0}, u32
Vd = {Vd’, Vd] = {{D1}, {D0}}, f64
D1 = T1, D0 = T0 Преобразование из uint32 в float64 VCVHF Vt, VVd Vt = {T3, T2, T1, T0}, i16
Vd = {Vd’, Vd] = {{D3, D1}, {D2, D0}}, f64
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из i16 в float32 VCVHFU Vt, VVd Vt = {T3, T2, T1, T0}, u16
Vd = {Vd’, Vd} = {{D3, D1}, {D2, D0}}, f64
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из u16 в float32 VCVIH Vt, Vs, Vd Vt = {T1, T0}, i32
Vs = {S1, S0}, i32
Vd = {D3, D2, D1, D0}, f16
D3 = S1, D2 = T1, D1 = S0, D0 = T0 Преобразование из i32 в float16 VCVIHU Vt, Vs, Vd Vt = {T1, T0}, u32
Vs = {S1, S0}, u32
Vd = {D3, D2, D1, D0}, f16
D3 = S1, D2 = T1, D1 = S0, D0 = T0 Преобразование из u32 в float16 VCVLINHF Vt, Vd Vt = {T3, T2, T1, T0}, i16
Vd = {Vd’, Vd] = {{D3, D2}, {D1, D0}}, f64
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из i16 в float32 VCVLINHFU Vt, VVd Vt = {T3, T2, T1, T0}, u16
Vd = {Vd’, Vd} = {{D3, D2}, {D1, D0}}, f64
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из u16 в float32 VCVHH Vt, Vd Vt = {T3, T2, T1, T0}, i16
Vd = {D3, D2, D1, D0}, f16
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из i16 в float16 VCVHHU Vt, Vd Vt = {T3, T2, T1, T0}, u16
Vd = {D3, D2, D1, D0}, f16
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из u16 в float16 Векторные операции преобразования типов FLT ->INT VHCVH Vt, Vd
VHCVH.floor Vt, Vd
VHCVH.round Vt, Vd
VHCVH.ceil Vt, Vd
VHCVH.trunc Vt, Vd Vt = {T3, T2, T1, T0}, f16
Vd = {D3, D2, D1, D0}, i16
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из float16 в i16
Опциональное округление, принудительная сатурация VHCVHU Vt, Vd
VHCVHU.floor Vt, Vd
VHCVHU.round Vt, Vd
VHCVHU.ceil Vt, Vd
VHCVHU.trunc Vt, Vd Vt = {T3, T2, T1, T0}, f16
Vd = {D3, D2, D1, D0}, u16
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из float16 в u16
Опциональное округление, принудительная сатурация VHCVI Vt, VVd Vt = {T3, T2, T1, T0}, f16
VVd = {Vd’, Vd} = {{D3, D1}, {D2, D0}}, i32
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из float16 в i32, принудительная сатурация VHCVIU Vt, VVd Vt = {T3, T2, T1, T0}, f16
VVd = {Vd’, Vd} = {{D3, D1}, {D2, D0}}, u32
D3 = T3, D2 = T2, D1 = T1, D0 = T0 Преобразование из float16 в u32, принудительная сатурация VFCVD Vt, VVd Vt = {T1, T0}, f32
VVd = {Vd’, Vd} = {{D1}, {D0}}, i64
D1 = T1, D0 = T0 Преобразование из float32 в i64, принудительная сатурация VFCVDU Vt, VVd Vt = {T1, T0}, f32
VVd = {Vd’, Vd} = {{D1}, {D0}}, u64
D1 = T1, D0 = T0 Преобразование из float32 в u64, принудительная сатурация VFCVI Vt, Vd
VFCVI.floor Vt, Vd
VFCVI.round Vt, Vd
VFCVI.ceil Vt, Vd
VFCVI.trunc Vt, Vd Vt = {T1, T0}, f32
VVd = {D1, D0}, i32
D1 = T1, D0 = T0 Преобразование из float32 в i32
Опциональное округление, принудительная сатурация VFCVIU Vt, Vd
VFCVIU.floor Vt, Vd
VFCVIU.round Vt, Vd
VFCVIU.ceil Vt, Vd
VFCVIU.trunc Vt, Vd Vt = {T1, T0}, f32
VVd = {D1, D0}, u32
D1 = T1, D0 = T0 Преобразование из float32 в u32
Опциональное округление, принудительная сатурация VDCVD Vt, Vd
VDCVD.floor Vt, Vd
VDCVD.round Vt, Vd
VDCVD.ceil Vt, Vd
VDCVD.trunc Vt, Vd Vt = {T0}, f64
VVd = {D0}, i64
D0 = T0 Преобразование из float64 в i64
Опциональное округление, принудительная сатурация VDCVDU Vt, Vd
VDCVDU.floor Vt, Vd
VDCVDU.round Vt, Vd
VDCVDU.ceil Vt, Vd
VDCVDU.trunc Vt, Vd Vt = {T0}, f64
VVd = {D0}, u64
D0 = T0 Преобразование из float64 в u64
Опциональное округление, принудительная сатурация VDCVI Vt, Vs, Vd Vt = {T0}, f64
Vs = {S0}, f64
VVd = {D1, D0}, i32
D1 = S0, D0 = T0 Преобразование из float64 в i32, принудительная сатурация VDCVIU Vt, Vs, Vd Vt = {T0}, f64
Vs = {S0}, f64
VVd = {D1, D0}, u32
D1 = S0, D0 = T0 Преобразование из float64 в u32, принудительная сатурация VFCVH Vt, Vs, Vd
VFCVH.round Vt,Vs, Vd
VFCVH.trunc Vt, Vs, Vd
VFCVH.ceil Vt, Vs, Vd
VFCVH.floor Vt, Vs, Vd Vt = {T1, T0}, f32
Vs = {S1, S0}, f32
Vd = {D3, D2, D1, D0}, i16
D3 = S1, D2 = T1, D1 = S0, D0 = T0 Преобразование из float32 в i16
Опциональное округление, принудительная сатурация

Табл. 15.

Мнемоника команды Описание VREDD Vt, Vd Скользящая межсекционная целочисленная сумма. При условном исполнении записываются только элементы регистра назначения, выделенные предикатом, суммирование при этом идет последовательно по всем элементам.
Vt = {T[i].D}, Vd = {D[i].D}
D[i].D = sum(T[0].D, …, T[i].D), i=0…7 VREDRD Vt, Rd.D Операция межсекционной редукции по целочисленному сложению с помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
Rd.D = SUM(T[i]) VANDREDD Vt, Vd.D
VANDREDRD Vt, Rd.D Операция межсекционной редукции по логическому «И» с размножением результата по векторному регистру или помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
R = AND(T[i])
Векторный вариант:
Vd = {D[i]}, D[i].D = R, i64, i=0…7
Скалярный вариант:
Rd.D = R VORREDD Vt, Vd.D
VORREDRD Vt, Rd.D Операция межсекционной редукции по логическому «ИЛИ» с размножением результата по векторному регистру или помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
R = OR(T[i])
Векторный вариант:
Vd = {D[i]}, D[i].D = R, i64, i=0…7
Скалярный вариант:
Rd.D = R VEORREDD Vt, Vd.D
VEORREDRD Vt, Rd.D Операция межсекционной редукции по логическому исключающему «ИЛИ» с размножением результата по векторному регистру или помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
R = EOR(T[i])
Векторный вариант:
Vd = {D[i]}, D[i].D = R, i64, i=0…7
Скалярный вариант:
Rd.D = R VADDREDD Vt, Vd.D
VADDREDRD Vt, Rd.D Операция межсекционной редукции по целочисленному сложению с размножением результата по векторному регистру или помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
R = SUM(T[i])
Векторный вариант:
Vd = {D[i]}, D[i].D = R, i64, i=0…7
Скалярный вариант:
Rd.D = R VMAXREDD Vt, Vd.D
VMAXREDRD Vt, Rd.D Операция межсекционной редукции по целочисленному знаковому максимуму с размножением результата по векторному регистру или помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
R = MAX(T[i])
Векторный вариант:
Vd = {D[i]}, D[i].D = R, i64, i=0…7
Скалярный вариант:
Rd.D = R VMINREDD Vt, Vd.D
VMINREDRD Vt, Rd.D Операция межсекционной редукции по целочисленному знаковому минимуму с размножением результата по векторному регистру или помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
R = MIN(T[i])
Векторный вариант:
Vd = {D[i]}, D[i].D = R, i64, i=0…7
Скалярный вариант:
Rd.D = R VMAXREDDU Vt, Vd.D
VMAXREDRDU Vt, Rd.D Операция межсекционной редукции по целочисленному беззнаковому максимуму с размножением результата по векторному регистру или помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
R = MAX(T[i])
Векторный вариант:
Vd = {D[i]}, D[i].D = R, i64, i=0…7
Скалярный вариант:
Rd.D = R VMINREDDU Vt, Vd.D
VMINREDRDU Vt, Rd.D Операция межсекционной редукции по целочисленному беззнаковому минимуму с размножением результата по векторному регистру или помещением результата в скалярный регистр. При условном исполнении складываться должны только выделенные предикатом элементы, остальные должны быть проигнорированы. При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].D}, i=0…7
R = MINU(T[i])
Векторный вариант:
Vd = {D[i]}, D[i].D = R, i64, i=0…7
Скалярный вариант:
Rd.D = R VFADDRED Vt, Vd.L
VFADDREDR Vt, Rd.L Операция межсекционной редукции по сложению плавающей запятой с размножением результата по векторному регистру или помещением результата в скалярный регистр. Из каждой векторной секции используется только младший элемент.
При условном исполнении на вход подаются только выделенные предикатом младшие элементы каждой векторной секции, записываются все подсвеченые выходные элемнеты (не только младшие). При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].L}, i=0…15
R = FSUM(T[j*2]), j=0…7
Векторный вариант:
Vd = {D[i]}, D[i].L = R, f32, i=0…15
Скалярный вариант:
Rd.L = R VFMAXRED Vt, Vd.L
VFMAXREDR Vt, Rd.L Операция межсекционной редукции по максимуму плавающей запятой с размножением результата по векторному регистру или помещением результата в скалярный регистр. Из каждой векторной секции используется только младший элемент.
При условном исполнении на вход подаются только выделенные предикатом младшие элементы каждой векторной секции, записываются все подсвеченые выходные элемнеты (не только младшие). При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].L}, i=0…15
R = FMAX(T[j*2]), j=0…7
Векторный вариант:
Vd = {D[i]}, D[i].L = R, f32, i=0…15
Скалярный вариант:
Rd.L = R VFMINRED Vt, Vd.L
VFMINREDR Vt, Rd.L Операция межсекционной редукции по минимуму плавающей запятой с размножением результата по векторному регистру или помещением результата в скалярный регистр. Из каждой векторной секции используется только младший элемент.
При условном исполнении на вход подаются только выделенные предикатом младшие элементы каждой векторной секции, записываются все подсвеченые выходные элемнеты (не только младшие). При нулевом условии скалярная команда исполняется, в результат записывается ноль.
Vt = {T[i].L}, i=0…15
R = FMIN(T[j*2]), j=0…7
Векторный вариант:
Vd = {D[i]}, D[i].L = R, f32, i=0…15
Скалярный вариант:
Rd.L = R

Табл. 16.

Мнемоника команды Описание VSHUFBH Vt, Vs, Vd Vt: = {T63,…, T2, T1, T0}, i8
Vs = {S63,…, S2, S1, S0}, i8
Vdi: = {R31,…, R2, R1, R0}, u16
Vdo: = {D31,…, D2, D1, D0}, i16
VV = {S63, …, S0, T63, …, T0}
Di = sext_8→16(VV[R[i] & 0x7F]), i=0,1,…,31
Операция универсальной межсекционной выборки с расширением типа данных VSHUFBL Vt, Vs, Vd Vt: = {T63,…, T2, T1, T0}, i8
Vs = {S63,…, S2, S1, S0}, i8
Vdi: = {R15,…, R2, R1, R0}, u32
Vdo: = {D15,…, D2, D1, D0}, i32
VV = {S63, …, S0, T63, …, T0}
Di = sext_8→32(VV[R[i] & 0x7F]), i=0,1,…,31
Операция универсальной межсекционной выборки с расширением типа данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFHL Vt, Vs, Vd Vt = {T31,…, T2, T1, T0}, i16
Vs = {S31,…, S2, S1, S0}, i16
Vdi: = {R15,…, R2, R1, R0}, u32
Vdo: = {D15,…, D2, D1, D0}, i32
VV = {S31, …, S0, T31, …, T0}
Di = sext_16→32(VV[R[i] & 0x3F]), i=0,1,…,15
Операция универсальной межсекционной выборки с расширением типа данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFBHU Vt, Vs, Vd Vt: = {T63,…, T2, T1, T0}, u8
Vs = {S63,…, S2, S1, S0}, u8
Vdi: = {R31,…, R2, R1, R0}, u16
Vdo: = {D31,…, D2, D1, D0}, u16
VV = {S63, …, S0, T63, …, T0}
Di = zext_8→16(VV[R[i] & 0x7F]), i=0,1,…,31
Операция универсальной межсекционной выборки с расширением типа данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFBLU Vt, Vs, Vd Vt: = {T63,…, T2, T1, T0}, u8
Vs = {S63,…, S2, S1, S0}, u8
Vdi: = {R15,…, R2, R1, R0}, u32
Vdo: = {D15,…, D2, D1, D0}, u32
VV = {S63, …, S0, T63, …, T0}
Di = zext_8→32(VV[R[i] & 0x7F]), i=0,1,…,31
Операция универсальной межсекционной выборки с расширением типа данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFHLU Vt, Vs, Vd Vt = {T31,…, T2, T1, T0}, u16
Vs = {S31,…, S2, S1, S0}, u16
Vdi: = {R15,…, R2, R1, R0}, u32
Vdo: = {D15,…, D2, D1, D0}, u32
VV = {S31, …, S0, T31, …, T0}
Di = zext_16→32(VV[R[i] & 0x3F]), i=0,1,…,15
Операция универсальной межсекционной выборки с расширением типа данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFHB Vt, Vs, Vd Vt: = {T31…, T2, T1, T0}, i16
Vs = {S31…, S2, S1, S0}, i16
Vdi: = {R63…, R2, R1, R0}, u8
Vdo: = {D63…, D2, D1, D0}, i8
VV = {S31, …, S0, T31, …, T0}
Di = sat_i16→i8 (VV[R[i] & 0x3F]), i=0,1,…,63
Операция универсальной межсекционной выборки с принудительной сатурацией signed → signed в меньший тип данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFLB Vt, Vs, Vd Vt = {T15…, T2, T1, T0}, i31
Vs = {S15…, S2, S1, S0}, i31
Vdi: = {R63…, R2, R1, R0}, u8
Vdo: = {D63…, D2, D1, D0}, i8
VV = {S15, …, S0, T15, …, T0}
Di = sat_i32→u8 (VV[R[i] & 0x1F]), i=0,1,…,63
Операция универсальной межсекционной выборки с принудительной сатурацией signed → signed в меньший тип данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFLH Vt, Vs, Vd Vt: = {T15…, T2, T1, T0}, i32
Vs = {S15…, S2, S1, S0}, i32
Vdi: = {R31…, R2, R1, R0}, u16
Vdo: = {D31…, D2, D1, D0}, i16
VV = {S15, …, S0, T15, …, T0}
Di = sat_i32→i16 (VV[R[i] & 0x1F]), i=0,1,…,31
Операция универсальной межсекционной выборки с принудительной сатурацией signed → signed в меньший тип данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFHBU Vt, Vs, Vd Vt: = {T31…, T2, T1, T0}, u16
Vs = {S31…, S2, S1, S0}, u16
Vdi: = {R63…, R2, R1, R0}, u8
Vdo: = {D63…, D2, D1, D0}, u8
VV = {S31, …, S0, T31, …, T0}
Di = sat_i16→u8 (VV[R[i] & 0x3F]), i=0,1,…,63
Операция универсальной межсекционной выборки с принудительной сатурацией signed → unsigned в меньший тип данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFLBU Vt, Vs, Vd Vt = {T15…, T2, T1, T0}, u31
Vs = {S15…, S2, S1, S0}, u31
Vdi: = {R63…, R2, R1, R0}, u8
Vdo: = {D63…, D2, D1, D0}, u8
VV = {S15, …, S0, T15, …, T0}
Di = sat_i32→u8 (VV[R[i] & 0x1F]), i=0,1,…,63
Операция универсальной межсекционной выборки с принудительной сатурацией signed → unsigned в меньший тип данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же. VSHUFLHU Vt, Vs, Vd Vt: = {T15…, T2, T1, T0}, u32
Vs = {S15…, S2, S1, S0}, u32
Vdi: = {R31…, R2, R1, R0}, u16
Vdo: = {D31…, D2, D1, D0}, u16
VV = {S15, …, S0, T15, …, T0}
Di = sat_i32→u16 (VV[R[i] & 0x1F]), i=0,1,…,31
Операция универсальной межсекционной выборки с принудительной сатурацией signed → unsigned в меньший тип данных.
В качестве индексов берутся прежние значения регистра Vd, результат записывается в него же.

Табл. 17.

Мнемоника команды Описание VLUT0 Vt, Vs, Vr, Vd
VLUT1 Vt, Vs, Vr, Vd VLUTa T, S, R, D
Vt = {T63…, T2, T1, T0}, u8
Vs = {S63…, S2, S1, S0}, u8
Vr = {R63…, R2, R1, R0}, u8
Vd = {D63…, D2, D1, D0}, u8
VV = {R63, …, R0, S63, …, S0}, u8
if (T[7] == a) then Di = VV[T[i] & 0x7F], i=0,1,…,63
a - целочисленный 1-битный параметр, который может принимать значения: 0, 1;
T, S, R - входные 512-разрядные вектора;
D - выходной 512-разрядный вектор.
Входные и выходные вектора разделены на 64 байта. Вектор VV: = {Vr, Vs} содержит таблицу преобразования, точнее - половину этой таблицы, полная таблица преобразования содержится в двух векторах VV, соответствующих двум значениям параметра a. Вектор S T содержит преобразуемые данные.
Выбор данных из таблицы для каждого байта ti вектора T (i = 0,1,…,63) определяется его младшими семью битами согласно формуле: di = SVV[ti[6:0]].
Особенностью команды VLUT является то, что кроме собственно выходного вектора она формирует также побайтовую маску записи для этого вектора согласно формуле: mi = (ti[7]== a). Таким образом, в выходной регистр D записываются данные только из нужной таблицы.

Табл. 18.

Мнемоника команды Описание VHIST0 Vs, Vd
VHIST1 Vs, Vd
VHIST2 Vs, Vd
VHIST3 Vs, Vd VHISTa S, D
a - целочисленный 2-битный параметр, который может принимать значения: 0, 1, 2, 3;
S - входной 512-разрядный вектор;
D - выходной 512-разрядный вектор.
Входной и выходной вектор разделены на 64 байта. Для каждого i (i = 0,1,…,63) вычисляется количество байт, значение которых равно (64*a + i), и это количество записывается в i-й байт выходного вектора.
Для вычисления 256-уровневой гистограммы необходимо выполнить эту команду для всех четырех значений параметра a, затем преобразовать полученные 64-компонентные байтовые вектора с расширением до 16-разрядных или 32-разрядных беззнаковых целых, в зависимости от того, в каком формате будет производиться накопление бинов гистограммы, и произвести накопление.
Таким образом, для вычисления гистограмм потребуются также векторные команды расширения типа и целочисленного сложения. При компактном коде возможно вычисление 256-уровневой гистограммы для 64 пикселей примерно за 6 тактов.
Четыре значения параметра a могут быть реализованы в виде четырех различных команд. VHISTC0 Vs, VAd
VHISTC1 Vs, VAd
VHISTC2 Vs, VAd
VHISTC3 Vs, VAd Команда аналогичная VHIST*, только накопление результата идет в аккумуляторах. Используются по восемь 32-разрядных беззнаковых аккумуляторов в каждой векторной секции. Для подсчета количества всех входных значений требуется четыре аккумулятора.

Табл. 19.

Мнемоника команды Описание VPUSHD Vt, Vs, Vd Vt: = {T7…, T2, T1, T0}, u64
Vs = {S7…, S2, S1, S0}, u64
Vd = { S6, S5, S4, S3, S2, S1, S0, T7}
Операция кольцевого межсекционного сдвига на 8 байт. Извлекаемый элемент S7 теряется.
При условном исполнении команда исполняется в обычном режиме, но записываются только активные элементы согласно условию-предикату. VPUSHRD Rt.D, Vs, Vd Vs = {S7…, S2, S1, S0}, u64
Vd = { S6, S5, S4, S3, S2, S1, S0, Rt}
Rt.D = S7.
Операция кольцевого межсекционного сдвига на 8 байт с пересылкой скалярного регистра в нулевую секцию. Извлекаемый элемент возвращается в Rt.D.

Табл. 20.

Настоящее техническое решение относится к области микропроцессорной вычислительной техники. Технический результат заключается в повышении скорости работы и объема обрабатываемых данных за счёт параллельных скалярных и векторных вычислений. Технический результат достигается за счёт того, что скалярно-векторный процессор содержит блок редукции, соединенный со скалярным и векторным каналами процессора и реализующий функции их взаимодействия в операциях, где скалярный канал формирует и/или потребляет скаляр, требуемый и/или формируемый векторным каналом процессора; блок редукции выполняет, кроме того, операции над вектором в целом - операции перестановок (shuffle), LUT-преобразования, вычисления гистограмм; скалярный и векторный каналы процессора объединены дополнительно кольцеобразной шиной, позволяющей производить по ней обмен данными одновременно с выполнением вычислительных операций в скалярном и векторном каналах процессора и в блоке редукции. 43 з.п. ф-лы, 7 ил., 20 табл.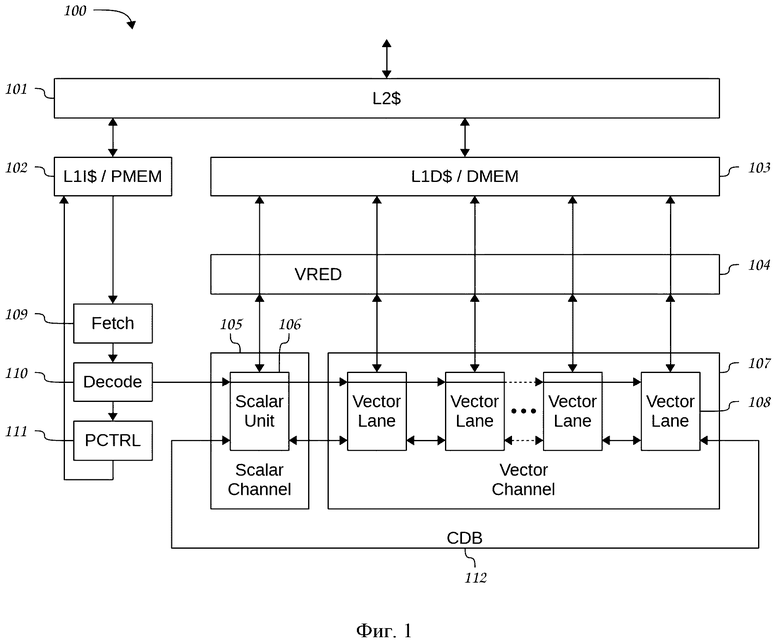

1. Скалярно-векторный процессор 100, содержащий соединенные кольцевой шиной CDB 112 скалярный и векторный каналы 105 и 107 обработки данных, которые соединены с блоком редукции VRED 104, а также с памятью данных первого уровня DMEM/L1D$ 103, которая соединена с кэш-памятью второго уровня L2$ 101, которая соединена с внешним интерфейсом процессора, который имеет доступ к внешней памяти вычислительной системы, а также соединена с памятью программ первого уровня PMEM/L1I$ 102, выход которой соединен с входом блока выборки команд FETCH 109, выход которого соединен с входом блока декодирования команд DECODE 110, первый выход которого соединен с входами скалярного и векторного каналов, а второй выход соединен с блоком программного управления PCTRL 111, выход которого соединен с входом памяти программ первого уровня PMEM/L1I$ 102, причем

- память программ первого уровня PMEM/L1I$ 102 и память данных первого уровня DMEM/L1D$ 103 выполнены с возможностью формирования обращений и передачи их в

- кэш-память второго уровня L2$ 101, которая выполнена с возможностью обслуживания обращений из памяти программ первого уровня РМЕМ/L1I$ 102 и памяти данных первого уровня DMEM/L1D$ 103, а также загрузки данных через внешний интерфейс из внешней памяти вычислительной системы и передачи данных в память данных первого уровня DMEM/L1D$ 103 и память программ первого уровня PMEM/L1I$ 102;

- блок выборки команд FETCH 109 выполнен с возможностью выборки команд из памяти программ PMEM/L1I$ 102 и передачи их в

- блок декодирования команд DECODE 110, выполненный с возможностью декодирования команд и формирования команд программного управления для исполнительных устройств процессора и передачи их в

- блок PCTRL, который выполнен с возможностью выполнения команд программного управления.

2. Процессор по п. 1, отличающийся тем, что память данных первого уровня DMEM/L1D$ 103 выполнена в виде кэш-памяти первого уровня L1D$ или в виде тесно связанной ТСМ (Tightly-Coupled Memory) статической памяти DMEM.

3. Процессор по п. 1, отличающийся тем, что память программ первого уровня РМЕМ/L1I$ 102 выполнена в виде кэш-памяти первого уровня L1I$ или в виде тесно связанной ТСМ (Tightly-Coupled Memory) статической памяти РМЕМ.

4. Процессор по п. 1, отличающийся тем, что на уровне вычислительного ядра имеет гарвардскую архитектуру с возможностью одновременного доступа к памяти программ первого уровня РМЕМ/L1$ 102 и памяти данных первого уровня DMEM/L1D$ 103 по отдельным шинам.

5. Процессор по п. 1, отличающийся тем, что кэш-память второго уровня L2$ 101 имеет фон-неймановскую архитектуру.

6. Процессор по п. 1, отличающийся тем, что команды программного управления выбраны из набора команд, содержащего команды программных переходов и команды программных циклов.

7. Процессор по п. 1, отличающийся тем, что команды объединены в инструкции, которые организованы в виде VLIW-пакета 201 (VLIW - Very Long Instruction Word).

8. Процессор по п. 7, отличающийся тем, что VLIW-пакет 201 содержит до восьми команд, из которых до четырех команд предназначены для исполнительных устройств скалярного канала обработки данных и до четырех команд предназначены для исполнительных устройств векторного канала обработки данных.

9. Процессор по п. 7, отличающийся тем, что VLIW-пакет 201 содержит до двух команд скалярных обменов данными и до двух векторных команд обмена данными с памятью данных DMEM/L1D$ 103.

10. Процессор по п. 1, отличающийся тем, что имеет систему команд, состоящую из команд программного управления, команд исполнительных устройств скалярного канала обработки данных и векторного канала обработки данных, а также команд блока редукции VRED 104.

11. Процессор по п. 1, отличающийся тем, что скалярный канал 105 содержит одну скалярную вычислительную секцию 106.

12. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит скалярный регистровый файл RF 301, который является многопортовым и в котором хранятся обрабатываемые скалярные данные.

13. Процессор по п. 12, отличающийся тем, что скалярный регистровый файл RF 301 содержит порты, связанные со скалярным каналом 105 обработки данных и выполненные с возможностью обмена данными с памятью данных DMEM/L1D$ 103.

14. Процессор по п. 12, отличающийся тем, что скалярный регистровый файл RF 301 содержит порты, связанные с исполнительными устройствами скалярной вычислительной секции 106 скалярного канала 105 обработки данных, выполненные с возможностью передачи исходных данных для выполнения вычислительных операций и записи результатов операций обратно в скалярный регистровый файл RF 301.

15. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит блоки обработки данных SLSE0 310, SLSE1 311, которые выполнены с возможностью обеспечения обмена данными между памятью данных DMEM/L1D$ 103 и скалярным регистровым файлом RF 301, в том числе выполнения команд пересылок данных между памятью данных DMEM/L1D$ 103 и скалярным регистровым файлом RF301.

16. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит блоки обработки данных ALU0 302, ALU1 303, ALU2 304, ALU3 305, выполняющие арифметические и логические операции над числами с фиксированной запятой.

17. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит блоки обработки данных FALU0 306, FALU1 307, выполняющие арифметические и логические операции над числами с плавающей запятой.

18. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит блоки обработки данных SMU0 308, SMU1 309, выполняющие операции умножения над числами с фиксированной и плавающей запятой.

19. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит блок обработки данных SH 312, выполняющий операции логического и арифметического сдвига.

20. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит блок обработки данных CONV 315, выполняющий операции преобразования типов данных.

21. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит блок обработки данных DIV 313, выполняющий операции деления.

22. Процессор по п. 1, отличающийся тем, что скалярная вычислительная секция 106 содержит блок обработки данных MF 314, выполняющий операции вычисления трансцендентных математических функций.

23. Процессор по п. 1, отличающийся тем, что векторный канал 107 состоит из нескольких векторных вычислительных секций 108, количество которых соответствует разрядности обрабатываемого вектора.

24. Процессор по п. 23, отличающийся тем, что векторная вычислительная секция 108 содержит векторный регистровый файл VRF 401, который является многопортовым и мультиформатным и в котором хранятся обрабатываемые векторные данные.

25. Процессор по п. 24, отличающийся тем, что векторный регистровый файл VRF 401 является мультиформатным, так что каждый 64-разрядный регистр 500 векторного регистрового файла VRF 401 может хранить либо одно 64-разрядное значение 501, либо два 32-разрядных значения 502, либо четыре 16-разрядных значения 503, либо восемь 8-разрядных значений 504.

26. Процессор по п. 24, отличающийся тем, что векторный регистровый файл VRF 401 содержит порты, связанные с внешним интерфейсом векторного канала 107 и выполненные с возможностью обмена данными с памятью данных DMEM/L1D$ 103.

27. Процессор по п. 24, отличающийся тем, что векторный регистровый файл VRF 401 содержит порты, связанные с исполнительными устройствами векторной вычислительной секции 108, выполненные с возможностью передачи исходных данных для выполнения вычислительных операций и записи результатов обратно.

28. Процессор по п. 24, отличающийся тем, что векторный регистровый файл VRF 401 выполнен с возможностью работы с различными форматами данных.

29. Процессор по п. 23, отличающийся тем, что векторная вычислительная секция 108 содержит блоки VLSE0 412, VLSE1 413, которые выполнены с возможностью обеспечения обмена данными между памятью данных DMEM/L1D$ 103 и векторным регистровым файлом VRF 401, в том числе и выполнения команд пересылок данных между памятью данных DMEM/L1D$ 103 и векторным регистровым файлом VRF 401.

30. Процессор по п. 23, отличающийся тем, что векторная вычислительная секция 108 содержит блоки VALU0 403, VALU1 404, VALU2 405, VALU3 406, выполненные с возможностью осуществления арифметических и логических операций над числами с фиксированной запятой.

31. Процессор по п. 23, отличающийся тем, что векторная вычислительная секция 108 содержит блоки VFALU0 407, VFALU1 408, выполненные с возможностью осуществления арифметических и логических операций над числами с плавающей запятой.

32. Процессор по п. 23, отличающийся тем, что векторная вычислительная секция 108 содержит блоки VMU0 409, VMU1 410, выполненные с возможностью осуществления операций умножения и умножения с накоплением над числами с фиксированной и плавающей запятой.

33. Процессор по п. 23, отличающийся тем, что векторная вычислительная секция 108 содержит векторный регистровый файл регистров-аккумуляторов VAC 402, выполненный с возможностью хранения данных, получаемых и используемых в результате выполнения операций умножения с накоплением, выполняемых блоками векторных умножителей VMU0 409, VMU1 410.

34. Процессор по п. 23, отличающийся тем, что векторная вычислительная секция 108 содержит блок VSH 411, выполненный с возможностью осуществления операций логического и арифметического сдвига над векторными операндами.

35. Процессор по п. 23, отличающийся тем, что векторная вычислительная секция 108 содержит блок VCONV 414, выполненный с возможностью осуществления операции преобразования типов данных над векторными операндами.

36. Процессор по п. 1, отличающийся тем, что блок редукции VRED 104 выполнен с возможностью вычисления функций редукции.

37. Процессор по п. 1, отличающийся тем, что блок редукции VRED 104 выполнен с возможностью вычисления функций редукции и при этом реализации функций взаимодействия скалярной и векторной частей процессора в разнообразных операциях, в которых скалярный канал 105 формирует и/или потребляет скаляр, требуемый и/или формируемый векторным каналом 107.

38. Процессор по п. 1, отличающийся тем, что блок редукции VRED 104 содержит блок RALU 601, выполненный с возможностью осуществления арифметико-логических межсекционных операций редукции.

39. Процессор по п. 1, отличающийся тем, что блок редукции VRED 104 содержит блок SHUFFLE 602, выполненный с возможностью осуществления операций межсекционных перестановок.

40. Процессор по п. 1, отличающийся тем, что блок редукции VRED 104 содержит блок LUT 603, выполненный с возможностью осуществления операций межсекционных табличных преобразований.

41. Процессор по п. 1, отличающийся тем, что блок редукции VRED 104 содержит блок HIST 604, выполненный с возможностью осуществления операций вычисления гистограмм.

42. Процессор по п. 1, отличающийся тем, что кольцевая шина CDB (Circular Data Bus) 112 выполнена с возможностью осуществления обмена данными одновременно с осуществлением вычислительных операций в скалярном и векторном каналах 105, 107 и в блоке редукции VRED 104.

43. Процессор по п. 1, отличающийся тем, что кольцевая шина CDB 112 выполнена с возможностью осуществления команд циклического сдвига, в результате выполнения которых регистр Ri скалярного регистрового файла RF 301 смещается в регистр Vj векторного регистрового файла VRF 401 нулевой векторной вычислительной секции 108: Vj.0=Ri; регистр Vj векторного регистрового файла VRF 401 старшей (N-1) векторной вычислительной секции 108 смещается в регистр Ri скалярного регистрового файла RF 301: Ri=Vj.N-1; регистры Vj векторных регистровых файлов VRF 401 остальных векторных вычислительных секций 108 смещаются на одну секцию в сторону старших секций: Vj.k=Vj.k-1, k=1,2,…,N-1.

44. Процессор по п. 1, отличающийся тем, что кольцевая шина CDB 112 выполнена с возможностью последовательного перемещения данных из векторного канала 107 в скалярный канал 105 с целью выполнения операций, имеющихся только в скалярном канале 105, с последующим возвращением преобразованных данных в векторный канал 107.

название	год	авторы	номер документа
УСТРОЙСТВО ДЛЯ ПАРАЛЛЕЛЬНОЙ ОБРАБОТКИ ДАННЫХ	1991	Кулик Борис Александрович Кулик Лия Ефимовна Федоров Виктор Федорович	RU2028664C1
СИСТЕМА И СПОСОБЫ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ВОЗДУШНОЙ ТУРБУЛЕНТНОСТИ	2007	Тиллотсон Брайан Синглтон Марисса	RU2470331C2
РЕГУЛИРУЕМЫЙ СТАБИЛИЗАТОР ПЕРЕМЕННОГО НАПРЯЖЕНИЯ	2013	Мустафа Георгий Маркович	RU2536875C2
АДАПТИВНАЯ СИСТЕМА ТЕРМИНАЛЬНОГО УПРАВЛЕНИЯ	2012	Детистов Владимир Анатольевич Таран Владимир Николаевич Смирнов Юрий Александрович Гужев Олег Юрьевич	RU2500009C1
Способ определения результатов векторно-матричных преобразований в параллельных акустооптических процессорах	1989	Соловьев Владимир Олегович Тигин Дмитрий Васильевич	SU1735836A1
СПОСОБ ПРОГНОЗИРОВАНИЯ ПАРАМЕТРОВ ЗЕМЛЕТРЯСЕНИЯ	2003	Давыдов В.Ф. Сорокин В.Н. Корольков А.В. Бронников С.В.	RU2254599C1
УСТРОЙСТВО ЗАХВАТА ИЗОБРАЖЕНИЯ И СИСТЕМА ЗАХВАТА ИЗОБРАЖЕНИЯ	2016	Тасиро Кадзуаки Годен Тацухито	RU2668949C2
СПОСОБ ДОСТАВКИ ИЗЛУЧЕНИЯ НА ДВИЖУЩИЙСЯ ОБЪЕКТ И КОМПЛЕКС ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ	1997	Земсков Е.М. Казанский В.М. Кочкин В.А. Кутаев Ю.Ф. Манкевич С.К.	RU2124740C1
БОРТОВОЙ СПЕЦВЫЧИСЛИТЕЛЬ	2013	Ефремов Николай Владимирович Злобин Сергей Леонидович Малыков Алексей Александрович Митькин Александр Викторович Осетров Павел Алексеевич Садовникова Антонина Иннокентьевна Сиренко Владимир Григорьевич Смородин Иннокентий Валерьевич Терешкин Виктор Тихонович Федоренко Владимир Андреевич Хрусталев Алексей Николаевич	RU2522852C1
СПОСОБ НЕРАЗРУШАЮЩЕГО ОБЪЕМНОГО ИЗМЕРЕНИЯ ВЕКТОРНОЙ ФУНКЦИИ МАГНИТНОЙ ИНДУКЦИИ НЕОДНОРОДНО РАСПРЕДЕЛЕННОГО В ПРОСТРАНСТВЕ И ПЕРИОДИЧЕСКИ ИЗМЕНЯЮЩЕГОСЯ ВО ВРЕМЕНИ МАГНИТНОГО ПОЛЯ	2012	Жильников Артем Александрович Жильников Тимур Александрович Жулев Владимир Иванович	RU2490659C1

US 8698817 B2, 15.04.2014
КОНВЕЙЕРНЫЙ ПРОЦЕССОР	1992	Соколов А.А. Агапов В.М. Бяков А.Ю. Губанов А.Ю. Зак Л.А. Жуковский В.А. Ли В.Л. Отто В.А. Чайковский Л.Ф. Смирнов В.И.	RU2032215C1
US 5430884 A, 04.07.1995
Ультразвуковой активатор жидких сред	1989	Штеле Владимир Иванович	SU1666174A1
US 7334110 B1, 19.02.2008
JP 5680697 B2, 05.09.2013.

СКАЛЯРНО-ВЕКТОРНЫЙ ПРОЦЕССОР Российский патент 2022 года по МПК G06F9/30 G06F17/16

Описание патента на изобретение RU2781355C1

Похожие патенты RU2781355C1

Иллюстрации к изобретению RU 2 781 355 C1

Реферат патента 2022 года СКАЛЯРНО-ВЕКТОРНЫЙ ПРОЦЕССОР

Формула изобретения RU 2 781 355 C1

Документы, цитированные в отчете о поиске Патент 2022 года RU2781355C1

RU 2 781 355 C1