Изобретение относится к информационно-измерительной технике, в частности к магнитометрии, и может быть использовано для неразрушающей регистрации в местах недоступных для механического проникновения мгновенных объемных состояний распределения магнитного поля, неоднородного в пространстве и периодически изменяющегося во времени. Результатом регистрации являются определенные в точках пространства и моменты времени значения векторной функции индукции, реконструированные посредством применения обратного преобразования Радона к измеренным проекциям магнитного потока, полученным путем управляемого пространственного перемещения рабочего органа, интегрирующего по плоскости векторную функцию поля.
Известен способ топографии магнитного поля, реализованный в устройстве [1], который основан на измерении магнитного поля одновременно в большом количестве точек плоскости посредством матричной регулярной структуры из столбцов и строк взаимосвязанных магниточувствительных элементов, расположенных на полупроводниковой пластине, помещенной в поле. Однако известные способ и реализующее его устройство не позволяют выполнять измерения в местах недоступных для механического проникновения полупроводниковой пластины и позволяют получить только одну составляющую векторной функции магнитной индукции, одинаково направленную с нормалью к полупроводниковой пластине. Также отсутствует возможность выполнять измерения в произвольных точках, так как все точки измерения определены матричной структурой магниточувствительных элементов. Кроме того, способ имеет ограничения по количеству магниточувствительных элементов и, как следствие, по разрешающей способности.
Известен способ сканирования магнитного поля, реализованный в устройстве [2], который основан на измерении магнитного поля поочередно в точках плоскости посредством последовательно соединенной матрицы чувствительных элементов, включающей N феррозондов, с последующей обработкой измеряемых напряжений с помощью ЭВМ. Однако известные способ и реализующее его устройство не позволяют выполнять измерения в местах недоступных для механического проникновения матрицы чувствительных элементов и позволяют получить только одну составляющую векторной функции магнитной индукции. Также отсутствует возможность выполнять измерения в произвольных точках, так как все точки измерения определены матричной структурой магниточувствительных элементов. Кроме того, способ имеет ограничения по количеству магниточувствительных элементов и, как следствие, по разрешающей способности.
Известен способ измерения и топографии магнитных полей рассеяния вблизи поверхности объекта, реализованный в устройстве [3], который основан на последовательном перемещении в соответствии с заданной траекторией с помощью измерительной штанги одного трехкомпонентного датчика Холла относительно объекта измерения посредством блока механических перемещений с поворотным столиком и подвижными каретками, приводимыми в движение шаговыми двигателями, с последующей статистической обработкой результатов измерения измерительно-вычислительным блоком. Однако известные способ и реализующее его устройство не позволяют выполнять измерения в местах недоступных для механического проникновения датчика Холла.
Наиболее близким к заявляемому является способ получения распределения векторной функции магнитной индукции периодического магнитного поля [4], реализованный в устройстве [5], основанный на последовательных поступательных и угловых перемещениях магниточувствительного рабочего органа, при этом исследуемый объем представляют совокупностью параллельных сечений, распределения магнитной индукции в которых получают посредством применения процедуры реконструкции вычислительной томографии к напряжениям, индуцируемым в соответствии с законом Фарадея в контурах, перемещающихся в магнитном поле. Однако известные способ и реализующее его устройство не позволяют выполнять измерения в местах недоступных для механического проникновения магниточувствительного рабочего органа.
Техническим результатом применения заявляемого способа является расширение функциональных возможностей магнитометрии, заключающееся в измерениях распределения векторной функции магнитной индукции периодически изменяющегося во времени поля в определенных точках исследуемого пространства для произвольно выбранных моментов времени на периоде. Заявленный способ основан на последовательно-поступательных перемещениях и поворотах на углы рабочего магнитоизмерительного органа и регистрации индуцируемых в нем напряжений, посредством применения обратного преобразования Радона к измеренным проекциям магнитного потока, полученным с помощью рабочего органа в ходе его управляемого пространственного перемещения в объеме измерения способом параллельного формирования исходных проекционных данных.
Технический результат, реализуемый в способе неразрушающего объемного измерения векторной функции магнитной индукции неоднородно распределенного в пространстве и периодически изменяющегося во времени магнитного поля, достигается тем, что измерения мгновенных объемных состояний распределения неоднородного в пространстве магнитного поля осуществляют в местах, недоступных для механического проникновения, а рабочий магнитоизмерительный орган выполняют в виде ориентируемого в пространстве одного контура, привязанного к сферической системе координат, причем в ходе его управляемого пространственного перемещения осуществляют способ параллельного формирования исходных проекционных данных функции индукции, для чего рабочим органом совершают движение, предполагающее чередование дискретных параллельных перемещений в направлении оси вектора нормали органа и поворотов направления этих перемещений, задаваемых зенитным и азимутальным углами сферической системы координат, таким образом, что дискретные параллельные перемещения многократно повторяют под разными углами, причем для зенитного в интервале от 0 до ½π, а для азимутального в интервале от 0 до π, а необходимые для алгоритма реконструкции исходные проекционные данные декартовых компонент распределения векторной функции магнитной индукции в объеме измерения в декартовой системе координат получают посредством тригонометрических преобразований:
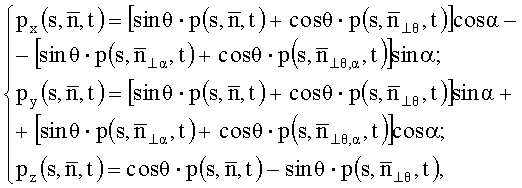
где 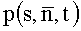
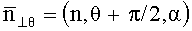
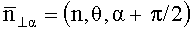
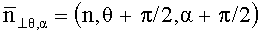
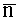
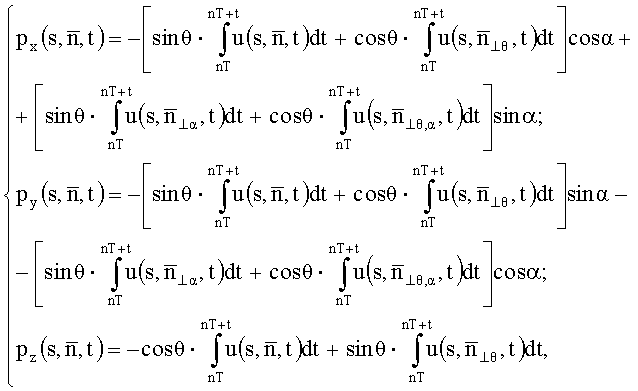
где u(t) - напряжения, индуцируемые изменением потока в контуре в момент времени t; T - период, в течение которого происходит одно полное изменение функции магнитной индукции; n=1, 2, … - номер периода, причем к исходным проекционным данным применяют обратное преобразование Радона, основанное на их свертке, осуществляющей фильтрацию с использованием свертывающей функции, являющейся обратным Фурье-преобразованием квадрата частоты пространственного спектра по формуле:
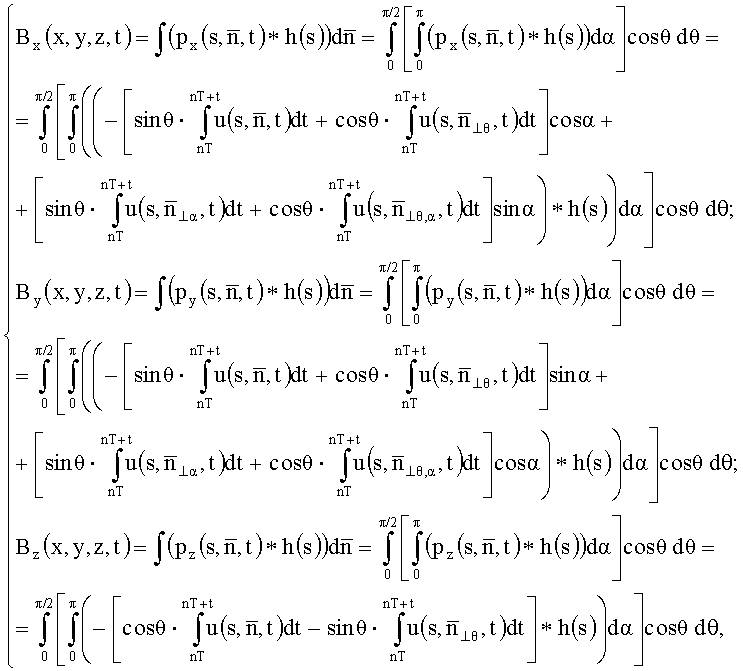
где символ «*» есть оператор свертки; h(s) - свертывающая функция; 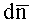
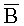
Суть способа неразрушающего объемного измерения векторной функции магнитной индукции неоднородно распределенного в пространстве и периодически изменяющегося во времени магнитного поля заключается в регистрации в местах, недоступных для механического проникновения, мгновенных объемных состояний распределения магнитного поля, благодаря чему определяются в конкретных точках пространства и моменты времени значения векторной функции индукции, получаемые реконструкцией посредством применения обратного преобразования Радона к измеренным проекциям магнитного потока, полученным с помощью магниточувствительного рабочего органа в ходе его управляемого пространственного перемещения в объеме измерения способом параллельного формирования исходных проекционных данных.
Магниточувствительный рабочий орган представляет собой плоский контур, на основе катушки индуктивности. Причем его размеры задаются таким образом, чтобы независимо от его положения в объеме измерения исходная векторная функция поля достаточно быстро убывала на границах этого контура.
Скалярное значение магнитного потока ФD исходной векторной функции магнитной индукции B(x,y,z,t) через поверхность D, образованную плоскостью контура, есть интеграл по плоскости, перпендикулярной вектору ее нормали 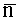
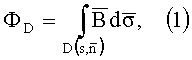
где 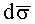
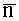
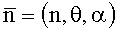
Технически регистрация магнитного потока осуществляется благодаря закону Фарадея, согласно которому напряжение u(t), наводимое в контуре, определяется выражением:
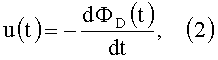
где dФD(t) - дифференциал потока векторной функции индукции; dt - дифференциал времени.
Благодаря введенному условию периодичности во времени, согласно которому поле точно повторяет свои мгновенные состояния через одинаковые промежутки времени равные периоду, продолжительность регистрации одного мгновенного объемного состояния распределения магнитного поля уже не ограничена по времени длительностью интервала дискретизации, потому что регистрировать состояние можно, осуществляя измерения в пространстве через интервалы времени, кратные периоду. И несмотря на то, что измерения значительно разнесены по времени, все они будут производиться для какого-то одного мгновенного состояния на периоде.
Интегрирование по времени t выраженного из равенства (2) дифференциала dФD(t) приводит к записи значения магнитного потока:
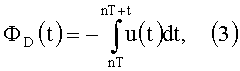
где T - период, в течение которого происходит одно полное изменение магнитной индукции; n=1, 2, … - номер периода.
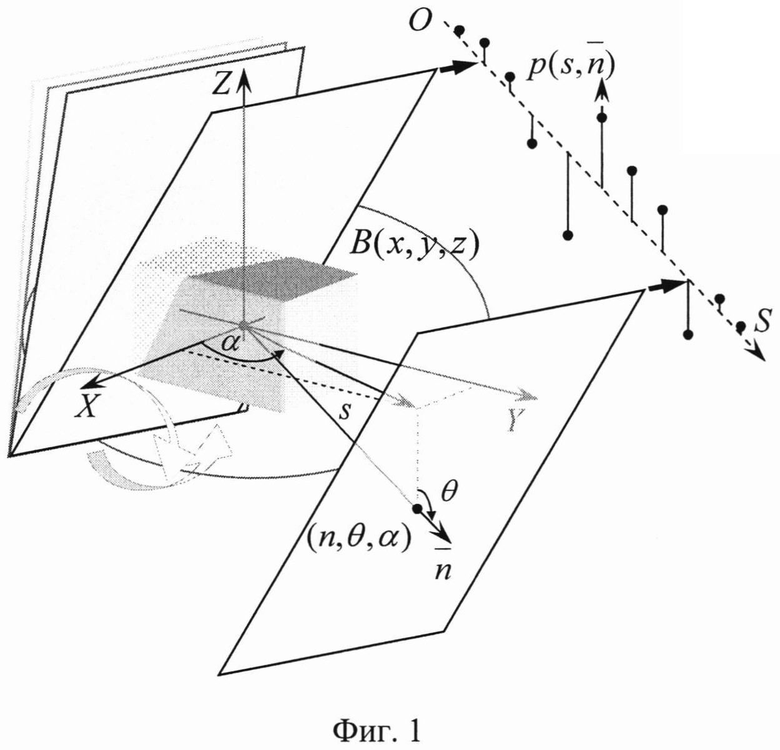
Измерение начинается с процедуры управляемого пространственного перемещения рабочего органа в объеме измерения с получением проекций, которая соответствует прямому преобразованию Радона для трехмерного пространства (фиг.1). Управляемое пространственное перемещение реализует способ параллельного формирования исходных проекционных данных, для которого рабочий орган совершает поступательно-поворотное движение, предполагающее чередование дискретных параллельных перемещений в направлении вектора нормали органа 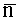
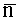
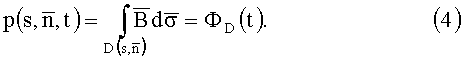
Принимая во внимание выражение (3), на основании (4) проекция значений интеграла исходной функции индукции 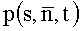
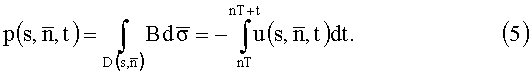
Уравнение (5) приведено для сферической системы координат, при этом в декартовой системе координат (X,Y,Z) выражение компонент данного равенства имеет вид:
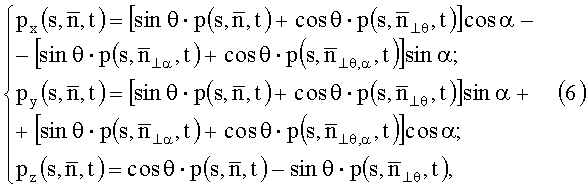
где 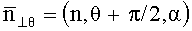
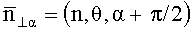
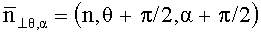
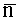
С учетом выражения (5), система уравнений (6) записывается в виде:
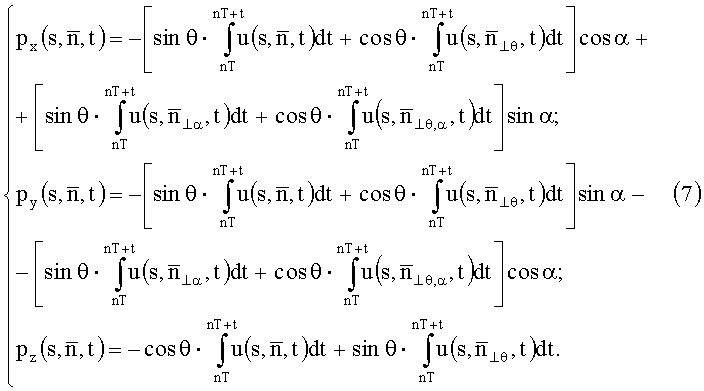
Декартовы компоненты распределения векторной функции индукции в объеме измерения получают посредством применения алгоритма реконструкции к исходным проекционным данным (7), полученным в ходе управляемого пространственного перемещения рабочего органа (фиг.2).
Задача реконструкции декартовых компонент в способе неразрушающего объемного измерения сводится к решению основного интегрального уравнения (7) с нахождением распределения компонент Bx, By, Bz по измеренным значениям плоскостных проекций px, py, pz. Решение основного интегрального уравнения (7) предполагает использование алгоритма реконструкции, основанного на обратном преобразовании Радона, посредством обратной проекции с Фурье-фильтрацией. Фурье-фильтрация осуществляется путем свертки проекций компонент непосредственно в пространстве оригинала Фурье-преобразования с соответствующей реализующей фильтрацию пространстве оригинала Фурье-преобразования с соответствующей реализующей фильтрацию свертывающей функцией h(s), являющейся обратным Фурье-преобразованием F-1[] квадрата частоты K пространственного спектра [6]. Так из (7) получают:
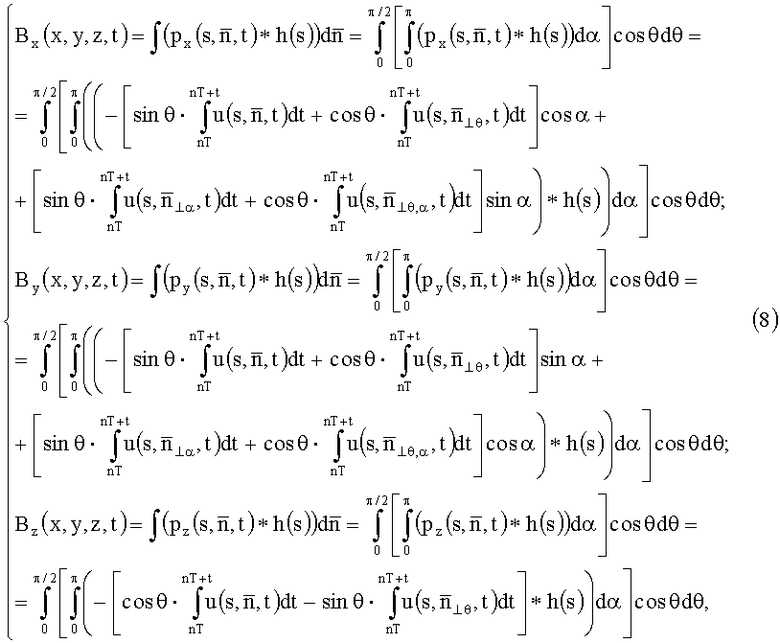
где символ «*» есть оператор свертки; 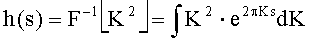
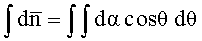
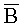
Таким образом, предложенный способ позволяет получить в местах, недоступных для механического проникновения, в объеме измерения распределения компонент векторной функции магнитной индукции неоднородно распределенного в пространстве и периодически изменяющегося во времени магнитного поля, реконструированные посредством применения принципа обратного преобразования Радона к измеренным проекциям магнитного потока, полученным путем управляемого пространственного перемещения рабочего органа, интегрирующего по плоскости векторную функцию поля.
Литература
1. Авторское свидетельство СССР №1652951, кл. G01R 33/02, опубл. 30.05.1991.
2. Авторское свидетельство СССР №1762282, кл. G01R 33/02, опубл. 15.09.1992.
3. Авторское свидетельство СССР №1684761, кл. G01R 33/06, опубл. 15.10.1991.
4. Патент РФ №2179323, кл. G01R 33/02, опубл. 10.02.2002.
5. Патент РФ №2174235, кл. G01R 33/02, опубл. 27.09.2001.
6. J. Radon. Uber die Bestimmung von Funktionen durch ihre Integralwerte langs gewisser Mannigfaltigkeiten // Berichte Sachsische Akademie der Wissenschaften, Bande 29, s.262-277, Leipzig, 1917.
Предложен способ неразрушающего объемного измерения векторной функции магнитной индукции неоднородного периодически меняющегося магнитного поля. В способе измерения мгновенных объемных состояний распределения неоднородного в пространстве магнитного поля осуществляются в местах, недоступных для механического проникновения. Рабочий магнитоизмерительный орган выполняется в виде ориентируемого в пространстве одного контура, привязанного к сферической системе координат. Рабочий орган совершает движение, предполагающее чередование дискретных параллельных перемещений в направлении оси вектора нормали органа и поворотов направления этих перемещений, задаваемых зенитным и азимутальным углами сферической системы координат, таким образом, что дискретные параллельные перемещения многократно повторяются под разными углами. Техническим результатом является расширение функциональных возможностей магнитометрии. 2 ил.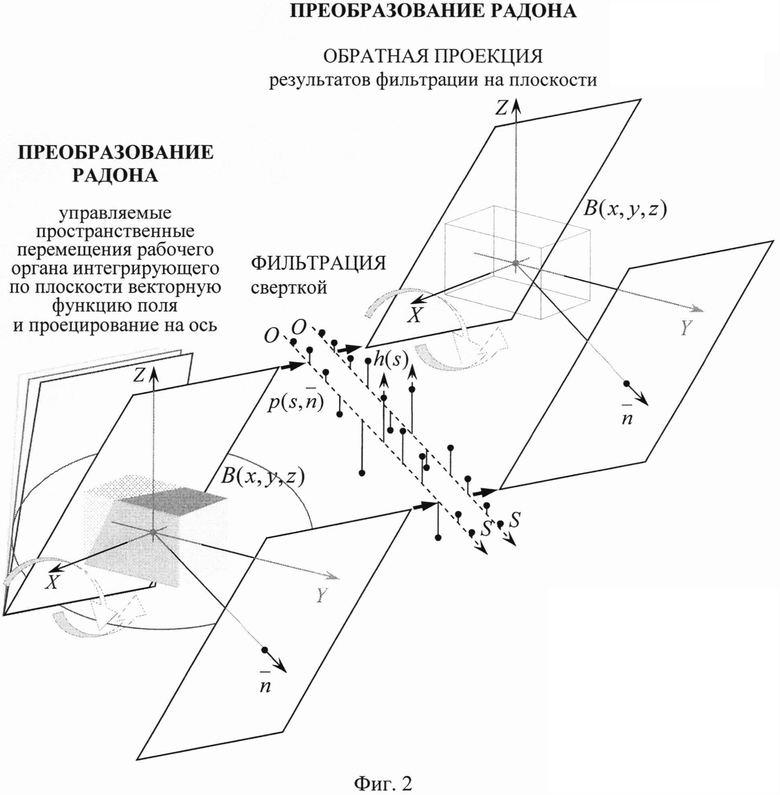
Способ неразрушающего объемного измерения векторной функции магнитной индукции неоднородно распределенного в пространстве и периодически изменяющегося во времени магнитного поля, заключающийся в измерениях распределения векторной функции магнитной индукции периодически изменяющегося во времени поля в определенных точках исследуемого пространства для произвольно выбранных моментов времени на периоде и основанный на последовательно-поступательных перемещениях и поворотах на углы рабочего магнитоизмерительного органа и регистрации индуцируемых в нем напряжений, отличающийся тем, что измерения мгновенных объемных состояний распределения неоднородного в пространстве магнитного поля осуществляют в местах, недоступных для механического проникновения, а рабочий магнитоизмерительный орган выполняют в виде ориентируемого в пространстве одного контура, привязанного к сферической системе координат, причем в ходе его управляемого пространственного перемещения осуществляют способ параллельного формирования исходных проекционных данных функции индукции, для чего рабочим органом совершают движение, предполагающее чередование дискретных параллельных перемещений в направлении оси вектора нормали органа и поворотов направления этих перемещений, задаваемых зенитным и азимутальным углами сферической системы координат, таким образом, что дискретные параллельные перемещения многократно повторяют под разными углами, причем для зенитного в интервале от 0 до 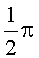
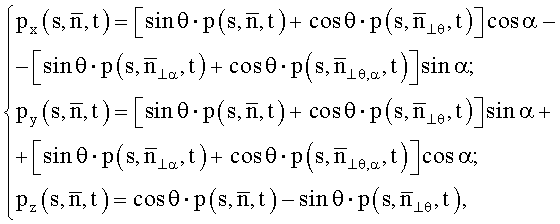
где 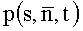
s - координата оси направления управляемого пространственного перемещения рабочего органа;
θ и α - зенитный и азимутальный углы отклонения рабочего органа, соответственно;
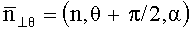
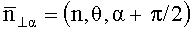


t - время;
px, py, pz - исходные проекционные данные x-, y-, z-компонент векторной функции магнитной индукции, которые записывают через магнитные потоки, численно равные интегралам по времени напряжений, индуцируемых в контуре:
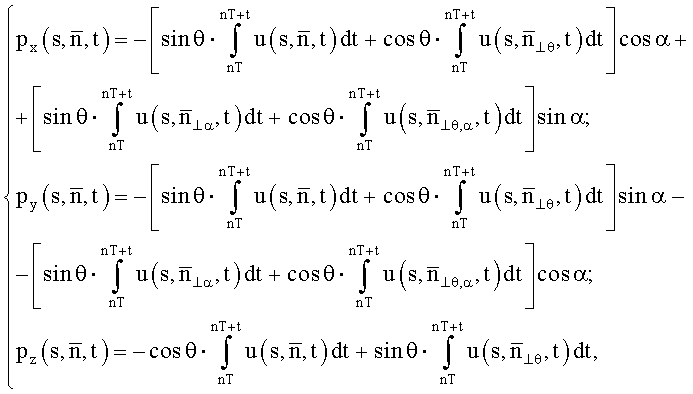
где u(t) - напряжения, индуцируемые изменением потока в контуре в момент времени t;
T - период, в течение которого происходит одно полное изменение функции магнитной индукции;
n=1, 2, … - номер периода, причем к исходным проекционным данным применяют обратное преобразование Радона, основанное на их свертке, осуществляющей фильтрацию с использованием свертывающей функции, являющейся обратным Фурье-преобразованием квадрата частоты пространственного спектра по формуле
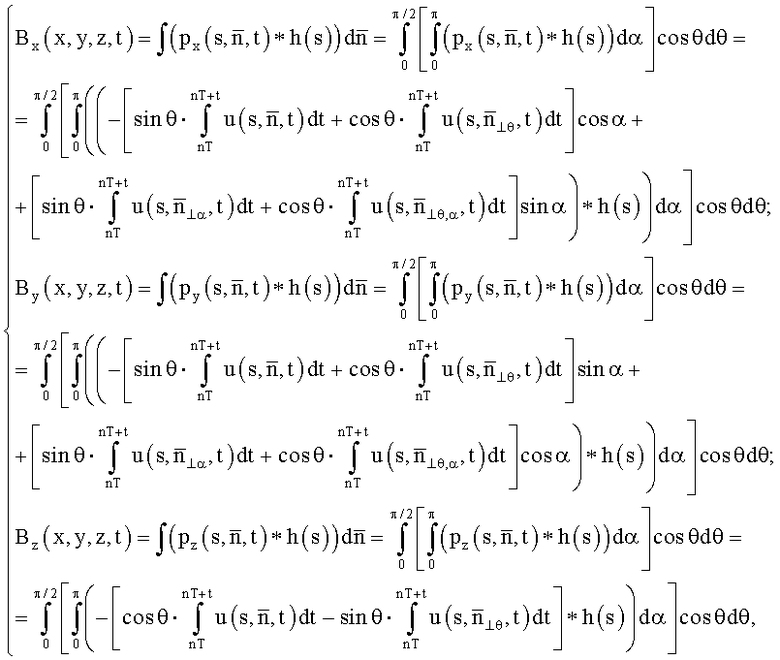
где символ «*» есть оператор свертки;
h(s) - свертывающая функция;
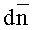
dθ и dα - дифференциалы зенитного и азимутального углов соответственно;
Bx(x,y,z,t0), By(x,y,z,t0), Bz(x,y,z,t0), где x, y, z - компоненты векторной функции магнитной индукции В соответственно, благодаря чему реконструируют декартовы компоненты распределения векторной функции магнитной индукции в пространстве.
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ПЕРИОДИЧЕСКИХ МАГНИТНЫХ ПОЛЕЙ И ПОЛУЧЕНИЯ ИХ РАСПРЕДЕЛЕНИЙ В ПРОСТРАНСТВЕ И ВО ВРЕМЕНИ | 2000 |
|
RU2174235C1 |
| СПОСОБ ПОЛУЧЕНИЯ РАСПРЕДЕЛЕНИЯ ВЕКТОРНОЙ ФУНКЦИИ МАГНИТНОЙ ИНДУКЦИИ ПЕРИОДИЧЕСКОГО МАГНИТНОГО ПОЛЯ | 2000 |
|
RU2179323C1 |
| Устройство для сканирования магнитных полей | 1989 |
|
SU1762282A1 |
| JP 11083963 A, 26.03.1999. | |||
Авторы
Даты
2013-08-20—Публикация
2012-04-20—Подача