Настоящее изобретение относится, к криптографии, в частности к
вычислению гаммы при поточном шифровании.
С широким распространением цифровой связи возрастает потребность в защите соответствующих каналов связи. Например, современные технологии позволяют пользователям осуществлять дистанционный доступ к банковским счетам, медицинским данным и другой конфиденциальной и секретной информации.
В настоящее время в симметричном шифровании широко используются два вида шифров – блочный и поточный. Блочный шифр оперирует с большим блоком данных. Поточный шифр, с другой стороны, оперирует с относительно малыми элементами текста (такими как биты, байты). Поточные шифры могут работать гораздо быстрее, чем блочные шифры.
Алгоритмы поточного шифрования, в отличие от блочного шифрования выполняют преобразование информации в текущий момент времени i, поступающей от источника сообщений Xi , по одному биту путём сложения Xiпо модулю два со значением ki, вырабатываемым генератором гаммы, и также имеющим значение один бит. Генератор гаммы как на стороне отправителя сообщения, так и на стороне получателя сообщения вырабатывает одинаковую последовательность нулей и единиц- гамму ki. Поточный шифр устраняет необходимость разбивать исходное сообщение (открытый текст) на блоки одинаковой длины по 64 бит или по 128 бит,как это делается в алгоритмах блочного шифрования, таких как DES или AES.Следовательно, поточный шифр может работать в реальном времени и при передаче сообщения, представленного в виде последовательности цифр в двоичном коде, то есть в виде нулей и единиц,каждая цифра может шифроваться и передаваться мгновенно.
При использовании гаммирования, ключом является последовательность чисел-гамма, то есть последовательность битов k1, k2,..., kn с которой производится сложение открытого текста.
В настоящее время для выработки гаммы применяются: линейный конгруэнтный генератор псевдослучайных чисел, метод Фибоначчи с запаздыванием, генератор псевдослучайных чисел на основе алгоритма BBS, отдельные режимы работы алгоритма DES,алгоритм RC4,или аналогичные шифры, которые вырабатывают последовательность чисел ki.
Способ поточного шифрования с использованием алгоритма RC4 (Рябко Б.Я., Фионов А.Н., Криптография в информационном мире, стр.201-203,-М.: Горячая линия-Телеком, 2018г, -300с.ил) является ближайшим к данному изобретению.RC4 относится к классу алгоритмов, определяемых размером его блока или слова – параметром n[1]. Внутреннее состояние RC4 состоит из последовательности чисел размером 2n слов, при n=4 количество чисел данной последовательности равено-16 и может быть записано в десятичной форме - 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 и двух счетчиков - i-й и j-й счётчики, оба при n=4 являются 4-битовыми. Все вычисления проводятся по модулю 2n, то есть при n=4-это означает, что вычисления будут проводиться по модулю 16.
В RC4- последовательность чисел используется как таблица замен (S-бокс), и обозначается как S и при n=4 массив Sбудет состоять из 24 =16 элементов, как отмечено выше, то есть из чисел 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15. В каждый момент времени таблица S содержит все возможные n-битовые (в нашем случае 4-битовые) числа от 0 до 15 в перемешанном виде. Конкретная перестановка значений в таблице определяется ключом К, который представляет – произвольный набор чисел. Если длина ключа меньше чем 2n , а в данном случае меньше чем 16, то ключ повторяется несколько раз, пока количество цифр в ключе не будет равно 2n.После того как все числа будут перемешаны закончится этап №1, а на втором этапе производится выборка псевдослучайного слова (числа).
Для этого счетчикам i и j присваивается начальное значение ноль. Затем для получения каждого нового значения zi выполняются следующие действия (этап №2 ):
i = (i + 1) mod 16;
j = (j + Si) mod 16;
поменять местами Si и Sj;
t = (Si + Sj) mod 16;
zi = St.
Значение zi вычисляется в десятичной форме записи, то есть как одно из чисел в диапазоне от 0 до 15.Для получения гаммы, то есть ki, вычисляемые на каждом шаге последовательности чисел ziзаписываем в двоичном виде и суммируются побитно по модулю два с открытым текстом xi. В результате получается зашифрованное значениеyi.
При использовании в известном способе поточного шифрования алгоритма RC4, которое происходит в два этапа, нет возможности оперативно менять гамму, так как надо менять ключ-матрицу К, кроме того для перемешивания матрицы состояния необходимо использовать два счетчика (i и j) на первом этапе, и использовать программу выборки чисел на втором этапе.
Задачей на которую направлено данное изобретение, является улучшение качества шифрования, за счёт вычисления новой вспомогательной матрицы – ключа KQ (или выборки её из библиотеки) в каждом новом цикле шифрования.
Техническим результатом изобретения является сокращение временных затрат на шифрование исходного (открытого) текста и улучшение качества шифрования за счёт вычисления новой вспомогательной матрицы – ключа KQ (или выборки её из библиотеки) в каждом новом цикле шифрования.
Кроме того, данный способ позволяет менять вспомогательную матрицу – ключ KQ с помощью матричных вычислений и таким образом, улучшается качество шифрования.
Для достижения названного технического результата в предлагаемом способе генерации гаммы, используемом при поточном шифровании:
создают матрицу состояния SQ;
производят вычисление вспомогательной матрицы-ключа KQ, значение матрицы-ключа KQ можно вычислять заранее и хранить в библиотеке, как на стороне получателя, так и на стороне отправителя информации;
производят вычисление результирующей матрицы состояний SQL путем выполнения арифметических действий с матрицами SQ и KQ;
используют счетчик элементов результирующей матрицы состояний SQL, для организации нового цикла вычислений путём вычисления новой матрицы KQ или использования матрицыKQ из библиотеки;
формируют последовательность Ki, путем перевода чисел результирующей матрицы состояний SQL из десятичной системы счисления в двоичную.
Вычисление результирующей матрицы SQL осуществляют путем сложения матрицы состояний SQ и матрицы-ключа KQ по модулю 2n.
Вычисление результирующей матрицы SQL осуществляют путем сложения матрицы состояний SQ и транспонированной матрицы-ключа KQ по модулю 2n.
Вычисление результирующей матрицы SQL осуществляют путем перемножения матрицы состояний SQ на матрицу-ключ KQ, по модулю 2n.
Вычисление результирующей матрицы SQL осуществляют путём сложения матрицы состояний SQ с матрицей-ключом KQ, умноженной на постоянное число 1 <µ <2n -1, по модулю 2n.
В предлагаемом способе генерации гаммы, состоящем из циклов - в каждом цикле используют матричный подход к построению как матрицы состояния SQ (аналог матрицы S), так и вспомогательной матрицы КQ, которая является аналогом ключа К в RC4 и вычисляется результирующая матрица SQL в результате матричных преобразований над матрицами SQ и KQ. Элементы результирующей матрицы SQL формируют последовательность Ki, путем перевода чисел результирующей матрицы состояний SQLij из десятичной системы счисления в двоичную.
В матричном подходе определяющим параметром является размер матрицы N, который может быть выражен через n, внутреннее состояние и определяется квадратной матрицей SQ размером N*N, где
N2 = 2n или N= 2n\2, (1)
то есть при n=4 N=4, при n=8 N=16, при n=10 N=32 и т.д.
Квадратная матрица SQ, используется как таблица замен S (S-бокс) в RC4. В начальный момент времени матрица SQ также как и таблица замен S содержит все возможные n-битовые числа, записанные либо по порядку, либо в перемешенном виде, то есть записанные в соответствии с заранее согласованной (между отправителем и получателем) последовательности.
Матричный алгоритм состоит из двух этапов. На первом, подготовительном этапе производится инициализация матрицы состояния SQ и вычисление вспомогательной матрицы КQ, которая является аналогом ключа К в RC4, по формуле
КQ= L*Mmod2n, (2),
где L - матрица порядка N*1, а M порядка 1*N, причём числа входящие в данные матрицы выбираются произвольным образом из чисел, входящих в матрицу состояния SQ, а элементы вспомогательной матрицы КQ вычисляются по модулю 2n.
На втором, основном этапе вычисляется по модулю 2n матрица SQL по формуле SQL = (SQ +KQ)mod2nилиSQL =(SQ *KQ)mod2n(3)
и производится выборка чисел, которыми будут являться элементы данной матрицы SQL, то есть SQLij - это числа, переведённые из десятичной системы счисления в двоичную систему счисления, и будут числами ki.
Матрицы SQL, SQ и KQ имеют одинаковый порядок, и представляют собой квадратные матрицы размера N*N.
Рассмотрим принцип работы матричного подхода при n=4. В этом случае количество всех чисел, входящих в массив S или в матрицу состояния SQ будет равно 24 = 16, а сами числа будут находиться в диапазоне от 0 до 15. Тогда N, вычисляемое по формуле (1) будет равно 4 и матрица SQ может быть представлена, в матричном виде как квадратная матрица размером N*N = 4*4. В дальнейшем для упрощения понятия принципа работы матричного подхода в матрицу состояния SQ запишем числа от 0 до 15 по порядку, хотя их порядок может быть изменён - по согласованию, между отправителем и получателем информации. Так как n=4 то все вычисления будут производиться по модулю 2n = 24 =16.
С учётом этого на первом этапе вычислений матрица состояния SQ может быть представлена, в следующем виде:

Так как вспомогательная матрица КQ вычисляется по формуле (2), то есть:
КQ= L*Mmod2n,
то заметим, что вычисление значений матрицы КQ производится с применением двух матриц- L (N*1) и М(1*N), и числа, входящие в данные матрицы, могут выбираться произвольным образом из чисел, входящих в матрицу состояния SQ, как было указано ранее. Для простоты и наглядности вычислений примем, что матрица М равна транспонированной матрице L, а в качестве произвольных чисел выберем значения 1,2,3,4.
Тогда вспомогательная матрица КQ вычисляется по модулю 16 следующим образом

Значение результирующей матрицы SQL вычисляется в соответствии с уравнением (3) - суммируя матрицы SQ и КQ по модулю 16,получим

Выборка чисел, для применения в поточном шифровании в качестве гаммы, может быть произведена любым способом, как по порядку (первая строка, вторая и т.д.), так и начиная с последнего элемента данной таблицы к первому, а после этого производится перевод перевода выбранных чисел из десятичной в двоичную систему счисления.
Данный матричный подход даёт возможность применения различных вариантов для дальнейших вычислений результирующей матрицы SQL и её составляющих, таких как матрица состояния SQ, и вспомогательная матрица КQ.
Например, можно получить новое значение результирующей матрицы SQL как результат произведения матриц SQ и КQ, то есть
SQL = SQ *КQ, (4),
учитывая, что все вычисления производятся по модулю 16 , как в рассмотренном выше примере.
Применительно к вспомогательной матрице КQ для получения новых значений также возможны следующие варианты:
во-первых, возможно преобразовать вспомогательную матрицу КQ с помощью выбора новых чисел(произвольных) в матрицах L, M или например, можно выбрать в качестве матрицы L- i-ый столбец матрицы состояния SQ, а в качестве матрицы М- j-ую строку матрицы SQ;
во-вторых, сдвинув «старые» элементы матриц L, М на определённое число позиций (одинаковое или разное выбранное по заранее согласованному алгоритму) и получить в результате их перемножения новое значение вспомогательной матрицы КQ;
в-третьих, можно ввести новый элемент – число µ, где µ - скалярная величина, находящаяся в диапазоне 1 < µ ≤ 2n-1 и умножить вспомогательную матрицу КQ, полученную на предыдущем этапе вычислений на µ- в результате чего все элементы вспомогательной матрицы KQ будут умножены на данный коэффициент и после применения к ним операции вычисления по модулю 2n, в результате будет получено новое значение вспомогательной матрицы КQ на новом этапе вычислений;
в-четвёртых, для вычисления результирующей матрицы SQL можно использовать транспонированное значение вспомогательной матрицы KQ.
После этих преобразований, учитывая полученное обновлённое значение вспомогательной матрицы КQ, можно вычислить новое значение результирующей матрицы SQL, элементы которой, то есть числа SQLij в двоичной форме записи могут быть использованы как числа ki .Предлагаемый матричный подход может использоваться для получения последовательности псевдослучайных чисел(гамма) в поточном шифровании.
Предлагаемый способ поясняется чертежами, на которых показаны:
Фиг.1 – Схема работы поточного шифра
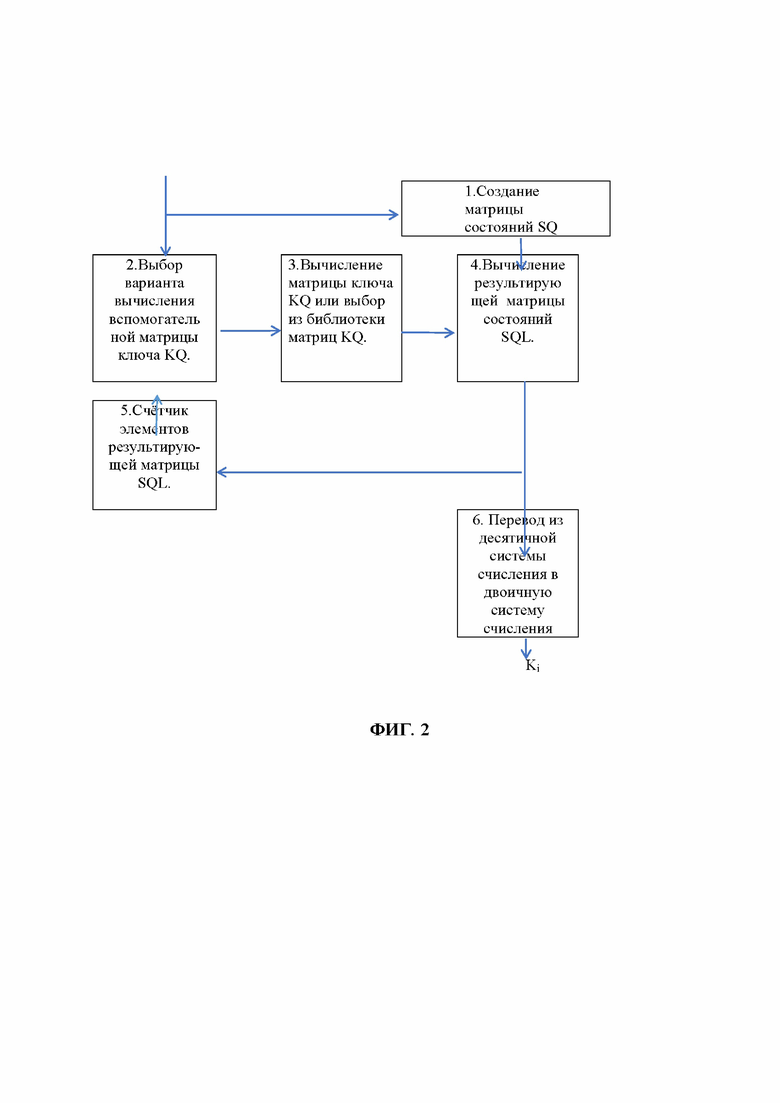
Фиг.2 - Блок-схема операций способа генерации гаммы – ki.
Способ состоит из циклов и осуществляется следующим образом.
Цикл работы состоит из нескольких этапов. На первом этапе производится инициализация матрицы состояния SQ (блок №1), то есть запись чисел в данную матрицу (блок №1), например от 0 до 15, если n=4 или от 0 до 255, если n=8, или от 0 до 1023 если n=10 и т.д. Так как матричный подход даёт возможность построения матрицы ключа различными способами по модулю 2n (например, перемножением i-ого столбца на j-ую строку или умножением полученного результата на константу 1<µ<2n-1, транспонированием полученного результата или выборки из библиотек и т.д.), то на втором этапе происходит выбор варианта построения вспомогательной матрицы ключа KQ (блок №2). На третьем этапе происходит вычисление вспомогательной матрицы ключа KQ (блок №3) для выбранного варианта. На данном этапе также возможно использование вспомогательной матрицы KQ из библиотеки, содержащей заранее вычисленные значения данной матрицы. Результат этого этапа поступает, на первый вход блока № 4, на второй вход которого поступают элементы матрицы состояний SQ и на выходе блока № 4 получается результирующая матрица SQL. Элементы результирующей матрицы, то есть числа SQLij , где ( i, j = 0….2n-1), выбранные, например, по порядку то есть sql00,sql01…sqln-1 n-1 поступают на вход блоков № 5 и № 6. Блок № 5 является счётчиком и после подсчёта количества чисел матрицы SQLij, где ( i, j = 0….2n-1) начинает новый цикл шифрования путём вычисления новой вспомогательной матрицы KQ или взятия её из библиотеки матриц KQ, в блоке № 6 данные числа переводятся из десятичной системы счисления в двоичную и формируют последовательность Ki (гамму), которая складывается с открытым текстом Xi и образует зашифрованный текст Yi.
осле того как будут выбраны все числа результирующей матрицы SQL, по команде от счётчика (блок № 5), можно будет изменить вспомогательную матрицу KQ, например, умножить полученный результат - вспомогательную матрицу KQ на константу 1<µ<2n-1или транспонировать её и сложить с матрицей состояния SQ, или перемножить матрицы SQL и KQ, и кроме того можно использовать заранее вычисленные значения вспомогательной матрицы ключа KQ, находящиеся в библиотеке, а после этого повторить весь цикл заново.
С учетом того, что перемешивание чисел в результирующей матрице SQL производится за счёт матричных преобразований, нет необходимости в использовании i-го и j-го счётчиков и в применении специальной программы выборки чисел, а оперативное изменение вспомогательной матрицы ключа KQ, затруднит дешифрование текста для противника.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОБАЙТНОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ С ПОМОЩЬЮ ПОТОЧНОГО ШИФРОВАНИЯ | 2023 |
|
RU2811065C1 |
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ СОСТАВНОГО КЛЮЧА | 2024 |
|
RU2831832C1 |
| СПОСОБ ИТЕРАТИВНОГО КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ | 2012 |
|
RU2504911C1 |
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 2009 |
|
RU2423799C2 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ RDOZEN | 2015 |
|
RU2591015C1 |
| СПОСОБ ФОРМИРОВАНИЯ ОБЩЕГО СЕКРЕТНОГО КЛЮЧА ДВУХ УДАЛЕННЫХ АБОНЕНТОВ | 2009 |
|
RU2420892C1 |
| СПОСОБ ПОТОЧНОГО ШИФРОВАНИЯ ДАННЫХ | 2005 |
|
RU2291578C1 |
| СПОСОБ ШИФРОВАНИЯ БЛОКА ДВОИЧНЫХ ДАННЫХ | 2014 |
|
RU2542880C1 |
| СПОСОБ ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1993 |
|
RU2091983C1 |
| СПОСОБ НЕЛИНЕЙНОГО ТРЕХМЕРНОГО МНОГОРАУНДОВОГО ПРЕОБРАЗОВАНИЯ ДАННЫХ DOZEN | 2012 |
|
RU2503994C1 |

Изобретение относится к криптографии, в частности к вычислению гаммы в поточном шифровании. Техническим результатом является сокращение временных затрат на шифрование исходного текста и улучшение качества шифрования за счёт вычисления новой вспомогательной матрицы – ключа KQ. Для этого в способе генерации гаммы в каждом цикле используют матричный подход к построению как матрицы состояния SQ, так и вспомогательной матрицы КQ, в результате матричных преобразований над матрицами SQ и KQ вычисляют результирующую матрицу SQL. Элементы матрицы SQL формируют последовательность Ki, путем перевода чисел результирующей матрицы состояний SQLij из десятичной системы счисления в двоичную. После подсчёта количества чисел матрицы SQLij, если количество чисел равно N2, то начинается новый цикл путём вычисления или выбора из библиотеки новой матрицы ключа KQ. 4 з.п. ф-лы, 2 ил.
1. Способ генерации гаммы, используемый при поточном шифровании, в котором:
создают матрицу состояния SQ;
выбирают вариант построения вспомогательной матрицы ключа KQ;
производят вычисление вспомогательной матрицы-ключа KQ, при этом значение матрицы-ключа KQ можно вычислять заранее и хранить в библиотеке, как на стороне получателя, так и на стороне отправителя информации;
производят вычисление результирующей матрицы состояний SQL путем выполнения арифметических действий с матрицами SQ и KQ;
используют счетчик элементов результирующей матрицы состояний SQL, для организации нового цикла вычислений путём вычисления новой матрицы KQ или использования матрицы KQ из библиотеки;
формируют последовательность Ki-гамму, путем перевода элементов результирующей матрицы состояний SQL из десятичной системы счисления в двоичную.
2. Способ по п. 1, отличающийся тем, что вычисление результирующей матрицы SQL осуществляют путем сложения матрицы состояний SQ и матрицы-ключа KQ по модулю 2n.
3. Способ по п. 1, отличающийся тем, что вычисление результирующей матрицы SQL осуществляют путем сложения матрицы состояний SQ и транспонированной матрицы-ключа KQ по модулю 2n.
4. Способ по п. 1, отличающийся тем, что вычисление результирующей матрицы SQL осуществляют путем перемножения матрицы состояний SQ на матрицу-ключ KQ, по модулю 2n.
5. Способ по п. 1, отличающийся тем, что вычисление результирующей матрицы SQL осуществляют путём сложения матрицы состояний SQ с матрицей-ключом KQ, умноженной на постоянное число 1 <µ <2n -1, по модулю 2n.
| РЯБКО Б.Я | |||
| и др., Криптография в информационном мире, Горячая линия-Телеком, 2018, стр | |||
| Питательное приспособление к трепальным машинам для лубовых растений | 1922 |
|
SU201A1 |
| Устройство для пуска двигателей многомоторного электропривода | 1949 |
|
SU82890A1 |
| СПОСОБ СКРЫТОЙ ПЕРЕДАЧИ ЗАШИФРОВАННОЙ ИНФОРМАЦИИ ПО МНОЖЕСТВУ КАНАЛОВ СВЯЗИ | 2011 |
|
RU2462825C1 |
| US 5297208 A1, 22.03.1994. | |||
Авторы
Даты
2022-11-14—Публикация
2021-10-25—Подача