СПОСОБ ПОБАЙТНОЙ ПЕРЕДАЧИ ИНФОРМАЦИИ С ПОМОЩЬЮ ПОТОЧНОГО ШИФРОВАНИЯ Российский патент 2024 года по МПК H04L9/06 H04L9/16 

Изобретение относится к криптографии, в частности к способам поточного шифрования, в которых используется побайтная передача информации на основе таблицы кодирования символов ASCII.

В описании использованы следующие термины.

ASCII – (англ. American standard code for information interchange) - название таблицы (кодировки, набора), в которой некоторым распространённым печатным и непечатным символам сопоставлены числовые коды.

Алгоритмы шифрования делятся на две группы: алгоритмы симметричного шифрования и алгоритмы ассиметричного шифрования. В алгоритмах симметричного шифрования, которые также делятся на две большие группы: поточные и блочные, отправитель информации и получатель информации имеют одинаковые ключи, а в алгоритмах ассиметричного шифрования отправитель информации и получатель информации имеют по два ключа каждый – открытый и закрытый.

В алгоритмах симметричного шифрования передача ключей шифрования является слабым местом. Например, если фирма состоит из t филиалов, включая головной офис, то для обеспечения обмена информацией между всеми филиалами необходимо t·(t-1)/2, но время от времени старые ключи необходимо менять на новые ключи, что усложняет работу.

В настоящее время для шифрования открытого текста широкое применение нашли алгоритмы поточного шифрования, которые в отличие от блочного шифрования выполняют преобразование информации, поступающей от источника сообщений как по одному биту, так по 1 байту (8 бит). Таким образом, алгоритм поточного шифрования может преобразовывать поступающую информацию в момент её получения.

Недостатком поточного шифрования, как было отмечено ранее, является необходимость получения нового ключа (гаммы) для шифрования, поступающей информации. Возможно вместо передачи нового ключа произвести его вычисление, как на стороне отправителя, так и получателя информации по одинаковому алгоритму путем матричных преобразований на основе передаваемых коэффициентов.

То есть вместо передачи ключа произвести обмен коэффициентами между отправителем и получателем информации и на их основе c помощью матричных преобразований вычислять ключи.

Известны алгоритм шифрования RC-4 – класс алгоритмов, определяемых размером его блока или слова – параметром n. В том случае, когда n = 8 бит или 1 байт, то тогда внутреннее состояние RC-4(S-бокс) состоит из массива размером 2⁸ слов, то есть внутреннее состояние включает 256 элементов (0,1,2,….255).

Наиболее близким аналогом к заявляемому изобретению является способ шифрование, известный из патента RU 2783406, в котором рассматривается побитовое поточное шифрование с использованием матричных преобразований.

Однако при использование данного технического решения каждый символ открытого текста нужно переводить в набор нулей и единиц в соответствии с используемым алфавитом и складывать по модулю два с набором нулей и единиц матрицы SQL и отправлять получателю данную информацию.

Преимуществом заявляемого изобретения является использование стандартной таблицы кодирования символов ASCII при поточном шифровании.

Техническим результатом изобретения является упрощение процесса шифрования и расшифрования текста, сокращение временных и вычислительных затрат.

В предлагаемой заявке нет необходимости каждый символ открытого текста переводить в набор нулей и единиц – каждому символу соответствует своё число в двоичной системе счисления, которое будет суммироваться по модулю два с элементом результирующей матрицы SQL, также представленным в соответствующей форме и отправляться получателю информации.

Сущность заявляемого изобретения заключается в том, что в способе побайтной передачи информации с помощью поточного шифрования создают матрицу состояния SQ, записывая числа по порядку от 0 до 255; выбирают вариант построения вспомогательной матрицы-ключа KQ; производят вычисление вспомогательной матрицы-ключа KQ; производят вычисление результирующей матрицы SQL по формуле: SQL = SQ ⊕ KQ mod 256. Элементы результирующей матрицы SQL(sql_ij) и будут являться гаммой(ключом) используемыми при сложении с символами открытого текста. Полученные числовые значения элементов матрицы SQL переводят в двоичную систему счисления, соответствующую таблице символов ASCII, символы открытого текста записывают с помощью таблицы символов ASCII, получая значение символа X_i, соответствующее символу открытого текста, записанное в двоичной системе счисления и далее суммируют по модулю два один байт символов ASCII, соответствующий символу открытого текста X_i с элементом матрицы sql_ij, получая зашифрованное сообщение Y_i, передают зашифрованное сообщение Y_i.

Применение n = 8 даёт возможность использовать таблицу символов, например, ASCII, в которой символы – буквы алфавита, цифры, арифметические операции, и другие знаки также представлены в виде 8 битовых значений, например символ A – 01000001, символ B – 01000010, символ C – 01000011 и так далее.

С другой стороны, с помощью подхода, основанного на матричных преобразованиях [Дедов О.П. Применение матричного подхода к поточному шифрованию. Электронный научный журнал «E-Scio.ru», 2021.-5с, далее – Источник 1] возможно сформировать результирующую матрицу, элементы которой являются гаммой (ключом), также состоящую из 256 чисел, записанных в виде 8 битовых значений символов: 0 – 00000000, 1 – 00000001, 2 – 00000010 и т.д., и суммируя символы открытого текста и вычисленные с помощью матричных преобразований элементы результирующей матрицы (гаммы), по модулю два производить побайтовое шифрование открытого текста.

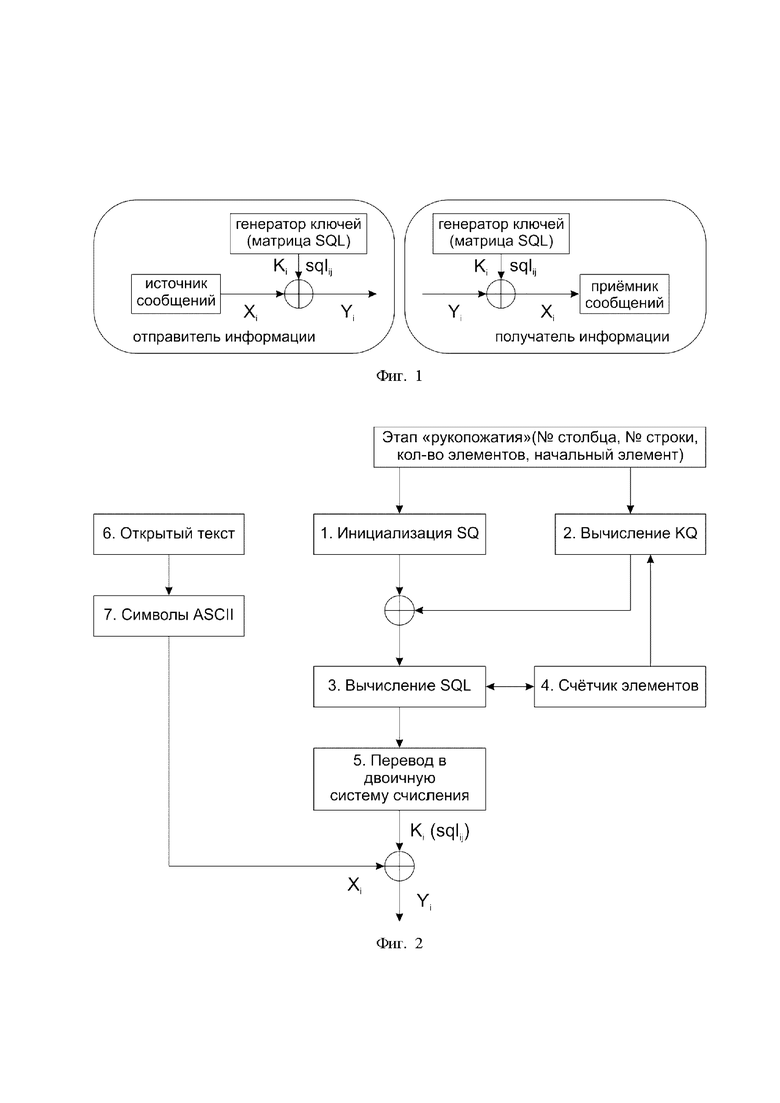
Заявляемое изобретение поясняется фигурами 1-2, на которых показаны:

- фиг. 1 – схема алгоритма поточного шифрования;

- фиг. 2 – блок-схема предлагаемого алгоритма поточного шифрования.

На фигуре 1 X_i i-ый байт открытого текста и sql_ij элемент матрицы SQL, записанный в виде одного байта, находящийся в ячейке – K_i, где 0 ≤ i<≤255.

SQL – результирующая матрица, элементы которой sql_ij [Источник 1, С.А.Белецкий, О.П.Дедов, С.И.Журавлёв. Построение многослойной и бесконечной гаммы для поточного шифрования. Промышленные АСУ и Контроллеры. DOI: 10.25791/ asu.10.2022.1392 стр.39-43 – далее Источник 2] вычисляются по формуле

SQL= SQ + KQ mod 2ⁿ, (1)

где SQ – матрица состояния;

КQ – матрица-ключа;

SQL – результирующая матрица, элементы которой, переведённые в двоичную систему счисления, будут выступать в роли гаммы.

Причём в Источнике 1 было показано, что при n = 4 параметр N, определяющий размер квадратных матриц SQ, КQ и SQL, вычисляется по формуле (1).

N= 2^4/2= 2² = 4, (2)

То есть матрицы SQ, КQ и SQL при n = 4 являются квадратными матрицами размера 4×4, а при n = 8 N будет равно 16, а это значит, что матрицы SQ, КQ и SQL будут квадратными матрицами размера 16×16, и каждая из них содержат по 256 элементов (чисел). Каждый элемент матрицы SQL (sgl_ij) может быть представлен как последовательность восьми нулей и единиц, то есть одним байтом.

Таким образом, каждый символ открытого текста X_i c помощью таблицы символов ASCII, записанный в виде последовательности 8 битов, то есть одним байтом, может быть сложен по модулю два с элементами матрицы SQL (sgl_ij), каждый из которых также записан виде восьми битовой последовательности (одним байтом), а в результате данного сложения получается Y_i – зашифрованное значение X_{i ,}которое поступает вход получателя информации и расшифровывается там в обратном порядке, то есть сложением по модулю два с элементами результирующей матрицы SQL(sgl_ij), вычисленным по аналогичному алгоритму.

В Источнике 2 было рассмотрено вычисление квадратных матриц SQ, КQ и SQL для n=4 и следовательно N= 2^4/2= 2² = 4, и матрицы SQ, КQ , SQL имеют размер 4×4 , различными способами.

То есть на первом этапе есть матрица состояния S (в алгоритме RС 4) и матрица SQ в предлагаемом алгоритме шифрования (n = 4 и 2⁴ = 16), которая включает 16 элементов числа – 0,1,2,….15 , расставленные по порядку. На втором этапе вычисляется матрица ключ KQ – аналог матрицы ключа К в алгоритме шифрования RС 4 (различными способами [Источник 2]). На третьем этапе вычисляется результирующая матрица SQL как сумма матриц SQ и КQ. Все матрицы SQ, КQ и SQL в [Источник 2] имеют одинаковый размер – 4×4.

Матричный подход позволяет вычислять матрицу-ключ KQ различными способами [Источник 2], например, как произведение матрицы-столбца размера 4×1, на матрицу строку размера 1×4 по модулю 2ⁿ , а элементы матрицы столбца и матрицы строки могут выбираться также различными способам, либо с помощью датчика случайных чисел ДСЧ (среди чисел, находящихся в диапазоне от 1 до 2ⁿ -1) или выбираться как произведение матрицы-столбца на матрицу-строку (обе матрицы получены из матрицы состояний S( RC-4) или SQ [Источники 1, 2].

В Источниках 1,2 и наиболее близком аналоге рассмотрено вычисление матриц SQ, KQ, SQL для n=4.

Так как n = 4, то все вычисления будут производиться по модулю 2⁴ , то есть по модулю 16.

При n = 4 матрица состояний SQ, состоит из 2⁴ элементов и имеет вид:

SQ =

Вычислим матрицу-ключа KQ одним из способов, рассмотренных в Источнике 2, как произведение второго столбца матрицы SQ на третью строку данной матрицы по модулю 16, то есть

KQ = 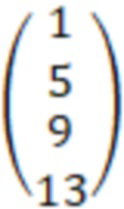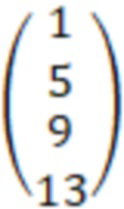×( 8 9 10 11) = mod 16 (3)

Элементы результирующей матрицы SQL будут вычисляться как сумма соответствующих элементов матриц SQ и KQ по модулю 16.

SQL = SQ ⊕ KQ = 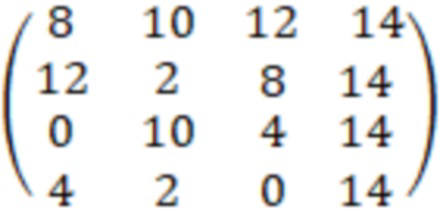mod 16

Данную результирующую матрицу SQL, полученную в результате однократного сложения матриц SQ и KQ назовём однослойной [Источник 2] и обозначим как SQL₁. В Источнике 2 показано вычисление двух, трёхслойных матриц и многослойных матриц различными способами, в том числе умножением матрицы-ключа KQ на константу µ ( 1 < µ ≤ 15 ) n=4.

Матрица SQL₂ будет вычисляться по формуле (1) и называется двухслойной матрицей.

SQL₂ = SQL₁ ⊕ KQ mod 16

SQL₂ =

В том случае, когда происходит передача информации по одному байту, то есть при n = 8 , все рассматриваемые матрицы: матрица состояний SQ, матрица ключа KQ и результирующая матрица SQL будут иметь размерность 16×16 и состоять из 256 элементов каждая. Матрица состояния SQ, состоящая из 256 элементов, записанных по порядку будет иметь вид:

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 223 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255

Предположим, что матрица KQ (для n = 8) вычисляется аналогично вычислению KQ (для n = 4), как в рассмотренном ранее примере, то есть как произведение второго столбца матрицы SQ - ST(2,1) на третью строку STR(3,1) данной матрицы, но по модулю 256 вместо 16 (для n = 4).То есть

KQ= ST(2) * STR(3)= *[32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47] mod 256 (4)

Таким образом, матрица KQ будет иметь вид:

32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 32 49 66 83 100 117 134 151 168 185 202 219 236 253 14 31 32 65 98 131 164 197 230 7 40 73 106 139 172 205 238 15 32 81 130 179 228 21 70 119 168 217 10 59 108 157 206 255 32 97 162 227 36 101 166 231 40 105 170 235 44 109 174 239 32 113 194 19 100 181 6 87 168 249 74 155 236 61 142 223 32 129 226 67 164 5 102 199 40 137 234 75 172 13 110 207 32 145 2 115 228 85 198 55 168 25 138 251 108 221 78 191 32 161 34 163 36 165 38 167 40 169 42 171 44 173 46 175 32 177 66 211 100 245 134 23 168 57 202 91 236 125 14 159 32 193 98 3 164 69 230 135 40 201 106 11 172 77 238 143 32 209 130 51 228 149 70 247 168 89 10 187 108 29 206 127 32 225 162 99 36 229 166 103 40 233 170 107 44 237 174 111 32 241 194 147 100 53 6 215 168 121 74 27 236 189 142 95 32 1 226 195 164 133 102 71 40 9 234 203 172 141 110 79 32 17 2 243 228 213 198 183 168 153 138 123 108 93 78 63

Тогда матрица SQL которая равна сумме матриц SQ и KQ вычисляется по формуле

SQL = SQ ⊕ KQ mod 256, (5)

примет следующий вид:

32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 48 66 84 102 120 138 156 174 192 210 228 246 8 26 44 62 64 98 132 166 200 234 12 46 80 114 148 182 216 250 28 62 80 130 180 230 24 74 124 174 224 18 68 118 168 218 12 62 96 162 228 38 104 170 236 46 112 178 244 54 120 186 252 62 112 194 20 102 184 10 92 174 0 82 164 246 72 154 236 62 128 226 68 166 8 106 204 46 144 242 84 182 24 122 220 62 144 2 116 230 88 202 60 174 32 146 4 118 232 90 204 62 160 34 164 38 168 42 172 46 176 50 180 54 184 58 188 62 176 66 212 102 248 138 28 174 64 210 100 246 136 26 172 62 192 98 4 166 72 234 140 46 208 114 20 182 88 250 156 62 208 130 52 230 152 74 252 174 96 18 196 118 40 218 140 62 224 162 100 38 232 170 108 46 240 178 116 54 248 186 124 62 240 194 148 102 56 10 220 174 128 82 36 246 200 154 108 62 0 226 196 166 136 106 76 46 16 232 212 182 152 122 92 62 16 2 244 230 216 202 188 174 160 146 132 118 104 90 76 62

В общем виде матрица SQL_i вычисляется по формуле:

SQL_i= SQL_i-1 + KQ mod 16, (6)

Каждый элемент данной матрицы sql_ij, записанный в двоичном виде с помощью 8 бит, поступает на первый вход сумматора по модулю два (фиг.1), где складывается с символом открытого текста X_i, который также записан в виде 8 бит (при применении ASCII), и на выходе сумматора получается зашифрованный символ Y_i, а дешифрование производится в обратном порядке на стороне получателя информации.

Таким образом, каждый символ открытого текста может быть зашифрован и передан получателю информации.

Заметим, что при шифровании можно использовать элементы матрицы sql_ij как по порядку, то есть начиная с первого sql₁₁ (первый символ открытого текста будет суммироваться по модулю два с sql₁₁) и заканчивая последним sql_255,255 или, как было указано в Источнике 1, элементы данной матрицы могут быть использованы в обратном порядке, то есть от sql_255,255 до sql₁₁.

Кроме этого при применении матричного подхода, возможно, использовать группу элементов (40-100) матрицы SQL₁ для шифрования части открытого текста, а потом перейти к таким же элементам матрицы SQL₂ для шифрования второй части открытого текста т.д.

Данный алгоритм может быть реализован следующим образом. Во- первых, можно заранее обменяться значениями матриц SQL – на определённый срок (день, месяц) между отправителем и получателем информации. Во- вторых, на этапе «рукопожатие» («Handshakes») (фиг. 2) между отправителем и получателем информации происходит обмен коэффициентами, в качестве которых могут применяться числа, либо вырабатываемые с помощью ДСЧ выбираются элементы из чисел от 1 до 255, соответствующие элементам матрицы-столбца (16 чисел) и матрицы строки (16 чисел), а матрица KQ вычисляется как их произведение, либо как в рассмотренных ранее примерах можно указать номер столбца (α1) и номер строки (α2), при умножении которых по модулю 256 получается матрица ключа KQ, также можно указать значение коэффициента µ (α3), который может применяться при вычислении матрицы KQ [Источник 2] (в данной работе он был равен 5), а также указать количество элементов (α4), используемых при шифровании, если принято решение использовать при шифровании 40-100 символов матрицы SQL₁ , а потом перейти к матрице SQL₂ и далее к матрице SQL_i и в этом случае необходимо указать номер элемента K_i (α5) с которого начинается отчёт. Все эти коэффициенты могут быть сведены в таблицу №1.

Таблица № 1.

Номер столбца (α1) Номер строки (α2) Коэффициент ( µ=5) (α3) Кол-во элементов (α4) Номер элемента K_i (α5) 2 3 5 40 100

Заметим, что в качестве коэффициента µ могут быть использованы числа, входящие в матрицу-столбец (α1) или матрицу-строку (α2).

На фигуре 2 представлена блок-схема алгоритма поточного шифрования, где:

- блок № 1– блок инициализации матрицы SQ;

- блок № 2 – программа вычисления матрицы ключа KQ;

- блок № 3 – вычисление результирующей матрицы состояний SQL;

- блок № 4 – счётчик элементов результирующей матрицы состояний SQL;

- блок № 5 – перевод из десятичной системы счисления в двоичную систему счисления;

- блок № 6 – открытый текст;

- блок №7 – блок перевода открытого теста в символы ASCII.

Способ осуществляют следующим образом.

Цикл работы состоит из нескольких этапов. На первом этапе производится инициализация матрицы SQ (блок № 1), то есть запись чисел в данную матрицу по порядку от 0 до 255 (при n = 8) и вычисление матрицы-ключа KQ на основе коэффициентов из таблицы №1 или другим способом, например, с помощью ДСЧ выбираются элементы из чисел от 1 до 255, соответствующие элементам матрицы-столбца (16 чисел) и матрицы-строки (16 чисел), а матрица KQ вычисляется как их произведение (3,4).

На втором этапе по формуле (3) с учётом вычисленных значений матрицы KQ и значений матрицы SQ вычисляется матрица SQL.

На третьем этапе происходит перевод числовых значений элементов матрицы SQL в двоичную систему счисления, соответствующую таблице символов ASCII.

На четвёртом этапе символы открытого текста записываются с помощью таблицы символов ASCII (блок № 6 и блок № 7), и на выходе блока № 7 получают значение символа X_i, соответствующее символу открытого текста, но записанное в двоичной системе счисления.

На пятом этапе после суммирования по модулю два 8 бит символов, поступивших из блока №5, и 8 бит символов, поступивших из блока № 7, получают зашифрованное сообщение Y_i.

Нет проблемы возникающей из-за наличия байтов вне диапазона. Все байты, как преобразующие символы открытого текста, так и байты для шифрования (элементы матрицы SQL) находятся в диапазоне от 0 до 255, и после сложения по модулю два они также будут находиться в этом диапазоне. То есть, производится сложение слова из 8бит(1 байт), соответствующего символу открытого текста с элементом матрицы sql_ij ,также состоящим из 8 бит по модулю два и в результате получается слово из 8 бит(1байт).

В том случае, если размер открытого текста, то есть количество символов открытого текста равно 256, то для их шифрования достаточно элементов матрицы SQL₁ (число которых равно 256), а если больше, чем 256 ,то по команде со счётчика элементов будет сформирована новая матрица SQL₂ (число элементов которой также равно 256) и т.д.

Кроме этого возможно использование определённого количества символов (40-100) из матрицы SQL₁, а потом из матрицы SQL₂ и тд., что сделает невозможным расшифрование зашифрованного текста.

В заявляемом способе производятся матричные операции, не требующие больших вычислительных и, как следствие, временных затрат: матрицы не возводятся в степень и нет вычисления обратных матриц (которые могут и не существовать), что значительно упрощает применение данного метода в реальной практике.

Изобретение относится к способам поточного шифрования. Техническим результатом изобретения является сокращение времени шифрования и расшифрования текста. Создают матрицу состояния SQ, записывая числа по порядку от 0 до 255. Выбирают вариант построения вспомогательной матрицы-ключа KQ. Производят вычисление вспомогательной матрицы-ключа KQ. Производят вычисление результирующей матрицы состояний SQL по формуле: SQL = SQ ⊕ KQ mod 256. Переводят числовые значения элементов матрицы SQL в двоичную систему счисления, соответствующую таблице символов ASCII. Символы открытого текста записывают с помощью таблицы символов ASCII, получая значение символа X_i, соответствующее символу открытого текста, записанное в двоичной системе счисления. Суммируют по модулю два один байт символов ASCII и один байт элемента матрицы SQL и один байт символов X_i, получая зашифрованное сообщение Y_i. Передают зашифрованное сообщение Y_i. 1 з.п. ф-лы, 2 ил., 1 табл.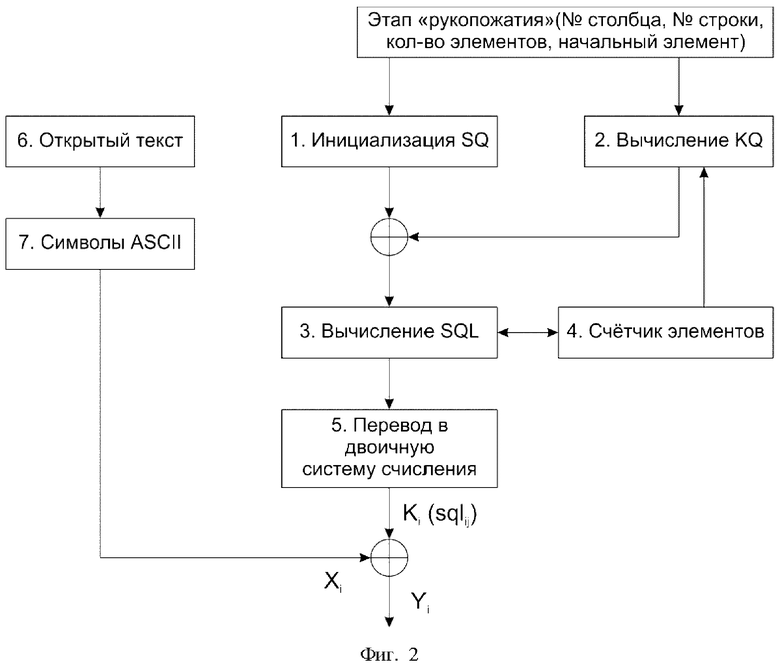

1. Способ побайтной передачи информации с помощью поточного шифрования, характеризующийся тем, что:

- создают матрицу состояния SQ, записывая числа по порядку от 0 до 255;

- выбирают вариант построения вспомогательной матрицы-ключа KQ;

- производят вычисление вспомогательной матрицы-ключа KQ;

- производят вычисление результирующей матрицы состояний SQL по формуле:

SQL = SQ ⊕ KQ mod256;

- переводят числовые значения элементов матрицы SQL в двоичную систему счисления, соответствующую таблице символов ASCII;

- символы открытого текста записывают с помощью таблицы символов ASCII, получая значение символа X_i, соответствующее символу открытого текста, записанное в двоичной системе счисления;

- суммируют по модулю два один байт символов ASCII матрицы SQL и один байт символов X_i, получая зашифрованное сообщение Y_i.

- передают зашифрованное сообщение Y_i.

2. Способ по п.1, характеризующийся тем, что KQ вычисляют с помощью датчика случайных чисел.