Изобретение относится к измерительной технике и может быть использовано для измерения коэффициента кинематической вязкости при различных скоростях сдвиговой деформации, температуре и давлении для неньютоновских жидкостей, обладающих способностью отражать когерентное излучение.
Известны способы измерения коэффициента динамической вязкости (далее вязкости) сред, включающие определение момента силы трения на поверхности погруженного в испытуемую среду шпинделя формы цилиндр (конус, диск) при различных сдвиговых скоростях деформаций, реализованные в ротационных вискозиметрах. (Мидлман С. Течение полимеров. Пер. с англ. Ю.Н. Панова под ред. А.Я. Малкина. - М.: Мир, 1971. - 360 с., Шрамм Г. Основы практической реологии и реометрии. Пер. с англ. И.А. Лавыгина. - М: КолосС, 2003. - 312 с.).
Известен способ, включающий прокачку испытуемой среды через канал известного размера и определение напряжения и сдвиговой скорости деформации на стенке канала, реализованный в капиллярных вискозиметрах (патент SU №1716388, МПК G01N 11/04, публ. 1992 г.).
Общим недостатком этих способов является невозможность создания условий однородности полей механических величин на поверхности шпинделя (для ротационных вискозиметров) и в объеме канала (для капиллярных вискозиметров), что ведет к возникновению погрешности расчета касательных напряжений, сдвиговых скоростей деформаций и, как следствие, вязкости.
Наиболее близким по физическим условиям течения испытуемой среды и технической реализации используемого вискозиметра является способ, включающий прокачку испытуемой среды через канал формы тор под действием изменяющихся во времени сил инерции и трения среды, возникших в результате резкой остановки вращающегося вокруг своей оси тора, и определение параметров движения среды, а именно, касательного напряжения и сдвиговой скорости деформации на поверхности канала (патент RU №2589753, МПК G0lN l1/04, публ. 2016 г.).
Недостатками этого способа являются допущение о профиле скорости в канале, что вносит дополнительную погрешность в вычисление скорости сдвиговой деформации, а также габариты вискозиметра, и, как следствие, необходимость в большом объеме испытуемой жидкости (300 мл).
Техническая задача состоит в повышении точности измерения вязкости как функции от сдвиговых скоростей деформаций, давления и температуры для неньютоновских жидкостей, обладающих способностью отражать когерентное излучение, при минимальном количестве измеряемых параметров.
Техническая задача достигается тем, что инерционный способ измерения вязкости неньютоновских жидкостей включает плавный разгон и резкую остановку вращающегося вокруг своей оси замкнутого прозрачного тора, заполненного испытуемой жидкостью со светоотражающими свойствами, и определение кинематических параметров инерционного течения, а именно, скорости сдвиговой деформации на поверхности течения и объемного расхода, по которым из упрощенного уравнения Навье-Стокса численно определяют кинематическую вязкость жидкости, при этом измерение кинематических характеристик производят косвенно с помощью предварительно обученной сверточной нейронной сети ResNetl8, на вход которой подаются изображения течения жидкости, освещенной когерентным излучением, в фиксированные моменты времени, полученные с помощью высокоскоростной КМОП-камеры, в выходном слое нейронной сети вычисляются значения скорости сдвиговой деформации и объемного расхода.
Технический результат заключается в повышении точности измерений вязкости неньютоновских жидкостей, зависящей от давления, скоростей сдвиговых деформаций и температуры при минимальном количестве измеряемых параметров, что позволяет отказаться от гипотезы о профиле скорости в канале и приближенного вычисления скорости сдвиговой деформации, а также отказаться от измерения крутящего момента. Вместо этого, скорость сдвиговой деформации определяется с помощью сверточной нейронной сети, предварительно обученной на размеченной обучающей выборке, представляющей собой совокупность изображений течения в тонкой прозрачной трубке в каждый момент времени и вычисленные аналитически значения скорости сдвиговой деформации и объемного расхода.
Для достижения технического результата необходимо произвести следующее.
Плавно разгоняют и резко останавливают тор, характеризуемый радиусом образующей окружности r и расстоянием R от центра оси симметрии тора до центра образующей окружности. Вязкая среда закачана в тор под давлением р0. Исследованию подлежит инерционное движение жидкости, возникшее в результате резкой остановки тора. Предполагается, что до начального момента времени (момента остановки тора) окружная скорость всех частиц среды составляет V0, после остановки тора среда продолжает движение под действием сил инерции и трения. Предполагается также, что в исследуемый промежуток времени действие силы гравитации незначительно, а движение жидкости происходит по стационарным линиям тока, образованным множеством соосных окружностей.
Основными уравнениями, описывающими этот процесс, являются уравнения Навье-Стокса, неразрывности и конвективной теплопроводности (Лойцянский, Л.Г. Механика жидкости и газа. М.: Дрофа, 2003. - 870 с.). Эти уравнения удобнее записать в тороидальной системе координат с коэффициентами Лямэ (Корн Г., Корн Т. Справочник по математике для научных работников и инженеров: Определения. Теоремы. Формулы. Пер. И.Г. Арамановича. - 6. изд., стер. - СПб.: Лань, 2003. - 831 с.): Н1=1, Н2=β1 cos β3+R, Н3=β1. Переход к криволинейной системе координат позволяет значительно упростить модель, во-первых, поле скоростей будет иметь одну ненулевую компоненту  во-вторых, упростится форма записи граничных условий. А уравнение неразрывности примет тривиальный вид: ∂υ2/∂β2=0. Из последнего следует, что υ2 не зависит от координаты β2, т.е. υ2=υ(β1, β3).
во-вторых, упростится форма записи граничных условий. А уравнение неразрывности примет тривиальный вид: ∂υ2/∂β2=0. Из последнего следует, что υ2 не зависит от координаты β2, т.е. υ2=υ(β1, β3).
Так как среда закачана в тор под некоторым постоянным давлением р0, тогда в силу симметрии области течения давление является функцией двух координат p(β1, β3).
Для определения условий однородности полей давления и температур, уравнения математической модели представлены в безразмерном виде. Обезразмеривающие величины выбирались так, чтобы безразмерные координаты и функции изменялись в диапазоне [0,1]. Способ обезразмеривания представлен в таблице.

Основные уравнения (Навье-Стокса и теплового баланса), описывающие исследуемый процесс в безразмерном виде в криволинейных координатах βi с учетом принятых в постановке задачи допущений, примут вид:

где  - аналог критерия Эйлера (далее критерий Эйлера);
- аналог критерия Эйлера (далее критерий Эйлера);
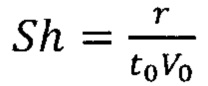 - критерий Струхаля;
- критерий Струхаля;
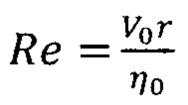 - критерий Рейнольдса;
- критерий Рейнольдса;
 - критерий Прандтля;
- критерий Прандтля;
 - критерий Эккерта;
- критерий Эккерта;
 - безразмерные геометрические критерий;
- безразмерные геометрические критерий;
V0=ωR - характерная скорость (максимальная) течения жидкости;
t0 - время инерционного течения жидкости до остановки;
ΔТ - изменение температуры жидкости;
η0 - характерная кинематическая вязкость исследуемой жидкости;
ρ - плотность исследуемой жидкости.
По первому и третьему уравнению системы (1) можно определить условие однородности поля давлений. Правые части этих уравнений являются пренебрежимо малыми по сравнению с компонентами градиента давления в левой части уравнений при условии:

Условие (2) определяет соотношение аналога критерия Эйлера 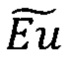 с геометрическим параметром γ. Значение геометрического параметра определено размером конструкции устройства и имеет порядок γ~101. Из условия (2) можно определить условия для окружной скорости течения V0 при фиксированных значениях геометрического параметра, характерного давления и плотности жидкости.
с геометрическим параметром γ. Значение геометрического параметра определено размером конструкции устройства и имеет порядок γ~101. Из условия (2) можно определить условия для окружной скорости течения V0 при фиксированных значениях геометрического параметра, характерного давления и плотности жидкости.
Первое слагаемое в правой части четвертого уравнения системы (1) отвечает за перенос тепла от слоя к слою жидкости. Порядок этого слагаемого зависит от критерия Прандтля Pr и безразмерного геометрического параметра γ. Второе слагаемое в правой части четвертого уравнения системы (1) характеризует перенос тепла за счет вынужденной конвекции. Порядок этого слагаемого зависит от критерия Эккерта Ec. Порядок величины левой части четвертого уравнения зависит от критерия Струхаля Sh и Рейнольдса Re. Таким образом, добиться однородности температурного поля в канале можно накладыванием следующего условия на эти критерии:

Выражение (3) определяет условия, при которых слагаемые в правой части четвертого уравнения (1) являются пренебрежимо малыми по сравнению с левой частью уравнения. Порядок числа Рейнольдса определяется из условия (3) при фиксированном значении радиуса тора r и характерной вязкости η0. Критерий Прандтля Pr определяется свойствами среды. Число Эккерта Ec зависит от характерной скорости, определяемой по условию (3), а также от величины ΔТ, поэтому при оценке его порядка учитывалось условие незначительного перепада температур [10-1; 100]. Из условия (3) определяется порядок величины характерного времени t0 инерционного движения жидкости в рассматриваемом канале.
Таким образом, можно определить условия однородности полей давлений и температур из условий (2), (3). Можно определить значения окружной скорости движения тора V0 до остановки по условию (2) и времени течения жидкости после остановки тора по условию (3), в течение которого необходимо проводить измерения. При этом остальные параметры фиксируются заранее.
Анализируя слагаемые второго уравнения системы (1) с учетом выполнения условий (2), (3), получится упрощенное уравнение, которое для дальнейших вычислений удобнее записать в размерном виде:

где υ=υ(β1) осевая компонента скорости;
η - коэффициент кинематической вязкости исследуемой жидкости.
Уравнение (4) можно использовать для определения кинематической вязкости при заданном поле скоростей. Для этого его можно проинтегрировать по толщине канала, с учетом граничного условия 

После некоторых преобразований левой части уравнения, заменяя 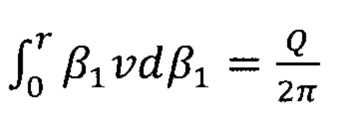 можно получить следующее выражение:
можно получить следующее выражение:
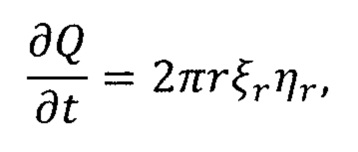
где  - значение скорости сдвига на поверхности течения; ηr - значение кинематической вязкой на поверхности течения (далее η), зависит от ξr; Q - объемный расход жидкости через сечение.
- значение скорости сдвига на поверхности течения; ηr - значение кинематической вязкой на поверхности течения (далее η), зависит от ξr; Q - объемный расход жидкости через сечение.
Производную в левой части уравнения можно заменить на центральную конечную разность. Тогда кинематическую вязкость можно определять через скорость сдвиговой деформации и изменение расхода в каждый момент времени tk:

где ξk - значения скорости сдвига на поверхности течения в каждый момент времени tk;
Qk+1, Qk-1 - значение расхода на предыдущем и следующем шаге по времени;
Δt=tk+1-tk - шаг по времени, постоянный.
Значения скорости сдвига на поверхности  и значения расхода Qk в каждый момент времени tk определяется с помощью программы расчета, в основу которой заложена предварительно обученная сверточная нейронная сеть. Изображения течения жидкости, полученные через равные промежутки времени Δt, подаются на вход нейронной сети, сверточные слои которой преобразуют эти изображения и передают на слои аппроксиматора, выходной слой сети содержит два нейрона (для скорости сдвиговой деформации и объемного расхода). Таким образом, за время измерений t0 (время инерционного течения в торе) определяется массив значений скорости сдвига и объемного расхода, по которым с помощью итерационной формулы (5), полученной из уравнения Навье-Стокса, рассчитываются соответствующие значения кинематической вязкости.
и значения расхода Qk в каждый момент времени tk определяется с помощью программы расчета, в основу которой заложена предварительно обученная сверточная нейронная сеть. Изображения течения жидкости, полученные через равные промежутки времени Δt, подаются на вход нейронной сети, сверточные слои которой преобразуют эти изображения и передают на слои аппроксиматора, выходной слой сети содержит два нейрона (для скорости сдвиговой деформации и объемного расхода). Таким образом, за время измерений t0 (время инерционного течения в торе) определяется массив значений скорости сдвига и объемного расхода, по которым с помощью итерационной формулы (5), полученной из уравнения Навье-Стокса, рассчитываются соответствующие значения кинематической вязкости.
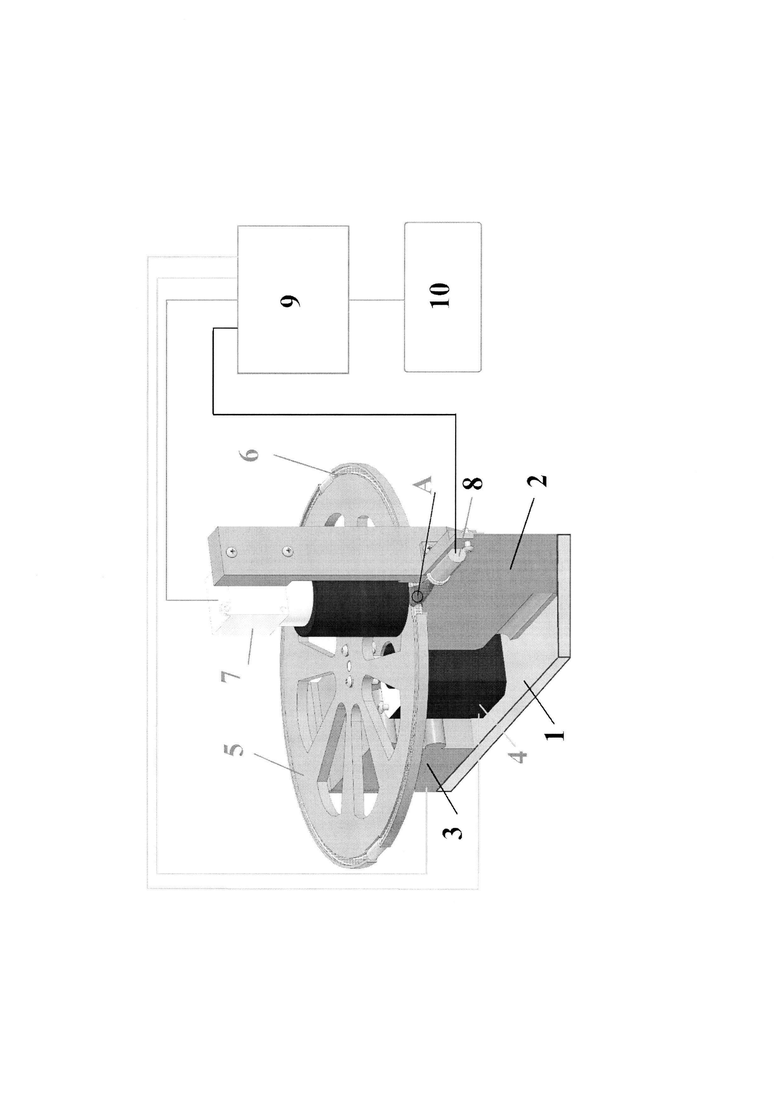
Для осуществления способа использовано устройство, содержащие опору 1, на которой установлены стойка 2, тормозной механизм 3 и шаговый двигатель 4. На шаговом двигателе 4 установлен диск 5. На диске 5 закреплен тор 6. На стойке 2 закреплены КМОП-камера 7 и источник 8 когерентного излучения. Шаговый двигатель 4, тормозной механизм 3, источник 8 когерентного излучения и КМОП-камера 7 соединены с блоком 9 обработки информации. Блок 9 обработки информации соединен с блоком 10 отображения информации.
Способ осуществляется следующим образом.
В тор 6, установленный на диске 5, под давлением р0 закачивают испытуемую жидкость со светоотражающими свойствами. Включают шаговый двигатель 4. Установленный на нем диск 5 с тором 6 плавно разгоняют до окружной скорости V0, затем выключают шаговый двигатель 4 и включают тормозной механизм 3, при этом диск 5 с тором 6 резко останавливается. После остановки тора 6 жидкость совершает инерционное движение. В течение времени инерционного движения с помощью системы технического зрения, которая включает в себя КМОП-камеру 7 и источник 8 когерентного излучения, происходит фиксация изображений течения жидкости в точке А. Полученную информацию передают в блок 9 обработки информации, например, мини-компьютер JetsonNano с ядрами CUDA, где она обрабатывается косвенно с помощью предварительно обученной сверточной нейронной сети, и по результатам проведенной обработки производят расчет кинематических характеристик жидкости: скорости сдвиговой деформации на поверхности течения  и объемного расхода Qfe4epe3 равные промежутки времени Δt. Затем по полученным значениям кинематических характеристик с помощью итерационной формулы, полученной из уравнения Навье-Стокса, вычисляют значения кинематической вязкости испытуемой жидкости для каждого значения скорости сдвиговой деформации. Полученные данные передают на блок 10 отображения информации.
и объемного расхода Qfe4epe3 равные промежутки времени Δt. Затем по полученным значениям кинематических характеристик с помощью итерационной формулы, полученной из уравнения Навье-Стокса, вычисляют значения кинематической вязкости испытуемой жидкости для каждого значения скорости сдвиговой деформации. Полученные данные передают на блок 10 отображения информации.
Предложенный способ измерения вязкости позволяет исследовать вязкость сред со сложными реологическими свойствами, зависящими одновременно от сдвиговых скоростей деформаций, давления и температуры в широком диапазоне вышеназванных параметров, и в отличие от прототипа имеет более высокую точность определения скорости сдвиговой деформации за счет применения сверхточных нейронных сетей, что повышает точность расчета самой вязкости.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИНЕРЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ ВЯЗКОСТИ | 2014 |
|
RU2589753C2 |
| ИНЕРЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ ВЯЗКОСТИ | 2012 |
|
RU2517819C1 |
| ИНЕРЦИОННЫЙ ВИСКОЗИМЕТР | 2012 |
|
RU2522718C2 |
| Способ измерения вязкости неньютоновских жидкостей | 1989 |
|
SU1716388A1 |
| Устройство для определения реологических характеристик газосодержащих пищевых масс | 1984 |
|
SU1241103A1 |
| СПОСОБ ПЕРЕМЕШИВАНИЯ ЖИДКОСТИ | 2013 |
|
RU2543204C2 |
| СПОСОБ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ СВЯЗИ ФИЛЬТРАЦИИ/ПОВРЕЖДЕНИЙ/НАПРЯЖЕНИЙ ПРИ ВПРЫСКЕ ВОДЫ В КАМЕННОУГОЛЬНЫЙ МАССИВ ПРИ РАЙОНИРОВАНИИ | 2018 |
|
RU2743121C1 |
| СПОСОБ ВИБРАЦИОННОЙ ДИАГНОСТИКИ РОТОРНЫХ СИСТЕМ | 2020 |
|
RU2753151C1 |
| СПОСОБ СНИЖЕНИЯ СОПРОТИВЛЕНИЯ ТРЕНИЯ ТЕЛА ПОСРЕДСТВОМ ФОРМИРОВАНИЯ ВЯЗКОУПРУГОГО ПОКРЫТИЯ | 2001 |
|
RU2250175C2 |
| Способ определения реологических параметров неньютоновских жидкостей и ротационный вискозиметр для его осуществления | 1977 |
|
SU661297A1 |
Изобретение относится к измерительной технике и может быть использовано для измерения коэффициента кинематической вязкости при различных скоростях сдвиговой деформации, температуре и давлении для неньютоновских жидкостей, обладающих способностью отражать когерентное излучение. Инерционный способ измерения вязкости неньютоновских жидкостей включает плавный разгон и резкую остановку вращающегося вокруг своей оси замкнутого прозрачного тора, заполненного испытуемой жидкостью со светоотражающими свойствами, и определение кинематических параметров инерционного течения, а именно скорости сдвиговой деформации на поверхности течения и объемного расхода, по которым из упрощенного уравнения Навье-Стокса численно определяют кинематическую вязкость жидкости, при этом измерение кинематических характеристик производят косвенно с помощью предварительно обученной сверточной нейронной сети, на вход которой подаются изображения течения жидкости, освещенной когерентным излучением, в фиксированные моменты времени, полученные с помощью высокоскоростной КМОП-камеры. Техническим результатом является повышение точности измерений вязкости неньютоновских жидкостей. 1 ил., 1 табл.
Инерционный способ измерения вязкости неньютоновских жидкостей, включающий плавный разгон и резкую остановку вращающегося вокруг своей оси замкнутого прозрачного тора, заполненного испытуемой жидкостью со светоотражающими свойствами, и определение кинематических параметров инерционного течения, а именно скорости сдвиговой деформации на поверхности течения и объемного расхода, по которым из упрощенного уравнения Навье-Стокса численно определяют кинематическую вязкость жидкости, при этом измерение кинематических характеристик производят косвенно с помощью предварительно обученной сверточной нейронной сети, на вход которой подаются изображения течения жидкости, освещенной когерентным излучением, в фиксированные моменты времени, полученные с помощью высокоскоростной КМОП-камеры.
| ИНЕРЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ ВЯЗКОСТИ | 2014 |
|
RU2589753C2 |
| Способ измерения вязкости неньютоновских жидкостей | 1989 |
|
SU1716388A1 |
| ИНЕРЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ ВЯЗКОСТИ | 2012 |
|
RU2517819C1 |
| JP 2011027593 A, 10.02.2011. | |||
Авторы
Даты
2023-02-07—Публикация
2022-05-05—Подача