ИНЕРЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ ВЯЗКОСТИ Российский патент 2014 года по МПК G01N11/04 

Изобретение относится к измерительной технике и может быть использовано для измерения коэффициента динамической вязкости текучих сред со сложными реологическими свойствами, зависящими от скорости сдвига, давления и температуры.

Известен способ измерения коэффициента динамической вязкости (далее вязкости) сред, включающий определение момента силы трения на поверхности погруженного в испытуемую среду шпинделя формы цилиндр (конус, диск) при различных скоростях сдвига для испытуемой и эталонной сред (Мидлман С. Течение полимеров. Пер. с англ. Ю.Н.Панова под ред. А.Я.Малкина. - М.: Мир, 1971. - 360 с.). Способ реализован в ротационных вискозиметрах (Мидлман С. Течение полимеров. Пер. с англ. Ю.Н.Панова под ред. А.Я.Малкина. - М.: Мир, 1971. - 360 с.). Недостатком способа является невозможность создания на поверхности шпинделя условий однородности полей механических величин, что ведет к возникновению погрешности расчета касательных напряжений, сдвиговых скоростей деформаций и, как следствие, вязкости. Другим недостатком способа является сложность конструкции устройства, реализующего измерение вязкости при различных значениях гидростатического давления в испытуемой среде. Существенным совпадающим признаком аналога с заявляемым изобретением является процедура измерения момента силы трения на поверхности контакта среды и элемента устройства измерения вязкости.

Наиболее близким по физическим условиям течения испытуемой среды является способ, включающий прокачку испытуемой среды через канал известного размера и определение напряжения и скорости сдвига на стенке канала (Патент СССР №1716388, МПК G01N 11/04, опубл. 1992 г.). Способ реализован в капиллярных вискозиметрах. Недостатком способа является невозможность создания в объеме и на поверхности канала условий однородности гидростатического давления, так как процесс течения испытуемой среды обеспечивается именно перепадом давления по длине канала, что ведет к невозможности исследования сред, реологические свойства которых зависят от величины гидростатического давления. Существенными совпадающими признаками аналога (прототипа) с заявляемым изобретением являются физические условия течения, а именно реализация Пуазейлевского течения (Мидлман С. Течение полимеров. Пер. с англ. Ю.Н.Панова под ред. А.Л.Малкина. - М.: Мир, 1971. - 360 с.), а также наличие процедуры определения касательного напряжения и сдвиговой скорости деформации на поверхности канала.

Задача, на решение которой направлено изобретение, состоит в получении способа измерения вязкости сред со сложными реологическими свойствами, зависящими от скорости сдвига, давления и температуры.

Поставленная задача достигается тем, что в отличие от прототипа течение испытуемой среды происходит в замкнутом канале формы тор под действием сил инерции и трения. Такое течение при определенных геометрических, кинематических и статических параметрах устройства обеспечивает с требуемой точностью выполнение требуемых условий однородности полей термомеханических величин. Определение величин касательного напряжения, скорости сдвиговой деформации и температуры испытуемой среды на поверхности тора, а также гидростатического давления во всем объеме тора, позволяет определить величину вязкости при различных значениях выше перечисленных параметров. Предлагаемый способ заключается в плавном разгоне и резкой остановке тора с испытуемой средой с последующим в процессе инерционного торможения измерением момента силы трения и профиля скорости среды вблизи стенки тора.

Сущность изобретения заключается в следующем.

По сути, вязкость является коэффициентом пропорциональности между компонентами девиатора напряжений и девиатора скоростей деформаций в обобщенном законе Р.Гука, описывающем реологическое поведение изотропных вязкопластичных сред в рамках основных положений механики сплошных сред и безмоментной теории напряжений (Кучеряев Б.В. Механика сплошных сред (теоретические основы обработки давлением композитных металлов с задачами и решениями, примерами и упражнениями): Учебник для вузов. М.: МИСиС, 2006. - 604 с.):

$$D_{\sigma }=2\mu D_{\xi },\left(1\right)$$

где D_σ - девиатор напряжений с компонентами s_ij;

µ - вязкость;

D_ξ - девиатор скоростей деформаций с компонентами e_ij.

Поэтому для определения вязкости необходимо знать значения соответствующих компонент тензора напряжений и скоростей деформаций в какой-либо малой окрестности движущейся среды. В случае если поля физических величин обладают свойством однородности на какой-то поверхности и (или) в каком-то объеме, то значения выше названных компонент могут быть определены по сравнительно легко измеряемым интегральным характеристикам. Например, по известному моменту силы трения на поверхности контакта с испытуемой средой при условии, что вид напряженного состояния известен и напряженное состояние является однородным, на этой поверхности можно легко найти значение касательного напряжения.

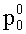
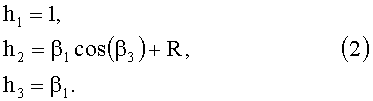
Рассмотрим изотермическое инерционное тормозящееся течение вязкой несжимаемой среды в канале формы тор, характеризуемом радиусом образующей окружности r и расстоянием от центра оси симметрии тора до центра образующей окружности R. Среда закачана в тор под давлением $$p_0^0$$ . Исследуется инерционное движение среды, возникшее в результате резкой остановки тора. До момента остановки тор достаточное количество времени вращался с угловой скоростью ω⁰, поэтому угловая скорость всех материальных частиц среды одинакова и равна ω⁰, средняя линейная скорость составляет V⁰=ω⁰R. В начальный момент времени тор останавливается, среда при этом продолжает движение под действием сил инерции и трения. Предполагается, что в исследуемый промежуток времени действие силы гравитации незначительно, а движение среды происходит по стационарным линиям тока, образованным множеством соосных окружностей. Вводятся криволинейные ортогональные координаты: β₁ - радиальная координата в плоскости образующей окружности, 0≤β₁≤r; β₂ - угловая координата в плоскости, перпендикулярной оси тора, 0≤β₂≤2π; β₃ - угловая координата в плоскости образующей окружности, перпендикулярной оси тора, 0≤β₃≤2π. Коэффициенты Г.Лямэ h_i преобразования координат составят:

$$\begin{array}{l}{h}_1=\mathrm{1,}\\ h_2={\beta }_1\cos \left({\beta }_3\right)+R,\left(2\right)\\ h_3={\beta }_1.\end{array}$$

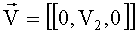
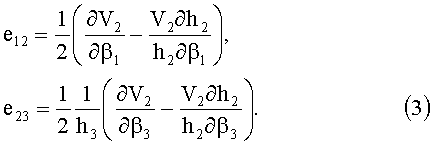
В криволинейных координатах скорость движения среды характеризуется однокомпонентным вектором скорости $$\overrightarrow{V}=\left[\left[\mathrm{0,}{V}_2\mathrm{,0}\right]\right]$$ , компоненты девиатора скоростей деформаций согласно формуле Дж.Стокса (Кучеряев Б.В. Механика сплошных сред (теоретические основы обработки давлением композитных металлов с задачами и решениями, примерами и упражнениями): Учебник для вузов. М.: МИСиС, 2006. - 604 с.) определяются по формуле:

$$\begin{array}{l}{e}_{12}=\frac{1}{2}\left(\frac{\partial V_2}{\partial {\beta }_1}-\frac{V_2\partial h_2}{h_2\partial {\beta }_1}\right),\\ e_{23}=\frac{1}{2}\frac{1}{h_3}\left(\frac{\partial V_2}{\partial {\beta }_3}-\frac{V_2\partial h_2}{h_2\partial {\beta }_3}\right).\left(3\right)\end{array}$$

Уравнения движения с учетом симметрии полей исследуемых термомеханических величин относительно оси тора ∂/∂β₂=0, что для поля скоростей совпадает с условием несжимаемости среды, имеют вид:

$$\begin{array}{l}\frac{\partial p_0}{\partial {\beta }_1}={\rho }_{ж}\frac{V_2^2\partial h_2}{h_2\partial {\beta }_1},\\ \frac{\partial V_2}{\partial t}=-\frac{1}{h_2^2{h}_3{\rho }_{ж}}\left[\frac{\partial }{\partial {\beta }_1}\left(h_2^2{h}_3{s}_{12}\right)+\frac{\partial }{\partial {\beta }_3}\left(h_2^2{s}_{23}\right)\right],\left(4\right)\\ \frac{\partial p_0}{\partial {\beta }_3}={\rho }_{ж}\frac{V_2^2}{h_2}\frac{\partial h_2}{\partial {\beta }_3},\end{array}$$

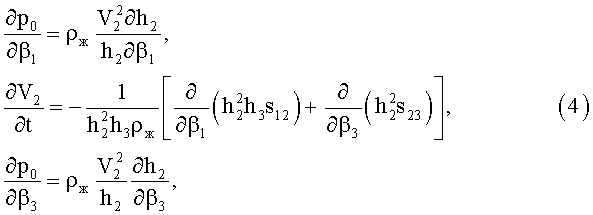
где p₀ - гидростатическое давление;

ρ_ж - плотность среды (жидкости).

Используя аппарат теории подобия и анализа размерностей, можно выполнить оценку геометрических параметров тора, начальной скорости его вращения, а также свойств среды, при которых характеристики напряженно-деформированного состояния движущейся среды на поверхности тора и поле давления во всем объеме тора будут с достаточной степенью точности однородны. Процедура обезразмеривания переменных величин представлена в таблице 1. В качестве обезразмеривающей величины вязкости µ₀ предлагается использовать вязкость, близкой по свойствам ньютоновской жидкости, а в качестве обезразмеривающей величины времени t₀ - время инерционного движения среды с момента остановки тора до момента остановки среды.

Компоненты градиента скорости ∂V₂/∂β₁ и (1/h₃)(∂V₂/∂β₃) вблизи поверхности тора можно сравнить в начальный момент времени, тогда компонента ∂V₂/∂β₁ обусловлена перепадом в результате условия прилипания среды к неподвижной стенке тора и при допущении о линейности составит приблизительно ∂V₂/∂β₁≈ω₀R/r, компонента (1/h₃)(∂V₂/∂β₃) обусловлена разницей окружных скоростей и составит приблизительно (1/h₃)(∂V₂/∂β₃)≈ω₀2r/πr. Отношение компонент градиента составит приблизительно R/r, поэтому при значительной разнице радиусов вкладом компоненты градиента (1/h₃)(∂V₂/∂β₃) в вектор градиента можно пренебречь.

Таблица 1 Обезразмеривание параметров уравнений (1)-(4) Обозначение безразмерной величины Способ определения безразмерной величины Пределы изменения безразмерной
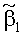
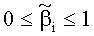
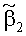
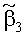
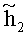
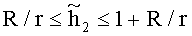
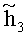
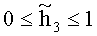
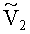
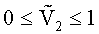
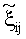
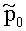
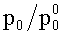
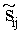
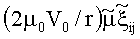
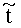
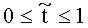
величины (если известны) $${\tilde{\beta }}_1$$ β1/r $$0\le {\tilde{\beta }}_i\le 1$$ $${\tilde{\beta }}_2$$ β₂/2π $${\tilde{\beta }}_3$$ β₃/2π $${\tilde{h}}_2$$ h₂/r $$R/r\le {\tilde{h}}_2\le 1+R/r$$ $${\tilde{h}}_3$$ h₃/r $$0\le {\tilde{h}}_3\le 1$$ $${\tilde{V}}_2$$ V₂/V ₀ $$0\le {\tilde{V}}_2\le 1$$ $${\tilde{\xi }}_{ij}$$ rξ_ij/V₀ - $${\tilde{p}}_0$$ $$p_0/p_0^0$$ - $${\tilde{s}}_{ij}$$ $$\left(2{\mu }_0{V}_0/r\right)\tilde{\mu }{\tilde{\xi }}_{ij}$$ - $$\tilde{t}$$ t/t₀ $$0\le \tilde{t}\le 1$$

С целью оценки значимости отдельных членов в уравнениях (1)-(4) вводятся безразмерный геометрический критерий γ=r/R, число Рейнольдса Re=(rV₀ρ_ж)/µ₀, число Струхаля Sh=r/(t₀V₀) и аналог числа Эйлера 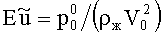$$E\tilde{u}=p_0^0/\left({\rho }_{ж}{V}_0^2\right)$$ . Порядок величин компонент девиатора скоростей деформаций и правых частей уравнений движения представлен в таблице 2.

Таким образом, при условии малости геометрического параметра (γ≤10^-2) можно с погрешностью порядка γ утверждать, что компоненты девиатора скоростей деформаций (3) имеют вид:

$$\begin{array}{l}{e}_{12}=\frac{1}{2}\frac{\partial V_2}{\partial {\beta }_1},\\ e_{23}=0.\left(5\right)\end{array}$$

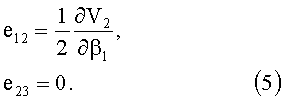
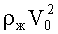
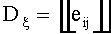
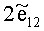
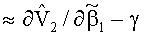
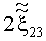
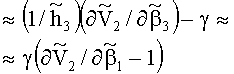
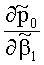
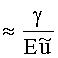
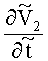
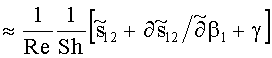
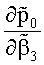
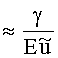
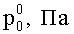
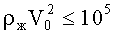
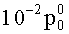
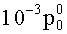
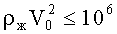
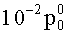
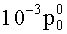
Девиатор скоростей деформаций (5) однороден по всей поверхности тора. Для выполнения с заданной точностью условия однородности поля давления p₀ по всему объему тора гидродинамический напор $${\rho }_{ж}{V}_0^2$$ следует выбирать согласно рекомендациям, приведенным в таблице 3.

Таблица 2 Порядок величин членов уравнений (1)-(4) Элемент математической модели Физическая величина или слагаемое уравнения Порядок величины Примечание Девиатор скоростей деформаций $$D_{\xi }=\lfloor \lfloor e_{ij}\rfloor \rfloor$$ $$2{\tilde{e}}_{12}$$ $$\approx \partial {\widehat{V}}_2/\partial {\tilde{\beta }}_1-\gamma$$ γ≤10^-2 $$2{\tilde{\tilde{\xi }}}_{23}$$ $$\begin{array}{l}\approx \left(1/{\tilde{h}}_3\right)\left(\partial {\tilde{V}}_2/\partial {\tilde{\beta }}_3\right)-\gamma \approx \\ \approx \gamma \left(\partial {\tilde{V}}_2/\partial {\tilde{\beta }}_1-1\right)\end{array}$$ Уравнение движения:   проекция на ось β₁ $$\frac{\partial {\tilde{p}}_0}{\partial {\tilde{\beta }}_1}$$ $$\approx \frac{\gamma }{E\tilde{u}}$$ γ≤10^-2 проекция на ось β₂ $$\frac{\partial {\tilde{V}}_2}{\partial \tilde{t}}$$ $$\approx \frac{1}{\mathrm{Re}}\frac{1}{Sh}\left[{\tilde{s}}_{12}+\partial {\tilde{s}}_{12}/\tilde{\partial }{\beta }_1+\gamma \right]$$ γ≤10^-2 проекция на ось β₃ $$\frac{\partial {\tilde{p}}_0}{\partial {\tilde{\beta }}_3}$$ $$\approx \frac{\gamma }{E\tilde{u}}$$ γ≤10^-2

Таблица 3 Условия однородности поля давления γ $$p_0^0,\text{ Па}$$ Рекомендуемая величина гидродинамического напора, Па Порядок величины перепада давления по направлению, Па 0≤β₁≤r 0≤β₃≤π 10^-2 10⁵ $${\rho }_{ж}{V}_0^2\le {10}^5$$ $${10}^{-2}{p}_0^0$$ 10^-3 10⁵ $${10}^{-3}{p}_0^0$$ 10^-2 10⁶ $${\rho }_{ж}{V}_0^2\le {10}^6$$ $${10}^{-2}{p}_0^0$$ 10^-3 10⁶ $${10}^{-3}{p}_0^0$$

Таким образом, при выполнении условий малости геометрического параметра (γ≤10^-2), а также кинематических и статических условий

таблицы 3 можно с точностью порядка 10⁰% и меньше определять вязкость испытуемой среды по формуле:

$$\mu =s_{12}/\left(\frac{\partial V_2}{\partial {\beta }_1}\right).\left(6\right)$$

Компонента девиатора напряжений s₁₂ является, по сути, касательным напряжением на поверхности тора, возникающим по причине инерционного тормозящегося течения испытуемой среды, и может быть определена на поверхности тора по известному моменту силы трения М:

$$s_{12}=M/\left({\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\left(r\cos {\beta }_3+R\right)}^{2}rd{\beta }_{2}d{\beta }_3}}\right)\approx M/\left(2{\pi }^2{R}^{2}r\right).\left(7\right)$$

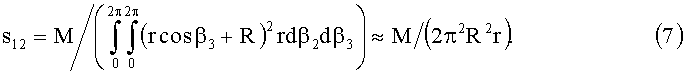
Градиент скорости ∂V₂/∂β₁ может быть определен по результатам измерения скорости течения с помощью доплеровского измерителя скорости (Мидлман С. Течение полимеров. Пер. с англ. Ю.Н.Панова под ред. А.Я.Малкина. - М.: Мир, 1971. - 360 с.).

Способ осуществляется следующим образом.

В тор под давлением 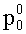$$p_0^0$$ закачивается испытуемая среда. Затем тор плавно разгоняется до угловой скорости ω⁰, удовлетворяющей рекомендациям по величине гидродинамического напора (таблица 3), и резко останавливается. После остановки тора жидкость продолжает движение, в течение этого времени показания датчиков скорости и крутящего момента передаются на ЭВМ. Затем в фиксированный момент времени вычисляется величина касательного напряжения на поверхности тора по формуле (7) и градиент скорости жидкости на поверхности тора в виде конечно-разностного аналога производной: ∂V₂/∂β₁≈ΔV₂/Δβ₁. По формуле (6) определяется вязкость.

Предложенный способ измерения вязкости позволяет исследовать вязкость сред со сложными реологическими свойствами, зависящими одновременно от скорости сдвига, давления и температуры в широком диапазоне выше названных параметров. Выработанные рекомендации по выбору параметров и условий исследования позволяют производить высокоточные измерения вязкости.

Изобретение относится к измерительной технике и может быть использовано для измерения коэффициента динамической вязкости текучих сред со сложными реологическими свойствами, зависящими от скорости сдвига, давления и температуры. Способ измерения вязкости включает прокачку испытуемой среды через канал круглой формы поперечного сечения и определение параметров движения среды, а именно касательного напряжения и сдвиговой скорости деформации на поверхности канала, по которым определяют вязкость среды. При этом канал имеет замкнутую форму тора, а прокачка испытуемой среды происходит под действием сил инерции и трения среды, возникших в результате резкой остановки вращающегося вокруг своей оси тора. Техническим результатом является повышение точности определения вязкости сред со сложными реологическими свойствами, зависящими одновременно от скорости сдвига, давления и температуры в широком диапазоне перечисленных параметров. 3 табл.

Способ измерения вязкости, включающий прокачку испытуемой среды через канал круглой формы поперечного сечения и определение параметров движения среды, а именно касательного напряжения и сдвиговой скорости деформации на поверхности канала, по которым определяют вязкость среды, отличающийся тем, что канал имеет замкнутую форму тора, а прокачка испытуемой среды происходит под действием изменяющихся во времени сил инерции и трения среды, возникших в результате резкой остановки вращающегося вокруг своей оси тора.