Изобретение относится к измерительной технике и может быть использовано для измерения коэффициента динамической вязкости сред со сложными реологическими свойствами, зависящими от сдвиговых скоростей деформаций, давления и температуры.
Известны способы измерения коэффициента динамической вязкости (далее вязкости) сред, включающие определение момента силы трения на поверхности погруженного в испытуемую среду шпинделя формы цилиндр (конус, диск) при различных сдвиговых скоростях деформаций (Мидлман С. Течение полимеров. Пер. с англ. Ю.Н. Панова под ред. А.Я. Малкина. - М.: Мир, 1971. - 360 с.). Способ реализован в ротационных вискозиметрах. Известен способ, включающий прокачку испытуемой среды через канал известного размера и определение напряжения и сдвиговой скорости деформации на стенке канала (SU №1716388, МПК G01N 11/04, заяв. 30.05.1989 г., опубл. 29.02.1992 г., бюл. №8). Способ реализован в капиллярных вискозиметрах.
Общим недостатком этих способов является невозможность создания условий однородности полей механических величин на поверхности шпинделя (для ротационных) и в объеме канала (для капиллярных), что ведет к возникновению погрешности расчета касательных напряжений, сдвиговых скоростей деформаций и, как следствие, вязкости.
Наиболее близким по физическим условиям течения испытуемой среды и технической реализации используемого вискозиметра является способ, включающий прокачку испытуемой среды в замкнутом канале формы тор под действием сил инерции и трения (RU №2517819, МПК G01N 11/04, заяв. 06.11.2012 г., опубл. 27.05.2014 г., бюл. №15). Такое течение при определенных геометрических, кинематических и статических параметрах устройства обеспечивает с требуемой точностью выполнение требуемых условий однородности полей термомеханических величин. Определение величин касательного напряжения, сдвиговой скорости деформации и температуры испытуемой среды на поверхности тора, а также гидростатического давления во всем объеме тора позволяет определить величину вязкости при различных значениях выше перечисленных параметров. Способ заключается в плавном разгоне и резкой остановке тора с испытуемой средой, с последующим в процессе инерционного торможения измерением момента силы трения и профиля скорости среды вблизи стенки тора.
Недостатком этого способа является необходимость применения приборов для измерения скорости потока по толщине канала, что ограничивает выбор материала тора и увеличивает стоимость вискозиметра. Также возникает необходимость приближенного вычисления сдвиговой скорости деформации путем численного интегрирования экспериментальных данных, что приводит к возникновению существенной погрешности. Существенными совпадающими признаками аналога (прототипа) с заявляемым изобретением являются физические условия течения, а именно инерционное течение в замкнутом торе, а также процедура измерения момента силы трения на поверхности тора.
Задача, на решение которой направлено изобретение, состоит в получении способа измерения вязкости сред со сложными реологическими свойствами, зависящими от сдвиговых скоростей деформаций, давления и температуры при минимальном количестве измеряемых параметров.
Поставленная задача достигается тем, что прокачка испытуемой среды происходит в устройстве по патенту RU №2522718, МПК G01N 11/14, заяв. 06.11.2012 г., опубл. 20.07.2014 г., бюл. №20. Такое течение при определенных геометрических, кинематических и статических параметрах обеспечивает с требуемой точностью выполнение требуемых условий однородности полей термомеханических величин.
Предлагаемый инерционный способ включает прокачку испытуемой среды через канал формы тор под действием изменяющихся во времени сил инерции и трения среды, возникших в результате резкой остановки вращающегося вокруг своей оси тора, и определение параметров движения среды, а именно касательного напряжения и сдвиговой скорости деформации на поверхности канала, и отличается от прототипа тем, что измеряют в процессе инерционного движения среды только момент результирующей силы трения, по значениям которого в каждый момент времени определяют величину касательного напряжения, затем численным решением уравнения движения сплошной среды определяют сдвиговую скорость деформации и вязкость. Таким образом, предлагаемый способ позволяет отказаться от дополнительного устройства измерения скорости слоев жидкости и дальнейшего определения сдвиговой скорости деформации путем численного дифференцирования экспериментальных данных. Вместо этого сдвиговая скорость деформации определяется из уравнения движения Навье-Стокса с учетом допущений, обоснованных с применением аппарата теории подобия и анализа размерностей.
Технический результат, который может быть получен при осуществлении заявленного способа, заключается в повышении точности измерений вязкости сред со сложными реологическими свойствами, зависящими от давления, сдвиговых скоростей деформаций и температуры при минимальном количестве измеряемых параметров.
Сущность изобретения заключается в следующем.
Вязкость определяется из обобщенного закона Гука, описывающего реологическое поведение изотропных вязкопластичных сред в рамках основных положений механики сплошных сред и безмоментной теории напряжений (Кучеряев Б.В. Механика сплошных сред (теоретические основы обработки давлением композитных металлов с задачами и решениями, примерами и упражнениями): Учебник для вузов. - М.: МИСиС, 2006. - 604 с.), и является коэффициентом пропорциональности между компонентами девиатора тензора напряжений и девиатора тензора скоростей деформаций:

где Dσ - девиатор тензора напряжений с компонентами sij;
µ - вязкость;
Dξ - девиатор тензора скоростей деформаций с компонентами eij.
Таким образом, для определения вязкости необходимо знать значения соответствующих компонент тензора напряжений и сдвиговых скоростей деформаций в какой-либо малой окрестности движущейся среды. В случае, если поля физических величин обладают свойством однородности на какой-то поверхности и (или) в каком-то объеме, то значения выше названных компонент могут быть определены по сравнительно легко измеряемым интегральным характеристикам. Например, по известному моменту силы трения на поверхности контакта с испытуемой средой, при условии, что вид напряженного состояния известен и напряженное состояние является однородным, на этой поверхности можно определить значение касательного напряжения.
Предлагаемый способ заключается в прокачке испытуемой среды через канал формы тор, характеризуемый радиусом образующей окружности r и расстоянием от центра оси симметрии тора до центра образующей окружности R. Вязкая среда закачана в тор под давлением Р0. Исследуется инерционное движение жидкости, возникшее в результате резкой остановки тора. Предполагается, что до начального момента времени (момента остановки тора) окружная скорость всех частиц среды составляет V0, после остановки тора среда продолжает движение под действием сил инерции и трения. Предполагается также, что в исследуемый промежуток времени действие силы гравитации незначительно, а движение жидкости происходит по стационарным линиям тока, образованным множеством соосных окружностей.
Для упрощения задания граничных условий и решения основных уравнений, описывающих данный процесс, была введена в рассмотрение криволинейная ортогональная система координат βi, характеризуемая коэффициентами Лямэ:

где β1 - радиальная координата в плоскости образующей окружности;
β2 - угловая координата в плоскости, перпендикулярной оси тора;
β3 - угловая координата в плоскости образующей окружности, перпендикулярной оси тора.
Основные уравнения (Навье-Стокса и теплового баланса), описывающие исследуемый процесс в безразмерном виде в криволинейных координатах βi с учетом принятых в постановке задачи допущений, имеют вид:
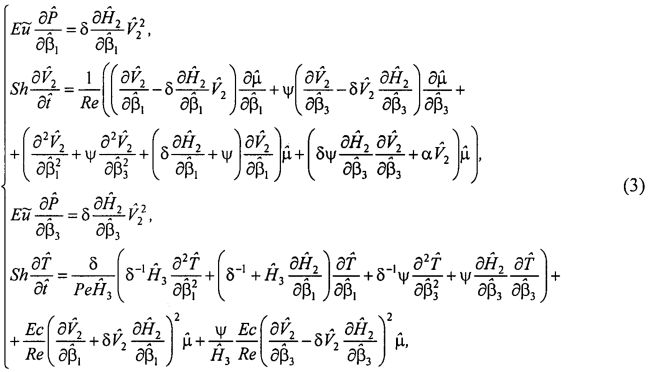
где 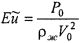 - число Эйлера;
- число Эйлера;
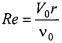 - число Рейнольдса;
- число Рейнольдса;
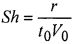 - число Струхаля;
- число Струхаля;
Pe=PrRe - число Пекле;
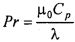 - число Прандтля;
- число Прандтля;
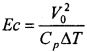 - число Эккерта;
- число Эккерта;
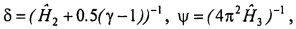
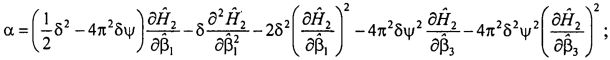
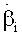
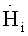
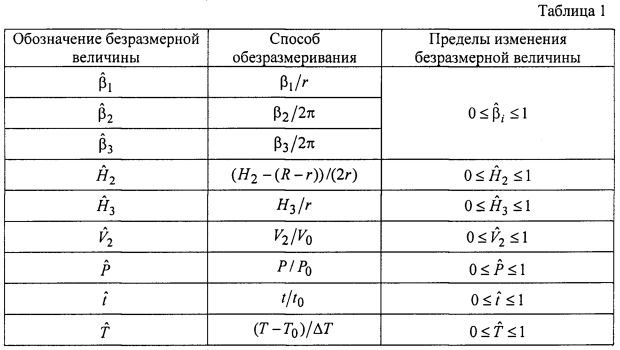
Способ обезразмеривания параметров математической модели приведен в табл. 1 для каждой неизвестной функции и независимых координат. В качестве обезразмеривающей величины вязкости µ0 предлагается использовать вязкость базовой жидкости, например воды при комнатной температуре, а в качестве обезразмеривающей величины времени t0 - время инерционного движения жидкости с момента остановки тора до момента остановки жидкости. Для обезразмеривания координат используются характерные геометрические размеры области течения (масштабы).
Используя аппарат теории подобия и анализа размерностей (Л.И. Седов. Методы подобия и размерности в механике: 8-е изд., перераб. - М.: Наука, 1977. - 440 с.), можно выполнить оценку слагаемых в безразмерных уравнениях движения и конвективной теплопроводности в системе уравнений (3) для того, чтобы определить условия однородности полей давления и температуры.
Компоненты градиента давления входят только в первое и третье уравнение системы (3). Поле давлений будет однородным, если безразмерные коэффициенты, стоящие при безразмерных компонентах градиента давления, значительно превосходят коэффициенты перед слагаемыми в правой части, т.е. выполняется условие:

Из условия (4) можно определить порядок величины скоростного напора 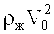
Для определения условия однородности поля температур необходимо проанализировать уравнение конвективной теплопроводности, полученного из закона сохранения энергии для случая вязкой несжимаемой жидкости (Н.А. Слезкин. Динамика вязкой несжимаемой жидкости. - М.: Государственное издательство технико-технической литературы, 1955. - 519 с.). В правой части последнего безразмерного уравнения системы (3) первое слагаемое отвечает за перенос тепла от слоя к слою жидкости и его порядок определяется безразмерным гидродинамическим критерием подобия - числом Pe и геометрическим параметром δ. Два других слагаемых характеризуют перенос тепла за счет вынужденной конвекции и их порядок определяется числами Ec и Re, а также геометрическим параметром ψ. Левая часть уравнения, в силу введенных допущений о характере движения, содержит только частную производную температуры по времени, и порядок этого слагаемого, т.е. меры нестационарности процесса, определяется числом Sh. Поле температур будет однородным, если коэффициент перед слагаемым в левой части будет являться величиной более высокого порядка, чем коэффициенты перед слагаемыми в правой части. Тогда это условие можно формализовано записать в виде:

Порядок величины числа Рейнольдса определяется по величине гидродинамического напора из условия (4), обеспечивающего однородность поля давлений. Критерий Прандтля определяется свойствами среды и, например, для воды составляет величину порядка 101 (М.А. Михеев, И.М. Михеева. Основы теплопередачи. Изд. 2-ое стереотип. - М.: «Энергия», 1977. - 341 с.). Число Эккерта зависит от характерной скорости, определяемой из условия (5), а также от величины ΔT, поэтому при оценке его порядка рассматривается необходимый незначительный перепад температур [10-1; 100]. Из условия (5) определяется порядок величины характерного времени t0 инерционного движения жидкости в рассматриваемом канале. В качестве примера для воды в таблице 2 приведены оценки критериев подобия, обеспечивающие условие однородности поля давлений и температур.

Таким образом, при проведении эксперимента необходимо задавать входные параметры в установленном диапазоне, определяемом условиями (4) и (5), чтобы добиться однородности поля давлений и температур, что обеспечит измерение вязкости при фиксированных значениях этих величин.
В системе уравнений (3) в таком случае остается только второе уравнение с двумя неизвестными функциями скорости и вязкости. Учитывая полученные условия, а также порядок безразмерных критериев подобия и геометрических параметров δ~ψ~γ-2, второе уравнение системы (3) примет вид:
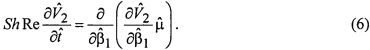
Учитывая полученные выше допущения, вязкость можно выразить из обобщенного закона Гука:

Заменив производную в левой части (6) конечной разностью, а правую часть записав на текущем шаге по времени, предварительно заметив, что слагаемое под операцией дифференцирования в правой части является не что иное, как оставшаяся ненулевая компонента девиатора тензора напряжений 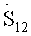

которое решается, добавляя граничное условие 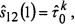 т.е значение касательного напряжения на поверхности тора, вычисленное по измеренному в каждый момент времени tk моменту силы трения. Поле скоростей при k=Nt+1, т.е. в момент остановки тора задается как
т.е значение касательного напряжения на поверхности тора, вычисленное по измеренному в каждый момент времени tk моменту силы трения. Поле скоростей при k=Nt+1, т.е. в момент остановки тора задается как 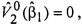 тогда после интегрирования по толщине канала уравнение (9) примет вид:
тогда после интегрирования по толщине канала уравнение (9) примет вид:
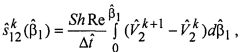
применяя граничное условие на поверхности тора в каждый фиксированный момент времени tk, как косвенно измеренное значение касательного напряжения, получено уравнение:
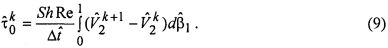
Для определения вязкости из соотношения (1) требуется знать значение производной скорости, для этого условия (9) не достаточно, поэтому в рамках рассматриваемой задачи и полученных на основе анализа размерностей допущений, вводится предположение о профиле скорости на промежутке 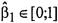 в виде полинома второй степени, удовлетворяющего граничным условиям на стенке и в центре канала соответственно:
в виде полинома второй степени, удовлетворяющего граничным условиям на стенке и в центре канала соответственно:
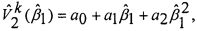
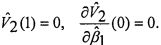
Тогда функцию скорости можно определить в виде:

Для определения коэффициента а0 в фиксированный момент времени tk, используется условие (9):
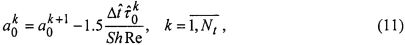
с учетом того, что в момент остановки течения 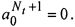
Тогда профиль скорости и сдвиговая скорость деформации примут вид соответственно:
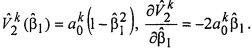
Безразмерная сдвиговая скорость деформации на поверхности тора будет определяться в каждый фиксированный момент времени tk:
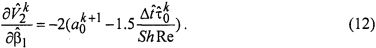
Таким образом, определив значение касательного напряжения по измеряемому моменту силы трения Mk на поверхности тора в фиксированные моменты времени tk:
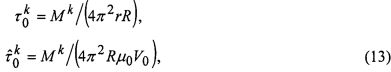
а сдвиговую скорость деформации по формуле (12) на поверхности тора при заданных значениях 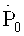
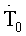
Предложенный способ измерения вязкости позволяет исследовать вязкость сред со сложными реологическими свойствами, зависящими одновременно от сдвиговых скоростей деформаций, давления и температуры в широком диапазоне выше названных параметров, и в отличие от прототипа, отсутствует необходимость в дополнительном оборудовании для измерения скорости в слоях жидкости и дальнейшем вычислении сдвиговой скорости деформации путем численного дифференцирования экспериментальных данных.
Способ осуществляется следующим образом.
В тор под давлением P0 закачивается испытуемая среда. Затем тор плавно разгоняется до окружной скорости V0, удовлетворяющей рекомендациям по величине скоростного напора (табл. 1) и резко останавливается. После резкой остановки тора испытуемая среда продолжает движение по инерции, то есть происходит прокачка испытуемой среды под действием изменяющихся во времени сил инерции и трения. В процессе инерционного движения среды измеряется момент результирующей силы трения, по значениям которого в каждый момент времени вычисляется величина касательного напряжения на внутренней поверхности тора по формуле (13) и сдвиговая скорость деформации на внутренней поверхности тора по формуле (12). Из формулы (7) определяется вязкость в безразмерном виде, которая приводится к размерному виду умножением на некоторую обезразмеривающую величину вязкости µ0 базовой жидкости.
| название | год | авторы | номер документа |
|---|---|---|---|
| ИНЕРЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ ВЯЗКОСТИ | 2012 |
|
RU2517819C1 |
| ИНЕРЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ ВЯЗКОСТИ НЕНЬЮТОНОВСКИХ ЖИДКОСТЕЙ | 2022 |
|
RU2789667C1 |
| ИНЕРЦИОННЫЙ ВИСКОЗИМЕТР | 2012 |
|
RU2522718C2 |
| Способ измерения вязкости неньютоновских жидкостей | 1989 |
|
SU1716388A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОБЪЕМНОГО И МАССОВОГО ГАЗО/ПАРОСОДЕРЖАНИЯ ДВИЖУЩЕГОСЯ ДВУХФАЗНОГО ПОТОКА В ТРУБОПРОВОДЕ | 2024 |
|
RU2838748C1 |
| ПОРОДОРАЗРУШАЮЩИЙ ИНСТРУМЕНТ | 1997 |
|
RU2127349C1 |
| СПОСОБ ОЦЕНКИ ПРЕДЕЛЬНОГО НАПРЯЖЕННОГО СОСТОЯНИЯ ГОРНЫХ ПОРОД И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1995 |
|
RU2106493C1 |
| СПОСОБ СНИЖЕНИЯ СОПРОТИВЛЕНИЯ ТРЕНИЯ ТЕЛА ПОСРЕДСТВОМ ФОРМИРОВАНИЯ ВЯЗКОУПРУГОГО ПОКРЫТИЯ | 2001 |
|
RU2250175C2 |
| СПОСОБ НЕМОНОТОННОГО ДЕФОРМИРОВАНИЯ АНИЗОТРОПНЫХ МАТЕРИАЛОВ И УСТРОЙСТВО ДЛЯ РЕАЛИЗАЦИИ СПОСОБА | 2021 |
|
RU2781869C1 |
| Устройство для оценки смазывающей способности масел | 1981 |
|
SU998922A1 |
Изобретение относится к измерительной технике и может быть использовано для измерения коэффициента динамической вязкости текучих сред со сложными реологическими свойствами, зависящими от сдвиговых скоростей деформаций, давления и температуры. Инерционный способ измерения вязкости включает прокачку испытуемой среды через канал формы тор под действием изменяющихся во времени сил инерции и трения среды, возникших в результате резкой остановки вращающегося вокруг своей оси тора, и определение параметров движения среды, а именно касательного напряжения и сдвиговой скорости деформации на поверхности канала. При этом в процессе инерционного движения среды измеряют только момент результирующей силы трения, по значениям которого в каждый момент времени определяют величину касательного напряжения, затем численным решением уравнения движения сплошной среды определяют сдвиговую скорость деформации и вязкость. Техническим результатом является повышение точности при минимальном количестве измеряемых параметров определять вязкость сред со сложными реологическими свойствами, зависящими одновременно от сдвиговых скоростей деформаций, давления и температуры в широком диапазоне перечисленных параметров. 2 табл.
Инерционный способ измерения вязкости, включающий прокачку испытуемой среды через канал формы тор под действием изменяющихся во времени сил инерции и трения среды, возникших в результате резкой остановки вращающегося вокруг своей оси тора, и определение параметров движения среды, а именно касательного напряжения и сдвиговой скорости деформации на поверхности канала, отличающийся тем, что измеряют в процессе инерционного движения среды только момент результирующей силы трения, по значениям которого в каждый момент времени определяют величину касательного напряжения, затем численным решением уравнения движения сплошной среды определяют сдвиговую скорость деформации и вязкость.
| ИНЕРЦИОННЫЙ СПОСОБ ИЗМЕРЕНИЯ ВЯЗКОСТИ | 2012 |
|
RU2517819C1 |
| ИНЕРЦИОННЫЙ ВИСКОЗИМЕТР | 2012 |
|
RU2522718C2 |
| CN 101556233 14.10.2009 | |||
| JP 2011027593 A 10.02.2011 | |||
| Способ измерения вязкости неньютоновских жидкостей | 1989 |
|
SU1716388A1 |
Авторы
Даты
2016-07-10—Публикация
2014-09-10—Подача