Изобретение относится к области машиностроения, а именно к технологии динамической балансировки ротора, например, центробежных насосов, компрессоров, экстракторов, центрифуг. Способ заключается в том, что выполняют последовательность измерительных операций, в которых закрепляют на установленном в подшипниковой опоре роторе две корректирующие массы в двух плоскостях коррекции и измеряют скорость вибрации подшипниковой опоры измерительным устройством при вращении ротора, последовательность расчетных операций, в которых рассчитывают с использованием математической модели в расчетном устройстве параметры корректирующих масс, и контрольной измерительной операции, в которой с изготовленными с расчетными параметрами корректирующими массами измеряют минимальную скорость вибрации подшипниковой опоры, соответствующую допустимому остаточному дисбалансу ротора.
Известен способ балансировки ротора в одной плоскости коррекции по патенту RU 2499985, G01M 1/16, опубликован 27.11.2013 бюллетень №33, заключающийся в том, что в опоры балансировочного стенда устанавливают ротор с двумя плоскостями коррекции - балансировочной и пробной, при вращении ротора определяют амплитуды и фазы вибраций обеих опор, повторяют эти операции с поочередно прикрепляемыми к каждой из плоскостей коррекции пробными грузами, рассчитывают коэффициенты балансировочной чувствительности стенда и коэффициенты взаимовлияния плоскостей коррекции, определяют значения и углы векторов начальных дисбалансов в каждой плоскости коррекции, находят начальные значения параметров массо-инерционной асимметрии ротора, при превышении хотя бы одним из них заданного предельно допустимого значения создают балансировочный дисбаланс в балансировочной плоскости коррекции, предварительно произведя расчет его значения и углового положения, после чего определяют остаточные значения параметров массо-инерционной асимметрии с использованием процедуры моделирования дисбалансов в обеих плоскостях.
Недостатком этого способа является необходимость многократного повторения итерационного цикла операций корректировки балансировочных дисбалансов в обеих плоскостях коррекции, обусловленная изменяющимися коэффициентами взаимовлияния плоскостей коррекции и коэффициентами балансировочной чувствительности стенда. Кроме того, способ основан на априорном знании параметров ротора: массы, расстояния от центра масс до плоскостей коррекции, значениям аксиального и экваториального моментов инерции. Отсутствие численного примера обработки экспериментальных данных с получением искомых параметров балансировочных грузов затрудняет воспроизведение предложенного способа и проверку его корректности.
Известен способ вертикальной динамической балансировки изделия по патенту RU 2674423, G01M 1/16, опубликован 10.12.2018 бюллетень №34, заключающийся в том, что изделие устанавливают на промежуточной платформе, приводят изделие во вращение и измеряют динамические реакции между промежуточной платформой и опорным основанием с помощью весоизмерительных тензометрических датчиков, причем, используют трехточечную схему установки опорно-поворотного устройства на промежуточную платформу, а изделие приводят во вращение с помощью собственного привода вращения балансируемого изделия. Сигналы с датчиков вводят в компьютер с программным обеспечением для расчета корректирующих операций. После устранения статического дисбаланса производят вертикальную динамическую балансировку традиционными методами, например, добавлением, удалением или перемещением пары балансировочных грузов, устанавливаемых в двух плоскостях коррекции.
Недостатком этого способа является необходимость многократного повторения итерационного цикла операций корректировки балансировочных дисбалансов в обеих плоскостях коррекции, обусловленная неодновременностью операций устранения статического дисбаланса и вертикальной динамической балансировки изделия, подробности которой отсутствуют в тексте описания способа. Отсутствие численного примера обработки экспериментальных данных с получением искомых параметров балансировочных грузов затрудняет воспроизведение предложенного способа и проверку его корректности.
Известен способ и устройство для балансировки ротора по патенту RU 2756710, G01M 1/32, опубликован 04.10.2021 бюллетень №28, заключающийся в том, что на роторе, установленном в двух или более подшипниках в подшипниковой опоре и содержащим множество плоскостей коррекции, в повторяющемся цикле прогонов закрепляют балансировочные грузики при разных сочетаниях их масс и углов закрепления, при вращении ротора с заданной частотой измеряют вибрации подшипниковой опоры установленными в зоне подшипников датчиками, после чего полученные данные вводят в расчетное устройство с программным обеспечением, в котором в соответствии с заданной математической моделью рассчитывают очередное приближение параметров дисбаланса балансировочных грузиков. Математическая модель основана на системе нелинейных уравнений взаимосвязи измеренной скорости вибрации с параметрами балансировочных грузиков, которую решают с использованием известных оптимизационных численных методов.
Недостатком этого способа является необходимость многократного повторения итерационного цикла операций корректировки балансировочных грузиков в плоскостях коррекции. Отсутствие подробного описания математической модели и явного представления ее системой нелинейных уравнений по результатам измерений вибрации и численного примера обработки экспериментальных данных с получением искомых параметров балансировочных грузиков затрудняет воспроизведение предложенного способа и проверку его корректности.
Известен способ балансировки роторов по патенту RU 2163008, G01M 1/00, опубликован 10.02.2001 бюллетень №4, заключающийся в том, что измеряют дисбалансы, определяют параметры корректирующих воздействий, отвечающих условию равенства нулю остаточных дисбалансов в двух плоскостях коррекции с учетом смещений центров корректирующих масс через процедуру моделирования ожидаемых последствий корректирующих воздействий, сначала для статической балансировки, а затем для моментной балансировки добиваются приведения к нулю ожидаемых равных по модулю и противолежащих остаточных дисбалансов, и производят корректировку масс ротора. Предложен алгоритм преобразования измеренных дисбалансов в параметры корректирующих воздействий, построенный на процедуре имитационного моделирования ожидаемых последствий реализации найденных параметров при корректировке масс ротора и внесении итерационных поправок к входным данным раздельно в каждой плоскости коррекции. Итерационный расчет остаточных дисбалансов по предложенному алгоритму производится поочередно, сначала для вектора центробежного момента инерции, а затем для противолежащих векторов дисбалансов.
Недостатком этого способа является необходимость многократного повторения итерационного цикла операций корректировки корректирующих воздействий в плоскостях коррекции. Кроме того, способ основан на априорном знании расстоянии от центра масс ротора до плоскостей коррекции. Отсутствие математической модели с формулой расчета корректирующих масс по результатам измерений вибрации затрудняет воспроизведение предложенного способа и проверку его корректности.
Известен способ и устройство динамической балансировки роторов по патенту RU 2208772, G01M 1/32, опубликован 20.07.2003, бюллетень №20, заключающийся в том, что закрепляют корректирующую массу на поверхности ротора в плоскости, проходящей через центр масс, закрепляют ротор на оси консольно относительно опор оси, приводят ротор во вращение и, изменяя корректирующую массу, компенсируют дисбаланс до минимального значения, по величине изменяемой корректирующей массы определяют корректирующие массы для боковых плоскостей коррекции, размещенных по разные стороны от центра масс ротора, пропорционально расстояниям каждой плоскости коррекции от центра масс, закрепляют каждую массу в соответствующей плоскости коррекции и окончательно устраняют дисбаланс, изменяя корректирующую массу в плоскости коррекции, ближней к опорам оси. Устройство для динамической балансировки роторов содержит вращающийся вал, установленный с возможностью консольного закрепления балансируемого ротора. Если ротор несимметричен и его диаметры в плоскостях коррекции различны, или центр масс находится на разных расстояниях от плоскости коррекции, то корректирующую массу разделяют на части, пропорциональные расстояниям от каждой плоскости коррекции до центра масс.Математическая модель обработки результатов основана на величине суммарного вектора дисбалансов, которая аналогично ГОСТ 22061-76 представлена в виде суммы главного вектора дисбалансов ротора и главного момента дисбалансов ротора, нормированного на расстояние между плоскостями коррекции.
Недостатком этого способа является необходимость многократного повторения итерационного цикла операций корректировки корректирующих масс в плоскостях коррекции. Кроме того, балансируемый ротор балансируется не в своих подшипниках и не со своим приводом, а способ основан на априорном знании массы ротора и расстояния от центра масс ротора до плоскостей коррекции и измерении эксцентриситета ротора датчиком перемещения, на основе которых рассчитывают дисбаланс ротора и его азимутальный угол, что является грубым приближением этих параметров ротора. Отсутствие подробного описания математической модели с формулой расчета корректирующих масс по результатам измерений вибрации затрудняет воспроизведение предложенного способа и проверку его корректности.
Данное техническое решение выбрано в качестве прототипа.
Целью изобретения является достижение технического результата, заключающегося в уменьшении длительности и трудоемкости процедуры балансировки и уменьшении остаточного дисбаланса ротора до величины, соответствующей скорости вибрации в интервале погрешности ее измерения, при минимальной величине корректирующих масс и отсутствии необходимости априорного знания массы ротора и расстояния от центра его масс до плоскостей коррекции, за счет разработки новой математической модели обработки результатов измерений в процедуре расчета параметров корректирующих дисбалансов, применения новых операций корректировки измеренной скорости вибрации, их последовательности и режимов проведения.
Технический результат достигается тем, что в способе балансировки ротора в двух плоскостях коррекции, включающий последовательность измерительных операций, в которых закрепляют на установленном в подшипниковой опоре роторе две корректирующие массы в двух плоскостях коррекции и измеряют скорость вибрации подшипниковой опоры измерительным устройством при вращении ротора, последовательность расчетных операций, в которых рассчитывают с использованием математической модели в расчетном устройстве параметры корректирующих масс, и контрольного измерения, в котором с изготовленными с расчетными параметрами корректирующими массами измеряют минимальную скорость вибрации, соответствующую допустимому остаточному дисбалансу ротора, в котором в первой последовательности измерительных операций, далее по тексту-пробный опыт, размещают обе плоскости коррекции с одной стороны от центра масс ротора, закрепляют корректирующие массы диаметрально противоположно друг другу, устанавливают дисбаланс корректирующей массы, условно первой, в ближайшей к центру масс ротора плоскости коррекции большим аналогичной величины другой корректирующей массы, условно второй, в первой последовательности расчетных операций полученные экспериментальное данные аппроксимируют с использованием математической модели суммарного вектора дисбалансов, в форме уравнения явной зависимости скорости вибрации от параметров корректирующих масс, выбирают из полученного множества решений одну совокупность дисбалансов корректирующих масс с соответствующей минимальной скоростью вибрации, уменьшают совокупность экспериментальной скорости вибрации на разность между ее минимальной аппроксимированной величиной и погрешностью измерительного устройства с получением зависимости скорректированной скорости вибрации от азимутального угла одной корректирующей массы, аппроксимируют ее по упомянутой модели, выбирают из полученного множества решений одну совокупность дисбалансов контрольных корректирующих масс со своими параметрами, а в контрольном измерении с упомянутыми выбранными корректирующими массами получают минимальную величину скорости вибрации, находящуюся внутри интервала погрешности измерительного устройства, и соответствующую минимальному остаточному дисбалансу ротора.
Упомянутые отличительные признаки заявленного способа балансировки ротора в двух плоскостях коррекции в форме новых операций, их последовательности и режимов проведения, позволяют получить новый технический результат, заключающийся в уменьшении количества экспериментов до 8-12 измерений скорости вибрации подшипниковой опоры, далее по тексту-виброскорость, уменьшении остаточного дисбаланса ротора до величины, соответствующей минимальной виброскорости в интервале погрешности ее измерения измерительным устройством при минимальной величине корректирующих масс и отсутствии необходимости априорного знания параметров дисбаланса ротора, за счет разработки новой математической модели обработки результатов измерений в процедуре расчета дисбалансов корректирующих масс и применения новых операций корректировки измеренной виброскорости, их последовательности и режимов проведения.
Сущность изобретения поясняется Фиг. 1 - Фиг. 13.
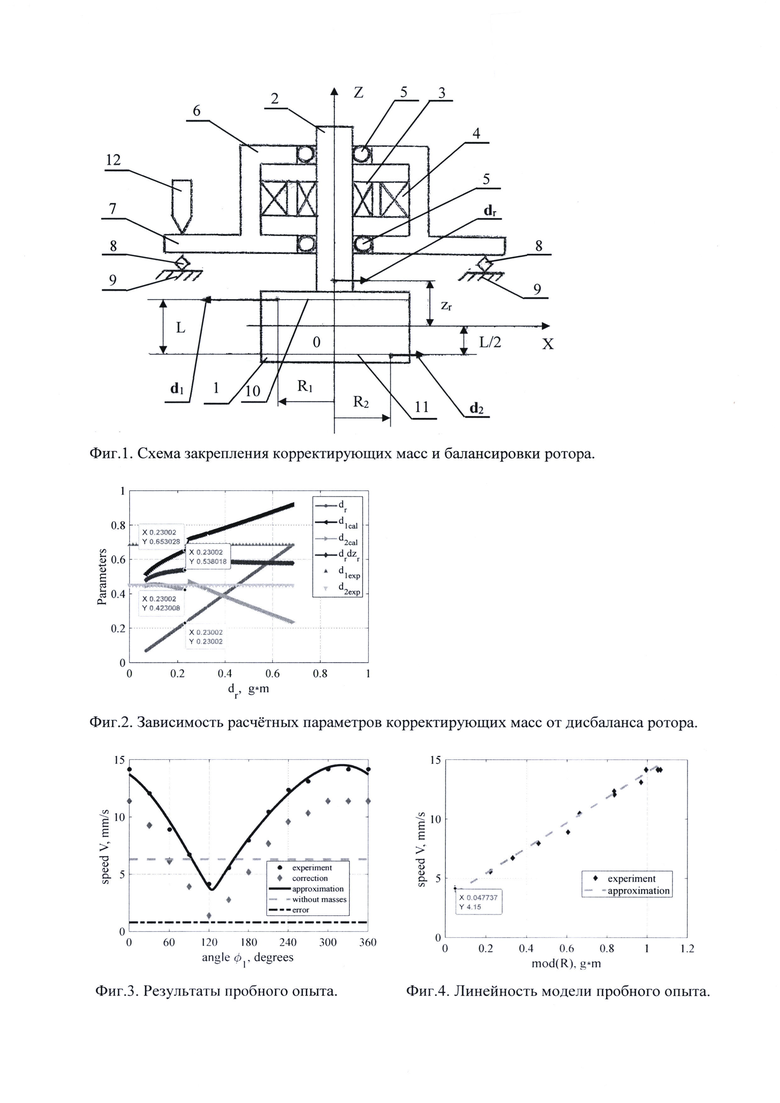
На Фиг. 1 представлена схема закрепления корректирующих масс с дисбалансами d1 и d2 в своих плоскостях коррекции в привязке их к геометрии и системам координат балансируемого ротора.
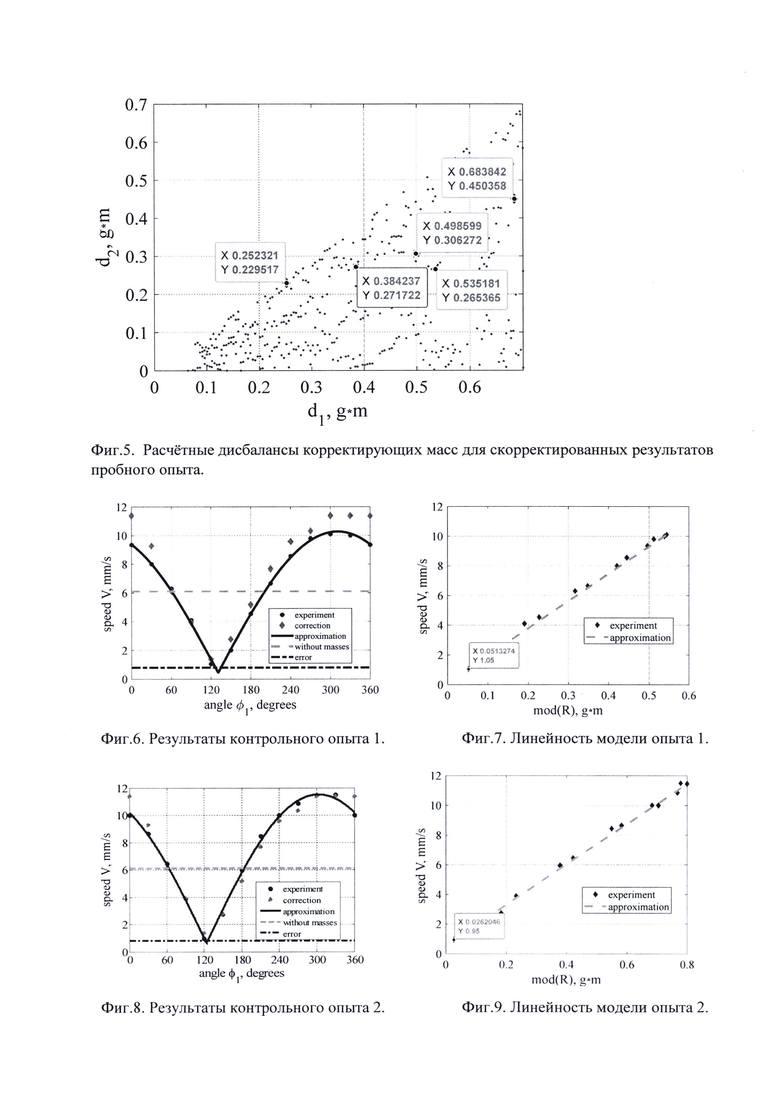
На Фиг. 2 представлена зависимость расчетных параметров корректирующих масс от дисбаланса dr ротора, g⋅m (г⋅м), полученных в процедуре аппроксимации предложенной моделью результатов пробного опыта, где d1cal, d2cal и d1exp, d2exp - расчетные и экспериментальные (постоянные) соответственно дисбалансы первой и второй корректирующих масс, г⋅м; dzr - безразмерная zr координата ротора.
На Фиг. 3 представлена зависимость виброскорости V, mm/s (мм/с), от азимутального угла φ1, degrees (градусах) первой корректирующей массы, для дисбалансов расчетных корректирующих масс, отмеченных маркерами на Фиг. 2, и ее аппроксимация предложенной моделью с указанием дискретных значений корректированной виброскорости, где, experiment и approximation - экспериментальные значения виброскорости, мм/с и их аналитическая аппроксимация предложенной моделью, correction - корректированная виброскорость, мм/с, without masses - виброскорость (постоянная) без корректирующих масс, мм/с, error - среднее значение погрешности измерительного устройства (постоянное), мм/с.
На Фиг. 4 представлена зависимость виброскорости V, mm/s (мм/с), указанной на Фиг. 3, от модуля суммарного вектора R дисбалансов mod(R), g⋅m (г⋅м) для дисбалансов расчетных корректирующих масс, отмеченных маркерами на Фиг. 2, и ее линейная аппроксимация, где experiment и approximation - экспериментальные значения виброскорости, отмеченные маркерами на Фиг. 3.
На Фиг. 5 представлена зависимость расчетных дисбалансов d1 и d2, g⋅m (г⋅м) корректирующих масс, полученных в процедуре аппроксимации предложенной моделью скорректированных результатов, отмеченных маркерами на Фиг. 3 для пробного опыта, где маркерами отмечены одна пара экспериментальных дисбалансов корректирующих масс в пробном опыте и 4 пары расчетных дисбалансов корректирующих масс для контрольного измерения.
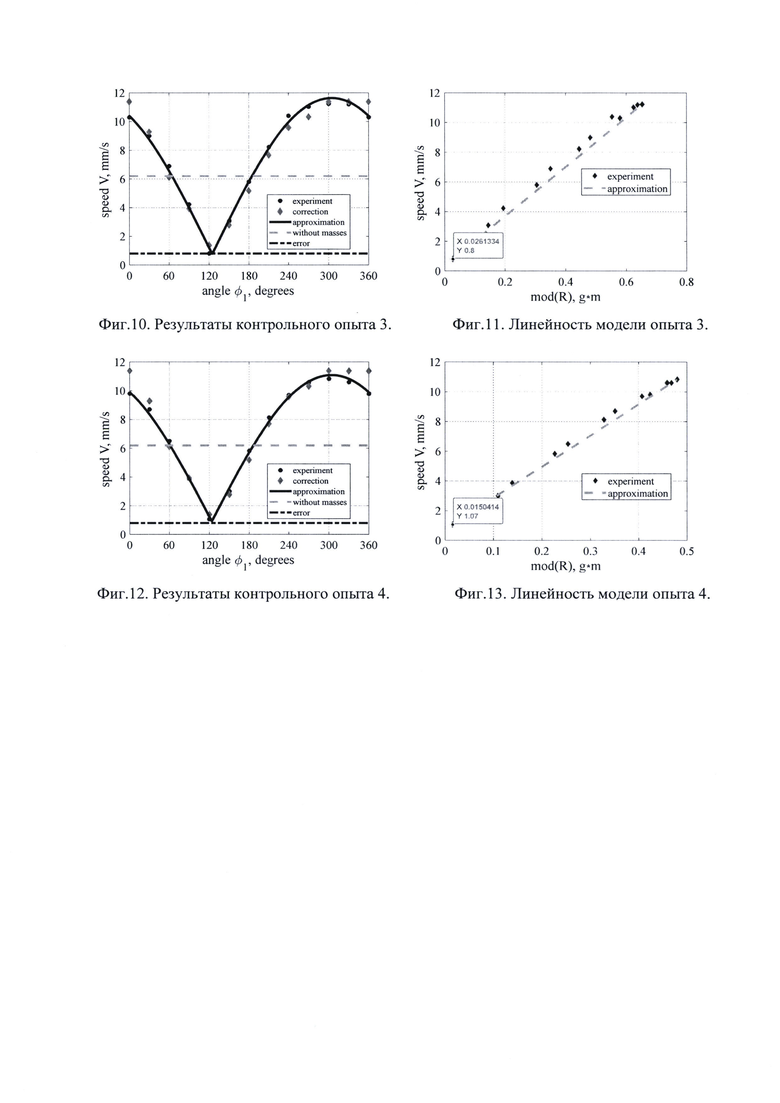
На Фиг. 6 и Фиг. 7 представлены зависимости виброскорости speed V, mm/s (мм/с), от азимутального угла φ1 degrees (градусах) первой корректирующей массы и от модуля суммарного вектора R дисбалансов mod(R), g⋅m (г⋅м) с линейной аппроксимацией, для дисбалансов контрольных корректирующих масс d1=0,537 г⋅м и d2=0,265 г⋅м из Фиг. 5, аналогичные результатам, представленным на Фиг. 3 и Фиг. 4 с аналогичной экспликацией всех обозначений.
На Фиг. 8 и Фиг. 9 представлены зависимости виброскорости V, mm/s (мм/с), от азимутального угла φ1, degrees (градусах) первой корректирующей массы и от модуля суммарного вектора R дисбалансов mod(R), g⋅m (г⋅м) с линейной аппроксимацией, для дисбалансов контрольных корректирующих масс d1=0,497 г⋅м и d2=0,306 г⋅м из Фиг. 5, аналогичные результатам, представленным на Фиг. 3 и Фиг. 4 с аналогичной экспликацией всех обозначений.
На Фиг. 10 и Фиг. 11 представлены зависимости виброскорости V, mm/s (мм/с), от азимутального угла φ1, degrees (градусах) первой корректирующей массы и от модуля суммарного вектора R дисбалансов mod(R), g⋅m (г⋅м) с линейной аппроксимацией, для дисбалансов контрольных корректирующих масс d1=0,383 г⋅м и d2=0,272 г⋅м из Фиг. 5, аналогичные результатам, представленным на Фиг. 3 и Фиг. 4 с аналогичной экспликацией всех обозначений.
На Фиг. 12 и Фиг. 13 представлены зависимости виброскорости V, mm/s (мм/с), от азимутального угла φ1, degrees (градусах) первой корректирующей массы и от модуля суммарного вектора R дисбалансов mod(R), g⋅m (г⋅м) с линейной аппроксимацией, для дисбалансов контрольных корректирующих масс d1=0,252 г⋅м и d2=0,230 г⋅м из Фиг. 5, аналогичные результатам, представленным на Фиг. 3 и Фиг. 4 с аналогичной экспликацией всех обозначений.
Пример осуществления способа.
Балансируют узел ротора с приводом и подшипниковой опорой центробежного экстрактора ЭЦ125Ф конструкции АО НИКИМТ-Атомстрой с вертикальной осью вращения без заполнения ротора жидкостью, показанный схематично на Фиг. 1. Ротор (1) экстрактора цилиндрической формы с размерами D×H ≈ 160 мм × 170 мм закреплен жестко, соосно и консольно на валу (2) электродвигателя асинхронного АИС 71В4У3 со своим ротором (3) и статором (4), размещенными между подшипниками (5) электродвигателя, установленными в подшипниковой опоре (6) с посадочным фланцем (7), который закрепляют пружинами (8) на неподвижном фланце (9) балансировочного устройства. В роторе (1) в плоскостях коррекции верхней-первой (10) и нижней-второй (11), размещенных на расстоянии L=150 мм, изготавливают по 12 резьбовых отверстий М8 эквидистантно по окружности через 30° и с совпадением азимутальных углов центров соответствующих отверстий в обеих плоскостях с погрешностью меньше 1°, в которых закрепляют первую и вторую корректирующие массы с дисбалансами d1 и d2 на радиусах R1 и R2. Дисбаланс ротора dr размещен на своем эксцентриситете (на Фиг. 1 не показан) на расстоянии zr>L/2. Совмещают с осью ротора (1) ось z систем Декартовых и цилиндрических координат с совмещенным началом 0 обеих систем координат в средней точке между плоскостями коррекции (10) и (11) и ориентируют ее положительное направление вверх от нижней-второй (11) к верхней-первой (10) плоскостей коррекции. Измерительный щуп (12) измерительного устройства устанавливают в заданной точке периферийной зоны поверхности посадочного фланца (7) подшипниковой опоры (6) при вертикальной его ориентации.
Заявленный способ реализуют проведением следующей последовательности операций:
1. Уточняют математическую модель явной зависимости, измеренной виброскорости от параметров дисбаланса ротора и обеих корректирующих масс.
2. Измеряют виброскорости в пробном опыте с пробными корректирующими массами при нескольких диаметрально противоположных азимутальных углах их закрепления на роторе.
3. Аппроксимируют полученные экспериментальные результаты виброскорости предложенной моделью, из множества полученных решений для расчетных дисбалансов корректирующих масс выбирают одно решение, для которого рассчитывают минимальною величину аппроксимированной виброскорости.
4. Корректируют полученные экспериментальные результаты виброскорости с получением псевдоэкспериментальной зависимости корректированного распределения виброскорости от азимутального угла первой корректирующей массы.
5. Аппроксимируют полученное корректированное распределение виброскорости предложенной моделью, из множества полученных решений для расчетных дисбалансов корректирующих масс выбирают одно решение, для которого изготавливают новые корректирующие массы для контрольного измерения.
6. Выполняют контрольное измерение виброскорости с корректирующими массами с расчетными дисбалансами и азимутальными углами, подтверждающими достижение минимальной виброскорости, находящейся в интервале погрешности устройства ее измерения и соответствующей минимальному остаточному дисбалансу ротора.
Для устранения недостатка прототипа разрабатывают новую математическую модель явной зависимости виброскорости от параметров дисбалансов ротора и корректирующих масс в форме ее линейной зависимости от модуля суммы двух векторов: главного вектора дисбаланса и вектора главного момента дисбалансов в единой функциональной зависимости среднего квадратического значения виброскорости с неизвестными параметрами дисбаланса ротора с валом, далее по тексту - ротора, от заданных параметров дисбалансов обеих корректирующих масс. В представленной на Фиг. 1 системе координат главный вектор дисбалансов D и вектор главного момента дисбалансов М имеют вид:

где D - главный вектор дисбалансов, г⋅м; М - вектор главного момента дисбалансов, г⋅м2; d1, d2 и dr - модули векторов дисбалансов, далее по тексту-дисбалансы, соответственно первой и второй корректирующих масс, и ротора, г⋅м; ϕ1, ϕ2 и ϕr - азимутальные углы центров масс соответственно первой и второй корректирующих масс, и ротора, радиан; L>0 - заданное расстояние вдоль оси z между обеими плоскостями коррекции, м; zr>L/2 - неизвестная координата z до центра масс ротора, м; i и j - орты Декартовых координат по осям х и у соответственно.
Разделяют вектор М на заданное расстояние L>0 и получают его нормированные компоненты M/L, имеющие одинаковую размерность г⋅м с компонентами вектора D, которые также подлежат одновременному уменьшению в процедуре балансировки, и поэтому могут суммироваться с учетом знаков вместе с компонентами вектора D. С учетом предложенной модификации вектора М в вектор M/L формируют соответствующую векторную величину R=D+M/L с размерностью дисбаланса г⋅м, аналогичная величина которой в ГОСТ 22061-76 названа «суммарный вектор дисбалансов», с отличием того, что в нем расстояние L является расстоянием между серединами опор (подшипников) двухопорного ротора. Таким образом аналог суммарного вектора дисбалансов R, далее по тексту - вектор R, полностью определяет динамическую неуравновешенность ротора и позволяет осуществить процедуру балансировки ротора при одновременном учете в единой функциональной зависимости его главного вектора дисбаланса с учетом корректирующих масс и вектора главного момента дисбалансов.
С учетом известного представления вектора М в виде векторного произведения, зависящего от начала системы координат, компоненты упомянутого вектора R имеют вид:
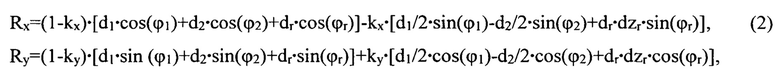
где kx, ky - неизвестные безразмерные коэффициенты, учитывающие вклад компоненты нормированного момента дисбалансов в долях от соответствующей суммы со вкладом компоненты дисбаланса, 0≤kx≤1, 0≤ky≤1; dzr=zr/L>0 - неизвестная безразмерная zr координата центра масс ротора.
Таким образом новую математическую модель, далее по тексту - модель R, представляют в форме линейной зависимости виброскорости от модуля вектора R в виде уравнения:

где V - измеренная виброскорость, мм/с; kv, мм/с и kr, (кг⋅с)-1 - неизвестные коэффициенты линейной зависимости, причем коэффициент kv не меньше погрешности устройства измерения виброскорости, далее по тексту- погрешность виброскорости.
В каждом из выражений для Rx и Ry знаки компонент векторов d1 и dr совпадают, поэтому одновременное уменьшение упомянутых выражений до нуля или до допустимо малой величины возможно при диаметрально противоположном направлении векторов d1 и dr или |ϕ1-ϕr|=π. При этом знаки компонент векторов d1 и d2 в каждом из выражений для Rx и Ry в одном слагаемом суммы совпадают, а в другом противоположны, поэтому одновременное уменьшение упомянутых выражений до нуля или до допустимо малой величины возможно, как при диаметрально противоположном, так и при совпадающем их направлении, в зависимости от углов ϕ1, ϕ2 и ϕr и коэффициентов kx и ky.
Для схемы диаметрально противоположного закрепления обеих корректирующих масс |ϕ1-ϕ2|=π компоненты вектора R в зависимости от азимутального угла, например, первой корректирующей массы ϕ1 при заданных d1 и d2, преобразуют к виду
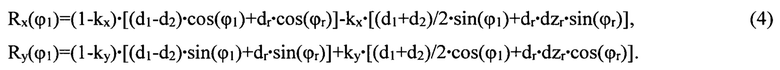
В этом варианте модель R по уравнениям (3) и (4) зависит от одного аргумента ϕ1 и подлежащих расчету девяти параметров: d1, d2, dr, dzr, ϕr, kx, ky, kr и kv. При этом аппроксимации подлежит одномерная зависимость виброскорости (3) от одного аргумента ϕ1, что упрощает процедуру аппроксимации и уменьшает погрешность результатов. В варианте аппроксимации экспериментальных данных, полученных с заданными d1 и d2, модель R по уравнениям (3) и (4) зависит от одного аргумента ϕ1, двух заданных параметров d1 и d2 и подлежащих расчету семи параметров: dr, dzr, ϕr, kx, ky, kr и kv.
Достижение минимальной виброскорости получают из условия |ϕ1-ϕr|=π, при котором упомянутые компоненты вектора R в (4) преобразуют к виду:
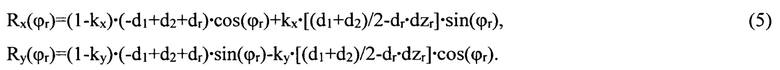
Из анализа этих уравнений следует, что независимо от значения коэффициентов kx и ky и угла ϕr обе компоненты вектора R одновременно обращаются в ноль Rx(ϕr)=Ry(ϕr)=0 при необходимых и достаточных условиях:

выполнение которых предопределяет корректность использования модели R для уменьшения виброскорости и остаточного дисбаланса теоретически вплоть до нуля. Из системы двух уравнений (6) с четырьмя неизвестными d1, d2, dr и dzr следуют эквивалентные равенства:
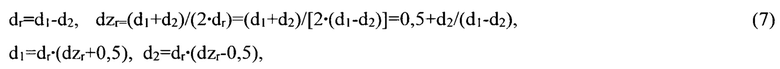
из которых независимо от dr при условии, например, d1>d2 следует dzr>0,5, в связи с чем центр масс ротора при этом условии должен располагаться вне промежутка L между плоскостями коррекции. В частности, упомянутую схему можно применить в варианте консольного закрепления ротора на валу при размещении центра масс ротора с валом вне подшипниковой опоры. При этом обе компоненты дисбалансов d2 и dr суммируются, так как имеют одинаковый знак, противоположный знаку компонент дисбаланса d1 (Фиг. 1), и одновременно обе компоненты нормированных моментов M1/L и М2/L дисбалансов d1 и d2 суммируются, так как имеют одинаковый знак, противоположный знаку компонент нормированного момента Mr/L дисбаланса dr.
Система двух уравнений (6) с четырьмя неизвестными d1, d2, dr и dzr при заданных любых двух из них, например, d1 и d2, имеет единственное решение (7) относительно оставшихся двух переменных, в связи с чем упрощают модель R подстановкой dr и dzr из (7) в (5) и получают компоненты вектора R в виде
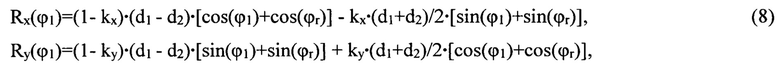
зависящим от заданных d1 и d2 только через их совокупности d1 - d2 и d1+d2. В этом варианте модель R по уравнениям (3) и (8) зависит от одного аргумента ϕ1 и подлежащих расчету семи параметров: d1, d2, ϕr, kx, ky, kr и kv и не зависит явным образом от параметров дисбаланса ротора dr и dzr. Подстановкой |ϕ1-ϕr|=π в равенства (8) аналогично (5) гарантированно получают к Rx(ϕ1)=Ry(ϕ1)=0 независимо от kx, ky и ϕr, что подтверждает корректность модели R. В действительности за счет погрешностей исходных данных упомянутая подстановка приводит к получению отличной от нуля минимальной виброскорости Vmin. Максимальную виброскорость Vmax получают подстановкой ϕ1=фr в (8), причем, разность ΔV=Vmax-Vmin также не зависит от параметров дисбаланса ротора dr и dzr, что будет использовано далее в реализации предложенного способа при корректировке экспериментальных данных виброскорости.
В варианте аппроксимации экспериментальных данных, полученных с заданными d1 и d2, обеспечивающими предположительно окончательную балансировку ротора, модель R по уравнениям (3) и (8) зависит от одного аргумента ϕ1, двух заданных параметров d1 и d2 и подлежащих расчету пяти параметров: ϕr, kx, ky, kг и kv. С использованием полученного в процедуре аппроксимации решения, включающего расчетные d1c и d2c, по уравнениям (7) рассчитывают dr и dzr.
Из анализа упомянутых уравнений (4) и (8) следует, что одновременный учет вкладов компонент дисбалансов и их нормированных моментов в алгебраической сумме в обеих компонентах Rx и Ry обеспечивает возможность их взаимной компенсации и достижение допустимого остаточного дисбаланса при меньших одновременно величинах корректирующих масс. Кроме того, несмотря на единственность действительных параметров dr и dzr, присущих балансируемому ротору, из необходимости и достаточности условий (6), эквивалентных им равенств (7) и уравнений (8) следует, что возможно множество решений d1 и d2 в совокупности с такими расчетными dr и dzr из (7), которые могут быть существенно отличны от упомянутых единственных действительных параметров dr и dzr. Таким образом модель R в представленном виде (8) является универсальной, поскольку не требует в процедуре балансировки ротора априорного знания параметров его дисбаланса dr и dzr, так как не зависит от них.
Перед проведением опытов с пробными корректирующими массами измеряют величины корректирующих масс весами «Kromatech МН-999» с погрешностью 0,01 г, рассчитывают их центры масс с использованием их известной геометрии, устанавливают радиусы размещения этих центров в привязке к геометрии ротора экстрактора с использованием штангенциркуля «ШЦ-1-150» с погрешностью 0,1 мм. Виброскорость измеряют виброметром «Диамех 2000 ОПАЛ» в заданной точке периферийной зоны поверхности посадочного фланца подшипниковой опоры, указанной на Фиг. 1, при вертикальной ориентации измерительного щупа (12). Рассчитывают погрешность виброскорости Ve этим виброметром при полном отсутствии вибрации по результатам 24 измерений, среднее значение которой оказалось равным Ve=0,7958 мм/с, а ее дисперсия σе=0,1197 мм/с. Поэтому в предположении нормального распределения этой случайной величины с вероятностью 0,997 она находится в интервале от Vemin=Ve-3σe=0,4367 мм/с до Vemax=Ve+3σe=l,155 мм/с. Для наглядности визуализации результатов измеряют виброскорость подшипниковой опоры без закрепленных корректирующих масс, среднее значение которой оказалось равным V0=6,3 мм/с.
Закрепляют на остановленном роторе последовательно при каждом значении азимутального угла 0°≤ϕ1≤360° из заданной их совокупности через 30° произвольно выбранные пробные корректирующие массы с дисбалансами, например, d1=0,6838 г⋅м и d2=0,4504 г⋅м с суммой d1+d2=1,1342 г⋅м и отношением d2/d1=0,6586, в резьбовых отверстиях в верхней-первой и нижней-второй плоскостях коррекции соответственно по схеме диаметрально противоположного закрепления (Фиг. 1). Приводят ротор во вращение, и при каждом значении азимутального угла ϕ1 первой корректирующей массы измеряют значение виброскорости - всего 12 измерений, в результате чего получают 13 экспериментальных данных, с учетом совпадения виброскорости при углах ϕ1=0° и ϕ1=360°, представленных в таблице 1 строка «Эксперимент».
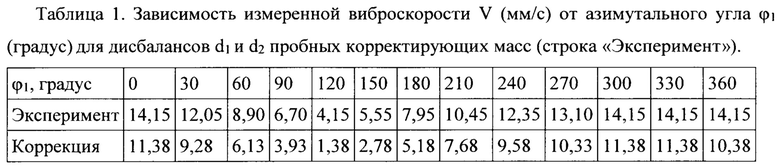
Перед обращением к процедуре аппроксимации устанавливают равные подынтервалы для искомых величин дисбаланса dr, разделяя исходный интервал, например, 0,1⋅d1≤dri≤d1 несколькими, например, N=100 равноотстоящими точками с номерами l≤i≤N на N-1 подынтервалов между монотонно возрастающими величинами dri. С учетом равенств (6) устанавливают соответствующие монотонно убывающие подынтервалы для искомых величин dzri=(d1+d2)/(2-dri) между монотонно убывающими величинами dzri. С использованием экспериментальных данных таблицы 1 устанавливают постоянный интервал для искомой величины ϕr с границами, равными соседними с минимальными значениями углов в сумме с 180°, в этом примере от 90°+180°=270° до 150о+180°=330о. Интервалы для остальных четырех искомых параметров устанавливают также постоянными, например, 0≤kx≤1, 0≤ky≤1, 0≤kг≤40, 0≤kv≤4,15, причем, максимальное значение kv устанавливают равным минимальному значению виброскорости из таблицы 1 (Строка «Эксперимент»). В качестве начальных значений всех искомых параметров для процедуры аппроксимации устанавливают, например, средние значения двух границ соответствующих интервалов.
Вводят исходные данные таблицы 1 в расчетное устройство, где в одном программном цикле по текущему возрастающему номеру точки i в интервале 2≤i≤N-l для текущего интервала от dri-1 до dri+1 и соответствующего ему текущего интервала от dzri+1 до dzri-1 в связи с обратной пропорциональностью с dri аппроксимируют заданные в таблице 1 (Строка «Эксперимент») экспериментальные данные виброскорости от одного аргумента ϕ1 по модели R и уравнениям (3) и (4) и получают точечные оценки всех ее искомых параметров в предустановленных интервалах. Выполняют упомянутые вычисления с использованием известной оптимизационной процедуры подбора нескольких параметров заданной таблично дискретными значениями функции, например, с использованием функций cftool и fit в приложении Curve Fitting Toolbox пакета прикладных программ MATLAB. Таким образом в процедуре аппроксимации для заданных пробных d1 и d2 рассчитывают 7 параметров dr, dzr, ϕr, kx, ky, kr и kv, причем, отбирают только такие решения в форме совокупностей точечной оценки всех параметров, которые находятся строго внутри своих заданных интервалов в локальных минимумах. С использованием полученных параметров dr и dzr рассчитывают по формулам (7) расчетные d1c и d2c, которые в общем случае не совпадают с заданными пробными d1 и d2.
После выхода из программного цикла из полученных результатов дополнительно отбирают только такие решения, которые удовлетворяют заданным критериям качества аппроксимации, основанным на известном методе наименьших квадратов с учетом числа степеней свободы аппроксимируемых данных, равного разности между числом значений аргумента и количеством искомых параметров аппроксимируемой функции, с учетом равных единице весовых коэффициентов измерений. В качестве таких критериев используют являющиеся выходными данными упомянутых функций величину rmse с размерностью мм/с, основанную на сумме квадратов отклонений аппроксимированных значений от экспериментальных величин с учетом числа степеней свободы, и основанные на ее использовании безразмерные критерии adjrsquare и rsquare. В описании упомянутого вычислительного пакета утверждается, что качество аппроксимации улучшается при приближении величины raise к 0 и приближении величин rsquare и adjrsquare к 1.
Из множества полученных решений выбирают решения, удовлетворяющие установленным критериям, например, rsquare>0,990 и adjrsquare>0,986 и rmse<0,426, которые, представлены на Фиг. 2 в зависимости от переменной dr. Из анализа полученных решений следует, что все они имеют разные параметры 0,068<dr<0,684 и 0,845<dzr<7,017, а также суммы 0,960<d1cal+d2cal<l,194 г⋅м и отношения 0,256<d2cal/d1cal<0,867, отличающиеся от аналогичных величин для пробных корректирующих масс с суммой d1+d2=1,134 г⋅м и отношением d2/d1=0,6586. Кроме того, из Фиг. 2 следует, что все представленные решения удовлетворяют условиям (6) для dr,dzr=(d1+d2)/2. Представленные результаты подтверждают корректность модели R в аспекте аппроксимирования с установленным критерием качества аппроксимации заданной совокупности дискретных экспериментальных данных и получения множества различных решений для искомых параметров безотносительно к неизвестным действительным величинам dr и dzr данного балансируемого ротора, которые неизменны и единственны. Для произвольно выбранного из множества расчетных совокупностей решения, например, указанного на Фиг. 2 текстовыми полями в соответствующих маркерах с отображением обеих координат, например, ближайшего к пробным d1 и d2 при dr=0,2300 г⋅м, d1=0,6530 г⋅м и d2=0,4230 г⋅м на Фиг. 3 представлена визуализация его аппроксимации по модели R, а в таблице 2 представлена совокупность его расчетных параметров.

Основная цель аппроксимации пробных экспериментальных данных виброскорости заключается в расчете минимального аппроксимированного значения Vmin по уравнениям (5), и ΔV=Vmax - Vmin, где Vmax рассчитывают по уравнениям (4) подстановкой ϕ1=ϕr. Критерии качества аппроксимации экспериментальных данных составляют: rsquare=0,991, adjrsquare=0,988, rmse=0,401. При этом, минимальное экспериментальное значение виброскорости 4,15 мм/с из таблицы 1, расположенное при угле 120°, немного превышает аналогичное расчетное значение 3,57 мм/с из таблицы 2, расположенное при немного большем расчетном угле: 0,848⋅360°-180°=125,3o. Для всех остальных без исключения указанных маркерами на Фиг. 2 совокупностей решений их графическое представление аналогично Фиг. 3 до такой степени, что они визуально практически неотличимы друг от друга, что обусловлено удовлетворительными величинами всех упомянутых критериев качества аппроксимации. Это обстоятельство подтверждает обоснованность произвольности выбора конкретного решения на этом этапе расчетов по модели R.
С использованием упомянутых ранее процедур cftool и fit пакета MATLAB рассчитывают по результатам таблицы 2 величину модуля |R|=(V-kv)/kr, которую затем вместе с соответствующими величинами виброскорости V сортируют по монотонному возрастанию |R|. На Фиг. 4 представлены результаты аналогичной уравнению (3) линейной аппроксимации модели R в виде

где р0=3,310 мм/с и p1=10,44 (кг⋅с)-1 - коэффициенты линейной зависимости, немного отличающиеся от упомянутых коэффициентов kv и kr из таблицы 2. При этом критерии качества линейной аппроксимации экспериментальных данных составляют: rsquare=0,990, adjrsquare=0,990 и rmse=0,368, что подтверждает корректность линейности модели R.
Полученные для пробных корректирующих масс экспериментальные данные виброскорости, представленные в таблице 1 (строка «Эксперимент»), преднамеренно и целенаправленно корректируют до такого гипотетического распределения, которое предположительно должно соответствовать по модели R распределению виброскорости при окончательной балансировке ротора с достижением минимальной виброскорости, находящейся в интервале ее погрешности. Для этого с учетом погрешности виброскорости Ve и аппроксимированного минимального значения Vmin уменьшают все ординаты экспериментальных значений виброскорости эквидистантно на разность ΔV=Vmin-Ve=3,57-0,7958=2,774 мм/с и получают псевдоэкспериментальную скорректированную зависимость виброскорости от азимутального угла ϕ1, представленную в таблице 1 (строка «Коррекция») и маркерами на Фиг. 3. При этом, минимальная скорректированная виброскорость составляет 4,15-2,774=1,38 мм/с и немного превышает верхнюю границу интервала погрешности виброскорости 1,155 мм/с.
Полученные скорректированные величины зависимости виброскорости от одного аргумента ϕ1, представленные в таблице 1 (Строка «Коррекция»), аппроксимируют по модели R и уравнениям (3) и (8) в двух вложенных циклах, например, по монотонно возрастающим значениям искомых d1 и d2, с получением решений для всех семи искомых параметров d1, d2, ϕr, kx, ky, kr и kv при всех возможных сочетаниях их заданных узких интервалов. Наружный программный цикл устанавливают, например, по монотонному возрастанию d1i, размещенных в средней точке между двумя соседними подынтервалами Δi, для чего интервал для d1, например, 0≤d1≤0,7 г⋅м разделяют несколькими, например, N1=300 равноотстоящими точками d1i с номерами 1≤i≤N1 на N1-1 равных подынтервалов. Внутренний программный цикл устанавливают, например, по монотонному возрастанию d2j, размещенных в середине подынтервалов Δj, для чего формируют с учетом текущего значения d1i и неравенств 0≤(d2/d1)≤1 текущий интервал, например, от 0 до d1i и разделяют его несколькими, например, N2=300 равноотстоящими точками d2j с номерами 1<j<N2 на N2-1 равных подынтервалов. Для остальных пяти искомых параметров ϕr, kx, ky, kг и kv устанавливают постоянные в обоих циклах интервалы, например, 0,75≤ϕr/(2⋅π)≤0,92, 0≤kx≤1, 0≤ky≤1, 0≤kr≤40, 0,437≤kv≤1,155, причем, интервал kv устанавливают равным интервалу погрешности виброскорости. В качестве начальных значений всех искомых параметров устанавливают, например, средние значения двух границ соответствующих интервалов. В качестве выходных данных расчетного устройства получают множество решений в виде совокупностей всех семи параметров: d1, d2, ϕr, kx, ky, kr и kv, из которых выбирают любую совокупность d1 и d2, удовлетворяющую дополнительным критериям отбора, например, с меньшей суммой d1+d2 и более близким к 1 отношением d2/d1 для удобства изготовления и закрепления на роторе. Результаты аппроксимации с выбранными d1 и d2 для контрольных опытов представлены в таблице 3 и на Фиг. 5.
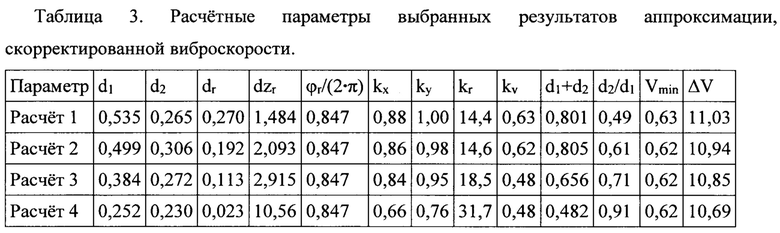
Критерии качества аппроксимации для всех результатов таблицы 3 составили: rsquare>0,99, adjrsquare>0,98 и rmse<0,5. Выбор данных из Фиг. 5 и таблицы 3 (строка «Расчет 4») совокупности d1 и d2 с минимальной суммой d1+d2=0,482 г⋅м был ограничен только тем обстоятельством, что в связи с малой величиной корректирующих масс было уже затруднительно изготовить их в форме шпилек с резьбой М8 и закрепить в предназначенных для них резьбовых отверстиях ротора.
Для подтверждения корректности модели R в аспекте достижения минимального остаточного дисбаланса ротора изготавливают контрольные корректирующие массы с таким d1 и d2, приведенными в таблице 4, которые отличаются от приведенных в таблице 2 расчетных дисбалансов меньше чем на 0,4%, закрепляют их по диаметрально противоположной схеме (Фиг. 1) и выполняют контрольные измерения виброскорости аналогично процедуре с пробными корректирующими массами с получением результатов, представленных в таблице 5.
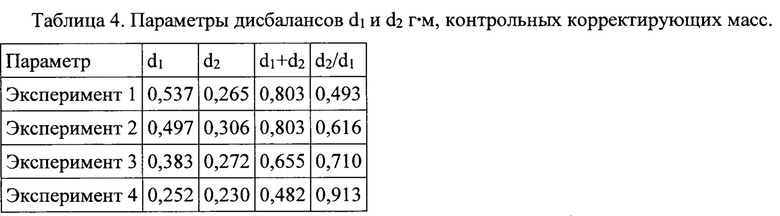
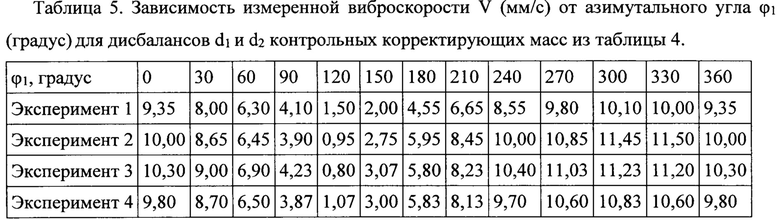
Анализ представленных в таблице 5 данных подтверждает достижение во всех четырех опытах малой величины виброскорости в зоне угла ϕ1≈120°, которая уже находится внутри интервала погрешности виброскорости, но еще превышает минимально возможную виброскорость в связи с тем, что она достигается в промежуточном угле между соседними позициями 120°<ϕ1<150° закрепления первой корректирующей массы с синхронным закреплением второй корректирующей массы на угле ϕ2=ϕ1+π.
Экспериментальные результаты в таблице 5 зависимости виброскорости от одного аргумента ϕ1 для заданных дисбалансов d1 и d2 в таблице 4 аппроксимируют по модели R и уравнениям (3) и (8). Перед обращением к процедуре аппроксимации устанавливают интервалы всех искомых параметров, например, такие же как в процедуре аппроксимации скорректированной виброскорости. В результате получают точечные оценки всех пяти искомых параметров: ϕr, kx, ky, kг и kv и рассчитывают из равенств (7) dr и dzr, представленные в таблице 6, а визуализация аппроксимации по зависимости (3) представлена на Фиг. 6, Фиг. 8, Фиг. 10, Фиг. 12.


Расчетные параметры величин d1 и d2 в таблице 6 совпадают с аналогичными исходными величинами таблице 4 с погрешностью меньше 0,5%, что подтверждает корректность модель R в варианте аппроксимации экспериментального распределения виброскорости при таких величинах d1 и d2, которые обеспечивают окончательную балансировку ротора. Расчетные критерии качества аппроксимации для всех расчетных результатов таблицы 6 составили: rsquare>0,99, adjrsquare>0,99 и rmse<0,29. Сравнение величин Vmin и ΔV из таблиц 2 и 6 показывает, что при существенном уменьшении Vmin величина ΔV изменяется незначительно, что подтверждает возможность использования корректированной виброскорости из таблицы 1 для последующего расчета контрольных дисбалансов d1 и d2, в процедуре аппроксимации предложенной моделью. Это обстоятельство подчеркнуто визуально на Фиг. 6, Фиг. 8, Фиг. 10 и Фиг. 12, где маркерами указаны те же данные корректированной виброскорости, что и на Фиг. 3. Представленные таблице 5 измеренные минимальные экспериментальные величины виброскорости при ϕ1=120° и представленные в таблице 6 расчетные величины Vmin ограничены только погрешностью использованного виброметра и могут быть уменьшены еще ближе к нулю за счет применения более точного измерительного устройства без изменения процедуры балансировки.
Проверка линейности модели R для контрольных корректирующих масс из таблицы 6 выполнена по описанной ранее процедуре в соответствии с уравнением (9) и представлена в таблице 7, а визуализация линейной аппроксимации по зависимости (3) представлена на Фиг. 7, Фиг. 9, Фиг. 11, Фиг. 13.

Критерии качества линейной аппроксимации для всех расчетных результатов таблицы 7 составили: rsquare>0,99, adjrsquare>0,99 и rmse<0,27. При этом параметры р0 и p1 таблицы 7 немного отличаются от параметров kv и kr таблицы 6.
Представленные на Фиг. 6, Фиг. 8, Фиг. 10, Фиг. 12. графики, аппроксимирующей экспериментальные данные функции (3) для совокупности корректирующих масс, соответствующих достижению минимальной виброскорости, имеют в зоне этого минимума характерный заостренный вид с резким изменением знака первой производной этой функции от отрицательного до положительного значения при монотонном увеличении угла ϕ1. Это обусловлено теоретической разрывностью первой производной этой функции по аргументу ϕ1 в упомянутой зоне, в связи с ее аналитическим видом в виде дробного выражения, величина знаменателя которого (Rx2+Ry2)0,5 близка к нулю в соответствии с уравнениями (8) при подстановке |ϕ1-ϕr|=π, что подтверждает соответствие модели R ее физическому смыслу.
Дополнительными расчетами установлено, что все зависимости аппроксимированной виброскорости от угла, представленные графиками на Фиг. 6, Фиг. 8, Фиг. 10, Фиг. 12 симметричны относительно угла ϕr с максимальной погрешностью менее 0,4% в зоне углов ϕr±90°, хотя это и не следует явным образом из уравнений (3) и (8). Аналогичная величина для графика на Фиг. 3 составляет ~10% в той же зоне углов. Эти обстоятельства позволяют упростить процедуру балансировки за счет измерения и приведения к равенству виброскорости, с существенно отличной от нуля величиной, только в двух по указанным углам позициях закрепления корректирующих масс путем варьирования их дисбалансов, но при наличии предварительной оценки величины ϕr.
Сравнение результатов, представленных на Фиг. 4 и Фиг. 7 показывает, что при практически одинаковой расчетной минимальной величине ~0,05 г⋅м модуля вектора R соответствующая виброскорость для пробного опыта в ~4 раза больше, чем для контрольного опыта. Следовательно, необходимым и достаточным условием для окончания процедуры балансировки ротора является одновременное достижение минимальных величин модуля вектора R и соответствующей виброскорости, а не только минимального остаточного дисбаланса ротора. При этом, в обеих расчетных последовательностях аппроксимации экспериментальных данных рассчитывают по 7 параметров, в связи с чем целесообразно получить для этого не менее 8 пар экспериментальных данных аргумента и функции.
Кроме рассчитанного азимутального угла дисбаланса ротора оценку остальных действительных параметров вектора дисбаланса ротора - его модуля и z координаты центра масс выполняют следующим образом. Поученное множество решений в процедуре аппроксимации моделью R скорректированных результатов пробного опыта для расчетных дисбалансов корректирующих масс, представленных на Фиг. 5 сортируют в порядке возрастания суммы коэффициентов kx и ky и отбирают первые несколько из них, например, 10 решений с минимальной отличной от нуля их суммой. Поскольку эти решения соответствуют практическому отсутствию вклада моментов в вектор R, параметры дисбаланса ротора dr и dzr рассчитывают по модели R и формулам (7) в форме среднего mean(dr)=0,0630 г⋅м и mean(dzr)=0,5897 и дисперсии σ(dr)=0,0003 г⋅м и σ(dzr)=0,0803 отобранных результатов. Следовательно, в предположении нормального распределения этих случайных величин с вероятностью 0,997 они находится в интервалах 0,062 г⋅M<dr<0,064 г⋅м и 0,349<dzr<0,831.
После разборки центробежного экстрактора и электродвигателя, и последующей сборки совокупности вращающихся элементов ротора экстрактора (без корректирующих масс) и вала с ротором электродвигателя измерили координату центра масс совокупности вращающихся элементов dzr, которая оказалась равной ~0,55 и, следовательно, расположена внутри упомянутого расчетного интервала. Полученная оценка величины dr оказалась примерно в 4 раза меньше величин минимальных контрольных корректирующих масс d1 и d2 из таблицы 6 (строка Расчет 4), необходимых для балансировки ротора. Из фиг. 5 следует возможность изготовления контрольных корректирующих масс и с меньшими дисбалансами d1 и d2, например, ~0,1 г⋅м и меньше, что сравнимо с оценкой величины dr, поэтому для принятой схемы закрепления корректирующих масс справедлива максимальная оценка дисбаланса ротора dr<d1. Оценку эксцентриситета центра масс ротора, однозначно связанную с его дисбалансом и массой, здесь не проводили. Таким образом, предложенный способ, основанный на модели R, кроме достижения основной цели изобретения позволяет дополнительно рассчитать интервальные оценки всех неизвестных параметров дисбаланса ротора.
Таким образом использование заявленного изобретения позволяет получить новый технический результат, заключающийся в уменьшении количества экспериментов до 8-12 измерений виброскорости, уменьшении остаточного дисбаланса ротора до величины, соответствующей виброскорости в интервале погрешности ее измерения при минимальной величине корректирующих масс и отсутствии необходимости априорного знания массы ротора и расстояния от центра его масс до плоскостей коррекции, совокупность признаков которого неизвестна из настоящего уровня техники, обладает новизной по сравнению с выбранным прототипом, технически выполнимо и промышленно применимо, что соответствует критериям, характеризующим способ.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ БАЛАНСИРОВКИ РОТОРОВ | 1999 |
|
RU2163008C2 |
| СПОСОБ БАЛАНСИРОВКИ РОТОРА В ОДНОЙ ПЛОСКОСТИ КОРРЕКЦИИ | 2018 |
|
RU2694142C1 |
| СПОСОБ БАЛАНСИРОВКИ РОТОРА | 2004 |
|
RU2292534C2 |
| СПОСОБ БАЛАНСИРОВКИ РОТОРА С ПРИВОДНОЙ МУФТОЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2009 |
|
RU2387962C1 |
| СПОСОБ БАЛАНСИРОВКИ РОТОРА В ОДНОЙ ПЛОСКОСТИ КОРРЕКЦИИ | 2012 |
|
RU2499985C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛА И МАССЫ ПРОТИВОВЕСА (ВАРИАНТЫ) | 2001 |
|
RU2205376C2 |
| СПОСОБ БАЛАНСИРОВКИ ГИБКИХ РОТОРОВ | 2009 |
|
RU2399428C1 |
| СПОСОБ И УСТРОЙСТВО ДИНАМИЧЕСКОЙ БАЛАНСИРОВКИ РОТОРОВ | 2000 |
|
RU2208772C2 |
| СПОСОБ БАЛАНСИРОВКИ ШЛИФОВАЛЬНОГО КРУГА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2173629C1 |
| СПОСОБ НАСТРОЙКИ БАЛАНСИРОВОЧНОГО СТЕНДА ДЛЯ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МАССОИНЕРЦИОННОЙ АСИММЕТРИИ РОТОРОВ | 2011 |
|
RU2453818C1 |
Изобретение относится к области машиностроения, а именно к технологии динамической балансировки ротора, например, центробежных насосов, компрессоров, экстракторов, центрифуг. Способ заключается в том, что выполняют несколько последовательностей измерительных операций, в которых закрепляют корректирующие массы на неподвижном роторе в двух плоскостях коррекции и измеряют скорость вибрации подшипниковой опоры при вращении ротора, расчетных операций, в которых рассчитывают очередное приближение параметров дисбаланса корректирующих масс и контрольного измерения с расчетными корректирующими массами, в котором подтверждают уменьшение скорости вибрации до величины, при которой остаточный дисбаланс ротора не превышает допустимой величины. Техническим результатом является уменьшение количества экспериментов до 8-12 измерений скорости вибрации, уменьшение остаточного дисбаланса ротора до величины, соответствующей минимальной скорости вибрации в интервале погрешности ее измерения измерительным устройством при минимальной величине корректирующих масс. Технический результат достигается тем, что в способе балансировки ротора в двух плоскостях коррекции, включающем операции, в которых закрепляют корректирующие массы на неподвижном роторе в двух плоскостях коррекции, измеряют скорость вибрации подшипниковой опоры при вращении ротора, рассчитывают очередное приближение параметров дисбаланса корректирующих масс и проводят контрольный опыт, подтверждающий уменьшение скорости вибрации до величины, при которой остаточный дисбаланс ротора не превышает допустимой величины, размещают обе плоскости коррекции с одной стороны от центра масс ротора, закрепляют исходные корректирующие массы диаметрально противоположно друг другу, устанавливают исходный дисбаланс корректирующей массы, условно первой, в ближайшей к центру масс ротора плоскости коррекции большим аналогичной величины другой корректирующей массы, условно второй, полученные экспериментальное данные аппроксимируют с использованием математической модели в форме уравнения явной зависимости скорости вибрации от параметров корректирующих масс, выбирают из полученного множества решений одну совокупность дисбалансов контрольных корректирующих масс, с которыми измеряют скорость вибрации, находящуюся внутри интервала погрешности измерительного устройства и соответствующую минимальному остаточному дисбалансу ротора. 6 з.п. ф-лы, 13 ил., 7 табл.
1. Способ динамической балансировки ротора в двух плоскостях коррекции, включающий последовательность измерительных операций, в которых закрепляют на установленном в подшипниковой опоре роторе две корректирующие массы в двух плоскостях коррекции и измеряют скорость вибрации подшипниковой опоры измерительным устройством при вращении ротора, последовательность расчетных операций, в которых рассчитывают с использованием математической модели в расчетном устройстве параметры корректирующих масс, и контрольного измерения, в котором с изготовленными с расчетными параметрами корректирующими массами измеряют минимальную скорость вибрации, соответствующую допустимому остаточному дисбалансу ротора, отличающийся тем, что в первой последовательности измерительных операций размещают обе плоскости коррекции с одной стороны от центра масс ротора, закрепляют корректирующие массы диаметрально противоположно друг другу, устанавливают дисбаланс корректирующей массы, условно первой, в ближайшей к центру масс ротора плоскости коррекции большим аналогичной величины другой корректирующей массы, условно второй, в первой последовательности расчетных операций полученные экспериментальные скорости вибрации аппроксимируют с использованием математической модели в системе координат с центром в средней точке между плоскостями коррекции и продольной осью z, совпадающей с осью ротора, в форме уравнения линейной зависимости
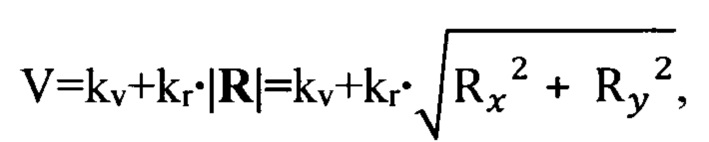
и компонентами вектора R с размерностью дисбаланса, зависящими от одного аргумента ϕ1 по уравнениям
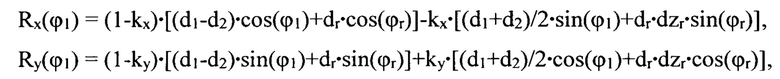
где V - измеренная скорость вибрации; kv, kr - коэффициенты линейной зависимости; d1, d2, dr - дисбалансы первой и второй корректирующих масс и ротора; dzr=zr/h - безразмерная zr координата центра масс ротора, нормированная на заданное расстояние h между плоскостями коррекции; ϕ1, ϕr - азимутальные углы центров масс первой корректирующей массы и ротора; kx, ky - безразмерные коэффициенты, учитывающие вклад компоненты нормированного момента дисбалансов в долях от соответствующей суммы со вкладом компоненты дисбаланса по соответствующей координате;
рассчитывают удовлетворяющие заданным критериям качества аппроксимации множество решений, в виде расчетных совокупностей семи параметров dr, dzr, ϕr, kx, ky, kr, kv, выбирают из него одно решение с соответствующей минимальной аппроксимированной скоростью вибрации и уменьшают полученные экспериментальные скорости вибрации эквидистантно до псевдоэкспериментального скорректированного распределения с минимальной аппроксимированной скоростью вибрации, равной среднему значению погрешности измерительного устройства, во второй последовательности расчетных операций полученную скорректированную скорость вибрации аппроксимируют с использованием математической модели при условиях
d1-d2-dr=0,
(d1+d2)/2-dr⋅dzr=0,
с компонентами вектора R, зависящими от одного аргумента ϕ1 по уравнениям
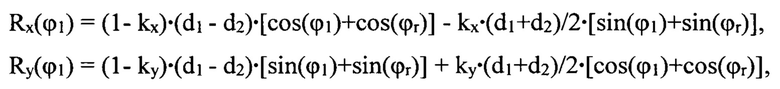
рассчитывают удовлетворяющие заданным критериям качества аппроксимации множество решений в виде расчетных совокупностей семи параметров d1, d2, ϕr, kx, ky, kr, kv и выбирают из него одну совокупность параметров d1, d2, ϕr, а в контрольной измерительной операции закрепляют первую корректирующую массу с дисбалансом d1 на азимутальном угле ϕ1, удовлетворяющему условию |ϕ1-ϕr|=π, и вторую корректирующую массу с дисбалансом d2 на азимутальном угле ϕ2=ϕr, и измеряют скорость вибрации, находящуюся внутри интервала погрешности измерительного устройства.
2. Способ динамической балансировки ротора в двух плоскостях коррекции по п. 1, отличающийся тем, что в первой последовательности измерительных операций корректирующие массы закрепляют на роторе не менее чем в восьми позициях, преимущественно эквидистантно по азимутальному углу, например, через 30-45°.
3. Способ динамической балансировки ротора в двух плоскостях коррекции по п. 1, отличающийся тем, что в первой последовательности расчетных операций, полученные экспериментальное данные скорости вибрации для заданных дисбалансов d1 и d2 корректирующих масс, аппроксимируют в одном цикле с монотонно изменяющимися границами интервала искомого дисбаланса dr, с монотонно изменяющимися границами интервала искомого параметра dzr, удовлетворяющих условию
dzr=(d1+d2)/(2⋅dr),
с постоянными границами интервала от 0 до 1 для искомых коэффициентов kx, ky, и большей границей постоянного интервала искомого коэффициента kv, не превышающей минимальной экспериментальной скорости вибрации.
4. Способ динамической балансировки ротора в двух плоскостях коррекции по п. 1, отличающийся тем, что в первой последовательности расчетных операций из множества решений аппроксимации экспериментальных данных скорости вибрации выбирают совокупность расчетных параметров с такими дисбалансами d1 и d2, для которых, например, сумма модулей разности с аналогичными величинами для заданных дисбалансов корректирующих масс достигает минимальной величины.
5. Способ динамической балансировки ротора в двух плоскостях коррекции по п. 1, отличающийся тем, что во второй последовательности расчетных операций аппроксимации скорректированной скорости вибрации ее аппроксимируют в двух вложенных циклах с монотонно изменяющимися границами интервалов искомых параметров, например, дисбалансов d1 и d2, с постоянными границами интервала от 0 до 1 для искомых коэффициентов kx и ky и постоянным интервалом искомого коэффициента kv, равным интервалу погрешности измерительного устройства.
6. Способ динамической балансировки ротора в двух плоскостях коррекции по п. 1, отличающийся тем, что во второй последовательности расчетных операций из множества решений аппроксимации скорректированной скорости вибрации выбирают для контрольной измерительной операции дисбалансы d1 и d2, например, с минимальной их суммой и более близким к единице отношением d2/d1.
7. Способ динамической балансировки ротора в двух плоскостях коррекции по п. 1, отличающийся тем, что в качестве расчетного устройства используют процессор с программным обеспечением для аппроксимации дискретных экспериментальных данных функции, зависящей от одного аргумента и нескольких искомых параметров, при равных единице весовых коэффициентах измерений, например, входящими в состав пакета прикладных программ MATLAB расчетными функциями cftool и fit и критериями качества аппроксимации, основанных на известном методе наименьших квадратов: безразмерными adjrsquare>0,98 и rsquare>0,98 и с размерностью скорости вибрации rmse<0,3.
| СПОСОБ И УСТРОЙСТВО ДИНАМИЧЕСКОЙ БАЛАНСИРОВКИ РОТОРОВ | 2000 |
|
RU2208772C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ БАЛАНСИРОВКИ РОТОРА | 2019 |
|
RU2759651C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ БАЛАНСИРОВКИ РОТОРА | 2019 |
|
RU2756710C1 |
| US 20150128698 A1, 14.05.2015 | |||
| US 5214585 A1, 25.05.1993. | |||
Авторы
Даты
2023-02-28—Публикация
2022-09-20—Подача