Область техники, к которой относится изобретение
Предлагаемое изобретение относится к информационным технологиям и может быть использовано для построения крипто-кодовых конструкций контроля и восстановления целостности структурированных массивов данных на основе применения криптографических хэш-функций и кодов, корректирующих ошибки, в условиях деградации многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования.
Уровень техники
а) Описание аналогов
Известны способы построения криптографических конструкций контроля целостности структурированных массивов данных за счет применения криптографических хэш-функций (Патент на изобретение RUS №2730365, 21.08.2020; Патент на изобретение RUS №2758194, 26.10.2021; Патент на изобретение RUS №2759240, 11.11.2021; Патент на изобретение RUS №2771146, 27.04.2022; Патент на изобретение RUS №2771209, 28.04.2022; Патент на изобретение RUS №2771236, 28.04.2022; Патент на изобретение RUS №2771273, 29.04.2022; Патент на изобретение RUS №2774099, 15.06.2022; Шеннон, К. Работы по теории информации и кибернетике / К. Шеннон. - М.: Изд-во иностранной литературы, 1963. - 829 с.: Шнайер, Б. Секреты и ложь. Безопасность данных в цифровом мире / Б. Шнайер. -СПб.: Питер, 2003. - 367 с.).
Недостатками данных способов являются:
- отсутствие возможности восстановления целостности данных;
- отсутствие возможности контроля целостности данных при изменении их структуры в условиях деградации многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования.
Известны способы построения кодовых конструкций восстановления целостности структурированных массивов данных за счет применения кодов, корректирующих ошибки (Патент на изобретение RUS №2680033, 14.02.2019; Патент на изобретение RUS №2680350, 19.02.2019; Патент на изобретение RUS №2758943, 03.11.2021; Патент на изобретение RUS №2771238, 28.04.2022; Морелос-Сарагоса, Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / Р. Морелос-Сарагоса; перевод с англ. В.Б.Афанасьев. М.: Техносфера, 2006. 320 с.; Хемминг, Р.В. Теория кодирования и теория информации / Р.В.Хемминг; перевод с англ. М.: «Радио и связь», 1983. 176 с.).
Недостатками данных способов являются:
- контроль целостности данных выполняется с определенной для применяемого кода, корректирующего ошибки, вероятностью;
- отсутствие возможности восстановления целостности данных при изменении их структуры в условиях деградации многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования.
Известны способы, основанные на построении крипто-кодовых конструкций контроля и восстановления целостности структурированных массивов данных за счет применения криптографических методов и методов теории надежности (Патент на изобретение RUS №2680739, 26.02.2019; Патент на изобретение RUS №2696425, 02.08.2019; Патент на изобретение RUS №2707940, 02.12.2019).
Недостатками данных способов являются:
- контроль и восстановление целостности данных выполняется для изначально определенной структуры данных, подлежащих хранению;
- отсутствие возможности контроля и восстановления целостности данных при изменении их структуры в условиях деградации многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования.
б) Описание ближайшего аналога (прототипа)
Наиболее близким по технической сущности к заявленному изобретению (прототипом) является способ контроля и восстановления целостности многомерных массивов данных, в котором крипто-кодовая конструкция строится для контроля и восстановления целостности данных, представленных в виде многомерных структурированных массивов данных размерности k (фиг. 1), от элементов которых предварительно посредством применения хэш-функции вычисляются эталонные хэш-коды, значения которых в последующем при контроле целостности данных сравниваются со значениями хэш-кодов, вычисляемых уже от проверяемых блоков данных, при запросе на их использование. От полученных хэш-кодов, а также от элементов многомерных структурированных массивов данных посредством математического аппарата кодов, корректирующих ошибки, для обеспечения возможности восстановления целостности данных вычисляются избыточные блоки (Алиманов П.Е., Диченко С.А., Самойленко Д.В., Финько О.А. [и др.]. Способ контроля и восстановления целостности многомерных массивов данных // Патент на изобретение RUS №2771208, 28.04.2022).
Недостатком известного способа является отсутствие возможности контроля и восстановления целостности данных при изменении их структуры в условиях деградации многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования.
Раскрытие изобретения
а) Технический результат, на достижение которого направлено изобретение Целью настоящего изобретения является разработка способа построения крипто-кодовых конструкций контроля и восстановления целостности структурированных массивов данных на основе применения криптографических хэш-функций и кодов, корректирующих ошибки, с возможностью контроля и восстановления целостности данных при изменении их структуры в условиях деградации многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования.
б) Совокупность существенных признаков
Поставленная цель достигается тем, что в известном способе контроля и восстановления целостности многомерных массивов данных, заключающемся в том, что крипто-кодовые конструкции контроля и восстановления целостности данных строятся на основе массивов данных размерности k, состоящих из блоков данных, которые для обеспечения возможности контроля их целостности размещаются в массиве размерности k+1, к которым для возможности обнаружения признаков нарушения целостности применяется хэш-функция h, при этом вычисленные хэш-коды размещаются в свободных блоках массива и являются эталонными, значения которых при запросе на использование данных сравниваются со значениями хэш-кодов, вычисляемых уже от проверяемых блоков данных, при восстановлении целостности блоки данных, подлежащие защите, а также вычисленные от них эталонные хэш-коды интерпретируются как элементы GF(2') и являются наименьшими полиномиальными вычетами, при этом полученный массив данных рассматривается как единый суперблок модулярного полиномиального кода, над которым выполняется операция расширения путем введения n-k избыточных оснований, для которых вычисляются соответствующие им избыточные вычеты, дополнительно вводимые для коррекции ошибки, в случае возникновения которой восстановление блоков данных без ущерба для однозначности их представления осуществляется посредством реконфигурации системы путем исключения из вычислений блока данных с признаками нарушения целостности, в представленном же способе для построения крипто-кодовых конструкций контроля и восстановления целостности данных на основе информационного подхода накапливаемая в рассматриваемых многомерных системах хранения данных информация представляется в виде р-мерных структурированных массивов данных посредством предварительной сортировки большого многомерного массива данных, поступающего на хранение, на кластеры данных, являющиеся объектами р-мерного пространства и обладающие ценностью для принятия пользователем информационной системы, в интересах которой применяются многомерные системы хранения данных, решения, полученный при этом структурированный массив данных, состоящий из элементов 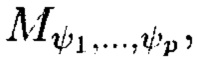 где индексы
где индексы  принимают значения от 1 до
принимают значения от 1 до 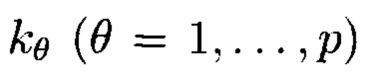 соответственно, содержащий k1×k2×…×kp элементов и обозначаемый как
соответственно, содержащий k1×k2×…×kp элементов и обозначаемый как 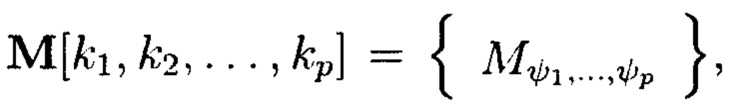 является математическим множеством, имеющим определенную структуру и аксиоматические правила, что позволяет рассматривать его аналогично пространству данных и считающийся дискретным метрическим пространством, так как содержит в своей структуре точки, представленные элементами
является математическим множеством, имеющим определенную структуру и аксиоматические правила, что позволяет рассматривать его аналогично пространству данных и считающийся дискретным метрическим пространством, так как содержит в своей структуре точки, представленные элементами 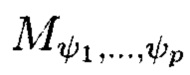 массива, изолированными друг от друга и располагаемыми вдоль абстрактных прямых, параллельных осям координат, на одинаковых расстояниях друг от друга, что позволяет контролировать и восстанавливать целостность полученного структурированного массива данных посредством применения ϕ-функции, отображающей его элементы посредством разных видов преобразований, основанных на применении функций хэширования h и кодирования
массива, изолированными друг от друга и располагаемыми вдоль абстрактных прямых, параллельных осям координат, на одинаковых расстояниях друг от друга, что позволяет контролировать и восстанавливать целостность полученного структурированного массива данных посредством применения ϕ-функции, отображающей его элементы посредством разных видов преобразований, основанных на применении функций хэширования h и кодирования 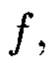 в контрольные символы, при этом с полученными крипто-кодовыми конструкциями контроля и восстановления целостности данных в случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация на массивы меньшей размерности или массивы, являющиеся объектами, принадлежащими их подпространствам, при этом содержащаяся в них информация продолжает обладать ценностью для принятия пользователем информационной системы решения, и обеспечивается возможность контроля и восстановления целостности структурированных массивов данных с измененной структурой.
в контрольные символы, при этом с полученными крипто-кодовыми конструкциями контроля и восстановления целостности данных в случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация на массивы меньшей размерности или массивы, являющиеся объектами, принадлежащими их подпространствам, при этом содержащаяся в них информация продолжает обладать ценностью для принятия пользователем информационной системы решения, и обеспечивается возможность контроля и восстановления целостности структурированных массивов данных с измененной структурой.
Сопоставительный анализ заявленного решения и прототипа показывает, что предлагаемый способ отличается от известного тем, что поставленная цель достигается за счет представления на основе информационного подхода накапливаемой в рассматриваемых многомерных системах хранения данных информации в виде р-мерных структурированных массивов данных, по правилам применения ϕ-функции во времени и пространстве, отображающей их элементы посредством разных видов преобразований, основанных на применении функций хэширования h и кодирования 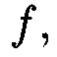 в контрольные символы, строятся крипто-кодовые конструкции.
в контрольные символы, строятся крипто-кодовые конструкции.
В случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация первоначальных структурированных массивов данных, при этом содержащаяся в полученных массивах информация продолжает обладать ценностью, достаточной для принятия пользователем информационной системы решения, что позволит в момент времени t из полученных в результате фрагментации структурированных массивов данных на основе применения ϕ-функции построить крипто-кодовые конструкции с возможностью контроля и восстановления их целостности при изменении их структуры. Новым является то, что для построения крипто-кодовых конструкций контроля и восстановления целостности данных на основе информационного подхода накапливаемая в рассматриваемых многомерных системах хранения данных информация представляется в виде р-мерных структурированных массивов данных. Новым является то, что выполняется предварительная сортировка большого многомерного массива данных на кластеры данных, являющиеся объектами р-мерного пространства, каждый из которых обладает ценностью для принятия пользователем информационной системы решения, полученный структурированный массив данных, является математическим множеством, имеющим определенную структуру и аксиоматические правила, что позволяет рассматривать его аналогично пространству, а содержащиеся в нем блоки данных 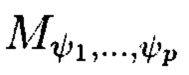 как точки пространства, являющийся пространством данных и считающийся дискретным метрическим пространством, так как содержит в своей структуре точки, представленные элементами массива, изолированными друг от друга и располагаемые вдоль абстрактных прямых, параллельных осям координат, на одинаковых расстояниях. Новым является то, что выполняются преобразования со структурированными массивами данных, приводящими к получению крипто-кодовых конструкций контроля и восстановления их целостности, правила построения которых определяются посредством применения ϕ-функции во времени и пространстве, отображающей элементы структурированных массивов данных посредством разных видов преобразований, основанных на применении функций хэширования h и кодирования
как точки пространства, являющийся пространством данных и считающийся дискретным метрическим пространством, так как содержит в своей структуре точки, представленные элементами массива, изолированными друг от друга и располагаемые вдоль абстрактных прямых, параллельных осям координат, на одинаковых расстояниях. Новым является то, что выполняются преобразования со структурированными массивами данных, приводящими к получению крипто-кодовых конструкций контроля и восстановления их целостности, правила построения которых определяются посредством применения ϕ-функции во времени и пространстве, отображающей элементы структурированных массивов данных посредством разных видов преобразований, основанных на применении функций хэширования h и кодирования 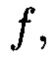 в контрольные символы. Новым является то, что в случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация первоначальных структурированных массивов данных, в результате которой выполняется их разбиение на массивы меньшей размерности или массивы, являющиеся объектами, принадлежащими их подпространствам, при этом содержащаяся в них информация продолжает обладать ценностью, достаточной для принятия пользователем информационной системы решения, из полученных в результате фрагментации структурированных массивов данных на основе применения ϕ-функции строятся крипто-кодовые конструкции с возможностью контроля и восстановления их целостности при изменении их структуры.
в контрольные символы. Новым является то, что в случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация первоначальных структурированных массивов данных, в результате которой выполняется их разбиение на массивы меньшей размерности или массивы, являющиеся объектами, принадлежащими их подпространствам, при этом содержащаяся в них информация продолжает обладать ценностью, достаточной для принятия пользователем информационной системы решения, из полученных в результате фрагментации структурированных массивов данных на основе применения ϕ-функции строятся крипто-кодовые конструкции с возможностью контроля и восстановления их целостности при изменении их структуры.
в) Причинно-следственная связь между признаками и техническим результатом
Благодаря новой совокупности существенных признаков в способе реализована возможность:
- представления накапливаемой в рассматриваемых многомерных системах хранения данных информации на основе информационного подхода в виде р-мерных структурированных массивов данных;
- предварительной сортировки большого многомерного массива данных на кластеры данных, являющиеся объектами р-мерного пространства, каждый из которых обладает ценностью для принятия пользователем информационной системы решения;
- выполнения преобразований со структурированными массивами данных, приводящим к получению посредством применения ϕ-функции во времени и пространстве крипто-кодовых конструкций контроля и восстановления их целостности;
- выполнения фрагментации первоначальных структурированных массивов данных, в результате которой происходит их разбиение на массивы меньшей размерности или массивы, являющиеся объектами, принадлежащими их подпространствам;
- контроля и восстановления целостности данных при изменении их структуры в условиях деградации многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущений среды функционирования.
Доказательства соответствия заявленного изобретения условиям патентоспособности «новизна» и «изобретательский уровень»
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна».
Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность отличительных существенных признаков, обуславливающих тот же технический результат, который достигнут в заявленном способе. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
Краткое описание чертежей
Заявленный способ поясняется чертежами, на которых показано:
фиг. 1 схема, иллюстрирующая общий вид крипто-кодовой конструкции контроля и восстановления целостности многомерных массивов данных;
фиг. 2 - примеры возможных кластеров данных;
фиг. 3 - примеры получаемых структурированных массивов данных;
фиг. 4 - расположение векторов: а) перпендикулярное, б) параллельное однонаправленное, в) параллельное противоположно направленное;
фиг. 5 - представления гиперкуба данных: а) 2-мерный гиперкуб (квадрат), б) 3-мерный гиперкуб (куб), в) 4-мерный гиперкуб (тессеракт), г) 5-мерный гиперкуб (пентеракт);
фиг. 6 схема, иллюстрирующая общий вид 3-мерного куба, содержащего блоки данных 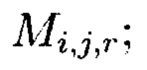
фиг. 7 - порядок расположения к блоков данных на ребре гиперкуба;
фиг. 8 - схема, иллюстрирующая единичный блок данных в 3-мерном массиве данных;
фиг. 9 - схема, иллюстрирующая 1-мерный подмассив данных в 3-мерном массиве данных;
фиг. 10 - схема, иллюстрирующая 2-мерный подмассив данных в 3-мерном массиве данных;
фиг. 11 - схема, иллюстрирующая 3-мерный куб данных размерности k=6;
фиг. 12 - схема 3-мерного куба данных нечетной размерности с изображением центра
симметрии;
фиг. 13 - плоскости симметрии, проходящие через центр 3-мерного куба данных размерности k=6;
фиг. 14 схема, иллюстрирующая маршрут между двумя произвольными блоками данных;
фиг. 15 - схема, иллюстрирующая отсутствие маршрута между блоками данных; фиг. 16 - схема, иллюстрирующая порядок контроля и восстановления целостности информации на основе применения крипто-кодовых конструкций; фиг. 17 схема с графическим представлением 2-мерного массива данных; фиг. 18 - схема, иллюстрирующая порядок выполнения преобразований над элементами строк 2-мерного массива данных;
фиг. 19 схема, иллюстрирующая порядок выполнения преобразований над элементами столбцов 2-мерного массива данных;
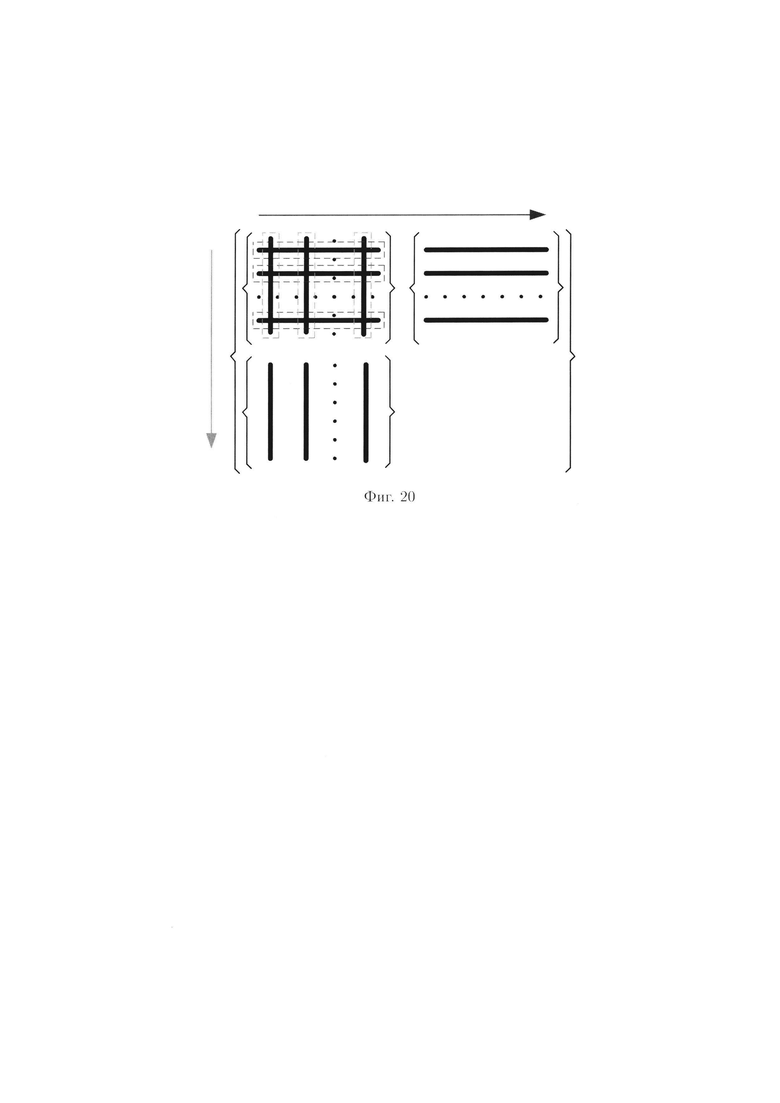
фиг. 20 схема, иллюстрирующая преобразования, одновременно выполняемые над элементами строк и столбцов 2-мерного массива данных;
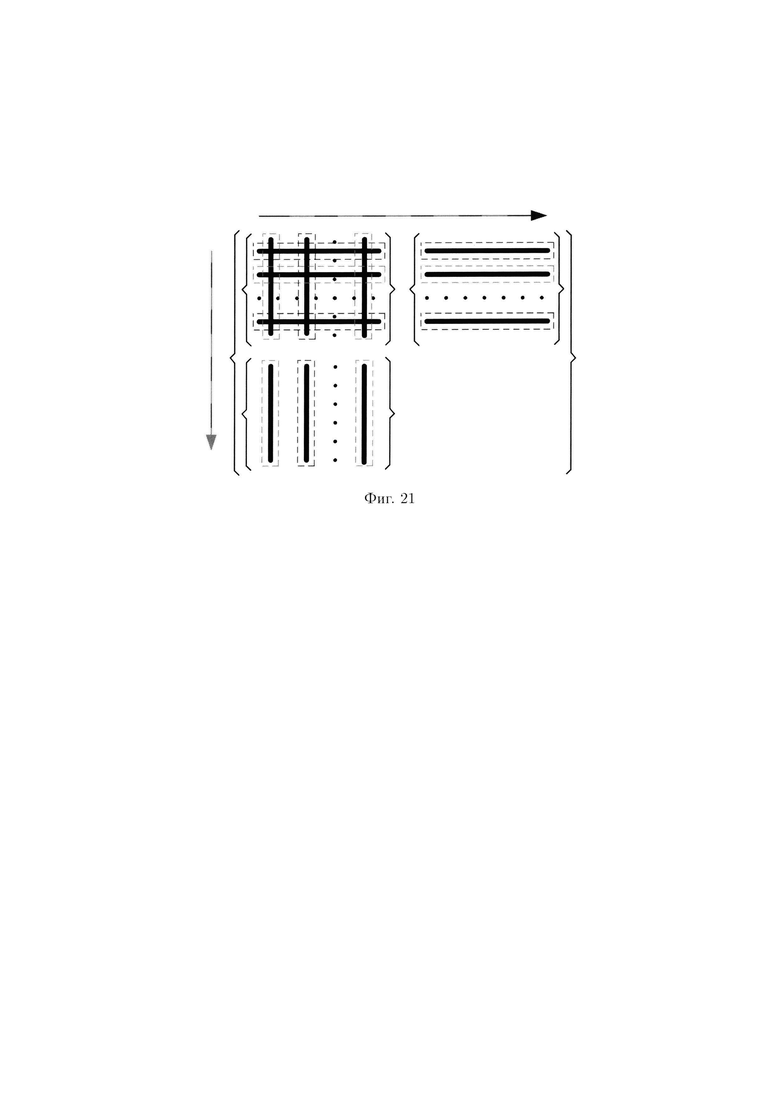
фиг. 21 - схема, иллюстрирующая преобразования над элементами 2-мерного массива данных, выполняемые с чередованием правил по отношению к его строкам и столбцам;
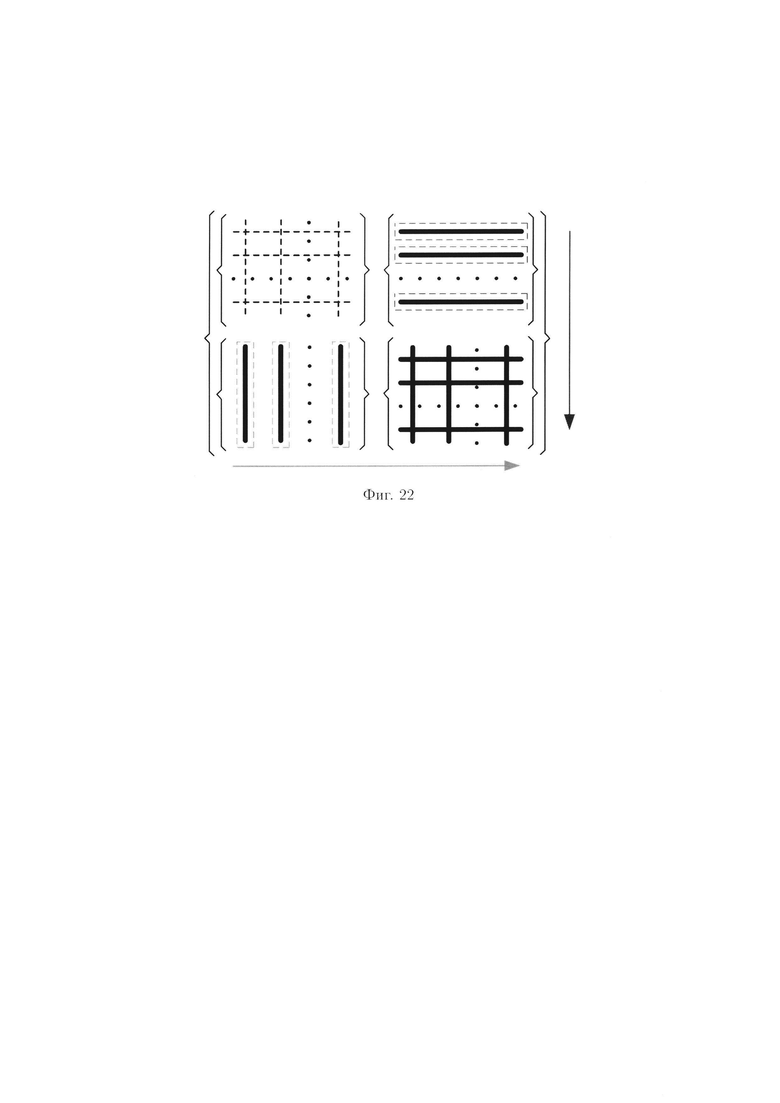
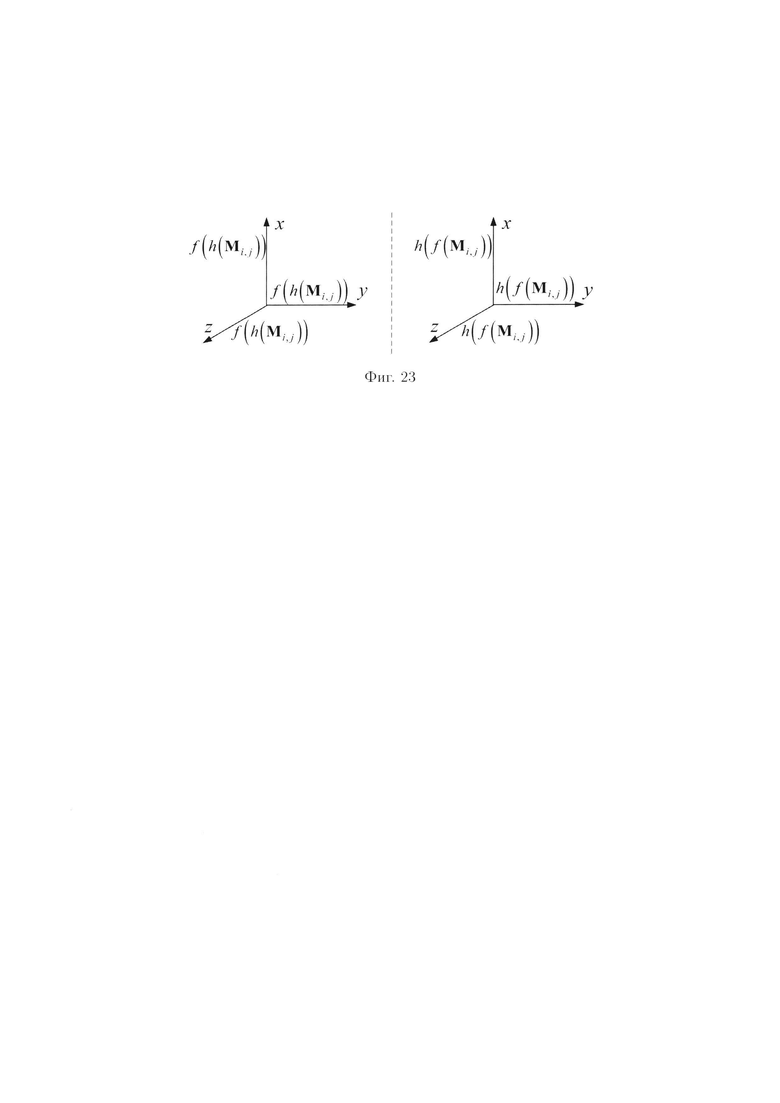
фиг. 22 - схема, иллюстрирующая преобразования над контрольными символами; фиг. 23 - схема, иллюстрирующая применение ϕ-функции во времени, при 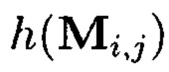 и
и 
фиг. 24 - схема, иллюстрирующая применение ϕ-функции во времени, при 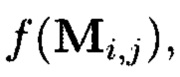
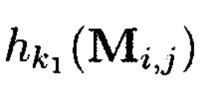 и
и 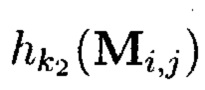 (k1, k2 - секретные ключи),
(k1, k2 - секретные ключи),
фиг. 25 - схема фрагментации 3-мерного куба данных на две треугольные 3-мерные призмы данных;
фиг. 26 - схема фрагментации 3-мерного массива данных на 2-мерные массивы данных;
фиг. 27 - схема фрагментации 2-мерного массива данных на 1-мерные массивы данных;
фиг. 28 - схема фрагментации 2-мерного массива данных на 2-мерные массивы данных разных размеров;
фиг. 29 - схема тетраэдра данных;
фиг. 30 - схема фрагментации 3-мерного куба данных на три равные 3-мерные пирамиды данных с четырехугольным основанием;
фиг. 31 - схема 3-мерной пирамиды данных с четырехугольным основанием;
фиг. 32 - схема двух 3-мерных тетраэдров данных.
Осуществление изобретения
Рассматриваемые многомерные системы хранения данных (СХД) предназначены для обработки и хранения больших объемов данных и их представления пользователям информационных систем (ИС) для оперативного анализа и принятия решения. Ввиду того, что функционирование многомерных СХД является целевым, поэтому при разработке способов контроля и восстановления целостности накапливаемых в них данных в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования наиболее важными являются качественные (семантические и прагматические) характеристики информации.
Это объясняется тем, что методы статистической теории информации (Шеннон, К. Работы по теории информации и кибернетике / К. Шеннон. М.: Изд-во иностранной литературы, 1963. - 829 с.; Стратонович, Р.Л. Теория информации / Р.Л. Стратонович. М.: Сов. радио, 1975. 424 с.), характеризующие лишь количественную (синтаксическую) сторону информационных массивов, не отражают связи с достижением цели функционирования рассматриваемых многомерных СХД и поэтому являются мало эффективными.
В свою очередь, применение информационного подхода (Горский, Ю.М. Информационные аспекты управления и моделирования / Ю.М. Горский; Акад. наук СССР, Сибирский энергетический ин-т, Науч. совет по комплекс, пробл. энергетики. - М.: Наука, 1978. - 223 с.; Ловцов, Д.А. Модели измерения информационного ресурса автоматизированной системы управления / Д.А. Ловцов // Автоматика и телемеханика. - 1996. - 9. - С. 3-17) дает возможность рассматривать непрерывно накапливаемую в СХД информацию на более высоком уровне, как структурированные массивы данных, ценность которых напрямую влияет на качество принимаемого пользователем ИС решения. Поэтому разрабатываемые механизмы защиты должны быть направлены на обеспечение неизменности смысла (семантические и прагматические характеристики) накапливаемой в СХД информации, и, как следствие, ее ценности. В этом случае ценность информации будет определяться как приращение вероятности достижения цели в результате использования данной информации. Поэтому кроме содержательности, своевременности и оперативности ценность информации главным образом будет выражается в таких понятиях, как ее полнота и достоверность.
Для построения крипто-кодовых конструкций контроля и восстановления целостности данных на основе информационного подхода накапливаемая в рассматриваемых многомерных СХД информация представляется в виде р-мерных структурированных массивов данных. Для этого посредством кластеризации данных выполняется предварительная сортировка большого многомерного массива данных, накапливаемых в рассматриваемых многомерных СХД, на группы данных (кластеры), каждая из которых обладает ценностью для принятия пользователем ИС решения.
Операция кластеризации данных заключается в следующем: имеется обучающая выборка  и функция расстояния между объектами требуется
и функция расстояния между объектами требуется 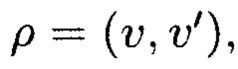 разбить выборку на непересекающиеся подмножества, называемые кластерами, так. чтобы каждый кластер состоял из объектов, близких по метрике ρ, а объекты разных кластеров существенно отличались. При этом каждому объекту
разбить выборку на непересекающиеся подмножества, называемые кластерами, так. чтобы каждый кластер состоял из объектов, близких по метрике ρ, а объекты разных кластеров существенно отличались. При этом каждому объекту 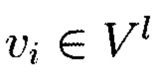 приписывается метка (номер) кластера
приписывается метка (номер) кластера 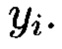
Целями кластеризации являются:
- понимание данных путем выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа;
- сжатие данных. Если исходная выборка избыточно большая, то можно сократить ее, оставив по одному наиболее типичному представителю от каждого кластера;
- обнаружение новизны. Выделяются нетипичные объекты, которые не удается присоединить ни к одному из кластеров.
Может применяться иерархическая кластеризация, когда крупные кластеры дробятся на более мелкие, те в свою очередь дробятся еще мельче и т.д.
При этом к методам кластеризации (Мандель, И.Д. Кластерный анализ / И.Д. Мандель. - М.: Финансы и статистика, 1988. 176 с.) можно отнести:
- вероятностный подход (каждый рассматриваемый объект относится к одному из к классов: K-средних, K-медиан, ЕМ-алгоритм, алгоритмы семейства FOREL, дискри-минантный анализ);
- подходы на основе систем искусственного интеллекта: метод нечеткой кластеризации С-средних, нейронная сеть Кохонена, генетический алгоритм;
- логический подход (деревья решений);
- теоретико-графовый подход (графовые алгоритмы кластеризации);
- иерархический подход (наличие вложенных групп кластеров различного порядка). Алгоритмы в свою очередь подразделяются на агломеративные (объединительные) и дивизивные (разделяющие);
- другие методы, невошедшие в предыдущие группы.
Методы кластеризации также применяются для интеллектуальной группировки результатов при поиске файлов и других объектов, предоставляя пользователю возможность быстрой навигации. При сегментации изображений кластеризация может быть использована для разбиения цифрового изображения на отдельные области с целью обнаружения границ или распознавания объектов. При интеллектуальном анализе данных кластеризация приобретает ценность тогда, когда она выступает одним из этапов анализа данных, построения законченного аналитического решения. Аналитику часто легче выделить группы схожих объектов, изучить их особенности и построить для каждой группы отдельную модель, чем создавать одну общую модель для всех данных.
Получаемые кластеры по своему внешнему виду отдаленно напоминают различные геометрические фигуры, являющиеся объектами многомерного (р-мерного, где р количество признаков, по которым выполнялась кластеризация) пространства. На фиг. 2 представлены примеры возможных кластеров данных, полученных из многомерного массива данных, накапливаемых в многомерных СХД.
Для обеспечения возможности формализации и последующего обеспечения целостности информации в рассматриваемых многомерных СХД получаемые кластеры данных преобразовываются в структурированные многомерные (в зависимости от количества признаков, по которым выполнялась кластеризация) массивы данных (фиг. 3).
Многомерная модель данных, лежащая в основе построения рассматриваемых СХД, применяемых в интересах ИС, предназначенных для оперативного анализа больших объемов данных, опирается на концепцию многомерных кубов (Codd, E.F. Providing OLAP to User-Analysts: An IT Mandate / E.F. Codd // Computer World. 1993. - Vol. 27. - No. 30. - P. 13-27; Thomsen, E. OLAP Solutions: Building Multidimensional Information Systems. Second Edition / E. Thomsen. Wiley Computer Publishing John Wiley & Sons, Inc., 2002. 688 p.) или гиперкубов.
По аналогии с теорией многомерных матриц (Соколов, Н.П. Введение в теорию многомерных матриц / Н.П. Соколов. - Киев: Наукова думка, 1972. - 175 с.) многомерный массив данных представляется в виде р-мерного массива, состоящего из элементов 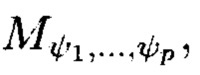 где индексы
где индексы  принимают значения от 1 до
принимают значения от 1 до 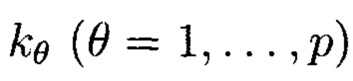 соответственно.
соответственно.
При этом р-мерный массив данных будет содержать k1×k2×…×kp элементов и обозначаться как
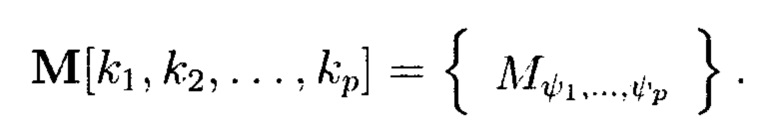
Многомерный массив данных 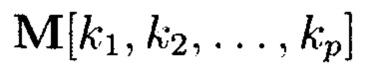 является математическим множеством, имеющим определенную структуру и аксиоматические правила, что позволяет рассматривать его аналогично пространству, а содержащиеся в нем элементы (блоки данных
является математическим множеством, имеющим определенную структуру и аксиоматические правила, что позволяет рассматривать его аналогично пространству, а содержащиеся в нем элементы (блоки данных 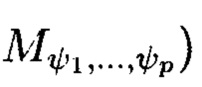 как точки пространства. Такое пространство будем называть пространством данных и считаться дискретным метрическим пространством, так как содержит в своей структуре точки, представленные элементами массива, изолированными друг от друга в некотором смысле. Внутри многомерного массива данных
как точки пространства. Такое пространство будем называть пространством данных и считаться дискретным метрическим пространством, так как содержит в своей структуре точки, представленные элементами массива, изолированными друг от друга в некотором смысле. Внутри многомерного массива данных 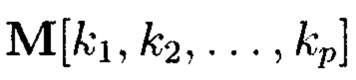 все элементы (блоки данных
все элементы (блоки данных 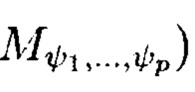 располагаются вдоль абстрактных прямых, параллельных осям координат, на одинаковых расстояниях друг от друга.
располагаются вдоль абстрактных прямых, параллельных осям координат, на одинаковых расстояниях друг от друга.
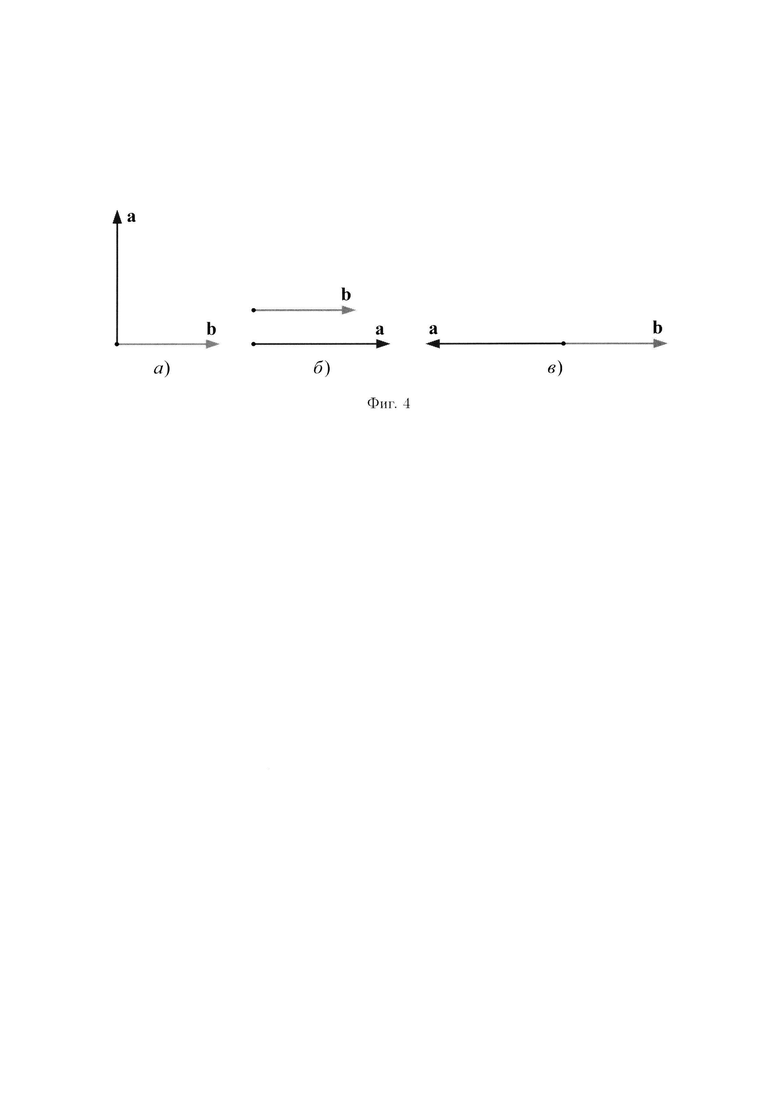
Пространство данных будет являться евклидовым пространством, так как в нем можно ввести понятие скалярного произведения. Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла между ними (Данилов, Ю.М. Математика: учебное пособие для студентов высших учебных заведений, обучающихся по техническим специальностям / Ю.М. Данилов [и др.]; под ред. Л.Н. Журбенко, Г.А. Никоновой; М-во образования и науки Рос. Федерации, Казан, гос. технол. ун-т. - М.: ИНФРА-М, 2009. - 495 с.).
В связи с тем, что все вектора пространства данных располагаются параллельно осям координат, скалярное произведение двух векторов пространства данных будет иметь лишь три состояния, зависящих от значения cos α, где α - угол между векторами.
Из определения скалярного произведения следует, что 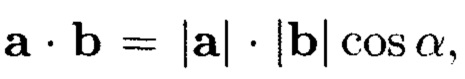 где a и b произвольные вектора пространства данных. При этом cos α в пространстве данных может принимать только три значения:
где a и b произвольные вектора пространства данных. При этом cos α в пространстве данных может принимать только три значения:
- при α=90°, cos α=0. Вектора расположены перпендикулярно (фиг. 4 а), следовательно, независимо от длин векторов их скалярное произведение равно 0;
- при α=0°, cos α=1. Вектора а и b параллельные однонаправленные (фиг. 4 б). Их скалярное произведение всегда равно произведению длин векторов. Из этого следует, что скалярный квадрат а2 вектора а равен квадрату его длины: 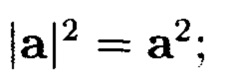
- при α=180°, cos α=- 1. Вектора а и b параллельные противоположно направленные фиг. 4 в). Их скалярное произведение всегда равно произведению длин векторов со знаком минус.
Многомерный массив данных можно представить в виде геометрических фигур евклидовых конечномерных пространств данных разных размерностей. Значит, для пространства данных любой размерности можно построить базис. Базис пространства данных - это линейная независимая система векторов.
Базис состоит из минимального количества векторов, с помощью которых можно получить любой вектор пространства всего лишь применив к ним арифметические операции сложения, вычитания векторов и умножение их на скаляр.
Пример 1. Базисом 3-мерного евклидова пространства является:
Пусть 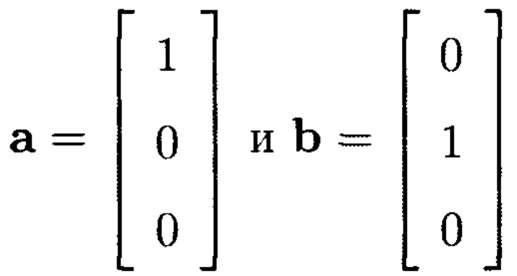 вектора базиса 3-мерного пространства.
вектора базиса 3-мерного пространства.
Найдем их скалярное произведение: а⋅b=1⋅1 cos 90°=0, следовательно, вектора будут ортогональными (перпендикулярными).
Базис является ортонормированным, так как все его вектора попарно ортогональны и единичны.
Все базисы пространства данных состоят из конечного числа элементов. Это позволяет дать корректность определению размерности пространства. Размерность пространства данных определяется максимальным количеством независимых векторов, по которым будут формироваться геометрическое представление массивов данных.
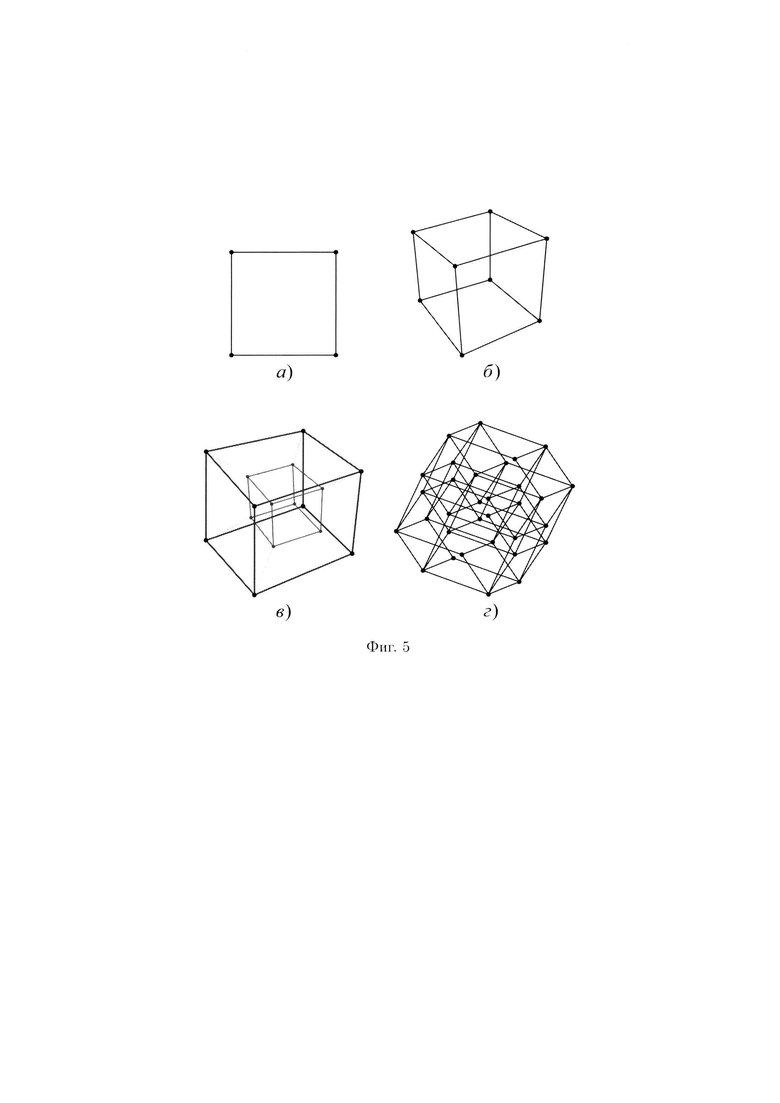
Существует множество представлений гиперкуба данных в пространстве разной размерности (фиг. 5). При этом под гиперкубом понимается обобщение куба на случай с произвольным числом измерений.
Пример 2. На фиг. 5 в) идеалистическое представление тессеракта. На нем представлены два 3-мерных куба разных размеров. Оба куба соединены ребрами в соответствующих вершинах. На самом деле все ребра тессеракта, которые сходятся к одной из его вершин, перпендикулярны друг другу, но мы не можем представить четыре попарно перпендикулярных вектора. Наши органы чувств позволяют нам видеть лишь трехмерную проекцию 4-мерного гиперкуба. На фиг. 5 г) ребра и грани пентеракта пересекаются, но это лишь иллюзия, на самом деле этого не происходит.
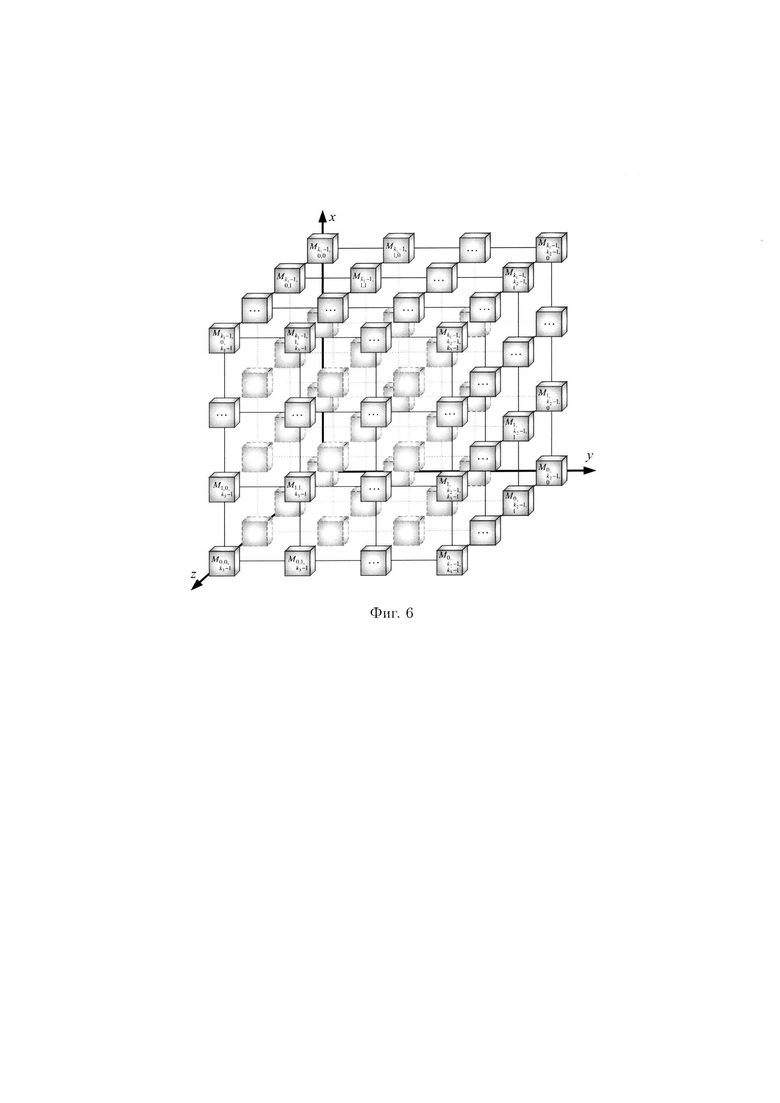
Пример 3. Рассмотрим 3-мерный массив данных 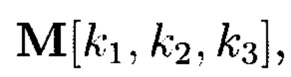 который может быть представлен в виде 3-мерного куба (фиг. 6), содержащего систему координат с осями: х, у, z, по которым откладываются блоки данных
который может быть представлен в виде 3-мерного куба (фиг. 6), содержащего систему координат с осями: х, у, z, по которым откладываются блоки данных 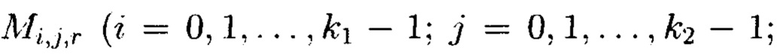

С помощью сечений ориентации (z) 3-мерный массив данных 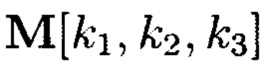 может быть представлен в следующем виде:
может быть представлен в следующем виде:
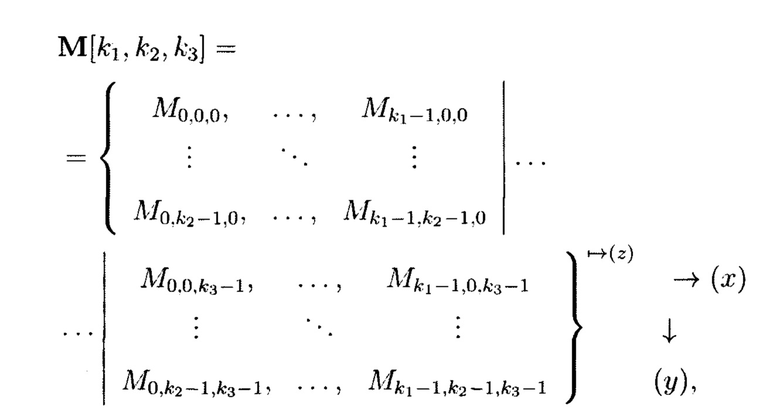
где стрелка 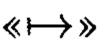 с индексом (z) показывает порядок представления массива посредством сечений, ориентированных по оси z; стрелки
с индексом (z) показывает порядок представления массива посредством сечений, ориентированных по оси z; стрелки  и
и  с индексами (х) и (у) указывают направления, в которых возрастают соответствующие индексы элементов массива по осям х и у.
с индексами (х) и (у) указывают направления, в которых возрастают соответствующие индексы элементов массива по осям х и у.
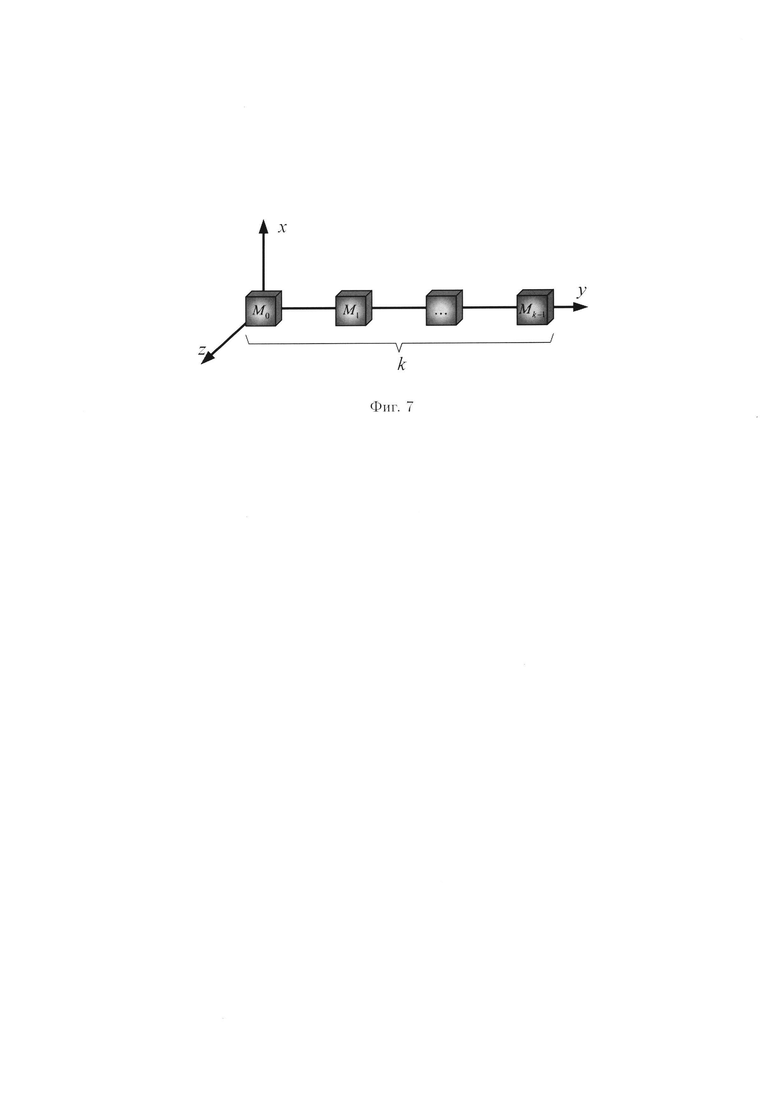
Если все измерения гиперкуба, содержащего блоки данных, будут иметь одинаковые значения:
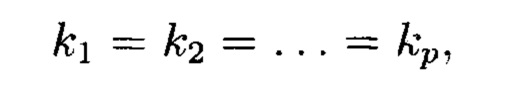
то он будет являться правильной фигурой и его размер может быть описан одним числом к, равным количеству блоков данных, расположенных на его ребре (фиг. 7). Такой гиперкуб будем называть гиперкубом размерности k.
При этом 3-мерный массив данных 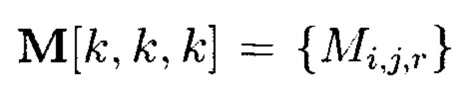 размерности к с помощью сечений ориентации (z) может быть представлен в следующем виде:
размерности к с помощью сечений ориентации (z) может быть представлен в следующем виде:

где i, j, r=0, …, k-1.
Блоки данных 3-мерного массива данных M[k, k, k] могут интерпретироваться как:
- целые неотрицательные числа, представленные в двоичной системе счисления: 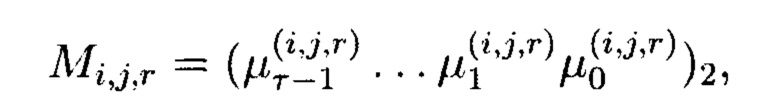 где
где 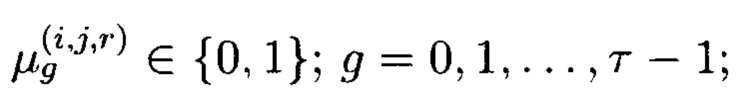
- элементы расширенного поля 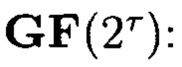
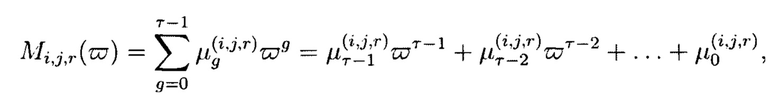
где  - фиктивная переменная:
- фиктивная переменная: 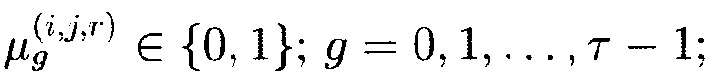
- векторы:
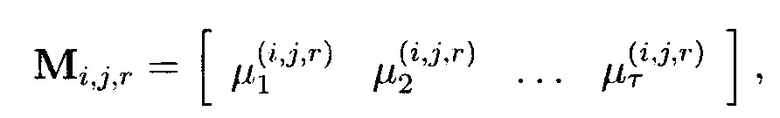
где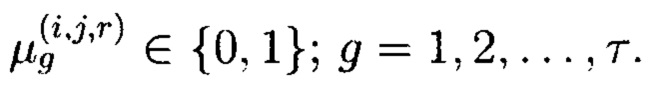
Получаемые структурированные массивы данных могут различаться в зависимости от мерности пространства. Подпространством для многомерного структурированного массива данных является пространство данных меньшей размерности. При этом объекты нульмерного (0-мерного), одномерного (1-мерного) и двумерного (2-мерного) пространств данных будут являться объектами подпространств трехмерного (3-мерного) пространства данных. В то же время, 3-мерное пространство будет являться подпространством 4-мерного пространства данных.
Минимальным значением размерности пространства данных является 0. Такое пространство будет называться 0-мерным пространством данных.
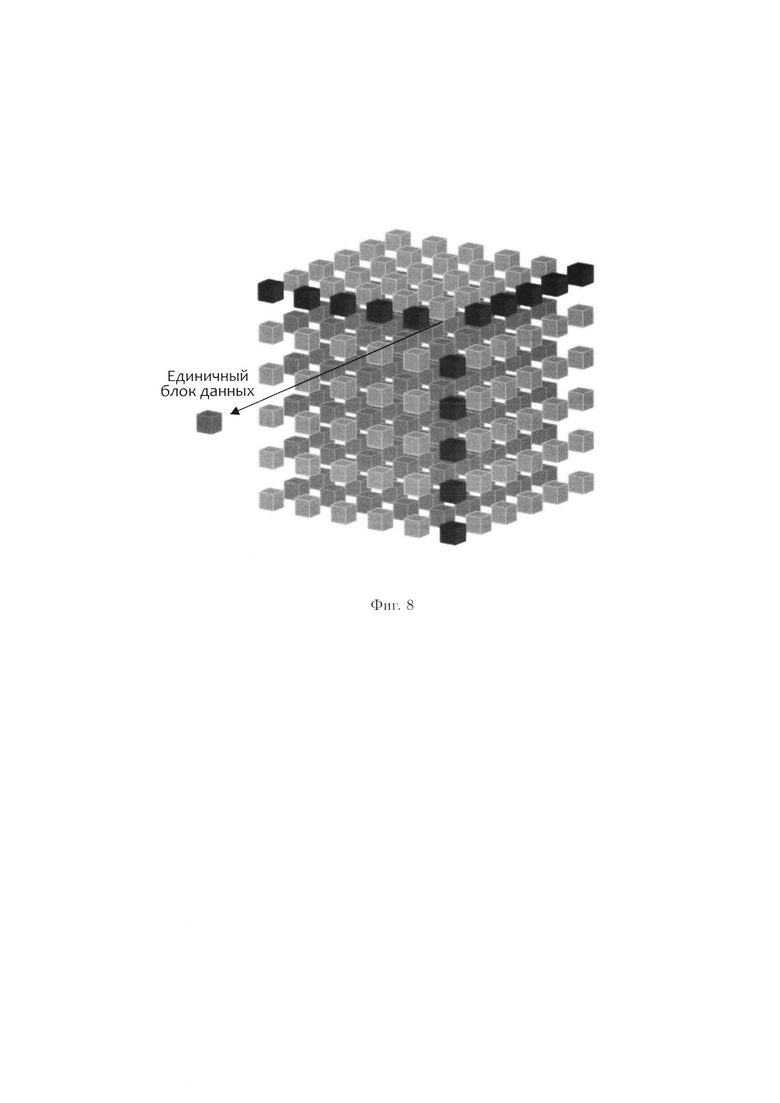
Пример 4. Примером 0-мерного пространства данных будет являться единичный блок данных (фиг 8). 0-мерное пространство будет представлять собой массив данных, состоящий из одного элемента (единичного блока данных М). При этом в пространстве данных, состоящем из одного блока данных М, линейно независимые подмножества отсутствуют. Единичный блок данных М является метрикой для пространств данных, его нельзя разбить на составные части.
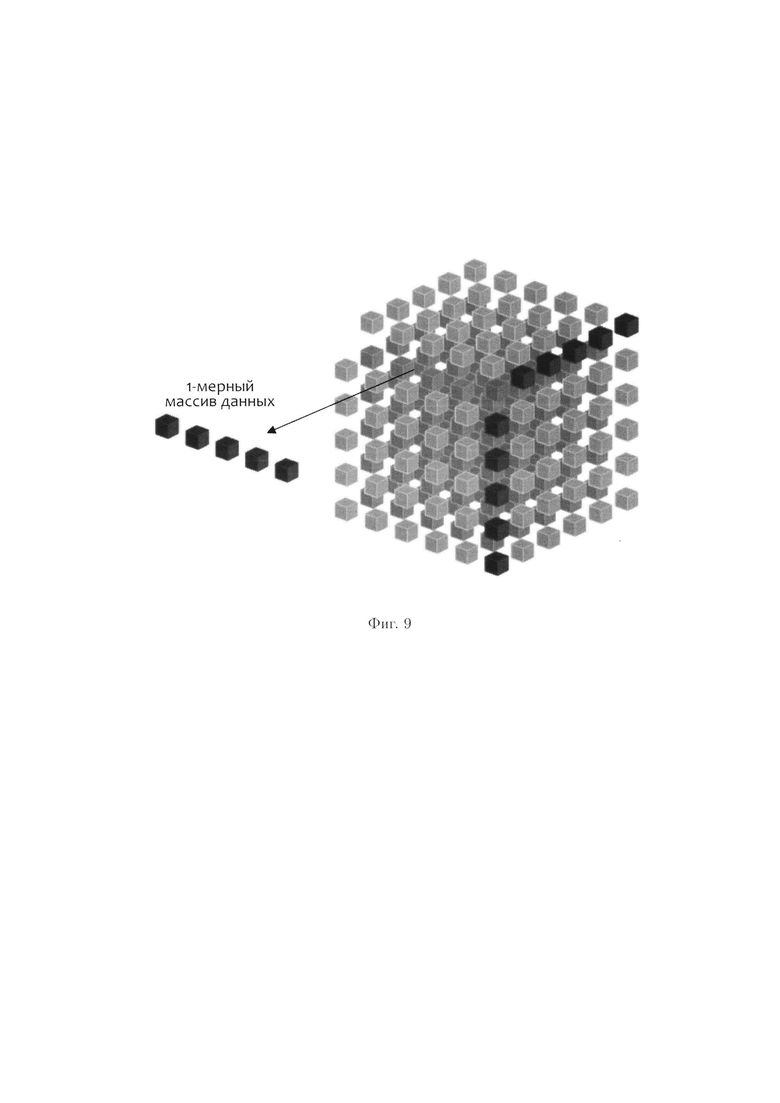
Под 1-мерным пространством данных будет пониматься совокупность блоков данных, расположение которых можно охарактеризовать с помощью одной оси координат.
Пример о. Примером 1-мерного пространства данных будет являться множество блоков данных, идущих друг за другом вдоль одной прямой (1-мерный массив данных) (фиг. 9). Если такое множество является конечным, то оно является отрезком пространства данных. Количество блоков данных, принадлежащих отрезку данных, определяет его длину. Если отрезку пространства данных задать направление, то есть обозначить крайние блоки данных за начало и конец отрезка, то такой отрезок можно считать вектором пространства данных.
При декомпозиции многомерного массива данных на 1-мерные массивы данных получим блоки данных Mi, где i=0, 1, …, k-1. При этом 1-мерный массив данных М[k] может быть представлен в следующем виде:
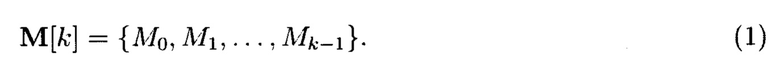
Блоки данных 1-мерного массива данных M[k] могут интерпретироваться как:
- целые неотрицательные числа, представленные в двоичной системе счисления:
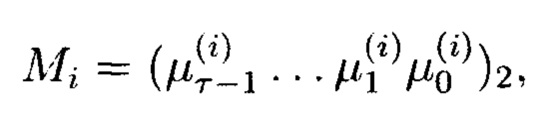
где 
- элементы расширенного поля 
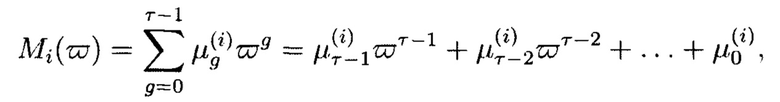
где  - фиктивная переменная;
- фиктивная переменная; 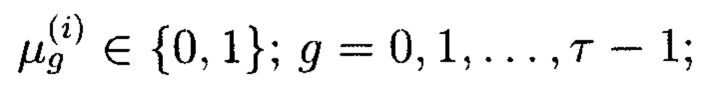
- векторы:
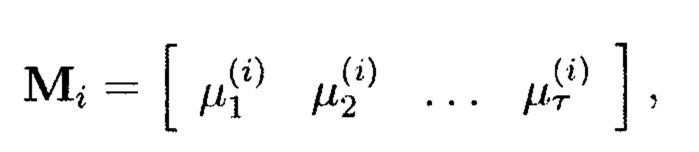
где 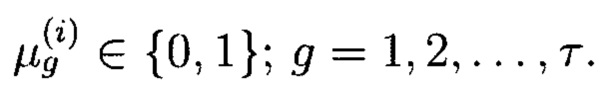
Под 2-мерным пространством данных будет пониматься совокупность блоков данных, расположение которых можно задать, в отличии от 1-мерного пространства, двумя параметрами. Общепринятым представлением 2-мерного пространства является плоскость. Объектами 2-мерного пространства являются плоские объекты, размеры которых можно охарактеризовать не только длинной, как 1-мерные объекты, но и шириной.
Пример 6. Примером 2-мерного пространства данных будет являться множество блоков данных, принадлежащих склеенным параллельным векторам данных, расположенным перпендикулярно одной общей прямой (2-мерный массив данных) (фиг. 10).
При декомпозиции многомерного массива данных на 2-мерные массивы данных получим блоки данных 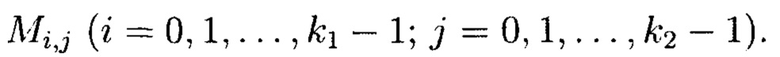 При этом 2-мерный массив данных
При этом 2-мерный массив данных 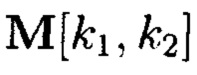 может быть представлен в следующем виде:
может быть представлен в следующем виде:
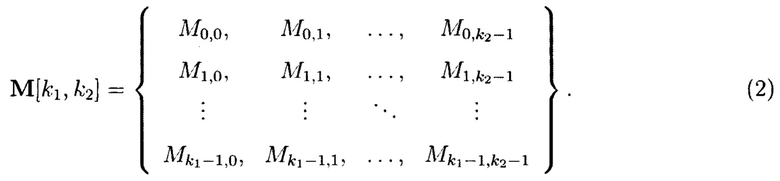
В этом случае блоки данных 2-мерного массива данных 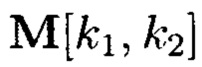 могут интерпретироваться как:
могут интерпретироваться как:
- целые неотрицательные числа, представленные в двоичной системе счисления:
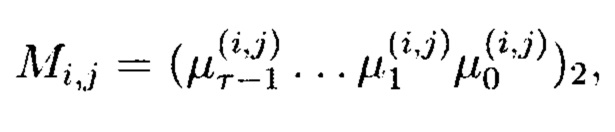
где 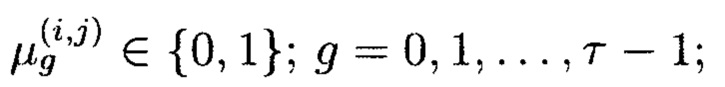
- элементы расширенного поля 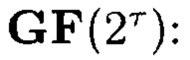
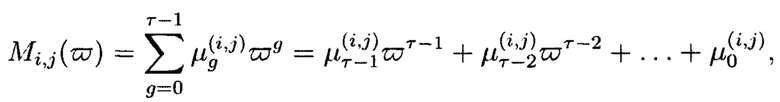
где  - фиктивная переменная;
- фиктивная переменная; 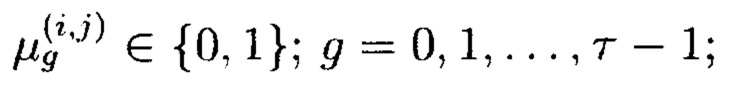
- векторы:
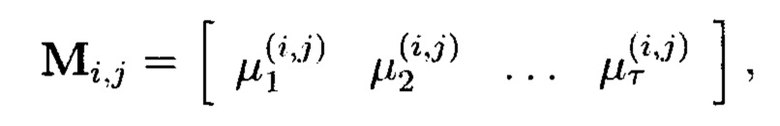
где 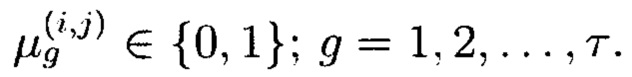
Свойства структурированных массивов данных могут быть рассмотрены на примере 3-мерного куба данных, который является объектом 3-мерного пространства данных, имеющего три однородных измерения: длину, ширину и высоту. Рассматриваемый куб данных будет являться правильной фигурой (то есть все три измерения имеют одинаковые значения) с размерностью к.
На фиг. 11 представлен 3-мерный куб данных размерности k=6 (на его ребре расположено шесть блоков данных).
С точки зрения аналитической геометрии 3-мерный куб данных представляет собой множество точек, которые можно описать набором из трех величин координат. Три взаимно-перпендикулярных вектора, пересекающиеся в одной точке, будут считаться координатными осями, а точка их пересечения началом координат. Такое представление позволяет описать положение блоков данных в пространстве данных относительно осей координат с помощью трех чисел, каждое из которых задает расстояние от начала координат вдоль одной из осей координат до проекции этой точки на плоскости, образованной двумя другими осями. В линейной алгебре, благодаря понятию линейной независимости, любое расположение блока данных можно задать с помощью трех ортогональных векторов.
Представленный 3-мерный куб данных (фиг. 11), является многоугольником 3-мерного евклидова пространства, который обладает симметрией. Его можно разложить на другие геометрические фигуры с учетом минимальной единицы объема, которой является неделимый блок данных.
При этом 3-мерный куб данных имеет центр симметрии. Для 3-мерного куба данных нечетной размерности центром симметрии будет являться блок данных, равноудаленный от всех граней куба данных, как показано на фиг. 12.
Для 3-мерного куба данных четной размерности центр симметрии будет располагаться в пространстве, находящемся в точке пересечения прямых, проходящих через центры противоположных граней куба данных, как показано на фиг. 13. В то же время, 3-мерный куб данных имеет девять плоскостей симметрии. Три плоскости проходят через центр симметрии параллельно граням. Остальные шесть плоскостей проходят через центр симметрии по диагоналям параллельных граней куба данных, но разбить куб данных по этим плоскостям невозможно, для этого пришлось бы разбивать единичные блоки данных.
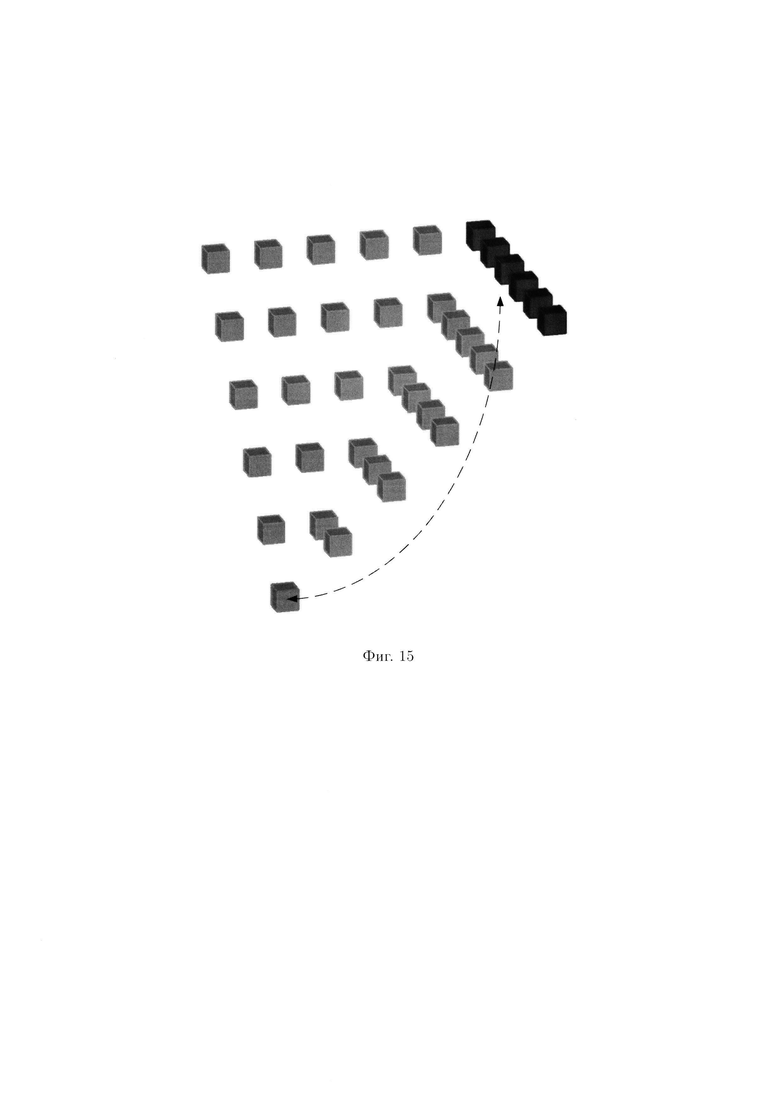
Таким образом, под объектом пространства данных будет пониматься единичный или совокупность блоков данных, объединенных в единую структуру так, что между двумя любыми блоками данных одного объекта можно построить прямую или ломаную линию, соединяющую блоки данных. Такая линия будет называться маршрутом.
На фиг. 14 представлен пример маршрута между двумя произвольными блоками данных объекта 3-мерного пространства данных.
Несмотря на хаотичность расположения блоков данных, объект 3-мерного пространства данных, представленный на фиг. 14, является единым. Каждый блок данных можно соединить с любым другим блоком данных этого объекта, передвигаясь по соседствующим блокам данных, образующим маршрут. Обратный случай представлен на фиг. 15. В объекте 3-мерного пространства данных, представленном на фиг. 15, блоки равномерно распределены по фигуре, однако некоторые ее части обособлены друг от друга и между ними невозможно построить маршрут. Произвольный 1-мерный массив данных не связан с блоками данных, расположенными ниже (из него нельзя попасть к указанному единичному блоку данных).
Таким образом, в случае возможной деградации рассматриваемой СХД, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, не представляется возможным обеспечить целостность данных, представленных в виде объектов, не являющихся едиными (частный случай, объект 3-мерного пространства данных, представленный на фиг. 15).
Для контроля и восстановления целостности полученных на основе информационного подхода структурированных массивов данных предлагается подход, основанный на агрегировании методов из области обеспечения безопасности информации (БИ) и теории надежности, в частности:
- для возможности осуществления криптографического контроля целостности информации используется функция хэширования (область обеспечения БИ);
- для восстановления целостности информации с возможностью гибкого введения избыточности по сравнению с другими методами теории надежности - коды, корректирующие ошибки.
При этом совместное использование функции хэширования и кодов, корректирующих ошибки, позволяет построить крипто-кодовые конструкции контроля и восстановления целостности информации, обеспечивающие возможность подтверждения с криптографической достоверностью ее целостности после выполнения процедуры восстановления (фиг. 16).
Под крипто-кодовой конструкцией будет пониматься конструкция, полученная в результате преобразований, выполняемых над элементами структурированного массива данных, посредством разных видов преобразований, основанных на применении функции хэширования и кодов, корректирующих ошибки, соответственно.
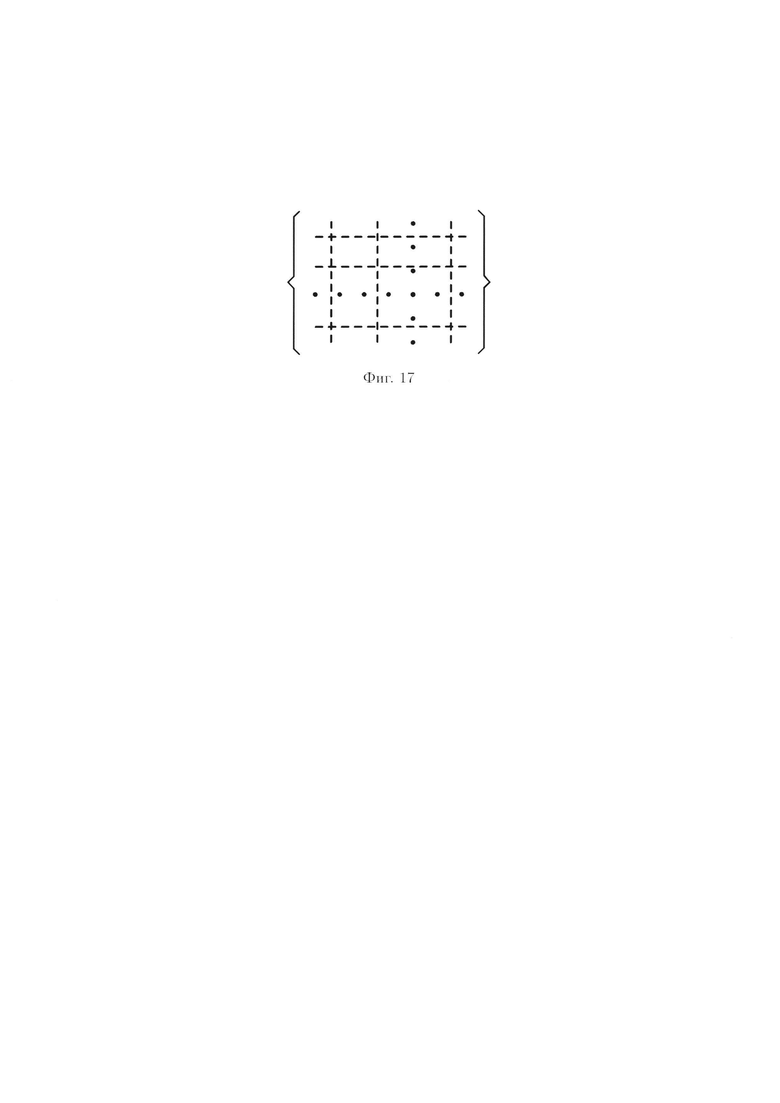
Для получения крипто-кодовых конструкций контроля и восстановления целостности информации выполняются преобразования со структурированными массивами данных, которые будут поясняться на примере 2-мерного массива данных размерности к при векторной интерпретации его элементов:
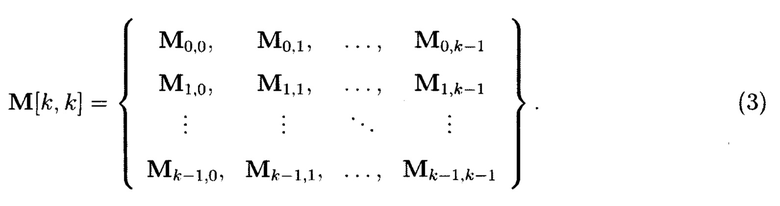
Для графического описания порядка выполнения преобразований 2-мерный массив данных (3) будет представлен, как показано на фиг. 17.
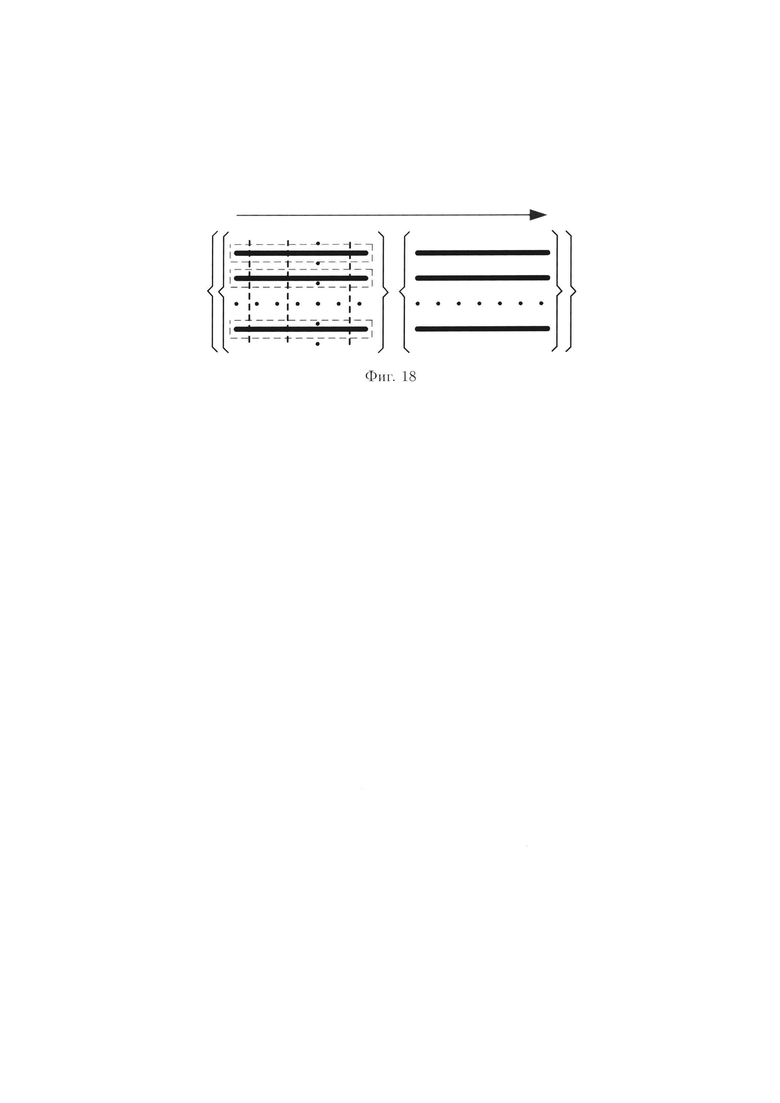
Преобразования над элементами строк 2-мерного массива данных иллюстрируются на фиг. 18.
При этом массив (3) примет следующий вид:
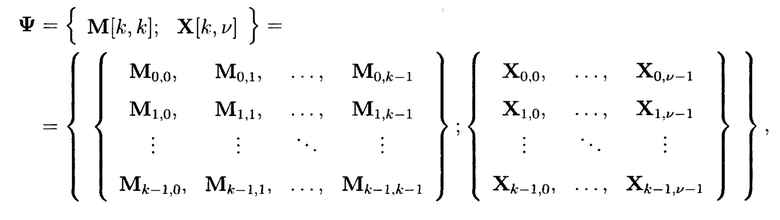
где 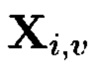 - элемент массива
- элемент массива 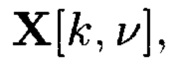 обозначающий контрольный символ, полученный в
обозначающий контрольный символ, полученный в
результате преобразований над элементами строк массива 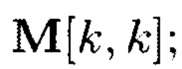
 Причем выполняемые преобразования могут быть связаны как с применением, функции хэширования, так и кодов, корректирующих ошибки.
Причем выполняемые преобразования могут быть связаны как с применением, функции хэширования, так и кодов, корректирующих ошибки.
Здесь 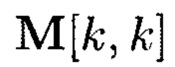 и
и 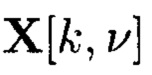 меньшие массивы, размеры которых очевидным образом дополняют друг друга до размера массива
меньшие массивы, размеры которых очевидным образом дополняют друг друга до размера массива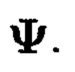
Массив 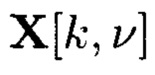 будет называться подмассивом, расположенным в строках и столбцах массива
будет называться подмассивом, расположенным в строках и столбцах массива 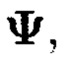 полученным в результате преобразований над элементами строк массива (3).
полученным в результате преобразований над элементами строк массива (3).
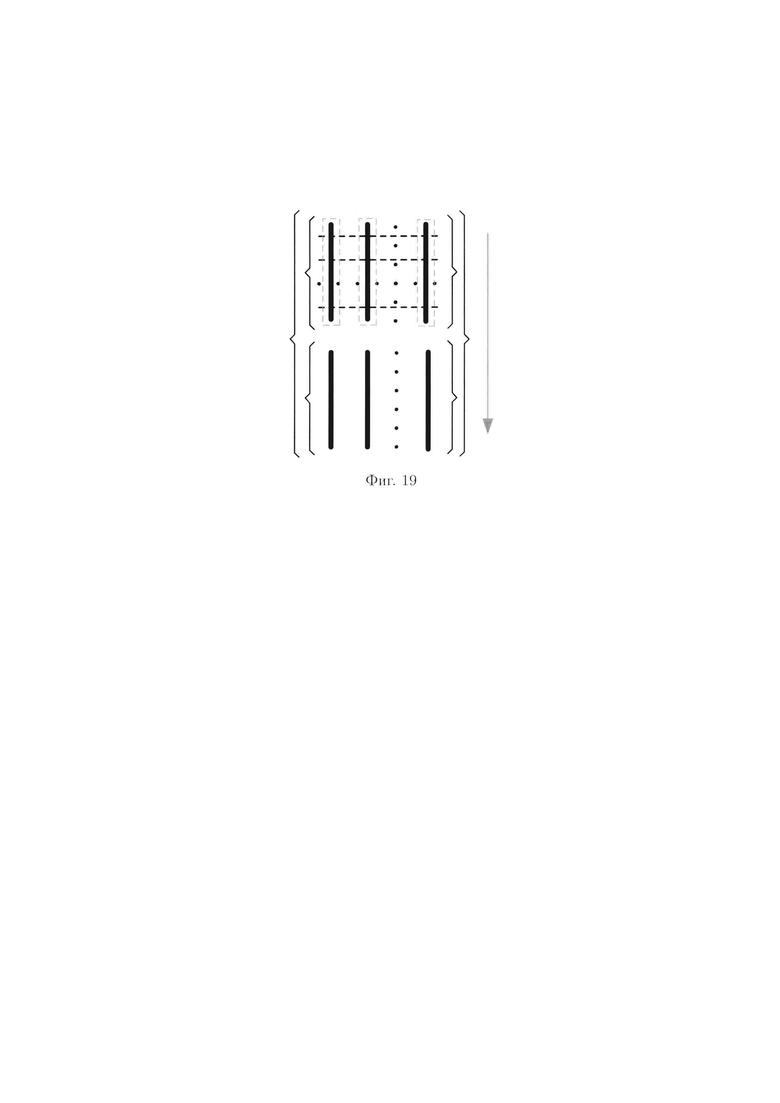
Преобразования над элементами столбцов 2-мерного массива данных иллюстрируются на фиг. 19.
При этом массив (3) примет следующий вид:

где 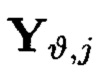 - элемент массива
- элемент массива 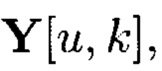 обозначающий контрольный символ, полученный в результате преобразований над элементами столбцов массива M[k, k];
обозначающий контрольный символ, полученный в результате преобразований над элементами столбцов массива M[k, k]; 
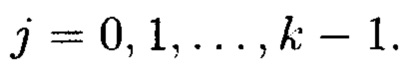
Выполняемые преобразования, в этом случае, могут быть связаны как с применением функции хэширования, так и кодов, корректирующих ошибки.
Здесь 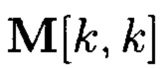 и меньшие
и меньшие 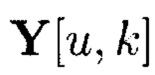 массивы, размеры которых очевидным образом дополняют друг друга до размера массива
массивы, размеры которых очевидным образом дополняют друг друга до размера массива 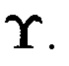
Полученный массив 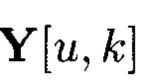 будет называться подмассивом, расположенным в строках и столбцах массива
будет называться подмассивом, расположенным в строках и столбцах массива 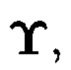 полученным в результате преобразований над элементами столбцов массива (3).
полученным в результате преобразований над элементами столбцов массива (3).
Для построения крипто-кодовых конструкций контроля и восстановления целостности структурированных массивов данных, представленных 2-мерным массивом данных, необходимы преобразования, одновременно выполняемые над элементами как строк, так и столбцов 2-мерного массива данных.
В результате одновременного выполнения над элементами строк и столбцов 2-мерного массива данных разных типов преобразований, основанных на применении функции хэширования и кодов, контролирующих ошибки, получим крипто-кодовую конструкцию контроля и восстановления целостности информации.
Порядок выполнения преобразований, одновременно выполняемых над элементами строк и столбцов 2-мерного массива данных, иллюстрируется на фиг. 20.
При этом массив (3) примет следующий вид:
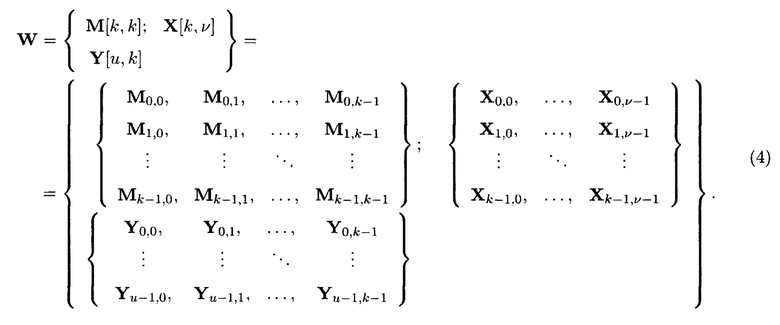
При условии, что элементы 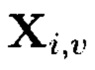 и
и 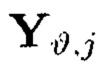 получены посредством разных видов преобразований, выражение вида (4) является крипто-кодовой конструкцией.
получены посредством разных видов преобразований, выражение вида (4) является крипто-кодовой конструкцией.
Крипто-кодовые конструкции, описываемые выражением (4), могут быть представлены в двух видах. В конструкциях первого вида элементы 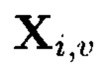 являются результатами преобразований над блоками данных Mi,j, расположенными на строках массива (4), а элементы
являются результатами преобразований над блоками данных Mi,j, расположенными на строках массива (4), а элементы 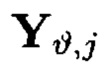 - результаты преобразований над блоками данных Mi,j, расположенными на столбцах массива (4), в конструкциях второго вида преобразования выполняются в обратном порядке.
- результаты преобразований над блоками данных Mi,j, расположенными на столбцах массива (4), в конструкциях второго вида преобразования выполняются в обратном порядке.
Пример 7. Дан массив данных:

состоящая из 4-х блоков данных 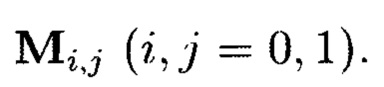
Возможными выражениями, описываемые крипто-кодовыми конструкциями, в которых в результате преобразований вычисляются по одному элементу от каждой строки и столбца массива (5), являются:
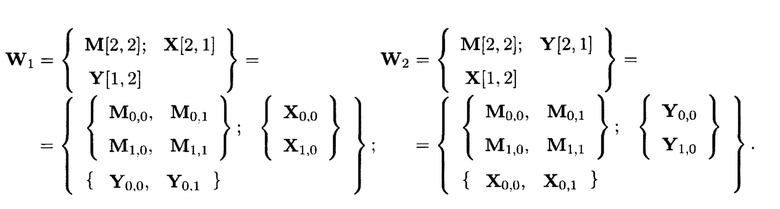
Также возможны преобразования над элементами строк и столбцов 2-мерного массива данных, выполняемые с чередованием правил. Данные преобразования могут выполняться с чередованием правил как по отношению к строкам и столбцам массива (3), так и по отношению к элементам массива независимо от места их нахождения.
Так преобразования над элементами 2-мерного массива данных, выполняемые с чередованием правил по отношению к его строкам и столбцам (частный случай), иллюстрируются на фиг. 21.
В этом случае над элементами четных строк массива (3) выполняются преобразования по правилам, идентичным правилам, по которым выполняются преобразования над элементами нечетных столбцов массива или в обратном порядке.
Массив (3) примет вид:
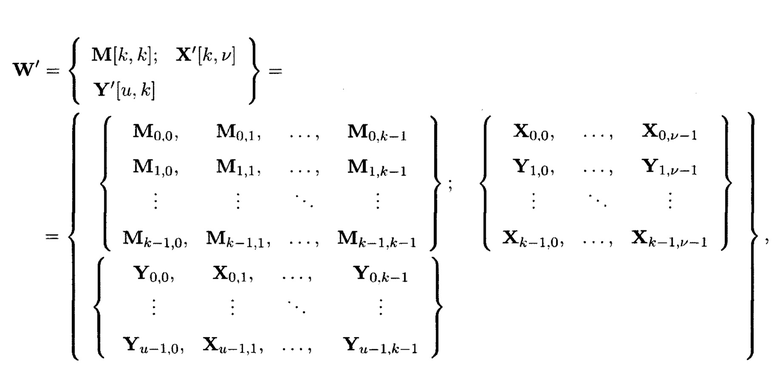
где  обозначает массив
обозначает массив  содержащий неоднородные элементы (полученные в результате разных видов преобразований), или массив
содержащий неоднородные элементы (полученные в результате разных видов преобразований), или массив  содержащий подмассивы, состоящие из неоднородных элементов; k - нечетное число (частный случай).
содержащий подмассивы, состоящие из неоднородных элементов; k - нечетное число (частный случай).
Для данных, представленных 2-мерным массивом данных, количество возможных сочетаний подобных видов преобразований будет зависить от значения k.
Пример 8. Дан массив (5).
Возможными выражениями, описываемые крипто-кодовыми конструкциями, в которых в результате преобразований вычисляются по одному элементу от каждой строки и столбца массива, являются:
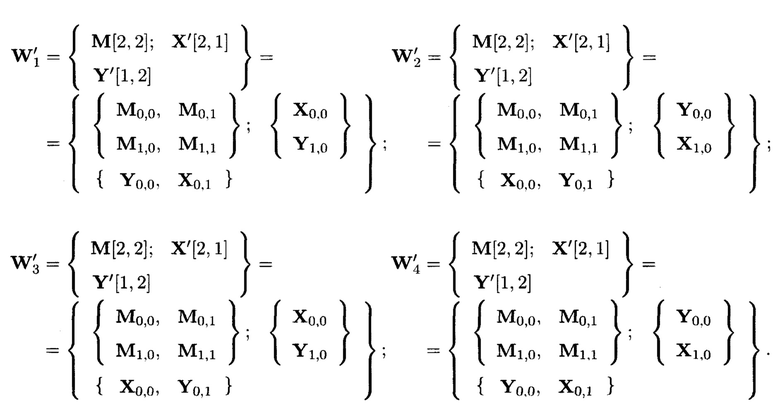
Также возможны преобразования, выполняемые с чередованием правил по отношению к самим элементам 2-мерного массива данных независимо от места их нахожденияих. Преобразования над элементами подмассива 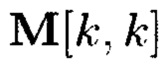 могут выполняться по правилам, определенным для вычисления отдельного элемента, расположенного независимо от номера строки и столбца подмассивов
могут выполняться по правилам, определенным для вычисления отдельного элемента, расположенного независимо от номера строки и столбца подмассивов 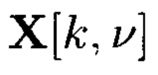 и
и 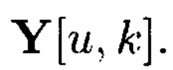
Пример 9. Для вычисления iv-элемента 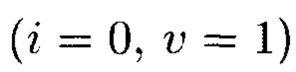 подмассива
подмассива 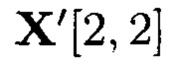 массива:
массива:
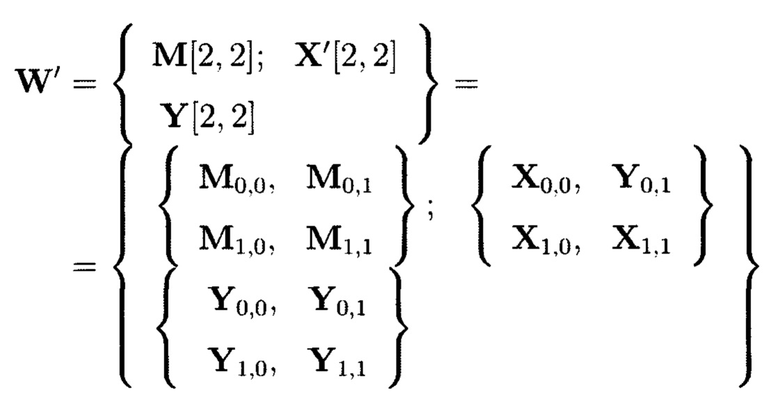
применяются правила, отличающиеся от правил, по которым вычисляется iv-элемент 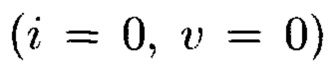 подмассива
подмассива 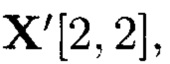 независимо от того, что они оба расположены на одной строке.
независимо от того, что они оба расположены на одной строке.
Также существуют крипто-кодовые конструкции, описываемые выражениями, в которых преобразования выполняются по правилам, определенным для наборов элементов подмассива 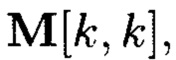 независимо от их нахождения в его строках и столбцах.
независимо от их нахождения в его строках и столбцах.
Массив (3) примет вид:
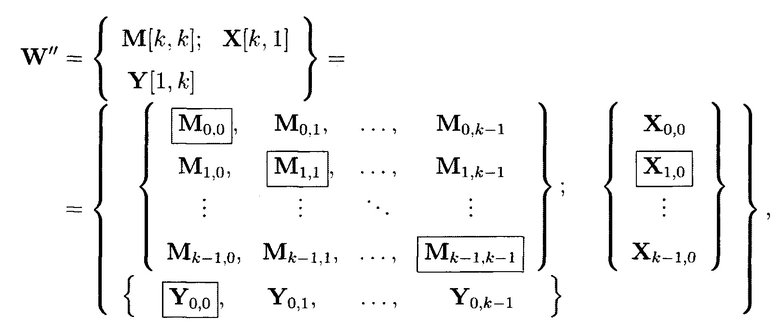
где элементы, обозначенные как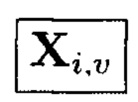 и
и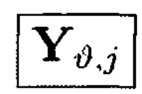 являются результатами преобразований над блоками данных, обозначенными как
являются результатами преобразований над блоками данных, обозначенными как 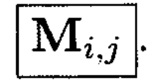
Пример 10. Элементы Х1,0 и Y0,0 массива являются результатами разных видов преобразований от одних и тех же блоков данных Mi,j:
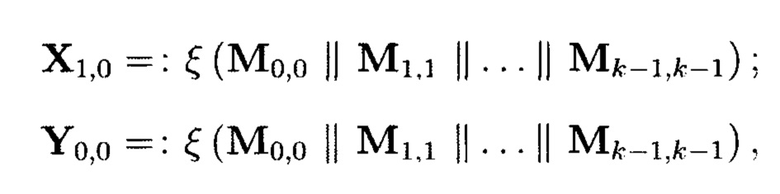
где 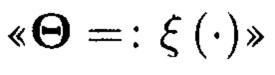 обозначает, что элемент
обозначает, что элемент  массива является результатом преобразования, выполненного по правилам, определенным функцией
массива является результатом преобразования, выполненного по правилам, определенным функцией 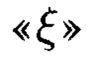 от аргумента
от аргумента 
Также могут выполняться преобразования над контрольными символами 2-мерного массива данных. Результатом преобразований контрольных символов 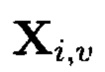 и
и 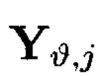 из множества
из множества 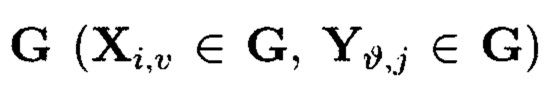 является однозначное определение дополнительных контрольных символов
является однозначное определение дополнительных контрольных символов 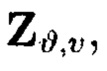 операции с которыми:
операции с которыми:
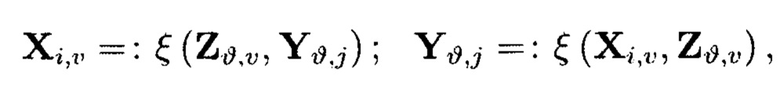
являются обратными. Такое свойство будет обеспечивать возможность подтверждения с криптографической достоверностью целостности ценной информации после выполнения процедуры восстановления.
Порядок выполнения преобразований над контрольными символами 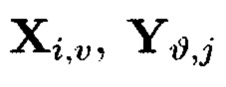 массива (4), иллюстрируется на фиг. 22.
массива (4), иллюстрируется на фиг. 22.
Массив (4) примет вид:
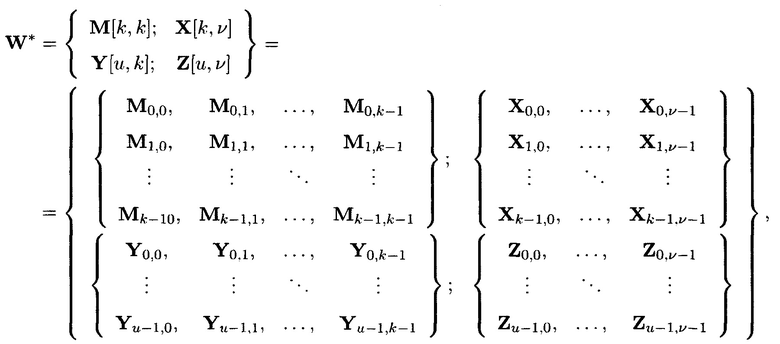
где 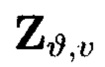 элемент массива W*, обозначающий дополнительный контрольный символ, полученный в результате преобразований над контрольными символами;
элемент массива W*, обозначающий дополнительный контрольный символ, полученный в результате преобразований над контрольными символами; 
Здесь 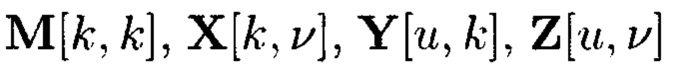 - меньшие массивы, размеры которых, очевидным образом, дополняют друг друга до размера массива W*.
- меньшие массивы, размеры которых, очевидным образом, дополняют друг друга до размера массива W*.
Массив 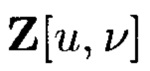 также будем называть подмассивом, расположенным в строках и столбцах массива W*.
также будем называть подмассивом, расположенным в строках и столбцах массива W*.
Сумма числа строк массива 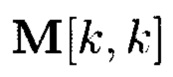 (или
(или 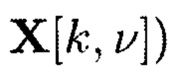 и числа строк массива (
и числа строк массива (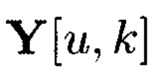 или
или 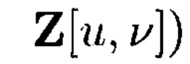 равна числу строк массива W*.
равна числу строк массива W*.
Аналогичное утверждение выполняется для столбцов массива W*.
В общем порядок построения крипто-кодовых конструкций контроля и восстановления целостности структурированных массивов данных определяется посредством применения ϕ-функции («фи-функции»).
Под ϕ-функцией будет пониматься функция, отображающая элементы массива данных - блоки данных, подлежащие защите, посредством разных видов преобразований, основанных на применении функции хэширования и кодов, корректирующих ошибки, в контрольные символы.
Определение понятия «ϕ-функции» поясняется на примере крипто-кодовых конструкций, описываемых 2-мерным массивом (4).
Пример 11. Под ϕ-функцией будет пониматься функция, отображающая блоки данных M/j массива (4) в контрольные символы 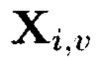 и
и 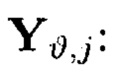
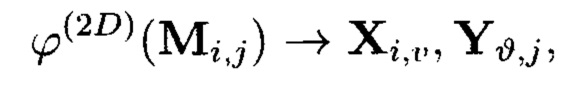
где блоки данных 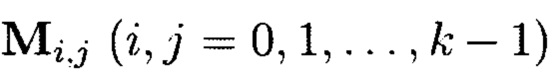 являются аргументами, контрольные символы
являются аргументами, контрольные символы 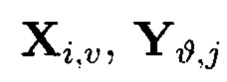 - значениями ϕ-функции
- значениями ϕ-функции 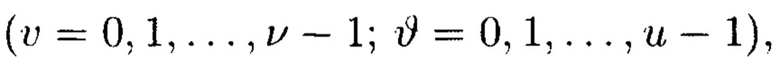 полученными в результате разных видов преобразований:
полученными в результате разных видов преобразований:
- элементы 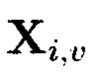 - к примеру, результаты преобразований, выполняемые по правилам применения функции хэширования
- к примеру, результаты преобразований, выполняемые по правилам применения функции хэширования 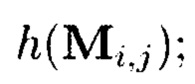
- элементы 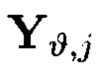 - результаты преобразований, выполняемые по правилам применения кодов, корректирующих ошибки,
- результаты преобразований, выполняемые по правилам применения кодов, корректирующих ошибки, 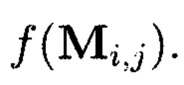
В общем виде представления «ϕ-функции» мерность пространства, в котором выполняются преобразования будет обозначаться как pD (р=1, 2, 3, … обозначает 1-, 2-, 3-мерное и т.д. пространство, соответственно).
Причем построение крипто-кодовых конструкций будет определятся на основе применения ϕ-функции как во времени, так и пространстве.
Применение ϕ-функции во времени будет определяться очередностью выполнения преобразований над ее аргументом, а в пространстве - мерностью пространства, в котором будут выполняться преобразования.
Пример 12. При применении ϕ-функции во времени существуют следующие очередности выполнения преобразований (фиг. 23):
- сначала вычисляются контрольные символы  являющиеся результатами преобразований, выполняемых по правилам применения функции хэширования, а затем контрольные символы
являющиеся результатами преобразований, выполняемых по правилам применения функции хэширования, а затем контрольные символы  являющиеся результатами преобразований, выполняемых по правилам применения кодов, корректирующих ошибки. Получим:
являющиеся результатами преобразований, выполняемых по правилам применения кодов, корректирующих ошибки. Получим:
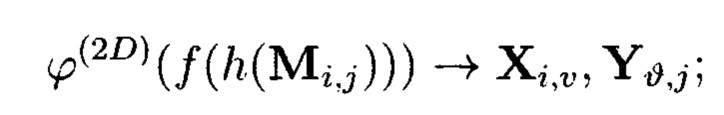
- или в обратном порядке:
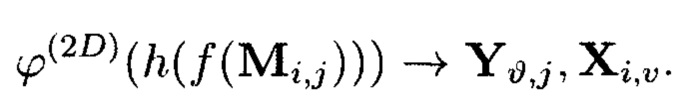
Пример 13. Порядок применения ϕ-функции во времени, где преобразования выполняются:
- по правилам применения кодов, корректирующих ошибки, 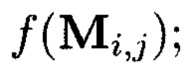
- по правилам применения нескольких функций хэширования: 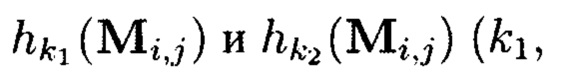
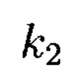 - секретные ключи), представлен на фиг. 24.
- секретные ключи), представлен на фиг. 24.
Применение таких крипто-кодовых конструкций контроля и восстановления целостности структурированных массивов данных характеризуется появлением нового эмерджентного свойства. Появляющаяся эмерджентность заключается в том, что используемому при кодировании 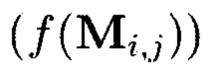 коду, корректирующему ошибки, для исправления ошибок достаточно обладать исправляющей способностью, равной его обнаруживающей. Такое преимущество обеспечивается тем, что обнаружение ошибки, приводящей к нарушению целостности информации, уже выполняются за счет использования функции хэширования (h(Mi,j)).
коду, корректирующему ошибки, для исправления ошибок достаточно обладать исправляющей способностью, равной его обнаруживающей. Такое преимущество обеспечивается тем, что обнаружение ошибки, приводящей к нарушению целостности информации, уже выполняются за счет использования функции хэширования (h(Mi,j)).
К тому же, с полученными крипто-кодовыми конструкциями контроля и восстановления целостности данных в случае возможной деградации рассматриваемых многомерных СХД, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, может быть выполнена фрагментация на массивы меньшей размерности или массивы, являющиеся объектами, принадлежащими их подпространствам, при этом содержащаяся в них информация продолжает обладать ценностью для принятия пользователем ИС решения.
Порядок фрагментации структурированных массивов данных будет рассмотрен на примере фрагментации объектов 3-мерного пространства данных, а также объектов его подпространств. Ввиду того, что 3-мерный куб данных обладает симметрией, один и тот же способ фрагментации куба данных в различных плоскостях будет давать одинаковые результаты. Поэтому фрагментация будет выполняться только в одной изометрии. При этом свойство неделимости блока данных, как минимальной структурной единицы многомерного массива данных, накладывает ограничения на способы разбиения 3-мерного объекта пространства данных.
Пример 14. Если в основании 3-мерного куба данных лежит квадрат, то при попытке фрагментировать его по диагонали на две треугольные призмы, блоки данных, принадлежащие диагонали основания, придется причислить к одной из получаемых призм, при этом призмы будут иметь разные размеры (фиг. 25).
Фрагментация объектов 3-мерного пространства данных на объекты, принадлежащие его подпространствам, может быть выполнена по линиям, параллельным осям координат.
Пример 15. Порядок фрагментации 3-мерного массива данных на 2-мерные массивы данных представлен на фиг. 26, а 2-мерного массива данных на 1-мерные массивы данных представлен на фиг. 27. При этом получаемые 1- и 2-мерные массивы данных могут быть представлены в виде (1) и (2) соответственно.
Фрагментация объектов 2-мерного пространства данных может быть выполнена на объекты по диагональным линиям (с учетом свойства неделимости единичных блоков данных).
Пример 16. Фрагментация 2-мерного массива данных на 2-мерные массивы данных разных размеров (фиг. 28). При этом получаемый 2-мерный массив данных 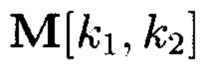 может быть представлен в следующем виде:
может быть представлен в следующем виде:
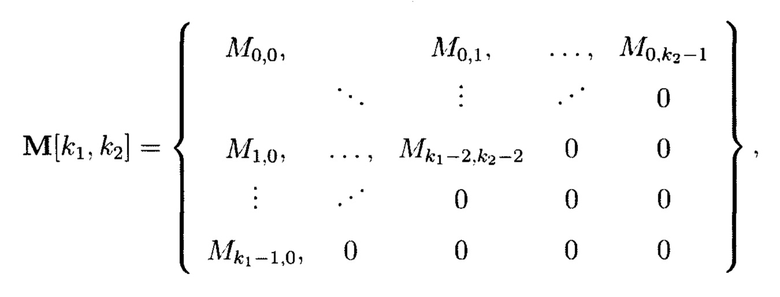
где «0» обозначает пустой элемент массива.
Также возможно выполнение фрагментации объектов 3-мерного пространства данных на объекты путем отсечения от него плоскостью одной из вершин.
Пример 17. Фрагментация 3-мерного куба данных на тетраэдр данных - пирамиду с треугольным основанием (фиг. 29).
С помощью сечений ориентации (z) тетраэдр данных - 3-мерный массив данных 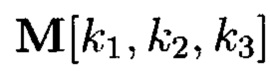 может быть представлен в следующем виде:
может быть представлен в следующем виде:

Полученный тетраэдр будет являться прямоугольной пирамидой, так как в нем присутствует вершина, грани которой попарно перпендикулярны.
Другие способы фрагментации объектов 3-мерного пространства данных. Фрагментация многомерных массивов данных может привести к получению фигур, которые не являются едиными объектами.
Пример 18. Фрагментация 3-мерного куба данных на три равные 3-мерные пирамиды данных с четырехугольным основанием (фиг. 30).
Полученную фигуру, размещенную в центре фиг. 30, нельзя рассматривать как объект 3-мерного пространства данных, так как она не является единым объектом, но ее можно рассматривать как совокупность объектов 0- и 1-мерного пространства данных.
В свою очередь, полученная 3-мерная пирамида данных с четырехугольным основанием, может быть рассмотрена как 3-мерный массив данных M[k1, k2, k3], который с помощью сечений ориентации (z) примет следующий вид:
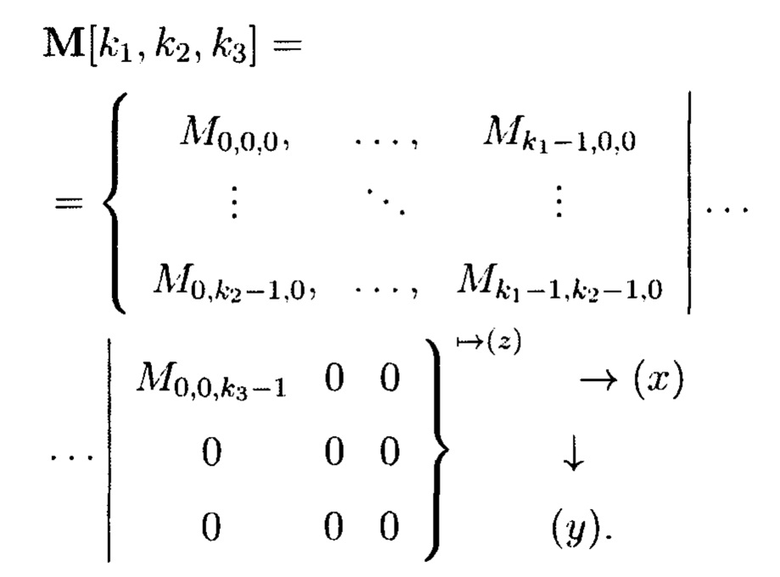
Полученная 3-мерная пирамида данных с четырехугольным основанием для наглядности представлена на фиг. 31.
При фрагментации 3-мерной пирамиды данных с четырехугольным основанием вдоль диагонали основания по направлению к вершине могут быть получены два 3-мерных тетраэдра данных (фиг. 32).
В отличие от тетраэдров данных, рассмотренных выше, полученные объекты не будут являться прямоугольными, так как не обладают вершиной, у которой все прилегающие грани попарно перпендикулярны. Такой тетраэдр данных обладает двумя равными гранями перпендикулярными граням, гипотенузы которых не сходятся к одной вершине.
Таким образом, на основе применения информационного подхода к представлению информации в рассматриваемых многомерных СХД по критерию ценности информации получены p-мерные структурированные массивы данных. При вынужденной деградации СХД в условиях деструктивных воздействий злоумышленника и возмущений среды функционирования фрагментацию полученных структурированных массивов данных требуется выполнять с учетом обеспечения возможности принятия пользователем ИС решения на основе информации, содержащейся в полученных массивах.
Это объясняется тем, что ценность информации, содержащейся в полученных структурированных массивах данных, будет напрямую влиять на достижение цели функционирования СХД и выражаться в таких понятиях как достоверность и полнота, которые, в свою очередь, будут оцениваться посредством измерения обноруживающей и исправляющей способностей разрабатываемых механизмов защиты при компенсации деструктивных воздействий.
Таким образом, на основе представленных правил применения ϕ-функции во времени и пространстве могут быть построены крипто-кодовые конструкции контроля и восстановления целостности структурированных массивов данных на основе применения криптографических хэш-функций и кодов, корректирующих ошибки, с возможностью контроля и восстановления целостности данных при изменении их структуры в условиях деградации многомерных СХД, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ В УСЛОВИЯХ КРИТИЧЕСКОЙ ДЕГРАДАЦИИ СИСТЕМ ИХ ХРАНЕНИЯ | 2023 |
|
RU2828227C1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ В УСЛОВИЯХ ДЕГРАДАЦИИ СИСТЕМ ХРАНЕНИЯ | 2022 |
|
RU2801124C1 |
| СПОСОБ СТРУКТУРНО-ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ ПРИ ВЫНУЖДЕННОМ СОКРАЩЕНИИ МЕРНОСТИ ПРОСТРАНСТВА КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ | 2022 |
|
RU2801198C1 |
| СПОСОБ ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КРИПТО-КОДОВЫХ СТРУКТУР ДЛЯ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ | 2023 |
|
RU2808758C1 |
| СПОСОБ ФОРМИРОВАНИЯ КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ В УСЛОВИЯХ СОКРАЩЕНИЯ МЕРНОСТИ ПРОСТРАНСТВА КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ | 2022 |
|
RU2806539C1 |
| СПОСОБ СТРУКТУРНО-ПАРАМЕТРИЧЕСКОГО СИНТЕЗА КРИПТО-КОДОВЫХ КОНСТРУКЦИЙ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ СТРУКТУРИРОВАННЫХ МАССИВОВ ДАННЫХ В УСЛОВИЯХ ПЕРЕХОДА К ПРОСТРАНСТВУ ДАННЫХ С БОЛЬШЕЙ МЕРНОСТЬЮ | 2022 |
|
RU2801082C1 |
| СПОСОБ ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ ПРИ ДЕГРАДАЦИИ МНОГОМЕРНЫХ СИСТЕМ ХРАНЕНИЯ | 2023 |
|
RU2833352C1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ ОДНОМЕРНЫХ МАССИВОВ ДАННЫХ НА ОСНОВЕ КОМПЛЕКСИРОВАНИЯ КРИПТОГРАФИЧЕСКИХ МЕТОДОВ И МЕТОДОВ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ | 2022 |
|
RU2786617C1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ | 2021 |
|
RU2771208C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ | 2021 |
|
RU2771236C1 |


















Изобретение относится к способу построения крипто-кодовых конструкций контроля и восстановления целостности структурированных массивов данных. Технический результат заключается в возможности контроля и восстановления целостности структурированных массивов данных на основе применения криптографических хэш-функций и кодов, корректирующих ошибки. В способе на основе накапливаемой в многомерных системах хранения данных информации в виде p-мерных структурированных массивов данных, по правилам применения ϕ-функции во времени и пространстве, отображающей их элементы посредством разных видов преобразований, основанных на применении функций хэширования h и кодирования 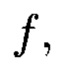 в контрольные символы, строятся крипто-кодовые конструкции, при этом в случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация первоначальных структурированных массивов данных, посредством чего содержащаяся в полученных массивах информация продолжает обладать ценностью, достаточной для принятия пользователем информационной системы решения. 32 ил.
в контрольные символы, строятся крипто-кодовые конструкции, при этом в случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация первоначальных структурированных массивов данных, посредством чего содержащаяся в полученных массивах информация продолжает обладать ценностью, достаточной для принятия пользователем информационной системы решения. 32 ил.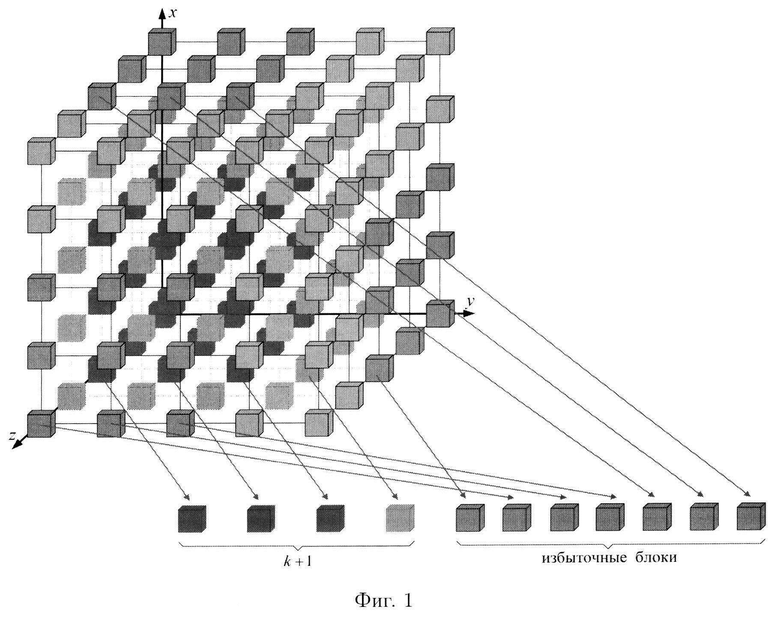
Способ построения крипто-кодовых конструкций контроля и восстановления целостности структурированных массивов данных, заключающийся в том, что крипто-кодовые конструкции контроля и восстановления целостности данных строятся на основе массивов данных размерности k, состоящих из блоков данных, которые для обеспечения возможности контроля их целостности размещаются в массиве размерности k+1, к которым для возможности обнаружения признаков нарушения целостности применяется хэш-функция h, при этом вычисленные хэш-коды размещаются в свободных блоках массива и являются эталонными, значения которых при запросе на использование данных сравниваются со значениями хэш-кодов, вычисляемых уже от проверяемых блоков данных, при восстановлении целостности блоки данных, подлежащие защите, а также вычисленные от них эталонные хэш-коды интерпретируются как элементы GF(2t) и являются наименьшими полиномиальными вычетами, при этом полученный массив данных рассматривается как единый суперблок модулярного полиномиального кода, над которым выполняется операция расширения путем введения n-k избыточных оснований, для которых вычисляются соответствующие им избыточные вычеты, дополнительно вводимые для коррекции ошибки, в случае возникновения которой восстановление блоков данных без ущерба для однозначности их представления осуществляется посредством реконфигурации системы путем исключения из вычислений блока данных с признаками нарушения целостности, отличающийся тем, что для построения крипто-кодовых конструкций контроля и восстановления целостности данных на основе информационного подхода накапливаемая в рассматриваемых многомерных системах хранения данных информация представляется в виде р-мерных структурированных массивов данных посредством предварительной сортировки большого многомерного массива данных, поступающего на хранение, на кластеры данных, являющиеся объектами р-мерного пространства и обладающие ценностью для принятия пользователем информационной системы, в интересах которой применяются многомерные системы хранения данных, решения, полученный при этом структурированный массив данных, состоящий из элементов 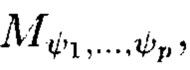 где индексы
где индексы  принимают значения от 1 до kθ (0=1, …, р) соответственно, содержащий k1×k2×…×kp элементов и обозначаемый как
принимают значения от 1 до kθ (0=1, …, р) соответственно, содержащий k1×k2×…×kp элементов и обозначаемый как 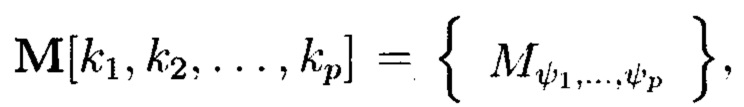 является математическим множеством, имеющим определенную структуру и аксиоматические правила, что позволяет рассматривать его аналогично пространству данных и считающийся дискретным метрическим пространством, так как содержит в своей структуре точки, представленные элементами
является математическим множеством, имеющим определенную структуру и аксиоматические правила, что позволяет рассматривать его аналогично пространству данных и считающийся дискретным метрическим пространством, так как содержит в своей структуре точки, представленные элементами 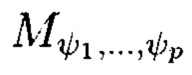 массива, изолированными друг от друга и располагаемыми вдоль абстрактных прямых, параллельных осям координат, на одинаковых расстояниях друг от друга, что позволяет контролировать и восстанавливать целостность полученного структурированного массива данных посредством применения ϕ-функции, отображающей его элементы посредством разных видов преобразований, основанных на применении функций хэширования h и кодирования
массива, изолированными друг от друга и располагаемыми вдоль абстрактных прямых, параллельных осям координат, на одинаковых расстояниях друг от друга, что позволяет контролировать и восстанавливать целостность полученного структурированного массива данных посредством применения ϕ-функции, отображающей его элементы посредством разных видов преобразований, основанных на применении функций хэширования h и кодирования 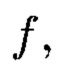 в контрольные символы, при этом с полученными крипто-кодовыми конструкциями контроля и восстановления целостности данных в случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация на массивы меньшей размерности или массивы, являющиеся объектами, принадлежащими их подпространствам, при этом содержащаяся в них информация продолжает обладать ценностью для принятия пользователем информационной системы решения, и обеспечивается возможность контроля и восстановления целостности структурированных массивов данных с измененной структурой.
в контрольные символы, при этом с полученными крипто-кодовыми конструкциями контроля и восстановления целостности данных в случае возможной деградации рассматриваемых многомерных систем хранения данных, вызванной деструктивными воздействиями злоумышленника и возмущениями среды функционирования, выполняется фрагментация на массивы меньшей размерности или массивы, являющиеся объектами, принадлежащими их подпространствам, при этом содержащаяся в них информация продолжает обладать ценностью для принятия пользователем информационной системы решения, и обеспечивается возможность контроля и восстановления целостности структурированных массивов данных с измененной структурой.
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ ДАННЫХ НА ОСНОВЕ КРИПТОГРАФИЧЕСКОЙ ПИРАМИДЫ ПАСКАЛЯ | 2020 |
|
RU2759240C1 |
| СПОСОБ КОНТРОЛЯ И ВОССТАНОВЛЕНИЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ | 2021 |
|
RU2771208C1 |
| СПОСОБ ДВУМЕРНОГО КОНТРОЛЯ И ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ | 2018 |
|
RU2696425C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ НА ОСНОВЕ ПРАВИЛ ПОСТРОЕНИЯ КВАДРАТНЫХ КОДОВ | 2021 |
|
RU2771209C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ МНОГОМЕРНЫХ МАССИВОВ ДАННЫХ НА ОСНОВЕ ПРАВИЛ ПОСТРОЕНИЯ ТРЕУГОЛЬНЫХ КОДОВ | 2021 |
|
RU2774099C1 |
| СПОСОБ КОНТРОЛЯ И ОБЕСПЕЧЕНИЯ ЦЕЛОСТНОСТИ ДАННЫХ | 2017 |
|
RU2680739C1 |
| СПОСОБ КОНТРОЛЯ ЦЕЛОСТНОСТИ ДАННЫХ НА ОСНОВЕ ПРАВИЛ ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКИХ КОДОВ | 2021 |
|
RU2758194C1 |
| Автомобиль-сани, движущиеся на полозьях посредством устанавливающихся по высоте колес с шинами | 1924 |
|
SU2017A1 |
Авторы
Даты
2023-04-06—Публикация
2022-10-26—Подача