Изобретение относится к лазерной технике и может быть использовано для выбора резонаторных зеркал датчиков лазерных гироскопов при использовании анизотропных кольцевых резонаторов, в частности резонаторов с неплоским контуром.
В настоящее время распространенным методом компенсации магнитного дрейфа зеемановских лазерных гироскопов (ЗЛГ) стал квази-четырехчастотный режим генерации [1], при котором обеспечивается попеременная работа на продольных модах с противоположной круговой поляризацией. Переключение с одной моды генерации на другую осуществляется путем изменения периметра кольцевого лазера [2]. Однако при наличии фазовой и амплитудной анизотропии зеркал, формирующих кольцевой резонатор с неплоским контуром, собственными поляризациями становятся не круговые поляризации с правым и левым направлениями вращения, а эллиптические поляризации с разными углами наклона и с разнодобротностью мод. При переключении лазерного гироскопа с одной моды на моду с противоположной поляризацией возникает дополнительная ошибка измерения скорости вращения и угла поворота при разной эллиптичности и неравных добротностях мод [1-3].
Для повышения точности измерений с помощью ЗЛГ важным является подбор зеркал при формировании кольцевых резонаторов с неплоским контуром таким образом, чтобы эллиптичность мод стремилась к единице, т.е. круговой поляризации, а разнодобротность мод уменьшалась до нуля.
Это достигается на основе проведения анализа влияния анизотропии каждого зеркала, формирующего кольцевой резонатор с учетом его положения, на степень эллиптичности ортогональных мод и выбор критерия допустимых значений анизотропии зеркал для достижения минимальной величины разно добротности мод.
Известен способ измерения углов между плоскостями моноблока резонатора кольцевого лазера с неплоским оптическим контуром [RU 2789240 C1, G01B 11/26, 31.01.2023], заключающийся в измерении углов между плоскостями моноблока с использованием гониометра для измерения угла между двумя соседними посадочными плоскостями, пирамидальности двух посадочных плоскостей по отношению к противоположным посадочным плоскостям и базовой плоскости и углов между каждой посадочной плоскостью и базовой плоскостью, причем, при измерении формируют прямое отражение светового луча гониометра от измеряемых плоскостей моноблока, располагая моноблок на установленном на предметном столике гониометра блоке формирования автоколлимационной марки.
Недостатком способа является относительно узкая область применения, поскольку, хотя известный способ и позволяет измерения углов между плоскостями моноблока резонатора кольцевого лазера с неплоским оптическим контуром, но не позволяет выбрать зеркала такого резонатора на основе минимизации разнодобротности мод.
Известен также способ сборки кольцевого резонатора [RU 2626725 C1, G01С 19/66, 31.07.2017], включающий установку зеркал, сварку электродов, электровакуумную обработку и герметизацию, при этом, перед установкой зеркал определяют рассеивающие свойства, по меньшей мере, одного зеркала на основе зарегистрированного трехмерного изображения его поверхности, выделяют анизотропную составляющую рассеяния, вызванную линейно структурированными дефектами в условиях лазерного излучения, падающего на зеркало под углом, характерным для данного типа резонатора, осуществляют выбор углового положения плоскости падения лазерного луча, соответствующего минимальной величине обратного рассеяния, затем осуществляют установку, по меньшей мере, одного зеркала на кольцевой резонатор таким образом, что угловое положение, соответствующее минимальной величине рассеяния, совмещается с плоскостью кольцевого резонатора.
Недостатком этого технического решения также является относительно узкая область применения, поскольку известный способ не позволяет выбрать зеркала такого резонатора на основе минимизации разнодобротности мод, которые обязательно наблюдаются при любой добротности зеркал.
Наиболее близким по технической сущности к предложенному является способ [А.В. Молчанов, А.Ю. Степанов, М.В. Чиркин. Статистические характеристики подложек зеркал и случайная погрешность лазерного гироскопа. //Авиакосмическое приборостроение. 2008, №3, с. 9-16], заключающийся в том, что каждое из четырех зеркал резонатора лазерного гироскопа с целью уменьшения погрешности в измерении угловой скорости и уменьшению порога чувствительности к качеству поверхности зеркал предъявляются повышенные требования - доля излучения, рассеянного зеркалом, не должна превышать 30 ppm (1 ppm=10-6).
Недостатком наиболее близкого технического решения является относительно узкая область применения, поскольку известный способ не позволяет выбрать зеркала такого резонатора на основе минимизации разнодобротности мод, которые обязательно наблюдаются при любой добротности зеркал.
Задача, которая решается в предложенном техническом решении, заключается в разработке способа выбора зеркал таких резонаторов на основе минимизации разнодобротности мод и их эллиптичности к единице с целью повышения точности измерений датчиков, использующих лазерные гироскопы.
Требуемый технический результат заключается в расширении области применения известного способа с целью повышения точности измерений датчиков, использующих лазерные гироскопы, на основе обеспечения возможности выбора зеркал резонатора кольцевого лазера путем минимизации разнодобротности мод и их эллиптичности к единице.
Поставленная задача решается, а требуемый технический результат достигается тем, что резонаторе кольцевого лазера, содержащем последовательно установленные и оптически соединенные первое отражающее зеркало, первое зеркало косого падения, второе отражающее зеркало и второе зеркало косого падения, оптически соединенное с первым отражающим зеркалом, зеркала выбирают из условия равенства величины суммарной фазовой анизотропии всех зеркал, равной нулю
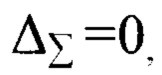
где 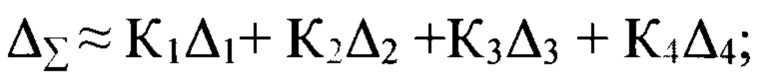
Δ1 - величина фазовой анизотропии первого отражающего зеркала;
Δ2 - величина фазовой анизотропии первого зеркала косого падения;
Δ3 - величина фазовой анизотропии второго отражающего зеркала;
Δ4 - величина фазовой анизотропии второго зеркала косого падения;
K1, К2, К3, К4 - весовые коэффициенты.
Кроме того, требуемый технический результат достигается тем, что весовые коэффициенты выбирают из условия: К1=0,13; К2=1, К3=1,3, К4=1.
На чертеже представлены:
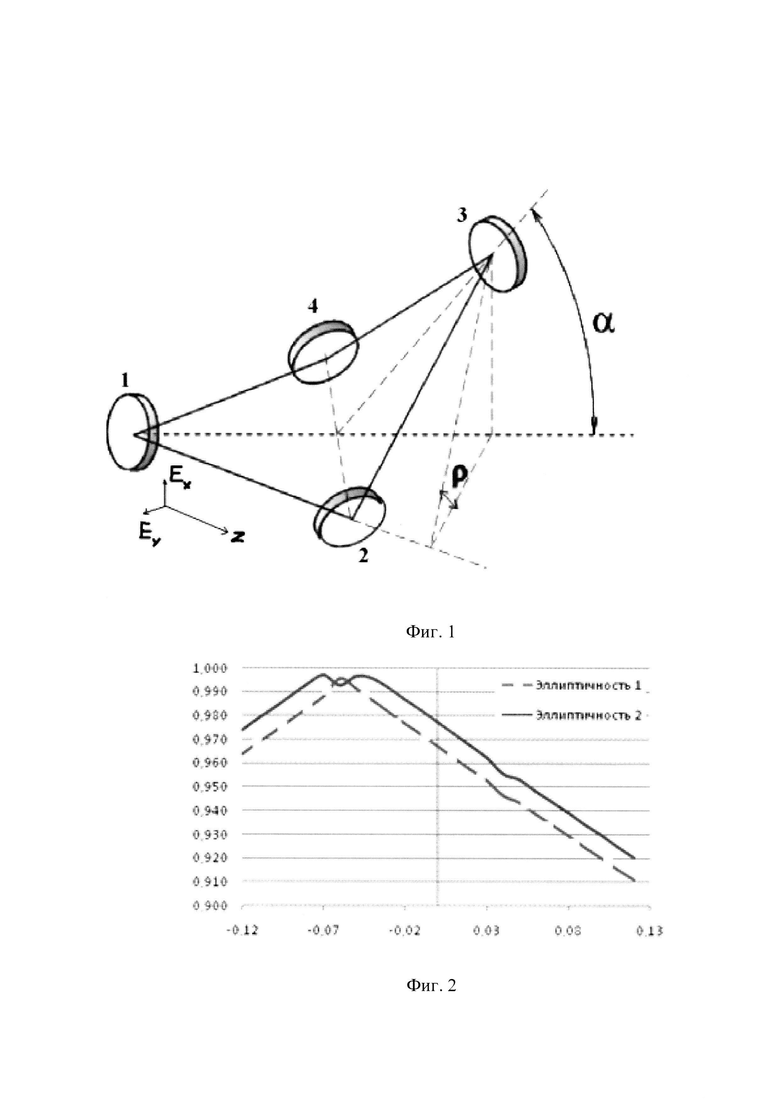
на фиг. 1 - оптическая схема резонатора кольцевого лазера с неплоским оптическим контуром, в котором в качестве примера реализуется предложенный способ;
на фиг. 2 - зависимость эллиптичности мод от Δ3;
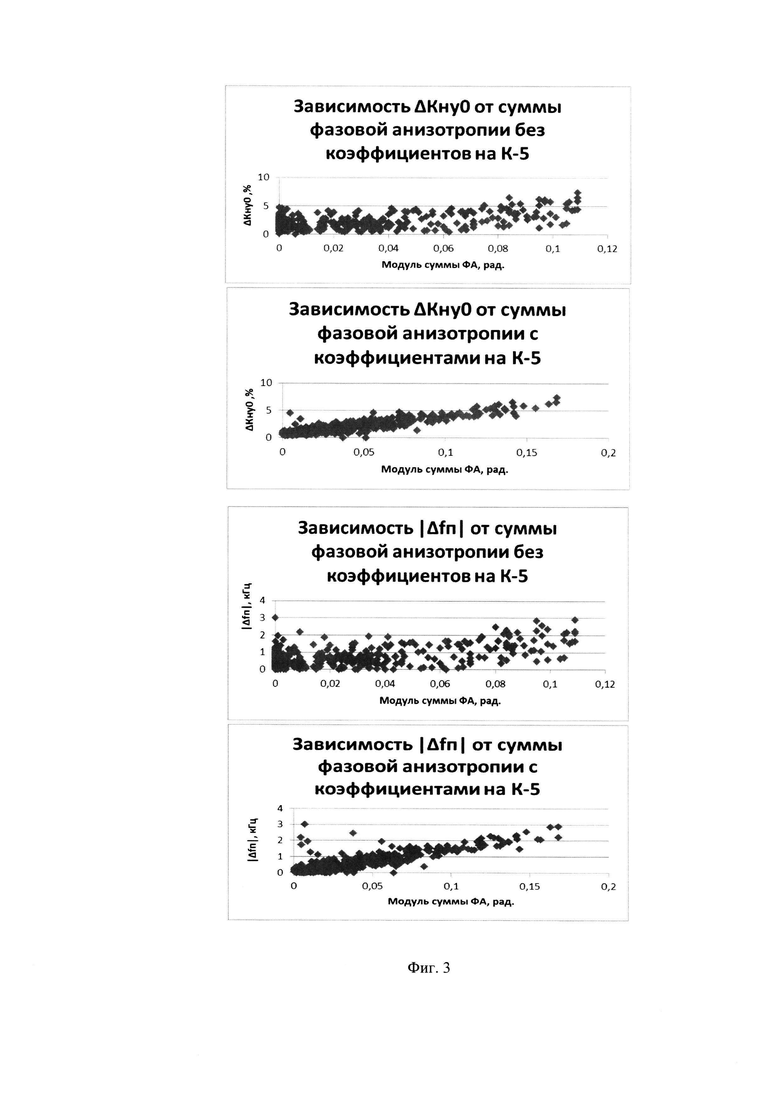
на фиг. 3 - зависимость между суммой фазовой анизотропии и разностью частот подставки. Степень влияния разных зеркал неодинакова. График отношения величин принимает вид линейной зависимости при введении поправочных коэффициентов - множителя 0,13 для фазовой анизотропии плоского зеркала и 1,31 для сферического.
Резонатор кольцевого лазера с неплоским оптическим контуром содержит последовательно установленные и оптически соединенные первое отражающее зеркало 1, первое зеркало 2 косого падения, второе отражающее зеркало 3 и второе зеркало 4 косого падения, оптически соединенное с первым отражающим зеркалом.
Реализуется предложенный способ следующим образом.
Предварительно проведем теоретическое обоснование способа.
Рассмотрение проведено для кольцевого резонатора с неплоским контуром (рис. 1) в приближении переключения поляризационных мод с одним и тем же продольным индексом.
Применение метода Джонса [4-7] для расчета собственных состояний поляризации заключается в решении поляризационного уравнения МЕ=ΔE, построении матрицы М при полном обходе контура резонатора, в нахождении собственных векторов Е и собственных значений λ данной матрицы. Рассматриваемый резонатор состоит из четырех зеркал, угол излома резонатора α, угол поворота плоскости поляризации ρ.
Математическая модель расчета
Обозначим матрицы зеркал М1…М4 в порядке прохождения их лучом света, S (ρ) и S (-ρ) - матрицы поворота. В реальных зеркалах существует фазовая анизотропия и коэффициенты отражения для ТЕ и ТМ поляризаций различны. Матрица зеркала Мn равна:
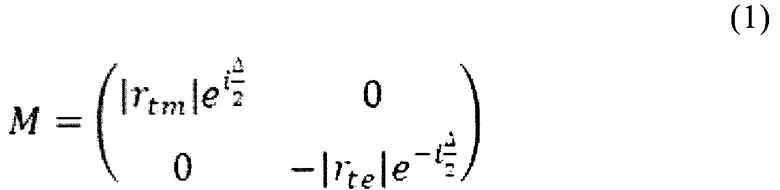
где Δ - фазовая анизотропия зеркала.
Для каждого зеркала рассчитываются значения коэффициентов отражения для ТЕ и ТМ поляризаций и фазовая анизотропия. Матрица полного обхода резонатора имеет следующий вид:
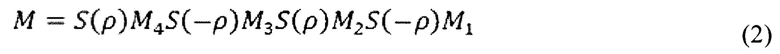
Собственные значения λ1 и λ2 вычисляются через элементы матрицы резонатора
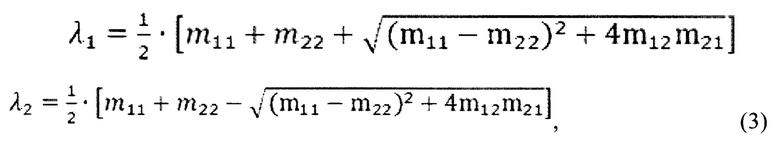
где mn1 - элементы матрицы М.
Собственные значения в общем случае комплексные величины. Модуль собственного значения матрицы обхода М определяет амплитудное пропускание, аргумент - фазовый набег. Потери резонатора определяются выражением:
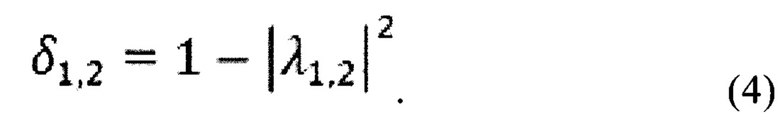
Комплексный поляризационный параметр 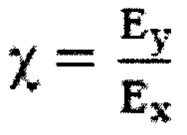 позволяет определить эллиптичность ε (отношение малой оси эллипса поляризации к большой) и азимут β (угол наклона большой полуоси эллипса поляризации к оси х). В работах [6, 7] с помощью метода матриц Джонса были получены следующие уравнения:
позволяет определить эллиптичность ε (отношение малой оси эллипса поляризации к большой) и азимут β (угол наклона большой полуоси эллипса поляризации к оси х). В работах [6, 7] с помощью метода матриц Джонса были получены следующие уравнения:
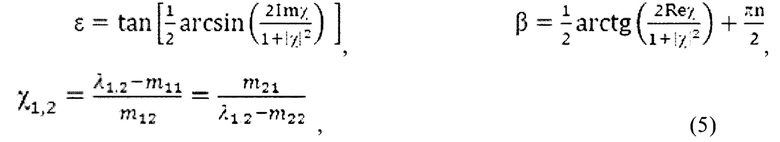
где n=0,1 для различных поляризационных мод.
Результаты расчетов
Расчеты проводили по формулам (1-5) с перебором фазовой и амплитудной анизотропии зеркал. Эти расчеты показали, что круговую поляризацию мод в резонаторе с неидеальными зеркалами можно получить при условии равенства нулю суммы анизотропий всех зеркал с учетом весовых коэффициентов каждого зеркала.
Величины фазовой анизотропии зеркал, поворачивающих плоскость поляризации при отражении Δ2 и Δ4 должны быть равны. Влияние фазовой анизотропии зеркала 3 - максимально и величина Δ3 должна компенсировать сумму анизотропий зеркал (2 и 4) с коэффициентом приблизительно 1,3 при равенстве фазовой анизотропии пропускающего зеркала (1) нулю.
При неравенстве нулю фазовой анизотропии этого зеркала ее следует учитывать при расчете суммы с коэффициентом, приблизительно равным 0,1.
В качестве примера расчета на фиг. 2 приведены значения эллиптичности собственных колебаний в зависимости от фазовой анизотропии 3-го зеркала (Δ3 в радианах).
Из чертежа следует, что эллиптичности мод равны и близки к круговой поляризации при Δ2+Δ4 ≈ 1,3Δ3. (Δ1=0, Δ2=Δ4=0,04 рад.)
Статистика экспериментальных результатов
В результате экспериментальных исследований получены значения поправочных коэффициентов путем алгоритмического перебора с целью максимизации коэффициента корреляции Пирсона между модулем суммы фазовой анизотропии и модулем разности частот подставки, пропорциональной разности потерь мод (фиг. 3).
Начальные значения для перебора коэффициентов взяты из результатов, полученных в работе [8]. Результаты статистики хорошо согласуются с расчетными коэффициентами, а именно оптимальная величина суммарной фазовой анизотропии ΔΣ≈0,13Δ1+Δ2+1,3Δ3+Δ4.
Таким образом, на основе матричного метода Джонса расчетным путем определены весовые коэффициенты фазовой анизотропии каждого зеркала, при которых эллиптичности поляризационных мод стремятся к единице, а разнодобротность мод к нулю. Эти выводы хорошо согласуются с проведенными экспериментальными исследованиями.
В соответствии с представленным выше описанием можно сделать вывод, что в предложении достигается требуемый технический результат, который заключается в расширении области применения известного способа с целью обеспечения возможности выбора зеркал резонатора кольцевого лазера с неплоским оптическим контуром на основе минимизации разнодобротности мод и их эллиптичности к единице, что повышает точность проводимых измерений с использованием датчиков гироскопа.
ЛИТЕРАТУРА
1. Вахитов Н.Г., Голяев Ю.Д., Дронов И.В, Иванов М.А., Колбас Ю.Ю., Крутиков А.П. Зеемановский лазерный гироскоп с переключением продольных мод генерации// Вестник МГТУ им. Н.Э. Баумана. Серия «Приборостроение».
2. Азарова В.В., Голяев Ю.Д., Дмитриев В.Г. Кольцевые газовые лазеры с магнитооптическим управлением в лазерной гироскопии // Квантовая электроника. 2000, т. 30, №2, с.96-104.
3. Кудрявцев А.С., Ларионцев Е.Г., Савельев И.И. Режим биений встречных волн в Зеемановском кольцевом лазере в поле сильного магнита //Квантовая электроника. 2021, т. 51, №11, с.1004-1008.
4. Молчанов В.Я., Скроцкий Г.В. Матричный метод вычисления собственных состояний поляризации анизотропных оптических резонаторов //Квантовая электроника, 1971, №4, с.3-26.
5. A.Gerrard, J.M. Burch. Introduction to Matrix Methods in Optics. A Wiley-Interscience Publication. John Wiley &Sons/ London, New-York, Sydney, Toronto. 1975.
6. Nilsson A.C., Gustafson E.K., Byer R.L. IEEE J. Quantum Electronics, 1989, V.25, P. 767.
7. Мамаев Ю.А., Хандохин П.А., Неортогональность собственных состояний поляризации в анизотропных резонаторах //Квантовая электроника, 2011, т. 41, №6, с. 571-576.
8. Азарова В.В., Макеев А.П., Сухов Е.В. Поляризационные характеристики кольцевых резонаторов с неплоским контуром для лазерных гироскопов//Контенант, 2019, т. 18, №3, с.16-22.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЛАЗЕР С КОНТРОЛИРУЕМОЙ ПОЛЯРИЗАЦИЕЙ | 1997 |
|
RU2113044C1 |
| ЧЕТЫРЕХМОДОВЫЙ ГИРОСКОП НА СТАБИЛИЗИРОВАННОМ ТВЕРДОТЕЛЬНОМ ЛАЗЕРЕ БЕЗ ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ | 2006 |
|
RU2382333C2 |
| СПОСОБ ЛАЗЕРНОЙ ПОЛЯРИЗАЦИОННОЙ СПЕКТРОСКОПИИ | 1989 |
|
RU2039351C1 |
| Кольцевой лазер | 1978 |
|
SU698468A1 |
| ЛАЗЕРНЫЙ ГИРОСКОП | 2016 |
|
RU2627566C1 |
| КОЛЬЦЕВОЙ ЛАЗЕР | 2001 |
|
RU2188488C1 |
| ТВЕРДОТЕЛЬНЫЙ ЛАЗЕРНЫЙ ГИРОСКОП С МЕХАНИЧЕСКИ АКТИВИРУЕМОЙ УСИЛИВАЮЩЕЙ СРЕДОЙ | 2007 |
|
RU2437062C2 |
| СПОСОБ И ПРИСПОСОБЛЕНИЕ ДЛЯ ЮСТИРОВКИ И СБОРКИ СИММЕТРИЧНОГО ЛАЗЕРНОГО ГИРОСКОПА С ПРИЗМАМИ ПОЛНОГО ВНУТРЕННЕГО ОТРАЖЕНИЯ И СИММЕТРИЧНЫЙ ЛАЗЕРНЫЙ ГИРОСКОП | 1998 |
|
RU2155936C2 |
| СПОСОБ РЕГУЛИРОВАНИЯ ПЕРИМЕТРА РЕЗОНАТОРА ЧЕТЫРЕХЧАСТОТНОГО ЛАЗЕРНОГО ГИРОСКОПА | 2022 |
|
RU2794241C1 |
| Лазер | 1978 |
|
SU813570A1 |
Изобретение относится к лазерной технике и может быть использовано для выбора резонаторных зеркал датчиков лазерных гироскопов при использовании резонаторов с неплоским контуром. Способ выбора резонаторных зеркал датчиков лазерных гироскопов заключается в том, что в резонаторе кольцевого лазера с неплоским оптическим контуром, содержащем последовательно установленные и оптически соединенные первое отражающее зеркало, первое зеркало косого падения, второе отражающее зеркало и второе зеркало косого падения, оптически соединенное с первым отражающим зеркалом, зеркала выбирают из условия равенства величины суммарной фазовой анизотропии всех зеркал, равной нулю 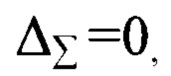 где
где 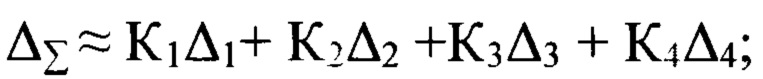 Δ1 - величина фазовой анизотропии первого отражающего зеркала; Δ2 - величина фазовой анизотропии первого зеркала косого падения; Δ3 - величина фазовой анизотропии второго отражающего зеркала; Δ4 - величина фазовой анизотропии второго зеркала косого падения. Технический результат - повышение точности измерений датчиками, использующими лазерные гироскопы. 1 з.п. ф-лы, 3 ил.
Δ1 - величина фазовой анизотропии первого отражающего зеркала; Δ2 - величина фазовой анизотропии первого зеркала косого падения; Δ3 - величина фазовой анизотропии второго отражающего зеркала; Δ4 - величина фазовой анизотропии второго зеркала косого падения. Технический результат - повышение точности измерений датчиками, использующими лазерные гироскопы. 1 з.п. ф-лы, 3 ил.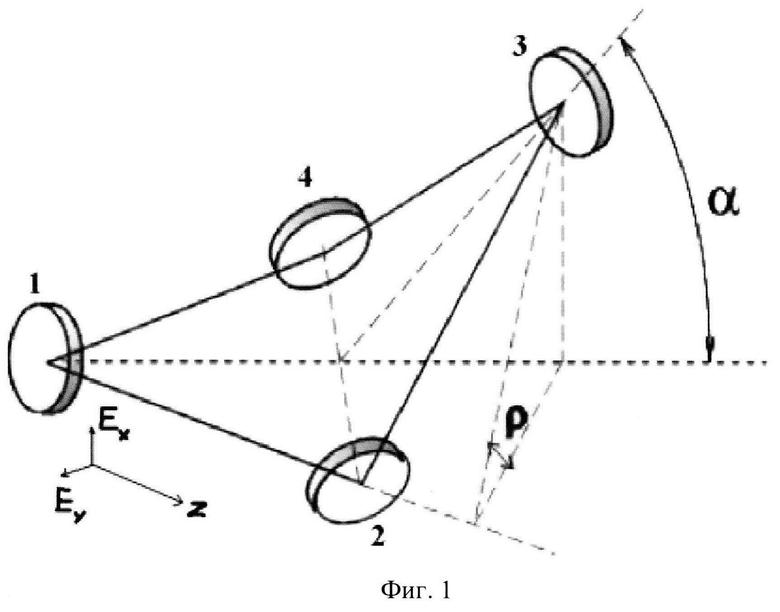
1. Способ выбора резонаторных зеркал датчиков лазерных гироскопов, заключающийся в том, что в резонаторе кольцевого лазера с неплоским оптическим контуром, содержащем последовательно установленные и оптически соединенные первое отражающее зеркало, первое зеркало косого падения, второе отражающее зеркало и второе зеркало косого падения, оптически соединенное с первым отражающим зеркалом, зеркала выбирают из условия равенства величины суммарной фазовой анизотропии всех зеркал, равной нулю
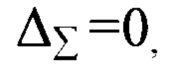 где
где 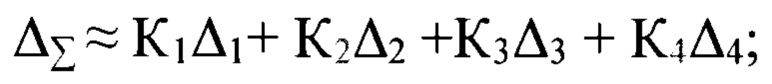
Δ1 - величина фазовой анизотропии первого отражающего зеркала;
Δ2 - величина фазовой анизотропии первого зеркала косого падения;
Δ3 - величина фазовой анизотропии второго отражающего зеркала;
Δ4 - величина фазовой анизотропии второго зеркала косого падения;
К1, К2, К3, К4 - весовые коэффициенты.
2. Способ по п. 1, отличающийся тем, что весовые коэффициенты выбирают из условия: К1=0,13, К2=1, К3=1,3, К4=1.
| СПОСОБ СБОРКИ КОЛЬЦЕВОГО РЕЗОНАТОРА ЛАЗЕРНОГО ГИРОСКОПА (ВАРИАНТЫ) | 2016 |
|
RU2626725C1 |
| Способ измерения углов между плоскостями моноблока резонатора кольцевого лазера с неплоским оптическим контуром и устройство для его реализации | 2022 |
|
RU2789240C1 |
| СПОСОБ ПОЛУЧЕНИЯ 2-ОКСИ-З-АМИНОПРОПИЛОВЫХ ЭФИРОВ АКРИЛОВОЙ И МЕТАКРИЛОВОЙ КИСЛОТ | 0 |
|
SU185343A1 |
| ПЕСКОСТРЕЛЬНЫЙ ПУЛЬСИРУЮЩИЙ ПОЛУАВТОМАТ | 0 |
|
SU181779A1 |
| US 5098188 A1, 24.03.1992. | |||
Авторы
Даты
2023-09-06—Публикация
2023-03-06—Подача